Abstract
This paper introduces an innovative artificial neural networks-based analytical solver for fractional partial differential equations (fPDEs), combining neural networks (NNs) with symbolic computation. Leveraging the powerful function approximation ability of NNs and the exactness of symbolic methods, our approach achieves notable improvements in both computational speed and solution precision. The efficacy of the proposed method is validated through four numerical examples, with results visualized using three-dimensional surface plots, contour mappings, and density distributions. Numerical experiments demonstrate that the proposed framework successfully derives exact solutions for fPDEs without relying on data samples. This research provides a novel methodological framework for solving fPDEs, with broad applicability across scientific and engineering fields.
1. Introduction
In recent years, fractional operators have emerged as a powerful mathematical tool for modeling complex systems [1,2,3,4], offering superior capabilities over integer-order calculus in capturing memory effects, hereditary properties, and non-local dynamics with greater accuracy. By incorporating non-local memory effects and capturing anomalous dynamics [5,6], fractional-order models provide a more accurate and flexible framework for describing phenomena such as viscoelasticity, diffusion in heterogeneous media, and biological processes with long-range dependencies. Their ability to characterize multi-scale behaviors and fit real-world data more precisely makes them invaluable in physics, engineering, and biology. Nevertheless, solving fractional partial differential equations (fPDEs) presents significantly greater complexity. The development of effective numerical methods to approximate fPDEs has been the goal of some researchers. The traditional solving methods include finite-difference method [7,8], finite element method [9,10], spectral method [11,12] and virtual-element method [13,14], etc. However, these algorithms require discretization, which incurs significant time costs due to the vast amount of data processing and introduces approximate errors.
The rapid development of artificial intelligence has driven widespread applications of deep learning in scientific and technological domains [15,16,17,18]. This trend is primarily propelled by the strong function approximation capability [19,20,21] of neural networks (NNs), which has established them as powerful computational tools for solving differential and integral equations [22,23]. Particularly in computational mathematics, physics-informed neural networks (PINNs) have emerged as a significant methodology for solving partial differential equations (PDEs), attracting considerable scholarly attention [24,25,26,27]. PINNs are machine learning models that combine deep learning with physical knowledge. By serving as a surrogate model, NNs establish a mapping between spatio-temporal points and the corresponding PDE solutions. The residual information of PDEs is embedded into the loss function of NNs, thereby optimizing the training process through minimization with respect to the parameters of NNs, ultimately leading to the derivation of an optimal model. Due to the inapplicability of the standard chain rule in fractional calculus, automatic differentiation cannot be directly used with fractional operators. To solve this problem, fractional physics-informed neural networks (fPINNs) [28,29,30] discretize the fractional operators numerically. By employing automatic differentiation for integer-order operators and numerical approximation for fractional operators, the residual information from fPDEs can be integrated into the NN’s loss function during training. However, fPINNs require numerical discretization to solve fPDEs, which inherently introduces approximation errors. The fPINNs are data-driven models [31,32,33] that require a large number of training points for training and have high time costs. During network training, the NNs often become stuck in the local optimal value and cannot find the global optimal value. Consequently, enhancing NN training efficiency and developing advanced optimization algorithms remain active research priorities.
Nevertheless, existing approaches universally employ NNs to compute numerical approximations for diverse classes of fPDEs. While numerical solutions of fPDEs have broad applicability in practical applications, analytical solutions still possess irreplaceable value in pursuing accuracy and theoretical depth. Generally, it becomes difficult to find exact analytical solutions of fPDEs. In prior work [34,35,36], we developed an NN framework that derives exact PDE solutions through equation-specific trial functions constructed via NN architectures. Currently, NNs have not yet been employed to obtain exact analytical solutions of fPDEs.
Motivated by these advances, a novel artificial neural networks-based analytical solver is newly introduced herein, addressing fPDEs through an unprecedented computational paradigm. This novel approach integrates NNs with a symbolic computation strategy, enabling the rapid acquisition of precise analytical solutions to fPDEs. The proposed method solely employs the feedforward computation of NNs to obtain exact solutions for fPDEs without involving any training mechanisms, thereby significantly improving computational efficiency and accuracy. Moreover, this analytical method exhibits high customizability and flexibility, allowing the construction of diverse trial functions by adjusting the parameter configuration of NNs, making it widely applicable to various types of fPDEs. The main focus of our contributions lies in the following aspects:
- We introduce an innovative framework for deriving exact analytical solutions to fPDEs, ensuring mathematically rigorous results free from computational errors.
- Potential analytical solutions of fPDEs are constructed via NN architectures. Transformed inputs undergo feedforward propagation to yield network outputs, which subsequently serve as trial functions in the fPDE solutions framework.
- Our approach simplifies the fPDE into computationally feasible algebraic systems through trial function application. The synaptic weights and biases of NNs are then resolved through undetermined coefficient optimization.
- Exact analytical solutions for fPDEs are obtained in a data-independent manner through this computational framework. NNs are employed to impose structural constraints on trial function formulation, enhancing mathematical tractability.
The paper adopts the following structure: Theoretical principles of the proposed solver are formalized within the Section 2. In Section 3, the accuracy and feasibility of the artificial neural networks-based analytical solver for fPDEs are verified through fractional wave equation [37], fractional telegraph equation [38], fractional Sharma–Tasso–Olever equation [39], and fractional biological population model [40]. In Section 4, the proposed method is discussed. Finally, the conclusions of this paper are given in Section 5.
2. Methodology
In this section, we introduce the idea of an artificial neural network-based analytical solver for finding solutions of fPDEs. Analytical solutions of fPDEs are obtained by embedding NNs as explicit functional representations. The novelty of the technique stems from its ability to impose explicit mathematical constraints on the solution space representation. Consider the following general fractional partial differential equation
where the function satisfies the governing equation, the fractional orders and , and are the conformable fractional derivatives of with respect to t and x, respectively.
We employ a precisely formulated explicit model during the forward propagation phase of the NNs to compute the solution for Equation (1). The neuron model is composed of input, output, and computational functions. The input can be analogized as dendrites of neurons, while the output can be analogized as axons of neurons, and the computing can be analogized as the nucleus. Figure 1 shows a neuron model with three inputs, one output, and two computational functions. The arrow lines in Figure 1 are called connections, and each connection has a weight on it. In this networks, the weighted sum of the three inputs , , and is first computed as . Subsequently, they go through a nonlinear transformation to obtain
here, f denotes the activation function, enhancing the neuron’s ability to model nonlinear relationships, while b represents the bias term. Consequently, the solution to the equation can be explicitly represented by a single neuron’s output. Given the high expressive power of neural networks in approximating functions, solutions to fPDEs can be computed using NNs with limited neurons or hidden layers. In this work, we employ an NN-based model to approximate the solution of the fPDEs, as illustrated in Figure 2. Where X and T are inputs of the NNs, and
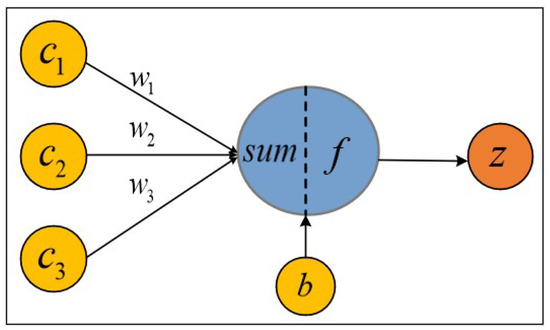
Figure 1.
Graphical depiction of neuron structure.
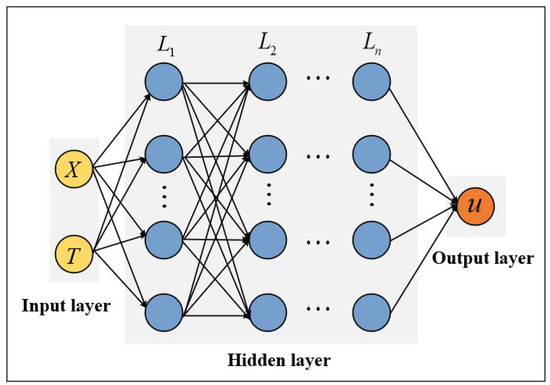
Figure 2.
Architecture of NNs.
After applying the aforementioned independent variable transformation, all fractional derivatives in Equation (1) are converted into integer-order derivatives
thus simplifying the subsequent calculation. Consider an NN architecture comprising n hidden layers, with each layer containing m neurons. For the first hidden layer (), the output of its n-th neuron () can be expressed as
where f is the activation function, while and denote the weights linking the n-th neuron to inputs X and T, respectively. The output of the n-th neuron in layer () can be expressed as
let denote the activation value of the first neuron in the -th hidden layer, and represent the output of the m-th neuron in the same layer. The connection weight from neuron to is denoted as , whereas represents the weight between and . The system’s final output is computed as the weighted linear combination of all activation outputs from the final layer’s neurons. Consequently, the potential closed-form solution of the fPDEs, derived via the NNs framework, takes the following form:
The trial function takes the expanded representation when neuronal outputs contain bias components.
In the realm of mathematical modeling for physical phenomena, utilizing the trial function method to derive analytical solutions for field partial differential equations related to these domains is a prevalent technique. Nevertheless, the cornerstone of this methodology lies in the artful construction of the trial function itself, which necessitates a meticulous and strategic construction process. This paper presents an analytical solver based on an NN architecture, employing its explicit mathematical formulation as the trial solution for fPDEs. The architecture of the NNs is designed to be regular, and the overall flow of the proposed method is shown in Figure 3.
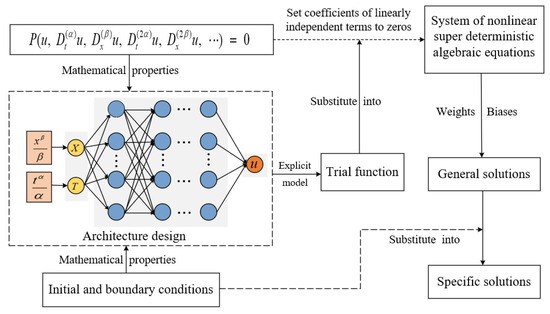
Figure 3.
Overall flow of the proposed analytical method.
The method uses the trial function method to construct potential analytical solutions of fPDEs. The potential analytical solutions to fPDEs may incorporate various elementary functions, including rational term (), trigonometric components (, ), and exponential term (), etc. This is directly related to the activation function of the selected NNs. Fortunately, the selection of the activation function can be facilitated by leveraging the initial or boundary conditions as a guiding principle, significantly expediting the process of designing the architecture of NNs. The NNs have a structured architecture with a standardized pattern, mainly requiring specification of hidden layer neuron quantities and individual neuron activation functions, as detailed in Table 1. Consequently, the proposed methodology significantly reduces the difficulties involved in formulating trial functions.

Table 1.
Architectural configuration of NNs for analytical solution.
Suppose there is an architecture of NNs with one hidden layer and two neurons, and is chosen as the activation function for each neuron. If and are taken as inputs to the NNs, the explicit model of the NNs can be expressed as
the connection weights between neurons are denoted by w, while b corresponds to the bias term in each neuron’s output. By substituting the Equation (8) into the Equation (4), a nonlinear equation about weights and biases is obtained:
by combining the similar terms of Equation (9), extracting the coefficients, and setting all coefficients to zero, we derive a system of nonlinear algebraic equations. Finally, the weight coefficients, biases, and Equation (3) obtained by the solution are substituted into the NN model Equation (8), and the analytical solution of the Equation (1) can be obtained.
To facilitate the practical application of our analytical methodology, we have implemented a dedicated Maple-based computational tool that automates all solution procedures.
3. Applications
In this section, we demonstrate the accuracy and feasibility of an artificial neural network-based analytical solver to solve fPDEs by fractional wave equation [37], fractional telegraph equation [38], fractional Sharma–Tasso–Olever equation [39], and fractional biological population model [40].
3.1. Fractional Wave Equation
The fractional wave equation under consideration takes the form
with the following initial condition
where k is a positive coefficient, , , , , the function satisfies the governing equation.
Via the variable transformation Equation (3), Equation (10) is rewritten as its integer-order counterpart:
Case I: To obtain analytical solutions for the fractional wave equation, the NNs architecture is utilized. Design considerations incorporate the initial condition of the equation. We implement a network with two hidden layers, each consisting of two neurons. The corresponding architectural schematic appears in Figure 4a. Using neural networks, the trial function is parameterized by weights and biases. Therefore, the mathematical representation of the explicit model can be expressed as follows:
where , , denote the exact solution of the Equation (10). In the networks architecture, the initial hidden layer generates outputs and from its first and second neurons, respectively, followed by outputs and from the subsequent layer’s corresponding neurons, , , , , , , , , , are the weights between the each neurons, , , , are the activation functions. The bias terms are denoted as , , , , and , corresponding to each neuron’s offset parameter. Within the NNs framework, the trial solution for Equation (13) is parameterized by both connection weights and these bias components.
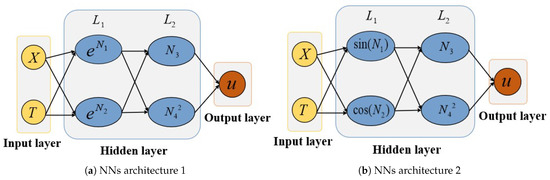
Figure 4.
Architectural design of NNs for deriving analytical solutions to the fractional wave equation.
The first hidden layer employs exponential functions for all neuronal activations, while in the second hidden layer, the third and fourth neurons utilize and activation mappings, respectively. Consequently, the explicit model admits the following mathematical representation:
By collecting terms involving the basis set and enforcing zero coefficients for each independent component, we derive the following equation system.
Through the systematic solving of the equation system, we derive 20 constraint conditions, where each condition corresponds to a general solution in the solution space. Due to limited space, a few representative examples are cited below:
Solution 1:
The general solution for this system of constraints can be expressed as follows:
Substituting , into the Equation (18) yields the exact solution
Solution 2:
and for the given constraints, the general solution takes the following form:
Solution 3:
A fully connected NN structure can better approximate the analytical solution of an equation. However, the weight coefficients in the constraint conditions corresponding to the three examples introduced above are not all non-zero, which means the corresponding NNs are not fully connected network structures. For example, the network structure corresponding to the set of constraints Equation (17) of the equation only utilizes the second and fourth neurons. Due to limited space, we provide the constraint conditions corresponding to a fully connected NN structure as follows
and the general solution for this system of constraints can be expressed as follows:
In order to further simplify the general solution of the Equation (23), we substitute the initial condition into Equation (23) to obtain
where and .
If one chooses coefficients in the Equation (24), the results are shown in Figure 5. In this way, the solution’s performance becomes more apparent. Figure 5a presents a 3D plot illustrating the solution over the spatio-temporal domain . To observe the local behavior of the solution, we plot the x-curves in Figure 5b at interval . In Figure 5c,d, we illustrate the contour and density representations of the fractional wave equation. As can be seen from the figure, the initial condition takes on a parabolic shape. Over time, the shape and size of the solution evolve, forming distinct peaks and troughs while exhibiting characteristics of propagation and diffusion. The variation in color intuitively reflects the dynamic changes in the solution, providing a crucial visualization tool for understanding the solutions to the fractional wave equation.
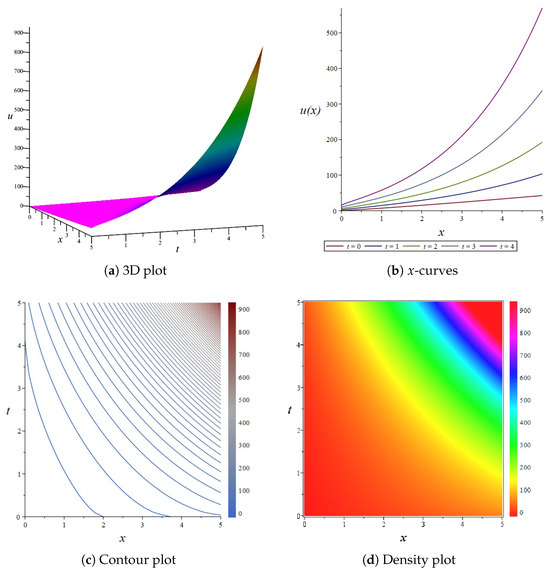
Figure 5.
The 3D plot, curve plot, contour plot, and density plot of the exact solution Equation (24).
Case II: Therefore, the artificial neural networks-based analytical solver can effectively obtain the exact solutions of the Equation (10). Further demonstrating the adjustable nature of our approach, we employed a different NN parameter configuration for Equation (10), visible in Figure 4b. In this case, we take the activation functions of neurons in the second hidden layer as the and the , respectively, while other settings in the NN structure remain unchanged. According to the analytical formulation Equation (13), the following trial function can be constructed:
Substituting Equation (25) into Equation (12) and combining similar terms involving . Setting every coefficient equal to zero generates 20 distinct constraint groups, each associated with a generalized solution of the equation that includes weights and biases. We give an example of the constraint conditions corresponding to a fully connected NN structure (where the weights are all non-zero), as shown below:
and the general solution takes the form
where and .
With the coefficients configuration specified in Equation (28), the 3D plot, x-curves plot, contour lines, and density patterns of the Equation (10) are collectively illustrated in Figure 6. The Figure 6 exhibits a distinct wave-like pattern, indicating that the solution possesses wave characteristics in both space and time. The amplitudes of the wave peaks and troughs gradually change over time, revealing the dynamic evolution of the wave properties. In the spatial direction, the waveform displays a certain periodicity, suggesting that the solution exhibits periodic wave characteristics in space. In the Figure 6b, it is also evident that the phase of the curves shifts at different time points, indicating the presence of phase variation as the solution evolves dynamically over time.
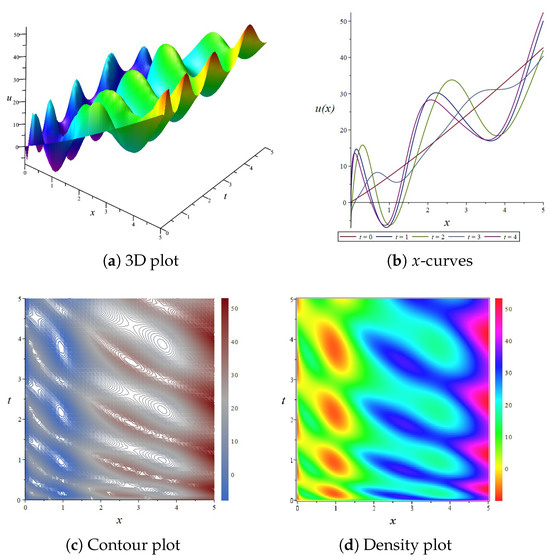
Figure 6.
The 3D plot, curves plot, contour plot, and density plot of the exact solution Equation (28).
3.2. Fractional Telegraph Equation
The following fractional telegraph equation is investigated:
with the following initial condition
where , , , , the function satisfies the equation.
Case I: Following the same approach, the NNs framework is employed to derive exact solutions for the fractional telegraph equation, where the initial conditions serve as the basis for designing the network structure. NN architecture 3, as shown in Figure 7a, is used to solve the equation. The network configuration consists of two hidden layers, both containing two neuronal units. Neurons in the initial hidden layer utilize exponential activation , whereas the subsequent layer adopts reciprocal activation . According to the analytical formulation Equation (13), we can determine the trial function
where and .
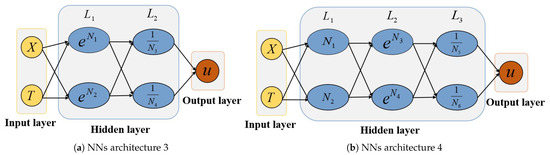
Figure 7.
Architectural design of NNs for deriving analytical solutions to the fractional telegraph equation.
Substituting Equation (32) into Equation (31) and grouping similar terms involving . Setting every coefficient equal to zero generates 18 distinct constraint groups, each associated with a generalized solution of the equation that includes weights and biases. We give an example of the constraint conditions corresponding to a fully connected NN structure, as shown below:
and the analytical solution takes the form
where and , and by substituting the Equation (30) into the above equation, we obtain the analytic solution in the following form
where , , , and .
Case II: Furthermore, the NNs architecture 4 as shown in Figure 7b is used to solve the fractional telegraph equation. The network structure includes three hidden layers, and the activation functions of neurons in the first hidden layer, second hidden layer, and the third hidden layer are set to identity mapping , , and reciprocal , respectively. Following the architecture of the established NNs, we formulate the novel trial function as
where , , and .
Compared with previously discussed trial functions, this formulation exhibits significantly greater complexity. Substituting Equation (36) into Equation (31) and grouping similar terms involving . When all coefficients are set to zero, the system yields 25 constraint groups, mapping to 18 weighted solutions of the equation with bias terms. We give an example of the constraint conditions corresponding to a fully connected NN structure, as shown below:
Consequently, the exact solution satisfying these constraint conditions can be expressed as
where , , , and .
By substituting the initial condition into Equation (38), we obtain the solution in the following form:
where , , , and .
With the coefficients configuration specified in Equation (39), the various figures of the Equation (29) are collectively illustrated in Figure 8. The exact solution of the fractional telegraph equation exhibits a smooth and monotonically decreasing behavior as the absolute values of x and t increase. The 3D plot, x-curves, contour plot, and density plot all consistently show this trend, with the solution starting higher at and and gradually declining as x and t change. The visualizations provide a clear understanding of the spatio-temporal dynamics of the solution.
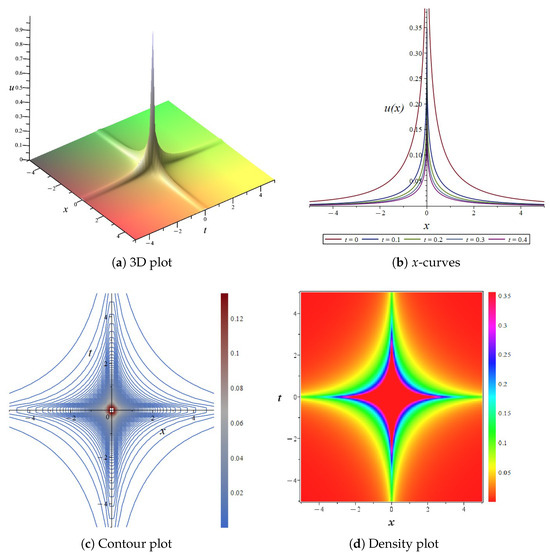
Figure 8.
The 3D plot, curves plot, contour plot, and density plot of the exact solution Equation (39).
3.3. Fractional Sharma–Tasso–Olever Equation
Let us examine the fractional-order Sharma–Tasso–Olever equation expressed as
where a is an arbitrary constant, , .
Case I: The NNs architecture depicted in Figure 9a, featuring two hidden layers with two neurons each, is employed to solve the governing equation. The first hidden layer employs distinct activation functions, with for its first neuron and for the second, while all neurons in the second hidden layer utilize identity mapping . According to the analytical formulation Equation (13), we can derive the trial function
where and .
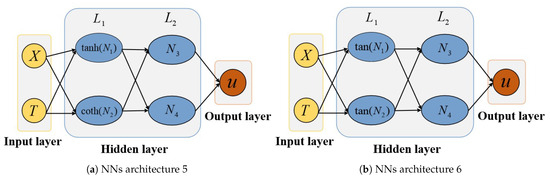
Figure 9.
Architectural design of NNs for deriving analytical solutions to fractional Sharma–Tasso–Olever equation.
Substituting Equation (42) into Equation (41) and grouping similar terms involving . When all coefficients are set to zero, the system yields 19 constraint groups, mapping to 18 weighted solutions of the equation with bias terms. We give an example of the constraint conditions corresponding to a fully connected NN structure, as shown below:
and the exact solution satisfying this constraint condition can be expressed as
where , , , and are denoted by Equation (43), and .
If one chooses coefficients in the Equation (44), the results are shown in Figure 10. In this way, the solution’s performance becomes more apparent. Figure 10a presents a 3D plot illustrating the solution over the spatio-temporal domain . To observe the local behavior of the solution, we plot the x-curves in Figure 10b at interval . And the contour and density plots of the Equation (40) are shown in Figure 10c and Figure 10d, respectively. From the figure, it can be observed that the solution exhibits a series of fine oscillations, which emerge abruptly on a smooth plane, demonstrating distinct soliton characteristics. The oscillations are unevenly distributed across the plane, with larger amplitudes in certain regions and smaller amplitudes in others. The frequency and amplitude of the oscillations vary both spatially and temporally. The density plot clearly illustrates the vibrational patterns and peaks of the waveform.
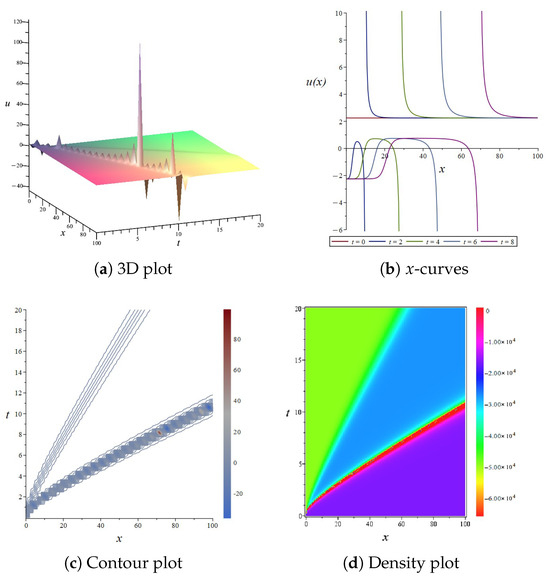
Figure 10.
The 3D plot, curves plot, contour plot, and density plot of the exact solution Equation (44).
Case II: Furthermore, the NNs architecture 6 as shown in Figure 9b is employed to analytically solve the Equation (40). We configure tan(·) activation for all first hidden layer neurons, while implementing identity mapping across the second hidden layer. According to the corresponding analytical formulation Equation (13), we derive
where and .
Substituting Equation (45) into Equation (41) and grouping similar terms involving . Setting every coefficient equal to zero generates 19 distinct constraint groups, each associated with a generalized solution of the equation that includes weights and biases. We give an example of the constraint conditions corresponding to a fully connected NN structure, as shown below:
Consequently, the analytical solution associated with this constraint condition can be expressed as
where and are denoted by Equation (46), and .
If one chooses coefficients in the Equation (47), the results are shown in Figure 11. In this way, the solution’s performance becomes more apparent. The surface of the image exhibits significant sharp peaks and depressions in certain regions, indicating abrupt changes in the solution within these areas. The distribution of sharp peaks and depressions reveals the nonlinear behavior of the solution in both space and time. The distribution of colors in the density plot exhibits a complex wave-like pattern. This wave-like structure indicates that the solution undergoes periodic or quasi-periodic variations in both space and time, while the changes in color intensity reveal the amplitude and frequency characteristics of the solution.
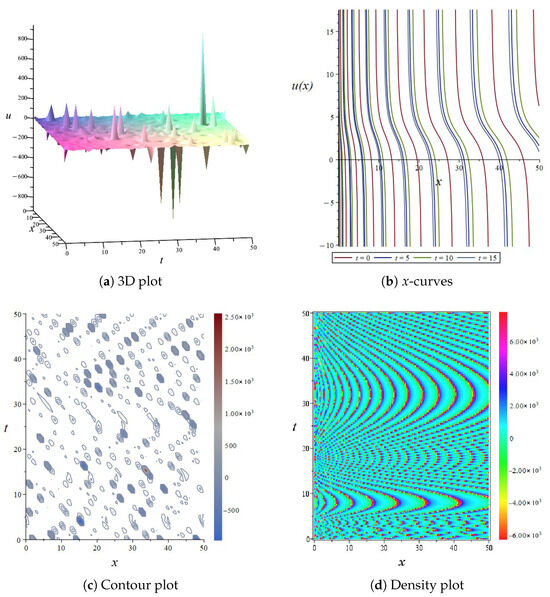
Figure 11.
The 3D plot, curves plot, contour plot, and density plot of the exact solution Equation (47).
3.4. Fractional Biological Population Model
We investigate a fractional biological population model in (2 + 1) dimensions with the following formulation:
where h and r are arbitrary constants, , , .
Case I: The NNs architecture 7 as shown in Figure 12a is used to solve the equation. The network architecture consists of three inputs, two hidden layers with two neurons each. For the first hidden layer, we adopt the exponential activation function , whereas is implemented throughout the second hidden layer. According to the corresponding analytical formulation, we derive
where , , and .
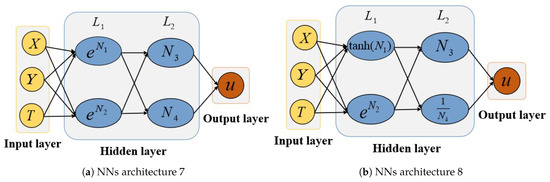
Figure 12.
Architectural design of NNs for deriving analytical solutions to the fractional biological population model.
Substituting Equation (51) into Equation (50) and grouping similar terms involving . Setting every coefficient equal to zero generates four distinct constraint groups, each associated with a generalized solution of the equation that includes weights and biases. We give an example of the constraint conditions, as shown below:
Based on the aforementioned constraints, we arrive at the following general solution
where , , and .
By selecting the appropriate values in Equation (53), the results are shown in Figure 13, which displays the various plots of the Equation (48) over the spatial domain . This set of images presents the characteristics of the fractional biological population model from various perspectives, aiding in a more comprehensive understanding of the model’s behavior and evolutionary trends. The figure shows that u increases with the growth of x and y, presenting a smooth, rainbow-like gradient, indicating that the value of u varies continuously in space. From the curve plots, it can be observed that as x and y increase, the curve shifts upward overall and the rate of growth accelerates. From the contour plot, it can be observed that the population density exhibits a gradient trend in both the x and y directions, with the density of the contour lines reflecting the rate of change in population density.
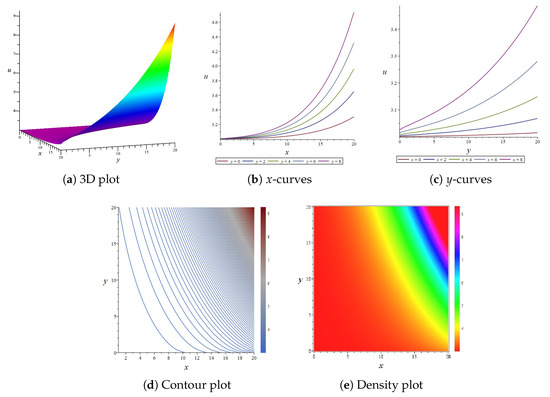
Figure 13.
The 3D plot, curve plots, contour plot, and density plot of the exact solution Equation (53).
Case II: The NNs architecture 8 as shown in Figure 12b is utilized to solve the equation. For the first hidden layer, we adopt exponential activation functions and , whereas identity mapping and reciprocal are implemented throughout the second hidden layer. According to the analytical formulation, the new trial function is
where , , and .
Substituting Equation (54) into Equation (50) and combining similar terms involving . Setting every coefficient equal to zero generates 10 distinct constraint groups, each associated with a generalized solution of the equation that includes weights and biases. We give an example of the constraint conditions, as shown below:
Based on the aforementioned constraints, we arrive at the following general solution
where is denoted by Equation (55), , , and .
By selecting the appropriate values in Equation (56), the results are shown in Figure 14, which displays the various plots of the Equation (48) over the spatial domain . From the figures, it can be observed that the image of the solution abruptly transitions from a smooth plane to a surface characterized by a series of sharp peaks and depressions. The diagonal structures in the Figure 14d,e suggest that the waveform evolves steadily with spatial progression.
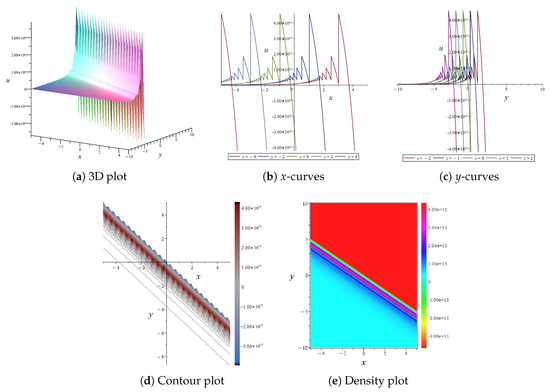
Figure 14.
The 3D plot, curve plots, contour plot, and density plot of the exact solution Equation (56).
Remark 1.
To validate the correctness of the derived solutions, they are substituted back into the original equations, yielding exact agreement on both sides. Furthermore, all equation solutions computed by the proposed analytical method are verified using Maple.
Remark 2.
Several tailored NNs configurations are presented for obtaining analytical solutions to fPDEs, including the fractional wave equation, fractional telegraph equation, fractional Sharma–Tasso–Olever equation, and fractional biological population model. Owing to its adaptable framework, the approach permits alternative network designs to solve these and extended classes of fPDEs.
4. Discussions
In recent years, deep learning approaches have emerged as promising and popular methods for solving various numerical problems of partial differential equations. An NN serves as a computational surrogate to establish the mapping from input variables to the output solution . The fundamental innovation of PINNs resides in embedding the residual terms of governing equations within the NN’s loss function during optimization. However, PINNs can only provide numerical solutions for solving the equation. Although PINNs have achieved great success in solving equations, there are still many deficiencies. PINNs are data-driven models, thus requiring a large amount of data for training. Optimizing NN parameters necessitates employing iterative algorithms for progressive refinement. Therefore, solving equations using PINNs entails significant computational costs and involves approximation errors.
Owing to their exceptional function approximation properties, NNs enable the derivation of analytical solutions for fPDEs. This work specifically leverages mathematical architectures of NNs to formulate closed-form expressions that solve these equations. Since shallow NNs also possess strong function approximation capabilities, this significantly reduces the complexity of the model. Through judicious configuration of activation functions, layer depth, and neuron density, customized trial solutions can be formulated for diverse fPDE classes. Moreover, the present methodology selectively adopts only the structural framework of neural networks, explicitly excluding their parameter optimization processes. The proposed method utilizes trial functions constructed using NNs to convert the calculation of fPDEs into the computation of a set of nonlinear algebraic equations containing weights and biases. Modifications to the governing equation’s boundary or initial conditions necessitate that PINNs repeat their training procedure. The process requires reformulating the objective function to include the updated physical relationships and then performing full network retraining. Thus, the computational load is heavy and the efficiency is low. Once the general solution to the equation is obtained using the analytical solver, only the corresponding different conditions need to be substituted into the general solution for computation, without the need for repeated calculations.
To validate the computational efficiency of the analytical method in this research, a comparison of numerical examples will be conducted between PINNs and our proposed method.
4.1. Neural Networks-Based Analytical Solver
The proposed methodology is employed to obtain exact solutions for the fractional wave equation under varying initial and boundary conditions, yielding multiple analytical solutions to the Equation (10). The proposed method is implemented using Maple 2024.0 for computation.
Case I: Consider Equation (10) with initial condition Equation (11). Since the general solution to the equation has already been obtained in Section 3.1, the general solution requires substitution of the specified initial and boundary conditions to obtain particular solutions. Substitute Equation (11) into a general solution Equation (19) of Equation (10) to obtain a particular solution.
where and .
For enhanced solution characterization, we adopt the parameter configuration specified in Equation (57). The solution’s spatio-temporal behavior is visualized through multiple representations in Figure 15, including three-dimensional surface visualization, spatial profile analysis, contour mapping, and density distribution.
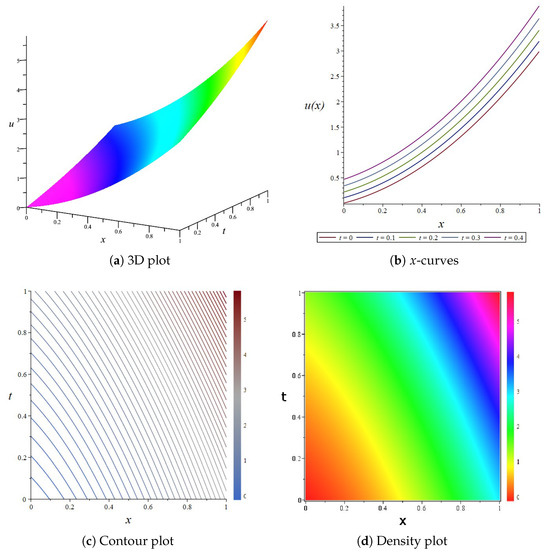
Figure 15.
The 3D plot, curve plot, contour plot, and density plot of the exact solution Equation (57).
Case II: The Equation (10) is investigated under the following initial and boundary conditions:
For enhanced solution characterization, we adopt the parameter configuration specified in Equation (59). The solution’s spatio-temporal behavior is visualized through multiple representations in Figure 16, including three-dimensional surface visualization, spatial profile analysis, contour mapping, and density distribution.
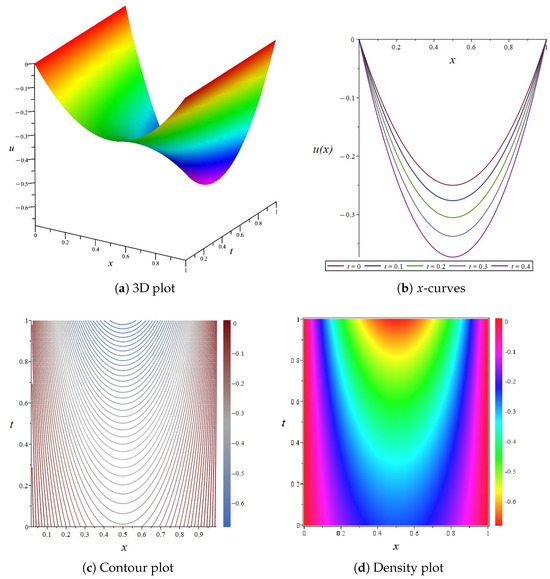
Figure 16.
The 3D plot, curve plot, contour plot, and density plot of the exact solution Equation (59).
4.2. Physics-Informed Neural Networks
We employ PINNs to numerically solve both Case I and Case II presented in Section 4.1, subsequently conducting a systematic comparison between the computational performance and solution accuracy of PINNs and our proposed methodology. The spatio-temporal domain is and in Case I and Case II. The physics-informed loss function in PINNs depends on the governing equation’s initial or boundary conditions. Consequently, varying conditions between Case I and Case II require distinct loss formulations, mandating separate network training procedures for each scenario. We use the following form of relative error
mean absolute error, and maximum absolute error to measure the performance of the NNs, where the neural approximation and analytical solution u are evaluated at discrete test locations for each sample point index i.
The computational framework is implemented in Python 3.9, leveraging TensorFlow’s built-in automatic differentiation functionality. For optimization, we employ the Adam stochastic gradient descent algorithm to minimize the loss function. We initialize the NN parameters using normalized Glorot initialization. For these computational tasks, we implement an NN architecture consisting of 4 hidden layers with a uniform width of 50 neurons per layer. Some other hyperparameters of the NNs, such as the learning rate, the activation function, and the training epoch, are set to , , and 20,000, respectively. A total of 1000 points are sampled within the spatio-temporal domain, with 500 points sampled on both the initial and boundary conditions.
The performance comparison results between PINNs and our analytical solution method are summarized in Table 2. Since PINNs require an iterative training mechanism to optimize the loss function, the training time is relatively long, and the values 0.0210 and 0.0240 in Table 2 represent the inference time of the NNs. PINNs can obtain approximate solutions to the equations with a certain error, as illustrated in Figure 17 and Figure 18.

Table 2.
Computational performance comparison between the two approaches.
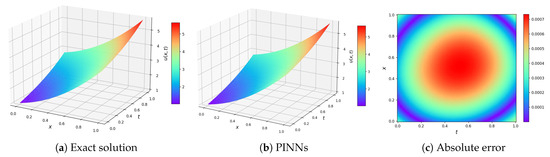
Figure 17.
Calculation results by PINNs for Case I.
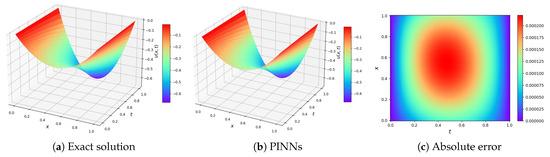
Figure 18.
Calculation results by PINNs for Case II.
Therefore, compared with PINNs, this symbolic computation method can obtain exact solutions for equations without data samples, and it reduces computational costs. To facilitate comparison, Table 3 summarizes the performance metrics of both methodologies. The proposed framework presents an innovative technique for deriving exact solutions to fPDEs, offering significant potential for advancing computational mathematics through its elimination of extensive data requirements and iterative optimization procedures.

Table 3.
Comparison between two approaches.
5. Conclusions
In this paper, an artificial neural networks-based analytical solver that combines NNs with a symbolic computation method is proposed to analytically solve fPDEs. The computational capability of this analytical approach is verified through successful solutions to the fractional wave equation, fractional telegraph equation, fractional Sharma–Tasso—Olever equation, and fractional biological population model. Employing NN architecture, the solver establishes analytical solutions for fPDEs. New trial formulations emerge from the flexible implementation of different activation functions across multiple network models. This study establishes that 3D surface plots, contour diagrams, and density heatmaps collectively provide a robust framework for analyzing solution dynamics. This research introduces an innovative solution strategy for fPDEs with significant potential for cross-disciplinary implementation in both fundamental and applied research domains.
Compared with traditional numerical methods, the method completely avoids approximation errors and significantly improves the computational efficiency of fPDEs. In contrast to the existing bilinear neural network method [41], our methodology removes the requirement for bilinear transformation, significantly improving accessibility for research workers. Furthermore, not all equations possess a bilinear form. The neural network architecture in our proposed framework exhibits significant adaptability, enabling application to diverse fractional PDEs through customizable configurations of network depth, node density, and nonlinear activation selection. For the first time, NNs are employed to derive exact solutions for fPDEs. However, as an exact solution methodology, the proposed technique is specifically designed for obtaining analytical solutions to fPDEs, rather than numerical approximations. The method employs some basic functions to construct potential analytical solutions for fPDEs, and the activation function provides the basic function for this method. For equations without initial and boundary conditions, the selection of activation functions becomes blind. As the complexity of differential equations and NN models increases, it may lead to higher computational complexity. In the future, we will further apply this method to more complex equations, including high-dimensional fPDEs and nonlinear coupled systems, and attempt to construct new activation functions to reduce computational parameters.
Author Contributions
Conceptualization, Y.L. and L.Y.; Methodology, Y.L. and L.Y.; Software, R.Z.; Validation, S.W.; Visualization, S.Y.; Writing-original draft preparation, S.Y.; Writing-review and editing, Y.L. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Natural Science Foundation of Shandong Province (No. ZR2023MA062), the Belt and Road Special Foundation of The National Key Laboratory of Water Disaster Prevention (No. 2023491911), Tianyuan Fund for Mathematics of the National Natural Science Foundation of China (No. 12426105), and the Scientific and Technological Innovation Programs (STIP) of Higher Education Institutions in Shanxi (No. 2024L022).
Data Availability Statement
No new data were created or analyzed in this study. Data sharing is not applicable to this article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Cristofaro, L.; Garra, R.; Scalas, E.; Spassiani, I. A fractional approach to study the pure-temporal Epidemic Type Aftershock Sequence (ETAS) process for earthquakes modeling. Fract. Calc. Appl. Anal. 2023, 26, 461–479. [Google Scholar] [CrossRef]
- Zhang, Y.; Sun, H.G.; Stowell, H.H.; Zayernouri, M.; Hansen, S.E. A review of applications of fractional calculus in Earth system dynamics. Chaos Solitons Fractals 2017, 102, 29–46. [Google Scholar] [CrossRef]
- Molina, M.I. Fractional electrical impurity. New J. Phys. 2024, 26, 013020. [Google Scholar] [CrossRef]
- Yang, Y.Q.; Qi, Q.W.; Hu, J.Y.; Dai, J.S.; Yang, C.D. Adaptive fault-tolerant control for consensus of nonlinear fractional-order multi-agent systems with diffusion. Fractal Fract. 2023, 7, 760. [Google Scholar] [CrossRef]
- Baliarsingh, P.; Nayak, L. Fractional derivatives with variable memory. Iran. J. Sci. Technol. Trans. A Sci. 2022, 46, 849–857. [Google Scholar] [CrossRef]
- Hu, J.B. Studying the memory property and event-triggered control of fractional systems. Inf. Sci. 2024, 662, 120218. [Google Scholar] [CrossRef]
- Guo, J.; Xu, D.; Qiu, W.L. A finite difference scheme for the nonlinear time-fractional partial integro-differential equation. Math. Methods Appl. Sci. 2020, 43, 3392–3412. [Google Scholar] [CrossRef]
- Qiao, H.L.; Cheng, A.J. A fast finite difference method for 2D time variable fractional mobile/immobile equation. J. Appl. Math. Comput. 2024, 70, 551–577. [Google Scholar] [CrossRef]
- Hu, H.Z.; Chen, Y.P.; Zhou, J.W. Two-grid finite element method for time-fractional nonlinear schrodinger equation. J. Comput. Math. 2024, 42, 1124–1144. [Google Scholar] [CrossRef]
- Sheng, Z.H.; Liu, Y.; Li, Y.H. Finite element method combined with time graded meshes for the time-fractional coupled Burgers’ equations. J. Appl. Math. Comput. 2024, 70, 513–533. [Google Scholar] [CrossRef]
- Jiao, Y.J.; Li, T.T.; Zhang, Z.Q. Jacobi spectral collocation method of space-fractional Navier-Stokes equations. Appl. Math. Comput. 2025, 488, 129111. [Google Scholar] [CrossRef]
- Zhang, X.X.; Wang, J.H.; Wu, Z.S.; Tang, Z.Y.; Zeng, X.Y. Spectral Galerkin methods for Riesz space-fractional convection–diffusion equations. Fractal Fract. 2024, 8, 431. [Google Scholar] [CrossRef]
- Gu, Q.L.; Chen, Y.P.; Zhou, J.W.; Huang, J. A fast linearized virtual element method on graded meshes for nonlinear time-fractional diffusion equations. Numer. Algorithms 2024, 97, 1141–1177. [Google Scholar] [CrossRef]
- Gu, Q.L.; Chen, Y.P.; Zhou, J.W.; Huang, Y.Q. A two-grid virtual element method for nonlinear variable-order time-fractional diffusion equation on polygonal meshes. Int. J. Comput. Math. 2023, 100, 2124–2139. [Google Scholar] [CrossRef]
- Yu, S.S.; Guo, M.; Chen, X.Y.; Qiu, J.L.; Sun, J.Q. Personalized movie recommendations based on a multi-feature attention mechanism with neural networks. Mathematics 2023, 11, 1355. [Google Scholar] [CrossRef]
- Li, S.A.; Cao, J.D.; Liu, H.; Huang, C.D. Delay-dependent parameters bifurcation in a fractional neural network via geometric methods. Appl. Math. Comput. 2024, 478, 128812. [Google Scholar] [CrossRef]
- Choudhary, K.; DeCost, B.; Chen, C.; Jain, A.; Tavazza, F.; Cohn, R.; Park, C.W.; Choudhary, A.; Agrawal, A.; Billinge, S.J.L.; et al. Recent advances and applications of deep learning methods in materials science. NPJ Comput. Mater. 2022, 8, 59. [Google Scholar] [CrossRef]
- Liu, Z.P.; Zhang, Z.M.; Lei, Z.V.; Omura, M.; Wang, R.L.; Gao, S.C. Dendritic deep learning for medical segmentation. IEEE/CAA J. Autom. Sin. 2024, 11, 803–805. [Google Scholar] [CrossRef]
- Liu, Y.Q.; Mao, T.; Zhou, D.X. Approximation of functions from Korobov spaces by shallow neural networks. Inf. Sci. 2024, 670, 120573. [Google Scholar] [CrossRef]
- Anastassiou, G.A.; Kouloumpou, D. Neural network approximation for time splitting random functions. Mathematics 2023, 11, 2183. [Google Scholar] [CrossRef]
- Principe, J.C.; Chen, B.D. Universal approximation with convex optimization: Gimmick or reality? IEEE Comput. Intell. Mag. 2015, 10, 68–77. [Google Scholar] [CrossRef]
- Zhang, Z.Z.; Bao, F.; Ju, L.L.; Zhang, G.N. Transferable neural networks for partial differential equations. J. Sci. Comput. 2024, 99, 2. [Google Scholar] [CrossRef]
- Li, Y.; Gao, W.; Ying, S.H. RBF-Assisted hybrid neural network for solving partial differential equations. Mathematics 2024, 12, 1617. [Google Scholar] [CrossRef]
- Lu, L.; Meng, X.H.; Mao, Z.P.; Karniadakis, G.E. DeepXDE: A deep learning library for solving differential equations. SIAM Rev. 2021, 63, 208–227. [Google Scholar] [CrossRef]
- Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J. Comput. Phys. 2019, 378, 686–707. [Google Scholar] [CrossRef]
- Cai, S.Z.; Mao, Z.P.; Wang, Z.C.; Yin, M.L.; Karniadakis, G.E. Physics-informed neural networks (PINNs) for fluid mechanics: A review. Acta Mech. Sin. 2021, 37, 1727–1738. [Google Scholar] [CrossRef]
- Hou, Q.Z.; Li, Y.X.; Singh, V.P.; Sun, Z.W. Physics-informed neural network for diffusive wave model. J. Appl. Math. Comput. 2024, 637, 131261. [Google Scholar] [CrossRef]
- Pang, G.F.; Lu, L.; Karniadakis, G.E. fPINNs: Fractional physics-informed neural networks. SIAM J. Sci. Comput. 2019, 41, A2603–A2626. [Google Scholar] [CrossRef]
- Wang, S.P.; Zhang, H.; Jiang, X.Y. Fractional physics-informed neural networks for time-fractional phase field models. Nonlinear Dyn. 2022, 110, 2715–2739. [Google Scholar] [CrossRef]
- Ren, H.P.; Meng, X.Y.; Liu, R.R.; Hou, J.; Yu, Y.G. A class of improved fractional physics informed neural networks. Neurocomputing 2023, 562, 126890. [Google Scholar] [CrossRef]
- Wu, G.C.; Wu, Z.Q.; Zhu, W. Data-driven discrete fractional chaotic systems, new numerical schemes and deep learning. Chaos 2024, 34, 093144. [Google Scholar] [CrossRef]
- Yuan, B.; Wang, H.; Heitor, A.; Chen, X.H. f-PICNN: A physics-informed convolutional neural network for partial differential equations with space-time domain. J. Comput. Phys. 2024, 515, 113284. [Google Scholar] [CrossRef]
- Wang, S.P.; Zhang, H.; Jiang, X.Y. Physics-informed neural network algorithm for solving forward and inverse problems of variable-order space-fractional advection—Diffusion equations. Neurocomputing 2023, 535, 64–82. [Google Scholar] [CrossRef]
- Zhang, R.F.; Li, M.C.; Albishari, M.; Zheng, F.C.; Lan, Z.Z. Generalized lump solutions, classical lump solutions and rogue waves of the (2+1)-dimensional Caudrey-Dodd-Gibbon-Kotera-Sawada-like equation. Appl. Math. Comput. 2021, 403, 126201. [Google Scholar] [CrossRef]
- Zhang, R.F.; Li, M.C.; Cherraf, A.; Vadyala, S.R. The interference wave and the bright and dark soliton for two integro-differential equation by using BNNM. Nonlinear Dyn. 2023, 111, 8637–8646. [Google Scholar] [CrossRef]
- Zhang, R.F.; Li, M.C.; Gan, J.Y.; Li, Q.; Lan, Z.Z. Novel trial functions and rogue waves of generalized breaking soliton equation via bilinear neural network method. Chaos Solitons Fractals 2022, 154, 111692. [Google Scholar] [CrossRef]
- Jumarie, G. Fractional Partial Differential Equations and Modified Riemann-liouville Derivative New Methods for Solution. J. Appl. Math. Comput. 2007, 8, 31–48. [Google Scholar] [CrossRef]
- Mahdy, A.; Marai, G. Fractional complex transform for solving the fractional differential equations. Glob. J. Pure Appl. Math. 2018, 14, 17–37. [Google Scholar]
- Song, L.N.; Wang, Q.; Zhang, H.Q. Rational approximation solution of the fractional Sharma—Tasso—Olever equation. J. Comput. Appl. Math. 2009, 224, 210–218. [Google Scholar] [CrossRef]
- Zhang, S.; Zhang, H.Q. Fractional sub-equation method and its applications to nonlinear fractional PDEs. Phys. Lett. A 2011, 375, 1069–1073. [Google Scholar] [CrossRef]
- Zhang, R.F.; Bilige, S. Bilinear neural network method to obtain the exact analytical solutions of nonlinear partial differential equations and its application to p-gBKP equation. Nonlinear Dyn. 2019, 95, 3041–3048. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).