Fractional Dynamics of Information Entropy in Quantum Wire System Under Rashba Interaction

Abstract

We present a theoretical examination of the fractional dynamics of information entropy within a semiconductor nanowire system influenced by Rashba spin–orbit interaction and external magnetic fields. Moreover, we determine the fractional nanowire state through the analytical solution of the fractional Schrödinger equation, considering various initial states of the nanowire system. Our research emphasizes the impact of the fractional order and the interaction parameters on the behavior of information entropy. Our findings reveal that the temporal behavior of information entropy is highly sensitive to any variations in the magnetic field length, the Rashba spin–orbit interaction, and the fractional order parameter. The results demonstrate that these parameters are pivotal in determining the coherence and correlation properties of the nanowire system. Therefore, precise control of these factors paves the way for enhancing entanglement performance and facilitating information transfer in spintronic and quantum communication applications.

1. Introduction

Nanowire systems featuring Rashba spin–orbit interaction (SOI) offer an exciting avenue for investigating spintronic technologies and quantum computation [1,2]. The Rashba SOI is generated in systems without inversion symmetry, resulting in a coupling between an electron’s spin and its momentum [3,4]. Upon the application of a magnetic field on nanowire systems, it interacts with the spins of the electrons, allowing for the manipulation of their orientations [5,6]. Moreover, in the presence of a magnetic field, the dynamics of electrons within nanowires undergo notable transformations due to the combined influences of spin–orbit coupling and Zeeman splitting [7]. The magnetic field can lead to a division of energy levels that depends on the electron’s spin state, which can be applied in the development of qubits for quantum computing [8]. The fusion of Rashba SOI and magnetic fields provides an expansive field for academic research and technological advancement in condensed matter physics and nanotechnology [9,10].

The influence of Rashba spin–orbit interaction and magnetic fields on nanowires has been extensively studied both theoretically and experimentally. For example, the influence of inhomogeneous SOI in the presence of magnetic fields can produce equilibrium spin currents and modify subband structures, as presented in [7]. The first evidence of tunneling conductance signatures that correspond to Majorana zero modes in proximitized Rashba nanowires exposed to magnetic fields is supplied by Mourik et al. [11]. Moreover, the impact of Rashba SOI and the intensity of magnetic fields on quantum Fisher information has been investigated for their possible future applications in quantum estimation theory [12]. A recent experimental study conducted by Bhowmik et al. (2025) demonstrated that the implementation of engineered Rashba–Zeeman coupling in hybrid nanowires improves the efficiencies of superconducting diodes, facilitating nonreciprocal current flow with significant tunability [13]. Both theoretical and experimental studies affirm that the integration of Rashba SOI with magnetic fields forms a robust combination that supports the development of spin filters, superconducting diodes, and potentially topological quantum devices [14,15,16,17]. Consequently, in our research, we explore how the Rashba SOI, in conjunction with varying magnetic field strengths, affects the measurement of information entropy, which serves as a metric for quantum entanglement and the transfer of information across nanowire subsystems.

Quantum information entropy is a powerful tool for characterizing correlations, decoherence, and information flow in quantum systems [18,19]. It is based on the classical Shannon entropy [20], and quantum extensions like von Neumann entropy [21], Rényi entropy [22], and linear entropy [23] offer metrics for assessing uncertainty and entanglement across diverse models. Several studies have examined these concepts thoroughly in the realms of quantum optics [24], condensed matter physics [25], and nanostructured systems [26]. Due to the rise of intriguing new properties of entanglement, which are rapidly developing with transformative innovations in the fields of quantum communication, quantum information processing, and quantum computing, the quantum information entropy and multi-qubit entanglement have been analyzed in [27]. As referenced in [28], the entropy of quantum information in multi-qubit Rabi systems exhibits greater sensitivity to temporal evolution compared with von Neumann entropy, thereby offering enhanced dynamical precision in the presence of variations in detuning and coupling. In addition, more recent research has explicitly examined entropy in semiconductor nanowires, such as linear entropy and mutual information in Rashba-coupled nanowires, revealing that applied magnetic fields have a substantial impact on quantum coherence and entanglement, as discussed in [29]. Meanwhile, in ref. [30], Shannon entropy effectively serving as a tracker for decoherence processes in dissipative nanowires has been illustrated, thereby affirming entropy as a crucial indicator of quantum-to-classical transitions. These results emphasize that entropy metrics connect microscopic models of nanowires influenced by Rashba SOI with the broader context of quantum information theory, rendering them crucial instruments for investigating both fundamental physics and prospective quantum computing platforms. Thus, this study focuses on the fractional dynamics of information entropy within a quantum wire system influenced by Rashba interaction.

The examination of quantum systems has historically depended on integer-order calculus for the description of time evolution and system dynamics. Nevertheless, recent developments in fractional calculus have offered fresh insights into the nonlocal and memory-dependent characteristics of physical systems. The fractional dynamics associated with quantum systems present a robust mathematical framework for modeling anomalous diffusion, long-range correlations, and intricate relaxation processes that traditional Schrödinger dynamics fail to account for. This methodology has been applied in open quantum systems, quantum transport phenomena, and studies of information entropy, where memory effects are of significant importance [31,32]. Furthermore, Fractional calculus broadens the notion of derivatives and integrals to encompass non-integer orders, allowing for the integration of history-dependent effects into dynamic equations. In the realm of quantum mechanics, the time-fractional Schrödinger equation (TFSE) has been introduced as a generalization of the traditional Schrödinger equation, where in the conventional time derivative is substituted with a fractional derivative, such as the Caputo or Riemann–Liouville derivative [33,34]. Additionally, fractional quantum dynamics reveals important insights into quantum information indicators like von Neumann entropy and Fisher information [35], drawing attention to non-exponential decay characteristics and peculiar uncertainty relations [36]. The scope of applications includes quantum optics and nanophysics as well as exciton transport in biological systems, indicating that fractional approaches are advantageous for the progression of durable quantum technologies [37].

The structure of this paper is as follows: in Section 2, we describe the theoretical model and Hamiltonian formalism used to characterize the nanowire structure. Section 3 develops the mathematical framework based on fractional calculus to investigate the fractional nanowire state through an analytical solution to the fractional Schrödinger equation. In Section 4, we explain the entropy concepts employed to analyze quantum coherence, entanglement, and information transfer for nanowire systems. Section 5 presents the analytical and numerical findings, highlighting the impact of fractional parameters, Rashba interaction, and magnetic fields on entropy dynamics. Finally, Section 6 summarizes the main outcomes and conclusion.

2. The Quantum Wire System

The Hamiltonian governing the physical properties of a nanowire system is contingent upon the unique characteristics of the wire, including its dimensionality, which is considered here along the y-axis, the confinement potential in the x-direction, denoted as $V\left(x\right)={\displaystyle \frac{1}{2}}m{\omega }^2{x}^2$, with the effective mass of the electron m and harmonic oscillator frequency $\omega$, and the external magnetic fields oriented in the z-direction $(\overrightarrow{B}=B{\widehat{e}}_z)$. The proposed theoretical framework is predicated on the interaction between a two-level state and Rashba spin–orbit interaction $H_{SO}=-{\displaystyle \frac{{\alpha }_r}{\hslash }}{\left[(\overrightarrow{p}+e\overrightarrow{A})\times \overrightarrow{\sigma }\right]}_z$ with Rashba coupling constant ${\alpha }_r$ that can be controlled by an electric field E, and vector potential $\overrightarrow{A}=xB{\widehat{e}}_y$. Therefore, the general form of the Hamiltonian for a quasi-1D semiconductor nanowire (like InAs or InSb) with Rashba spin–orbit interaction (RSOI) is given as [26,38,39,40]:

$$\widehat{H}={\displaystyle \frac{\left[p_x^2+{(p_y+eBx)}^2\right]}{2m}}+V\left(x\right)+eEx+H_Z+H_{SO}.$$

(1)

Here, $H_Z={\displaystyle \frac{g{\mu }_B}{2}}(\overrightarrow{\sigma }.\overrightarrow{B})$ represents the Zeeman effect with Lande’s g-factor, and Bohr magneton ${\mu }_B$, also $\overrightarrow{p}=(p_x,p_y)$ indicates the momentum operators, e refers to the electron’s charge, and $\overrightarrow{\sigma }=\left({\widehat{\sigma }}_x,{\widehat{\sigma }}_y,{\widehat{\sigma }}_z\right)$ is the Pauli matrix representing spin in the x, y, and z-directions, which can expressed in the Dirac notation as ${\widehat{\sigma }}_x=|\mathrm{e}⟩⟨\mathrm{g}|+|\mathrm{g}⟩⟨\mathrm{e}|,{\widehat{\sigma }}_y=-i|\mathrm{e}⟩⟨\mathrm{g}|+i|\mathrm{g}⟩⟨\mathrm{e}|,\mathrm{and}{\widehat{\sigma }}_z=|\mathrm{e}⟩⟨\mathrm{e}|-|\mathrm{g}⟩⟨\mathrm{g}|$, where $|\mathrm{e}⟩$ and $|\mathrm{g}⟩$ signify the excited and ground state of the electron.

In a nanowire system, particularly when subjected to harmonic confinement or when examining quantized energy levels, it is frequently advantageous to express the Hamiltonian utilizing ladder operators $\widehat{a}$, and ${\widehat{a}}^{†}$. Consequently, the Hamiltonian (1) articulated in units of $\hslash {\omega }_o$ can be formulated in the quantization framework by employing ladder operators ($\widehat{a}$, and ${\widehat{a}}^{†}$), which signifies the shifted harmonic oscillator in dimensionless lengths form as:

$$\begin{array}{cc}\hfill {\displaystyle \frac{\widehat{H}}{\hslash {\omega }_o}}=& \Omega \left({\widehat{a}}^{†}\widehat{a}+{\displaystyle \frac{1}{2}}\right)+{\displaystyle \frac{\eta }{2}}+{\displaystyle \frac{1}{2}}\left(\begin{array}{c}{\zeta }_1+{\zeta }_2({\widehat{a}}^{†}+\widehat{a})\\ i{\zeta }_3(\widehat{a}-{\widehat{a}}^{†})\\ \delta \end{array}\right).\overrightarrow{\sigma }\hfill \\ \hfill =& \Omega \left({\widehat{a}}^{†}\widehat{a}+{\displaystyle \frac{1}{2}}\right)+{\displaystyle \frac{\eta }{2}}+{\displaystyle \frac{1}{2}}\left({\zeta }_1{\widehat{\sigma }}_x+{\zeta }_2({\widehat{a}}^{†}+\widehat{a}){\widehat{\sigma }}_x+i{\zeta }_3(\widehat{a}-{\widehat{a}}^{†}){\widehat{\sigma }}_y+\delta {\widehat{\sigma }}_z\right).\hfill \end{array}$$

(2)

Here, three different length scales delineate the relative strengths in the dynamics of confinement, magnetic field B, and spin–orbit interaction (SOI),

$$L_O=\sqrt{{\displaystyle \frac{\hslash }{m{\omega }_o}}}{L}_B=\sqrt{{\displaystyle \frac{\hslash }{eB}}}{L}_{SO}={\displaystyle \frac{{\hslash }^2}{2m{\alpha }_r}},$$

(3)

while the parameters referenced in the preceding equations are delineated as follows:

$$\begin{array}{cc}\hfill & \Omega =\sqrt{1+{\left({\displaystyle \frac{L_O}{L_B}}\right)}^4},\eta ={\left(L_{O}k\right)}^2-{\left({\displaystyle \frac{\Omega {\chi }_c}{L_O}}\right)}^2,{\chi }_c={\left({\displaystyle \frac{L_O}{\Omega }}\right)}^2\left[{\displaystyle \frac{eE}{\hslash {\omega }_o}}+k{\left({\displaystyle \frac{L_O}{L_B}}\right)}^2\right],\hfill \\ \hfill & \delta ={\displaystyle \frac{g}{2}}{\displaystyle \frac{m}{m_o}}{\left({\displaystyle \frac{L_O}{L_B}}\right)}^2,{\zeta }_1={\displaystyle \frac{L_O^2}{L_{SO}}}\left(k-{\displaystyle \frac{{\chi }_c}{L_B^2}}\right),{\zeta }_2={\displaystyle \frac{1}{\sqrt{2\Omega }}}{\displaystyle \frac{L_O}{L_{SO}}}{\left({\displaystyle \frac{L_O}{L_B}}\right)}^2,and{\zeta }_3=\sqrt{{\displaystyle \frac{\Omega }{2}}}{\displaystyle \frac{L_O}{L_{SO}}}.\hfill \end{array}$$

(4)

In the situation of lacking an external electric field, the proposed Hamiltonian (2) transforms into the following form:

$$\widehat{H}=\Omega \left({\widehat{a}}^{†}\widehat{a}+{\displaystyle \frac{1}{2}}\right)+{\displaystyle \frac{\delta }{2}}{\widehat{\sigma }}_z+\gamma \left({\widehat{a}}^{†}{\widehat{\sigma }}_{-}+\widehat{a}{\widehat{\sigma }}_{+}\right),$$

(5)

where $\gamma ={\displaystyle \frac{1}{2}}({\zeta }_2+{\zeta }_3)$ signifies the coefficient associated with spin–orbit coupling, and the Raising $\left({\widehat{\sigma }}_{+}\right)$ and Lowering $\left({\widehat{\sigma }}_{-}\right)$ operators ${\widehat{\sigma }}_{\pm }={\widehat{\sigma }}_x\pm i{\widehat{\sigma }}_y$, which are represented in the Dirac notation as ${\widehat{\sigma }}_{+}=|\mathrm{e}⟩⟨\mathrm{g}|,and{\widehat{\sigma }}_{-}=|\mathrm{g}⟩⟨\mathrm{e}|$.

3. The Time-Fractional Evolution of a Nanowire State

To formulate the generalized nanowire state (NS) dictated by the Hamiltonian presented in (5), we employ the time-fractional Schrödinger equation (TFSE), defined as follows [32,35,41]:

$$\begin{array}{c}\hfill i^{\alpha }\hslash T_C^{\alpha -1}{\displaystyle \frac{{\partial }^{\alpha }}{\partial t}}|\Psi (\alpha ,t)⟩=\widehat{H}|\Psi (\alpha ,t)⟩,\end{array}$$

(6)

where $|\Psi (\alpha ,t)⟩$ represents the state vector of the NS, and ${\displaystyle \frac{{\partial }^{\alpha }}{\partial t}}$ is the Caputo fractional derivative of order $\alpha$, which indicates the memory effect of Equation (6) given by

$${\displaystyle \frac{{\partial }^{\alpha }}{\partial t^{\alpha }}}f\left(t\right){=}_0^C{D}_t^{\alpha }f\left(t\right)={\displaystyle \frac{1}{\Gamma (1-\alpha )}}{\mathsf{\int }}_0^t{\displaystyle \frac{f^{\prime }\left(\tau \right)}{{(t-\tau )}^{\alpha }}}d\tau (0<\alpha \le 1),$$

where $f^{\prime }\left(\tau \right)$ represents the first order time derivative, and $\Gamma (1-\alpha )$ is the Gamma function. As $\alpha =1$, the TFSE presented in Equation (6) loses its memory characteristics and reverts to the conventional Schrödinger equation. Conversely, as $0<\alpha <1$, TFSE exhibits complete memory retention. The existence and uniqueness results for solutions of the fractional Schrödinger Equation (6) have been established in the literature [33,42].

Considering that the value of the fractional time constant $T_C$ can be modified, we will assume that $\hslash T_C^{\alpha -1}=1$ for the purposes of this discussion [32,42]. Consequently, based on the comprehensive analysis of fractional differential linear systems [41,43], the solution to Equation (6) is expressed as

$$\begin{array}{c}\hfill |\Psi (\alpha ,t)⟩=C_1{E}_{\alpha }\left(k_1{i}^{-\alpha }{t}^{\alpha }\right)|{\eta }_1⟩+C_2{E}_{\alpha }\left(k_2{i}^{-\alpha }{t}^{\alpha }\right)|{\eta }_2⟩+...+C_n{E}_{\alpha }\left(k_n{i}^{-\alpha }{t}^{\alpha }\right)|{\eta }_n⟩,\end{array}$$

(7)

where $C_i$ are arbitrary constants, $k_i$ and ${\eta }_i$ ($i=1,2,...,n$) are the eigenvalues and their associated eigenvectors of the Hamiltonian $\widehat{H}$. Meanwhile, $E_{\alpha }\left(s\right)$ represents the Mittag–Leffler function of a single parameter $\alpha$ in the context of fractional calculus, which is expressed in the following manner [44]:

$$\begin{array}{c}\hfill E_{\alpha }\left(s\right)=\sum _{j=0}^{\infty }{\displaystyle \frac{s^j}{\Gamma (\alpha j+1)}},\alpha >0,s\in \mathcal{C}.\end{array}$$

(8)

In order to solve Equation (6), we posited that the RSOI–nanowire system is set up in distinct initial states:

Case 1: We assume that the NS was initially established in the following form:

$$|{\Psi }_1\left(0\right)⟩=cos\left({\displaystyle \frac{\theta }{2}}\right)|\mathrm{e},0⟩+sin\left({\displaystyle \frac{\theta }{2}}\right)|\mathrm{g},1⟩,$$

(9)

the notation $|0⟩$ and $|1⟩$ denote the lowest and highest states of the harmonic oscillator, whereas $|\mathrm{e}⟩$ and $|\mathrm{g}⟩$ signify the excited and ground state of the electron.

Using the space electron-harmonic states $\left\{\right|\mathrm{e},0⟩,|\mathrm{g},1⟩\}$, the system’s Hamiltonian (5) is calculated as

$$\widehat{H}=\left(\begin{array}{cc}{\displaystyle \frac{\Omega +\delta }{2}}& \gamma \\ \gamma & {\displaystyle \frac{3\Omega -\delta }{2}}\end{array}\right).$$

(10)

The eigenvalues and eigenvectors that correspond to $\widehat{H}$ can be computed straightforwardly as

$$\begin{array}{c}\hfill k_{1\left(2\right)}=\Omega \pm P_2,|{\eta }_{1\left(2\right)}⟩=\left(\begin{array}{c}{\displaystyle \frac{1}{\gamma }}\left(P_1\pm P_2\right)\\ 1\end{array}\right),\end{array}$$

(11)

where $P_1={\displaystyle \frac{\delta -\Omega }{2}}$, and $P_2=\sqrt{P_1^2+{\gamma }^2}$.

As a result, the solution to Equation (7) is articulated as follows:

$$|{\Psi }_1(\alpha ,t)⟩=C_1\left(\begin{array}{c}{\displaystyle \frac{1}{\gamma }}\left(P_1+P_2\right)\\ 1\end{array}\right)E_{\alpha }\left((\Omega +P_2)i^{-\alpha }{t}^{\alpha }\right)+C_2\left(\begin{array}{c}{\displaystyle \frac{1}{\gamma }}\left(P_1-P_2\right)\\ 1\end{array}\right)E_{\alpha }\left((\Omega -P_2)i^{-\alpha }{t}^{\alpha }\right).$$

(12)

After applying some computations on Equations (9) and (12), the constants $C_1$ and $C_2$ can be derived as follows:

$$\begin{array}{c}\hfill C_1={\displaystyle \frac{1}{2P_2}}\left[\gamma cos\left({\displaystyle \frac{\theta }{2}}\right)-(P_1-P_2)sin\left({\displaystyle \frac{\theta }{2}}\right)\right]\\ \hfill C_2={\displaystyle \frac{1}{2P_2}}\left[(P_1+P_2)sin\left({\displaystyle \frac{\theta }{2}}\right)-\gamma cos\left({\displaystyle \frac{\theta }{2}}\right)\right].\end{array}$$

(13)

Ultimately, the total density matrix for the time-fractional evolution of the NS is computed as

$$\widehat{{\rho }_1}\left(t\right)=\left(\begin{array}{ccc}{\rho }_{11}& & {\rho }_{12}\\ {\rho }_{21}& & {\rho }_{22}\end{array}\right)={\displaystyle \frac{1}{N_1}}\left(\begin{array}{ccc}|X_1{|}^2& & X_1{X}_2^{*}\\ & & & \\ X_2{X}_1^{*}& & |X_2{|}^2\end{array}\right),$$

(14)

where

$$\begin{array}{cc}\hfill X_1& ={\displaystyle \frac{cos\left(\frac{\theta }{2}\right)}{2P_2}}\left[r_{+}{E}_{{\alpha }_{+}}-r_{-}{E}_{{\alpha }_{-}}\right]+{\displaystyle \frac{\gamma sin\left(\frac{\theta }{2}\right)}{2P_2}}\left[E_{{\alpha }_{+}}-E_{{\alpha }_{-}}\right]\hfill \\ \hfill X_2& ={\displaystyle \frac{\gamma cos\left(\frac{\theta }{2}\right)}{2P_2}}\left[E_{{\alpha }_{+}}-E_{{\alpha }_{-}}\right]+{\displaystyle \frac{sin\left(\frac{\theta }{2}\right)}{2P_2}}\left[r_{+}{E}_{{\alpha }_{-}}-r_{-}{E}_{{\alpha }_{+}}\right]\hfill \\ \hfill N_1& =|X_1{|}^2+{\left|X_2\right|}^2.\hfill \end{array}$$

(15)

Here, $E_{{\alpha }_{\pm }}=E_{\alpha }\left((\Omega \pm P_2)i^{-\alpha }{t}^{\alpha }\right)$, and $r_{\pm }=P_1\pm P_2$.

Case 2: In this case, we posit that the NS was initially set up in the following format:

$$|{\Psi }_2\left(0\right)⟩={\displaystyle \frac{1}{2}}\left(|\mathrm{g},0⟩+|\mathrm{g},1⟩+|\mathrm{e},0⟩+|\mathrm{e},1⟩\right).$$

(16)

By employing the basis $\left\{\right|\mathrm{g},0⟩,|\mathrm{g},1⟩,|\mathrm{e},0⟩,|\mathrm{e},1⟩\}$, the Hamiltonian (5) may be represented as

$$\widehat{H}=\left(\begin{array}{cccc}{\displaystyle \frac{\Omega -\delta }{2}}& 0& 0& 0\\ 0& {\displaystyle \frac{3\Omega -\delta }{2}}& \gamma & 0\\ 0& \gamma & {\displaystyle \frac{\Omega +\delta }{2}}& 0\\ 0& 0& 0& {\displaystyle \frac{3\Omega +\delta }{2}}\end{array}\right).$$

(17)

Consequently, the relevant eigenvalues and eigenvectors of $\widehat{H}$ are determined as

$$\begin{array}{cc}\hfill k_1& =-P_1,k_2=\Omega +P_2,k_3=\Omega -P_2,k_4={\displaystyle \frac{3\Omega +\delta }{2}}.\hfill \\ \hfill |{\eta }_1⟩& =\left(\begin{array}{c}1\\ 0\\ 0\\ 0\end{array}\right),|{\eta }_2⟩=\left(\begin{array}{c}0\\ {\displaystyle \frac{1}{\gamma }}\left(P_2-P_1\right)\\ 1\\ 0\end{array}\right),|{\eta }_3⟩=\left(\begin{array}{c}0\\ {\displaystyle \frac{-1}{\gamma }}\left(P_2+P_1\right)\\ 1\\ 0\end{array}\right),|{\eta }_4⟩=\left(\begin{array}{c}0\\ 0\\ 0\\ 1\end{array}\right).\hfill \end{array}$$

(18)

Based on Equations (6), (7), and (16), the ultimate NS can be articulated as

$$\begin{array}{cc}\hfill |{\Psi }_2(\alpha ,t)⟩=& C_1\left(\begin{array}{c}1\\ 0\\ 0\\ 0\end{array}\right)E_{\alpha }\left(-P_1{i}^{-\alpha }{t}^{\alpha }\right)+C_2\left(\begin{array}{c}0\\ {\displaystyle \frac{1}{\gamma }}\left(P_2-P_1\right)\\ 1\\ 0\end{array}\right)E_{\alpha }\left((\Omega +P_2)i^{-\alpha }{t}^{\alpha }\right)\hfill \\ \hfill & +C_3\left(\begin{array}{c}0\\ {\displaystyle \frac{-1}{\gamma }}\left(P_2+P_1\right)\\ 1\\ 0\end{array}\right)E_{\alpha }\left((\Omega -P_2)i^{-\alpha }{t}^{\alpha }\right)+C_4\left(\begin{array}{c}0\\ 0\\ 0\\ 1\end{array}\right)E_{\alpha }\left(\left({\displaystyle \frac{3\Omega +\delta }{2}}\right)i^{-\alpha }{t}^{\alpha }\right).\hfill \end{array}$$

(19)

The values of parameters $C_1,C_2,C_3$, and $C_4$ can be established by utilizing Equation (16):

$$\begin{array}{c}\hfill C_1=C_4={\displaystyle \frac{1}{2}},C_2={\displaystyle \frac{P_2+P_1+\gamma }{4P_2}},C_3={\displaystyle \frac{P_2-P_1-\gamma }{4P_2}}.\end{array}$$

(20)

Therefore, the final NS for the initial state $|{\Psi }_2\left(0\right)⟩$ is given as

$$\begin{array}{c}\hfill |{\Psi }_2(\alpha ,t)⟩={\displaystyle \frac{1}{N_2}}\left(A_1|\mathrm{g},0⟩+A_2|\mathrm{g},1⟩+A_3|\mathrm{e},0⟩+A_4|\mathrm{e},1⟩\right),\end{array}$$

(21)

where

$$\begin{array}{cc}\hfill A_1& ={\displaystyle \frac{1}{2}}{E}_{\alpha }\left(-P_1{i}^{-\alpha }{t}^{\alpha }\right)\hfill \\ \hfill A_2& ={\displaystyle \frac{1}{4P_2}}\left[(\gamma -r_{-})E_{\alpha }\left((\Omega +P_2)i^{-\alpha }{t}^{\alpha }\right)-(\gamma -r_{+})E_{\alpha }\left((\Omega -P_2)i^{-\alpha }{t}^{\alpha }\right)\right]\hfill \\ \hfill A_3& ={\displaystyle \frac{1}{4P_2}}\left[(\gamma +r_{+})E_{\alpha }\left((\Omega +P_2)i^{-\alpha }{t}^{\alpha }\right)-(\gamma +r_{-})E_{\alpha }\left((\Omega -P_2)i^{-\alpha }{t}^{\alpha }\right)\right]\hfill \\ \hfill A_4& ={\displaystyle \frac{1}{2}}{E}_{\alpha }\left(\left({\displaystyle \frac{3\Omega -\delta }{2}}\right)i^{-\alpha }{t}^{\alpha }\right)\hfill \\ \hfill N_2& =|A_1{|}^2+|A_2{|}^2+|A_3{|}^2+{\left|A_4\right|}^2.\hfill \end{array}$$

(22)

4. Information Entropy

The concept of information entropy is a pivotal element in information theory, serving to quantify the level of uncertainty or unpredictability within a system. First introduced by Claude Shannon in 1948 [20], it assesses the average information content generated by a random variable or data source. Moreover, the information entropy has been significant in the analysis of quantum-mechanical systems and in elucidating several fundamental concepts. Namely, it quantifies the mixedness of a quantum state and is essential for measuring entanglement and the flow of information between subsystems.

Consequently, the information entropies of the atomic operator ${\widehat{\sigma }}_z$ for any arbitrary quantum state, which corresponds to the probability distribution $P_i\left({\widehat{\sigma }}_z\right)$ for N potential measurement outcomes, are expressed as follows [45,46,47,48]:

$$H\left({\widehat{\sigma }}_z\right)=-\sum _{i=1}^{N}ln{P}_i{\left({\widehat{\sigma }}_z\right)}^{P_i\left({\widehat{\sigma }}_z\right)},$$

(23)

where $P_i\left({\widehat{\sigma }}_z\right)=⟨{\Psi }_i|\rho \left(t\right)|{\Psi }_i⟩$ with $|{\Psi }_i⟩$ is an eigenvector of the operator ${\widehat{\sigma }}_z$.

Then, by using the density matrix $\rho \left(t\right)$ for the proposed nanowire system with N state, we obtain that the information entropy of the operator ${\widehat{\sigma }}_z$ can be written in the following form:

$$H\left({\widehat{\sigma }}_z\right)=-\sum _{i=1}^N{\rho }_{ii}ln\left({\rho }_{ii}\right),$$

(24)

where ${\rho }_{ii}$ in case (1) represents the elements of the density matrix $\widehat{{\rho }_1}\left(t\right)$ in Equation (14) as follows:

$${\rho }_{11}={\displaystyle \frac{1}{N_1}}|X_1{|}^2,and{\rho }_{22}={\displaystyle \frac{1}{N_1}}{\left|X_2\right|}^2.$$

(25)

Meanwhile, ${\rho }_{ii}$ in case (2) is given by

$${\rho }_{11}={\displaystyle \frac{1}{N_2}}|A_1{|}^2,{\rho }_{22}={\displaystyle \frac{1}{N_2}}|A_2{|}^2,{\rho }_{33}={\displaystyle \frac{1}{N_2}}|A_3{|}^2,and{\rho }_{44}={\displaystyle \frac{1}{N_2}}{|A_4|}^2.$$

(26)

5. Results and Discussion

Our discussion focuses on how the memory parameter $\left(\alpha \right)$ in the time-fractional Schrödinger equation affects the dynamics of information entropy $H\left({\widehat{\sigma }}_z\right)$. Additionally, the influences of various values for the interaction parameters, specifically the magnetic field $\left(L_B\right)$ and spin–orbit interaction ($L_{SO}$) strengths on $H\left({\widehat{\sigma }}_z\right)$ will be examined. Furthermore, we proposed that the NS is set up in distinct two initial states $|{\Psi }_1\left(0\right)⟩$, and $|{\Psi }_2\left(0\right)⟩$.

In Figure 1, the analysis of information entropy behaves, and $H\left({\widehat{\sigma }}_z\right)$ is conducted for various magnetic field strength values $\left(L_B\right)$, considering the NS initially set in an uncorrelated state $|{\Psi }_1\left(0\right)⟩=|\mathrm{e},0⟩$.

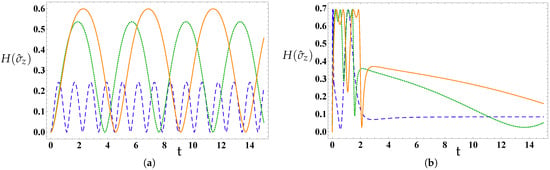
Figure 1. The time evolution of the information entropy, $H\left({\widehat{\sigma }}_z\right)$, for various values of the magnetic field strength ($L_B$): $L_B=L_O$ (dashed plots), $L_B=3L_O$ (dotted plots), and $L_B=5L_O$ (solid plots), with the SOI strength $L_{SO}=L_O$, when the NS is initially prepared in the uncorrelated state $|{\Psi }_1\left(0\right)⟩=|\mathrm{e},0⟩$, where $\theta =0$. In (a) $\alpha =1$, whereas (b) $\alpha =0.3$.

Figure 1a illustrates that the information entropy demonstrates oscillatory behavior, varying between its maximum and zero values. These oscillation frequencies are contingent upon the strength of the magnetic field; notably, the number of oscillations of $H\left({\widehat{\sigma }}_z\right)$ significantly diminishes as the magnetic field intensifies. Conversely, the upper limits of $H\left({\widehat{\sigma }}_z\right)$ rise as $L_B$ increases. Consequently, higher values of the magnetic field lead to a more sustained quantum entanglement between the spin and orbital components of the nanowire system. In addition, the role of the fractional order parameter, $\alpha$, is depicted in Figure 1b. It is noted that the information entropy fluctuates between its lower and upper limits for a brief period before stabilizing at its stationary values, yet it does not approach zero. This behavior occurs when $L_B=L_O$. In contrast, as the magnetic field intensifies, $H\left({\widehat{\sigma }}_z\right)$ begins from its initial value of $H\left({\widehat{\sigma }}_z\right)=0$, continuing to increase until it reaches its maximum potential value. Subsequently, it oscillates for a short duration of time $t<2$, and ultimately, $H\left({\widehat{\sigma }}_z\right)$ experiences a rapid decline as time t approaches infinity.

Based on Figure 1, it can be inferred that the strength of the magnetic field and the memory effect of TFSE can act as control parameters to improve information entropy, and quantum entanglement.

To examine how the initial state influences the behavior of information entropy, we posit that the NS is initially configured in a correlated state with $\theta ={\displaystyle \frac{\pi }{2}}$, as shown in Figure 2. From Figure 2a, we can see that $H\left({\widehat{\sigma }}_z\right)$ commences at its utmost possible values and declines until it arrives at the nadir of its possible values, which never completely disappear. As the magnetic field strength rises, the frequency of oscillations and the lower bounds in $H\left({\widehat{\sigma }}_z\right)$ significantly diminish. Moreover, the anticipated lower bounds are considerably superior to those illustrated in Figure 1a, which never approaches zero. In this case, Figure 2b reveals the memory effect of TFSE on information entropy. It is evident that the information entropy begins at its maximum value of $H\left({\widehat{\sigma }}_z\right)=0.7$ and decreases until it attains its minimum possible value. Subsequently, it oscillates for a brief period before stabilizing at $H\left({\widehat{\sigma }}_z\right)=0.1$, which occurs exclusively when $L_B=L_O$. However, when the magnetic field strength is increased to $L_B=3L_O$ and $5L_O$, the behavior of the information entropy exhibits intensified oscillations for a short time, followed by a gradual slowing of oscillations as time progresses, and the frequency of oscillations significantly diminishes with increasing magnetic field strength.

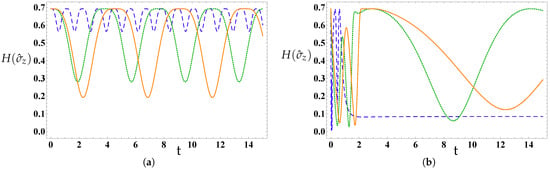
Figure 2. As Figure 1 but, when the NS initially prepared in the correlated state $|{\Psi }_1\left(0\right)⟩={\displaystyle \frac{1}{\sqrt{2}}}\left(\right|\mathrm{e},0⟩+|\mathrm{g},1⟩)$ where $(\theta ={\displaystyle \frac{\pi }{2}})$. In (a) $\alpha =1$, whereas (b) $\alpha =0.3$.

The information entropy, as depicted in Figure 1 and Figure 2, reveals a notable sensitivity to any variations in magnetic field strength, the memory effect of TFSE, and the initial state of the system.

Figure 3 displays the impact of spin–orbit interaction strength $\left(L_{SO}\right)$ on the temporal progression of information entropy, when the system is initially in an uncorrelated state $|{\Psi }_1\left(0\right)⟩=|\mathrm{e},0⟩$. Observations from Figure 3a indicate that $H\left({\widehat{\sigma }}_z\right)$ initiates at an initial value of $H\left({\widehat{\sigma }}_z\right)=0$ and progressively increases until it attains its maximum potential values, after which it exhibits regular fluctuations as time progresses. Additionally, with an increase in SOI strength, there is a notable reduction in both the upper bounds and the number of fluctuations of $H\left({\widehat{\sigma }}_z\right)$. These fluctuation frequencies are for $H\left({\widehat{\sigma }}_z\right)$ based on the memory impact of TFSE, $\alpha$, with regular fluctuations becoming evident at elevated $\alpha$ values. Conversely, increased $\alpha$ values lead to a more enduring quantum entanglement. Furthermore, there are instances of temporary sudden death and rebirth of quantum entanglement that transpire briefly before it attains its minimum potential values, subsequently stabilizing at stationary values for lower $\alpha$ values, as shown in Figure 3b.

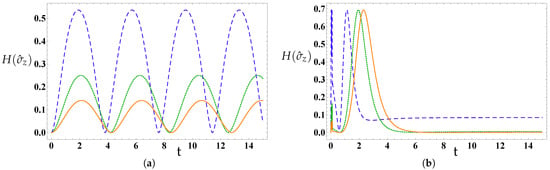
Figure 3. The time evolution of the information entropy, $H\left({\widehat{\sigma }}_z\right)$, for various values of the SOI ($L_{SO}$): $L_{SO}=L_O$ (dashed plots), $L_{SO}=2L_O$ (dotted plots), and $L_{SO}=3L_O$ (solid plots), with the magnetic field strength $L_B=3L_O$, when the NS is initially prepared in the uncorrelated state $|{\Psi }_1\left(0\right)⟩=|\mathrm{e},0⟩$, where $\theta =0$. In (a), $\alpha =1$, whereas in (b) $\alpha =0.3$.

The behaviors of $H\left({\widehat{\sigma }}_z\right)$ over time for different spin–orbit interaction strengths, when the system is initially in a correlated state $|{\Psi }_1\left(0\right)⟩={\displaystyle \frac{1}{\sqrt{2}}}\left(\right|\mathrm{e},0⟩+|\mathrm{g},1⟩)$, are displayed in Figure 4. It is apparent that the SOI strength has a pronounced impact on $H\left({\widehat{\sigma }}_z\right)$. With an increase in the $\left(L_{SO}\right)$, there is a notable reduction in the number of fluctuations. At the same time, the lower bounds increase until they reach the maximum values as seen in Figure 4a. Additionally, when the memory effect lessens, the information entropy experiences swift irregular fluctuations initially, followed by a significant decrease in fluctuations as time advances, leading to a more regular pattern, as demonstrated in Figure 4b.

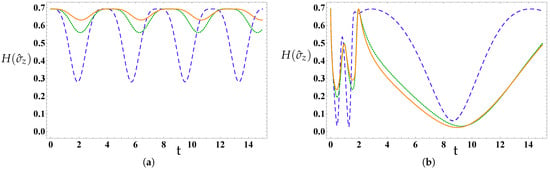
Figure 4. As Figure 3, but when the NS is initially prepared in the correlated state $|{\Psi }_1\left(0\right)⟩={\displaystyle \frac{1}{\sqrt{2}}}\left(\right|\mathrm{e},0⟩+|\mathrm{g},1⟩)$, where $(\theta ={\displaystyle \frac{\pi }{2}})$. In (a), $\alpha =1$, whereas in (b) $\alpha =0.3$.

In summary, the results presented in Figure 1, Figure 2, Figure 3 and Figure 4 reveal that information entropy, which quantifies quantum entanglement, has highly pronounced sensitivity to any modifications in the magnetic field and spin–orbit interaction strengths.

Figure 5 presents a distinct representation of how the fractional memory effect of TFSE ($\alpha$) affects information entropy when the NS initially set in both a correlated and uncorrelated states. As we show in Figure 5a, the information entropy exhibits rapid and irregular oscillations when $\alpha$ is within the range of $[0.1,0.5]$. However, as $\alpha$ is increased to the interval $[0.5,1]$, the frequency of oscillations diminishes and becomes more regular, while simultaneously, minor upper bounds are noted until a stationary state is achieved. Moreover, Figure 5b demonstrates how the $H\left({\widehat{\sigma }}_z\right)$ behaves when the NS is initially configured in a correlated state. It is evident that the number of fluctuations significantly diminishes and becomes more regular, while the lower bounds rise, as the $\alpha$ value is increased. This implies that the characteristics of information entropy and quantum entanglement can be managed by any variations in the fractional parameter $\alpha$.

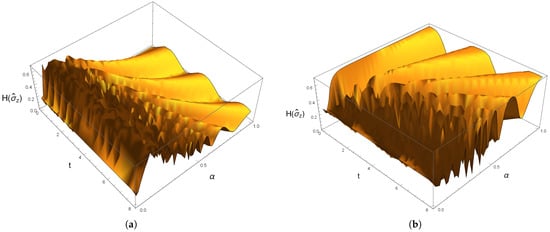
Figure 5. The time evolution of the information entropy $H\left({\widehat{\sigma }}_z\right)$. In (a), $\theta =0$ and $L_B=L_{SO}=2L_O$, whereas in (b) $\theta ={\displaystyle \frac{\pi }{2}}$, $L_B=3L_O$, and $L_{SO}=L_O$.

Currently, we are exploring the information entropy of the nanowire system that was initially established in the two-level state $|{\Psi }_2\left(0\right)⟩$. The influence of the magnetic field strength $\left(L_B\right)$ and fractional memory effect of TFSE $\left(\alpha \right)$ on $H\left({\widehat{\sigma }}_z\right)$ is presented in Figure 6. As illustrated in Figure 6a, the information entropy exhibits consistent fluctuations and begins at its potential maximum value of $H\left({\widehat{\sigma }}_z\right)=1.4$, as anticipated when $N=4$ states are considered. With an increase in $L_B$, both the frequency of fluctuations and the lower bounds experience a significant reduction. Additionally, the upper bounds of $H\left({\widehat{\sigma }}_z\right)$ maintain maximum values of $H\left({\widehat{\sigma }}_z\right)=1.4$ for a certain duration before ultimately declining to their potential minimum values, which diminishes with the rise in $L_B$. In the case of small fractional order values, specifically $\alpha =0.3$, the information entropy demonstrates erratic fluctuations for a limited time, commencing from a peak value of $H\left({\widehat{\sigma }}_z\right)=1.4$, subsequently declining to its lowest value before attaining a stationary state when $L_B=L_O$. In contrast, for $L_B=3L_O$ or $L_B=5L_O$, the information entropy similarly experiences irregular fluctuations for a brief interval $t<5$, but thereafter, $H\left({\widehat{\sigma }}_z\right)$ shows consistent and reduced fluctuations as time progresses, without converging to a stationary state (see Figure 6b).

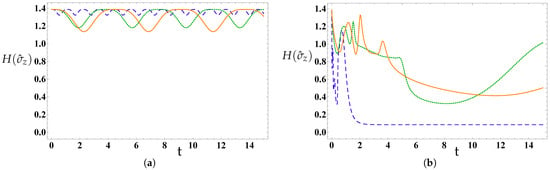
Figure 6. As Figure 1 but, when the NS initially prepared in case 2 state $|{\Psi }_2\left(0\right)⟩$. In (a), $\alpha =1$, whereas in (b) $\alpha =0.3$.

Figure 7 demonstrates how the strength of the SOI $\left(L_{SO}\right)$ influences information entropy when the NS is initially set in the state $|{\Psi }_2\left(0\right)⟩$. When the fractional parameter $\alpha$ assumes integer order derivative values of $\alpha =1$, we can illustrate that the lower bounds of $H\left({\widehat{\sigma }}_z\right)$ grow until they reach their highest possible values as the SOI escalates. Furthermore, the fluctuations diminish until they stabilize at the maximum value of $H\left({\widehat{\sigma }}_z\right)=1.4$ with an increase in $L_{SO}$. This indicates that in order to attain maximum quantum entanglement states in nanowire system, it is essential to utilize high values of SOI (show Figure 7a). On the other hand, when the fractional parameter exhibits full memory for $\alpha \to 0$, as depicted in Figure 7b) with $\alpha =0.3$, the information entropy initiates at its highest value of $H\left({\widehat{\sigma }}_z\right)=1.4$, and then experiences short oscillations before diminishing over time, which suggests that $H\left({\widehat{\sigma }}_z\right)$ is controllable through the fractional parameter $\alpha$.

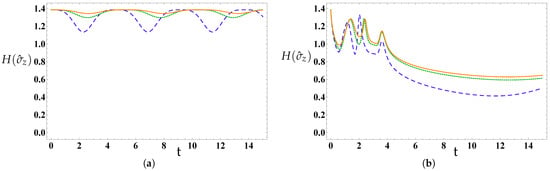
Figure 7. As Figure 3, but when the NS is initially prepared in case 2 state $|{\Psi }_2\left(0\right)⟩$, and $L_B=5L_O$. In (a), $\alpha =1$, whereas in (b) $\alpha =0.3$.

To exhibit the evident influence of the fractional parameter on $H\left({\widehat{\sigma }}_z\right)$ in relation to the $|{\Psi }_2\left(0\right)⟩$ state, refer to Figure 8. It is apparent that the information entropy experiences rapid and erratic fluctuations when $\alpha \in [0.1,0.5]$. Following this, the $H\left({\widehat{\sigma }}_z\right)$ demonstrates regular fluctuations with $\alpha \in [0.5,1]$, while the lower bounds of $H\left({\widehat{\sigma }}_z\right)$ rise with increasing $\alpha$, as previously shown in Figure 7.

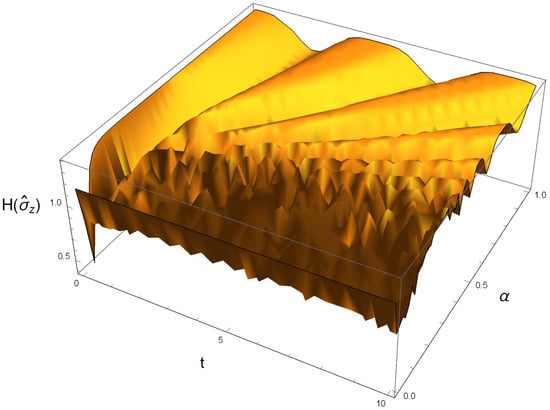
Figure 8. The time evolution of the information entropy, $H\left({\widehat{\sigma }}_z\right)$, when the NS is initially prepared in case 2 state $|{\Psi }_2\left(0\right)⟩$, with $L_B=5L_O$, and $L_{SO}=L_O$.

To summarize our findings, the dynamics of information entropy and quantum entanglement in a nanowire system can be regulated by any variations in all the parameters mentioned earlier, specifically the strengths of the magnetic field $\left(L_B\right)$, the spin–orbit interaction $\left(L_{SO}\right)$, and the fractional parameter $\left(\alpha \right)$ when the NS is set in various initial states. This highlights that these parameters play a crucial role in the control of the nanowire system’s behavior. Consequently, careful adjustment of these factors is vital for optimizing quantum entanglement performance.

6. Conclusions

In this work, we investigated the characterizing quantum coherence, entanglement, and information transfer within nanowire structures through quantum information entropy. By employing fractional calculus and solving the fractional Schrödinger equation, we were able to precisely investigate the fractional nanowire state when the system was prepared in two different initial states, providing a unique lens to analyze the system’s behavior. Our analytical and numerical findings confirm that the dynamics of information entropy are highly sensitive to the fractional parameter. Specifically, our results reveal that as the fractional memory effect, $\alpha$, increases to the range $[0.5,1]$, the oscillation frequency decreases and becomes more regular, while simultaneously, slight upper and lower bounds are observed before reaching their stationary state.

Additionally, we analyzed how interaction parameters, including Rashba spin–orbit interaction and external magnetic fields, influence information entropy. Our observations indicate that the strength of the magnetic field and Rashba SOI exerted distinct yet interrelated impacts on the dynamics of information entropy. Notably, elevated magnetic field strengths contribute to a more enduring quantum entanglement between the spin and orbital aspects of the nanowire system. Furthermore, as the strength of the SOI increases, there is a significant decrease in both the upper limits and the frequency of fluctuations of $H\left({\widehat{\sigma }}_z\right)$, which in turn influences the quantum entanglement of the nanowire states.

The ability to manipulate information entropy dynamics by tuning these parameters provides fundamental insights into quantum systems and opens new avenues for practical applications. This research demonstrates that the fractional memory effect is a powerful tool for controlling and optimizing information flow in quantum wires. Our findings create new perspectives for the development of nanowire systems with potential future applications in the fields of quantum estimation, quantum computing, and quantum information, where precise control over quantum states is paramount.