Dynamic Analysis of a Fractional-Order Model for Vector-Borne Diseases on Bipartite Networks
Abstract
1. Introduction
- (i)
- The long-memory behavior of the infected population during the recovery period is represented by a power-law tail distribution and described using an -order Riemann–Liouville fractional integral.
- (ii)
- Using the unique topology of bipartite networks, the model of the basic reproduction number with fractional-order effects is derived. As a critical threshold, it differentiates the stability regions of disease-free and endemic equilibrium points, and defines the conditions of the stability in the model.
- (iii)
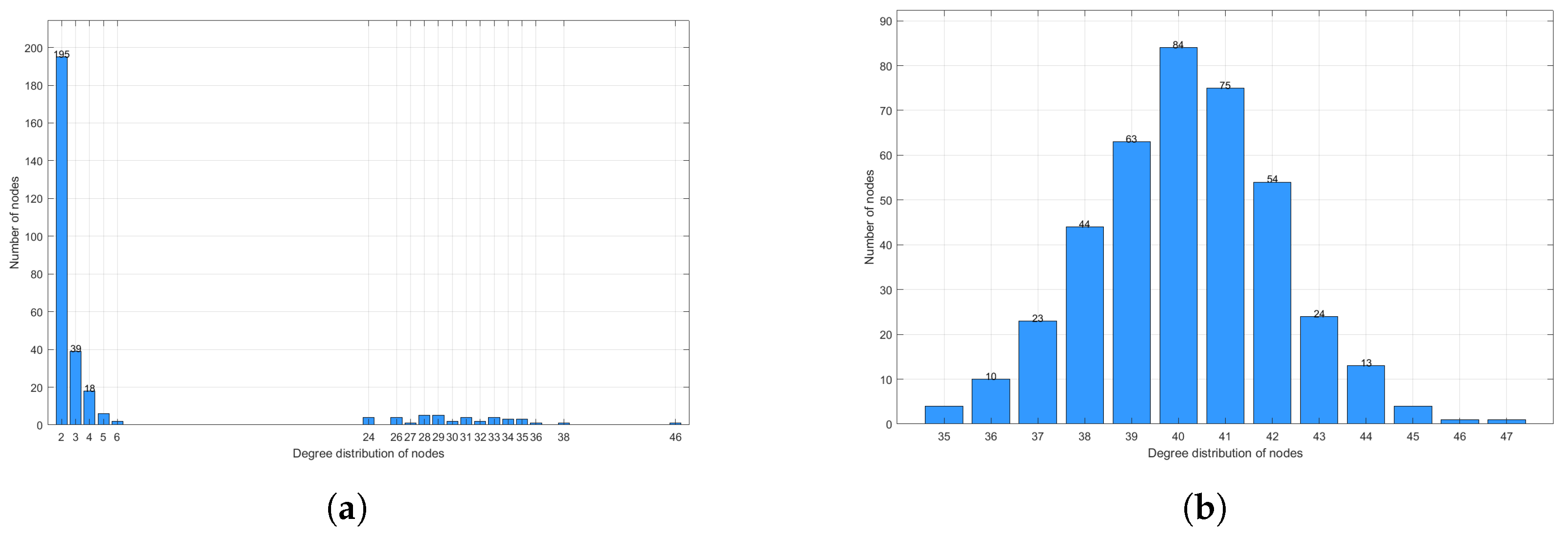
- Using scale-free and small-world networks as case studies, simulation results aligning with theoretical findings are derived, which furnish evidence for relevant models in complex networks.
2. Preliminaries and Problem Formulation
2.1. Preliminaries
- (H1) D is simply connected, where ;
- (H2) There is a compact absorbing set ;
- (H3) The dynamical system satisfies the Poincaré–Bendixson property;
- (H4) is a unique equilibrium point of the dynamical system in D provided it is stable.
2.2. Survival Probability in the Recovery Process
2.3. Dynamic Equations of the Fractional-Oder SIS-SI Model on Bipartite Networks
3. Model Analysis
3.1. Boundedness and Non-Negative of Solutions, the Basic Reproduction Number
3.2. Stability Analysis
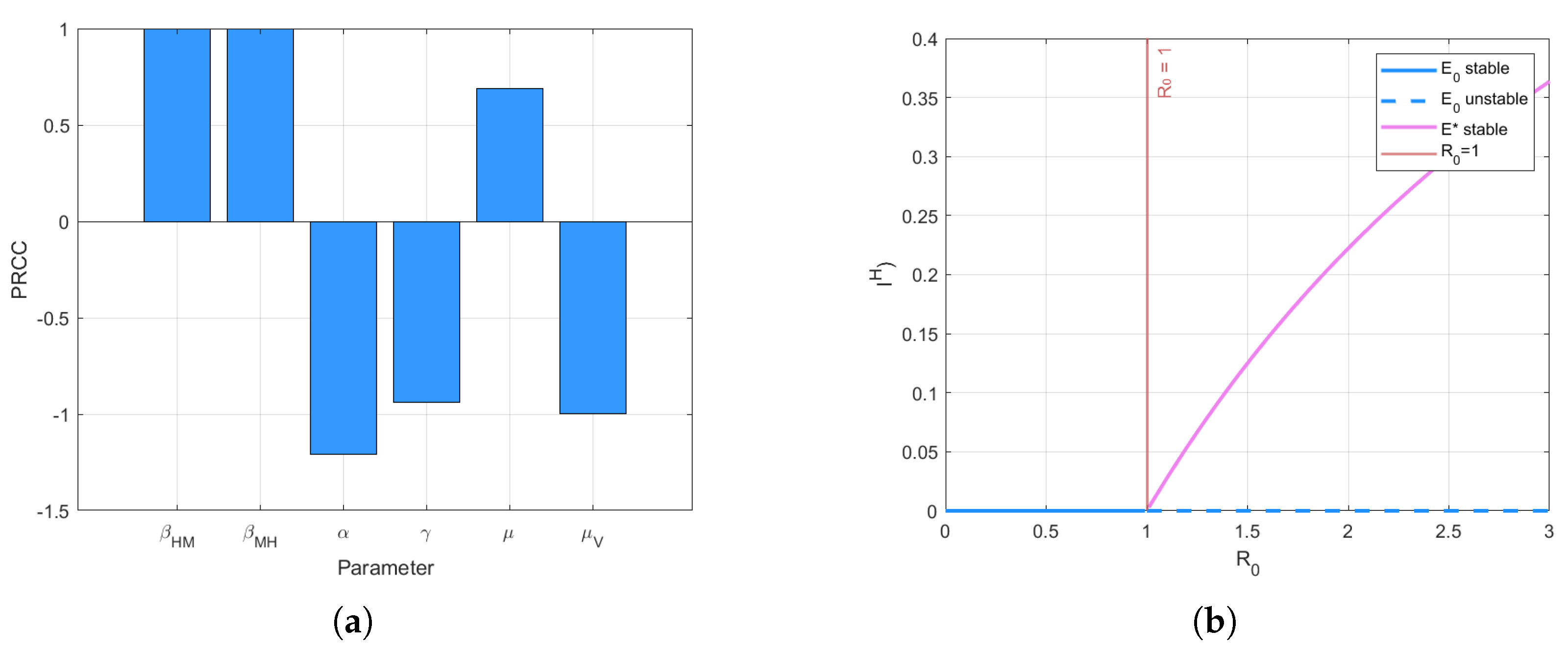
- (i)
- If , it has a unique disease-free equilibrium point which is locally asymptotically stable;
- (ii)
- If , the disease-free equilibrium point is neutrally stable;
- (iii)
- If , the disease-free equilibrium point is unstable, and the endemic equilibrium point is locally asymptotically stable.
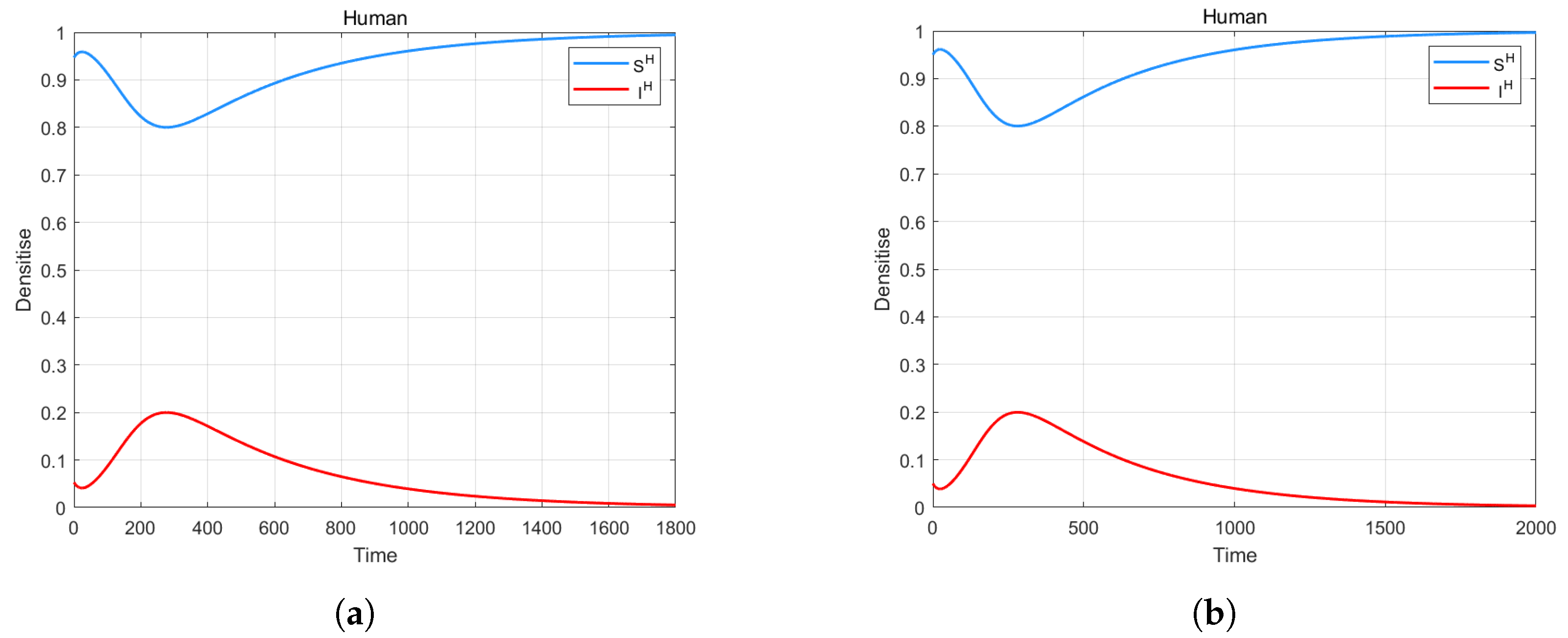
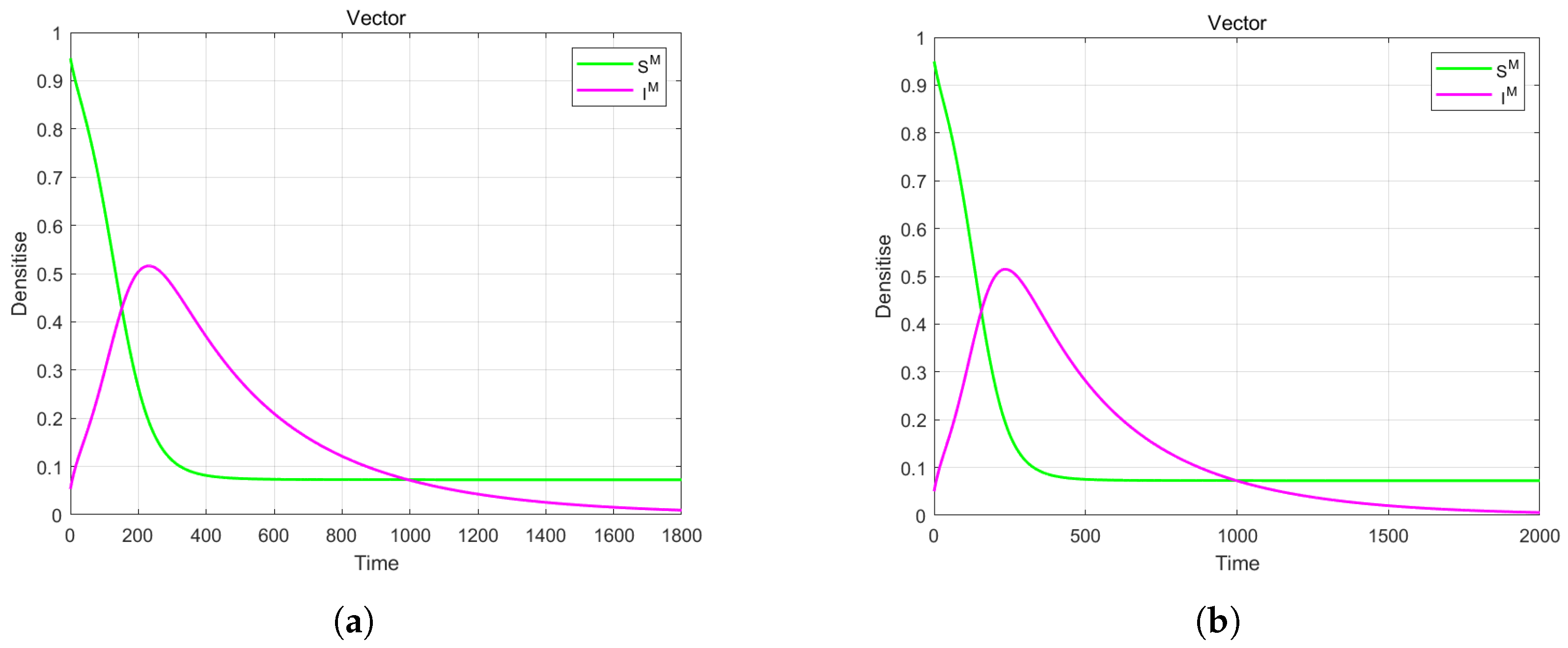
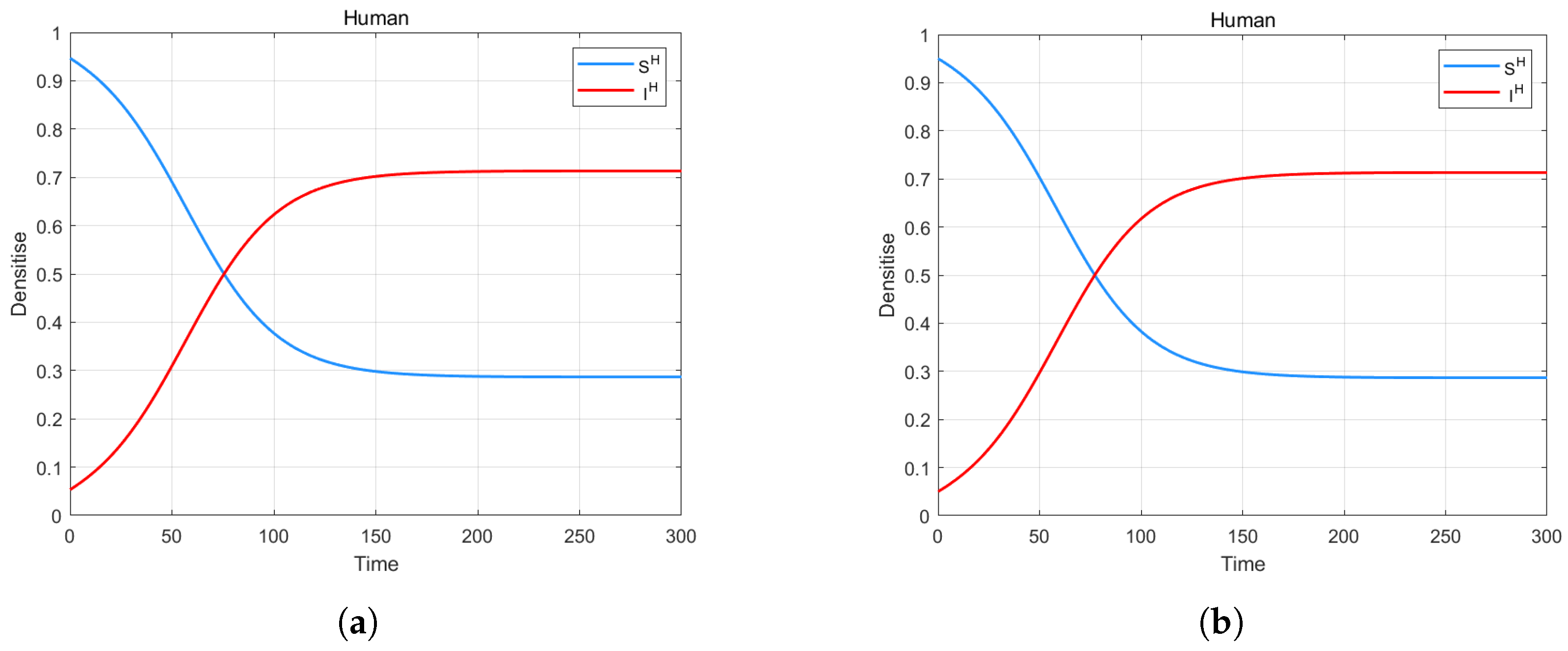
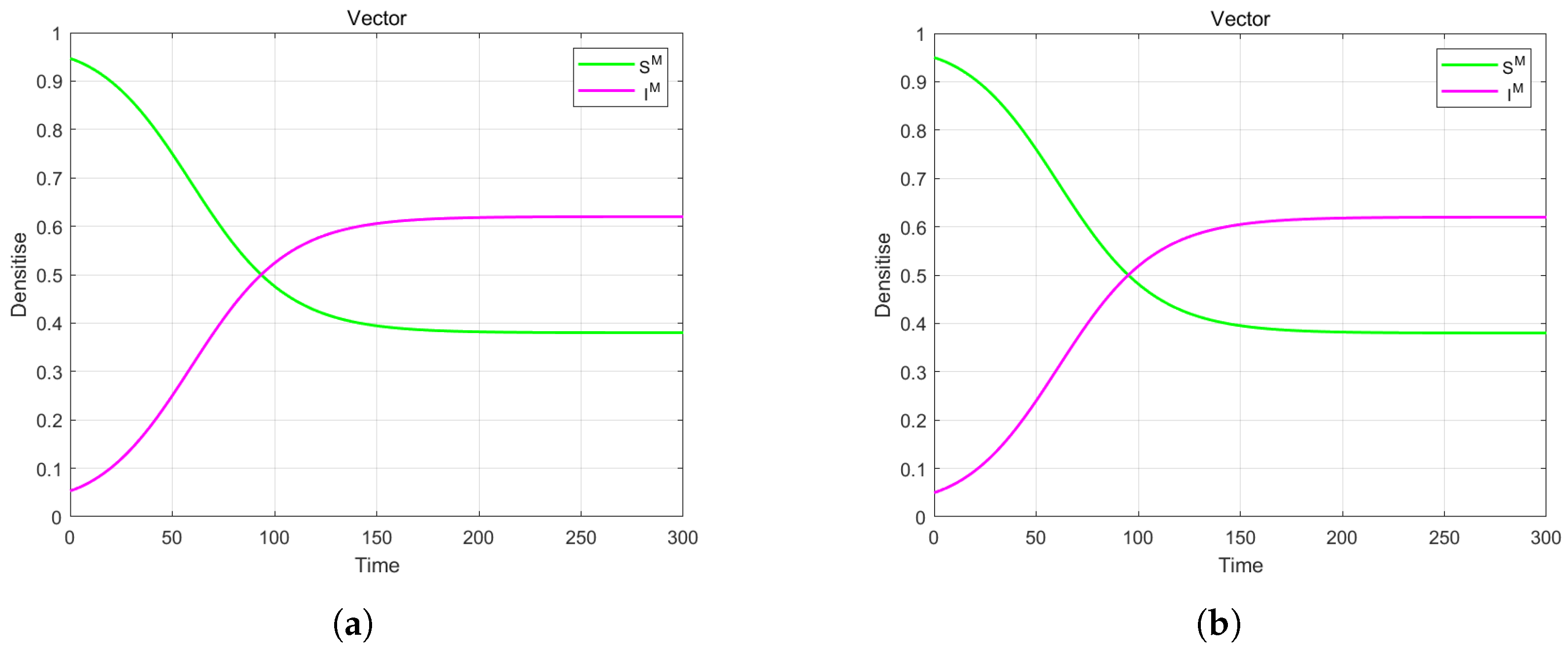
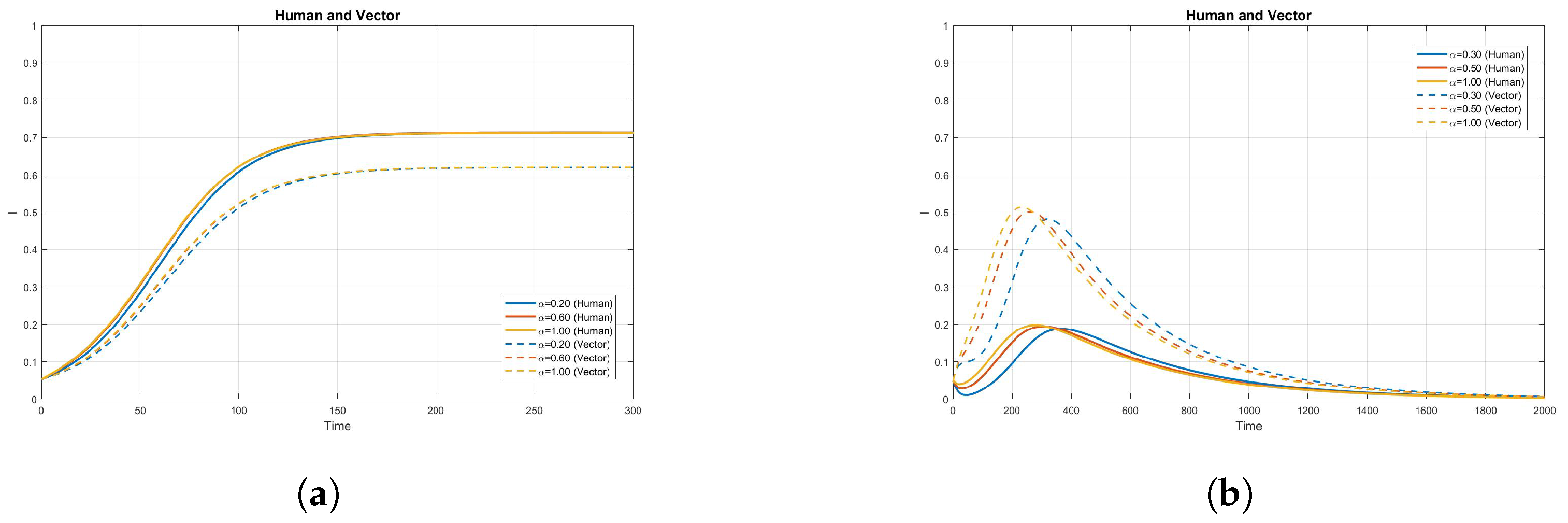
4. Numerical Simulation
5. Conclusions
5.1. Limitations of the Proposed Approach
5.2. Directions for Future Research
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ross, R. The Prevention of Malaria; John Murray: London, UK, 1911. [Google Scholar]
- Wonham, M. The mathematics of mosquitoes and West Nile virus. Pi Sky 2004, 8, 5–9. [Google Scholar]
- Bergsman, L.D.; Hyman, J.M.; Manore, C.A. A mathematical model for the spread of West Nile virus in migratory and resident birds. Math. Biosci. Eng. 2016, 13, 401–424. [Google Scholar] [CrossRef] [PubMed]
- Eguda, A.J.; Yakubu, F. Analysis of a mathematical model to investigate the dynamics of dengue fever. J. Appl. Sci. Environ. Manag. 2017, 21, 626–638. [Google Scholar] [CrossRef]
- Qu, Z.; Xue, L.; Hyman, J.M. Modeling the transmission of Wolbachia in mosquitoes for controlling mosquito-borne diseases. SIAM J. Appl. Math. 2018, 78, 826–852. [Google Scholar] [CrossRef]
- Njoroge, K.P. Mathematical Modeling and Analysis of Transmission of Rift Valley Fever. Ph.D. Thesis, Kenyatta University, Nairobi, Kenya, 2019. [Google Scholar]
- Gebremeskel, A.A.; Krogstad, H.E. Mathematical modelling of endemic malaria transmission. Am. J. Appl. Math. 2015, 3, 36–46. [Google Scholar] [CrossRef]
- Masuda, N.; Konno, N. Multi-state epidemic processes on complex networks. J. Theor. Biol. 2006, 243, 64–75. [Google Scholar] [CrossRef]
- Bisanzio, D.; Bertolotti, L.; Tomassone, L.; Amore, G.; Ragagli, C.; Mannelli, A.; Giacobini, M.; Provero, P. Modeling the spread of vector-borne diseases on bipartite networks. PLoS ONE 2010, 5, e13796. [Google Scholar] [CrossRef]
- Zhang, R. Global dynamic analysis of a model for vector-borne diseases on bipartite networks. Phys. A Stat. Mech. Its Appl. 2020, 545, 123813. [Google Scholar] [CrossRef]
- Tanimoto, S. Epidemic spreading with immunization on bipartite networks. arXiv 2011, arXiv:1105.3265. [Google Scholar] [CrossRef]
- Hernandez, D.G.; Risau-Gusman, S. Epidemic thresholds for bipartite networks. Phys. Rev. E-Nonlinear Soft Matter Phys. 2013, 88, 052801. [Google Scholar] [CrossRef]
- Zhang, R.; Li, D.; Jin, Z. Dynamic analysis of a delayed model for vector-borne diseases on bipartite networks. Appl. Math. Comput. 2015, 263, 342–352. [Google Scholar] [CrossRef]
- Zhao, R.; Liu, Q.; Zhang, H. Dynamical behaviors of a vector-borne diseases model with two time delays on bipartite networks. Math. Biosci. Eng. 2021, 18, 3073–3091. [Google Scholar] [CrossRef] [PubMed]
- Latha, V.P.; Rihan, F.A.; Rakkiyappan, R.; Velmurugan, G. A fractional-order model for Ebola virus infection with delayed immune response on heterogeneous complex networks. J. Comput. Appl. Math. 2018, 339, 134–146. [Google Scholar] [CrossRef]
- Yusuf, A.; Acay, B.; Mustapha, U.T.; Inc, M.; Baleanu, D. Mathematical modeling of pine wilt disease with Caputo fractional operator. Chaos Solitons Fractals 2021, 143, 110569. [Google Scholar] [CrossRef]
- Muhammad, G.; Akram, M. Fuzzy fractional epidemiological model for Middle East respiratory syndrome coronavirus on complex heterogeneous network using Caputo derivative. Inf. Sci. 2024, 659, 120046. [Google Scholar] [CrossRef]
- Zhou, J.C.; Salahshour, S.; Ahmadian, A.; Senu, N. Modeling the dynamics of COVID-19 using fractal-fractional operator with a case study. Results Phys. 2022, 33, 105103. [Google Scholar] [CrossRef]
- Angstmann, C.N.; Henry, B.I.; McGann, A.V. A fractional-order infectivity SIR model. Phys. A 2016, 452, 86–93. [Google Scholar] [CrossRef]
- Angstmann, C.N.; Henry, B.I.; McGann, A.V. A fractional order recovery SIR model from a stochastic process. Bull. Math. Biol. 2016, 78, 468–499. [Google Scholar] [CrossRef]
- Angstmann, C.N.; Henry, B.I.; McGann, A.V. A general framework for fractional order compartment models. SIAM Rev. 2021, 63, 375–392. [Google Scholar] [CrossRef]
- Hirsch, W.M.; Herman, H.; Jean, P.G. Differential equation models of some parasitic infections: Methods for the study of asymptotic behavior. Commun. Pure Appl. Math. 1985, 38, 733–753. [Google Scholar] [CrossRef]
- Hirsch, M.W.; Smale, S.; Devaney, R.L. Differential Equations, Dynamical Systems, and an Introduction to Chaos; Academic Press: San Diego, CA, USA, 2013. [Google Scholar]
- Li, M.Y.; Muldowney, J.S. A geometric approach to global-stability problems. SIAM J. Math. Anal. 1996, 27, 1070–1083. [Google Scholar] [CrossRef]
- Li, M.Y.; Wang, L. Global Stability in Some SEIR Epidemic Models. In Mathematical Approaches for Emerging and Reemerging Infectious Diseases: Models, Methods, and Theory; Castillo-Chavez, C., Blower, S., Driessche, P., Kirschner, D., Yakubu, A., Eds.; Springer: New York, NY, USA, 2002; pp. 295–311. [Google Scholar]
- Gandica, Y.; Carvalho, J.; Aidos, F.S.D.; Lambiotte, R.; Carletti, T. Stationarity of the inter-event power-law distributions. PLoS ONE 2017, 12, e0174509. [Google Scholar] [CrossRef]
- Gandica, Y.; Carvalho, J. The origin of bursts and heavy tails in human dynamics. J. Phys. A Math. Theor. 2005, 38, 207–211. [Google Scholar]
- Vazquez, A.; Balazs, R.; Andras, L.; Barabasi, A. Impact of non-Poissonian activity patterns on spreading processes. Phys. Rev. Lett. 2007, 98, 158702. [Google Scholar] [CrossRef] [PubMed]
- Jo, H.H.; Moon, E.; Kaski, K. Optimized reduction of uncertainty in bursty human dynamics. Phys. Rev. E-Nonlinear Soft Matter Phys. 2012, 85, 016102. [Google Scholar] [CrossRef] [PubMed]
- Oliveira, J.G.; Barabási, A.L. Darwin and Einstein correspondence patterns. Nature 2005, 437, 1251. [Google Scholar] [CrossRef]
- Gonçalves, B.; Ramasco, J.J. Human dynamics revealed through Web analytics. Phys. Rev. E-Nonlinear Soft Matter Phys. 2008, 78, 026123. [Google Scholar] [CrossRef]
- Candia, J.; González, M.C.; Wang, P.; Schoenharl, T.; Madey, G.; Barabási, A.-L. Uncovering individual and collective human dynamics from mobile phone records. J. Phys. A Math. Theor. 2008, 41, 224015. [Google Scholar] [CrossRef]
- Radicchi, F. Human activity in the web. Phys. Rev. E-Nonlinear Soft Matter Phys. 2009, 80, 026118. [Google Scholar] [CrossRef]
- Chaintreau, A.; Hui, P.; Crowcroft, J.; Diot, C.; Gass, R.; Scott, J. Impact of human mobility on opportunistic forwarding algorithms. IEEE Trans. Mob. Comput. 2006, 6, 620. [Google Scholar]
- Freedman, H.L.; Ruan, S.; Tang, M. Uniform persistence and flows near a closed positively invariant set. J. Dyn. Differ. Equ. 1994, 6, 583–600. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, W.; Lu, Z.; Wang, C.; Han, Y.; Yu, Y. Dynamic Analysis of a Fractional-Order Model for Vector-Borne Diseases on Bipartite Networks. Fractal Fract. 2025, 9, 742. https://doi.org/10.3390/fractalfract9110742
Xu W, Lu Z, Wang C, Han Y, Yu Y. Dynamic Analysis of a Fractional-Order Model for Vector-Borne Diseases on Bipartite Networks. Fractal and Fractional. 2025; 9(11):742. https://doi.org/10.3390/fractalfract9110742
Chicago/Turabian StyleXu, Weiyi, Zhenzhen Lu, Chengyi Wang, Yuxuan Han, and Yongguang Yu. 2025. "Dynamic Analysis of a Fractional-Order Model for Vector-Borne Diseases on Bipartite Networks" Fractal and Fractional 9, no. 11: 742. https://doi.org/10.3390/fractalfract9110742
APA StyleXu, W., Lu, Z., Wang, C., Han, Y., & Yu, Y. (2025). Dynamic Analysis of a Fractional-Order Model for Vector-Borne Diseases on Bipartite Networks. Fractal and Fractional, 9(11), 742. https://doi.org/10.3390/fractalfract9110742






