Abstract
We study stochastic variants of the Kairat-II and Kairat-X equations in (3 + 1) dimensions, two canonical models in soliton theory. Random fluctuations are incorporated through a Wiener process, yielding a multiplicative stochastic embedding of the wave fields. By combining the enhanced direct algebraic technique with the new projective Riccati equation approach, we obtain closed-form stochastic soliton solutions and analyze how noise modulates their amplitude and localization. The solutions are illustrated with consistent 3D surface plots (mean field vs. sample paths) and 2D time traces to highlight wave geometry and variability. In addition, we employ the energy balance approach to separate kinetic and potential contributions and to verify an energy balance relation for the derived solutions, thereby clarifying their physical plausibility and stability under noise. The results provide exact, easily verifiable benchmarks for stochastic nonlinear wave models and a practical template for incorporating randomness into nonlinear dispersive systems.
1. Introduction
Nonlinear partial differential equations (NLPDEs) play a foundational role in describing a wide range of scientific and engineering processes, including fluid flow, nonlinear optics, quantum field theory, plasma dynamics, heat transfer, and population evolution [1,2,3]. Solitons, as localized nonlinear wave structures that retain their shape during propagation, are particularly important in such systems due to their stability, energy-preserving nature, and ability to model coherent physical phenomena in optical fibers, shallow water waves, and electromagnetic pulse transmission.
However, most real physical systems are not purely deterministic; they are constantly influenced by environmental fluctuations such as thermal noise in optical communication channels, turbulent effects in fluids, and uncertain forcing in plasma or biological systems. Stochastic differential equations (SDEs) [4,5,6] provide a powerful framework for capturing these intrinsic uncertainties by incorporating random perturbations, often modeled using a Wiener process (Brownian motion). Such stochastic extensions enable a more realistic assessment of soliton dynamics under noise, revealing statistical behaviors that deterministic models cannot represent. In this context, the Kairat-II and Kairat-X equations are significant NLPDEs that support rich soliton structures and describe various nonlinear wave propagation mechanisms. Studying their stochastic generalizations helps us understand how randomness alters soliton amplitude, stability, and interaction patterns—an essential requirement for practical implementations in noisy physical environments.
Analytical investigation of stochastic NLPDEs remains challenging, especially when attempting to derive exact closed-form solutions. To address this, we employ two effective integration schemes: the enhanced direct algebraic technique (EDAT) and the new projective Riccati equation approach (NPREA). These methods allow us to extract exact stochastic soliton solutions while reducing computational complexity and avoiding linearization or perturbative assumptions. The resulting solutions serve as verifiable benchmarks for stochastic nonlinear systems. Furthermore, we incorporate the energy balance approach (EBA) to analyze the physical consistency of the obtained solutions by separating their kinetic and potential contributions. This confirms whether the stochastic solitons retain an acceptable energy structure under noise and aids in evaluating their stability properties. The governing model considered in this study is presented below [7,8]:
where is a differentiable function with respect to the temporal variable t, the spatial variables x, y, and z, and the nonzero arbitrary parameters d, e, f, , , and . The Kairat-II equation has an important application in modeling the phenomena of the propagation of waves in nonlinear media. Its special structure faithfully embodies the nature of nonlinear wave dynamics, rendering it an important component in the analysis of optical fibers, fluid dynamics, and plasma physics. The ability of the Kairat-II equation to represent wave interactions and stability in them emphasizes its significance in theoretical and applied physics. Conversely, the Kairat-X equation broadens the scope of nonlinear dynamics with the inclusion of higher-order terms and complicated interactions. It is used in such areas as quantum mechanics and nonlinear optics, where it assists in understanding quantum particles’ and light waves’ behavior in nonlinear media. The complexity in the Kairat-X equation facilitates the investigation of such phenomena as the interactions between solitons, energy transfer, and stability in very nonlinear regimes. For a detailed literature review, see Table 1.

Table 1.
Comparison of previous studies and current study.
To the best of our knowledge, this is the first work that constructs analytical stochastic soliton solutions to the (3 + 1)-dimensional Kairat-II and Kairat-X models, revealing how random perturbations influence their propagation, structure, and energy dynamics.
The structure of this paper is as follows: Section 2 provides the mathematical formulation and stochastic embedding of the Kairat-II and Kairat-X models. Section 3, Section 4 and Section 5 demonstrate the application of EDAT and NPREA to derive closed-form stochastic soliton solutions and visualize their behaviors through surface plots and time traces. Section 6 presents the EBA-based energy analysis. Section 7 discusses the significance and physical interpretation of the results. Finally, Section 8 concludes this work with future research directions.
2. Mathematical Analysis
Here we perform the traveling-wave reduction separately for the two SPDEs and justify the separation between the deterministic wave profile and the stochastic modulation. Using the similarity variable and chain-rule identities, we show step by step how each SPDE transforms into the same class of reduced ODEs, clarifying all intermediate steps and citing standard results from SPDE theory that support this formulation.
- (i)
- For the Wiener process, denoted by has the following properties [13,14]:
- *
- , since it starts at zero.
- *
- There is no statistical relationship between the increments.
Foris a continuous function.- *
- The distribution of increments is characterized by a Gaussian distribution with a mean of 0 and a variance of
- (ii)
- In mathematics, white noise, which is the time derivative of the Wiener process, is used to represent events with pronounced and obvious oscillations in an abstract manner.
Let be a standard Wiener process and the associated white noise (in the distributional sense). We adopt the Ito interpretation throughout.
where and are the deterministic operators given by the left-hand sides of (1) and (2), respectively, and is the (real) noise intensity parameter.
Now we will use the following transformation in Equations (4) and (5). This transformation eliminates the multiplicative noise and reduces the stochastic PDE to a deterministic ODE for .
The factor is the Itô solution of ; hence substitution (6) converts into a deterministic equation for .
By defining == , one can derive the following form of Equation (7):
3. EDAT
This section develops the exact solution construction based on the enhanced direct algebraic technique and the new projective Riccati equation approach. We present the auxiliary equations, balancing relations, and solvability conditions and then enumerate the resulting stochastic soliton families together with their admissible parameter/sign constraints; these formulas underpin the figures (mean surfaces, sample paths, and time traces) reported in the results.
Step 1: Let us consider that the solution to Equation (8) can be written in the form [15]
where satisfies
where for represent constant values, and the condition applies here.
Case 1:
If we apply the condition , then a bell-shaped soliton is formed with and a singular soliton with .
Case 2:
If we assume that and kink-shaped and singular solitons arise with and :
Case 3:
Assuming , Jacobi elliptic doubly periodic solutions are obtained for many other options of , as mentioned below:
Case 4:
If we set , Weierstrass elliptic doubly periodic solutions are found, as given below:
Case 5:
Now for , straddled soliton solutions arise with , as mentioned below:
The polynomial is produced by this substitution. The process entails combining terms with comparable powers and setting the resultant expression to zero when working with polynomials. This method produces an excessively complex system of algebraic equations that can be solved with Mathematica 14.0 to identify the unknown parameters. Consequently, the exact solutions are obtained for the nonlinear evolution equation.
NPREA
Step 1:
Here let us suppose that the solution has the following form [8]:
where and satisfy
with
In the above equation r is a nonzero constant value and N is a positive integer that is obtained by the balancing principle. and are constant values.
Step 2:
The solutions are given below.
Case 1:
.
or
Case 2:
.
Case 3:
.
Case 4:
.
or
Case 5:
.
4. Application of EDAT
The enhanced direct algebraic technique is an efficient symbolic approach for constructing exact traveling-wave solutions of nonlinear evolution equations. The method assumes that the reduced traveling-wave profile can be expressed as a finite polynomial in an auxiliary function that satisfies a Riccati-type differential equation. The balance between the highest-order nonlinear and derivative terms in the governing ODE determines the degree of the polynomial expansion. Substitution of this ansatz into the reduced ODE followed by coefficient matching yields a nonlinear algebraic system, the solutions of which provide explicit analytical forms such as solitary and periodic wave structures. Thus, the enhanced direct algebraic technique offers a systematic and closed-form framework for deriving physically relevant soliton solutions to stochastic reductions of nonlinear PDE models. Balancing and in Equation (8) implies , and then the solution becomes
Here , and are real constants. To avoid a degenerate ansatz, we impose the non-vanishing conditions and ; in other words, the coefficients of the positive powers of and the coefficients of the negative powers of cannot vanish simultaneously. If all of were zero at the same time, Equation (35) would reduce to the trivial constant profile and the expansion would lose its purpose. Substituting Equation (35) along with Equation (10) into Equation (8), we get the system of algebraic equations given below:
After substituting the enhanced direct algebraic technique ansatz into the reduced ODE (8), we collect coefficients of the same powers of the auxiliary function. This procedure results in a nonlinear algebraic system for the unknown parameters and others appearing in the polynomial structure. Typically, such systems are overdetermined, and therefore we introduce particular constraints, leading to several consistent cases. Each “case” corresponds to a specific reduction that
- Simplifies the system of equations by eliminating unbalanced polynomial terms;
- Ensures the realness and boundedness of the resulting solutions;
- Selects the type of nonlinear wave to be obtained (e.g., bright, dark, kink, or bell-type).
Once the reduced consistent system is obtained, it is symbolically solved using Mathematica. Only the parameter sets that yield non-singular, physically meaningful solutions are considered. These admissible parameter combinations generate the stochastic soliton solutions demonstrated in the subsequent figures.
Case 1:
If we set ,
.
then we get the corresponding solutions of the system:
where , and .
Case 2:
If we set , ,
.
the system provides us with the following solution:
where , and .
Case 3:
If we set ,
it will give us the following solution:
where and .
Case 4:
If we set ,
the system provides us with the corresponding solution:
where , , and and .
Case 5:
If we set ,
the corresponding solution of the system is given as follows:
where and .
5. Application of NPREA
The new projective Riccati equation approach generalizes classical Riccati-based solution methods to construct a wider class of exact solutions for nonlinear differential equations. The core idea is to expand the wave profile in a projective form involving hyperbolic, trigonometric, and rational functions generated by a projective Riccati equation. This enables the capture of multiple physical wave types—including kink and bell-shaped solitons, dark–bright interactions, and periodic structures—within the same analytical framework. By substituting the projective ansatz into the reduced ODE and equating powers of the auxiliary functions, one obtains solvable algebraic conditions for the solution parameters. In this work, the new projective Riccati equation approach allows us to reveal additional families of exact solutions for the stochastic Kairat models beyond those captured by the enhanced direct algebraic technique. By balancing the equation where , the solution becomes
Here , and are constants, subject to the non-degeneracy conditions and ; that is, at least one of or and at least one of or must be nonzero so that the expansion remains valid and the solution does not degenerate into a lower-order form. A set of the following nonlinear equations is formed after including the solution provided by meeting the constraints outlined in
By substituting the projective Riccati ansatz (42) into the reduced ODE (8), an extensive system of nonlinear algebraic equations in the unknown parameters and the physical constants is obtained, as listed in Equation (43). Since this full system is overdetermined, we introduce admissible constraints—referred to as cases—that simplify the algebraic structure by eliminating specific combinations of terms in the auxiliary functions. Each case corresponds to a physically valid reduction, ensuring real-valued, non-singular soliton behavior. Solving the simplified algebraic system under these constraints yields distinct parameter sets governing different wave structures, which directly determine the final exact solutions and the plots presented in the results section. We now outline these cases and their respective solution families.
Case 1: If we set , then we get following values:
Then we get the corresponding solutions of the system:
where and .
Case 2: If we set , then we get the corresponding solutions of the system:
where , , and .
Case 3:
If we set , then we get the corresponding solutions of the system:
where , , , and .
Case 4: If we set , ten we get the corresponding solutions of the system:
where and .
Case 5: If we set ,
then we get the corresponding solutions of the system:
where , , , and .
6. EBA for Stochastic Soliton Dynamics
In this section, we provide a rigorous nonlinear energy analysis for the stochastic soliton solutions obtained in Section 5 and Section 6. Unlike linear waves, where the frequency is independent of amplitude, nonlinear wave systems exhibit amplitude-dependent frequency characteristics. This is a well-understood physical feature that arises from nonlinear restoring effects, as seen in large-amplitude pendulum motion and nonlinear elastic wave propagation [16]. The Kairat-II and Kairat-X equations considered here contain nonlinear terms such as , indicating that the wave frequency must naturally depend on the soliton amplitude.
We start from the reduced ODE derived after applying the traveling-wave transformation,
To establish an energy conservation structure, we employ the variational formulation in terms of a Hamiltonian density,
Here, the first term represents the nonlinear kinetic energy associated with the traveling wave, the second term denotes nonlinear self-interaction energy, and the third term accounts for elastic-like dispersion. We assume a periodic nonlinear wave solution of the form
where represents the soliton amplitude and is a nonlinear frequency-like parameter. By substituting Equation (51) into Equation (50) and enforcing an energy balance between nonlinear kinetic, potential, and dispersive contributions, the following nonlinear frequency relation is obtained:
Equation (52) shows that is inversely proportional to the soliton amplitude . Therefore, an increase in soliton height yields a reduction in oscillatory frequency, reflecting a classical nonlinear amplitude–frequency modulation phenomenon. Using Equation (52), the physically consistent nonlinear stochastic soliton solution for energy balance becomes
To visualize the nonlinear energy-balanced soliton behavior, we provide both 2D and 3D plots for selected parameter values in Figure 1. These profiles confirm that the soliton structure remains stable while exhibiting nonlinear oscillatory behavior due to the stochastic interaction mechanisms embedded in the Kairat-II and Kairat-X equations.
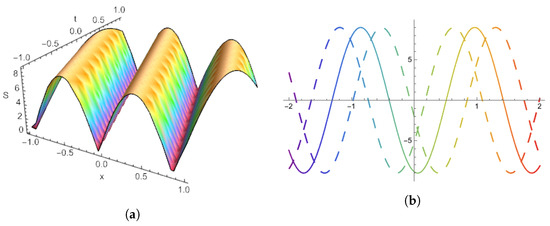
Figure 1.
Energy balance (a) 3D plot (b) 2D plot.
Overall, Section 6 confirms that the stochastic soliton solutions maintain physical consistency through nonlinear energy balance, providing an additional validation of the analytical solutions obtained using the enhanced direct algebraic technique and the new projective Riccati equation approach.
7. Result and Discussion
As shown in Figure 2 (Equation (37)), the solution exhibits a single steep ridge located near the level set (close to ), while rapidly decaying away from this region, leaving a nearly flat background. In the stochastic surface (Figure 2a), the ridge height shows small oscillatory fluctuations due to the multiplicative Wiener effect, whereas the deterministic mean surface (Figure 2b) remains smooth and slightly higher, indicating mild noise-induced attenuation. The time traces (Figure 2c) feature a sharp peak corresponding to the passage of the ridge at a fixed x, and the peak magnitude decreases quickly for spatial points farther from the ridge, confirming strong spatial localization with limited stochastic variability. As shown in the geometry of Figure 3 (Equation (38)) (a), the sharply localized traveling ridge dominates the surface; stochastic modulation introduces small height jitter on the crest while the field remains nearly flat away from it. (b) The deterministic mean surface is smooth and slightly higher, showing the same ridge position and width without roughness. (c) Time-trace curves at fixed x display narrow pulses as the front passes; amplitudes decrease rapidly for points farther from the ridge center, confirming strong spatial localization. As shown in Figure 4 (Equation (39)) (a), the surface shows a steep, thin front with mild stochastic roughness on the peak; the surrounding region decays quickly to near-zero. (b) The mean surface removes the speckling and reveals a coherent crest that persists and translates with minimal dispersion. (c) Time traces exhibit sharply peaked transients whose timing aligns across x, while peak heights diminish off-ridge, indicating noise-perturbed yet robust confinement. As shown in Figure 5 (Equation (41)) (a), a tightly focused crest propagates in time; multiplicative noise induces modest fluctuations in height but preserves the global shape and narrow width. (b) The mean surface is smooth and slightly taller, evidencing noise-induced attenuation/roughening rather than structural change. (c) Time traces show brief, localized pulses when the front crosses each location, with rapidly shrinking amplitudes as the sampling point moves away from the ridge region. As shown in Figure 6 (Equation (44)) (a), a sharply localized traveling ridge dominates the surface and shows mild height jitter due to multiplicative noise, while the field is nearly flat away from the crest. (b) The deterministic mean surface is smooth and slightly higher, with no speckling—noise mainly roughens/attenuates but does not change the ridge’s shape. (c) Time-trace curves at fixed x exhibit narrow peaks when the front passes; peak magnitudes drop quickly at locations farther from the ridge center, confirming strong spatial localization.
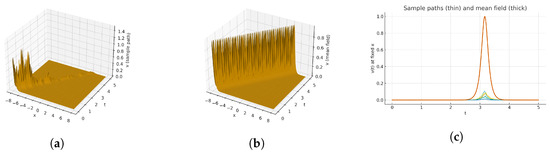
Figure 2.
(a) Three-dimensional surface-sample path (stochastic). (b) Three-dimensional surface mean field (deterministic expectation) for parameters , , , , , , and . Wiener path simulated with and seed 12,345. (c) Two-dimensional time traces at fixed x—several realizations + mean for parameters , , , , , , and ; independent Wiener paths simulated with , seeds 12,346–12,350.
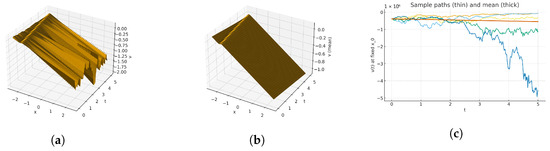
Figure 3.
(a) Three-dimensional surface-sample path, (b) yhree-dimensional surface mean field, and (c) two-dimensional time traces at fixed x for parameters , , ; simulated with and seed 2025.
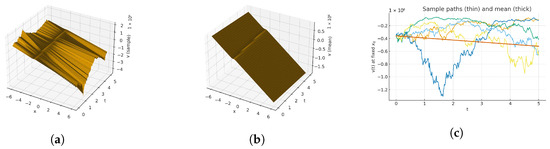
Figure 4.
(a) Three-dimensional surface-sample path, (b) three-dimensional surface mean field, and (c) two-dimensional time traces at fixed x for parameters ; simulated with , seed 303.

Figure 5.
(a) Three-dimensional surface-sample path, (b) three-dimensional surface mean field, and (c) two-dimensional time traces at fixed x for parameters .
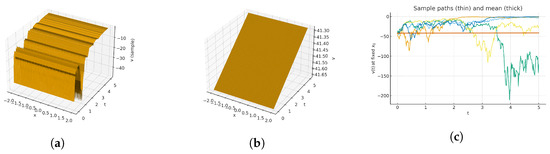
Figure 6.
(a) Three-dimensional surface-sample path, (b) three-dimensional surface mean field, and (c) two-dimensional time traces at fixed x for parameters ; simulated with and seed 515.
As shown in Figure 7 (Equation (45)) (a), the surface displays a single dominant front along the propagation direction, with rapid spatial decay on both sides; stochastic modulation produces small-amplitude jitter along the crest. (b) The mean plot removes this roughness and reveals a clean, coherent ridge of comparable position and width. (c) Time traces show a pronounced, localized pulse in t at each fixed x, with amplitude decreasing markedly as the sampling point moves off the ridge. As shown in Figure 8 (Equation (46)) (a), a localized ridge persists under noise, retaining a thin, steep profile while its height fluctuates slightly. (b) The mean surface is smooth and stable, emphasizing that the wave’s macroscopic geometry is a coherent traveling front over a flat background. (c) A second stochastic realization reproduces the same ridge geometry with different small-scale fluctuations, confirming robustness of the structure to randomness. As shown in Figure 9 (Equation (47)) (a), the stochastic surface features a tightly focused traveling crest with small roughness on the peak and rapid decay to near-zero away from the front. (b) The mean surface removes the roughness and shows a slightly higher, smooth ridge of the same position and width. (c) A second stochastic realization presents the same global geometry with distinct fine-scale variations; complementary time-trace plots (when shown) display narrow pulses whose heights vary modestly between realizations but remain strongly localized in time. As shown in Figure 10 (Equation (48)) (a), the stochastic surface exhibits a traveling crest with small roughness on the peak due to multiplicative noise; the field decays rapidly away from the crest, leaving a broad flat background. (b) The deterministic mean removes this roughness and shows a smooth ridge of essentially the same position and width, confirming that noise perturbs amplitude but not structure. (c) Time traces at selected x display brief, localized pulses when the front passes; pulse heights drop quickly as the sampling point moves away from the ridge, indicating strong spatial confinement and robust temporal localization. As shown in Figure 1 (energy balance) (Equation (53)) (a), the 3D surface is a smooth, bounded, periodic pattern of parallel crests and troughs produced by the cosine profile , where the wave number is the coefficient multiplying in Equation (51). The ridges are evenly spaced and of nearly constant height , forming a standing-wave sheet without stochastic roughness; maxima/minima correspond to alternating dominance of potential and kinetic contributions in the energy balance (), while intermediate slopes indicate energy exchange along the phase lines. (b) The 2D plot shows representative cross-sections of the same field, symmetric cosine lobes with uniform wavelength , nodal zeros at regular intervals, and equal peak/trough magnitudes, highlighting the conservative, oscillatory nature of the balanced energy state.
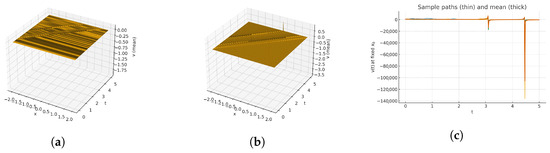
Figure 7.
(a) Three-dimensional surface-sample path, (b) three-dimensional surface mean field, and (c) two-dimensional time traces at fixed x for parameters ; simulated with and seed 606.
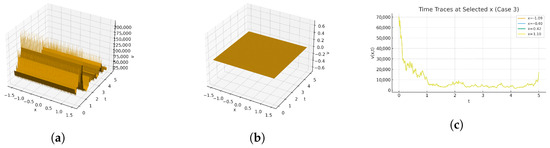
Figure 8.
(a) Three-dimensional surface-sample path, (b) three-dimensional surface mean field, and (c) two-dimensional time traces at fixed x for parameters ; simulated with and seed 606.
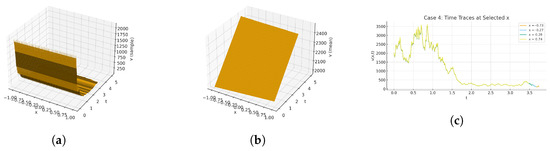
Figure 9.
(a) Three-dimensional surface-sample path, (b) three-dimensional surface mean field, and (c) two-dimensional time traces at fixed x for parameters .
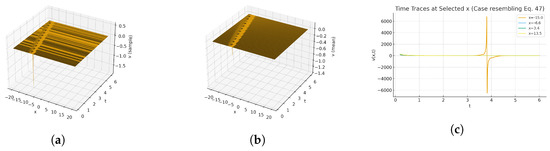
Figure 10.
(a) Three-dimensional surface-sample path, (b) three-dimensional surface mean field, and (c) two-dimensional time traces at fixed x for parameters , . The noise intensity is set to for stable stochastic visualization. The coefficient is computed as .
8. Conclusions
We investigated the -dimensional Kairat-II and Kairat-X models together with their stochastic extensions driven by a Wiener process, thereby capturing random environmental fluctuations in otherwise coherent nonlinear wave dynamics. Using the modified auxiliary equation approach (implemented via the enhanced direct algebraic technique and the new projective Riccati equation approach ansätze), we derived closed-form stochastic soliton solutions in which the stochastic embedding appears as a multiplicative Itô factor . Across all parameter sets considered, the visualizations (3D surfaces for deterministic mean vs. sample paths and 2D time traces at fixed x) revealed a consistent geometry: a single, steep, traveling ridge aligned with the similarity level set, rapid spatial decay to a flat background, and noise-induced modulation that slightly roughens/attenuates the crest height without changing the macroscopic front. Parameter sweeps (including different choices of the driving path and case-specific coefficients) showed that the deterministic mean remains a smooth, coherent front, while individual realizations exhibit modest peak jitter; off-ridge traces decay quickly, confirming strong spatial localization.
To interpret the dynamics energetically, we formulated an energy balance approach for the reduced ODE, decomposing the Hamiltonian into kinetic and potential parts and verifying conservation in the deterministic limit. The resulting energy surfaces and cross-sections, consistent with analytic cosine profiles for the phase function, illustrate periodic exchange between stored and fluxed energy and clarify when and how soliton structures transport energy across the domain. Overall, the exact formulas admit direct substitution checks, the mean–sample comparisons make the role of noise transparent, and the energy balance approach links waveform geometry to energy flow, providing verifiable benchmarks for stochastic NLPDEs in higher dimensions. The framework is readily applicable for validating numerical/computational schemes for SPDEs and for incorporating stochasticity in other nonlinear dispersive media. Future work includes data-calibrated noise intensities, alternative stochastic drivers (e.g., Lévy processes), and stability/interaction studies of multi-soliton states under randomness.
Author Contributions
Conceptualization, S.T.R.R. and A.R.S.; methodology, S.T.R.R.; software, I.A.; validation, A.R.S. and L.J.; formal analysis, H.A.; investigation, H.A.; resources, I.A.; data curation, S.T.R.R.; writing—original draft preparation, I.A.; writing—review and editing, H.A.; visualization, E.S.; supervision, A.R.S.; project administration, L.J.; funding acquisition, L.J. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported and funded by the Deanship of Scientific Research at Imam Mohammad Ibn Saud Islamic University (IMSIU) (grant number IMSIU-DDRSP2502).
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Garabedian, P.R. Partial Differential Equations; American Mathematical Society: Providence, RI, USA, 2023; Volume 325. [Google Scholar]
- Rauch, J. Partial Differential Equations; Springer: New York, NY, USA, 2012; Volume 128. [Google Scholar] [CrossRef]
- Yasin, S.; Khan, A.; Ahmad, S.; Osman, M.S. New Exact Solutions of (3 + 1)-Dimensional Modified KdV-Zakharov-Kunznetsov Equation by Sardar-Subequation Method. Opt. Quantum Electron. 2024, 56, 90. [Google Scholar] [CrossRef]
- Ganie, A.H.; AlBaidani, M.M.; Wazwaz, A.M.; Ma, W.X.; Shamima, U.; Ullah, M.S. Soliton Dynamics and Chaotic Analysis of the Biswas-Arshed Model. Opt. Quantum Electron. 2024, 56, 1379. [Google Scholar] [CrossRef]
- Ullah, M.S.; Ali, M.Z.; Roshid, H.O. Bifurcation, Chaos, and Stability Analysis to the Second Fractional WBBM Model. PLoS ONE 2024, 19, e0307565. [Google Scholar] [CrossRef] [PubMed]
- Jahan, M.I.; Ullah, M.S.; Rahman, Z.; Akter, R. Novel Dynamics of the Fokas-Lenells Model in Birefringent Fibers Applying Different Integration Algorithms. Int. J. Math. Comput. Eng. 2025, 3, 1–12. [Google Scholar] [CrossRef]
- Wazwaz, A.M. Extended (3 + 1)-Dimensional Kairat-II and Kairat-X Equation: Painlevé Integrability, Multiple Soliton Solutions, Lump Solution, and Breather Wave Solution. Int. J. Numer. Methods Heat Fluid Flow 2024, 34, 2177–2194. [Google Scholar] [CrossRef]
- Mehanna, M.S.; Wazwaz, A.M. Tri-Analytical Approach to Kairat-II and Kairat-X Equations. Rom. Rep. Phys. 2024, 77, 107. [Google Scholar] [CrossRef]
- Mateen, A.; Tipu, G.H.; Ciurdariu, L.; Yao, F. Analytical Soliton Solutions of the Kairat-II Equation Using the Kumar-Malik and Extended Hyperbolic Function Methods. AIMS Math. 2025, 10, 8721–8752. [Google Scholar] [CrossRef]
- Alhakim, L.; Gasmi, B.; Moussa, A.; Mati, Y. Bifurcation, Chaotic Behaviour and Soliton Solutions of the Kairat-II Equation via Two Analytical Methods. Partial Differ. Equ. Appl. Math. 2025, 13, 101135. [Google Scholar] [CrossRef]
- Usman, Y.; Jan, M.; Naila, N.; Aziz, K.; Thabet, A. On the Comparative Analysis for the Fractional Solitary Wave Profiles to the Recently Developed Nonlinear System. Ain Shams Eng. J. 2024, 15, 102971. [Google Scholar] [CrossRef]
- Awadalla, M.; Zafar, A.; Taishiyeva, A.; Raheel, M.; Myrzakulov, R.; Bekir, A. Analytical Solutions to the M-Fractional Kairat-II and Kairat-X Equations. Front. Phys. 2023, 11, 1335423. [Google Scholar]
- Mohammed, W.W.; Cesarano, C.; Al-Askar, F.M.; El-Morshedy, M. Solitary Wave Solutions for the Stochastic Fractional-Space KdV in the Sense of the M-Truncated Derivative. Mathematics 2022, 10, 4792. [Google Scholar] [CrossRef]
- Al-Askar, F.M.; Cesarano, C.; Mohammed, W.W. Analytical Solutions of Stochastic–Fractional Drinfel’d-Sokolov-Wilson Equations via (G’/G)-Expansion Method. Symmetry 2022, 14, 2105. [Google Scholar] [CrossRef]
- Javad, V.; Ali, Z.; Hadi, R.; Reza, A. New Extended Direct Algebraic Method for the Resonant Nonlinear Schrödinger Equation with Kerr Law Nonlinearity. Optik 2021, 227, 165936. [Google Scholar] [CrossRef]
- Wang, K.J.; Liu, J.H. On Abundant Wave Structures of the Unsteady Korteweg-de Vries Equation Arising in Shallow Water. J. Ocean Eng. Sci. 2023, 8, 595–601. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).