Numerical Treatment of the Time-Fractional Kuramoto–Sivashinsky Equation Using a Combined Chebyshev-Collocation Approach

Abstract

In this paper, we present a collocation algorithm for numerically treating the time-fractional Kuramoto–Sivashinsky equation (TFKSE). Certain orthogonal polynomials, which are expressed as combinations of Chebyshev polynomials, and their shifted polynomials are introduced. Some new theoretical formulas regarding these polynomials have been developed, including their operational matrices of both integer and fractional derivatives. The derived formulas will be the foundation for designing the proposed numerical algorithm, which relies on converting the governing problem with its underlying conditions into a nonlinear algebraic system, which can be solved using Newton’s iteration technique. A rigorous error analysis for the proposed combined Chebyshev expansion is presented. Some numerical examples are given to ensure the applicability and efficiency of the presented algorithm. These results demonstrate that the proposed algorithm attains superior accuracy with fewer expansion terms.

1. Introduction

Memory effects and non-local interactions are key features of fractional differential equations (FDEs) that distinguish them from classical differential equations (DEs). These features make FDEs ideal for modelling real-world processes. If your system displays complex dynamical behaviour, anomalous diffusion, or genetic effects, FDEs will be a better fit. Therefore, their significance is growing in numerous domains, including physics, engineering, biology, and finance [1,2]. The fields of viscoelasticity, heat conduction, electromagnetism, and signal processing—all of which can significantly benefit from contemporary computer technology—are where FDEs are utilized in the physical and engineering sciences. For some applications, one can refer to [3,4].

Numerous numerical techniques were followed to treat different types of FDEs. Some of them can be listed as follows:

• The series–based methods, such as the Laplace–residual power series method [5], and the fractional power series method [6].
• The mesh-based methods, such as the predictor–corrector methods [7,8,9], the three–step Adams–Bashforth scheme [10], the spatial sixth-order finite-difference scheme [11], and the spectral element approach [12].
• The wavelets and semi-analytic methods, such as Hahn–wavelets collocation method [13], the Fibonacci-wavelets operational-matrix technique [14], and the spectral method in [15].
• The neural method, such as the Chebyshev neural-network scheme [16].
• A hybrid numerical approach that mixes more than one method, such as the method in [17] that combines the Gauss quadrature rule and finite difference scheme.

Chebyshev polynomials (CPs) play a crucial role in several branches of applied mathematics. They are important in numerical analysis and approximation theory. The first four types of CPs are most often used because of the intuitive trigonometric formulas associated with them. Several publications, both recent and old, use these polynomials in several applications. The authors of [18] created some differentiation matrices of CPs for handling certain nonlinear DEs. In [19], certain modified third-kind CPs were used to treat the multidimensional hyperbolic telegraph equations. In other publications, various modifications and generalizations of CPs have been introduced and used to treat several DEs. For instance, the sixth kind of CPs was used in [20] to treat some fractional partial FDEs. The eighth kind of CPs was utilized in [21] to treat the nonlinear time-fractional generalized Kawahara equation. A set of unified CPs was constructed and employed in [22] to treat the time-fractional heat DEs. Two generalized kinds of CPs were introduced, respectively, in [23,24] to solve some FDEs.

Spectral methods are popular methods to treat DEs. Such approaches are excellent for solving FDEs and high-order ordinary DEs. Their primary benefit over more conventional numerical approaches is the extreme precision they may attain for smooth problems via exponential or high-order convergence. These techniques provide accurate approximations with few degrees of freedom by expressing the numerical solution using special functions or special polynomials. Spectral methods have found practical applications in many domains, including the modelling of biological systems, fluid dynamics, and quantum physics. One can refer to [25,26,27] for a few examples of spectral methods applications. Collocation, tau, and Galerkin are the three primary spectral approaches. Every method has its characteristics and advantages. The collocation method can be applied to all types of DEs due to its simplicity in application, see for example [28,29,30,31]. The Galerkin method can be applied to linear equations and some non-linear ones, see for instance [32,33,34]. For instance, as demonstrated in [35,36,37], the flexibility of the basis function choices makes the tau technique more adaptable compared to the Galerkin method.

An essential tool for modelling complex spatiotemporal dynamics like turbulence and chaos is the fourth-order nonlinear partial differential equation known as the Kuramoto-Sivashinsky equation (KSE). Its development by Yoshiki Kuramoto and Gregory Sivashinsky in the late 1970s was the beginning of its evolution into an indispensable tool in numerous technological and scientific domains. The KSE describes various physical and chemical processes, including chemical reaction-diffusion, plasma instability, problems with viscous flow, growth of flame fronts, and magnetized plasmas [38,39]. Since the KSE and its variants are so important, numerous authors have investigated numerical approaches for handling them using various algorithms. For example, a fractional power series method was presented in [6] to treat the nonlinear KSE. A finite difference scheme was followed in [40] to treat the TFKSE. A kernel smoothing technique was introduced in [41] for the numerical approximation of generalized TFKSEs. Chebyshev cardinal functions were employed in [42] to solve the variable-order fractional version of the two-dimensional equation. Another spline approach was proposed in [43] to treat the fourth-order time-dependent PDEs, including the TFKSE. Certain shifted Morgan–Voyce polynomials were utilized in [44] to treat the TFKSE. Several other methods were employed in [45,46,47,48] for the treatment of these equations.

The employment of the operational matrices of derivatives (OMDs) is pivotal in obtaining numerical solutions of several DEs. The philosophy of the use of these matrices relies on converting the integer and fractional operators into algebraic forms, which enable the reduction of the equation under investigation into a solvable system of equations. This approach decreases the computational cost, making it a powerful technique for treating complex models in applied mathematics, physics, and engineering. The use of OMDs allows various families of orthogonal and non-orthogonal polynomials to be employed in constructing numerical algorithms that are both reliable and versatile. Many publications have been devoted to introducing and employing different OMDs for various DEs. For example, an operational matrix in the Caputo sense was introduced in [49], with applications to fractional models. A matrix approach was followed in [50] for the treatment of a fractional-order computer virus model. The shifted Lucas polynomial collocation scheme, relying on its operational matrix, was presented in [51] for solving the time-fractional FitzHugh–Nagumo equation. An efficient method based on the Chelyshkov operational matrix for the time-space fractional reaction–diffusion equations was developed in [52]. A collocation method employing the fractional-order Lagrange operational matrix was described in [53] for the space-time fractional PDEs. A new operational matrix approach was designed in [54] to solve nonlinear FDEs. Vieta–Fibonacci operational matrices were introduced in [55] to construct spectral solutions for variable-order fractional integro–DEs.

The primary objective of the current paper is to propose a numerical approach that uses the spectral collocation approach to address the TFKSE. To accomplish this, a family of basis functions known as shifted combined Chebyshev polynomials (SCCPs) is presented. The proposed approach can be better designed with the help of specific new formulas that are related to these polynomials.

This paper’s originality is illustrated in the following aspects:

• Introducing some new fundamental formulas regarding the combined Chebyshev polynomials (CCPs) and their shifted polynomials.
• Establishing new integer and fractional OMDs of these polynomials, which are the fundamental basis for designing the proposed numerical algorithm.
• Presenting a rigorous convergence and error analysis of the proposed combined Chebyshev expansion.

The following is the outline for the remainder of the article. An outline of the two main kinds of CPs, along with some key definitions, is provided in the next section. Furthermore, an account of the CCPs and their shifted polynomials is given. Section 3 is dedicated to constructing new formulas for the SCCPs that will be pivotal in our study. Section 4 examines the collocation algorithm developed for handling the TFKSE. In Section 5, the upper bound on the error is provided. In Section 6, some numerical examples are displayed, supported by some comparisons with some other methods. In Section 7, a few last thoughts are reported.

2. Some Essential Definitions and Relations

This section presents some key concepts of fractional calculus. It also presents some features of CPs and their shifted polynomials. In addition, some properties of the CCPs and their shifted polynomials are given.

2.1. Caputo’s Fractional Derivative

Definition 1

([56]). In Caputo’s sense, the fractional-order derivative of $\psi \in C^k[0,s]$, where $k=\lceil \nu \rceil$ is defined as:

$${\displaystyle D_t^{\nu }\psi \left(s\right)=\frac{1}{\Gamma (k-\nu )}{\int }_0^s{(s-t)}^{k-\nu -1}{\psi }^{\left(k\right)}\left(t\right)dt,\nu >0,s>0,k-1<\nu \le k,k\in \mathbb{N}.}$$

(1)

For $D_t^{\nu }$ with $k-1<\nu \le k,k\in \mathbb{N}$, the relations listed below are valid:

$$\begin{array}{cc}\hfill D_t^{\nu }B& =0,B\mathrm{is}\mathrm{a}\mathrm{constant},\hfill \end{array}$$

(2)

$$\begin{array}{cc}\hfill D_t^{\nu }{s}^k& =\left\{\begin{array}{cc}0,\hfill & \mathrm{if}k\in {\mathbb{N}}_0\mathrm{and}k<\lceil \nu \rceil ,\hfill \\ {\displaystyle \frac{\left(k\right)!}{\Gamma (k-\nu +1)}}{s}^{k-\nu },\hfill & \mathrm{if}k\in {\mathbb{N}}_0\mathrm{and}k\ge \lceil \nu \rceil ,\hfill \end{array}\right.\hfill \end{array}$$

(3)

where $\mathbb{N}=\{1,2,\dots \}$ and ${\mathbb{N}}_0=\{0,1,2,\dots \}$, and $\lceil \nu \rceil$ represents the ceiling function.

Remark 1.

The notation $C^k[0,s]$ denotes the space of functions that are k-times continuously differentiable on the interval $[0,s]$.

2.2. An Overview of CPs

We give here some elementary properties of the first and second kinds of CPs and their shifted polynomials.

The first- and second-kinds of CPs: $T_k\left(x\right)$ and $U_k\left(x\right)$ are defined as [57])

$$\begin{array}{cccc}\hfill & T_k\left(x\right)=cos\left(k\varphi \right),\hfill & \hfill & {\displaystyle U_k\left(x\right)=\frac{sin\left((k+1)\varphi \right)}{sin\varphi },}\hfill \end{array}$$

(4)

where $\varphi ={cos}^{-1}\left(x\right)$.

$T_k\left(x\right),$ and $U_k\left(x\right)$ have the following series representations:

$$\begin{array}{cc}\hfill T_k\left(x\right)& =k\sum _{r=0}^{⌊{\displaystyle \frac{k}{2}}⌋}{\displaystyle \frac{{(-1)}^r{2}^{-1+k-2r}(k-r-1)!}{r!(k-2r)!}}{x}^{k-2r},\hfill \end{array}$$

(5)

$$\begin{array}{cc}\hfill U_k\left(x\right)& =\sum _{r=0}^{⌊{\displaystyle \frac{k}{2}}⌋}{\displaystyle \frac{{(-1)}^r{2}^{k-2r}(k-r)!}{(k-2r)!r!}}{x}^{k-2r}.\hfill \end{array}$$

(6)

The shifted CPs on $[0,1]$ denoted by $T_k^{\ast }\left(x\right)$, and $U_k^{\ast }\left(x\right)$ can be defined as

$$\begin{array}{c}\hfill T_k^{\ast }\left(x\right)=T_k\left(2x-1\right),U_k^{\ast }\left(x\right)=U_k\left(2x-1\right),\end{array}$$

(7)

and they may be expressed as

$$\begin{array}{cc}\hfill T_k^{\ast }\left(x\right)& =k\sum _{r=0}^k{\displaystyle \frac{{(-1)}^r{2}^{2(k-r)}(2k-r-1)!}{(2k-2r)!r!}}{x}^{k-r},\hfill \end{array}$$

(8)

$$\begin{array}{cc}\hfill U_k^{\ast }\left(x\right)& =\sum _{r=0}^k{\displaystyle \frac{{(-1)}^r{2}^{2(k-r)}(2k-r+1)!}{(2k-2r+1)!r!}}{x}^{k-r}.\hfill \end{array}$$

(9)

2.3. Combined Chebyshev Polynomials on $[-1,1]$

In [58], Chihara introduced the following orthogonal CCPs on $[-1,1]$ defined as

$$C_k^{\left(\xi \right)}\left(x\right)={\displaystyle \frac{1}{2^{k-1}}}\left(T_k\left(x\right)+\left(1-{\displaystyle \frac{1}{\xi }}\right)U_{k-2}\left(x\right)\right),k\ge 0.$$

(10)

Based on the connection formula [57]:

$$T_k\left(x\right)={\displaystyle \frac{1}{2}}\left(U_k\left(x\right)-U_{k-2}\left(x\right)\right),k\ge 0,$$

(11)

$C_k^{\left(\xi \right)}\left(x\right)$ can also be expressed in the following form:

$$C_k^{\left(\xi \right)}\left(x\right)={\displaystyle \frac{1}{2^k}}\left(U_k\left(x\right)+\left(1-{\displaystyle \frac{2}{\xi }}\right)U_{k-2}\left(x\right)\right),k\ge 0.$$

(12)

Remark 2.

The polynomials $C_k^{\left(\xi \right)}\left(x\right)$ are extensions of the first and second kinds of CPs, as is evident from the two equations in (10) and (12). To be more specific, we have

$$T_k\left(x\right)=2^{k-1}{C}_k^{\left(1\right)}\left(x\right),U_k\left(x\right)=2^k{C}_k^{\left(2\right)}\left(x\right).$$

(13)

One of the significant formulas of $C_j^{\left(\xi \right)}\left(x\right)$ is the following three-term recurrence relation [58]:

$$C_j^{\left(\xi \right)}\left(x\right)=x{C}_{j-1}^{\left(\xi \right)}\left(x\right)-{\displaystyle \frac{1}{4}}{C}_{j-2}^{\left(\xi \right)}\left(x\right),j\ge 2.$$

(14)

The set of polynomials ${\left\{C_k^{\left(\xi \right)}\right\}}_{k\ge 0}$ are orthogonal on $[-1,1]$ with respect to the weight function ${\displaystyle w^{\left(\xi \right)}\left(x\right)=\frac{\sqrt{1-x^2}}{1-\xi (2-\xi )x^2}}$ in the sense that [59]

$${\int }_{-1}^1{w}^{\left(\xi \right)}\left(x\right)C_m^{\left(\xi \right)}\left(x\right)C_j^{\left(\xi \right)}\left(x\right)dx=\left\{\begin{array}{cc}0,\hfill & m\ne j,\hfill \\ {\displaystyle \frac{4\pi }{{\xi }^3},}\hfill & m=j=0,\hfill \\ {\displaystyle \frac{\pi }{{\xi }^2{2}^{2m-1}},}\hfill & m=j>0.\hfill \end{array}\right.$$

(15)

2.4. Some Properties of the SCCPs

It is useful to introduce the SCCPs on $[0,1]$ defined as

$${\theta }_i^{\left(\xi \right)}\left(x\right)=C_i^{\left(\xi \right)}(2x-1).$$

(16)

These polynomials are orthogonal on $[0,1]$ in the sense that [59]:

$${\int }_0^1{\theta }_i^{\left(\xi \right)}\left(x\right){\theta }_j^{\left(\xi \right)}\left(x\right){\overline{w}}^{\left(\xi \right)}\left(x\right)dx=h_i^{\left(\xi \right)}{\delta }_{i,j},$$

(17)

where

$$\begin{array}{cc}\hfill {\overline{w}}^{\left(\xi \right)}\left(x\right)& {\displaystyle =\frac{\sqrt{x(1-x)}}{\xi (\xi -2){(1-2x)}^2+1},}\hfill \\ \hfill h_i^{\left(\xi \right)}& =\left\{\begin{array}{cc}{\displaystyle \frac{\pi }{{\xi }^3},}\hfill & i=0,\hfill \\ {\displaystyle \frac{\pi }{{\xi }^2{2}^{2i+1}},}\hfill & i\ge 1.\hfill \end{array}\right.\hfill \end{array}$$

From (12), by replacing x with $(2x-1)$, the SCCPs can be written as combinations of the shifted second kind of CPs as

$${\theta }_j^{\left(\xi \right)}\left(x\right)=2^{-j}\left({\displaystyle \frac{(\xi -2)}{\xi }}{U}_{j-2}^{\ast }\left(x\right)+U_j^{\ast }\left(x\right)\right).$$

(18)

Furthermore, based on the series representation of $U_j^{\ast }\left(x\right)$ in (9) along with the combination in (12), they may be represented explicitly as

$${\theta }_i^{\left(\xi \right)}\left(x\right)=\sum _{r=0}^j{\lambda }_{r,j}{x}^{j-r},$$

(19)

where

$${\lambda }_{r,j}={\displaystyle \frac{{(-1)}^{j+1}{2}^{-j}(2j-r-1)!\left(\genfrac{}{}{0pt}{}{j}{r}\right)\Gamma \left(-j+r-\frac{1}{2}\right)\left(\xi \left(2j^2-2jr+j+(r-1)r\right)-r^2+r\right)}{\sqrt{\pi }\xi j!}}.$$

(20)

The previous power formula can be rewritten in another form as

$${\theta }_i^{\left(\xi \right)}\left(x\right)=\sum _{r=0}^j{G}_{r,j}{x}^r,$$

(21)

where

$$G_{r,j}={\displaystyle \frac{{(-1)}^{1+j}{2}^{-j}\left(\genfrac{}{}{0pt}{}{j}{j-r}\right)\Gamma \left(-\frac{1}{2}-r\right)(j+r-1)!\left(j+2jr+j^2(-1+\xi )+r(1+r)(-1+\xi )\right)}{\sqrt{\pi }\xi j!}}.$$

(22)

3. Some New Formulas of the CCPs and SCCPs

This section derives some new formulas concerned with the CCPs and SCCPs, which will be pivotal in deriving the suggested numerical scheme. More precisely, the following formulas will be established:

• The connection formula between the second kind CPs and the CCPs, that is, we will determine explicitly the connection coefficients $A_{m,i}$ in the following connection formula:

  $$U_i\left(x\right)=\sum _{m=0}^{⌊\frac{i}{2}⌋}{A}_{m,i}{C}_{i-2m}^{\left(\xi \right)}\left(x\right).$$

  (23)
  Formula (23) will lead immediately to the following connection formula between the shifted second kind Chebyshev polynomials $U_i^{\ast }\left(x\right)$ and the SCCPs:

  $$U_i^{\ast }\left(x\right)=\sum _{m=0}^{⌊\frac{i}{2}⌋}{A}_{m,i}{\theta }_{i-2m}^{\left(\xi \right)}\left(x\right),$$

  (24)

  only by replacing x by $(2x-1)$ in the connection formula (23).
• The inversion formula for the series representation for the SCCPs in (19), that is, we will determine explicitly the inversion coefficients $Z_{r,m}$ in the following formula:

  $$x^m=\sum _{r=0}^m{Z}_{r,m}{\theta }_{m-r}^{\left(\xi \right)}\left(x\right),$$

  (25)

  for every nonnegative integer m.
• The high-order derivatives formula for the SCCPs as a combination of their original polynomials, that is, we will derive an expression for $D^q{\theta }_j^{\left(\xi \right)}\left(x\right)$ in the following form:

  $$D^q{\theta }_j^{\left(\xi \right)}\left(x\right)=\sum _{m=0}^{j-q}{V}_{j-m-q,r,j}^{\left(q\right)}{\theta }_m^{\left(\xi \right)}\left(x\right),j\ge q.$$

  (26)
• The establishment of the OMDs of the SCCPs, that is, we define the vector

  $${\mathit{\theta }}^{\left(\mathit{\xi }\right)}\left(x\right)={[{\theta }_0^{\left(\xi \right)}\left(x\right),{\theta }_1^{\left(\xi \right)}\left(x\right),\dots ,{\theta }_{\mathcal{N}}^{\left(\xi \right)}\left(x\right)]}^T,$$

  (27)

  and we will find explicitly the operational matrix of derivatives ${\mathit{V}}^q$ such that the following identity holds:

  $${\displaystyle \frac{d^q{\mathit{\theta }}^{\left(\mathit{\xi }\right)}\left(x\right)}{d{x}^q}}={\mathit{V}}^q{\mathit{\theta }}^{\left(\mathit{\xi }\right)}\left(x\right).$$

  (28)
• The expression of the fractional derivatives of the SCCPs, that is, we will determine the coefficients ${\mathcal{Q}}_{n,j}$ such that for $\gamma \in (0,1)$, we have the following expression:

  $$D_t^{\gamma }{\theta }_j^{\left(\xi \right)}\left(t\right)=t^{-\gamma }\sum _{n=0}^j{\mathcal{Q}}_{n,j}{\theta }_n^{\left(\xi \right)}\left(t\right).$$

  (29)
• Constructing the operational matrix of fractional derivatives of the SCCPs. It can be constructed from the above fractional derivative expression. In fact, from (29), we can write

  $${\displaystyle \frac{d^{\gamma }{\mathit{\theta }}^{\left(\mathit{\xi }\right)}\left(t\right)}{d{t}^{\gamma }}}=t^{-\gamma }{\mathit{D}}^{\gamma }{\mathit{\theta }}^{\left(\mathit{\xi }\right)}\left(t\right),$$

  (30)

  where ${\mathit{D}}^{\gamma }=\left({\mathcal{Q}}_{n,j}\right)$.

We now proceed to prove our theoretical results that will be pivotal in what follows.

Theorem 1.

$U_i\left(x\right)$ are connected with $C_i^{\left(\xi \right)}\left(x\right)$ by the following formula:

$$U_i\left(x\right)=\sum _{m=0}^{⌊{\displaystyle \frac{i}{2}}⌋}{\zeta }_{i-2m}{2}^{i-2m}{\left({\displaystyle \frac{2-\xi }{\xi }}\right)}^m{C}_{i-2m}^{\left(\xi \right)}\left(x\right),i\ge 0,$$

(31)

where

$${\zeta }_j=\left\{\begin{array}{cc}{\displaystyle \frac{\xi }{2},}\hfill & j=0,\hfill \\ 1,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

(32)

Proof. 

The idea of the proof depends on proving that the right-hand side of (31) satisfies the same recurrence relation of $U_i\left(x\right)$ with the same initials. For this end, assume the following polynomials:

$${\rho }_i\left(x\right)=\sum _{m=0}^{⌊{\displaystyle \frac{i}{2}}⌋}{\zeta }_{i-2m}{2}^{i-2m}{\left({\displaystyle \frac{2-\xi }{\xi }}\right)}^m{C}_{i-2m}^{\left(\xi \right)}\left(x\right).$$

(33)

Noting that ${\rho }_0\left(1\right)=1,{\rho }_1\left(x\right)=2x$, then to prove that (31) holds for $i\ge 2$, it remains to show that the following identity holds:

$${\eta }_i\left(x\right)={\rho }_{i+2}\left(x\right)-2x{\rho }_{i+1}\left(x\right)+{\rho }_i\left(x\right)=0,i\ge 0.$$

(34)

Using Formula (33), ${\eta }_i\left(x\right)$ can be written in the following form:

$$\begin{array}{cc}\hfill {\eta }_i\left(x\right)& =\sum _{m=0}^{⌊{\displaystyle \frac{i+2}{2}}⌋}{\zeta }_{i-2m+2}{2}^{i-2m+2}{\left({\displaystyle \frac{2-\xi }{\xi }}\right)}^m{C}_{i-2m+2}^{\left(\xi \right)}\left(x\right)-2x\sum _{m=0}^{⌊{\displaystyle \frac{i+1}{2}}⌋}{\zeta }_{i-2m+1}{2}^{i-2m+1}{\left({\displaystyle \frac{2-\xi }{\xi }}\right)}^m{C}_{i-2m+1}^{\left(\xi \right)}\left(x\right)\hfill \\ \hfill & +\sum _{m=0}^{⌊{\displaystyle \frac{i}{2}}⌋}{\zeta }_{i-2m}{2}^{i-2m}{\left({\displaystyle \frac{2-\xi }{\xi }}\right)}^m{C}_{i-2m}^{\left(\xi \right)}\left(x\right).\hfill \end{array}$$

(35)

We will prove the validity of the following two identities:

$${\eta }_{2i}\left(x\right)=0,{\eta }_{2i+1}\left(x\right)=0,i\ge 0.$$

(36)

It is possible to divide Equation (35) into the following two identities:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\eta }_{2i}\left(x\right)& =\sum _{m=0}^{i+1}{\zeta }_{2i-2m+2}{2}^{2i-2m+2}{\left({\displaystyle \frac{2-\xi }{\xi }}\right)}^m{C}_{2i-2m+2}^{\left(\xi \right)}\left(x\right)-2x\sum _{m=0}^i{\zeta }_{2i-2m+1}{2}^{2i-2m+1}{\left({\displaystyle \frac{2-\xi }{\xi }}\right)}^m{C}_{2i-2m+1}^{\left(\xi \right)}\left(x\right)\hfill \\ \hfill & +\sum _{m=0}^i{\zeta }_{2i-2m}{2}^{2i-2m}{\left({\displaystyle \frac{2-\xi }{\xi }}\right)}^m{C}_{2i-2m}^{\left(\xi \right)}\left(x\right),\hfill \end{array}\end{array}$$

(37)

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\eta }_{2i+1}\left(x\right)=& \sum _{k=0}^{i+1}{2}^{2i-2k+3}{\left({\displaystyle \frac{2-\xi }{\xi }}\right)}^k{\zeta }_{2i-2k+3}{C}_{2i-2k+3}^{\left(\xi \right)}\left(x\right)-2x\sum _{k=0}^{i+1}{2}^{2i-2k+2}{\left({\displaystyle \frac{2-\xi }{\xi }}\right)}^k{\zeta }_{2i-2k+2}{C}_{2i-2k+2}^{\left(\xi \right)}\left(x\right)\hfill \\ \hfill & +\sum _{k=0}^i{2}^{2i-2k+1}{\left({\displaystyle \frac{2-\xi }{\xi }}\right)}^k{\zeta }_{2i-2k+1}{C}_{2i-2k+1}^{\left(\xi \right)}\left(x\right).\hfill \end{array}\end{array}$$

(38)

We prove that ${\eta }_{2i}\left(x\right)=0$. The proof of ${\eta }_{2i+1}=0$ is similar.

Now, if we make use of the recurrence relation (14) written as

$$x{C}_j^{\left(\xi \right)}\left(x\right)=C_{j+1}^{\left(\xi \right)}\left(x\right)+\frac{1}{4}{C}_{j-1}^{\left(\xi \right)}\left(x\right),$$

(39)

then Formula (37) turns into following form:

$$\begin{array}{cc}\hfill {\eta }_{2i}\left(x\right)& =\sum _{m=0}^{i+1}{\zeta }_{2i-2m+2}{2}^{2i-2m+2}{\left({\displaystyle \frac{2-\xi }{\xi }}\right)}^m{C}_{2i-2m+2}^{\left(\xi \right)}\left(x\right)\hfill \\ \hfill & -2\sum _{m=0}^i{\zeta }_{2i-2m+1}{2}^{2i-2m+1}{\left({\displaystyle \frac{2-\xi }{\xi }}\right)}^m\left(C_{2i-2m+2}^{\left(\xi \right)}\left(x\right)+\frac{1}{4}{C}_{2i-2m}^{\left(\xi \right)}\left(x\right)\right)\hfill \\ \hfill & +\sum _{m=0}^i{\zeta }_{2i-2m}{2}^{2i-2m}{\left({\displaystyle \frac{2-\xi }{\xi }}\right)}^m{C}_{2i-2m}^{\left(\xi \right)}\left(x\right),\hfill \end{array}$$

(40)

of which the following form is also possible to express:

$$\begin{array}{cc}\hfill {\eta }_{2i}\left(x\right)& =\sum _{m=-1}^i{\zeta }_{2i-2m}{2}^{2i-2m}{\left({\displaystyle \frac{2-\xi }{\xi }}\right)}^{m+1}{C}_{2i-2m}^{\left(\xi \right)}\left(x\right)-2\sum _{m=-1}^{i-1}{\zeta }_{2i-2m-1}{2}^{2i-2m-1}{\left({\displaystyle \frac{2-\xi }{\xi }}\right)}^{m+1}{C}_{2i-2m}^{\left(\xi \right)}\left(x\right)\hfill \\ \hfill & -\frac{1}{2}\sum _{m=0}^i{\zeta }_{2i-2m+1}{2}^{2i-2m+1}{\left({\displaystyle \frac{2-\xi }{\xi }}\right)}^m{C}_{2i-2m}^{\left(\xi \right)}\left(x\right)+\sum _{m=0}^i{\zeta }_{2i-2m}{2}^{2i-2m}{\left({\displaystyle \frac{2-\xi }{\xi }}\right)}^m{C}_{2i-2m}^{\left(\xi \right)}\left(x\right).\hfill \end{array}$$

(41)

Now, after some algebraic manipulation, we can write

$$\begin{array}{cc}\hfill {\eta }_i\left(x\right)& =\sum _{m=0}^i{M}_{m,i}{C}_{2i-2m}^{\left(\xi \right)}\left(x\right)+{\displaystyle \frac{2}{\xi }}{\left({\displaystyle \frac{2-\xi }{\xi }}\right)}^{i+1}{\zeta }_{-1}+2^{2+2i}\left(-{\zeta }_{2i+1}+{\zeta }_{2i+2}\right)C_{2i+2}^{\left(\xi \right)}\left(x\right),\hfill \end{array}$$

(42)

where

$$M_{m,i}=\left\{\begin{array}{cc}{\displaystyle \frac{{\left(\frac{2}{\xi }-1\right)}^i(\xi -2)}{\xi }},\hfill & m=i,\hfill \\ 0,\hfill & 0\le m\le i-1.\hfill \end{array}\right.$$

(43)

Based on the definition of ${\zeta }_i$ in (32), it follows that $c_{-1}=1$ and $c_{2i+1}=c_{2i+2}=1$, and hence the formula of $M_{m,i}$ leads to

$${\eta }_{2i}\left(x\right)=0.$$

(44)

This ends the proof. □

Corollary 1.

The following is the connection formula between $U_i^{\ast }\left(x\right)$ and ${\theta }_i^{\left(\xi \right)}\left(x\right)$:

$$U_i^{\ast }\left(x\right)=\sum _{m=0}^{⌊\frac{i}{2}⌋}{\zeta }_{i-2m}{2}^{i-2m}{\left(\frac{2-\xi }{\xi }\right)}^m{\theta }_{i-2m}^{\left(\xi \right)}\left(x\right).$$

(45)

Proof. 

Equation (45) follows directly from (31) when x is substituted with $(2x-1)$. □

The following formula derives the inversion formula of the SCCPs.

Theorem 2.

Let m be any non-negative integer. $x^m$ can be expressed in terms of the CCPs as

$$x^m=\sum _{r=0}^m{Z}_{r,m}{\theta }_{m-r}^{\left(\xi \right)}\left(x\right),$$

(46)

where

$$Z_{r,m}=\left\{\begin{array}{cc}{\displaystyle \sum _{\ell =0}^{⌊\frac{r}{2}⌋}\frac{(2m+1)!(-2\ell +m+1)2^{-m-r+1}{\zeta }_{m-r}{\left(\frac{2}{\xi }-1\right)}^{\frac{r}{2}-\ell }}{(2\ell )!(-2\ell +2m+2)!},}\hfill & r\mathrm{even},\hfill \\ {\displaystyle \sum _{\ell =0}^{⌊\frac{r-1}{2}⌋}\frac{(2m+1)!(m-2\ell )2^{-m-r+1}{\zeta }_{m-r}{\left(\frac{2}{\xi }-1\right)}^{\frac{1}{2}(-2\ell +r-1)}}{(2\ell +1)!(-2\ell +2m+1)!},}\hfill & r\mathrm{odd},\hfill \end{array}\right.$$

(47)

where ${\zeta }_j$ is as given in (32).

Proof. 

We start from the following inversion formula of $U_i^{\ast }\left(x\right)$:

$$x^m=\sum _{r=0}^m{\displaystyle \frac{2^{1-2m}(1+m-r)(1+2m)!}{(2+2m-r)!r!}}{U}_{m-r}^{\ast }\left(x\right).$$

(48)

Applying Formula (45) to (48) yields the following formula:

$$x^m=\sum _{r=0}^m{\displaystyle \frac{2^{1-2m}(1+m-r)(1+2m)!}{(2+2m-r)!r!}}\sum _{k=0}^{⌊\frac{m-r}{2}⌋}{\zeta }_{m-r-2k}{2}^{m-r-2k}{\left(\frac{2-\xi }{\xi }\right)}^k{\theta }_{m-r-2k}^{\left(\xi \right)}\left(x\right).$$

(49)

Some lengthy manipulations enable one to write the last formula into the following formula:

$$\begin{array}{c}\hfill x^m=\sum _{r=0}^{⌊\frac{m}{2}⌋}{S}_{r,m}{\theta }_{m-2r}^{\left(\xi \right)}\left(x\right)+\sum _{r=0}^{⌊\frac{m-1}{2}⌋}{\overline{S}}_{r,m}{\theta }_{m-2r-1}^{\left(\xi \right)}\left(x\right),\end{array}$$

(50)

with

$$\begin{array}{cc}\hfill S_{r,m}& =\sum _{\ell =0}^r{\displaystyle \frac{{\zeta }_{m-2r}{2}^{1-m-2r}{\left(-1+\frac{2}{\xi }\right)}^{-\ell +r}(1-2\ell +m)(1+2m)!}{(2\ell )!(2-2\ell +2m)!}},\hfill \end{array}$$

(51)

$$\begin{array}{cc}\hfill {\overline{S}}_{r,m}& =\sum _{\ell =0}^r{\displaystyle \frac{{\zeta }_{m-2r-1}{2}^{-m-2r}{\left(-1+\frac{2}{\xi }\right)}^{-\ell +r}(-2\ell +m)(1+2m)!}{(2\ell +1)!(1-2\ell +2m)!}}.\hfill \end{array}$$

(52)

Formula (50) may be expressed as

$$x^m=\sum _{r=0}^m{Z}_{r,m}{\theta }_{m-r}^{\left(\xi \right)}\left(x\right),$$

(53)

with

$$Z_{r,m}=\left\{\begin{array}{cc}{\displaystyle \sum _{\ell =0}^{⌊\frac{r}{2}⌋}\frac{(2m+1)!(m+1-2\ell )2^{-m-r+1}{\zeta }_{m-r}{\left(\frac{2}{\xi }-1\right)}^{\frac{r}{2}-\ell }}{(2\ell )!(2m+2-2\ell )!},}\hfill & r\mathrm{even},\hfill \\ {\displaystyle \sum _{\ell =0}^{⌊\frac{r-1}{2}⌋}\frac{(2m+1)!(m-2\ell )2^{-m-r+1}{\zeta }_{m-r}{\left(\frac{2}{\xi }-1\right)}^{\frac{r-1}{2}-\ell }}{(2\ell +1)!(2m+1-2\ell )!},}\hfill & r\mathrm{odd}.\hfill \end{array}\right.$$

(54)

This ends the proof. □

Theorem 3.

Let $j,q$ be two positive integers with $j\ge q$. We can write

$${\displaystyle D^q{\theta }_j^{\left(\xi \right)}\left(x\right)=\sum _{m=0}^{j-q}{V}_{j-m-q,r,j}^q{\theta }_m^{\left(\xi \right)}\left(x\right),}$$

(55)

with

$$V_{m,r,j}^q=\sum _{r=0}^m{\lambda }_{r,j}{(j-q-r+1)}_q{Z}_{m-r,j-q-r},$$

(56)

where ${\lambda }_{r,j}$ is given in (20), and $Z_{r,m}$ is given in (54).

Proof. 

Differentiating the analytic form in (19) yields the following formula:

$$D^q{\theta }_j^{\left(\xi \right)}\left(x\right)=\sum _{r=0}^{j-q}{\lambda }_{r,j}{(j-r-q+1)}_q{x}^{j-r-q}.$$

(57)

Based on the inversion formula (46), the last equation may be converted into

$$D^q{\theta }_j^{\left(\xi \right)}\left(x\right)=\sum _{r=0}^{j-q}{\lambda }_{r,j}{(j-r-q+1)}_q\sum _{t=0}^{j-r-q}{Z}_{t,j-r-q}{\theta }_{j-r-q-t}^{\left(\xi \right)}\left(x\right),$$

(58)

which can be written alternatively as

$$D^q{\theta }_j^{\left(\xi \right)}\left(x\right)=\sum _{m=0}^{j-q}\left(\sum _{r=0}^m{\lambda }_{r,j}{(j-r-q+1)}_q{Z}_{m-r,j-r-q}\right){\theta }_{j-q-m}^{\left(\xi \right)}\left(x\right),$$

(59)

which give Formula (55). □

Remark 3.

Based on the high-order derivative formula of the SCCPs in (55), the OMDS of these polynomials may be deduced. This outcome is given in the following corollary.

Corollary 2.

Assume the following vector:

$${\mathit{\theta }}^{\left(\mathit{\xi }\right)}\left(x\right)={[{\theta }_0^{\left(\xi \right)}\left(x\right),{\theta }_1^{\left(\xi \right)}\left(x\right),\dots ,{\theta }_{\mathcal{N}}^{\left(\xi \right)}\left(x\right)]}^T.$$

(60)

The first-, second-, and fourth-order derivatives of the vector ${\mathit{\theta }}^{\left(\mathit{\xi }\right)}\left(x\right)$ may be expressed as

$$\begin{array}{cc}\hfill & {\displaystyle \frac{d{\mathit{\theta }}^{\left(\mathit{\xi }\right)}\left(x\right)}{dx}}=\mathit{U}{\mathit{\theta }}^{\left(\mathit{\xi }\right)}\left(x\right),\hfill \\ & {\displaystyle \frac{d^2{\mathit{\theta }}^{\left(\mathit{\xi }\right)}\left(x\right)}{d{x}^2}}=\mathit{V}{\mathit{\theta }}^{\left(\mathit{\xi }\right)}\left(x\right),\hfill \\ & {\displaystyle \frac{d^4{\mathit{\theta }}^{\left(\mathit{\xi }\right)}\left(x\right)}{d{x}^4}}=\mathit{K}{\mathit{\theta }}^{\left(\mathit{\xi }\right)}\left(x\right),\hfill \end{array}$$

(61)

where $\mathit{U}=\left(V_{j-m-1,r,j}^1\right)$, $\mathit{V}=\left(V_{j-m-2,r,j}^2\right)$, and $\mathit{K}=\left(V_{j-m-4,r,j}^4\right)$ are the OMDS each of order ${(\mathcal{N}+1)}^2$.

For example, the matrices $\mathit{U},\mathit{V}$ and $\mathit{K}$ take the following form for $\mathcal{N}=7$:

$$\begin{array}{cc}\hfill & \mathit{U}=\left(\begin{array}{cccccccc}0& 0& 0& 0& 0& 0& 0& 0\\ \xi & 0& 0& 0& 0& 0& 0& 0\\ 0& 4& 0& 0& 0& 0& 0& 0\\ 1-{\displaystyle \frac{\xi }{4}}& 0& 6& 0& 0& 0& 0& 0\\ 0& {\displaystyle \frac{2}{\xi }}& 0& 8& 0& 0& 0& 0\\ {\displaystyle \frac{(\xi -4)\xi +8}{16\xi }}& 0& {\displaystyle \frac{1}{2}}+{\displaystyle \frac{2}{\xi }}& 0& 10& 0& 0& 0\\ 0& {\displaystyle \frac{(\xi -2)\xi +4}{4{\xi }^2}}& 0& {\displaystyle \frac{\xi +2}{\xi }}& 0& 12& 0& 0\\ {\displaystyle \frac{16-{(\xi -4)}^2\xi }{64{\xi }^2}}& 0& {\displaystyle \frac{3}{8}}+{\displaystyle \frac{1}{{\xi }^2}}-{\displaystyle \frac{1}{2\xi }}& 0& {\displaystyle \frac{3}{2}}+{\displaystyle \frac{2}{\xi }}& 0& 14& 0\end{array}\right),\hfill \end{array}$$

(62)

$$\begin{array}{cc}& \mathit{V}=\left(\begin{array}{cccccccc}0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0\\ 4\xi & 0& 0& 0& 0& 0& 0& 0\\ 0& 24& 0& 0& 0& 0& 0& 0\\ -2(\xi -5)& 0& 48& 0& 0& 0& 0& 0\\ 0& 2+{\displaystyle \frac{28}{\xi }}& 0& 80& 0& 0& 0& 0\\ {\displaystyle \frac{3\xi }{4}}-3+{\displaystyle \frac{9}{\xi }}& 0& {\displaystyle \frac{12(\xi +3)}{\xi }}& 0& 120& 0& 0& 0\\ 0& {\displaystyle \frac{22-6\xi }{{\xi }^2}}+5& 0& 26+{\displaystyle \frac{44}{\xi }}& 0& 168& 0& 0\end{array}\right),\hfill \end{array}$$

(63)

$$\begin{array}{cc}& \mathit{K}=\left(\begin{array}{cccccccc}0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0\\ 192\xi & 0& 0& 0& 0& 0& 0& 0\\ 0& 1920& 0& 0& 0& 0& 0& 0\\ -192(\xi -7)& 0& 5760& 0& 0& 0& 0& 0\\ 0& {\displaystyle \frac{960(\xi +6)}{\xi }}& 0& 13440& 0& 0& 0& 0\end{array}\right).\hfill \end{array}$$

(64)

The following theorem is concerned with deriving an expression that computes the fractional derivatives of the SCCPs.

Theorem 4.

For $\gamma \in (0,1),D_t^{\gamma }{\theta }_j^{\left(\xi \right)}\left(t\right)$ can be expressed as

$$D_t^{\gamma }{\theta }_j^{\left(\xi \right)}\left(t\right)=t^{-\gamma }\sum _{n=0}^j{\mathcal{Q}}_{n,j}{\theta }_n^{\left(\xi \right)}\left(t\right),$$

(65)

where

$${\mathcal{Q}}_{n,j}=\sum _{k=0}^j{\displaystyle \frac{(k+1)!G_{k+1,j}{Z}_{k-n+1,k+1}}{\Gamma (k-\gamma +2)}}.$$

(66)

Proof. 

Based on (3) together with Formula (21), we can write

$$D_t^{\gamma }{\theta }_j^{\left(\xi \right)}\left(t\right)=t^{-\gamma }\sum _{p=1}^j{\displaystyle \frac{p!G_{p,j}}{\Gamma (p-\gamma +1)}}{t}^p.$$

(67)

Formula (46) turns (67) into the following one:

$$D_t^{\beta }{\theta }_j^{\left(\xi \right)}\left(t\right)=t^{-\gamma }\sum _{p=1}^j\sum _{s=0}^p{\displaystyle \frac{p!G_{p,j}{Z}_{p-s,p}}{\Gamma (p-\gamma +1)}}{\theta }_s^{\left(\xi \right)}\left(t\right),$$

(68)

which can be rearranged to give

$$D_t^{\gamma }{\theta }_j^{\left(\xi \right)}\left(t\right)=t^{-\gamma }\sum _{n=0}^j{\mathcal{Q}}_{n,j}{\theta }_n^{\left(\xi \right)}\left(t\right),$$

(69)

where

$${\mathcal{Q}}_{n,j}=\sum _{k=0}^j{\displaystyle \frac{(k+1)!G_{k+1,j}{Z}_{k-n+1,k+1}}{\Gamma (k-\gamma +2)}}.$$

(70)

This completes the proof of this theorem. □

Corollary 3.

The fractional derivative of ${\mathit{\theta }}^{\left(\mathit{\xi }\right)}\left(t\right)$ can be represented as

$${\displaystyle \frac{d^{\gamma }{\mathit{\theta }}^{\left(\mathit{\xi }\right)}\left(t\right)}{d{t}^{\gamma }}}=t^{-\gamma }{\mathit{D}}^{\gamma }{\mathit{\theta }}^{\left(\mathit{\xi }\right)}\left(t\right),$$

(71)

where ${\mathit{D}}^{\gamma }=\left({\mathcal{Q}}_{n,j}\right)$.

Proof. 

It is a direct consequence of Formula (65). □

For example, and for the following choices:

$$\gamma ={\displaystyle \frac{1}{2}},\xi =3,\mathcal{N}=7,$$

the matrix ${\mathit{D}}^{\gamma }$ takes the following form:

$${\mathit{D}}^{\gamma }=\left(\begin{array}{cccccccc}0& 0& 0& 0& 0& 0& 0& 0\\ {\displaystyle \frac{5}{\sqrt{\pi }}}& 0& 0& 0& 0& 0& 0& 0\\ -{\displaystyle \frac{10}{\sqrt{\pi }}}& {\displaystyle \frac{38}{3\sqrt{\pi }}}& 0& 0& 0& 0& 0& 0\\ {\displaystyle \frac{155}{12\sqrt{\pi }}}& -{\displaystyle \frac{38}{\sqrt{\pi }}}& {\displaystyle \frac{464}{15\sqrt{\pi }}}& 0& 0& 0& 0& 0\\ -{\displaystyle \frac{40}{3\sqrt{\pi }}}& {\displaystyle \frac{608}{9\sqrt{\pi }}}& -{\displaystyle \frac{1856}{15\sqrt{\pi }}}& {\displaystyle \frac{2616}{35\sqrt{\pi }}}& 0& 0& 0& 0\\ {\displaystyle \frac{575}{48\sqrt{\pi }}}& -{\displaystyle \frac{551}{6\sqrt{\pi }}}& {\displaystyle \frac{12644}{45\sqrt{\pi }}}& -{\displaystyle \frac{2616}{7\sqrt{\pi }}}& {\displaystyle \frac{101776}{567\sqrt{\pi }}}& 0& 0& 0\\ -{\displaystyle \frac{235}{24\sqrt{\pi }}}& {\displaystyle \frac{2527}{24\sqrt{\pi }}}& -{\displaystyle \frac{21344}{45\sqrt{\pi }}}& {\displaystyle \frac{36188}{35\sqrt{\pi }}}& -{\displaystyle \frac{203552}{189\sqrt{\pi }}}& {\displaystyle \frac{891680}{2079\sqrt{\pi }}}& 0& 0\\ {\displaystyle \frac{1435}{192\sqrt{\pi }}}& -{\displaystyle \frac{3857}{36\sqrt{\pi }}}& {\displaystyle \frac{3306}{5\sqrt{\pi }}}& -{\displaystyle \frac{14606}{7\sqrt{\pi }}}& {\displaystyle \frac{5979340}{1701\sqrt{\pi }}}& -{\displaystyle \frac{891680}{297\sqrt{\pi }}}& {\displaystyle \frac{11816032}{11583\sqrt{\pi }}}& 0\end{array}\right).$$

(72)

4. Treatment of the TFKSE Using the Collocation Method

In this section, we consider the following TFKSE: [60]:

$$\begin{array}{cc}\hfill {\displaystyle \frac{{\partial }^{\gamma }\zeta (\sigma ,t)}{\partial t^{\gamma }}}& +a_1(\sigma ,t)\zeta (\sigma ,t){\displaystyle \frac{\partial \zeta (\sigma ,t)}{\partial \sigma }}+a_2(\sigma ,t){\displaystyle \frac{{\partial }^2\zeta (\sigma ,t)}{\partial {\sigma }^2}}\hfill \\ & +a_3(\sigma ,t){\displaystyle \frac{{\partial }^4\zeta (\sigma ,t)}{\partial {\sigma }^4}}=f(\sigma ,t),(\sigma ,t)\in (0,1)\times (0,1],\hfill \end{array}$$

(73)

subject to the following conditions:

$$\begin{array}{cc}\hfill \zeta (\sigma ,0)& =g\left(\sigma \right),\hfill \end{array}$$

(74)

$$\begin{array}{cc}\hfill \zeta (0,t)& =g_0\left(t\right),\zeta (1,t)=g_1\left(t\right),\hfill \end{array}$$

(75)

$$\begin{array}{cc}\hfill {\displaystyle \frac{\partial \zeta (0,t)}{\partial \sigma }}& =0,{\displaystyle \frac{\partial \zeta (1,t)}{\partial \sigma }}=0,\hfill \end{array}$$

(76)

or

$$\begin{array}{cc}\hfill \zeta (\sigma ,0)& =g\left(\sigma \right),\hfill \end{array}$$

(77)

$$\begin{array}{cc}\hfill \zeta (0,t)& =g_0\left(t\right),\zeta (1,t)=g_1\left(t\right),\hfill \end{array}$$

(78)

$$\begin{array}{cc}\hfill {\displaystyle \frac{{\partial }^2\zeta (0,t)}{\partial {\sigma }^2}}& =0,{\displaystyle \frac{{\partial }^2\zeta (1,t)}{\partial {\sigma }^2}}=0,\hfill \end{array}$$

(79)

where $a_1(\sigma ,t)$, $a_2(\sigma ,t)$, and $a_3(\sigma ,t)$ are real-valued functions of $\sigma$ and t, $a_2(\sigma ,t)$ and $a_3(\sigma ,t)$ are connected to the growth of linear stability and surface tension [61], respectively. It is assumed that $a_1(\sigma ,t)$, $a_2(\sigma ,t)$, $a_3(\sigma ,t)$, $f(\sigma ,t)$, $g\left(\sigma \right)$, $g_0\left(t\right)$, and $g_1\left(t\right)$ are sufficiently smooth functions.

Now, consider the following space:

$${\mathcal{W}}^{\mathcal{N}}=\mathrm{span}\{{\theta }_m^{\left(\xi \right)}\left(\sigma \right){\theta }_n^{\left(\xi \right)}\left(t\right):0\le m,n\le \mathcal{N}\},$$

(80)

and therefore, every function ${\zeta }^{\mathcal{N}}(\sigma ,t)\in {\mathcal{W}}^N$ may be written as

$${\zeta }^{\mathcal{N}}(\sigma ,t)=\sum _{m=0}^{\mathcal{N}}\sum _{n=0}^{\mathcal{N}}{\widehat{\zeta }}_{mn}{\theta }_m^{\left(\xi \right)}\left(\sigma \right){\theta }_n^{\left(\xi \right)}\left(t\right)={\mathit{\theta }}^{\left(\mathit{\xi }\right)}{\left(\sigma \right)}^T\widehat{\mathbf{\zeta }}{\mathit{\theta }}^{\left(\mathit{\xi }\right)}\left(t\right),$$

(81)

where ${\mathit{\theta }}^{\left(\mathit{\xi }\right)}\left(\sigma \right)$ is as given in (60), and $\widehat{\mathbf{\zeta }}={\left({\widehat{\zeta }}_{mn}\right)}_{0\le m,n\le \mathcal{N}}$ is the matrix to be determined with order ${(\mathcal{N}+1)}^2$.

Now, the residual ${\mathcal{R}}_{\mathcal{N}}(\sigma ,t)$ of Equation (73) may be expressed as

$$\begin{array}{cc}\hfill {\mathcal{R}}_{\mathcal{N}}(\sigma ,t)={\displaystyle \frac{{\partial }^{\gamma }{\zeta }^{\mathcal{N}}(\sigma ,t)}{\partial t^{\gamma }}}& +a_1(\sigma ,t){\zeta }^{\mathcal{N}}(\sigma ,t){\displaystyle \frac{\partial {\zeta }^{\mathcal{N}}(\sigma ,t)}{\partial \sigma }}+a_2(\sigma ,t){\displaystyle \frac{{\partial }^2{\zeta }^{\mathcal{N}}(\sigma ,t)}{\partial {\sigma }^2}}\hfill \\ & +a_3(\sigma ,t){\displaystyle \frac{{\partial }^4{\zeta }^{\mathcal{N}}(\sigma ,t)}{\partial {\sigma }^4}}-f(\sigma ,t).\hfill \end{array}$$

(82)

In virtue of Corollaries 2 and 3, ${\mathcal{R}}_{\mathcal{N}}(\sigma ,t)$ may be rewritten in the following form:

$$\begin{array}{cc}\hfill {\mathcal{R}}_{\mathcal{N}}(\sigma ,t)& ={\mathit{\theta }}^{\left(\mathit{\xi }\right)}{\left(\sigma \right)}^T\widehat{\mathbf{\zeta }}\left(t^{-\gamma }{\mathit{D}}^{\gamma }{\mathit{\theta }}^{\left(\mathit{\xi }\right)}\left(t\right)\right)+a_1(\sigma ,t)\left[{\mathit{\theta }}^{\left(\mathit{\xi }\right)}{\left(\sigma \right)}^T\widehat{\mathbf{\zeta }}{\mathit{\theta }}^{\left(\mathit{\xi }\right)}\left(t\right)\right]\left[{\left(\mathit{U}{\mathit{\theta }}^{\left(\mathit{\xi }\right)}\left(\sigma \right)\right)}^T\widehat{\mathbf{\zeta }}{\mathit{\theta }}^{\left(\mathit{\xi }\right)}\left(t\right)\right]\hfill \\ & +a_2(\sigma ,t)\left[{\left(\mathit{V}{\mathit{\theta }}^{\left(\mathit{\xi }\right)}\left(\sigma \right)\right)}^T\widehat{\mathbf{\zeta }}{\mathit{\theta }}^{\left(\mathit{\xi }\right)}\left(t\right)\right]+a_3(\sigma ,t)\left[{\left(\mathit{K}{\mathit{\theta }}^{\left(\mathit{\xi }\right)}\left(\sigma \right)\right)}^T\widehat{\mathbf{\zeta }}{\mathit{\theta }}^{\left(\mathit{\xi }\right)}\left(t\right)\right]-f(\sigma ,t).\hfill \end{array}$$

(83)

Applying the collocation method, we may force the residual ${\mathcal{R}}_{\mathcal{N}}(\sigma ,t)$ to vanish at suitable collocation nodes $\left({\sigma }_m,t_n\right)$ in order to obtain the expansion coefficients ${\widehat{\zeta }}_{mn}$, that is

$${\mathcal{R}}_{\mathcal{N}}\left({\sigma }_m,t_n\right)=0,1\le m\le \mathcal{N}-3,1\le n\le \mathcal{N},$$

(84)

where $\{({\sigma }_m,t_n):m,n=1,2,\dots ,\mathcal{N}+1\}$ are the first distinct roots of ${\theta }_{\mathcal{N}+1}^{\left(\xi \right)}\left(x\right)$.

In addition, the conditions (74)–(76) lead to the following equations:

$$\begin{array}{cc}\hfill & \mathit{\theta }{\left({\sigma }_m\right)}^T\widehat{\mathbf{\zeta }}\mathit{\theta }\left(0\right)=g\left({\sigma }_m\right),1\le m\le \mathcal{N}+1,\hfill \end{array}$$

(85)

$$\begin{array}{cc}\hfill & \mathit{\theta }{\left(0\right)}^T\widehat{\mathbf{\zeta }}\mathit{\theta }\left(t_n\right)=g_0\left(t_n\right),1\le n\le \mathcal{N},\hfill \end{array}$$

(86)

$$\begin{array}{cc}\hfill & \mathit{\theta }{\left(1\right)}^T\widehat{\mathbf{\zeta }}\mathit{\theta }\left(t_n\right)=g_1\left(t_n\right),1\le n\le \mathcal{N},\hfill \end{array}$$

(87)

$$\begin{array}{cc}\hfill & {\left(\mathit{U}\mathit{\theta }\left(0\right)\right)}^T\widehat{\mathbf{\zeta }}\mathit{\theta }\left(t_n\right)=0,1\le n\le \mathcal{N},\hfill \end{array}$$

(88)

$$\begin{array}{cc}\hfill & {\left(\mathit{U}\mathit{\theta }\left(1\right)\right)}^T\widehat{\mathbf{\zeta }}\mathit{\theta }\left(t_n\right)=0,1\le n\le \mathcal{N},\hfill \end{array}$$

(89)

while the conditions (77)–(79) lead to the following equations:

$$\begin{array}{cc}\hfill & \mathit{\theta }{\left({\sigma }_m\right)}^T\widehat{\mathbf{\zeta }}\mathit{\theta }\left(0\right)=g\left({\sigma }_m\right),1\le m\le \mathcal{N}+1,\hfill \end{array}$$

(90)

$$\begin{array}{cc}\hfill & \mathit{\theta }{\left(0\right)}^T\widehat{\mathbf{\zeta }}\mathit{\theta }\left(t_n\right)=g_0\left(t_n\right),1\le n\le \mathcal{N},\hfill \end{array}$$

(91)

$$\begin{array}{cc}\hfill & \mathit{\theta }{\left(1\right)}^T\widehat{\mathbf{\zeta }}\mathit{\theta }\left(t_n\right)=g_1\left(t_n\right),1\le n\le \mathcal{N},\hfill \end{array}$$

(92)

$$\begin{array}{cc}\hfill & {\left(\mathit{V}\mathit{\theta }\left(0\right)\right)}^T\widehat{\mathbf{\zeta }}\mathit{\theta }\left(t_n\right)=0,1\le n\le \mathcal{N},\hfill \end{array}$$

(93)

$$\begin{array}{cc}\hfill & {\left(\mathit{V}\mathit{\theta }\left(1\right)\right)}^T\widehat{\mathbf{\zeta }}\mathit{\theta }\left(t_n\right)=0,1\le n\le \mathcal{N}.\hfill \end{array}$$

(94)

To obtain ${\widehat{\zeta }}_{mn}$, one can use Newton’s iterative technique to solve the ${(\mathcal{N}+1)}^2$ nonlinear system of equations that is created by Equations (85)–(89) or (90)–(94), in addition to (84).

Remark 4.

It is worth mentioning here that Newton’s method for solving the ${(\mathcal{N}+1)}^2$ nonlinear system of equations is convergent under the following conditions:

• Choosing a suitable initial guess ${\widehat{\zeta }}_{mn}={10}^{-m-n}$ that ensure the convergence.
• There is no singular Jacobian while solving the system in (85)–(89) or (90)–(94), in addition to (84).

5. Error Bound

The main aim of this section is to find an estimation of $\left.∥\zeta (\sigma ,t)-{\zeta }^{\mathcal{N}}(\sigma ,t)\right\}{\parallel }_{\infty },$ such that $\left|\right|\zeta (\sigma ,t)-{\zeta }^{\mathcal{N}}(\sigma ,t){\left|\right|}_{\infty }\to 0$ as $\mathcal{N}\to \infty .$

Theorem 5.

Let ${\zeta }^{\mathcal{N}}(\sigma ,t)\in {\mathcal{W}}^{\mathcal{N}}$ be the best approximation of $\zeta (\sigma ,t)$. The following inequality holds:

$$\left|\right|\zeta (\sigma ,t)-{\zeta }^{\mathcal{N}}(\sigma ,t){\left|\right|}_{\infty }\lesssim {\displaystyle \frac{2^{-2\mathcal{N}-1}((\xi -1)\mathcal{N}+\xi )}{\xi \Gamma (\mathcal{N}+2)}},$$

(95)

where $s_1\lesssim s_2$ means that there is a constant ν such that $s_1\le \nu s_2.$

Proof. 

Since ${\zeta }^{\mathcal{N}}(\sigma ,t)\in {\mathcal{W}}^{\mathcal{N}}$ is the best approximation of $\zeta (\sigma ,t)$; then, we can write the following inequality:

$$\left|\right|\zeta (\sigma ,t)-{\zeta }^{\mathcal{N}}{(\sigma ,t)\left|\right|}_{\infty }\le \left|\right|\zeta (\sigma ,t)-{\widehat{\zeta }}^{\mathcal{N}}(\sigma ,t){\left|\right|}_{\infty },\forall {\widehat{\zeta }}^{\mathcal{N}}(\sigma ,t)\in {\mathcal{W}}^{\mathcal{N}}.$$

(96)

In addition, (96) holds if ${\widehat{\zeta }}^{\mathcal{N}}(\sigma ,t)$ represents the interpolating polynomial for $\zeta (\sigma ,t)$ at points $({\sigma }_i,t_j)$, where ${\sigma }_i$ are the zeros of ${\theta }_i^{\left(\xi \right)}\left(\sigma \right)$, while $t_j$ are the zeros of ${\theta }_j^{\left(\xi \right)}\left(t\right)$. Now, if we take similar steps as in [62,63], we get

$$\begin{array}{cc}\hfill \zeta (\sigma ,t)-{\widehat{\zeta }}^{\mathcal{N}}(\sigma ,t)& ={\displaystyle \frac{{\partial }^{\mathcal{N}+1}\zeta (\eta ,t)}{\partial {\sigma }^{\mathcal{N}+1}(\mathcal{N}+1)!}}\prod _{i=0}^{\mathcal{N}}(\sigma -{\sigma }_i)+{\displaystyle \frac{{\partial }^{\mathcal{N}+1}\zeta (\sigma ,\mu )}{\partial t^{\mathcal{N}+1}(\mathcal{N}+1)!}}\prod _{j=0}^{\mathcal{N}}(t-t_j)\hfill \\ & -{\displaystyle \frac{{\partial }^{2\mathcal{N}+2}\zeta (\widehat{\eta },\widehat{\mu })}{\partial {\sigma }^{\mathcal{N}+1}\partial t^{\mathcal{N}+1}{((\mathcal{N}+1)!)}^2}}\prod _{i=0}^{\mathcal{N}}(\sigma -{\sigma }_i)\prod _{j=0}^{\mathcal{N}}(t-t_j).\hfill \end{array}$$

(97)

where $\eta ,\widehat{\eta },\mu ,\widehat{\mu }\in [0,1].$

Now, we can write

$$\begin{array}{cc}\hfill \left|\right|\zeta (\sigma ,t)-{\widehat{\zeta }}^{\mathcal{N}}(\sigma ,t){\left|\right|}_{\infty }& \le \underset{(\sigma ,t)\in \mathrm{\Omega }}{max}\left|{\displaystyle \frac{{\partial }^{\mathcal{N}+1}\zeta (\eta ,t)}{\partial {\sigma }^{\mathcal{N}+1}}}\right|{\displaystyle \frac{\left|\right|{\prod }_{i=0}^{\mathcal{N}}(\sigma -{\sigma }_i){\left|\right|}_{\infty }}{(\mathcal{N}+1)!}}\hfill \\ & +\underset{(\sigma ,t)\in \mathrm{\Omega }}{max}\left|{\displaystyle \frac{{\partial }^{\mathcal{N}+1}\zeta (\sigma ,\mu )}{\partial t^{\mathcal{N}+1}}}\right|{\displaystyle \frac{\left|\right|{\prod }_{j=0}^{\mathcal{N}}(t-t_j){\left|\right|}_{\infty }}{(\mathcal{N}+1)!}}\hfill \\ & +\underset{(\sigma ,t)\in \mathrm{\Omega }}{max}\left|{\displaystyle \frac{{\partial }^{2\mathcal{N}+2}\zeta (\widehat{\eta },\widehat{\mu })}{\partial {\sigma }^{\mathcal{N}+1}\partial t^{\mathcal{N}+1}}}\right|{\displaystyle \frac{\left|\right|{\prod }_{i=0}^{\mathcal{N}}(\sigma -{\sigma }_i){\left|\right|}_{\infty }\left|\right|{\prod }_{j=0}^{\mathcal{N}}(t-t_j){\left|\right|}_{\infty }}{{((\mathcal{N}+1)!)}^2}}.\hfill \end{array}$$

(98)

Since $\zeta$ is a smooth function on $\mathrm{\Omega }={[0,1]}^2$, then there exist three constants ${\sigma }_1,{\sigma }_2$ and ${\sigma }_3$, such that

$$\underset{(\sigma ,t)\in \mathrm{\Omega }}{max}\left|{\displaystyle \frac{{\partial }^{\mathcal{N}+1}\zeta (\eta ,t)}{\partial {\sigma }^{\mathcal{N}+1}}}\right|\le {\sigma }_1,\underset{(\sigma ,t)\in \mathrm{\Omega }}{max}\left|{\displaystyle \frac{{\partial }^{\mathcal{N}+1}\zeta (\sigma ,\mu )}{\partial t^{\mathcal{N}+1}}}\right|\le {\sigma }_2,\underset{(\sigma ,t)\in \mathrm{\Omega }}{max}\left|{\displaystyle \frac{{\partial }^{2\mathcal{N}+2}\zeta (\widehat{\eta },\widehat{\mu })}{\partial {\sigma }^{\mathcal{N}+1}\partial t^{\mathcal{N}+1}}}\right|\le {\sigma }_3.$$

(99)

To minimize the factor $\left|\right|{\prod }_{i=0}^{\mathcal{N}}(\sigma -{\sigma }_i){\left|\right|}_{\infty }$, we use the one-to-one mapping $\sigma ={\displaystyle \frac{1}{2}}(z+1)$ between the intervals $[-1,1]$ and $[0,1]$ to deduce that

$$\begin{array}{cc}\hfill \underset{{\sigma }_i\in [0,1]}{min}\underset{\sigma \in [0,1]}{max}\left|\prod _{i=0}^{\mathcal{N}}(\sigma -{\sigma }_i)\right|& =\underset{z_i\in [-1,1]}{min}\underset{z\in [-1,1]}{max}\left|\prod _{i=0}^{\mathcal{N}}{\displaystyle \frac{1}{2}}(z-z_i)\right|\hfill \\ & ={\left({\displaystyle \frac{1}{2}}\right)}^{\mathcal{N}+1}\underset{z_i\in [-1,1]}{min}\underset{z\in [-1,1]}{max}\left|\prod _{i=0}^{\mathcal{N}}(z-z_i)\right|\hfill \\ & ={\left({\displaystyle \frac{1}{2}}\right)}^{\mathcal{N}+1}\underset{z_i\in [-1,1]}{min}\underset{z\in [-1,1]}{max}\left|{\displaystyle \frac{C_{\mathcal{N}+1}^{\left(\xi \right)}\left(z\right)}{\overline{C_{\mathcal{N}}^{\left(\xi \right)}}}}\right|,\hfill \end{array}$$

(100)

where $\overline{C_{\mathcal{N}}^{\left(\xi \right)}}=1$ is the leading coefficient of $C_{\mathcal{N}+1}^{\left(\xi \right)}\left(z\right)$ and $z_i$ are the zeros of $C_{\mathcal{N}+1}^{\left(\xi \right)}\left(z\right).$

Similarly, the factor $\left|\right|{\prod }_{j=0}^{\mathcal{N}}(t-t_j){\left|\right|}_{\infty }$, can be minimized by using the one-to-one mapping $t={\displaystyle \frac{1}{2}}(\overline{t}+1)$ between the intervals $[-1,1]$ and $[0,1]$ to deduce that

$$\underset{t_j\in [0,1]}{min}\underset{t\in [0,1]}{max}\left|\prod _{j=0}^{\mathcal{N}}(t-t_j)\right|={\left({\displaystyle \frac{1}{2}}\right)}^{\mathcal{N}+1}\underset{{\overline{t}}_j\in [-1,1]}{min}\underset{\overline{t}\in [-1,1]}{max}\left|{\displaystyle \frac{C_{\mathcal{N}+1}^{\left(\xi \right)}\left(\overline{t}\right)}{{\overline{C^{\left(\xi \right)}}}_{\mathcal{N}}}}\right|,$$

(101)

Now, we can write

$$\begin{array}{cc}\hfill \underset{z\in [-1,1]}{max}\left|C_{\mathcal{N}+1}^{\left(\xi \right)}\left(z\right)\right|& =\underset{z\in [-1,1]}{max}\left|2^{-(\mathcal{N}+1)}\left({\displaystyle \frac{(\xi -2)}{\xi }}{U}_{\mathcal{N}-1}\left(z\right)+U_{\mathcal{N}+1}\left(z\right)\right)\right|\hfill \\ \hfill & ={\displaystyle \frac{2^{-\mathcal{N}}((\xi -1)\mathcal{N}+\xi )}{\xi }},\hfill \end{array}$$

(102)

And hence, inequality (99) along with Equations (100)–(102) help us to obtain the following required result:

$$\begin{array}{cc}\hfill \left|\right|\zeta (\sigma ,t)-{\zeta }^{\mathcal{N}}(\sigma ,t){\left|\right|}_{\infty }& \le \left|\right|\zeta (\sigma ,t)-{\widehat{\zeta }}^{\mathcal{N}}(\sigma ,t){\left|\right|}_{\infty }\hfill \\ & <{\sigma }_1{\displaystyle \frac{2^{-2\mathcal{N}-1}((\xi -1)\mathcal{N}+\xi )}{\xi \Gamma (\mathcal{N}+2)}}+{\sigma }_2{\displaystyle \frac{2^{-2\mathcal{N}-1}((\xi -1)\mathcal{N}+\xi )}{\xi \Gamma (\mathcal{N}+2)}}\hfill \\ & +{\sigma }_3{\displaystyle \frac{4^{-2\mathcal{N}-1}{((\xi -1)\mathcal{N}+\xi )}^2}{{\xi }^2\Gamma {(\mathcal{N}+2)}^2}}\hfill \\ & \lesssim {\displaystyle \frac{2^{-2\mathcal{N}-1}((\xi -1)\mathcal{N}+\xi )}{\xi \Gamma (\mathcal{N}+2)}}.\hfill \end{array}$$

(103)

□

6. Some Numerical Examples

This section presents some numerical examples to ensure the applicability and high accuracy of our proposed algorithm. In addition, comparisons with some other algorithms are presented.

Example 1

([60]). Consider the following equation:

$$\begin{array}{cc}\hfill {\displaystyle \frac{{\partial }^{\gamma }\zeta (\sigma ,t)}{\partial t^{\gamma }}}& -2\zeta (\sigma ,t){\displaystyle \frac{\partial \zeta (\sigma ,t)}{\partial \sigma }}+4{\displaystyle \frac{{\partial }^2\zeta (\sigma ,t)}{\partial {\sigma }^2}}+{\displaystyle \frac{{\partial }^4\zeta (\sigma ,t)}{\partial {\sigma }^4}}=f(\sigma ,t),(\sigma ,t)\in (0,1)\times (0,1],\hfill \end{array}$$

(104)

governed by the following conditions:

$$\zeta (\sigma ,0)=\zeta (0,t)=\zeta (1,t)={\displaystyle \frac{\partial \zeta (0,t)}{\partial \sigma }}={\displaystyle \frac{\partial \zeta (1,t)}{\partial \sigma }}=0,$$

(105)

where $f(\sigma ,t)$ is selected to meet the the exact solution of (104) given by

$$\zeta (\sigma ,t)=t^4{\sigma }^2\left({\sigma }^3-{\displaystyle \frac{5{\sigma }^2}{2}}+2\sigma -{\displaystyle \frac{1}{2}}\right).$$

(106)

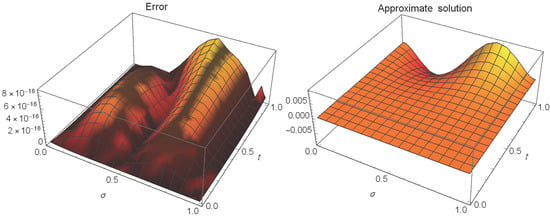
Table 1 and Table 2 present a comparison of $L_{\infty }$ and $L^2$ errors, respectively, between our method at different values of γ with the method in [60]. Table 3 presents the $L_{\infty }$ errors at different values of ξ and γ when $\mathcal{N}=5$. Figure 1 shows the absolute errors (left) and approximate solution (right) at $\gamma =0.2$ and $\xi =1$ when $\mathcal{N}=5$.

Table 1. Comparison of $L_{\infty }$ errors for Example 1.

$\mathit{\gamma }$	Method in [60] at ${\mathit{N}}_{\mathit{s}}=160,{\mathit{M}}_{\mathit{t}}=320$	Proposed Method at $\mathcal{N}=5$
		$\mathit{\xi }=\mathbf{1}$	$\mathit{\xi }=\mathbf{2}$	$\mathit{\xi }=\mathbf{3}$
0.3	$4.0055\times {10}^{-12}$	$9.51588\times {10}^{-16}$	$2.24918\times {10}^{-16}$	$1.96003\times {10}^{-16}$
0.5	$7.3038\times {10}^{-12}$	$8.80678\times {10}^{-16}$	$2.29253\times {10}^{-16}$	$2.39325\times {10}^{-16}$
0.8	$5.0390\times {10}^{-11}$	$9.10954\times {10}^{-16}$	$2.2734\times {10}^{-16}$	$2.21425\times {10}^{-16}$

Table 2. Comparison of $L^2$ errors for Example 1.

$\mathit{\gamma }$	Method in [60] at ${\mathit{N}}_{\mathit{s}}=160,{\mathit{M}}_{\mathit{t}}=320$	Proposed Method at $\mathcal{N}=5$
		$\mathit{\xi }=\mathbf{1}$	$\mathit{\xi }=\mathbf{2}$	$\mathit{\xi }=\mathbf{3}$
0.3	$8.2604\times {10}^{-13}$	$2.4914\times {10}^{-15}$	$1.87817\times {10}^{-15}$	$4.21728\times {10}^{-16}$
0.5	$9.0548\times {10}^{-12}$	$2.31524\times {10}^{-16}$	$1.09774\times {10}^{-15}$	$5.44158\times {10}^{-15}$
0.8	$3.1675\times {10}^{-11}$	$2.47329\times {10}^{-16}$	$5.02686\times {10}^{-16}$	$4.70814\times {10}^{-15}$

Table 3. $L_{\infty }$ errors for Example 1.

$\mathit{\gamma }$	$\mathit{\xi }=0.6$	$\mathit{\xi }=1$	$\mathit{\xi }=1.5$	$\mathit{\xi }=2$	$\mathit{\xi }=2.5$	$\mathit{\xi }=3$	$\mathit{\xi }=3.5$
0.3	$1.62276\times {10}^{-16}$	$9.51588\times {10}^{-16}$	$2.12504\times {10}^{16}$	$2.24918\times {10}^{-16}$	$1.6694\times {10}^{-16}$	$1.96003\times {10}^{-16}$	$2.25497\times {10}^{-16}$
0.5	$2.30089\times {10}^{-16}$	$8.80678\times {10}^{-16}$	$1.33319\times {10}^{-16}$	$2.29253\times {10}^{-16}$	$2.26395\times {10}^{-16}$	$2.39325\times {10}^{-16}$	$1.71556\times {10}^{-16}$
0.8	$2.30243\times {10}^{-16}$	$9.10954\times {10}^{-16}$	$2.289\times {10}^{-16}$	$2.2734\times {10}^{-16}$	$2.23061\times {10}^{-16}$	$2.21425\times {10}^{-16}$	$1.71799\times {10}^{-16}$

Figure 1. The absolute errors (left) and approximate solution (right) of Example 1.

Remark 5.

It is noticed from the results of Table 3 that the two cases correspond to the classical CPs, case $\xi =1$ corresponds to the first kind of CPs, $\xi =2$ that corresponds to the second kind of CPs, do not always yield the smallest $L_{\infty }$ errors. This demonstrates that our idea to introduce the CCPs and their shifted versions that generalize both the standard first and second kinds of CPs and their shifted versions is significant.

Example 2.

Consider the following equation:

$$\begin{array}{cc}\hfill {\displaystyle \frac{{\partial }^{\gamma }\zeta (\sigma ,t)}{\partial t^{\gamma }}}& +\sigma \zeta (\sigma ,t){\displaystyle \frac{\partial \zeta (\sigma ,t)}{\partial \sigma }}+\sigma {\displaystyle \frac{{\partial }^2\zeta (\sigma ,t)}{\partial {\sigma }^2}}+{\displaystyle \frac{{\partial }^4\zeta (\sigma ,t)}{\partial {\sigma }^4}}\hfill \\ \hfill & =f(\sigma ,t),(\sigma ,t)\in (0,1)\times (0,1].\hfill \end{array}$$

(107)

governed by the following conditions:

$$\zeta (\sigma ,0)=\zeta (0,t)=\zeta (1,t)={\displaystyle \frac{{\partial }^2\zeta (0,t)}{\partial {\sigma }^2}}={\displaystyle \frac{{\partial }^2\zeta (1,t)}{\partial {\sigma }^2}}=0,$$

(108)

where $f(\sigma ,t)$ is selected to meet the exact solution of (107) given by

$$\zeta (\sigma ,t)=t^{4}sin\left(\pi \sigma \right).$$

(109)

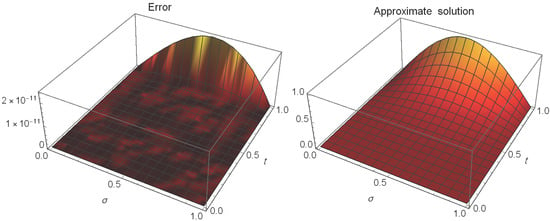
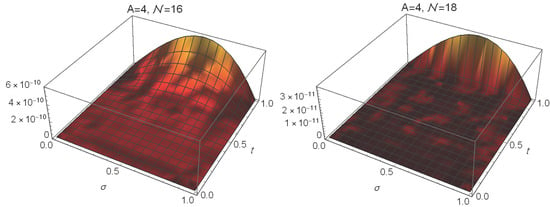
Figure 2 shows the absolute errors (left) and approximate solution (right) at $\gamma =0.2$ and $\xi =1$ when $\mathcal{N}=18$. Table 4 reports the absolute errors and also the CPU times (in seconds) (in seconds) for our numerical method at $\gamma =0.8$ and $\xi =2$ when $\mathcal{N}=18$. Figure 3 shows the absolute errors at different values of $\mathcal{N}$ when $\gamma =0.5$. Table 5 reports the absolute errors and also the CPU times (in seconds) for our numerical method at $\gamma =0.9$ and $\xi =2$ when $\mathcal{N}=18$.

Figure 2. The absolute errors (left) and approximate solution (right) of Example 2.

Table 4. The absolute errors of Example 2.

$\mathit{\sigma }$	$\mathit{t}=0.3$	CPU Time	$\mathit{t}=0.6$	CPU Time	$\mathit{t}=0.9$	CPU Time
0.1	$7.17829\times {10}^{-15}$		$6.43166\times {10}^{-14}$		$3.08337\times {10}^{-13}$
0.2	$1.39116\times {10}^{-14}$		$1.24803\times {10}^{-13}$		$5.97689\times {10}^{-13}$
0.3	$1.97793\times {10}^{-14}$		$1.7758\times {10}^{-13}$		$8.49432\times {10}^{-13}$
0.4	$2.43382\times {10}^{-14}$		$2.18783\times {10}^{-13}$		$1.04439\times {10}^{-12}$
0.5	$2.71276\times {10}^{-14}$	130.876	$2.4436\times {10}^{-13}$	131.048	$1.16374\times {10}^{-12}$	131.204
0.6	$2.77382\times {10}^{-14}$		$2.50369\times {10}^{-13}$		$1.18894\times {10}^{-12}$
0.7	$2.57121\times {10}^{-14}$		$2.32731\times {10}^{-13}$		$1.10123\times {10}^{-12}$
0.8	$2.06458\times {10}^{-14}$		$1.8742\times {10}^{-13}$		$8.8346\times {10}^{-13}$
0.9	$1.21465\times {10}^{-14}$		$1.10557\times {10}^{-13}$		$5.19168\times {10}^{-13}$

Figure 3. The absolute errors of Example 2 at $\gamma =0.5$.

Table 5. The absolute errors of Example 2.

$\mathit{\sigma }$	$\mathit{t}=0.2$	CPU Time	$\mathit{t}=0.5$	CPU Time	$\mathit{t}=0.8$	CPU Time
0.1	$1.38691\times {10}^{-14}$		$4.51583\times {10}^{-14}$		$2.09416\times {10}^{-13}$
0.2	$2.67414\times {10}^{-14}$		$8.75133\times {10}^{-14}$		$4.05592\times {10}^{-13}$
0.3	$3.76216\times {10}^{-14}$		$1.24317\times {10}^{-13}$		$5.75373\times {10}^{-13}$
0.4	$4.56189\times {10}^{-14}$		$1.52871\times {10}^{-13}$		$7.05769\times {10}^{-13}$
0.5	$4.99646\times {10}^{-14}$	128.204	$1.70336\times {10}^{-13}$	128.36	$7.83984\times {10}^{-13}$	128.516
0.6	$4.99748\times {10}^{-14}$		$1.74034\times {10}^{-13}$		$7.98139\times {10}^{-13}$
0.7	$4.51958\times {10}^{-14}$		$1.6126\times {10}^{-13}$		$7.36244\times {10}^{-13}$
0.8	$3.52986\times {10}^{-14}$		$1.29452\times {10}^{-13}$		$5.88113\times {10}^{-13}$
0.9	$2.01427\times {10}^{-14}$		$7.6085\times {10}^{-14}$		$3.43864\times {10}^{-13}$

Example 3

([60]). Consider the following equation:

$$\begin{array}{cc}\hfill {\displaystyle \frac{{\partial }^{\gamma }\zeta (\sigma ,t)}{\partial t^{\gamma }}}+e^{-20t}\zeta (\sigma ,t){\displaystyle \frac{\partial \zeta (\sigma ,t)}{\partial \sigma }}+(1+100\sigma ){\displaystyle \frac{{\partial }^2\zeta (\sigma ,t)}{\partial {\sigma }^2}}& =f(\sigma ,t),\hfill \\ \hfill (\sigma ,t)\in (0,1)\times (0,1].\end{array}$$

(110)

governed by the following conditions:

$$\zeta (\sigma ,0)=\zeta (0,t)=\zeta (1,t)={\displaystyle \frac{\partial \zeta (0,t)}{\partial \sigma }}={\displaystyle \frac{\partial \zeta (1,t)}{\partial \sigma }}=0,$$

(111)

where $f(\sigma ,t)$ is selected to meet the exact solution of (110) given by

$$\zeta (\sigma ,t)=t^4{\sigma }^3{(1-\sigma )}^3.$$

(112)

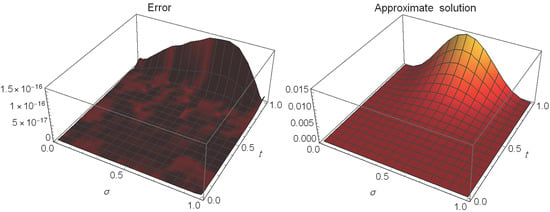
Table 6 presents a comparison of $L_{\infty }$ errors between our method at different values of γ with the method in [60]. Figure 4 shows the absolute errors (left) and approximate solution (right) at $\gamma =0.5$ and $\xi =4$ when $\mathcal{N}=6$. Table 7 reports the absolute errors and also the CPU times (in seconds) for our numerical method when $\gamma =0.3$ and $\xi =1$ when $\mathcal{N}=5$.

Table 6. Comparison of $L_{\infty }$ errors for Example 3.

$\mathit{\gamma }$	Method in [60] at ${\mathit{N}}_{\mathit{s}}=128,{\mathit{M}}_{\mathit{t}}=64$	Proposed Method at $\mathcal{N}=5$
		$\mathit{\xi }=\mathbf{4}$	$\mathit{\xi }=\mathbf{6}$	$\mathit{\xi }=\mathbf{9}$
0.6	$4.2262\times {10}^{-10}$	$5.36161\times {10}^{-17}$	$5.23705\times {10}^{-17}$	$5.91998\times {10}^{-17}$
0.8	$3.9223\times {10}^{-10}$	$2.05108\times {10}^{-16}$	$2.68635\times {10}^{-17}$	$2.4015\times {10}^{-17}$
0.95	$3.3087\times {10}^{-10}$	$5.56566\times {10}^{-17}$	$9.94028\times {10}^{-18}$	$1.01048\times {10}^{-16}$

Figure 4. The absolute errors (left) and approximate solution (right) of Example 3.

Table 7. The absolute errors of Example 3.

$\mathit{\sigma }$	$\mathit{t}=0.2$	CPU Time	$\mathit{t}=0.5$	CPU Time	$\mathit{t}=0.8$	CPU Time
0.1	$2.64486\times {10}^{-19}$		$6.77626\times {10}^{-20}$		$2.54788\times {10}^{-18}$
0.2	$7.86047\times {10}^{-19}$		$1.0842\times {10}^{-19}$		$6.93889\times {10}^{-18}$
0.3	$7.45389\times {10}^{-19}$		$3.25261\times {10}^{-19}$		$8.23994\times {10}^{-18}$
0.4	$4.13352\times {10}^{-19}$		$2.1684\times {10}^{-19}$		$9.54098\times {10}^{-18}$
0.5	$5.75982\times {10}^{-19}$	3.514	0	3.53	$1.38778\times {10}^{-17}$	3.53
0.6	$7.04731\times {10}^{-19}$		$6.50521\times {10}^{-19}$		$1.64799\times {10}^{-17}$
0.7	$1.15196\times {10}^{-18}$		$7.58942\times {10}^{-19}$		$1.77809\times {10}^{-17}$
0.8	$1.05032\times {10}^{-18}$		$8.67362\times {10}^{-19}$		$1.47451\times {10}^{-17}$
0.9	$1.999\times {10}^{-19}$		$4.47233\times {10}^{-19}$		$4.71628\times {10}^{-18}$

Example 4.

Consider the following equation:

$$\begin{array}{cc}\hfill {\displaystyle \frac{{\partial }^{\gamma }\zeta (\sigma ,t)}{\partial t^{\gamma }}}+\sigma \zeta (\sigma ,t){\displaystyle \frac{\partial \zeta (\sigma ,t)}{\partial \sigma }}+\sigma {\displaystyle \frac{{\partial }^2\zeta (\sigma ,t)}{\partial {\sigma }^2}}+{\displaystyle \frac{{\partial }^4\zeta (\sigma ,t)}{\partial {\sigma }^4}}& =f(\sigma ,t),\hfill \\ \hfill (\sigma ,t)\in (0,1)\times (0,1].\end{array}$$

(113)

governed by the following conditions:

$$\zeta (\sigma ,0)=\zeta (0,t)=\zeta (1,t)={\displaystyle \frac{{\partial }^2\zeta (0,t)}{\partial {\sigma }^2}}={\displaystyle \frac{{\partial }^2\zeta (1,t)}{\partial {\sigma }^2}}=0,$$

(114)

where $f(\sigma ,t)$ is selected to meet the exact solution of (113) given by

$$\zeta (\sigma ,t)=t^{4+\alpha }sin\left(\pi \sigma \right).$$

(115)

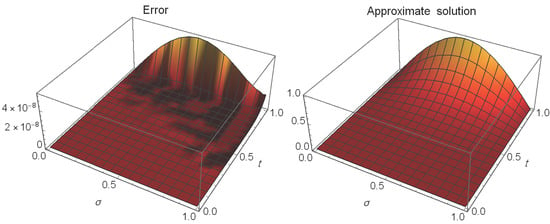
Table 8 reports the absolute errors and also the CPU times (in seconds) for our numerical method at $\gamma =0.5$ and $\xi =1$ when $\mathcal{N}=18$. Figure 5 illustrates the absolute errors and approximate solution at $\gamma =0.8$ and $\xi =3$ when $\mathcal{N}=18$.

Table 8. The absolute errors of Example 4.

$\mathit{\sigma }$	$\mathit{t}=0.3$	CPU Time	$\mathit{t}=0.6$	CPU Time	$\mathit{t}=0.9$	CPU Time
0.1	$1.29728\times {10}^{-10}$		$1.46848\times {10}^{-10}$		$9.63238\times {10}^{-10}$
0.2	$2.46753\times {10}^{-10}$		$2.7931\times {10}^{-10}$		$1.83216\times {10}^{-9}$
0.3	$3.39616\times {10}^{-10}$		$3.84417\times {10}^{-10}$		$2.52169\times {10}^{-9}$
0.4	$3.99227\times {10}^{-10}$		$4.51879\times {10}^{-10}$		$2.96434\times {10}^{-9}$
0.5	$4.19752\times {10}^{-10}$	131.47	$4.75101\times {10}^{-10}$	131.626	$3.1168\times {10}^{-9}$	131.783
0.6	$3.99187\times {10}^{-10}$		$4.51818\times {10}^{-10}$		$2.96418\times {10}^{-9}$
0.7	$3.3955\times {10}^{-10}$		$3.84318\times {10}^{-10}$		$2.52143\times {10}^{-9}$
0.8	$2.46683\times {10}^{-10}$		$2.79214\times {10}^{-10}$		$1.83191\times {10}^{-9}$
0.9	$1.29681\times {10}^{-10}$		$1.4679\times {10}^{-10}$		$9.63091\times {10}^{-10}$

Figure 5. The absolute errors and approximate solution of Example 4 at $\gamma =0.8$.

Remark 6.

The algorithm designed in this paper was suitable for handling Equation (73) in the square domain. The same problem has been solved through other numerical algorithms, such that was those developed in [60]. The numerical results in this section showed the high accuracy and applicability of our algorithm using the combined CPs.

Remark 7.

To handle the problem defined on irregular domains, the method can be extended by employing a suitable curvilinear coordinate transformation, which maps an irregular physical domain into a square domain; however, this requires a comprehensive analysis. We aim to investigate this problem in a separate study in future work.

7. Concluding Remarks

In this work, an efficient collocation framework is analyzed for the numerical solution of the time-fractional Kuramoto–Sivashinsky equation. Certain combined orthogonal polynomials were utilized for this purpose. Some theoretical results of these polynomials, such as the power form representation and their inversion formula, were pivotal in establishing the integer and fractional operational matrices of derivatives. These formulas were essential in designing the numerical algorithm. Through a series of numerical experiments, the method has shown excellent agreement with exact solutions and significant improvements over recently developed algorithms. We expect that other classes of differential equations may be treated using the CCPs. In addition, we aim to introduce other combined orthogonal polynomials and utilize them in numerical analysis. All codes were written and debugged using Mathematica 11 on an HP Z420 Workstation, with an Intel(R) Xeon(R) CPU E5-1620 processor, v2, 3.70 GHz; 16 GB of RAM, DDR3; and 512 GB of storage.