Fractional-Order Black-Winged Kite Algorithm for Moving Target Search by UAV

Abstract

The nonlocality (capable of associating target dynamics across multiple time moments) and memory properties (able to retain historical trajectories) of fractional calculus serve as the core theoretical approach to resolving the “dynamic information association deficiency” in UAV mobile target search. This paper proposes the Fractional-order Black-winged Kite Algorithm (FOBKA), which transforms the search problem into an adaptability function optimization model aimed at “maximizing target capture probability” based on Bayesian theory. Addressing the limitations of the standard Black-winged Kite Algorithm (BKA), the study incorporates fractional calculus theory for enhancement: A fractional-order operator is embedded in the migration behavior phase, leveraging the memory advantage of fractional-orders to precisely capture the temporal span, spatial position, and velocity evolution of targets, thereby enhancing global detection capability and convergence accuracy. Simultaneously, population individuals are initialized using motion-encoding, and the attack behavior phase combines alternating updates with a Lévy flight mechanism to balance local exploration and global search performance. To validate FOBKA’s superiority, comparative experiments were conducted against eight newly proposed meta-heuristic algorithms across six distinct test scenarios. Experimental data demonstrate that FOBKA significantly outperforms the comparison algorithms in convergence accuracy, operational robustness, and target capture probability.

1. Introduction

In recent years, unmanned aerial vehicles (UAVs) have become a key technological enabler driving intelligent transformation across various industries, including public safety surveillance [1,2], emergency disaster search [3,4,5], and rescue operations [6,7,8,9], with these capabilities being empowered by advances in autonomous navigation, efficient vision perception [10] and real-time decision-making systems. Consequently, related research and applications have garnered significant attention from both academia and industry. The use of UAVs for missing person searches represents a core research direction within emergency response to disasters. During such searches, the probability of detection of the target decreases significantly over time due to the degradation of initial information and interference from external dynamic factors such as weather, terrain, and target status. Consequently, these missions feature a critical ’golden time’ period in which the probability of detection must be maintained at the highest levels. Given these constraints, the core requirement for UAV search operations can be defined as follows: under specified initial target locations and search constraints, plan an optimal path within a limited flight duration that maximizes the probability of target detection.

In the research of UAV-based target search, path planning algorithms are generally divided into four categories: (1) graph search-based, (2) potential field-based, (3) sample-based, and (4) intelligent algorithms [11]. Graph search-based rely on pre-constructed static graphs and cannot dynamically incorporate target probability information. Potential field-based are prone to local optima and cannot adjust paths based on real-time changes in target probability. Sample-based suffer from excessive computational load at high sampling densities, while low densities risk overlooking high-probability paths. Dynamic target trajectory changes necessitate frequent reconstruction of sample trees, exacerbating latency. Mobile target search involves multiple probabilistic variables; as search dimensions expand and flight duration increases, the number of candidate solutions grows exponentially, making this problem inherently NP-hard (Non-deterministic Polynomial-time hard) [12,13]. Thus, algorithms from categories (1), (2), and (3) have low practical feasibility for solving high-probability path problems. By contrast, metaheuristic algorithms (a subset of category 4) offer more promising solutions for UAV path planning. Derived from nature-inspired heuristic rules, they simulate biological evolution, animal group behavior, and natural selection to find optimal solutions [14]. Their key advantage is independence from specific problem modeling—they approach optimal solutions via iterative search and optimization, and excel at handling complex nonlinear or nonconvex problems, achieving global search, and exploring large-scale solution spaces [15].

UAV path planning for moving target search is a specialized branch in the field of path planning focusing on “target dynamics and position uncertainty” [16]. Its core requirement is that the UAV must address the probabilistic ambiguity of the target’s position while adapting to the target’s dynamic displacement over time, and thus design paths with real-time adjustment capabilities, ultimately maximizing the cumulative target detection probability in the early stage of the search when the detection probability is highest. The core difference between this requirement and traditional static path planning lies in that the former needs to continuously respond to the dynamic adjustment of the solution space caused by the target’s dynamic migration and changes in position probability, while the latter does not need to deal with such real-time changes.

In recent years, to address the challenge of searching for moving targets, the academic community has proposed various swarm intelligence approaches. For example, Phung et al. incorporated motion encoding mechanisms into various swarm intelligence algorithms to enhance the efficiency of drone path planning, thereby generating optimal paths through the proposed novel algorithm [16,17,18,19]. Ma et al. propose a Convex Combination Multiple Populations Competitive Swarm Optimization algorithm (CDCSO), which employs a multi-population strategy and convex combination update policy to coordinate two subpopulations in jointly seeking the global optimum solution for mobile target search problems [20]. Garg proposes an Exploration Enhanced Robotic Ground-Based Object Search (E2RGWO) to address multi-object search problems in uncharted environments. This algorithm incorporates random individuals into the position update equation to enhance exploration capabilities. Test results indicate that E2RGWO achieves high detection rates when searching for static objects but exhibits poor diversity during dynamic target searches [21]. Although heuristic algorithms offer numerous advantages in solving moving target search problems, the difficulty of finding optimal solutions increases as the number of moving targets grows, often leading them to become trapped in local optima.

In this case, to overcome the defects of the metaheuristic algorithm and further improve its performance, this paper embeds fractional calculus into the metaheuristic algorithm to enhance its development capabilities and improve the algorithm’s convergence accuracy. Compared to integer-order calculus, fractional calculus fully captures the memory of historical events [22]. In recent years, fractional calculus has been repeatedly applied in meta-heuristic algorithms to enhance their performance. Guo et al. proposed the Fractional-Order Fish Migration Optimization Algorithm (FOFMO) based on fractional calculus theory [23]. This algorithm avoids the tendency of integer-order methods to “skip optimal solutions,” thereby enhancing optimization accuracy. However, it has only been validated for simple PID systems and has not been compared with commonly used industrial PID tuning algorithms, resulting in its engineering application value not being fully demonstrated. Cui et al. incorporated the memory properties of fractional calculus into the observation phase, enhancing the algorithm’s local search capability by utilizing historical foraging data to assist new solution generation [24]. This effectively improved global optimization accuracy. However, core parameters such as the fractional order and number of memory terms in this improved algorithm exhibit poor generalizability. When the optimization problem dimension increased from 10 to 50, performance maintenance required readjusting the memory terms. Xia et al. employed fractional calculus strategies to dynamically adjust and optimize regional boundaries, enabling the algorithm to precisely target potential optimization zones [25]. The improved algorithm was applied to six practical industrial engineering optimization scenarios, yielding excellent results in each case. This further demonstrates the application potential of fractional calculus in complex engineering contexts. In summary, incorporating fractional-order calculus into meta-heuristic algorithms effectively addresses the performance limitations of traditional integer-order methods, significantly enhancing optimization accuracy and scenario adaptability. This provides robust literature support and theoretical justification for the algorithmic improvements proposed in this paper.

Based on the insights from applying fractional calculus to enhance the performance of meta-heuristic algorithms, and considering the core requirements of maximizing target capture probability and search efficiency within limited time for UAV mobile target search tasks, this study aims to design an efficient and stable path planning search algorithm tailored for this scenario. This approach addresses the critical issues of low positioning accuracy and insufficient search robustness in dynamic target search. The Black-winged Kite Algorithm (BKA), while possessing swarm search characteristics, exhibits significant shortcomings in dynamic target search: First, the limited search space during the initialization phase results in insufficient population diversity, leading to low target localization probability. Second, the absence of mutation mechanisms during the attack phase makes it prone to getting stuck in local optima. Third, the migration phase fails to retain historical search information, resulting in poor dynamic adaptability to target trajectories. To address the limitations of the BKA algorithm, this paper proposes a Fractional-order Black-winged Kite Algorithm (FOBKA) for UAV mobile target search tasks. By incorporating a fractional-order strategy and leveraging its memory characteristics, this algorithm effectively identifies high-probability target regions and generates paths with optimized search probabilities, thereby enhancing overall search performance. From the perspective of practical application value, this research holds two significant implications: On one hand, it provides actionable algorithmic solutions for optimizing the performance of UAV mobile target search missions, thereby enhancing mission execution efficiency and accuracy. On the other hand, it advances the continuous improvement of UAV autonomy and intelligence, strengthening their search and monitoring capabilities in complex environments.

The main contributions of this paper are as follows: (1) Designing a novel motion encoding mechanism during the initialization phase of the BKA: Addressing the limitation of BKA’s finite search space, this mechanism expands the search range to enhance population diversity and improve the probability of locating dynamic targets, making it more suitable for complex scenarios such as dynamic target search. (2) Introduction of alternating updates and Lévy flight mechanisms during the attack phase: To address BKA’s susceptibility to local optima, these mechanisms enhance global search capabilities by increasing mutation variability. (3) Integration of fractional-order strategies during the migration phase: To overcome BKA’s inability to retain historical information, fractional-order memory properties are employed to accurately model temporal and spatial variations in target trajectories, thereby improving convergence accuracy.

The structure of this paper is as follows: Section 2 introduces the mathematical model for the mobile target search problem using UAVs. Section 3 describes the standard BKA algorithm. Section 4 presents the FOBKA method. Section 5 applies the novel algorithm to simulate and experimentally demonstrate the path planning problem for UAV mobile target search. Section 6 analyzes the simulation results, while Section 7 summarizes the findings of this study.

2. Problem Formulation

Moving target search using UAVs is a critical challenge in UAV applications, aiming to determine a drone path that maximizes the target’s observation probability within a short time. The objective function is formulated based on the target, sensor, and belief graph models.

2.1. Moving Target

In the search problem for moving targets, the target’s spatial position is represented by the variable m. Due to uncertainty in the target’s location prior to search initiation, a mathematical model based on a probability distribution function is employed to quantify positional possibilities before the UAV commences search operations. This model is determined by whether the target’s last known position is missing. When the last known position is available, the probability distribution function is typically modeled as a normal distribution centered on that last position. When the last known position is missing, the probability distribution function becomes a uniform distribution, reflecting the uncertainty surrounding the last known location. To concretize this probability distribution function within the search space, the search domain R can be defined as an $S_r\times S_c$ discrete grid, forming a belief map $g\left(m_0\right)$. Each grid cell corresponds to a probability, and the sum of probabilities across the $S_r\times S_c$ grid cells equals ${\sum }_{m_0\in R}g\left(m_0\right)=1$.

In the process of UAV moving target search, the probability of the target’s future position depends only on its current position; thus, the target motion pattern is modeled as a Markov process. This characteristic can not only adapt to the limitation that UAVs can only obtain real-time or recent information but also support the dynamic update of the belief map based on recursive Bayesian estimation, while reducing the problem complexity to meet real-time search requirements. Since all the targets in this study have specific conditions, the motion of the target depends only on its initial position $m_0$. In this context, the probability of the target transitioning from grid $m_{t-1}$ to grid $m_t$ is denoted as $P(m_t\mid m_{t-1})$. Since the probabilities of all cells are known, according to Bayes’ theorem, if the initial position of the target is known, the complete trajectory of movement of the target can be obtained.

2.2. Sensor Model

To achieve search and detection objectives, the UAV is equipped with a sensor system. At every time step t, an observation is made and a detection algorithm is implemented, returning a result for each observation, denoted as $O_t$. If the target is successfully captured, record it as $O_t=H_t$; otherwise, record it as $O_t={\overline{H}}_t$. Since the target is moving and there is inherent latency in the sensors and search algorithms, even when a target is detected (i.e., $O_t=H_t$), it cannot be guaranteed that the target remains at position $m_t$. For such scenarios, the probability that a target is present at a given position $m_t$ but remains undetected can be calculated using Equation (1).

$$P(\overline{H_t}\mid m_t)=1-P(H_t\mid m_t).$$

(1)

2.3. Belief Graph Update

After $g\left(m_0\right)$ is determined, the system dynamically updates the belief map using Bayesian methods [26] and the sensor-acquired detection sequence $O_{1:t}=O_1,O_2,\cdots ,O_t$, thereby determining the belief map for the target location. This technique operates through two main phases: recursive prediction and recursive update, known as the recursive Bayesian estimation method. As time progresses, predicting the next belief map based on the target motion model is crucial during dynamic optimization. Given the known belief map $g\left(m_{t-1}\right)$, the next belief map at time t is predicted as follows:

$$\widehat{g}\left(m_t\right)=\sum _{m_{t-1}\in R}P(m_t\mid m_{t-1})g\left(m_{t-1}\right).$$

(2)

From Equation (2), it follows that when the target is at grid $m_{t-1}$, its belief map is $g\left(m_{t-1}\right)$. This also represents the conditional probability of the target from time 1 to time $t-1$, i.e., $g\left(m_{t-1}\right)=P\left(m_{t-1}\right|O_{1:t-1})$. Given the known target position $m_t$, the predicted belief map $g\left(m_t\right)$ at time t can be derived from Equation (2). Multiplying this by the computed conditional probability $g\left(m_t\right)=P\left(m_t\right|O_t)$ yields the belief map update formula, as shown below:

$$g\left(m_t\right)={\gamma }_{t}P(O_t\mid m_t)\widehat{g}\left(m_t\right),$$

(3)

$${\gamma }_t={\displaystyle \frac{1}{{\sum }_{m_t\in R}P(O_t\mid m_t)\widehat{g}\left(m_t\right)}},$$

(4)

here ${\gamma }_t$ functions as a normalization factor, ensuring the target stays within the search domain. Essentially, ${\gamma }_t$ guarantees that ${\sum }_{m_t\in R}g\left(m_t\right)=1$ holds true.

2.4. Fitness Function for Moving Target Search

According to Bayes’ theorem, when the sensor is performing detection, the conditional probability that the target was not detected from time 1 to time $t-1$ can be expressed as ${\delta }_t=P(\overline{H_t}\mid O_{1:t-1})$. The specific calculation method is shown in the following equation:

$${\delta }_t=\sum _{m_t\in R}P({\overline{H}}_t\mid m_t)\widehat{g}\left(m_t\right),$$

(5)

according to Equations (4) and (5), the relationship ${\delta }_t=1/{\gamma }_t$ can be derived.

When the observation event $O_t$ corresponds to “no target detected at time t” (i.e., $O_t={\overline{H}}_t$), the undetected state is triggered. By accumulating the undetected probabilities at each time point, the joint probability of continuous undetection from time 1 to time t, ${\beta }_t=P\left({\overline{H}}_{1:t}\right)$, can be calculated, yielding its expression of probability,

$${\beta }_t=\prod _{l=1}^t{\delta }_l={\beta }_{t-1}·{\delta }_t.$$

(6)

Therefore, if the target is first detected at time t, its probability is calculated according to Equation (7).

$$P_t=\prod _{l=1}^{t-1}{\delta }_l(1-{\delta }_t)={\beta }_{t-1}·(1-{\delta }_t),$$

(7)

by summing the $p_t$ values calculated from time 1 to t using Equation (7), the probability ${\chi }_t$ of detecting the target throughout the entire detection process. A higher value indicates that the algorithm’s Bayesian inference has concentrated on a ‘high-probability target region,’ increasing the likelihood of target detection and providing more reliable positional reference for subsequent capture actions. The calculation method is as follows:

$${\chi }_t=\sum _{l=1}^t{P}_l={\chi }_{t-1}+P_t.$$

(8)

Equations (6) and (8) respectively give the relationship between the “probability of not finding the target” ${\beta }_t$ and the “probability of finding the target” ${\chi }_t$ during the time interval from the start to time t, as follows:

$${\chi }_t=1-{\beta }_t.$$

(9)

The objective of the problem is to find an optimal detection path $w=w_1,w_2,\cdots ,w_T$ that maximizes the cumulative probability ${\chi }_t$ within a given search time interval $1,2,\cdots T$. Therefore, the fitness function for the search problem can be expressed as Equation (10).

$$C=\sum _{t=1}^T{\chi }_t.$$

(10)

3. Sand Black-Winged Kite Algorithm

The BKA is a new metaheuristic algorithm inspired by the survival strategy of black-winged kites [27]. It mainly consists of two different stages: attack behavior and migration behavior.

3.1. Initialization Phase

During the initialization phase of the BKA, a set of solutions is first randomly generated based on the problem’s given constraints using Equation (11). Here, a matrix is used to represent the position of each black-winged kite in the population:

$$X=\left[\begin{array}{cccc}{x}_{1,1}& x_{1,2}& \cdots & x_{1,\dim }\\ x_{2,1}& x_{2,2}& \cdots & x_{2,\dim }\\ ⋮& ⋮& \ddots & ⋮\\ x_{N,1}& x_{N,2}& \cdots & x_{N,\dim }\end{array}\right]$$

(11)

in this context, N denotes the number of individuals contained within the group, $dim$ denotes the number of dimensions in the problem, and $x_{ij}$ indicates the position of the $i\text{-}th$ black-winged kite in the $j\text{-}th$ dimension. The individuals in population X are generated by Equation (12).

$$x_i=x_{\mathrm{lb}}+rand(x_{\mathrm{ub}}-x_{\mathrm{lb}}),$$

(12)

where i denotes integers from 1 to N, where the lower and upper bounds of the black-winged kite’s position are $x_{lb}$ and $x_{ub}$, respectively. Meanwhile, $rand$ represents a random value generated within the interval $[0,1]$.

During the initialization phase, the BKA ranks the fitness values of all individuals in the population and selects the optimal individual as the leader $X_L$. Taking the minimization of a problem as an example, $X_L$ is represented as follows:

$$f_{\mathrm{best}}=min\left(f\left(x_i\right)\right),$$

(13)

$$X_L=x\left(find(f_{\mathrm{best}}=f\left(x_i\right))\right).$$

(14)

3.2. Attacking Behavior

The black-winged kite feeds on small animals and insects. During hunting, it adjusts the angle of its wings and tail feathers according to wind speed while flying, circling overhead to observe prey before launching a swift dive attack. This strategy incorporates multiple attack behaviors for comprehensive exploration and search. Its mathematical model is as shown in Equation (15).

$$x_i(t+1)=\left\{\begin{array}{cc}{x}_i\left(t\right)+n(1+sin\left(r\right))\times x_i\left(t\right)\hfill & p<r,\hfill \\ x_i\left(t\right)+n\times (2r-1)\times x_i\left(t\right)\hfill & \mathrm{else},\hfill \end{array}\right.$$

(15)

$$n=0.05\times e^{-2\times {(t/T)}^2},$$

(16)

in this context, $x_i\left(t\right)$ and $x_i(t+1)$ denote the positions of the ith black-winged kite at iterations t and $t+1$, respectively. where $r\in [0,1]$ and $p=0.9$. T denotes the total number of iterations, while t indicates the current iteration number.

3.3. Migration Behavior

Bird migration is a complex behavior driven by environmental conditions such as climate change and the distribution of food resources, demonstrating adaptability to seasonal shifts. Many bird species migrate southward from the north during winter to access more favorable resources. During migration, the lead bird typically takes the lead, and its navigational abilities are critical to the group’s success. Based on this hypothesis: When the current flock’s adaptability falls below that of a random group, the lead bird relinquishes its position and rejoins the flock, indicating its unsuitability for leadership. Conversely, it continues guiding the flock forward to reach the destination. This approach dynamically selects superior leaders, ensuring the successful completion of migration. Its mathematical model is as shown in Equation (17).

$$x_i(t+1)=\left\{\begin{array}{cc}{x}_i\left(t\right)+C(0,1)\times \left(x_i\left(t\right)-L_t\right)\hfill & F_i<F_{ri},\hfill \\ x_i\left(t\right)+C(0,1)\times \left(L_t-m·x_i\left(t\right)\right)\hfill & \mathrm{else},\hfill \end{array}\right.$$

(17)

$$m=2\times \sin (r+\pi /2),$$

(18)

$L_t$ indicates that the black-winged kite is the leader in terms of score in the t-th iteration. At iteration t, $F_i$ denotes the fitness value of the tth individual. $F_{ri}$ represents the fitness value of any individual. $C(0,1)$ indicates Cauchy mutation.

Equation (19) is an expression for the one-dimensional Cauchy distribution function.

$$f(x,\delta ,\mu )={\displaystyle \frac{1}{\pi }}·{\displaystyle \frac{\delta }{{\delta }^2+{(x-\mu )}^2}},-\infty <x<+\infty ,$$

(19)

when $\delta =1$ and $\mu =0$, the function assumes its standard form, whose exact formula is as follows:

$$f(x,\delta ,\mu )={\displaystyle \frac{1}{\pi }}·{\displaystyle \frac{1}{x^2+1}},-\infty <x<+\infty .$$

(20)

The pseudocode for BKA is shown in Algorithm 1.

Algorithm 1: Algorithm Pseudocode of BKA

Input: Population initialization parameters: population size $pop$, maximum iterations T, dimension $dim$ Output: Best fitness $F\left(X_{\mathrm{best}}\right)$, best position $X_{\mathrm{best}}$ 1: Initialize black-winged kite population 2: Set parameter $p=0.9$ and calculate initial fitness values 3: for $t=1$ to T do 4:     Calculate fitness for each individual and determine current optimal value 5:     for $i=1$ to $pop$ do 6:         Execute attack behavior 7:         if $p<r$ then 8:            Update $x_i$ using Equation (15)             ▹ p < r 9:         else 10:            Update $x_i$ using Equation (15)            ▹ p > r 11:         end if 12:         Execute migration behavior 13:         if $F_i<F_{ri}$ then 14:            Update $x_i$ using Equation (17)         ▹$F_i<F_{ri}$ 15:         else 16:            Update $x_i$ using Equation (17)         ▹$F_i>F_{ri}$ 17:         end if 18:     end for 19:     Update global optimal solution 20: end for

4. Proposed Work

The motion target search problem tackled in this study poses considerable computational challenges in optimization. Specifically, as the problem scale expands, the time required to globally traverse feasible paths and find optimal solutions grows exponentially. To tackle this issue, the BKA is adopted as the solution method for dynamic goal search problems. However, considering the inherent limitations of this algorithm, three enhancement strategies are further integrated to strengthen its optimization capabilities. The specific improvement methods are detailed below.

4.1. Population Initialization Method Using Motion-Encoded Mechanism

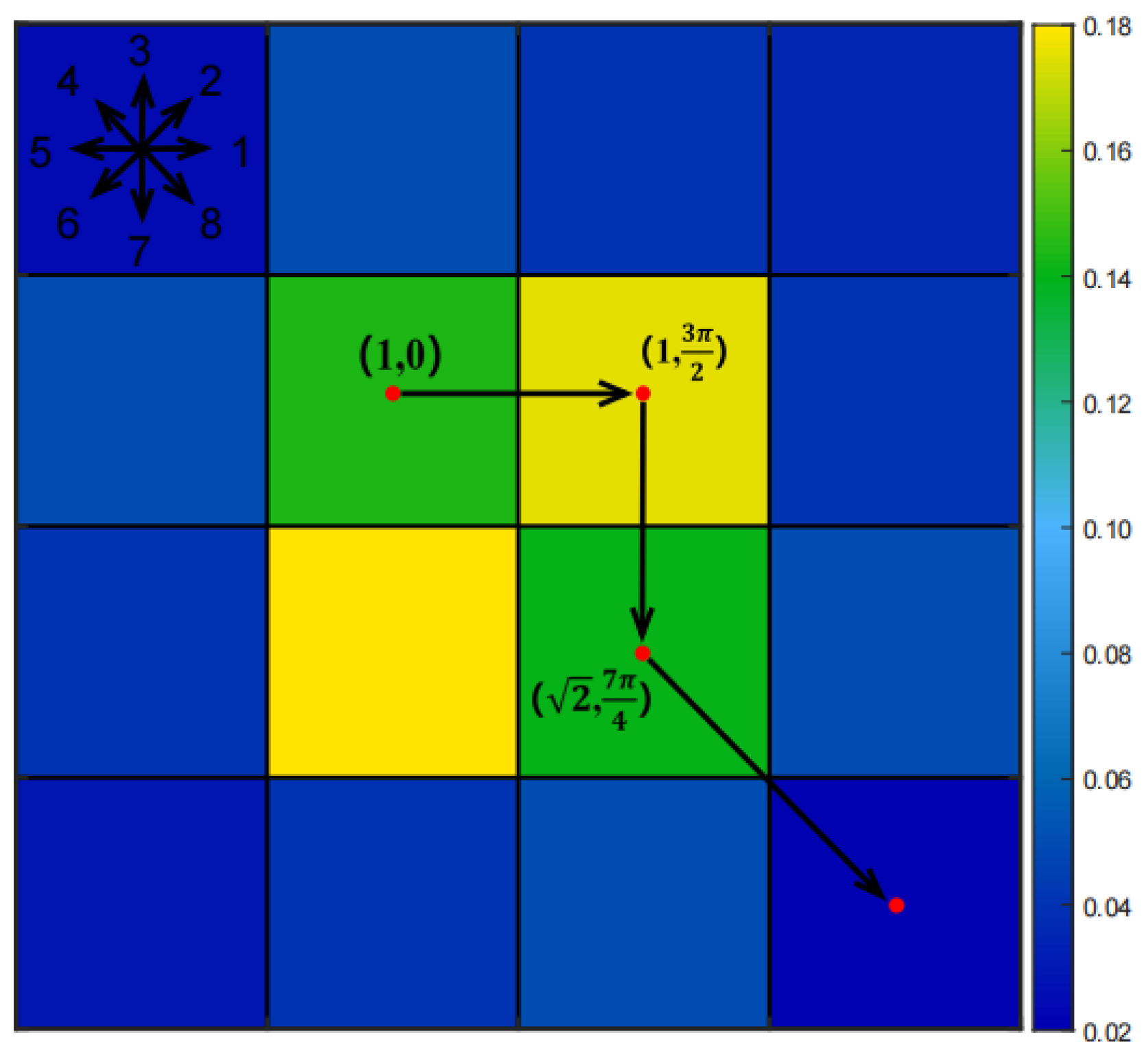
In the problem of using UAVs to search for dynamic targets in complex environments, the most common approach involves encoding the positions of individual population members and gradually seeking a global optimal solution. Individuals’ positions in Cartesian space are represented by vectors containing search path points (e.g., $W_i=\{w_{i,1},w_{i,2},\cdots ,w_{i,n}\}$, where $w_{i,1}$ denotes a point in the belief graph grid). Due to insufficient coverage of adjacent nodes, this method is prone to generating invalid paths.

In contrast, methods such as angle encoding [28] and priority encoding [29] for individuals can better search for the optimal path. Therefore, it is necessary to perform motion encoding on the positions of the initial population individuals. Firstly, the search path is represented as a set of UAV movement segments, denoted as $S_i=\{s_{i,1},s_{i,2},\cdots ,s_{i,n}\}$. Each search path contains n motion segments, and each segment corresponds to the movement of the drone between grids in a single time period (motion vector $s_{i,t}=({\phi }_{i,t},{\theta }_{i,t}),t\in (1,n)$, where ${\phi }_{i,t}$ and ${\theta }_{i,t}$ represent the amplitude and direction of motion in the time domain), its motion process is shown in the Figure 1. The position of the ith individual in the population serves as the counterpart of the search path $S_i$.

Figure 1. An example of a search path based on motion-encoding, where colors on the discrete grid represent the probability of target appearance (see probability bar on the right). The red dot indicates the UAV’s position, and directional arrows show the eight possible movement directions between the UAV and the target.

During the search, $S_i$ is mapped to the node path $W_i$ to evaluate fitness. The UAV is restricted to moving only along the eight adjacent grids to the location of the previous time point during a single time interval. ${\phi }_{i,t}$ is then normalized, and ${\theta }_{i,t}$ is calculated as follows.

$${\phi }_{i,t}^{\ast }=1,$$

(21)

$${\theta }_{i,t}^{\ast }={45}^{\circ }⌊{\theta }_{i,t}/{45}^{\circ }⌉,$$

(22)

among them, is the integer symbol. Next, calculate the node position of the UAV in Cartesian space using Equation (23).

$$w_{i,t+1}=w_{i,t}+s_{i,t}^{\ast },$$

(23)

where $s_{i,t}^{\ast }=\left(⌊cos{\theta }_{i,t}^{\ast }⌉,⌊sin{\theta }_{i,t}^{\ast }⌉\right)$.

The motion-encoding mechanism preserves the iterative update steps inherent to the BKA. Compared to traditional Cartesian coordinate systems, the BKA integrated with motion encoding enables autonomous exploration within the search space, with each movement restricted to adjacent cells. This movement pattern aligns precisely with the operational mode of unmanned aerial vehicles, thereby enhancing the feasibility of the algorithm’s generated paths.

4.2. Attack Behavior Based on the Lévy Flight

Many flying animals exhibit flight behavior characterized by Lévy flight [30]. Lévy flight is a random walk strategy in which the step lengths follow a distribution with a long-tail characteristic, exhibiting a “jumping” feature. This means that individuals following this pattern will exhibit periodic “large step” movements interspersed with numerous frequent “small step” movements [31]. The Lévy distribution and the calculation of Lévy flight step lengths are given by Equations (24) and (25).

$$\mathrm{L}é\mathrm{vy}\left(\beta \right)\sim {\left|s\right|}^{-\beta },1<\beta <3,$$

(24)

$$s={\displaystyle \frac{u}{{\left|v\right|}^{1/\beta }}},0<\beta <2,$$

(25)

in this study, $\beta =1.5$; u and v are both random numbers that follow a normal distribution, i.e., $u\sim N(0,{\sigma }_u^2)$,$v\sim N(0,{\sigma }_v^2)$, where ${\sigma }_v=1$, and ${\sigma }_u$ is given by the following formula:

$${\sigma }_u={\left\{{\displaystyle \frac{\mathsf{\Gamma }(1+\beta )·sin(\pi \beta /2)}{\mathsf{\Gamma }\left(\frac{1+\beta }{2}\right)·\beta ·2^{(\beta -1)/2}}}\right\}}^{1/\beta },$$

(26)

where $\mathsf{\Gamma }$ denotes the gamma function. To enhance the algorithm’s global exploration capabilities and enable it to better adapt to target searches in dynamic environments. An alternating update mechanism is introduced in the attack behavior phase of BKA algorithm. When the random number $\epsilon >0.2$, the algorithm updates individuals using Equation (15); when the random number $\epsilon <0.2$, the algorithm updates individuals using Equation (27).

$$x_i(t+1)=x_i\left(t\right)+(X_{\mathrm{L}}-x_i\left(t\right))·\mathrm{L}é\mathrm{vy}\left(\beta \right),$$

(27)

$X_{\mathrm{L}}$ represents the position of the current global optimal individual and $\beta =1.5$.

4.3. Fractional-Order Migration Behavior

Fractional calculus, as a branch of mathematical analysis, is an extension of the classical integer-order calculus concepts. This calculus method not only exhibits superior memory and hereditary characteristics [24] but also represents a significant breakthrough in the field of integer-order calculus. Fractional calculus has multiple definitions, with commonly used definitions including the Grünwald-Letnikov (G-L) [32], Riemann-Liouville [33], and Caputo [34]. The G-L definition, due to its discretization properties, is frequently used in numerical simulations and serves as the foundation for numerical computations. Therefore, this study primarily employs the G-L definition of fractional calculus for mathematical derivations. The commonly used expression for the G-L definition is as follows:

$$D^{\alpha }\left[x\left(t\right)\right]=\underset{h\to 0}{lim}\left[{\displaystyle \frac{1}{h^{\alpha }}}\sum _{k=0}^{+\infty }{\displaystyle \frac{{(-1)}^k\mathsf{\Gamma }(\alpha +1)x(t-kh)}{\mathsf{\Gamma }(k+1)\mathsf{\Gamma }(\alpha -k+1)}}\right],$$

(28)

where $\alpha$ represents the order (when $\alpha >0$, it is the fractional derivative; when $\alpha <0$, it is the fractional integral), h is the step size, which approaches 0 in the limit; $\mathsf{\Gamma }$ is the gamma function. The discrete expression of Equation (28) is as follows:

$$D^{\alpha }\left[x\left(t\right)\right]={\displaystyle \frac{1}{T^{\alpha }}}\sum _{k=0}^r{\displaystyle \frac{{(-1)}^k\mathsf{\Gamma }(\alpha +1)x(t-kT)}{\mathsf{\Gamma }(k+1)\mathsf{\Gamma }(\alpha -k+1)}},$$

(29)

where T is the sampling period and r is the cut-off order. To achieve discretization in the most concise form and facilitate subsequent calculations, let $T=1$. From Equation (29), the weights of each historical term decay rapidly as k increases, making the contribution of terms with $r\ge 4$ negligible. Furthermore, the summation approximation renders the computational complexity linearly proportional to r. Overall, $r=4$ suffices to capture effective memory. Expanding Equation (29) yields the following:

$$\begin{array}{cc}\hfill D^{\alpha }\left[x(t+1)\right]& =x(t+1)-\alpha x\left(t\right)+{\displaystyle \frac{1}{2}}\alpha (\alpha -1)x(t-1)-\hfill \\ & {\displaystyle \frac{1}{6}}\alpha (\alpha -1)(\alpha -2)x(t-2)+{\displaystyle \frac{1}{24}}\alpha (\alpha -1)\hfill \\ & (\alpha -2)(\alpha -3)x(t-3).\hfill \end{array}$$

(30)

To avoid the BKA falling into a local optimum trap, this study introduces a fractional-order strategy into the migration behavior of the BKA to balance the global search and local detection capabilities of the algorithm. By rearranging the mathematical model Equation (17) for the migration behavior in the BKA, the following formula can be obtained:

$$x_i(t+1)-x_i\left(t\right)=C(0,1)\times (x_i\left(t\right)-L_t),F_i<F_{ri},$$

(31)

$$x_i(t+1)-x_i\left(t\right)=C(0,1)\times \left(L_t-m\times x_i\left(t\right)\right),\mathrm{else}.$$

(32)

According to the $G-L$ definition, the leftmost part of Equations (31) and (32) is the discrete form of the first derivative (assuming $T=1$), which leads to the following formula:

$$D^{\alpha }\left[x(t+1)\right]=C(0,1)\times (x_i\left(t\right)-L_t),F_i<F_{ri},$$

(33)

$$D^{\alpha }\left[x(t+1)\right]=C(0,1)\times \left(L_t-m\times x_i\left(t\right)\right),\mathrm{else}.$$

(34)

Substituting the Equation (30) for the fractional-order differential expansion into Equation (33) and (34), the fractional-order individual update formula for migration behavior can be obtained:

$$\begin{array}{cc}\hfill x_i(t+1)& =\alpha x_i\left(t\right)-{\displaystyle \frac{1}{2}}\alpha (\alpha -1)x_i(t-1)+{\displaystyle \frac{1}{6}}\alpha (\alpha -1)(\alpha -2)\hfill \\ & x_i(t-2)-{\displaystyle \frac{1}{24}}\alpha (\alpha -1)(\alpha -2)(\alpha -3)x_i(t-3)+\hfill \\ & C(0,1)\times \left(x_i\left(t\right)-L_t\right),F_i<F_{ri},\hfill \end{array}$$

(35)

$$\begin{array}{cc}\hfill x_i(t+1)& =\alpha x_i\left(t\right)-{\displaystyle \frac{1}{2}}\alpha (\alpha -1)x_i(t-1)+{\displaystyle \frac{1}{6}}\alpha (\alpha -1)(\alpha -2)\hfill \\ \hfill & x_i(t-2)-{\displaystyle \frac{1}{24}}\alpha (\alpha -1)(\alpha -2)(\alpha -3)x_i(t-3)+\hfill \\ & C(0,1)\times \left(L_t-m\times x_i\left(t\right)\right),\mathrm{else}.\hfill \end{array}$$

(36)

From Equations (35) and (36), it can be seen that the current fractional-order differential results are correlated with the individual state values of the previous three generations, and these historical state values have a gradually decreasing influence on the current state as time progresses. Its unique memory characteristic enables it to more accurately describe processes with changes in time, spatial position, and speed. Therefore, introducing fractional-order differential into the migration behavior of the BKA can dynamically adjust the search direction, enhance global exploration ability, and avoid local optimality.

4.4. Algorithm FOBKA Steps and Flow Chart

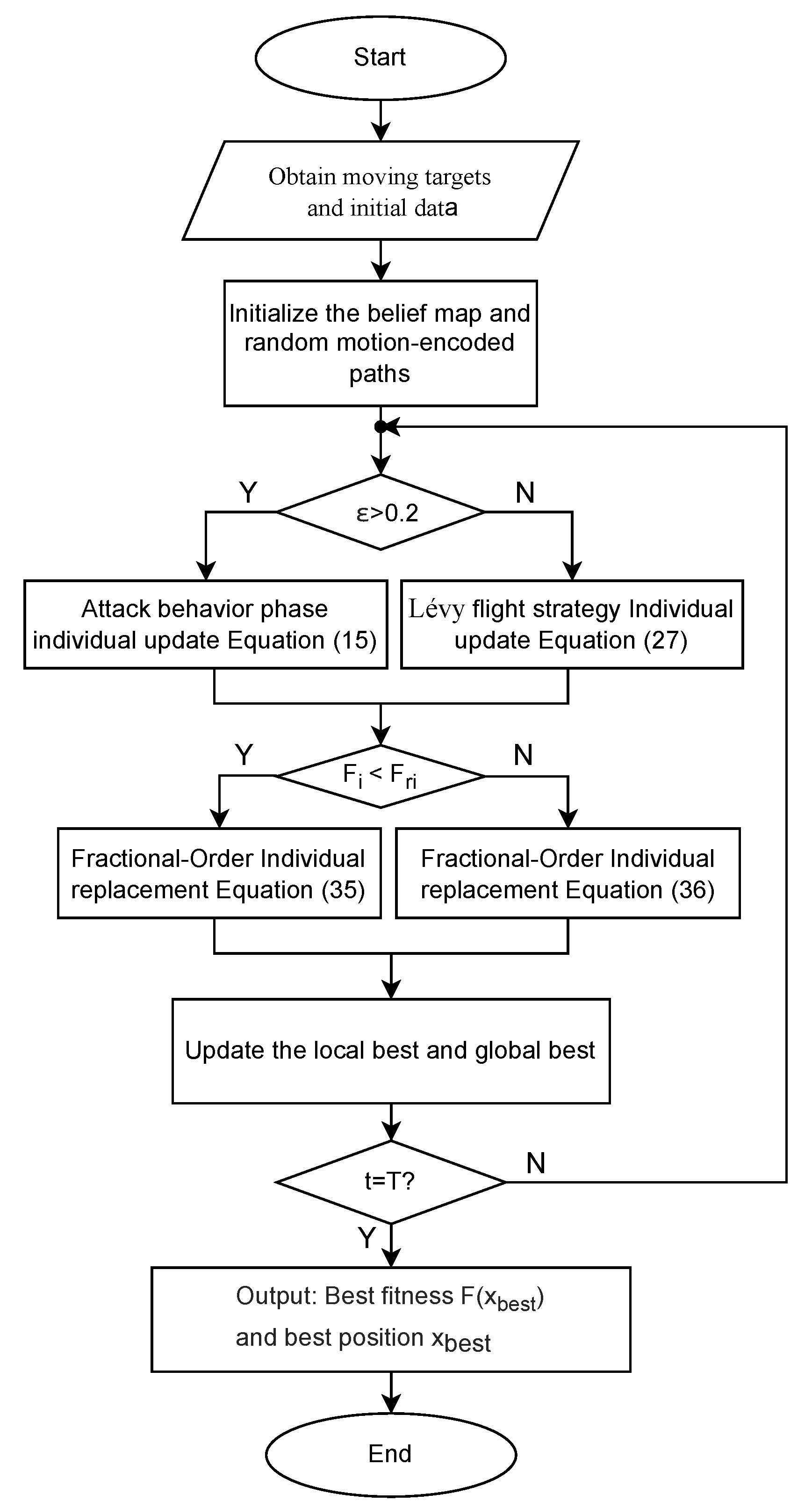
This section explains how the FOBKA optimizer works. By incorporating innovative elements such as the innovative motion encoding mechanism, Lévy flight strategy, and fractional-order strategy into the BKA, the optimization accuracy and computational efficiency of the algorithm have been significantly improved. The specific implementation steps are as follows:

Setp 1. Initialize population individuals: Based on belief graph information, randomly generate population individuals using an innovative movement encoding mechanism.

Step 2. Solve the objective function value: Decode the motion-encoded path using Equation (23), compute the fitness function value after obtaining the Cartesian space path, synchronously update the belief map, and determine the initial leader of the population.

Setp 3. Individual position update stage: Update the individual’s movement encoding path by performing attack behavior using Equation (15) or Equation (27) and performing fractional migration behavior using Equation (35) or Equation (36).

Setp 4. Execution termination: If the termination condition is met, record the optimal solution; otherwise, return to step 2 and continue running.

The pseudocode for FOBKA is shown in Algorithm 2. The FOBKA algorithm flowchart is shown in Figure 2.

Algorithm 2: Algorithm Pseudocode of FOBKA

Input: Population Initialization parameters: population size $pop$, maximum iterations T Output: Best fitness $F\left(x_{\mathrm{best}}\right)$, best position $x_{\mathrm{best}}$ 1: Obtain moving targets and initial data 2: Construct belief map 3: Initialize algorithm parameter p 4: for $t=1$ to T do 5:     for each individual $i=1$ to $pop$ do 6:         Generate random motion-encoded paths $S_i$ 7:         Calculate cost value for individual i 8:     end for 9:     Determine current optimal solution 10:     for $i=1$ to $pop$ do 11:         Execute Lévy flight attack behavior 12:         if $\epsilon >0.2$ then 13:            Update $x_i$ using Equation (15) 14:         else 15:            Update $x_i$ using Equation (27) 16:         end if 17:         Execute Fractional-order migration behavior 18:         if $F_i<F_{ri}$ then 19:            Update $x_i$ using Equation (35) 20:         else 21:            Update $x_i$ using Equation (36) 22:         end if 23:     end for 24:     Update global optimal solution 25: end for

Figure 2. FOBKA Algorithm Flowchart.

4.5. Time Complexity Analysis

Time complexity analysis is the core quantitative indicator for evaluating the real-time performance and target search response speed of an algorithm. The industry commonly uses the Big -O notation to describe the trend of its growth with the increase in input size. The detailed derivation of the time complexity of the BKA and the FOBKA is as follows.

4.5.1. The BKA Algorithm

Assume that the BKA algorithm has a population size of N, a dimension of the optimization problem of $Dim$, and a maximum number of iterations of $MaxIter$. Based on the core execution flow of the BKA algorithm, the complexity is decomposed into phases as follows:

Initialization phase: This phase requires completing the initialization of the Dim-dimensional positions of N population individuals, where the dimensional parameters of each individual are independently assigned. The time complexity is $O(N\times Dim)$.

Fitness evaluation phase: In each iteration, the fitness values of N population individuals need to be calculated one by one. By default, the time complexity of a single fitness calculation is $O\left(1\right)$, so the overall time complexity of this phase is $O\left(N\right)$.

Individual update phase: In each iteration, the Dim-dimensional positions of N individuals are independently updated based on the algorithm’s search strategy. The time complexity is $O(N\times Dim)$.

Since the fitness evaluation and individual update need to be executed cyclically for $MaxIter$ iterations, and the impact of the low-order term $O\left(N\right)$ on the overall complexity trend is negligible, the overall time complexity of the BKA algorithm is $O(N\times Dim\times MaxIter)$.

4.5.2. The FOBKA Algorithm

The core parameters of the algorithm are defined as follows: population size N, dimension of the optimization problem $Dim$, and maximum number of iterations $Maxlter$. Based on the execution flow of the algorithm, the complexity is decomposed into phases as follows:

Initialization phase: This phase requires completing the initialization of the Dim-dimensional parameters of N population individuals, which is a one-time operation before iterations. The time complexity is $O(N\times Dim)$.

Fitness evaluation phase: In each iteration, the fitness values of N individuals need to be calculated one by one. By default, the time complexity of a single fitness calculation is $O\left(1\right)$, so the time complexity of this phase is $O\left(N\right)$.

Individual update phase: In each iteration, the Dim-dimensional positions of N individuals are independently updated based on the algorithm’s strategy, without high-order nested operations. The time complexity is $O(N\times Dim)$.

Since fitness evaluation and individual update need to be executed cyclically for $MaxIter$ iterations, and the impact of the low-order term $O\left(N\right)$ on the overall complexity trend is negligible, the overall time complexity of the FOBKA algorithm is $O(N\times Dim\times MaxIter)$.

To summarize, the FOBKA shares the same time complexity as the BKA. This demonstrates that while achieving enhanced performance, it does not introduce additional complexity overhead, thereby striking a balanced compromise between optimization efficacy and computational efficiency.

5. Simulation Experiment

To investigate the algorithmic performance of the FOBKA in solving move target search problems, a series of simulation and comparative experiments were conducted, the details of which are described below.

5.1. Scenarios Setup

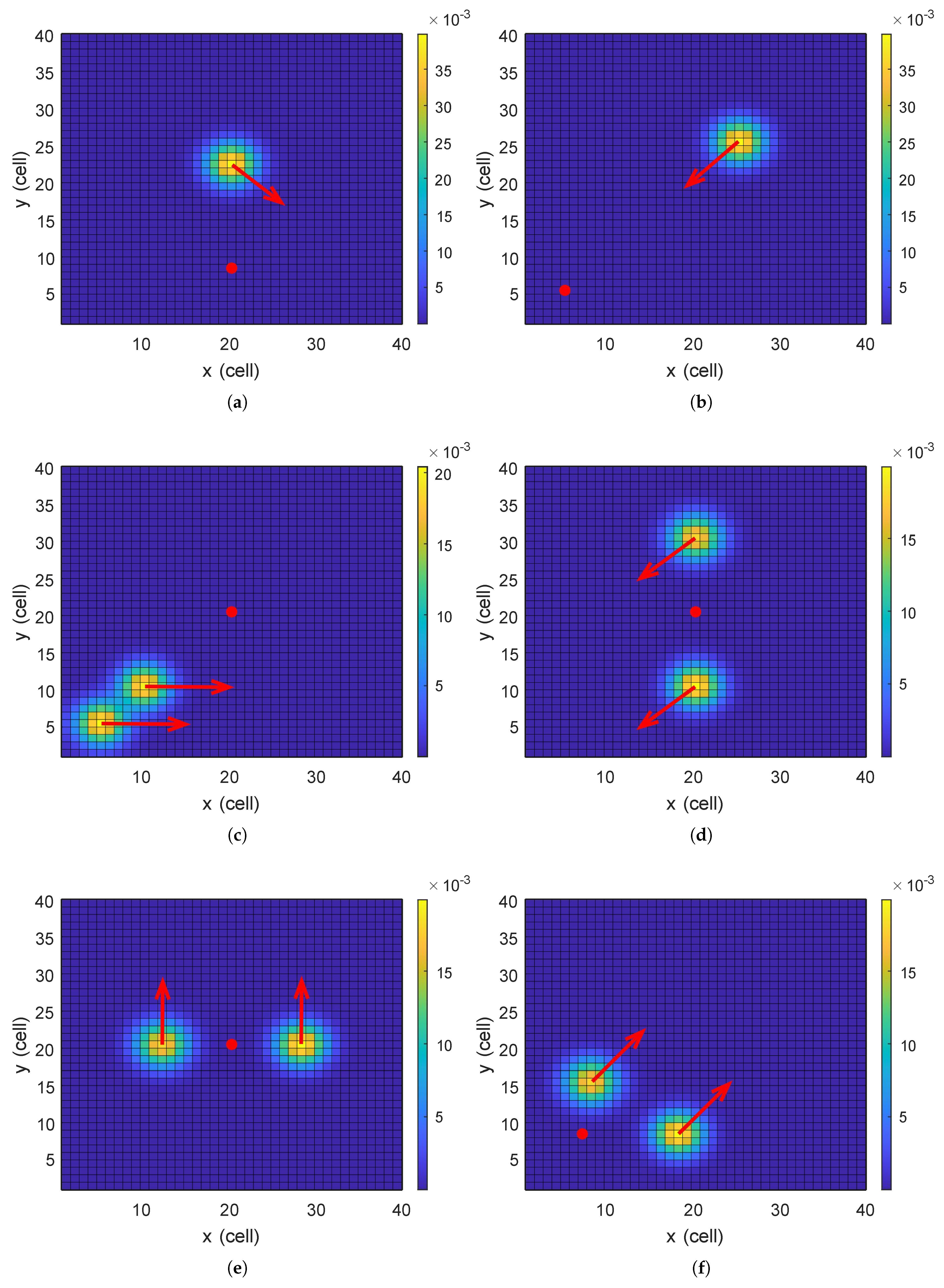
To examine the performance characteristics of the FOBKA, this study established six distinct search scenarios and conducted comprehensive testing and analysis of the algorithm’s performance across various dimensions. All scenarios are set with the same map size $S_r=S_c=40$, but differ in the initial position of the UAV, the target motion model $P\left(m_t\right|m_{t-1})$, and the initial belief map $b\left(x_0\right)$. Different colors in the figure correspond to different probabilities; specific values can be found in Figure 1. Red arrows indicate the target’s dynamic movement direction, while red dots mark the initial position of the UAV. The situations of each Scenario are shown in Figure 3.

Figure 3. Algorithm performance testing scenarios. (a–f) correspond to scenarios (1)–(6), respectively. Red dots indicate the initial positions of the UAV, and arrows indicate the direction of target movement.

Scenario 1: Single-Target Circumnavigation Test Scenario. There is only one moving target with coordinates $(20,22)$, and the UAV’s initial position is (20, 8). The moving target is directly north of the UAV’s initial position, and it moves toward the southeast during the UAV’s search process. This scenario contains no multi-target interference, enabling testing of the algorithm’s exploration and adaptive capabilities under basic mission mode.

Scenario 2: Single-Target Opposite-Direction Test Scenario. There is only one moving target with coordinates (5, 5), and the UAV’s initial position is (5, 5). The moving target is directly northeast of the UAV’s initial position, and it moves toward the southwest during the UAV’s search process. As the target moves toward the UAV’s initial position, this scenario further tests the search algorithm’s adaptability. The test emphasizes evaluating the algorithm’s convergence speed.

Scenario 3: Dual-Target Side-by-Side Co-directional Test Scenario. There are two independently moving targets, with coordinates (5, 5) and (10, 10) respectively. The UAV’s initial position is (20, 20), and both moving targets are directly southwest of the UAV’s initial position. During the UAV’s search process, the two targets are adjacent to each other and both move toward the east. This scenario tests the algorithm’s ability to distinguish between similar-featured targets and avoid redundant paths.

Scenario 4: Dual-Target Symmetrical Surrounding Diagonal Test Scenario.There are two independently moving targets, with coordinates (20, 10) and (20, 30) respectively. The UAV’s initial position is (20, 20), and the two moving targets are located directly south and directly north of the UAV’s initial position respectively. During the UAV’s search process, the two targets are distributed on the south and north sides of the UAV and both move toward the southwest. This scenario tests the algorithm’s dynamic allocation of tracking priority during dispersed target tracking. The algorithm must rapidly detect and locate high-probability areas where moving targets are present.

Scenario 5: Dual-Target Symmetrical Surrounding Co-Directional Test Scenario. There are two independently moving targets, with coordinates (12, 20) and (28, 20) respectively. The UAV’s initial position is (20, 20), and the two moving targets are located directly east and directly west of the UAV’s initial position respectively. During the UAV’s search process, the two targets are distributed on the east and west sides of the UAV and both move toward the north. This test scenario evaluates the algorithm’s task coordination capability between “covering static high-probability areas” and “tracking dynamic targets.”

Scenario 6: Dual-Target Divergence Co-Directional Test Scenario. There are two independently moving targets, with coordinates (8, 15) and (18, 8) respectively. The UAV’s initial position is (7, 8), and the two moving targets are located in the northeast direction close to the UAV’s initial position. During the UAV’s search process, the two targets are adjacent to each other and both move toward the northwest. This scenario tests the algorithm’s path extension capability and search range adjustment ability under the “area departure” scenario.

Comparative experiments were conducted with optimization algorithms from recent years, such as the Subtraction-Average-Based Optimizer (SABO) [35], the Parrot Optimizer (PO) [36], Crested Porcupine Optimizer (CPO) [37], Pelican Optimization Algorithm (POA) [38], Sand Cat Swarm Optimization Algorithm (SCSO) [39], The Hiking Optimization Algorithm (HOA) [40], and Polar Lights Optimization (PLO) [41]. The population size for all nine algorithms tested was set to 100, with a maximum iteration limit of 200. Detailed specifications of the key parameters for each optimization algorithm are provided in Table 1.

Table 1. Parameter Values of Different Algorithms.

Algorithms	Parameter Values
SABO	Velocity vector $\overrightarrow{v}\in [1,2]$; Random parameter $r_i\in (0,1)$
PO	Weight factor $\gamma =1.5$
CPO	Iteration factor $T=2$
POA	Index set $I=\{1,2\}$; Random coefficient $R=0.2$
SCSO	Search step $SS=5$
HOA	Angle parameter $\theta \in [0,{50}^{\circ }]$; Amplitude parameter $aa\in [1,3]$
PLO	Population size $m=100$; Coefficient $a=[1,1.5]$
BKA	Attack probability $p=0.9$
FOBKA	Attack probability $p=0.9$; Fractional order $\alpha =0.9$

5.2. Sensitive Analysis of the Fractional-Order $\alpha$ and Probability Threshold

In the FOBKA, the fractional-order $\alpha$ serves as the core hyperparameter, while the probability threshold in the alternating update mechanism acts as the key control parameter for balancing algorithmic exploration and exploitation. Both significantly influence the algorithm’s overall performance. Therefore, this section conducts a systematic sensitivity analysis with multiple quantitative comparison experiments to verify the optimal values and rationality of the fractional-order $\alpha$ and probability threshold. To ensure the objectivity and relevance of the analysis, this experiment strictly adheres to the control variable method and is conducted within the experimental scenario 1 defined in this paper. The specific experimental design is as follows: While keeping all other parameters of the FOBKA algorithm fixed, the core parameters were independently adjusted and tested. First, for the fractional order $\alpha$, discrete values were selected within the interval $[0.1,0.9]$ with a step size of $0.1$, constructing 9 sets of comparative experiments. Second, for the probability threshold, discrete values were also selected within the range $[0.1,0.9]$ with increments of $0.1$, simultaneously constructing 9 comparative experiments. The experiment selected “target detection probability,” aligned with the research objectives of this paper, as the core quantitative evaluation metric. Through 30 independent repeated tests, the best value, worst value, average, and standard deviation for each experimental group were statistically recorded. This comprehensively and systematically characterized the algorithm’s computational accuracy and operational stability under different parameter configurations.

The sensitivity experiment data for the fractional-order $\alpha$ are shown in Table 2. The sensitivity experiment data for the probability threshold in the alternating update mechanism are shown in Table 3.

Table 2. The FOBKA algorithm was run independently 30 times with different values of $\alpha$ to obtain the fitness function values. Bold text indicates the optimal comparison results.

Fractional-Order $\mathit{\alpha }$	0.1	0.2	0.3	0.4	0.5	0.6	0.7	0.8	0.9
Best	0.3422	0.3482	0.3509	0.3469	0.3511	0.3609	0.3627	0.3627	0.3884
Worst	0.3082	0.2907	0.3114	0.3138	0.3153	0.3177	0.3201	0.3087	0.3217
Mean	0.3179	0.3245	0.3314	0.3342	0.3348	0.3349	0.3402	0.3382	0.3535
Std	0.0101	0.0162	0.0121	0.0116	0.0128	0.0129	0.0139	0.0168	0.0157

Table 3. The FOBKA algorithm was run independently 30 times with different values in the alternating update mechanism, and then obtains the result of the fitness function values. Bold text indicates the optimal comparison results.

Probability Threshold	0.1	0.2	0.3	0.4	0.5	0.6	0.7	0.8	0.9
Best	0.3792	0.3884	0.3787	0.3672	0.3618	0.3643	0.3616	0.365	0.3627
Worst	0.3182	0.3217	0.3031	0.3098	0.2963	0.3002	0.2942	0.2896	0.287
Mean	0.3478	0.3535	0.3421	0.3443	0.3344	0.3328	0.3305	0.3348	0.3245
Std	0.0161	0.0157	0.0151	0.0132	0.0177	0.0185	0.0173	0.0196	0.0198

Based on the experimental data in Table 2, the optimality of $\alpha =0.9$ can be verified from two aspects: (1) Optimal solution accuracy: At $\alpha =0.9$, the experimental best value and average value both exhibit optimal performance among all values, indicating that the algorithm significantly improves capture accuracy in high-probability regions of the objective. This aligns closely with the pattern where the “memory effect” of fractional order strengthens as increases. (2) Balanced stability: The standard deviation at $\alpha =0.9$ remains at an intermediate level among all values. This avoids both significant stability degradation caused by excessive precision pursuit and precision loss due to excessive conservatism, thereby achieving an optimal trade-off between precision and stability.

The experimental data in Table 3 show that when the probability threshold is set to $0.2$ (i.e., $\epsilon >0.2$), the algorithm achieves the best overall performance in terms of the optimal solution, average value, and worst value, and is the optimal probability threshold for balancing exploration and exploitation.

5.3. Experiment Findings

Table 4 presents the simulation validation results across six search scenarios, covering four key cumulative probability metrics—optimal value, worst value, average value, and standard deviation from 30 independent runs of all comparison algorithms in each scenario. The optimal data for each scenario is highlighted in bold for clear distinction. The data reveal that in Scenarios 1 and 3–5, the FOBKA consistently outperforms all other comparison algorithms across all four cumulative probability metrics. In Scenario 2, FOBKA maintains advantages in the first three metrics, with only the PLO algorithm achieving the optimal standard deviation. In Scenario 6, the FOBKA outperformed other comparison algorithms only in the optimal value and average value of cumulative probability, while its worst value and standard deviation were slightly inferior to the CPO algorithm. These results demonstrate that the proposed FOBKA algorithm achieves significant performance improvements over existing comparison algorithms: Compared to the baseline BKA algorithm, FOBKA exhibits substantially enhanced search capability and robustness. It more efficiently supports rapid identification and tracking of moving targets by UAVs, thereby providing effective support for planning high-probability search paths for UAVs.

Table 4. All algorithms were run independently 30 times to obtain the fitness function values. The best matching results are highlighted in bold.

	Result	Algorithm
		FOBKA	BKA	POA	SCSO	HOA	PLO	CPO	PO	SABO
1	Best	0.3884	0.3390	0.3159	0.3594	0.3646	0.3575	0.3478	0.3377	0.3310
	Worst	0.3217	0.2476	0.1574	0.1966	0.2528	0.2657	0.2277	0.2396	0.2341
	Mean	0.3535	0.2986	0.2320	0.2923	0.3160	0.3175	0.2993	0.2971	0.2752
	Std	0.0157	0.0243	0.0352	0.0407	0.0289	0.0206	0.0302	0.0278	0.0242
2	Best	0.2593	0.2071	0.2074	0.2108	0.2186	0.2115	0.2265	0.2071	0.1815
	Worst	0.1941	0.1513	0.1316	0.1136	0.1566	0.1476	0.1559	0.1464	0.1011
	Mean	0.2254	0.1844	0.1544	0.1568	0.1845	0.1714	0.1809	0.1781	0.1398
	Std	0.0172	0.0203	0.0165	0.0195	0.0143	0.0140	0.0159	0.1411	0.0211
3	Best	0.1864	0.1813	0.1733	0.1756	0.1622	0.1711	0.1812	0.1822	0.1443
	Worst	0.1713	0.10796	0.1148	0.0899	0.0781	0.1309	0.1519	0.1519	0.0847
	Mean	0.1815	0.1676	0.1533	0.1488	0.1261	0.1485	0.1671	0.1706	0.1154
	Std	0.0040	0.0167	0.0142	0.0216	0.0189	0.0103	0.0077	0.0077	0.0150
4	Best	0.2222	0.1924	0.1753	0.2108	0.2015	0.2039	0.1988	0.2088	0.1916
	Worst	0.1802	0.1436	0.0880	0.1059	0.0824	0.1593	0.1153	0.1250	0.1419
	Mean	0.1928	0.1718	0.1249	0.1849	0.1565	0.1861	0.1615	0.1792	0.1655
	Std	0.0095	0.0104	0.0229	0.0214	0.0238	0.0093	0.0203	0.0206	0.0144
5	Best	0.2305	0.2062	0.1988	0.2119	0.2184	0.2126	0.2204	0.2086	0.1936
	Worst	0.1949	0.1336	0.1306	0.1268	0.1704	0.1753	0.1671	0.1662	0.1432
	Mean	0.2088	0.1823	0.1591	0.1811	0.1959	0.1907	0.1934	0.1893	0.1664
	Std	0.0085	0.0185	0.0198	0.0233	0.0103	0.0086	0.0140	0.01193	0.0121
6	Best	0.1858	0.1616	0.1671	0.1707	0.1738	0.1616	0.1705	0.1724	0.1253
	Worst	0.1544	0.0656	0.1115	0.0309	0.1494	0.0943	0.1583	0.1419	0.0254
	Mean	0.1681	0.1453	0.1411	0.1137	0.1658	0.1291	0.1586	0.1602	0.0545
	Std	0.0070	0.0185	0.0141	0.0420	0.0070	0.0164	0.0069	0.0071	0.0267

These results, obtained by independently running the nine algorithms 30 times in each scenario, underwent Wilcoxon nonparametric statistical testing to determine whether there were statistically significant differences between the FOBKA algorithm and other alignment algorithms [42]. The p-values for FOBKA compared with the other eight algorithms are detailed in Table 5, with data exceeding the threshold of $0.05$ highlighted in bold. As shown in the table, the p-values of FOBKA compared with BKA, POA, PLO, CPO, PO, and SABO are all below the threshold of $0.05$, indicating stable and significant performance differences. Moreover, the p-values of FOBKA compared with SCSO in Scenario 4 and with HOA in Scenario 6 are both greater than the threshold of $0.05$. This indicates that there is no statistically significant difference in performance between FOBKA and SCSO in Scenario 4. The reason is that the setup of Scenario 4 weakens the improved advantages of FOBKA: although FOBKA’s motion encoding mechanism ensures path validity, SCSO’s path update can also meet the requirements of the target-moving-away scenario, resulting in minimal differences in their cumulative detection probabilities and convergence speeds. In addition, there is no statistically significant difference in performance between FOBKA and HOA in Scenario 6. This is because the target moves uniformly along the northeast diagonal with a predictable trajectory; the requirements of this scenario are highly compatible with HOA while weakening FOBKA’s improved strategies, leading to narrowed differences in the validity of the generated diagonal paths and cumulative detection probabilities between the two algorithms.

Table 5. Results of the p-value Wilcoxon rank-sum test comparing the 8 algorithms against the FOBKA algorithm across various scenarios.

No.	FOBKA VS
	BKA	POA	SCSO	HOA	PLO	CPO	PO	SABO
1	1.21 $\times {10}^{-10}$	3.02 $\times {10}^{-11}$	1.86 $\times {10}^{-9}$	1.39 $\times {10}^{-6}$	4.31 $\times {10}^{-8}$	1.29 $\times {10}^{-9}$	1.33 $\times {10}^{-10}$	4.5 $\times {10}^{-11}$
2	1.69 $\times {10}^{-9}$	5.49 $\times {10}^{-11}$	5.49 $\times {10}^{-11}$	7.37 $\times {10}^{-10}$	7.38 $\times {10}^{-11}$	8.09 $\times {10}^{-10}$	1.77 $\times {10}^{-10}$	3.01 $\times {10}^{-11}$
3	6.00 $\times {10}^{-8}$	3.68 $\times {10}^{-11}$	1.21 $\times {10}^{-10}$	3.01 $\times {10}^{-11}$	3.01 $\times {10}^{-11}$	1.85 $\times {10}^{-9}$	2.83 $\times {10}^{-8}$	3.01 $\times {10}^{-11}$
4	1.28 $\times {10}^{-9}$	3.01 $\times {10}^{-11}$	0.36322	7.77 $\times {10}^{-9}$	0.03513	3.49 $\times {10}^{-9}$	0.01501	5.96 $\times {10}^{-9}$
5	4.31 $\times {10}^{-8}$	6.69 $\times {10}^{-11}$	8.19 $\times {10}^{-7}$	1.16 $\times {10}^{-5}$	5.96 $\times {10}^{-9}$	8.88 $\times {10}^{-6}$	5.53 $\times {10}^{-8}$	3.01 $\times {10}^{-11}$
6	3.47 $\times {10}^{-10}$	2.03 $\times {10}^{-9}$	3.49 $\times {10}^{-9}$	0.46426	5.49 $\times {10}^{-11}$	2.59 $\times {10}^{-5}$	0.000189	3.02 $\times {10}^{-11}$

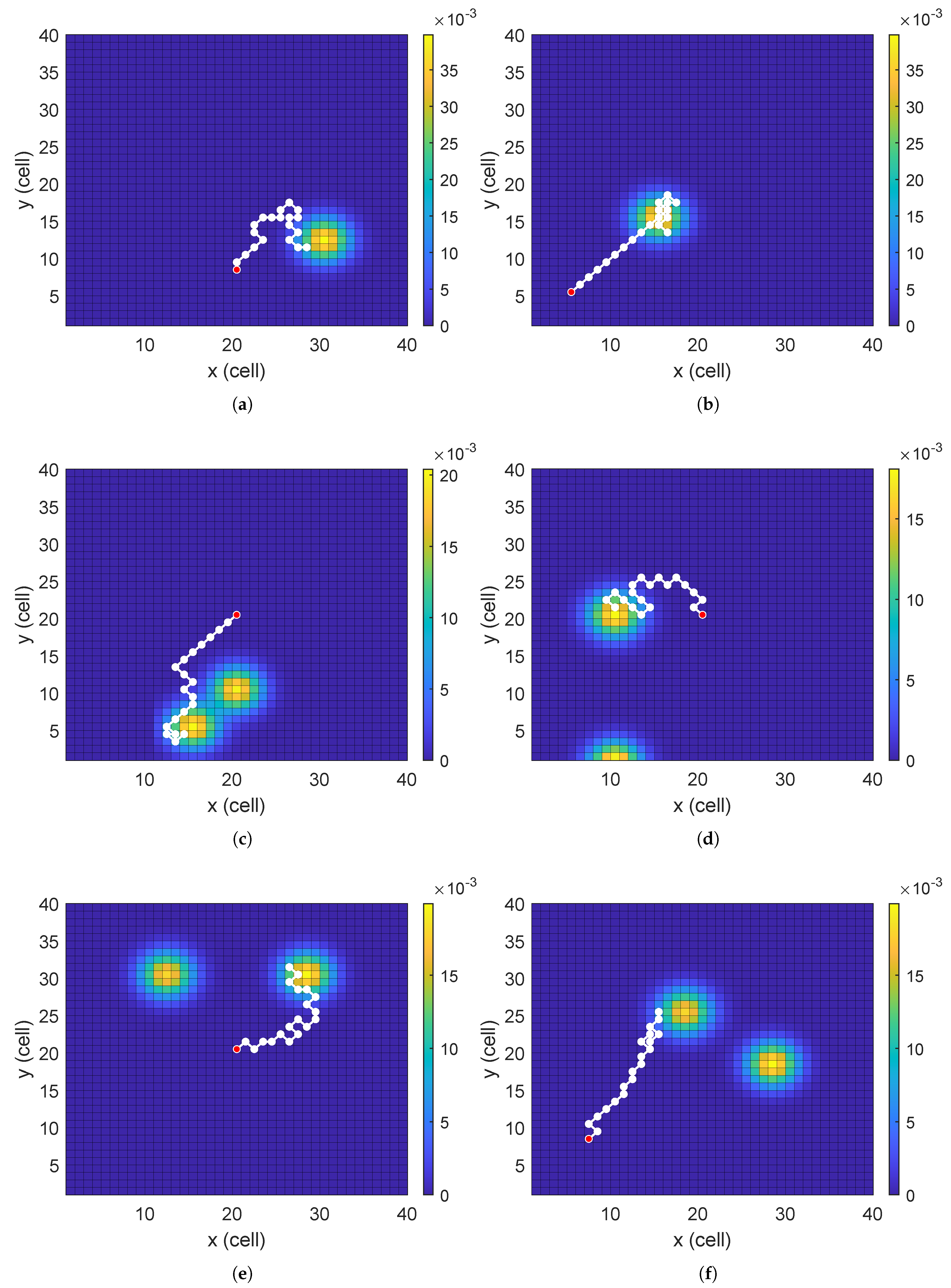
Figure 4 shows the optimal search paths generated by the FOBKA algorithm after running independently 30 times in six scenarios. In all scenarios, the algorithm accurately identifies high-probability areas and plans effective flight paths for drones. For scenarios 1 and 2, which have only a single high-probability area, the cumulative probability value is high because the opportunity to detect targets is not dispersed across other areas. It should be noted that the probability map only reflects the confidence level of the target at the final moment, while the search path shows the dynamic tracking process of high-probability areas over time. Comparing the initial positions of the target and the drone in Figure 3, it can be seen that the search path can be adjusted according to the dynamic characteristics of the target, thereby maximizing the cumulative detection probability.

Figure 4. Best search paths for each scenario produced by FOBKA. (a–f) correspond to scenarios (1)–(6), respectively. Red dots are the initial positions of the UAV, and white dots are the nodes on the UAV’ optimal search paths.

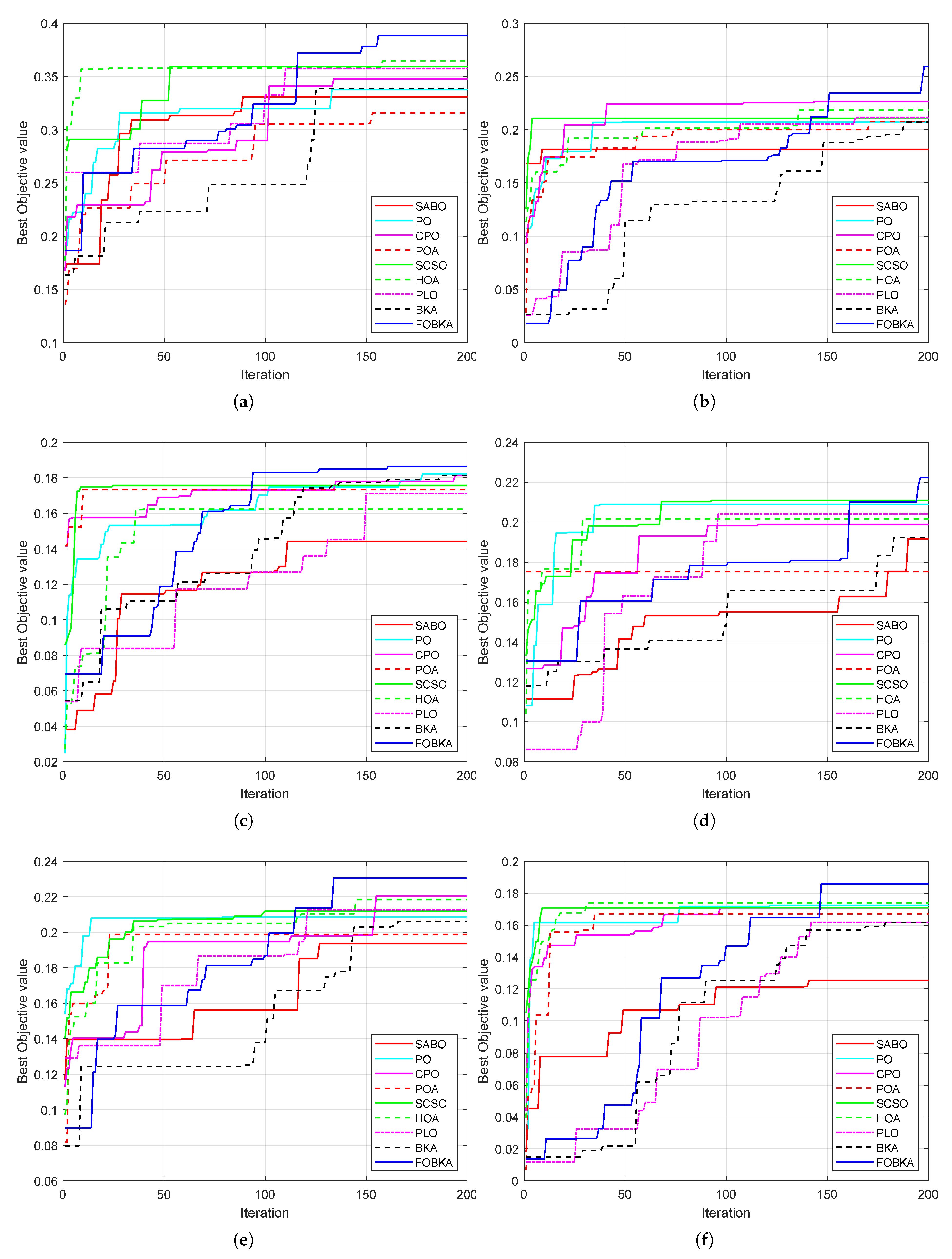
As shown in Figure 5, the FOBKA demonstrates a fast convergence speed and high convergence accuracy in various scenarios, highlighting its strong robustness, independence from specific scene layouts, and superior generalization capabilities. The SCSO also performs well in the six scenarios, but is prone to getting stuck in local optima. The BKA algorithm ranks high in convergence speed in the six scenarios, but its convergence accuracy is suboptimal. In general, the FOBKA demonstrates significant advantages over other algorithms, particularly in dynamic target search scenarios.

Figure 5. Comparison of convergence curves for the best objective values obtained by running nine algorithms independently 30 times across six scenarios. (a–f) correspond to scenarios (1)–(6), respectively.

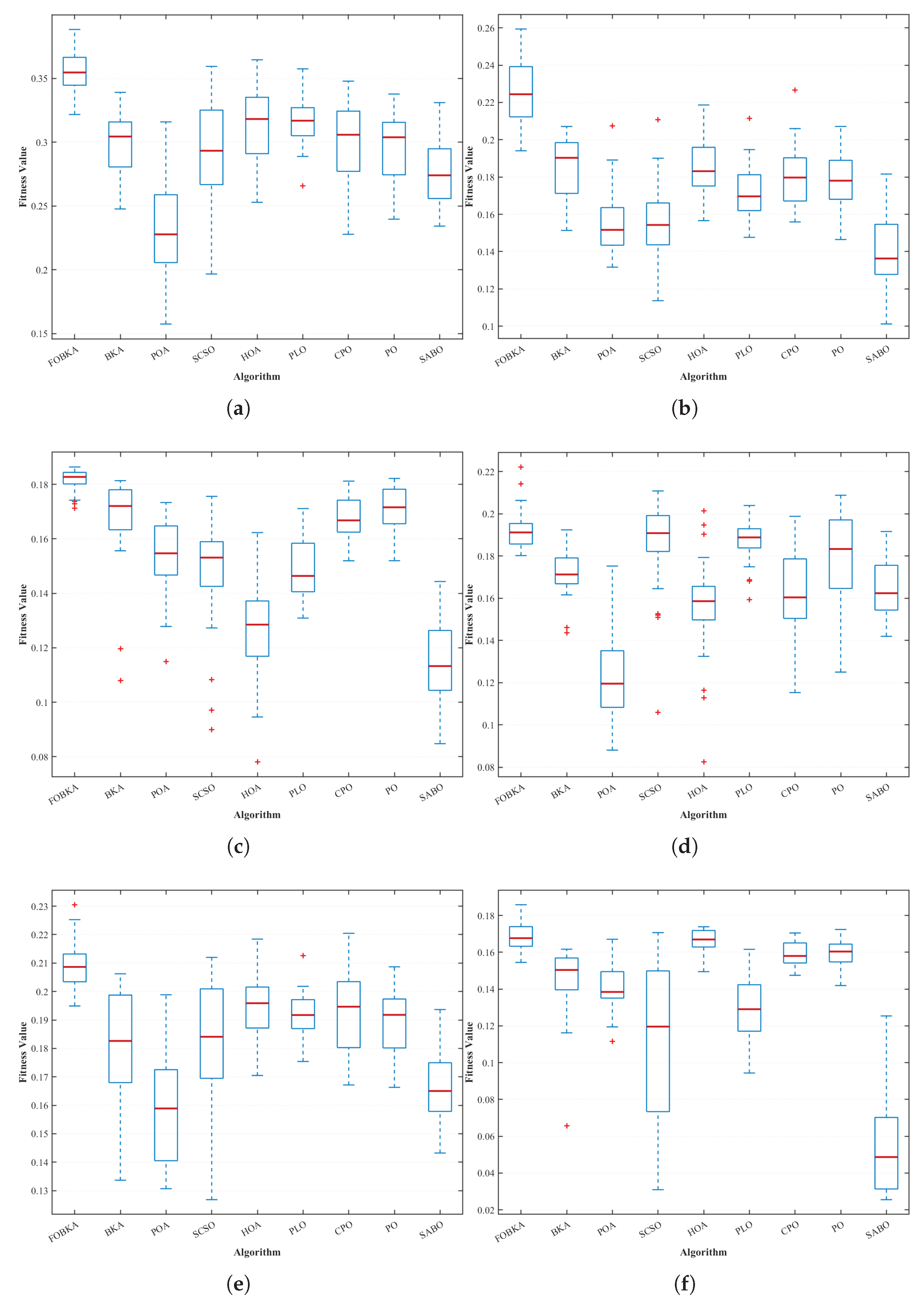
Figure 6 shows the box plots of the fitness values distributed in 30 independent runs of each of the 9 algorithms. By examining the position, length, and outliers (red plus signs) of the box plots, one can visually compare the central tendency and dispersion of the results from each algorithm, thereby assessing their stability. As shown in the figure, FOBKA consistently ranks among the top in terms of median fitness values in six scenarios (with the red line within the box being relatively high), exhibits concentrated results (short box length), and demonstrates superior stability and performance; SABO often exhibits low fitness values and high dispersion; POA shows significant dispersion in scenarios 1 and 4–5; SCSO exhibits significant dispersion and is prone to extreme values in scenarios 1–2 and 5–6, indicating poor stability.

Figure 6. Box plots of fitness values for all algorithms running independently 30 times in six scenarios. (a–f) correspond to scenarios (1)–(6), respectively. The special symbol “+” indicates outliers beyond the normal distribution range of the data.

5.4. Ablation Study

Among them, Type 1 is the BKA algorithm without any strategy, Type 2 is the BKA algorithm using only the motion-encoded mechanism, Type 3 is the BKA algorithm with the alternating update mechanism added on the basis of Type 2, and Type 4 is the algorithm that introduces the fractional-order strategy on the basis of Type 3, which is also the FOBKA algorithm proposed in this paper. It can be seen from the experimental conclusions in Table 6 that as the improved strategies are gradually added, the optimal value, average value, and worst value of the algorithm continue to increase, and the standard deviation continues to decrease. Moreover, Type 4, namely the FOBKA algorithm proposed in this paper, achieves the best comprehensive performance in the experimental results. All improved strategies have positive effects, and the effect is optimal when they are synergistically combined, which verifies the necessity and synergistic value of each improved strategy.

Table 6. Ablation results using different strategies on scenario 1. ✓ denotes that the variant adopts the corresponding improvement, and ✗ denotes that it does not.

	Strategies			Results
Variants	Motion-Encoded Mechanism	Alternating Update Mechanism	Fractional-Order Strategy	Best	Worst	Mean	Std
Type 1 (Base)	✗	✗	✗	0.3390	0.2476	0.2986	0.0243
Type 2	✓	✗	✗	0.3599	0.2483	0.3067	0.0259
Type 3	✓	✓	✗	0.3744	0.3093	0.3322	0.0159
Type 4	✓	✓	✓	0.3884	0.3217	0.3535	0.0157

6. Discussion Analysis

Comprehensive simulation verification and comparative analysis show that in the task of UAV moving space target search, the FOBKA optimizer can stably generate feasible and high-performance search paths. In six different search scenarios with various settings, through the evaluation of the maximum cumulative probability fitness function, FOBKA outperforms eight mainstream meta-heuristic algorithms in terms of cumulative detection probability, convergence accuracy, and operational robustness. Its superiority mainly stems from the targeted improvements in the three key stages of the algorithm.

First, a motion encoding mechanism is introduced during the algorithm’s initialization phase. This mechanism overcomes the exploration limitations inherent in traditional Cartesian coordinate systems. It not only ensures the physical feasibility of search paths from the outset but also enhances the algorithm’s adaptability to the movement trends of dynamic targets. Additionally, it improves search efficiency and stability in complex scenarios.

Second, an alternating update mechanism is designed during the algorithmic attack phase. This mechanism fully leverages the “long jumps + short explorations” characteristic of Lévy flights. Without altering the mathematical form of the original position update formula, it dynamically adjusts the step size distribution to enhance the algorithm’s global search volatility: When search becomes trapped in local optima, the random long jumps of Lévy flight enable the algorithm to rapidly escape these local peaks. Meanwhile, short exploration ensures precision in local refinement, achieving a balance between global detection and local exploration.

Third, incorporating fractional-order strategies into the algorithm’s migration behavior phase. Leveraging the inherent memory characteristics of fractional-orders, FOBKA can more accurately describe migration processes involving temporal spans, spatial position changes, and velocity variations. This decision mechanism, which relies on historical information, not only enhances the algorithm’s predictive capabilities for dynamic target trajectories but also avoids the global search deficiencies caused by traditional migration behaviors “forgetting historical information.” This further reduces the risk of getting stuck in local optima.

Experimental data further validate the effectiveness of the improvements: FOBKA outperforms the original BKA significantly in all 6 scenarios, demonstrating the statistical significance of the improvements. Furthermore, ablation experiments confirm that removing the motion encoding, alternating update, or fractional-order strategy leads to a respective decrease in algorithm performance, thus verifying the necessity of each module. Compared with the 8 comparative algorithms, FOBKA ranks first in both optimal values and average values, and its advantages are more pronounced especially in experimental environments with low-probability target interference.

However, this study still has clear limitations: First, there are discrepancies between the simulated experimental environment and real-scene environments, such as sensor noise and dynamic obstacles. Second, the current design is only adapted to single-UAV scenarios, while practical needs like full-area search and rescue, and environmental monitoring rely more on multi-UAV collaboration—yet core challenges including unsolved distributed target assignment, multi-UAV collision avoidance, and information fusion remain unaddressed. These limitations point out directions for future research: it is necessary to establish a real-scene experimental platform to verify the algorithm’s feasibility, and expand the multi-UAV collaboration framework based on FOBKA’s motion encoding mechanism to enhance its engineering applicability.

7. Conclusions

This study proposes a novel optimization algorithm, FOBKA, for solving the problem of optimal search for moving spatial targets by unmanned aerial vehicles, with the aim of generating high-probability, feasible search paths. The algorithm is built upon the BKA framework and introduces the following enhancements: during the initialization phase, a novel motion-encoding mechanism is employed to expand and diversify the search space; in the attack phase, an alternating update scheme is adopted and Lévy flight is incorporated to increase mutation, thereby helping to escape local optima and enhance global search capability; in the migration phase, a fractional-order strategy is introduced to exploit its memory characteristics in order to more accurately capture the target’s temporal evolution, spatial position, and velocity changes, thereby strengthening global exploration and convergence accuracy.

To validate the performance of FOBKA, a series of simulations were conducted across six different scenario settings. To further verify its superiority, FOBKA was compared with eight recently proposed metaheuristic algorithms. The experimental results indicate that FOBKA outperforms the comparison algorithms in convergence accuracy, robustness, and target capture probability. The findings demonstrate that FOBKA effectively addresses the key challenges of UAV search for moving spatial targets and provides efficient, feasible search paths.

Notwithstanding the demonstrated efficacy in simulation, several limitations warrant further investigation. The current experiments are based on predefined synthetic environments, and many real-world disturbances were not accounted for. Future work will establish a real-scene experimental platform using actual UAV hardware and environmental sensors to test FOBKA’s adaptability in real scenarios, thereby bridging the gap between simulation results and engineering applications. At present, FOBKA focuses on single-UAV search, which may be inadequate for large-scale or complex missions. In the future, FOBKA will be extended to a multi-UAV cooperative search framework suitable for operation in complex environments. Additionally, the fractional-order parameter in FOBKA presently requires manual tuning, reducing autonomy in complex scenarios. The next step is to explore adaptive optimization mechanisms that dynamically adjust the fractional-order order in response to real-time target motion characteristics and environmental complexity, further enhancing FOBKA’s autonomy and reducing human intervention.