Federated Incomplete Multi-View Unsupervised Feature Selection with Fractional Sparsity-Guided Whale Optimization and Tensor Alternating Learning
Abstract
1. Introduction
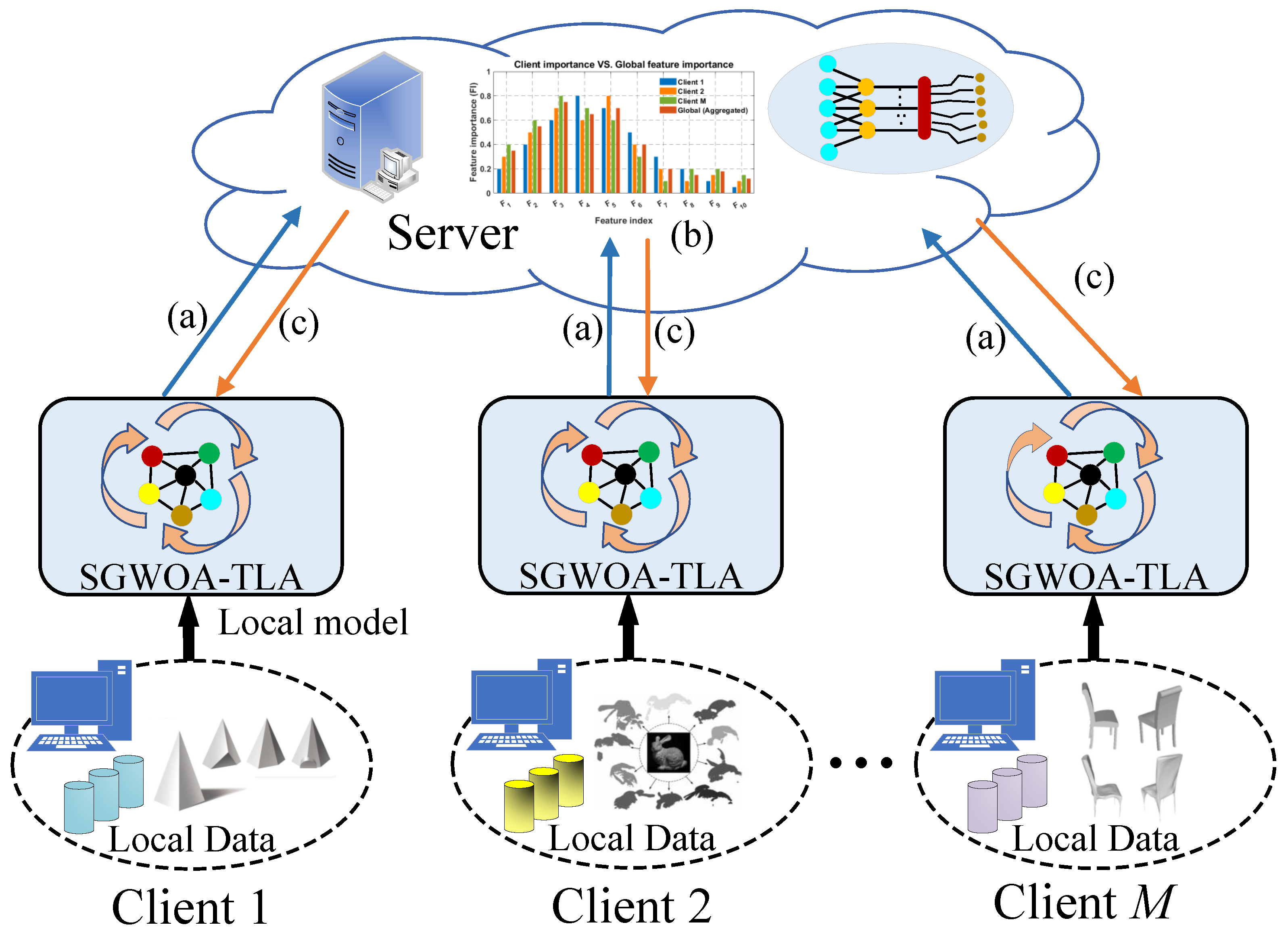
- We propose a novel Fed-IMUFS method that integrates federated learning with MUFS. Each client sequentially executes SGWOA and TAL to obtain an optimized FS weight matrix and compute its NMI. During federated training, the server employs an aggregation and distribution strategy driven by NMI to adaptively fuse the uploaded weight matrices and quality indicators into a global matrix, which is then redistributed to clients. This process safeguards data privacy while enhancing the quality and convergence of MUFS.
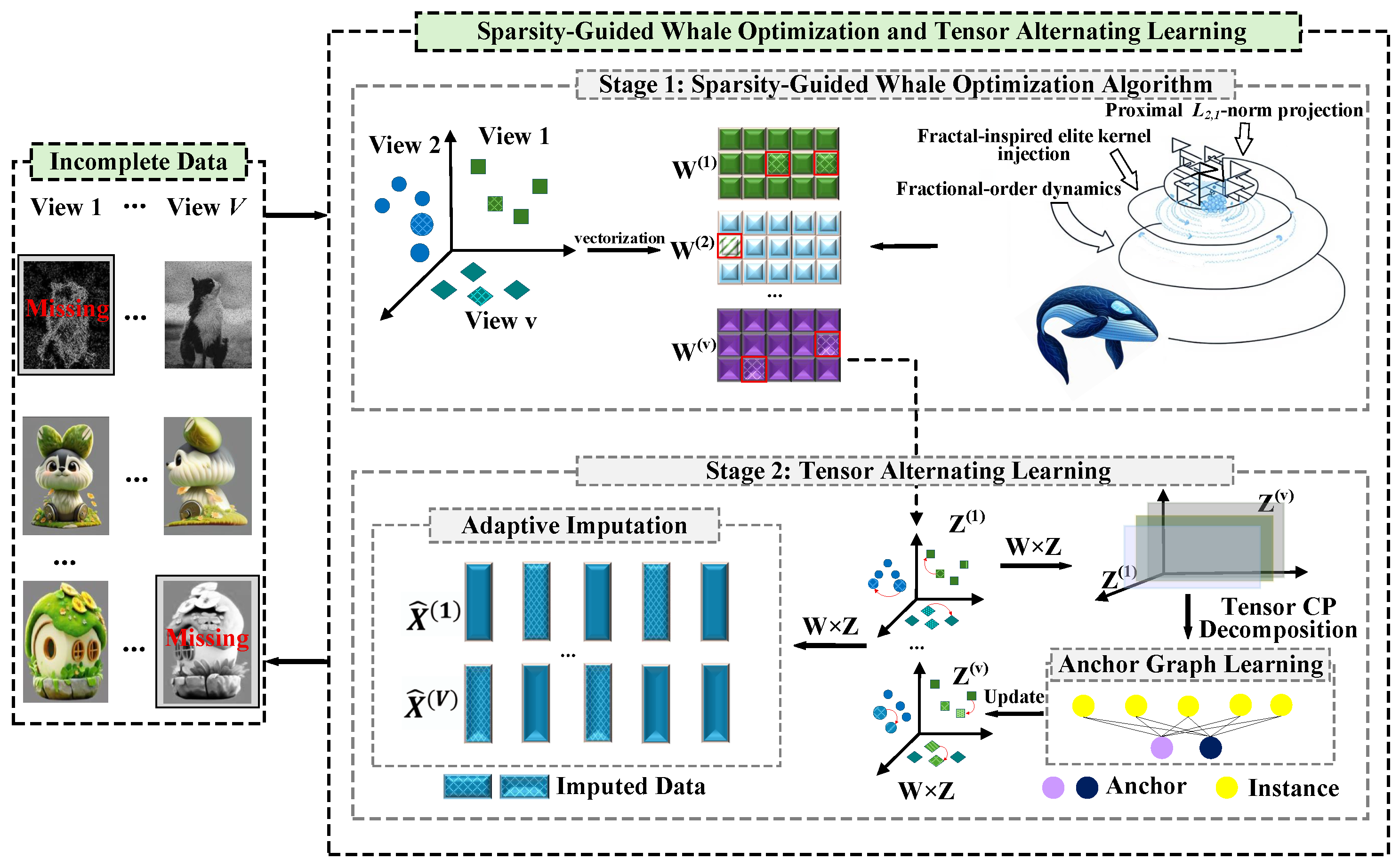
- We design an SGWOA for global search in the vectorized FS matrix space, integrating three mechanisms: (i) Prox- projection enforces row sparsity on W, enhancing stability and interpretability; (ii) fractional-order dynamics adaptively regulate parameters to avoid premature convergence; and (iii) fractal-inspired elite-kernel injection replaces poor solutions with samples near elites, sustaining diversity at low cost. Together, these mechanisms enable SGWOA to learn discriminative and robust weight matrices, forming a solid basis for data completion and representation learning.
- We introduce an aggregation and distribution strategy driven by NMI. Each client independently optimizes its FS matrix and computes its NMI, uploading only the FS matrix and NMI to the server. The server adaptively allocates weights using NMI to aggregate local matrices into a global FS matrix, which is then redistributed to clients for subsequent optimization rounds. This strategy eliminates raw data transmission, improves global performance and cross-client consistency, and further strengthens privacy protection by minimizing the risk of data leakage.
2. Related Work
2.1. Single-View Unsupervised Feature Selection
2.2. Multi-View Unsupervised Feature Selection
3. The Proposed Method
3.1. Whale Optimization Algorithm
- (1)
- Encircling and Searching
- (2)
- Spiral updating
3.2. MUFS Matrix Initialization
3.3. Sparsity-Guided Whale Optimization Algorithm and Tensor Alternating Learning
3.3.1. Stage 1: Sparsity-Guided Whale Optimization Algorithm
3.3.2. Stage 2: Tensor Alternating Learning
| Algorithm 1: Implementation of SGWOA-TAL |
 |
3.4. Federated Incomplete Multi-View Unsupervised Feature Selection via Sparsity-Guided Whale Optimization Algorithm and Tensor Alternating Learning
| Algorithm 2: Implementation of Fed-IMUFS |
 |
3.4.1. An Aggregation and Distribution Strategy Driven by Normalized Mutual Information
3.4.2. Privacy and Communication Overhead Analysis of Fed-IMUFS
3.4.3. Time Complexity Analysis of Fed-IMUFS
4. Experiments and Analysis
4.1. Experimental Setup
4.1.1. Dataset Description
4.1.2. Experimental Environment
4.1.3. Comparison Algorithms and Parameter Configuration
4.1.4. Comparison Schemes
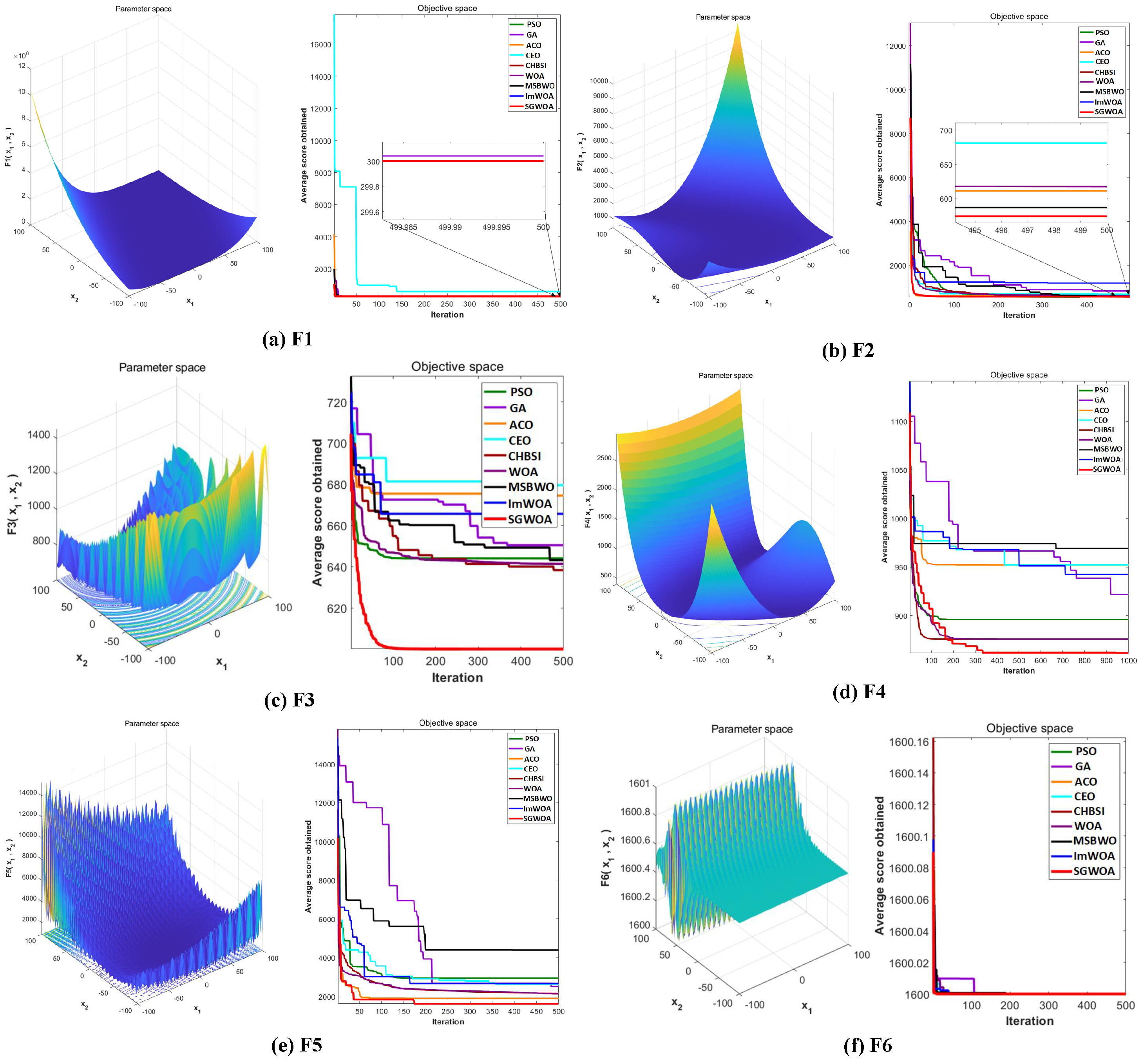
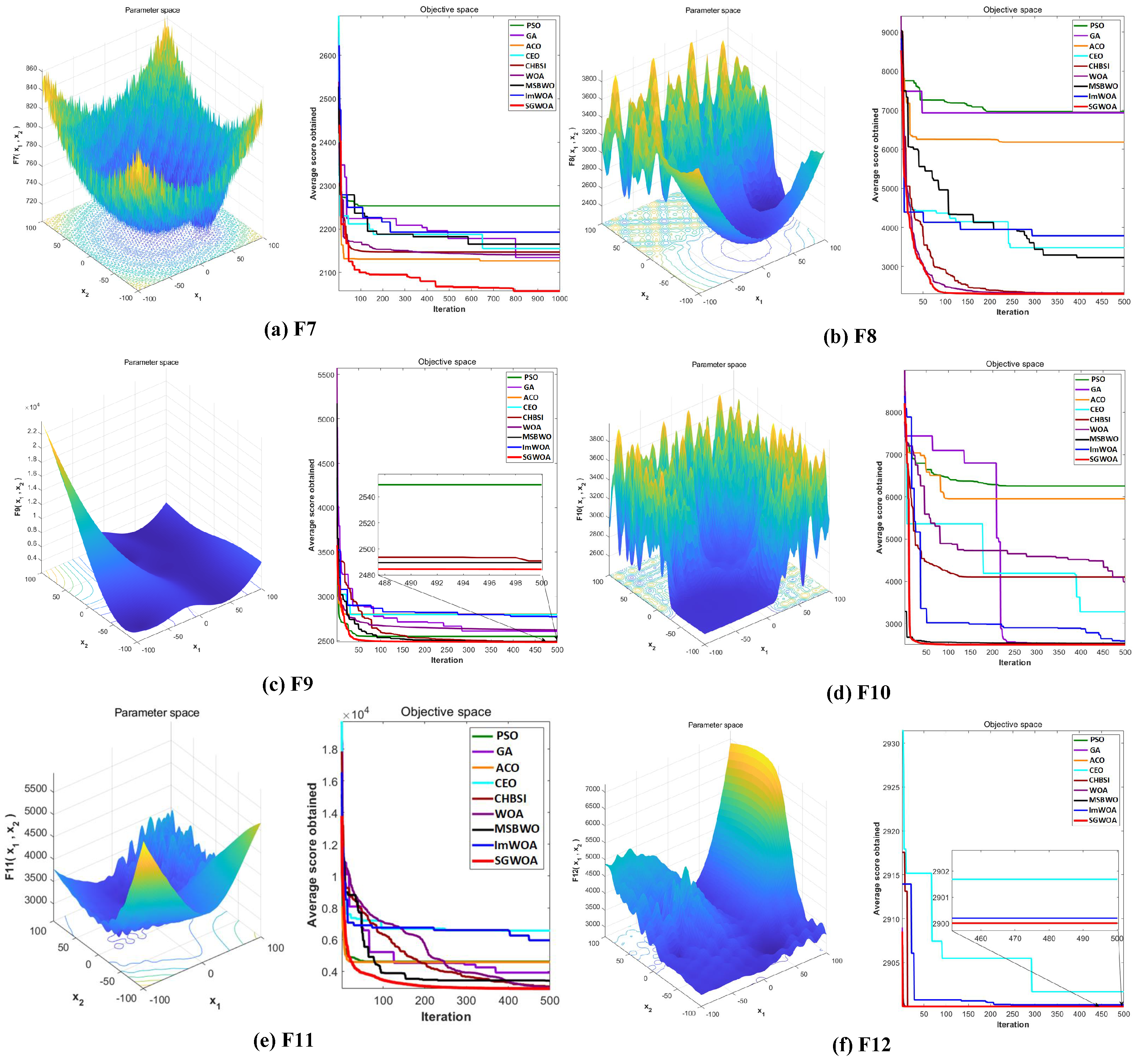
4.2. Global Optimization Analysis of SGWOA
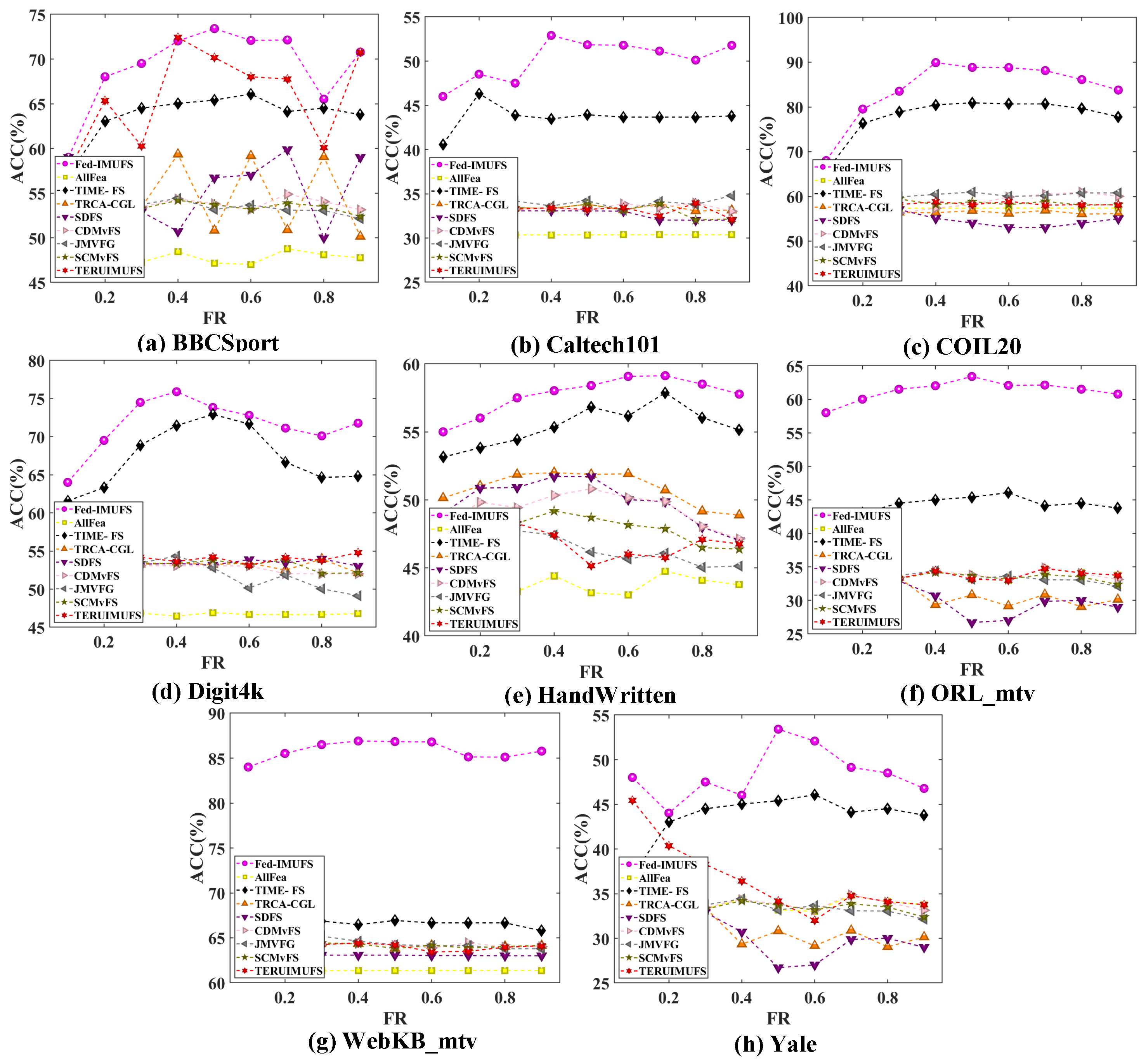
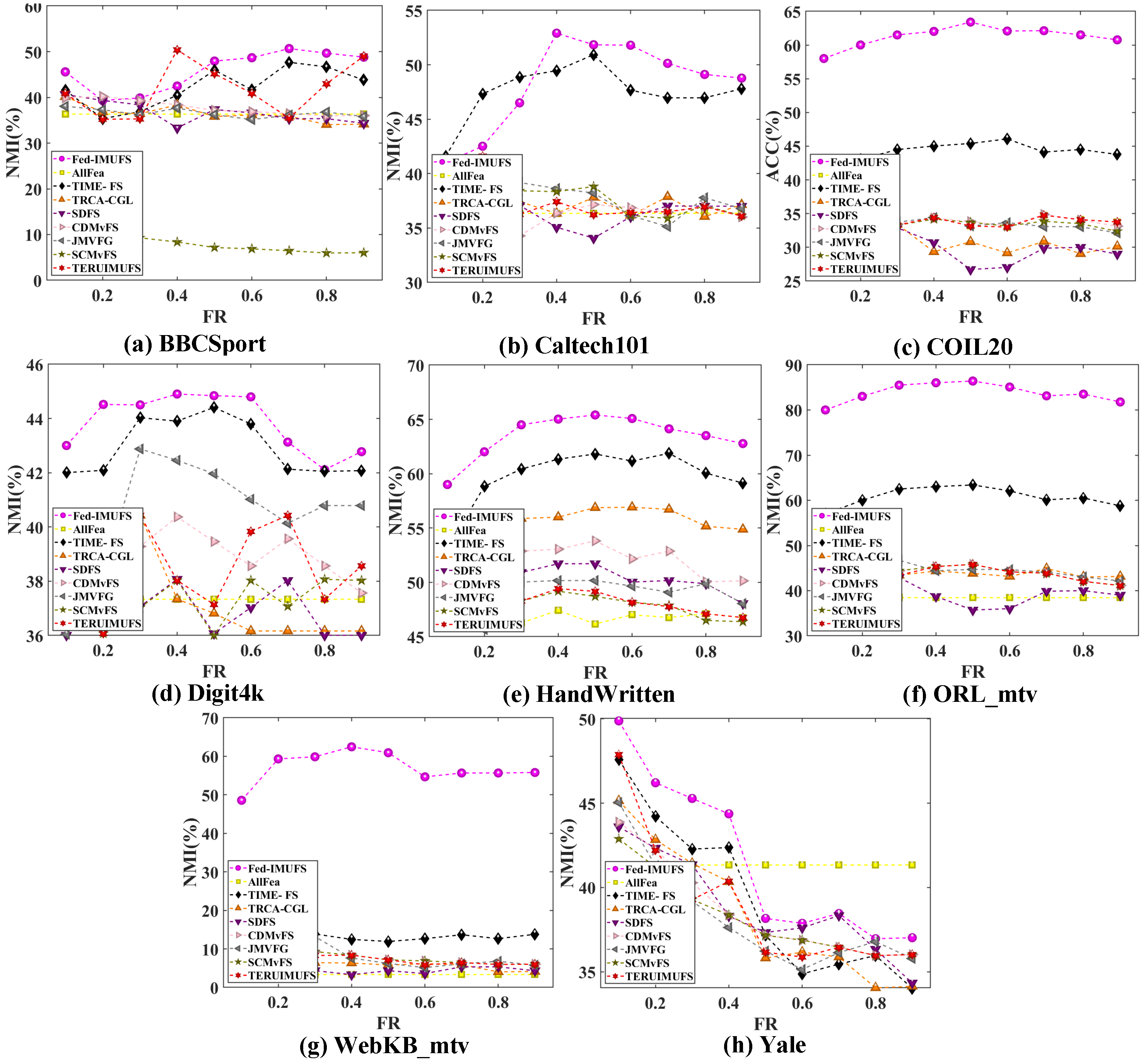
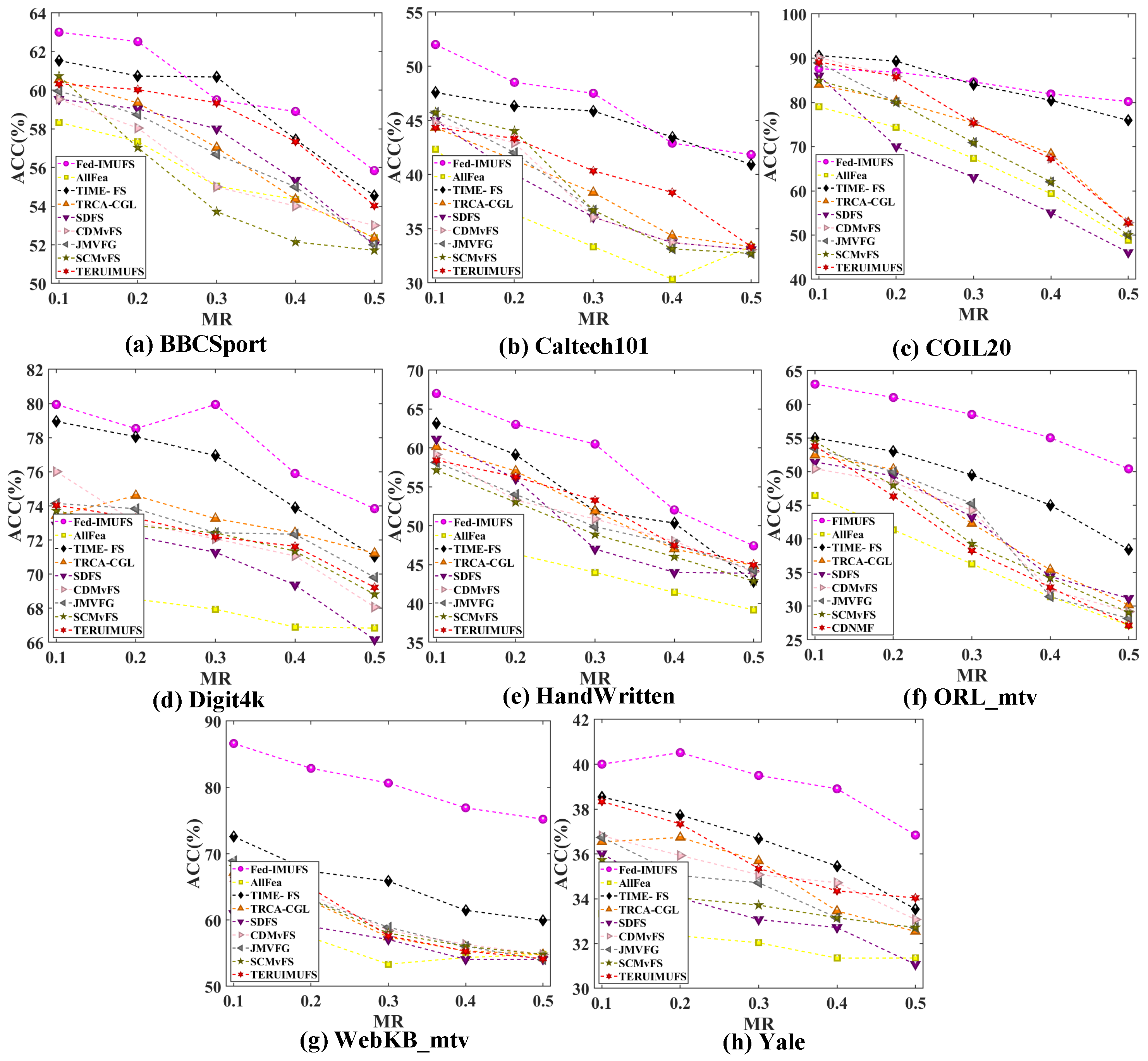
4.3. Comparative Performance Analysis of Fed-IMUFS
4.4. Ablation Study
4.5. Parameter Sensitivity Analysis
4.6. Analysis of Statistical Significance
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lv, J.; Kang, Z.; Wang, B.; Ji, L.; Xu, Z. Multi-view subspace clustering via partition fusion. Inf. Sci. 2021, 560, 410–423. [Google Scholar] [CrossRef]
- Wan, Y.; Sun, S.; Zeng, C. Adaptive similarity embedding for unsupervised multi-view feature selection. IEEE Trans. Knowl. Data Eng. 2020, 33, 3338–3350. [Google Scholar] [CrossRef]
- Tang, J.; Li, D.; Tian, Y. Image classification with multi-view multi-instance metric learning. Expert Syst. Appl. 2022, 189, 116117. [Google Scholar] [CrossRef]
- Ma, W.; Zhou, X.; Zhu, H.; Li, L.; Jiao, L. A two-stage hybrid ant colony optimization for high-dimensional feature selection. Pattern Recognit. 2021, 116, 107933. [Google Scholar] [CrossRef]
- Hao, P.; Gao, W.; Hu, L. Embedded feature fusion for multi-view multi-label feature selection. Pattern Recognit. 2025, 157. [Google Scholar] [CrossRef]
- Ran, W.; Yuan, W.; Zheng, Y. You Always Recognize Me (YARM): Robust Texture Synthesis Against MultiView Corruption. In Proceedings of the Forty-Second International Conference on Machine Learning, Vancouver, BC, Canada, 13–19 July 2025. [Google Scholar]
- Hu, R.; Gan, J.; Zhan, M.; Li, L.; Wei, M. Unsupervised Kernel-based Multi-view Feature Selection with Robust Self-representation and Binary Hashing. In Proceedings of the AAAI Conference on Artificial Intelligence, Philadelphia, PA, USA, 25 February–4 March 2025; Volume 39, pp. 17287–17294. [Google Scholar]
- Duan, M.; Song, P.; Zhou, S.; Mu, J.; Liu, Z. Consensus and discriminative non-negative matrix factorization for multi-view unsupervised feature selection. Digit. Signal Process. 2024, 154, 104668. [Google Scholar] [CrossRef]
- Liang, C.; Wang, L.; Liu, L.; Zhang, H.; Guo, F. Multi-view unsupervised feature selection with tensor robust principal component analysis and consensus graph learning. Pattern Recognit. 2023, 141, 109632. [Google Scholar] [CrossRef]
- Xu, W.; Huang, M.; Jiang, Z.; Qian, Y. Graph-based unsupervised feature selection for interval-valued information system. IEEE Trans. Neural Netw. Learn. Syst. 2023, 35, 12576–12589. [Google Scholar] [CrossRef]
- Mi, Y.; Chen, H.; Luo, C.; Horng, S.J.; Li, T. Unsupervised feature selection with high-order similarity learning. Knowl.-Based Syst. 2024, 285, 111317. [Google Scholar] [CrossRef]
- Li, Z.; Nie, F.; Bian, J.; Wu, D.; Li, X. Sparse PCA via ℓ2,p-Norm Regularization for Unsupervised Feature Selection. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 45, 5322–5328. [Google Scholar]
- Cao, Z.; Xie, X. Structure learning with consensus label information for multi-view unsupervised feature selection. Expert Syst. Appl. 2024, 238, 121893. [Google Scholar] [CrossRef]
- Fang, S.G.; Huang, D.; Wang, C.D.; Tang, Y. Joint multi-view unsupervised feature selection and graph learning. IEEE Trans. Emerg. Top. Comput. Intell. 2023, 8, 16–31. [Google Scholar] [CrossRef]
- Zhou, S.; Song, P.; Yu, Y.; Zheng, W. Structural regularization based discriminative multi-view unsupervised feature selection. Knowl.-Based Syst. 2023, 272, 110601. [Google Scholar] [CrossRef]
- Amara, A.; Taieb, M.A.H.; Aouicha, M.B. A multi-view GNN-based network representation learning framework for recommendation systems. Neurocomputing 2025, 619, 129001. [Google Scholar] [CrossRef]
- Yu, H.T.; Song, M. Mm-point: Multi-view information-enhanced multi-modal self-supervised 3d point cloud understanding. In Proceedings of the AAAI Conference on Artificial Intelligence, Vancouver, BC, Canada, 20–27 February 2024; Volume 38, pp. 6773–6781. [Google Scholar]
- Wang, X.; Zhang, Z.; Shen, G.; Lai, S.; Chen, Y.; Zhu, S. Multi-view knowledge graph convolutional networks for recommendation. Appl. Soft Comput. 2025, 169, 112633. [Google Scholar] [CrossRef]
- Han, T.; Gong, X.; Feng, F.; Zhang, J.; Sun, Z.; Zhang, Y. Privacy-preserving multi-source domain adaptation for medical data. IEEE J. Biomed. Health Inform. 2022, 27, 842–853. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Yao, M.; Chen, Y.; Xu, Y.; Liu, H.; Jia, W.; Wang, Y. Manifold-based incomplete multi-view clustering via bi-consistency guidance. IEEE Trans. Multimed. 2024, 26, 10001–10014. [Google Scholar] [CrossRef]
- Yin, J.; Wang, P.; Sun, S.; Zheng, Z. Incomplete Multi-View Clustering via Multi-Level Contrastive Learning. IEEE Trans. Knowl. Data Eng. 2025, 37, 4716–4727. [Google Scholar] [CrossRef]
- Huang, Y.; Lu, M.; Huang, W.; Yi, X.; Li, T. Time-fs: Joint learning of tensorial incomplete multi-view unsupervised feature selection and missing-view imputation. In Proceedings of the AAAI Conference on Artificial Intelligence, Philadelphia, PA, USA, 25 February–4 March 2025; Volume 39, pp. 17503–17510. [Google Scholar]
- Chen, X.; Ren, Y.; Xu, J.; Lin, F.; Pu, X.; Yang, Y. Bridging gaps: Federated multi-view clustering in heterogeneous hybrid views. In Proceedings of the Advances in Neural Information Processing Systems 37 (NeurIPS 2024), Vancouver, BC, Canada, 9–15 December 2024; pp. 37020–37049. [Google Scholar]
- Gao, M.; Zheng, H.; Feng, X.; Tao, R. Multimodal fusion using multi-view domains for data heterogeneity in federated learning. In Proceedings of the AAAI Conference on Artificial Intelligence, Philadelphia, PA, USA, 25 February–4 March 2025; Volume 39, pp. 16736–16744. [Google Scholar]
- Banerjee, S.; Bhuyan, D.; Elmroth, E.; Bhuyan, M. Cost-efficient feature selection for horizontal federated learning. IEEE Trans. Artif. Intell. 2024, 5, 6551–6565. [Google Scholar] [CrossRef]
- Mahanipour, A.; Khamfroush, H. FMLFS: A federated multi-label feature selection based on information theory in IoT environment. In Proceedings of the 2024 IEEE International Conference on Smart Computing (SMARTCOMP), Dublin, Ireland, 29 June–3 July; IEEE: Piscataway, NJ, USA, 2024; pp. 166–173. [Google Scholar]
- Bohrer, J.D.S.; Dorn, M. Enhancing classification with hybrid feature selection: A multi-objective genetic algorithm for high-dimensional data. Expert Syst. Appl. 2024, 255, 124518. [Google Scholar] [CrossRef]
- Song, X.; Zhang, Y.; Gong, D.; Liu, H.; Zhang, W. Surrogate sample-assisted particle swarm optimization for feature selection on high-dimensional data. IEEE Trans. Evol. Comput. 2022, 27, 595–609. [Google Scholar] [CrossRef]
- Marzbani, F.; Osman, A.H.; Hassan, M.S. Two-Stage Hybrid Feature Selection: Integrating ACO Algorithms with a Statistical Ensemble Technique for EV Demand Prediction. IEEE Trans. Ind. Appl. 2025, 61, 5091–5102. [Google Scholar] [CrossRef]
- Fathi, I.S.; El-Saeed, A.R.; Hassan, G.; Aly, M. Fractional Chebyshev Transformation for Improved Binarization in the Energy Valley Optimizer for Feature Selection. Fractal Fract. 2025, 9, 521. [Google Scholar] [CrossRef]
- Meng, Z.; Hu, Y.; Jiang, S.; Zheng, S.; Zhang, J.; Yuan, Z.; Yao, S. Slope Deformation Prediction Combining Particle Swarm Optimization-Based Fractional-Order Grey Model and K-Means Clustering. Fractal Fract. 2025, 9, 210. [Google Scholar] [CrossRef]
- Kartci, A.; Agambayev, A.; Farhat, M.; Herencsar, N.; Brancik, L.; Bagci, H.; Salama, K.N. Synthesis and optimization of fractional-order elements using a genetic algorithm. IEEE Access 2019, 7, 80233–80246. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The whale optimization algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Liang, Z.; Shu, T.; Ding, Z. A novel improved whale optimization algorithm for global optimization and engineering applications. Mathematics 2024, 12, 636. [Google Scholar] [CrossRef]
- Wu, L.; Xu, D.; Guo, Q.; Chen, E.; Xiao, W. A nonlinear randomly reuse-based mutated whale optimization algorithm and its application for solving engineering problems. Appl. Soft Comput. 2024, 167, 112271. [Google Scholar] [CrossRef]
- Miao, F.; Wu, Y.; Yan, G.; Si, X. A memory interaction quadratic interpolation whale optimization algorithm based on reverse information correction for high-dimensional feature selection. Appl. Soft Comput. 2024, 164, 111979. [Google Scholar] [CrossRef]
- Deng, L.; Liu, S. Deficiencies of the whale optimization algorithm and its validation method. Expert Syst. Appl. 2024, 237, 121544. [Google Scholar] [CrossRef]
- Li, L.L.; Fan, X.D.; Wu, K.J.; Sethanan, K.; Tseng, M.L. Multi-objective distributed generation hierarchical optimal planning in distribution network: Improved beluga whale optimization algorithm. Expert Syst. Appl. 2024, 237, 121406. [Google Scholar] [CrossRef]
- Wolpert, D.H.; Macready, W.G. No free lunch theorems for optimization. IEEE Trans. Evol. Comput. 2002, 1, 67–82. [Google Scholar] [CrossRef]
- He, X.; Cai, D.; Niyogi, P. Laplacian score for feature selection. In Proceedings of the Advances in Neural Information Processing Systems 18 (NIPS 2005), Vancouver, BC, Canada, 5–8 December 2005. [Google Scholar]
- Zhao, Z.; Liu, H. Spectral feature selection for supervised and unsupervised learning. In Proceedings of the 24th International Conference on Machine Learning, Corvallis, OR, USA, 20–24 June 2007; pp. 1151–1157. [Google Scholar]
- Shi, D.; Zhu, L.; Li, J.; Zhang, Z.; Chang, X. Unsupervised adaptive feature selection with binary hashing. IEEE Trans. Image Process. 2023, 32, 838–853. [Google Scholar] [CrossRef] [PubMed]
- Wang, C.; Wang, J.; Gu, Z.; Wei, J.M.; Liu, J. Unsupervised feature selection by learning exponential weights. Pattern Recognit. 2024, 148, 110183. [Google Scholar] [CrossRef]
- Li, T.; Qian, Y.; Li, F.; Liang, X.; Zhan, Z.H. Feature subspace learning-based binary differential evolution algorithm for unsupervised feature selection. IEEE Trans. Big Data 2025, 11, 99–114. [Google Scholar] [CrossRef]
- Fan, Z.; Xiao, Z.; Li, X.; Huang, Z.; Zhang, C. MSBWO: A Multi-Strategies Improved Beluga Whale Optimization Algorithm for Feature Selection. Biomimetics 2024, 9, 572. [Google Scholar] [CrossRef]
- Miao, F.; Wu, Y.; Yan, G.; Si, X. Dynamic multi-swarm whale optimization algorithm based on elite tuning for high-dimensional feature selection classification problems. Appl. Soft Comput. 2025, 169, 112634. [Google Scholar] [CrossRef]
- Pramanik, P.; Pramanik, R.; Naskar, A.; Mirjalili, S.; Sarkar, R. U-WOA: An unsupervised whale optimization algorithm based deep feature selection method for cancer detection in breast ultrasound images. In Handbook of Whale Optimization Algorithm; Academic Press: New York, NY, USA, 2024; pp. 179–191. [Google Scholar]
- Nie, F.; Zhu, W.; Li, X. Unsupervised feature selection with structured graph optimization. In Proceedings of the AAAI Conference on Artificial Intelligence, Phoenix, AZ, USA, 12–17 February 2016; Volume 30. [Google Scholar]
- Wang, Z.; Feng, Y.; Qi, T.; Yang, X.; Zhang, J.J. Adaptive multi-view feature selection for human motion retrieval. Signal Process. 2016, 120, 691–701. [Google Scholar] [CrossRef]
- Cao, Z.; Xie, X. Multi-view unsupervised complementary feature selection with multi-order similarity learning. Knowl.-Based Syst. 2024, 283, 111172. [Google Scholar] [CrossRef]
- Cao, Z.; Xie, X.; Li, Y. Multi-view unsupervised feature selection with consensus partition and diverse graph. Inf. Sci. 2024, 661, 120178. [Google Scholar] [CrossRef]
- Liu, Q.; Liu, S.; Liu, X.; Dai, J. Latent Semantics and Anchor Graph Multi-layer Learning for Multi-view Unsupervised Feature Selection. IEEE Trans. Knowl. Data Eng. 2025, 37, 6032–6045. [Google Scholar] [CrossRef]
- Yang, X.; Che, H.; Leung, M.F. Tensor-based unsupervised feature selection for error-robust handling of unbalanced incomplete multi-view data. Inf. Fusion 2025, 114, 102693. [Google Scholar] [CrossRef]
- Yu, H.W.; Wu, J.Y.; Wu, J.S.; Min, W. Confident local similarity graphs for unsupervised feature selection on incomplete multi-view data. Knowl.-Based Syst. 2025, 316, 113369. [Google Scholar] [CrossRef]
- Fan, S.; Wang, R.; Su, K. A novel metaheuristic algorithm: Advanced social memory optimization. Phys. Scr. 2025, 100, 055004. [Google Scholar] [CrossRef]
- Xie, X.; Li, Y.; Sun, S. Deep multi-view multiclass twin support vector machines. Inf. Fusion 2023, 91, 80–92. [Google Scholar] [CrossRef]
- Ma, Y.; Shen, X.; Wu, D.; Cao, J.; Nie, F. Cross-view approximation on grassmann manifold for multiview clustering. IEEE Trans. Neural Netw. Learn. Syst. 2024, 36, 7772–7777. [Google Scholar] [CrossRef]
- Lin, Y.; Gou, Y.; Liu, X.; Bai, J.; Lv, J.; Peng, X. Dual contrastive prediction for incomplete multi-view representation learning. IEEE Trans. Pattern Anal. Mach. Intell. 2022, 45, 4447–4461. [Google Scholar] [CrossRef] [PubMed]
- Chakraborty, S.; Sharma, S.; Saha, A.K.; Saha, A. A novel improved whale optimization algorithm to solve numerical optimization and real-world applications. Artif. Intell. Rev. 2022, 55, 4605–4716. [Google Scholar] [CrossRef]
- Mei, M.; Zhang, S.; Ye, Z.; Wang, M.; Zhou, W.; Yang, J.; Shen, J. A cooperative hybrid breeding swarm intelligence algorithm for feature selection. Pattern Recognit. 2026, 169, 111901. [Google Scholar] [CrossRef]
- Dong, Y.; Zhang, S.; Zhang, H.; Zhou, X.; Jiang, J. Chaotic evolution optimization: A novel metaheuristic algorithm inspired by chaotic dynamics. Chaos Solitons Fractals 2025, 192, 116049. [Google Scholar] [CrossRef]
- Li, J.; Cheng, K.; Wang, S.; Morstatter, F.; Trevino, R.P.; Tang, J.; Liu, H. Feature selection: A data perspective. ACM Comput. Surv. (CSUR) 2017, 50, 1–45. [Google Scholar] [CrossRef]

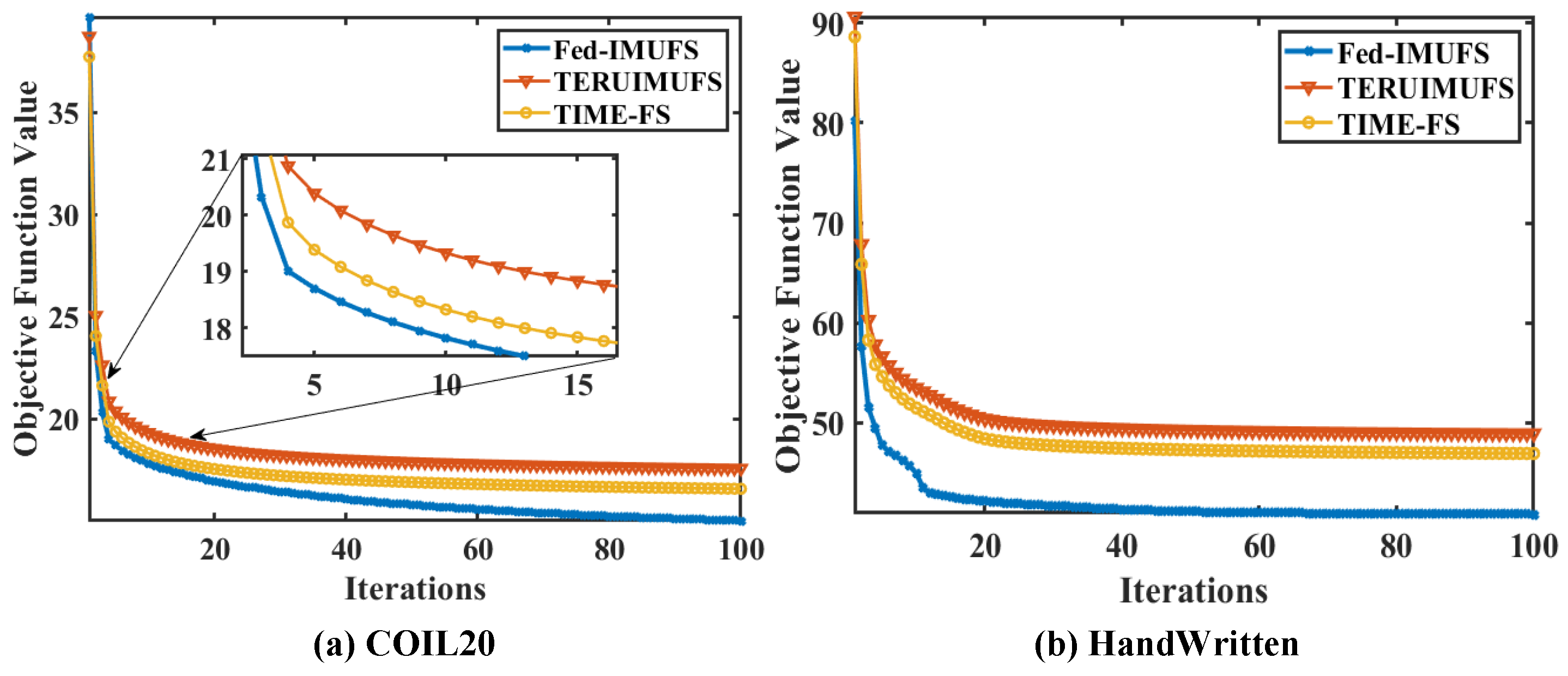
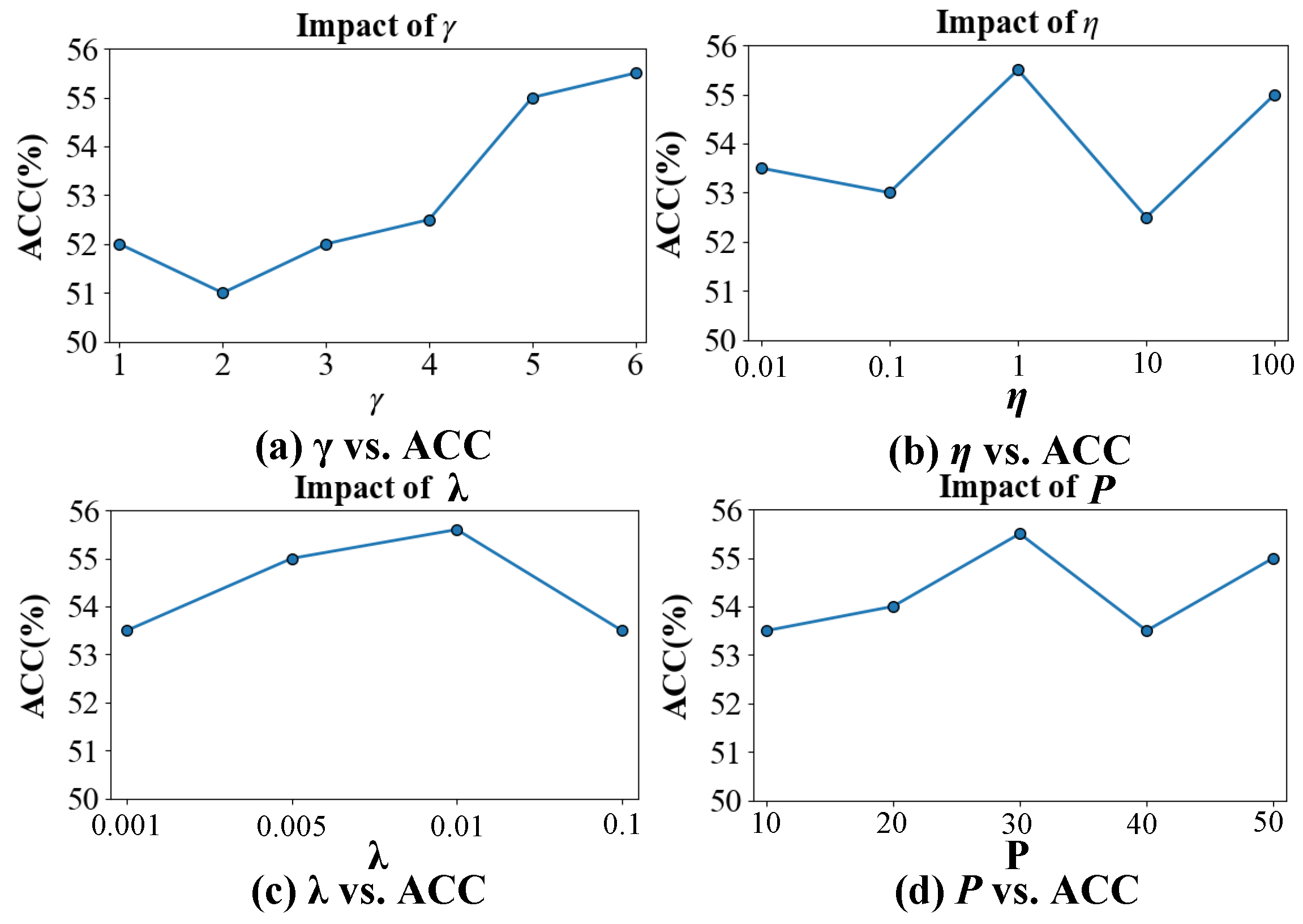
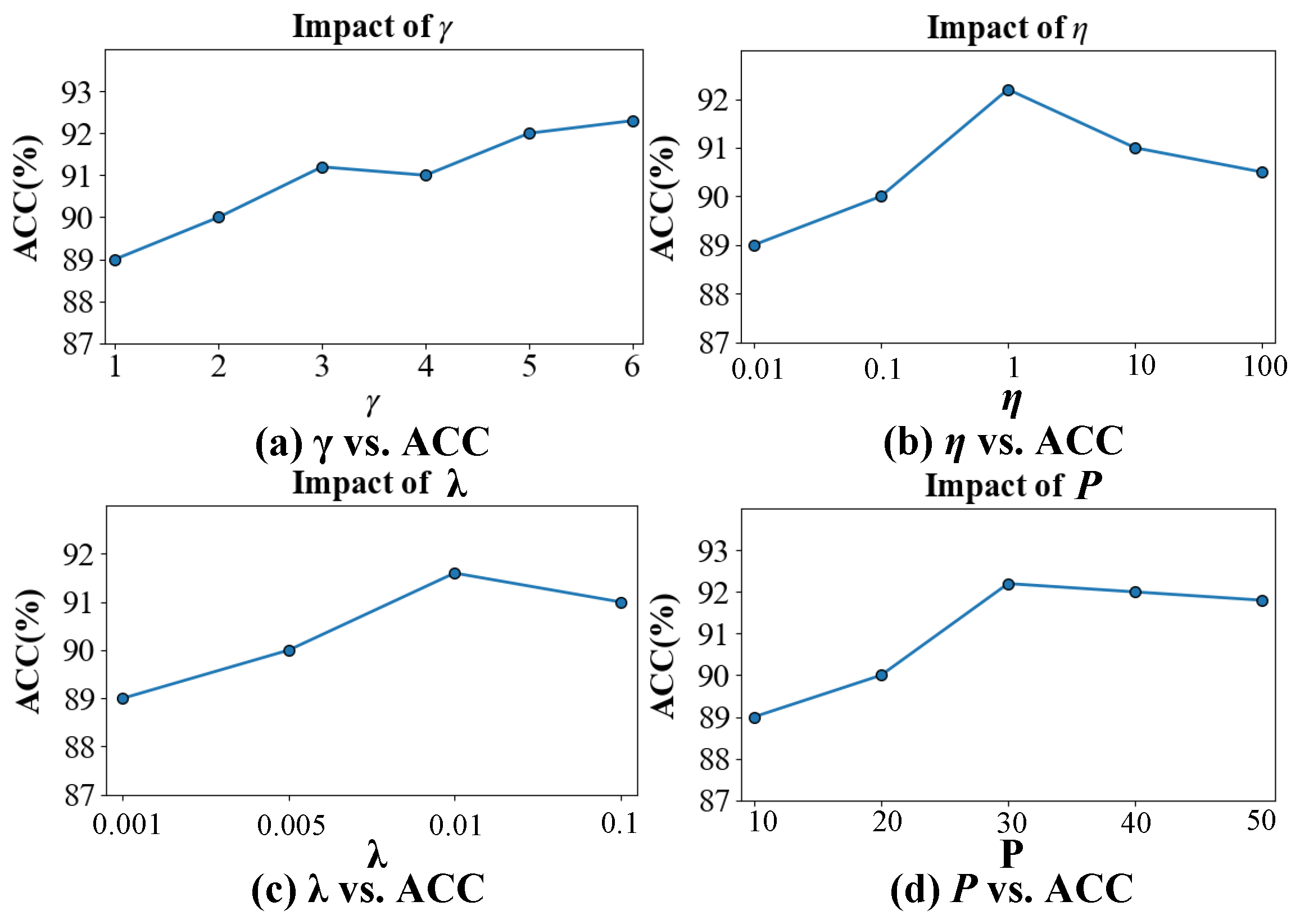
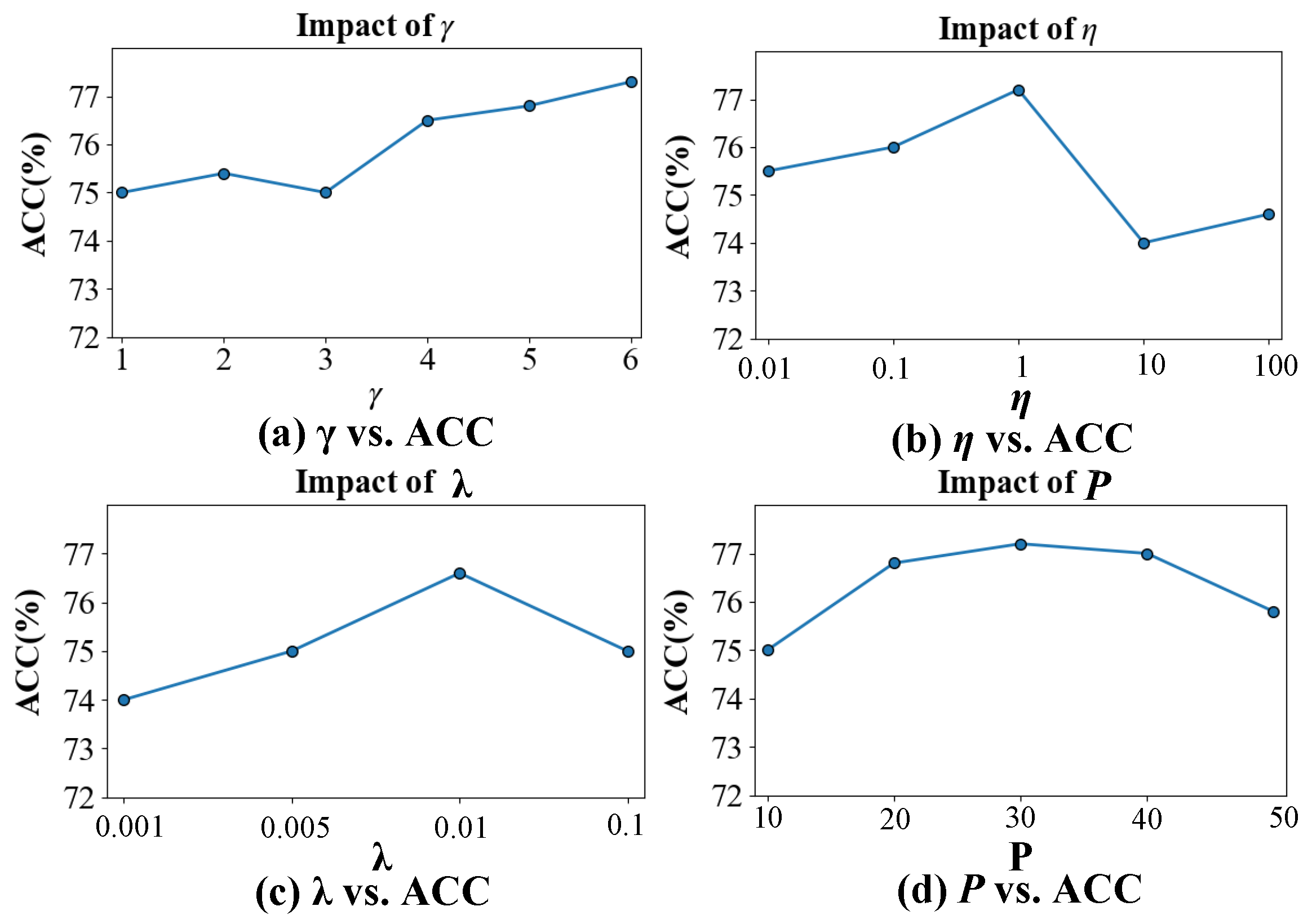
| Datasets | Views | Samples | Features | Classes |
|---|---|---|---|---|
| BBCSport | 2 | 544 | 7073/6935 | 5 |
| Caltech101 | 6 | 1474 | 48/40/254/1984/512/928 | 7 |
| COIL20 | 3 | 1440 | 30/19/30 | 20 |
| Digit4k | 4 | 2000 | 240/216/47/64 | 10 |
| HandWritten | 2 | 544 | 4657/1125 | 5 |
| ORL_mtv | 3 | 400 | 4096/3304/6750 | 40 |
| WebKB | 3 | 2100 | 540/640/256 | 21 |
| Yale | 2 | 165 | 1024/3304/6750 | 15 |
| Methods | COIL20 | Caltech101 | HandWritten | Time Complexity |
|---|---|---|---|---|
| Fed-IMUFS | 2.87 | 39.01 | 5.40 | |
| TIME-FS | 0.46 | 6.55 | 7.14 | |
| TRCA-CGL | 15.81 | 127.30 | 35.69 | |
| SDFS | 27.68 | 187.16 | 48.45 | |
| CDMvFS | 50.84 | 527.95 | 79.38 | |
| JMVFG | 3.22 | 68.75 | 12.45 | |
| SCMvFS | 19.05 | 256.84 | 27.64 | |
| TERUI-MUFS | 3.07 | 44.42 | 11.46 |
| Datasets | Fed-IMUFS | Fed-IMUFS-I | Fed-IMUFS-II | Fed-IMUFS-III | Fed-IMUFS-IV | Fed-IMUFS-V | Fed-IMUFS-VII | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ACC | NMI | ACC | NMI | ACC | NMI | ACC | NMI | ACC | NMI | ACC | NMI | ACC | NMI | |
| Caltech101 | 52.85 * | 53.42 * | 48.41 | 47.46 | 47.21 | 46.82 | 50.11 | 49.23 | 49.85 | 47.92 | 48.92 | 48.31 | 50.72 | 49.85 |
| COIL20 | 90.55 * | 96.12 * | 85.81 | 91.97 | 84.98 | 90.14 | 86.42 | 92.11 | 87.05 | 91.85 | 85.63 | 90.72 | 87.42 | 92.23 |
| Digit4k | 76.65 * | 45.64 * | 71.39 | 40.14 | 70.80 | 39.07 | 72.50 | 42.11 | 71.95 | 41.73 | 70.25 | 40.32 | 72.18 | 41.52 |
| HandWritten | 65.18 * | 65.43 * | 57.95 | 65.23 | 56.62 | 59.77 | 59.84 | 62.09 | 60.21 | 61.84 | 59.45 | 60.37 | 61.72 | 62.35 |
| ORL_mtv | 86.73 * | 87.27 * | 78.81 | 82.97 | 77.08 | 81.64 | 80.45 | 84.11 | 81.62 | 83.92 | 79.58 | 82.16 | 82.05 | 84.02 |
| WebKB | 87.10 * | 62.87 * | 80.44 | 50.59 | 79.82 | 47.15 | 82.21 | 55.42 | 81.95 | 54.83 | 80.25 | 52.62 | 82.65 | 55.72 |
| Methods | Superior | Comparable | Inferior | p-Value | Significance | Effect Size |
|---|---|---|---|---|---|---|
| Fed-IMUFS—TIME-FS | 6 | 1 | 1 | 1.1511 × 10−2 | + | 0.4547 |
| Fed-IMUFS—TRCA-CGL | 8 | 0 | 0 | 2.6441 × 10−2 | + | 0.74614 |
| Fed-IMUFS—SDFS | 8 | 0 | 0 | 4.3422 × 10−3 | + | 0.73443 |
| Fed-IMUFS—CDMvFS | 8 | 0 | 0 | 6.1702 × 10−4 | + | 0.73227 |
| Fed-IMUFS—JMVFG | 8 | 0 | 0 | 1.8360 × 10−3 | + | 0.63172 |
| Fed-IMUFS—SCMvFS | 8 | 0 | 0 | 3.2637 × 10−3 | + | 0.62534 |
| Fed-IMUFS—TERUIMUFS | 7 | 1 | 0 | 3.3042 × 10−2 | + | 0.54402 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yuan, Y.; Wu, W.; Xu, C.-A.; Zhang, W.; Jin, C. Federated Incomplete Multi-View Unsupervised Feature Selection with Fractional Sparsity-Guided Whale Optimization and Tensor Alternating Learning. Fractal Fract. 2025, 9, 717. https://doi.org/10.3390/fractalfract9110717
Yuan Y, Wu W, Xu C-A, Zhang W, Jin C. Federated Incomplete Multi-View Unsupervised Feature Selection with Fractional Sparsity-Guided Whale Optimization and Tensor Alternating Learning. Fractal and Fractional. 2025; 9(11):717. https://doi.org/10.3390/fractalfract9110717
Chicago/Turabian StyleYuan, Yufan, Wangyu Wu, Chang-An Xu, Weirong Zhang, and Chuan Jin. 2025. "Federated Incomplete Multi-View Unsupervised Feature Selection with Fractional Sparsity-Guided Whale Optimization and Tensor Alternating Learning" Fractal and Fractional 9, no. 11: 717. https://doi.org/10.3390/fractalfract9110717
APA StyleYuan, Y., Wu, W., Xu, C.-A., Zhang, W., & Jin, C. (2025). Federated Incomplete Multi-View Unsupervised Feature Selection with Fractional Sparsity-Guided Whale Optimization and Tensor Alternating Learning. Fractal and Fractional, 9(11), 717. https://doi.org/10.3390/fractalfract9110717








