Analytic Functions Related to a Balloon-Shaped Domain

Abstract

One of the fundamental parts of Geometric Function Theory is the study of analytic functions in different domains with critical geometrical interpretations. This article defines a new generalized domain obtained based on the quotient of two analytic functions. We derive various properties of the new class of normalized analytic functions $\mathcal{X}$ defined in the new domain, including the sharp estimates for the coefficients $a_2,a_3$, and $a_4$, and for three second-order and third-order Hankel determinants, ${\mathcal{H}}_{2,1}\mathcal{X},{\mathcal{H}}_{2,2}\mathcal{X}$, and ${\mathcal{H}}_{3,1}\mathcal{X}$. The optimality of each obtained estimate is given as well.

1. Introduction

Let $\mathcal{A}$ be the class of all analytic functions $\mathcal{X}$ defined in the open unit disc $\mathbf{U}=\{z\in \mathbb{C}:\left|z\right|<1\}$ with $\mathcal{X}\left(0\right)=0$ and ${\mathcal{X}}^{\prime }\left(0\right)=1.$ Thus, each analytic function in $\mathcal{A}$ has the following Taylor series representation

$$\mathcal{X}\left(z\right)=z+\sum _{t=2}^{\infty }{a}_t{z}^t.$$

(1)

Let $\mathcal{S}$ be the subclass of all analytic functions in $\mathcal{A}$ that are univalent in $\mathbf{U}$.

An analytic function $\mathcal{X}$ is said to be subordinate to an analytic function $\mathbf{g}$ in $\mathbf{U}$, denoted as $\mathcal{X}\prec \mathbf{g}$, if there exists a Schwarz function $\xi$ that is analytic in $\mathbf{U}$ with $\xi \left(0\right)=0$ and $\left|\xi \left(z\right)\right|$< 1, such that $\mathcal{X}\left(z\right)$ = $\mathbf{g}\left(\xi \right(z\left)\right)$. In particular (see [1]), if $\mathbf{g}$ is univalent in $\mathbf{U}$, then $\mathcal{X}\prec \mathbf{g}$ if and only if

$$\mathcal{X}\left(0\right)=\mathbf{g}\left(0\right)\mathrm{and}\mathcal{X}\left(\mathbf{U}\right)\subset \mathbf{g}\left(\mathbf{U}\right).$$

Using the concept of subordination, many subclasses have been defined and studied, such as ${\mathcal{S}}^{\ast },\mathcal{C},\mathcal{K}$ and $\mathcal{R}$ of starlike, convex, close to convex, and functions with bounded turnings, respectively. See [2,3,4,5,6] for the new results about more subclasses.

For two analytic functions $\mathcal{X}$ and $\zeta$ in $\mathcal{A}$ with the series representation of $\mathcal{X}$given in (1) and $\zeta \left(z\right)=z+{\displaystyle \sum _{t=2}^{\infty }}{b}_t{z}^t$ the convolution (Hadamard product) $\mathcal{X}\ast \zeta$ is defined by

$$\left(\mathcal{X}\ast \zeta \right)\left(z\right)=z+\sum _{t=2}^{\infty }{a}_t{b}_t{z}^t=\left(\zeta \ast \mathcal{X}\right)\left(z\right).$$

(2)

Shanmugam [7] generalized the idea of Padmanabhan et al. [8] and introduced the general form of function class ${\mathcal{S}}_h^{\ast }\left(\phi \right)$ as follows

$${\mathcal{S}}_h^{\ast }\left(\phi \right)=\left\{\mathcal{X}\in \mathcal{A}:\frac{z{(\mathcal{X}\ast h)}^{\prime }\left(z\right)}{(\mathcal{X}\ast h)\left(z\right)}\prec \phi \left(z\right),z\in \mathbf{U}\right\},$$

where h is a fixed function in $\mathcal{A}$ and $\phi$ is a convex univalent function on $\mathbf{U}$ with $\phi \left(0\right)=1$ and $Re\left(\phi \right(z\left)\right)>0$.

Ma and Minda [9] defined a more general form of function class ${\mathcal{S}}^{\ast }\left(\phi \right)$ by applying for some restrictions $h\left(z\right)=\frac{z}{1-z}$ (and hence $\mathcal{X}\ast h=\mathcal{X}$) with $\phi \left(0\right)=1$ and ${\phi }^{\prime }\left(0\right)>0$. The generic form of Ma and Minda-type class of starlike functions is defined as

$${\mathcal{S}}^{\ast }\left(\phi \right)=\left\{\mathcal{X}\in \mathcal{A}:\frac{z{\mathcal{X}}^{\prime }\left(z\right)}{\mathcal{X}\left(z\right)}\prec \phi \left(z\right),z\in \mathbf{U}\right\}.$$

(3)

In recent years, many authors have established important subfamilies of analytic functions by varying $\phi \left(z\right)$ in ${\mathcal{S}}^{\ast }\left(\phi \right)$, and they proved significant geometric properties of those subfamilies. For details, see [10,11,12,13,14].

We discuss the following two classes that have some interesting geometric properties.

(i)

For ${\phi }_1\left(z\right)=\sqrt{1+z}$, the class ${\mathcal{S}}^{\ast }\left(\phi \right)$ becomes ${\mathcal{S}}_L^{\ast }$, which was introduced by Sokol and Stankiewicz [15], and it contains those functions $\mathcal{X}\in \mathcal{A}$ such that $\frac{z{\mathcal{X}}^{{}^{\prime }}\left(z\right)}{\mathcal{X}\left(z\right)}$ lies in the region bounded by the right half of the lemniscate of Bernoulli defined by $\left|z^2-1\right|<1$.

(ii)

For ${\phi }_2\left(z\right)=\frac{2}{1+e^{-z}}$, the class ${\mathcal{S}}^{\ast }\left(\phi \right)$ becomes ${\mathcal{S}}_{sig}^{\ast }$, which was defined and investigated by Geol et al. [16]. Geometrically, a function $\mathcal{X}\in {\mathcal{S}}_{sig}^{\ast }$ if and only if $\frac{z{\mathcal{X}}^{{}^{\prime }}\left(z\right)}{\mathcal{X}\left(z\right)}$ lies in the region defined by $\left\{w\in \mathbb{C}:\left|log\left(\frac{w}{2-w}\right)\right|<1\right\}$.

By taking inspiration from all of the previous works mentioned, we introduce the following new class of analytic functions by using the quotient of ${\phi }_1\left(z\right)=\sqrt{1+z}$ and ${\phi }_2\left(z\right)=\frac{2}{1+e^{-z}}$.

Definition 1.

Let $\mathcal{X}\in \mathcal{A},$given in (1). We say $\mathcal{X}\in {\mathcal{R}}_{sl}$ if it satisfies the following condition

$${\mathcal{X}}^{\prime }\left(z\right)\prec \frac{2\sqrt{1+z}}{1+e^{-z}},z\in \mathbf{U}.$$

(4)

Geometrically, each $\mathcal{X}\in {\mathcal{R}}_{sl}$ maps the open unit disc into a balloon-shaped domain, which is symmetric about the real axis, as shown in the following Figure 1.

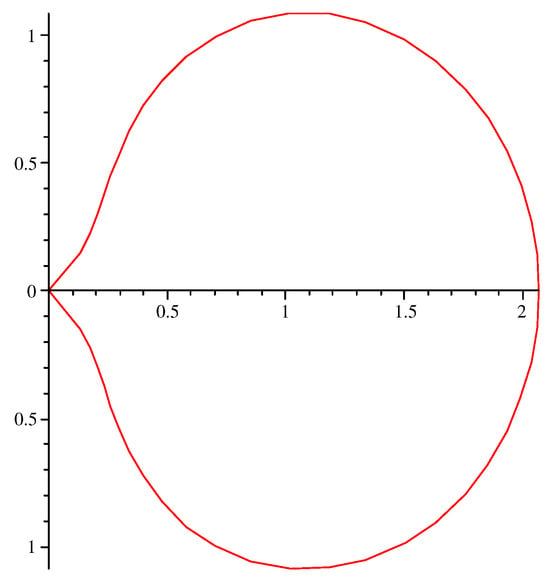
Figure 1. The geometry of the function $\mathsf{\varphi }$(z)=$\frac{2\sqrt{1+z}}{1+e^{-z}}$.

For $\mathcal{X}\in \mathcal{A}$ and $n,$$k\ge 0$, Pommerenke [17] defined the $k^{th}$ order Hankel determinant ${\mathcal{H}}_{k,n}$ by

$${\mathcal{H}}_{k,n}\left(\mathcal{X}\right)=\left|\begin{array}{cccccc}{a}_n& a_{n+1}& .& .& .& a_{n+k-1}\\ a_{n+1}& a_{n+2}& .& .& .& a_{n+k}\\ .& .& .& .& .& .\\ .& .& .& .& .& .\\ .& .& .& .& .& .\\ a_{n+k-1}& a_{n+k}& .& .& .& a_{n+2\left(k-1\right)}\end{array}\right|.$$

(5)

Recently, finding the sharp upper bounds of the Hankel determinants ${\mathcal{H}}_{k,n}\left(\mathcal{X}\right)$ for certain n and k for various subfamilies of analytic functions has been identified as an interesting and important problem. Many researchers have observed sharp upper bounds of Hankel determinants for many subfamilies of analytic functions. In particular, the upper bounds of second and third-order Hankel determinants have been estimated in [18,19,20,21,22,23] for several subclasses of normalized analytic function.

Hayman [24] was the first to give the sharp inequality for $\mathcal{X}\in \mathcal{S}$, and subsequently proved that $\left|{\mathcal{H}}_{2,n}\left(\mathcal{X}\right)\right|\le \lambda \sqrt{n}$, where $\lambda >0$. This inequality is further explained in [25] and showed that $\left|{\mathcal{H}}_{2,2}\left(\mathcal{X}\right)\right|\le \lambda$, where $1\le \lambda \le \frac{11}{3}$.

Janteng et al. [26] determined the sharp bounds of ${\mathcal{H}}_{2,2}\left(\mathcal{X}\right)$ for the subfamilies of $\mathcal{K}$, ${\mathcal{S}}^{\ast }$, and $\mathcal{R}$. Babalola [27] studied a third-order Hankel determinant for the subclasses of ${\mathcal{S}}^{\ast }$ and $\mathcal{C}$, while Zaprawa [28] amended Babalola’s results and gave the following estimates, which it is believed may not be the best possible results.

$$\left|{\mathcal{H}}_{3,1}\left(\mathcal{X}\right)\right|\le \left\{\begin{array}{c}\frac{49}{540}\left(\mathcal{X}\in \mathcal{K}\right),\\ 1\left(\mathcal{X}\in {\mathcal{S}}^{\ast }\right),\\ \frac{41}{60}\left(\mathcal{X}\in \mathcal{R}\right).\end{array}\right.$$

Kwon et al. [29] improved this determinant for starlike functions as $\left|{\mathcal{H}}_{3,1}\left(\mathcal{X}\right)\right|\le \frac{8}{9}.$ Zaprawa et al. [30] extended his work by estimating $\left|{\mathcal{H}}_{3,1}\left(\mathcal{X}\right)\right|\le \frac{5}{9}$ for $\mathcal{X}\in {\mathcal{S}}^{\ast }$.

Arif et al. [31] calculated the sharpness of the bounds of the coefficients and ${\mathcal{H}}_{3,1}\left(\mathcal{X}\right)$ for a subfamily of starlike functions related to sigmoid functions; see [32] for the modified sigmoid functions. Orhan et al. [33] estimated the sharp Hankel determinants for a subfamily of analytic functions associated with the lemniscate of Bernoulli. Moreover, Shi et al. [34,35] estimated the sharpness of Hankel determinants for the functions with bounded turning associated with a petal-shaped domain and inverse functions, respectively.

Moreover, the estimation of various bounds can be considered for many classes of functions; for example, see [36,37,38].

It is natural to ask what the upper bounds for the analytic functions in the newly defined class ${\mathcal{R}}_{sl}$ related to the coefficients of the Taylor series representation (1) and Hankel determinants are.

The aim and novelty of this article are the sharp upper bounds of the modulus of the coefficients $a_2,a_3$, and $a_4$ and the second-order and third-order Hankel determinants, ${\mathcal{H}}_{2,1}\mathcal{X},{\mathcal{H}}_{2,2}\mathcal{X}$, and ${\mathcal{H}}_{3,1}\mathcal{X}$, for the analytic functions in the new class ${\mathcal{R}}_{sl}$.

2. A Set of Lemmas

Let $\mathcal{P}$ represent the class of analytic functions p, such that $p\left(0\right)=1$, $Re\left(p\right(z\left)\right)>0$ for $z\in \mathbf{U}$, which has the following Taylor series form,

$$p\left(z\right)=1+\underset{t=1}{\sum ^{\infty }}{c}_t{z}^t.$$

(6)

The subsequent Lemmas 1–4 will help to demonstrate our main findings, where $c_t,c_{t+k}$, and $c_{t+2k}$ for $t,k\in \mathbb{N}$ are coefficients of the Taylor series (6).

Lemma 1.

([17]). Let $p\in \mathcal{P}$. Then, the following inequalities hold true

$$\begin{array}{ccc}\hfill \left|c_t\right|& \le & 2\mathrm{for}t\ge 1,\hfill \end{array}$$

(7)

$$\begin{array}{ccc}\hfill \left|c_{t+k}-\rho c_t{c}_k\right|& <& 2\mathrm{for}0\le \rho \le 1,\hfill \end{array}$$

(8)

$$\begin{array}{ccc}\hfill \left|c_{t+2k}-\rho c_t{c}_k^2\right|& \le & 2(1+2\rho ),\mathrm{for}0\le \rho \le 1,\hfill \end{array}$$

(9)

and

$$\left|c_2-\frac{c_1^2}{2}\right|\le 2-\frac{\left|c_1^2\right|}{2}.$$

(10)

Lemma 2.

Let $p\in \mathcal{P}$. Then there exists $q,\gamma$, and $\mu \in$$\mathbb{C}$ with $\left|q\right|\le 1,\left|\gamma \right|\le 1,$and $\left|\mu \right|\le 1$ such that

$$\begin{array}{ccc}\hfill c_2& =& \frac{1}{2}\left(c_1^2+q\left(4-c_1^2\right)\right),\hfill \end{array}$$

(11)

$$\begin{array}{ccc}\hfill c_3& =& \frac{1}{4}\left(c_1^3+2c_{1}q\left(4-c_1^2\right)-\left(4-c_1^2\right)c_1{q}^2+2\left(4-c_1^2\right)\left(1-{\left|q\right|}^2\right)\gamma \right),\hfill \end{array}$$

(12)

and

$$c_4=\frac{1}{8}\left(\begin{array}{c}{c}_1^4+q\left(4-c_1^2\right)(4q+(q^2-3q+3)c_1^2)-4\left(4-c_1^2\right)\left(1-{\left|q\right|}^2\right)(c(q-1)\gamma \\ -\mu \left(1-{\left|\gamma \right|}^2\right)+\overline{q}{\gamma }^2)\end{array}\right).$$

(13)

The inequalities given in (11)–(13) are due to [17,39,40], respectively.

Lemma 3.

([39]). If $p\in \mathcal{P}$, $0\le R\le 1$, and $R\left(2R-1\right)\le S\le R$, then the following inequality holds true

$$\left|c_3-2R{c}_1{c}_2+S{c}_1^3\right|\le 2.$$

(14)

Lemma 4.

([41]). Let $\alpha ,\beta ,\gamma$, and λ satisfying the conditions $0<\alpha <1,$

$0<\lambda <1$, and

$$8\lambda \left(1-\lambda \right)\left[{\left(\alpha \beta -2\gamma \right)}^2+{\left(\alpha \left(\lambda +\alpha \right)-\beta \right)}^2\right]+\alpha \left(1-\alpha \right){\left(\beta -2\lambda \alpha \right)}^2\le 4{\alpha }^2{\left(1-\alpha \right)}^2\lambda \left(1-\lambda \right).$$

Let $p\in \mathcal{P}$ be given in (6), then the following inequality holds true

$$\left|\gamma c_1^4+\lambda c_2^2+2\alpha c_1{c}_3-\frac{3}{2}\beta c_1^2{c}_2-c_4\right|\le 2.$$

(15)

3. Main Results

Theorem 1.

Let $\mathcal{X}\in {\mathcal{R}}_{sl}$. Then, the following inequalities for the coefficients in (1) are true.

$$\left|a_2\right|\le \frac{1}{2},\left|a_3\right|\le \frac{1}{3},\left|a_4\right|\le \frac{1}{4},\mathrm{and}\left|a_5\right|\le \frac{1}{5}.$$

The sharpness of these inequalities can be obtained using the function

$${\mathcal{X}}_n^{\prime }\left(z\right)=\frac{2\sqrt{1+z^n}}{1+e^{-z^n}},n\in \mathbb{N}.$$

In particular, if $n=1,2,3$, and 4, then we have

$$\begin{array}{ccc}\hfill {\mathcal{X}}_1& =& \underset{0}{\overset{z}{\int }}\left(\frac{2\sqrt{1+t}}{1+e^{-t}}\right)dt=z+\frac{1}{2}{z}^2+\frac{1}{24}{z}^3-\frac{1}{96}{z}^4-\frac{11}{1920}{z}^5,\hfill \end{array}$$

(16)

$$\begin{array}{ccc}\hfill {\mathcal{X}}_2& =& \underset{0}{\overset{z}{\int }}\left(\frac{2\sqrt{1+t^2}}{1+e^{-t^2}}\right)dt=z+\frac{1}{3}{z}^3+\frac{1}{40}{z}^5-\frac{1}{168}{z}^7,\hfill \end{array}$$

(17)

$$\begin{array}{ccc}\hfill {\mathcal{X}}_3& =& \underset{0}{\overset{z}{\int }}\left(\frac{2\sqrt{1+t^3}}{1+e^{-t^3}}\right)dt=z+\frac{1}{4}{z}^4+\frac{1}{56}{z}^7,\hfill \end{array}$$

(18)

$$\begin{array}{ccc}\hfill {\mathcal{X}}_4& =& \underset{0}{\overset{z}{\int }}\left(\frac{2\sqrt{1+t^4}}{1+e^{-t^4}}\right)dt=z+\frac{1}{5}{z}^5.\hfill \end{array}$$

(19)

Proof. 

As $\mathcal{X}\in {\mathcal{R}}_{ls}$, from (4), we obtain

$${\mathcal{X}}^{\prime }\left(z\right)=\frac{2\sqrt{1+\xi \left(z\right)}}{1+e^{-\xi \left(z\right)}}.$$

(20)

Then, (1) gives

$${\mathcal{X}}^{\prime }\left(z\right)=1+2a_{2}z+3a_3{z}^2+4a_4{z}^3+5a_5{z}^4....$$

(21)

Let$p\in \mathcal{P}$ be written by

$$p\left(z\right)=\frac{1+\xi \left(z\right)}{1-\xi \left(z\right)}=1+c_{1}z+c_2{z}^2+c_3{z}^3+c_4{z}^4+\dots .$$

This implies that

$$\begin{array}{ccc}\hfill \xi \left(z\right)& =& \frac{1}{2}{c}_{1}z+\left(\frac{1}{2}{c}_2-\frac{1}{4}{c}_1^2\right)z^2+\left(\frac{1}{8}{c}_1^3-\frac{1}{2}{c}_1{c}_2+\frac{1}{2}{c}_3\right)z^3\hfill \\ & & +\left(\frac{1}{2}{c}_4-\frac{1}{2}{c}_1{c}_3-\frac{1}{4}{c}_2^2-\frac{1}{16}{c}_1^4+\frac{3}{8}{c}_1^2{c}_2\right)z^4+\dots .\hfill \end{array}$$

Then,

$$\begin{array}{ccc}\hfill \frac{2\sqrt{1+\xi \left(z\right)}}{1+e^{-\xi \left(z\right)}}& =& 1+\left(\frac{1}{2}{c}_1\right)z+\left(\frac{1}{2}{c}_2-\frac{7}{32}{c}_1^2\right)z^2+\left(\frac{1}{2}{c}_3-\frac{7}{16}{c}_1{c}_2+\frac{17}{192}{c}_1^3\right)z^3\hfill \\ & & +\left(\frac{-203}{6144}{c}_1^4+\frac{17}{64}{c}_1^2{c}_2-\frac{7}{16}{c}_1{c}_3-\frac{7}{32}{c}_2^2+\frac{1}{2}{c}_4\right)z^4+....\hfill \end{array}$$

(22)

It follows from (21) and (22) that

$$\begin{array}{ccc}\hfill a_2& =& \frac{1}{4}{c}_1,\hfill \end{array}$$

(23)

$$\begin{array}{ccc}\hfill a_3& =& \frac{1}{6}{c}_2-\frac{7}{96}{c}_1^2,\hfill \end{array}$$

(24)

$$\begin{array}{ccc}\hfill a_4& =& \frac{17}{768}{c}_1^3-\frac{7}{64}{c}_1{c}_2+\frac{1}{8}{c}_3,\hfill \end{array}$$

(25)

$$\begin{array}{ccc}\hfill a_5& =& \frac{-203}{30720}{c}_1^4+\frac{17}{320}{c}_1^2{c}_2-\frac{7}{80}{c}_1{c}_3-\frac{7}{160}{c}_2^2+\frac{1}{10}{c}_4.\hfill \end{array}$$

(26)

Using Lemma 1, (23) and (24) imply

$$\left|a_2\right|\le \frac{1}{2}\mathrm{and}\left|a_3\right|\le \frac{1}{3}.$$

By (25),

$$\left|a_4\right|=\frac{1}{8}\left|c_3-\frac{7}{8}{c}_1{c}_2+\frac{17}{96}{c}_1^3\right|.$$

Using Lemma 3, we obtain

$$\left|a_4\right|\le \frac{1}{4}.$$

From (26), we have

$$\left|a_5\right|=\frac{1}{10}\left|\frac{203}{3072}{c}_1^4+\frac{7}{16}{c}_2^2+2\left(\frac{7}{16}\right)c_1{c}_3-\frac{17}{32}{c}_1^2{c}_2-c_4\right|.$$

By applying Lemma 4,

$$\left|a_5\right|\le \frac{1}{5}.$$

□

Theorem 2.

Let $\mathcal{X}\in {\mathcal{R}}_{ls}$. Then, the sharp upper bound for the following second-order Hankel determinant is given by

$$\left|{\mathcal{H}}_{2,1}\left(\mathcal{X}\right)\right|\le \frac{1}{3}.$$

(27)

The function (17) gives the sharpness of the inequality (27).

Proof. 

Applying to the identities (23) and (24),

$$\left|a_3-a_2^2\right|=\frac{1}{6}\left|c_2-\frac{13}{16}{c}_1^2\right|.$$

Using Lemma 1, we obtain

$$\left|{\mathcal{H}}_{2,1}\left(\mathcal{X}\right)\right|\le \frac{1}{3}.$$

It is easy to verify that the function ((17).) gives the sharpness of the inequality (27). □

Theorem 3.

Let $\mathcal{X}\in {\mathcal{R}}_{ls}$. Then, the sharp upper bound for the following second-order Hankel determinant is given by

$$\left|{\mathcal{H}}_{2,2}\mathcal{X}\right|\le \frac{1}{9}.$$

(28)

The function (17) gives the sharpness of the inequality (28).

Proof. 

By the identities (23)–(25),

$$\left|a_2{a}_4-a_3^2\right|=\left|\frac{1}{4608}{c}_1^4-\frac{7}{2304}{c}_1^2{c}_2+\frac{1}{32}{c}_3{c}_1-\frac{1}{36}{c}_2^2\right|.$$

Now, using Lemma 2, we have

$$\left|a_2{a}_4-a_3^2\right|=\frac{1}{4608}\left|-32t^2{q}^2-36t{q}^2{c}_1^2-72\gamma t{c}_1\left(1-q^2\right)+tq{c}_1^2-2c_1^4\right|.$$

Using the triangular inequality by taking $\left|c_1\right|=c\in \left[0,2\right]$, $t=4-c^2$, $\left|\gamma \right|\le 1$, and $\left|q\right|=b\in [0,1]$.

$$\left|a_2{a}_4-a_3^2\right|\le \frac{1}{4608}\left(32{\left(4-c^2\right)}^2{b}^2+36\left(4-c^2\right)b^2{c}^2+72c\left(4-c^2\right)\left(1-b^2\right)+\left(4-c^2\right)b{c}^2+2c^4\right).$$

Let

$$F\left(b,c\right)=\frac{1}{4608}\left(32{\left(4-c^2\right)}^2{b}^2+36\left(4-c^2\right)b^2{c}^2+72c\left(4-c^2\right)\left(1-b^2\right)+\left(4-c^2\right)b{c}^2+2c^4\right).$$

Then

$$\frac{\partial F}{\partial b}=\frac{1}{4608}\left(4-c^2\right)\left(256b+8b{c}^2-144bc+c^2\right)\ge 0,$$

which shows that $F\left(b,c\right)$ is an increasing function for all $b\in [0,1]$ and $c\in \left[0,2\right].$ Thus, the maximum value occurs at $b=1$. Consequently,

$$F\left(b,c\right)\le F\left(1,c\right)=\frac{1}{4608}\left(32{\left(4-c^2\right)}^2+36\left(4-c^2\right)c^2+\left(4-c^2\right)c^2+2c^4\right).$$

(29)

Let

$$G\left(c\right)=32{\left(4-c^2\right)}^2+36\left(4-c^2\right)c^2+\left(4-c^2\right)c^2+2c^4,$$

which implies

$$\frac{\partial G}{\partial c}=-12c\left(c^2+18\right)\le 0,$$

this shows that $G\left(c\right)$ is a decreasing function for all $c\in [0,2]$, and the maximum value occurs at $c=0$. By referring to (29), we can deduce the required inequality,

$$\left|{\mathcal{H}}_{2,2}\mathcal{X}\right|=\left|a_2{a}_4-a_3^2\right|\le \frac{1}{9}.$$

It is also easy to verify that the function (17) provides the sharpness of the inequality (28). □

Theorem 4.

Let $\mathcal{X}\in {\mathcal{R}}_{ls}.$ Then, we have the sharp upper bound for the following third-order Hankel determinant.

$$\left|{\mathcal{H}}_{3,1}\mathcal{X}\right|\le \frac{1}{16}.$$

(30)

The sharpness of this inequality can occur according to the function given in (18).

Proof. 

From (5), we have

$${\mathcal{H}}_{3,1}\left(\mathcal{X}\right)=2a_2{a}_3{a}_4-a_2^2{a}_5-a_3^3+a_3{a}_5-a_4^2.$$

(31)

Taking $c_1=c$ in the identities (23)–(26), we have

$${\mathcal{H}}_{3,1}\left(\mathcal{X}\right)=\frac{1}{1105920}\left(\begin{array}{c}-16c^6-309c^4{c}_2+1944c^3{c}_3-246c^2{c}_2^2-14976c^2{c}_4\\ -13184c_2^3+18432c_2{c}_4-17280c_3^2+25632c{c}_2{c}_3\end{array}\right).$$

(32)

Also, taking $4-c^2=t$ in Lemma 2, we can simplify the terms in (32).

$$\begin{array}{ccc}\hfill -309c^4{c}_2& =& -\frac{309}{2}{c}^6-\frac{309}{2}tq{c}^4,\hfill \\ \hfill 1944c^3{c}_3& =& 486c^6-486t{c}^4{q}^2+972t{c}^{4}q+972\left(1-{\left|q\right|}^2\right)t\gamma c^3,\hfill \\ \hfill -246c^2{c}_2^2& =& -\frac{123}{2}{c}^6-123c^{4}tq-\frac{123}{2}{c}^2{t}^2{q}^2,\hfill \\ \hfill -14976c^2{c}_4& =& -1872c^6-1872t{c}^4{q}^3+5616t{c}^4{q}^2-5616t{c}^{4}q+7488\left(1-{\left|q\right|}^2\right)t{c}^{3}q\gamma \hfill \\ & & -7488\left(1-{\left|q\right|}^2\right)t{c}^3\gamma -7488t{c}^2{q}^2+7488\left(1-{\left|q\right|}^2\right)t{c}^{2}q{\gamma }^2\hfill \\ & & -7488\left(1-{\left|q\right|}^2\right)t\left(1-{\left|\gamma \right|}^2\right)\mu c^2,\hfill \\ \hfill -13184c_2^3& =& -1648c^6-4944c^{4}tq-4944c^2{t}^2{q}^2-1648t^3{q}^3,\hfill \\ \hfill 18432c_2{c}_4& =& 1152c^6+1152c^{4}t{q}^3-3456c^{4}t{q}^2+4608c^{4}tq-4608\left(1-{\left|q\right|}^2\right)c^{3}tq\gamma \hfill \\ & & +4608\left(1-{\left|q\right|}^2\right)c^{3}t\gamma +1152c^2{t}^2{q}^4-3456c^2{t}^2{q}^3+3456c^2{t}^2{q}^2+4608c^{2}t{q}^2\hfill \\ & & -4608\left(1-{\left|q\right|}^2\right)c^{2}tq{\gamma }^2+4608\left(1-{\left|q\right|}^2\right)\left(1-{\left|\gamma \right|}^2\right)\mu c^{2}t-4608\left(1-{\left|q\right|}^2\right)c{t}^2{q}^2\gamma \hfill \\ & & +4608\left(1-{\left|q\right|}^2\right)c{t}^{2}q\gamma +4608t^2{q}^3-4608\left(1-{\left|q\right|}^2\right)t^2{q}^2{\gamma }^2\hfill \\ & & +4608\left(1-{\left|q\right|}^2\right)\left(1-{\left|\gamma \right|}^2\right)\mu t^{2}q,\hfill \\ \hfill -17280c_3^2& =& -1080c^6+2160c^{4}t{q}^2-4320c^{4}tq-4320c^3\left(1-{\left|q\right|}^2\right)t\gamma -1080c^2{t}^2{q}^4\hfill \\ & & +4320c^2{t}^2{q}^3-4320c^2{t}^2{q}^2+4320c\left(1-{\left|q\right|}^2\right)t^2{q}^2\gamma -8640c\left(1-{\left|q\right|}^2\right)t^{2}q\gamma \hfill \\ & & -4320{\left(1-{\left|q\right|}^2\right)}^2{t}^2{\gamma }^2,\hfill \\ \hfill 25632c{c}_2{c}_3& =& 3204c^6-3204c^{4}t{q}^2+9612c^{4}tq+6408\left(1-{\left|q\right|}^2\right)\gamma c^{3}t-3204c^2{t}^2{q}^3\hfill \\ & & +6408c^2{t}^2{q}^2+6408\left(1-{\left|q\right|}^2\right)\gamma c{t}^{2}q.\hfill \end{array}$$

Substituting the simplified terms into (32),

$${\mathcal{H}}_{3,1}\left(\mathcal{X}\right)=\frac{1}{1105920}\left(\begin{array}{c}26c^6-720c^{4}t{q}^3+630c^{4}t{q}^2+\frac{69}{2}{c}^{4}tq+2880c^3\left(1-{\left|q\right|}^2\right)tq\gamma \\ +180c^3\left(1-{\left|q\right|}^2\right)t\gamma +2880c^2\left(1-{\left|q\right|}^2\right)tq{\gamma }^2-288c\left(1-{\left|q\right|}^2\right)t^2{q}^2\gamma \\ -2880c^2\left(1-{\left|\gamma \right|}^2\right)\left(1-{\left|q\right|}^2\right)\mu t-2340c^2{t}^2{q}^3+\frac{1077}{2}{c}^2{t}^2{q}^2-2880c^{2}t{q}^2\\ +2376c\left(1-{\left|q\right|}^2\right)t^{2}q\gamma -4320{\left(1-{\left|q\right|}^2\right)}^2{t}^2{\gamma }^2-4608\left(1-{\left|q\right|}^2\right)t^2{q}^2{\gamma }^2\\ +72c^2{t}^2{q}^4+4608\left(1-{\left|\gamma \right|}^2\right)\left(1-{\left|q\right|}^2\right)t^{2}q-1648t^3{q}^3+4608t^2{q}^3\end{array}\right).$$

Since $t=4-c^2$,

$${\mathcal{H}}_{3,1}\left(\mathcal{X}\right)=\frac{1}{1105920}\left[m_1\left(c,q\right)+m_2\left(c,q\right)\gamma +m_3\left(c,q\right){\gamma }^2+\phi \left(c,q,\gamma \right)\mu \right],$$

where

$$\begin{array}{ccc}\hfill m_1\left(c,q\right)& =& 26c^6-\frac{1}{2}\left(4-c^2\right)q\left(\begin{array}{c}\left(4-c^2\right)q\left(1384c^{2}q-144c^2{q}^2-1077c^2+3968q\right)+\\ 5760c^{2}q-1260c^{4}q+1440c^4{q}^2-69c^4\end{array}\right),\hfill \\ \hfill m_2\left(c,q\right)& =& -36c\left(4-c^2\right)\left(1-{\left|q\right|}^2\right)\left(2\left(4-c^2\right)q\left(4q-33\right)-80c^{2}q-5c^2\right),\hfill \\ \hfill m_3\left(c,q\right)& =& -288\left(4-c^2\right)\left(1-{\left|q\right|}^2\right)\left(\left(4-c^2\right)\left(q^2+15\right)-10c^{2}q\right),\hfill \\ \hfill \phi \left(c,q,\gamma \right)& =& 576\left(4-c^2\right)\left(1-{\left|q\right|}^2\right)\left(1-{\left|\gamma \right|}^2\right)\left(8\left(4-c^2\right)q-5c^2\right).\hfill \end{array}$$

Let $\left|\gamma \right|=y$ and $\left|\mu \right|\le 1$, then

$$\begin{array}{ccc}\hfill \left|{\mathcal{H}}_{3,1}\left(\mathcal{X}\right)\right|& \le & \frac{1}{1105920}\left[\left|m_1\left(c,q\right)\right|+\left|m_2\left(c,q\right)\right|y+\left|m_3\left(c,q\right)\right|y^2+\left|\phi \left(c,q,\gamma \right)\right|\right]\hfill \\ & \le & \frac{1}{1105920}\left[\mathcal{G}\left(c,q,y\right)\right],\hfill \end{array}$$

(33)

where

$$\mathcal{G}\left(c,q,y\right)=n_1\left(c,q\right)+n_2\left(c,q\right)y+n_3\left(c,q\right)y^2+n_4\left(c,q\right)\left(1-y^2\right),$$

with

$$\begin{array}{ccc}\hfill n_1\left(c,q\right)& =& 26c^6+\frac{1}{2}\left(4-c^2\right)q\left[\begin{array}{c}\left(4-c^2\right)q\left(1384c^{2}q+144c^2{q}^2+1077c^2+3968q\right)\\ +5760c^{2}q+1260c^{4}q+1440c^4{q}^2+69c^4\end{array}\right],\hfill \\ \hfill n_2\left(c,q\right)& =& 36c\left(4-c^2\right)\left(1-{\left|q\right|}^2\right)\left[\left(4-c^2\right)q\left(8q+66\right)+80c^{2}q+5c^2\right],\hfill \\ \hfill n_3\left(c,q\right)& =& 288\left(4-c^2\right)\left(1-{\left|q\right|}^2\right)\left[\left(4-c^2\right)\left(q^2+15\right)+10c^{2}q\right],\hfill \\ \hfill n_4\left(c,q\right)& =& 576\left(4-c^2\right)\left(1-{\left|q\right|}^2\right)\left[8q\left(4-c^2\right)+5c^2\right].\hfill \end{array}$$

To find the maximum values of the function $\mathcal{G}\left(c,q,y\right)$ within the closed cuboid $▵=\left[0,2\right]\times \left[0,1\right]\times \left[0,1\right]$, we need to examine the function $\mathcal{G}\left(c,q,y\right)$ inside the cuboid, on its faces and along its edges. Let us divide the analysis into the following three cases.

I. 

Interior points of cuboid

Now, we find the maximum value of $\mathcal{G}\left(c,q,y\right)$ within the cuboid’s interior.

Let $\left(c,q,y\right)\in \left[0,2\right)\times \left[0,1\right)\times \left(0,1\right)$. By differentiating $\mathcal{G}\left(c,q,y\right)$ with respect to y, we obtain

$$\frac{\partial \mathcal{G}}{\partial y}=\left(\begin{array}{c}36c\left(4-c^2\right)\left(1-{\left|q\right|}^2\right)\left[\left(4-c^2\right)q\left(8q+66\right)+5c^2\left(16q+1\right)\right]\\ +576y\left(4-c^2\right)\left(1-{\left|q\right|}^2\right)\left[\left(4-c^2\right)\left(q-15\right)+10c^2\right]\left(q-1\right)\end{array}\right).$$

Putting $\frac{\partial \mathcal{G}}{\partial y}=0$, gives

$$y=\frac{c\left[2q\left(4-c^2\right)\left(4q+33\right)+5c^2\left(16q+1\right)\right]}{16\left[\left(4-c^2\right)\left(15-q\right)-10c^2\right]\left(q-1\right)}=y_1.$$

If $y_1$ is a critical point inside ▵, then $y_1\in \left(0,1\right)$, which is possible only if

$$5c^3\left(16q+1\right)+2cq\left(4-c^2\right)\left(4q+33\right)+16\left(4-c^2\right)\left(15-q\right)\left(1-q\right)<160\left(1-q\right)c^2,$$

(34)

and

$$c^2>\frac{4\left(15-q\right)}{25-q}.$$

(35)

To identify the critical point, we need to find a solution that satisfies the inequalities (34) and (35). Let $g\left(q\right)=\frac{4\left(15-q\right)}{25-q}$ with $g^{\prime }\left(q\right)=-\frac{40}{{\left(25-q\right)}^2}<0$, which shows that $g\left(q\right)$ is a decreasing function, so

$$c^2>\frac{7}{3}.$$

It follows from the simple calculations that (34) is not held for $q\in \left[\frac{15}{32},1\right)$. As a result, it can be concluded that the function $\mathcal{G}\left(c,q,y\right)$ does not possess any critical points within the interior of the cuboid $\left[0,2\right)\times \left[\frac{15}{32},1\right)\times \left(0,1\right)$.

Suppose $\left(c,q,y\right)$ is a critical point of $\mathcal{G}$ in the interior of the cuboid, satisfying the conditions $q\in \left[0,\frac{15}{32}\right)$ and $y\in \left(0,1\right)$ which leads us to $c^2>g\left(\frac{15}{32}\right)=\frac{372}{157}$. It can also be observed that

$$n_1\left(c,q\right)\le n_1\left(c,\frac{15}{32}\right)={\vartheta }_1\left(c\right).$$

Since $1-q^2\le 1$ and $0<q<\frac{15}{32}$, we have

$$\begin{array}{ccc}\hfill n_2\left(c,q\right)& \le & 36\left(4-c^2\right)\left[\left(4-c^2\right)\left(8c{\left(\frac{15}{32}\right)}^2+66c\left(\frac{15}{32}\right)\right)+5\left(16\left(\frac{15}{32}\right)+1\right)c^3\right],\hfill \\ & =& \frac{1024}{799}{n}_2\left(c,\frac{15}{32}\right)={\vartheta }_2\left(c\right).\hfill \end{array}$$

Similarly, we obtain

$$n_j\left(c,q\right)\le \frac{1024}{799}{n}_j\left(c,\frac{15}{32}\right)={\vartheta }_j\left(c\right)\left(j=3,4\right).$$

It follows that

$$\mathcal{G}\left(c,q,y\right)\le {\vartheta }_1\left(c\right)+{\vartheta }_4\left(c\right)+{\vartheta }_2\left(c\right)y+\left({\vartheta }_3\left(c\right)-{\vartheta }_4\left(c\right)\right)y^2=\Psi \left(c,y\right).$$

Differentiating with regard to “y”, we have

$$\frac{\partial \Psi }{\partial y}={\vartheta }_2\left(c\right)+2\left({\vartheta }_3\left(c\right)-{\vartheta }_4\left(c\right)\right)y.$$

Consider

$${\vartheta }_3\left(c\right)-{\vartheta }_4\left(c\right)=288\left(4-c^2\right)\left(\frac{7905}{256}-\frac{13345}{1024}{c}^2\right)\le 0,c\in \left(\sqrt{\frac{372}{157}},2\right).$$

Then, for all $c\in \left(\sqrt{\frac{372}{157}},2\right)$ and $y\in \left(0,1\right)$, we have

$$\begin{array}{ccc}\hfill \frac{\partial \Psi }{\partial y}& =& {\vartheta }_2\left(c\right)+2\left({\vartheta }_3\left(c\right)-{\vartheta }_4\left(c\right)\right)y\hfill \\ & \ge & {\vartheta }_2\left(c\right)+2\left({\vartheta }_3\left(c\right)-{\vartheta }_4\left(c\right)\right)\hfill \\ & =& 36\left(4-c^2\right)\left(\frac{1255}{128}{c}^3-\frac{13345}{64}{c}^2+\frac{4185}{32}c+\frac{7905}{16}\right)\hfill \\ & \ge & 0.\hfill \end{array}$$

Thus, we obtain

$$\Psi \left(c,y\right)\le \Psi \left(c,1\right)={\vartheta }_1\left(c\right)+{\vartheta }_2\left(c\right)+{\vartheta }_3\left(c\right)=\zeta \left(c\right),$$

where

$$\zeta \left(c\right)=-\frac{1269383}{131072}{c}^6-\frac{11295}{32}{c}^5+\frac{32362695}{16384}{c}^4-\frac{13185}{4}{c}^3-\frac{210375495}{8192}{c}^2+\frac{37665}{2}c+\frac{2348865}{32}.$$

It can be seen that ${\zeta }^{\prime }\left(c\right)\ne 0$, for any $c\in \left(\sqrt{\frac{372}{157}},2\right)$. Also, $\zeta \left(c\right)$ is a decreasing function and its maximum value occurs at $c\approx 1.53928554$, which is 37,437.

II. 

On the six faces of the cuboid

Next, we proceed to examine the maximum value of the function $\mathcal{G}\left(c,q,y\right)$ on all six faces of the cuboid ▵.

$\left(\mathrm{i}\right)$On the face $c=0$: $\mathcal{G}\left(0,q,y\right)$ becomes

$$h_1\left(q,y\right)=31744q^3+\left(4608\left(q-1\right)\left(q-15\right)y^2+73728q\right)\left(1-q^2\right),$$

then

$$\frac{\partial h_1}{\partial y}=-9216y\left(q^2-1\right)\left(q-1\right)\left(q-15\right)\ne 0\mathrm{for}y\in \left(0,1\right),$$

which implies that $h_1$ does not have any optimal points within the interval $\left(0,1\right)\times \left(0,1\right)$.

$\left(\mathrm{ii}\right)$ On the face $c=2$, we have

$$\mathcal{G}\left(2,q,y\right)=1664$$

(36)

$\left(\mathrm{iii}\right)$ On the face $q=0$, $\mathcal{G}\left(c,0,y\right)$ becomes

$$h_2\left(c,y\right)=26c^6+180c^{3}y\left(4-c^2\right)+7200c^4{y}^2-2880c^4-46080c^2{y}^2+11520c^2+69120y^2,$$

then $\frac{\partial h_2}{\partial y}=0$ gives

$$y=\frac{c^3}{16\left(5c^2-12\right)}=y_0.$$

(37)

For the provided range of $y,$$y_0\in$$\left(0,1\right)$, if $c>c_0\approx 1.5491933.$

Also, $\frac{\partial h_2}{\partial c}=0$ gives

$$12c\left(13c^4-75c^{3}y+2400c^2{y}^2-960c^2+180cy-7680y^2+1920\right)=0.$$

(38)

Putting (37) in (38), we obtain

$$14925c^9-1222920c^7+7916976c^5-17694720c^3+13271040c=0.$$

Solving for c within the range $\left(0,2\right)$, we find that $c\approx 1.4228$. This indicates that there is no optimal solution for $\mathcal{G}\left(c,0,y\right)$.

$\left(\mathrm{iv}\right)$ On the face $q=1$: $\mathcal{G}\left(c,1,y\right)$ becomes

$$h_3\left(c,y\right)=-820c^6+334c^4+4264c^2+31744,$$

then $\frac{\partial h_3}{\partial c}=0$ gives a critical point $c\approx 1.208$, where $h_3$ attains its maximum value; that is,

$$h_3\left(c,y\right)\le 36129.$$

(39)

$\left(\mathrm{v}\right)$ On the face $y=0$: $\mathcal{G}\left(c,q,0\right)$ becomes

$$\begin{array}{ccc}\hfill h_4\left(c,q\right)& =& 72c^6{q}^4-28c^6{q}^3-\frac{183}{2}{c}^6{q}^2-\frac{69}{2}{c}^{6}q+26c^6-576c^4{q}^4-5280c^4{q}^3\hfill \\ & & -1788c^4{q}^2+4746c^{4}q-2880c^4+1152c^2{q}^4+32064c^2{q}^3+8616c^2{q}^2\hfill \\ & & -36864c^{2}q+11520c^2-41984q^3+73728q.\hfill \end{array}$$

Thus,

$$\begin{array}{ccc}\hfill \frac{\partial h_4}{\partial c}& =& 432c^5{q}^4-168c^5{q}^3-549c^5{q}^2-207c^{5}q+156c^5-2304c^3{q}^4-21120c^3{q}^3-7152c^3{q}^2\hfill \\ & & +18984c^{3}q-11520c^3+2304c{q}^4+64128c{q}^3+17232c{q}^2-73728cq+23040c,\hfill \end{array}$$

$$\begin{array}{ccc}\hfill \frac{\partial h_4}{\partial q}& =& 288c^6{q}^3-84c^6{q}^2-183c^{6}q-\frac{69}{2}{c}^6-2304c^4{q}^3-15840c^4{q}^2-3576c^{4}q+4746c^4\hfill \\ & & +4608c^2{q}^3+96192c^2{q}^2+17232c^{2}q-36864c^2-125952q^2+73728.\hfill \end{array}$$

Computation shows that the system of equations $\frac{\partial h_4}{\partial c}=0$ and $\frac{\partial h_4}{\partial q}=0$ has no solutions in $\left(0,2\right)\times \left(0,1\right)$.

$\left(\mathrm{vi}\right)$ On the face $y=1$: $\mathcal{G}\left(c,q,1\right)$, becomes

$$\begin{array}{ccc}\hfill h_5\left(c,q\right)& =& 72c^6{q}^4-28c^6{q}^3-\frac{183}{2}{c}^6{q}^2-\frac{69}{2}{c}^{6}q+26c^6-288c^5{q}^4+504c^5{q}^3+468c^5{q}^2\hfill \\ & & -504c^{5}q-180c^5-864c^4{q}^4+2208c^4{q}^3-8700c^4{q}^2-2742c^{4}q+4320c^4\hfill \\ & & +2304c^3{q}^4+7488c^3{q}^3-3024c^3{q}^2-7488c^{3}q+720c^3+3456c^2{q}^4-16320c^2{q}^3\hfill \\ & & +52392c^2{q}^2+11520c^{2}q-34560c^2-4608c{q}^4-38016c{q}^3+4608c{q}^2+38016cq\hfill \\ & & -4608q^4+31744q^3-64512q^2+69120.\hfill \end{array}$$

It follows that

$$\begin{array}{ccc}\hfill \frac{\partial h_5}{\partial c}& =& 432c^5{q}^4-168c^5{q}^3-549c^5{q}^2-207c^{5}q+156c^5-1440c^4{q}^4+2520c^4{q}^3+2340c^4{q}^2\hfill \\ & & -2520c^{4}q-900c^4-3456c^3{q}^4+8832c^3{q}^3-34800c^3{q}^2-10968c^{3}q+17280c^3\hfill \\ & & +6912c^2{q}^4+22464c^2{q}^3-9072c^2{q}^2-22464c^{2}q+2160c^2+6912c{q}^4-32640c{q}^3\hfill \\ & & +104784c{q}^2+23040cq-69120c-4608q^4-38016q^3+4608q^2+38016q,\hfill \end{array}$$

$$\begin{array}{ccc}\hfill \frac{\partial h_5}{\partial q}& =& 288c^6{q}^3-84c^6{q}^2-183c^{6}q-\frac{69}{2}{c}^6-1152c^5{q}^3+1512c^5{q}^2+936c^{5}q-504c^5\hfill \\ & & -3456c^4{q}^3+6624c^4{q}^2-17400c^{4}q-2742c^4+9216c^3{q}^3+22464c^3{q}^2-6048c^{3}q\hfill \\ & & -7488c^3+13824c^2{q}^3-48960c^2{q}^2+104784c^{2}q+11520c^2-18432c{q}^3-114048c{q}^2\hfill \\ & & +9216cq+38016c-18432q^3+95232q^2-129024q.\hfill \end{array}$$

Also, the computation indicates that the system of equations $\frac{\partial h_5}{\partial c}=0$ and $\frac{\partial h_5}{\partial q}=0$ has no solutions in $\left(0,2\right)\times \left(0,1\right)$.

III. 

On the twelve edges of the cuboid

Finally, we need to find the maximum values of $\mathcal{G}\left(c,q,y\right)$ along the twelve edges.

$\left(\mathrm{i}\right)$ On $q=0$and $y=0$: $\mathcal{G}\left(c,0,0\right)$ becomes

$$h_6\left(c\right)=26c^6-2880c^4+11520c^2,$$

then $\frac{\partial h_6}{\partial c}=0$ gives the critical point $c\approx 1.4343$, where the maximum value is obtained as follows.

$$h_6\left(c\right)\le 11737.$$

(40)

$\left(\mathrm{ii}\right)$ On $q=0$ and $y=1$: $\mathcal{G}\left(c,0,1\right)$ becomes

$$h_7\left(c\right)=26c^6-180c^5+4320c^4+720c^3-34560c^2+69120.$$

It is clear that $\frac{\partial h_7}{\partial c}\le 0,$ for all $c\in [0,2]$. This indicates that $h_7\left(c\right)$ is a decreasing function and attains its maximum value at $c=0$.

$$h_7\left(c\right)\le 69120.$$

(41)

$\left(\mathrm{iii}\right)$ On $q=0$ and $c=0$: $\mathcal{G}\left(0,0,y\right)$ becomes

$$h_8\left(y\right)=66816y^2+2304.$$

Therefore, $\frac{\partial h_8}{\partial c}>0$ for the interval $[0,1],$ which shows that $h_8\left(y\right)$ is an increasing function. As a result, it attains its maximum value at $y=1$; that is,

$$h_8\left(y\right)\le 69120.$$

(42)

As the terms $\mathcal{G}\left(c,1,1\right)$ and $\mathcal{G}\left(c,1,0\right)$ are free from q, that is

$$h_9\left(c\right)=\mathcal{G}\left(c,1,0\right)=\mathcal{G}\left(c,1,1\right)=-56c^6-5778c^4+16488c^2+31744.$$

Putting $\frac{\partial h_9}{\partial c}=0$, we find a critical point $c\approx 1.1825$. At this critical point, $h_9\left(c\right)$ achieves its maximum value, which is

$$h_9\left(c\right)\le 43349.$$

(43)

$\left(\mathrm{iv}\right)$ On $q=1$ and $c=0$: $\mathcal{G}\left(0,1,y\right)$ becomes

$$h_{10}\left(y\right)=\mathcal{G}\left(0,1,y\right)=31744.$$

$\left(\mathrm{v}\right)$ On $c=2$:

$$\mathcal{G}\left(2,0,y\right)=\mathcal{G}\left(2,1,y\right)=\mathcal{G}\left(2,q,1\right)=\mathcal{G}\left(2,q,0\right)=1664.$$

$\left(\mathrm{vi}\right)$ On $c=0$ and $y=0$: $\mathcal{G}\left(0,q,0\right)$ becomes

$$h_{11}\left(q\right)=-1024q\left(41q^2-72\right),$$

and calculation shows that $\frac{\partial h_{11}}{\partial q}\le 0$ for all $q\in \left[0,1\right]$, which means $h_{11}\left(q\right)$ is a decreasing function and maximum value occurs at $q=0$; that is,

$$h_{11}\left(q\right)\le 0.$$

(44)

$\left(\mathrm{vii}\right)$ On $c=0$ and $y=1$: $\mathcal{G}\left(0,q,1\right)$ becomes

$$h_{12}\left(q\right)=-4608q^4+31744q^3-64512q^2+69120.$$

Let $\frac{\partial h_{12}}{\partial q}=0$, we then find a critical point $q=0,$ where the function $h_{12}\left(q\right)$ achieves its maximum value,

$$h_{12}\left(q\right)\le 69120.$$

(45)

Therefore, we can conclude that

$$\mathcal{G}\left(c,q,y\right)\le 69120.$$

And hence, we reach the following inequality as described by (33),

$$\left|{\mathcal{H}}_{3,1}\left(\mathcal{X}\right)\right|\le \frac{1}{16}.$$

□

4. Conclusions

In the present article, we defined a class of analytic functions by considering the ratio of two well-known functions. We investigated the sharp upper bounds of the modulus of coefficients $a_2,a_3$, and $a_4$; and the sharp upper bounds for the modulus of three second-order and third-order Hankel determinants, ${\mathcal{H}}_{2,1}\mathcal{X},{\mathcal{H}}_{2,2}\mathcal{X}$, and ${\mathcal{H}}_{3,1}\mathcal{X}$, for the normalized analytic functions $\mathcal{X}$ belonging to the newly defined class. These findings contribute to the existing body of knowledge and provide valuable insights for further research in the field. This work provides a direction to define more interesting generalized domains and to extend to new subclasses of starlike and convex functions by using quantum calculus.