Next Article in Journal
Analytic Functions Related to a Balloon-Shaped Domain
Previous Article in Journal
Adaptive Fuzzy Fault-Tolerant Control of Uncertain Fractional-Order Nonlinear Systems with Sensor and Actuator Faults
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Fractal Fract
Volume 7
Issue 12
10.3390/fractalfract7120863
fractalfract-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Fractal Features in Terrain Restoration of Jiuzhai Valley, a World Natural Heritage Site in China

by
Zan Zou
1,†,
Yue Du
2,† and
Huixing Song
1,*
1
College of Landscape Architecture, Sichuan Agricultural University, Chengdu 611130, China
2
College of Art, Sichuan Technology and Business University, Chengdu 610000, China
*
Author to whom correspondence should be addressed.
†
This author contributed equally to this work.
Fractal Fract. 2023, 7(12), 863; https://doi.org/10.3390/fractalfract7120863
Submission received: 7 October 2023 / Revised: 29 November 2023 / Accepted: 30 November 2023 / Published: 5 December 2023
(This article belongs to the Special Issue Fractal Analysis of Climate and Environmental Systems)
Browse Figures
Versions Notes

Abstract

:
Jiuzhai Valley, a World Natural Heritage Site, was significantly damaged by an earthquake in 2017. However, case studies on the restoration of World Natural Heritage sites are lacking. This study aimed to use the box-counting method to analyze fractal characteristics of the terrain in Shuzheng Valley. Research data were used to conduct artificial intervention restoration of the earthquake-damaged terrain. Our results showed that (i) the travertine terrain shows self-similarity at different scales. The fractal dimension was related to terrain complexity: the more complex the terrain, the higher the fractal-dimension value; (ii) a combined form of fractal generator elements at the same scale was related to terrain complexity—differences in the spatial combination of the fractal generator elements can be compared based on fractal dimension; and (iii) the newly restored dam terrain also showed fractal characteristics whose spatial combination form was similar to that of the surrounding terrain. The complexity of the terrain’s fractal element combination may be related to the influence of surrounding environmental factors and the different ecological functional requirements. This study provides basic data for the near natural restoration of the Sparkling Lake travertine terrain after an earthquake and proposes new concepts and strategies for restoring World Natural Heritage Site terrains.

1. Introduction

Jiuzhai Valley, a well-recognized Natural World Heritage Site, has a superior natural environment. The 7.0 magnitude earthquake (Mw 6.5) that occurred on 8 August 2017 (later referred to as the “8.8” earthquake) caused damage to the travertine terrain of Sparkling Lake in Jiuzhai Valley, resulting in vegetation erosion, drying up of the lake, and waterfall cutoff [1,2]. The earthquake tracking results indicated that the travertine terrain of Sparkling Lake had been exposed to air for an extended period following the “8.8” earthquake, caused by the dam break and subsequent drying up of the lake. In the event of disasters, such as rainstorms or earthquakes, striking again, a new round of damage is likely to occur, leading to a gradual breach of the dam downstream of Sparkling Lake and causing further damage to the overall travertine terrain [3]. Sparkling Lake is likely to face more serious disaster risks. Therefore, restoration of Sparkling Lake through artificial intervention is urgently needed.
Until recently, most restorations of heritage sites pertained to World Cultural Heritage sites such as castles, temples, and roads [4]. A worldwide dearth of restored natural heritage sites appears to exist. The protection and restoration of world natural heritage needs to follow the same principles regarding authenticity and integrity that govern the protection of World Cultural Heritage sites [5]. The guiding document of the World Heritage Convention, “Convention concerning the protection of the world cultural and natural heritage”, indicates that parts of this heritage possess exceptional qualities, considered to be of “outstanding universal value (OUV)”, and as such deserve special protection from the dangers that increasingly threaten them. Furthermore, it clarifies the duties of state parties to protect world cultural and natural heritage [5,6]. The Faro Convention emphasizes the importance of human and community participation in heritage protection. In addition to protecting historical buildings and materials, the protection of heritage sites must be beneficial to the general public, who need to recognize the value of natural landscapes. According to a report released by the United Nations Office for Disaster Risk Assessment, the number of natural disasters worldwide is increasing, but studies on disaster risk reduction are quite limited [7]. Currently, due to the lack of case studies on the restoration of World Natural Heritage sites, their restoration is difficult and requires a balance between restoration and protection of authenticity and integrity. The restoration of World Natural Heritage sites may be of practical significance to humanity as a whole by better protecting their OUV.
Reducing traces of artificial intervention when restoring natural landscapes remains a topic of broad and current interest [8,9]. Studies have investigated landscape restoration of natural coastal dune systems [10] and World Heritage sites [11,12] and evaluated their natural values following restoration [9,13]. However, traditional landscape restoration typically involves extracting data on landscape characteristics so that landscape designers can imitate the original landscape style and characteristics via restoration. This method involves subjectivity in the design process and cannot replicate the authenticity of the original landscape features. Concerning the current study, traditional landscape restoration methods were not supported by reliable data due to the absence of accurate field investigations and surveys pertaining to Sparkling Lake in Jiuzhai Valley before the earthquake. A previous study reconstructed a 3D computer graphics-based image of the Bam Adobe castle, a World Heritage Site, by analyzing the spatial structure of the castle and the relationship between its internal and external façades, which enabled its restoration [14]. This case reinforced the importance of effectively extracting the landscape and geomorphic features of Sparkling Lake for its restoration.
However, unlike artificial buildings, such as castles, natural terrain and vegetation are often irregular and complex, and may be explained by fractal theory. Although Euclidian shapes are composed of smooth lines, many natural shapes exhibit self-similarity at different spatial scales [15]. The fractal theory proposed by Mandelbrot can be used to analyze complex and irregular forms and structures in nature, including rivers, coastlines, and skylines, considered to have a fractal morphology, as well as their topography and geomorphology. It can also reveal the potential order or laws governing these natural landscapes [16,17,18,19,20,21]. More specifically, a local portion of the natural landscape may reflect the self-similarity characteristics of the entire landscape, which can be described quantitatively by the fractal dimension. Fractal geometry based on “self-similarity” helps determine the potential order or laws governing the external morphology of the landscape [16,17,18], and postulates that fractal morphology generally exists in natural landscapes, such as vegetation [22,23,24], coastlines [21,25], habitats and wetlands [26,27,28], among others. Fractal dimension characteristics can also be seen in artificial landscapes, such as terraces [29,30], artificial land use [31], building environments [32,33,34], traffic networks [35,36] and others. The practice of fractal geometry in landscape restoration of quarries, open-pit mines, and other damaged environments [37,38], as well as river shoreline restoration [39], urban skyline construction [40,41], urban spatial organization structure [42,43,44,45,46,47], and landscape restoration [11], has confirmed that the balance, congruence, and symmetry of fractal images enhance pleasure in perception and cognition. Therefore, any change in fractal dimensions may affect people’s visual judgment and preference for a landscape [48,49,50]. People prefer images with fractal features [51]. Accordingly, quantifying the self-similarity characteristics of natural landscapes via fractal dimensions is considered an effective means of describing their characteristics and one that may guide natural landscape restoration [15,40].
This study aimed to address the following questions. Can artificial restoration effectively restore the damaged terrain of World Natural Heritage? What kind of restoration methods should be implemented to minimize the traces of artificial intervention and align with the restoration principles of World Natural Heritage? What metrics should be used to assess the similarity between restored terrains and their surroundings to ensure a successful restoration outcome? To address these issues, this study explored the fractal dimension and characteristics of the terrain in Shuzheng Valley by quantifying the self-similarity characteristics of the natural landscape of this area using fractal geometry. In addition, the results were used to conduct artificial intervention restoration of the earthquake-damaged terrain. This could help to prevent geological disasters caused by dam breaks due to a lack of stability from recurring in Sparkling Lake and improve the ability to minimize disaster risks in the Shuzheng Valley area. The results of this study may help to facilitate other World Natural Heritage restoration projects, with our restoration experience serving as an important reference for natural landscape restoration.

2. Research Methods

In order to explore the fractal dimension and characteristics of the terrain in Shuzheng Valley, it is necessary to extract different scales of the terrain and conduct fractal analysis. Therefore, the terrain extraction process of Shuzheng Valley is essential. Moreover, a series of calculation processes are required to obtain the fractal dimension of Shuzheng Valley at different scales. After analyzing the results, the terrain characteristics of Shuzheng Valley can be applied to the terrain restoration of Sparkling Lake.

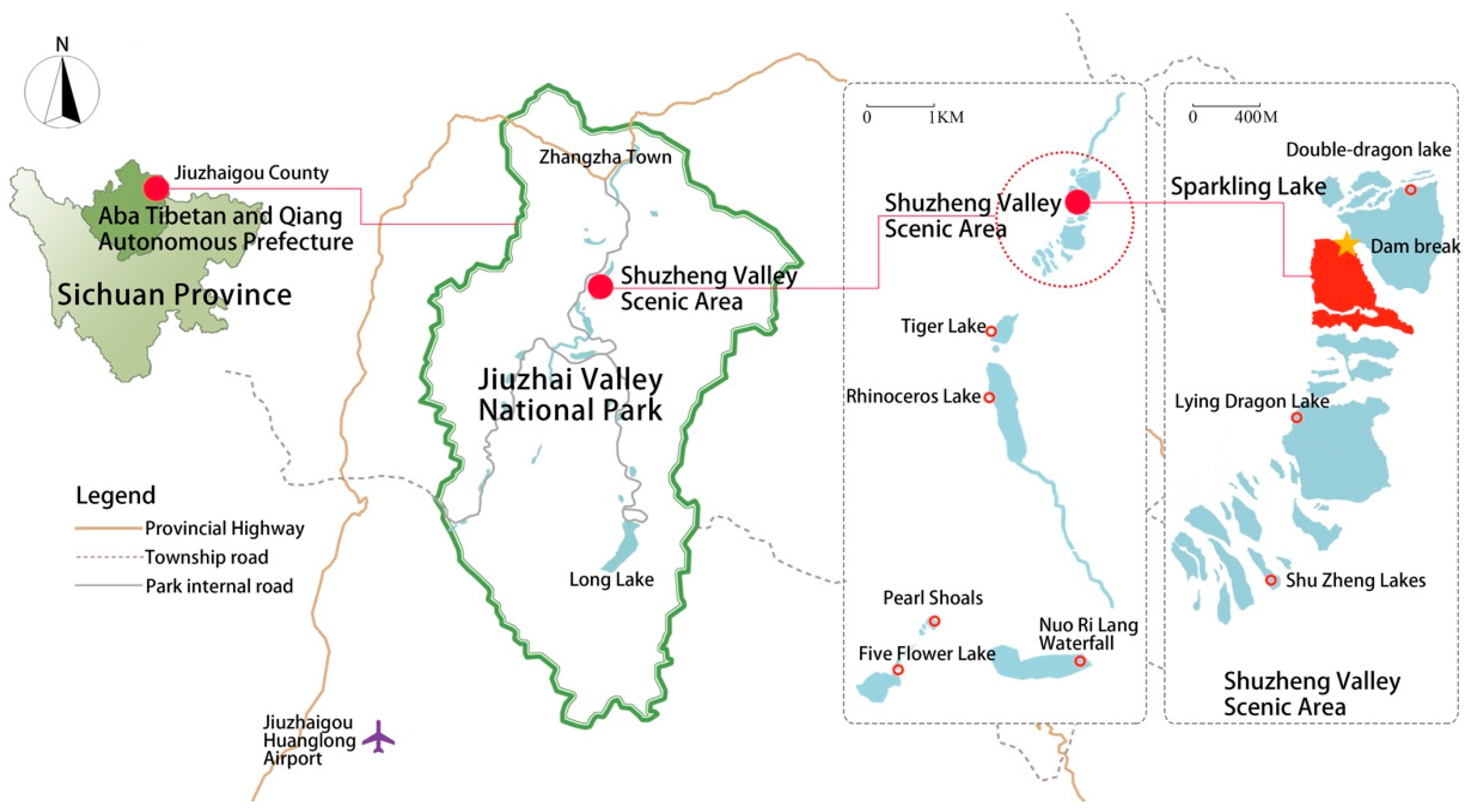
2.1. Study Area

The Jiuzhai Valley Scenic Area is a World Natural Heritage Site that functions as a national AAAAA tourist attraction (the highest level of tourist attractions in China), nature reserve, and geological park. Moreover, it is the first natural reserve in China whose main purpose is the protection of natural scenery. Its special geological conditions have led to the formation of large-scale travertine deposits via the combined action of water bodies and organisms. These deposits have formed natural landscapes in Shuzheng Valley, such as travertine dams and waterfalls with high ecological, aesthetic, and research value. Shuzheng Valley, including Shuzheng Falls, Shuzheng Lakes, Lying Dragon Lake, Sparkling Lake, Double-Dragon Lake, Reed Lake, and other scenic areas, is located at the starting point of the tourist route of the Jiuzhai Valley Scenic Area (Figure 1). The terrain is based on the accumulation of debris flow deposits in the river valley, followed by the deposition of travertine deposits, forming multiple lakes of different sizes stacked layer-by-layer along the valley. Here, the forests, lakes and waterfalls are connected in a staggered way, presenting a delightful landscape replete with “trees growing in the water, water flowing in the forest, and people swimming in the scenery” [52].
One of these scenic locations, Sparkling Lake, located 103°54′1″ E and 33°12′13″ N, has an elevation of 2211 m, a length of 294 m, and a width of 232 m. Before the earthquake, the lake was 16 m deep with a storage capacity of 45 × 104 m3 and contained various plants. The “8.8” earthquake destroyed the dam, forming a 40-m-long breach that was 15 and 12 m wide on the east and west sides, respectively, and approximately 13–15 m deep. The original vegetation on the dam was scoured (Figure 2). The breach caused Sparkling Lake to lose its water storage function, and the lake dried up. Moreover, after the earthquake, Shuzheng Valley was classified as an area that posed a potential risk of debris flow, with the potential to cause more severe damage in the area [53]. Therefore, artificial restoration was deemed urgent (Figure 3).

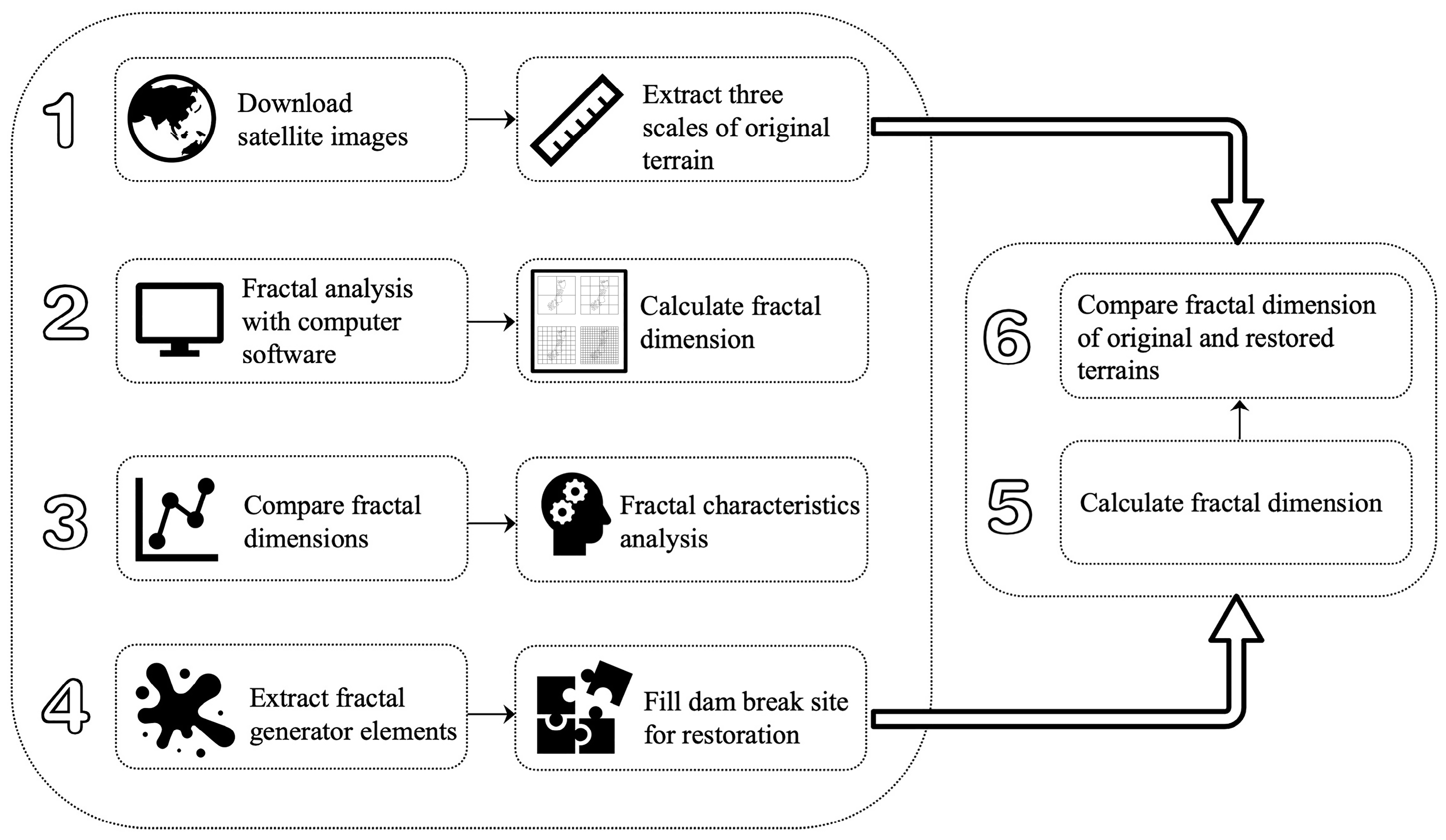
2.2. The Study Process

As observed in the flowchart in Figure 4, the fractal analysis and restoration design comprised the following main research processes.
Firstly, the original terrain information of Shuzheng Valley from before the earthquake was extracted and divided into three scales for analysis. Grids of different sizes were used to cover the extracted terrain and collect data. Data from the coverage grid were processed, and the slope of the scatterplot was calculated to obtain the fractal dimensions. We analyzed the fractal characteristics of Shuzheng Valley before the earthquake at different scales (steps 1–3). Secondly, we extracted fractal generator elements of different terrain scales in Shuzheng Valley and used them to fill and restore the Sparkling Lake terrain that was damaged by the earthquake (step 4). Finally, we calculated the fractal dimensions of the newly restored terrain using the same method. The restoration was quantified by comparing the newly restored Sparkling Lake terrain’s fractal characteristics with those of the original terrain (steps 5 and 6). If the fractal characteristics were dissimilar from those of the original terrain, it was recommended to return to step 4 for redesign. Thus, the design ensures the authenticity of World Natural Heritage sites.

2.3. Data Source and Processing

Using archived and new remote sensing data to analyze spatial structure through fractal methods, Thomas W. Crawford and others [54] showed that fractal characterization of Mytilus edulis L. spatial structure in intertidal landscapes was feasible. Other studies have also demonstrated the feasibility of this method [47,55].The original data used in the present study included Landsat-7TM remote sensing images acquired on 21 October 2015 (before the earthquake). After digitizing the remote-sensing images, the terrain was divided into three scales [56]. The division of these three scales was determined by the overall and partial relationship between the various scenic spots in Shuzheng Valley. The relationships between the primary scale terrain, the secondary scale terrain, and the tertiary scale terrain were overall and partial, respectively. The primary scale terrain was a whole, while the secondary scale terrain and tertiary scale terrain were parts of the primary scale terrain. At the same time, the tertiary scale terrain was also a part of the secondary scale terrain. The primary scale included the whole Shuzheng Valley section (including Shuzheng Lakes, Lying Dragon Lake, Sparkling Lake, and Double-Dragon Lake). The secondary scale included three terrain sections, comprising Double-Dragon Lake, Sparkling Lake, and Lying Dragon Lake. The tertiary scale, which was the smallest scale unit, included two terrain sections, comprising the west and east residual dams, located on either side of the Sparkling Lake dam breach. The division of these three different scales of terrain helps to explore the fractal characteristics between the overall and partial terrain of Shuzheng Valley. Next, we extracted the terrain (lines) from the edges of each sample at three different scale levels based on the boundary division of the landscape’s ecological patches (Figure 5).

2.4. Calculation of the Fractal Dimension

The Hausdorff–Besicovitch dimension is the theoretical definition of the fractal dimension [57]. The fractal dimension is a characteristic measure of fractals and can be used to describe the degree of space filled by fractal elements and indicate the size of the space occupied by them [58]. The fractal dimension provides a connection between different levels of scale that have self-similar elements [59]. However, some natural fractals do not have any strict self-similarity, and fractal dimension is often the only way to describe their nature [33]. The fractal dimension has been used in a lot of cases to describe the “self-similarity” of natural landscapes [16,22,24].
The box-counting method is a common method used to calculate the fractal dimension, and reflects the degree of space occupied by the fractal elements and allows shape calculations [58,60,61]. This method uses square grids of different unit scales to cover the measured figures and then generates statistics on the square grids occupied by the figures of different unit scales [15,62,63]. Finally, it is substituted into the calculation formula [33] (p. 5). Accordingly, the box-counting dimension method was used to calculate the fractal dimensions. The measured terrain was covered with grids of different sizes, divided 20 times in total, and the statistics of the grid-covered terrain images were obtained using the Quick Select (QSE) command in AutoCAD 2022 (Figure 6) [64]. The present study focused only on the fractal analysis of two-dimensional planes.
The specific steps involved were: (a) the creation of a circle as a marker symbol, using the Block command to create a new block of this circle, then naming it “Count”; (b) marking of all grids of the covered terrain with the circle named “Count”; (c) using the QSE command to count the number of circles named “Count”; and (d) importing the statistical data into Microsoft Excel and calculating the fractal dimension Db using the following formula [33] (p. 5):
D b = lim r → 0 ⁡ log ⁡ ( N r ) log ( ⁡ 1 r ) n
where Nr is the number of square grids covered by the graph during measurement and r is the unit size of the square grids during measurement. While the function slowly approaches the limit value, the slope of the regression line in the double-logarithmic graph with Nr versus r estimates the box-counting dimension. The box-counting dimension, Db, is equivalent to the fractal dimension.

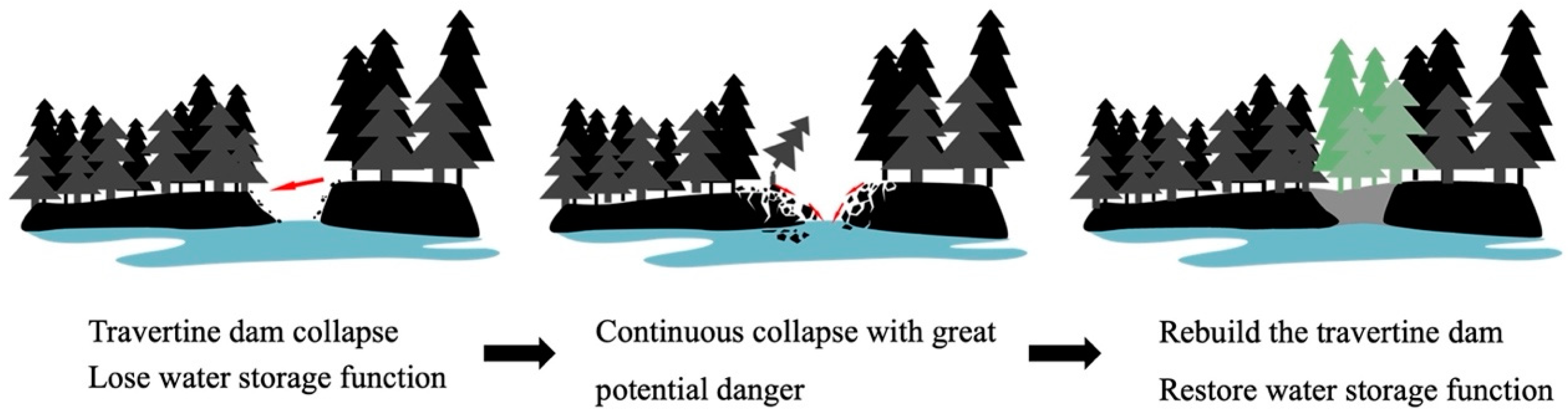
2.5. Design of Terrain Restoration for the Broken Sparkling Lake Dam

As fractal dimensions are key factors in quantitative restoration design, we attempted to quantitatively design a new dam terrain for Sparkling Lake that would be similar to the surrounding terrain by coordinating the relationship between the fractal dimension, Db, and the topography. However, this may involve selecting various fractal elements and different combination forms.

2.5.1. Selection of Fractal Elements

For the restoration design process, all terrain fractal generator elements at the three scales in the Shuzheng Valley area can be extracted, iterated, combined many times, continuously copied, shrunk, and enlarged, enabling suitable forms to be selected to fill the site, i.e., to restore it. After repeated attempts and coordination, a group of Sparkling Lake dam terrains “self-similar” with the surrounding terrain was able to be formed (Figure 7).
When selecting fractal elements, considering the impact of terrain restoration on water, soil, and vegetation is necessary. For example, water is the key link within the landscape of the Jiuzhaigou Natural World Heritage Site. However, the earthquake on 8 August 2017 severely disrupted the connectivity between the up- and downstream river systems, affecting the original aquatic ecosystem [65]. A restored Sparkling Lake dam terrain needs to assume the role of water exchange between Double-Dragon Lake and Lying Dragon Lake. In terms of terrain design, water flow channels from southwest to northeast must be preserved. Therefore, in the selection of fractal elements, selecting a strip-shaped terrain similar to the area of Shuzheng Lakes in Shuzheng Valley is necessary to facilitate the subsequent combination and formation of water flow channels.

2.5.2. Combination of Fractal Elements

Different combinations of fractal elements may affect terrain morphology, thereby affecting the flow direction, velocity, and rate of water flow. The design should comprehensively consider the total water storage capacity of Sparkling Lake after restoration and the differences between water volumes during the dry and wet seasons. By combining the design of the dam crest terrain, a suitable terrain morphology could be generated to ensure that Sparkling Lake is in a state of water conservation during both the wet and dry seasons, thereby forming an aesthetically pleasing landscape. The water flowing through the restored dam crest forms a waterfall whose shape is influenced by the water flow velocity and rate. Therefore, in the restoration design process, the tortuosity and undulation of the dam crest terrain should also be considered. Terrain morphology also affects plant growth [66,67]. With due consideration given to the subsequent vegetation restoration, it becomes necessary to reserve a plant-planting pool. Different terrain compositions can form planting ponds of different shapes, specifications, and slopes, thereby affecting the configuration of plant clusters. A terrain that is too narrow restricts plant growth. In the process of fractal element combination, sufficient planting areas should be reserved to provide sufficient growth space for plants to spread. Therefore, comprehensively considering various environmental factors and selecting an appropriate combination of fractal elements is necessary.
Previous studies have shown that the fractal dimension of terrain is significantly affected by land use, vegetation type, land area, and human disturbance [27]. Similarly, in terrain restoration design, environmental factors affect terrain morphology. Different combinations of fractal elements result in different fractal dimensions for the terrain. The spatial analysis of a site can be conducted by obtaining comparable fractal dimension values [43]. The current study compared the fractal dimension of the restored terrain of Sparkling Lake generated by combining fractal elements with the surrounding landscape terrain to determine whether the restored Sparkling Lake terrain is similar to the surrounding terrain and whether the combination form of fractal elements under this mode is appropriate. A fractal model used to study urban morphology delineated that fractal dimension was related to urban density [35]. Similar to the study on urban morphology, the present study filled the space created by the Sparkling Lake dam break for restoration in the most effective manner using fractal elements and observed that space-filling through fractal dimension changes ensured an appropriate -degree of filling (Figure 7). The appropriate degree of filling was similar to that of the surrounding terrain. Using the concept of fractals to plan and design the terrain form of a dam may be regarded as an objective and quantitative design method.

3. Results

After a series of calculations, the fractal dimensions of the Shuzheng Valley section at different scales and the newly restored Sparkling Lake dam were obtained. Then, these fractal dimensions were compared and analyzed.

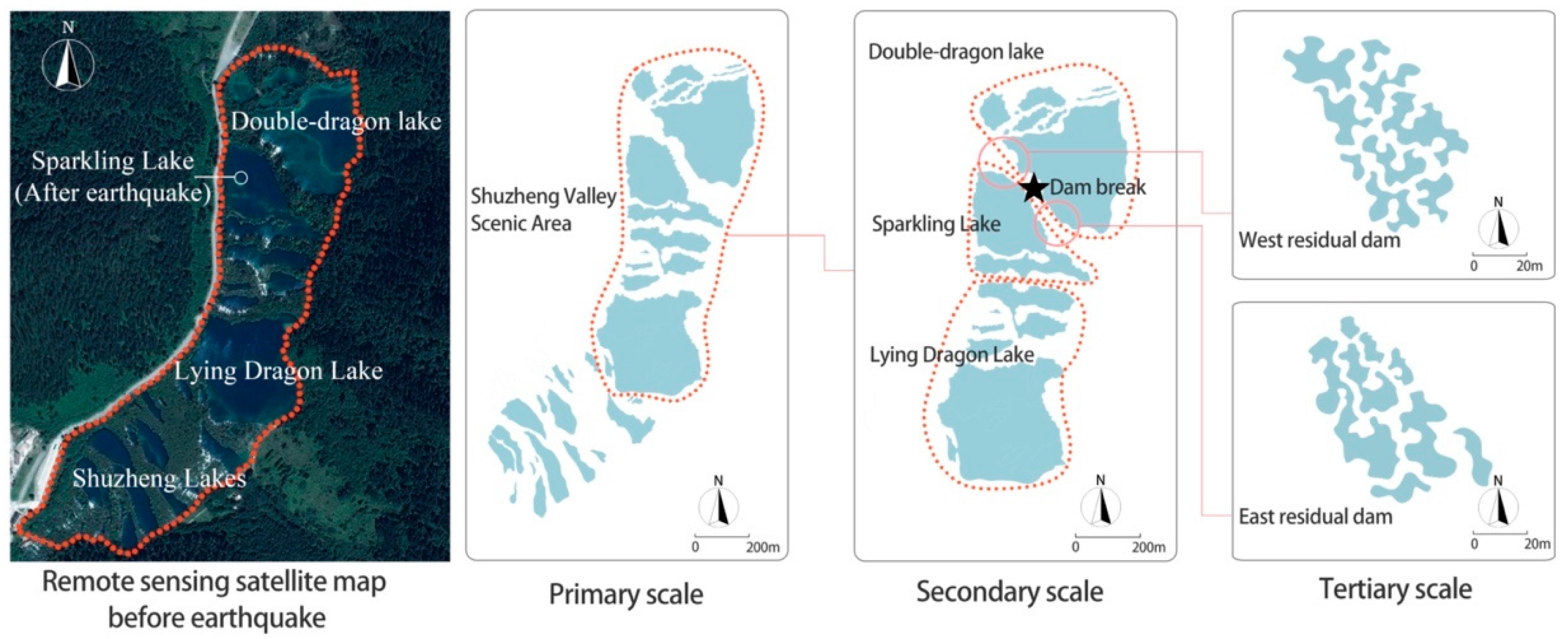
3.1. Fractal Analysis of Shuzheng Valley Terrain

The calculated fractal dimensions of the travertine terrains in the Shuzheng Valley—section of Jiuzhai Valley exhibited an apparent linear relationship at all three scales—(Figure 8). Comparing the fractal dimension values of travertine terrains in Jiuzhai Valley at different scales indicated that the fractal dimension of Shuzheng Valley at the primary scale was 1.3618 (R2 = 0.9938), while those of Double-Dragon Lake, Sparkling Lake, and Lying Dragon Lake at the secondary scale were 1.5235 (R2 = 0.9930), 1.3785 (R2 = 0.9891), and 1.6557 (R2 = 0.9973), respectively. The fractal dimension values of the western and eastern residual dams at the tertiary scale were 1.7533 (R2 = 0.9994) and 1.6975 (R2 = 0.9980), respectively. Fractal dimension values were in the order of primary-level scale < secondary-level scale < tertiary-level scale.

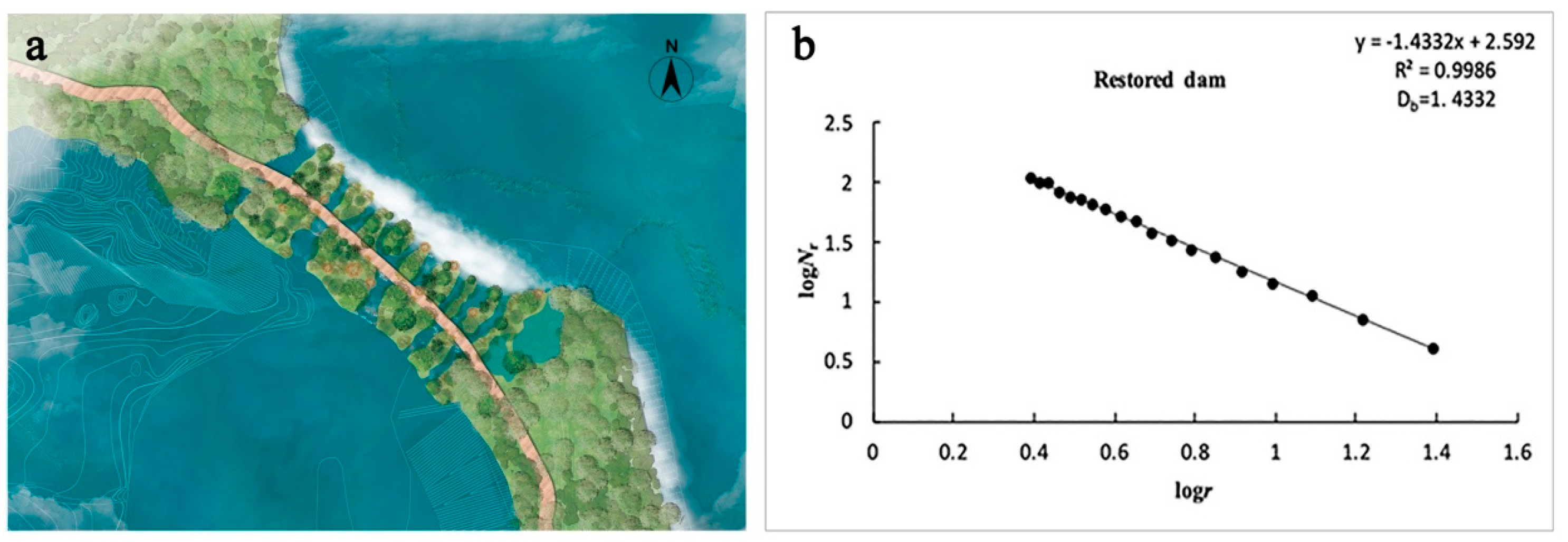
3.2. Fractal Analysis of Newly Restored Dam

Several factors must be considered in terrain design. Following careful consideration, the present study generated the restored terrain of the Sparkling Lake dam following an earthquake (Figure 9a) and conducted a fractal analysis of the restored dam terrain. The fractal analysis indicated that the restored Sparkling Lake dam terrain belonged to the tertiary level of the scale assumed in this study and possessed significant fractal characteristics (Figure 9b). Its fractal dimension was 1.4332 (R2 = 0.9986), which was closest to the value of the Sparkling Lake terrain fractal dimension at the secondary scale level.

4. Discussion

4.1. Self-Similarity of Terrains with Different Scales

Linear relationships indicate that the Shuzheng Valley section and its internal Double-Dragon Lake, Sparkling Lake, Lying Dragon Lake, and residual dams on the east and west sides possess obvious fractal self-similarity characteristics in external morphology. Fractal dimension values were in the order of primary-level scale < secondary-level scale < tertiary-level scale, indicating that in the Shuzheng Valley section of the Jiuzhai Valley, travertine terrain morphology in different areas was similar, but not identical. Due to insufficient analysis of larger-scale terrain in our study, Shuzheng Valley displayed fractal characteristics across all three selected scales. The terrain of Shuzheng Valley exhibits similar characteristics within a given scale range. This similarity is also found in trees [51]. While the observed patterns are not entirely replicated at different scales, they possess analogous fractal characteristics. Beyond this intuitive, more conceptual approach, it is possible to introduce measures that help describe the complex form of fractal objects by means of unique values. Therefore, if the terrain exhibits the particular features of fractal objects, we may conclude that despite its highly irregular aspect, it follows a well-defined spatial organization principle, which can be characterized by quantitative factors [62,68]. Previous studies discussed the fractal dimension of urban patterns, wherein the appropriate urban pattern fractal dimension scale was between 1.5 and 2 [35]. The spatial form with a fractal dimension close to 1.71 was considered the preferred mode, with the urban form pattern reaching a relatively stable and reasonable state in terms of both balance and agglomeration [69]. In the current study, the fractal dimension of the natural terrain of the Shuzheng Valley section was approximately 1.3–1.7. This result indicated that the terrain of natural environments had a lower fractal dimension value when compared to artificial environments.
The slope of the logarithmic graph usually varies with the scale when the box-counting dimension method is used. The estimated fractal dimension is a combination of these slopes and differs from the theoretical dimension. Martínez confirmed that the variability of Db is almost negligible within an appropriate scale range [46]. Generally, the smaller the scale range of the observation dimension, the greater the fluctuation. Loehle and Li [70] proposed establishing a multiscale fractal dimension profile to study the change in fractal dimension with scale. In the current study, we selected three different terrain scales to conduct our research. The fractal dimension value gradually increased, which suggests that the complexity of the terrain also increased as the scale of the sample decreased (Table 1), consistent with previous reports [19,20]. This accounts for the natural terrain being complex and seemingly irregular.
Previous studies have shown that the higher the fractal dimension, the more complex and irregular the spatial morphology [27,55]. Samples at the tertiary scale were from the overflow of travertine dams with several shallow water and low-lying areas. The fragmentation degree of the terrain is higher and more complex at the tertiary scale; therefore, the fractal dimension increases with the fragmentation degree of the terrain. However, both the primary- and secondary-scale terrain samples contained large lakes, which have large water areas and a high integrity of travertine terrain, resulting in low fractal dimension values. Landscape patch characteristics may be an important factor affecting fractal dimensions. Differences in landscape patch complexity may affect ecological diversity, stability, and function. A complex terrain has a more stable ecosystem with a higher fractal dimension. Contrastingly, a simple terrain has a relatively fragile ecosystem with a lower fractal dimension [23]. The fractal dimensions of Shuzheng Valley at the primary scale and Sparkling Lake at the secondary scale were low; therefore, their environments were fragile and vulnerable.
The relationship of travertine terrain samples among the primary-, secondary-, and tertiary-level scales indicates that coherence exists between the whole and its components. The fractal dimension of the primary scale is closest to that of the secondary scale of Sparkling Lake, reflecting significant self-similarity between the whole and parts of the fractal, which is repeated and expanded in countless microgeomorphic units [29,44].

4.2. Differences in the Composition of Terrain Fractal Elements at the Same Scale

4.2.1. The Primary Scale

The primary scale included three large lakes that form irregular and blocky fractal elements. The remaining areas were small, terraced lakes formed by overflow embankments that formed narrow-striped fractal elements. The fractal dimension can be considered a measure of an object’s ability to fill the space in which it resides [71]. Isabelle Thomas and others [55] conducted a fractal analysis on 18 urban agglomerations and found that the lowest value was obtained for Bayonne–Anglet–Biarritz (BAB) in France (1.51). The BAB is a set of cities strung along the coast with an elongated outline and scattered land use with many detached houses. Hence, the pattern is rather scattered and irregular, comprising a set of local clusters. The results are consistent with those of Isabelle Thomas and others. The number of elements formed by the terraced lake terrain in the primary-scale terrain is considerable, but the spatial distribution is loose and the space occupation intensity is low, which may explain the low fractal dimension value of the primary-scale terrain.

4.2.2. The Secondary Scale

By comparing the travertine terrain samples of Double-Dragon Lake, Sparkling Lake, and Lying Dragon Lake at the secondary level, both Double-Dragon Lake and Lying Dragon Lake contained multiple lakes and exhibited complex dam morphology, resulting in a high fractal dimension. Double-Dragon Lake and Lying Dragon Lake contain several travertine dams of different shapes, dividing large lakes into many areas of different sizes and shapes, finally forming travertine-terraced lakes. Their terrain composition is more complex than that of Sparkling Lake; therefore, they have higher fractal dimensions. Although Sparkling Lake also includes some overflow travertine dams, the scale of this patchy terrain is too small to be observed at the secondary-scale level; therefore, the complexity of the Sparkling Lake formation is lower than that of Double-Dragon Lake or Lying Dragon Lake.

4.2.3. The Tertiary Scale

At the tertiary scale, the fractal dimension of the western residual dam terrain of Sparkling Lake was slightly higher than that of the eastern residual dam terrain. On the west side, a large amount of flowing water passes through the west residual dam, with a large number of water channels and many shallow and low-lying areas, forming a large number of overflow dam terrain structures. Micro-terrain undulations and changes were complex, and the terrain was highly fragmented. On the east side, the water flowing through the east residual dam was relatively less than that flowing through the west residual dam. Compared with the western residual dam, the eastern residual dam had several but smaller water channels and a lower degree of terrain fragmentation. Therefore, the difference in terrain changes was slightly smaller in the two-dimensional plane, and the fractal dimension was lower than that of the western residual dam. This is consistent with the results of other research showing that the complexity of the edge of the Hani Terrace was affected by hydrological processes [72]. In general, differences in the fractal dimensions between the west and east residual dams were small (1.7533 vs. 1.6975), and the self-similarity characteristics were apparent.
Generally, fractals have three properties: heterogeneity, self-similarity, and characteristic length. These geometric features also apply to fractal generator elements in landscapes [23]. As the primary, secondary, and tertiary scales are affected by different environmental factors, the latter leads to differences in the size, quantity, and other characteristics of the fractal generator elements. Therefore, the composition of some elements within the three different scale levels and their fractal dimensions differ. The difference in fractal element composition at the same scale due to the difference between the numbers and sizes of fractal elements results in different terrain complexities and affects the fractal dimension value. This finding was consistent with the results of terrain fractal dimensions at different scales. However, travertine terrains all have fractal characteristics, indicating that they possess similar fractal elements. Such differences in combinations reflect the beauty of the order and irregularity of natural fractals. Evidently, the external morphology of the terrain is similar, but the combination form of the internal part of the fractal elements also affects its fractal dimension. In contrast, we may infer the similarities between terrains by comparing the dimensions of the terrain formed by different combinations of similar fractal elements. By comparing the fractal calculation results of each grid with the fractal terrains, the fractal value can be visualized and the terrain morphology of each part of the study area can be clarified [73]. Some studies have suggested that landscape habitats are more vulnerable to human interference than to natural processes, suggesting that natural ecosystems are significantly affected by human interference [23,74]. This may contribute to the restoration, reconstruction, and management of landscape ecological habitats; nevertheless, the degree of human intervention should be minimized in restoration designs.

4.3. Verification of Newly Restored Terrain Fractal Dimension

The fractal dimension of the newly restored Sparkling Lake at the secondary scale was close to that of Shuzheng Valley at the primary scale, indicating self-similarity between the restored dam terrain, Sparkling Lake, and Shuzheng Valley. The spatial structure of the terrain at different scale levels was similar and conformed to the characteristics of the overall and partial self-similarity of the fractal theory. The fractal dimension can be used as an important reference index to evaluate the planar morphology of the terrain.
However, some differences among the similarities were noted. This was substantiated by previous fractal analysis results of Shuzheng Valley (see, e.g., Section 4.2), which indicated that each terrain is affected by environmental factors, and some differences in the combined form of the fractal elements exist. However, fractal self-similarity is unaffected by this phenomenon. The restored terrain of the Sparkling Lake dam serves as the main channel for water exchange between Sparkling Lake and Double-Dragon Lake. Therefore, several water flow channels are present in the southwest to northeast direction, and the fractal- element morphology of the terrain is mostly elongated. The terrain complexity and fractal dimension value of the restored dam were lower than those of the residual dams on the east and west sides. This was the outcome of combining fractal elements, influenced by the environmental factors. This terrain was similar to what it was before earthquake.
Following verification of the fractal dimension, the Sparkling Lake dam was reconstructed according to the designed terrain (Figure 10a). After the construction of the Sparkling Lake dam, the lake was filled with water to the top of the dam (Figure 10b), causing the lake water to overflow, forming a waterfall (Figure 10c). To ensure the landscape effect of the waterfall, different fractal elements were used to design and combine terrain morphology, forming water flow channels with different widths, twists, and slopes to control the rate, water direction, and speed of water flow in various areas on top of the dam (Figure 10d).
In the specific implementation process, water flow channels were formed by stacking travertine stones, which are similar to the surrounding terrain in terms of overall terrain boundary morphology but also simulate the shape of natural travertine terrain in terms of local terrain color and undulation. After restoring the Sparkling Lake dam through this design, Sparkling Lake and its up- and downstream lakes had abundant water, and the travertine terrain was well-maintained under water coverage. A satellite image acquired on 10 September 2021 (Google Earth, 8192 × 4320 pixels) shows that the overall landscape of Shuzheng Valley had been successfully restored (Figure 10e).
Similarly, the fractal dimension, which remains unchanged over a wide range of scales, has also been applied in landscape ecology in an attempt to explain the interaction between population spatial patterns and ecological processes [22]. Researchers have conducted studies on the fractal characteristics of landscapes, particularly concerning vegetation [23,75]. However, the current study focused only on the terrain of Sparkling Lake and its surrounding areas. Future studies should also analyze the fractal characteristics of vegetation. Combining terrain and vegetation data can provide a more comprehensive understanding of the spatial distribution pattern of Sparkling Lake, which would be beneficial for its restoration. In addition, this study considered only large-scale terrain analysis, which only guided the design of the terrain boundary of the newly repaired Sparkling Lake dam. In the actual design process, consideration should also be given to the design of terrain on smaller scales, such as slope design and vertical design of terrain.

5. Conclusions

A fractal dimension objectively and effectively fills site space, thus providing effective guidance for terrain restoration. In the present study, a fractal dimension was applied to the terrain restoration design of the Sparkling Lake dam break in Jiuzhai, a World Natural Heritage Site. The rationality of the spatial layout of the designed terrain was quantified by comparing the fractal dimension values of the designed and surrounding terrains. The conclusions are as follows.
(1)
The travertine terrain at different scale levels exhibited an apparent linear relationship and self-similarity. The fractal dimension increased as the scale level decreased, reflecting terrain complexity. The terrain was more complex, and the fractal dimension value was higher than the simple terrain.
(2)
Differences were observed in the combinations of elements within the same scale. According to the complexity of the terrain, the number and size of terrain fractal elements in different combinations varied. Comparing the differences in fractal elements in spatial combinations using the fractal dimension value is possible.
(3)
The topography of the restored Sparkling Lake dam break shows fractal characteristics, and the fractal dimension value is close to that of Sparkling Lake at the secondary scale and that of Shuzheng Valley at the primary scale. The Sparkling Lake dam break had similar fractal characteristics, but its fractal element combination complexity was less than that of the residual dams on the east and west sides.
The application of fractal dimension helped to design and restore the natural morphology of the broken dam quantitatively. Moreover, it enabled the authenticity and integrity of the Sparkling Lake landscape of the Jiuzhaigou Valley Scenic and Historic Interest Area to be restored as much as possible. The reconstruction work on the collapsed dam prevented further collapse of downstream lakes in Sparkling Lake, thereby preventing secondary disasters. This study was able to achieve protection of the overall travertine terrain of Shuzheng Valley and improved the ability to minimize disaster risks in the Shuzheng Valley area, helping to protect the World Natural Heritage OUV of Jiuzhai Valley and contributing to the sustainable development of World Natural Heritage. In addition, the current study introduced novel concepts and strategies that may improve the artificial intervention process in relation to the restoration design of natural heritage sites.
In other applications of landscape restoration design, the fractal theory can also be applied to vegetation restoration, species distribution [22,76], and other designs of the Sparkling Lake dam. For example, in the present study, we projected plants vertically onto a two-dimensional plane and then conducted fractal analysis via grid coverage. Here, we primarily discussed the box-counting method when producing the fractal dimension. Another expression of the fractal dimension is the information dimension. The box-counting dimension indicates the occupation and utilization of space by the plant population, whereas the information dimension reflects the concentration intensity of the plant population. The fractal dimension, comprehensively analyzed by box-counting and information dimensions, can better reflect the space-filling potential of fractal elements. Therefore, when analyzing plant population patterns, both the box-counting and information dimension methods may be utilized to provide a more specific reference design scheme for the plane configuration of vegetation restoration.
Fractal design schemes can also be combined with aesthetic evaluation methods to assist landscape design via landscape aesthetic preference evaluation to improve theoretical research and practical planning and design of landscape terrain [77]. The present study focused only on the fractal analysis of two-dimensional planes. In future research, a combination of 2D and 3D fractal analysis could describe natural and non-natural environments by using LiDAR-derived DSM or Arc GIS for fractal analysis [45,73]. In summary, fractal theory quantifies the degree of space occupation in its unique geometric form, which may then be combined with various methods and widely applied in landscape design.

Author Contributions

Conceptualization, Z.Z., Y.D. and H.S.; methods, Z.Z. and Y.D.; software, Z.Z. and Y.D.; formal analysis, Z.Z. and Y.D.; investigation, Z.Z. and Y.D.; data curation, Z.Z. and Y.D.; writing—original draft preparation, Z.Z. and Y.D.; writing—review and editing, Z.Z. and Y.D.; visualization, Z.Z. and Y.D.; supervision, H.S.; project administration, H.S.; funding acquisition, H.S. All authors have read and agreed to the published version of the manuscript.

Funding

This work was partially supported by the Specialized Fund for the Post-Disaster Reconstruction and Heritage Protection in Sichuan (grant 5132202019000128) and the Research Project on Lake Swamping and Ecological Restoration of Jiuzhai Valley (grant 5132112022000246).

Data Availability Statement

Data are contained within the article.

Acknowledgments

Special thanks are extended to Jie Du and Weiyang Xiao for research help. The authors express their gratitude to the Jiuzhai Valley Administration Bureau for assistance.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Fan, X.M.; Scaringi, G.; Xu, Q.; Zhan, W.W.; Dai, L.X.; Li, Y.S.; Pei, X.J.; Yang, Q.; Huang, R.Q. Coseismic landslides triggered by the 8th August 2017 M-s 7.0 Jiuzhaigou earthquake (Sichuan, China): Factors controlling their spatial distribution and implications for the seismogenic blind fault identification. Landslides 2018, 15, 967–983. [Google Scholar] [CrossRef]
  2. Wang, D.P.; Zhou, Y.; Pei, X.J.; Ouyang, C.J.; Du, J.; Scaringi, G. Dam-break dynamics at Huohua Lake following the 2017 M-w 6.5 Jiuzhaigou earthquake in Sichuan, China. Eng. Geol. 2021, 289, 106145. [Google Scholar] [CrossRef]
  3. Hu, X.; Hu, K.; Zhang, X.; Wei, L.; Tang, J. Quantitative assessment of the impact of earthquake-induced geohazards on natural landscapes in Jiuzhaigou Valley. J. Mt. Sci. 2019, 16, 441–452. [Google Scholar] [CrossRef]
  4. Durrant, L.J.; Vadher, A.N.; Teller, J. Disaster risk management and cultural heritage: The perceptions of European world heritage site managers on disaster risk management. Int. J. Disaster Risk Reduct. 2023, 89, 103625. [Google Scholar] [CrossRef]
  5. UNESCO. Convention Concerning the Protection of the World’s Cultural and Natural Heritage. Available online: https://whc.unesco.org/en/conventiontext/ (accessed on 1 October 2023).
  6. UNESCO. Operational Guidelines for the Implementation of the World Heritage Convention (Revised 2021). Available online: https://whc.unesco.org/en/guidelines/ (accessed on 1 October 2023).
  7. Bahtiyar, T.B.; Disli, G. Risk management and preventive conservation of historic buildings: The case of Karatay Madrasah (Museum). Int. J. Disaster Risk Reduct. 2022, 77, 103079. [Google Scholar] [CrossRef]
  8. Yu, K. Large scale ecological restoration: Empowering the nature-based solutions inspired by ancient wisdom of farming. Acta Ecol. Sin. 2019, 39, 8733–8745. [Google Scholar] [CrossRef]
  9. Quintero-Uribe, L.C.; Navarro, L.M.; Pereira, H.M.; Fernandez, N. Participatory scenarios for restoring European landscapes show a plurality of nature values. Ecography 2022, 2022, e06292. [Google Scholar] [CrossRef]
  10. Austin, M.J.; Walker-Springett, G.R. Comment on: “Is ‘re-mobilisation’ nature restoration or nature destruction? A commentary”, by Delgado-Fernandez et al. J. Coast. Conserv. 2021, 25, 10. [Google Scholar] [CrossRef]
  11. Sugio, K. Large-scale Disasters on World Heritage and Cultural Heritage in Japan: Significant Impacts and Sustainable Management Cases. Landsc. Res. 2015, 40, 748–758. [Google Scholar] [CrossRef]
  12. Floor, J.R.; van Koppen, C.S.A.; van Tatenhove, J.P.M. Science, uncertainty and changing storylines in nature restoration: The case of seagrass restoration in the Dutch Wadden Sea. Ocean. Coast. Manag. 2018, 157, 227–236. [Google Scholar] [CrossRef]
  13. Swart, J.A.A.; van der Windt, H.J.; Keulartz, J. Valuation of nature in conservation and restoration. Restor. Ecol. 2001, 9, 230–238. [Google Scholar] [CrossRef]
  14. Matini, M.R.; Andaroodi, E.; Ono, K. A 3D approach to reconstitution of the adobe citadel of Bam after earthquake: A complementary interpretation of architectural heritage knowledge, aerial photogrammetry, and heterogeneous data. Int. J. Archit. Herit. 2019, 13, 600–618. [Google Scholar] [CrossRef]
  15. Mandelbrot Benoit, B. The Fractal Geometry of Nature; Freeman: New York, NY, USA, 1977; Volume 51, p. 468. [Google Scholar]
  16. Thomas, I.; Frankhauser, P.; Biernacki, C. The morphology of built-up landscapes in Wallonia (Belgium): A classification using fractal indices. Landsc. Urban Plan. 2008, 84, 99–115. [Google Scholar] [CrossRef]
  17. Falconer, K.J. The Hausdorff dimension of some fractals and attractors of overlapping construction. J. Stat. Phys. 1987, 47, 123–132. [Google Scholar] [CrossRef]
  18. Falconer, K.J.; Howroyd, J.D. Packing dimensions of projections and dimension profiles. Math. Proc. Camb. Philos. Soc. 1997, 121, 269–286. [Google Scholar] [CrossRef]
  19. Dickau, J.J. Fractal cosmology. Chaos Solitons Fractals 2009, 41, 2103–2105. [Google Scholar] [CrossRef]
  20. Sajid, M.; Husain, A.; Reddy, J.; Alresheedi, M.T.; Al Yahya, S.A.; Al-Rajy, A. Box dimension of the border of Kingdom of Saudi Arabia. Heliyon 2023, 9, E14846. [Google Scholar] [CrossRef]
  21. Husain, A.; Reddy, J.; Bisht, D.; Sajid, M. Fractal dimension of coastline of Australia. Sci. Rep. 2021, 11, 6304. [Google Scholar] [CrossRef]
  22. Kallimanis, A.S.; Sgardelis, S.P.; Halley, J.M. Accuracy of fractal dimension estimates for small samples of ecological distributions. Landsc. Ecol. 2002, 17, 281–297. [Google Scholar] [CrossRef]
  23. Li, B.L. Fractal geometry applications in description and analysis of patch patterns and patch dynamics. Ecol. Model. 2000, 132, 33–50. [Google Scholar] [CrossRef]
  24. Wang, J.Z.; Guo, Y. Fractal Dimension and Characteristic of Tree Branch Growth. Appl. Mech. Mater. 2014, 610, 246–250. [Google Scholar] [CrossRef]
  25. Zhu, X.; Wang, J. On Fractal Mechanism of Coastline—A Case Study of China. Chin. Geogr. Sci. 2002, 12, 47–50. [Google Scholar] [CrossRef]
  26. Ferrarini, A.; Rossi, P.; Rossi, O. Ascribing Ecological Meaning to Habitat Shape by Means of a Piecewise Regression Approach to Fractal Domains. Landsc. Ecol. 2005, 20, 799–809. [Google Scholar] [CrossRef]
  27. Liu, A.J.; Cameron, G.N. Analysis of landscape patterns in coastal wetlands of Galveston Bay, Texas (USA). Landsc. Ecol. 2001, 16, 581–595. [Google Scholar] [CrossRef]
  28. Boeye, J.; Kubisch, A.; Bonte, D. Habitat structure mediates spatial segregation and therefore coexistence. Landsc. Ecol. 2014, 29, 593–604. [Google Scholar] [CrossRef]
  29. Yuanmei, J.; Liping, Y. Multi-scale Research on the Fractal Beauty of Hani Terrace Based on Remote Sensing and Geographic Information System. J. Mt. Sci. 2008, 26, 339–346. [Google Scholar] [CrossRef]
  30. Zhang, Z.; Song, W. Canal System Structure Characteristics of Typical Irrigation Areas in Yuanyang Terraces Based on UAV Remote Sensing. Res. Soil Water Conserv. 2020, 27, 220–224. [Google Scholar] [CrossRef]
  31. Yue, W.; Xu, J.; Ai, N. Quantity Character Analysis and Fractal Model Study on the Mosaic Structure of the Landscape in a Mountaionous Area. J. Mt. Sci. 2002, 20, 150–156. [Google Scholar] [CrossRef]
  32. Katona, V. The Hidden Dimension of Façades: Fractal Analysis Reveals Composition Rules in Classical and Renaissance Architecture. Fractal Fract. 2023, 7, 257. [Google Scholar] [CrossRef]
  33. Lorenz, W.E.; Kulcke, M. Multilayered Complexity Analysis in Architectural Design: Two Measurement Methods Evaluating Self-Similarity and Complexity. Fractal Fract. 2021, 5, 244. [Google Scholar] [CrossRef]
  34. Kulcke, M.; Lorenz, W.E. Spherical Box-Counting: Combining 360° Panoramas with Fractal Analysis. Fractal Fract. 2023, 7, 327. [Google Scholar] [CrossRef]
  35. Chen, Y. Fractal analytical approach of urban form based on spatial correlation function. Chaos Solitons Fractals Interdiscip. J. Nonlinear Sci. Nonequilibrium Complex Phenom. 2013, 49, 47–60. [Google Scholar] [CrossRef]
  36. Rodin, V.; Rodina, E. The fractal dimension of Tokyo’s streets. Fractals-Complex Geom. Patterns Scaling Nat. Soc. 2000, 8, 413–418. [Google Scholar] [CrossRef]
  37. Rosario-Amado, I.n.d.; Pozo-Antonio, J.S.; Lorenzo-Salgueiro, G.; Feijoo-Conde, J.; Taboada-Castroe, J. Photorealistic simulated modelling from fractals applied to mined-out pit restoration. DYNA 2014, 81, 57–64. [Google Scholar] [CrossRef]
  38. Miao, K.J.; Tu, S.H.; Tu, H.S.; Liu, X.; Li, W.L.; Zhao, H.B.; Tang, L.; Ma, J.Y.; Li, Y. Research on Fractal Evolution Characteristics and Safe Mining Technology of Overburden Fissures under Gully Water Body. Fractal Fract. 2022, 6, 486. [Google Scholar] [CrossRef]
  39. Tang, H.; Hong, Q. Practice and Enlightenment of Shoreline Restoration in US-The Case of Hudson River Sustainable Shorelines Projects. Chin. Landsc. Archit. 2021, 37, 86–91. [Google Scholar] [CrossRef]
  40. Stamps, A.E. Fractals, skylines, nature and beauty. Landsc. Urban Plan. 2002, 60, 163–184. [Google Scholar] [CrossRef]
  41. Yan, J.; Qiu, B.; Mao, J. Evaluation and optimization of waterfront skyline of Yushan Lake in Maanshan city based on fractal theory. J. Anhui Agric. Univ. 2019, 46, 541–548. [Google Scholar] [CrossRef]
  42. Thomas, I.; Tannier, C.; Frankhauser, P. Is there a link between fractal dimension and residential environment at a regional level? Cybergeo 2008, 413, 24. [Google Scholar] [CrossRef]
  43. Chen, Y. The solutions to uncertainty problem of urban fractal dimension calculation. Entropy 2019, 21, 453. [Google Scholar] [CrossRef]
  44. Chen, Y. Fractal Modeling and Fractal Dimension Description of Urban Morphology. Entropy 2020, 22, 961. [Google Scholar] [CrossRef] [PubMed]
  45. Tara, A.; Patuano, A.; Lawson, G. Between 2D and 3D: Studying Structural Complexity of Urban Fabric Using Voxels and LiDAR-Derived DSMs. Fractal Fract. 2021, 5, 227. [Google Scholar] [CrossRef]
  46. Martinez, F.; Sepulveda, B.; Manriquez, H. Fractal Organization of Chilean Cities: Observations from a Developing Country. Land 2023, 12, 296. [Google Scholar] [CrossRef]
  47. Yilmaz, M.; Terzi, F. Measuring the patterns of urban spatial growth of coastal cities in developing countries by geospatial metrics. Land Use Policy 2021, 107, 105487. [Google Scholar] [CrossRef]
  48. Brielmann, A.A.; Buras, N.H.; Salingaros, N.A.; Taylor, R.P. What Happens in Your Brain When You Walk Down the Street? Implications of Architectural Proportions, Biophilia, and Fractal Geometry for Urban Science. Urban Sci. 2022, 6, 3. [Google Scholar] [CrossRef]
  49. Mehaffy, M.W. The Impacts of Symmetry in Architecture and Urbanism: Toward a New Research Agenda. Buildings 2020, 10, 249. [Google Scholar] [CrossRef]
  50. Salingaros, N.A. Spontaneous Cities: Lessons to Improve Planning for Housing. Land 2021, 10, 535. [Google Scholar] [CrossRef]
  51. Spehar, B.; Clifford, C.W.G.; Newell, B.R.; Taylor, R.P. Universal aesthetic of fractals. Comput. Graph.-Uk 2003, 27, 813–820. [Google Scholar] [CrossRef]
  52. JVNP. Jiuzhai Valley National Park: Shuzheng Lake Information. Available online: https://www.jiuzhai.com/about/scenic-spot/eature-spot/6105-2017-11-28-14 (accessed on 1 October 2023).
  53. Hu, X.; Hu, K.; Tang, J.; You, Y.; Wu, C. Assessment of debris-flow potential dangers in the Jiuzhaigou Valley following the August 8, 2017, Jiuzhaigou earthquake, western China. Eng. Geol. 2019, 256, 57–66. [Google Scholar] [CrossRef]
  54. Crawford, T.W.; Commito, J.A.; Borowik, A.M. Fractal characterization of Mytilus edulis L. spatial structure in intertidal landscapes using GIS methods. Landsc. Ecol. 2006, 21, 1033–1044. [Google Scholar] [CrossRef]
  55. Thomas, I.; Frankhauser, P.; Badariotti, D. Comparing the fractality of European urban neighbourhoods: Do national contexts matter? J. Geogr. Syst. 2012, 14, 189–208. [Google Scholar] [CrossRef]
  56. Fleischmann, M.; Romice, O.; Porta, S. Measuring urban form: Overcoming terminological inconsistencies for a quantitative and comprehensive morphologic analysis of cities. Environ. Plan. B-Urban Anal. City Sci. 2021, 48, 2133–2150. [Google Scholar] [CrossRef]
  57. Ostwald, M.J.; Vaughan, J. Analysing the Twentieth-Century House. In The Fractal Dimension of Architecture; Ostwald, M.J., Vaughan, J., Eds.; Springer International Publishing: Cham, Switzerland, 2016; pp. 135–157. [Google Scholar]
  58. Mandelbrot, B.B. How Long Is the Coast of Britain? Statistical Self-Similarity and Fractional Dimension. Science 1967, 156, 636–638. [Google Scholar] [CrossRef] [PubMed]
  59. Hausdorff, F. Dimension und äußeres Maß. Math. Ann. 1918, 79, 157–179. [Google Scholar] [CrossRef]
  60. Falconer, K. Fractal Geometry; Wiley: NewYork, NY, USA, 2003; pp. 76–89. [Google Scholar]
  61. Vicsek, T. Fractal Growth Phenomena; World Scientific: Singapore, 1989; p. 368. [Google Scholar]
  62. Rian, I.M.; Park, J.H.; Ahn, H.U.; Chang, D. Fractal geometry as the synthesis of Hindu cosmology in Kandariya Mahadev temple, Khajuraho. Build. Environ. 2007, 42, 4093–4107. [Google Scholar] [CrossRef]
  63. Sugihara, G.; May, R.M. Applications of fractals in ecology. Trends Ecol. Evol. 1990, 5, 79–86. [Google Scholar] [CrossRef]
  64. Cooper, J.; Su, M.L.; Oskrochi, R. The influence of fractal dimension and vegetation on the perceptions of streetscape quality in Taipei: With comparative comments made in relation to two British case studies. Environ. Plan. B-Plan. Des. 2013, 40, 43–62. [Google Scholar] [CrossRef]
  65. Xiong, Y.J.; Du, J.; Qiu, G.Y. Conserving the unique aquatic ecosystem of the Jiuzhai National Heritage Site after the 2017 earthquake: Achievements and challenges. Front. Environ. Sci. 2022, 10, 990185. [Google Scholar] [CrossRef]
  66. Jiang, Z.D.; Owens, P.R.; Ashworth, A.J.; Fuentes, B.A.; Thomas, A.L.; Sauer, T.J.; Wang, Q.B. Evaluating tree growth factors into species-specific functional soil maps for improved agroforestry system efficiency. Agrofor. Syst. 2022, 96, 479–490. [Google Scholar] [CrossRef]
  67. Mohamedou, C.; Tokola, T.; Eerikäinen, K. LiDAR-based TWI and terrain attributes in improving parametric predictor for tree growth in southeast Finland. Int. J. Appl. Earth Obs. Geoinf. 2017, 62, 183–191. [Google Scholar] [CrossRef]
  68. Frankhauser, P. Comparing the morphology of urban patterns in Europe: A fractal approach. Eur. Cities Insights Outskirts 2004, 2, 79–105. [Google Scholar] [CrossRef]
  69. Tian, D.; Zhou, Q. The development path of urban and rural space in the loess plateau from the perspective of fractal theory:A case study of Mizhi. J. Xi’an Univ. Archit. Technology. Nat. Sci. Ed. 2017, 49, 699–707. [Google Scholar] [CrossRef]
  70. Loehle, C.; Li, B.L. Statistical properties of ecological and geologic fractals. Ecol. Model. 1996, 85, 271–284. [Google Scholar] [CrossRef]
  71. Sun, W.; Xu, G.; Gong, P.; Liang, S. Fractal analysis of remotely sensed images: A review of methods and applications. Int. J. Remote Sens. 2006, 27, 4963–4990. [Google Scholar] [CrossRef]
  72. Jiao, Y.M.; Yang, L.P. The fractal characteristics of Hani terrace in Ailao Mountain. Acta Ecol. Sin. 2007, 27, 4583–4589. [Google Scholar]
  73. Fan, Q.D.; Mei, X.J.; Zhang, C.M.; Yang, X.Y. Research on Gridding of Urban Spatial Form Based on Fractal Theory. Isprs Int. J. Geo-Inf. 2022, 11, 622. [Google Scholar] [CrossRef]
  74. Dou, Y.; Cosentino, F.; Malek, Z.; Maiorano, L.; Thuiller, W.; Verburg, P.H. A new European land systems representation accounting for landscape characteristics. Landsc. Ecol. 2021, 36, 2215–2234. [Google Scholar] [CrossRef]
  75. Drake, J.B.; Weishampel, J.F. Multifractal analysis of canopy height measures in a longleaf pine savanna. For. Ecol. Manag. 2000, 128, 121–127. [Google Scholar] [CrossRef]
  76. Schmid, P.E. Fractal properties of habitat and patch structure in benthic ecosystems. Adv. Ecol. Res. 2000, 30, 339–401. [Google Scholar]
  77. Zhang, Z.; Qie, G.F.; Wang, C.; Jiang, S.S.; Li, X.; Li, M.X. Relationship between Forest Color Characteristics and Scenic Beauty: Case Study Analyzing Pictures of Mountainous Forests at Sloped Positions in Jiuzhai Valley, China. Forests 2017, 8, 63. [Google Scholar] [CrossRef]
Fractalfract 07 00863 g001
Figure 1. Restoration area. (Red circle: locations; Red graph: location of Sparkling Lake; Yellow pentagram: location of the dam break).
Figure 1. Restoration area. (Red circle: locations; Red graph: location of Sparkling Lake; Yellow pentagram: location of the dam break).
Fractalfract 07 00863 g001
Fractalfract 07 00863 g002
Figure 2. Image of Sparkling Lake damaged by the earthquake. (a) Satellite image of Sparkling Lake. (b) Drone image of Sparkling Lake after the earthquake. (c) Image of the dam break.
Figure 2. Image of Sparkling Lake damaged by the earthquake. (a) Satellite image of Sparkling Lake. (b) Drone image of Sparkling Lake after the earthquake. (c) Image of the dam break.
Fractalfract 07 00863 g002
Fractalfract 07 00863 g003
Figure 3. Collapse of Sparkling Lake and the necessity for restoration. (Dark trees: original plants; Green trees: newly restored plants).
Figure 3. Collapse of Sparkling Lake and the necessity for restoration. (Dark trees: original plants; Green trees: newly restored plants).
Fractalfract 07 00863 g003
Fractalfract 07 00863 g004
Figure 4. Flowchart of the research.
Figure 4. Flowchart of the research.
Fractalfract 07 00863 g004
Fractalfract 07 00863 g005
Figure 5. Terrain extraction at different scales.
Figure 5. Terrain extraction at different scales.
Fractalfract 07 00863 g005
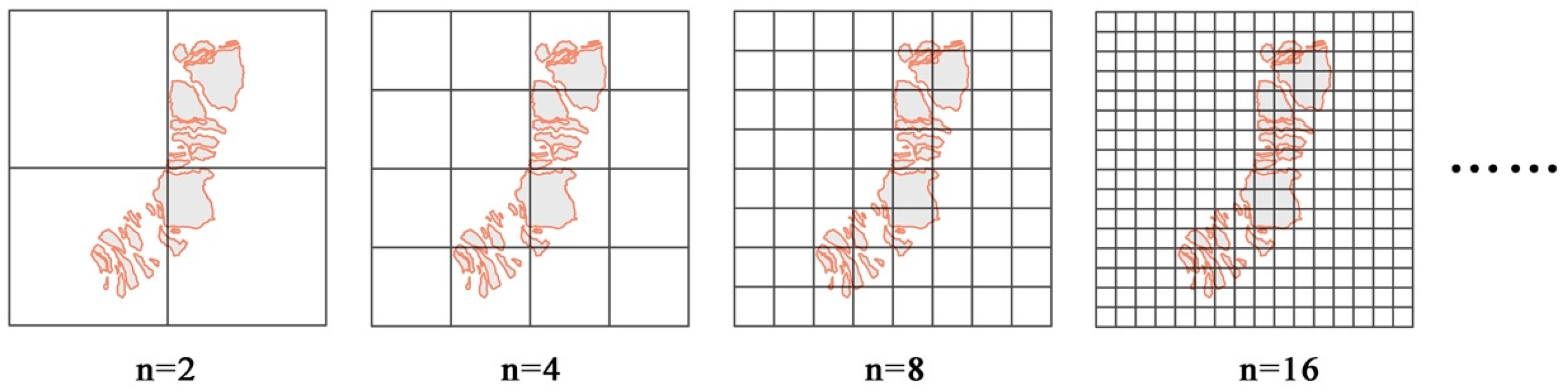
Fractalfract 07 00863 g006
Figure 6. Calculation process after covering the terrain with grids. (Dots: the subsequent terrain coverage and calculation).
Figure 6. Calculation process after covering the terrain with grids. (Dots: the subsequent terrain coverage and calculation).
Fractalfract 07 00863 g006
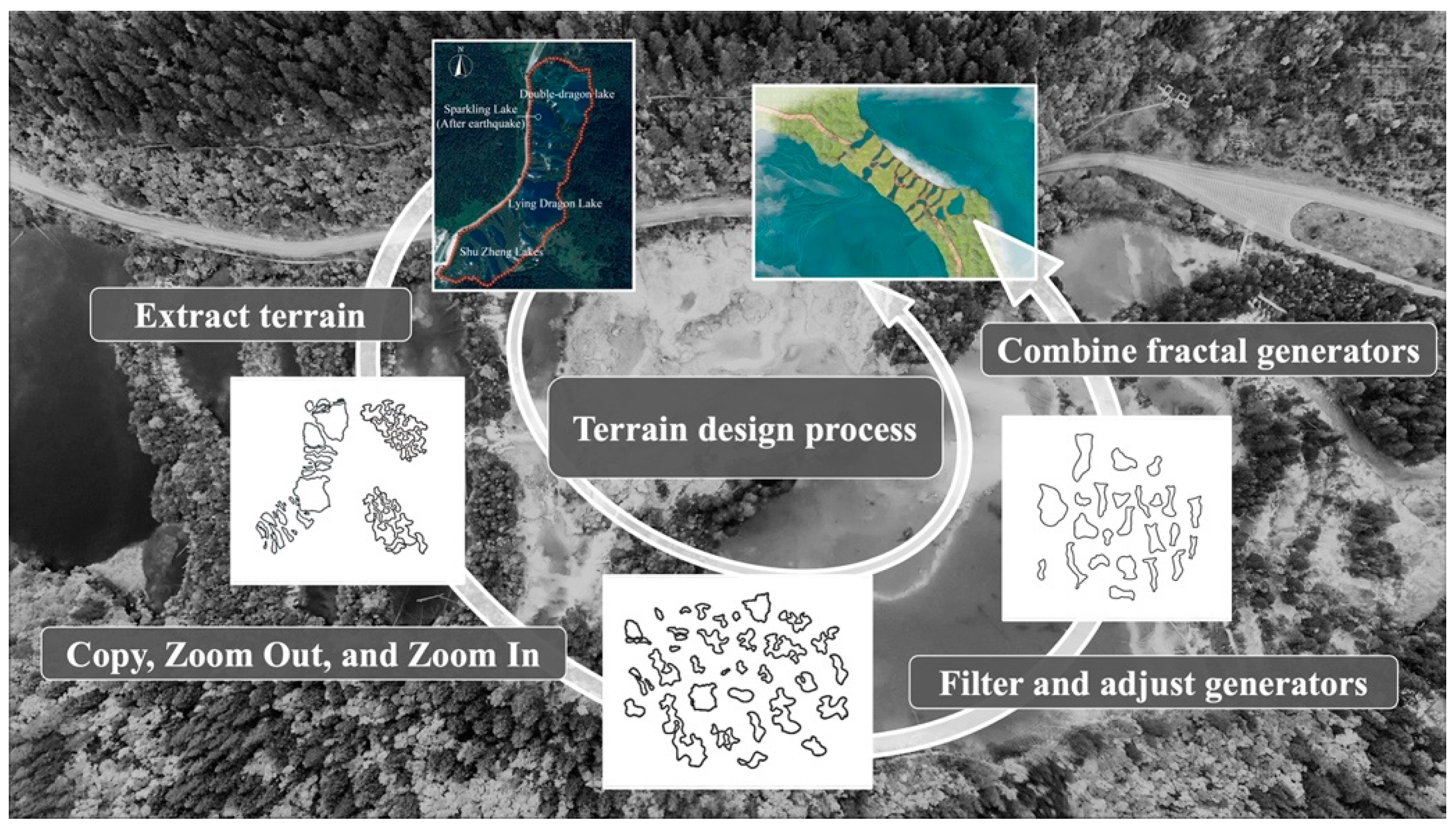
Fractalfract 07 00863 g007
Figure 7. Extraction and combination of terrain fractal elements.
Figure 7. Extraction and combination of terrain fractal elements.
Fractalfract 07 00863 g007
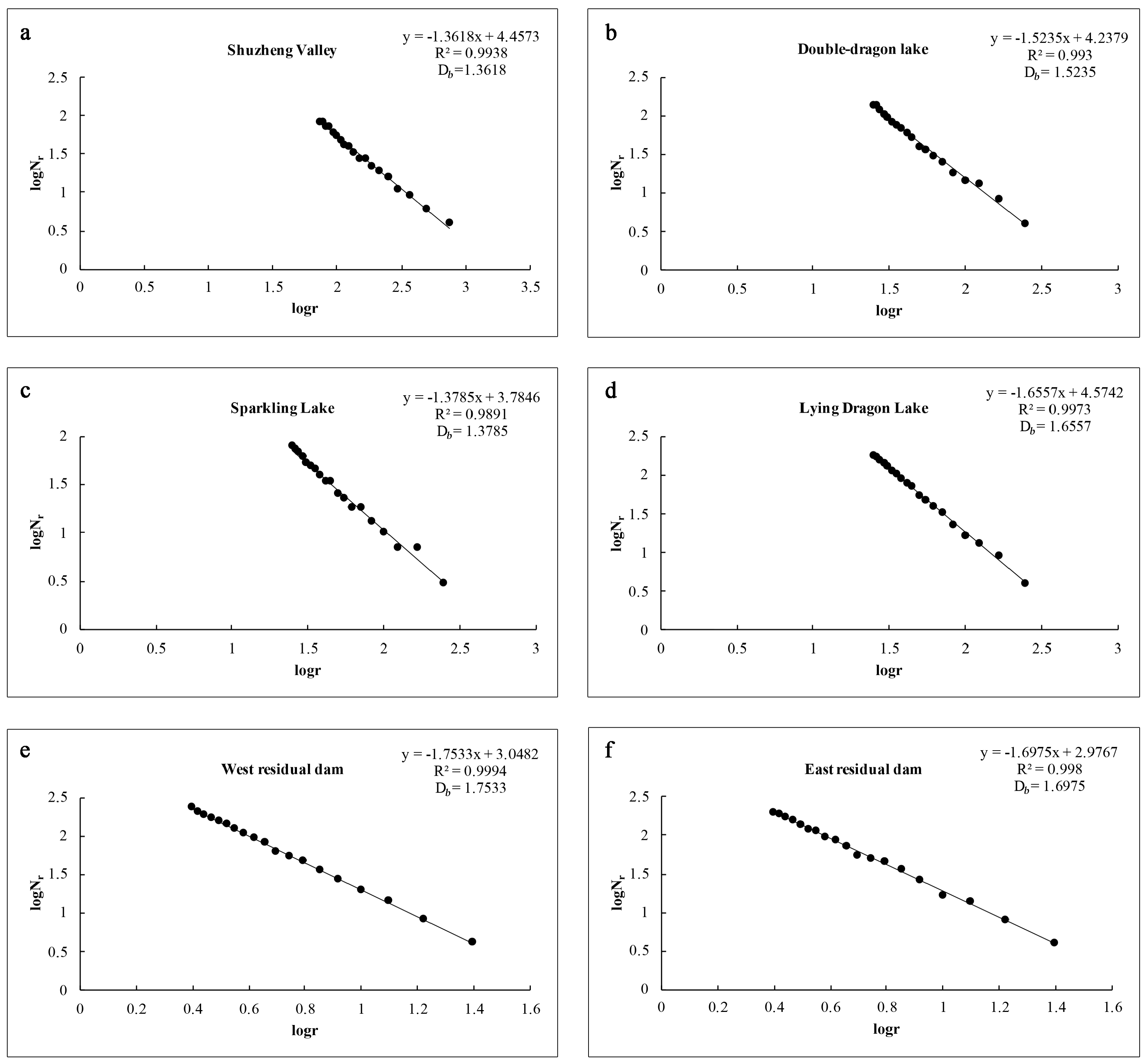
Fractalfract 07 00863 g008
Figure 8. Fractal dimension of travertine terrain. (a) Shuzheng Valley fractal dimension. (b) Double--Dragon Lake fractal dimension. (c) Sparkling Lake fractal dimension. (d) Lying Dragon Lake fractal dimension. (e) East residual dam fractal dimension. (f) West residual dam fractal dimension.
Figure 8. Fractal dimension of travertine terrain. (a) Shuzheng Valley fractal dimension. (b) Double--Dragon Lake fractal dimension. (c) Sparkling Lake fractal dimension. (d) Lying Dragon Lake fractal dimension. (e) East residual dam fractal dimension. (f) West residual dam fractal dimension.
Fractalfract 07 00863 g008
Fractalfract 07 00863 g009
Figure 9. Terrain design and fractal dimension. (a) Sparkling Lake restored dam terrain design. (b) Sparkling Lake restored dam fractal dimension.
Figure 9. Terrain design and fractal dimension. (a) Sparkling Lake restored dam terrain design. (b) Sparkling Lake restored dam fractal dimension.
Fractalfract 07 00863 g009
Fractalfract 07 00863 g010
Figure 10. Images of landscape and terrain restoration. (a) Sparkling Lake dam restoration. (b) Lake restoration. (c) Waterfall restoration. (d) Water flow channel restoration. (e) Overall view of Shuzheng Valley after restoration.
Figure 10. Images of landscape and terrain restoration. (a) Sparkling Lake dam restoration. (b) Lake restoration. (c) Waterfall restoration. (d) Water flow channel restoration. (e) Overall view of Shuzheng Valley after restoration.
Fractalfract 07 00863 g010
Table 1. Terrain characteristics.
Table 1. Terrain characteristics.
ScaleTerrain AreaFractal DimensionAltitudeSizeTerrain Characteristics
Primary scaleShuzheng
Valley		1.36182200–2280 m253–294 m long
2734 m wide		Contains three large lakes and some overflow dams. Terrain is generally complex, and spatial distribution is loose.
Secondary scaleDouble-Dragon Lake1.52352200 m333 m long
334 m wide
9 m deep		Contains a large lake and a small number of small overflow dams with complex terrain.
Sparkling Lake1.37852211 m294 m long
232 m wide
16 m deep		Contains a large lake and a large overflow dam with a relatively simple terrain.
Lying Dragon Lake1.65572220 m459 m long
293 m wide
24 m deep		Contains a large lake and a large number of overflow dams with complex terrain.
Tertiary scaleWest residual dam1.75332211 m70 m long
30 m wide
0.3–0.5 m deep		Located between the main road and the collapsed Sparkling Lake dam, it comprises a large amount of shallow and low-lying land with complex and irregular terrain.
East residual dam1.69752211 m70 m long
30 m wide
0.3–0.5 m deep		Located between the collapsed Sparkling Lake dam and the forest mountain. It comprises a large proportion of shallow and low-lying land with complex and irregular terrain.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Zou, Z.; Du, Y.; Song, H. Fractal Features in Terrain Restoration of Jiuzhai Valley, a World Natural Heritage Site in China. Fractal Fract. 2023, 7, 863. https://doi.org/10.3390/fractalfract7120863

AMA Style

Zou Z, Du Y, Song H. Fractal Features in Terrain Restoration of Jiuzhai Valley, a World Natural Heritage Site in China. Fractal and Fractional. 2023; 7(12):863. https://doi.org/10.3390/fractalfract7120863

Chicago/Turabian Style

Zou, Zan, Yue Du, and Huixing Song. 2023. "Fractal Features in Terrain Restoration of Jiuzhai Valley, a World Natural Heritage Site in China" Fractal and Fractional 7, no. 12: 863. https://doi.org/10.3390/fractalfract7120863

APA Style

Zou, Z., Du, Y., & Song, H. (2023). Fractal Features in Terrain Restoration of Jiuzhai Valley, a World Natural Heritage Site in China. Fractal and Fractional, 7(12), 863. https://doi.org/10.3390/fractalfract7120863

Article Metrics

Back to TopTop