Approximation Solution for Fuzzy Fractional-Order Partial Differential Equations

Abstract

In this article, the authors study the comparison of the generalization differential transform method (DTM) and fuzzy variational iteration method (VIM) applied to determining the approximate analytic solutions of fuzzy fractional KdV, K(2,2) and mKdV equations. Furthermore, we establish the approximation solution two-and three-dimensional fuzzy time-fractional telegraphic equations via the fuzzy reduced differential transform method (RDTM). Finding an exact or closed-approximation solution to a differential equation is possible via fuzzy RDTM. Finally, we present the fuzzy fractional variational homotopy perturbation iteration method (VHPIM) with a modified Riemann-Liouville derivative to solve the fuzzy fractional diffusion equation (FDE). Using this approach achieves a rapidly convergent sequence that approaches the exact solution of the equation. The proposed methods are investigated based on fuzzy fractional derivatives with some illustrative examples. The results reveal that the schemes are highly effective for obtaining the solutions to fuzzy fractional partial differential equations.

1. Introduction

The fuzzy fractional differential equations (FFDEs) are frequently employed as models in a variety of research fields, including the civil engineering, evaluation of weapon systems, population modeling, and electro-hydraulics modeling. Consequently, FFDEs have gained a lot of attention in the areas of mathematics and engineering. In particular, Agarwal et al. [1] originally developed FFDEs, ignoring the importance of fuzzy derivatives. In other words, they introduced a new class of FFDEs by incorporating fuzzy uncertainty into dynamic systems. Nonetheless, the growth of FFDEs has been significantly linked to the emergence of various forms of fuzzy derivatives. Allahviranloo et al. [2] proposed FFDEs under Riemann-Liouville Hukuhara differentiability, which is a straightforward extension of the fractional Riemann-Liouville derivative utilizing the Hukuhara difference. The authors of [3] presented the FFDEs based on the fuzzy fractional derivative of the Caputo type. Moreover, fuzzy derivatives based on the Hukuhara difference encounter some problems when the diameter of uncertainty increases with time. Therefore, generalizations of the Hukuhara derivative are acknowledged as an active research direction and constitute a substantial development. Considering the extensions of Bede and Gal [4] on the differentiability of fuzzy-valued functions, the references [5,6,7] introduced the generalized Hukuhara derivatives of interval-valued functions and fuzzy-valued functions. In [3,8], the generalized Caputo fractional derivative and the Riemann–Liouville fractional derivative were introduced together with their many applications.

Zhou [9] proposed the concept of DTM to solve the initial value problem of linearity–nonlinearity in polynomial form for circuit analysis, unlike traditional higher-order Taylor series that involve the symbolic computation of data functions derivatives. Later, this method was considered by many authors; see [10,11,12].

To overcome the lack of complex conversion of DTM, a reduced differential transform method (RDTM) was introduced by Keskin et al. [13,14], which is a reliable semi-analytical method used to find the approximate solutions of the partial differential equations (PDEs), and there have been few essential applications of RDTM [15,16,17]. In particular, [14] has shown that recursive RDTM equations produce all Poisson series coefficients for solutions altogether. However, recursive DTM equations entirely produce all Taylor solution coefficients, which is an advantage of the RDTM. Recently, the authors have used this method for solving some problems in the fuzzy environment; see [11,18,19].

He [20] created the HPM, which he applied to nonlinear problems by employing homotopy theory from topology [21]. The HPM has been the subject of numerous discussions by different authors. Particularly, the authors of [11] discussed the comparison of fuzzy HPM as well as other approaches to solving the fuzzy $(1+n)$-dimensional Burgers’ equation. Doan et al. [22] presented the new technique to efficiently approximate both linear buckling loads and associated mode shapes of finite element structures subject to perturbations. Noeiaghdam et al. [23] studied the dynamical strategy of HPM for solving second-kind integral equations using the CESTAC method. Osman et al. [18] compared HPM with different methods to solve fuzzy wave-like and heat-like equations.

In 1998, He first introduced the variational iteration method (VIM) [24]. Later, many researchers confirmed that VIM is a valuable method for solving some problems; see [25,26,27]. Moreover, various authors investigated the VIM in a fuzzy environment. In [28], the authors solved nonlinear fuzzy differential equations via the fuzzy VIM. Osman et al. [29] presented the comparison of VIM with another technique to obtain the solution of fuzzy wave-like and heat-like equations. Mungkasi [30] investigated the variational iteration with successive approximation techniques for an SIR epidemic model and constant vaccination strategy. Mustafa et al. [31] studied the fuzzy variational problem with fuzzy optimal control problem under granular differentiability. Chu et al. [32] proposed the fractional third-order dispersive PDEs utilizing Shehu decomposition and VIM. Hijaz et al. [33] studied a new method called the fractional iteration algorithm-I for solving nonlinear, noninteger-order partial differential equations numerically.

In the present paper, the authors compare the generalization of DTM with fuzzy VIM applied to obtain the solutions of fuzzy fractional KdV, K(2,2), and mKdV equations. The primary advantage of the VIM is its rapid solution convergence. The acquired numerical results confirm its extremely high level of precision. Moreover, we establish the approximation solution two-and three-dimensional fuzzy time-fractional telegraphic equations via the fuzzy RDTM. The technique is directly used without linearization, discretization, transformation, or restrictive assumptions. It is not difficult to apply this method to the multidimensional time-fractional order physical problems that crop up in a variety of engineering and scientific fields. Finally, we propose a fuzzy fractional VHPIM to obtain the solution to the fuzzy fractional diffusion equation. The numerical results demonstrated that the scheme is an effective and accurate technique for solving fuzzy time-fractional diffusion equations.

The present article has six sections. In Section 2, we will review several important definitions. In Section 3, we studied the comparison of the DTM and fuzzy VIM applied to determining the approximate analytic solutions of fuzzy fractional KdV, K(2,2), and mKdV equations. In Section 4, we investigate the approximation solution of fuzzy time-fractional telegraphic equations via fuzzy RDTM. Section 5 considers the fuzzy fractional VHPIM applied to solve the fuzzy fractional diffusion equation. The final part of the article, Section 6, presents the conclusions.

2. Preliminaries

Let us assume that $E^1$ is the set of fuzzy subsets of the real axis, if $\tilde{w}:R\to [0,1],$ and the following conditions hold:

i.

$\tilde{w}$ is upper semi-continuous on R;

ii.

$\tilde{w}$ is fuzzy convex;

iii.

$\tilde{w}$ is normal;

iv.

Closure of $\{x\in R|\tilde{w}\left(\mathsf{\Lambda }\right)>0\}$ is compact.

Then $E^1$ stands for the space of fuzzy numbers. For $0<\varrho \le 1$ denote $\tilde{w}\left(\varrho \right)=\left\{\mathsf{\Lambda }\in R^n|\tilde{w}\left(\mathsf{\Lambda }\right)\ge \varrho \right\}=[\underline{w}\left(\varrho \right),\stackrel{̲}{w}\left(\varrho \right)]$ and $\tilde{w}\left(0\right)=cl\{\mathsf{\Lambda }\in R^n|\tilde{w}\left(\mathsf{\Lambda }\right)>0\}.$ Then, from the above conditions, it follows that the $\varrho$-level set $\tilde{w}\left(\varrho \right)$ is the closed interval for any $0\le \varrho \le 1$. For arbitrary $\tilde{w},\tilde{\tau }\in E^1$ and $k\in R$, the addition and scalar multiplication are given by

(1)

$(\tilde{w}\oplus \tilde{\tau })\left(\varrho \right)=\tilde{w}\left(\varrho \right)+\tilde{\tau }\left(\varrho \right);$

(2)

$(k\odot \tilde{w})\left(\varrho \right)=[k\underline{w}\left(\varrho \right),k\stackrel{̲}{w}\left(\varrho \right)].$

For $d:E^1\times E^1\to R^{+}\cup \left\{0\right\}$, we denote the Hausdorff distance between fuzzy numbers by $d(\tilde{w},\tilde{\tau })={sup}_{0\le \varrho \le 1}max\left\{|\underline{w}\left(\varrho \right)-\underline{\tau }\left(\varrho \right)|,|\stackrel{̲}{w}\left(\varrho \right)-\stackrel{̲}{\tau }\left(\varrho \right)|\right\}.$ The metric space $(E^1,d)$ is complete, separable, and the following three conditions of the metric d are valid (see [34]):

   (1)

$d(\tilde{w}\oplus \tilde{\ell },\tilde{\tau }\oplus \tilde{\ell })=d(\tilde{w},\tilde{\tau }),\mathrm{for}\mathrm{all}\tilde{w},\tilde{\tau },\tilde{\ell }\in E^1;$

   (2)

$d(\tilde{w}\oplus \tilde{\tau },\tilde{\ell }\oplus \tilde{z})\le d(\tilde{w},\tilde{\tau })+d(\tilde{\ell },\tilde{z}),\tilde{w},\tilde{\tau },\tilde{\ell },\tilde{z}\in E^1;$

   (3)

$d\left(\lambda \tilde{w}\tilde{\oplus }\lambda \tilde{\tau }\right)=\left|\lambda \right|d(\tilde{w},\tilde{\tau }),\mathrm{for}\mathrm{all}\lambda \in R,\tilde{w},\tilde{\tau }\in E^1.$

The fuzzy-valued function $\tilde{w}:[a,b]\to E^1$ is represented at the $\varrho$-level as $\tilde{w}(\mathsf{\Lambda };\varrho )=[\underline{w}(\mathsf{\Lambda };\varrho ),\stackrel{̲}{w}(\mathsf{\Lambda };\varrho )]$, $\mathsf{\Lambda }\in [a,b]\mathrm{and}\varrho \in [0,1]$. Say that the fuzzy-valued function $\tilde{w}$ is integrable on $[a,b]$, if the function $\tilde{w}$ is continuous in the metric d, its definite integral exists. Moreover, we obtain

$${\int }_a^b\tilde{w}(\mathsf{\Lambda };\varrho )d\mathsf{\Lambda }=\left[{\int }_a^b\underline{w}(\mathsf{\Lambda };\varrho )d\mathsf{\Lambda },{\int }_a^b\stackrel{̲}{w}(\mathsf{\Lambda };\varrho )d\mathsf{\Lambda }\right].$$

Definition 1 ([7]).

Let us assume that $\tilde{w}\mathrm{and}\tilde{\tau }\in E^1$ are fuzzy numbers. Then, the gH-difference between $\tilde{w}\mathrm{and}\tilde{\tau }$ is defined as follows:

$$\tilde{w}{\ominus }_{gH}\tilde{\tau }=\tilde{\upsilon }\iff \left\{\begin{array}{c}\hfill \left(i\right)\tilde{w}=\tilde{\tau }\oplus \tilde{\upsilon },\hfill \\ \hfill or\left(ii\right)\tilde{\tau }=\tilde{w}\oplus (-\tilde{\upsilon }).\hfill \end{array}\right.$$

(1)

When it comes to the ϱ-level, we arrive at ${\left[\tilde{w}{\ominus }_{gH}\tilde{\tau }\right]}_{{}_{\varrho }}=[min\{{\underline{w}}_{\varrho }-{\underline{\tau }}_{\varrho },{\stackrel{̲}{w}}_{\varrho }-{\stackrel{̲}{\tau }}_{\varrho }\},max\{{\underline{w}}_{\varrho }-{\underline{\tau }}_{\varrho },{\stackrel{̲}{w}}_{\varrho }-{\stackrel{̲}{\tau }}_{\varrho }\}]$, as well as if the H-difference exists, then $\tilde{w}\ominus \tilde{\tau }=\tilde{w}{\ominus }_{gH}\tilde{\tau }$; the conditions for the existence of $\tilde{\upsilon }=\tilde{w}{\ominus }_{gH}\tilde{\tau }\in E^1$ are

$$\begin{array}{cc}\hfill Case\left(i\right)& \hfill \left\{\begin{array}{c}\hfill {\underline{\upsilon }}_{\varrho }={\underline{w}}_{\varrho }-{\underline{\tau }}_{\varrho }and{\stackrel{̲}{\upsilon }}_{\varrho }={\stackrel{̲}{w}}_{\varrho }-{\stackrel{̲}{\tau }}_{\varrho },for all\varrho \in [0,1],\hfill \\ \hfill with{\underline{\upsilon }}_{\varrho }increasing,{\stackrel{̲}{\upsilon }}_{\varrho }decreasing,{\underline{\upsilon }}_{\varrho }\le {\stackrel{̲}{\upsilon }}_{\varrho }.\hfill \end{array}\right.\hfill \end{array}$$

(2)

$$\begin{array}{cc}\hfill Case\left(ii\right)& \hfill \left\{\begin{array}{c}\hfill {\underline{\upsilon }}_{\varrho }={\stackrel{̲}{w}}_{\varrho }-{\stackrel{̲}{\tau }}_{\varrho }and{\stackrel{̲}{\upsilon }}_{\varrho }={\underline{w}}_{\varrho }-{\underline{\tau }}_{\varrho },for all\varrho \in [0,1],\hfill \\ \hfill with{\underline{\upsilon }}_{\varrho }increasing,{\stackrel{̲}{\upsilon }}_{\varrho }decreasing,{\underline{\upsilon }}_{\varrho }\le {\stackrel{̲}{\upsilon }}_{\varrho }.\hfill \end{array}\right.\hfill \end{array}$$

(3)

It is not difficult to show that the above two cases hold if and only if $\tilde{\upsilon }$ is a crisp number. The gH-difference between fuzzy numbers probably does not exist. To fix this, fuzzy numbers are differentiated [7].

Definition 2 ([35]).

A fuzzy-valued function $\tilde{w}$ of two variables is a rule that assigns to each ordered pair of real numbers, $(\mathsf{\Lambda },t)$, in a set D, denoted by $\tilde{w}(\mathsf{\Lambda },t)$, the unique fuzzy number. The domain of $\tilde{w}$ denotes D, and its range is the set of values that $\tilde{w}$ can take, so $\left\{\tilde{w}(\mathsf{\Lambda },t)\right|(\mathsf{\Lambda },t)\in D\}$.

Let us consider $\tilde{w}:D\to E^1$ is the parametric representation of the fuzzy-valued function. Then, for all $(\mathsf{\Lambda },t)\in D$ and $\varrho \in [0,1]$, the following inequality holds:

$$\tilde{w}(\mathsf{\Lambda },t;\varrho )=[\underline{w}(\mathsf{\Lambda },t;\varrho ),\stackrel{̲}{w}(\mathsf{\Lambda },t;\varrho )].$$

Definition 3 ([35]).

Let $\tilde{w}:D\to E^1$ be a fuzzy-valued function of two variables. Then, we say that the fuzzy limit of $f(\mathsf{\Lambda },t)$ as $(\mathsf{\Lambda },t)$ approaches $(a,b)$ is $L\in E^1$, and we write ${lim}_{(\mathsf{\Lambda },t)\to (a,b)}\tilde{w}(\mathsf{\Lambda },t)=L$ if for every number $\epsilon >0$, there is a corresponding number $\delta >0$ such that if $(\mathsf{\Lambda },t)\in D,\Vert (\mathsf{\Lambda },t)-(a,b)\Vert <\delta \Rightarrow D(\tilde{w}(\mathsf{\Lambda },t),L)<\epsilon$, where $\Vert ·\Vert$ denotes the Euclidean norm in $R^n$.

Fuzzy Fractional Calculus

The symbols ${\mathcal{C}}^{\mathcal{F}}[a,b]$ and ${\mathcal{L}}^{\mathcal{F}}[a,b]$ stand for the space of any fuzzy-valued functions which are continuous on the interval $[a,b]$ and the space of any Lebesgue integrable fuzzy-valued functions on the bounded interval $[a,b]\subset \mathbb{R}$, respectively.

Definition 4 (cf. [36]).

Let us assume that $\tilde{w}\left(\mathsf{\Lambda }\right)\in {\mathcal{C}}^{\mathcal{F}}[a,b]\cap {\mathcal{L}}^{\mathcal{F}}[a,b]$. The definition of the fuzzy Riemann–Liouville integral of fuzzy-valued function $\tilde{w}$ is as follows:

$$\left(I_{a+}^{\Im }\tilde{w}\right)\left(\mathsf{\Lambda }\right)=\frac{1}{\mathsf{\Gamma }(\Im )}{\int }_a^{\mathsf{\Lambda }}\frac{\tilde{w}\left(t\right)dt}{{(\mathsf{\Lambda }-t)}^{1-\Im }},\mathsf{\Lambda }>a,0<\Im ⩽1.$$

Let us assume the ϱ-level formula of a fuzzy-valued function, $\tilde{w}$, is written as $\tilde{w}(\mathsf{\Lambda };\varrho )=[\underline{w}(\mathsf{\Lambda };\varrho ),\stackrel{̲}{w}(\mathsf{\Lambda };\varrho )]$ for $\varrho \in [0,1]$; we may utilize the lower and upper functions to express the fuzzy Riemann–Liouville integral of $\tilde{w}$ in terms of the lower and upper functions as follows.

Theorem 1 ([36]).

Let us assume that $\tilde{w}\left(\mathsf{\Lambda }\right)\in {\mathcal{C}}^{\mathcal{F}}[a,b]\cap {\mathcal{L}}^{\mathcal{F}}[a,b]$. Then, the fuzzy Riemann–Liouville integral of fuzzy-valued function $\tilde{w}$ is defined as:

$$\left({\mathcal{I}}_{a+}^{\Im }\tilde{w}\right)(\mathsf{\Lambda };\varrho )=[\left({\mathcal{I}}_{a+}^{\Im }\underline{w}\right)(\mathsf{\Lambda };\varrho ),\left({\mathcal{I}}_{a+}^{\Im }\stackrel{̲}{w}\right)(\mathsf{\Lambda };\varrho )],$$

where $0\le \varrho \le 1$ and

$$\begin{array}{cc}\hfill \left({\mathcal{I}}_{a+}^{\Im }\underline{w}\right)(\mathsf{\Lambda };\varrho )& \hfill =\frac{1}{\mathsf{\Gamma }(\Im )}{\int }_a^{\mathsf{\Lambda }}\frac{\underline{w}(t;\varrho )\mathrm{d}t}{{(\mathsf{\Lambda }-t)}^{1-\Im }},0\le \varrho \le 1,\hfill \\ \hfill \left({\mathcal{I}}_{a+}^{\Im }\stackrel{̲}{w}\right)(\mathsf{\Lambda };\varrho )& \hfill =\frac{1}{\mathsf{\Gamma }(\Im )}{\int }_a^{\mathsf{\Lambda }}\frac{\stackrel{̲}{w}(t;\varrho )\mathrm{d}t}{{(\mathsf{\Lambda }-t)}^{1-\Im }},0\le \varrho \le 1.\hfill \end{array}$$

Definition 5.

Let us assume $\Im >0$. Then, the Mittag–Leffler function $E_{\Im }\left(t\right)$ is represented as follows:

$$E_{\Im }\left(t\right)=\sum _{n=0}^{\infty }\frac{t^n}{\mathsf{\Gamma }(\Im n+1)},\Im >0.$$

Definition 6 ([36,37]).

Let us assume that $\tilde{w}\in C^{\mathcal{F}}[a,b]\cap L^{\mathcal{F}}[a,b]$ is a fuzzy-valued function and that $\Im \in (0,1]$. Then, $\tilde{w}$ is said to be Caputo’s gH-differentiable at Λ when

$${}^{\mathcal{C}}{D}_a^{\Im }\tilde{w}(\mathsf{\Lambda };\varrho )=1/\mathsf{\Gamma }(1-\Im ){\int }_{{\mathsf{\Lambda }}_0}^{\mathsf{\Lambda }}{(\mathsf{\Lambda }-t)}^{-\Im }{\tilde{w}}^{\prime }(t;\varrho )dt.$$

Notice that later, we indicate ${}^{\mathcal{C}}{D}_0^{\Im }\tilde{w}(t;\varrho )$ using the expression ${}^{\mathcal{C}}{D}^{\Im }\tilde{w}(t;\varrho ).$

Theorem 2 ([37]).

Assume that $\tilde{w}\in C^{\mathcal{F}}[a,b]\cap L^{\mathcal{F}}[a,b],0<\Im \le 1$ and ${\mathsf{\Lambda }}_0\in (a,b)$. Then,

(i) 

Let $\tilde{w}$ be an (i)-differentiable fuzzy-valued function. Then, we have

$$\left({}_i^{\mathcal{C}}{D}_{{\mathsf{\Lambda }}_0}^{\Im }\right)\tilde{w}(\mathsf{\Lambda };\varrho )=\left[\left({}^{\mathcal{C}}{D}_{{\mathsf{\Lambda }}_0}^{\Im }\right)\underline{w}(\mathsf{\Lambda };\varrho ),\left({}^{\mathcal{C}}{D}_{{\mathsf{\Lambda }}_0}^{\Im }\right)\stackrel{̲}{w}(\mathsf{\Lambda };\varrho )\right],0\le \varrho \le 1.$$

(ii) 

Let $\tilde{w}$ be a (ii)-differentiable fuzzy-valued function. Then, we have

$$\left({}_{ii}^{\mathcal{C}}{D}_{{\mathsf{\Lambda }}_0}^{\Im }\right)\tilde{w}(\mathsf{\Lambda };\varrho )=\left[\left({}^{\mathcal{C}}{D}_{{\mathsf{\Lambda }}_0}^{\Im }\right)\stackrel{̲}{w}(\mathsf{\Lambda };\varrho ),\left({}^{\mathcal{C}}{D}_{{\mathsf{\Lambda }}_0}^{\Im }\right)\underline{w}(\mathsf{\Lambda };\varrho )\right],0\le \varrho \le 1.$$

3. Fuzzy Fractional Partial Differential Equations

In this section, we present the fuzzy fractional KdV, K(2,2), and mKdV equations using the generalized two-dimensional differential transform method with the fuzzy variational iteration method.

3.1. Generalized Two-Dimensional Differential Transform Method

Consider the real-valued function with two variables denoted by $w(\mathsf{\Lambda },t)$, and assume that it can be written as the product of two real-valued functions with a single parameter each, as shown by the equation $w(\mathsf{\Lambda },t)=f\left(\mathsf{\Lambda }\right)g\left(t\right)$. The function $w(\mathsf{\Lambda },t)$ can be calculated using the properties of generalized two-dimensional DTM as follows:

$$\begin{array}{cc}\hfill w(\mathsf{\Lambda },t)& \hfill =\sum _{\mathit{ȷ}=0}^{\infty }{\mathcal{F}}_{\Im }(\mathit{ȷ})·{(\mathsf{\Lambda }-{\mathsf{\Lambda }}_0)}^{\mathit{ȷ}\Im }\sum _{h=0}^{\infty }{\mathcal{G}}_{\beta }\left(h\right)·{(t-t_0)}^{h\beta }\hfill \\ \hfill & \hfill =\sum _{\mathit{ȷ}=0}^{\infty }\sum _{h=0}^{\infty }{W}_{\Im ,\beta }(\mathit{ȷ},h){(\mathsf{\Lambda }-{\mathsf{\Lambda }}_0)}^{\mathit{ȷ}\Im }{(t-t_0)}^{h\beta }\hfill \end{array}$$

(4)

where $0<\Im ,\beta \le 1$, $W_{\Im ,\beta }(\mathit{ȷ},h)={\mathcal{F}}_{\Im }(\mathit{ȷ}){\mathcal{G}}_{\beta }\left(h\right)$ denote the spectrum of $w(\mathsf{\Lambda },t)$. In the domain of interest, if the real-valued function $w(\mathsf{\Lambda },t)$ is analytic and continuously differentiated with respect to time t, then we define the generalized two-dimensional DTM of the function $w(\mathsf{\Lambda },t)$ as follows:

$$W_{\Im ,\beta }(\mathit{ȷ},h)=\frac{1}{\mathsf{\Gamma }(\Im \mathit{ȷ}+1)\mathsf{\Gamma }(\beta h+1)}{\left[{\left(D_{{\mathsf{\Lambda }}_0}^{\Im }\right)}^{\mathit{ȷ}}{\left(D_{t_0}^{\beta }\right)}^{h}w(\mathsf{\Lambda },t)\right]}_{({\mathsf{\Lambda }}_0,t_0)},$$

(5)

where ${\left(D_{{\mathsf{\Lambda }}_0}^{\Im }\right)}^{\mathit{ȷ}}=D_{{\mathsf{\Lambda }}_0}^{\Im }{D}_{{\mathsf{\Lambda }}_0}^{\Im }\cdots D_{{\mathsf{\Lambda }}_0}^{\Im }.$

The lowercase $u(\mathsf{\Lambda },t)$ denote the original real-valued function while the uppercase $U_{\Im ,\beta }(\mathit{ȷ},h)$ denote the transformed function. The generalized inverse DTM of $W_{\Im ,\beta }(\mathit{ȷ},h)$ is:

$$w(\mathsf{\Lambda },t)=\sum _{\mathit{ȷ}=0}^{\infty }\sum _{h=0}^{\infty }{W}_{\Im ,\beta }(\mathit{ȷ},h)·{(\mathsf{\Lambda }-{\mathsf{\Lambda }}_0)}^{\mathit{ȷ}\Im }{(t-t_0)}^{h\beta }.$$

(6)

In case of $\Im =1$ and $\beta =1$, the generalized two-dimensional DTM (5) reduces to the classical two-dimensional DTM [38]. Applying (5) and (6), some basic properties of the generalized two-dimensional DTM form are proposed.

Theorem 3.

If $w(\mathsf{\Lambda },t)=v(\mathsf{\Lambda },t)\pm q(\mathsf{\Lambda },t),then{W}_{\Im ,\beta }(\mathit{ȷ},h)=V_{\Im ,\beta }(\mathit{ȷ},h)\pm Q_{\Im ,\beta }(\mathit{ȷ},h).$

Theorem 4.

If $w(\mathsf{\Lambda },t)=\lambda v(\mathsf{\Lambda },t)$, then $W_{\Im ,\beta }(\mathit{ȷ},h)=\lambda V_{\Im ,\beta }(\mathit{ȷ},h).$

Theorem 5.

If $w(\mathsf{\Lambda },t)=v(\mathsf{\Lambda },t)q(\mathsf{\Lambda },t),$ then

$$W_{\Im ,\beta }(\mathit{ȷ},h)=\sum _{r=0}^{\mathit{ȷ}}\sum _{s=0}^h{V}_{\Im ,\beta }(r,h-s)W_{\Im ,\beta }(\mathit{ȷ}-r,s).$$

(7)

Theorem 6.

If $w(\mathsf{\Lambda },t)={(\mathsf{\Lambda }-{\mathsf{\Lambda }}_0)}^{ı\Im }{(t-t_0)}^{\mu \Im },$ then $W_{\Im ,\beta }(\mathit{ȷ},h)=\delta (\mathit{ȷ}-ı)\delta (h-m).$

Theorem 7.

If $w(\mathsf{\Lambda },t)=D_{{\mathsf{\Lambda }}_0}^{\Im }v(\mathsf{\Lambda },t)$ and $0<\Im \le 1$, then we obtain

$$W_{\Im ,\beta }(\mathit{ȷ},h)=\frac{\mathsf{\Gamma }(\Im (\mathit{ȷ}+1)+1)}{\mathsf{\Gamma }(\Im \mathit{ȷ}+1)}{V}_{\Im ,\beta }(\mathit{ȷ}+1,h).$$

(8)

3.2. Fuzzy Variational Iteration Method

The following is considered a fuzzy fractional differential equation:

$$\begin{array}{c}\hfill \mathcal{L}\tilde{w}(\mathsf{\Lambda },t)=\tilde{g}(\mathsf{\Lambda },t),t>0,\end{array}$$

(9)

where

$$\begin{array}{c}\hfill \mathcal{L}\tilde{w}(\mathsf{\Lambda },t)=D_t^{\Im }\tilde{w}(\mathsf{\Lambda },t)+\mathcal{L}\tilde{w}(\mathsf{\Lambda },t)+\mathcal{N}u(\mathsf{\Lambda },t),t>0,\end{array}$$

$m\in \mathcal{N},m-1<\Im \le m$, $\mathcal{N}$ denotes the nonlinear operator, $\mathcal{L}$ denotes the linear operator, $\tilde{g}(\mathsf{\Lambda },t;\varrho )=[\underline{g}(\mathsf{\Lambda },t;\varrho ),\stackrel{̲}{g}(\mathsf{\Lambda },t;\varrho )]$ is a known analytic fuzzy-valued function and $D_t^{\Im }$ is the fuzzy Caputo’s fractional derivative of order ℑ.

The initial conditions (9) are given in terms of the field variables and their integer order as follows:

$$\begin{array}{c}\hfill \frac{{\partial }^{\mu }\underline{w}(\mathsf{\Lambda },0)\left(\varrho \right)}{\partial t^{\mu }}={\underline{f}}_{\mu }(\mathsf{\Lambda };\varrho ),\mu =0,1,2,\cdots ,m-1,\\ \hfill \frac{{\partial }^{\mu }\stackrel{̲}{w}(\mathsf{\Lambda },0)\left(\varrho \right)}{\partial t^{\mu }}={\stackrel{̲}{f}}_{\mu }(\mathsf{\Lambda };\varrho ),\mu =0,1,2,\cdots ,m-1.\end{array}$$

where ${\tilde{f}}_{\mu }(\mathsf{\Lambda };\varrho )=[{\underline{f}}_{\mu }(\mathsf{\Lambda };\varrho ),{\stackrel{̲}{f}}_{\mu }(\mathsf{\Lambda };\varrho )]$ denote the fuzzy-valued functions. The solution of

$$\begin{array}{cc}\hfill \underline{w}(\mathsf{\Lambda },t;\varrho )& \hfill =\underset{\mu \to \infty }{lim}{\underline{w}}_n(\mathsf{\Lambda },t;\varrho ),\hfill \\ \hfill \stackrel{̲}{w}(\mathsf{\Lambda },t;\varrho )& \hfill =\underset{\mu \to \infty }{lim}{\stackrel{̲}{w}}_n(\mathsf{\Lambda },t;\varrho ).\hfill \end{array}$$

Equation (9) can be derived from the iteration formula,

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill {\underline{w}}_{\mu +1}(\mathsf{\Lambda },t;\varrho )& \hfill ={\underline{w}}_{\mu }(\mathsf{\Lambda },t;\varrho )-J^{\Im }\left[\mathcal{L}\underline{w}(\mathsf{\Lambda },t;\varrho )-\underline{g}(\mathsf{\Lambda },t;\varrho )\right],0<\Im \le 1,\hfill \\ \hfill {\underline{w}}_{\mu +1}(\mathsf{\Lambda },t;\varrho )& \hfill ={\underline{w}}_{\mu }(\mathsf{\Lambda },t;\varrho )-(\Im -1)J^{\Im }\left[\mathcal{L}\underline{w}(\mathsf{\Lambda },t;\varrho )-\underline{g}(\mathsf{\Lambda },t;\varrho )\right],1<\Im \le 2,\hfill \\ \hfill {\underline{w}}_{\mu +1}(\mathsf{\Lambda },t;\varrho )& \hfill ={\underline{w}}_{\mu }(\mathsf{\Lambda },t;\varrho )-(\Im -2)J^{\Im }\left[\mathcal{L}\underline{w}(\mathsf{\Lambda },t;\varrho )-\underline{g}(\mathsf{\Lambda },t;\varrho )\right],2<\Im \le 3,\hfill \\ \hfill ⋮\\ \hfill {\underline{w}}_{\mu +1}(\mathsf{\Lambda },t;\varrho )& \hfill ={\underline{w}}_{\mu }(\mathsf{\Lambda },t;\varrho )-\frac{(\Im -1)(\Im -2)\cdots (\Im -m+1)}{(\mu -1)!}{J}^{\Im }\left[\mathcal{L}\underline{w}(\mathsf{\Lambda },t;\varrho )-g(\mathsf{\Lambda },t;\varrho )\right],\hfill \\ \hfill & \hfill m-1<\Im \le m,\hfill \end{array}\right.\end{array}$$

(10)

and

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill {\stackrel{̲}{w}}_{\mu +1}(\mathsf{\Lambda },t;\varrho )& \hfill ={\stackrel{̲}{w}}_{\mu }(\mathsf{\Lambda },t;\varrho )-J^{\Im }\left[\mathcal{L}\stackrel{̲}{w}(\mathsf{\Lambda },t;\varrho )-\stackrel{̲}{g}(\mathsf{\Lambda },t;\varrho )\right],0<\Im \le 1,\hfill \\ \hfill {\stackrel{̲}{w}}_{\mu +1}(\mathsf{\Lambda },t;\varrho )& \hfill ={\stackrel{̲}{w}}_{\mu }(\mathsf{\Lambda },t;\varrho )-(\Im -1)J^{\Im }\left[\mathcal{L}\stackrel{̲}{w}(\mathsf{\Lambda },t;\varrho )-\stackrel{̲}{g}(\mathsf{\Lambda },t;\varrho )\right],1<\Im \le 2,\hfill \\ \hfill {\stackrel{̲}{w}}_{\mu +1}(\mathsf{\Lambda },t;\varrho )& \hfill ={\stackrel{̲}{w}}_{\mu }(\mathsf{\Lambda },t;\varrho )-(\Im -2)J^{\Im }\left[\mathcal{L}\stackrel{̲}{w}(\mathsf{\Lambda },t;\varrho )-\stackrel{̲}{g}(\mathsf{\Lambda },t;\varrho )\right],2<\Im \le 3,\hfill \\ \hfill ⋮\\ \hfill {\stackrel{̲}{w}}_{\mu +1}(\mathsf{\Lambda },t;\varrho )& \hfill ={\stackrel{̲}{w}}_{\mu }(\mathsf{\Lambda },t;\varrho )-\frac{(\Im -1)(\Im -2)\cdots (\Im -m+1)}{(\mu -1)!}{J}^{\Im }\left[\mathcal{L}\stackrel{̲}{w}(\mathsf{\Lambda },t;\varrho )-\stackrel{̲}{g}(\mathsf{\Lambda },t;\varrho )\right],\hfill \\ \hfill & \hfill m-1<\Im \le m,\hfill \end{array}\right.\end{array}$$

(11)

where $J^{\Im }$ denotes the fuzzy Riemann–Liouville fractional integral operator of order $\Im >0$, and $D_t^{\Im }$ denotes the fuzzy Caputo fractional derivative, of order $\Im >0.$ Applying the alternative approach of fuzzy VIM as follows

$$\begin{array}{cc}\hfill \underline{w}(\mathsf{\Lambda },t;\varrho )& \hfill =\sum _{\mu =0}^{\infty }{\underline{v}}_{\mu }(\mathsf{\Lambda },t;\varrho ),\hfill \end{array}$$

(12)

$$\begin{array}{cc}\hfill \stackrel{̲}{w}(\mathsf{\Lambda },t;\varrho )& \hfill =\sum _{\mu =0}^{\infty }{\stackrel{̲}{v}}_{\mu }(\mathsf{\Lambda },t;\varrho ).\hfill \end{array}$$

(13)

Using the iteration formula

$$\begin{array}{c}\hfill \left\{\begin{array}{c}\hfill {\underline{v}}_0(\mathsf{\Lambda },t;\varrho )=\sum _{\mu =0}^{m-1}\frac{{\underline{f}}_{\mu }(\mathsf{\Lambda };\varrho )}{\mu !}{t}^{\mu }\hfill \\ \hfill {\underline{v}}_{\mu +1}(\mathsf{\Lambda },t;\varrho )=-\frac{(\Im -1)(\Im -2)(\Im -3)\cdots (\Im -m+1)}{(m-1)!}\hfill \\ \hfill \times J^{\Im }\left(\mathcal{L}\left[\sum _{\varsigma =0}^{\mu }{v}_{\varsigma }(\mathsf{\Lambda },t;\varrho )\right]-g(\mathsf{\Lambda },t;\varrho )\right),\hfill \end{array}\right.\end{array}$$

(14)

and

$$\begin{array}{c}\hfill \left\{\begin{array}{c}\hfill {\stackrel{̲}{v}}_0(\mathsf{\Lambda },t;\varrho )=\sum _{\mu =0}^{m-1}\frac{{\stackrel{̲}{f}}_{\mu }(\mathsf{\Lambda };\varrho )}{\mu !}{t}^{\mu }\hfill \\ \hfill {\stackrel{̲}{v}}_{\mu +1}(\mathsf{\Lambda },t;\varrho )=-\frac{(\Im -1)(\Im -2)(\Im -3)\cdots (\Im -m+1)}{(m-1)!}\hfill \\ \hfill \times J^{\Im }\left(\mathcal{L}\left[\sum _{\varsigma =0}^{\mu }{v}_{\varsigma }(\mathsf{\Lambda },t;\varrho )\right]-g(\mathsf{\Lambda },t;\varrho )\right).\hfill \end{array}.\right.\end{array}$$

(15)

3.3. Applications

In this part, we apply the methods to obtain the solution of fuzzy partial differential equations.

Example 1.

We consider the following fuzzy fractional KdV equation

$$D_t^{\Im }\tilde{w}{\ominus }_{gH}3\odot {\left({\tilde{w}}^2\right)}_{\mathsf{\Lambda }}\oplus {\tilde{w}}_{\mathsf{\Lambda }\mathsf{\Lambda }\mathsf{\Lambda }}=\tilde{0},0<\Im \le 1,$$

(16)

under the initial condition

$$\tilde{w}(\mathsf{\Lambda },0)=[{(1+2\varrho )}^{ı},{(5-2\varrho )}^{ı}]{\ominus }_{gH}6\mathsf{\Lambda },ı=1,2,3,\dots$$

(17)

Case 1. The differential transform method

Applying the two-dimensional DTM of Equation (16), we obtain

$$\begin{array}{cc}\hfill \frac{\mathsf{\Gamma }(\Im (h+1)+1)}{\mathsf{\Gamma }(\Im h+1)}\underline{W}(\mathit{ȷ},h+1;\varrho )& \hfill =3(\mathit{ȷ}+1)\sum _{\iota =0}^{\mathit{ȷ}+1}\sum _{s=0}^h\underline{W}(\iota ,h-s;\varrho )\underline{W}(\mathit{ȷ}-\iota +1,s;\varrho ),\hfill \end{array}$$

$$\begin{array}{cc}\hfill & \hfill -(\mathit{ȷ}+1)(\mathit{ȷ}+2)(\mathit{ȷ}+3)\underline{W}(\mathit{ȷ}+3,h;\varrho )\hfill \end{array}$$

(18)

$$\begin{array}{cc}\hfill \frac{\mathsf{\Gamma }(\mathit{ȷ}(h+1)+1)}{\mathsf{\Gamma }(\Im h+1)}\stackrel{̲}{W}(\mathit{ȷ},h+1;\varrho )& \hfill =3(\mathit{ȷ}+1)\sum _{\iota =0}^{\mathit{ȷ}+1}\sum _{s=0}^h\stackrel{̲}{W}(\iota ,h-s;\varrho )\stackrel{̲}{W}(\mathit{ȷ}-\iota +1,s;\varrho ),\hfill \end{array}$$

$$\begin{array}{cc}\hfill & \hfill -(\mathit{ȷ}+1)(\mathit{ȷ}+2)(\mathit{ȷ}+3)\stackrel{̲}{W}(\mathit{ȷ}+3,h;\varrho ).\hfill \end{array}$$

(19)

Taking the initial condition (17), we obtain

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill \underline{W}(\mathit{ȷ},0)\left(\varrho \right)& \hfill ={(1+2\varrho )}^{ı},\mathit{ȷ}=0,2,3,\cdots \hfill \\ \hfill \underline{W}(1,0)\left(\varrho \right)& \hfill ={(1+2\varrho )}^{ı}-6,\hfill \end{array}\right.\end{array}$$

(20)

and

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill \stackrel{̲}{W}(\mathit{ȷ},0)\left(\varrho \right)& \hfill ={(5-2\varrho )}^{ı},\mathit{ȷ}=0,2,3,\cdots \hfill \\ \hfill \stackrel{̲}{W}(1,0)\left(\varrho \right)& \hfill ={(5-2\varrho )}^{ı}-6.\hfill \end{array}\right.\end{array}$$

(21)

Using (21) into (18), we can obtain some value of $\tilde{W}(\mathit{ȷ},h;\varrho )=\left[\underline{W}(\mathit{ȷ},h;\varrho ),\stackrel{̲}{W}(\mathit{ȷ},h;\varrho )\right]$ as

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill \underline{W}(\mathit{ȷ},1)\left(\varrho \right)& \hfill ={(1+2\varrho )}^{ı},\hfill \\ \hfill \underline{W}(1,1)\left(\varrho \right)& \hfill ={(1+2\varrho )}^{ı}-\left[\frac{6^3}{\mathsf{\Gamma }(\Im +1)}\right],\hfill \\ \hfill \underline{W}(\mathit{ȷ},2)\left(\varrho \right)& \hfill ={(1+2\varrho )}^{ı},\hfill \\ \hfill \underline{W}(1,2)\left(\varrho \right)& \hfill ={(1+2\varrho )}^{ı}-\left[\frac{2·6^5}{\mathsf{\Gamma }(2\Im +1)}\right],\hfill \\ \hfill \underline{W}(\mathit{ȷ},3)\left(\varrho \right)& \hfill ={(1+2\varrho )}^{ı},\hfill \\ \hfill \underline{W}(1,3)\left(\varrho \right)& \hfill ={(1+2\varrho )}^{ı}-\left[\frac{4·6^7}{\mathsf{\Gamma }(3\Im +1)}+\frac{6^7(2\Im +1)}{{\mathsf{\Gamma }}^2(\Im +1)\mathsf{\Gamma }(3\Im +1)}\right],\hfill \end{array}\right.\end{array}$$

(22)

and

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill \stackrel{̲}{W}(\mathit{ȷ},1)\left(\varrho \right)& \hfill ={(5-2\varrho )}^{ı},\hfill \\ \hfill \stackrel{̲}{W}(1,1)\left(\varrho \right)& \hfill ={(5-2\varrho )}^{ı}-\left[\frac{6^3}{\mathsf{\Gamma }(\Im +1)}\right],\hfill \\ \hfill \stackrel{̲}{W}(\mathit{ȷ},2)\left(\varrho \right)& \hfill ={(5-2\varrho )}^{ı},\hfill \\ \hfill \stackrel{̲}{W}(1,2)\left(\varrho \right)& \hfill ={(5-2\varrho )}^{ı}-\left[\frac{2·6^5}{\mathsf{\Gamma }(2\Im +1)}\right],\hfill \\ \hfill \stackrel{̲}{W}(\mathit{ȷ},3)\left(\varrho \right)& \hfill ={(5-2\varrho )}^{ı},\hfill \\ \hfill \stackrel{̲}{W}(1,3)\left(\varrho \right)& \hfill ={(5-2\varrho )}^{ı}-\left[\frac{4·6^7}{\mathsf{\Gamma }(3\Im +1)}+\frac{6^7(2\Im +1)}{{\mathsf{\Gamma }}^2(\Im +1)\mathsf{\Gamma }(3\Im +1)}\right].\hfill \end{array}\right.\end{array}$$

(23)

The solution for $\tilde{W}(\mathit{ȷ},h;\varrho )$ is

$$\begin{array}{cc}\hfill \underline{w}(\mathsf{\Lambda },t;\varrho )& \hfill ={(1+2\varrho )}^{ı}-\left[6\mathsf{\Lambda }+\frac{6^3}{\mathsf{\Gamma }(\Im +1)}\mathsf{\Lambda }{t}^{{}^{\Im }}+\frac{2·6^5}{\mathsf{\Gamma }(2\Im +1)}\mathsf{\Lambda }{t}^{2\Im }\right.\hfill \end{array}$$

$$\begin{array}{cc}\hfill & \hfill \left.+\left[\frac{4·6^7}{\mathsf{\Gamma }(3\Im +1)}+\frac{6^7(2\Im +1)}{{\mathsf{\Gamma }}^2(\Im +1)\mathsf{\Gamma }(3\Im +1)}\right]\mathsf{\Lambda }{t}^{3\Im }+\cdots \right]\hfill \end{array}$$

(24)

$$\begin{array}{cc}\hfill \stackrel{̲}{w}(\mathsf{\Lambda },t;\varrho )& \hfill ={(5-2\varrho )}^{ı}-\left[6\mathsf{\Lambda }+\frac{6^3}{\mathsf{\Gamma }(\Im +1)}\mathsf{\Lambda }{t}^{{}^{\Im }}+\frac{2·6^5}{\mathsf{\Gamma }(2\Im +1)}\mathsf{\Lambda }{t}^{2\Im }\right.\hfill \end{array}$$

$$\begin{array}{cc}\hfill & \hfill \left.+\left[\frac{4·6^7}{\mathsf{\Gamma }(3\Im +1)}+\frac{6^7(2\Im +1)}{{\mathsf{\Gamma }}^2(\Im +1)\mathsf{\Gamma }(3\Im +1)}\right]\mathsf{\Lambda }{t}^{3\Im }+\cdots \right].\hfill \end{array}$$

(25)

We can obtain the solution for $\Im =1,$ as:

$$\begin{array}{c}\hfill \tilde{w}(\mathsf{\Lambda },t;\varrho )=[{(1+2\varrho )}^{ı},{(5-2\varrho )}^{ı}]{\ominus }_{gH}\left[\frac{6\mathsf{\Lambda }}{1-36t}\right],\varrho \in [0,1].\end{array}$$

Case 2. Fuzzy variational iteration method

Applying (14) and (15) as the iteration formula for problem (16), we obtain

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill & \hfill {\underline{v}}_0(\mathsf{\Lambda },t;\varrho )={(1+2\varrho )}^{ı}-6\mathsf{\Lambda },\hfill \\ \hfill & \hfill {\underline{v}}_{\mu +1}(\mathsf{\Lambda },t;\varrho )=-J^{\Im }\left\{D_t^{\Im }\underline{v}(\mathsf{\Lambda },t;\varrho )-3{\left({\underline{v}}^2\right)}_{\mathsf{\Lambda }}(\mathsf{\Lambda },t;\varrho )+{\underline{v}}_{\mathsf{\Lambda }\mathsf{\Lambda }\mathsf{\Lambda }}(\mathsf{\Lambda },t;\varrho )\right\},\hfill \end{array}\end{array}$$

(26)

and

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill & \hfill {\stackrel{̲}{v}}_0(\mathsf{\Lambda },t;\varrho )={(5-2\varrho )}^{ı}-6\mathsf{\Lambda },\hfill \\ \hfill & \hfill {\stackrel{̲}{v}}_{\mu +1}(\mathsf{\Lambda },t;\varrho )=-J^{\Im }\left\{D_t^{\Im }\stackrel{̲}{v}(\mathsf{\Lambda },t;\varrho )-3{\left({\stackrel{̲}{v}}^2\right)}_{\mathsf{\Lambda }}(\mathsf{\Lambda },t;\varrho )+{\stackrel{̲}{v}}_{\mathsf{\Lambda }\mathsf{\Lambda }\mathsf{\Lambda }}(\mathsf{\Lambda },t;\varrho )\right\}.\hfill \end{array}\end{array}$$

(27)

Taking the mentioned iteration formula, we obtain

$$\left\{\begin{array}{cc}\hfill {\underline{v}}_1(\mathsf{\Lambda },t;\varrho )& \hfill ={(1+2\varrho )}^{ı}-\left[\frac{6^3\mathsf{\Lambda }}{\mathsf{\Gamma }(\Im +1)}{t}^{\Im }\right],\hfill \\ \hfill {\underline{v}}_2(\mathsf{\Lambda },t;\varrho )& \hfill ={(1+2\varrho )}^{ı}-\left[\frac{2·6^5\mathsf{\Lambda }}{\mathsf{\Gamma }(2\Im +1)}{t}^{2\Im }+\frac{6^7\mathsf{\Lambda }}{\mathsf{\Gamma }{(\Im +1)}^2}\frac{\mathsf{\Gamma }(2\Im +1)}{\mathsf{\Gamma }(3\Im +1)}{t}^{3\Im }\right],\hfill \\ \hfill {\underline{v}}_3(\mathsf{\Lambda },t;\varrho )& \hfill ={(1+2\varrho )}^{ı}-\left[\frac{4·6^7\mathsf{\Lambda }}{\mathsf{\Gamma }(3\Im +1)}{t}^{3\Im }\right.\hfill \\ \hfill & \hfill +\frac{\mathsf{\Gamma }(3\Im +1)}{\mathsf{\Gamma }(4\Im +1)}\left[\frac{2·6^9\mathsf{\Lambda }}{\mathsf{\Gamma }{(\Im +1)}^2}\frac{\mathsf{\Gamma }(2\Im +1)}{\mathsf{\Gamma }(3\Im +1)}+\frac{4·6^9\mathsf{\Lambda }}{\mathsf{\Gamma }(\Im +1)\mathsf{\Gamma }(2\Im +1)}\right]t^{4\Im },\hfill \\ \hfill & \hfill +\frac{\mathsf{\Gamma }(4\Im +1)}{\mathsf{\Gamma }(5\Im +1)}\left[\frac{4·6^{11}\mathsf{\Lambda }}{\mathsf{\Gamma }{(2\Im +1)}^2}+\frac{4·6^{11}\mathsf{\Lambda }}{\mathsf{\Gamma }{(\Im +1)}^3}\frac{\mathsf{\Gamma }(2\Im +1)}{\mathsf{\Gamma }(3\Im +1)}\right]t^{5\Im }\hfill \\ \hfill & \hfill +\frac{4·6^{13}\mathsf{\Lambda }}{\mathsf{\Gamma }{(\Im +1)}^2}\frac{\mathsf{\Gamma }(5\Im +1)}{\mathsf{\Gamma }(3\Im +1)\mathsf{\Gamma }(6\Im +1)}{t}^{6\Im }\hfill \\ \hfill & \hfill \left.+\frac{6^{15}\mathsf{\Lambda }}{\mathsf{\Gamma }{(\Im +1)}^4}\frac{\mathsf{\Gamma }{(2\Im +1)}^2\mathsf{\Gamma }{(3\Im +1)}^2}{\mathsf{\Gamma }{(6\Im +1)}^2\mathsf{\Gamma }(7\Im +1)}{t}^{7\Im }\right]\hfill \\ \hfill ⋮\end{array}\right.$$

and

$$\left\{\begin{array}{cc}\hfill {\stackrel{̲}{v}}_1(\mathsf{\Lambda },t;\varrho )& \hfill ={(5-2\varrho )}^{ı}-\left[\frac{6^3\mathsf{\Lambda }}{\mathsf{\Gamma }(\Im +1)}{t}^{\Im }\right],\hfill \\ \hfill {\stackrel{̲}{v}}_2(\mathsf{\Lambda },t;\varrho )& \hfill ={(5-2\varrho )}^{ı}-\left[\frac{2·6^5\mathsf{\Lambda }}{\mathsf{\Gamma }(2\Im +1)}{t}^{2\Im }+\frac{6^7\mathsf{\Lambda }}{\mathsf{\Gamma }{(\Im +1)}^2}\frac{\mathsf{\Gamma }(2\Im +1)}{\mathsf{\Gamma }(3\Im +1)}{t}^{3\Im }\right],\hfill \\ \hfill {\stackrel{̲}{v}}_3(\mathsf{\Lambda },t;\varrho )& \hfill ={(5-2\varrho )}^{ı}-\left[\frac{4·6^7\mathsf{\Lambda }}{\mathsf{\Gamma }(3\Im +1)}{t}^{3\Im }\right.\hfill \\ \hfill & \hfill +\frac{\mathsf{\Gamma }(3\Im +1)}{\mathsf{\Gamma }(4\Im +1)}\left[\frac{2·6^9\mathsf{\Lambda }}{\mathsf{\Gamma }{(\Im +1)}^2}\frac{\mathsf{\Gamma }(2\Im +1)}{\mathsf{\Gamma }(3\Im +1)}+\frac{4·6^9\mathsf{\Lambda }}{\mathsf{\Gamma }(\Im +1)\mathsf{\Gamma }(2\Im +1)}\right]t^{4\Im },\hfill \\ \hfill & \hfill +\frac{\mathsf{\Gamma }(4\Im +1)}{\mathsf{\Gamma }(5\Im +1)}\left[\frac{4·6^{11}\mathsf{\Lambda }}{\mathsf{\Gamma }{(2\Im +1)}^2}+\frac{4·6^{11}\mathsf{\Lambda }}{\mathsf{\Gamma }{(\Im +1)}^3}\frac{\mathsf{\Gamma }(2\Im +1)}{\mathsf{\Gamma }(3\Im +1)}\right]t^{5\Im }\hfill \\ \hfill & \hfill +\frac{4·6^{13}\mathsf{\Lambda }}{\mathsf{\Gamma }{(\Im +1)}^2}\frac{\mathsf{\Gamma }(5\Im +1)}{\mathsf{\Gamma }(3\Im +1)\mathsf{\Gamma }(6\Im +1)}{t}^{6\Im }\hfill \\ \hfill & \hfill \left.+\frac{6^{15}\mathsf{\Lambda }}{\mathsf{\Gamma }{(\Im +1)}^4}\frac{\mathsf{\Gamma }{(2\Im +1)}^2\mathsf{\Gamma }{(3\Im +1)}^2}{\mathsf{\Gamma }{(6\Im +1)}^2\mathsf{\Gamma }(7\Im +1)}{t}^{7\Im }\right]\hfill \\ \hfill ⋮.\end{array}\right.$$

For $\Im =1,$ we obtain the approximate solution as follows:

$$\begin{array}{c}\hfill \underline{u}(\mathsf{\Lambda },t;\varrho )\approx \sum _{\mu =0}^3{\underline{v}}_{\mu }(\mathsf{\Lambda },t;\varrho )={(1+2\varrho )}^{ı}-\left[6\mathsf{\Lambda }\left(1+36t+{36}^2{t}^2+\cdots \right)\right],\end{array}$$

(28)

$$\begin{array}{c}\hfill \stackrel{̲}{u}(\mathsf{\Lambda },t;\varrho )\approx \sum _{\mu =0}^3{\stackrel{̲}{v}}_{\mu }(\mathsf{\Lambda },t;\varrho )={(5-2\varrho )}^{ı}-\left[6\mathsf{\Lambda }\left(1+36t+{36}^2{t}^2+\cdots \right)\right],\end{array}$$

(29)

after some steps, the exact solution is obtained as follows:

$$\begin{array}{c}\hfill \underline{u}(\mathsf{\Lambda },t;\varrho )=\sum _{\mu =0}^{\infty }{\underline{v}}_{\mu }(\mathsf{\Lambda },t;\varrho )={(1+2\varrho )}^{ı}-\left[6\mathsf{\Lambda }\left(1+36t+{36}^2{t}^2+\cdots \right)\right]\end{array}$$

(30)

$$\begin{array}{c}\hfill \stackrel{̲}{u}(\mathsf{\Lambda },t;\varrho )=\sum _{\mu =0}^{\infty }{\stackrel{̲}{v}}_{\mu }(\mathsf{\Lambda },t;\varrho )={(5-2\varrho )}^{ı}-\left[6\mathsf{\Lambda }\left(1+36t+{36}^2{t}^2+\cdots \right)\right]\end{array}$$

(31)

Then, we obtain

$$\begin{array}{c}\hfill \tilde{w}(\mathsf{\Lambda },t;\varrho )=[{(1+2\varrho )}^{ı},{(5-2\varrho )}^{ı}]{\ominus }_{gH}\left[\frac{6\mathsf{\Lambda }}{1-36t}\right],\varrho \in [0,1].\end{array}$$

Meanwhile, the DTM and fuzzy VIM lower and upper solution of Equation (16) are demonstrated in Figure 1a, where $\mathsf{\Lambda }=0.2,t=0.3$ and $ı=1$ show the precision and compliance with the proposed theory.

Figure 1. The exact lower and upper solutions of Equation (16) at $\left(\mathbf{a}\right)\mathsf{\Lambda }=0.2,t=0.3,ı=1,$ for Equation (32) at $\left(\mathbf{b}\right)\mathsf{\Lambda }=0.00001,t=0.5,ı=2,$ and for Equation (50) at $\left(\mathbf{c}\right)\mathsf{\Lambda }=0.3,t=0.7,ı=3$.

Example 2.

We consider the following fuzzy fractional $K(2,2)$ equation

$$D_t^{\Im }\tilde{w}\oplus {\left({\tilde{w}}^2\right)}_{\mathsf{\Lambda }}\oplus {\left({\tilde{w}}^2\right)}_{\mathsf{\Lambda }\mathsf{\Lambda }\mathsf{\Lambda }}=\tilde{0},0<\Im \le 1,$$

(32)

under the initial condition

$$\tilde{w}(\mathsf{\Lambda },0)=\left[{(0.1+0.1\Im )}^{ı},{(0.3-0.1\Im )}^{ı}\right]\oplus \mathsf{\Lambda },ı=1,2,3,\cdots .$$

(33)

Case 1. The differential transform method

Using the two-dimensional DTM to (32), we obtain

$$\begin{array}{cc}\hfill \frac{\mathsf{\Gamma }(\Im (h+1)+1)}{\mathsf{\Gamma }(\Im h+1)}\underline{W}(\mathit{ȷ},h+1;\varrho )& \hfill =-(\mathit{ȷ}+1)\sum _{\iota =0}^{\mathit{ȷ}+1}\sum _{s=0}^h\underline{W}(\iota ,h-s;\varrho )\underline{W}(\mathit{ȷ}-\iota +1,s;\varrho ),\hfill \end{array}$$

$$\begin{array}{cc}\hfill & \hfill -(\mathit{ȷ}+1)(\mathit{ȷ}+2)(\mathit{ȷ}+3)\sum _{\iota =0}^{\mathit{ȷ}+3}\sum _{s=0}^h\underline{W}(\iota ,h-s;\varrho )\underline{W}(\mathit{ȷ}-\iota +3,s;\varrho ),\hfill \end{array}$$

(34)

$$\begin{array}{cc}\hfill \frac{\mathsf{\Gamma }(\Im (h+1)+1)}{\mathsf{\Gamma }(\Im h+1)}\stackrel{̲}{W}(\mathit{ȷ},h+1;\varrho )& \hfill =-(\mathit{ȷ}+1)\sum _{\iota =0}^{\mathit{ȷ}+1}\sum _{s=0}^h\stackrel{̲}{W}(\iota ,h-s;\varrho )\stackrel{̲}{W}(\mathit{ȷ}-\iota +1,s;\varrho ),\hfill \end{array}$$

$$\begin{array}{cc}\hfill & \hfill -(\mathit{ȷ}+1)(\mathit{ȷ}+2)(\mathit{ȷ}+3)\sum _{\iota =0}^{\mathit{ȷ}+3}\sum _{s=0}^h\stackrel{̲}{W}(\iota ,h-s;\varrho )\stackrel{̲}{W}(\mathit{ȷ}-\iota +3,s;\varrho ).\hfill \end{array}$$

(35)

Taking the initial condition (33), we obtain

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill \underline{W}(\mathit{ȷ},0)\left(\varrho \right)& \hfill ={(0.1+0.1\Im )}^{ı},\mathit{ȷ}=0,2,3,\cdots \hfill \\ \hfill \underline{W}(1,0)\left(\varrho \right)& \hfill =1+{(0.1+0.1\Im )}^{ı},\hfill \end{array}\right.\end{array}$$

(36)

and

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill \stackrel{̲}{W}(\mathit{ȷ},0)\left(\varrho \right)& \hfill ={(0.3-0.1\Im )}^{ı},\mathit{ȷ}=0,2,3,\cdots \hfill \\ \hfill \stackrel{̲}{W}(1,0)\left(\varrho \right)& \hfill =1+{(0.3-0.1\Im )}^{ı}.\hfill \end{array}\right.\end{array}$$

(37)

Using (37) into (34), we can obtain some value of $\tilde{W}(k,h;\varrho )=\left[\underline{W}(k,h;\varrho ),\stackrel{̲}{W}(k,h;\varrho )\right]$ as

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill \underline{W}(\mathit{ȷ},1)\left(\varrho \right)& \hfill ={(0.1+0.1\varrho )}^{ı},\hfill \\ \hfill \underline{W}(1,1)\left(\varrho \right)& \hfill ={(0.1+0.1\varrho )}^{ı}+\left[\frac{-2}{\mathsf{\Gamma }(\Im +1)}\right],\hfill \\ \hfill \underline{W}(\mathit{ȷ},2)\left(\varrho \right)& \hfill ={(0.1+0.1\varrho )}^{ı},\hfill \\ \hfill \underline{W}(1,2)\left(\varrho \right)& \hfill ={(0.1+0.1\varrho )}^{ı}+\left[\frac{2^3}{\mathsf{\Gamma }(2\Im +1)}\right],\hfill \\ \hfill \underline{W}(\mathit{ȷ},3)\left(\varrho \right)& \hfill ={(0.1+0.1\varrho )}^{ı},\hfill \\ \hfill \underline{W}(1,3)\left(\varrho \right)& \hfill ={(0.1+0.1\varrho )}^{ı}+\left[-\frac{2^5}{\mathsf{\Gamma }(3\Im +1)}-\frac{2^3\mathsf{\Gamma }(2\Im +1)}{{\mathsf{\Gamma }}^2(\Im +1)\mathsf{\Gamma }(3\Im +1)}\right],\hfill \end{array}\right.\end{array}$$

(38)

and

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill \stackrel{̲}{W}(\mathit{ȷ},1)\left(\varrho \right)& \hfill ={(0.3-0.1\varrho )}^{ı},\hfill \\ \hfill \stackrel{̲}{W}(1,1)\left(\varrho \right)& \hfill ={(0.3-0.1\varrho )}^{ı}+\left[\frac{-2}{\mathsf{\Gamma }(\Im +1)}\right],\hfill \\ \hfill \stackrel{̲}{W}(\mathit{ȷ},2)\left(\varrho \right)& \hfill ={(0.3-0.1\varrho )}^{ı},\hfill \\ \hfill \stackrel{̲}{W}(1,2)\left(\varrho \right)& \hfill ={(0.3-0.1\varrho )}^{ı}+\left[\frac{2^3}{\mathsf{\Gamma }(2\Im +1)}\right],\hfill \\ \hfill \stackrel{̲}{W}(\mathit{ȷ},3)\left(\varrho \right)& \hfill ={(0.3-0.1\varrho )}^{ı},\hfill \\ \hfill \stackrel{̲}{W}(1,3)\left(\varrho \right)& \hfill ={(0.3-0.1\varrho )}^{ı}+\left[-\frac{2^5}{\mathsf{\Gamma }(3\Im +1)}-\frac{2^3\mathsf{\Gamma }(2\Im +1)}{{\mathsf{\Gamma }}^2(\Im +1)\mathsf{\Gamma }(3\Im +1)}\right].\hfill \end{array}\right.\end{array}$$

(39)

The solution for $\tilde{W}(\mathit{ȷ},h;\varrho )$ is

$$\begin{array}{cc}\hfill \underline{w}(\mathsf{\Lambda },t;\varrho )& \hfill ={(0.1+0.1\Im )}^{ı}+\left[\mathsf{\Lambda }-\frac{2\mathsf{\Lambda }{t}^{\Im }}{\mathsf{\Gamma }(\Im +1)}+\frac{2^3\mathsf{\Lambda }{t}^{2\Im }}{\mathsf{\Gamma }(2\Im +1)}\right.\hfill \end{array}$$

$$\begin{array}{cc}\hfill & \hfill \left.-\left[\frac{2^5}{\mathsf{\Gamma }(3\Im +1)}+\frac{2^3\mathsf{\Gamma }(2\Im +1)}{{\mathsf{\Gamma }}^2(\Im +1)\mathsf{\Gamma }(3\Im +1)}\right]\mathsf{\Lambda }{t}^{3\Im }+\cdots \right],\hfill \end{array}$$

(40)

$$\begin{array}{cc}\hfill \stackrel{̲}{w}(\mathsf{\Lambda },t;\varrho )& \hfill ={(0.3-0.1\Im )}^{ı}+\left[\mathsf{\Lambda }-\frac{2\mathsf{\Lambda }{t}^{\Im }}{\mathsf{\Gamma }(\Im +1)}+\frac{2^3\mathsf{\Lambda }{t}^{2\Im }}{\mathsf{\Gamma }(2\Im +1)}\right.\hfill \end{array}$$

$$\begin{array}{cc}\hfill & \hfill \left.-\left[\frac{2^5}{\mathsf{\Gamma }(3\Im +1)}+\frac{2^3\mathsf{\Gamma }(2\Im +1)}{{\mathsf{\Gamma }}^2(\Im +1)\mathsf{\Gamma }(3\Im +1)}\right]\mathsf{\Lambda }{t}^{3\Im }+\cdots \right].\hfill \end{array}$$

(41)

For $\Im =1,$ we obtained the exact solutions as

$$\begin{array}{c}\hfill \tilde{w}(\mathsf{\Lambda },t;\varrho )=[{(0.1+0.1\varrho )}^{ı},{(0.3-0.1\varrho )}^{ı}]\oplus \left[\frac{\mathsf{\Lambda }}{1+2t}\right],0\le \varrho \le 1.\end{array}$$

Case 2. Fuzzy variational iteration method

Using the fuzzy iteration formula for problem (32), we obtain

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill & \hfill {\underline{v}}_0(\mathsf{\Lambda },t;\varrho )={(0.1+0.1\varrho )}^{ı}+\mathsf{\Lambda },\hfill \\ \hfill & \hfill {\underline{v}}_{\mu +1}(\mathsf{\Lambda },t;\varrho )=-J^{\Im }\left\{D_t^{\Im }\underline{v}(\mathsf{\Lambda },t;\varrho )+{\left({\underline{v}}^2\right)}_{\mathsf{\Lambda }}(\mathsf{\Lambda },t;\varrho )+{\left({\underline{v}}^2\right)}_{\mathsf{\Lambda }\mathsf{\Lambda }\mathsf{\Lambda }}(\mathsf{\Lambda },t;\varrho )\right\},\hfill \end{array}\end{array}$$

(42)

and

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill & \hfill {\stackrel{̲}{v}}_0(\mathsf{\Lambda },t;\varrho )={(0.3-0.1\varrho )}^{ı}+\mathsf{\Lambda },\hfill \\ \hfill & \hfill {\stackrel{̲}{v}}_{\mu +1}(\mathsf{\Lambda },t;\varrho )=-J^{\Im }\left\{D_t^{\Im }\stackrel{̲}{v}(\mathsf{\Lambda },t;\varrho )+{\left({\stackrel{̲}{v}}^2\right)}_{\mathsf{\Lambda }}(\mathsf{\Lambda },t;\varrho )+{\left({\stackrel{̲}{v}}^2\right)}_{\mathsf{\Lambda }\mathsf{\Lambda }\mathsf{\Lambda }}(\mathsf{\Lambda },t;\varrho )\right\}.\hfill \end{array}\end{array}$$

(43)

Taking the mentioned iteration formula, we obtain

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill {\underline{v}}_1(\mathsf{\Lambda },t;\varrho )& \hfill ={(0.1+0.1\varrho )}^{ı}-\left[\frac{2\mathsf{\Lambda }}{\mathsf{\Gamma }(\Im +1)}{t}^{\Im }\right],\hfill \\ \hfill {\underline{v}}_2(\mathsf{\Lambda },t;\varrho )& \hfill ={(0.1+0.1\varrho )}^{ı}+\left[\frac{2^3\mathsf{\Lambda }}{\mathsf{\Gamma }(2\Im +1)}{t}^{2\Im }-\frac{2^3\mathsf{\Lambda }}{\mathsf{\Gamma }{(\Im +1)}^2}\frac{\mathsf{\Gamma }(2\Im +1)}{\mathsf{\Gamma }(3\Im +1)}{t}^{3\Im }\right],\hfill \\ \hfill ⋮\end{array}\right.\end{array}$$

(44)

and

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill {\stackrel{̲}{v}}_1(\mathsf{\Lambda },t;\varrho )& \hfill ={(0.3-0.1\varrho )}^{ı}-\left[\frac{2\mathsf{\Lambda }}{\mathsf{\Gamma }(\Im +1)}{t}^{\Im }\right],\hfill \\ \hfill {\stackrel{̲}{v}}_2(\mathsf{\Lambda },t;\varrho )& \hfill ={(0.3-0.1\varrho )}^{ı}+\left[\frac{2^3\mathsf{\Lambda }}{\mathsf{\Gamma }(2\Im +1)}{t}^{2\Im }-\frac{2^3\mathsf{\Lambda }}{\mathsf{\Gamma }{(\Im +1)}^2}\frac{\mathsf{\Gamma }(2\Im +1)}{\mathsf{\Gamma }(3\Im +1)}{t}^{3\Im }\right],\hfill \\ \hfill ⋮.\end{array}\right.\end{array}$$

(45)

For $\Im =1,$ we obtain the approximate solution as follows:

$$\begin{array}{cc}\hfill \underline{w}(\mathsf{\Lambda },t;\varrho )\approx \sum _{\mu =0}^3{\underline{v}}_{\mu }(\mathsf{\Lambda },t;\varrho )& \hfill ={(0.1+0.1\varrho )}^{ı}+\left[\mathsf{\Lambda }\left(1-2t+4t^2+\cdots \right)\right]\hfill \end{array}$$

(46)

$$\begin{array}{cc}\hfill \stackrel{̲}{w}(\mathsf{\Lambda },t;\varrho )\approx \sum _{\mu =0}^3{\stackrel{̲}{v}}_{\mu }(\mathsf{\Lambda },t;\varrho )& \hfill ={(0.3-0.1\varrho )}^{ı}+\left[\mathsf{\Lambda }\left(1-2t+4t^2+\cdots \right)\right]\hfill \end{array}$$

(47)

The exact solution is obtained as:

$$\begin{array}{c}\hfill \underline{w}(\mathsf{\Lambda },t;\varrho )=\sum _{\mu =0}^{\infty }{\underline{v}}_{\mu }(\mathsf{\Lambda },t;\varrho )={(0.1+0.1\varrho )}^{ı}+\left[\mathsf{\Lambda }\left(1-2t+4t^2+\cdots \right)\right]\end{array}$$

(48)

$$\begin{array}{c}\hfill \stackrel{̲}{w}(\mathsf{\Lambda },t;\varrho )=\sum _{\mu =0}^3{\stackrel{̲}{v}}_{\mu }(\mathsf{\Lambda },t;\varrho )={(0.3-0.1\varrho )}^{ı}+\left[\mathsf{\Lambda }\left(1-2t+4t^2+\cdots \right)\right]\end{array}$$

(49)

We obtain

$$\begin{array}{c}\hfill \tilde{w}(\mathsf{\Lambda },t;\varrho )=\left[{(0.1+0.1\varrho )}^{ı},{(0.3-0.1\varrho )}^{ı}\right]\oplus \left[\frac{\mathsf{\Lambda }}{1+2t}\right],0\le \varrho \le 1.\end{array}$$

The DTM and fuzzy VIM lower and upper solution of Equation (32) are demonstrated in Figure 1b, where $\mathsf{\Lambda }=0.00001,t=0.5,$ and $ı=2$ show the precision and compliance with the proposed theory.

Example 3.

We consider the following fuzzy modified fractional KdV (mKdV) equation

$$D_t^{\Im }\tilde{w}\oplus \frac{1}{2}\odot {\left({\tilde{w}}^2\right)}_{\mathsf{\Lambda }}{\ominus }_{gH}{\tilde{w}}_{\mathsf{\Lambda }\mathsf{\Lambda }}=\tilde{0},0<\Im \le 1,$$

(50)

under the initial condition

$$\tilde{w}(\mathsf{\Lambda },0)=\left[{(0.2+0.2\varrho )}^{ı},{(0.6-0.2\varrho )}^{ı}\right]{\ominus }_{gH}\mathsf{\Lambda },ı=1,2,3,\cdots .$$

(51)

Case 1. The differential transform method.

Using the two-dimensional DTM to (50), we obtain

$$\begin{array}{cc}\hfill \frac{\mathsf{\Gamma }(\Im (h+1)+1)}{\mathsf{\Gamma }(\Im h+1)}\underline{W}(\mathit{ȷ},h+1;\varrho )& \hfill =-\frac{1}{2}(\mathit{ȷ}+1)\sum _{\iota =0}^{\mathit{ȷ}+1}\sum _{s=0}^h\underline{W}(\iota ,h-s;\varrho )\underline{W}(\mathit{ȷ}-\iota +1,s;\varrho ),\hfill \end{array}$$

$$\begin{array}{cc}\hfill & \hfill +(\mathit{ȷ}+1)(\mathit{ȷ}+2)U(\mathit{ȷ}+2,h;\varrho )\hfill \end{array}$$

(52)

$$\begin{array}{cc}\hfill \frac{\mathsf{\Gamma }(\Im (h+1)+1)}{\mathsf{\Gamma }(\Im h+1)}\stackrel{̲}{W}(\mathit{ȷ},h+1;\varrho )& \hfill =-\frac{1}{2}(\mathit{ȷ}+1)\sum _{\iota =0}^{\mathit{ȷ}+1}\sum _{s=0}^h\stackrel{̲}{W}(\iota ,h-s;\varrho )\stackrel{̲}{W}(\mathit{ȷ}-\iota +1,s;\varrho ),\hfill \end{array}$$

$$\begin{array}{cc}\hfill & \hfill +(\mathit{ȷ}+1)(\mathit{ȷ}+2)U(\mathit{ȷ}+2,h;\varrho ).\hfill \end{array}$$

(53)

Using the initial condition (51), we can obtain

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill \underline{W}(\mathit{ȷ},0)\left(\varrho \right)& \hfill ={(0.2+0.2\varrho )}^{ı},\mathit{ȷ}=0,2,3,\cdots \hfill \\ \hfill \underline{W}(1,0)\left(\varrho \right)& \hfill ={(0.2+0.2\varrho )}^{ı}-1,\hfill \end{array}\right.\end{array}$$

(54)

and

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill \stackrel{̲}{W}(\mathit{ȷ},0)\left(\varrho \right)& \hfill ={(0.6-0.2\varrho )}^{ı},\mathit{ȷ}=0,2,3,\cdots \hfill \\ \hfill \stackrel{̲}{W}(1,0)\left(\varrho \right)& \hfill ={(0.6-0.2\varrho )}^{ı}-1.\hfill \end{array}\right.\end{array}$$

(55)

From (55) into (52), we obtain

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill \underline{W}(\mathit{ȷ},1)\left(\varrho \right)& \hfill ={(0.2+0.2\varrho )}^{ı},\hfill \\ \hfill \underline{W}(1,1)\left(\varrho \right)& \hfill ={(0.2+0.2\varrho )}^{ı}-\left[\frac{-1}{\mathsf{\Gamma }(\Im +1)}\right],\hfill \\ \hfill \underline{W}(\mathit{ȷ},2)\left(\varrho \right)& \hfill ={(0.2+0.2\varrho )}^{ı},\hfill \\ \hfill \underline{W}(1,2)\left(\varrho \right)& \hfill ={(0.2+0.2\varrho )}^{ı}-\left[\frac{2}{\mathsf{\Gamma }(2\Im +1)}\right],\hfill \\ \hfill \underline{W}(\mathit{ȷ},3)\left(\varrho \right)& \hfill ={(0.2+0.2\varrho )}^{ı},\hfill \\ \hfill \underline{W}(1,3)\left(\varrho \right)& \hfill ={(0.2+0.2\varrho )}^{ı}-\left[-\frac{4}{\mathsf{\Gamma }(3\Im +1)}-\frac{\mathsf{\Gamma }(2\Im +1)}{{\mathsf{\Gamma }}^2(\Im +1)\mathsf{\Gamma }(3\Im +1)}\right],\hfill \end{array}\right.\end{array}$$

(56)

and

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill \stackrel{̲}{W}(\mathit{ȷ},1)\left(\varrho \right)& \hfill ={(0.6-0.2\varrho )}^{ı},\hfill \\ \hfill \stackrel{̲}{W}(1,1)\left(\varrho \right)& \hfill ={(0.6-0.2\varrho )}^{ı}-\left[\frac{-1}{\mathsf{\Gamma }(\Im +1)}\right],\hfill \\ \hfill \stackrel{̲}{W}(\mathit{ȷ},2)\left(\varrho \right)& \hfill ={(0.6-0.2\varrho )}^{ı},\hfill \\ \hfill \stackrel{̲}{W}(1,2)\left(\varrho \right)& \hfill ={(0.6-0.2\varrho )}^{ı}-\left[\frac{2}{\mathsf{\Gamma }(2\Im +1)}\right],\hfill \\ \hfill \stackrel{̲}{W}(\mathit{ȷ},3)\left(\varrho \right)& \hfill ={(0.6-0.2\varrho )}^{ı},\hfill \\ \hfill \stackrel{̲}{W}(1,3)\left(\varrho \right)& \hfill ={(0.6-0.2\varrho )}^{ı}-\left[-\frac{4}{\mathsf{\Gamma }(3\Im +1)}-\frac{\mathsf{\Gamma }(2\Im +1)}{{\mathsf{\Gamma }}^2(\Im +1)\mathsf{\Gamma }(3\Im +1)}\right].\hfill \end{array}\right.\end{array}$$

(57)

The solution for $\tilde{W}(\mathit{ȷ},h;\varrho )$ is

$$\begin{array}{cc}\hfill \underline{w}(\mathsf{\Lambda },t;\varrho )& \hfill ={(0.2+0.2\varrho )}^{ı}-\left[\mathsf{\Lambda }-\frac{\mathsf{\Lambda }{t}^{\Im }}{\mathsf{\Gamma }(\Im +1)}+\frac{2\mathsf{\Lambda }{t}^{2\Im }}{\mathsf{\Gamma }(2\Im +1)}\right.\hfill \end{array}$$

$$\begin{array}{cc}\hfill & \hfill \left.-\left[\frac{4}{\mathsf{\Gamma }(3\Im +1)}+\frac{\mathsf{\Gamma }(2\Im +1)}{{\mathsf{\Gamma }}^2(\Im +1)\mathsf{\Gamma }(3\Im +1)}\right]\mathsf{\Lambda }{t}^{3\Im }+\cdots \right],\hfill \\ \hfill \stackrel{̲}{w}(\mathsf{\Lambda },t;\varrho )& \hfill ={(0.6-0.2\varrho )}^{ı}-\left[\mathsf{\Lambda }-\frac{\mathsf{\Lambda }{t}^{\Im }}{\mathsf{\Gamma }(\Im +1)}+\frac{2\mathsf{\Lambda }{t}^{2\Im }}{\mathsf{\Gamma }(2\Im +1)}\right.\hfill \end{array}$$

(58)

$$\begin{array}{cc}\hfill & \hfill \left.-\left[\frac{4}{\mathsf{\Gamma }(3\Im +1)}+\frac{\mathsf{\Gamma }(2\Im +1)}{{\mathsf{\Gamma }}^2(\Im +1)\mathsf{\Gamma }(3\Im +1)}\right]\mathsf{\Lambda }{t}^{3\Im }+\cdots \right].\hfill \end{array}$$

(59)

We can obtain the solution for $\Im =1$ as follows:

$$\begin{array}{c}\hfill \tilde{w}(\mathsf{\Lambda },t;\varrho )=[{(0.2+0.2\varrho )}^{ı},{(0.6-0.2\varrho )}^{ı}]{\ominus }_{gH}\left[\frac{\mathsf{\Lambda }}{1+t}\right],0\le \varrho \le 1.\end{array}$$

Case 2. Fuzzy variational iteration method

Using the fuzzy iteration formula for problem (50), we deduce that

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill & \hfill {\underline{v}}_0(\mathsf{\Lambda },t;\varrho )={(0.2+0.2\varrho )}^{ı}-\mathsf{\Lambda },\hfill \\ \hfill & \hfill {\underline{v}}_{\mu +1}(\mathsf{\Lambda },t;\varrho )=-J^{\Im }\left\{D_t^{\Im }\underline{v}(\mathsf{\Lambda },t;\varrho )+\frac{1}{2}{\left({\underline{v}}^2\right)}_{\mathsf{\Lambda }}(\mathsf{\Lambda },t;\varrho )+{\underline{v}}_{\mathsf{\Lambda }\mathsf{\Lambda }}(\mathsf{\Lambda },t;\varrho )\right\},\hfill \end{array}\end{array}$$

(60)

and

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill & \hfill {\stackrel{̲}{v}}_0(\mathsf{\Lambda },t;\varrho )={(0.6-0.2\varrho )}^{ı}-\mathsf{\Lambda },\hfill \\ \hfill & \hfill {\stackrel{̲}{v}}_{\mu +1}(\mathsf{\Lambda },t;\varrho )=-J^{\Im }\left\{D_t^{\Im }\stackrel{̲}{v}(\mathsf{\Lambda },t;\varrho )+\frac{1}{2}{\left({\stackrel{̲}{v}}^2\right)}_{\mathsf{\Lambda }}(\mathsf{\Lambda },t;\varrho )+{\stackrel{̲}{v}}_{\mathsf{\Lambda }\mathsf{\Lambda }}(\mathsf{\Lambda },t;\varrho )\right\}.\hfill \end{array}\end{array}$$

(61)

Using the mentioned iteration formula, we infer that

$$\left\{\begin{array}{cc}\hfill {\underline{v}}_1(\mathsf{\Lambda },t;\varrho )& \hfill ={(0.2+0.2\varrho )}^{ı}+\left[\frac{\mathsf{\Lambda }}{\mathsf{\Gamma }(\Im +1)}{t}^{\Im }\right],\hfill \\ \hfill {\underline{v}}_2(\mathsf{\Lambda },t;\varrho )& \hfill ={(0.2+0.2\varrho )}^{ı}-\left[\frac{2\mathsf{\Lambda }}{\mathsf{\Gamma }(2\Im +1)}{t}^{2\Im }-\frac{\mathsf{\Lambda }}{\mathsf{\Gamma }{(\Im +1)}^2}\frac{\mathsf{\Gamma }(2\Im +1)}{\mathsf{\Gamma }(3\Im +1)}{t}^{3\Im }\right],\hfill \\ \hfill {\underline{v}}_3(\mathsf{\Lambda },t;\varrho )& \hfill ={(0.2+0.2\varrho )}^{ı}-\left[-\frac{2^2\mathsf{\Lambda }}{\mathsf{\Gamma }(3\Im +1)}{t}^{3\Im }\right.\hfill \\ \hfill & \hfill +\frac{\mathsf{\Gamma }(3\Im +1)}{\mathsf{\Gamma }(4\Im +1)}\left[\frac{2\mathsf{\Lambda }}{\mathsf{\Gamma }{(\Im +1)}^2}\frac{\mathsf{\Gamma }(2\Im +1)}{\mathsf{\Gamma }(3\Im +1)}+\frac{2^2\mathsf{\Lambda }}{\mathsf{\Gamma }(\Im +1)\mathsf{\Gamma }(2\Im +1)}\right]t^{4\Im },\hfill \\ \hfill & \hfill -\frac{\mathsf{\Gamma }(4\Im +1)}{\mathsf{\Gamma }(5\Im +1)}\left[\frac{2^2\mathsf{\Lambda }}{\mathsf{\Gamma }{(2\Im +1)}^2}+\frac{2\mathsf{\Lambda }}{\mathsf{\Gamma }{(\Im +1)}^3}\frac{\mathsf{\Gamma }(2\Im +1)}{\mathsf{\Gamma }(3\Im +1)}\right]t^{5\Im }\hfill \\ \hfill & \hfill +\frac{2^2\mathsf{\Lambda }}{\mathsf{\Gamma }{(\Im +1)}^2}\frac{\mathsf{\Gamma }(5\Im +1)}{\mathsf{\Gamma }(3\Im +1)\mathsf{\Gamma }(6\Im +1)}{t}^{6\Im }\hfill \\ \hfill & \hfill \left.-\frac{\mathsf{\Lambda }}{\mathsf{\Gamma }{(\Im +1)}^4}\frac{\mathsf{\Gamma }{(2\Im +1)}^2\mathsf{\Gamma }(6\Im +1)}{\mathsf{\Gamma }{(3\Im +1)}^2\mathsf{\Gamma }(7\Im +1)}{t}^{7\Im }\right]\hfill \\ \hfill ⋮\end{array}\right.$$

and

$$\left\{\begin{array}{cc}\hfill {\stackrel{̲}{v}}_1(\mathsf{\Lambda },t;\varrho )& \hfill ={(0.6-0.2\varrho )}^{ı}+\left[\frac{\mathsf{\Lambda }}{\mathsf{\Gamma }(\Im +1)}{t}^{\Im }\right],\hfill \\ \hfill {\stackrel{̲}{v}}_2(\mathsf{\Lambda },t;\varrho )& \hfill ={(0.6-0.2\varrho )}^{ı}-\left[\frac{2\mathsf{\Lambda }}{\mathsf{\Gamma }(2\Im +1)}{t}^{2\Im }-\frac{\mathsf{\Lambda }}{\mathsf{\Gamma }{(\Im +1)}^2}\frac{\mathsf{\Gamma }(2\Im +1)}{\mathsf{\Gamma }(3\Im +1)}{t}^{3\Im }\right],\hfill \\ \hfill {\stackrel{̲}{v}}_3(\mathsf{\Lambda },t;\varrho )& \hfill ={(0.6-0.2\varrho )}^{ı}-\left[-\frac{2^2\mathsf{\Lambda }}{\mathsf{\Gamma }(3\Im +1)}{t}^{3\Im }\right.\hfill \\ \hfill & \hfill +\frac{\mathsf{\Gamma }(3\Im +1)}{\mathsf{\Gamma }(4\Im +1)}\left[\frac{2\mathsf{\Lambda }}{\mathsf{\Gamma }{(\Im +1)}^2}\frac{\mathsf{\Gamma }(2\Im +1)}{\mathsf{\Gamma }(3\Im +1)}+\frac{2^2\mathsf{\Lambda }}{\mathsf{\Gamma }(\Im +1)\mathsf{\Gamma }(2\Im +1)}\right]t^{4\Im },\hfill \\ \hfill & \hfill -\frac{\mathsf{\Gamma }(4\Im +1)}{\mathsf{\Gamma }(5\Im +1)}\left[\frac{2^2\mathsf{\Lambda }}{\mathsf{\Gamma }{(2\Im +1)}^2}+\frac{2\mathsf{\Lambda }}{\mathsf{\Gamma }{(\Im +1)}^3}\frac{\mathsf{\Gamma }(2\Im +1)}{\mathsf{\Gamma }(3\Im +1)}\right]t^{5\Im }\hfill \\ \hfill & \hfill +\frac{2^2\mathsf{\Lambda }}{\mathsf{\Gamma }{(\Im +1)}^2}\frac{\mathsf{\Gamma }(5\Im +1)}{\mathsf{\Gamma }(3\Im +1)\mathsf{\Gamma }(6\Im +1)}{t}^{6\Im }\hfill \\ \hfill & \hfill \left.-\frac{\mathsf{\Lambda }}{\mathsf{\Gamma }{(\Im +1)}^4}\frac{\mathsf{\Gamma }{(2\Im +1)}^2\mathsf{\Gamma }(6\Im +1)}{\mathsf{\Gamma }{(3\Im +1)}^2\mathsf{\Gamma }(7\Im +1)}{t}^{7\Im }\right]\hfill \\ \hfill ⋮.\end{array}\right.$$

For $\Im =1,$ we can obtain the exact solution as:

$$\begin{array}{c}\hfill \tilde{w}(\mathsf{\Lambda },t;\varrho )=\left[{(0.2+0.2\varrho )}^{ı},{(0.6-0.2\varrho )}^{ı}\right]{\ominus }_{gH}\frac{\mathsf{\Lambda }}{1+t},0\le \varrho \le 1.\end{array}$$

Meanwhile, the DTM and fuzzy VIM lower and upper solution of Equation (50) are demonstrated in Figure 1c, where $\mathsf{\Lambda }=0.3,t=0.7,$ and $ı=3$ show the precision and compliance with the proposed theory.

4. Fuzzy Time-Fractional Telegraphic Equations

In the current section, we establish the fuzzy time-fractional telegraphic equations via the fuzzy reduced differential transform method. Let $\tilde{w}(\mathsf{\Lambda },\phi ,\varphi ;\varrho )=[\underline{w}(\mathsf{\Lambda },\phi ,\varphi ;\varrho ),$$\stackrel{̲}{w}(\mathsf{\Lambda },\phi ,\varphi ;\varrho )]$ and $\tilde{\hslash }(\mathsf{\Lambda },\phi ,\varphi ;\varrho )=[\underline{\hslash }(\mathsf{\Lambda },\phi ,\varphi ;\varrho ),\stackrel{̲}{\hslash }(\mathsf{\Lambda },\phi ,\varphi ;\varrho )]$ denote the electric voltage and the current in a double conductor.

• Consider the two-dimensional fuzzy fractional telegraphic equations of the form

  $$\begin{array}{c}\hfill \left.\begin{array}{cc}\hfill \frac{{\partial }^{2\Im }\tilde{w}}{\partial t^{2\Im }}\oplus 2p\odot \frac{{\partial }^{\Im }\tilde{w}}{\partial t^{\Im }}\oplus q^2\odot \tilde{w}& \hfill =\frac{{\partial }^2\tilde{w}}{\partial {\mathsf{\Lambda }}^2}\oplus \frac{{\partial }^2\tilde{w}}{\partial {\phi }^2}\oplus {\tilde{f}}_1(\mathsf{\Lambda },\phi ,t),\hfill \\ \hfill \frac{{\partial }^{2\Im }\tilde{\hslash }}{\partial t^{2\Im }}\oplus 2p\odot \frac{{\partial }^{\Im }\tilde{\hslash }}{\partial t^{\Im }}\oplus q^2\odot \tilde{\hslash }& \hfill =\frac{{\partial }^2\tilde{\hslash }}{\partial {\mathsf{\Lambda }}^2}\oplus \frac{{\partial }^2\tilde{\hslash }}{\partial {\phi }^2}\oplus {\tilde{f}}_1(\mathsf{\Lambda },\phi ,t),\hfill \end{array}\right\},(\mathsf{\Lambda },\phi ,t)\in \mathsf{\Psi },\end{array}$$

  (62)

  where $p>0,q>0,$ and $\mathsf{\Psi }=[a,b]\times [c,d]\times [e,f]\times [t>0].$
  Subject to the initial conditions

  $$\begin{array}{c}\hfill \left.\begin{array}{cc}\hfill \tilde{w}(\mathsf{\Lambda },\phi ,0)& \hfill ={\tilde{\psi }}_1(\mathsf{\Lambda },\phi ),\hfill \\ \hfill {\tilde{w}}_t(\mathsf{\Lambda },\phi ,0)& \hfill ={\tilde{\psi }}_2(\mathsf{\Lambda },\phi ),\hfill \\ \hfill \tilde{\hslash }(\mathsf{\Lambda },\phi ,0)& \hfill ={\tilde{\mathit{ȷ}}}_1(\mathsf{\Lambda },\phi ),\hfill \\ \hfill {\tilde{\hslash }}_t(\mathsf{\Lambda },\phi ,0)& \hfill ={\tilde{\mathit{ȷ}}}_2(\mathsf{\Lambda },\phi ),\hfill \end{array}\right\},(\mathsf{\Lambda },\phi )\in \mathsf{\Psi }.\end{array}$$

  (63)
• Consider the three-dimensional fuzzy fractional telegraphic equations of the form

  $$\begin{array}{c}\hfill \left.\begin{array}{cc}\hfill \frac{{\partial }^{2\Im }\tilde{w}}{\partial t^{2\Im }}\oplus 2p\odot \frac{{\partial }^{\Im }\tilde{w}}{\partial t^{\Im }}\oplus q^2\odot \tilde{w}& \hfill =\frac{{\partial }^2\tilde{w}}{\partial {\mathsf{\Lambda }}^2}\oplus \frac{{\partial }^2\tilde{w}}{\partial {\phi }^2}\oplus \frac{{\partial }^2\tilde{w}}{\partial {\varphi }^2}\oplus {\tilde{f}}_1(\mathsf{\Lambda },\phi ,\varphi ,t),\hfill \\ \hfill \frac{{\partial }^{2\Im }\tilde{\hslash }}{\partial t^{2\Im }}\oplus 2p\odot \frac{{\partial }^{\Im }\tilde{\hslash }}{\partial t^{\Im }}\oplus q^2\odot \tilde{\hslash }& \hfill =\frac{{\partial }^2\tilde{\hslash }}{\partial {\mathsf{\Lambda }}^2}\oplus \frac{{\partial }^2\tilde{\hslash }}{\partial {\phi }^2}\oplus \frac{{\partial }^2\tilde{w}}{\partial {\varphi }^2}\oplus {\tilde{f}}_1(\mathsf{\Lambda },\phi ,\varphi ,t),\hfill \end{array}\right\},(\mathsf{\Lambda },\phi ,\varphi ,t)\in \mathsf{\Psi },\end{array}$$

  (64)

  where $p>0,q>0,$ and $\mathsf{\Psi }=[a,b]\times [c,d]\times [e,f]\times [t>0].$
  Subject to the initial conditions

  $$\begin{array}{c}\hfill \left.\begin{array}{cc}\hfill {\tilde{w}}_t(\mathsf{\Lambda },\phi ,\varphi ,0)& \hfill ={\tilde{\tau }}_1(\mathsf{\Lambda },\phi ,\varphi ),\hfill \\ \hfill \tilde{w}(\mathsf{\Lambda },\phi ,\varphi ,0)& \hfill ={\tilde{\tau }}_2(\mathsf{\Lambda },\phi ,\varphi ),\hfill \\ \hfill \tilde{\hslash }(\mathsf{\Lambda },\phi ,\varphi ,0)& \hfill ={\tilde{\nu }}_1(\mathsf{\Lambda },\phi ,\varphi ),\hfill \\ \hfill {\tilde{\hslash }}_t(\mathsf{\Lambda },\phi ,\varphi ,0)& \hfill ={\tilde{\nu }}_2(\mathsf{\Lambda },\phi ,\varphi ),\hfill \end{array}\right\},(\mathsf{\Lambda },\phi ,\varphi )\in \mathsf{\Psi }\end{array}$$

  (65)

  where p and q denote constants.

4.1. Fuzzy Reduced Differential Transform Method

In this part, we give some basic definitions of fuzzy RDTM. Consider a fuzzy-valued function of some variables $\tilde{w}(\mathsf{\Lambda },\phi ,\varphi ,t;\varrho )=[\underline{w}(\mathsf{\Lambda },\phi ,\varphi ,t;\varrho ),\stackrel{̲}{w}(\mathsf{\Lambda },\phi ,\varphi ,t;\varrho )]$; where $\varrho \in [0,1]$, we can obtain

$$\begin{array}{c}\hfill \underline{w}(\mathsf{\Lambda },\phi ,\varphi ,t;\varrho )=\sum _{{\hslash }_1=0}^{\infty }\sum _{{\hslash }_2=0}^{\infty }\sum _{{\hslash }_3=0}^{\infty }\sum _{\wp =0}^{\infty }\underline{W}({\hslash }_1,{\hslash }_2,{\hslash }_3;\varrho ){\mathsf{\Lambda }}^{{\hslash }_1}{\phi }^{{\hslash }_2}{\varphi }^{{\hslash }_3}{t}^{\wp },\end{array}$$

(66)

$$\begin{array}{c}\hfill \stackrel{̲}{w}(\mathsf{\Lambda },\phi ,\varphi ,t;\varrho )=\sum _{{\hslash }_1=0}^{\infty }\sum _{{\hslash }_2=0}^{\infty }\sum _{{\hslash }_3=0}^{\infty }\sum _{\wp =0}^{\infty }\stackrel{̲}{W}({\hslash }_1,{\hslash }_2,{\hslash }_3;\varrho ){\mathsf{\Lambda }}^{{\hslash }_1}{\phi }^{{\hslash }_2}{\varphi }^{{\hslash }_3}{t}^{\wp }.\end{array}$$

(67)

where $\tilde{W}({\hslash }_1,{\hslash }_2,{\hslash }_3;\varrho )=\left[\underline{W}({\hslash }_1,{\hslash }_2,{\hslash }_3;\varrho ),\stackrel{̲}{W}({\hslash }_1,{\hslash }_2,{\hslash }_3;\varrho )\right]$ is called the spectrum function of $\tilde{w}(\mathsf{\Lambda },\phi ,\varphi ,t;\varrho )$. Let $R_D$ and $R_D^{-1}$ denote the RDTM operator and inverse RDTM operator, respectively.

Definition 7.

If the fuzzy-valued function $\tilde{w}(\mathsf{\Lambda },\phi ,\varphi ,t)$ is analytic and continuously differentiable with respect to space variables $\mathsf{\Lambda },\phi ,\varphi$ and time variable t in the domain of interest, then the spectrum function

$$\begin{array}{c}\hfill \left.\begin{array}{cc}\hfill R_D\left[\underline{w}(\mathsf{\Lambda },\phi ,\varphi ,t;\varrho )\right]\approx {\underline{W}}_{\mathit{ȷ}}(\mathsf{\Lambda },\phi ,\varphi ;\varrho )& \hfill =\frac{1}{\mathsf{\Gamma }(\mathit{ȷ}\Im +1)}{\left[\frac{{\partial }^{\mathit{ȷ}}}{\partial t^{\mathit{ȷ}}}\underline{w}(\mathsf{\Lambda },\phi ,\varphi ,t;\varrho )\right]}_{t=t_0},\hfill \\ \hfill R_D\left[\stackrel{̲}{w}(\mathsf{\Lambda },\phi ,\varphi ,t;\varrho )\right]\approx {\stackrel{̲}{W}}_{\mathit{ȷ}}(\mathsf{\Lambda },\phi ,\varphi ;\varrho )& \hfill =\frac{1}{\mathsf{\Gamma }(\mathit{ȷ}\Im +1)}{\left[\frac{{\partial }^{\mathit{ȷ}}}{\partial t^{\mathit{ȷ}}}\stackrel{̲}{w}(\mathsf{\Lambda },\phi ,\varphi ,t;\varrho )\right]}_{t=t_0},\hfill \end{array}\right\}\end{array}$$

(68)

is the fuzzy reduced transformed function of $\tilde{w}(\mathsf{\Lambda },\phi ,\varphi ,t).$ Consider that both functions $\tilde{w}(\mathsf{\Lambda },\phi ,\varphi ,t)$ and ${\tilde{W}}_{\mathit{ȷ}}(\mathsf{\Lambda },\phi ,\varphi )$ denote the original function and reduced transform function, respectively. The differential inverse fuzzy reduced transform of ${\tilde{W}}_{\mathit{ȷ}}(\mathsf{\Lambda },\phi ,\varphi ;\varrho )=[{\underline{W}}_{\mathit{ȷ}}(\mathsf{\Lambda },\phi ,\varphi ;\varrho ),{\stackrel{̲}{W}}_{\mathit{ȷ}}(\mathsf{\Lambda },\phi ,\varphi ;\varrho )]$ is defined as follows

$$\begin{array}{c}\hfill \left.\begin{array}{cc}\hfill R_D^{-1}\left[{\underline{W}}_{\mathit{ȷ}}(\mathsf{\Lambda },\phi ,\varphi ;\varrho )\right]\approx \underline{w}(\mathsf{\Lambda },\phi ,\varphi ,t;\varrho )& \hfill =\sum _{\mathit{ȷ}=0}^{\infty }{\underline{W}}_{\mathit{ȷ}}(\mathsf{\Lambda },\phi ,\varphi ;\varrho ){(t-t_0)}^{\mathit{ȷ}\Im }\hfill \\ \hfill R_D^{-1}\left[{\stackrel{̲}{W}}_{\mathit{ȷ}}(\mathsf{\Lambda },\phi ,\varphi ;\varrho )\right]\approx \stackrel{̲}{w}(\mathsf{\Lambda },\phi ,\varphi ,t;\varrho )& \hfill =\sum _{\mathit{ȷ}=0}^{\infty }{\stackrel{̲}{W}}_{\mathit{ȷ}}(\mathsf{\Lambda },\phi ,\varphi ;\varrho ){(t-t_0)}^{\mathit{ȷ}\Im }.\hfill \end{array}\right\}\end{array}$$

(69)

Combining (68) and (69), we obtain

$$\begin{array}{cc}\hfill \underline{w}(\mathsf{\Lambda },\phi ,\varphi ,t;\varrho )& \hfill =\sum _{\mathit{ȷ}=0}^{\infty }\frac{1}{\mathsf{\Gamma }(\mathit{ȷ}\Im +1)}{\left[\frac{{\partial }^{\mathit{ȷ}}}{\partial t^{\mathit{ȷ}}}\underline{w}(\mathsf{\Lambda },\phi ,\varphi ,t;\varrho )\right]}_{t=t_0}{(t-t_0)}^{\mathit{ȷ}\Im },\hfill \end{array}$$

(70)

$$\begin{array}{cc}\hfill \stackrel{̲}{w}(\mathsf{\Lambda },\phi ,\varphi ,t;\varrho )& \hfill =\sum _{\mathit{ȷ}=0}^{\infty }\frac{1}{\mathsf{\Gamma }(\mathit{ȷ}\Im +1)}{\left[\frac{{\partial }^{\mathit{ȷ}}}{\partial t^{\mathit{ȷ}}}\stackrel{̲}{w}(\mathsf{\Lambda },\phi ,\varphi ,t;\varrho )\right]}_{t=t_0}{(t-t_0)}^{\mathit{ȷ}\Im }.\hfill \end{array}$$

(71)

For $t=0,$ formulas (70) and (71) are given by

$$\begin{array}{cc}\hfill \underline{w}(\mathsf{\Lambda },\phi ,\varphi ,t;\varrho )& \hfill =\sum _{\mathit{ȷ}=0}^{\infty }\frac{1}{\mathsf{\Gamma }(\mathit{ȷ}\Im +1)}{\left[\frac{{\partial }^{\mathit{ȷ}}}{\partial t^{\mathit{ȷ}}}\underline{w}(\mathsf{\Lambda },\phi ,\varphi ,t;\varrho )\right]}_{t=t_0}{t}^{\mathit{ȷ}\Im },\hfill \end{array}$$

(72)

$$\begin{array}{cc}\hfill \stackrel{̲}{w}(\mathsf{\Lambda },\phi ,\varphi ,t;\varrho )& \hfill =\sum _{\mathit{ȷ}=0}^{\infty }\frac{1}{\mathsf{\Gamma }(\mathit{ȷ}\Im +1)}{\left[\frac{{\partial }^{\mathit{ȷ}}}{\partial t^{\mathit{ȷ}}}\stackrel{̲}{w}(\mathsf{\Lambda },\phi ,\varphi ,t;\varrho )\right]}_{t=t_0}{t}^{\mathit{ȷ}\Im }.\hfill \end{array}$$

(73)

Definition 8.

Let us assume $\tilde{w}\in E^1$ is the fuzzy valued function and that $v\in R$ is the real valued function. Then, $\tilde{w}(\mathsf{\Lambda },\phi ,\varphi ,t;\varrho )=R_D^{-1}[{\underline{W}}_{\mathit{ȷ}}(\mathsf{\Lambda },\phi ,\varphi ,t;\varrho ),{\stackrel{̲}{W}}_{\mathit{ȷ}}(\mathsf{\Lambda },\phi ,\varphi ,t;\varrho )],v(\mathsf{\Lambda },\phi ,\varphi ,t;\varrho )=R_D^{-1}[{\underline{V}}_{\mathit{ȷ}}(\mathsf{\Lambda },\phi ,\varphi ,t;\varrho ),{\stackrel{̲}{V}}_{\mathit{ȷ}}(\mathsf{\Lambda },\phi ,\varphi ,t;\varrho )]$, and the convolution ⊗ denotes the reduced differential transform version of multiplication; then, the basic operations of the RDTM are expressed as follows:

1. 

$$\begin{array}{c}\hfill \left.\begin{array}{cc}\hfill R_D\left[\underline{w}(\mathsf{\Lambda },\phi ,\varphi ,t;\varrho )\underline{v}(\mathsf{\Lambda },\phi ,\varphi ,t;\varrho )\right]& \hfill ={\underline{W}}_{\mathit{ȷ}}(\mathsf{\Lambda },\phi ,\varphi ;\varrho )\otimes {\underline{V}}_{\mathit{ȷ}}(\mathsf{\Lambda },\phi ,\varphi ;\varrho )\hfill \\ \hfill & \hfill =\sum _{\gamma =0}^{\mathit{ȷ}}{\underline{W}}_{\gamma }(\mathsf{\Lambda },\phi ,\varphi ;\varrho ){\underline{V}}_{R-\gamma }(\mathsf{\Lambda },\phi ,\varphi ;\varrho ),\hfill \\ \hfill R_D\left[\stackrel{̲}{w}(\mathsf{\Lambda },\phi ,\varphi ,t;\varrho )\stackrel{̲}{v}(\mathsf{\Lambda },\phi ,\varphi ,t;\varrho )\right]& \hfill ={\stackrel{̲}{W}}_{\mathit{ȷ}}(\mathsf{\Lambda },\phi ,\varphi ;\varrho )\otimes {\stackrel{̲}{V}}_{\mathit{ȷ}}(\mathsf{\Lambda },\phi ,\varphi ;\varrho )\hfill \\ \hfill & \hfill =\sum _{\gamma =0}^{\mathit{ȷ}}{\stackrel{̲}{W}}_{\gamma }(\mathsf{\Lambda },\phi ,\varphi ;\varrho ){\stackrel{̲}{V}}_{R-\gamma }(\mathsf{\Lambda },\phi ,\varphi ;\varrho ).\hfill \end{array}\right\}\end{array}$$

(74)

2. 

$$\begin{array}{c}\hfill \left.\begin{array}{cc}\hfill R_D[\Im \underline{w}(\mathsf{\Lambda },\phi ,\varphi ,t;\varrho )\pm \beta \underline{v}(\mathsf{\Lambda },\phi ,\varphi ,t;\varrho )]& \hfill =[\Im {\underline{W}}_{\mathit{ȷ}}(\mathsf{\Lambda },\phi ,\varphi ;\varrho )\pm \beta {\underline{V}}_{\mathit{ȷ}}(\mathsf{\Lambda },\phi ,\varphi ;\varrho )],\hfill \\ \hfill R_D[\Im \stackrel{̲}{w}(\mathsf{\Lambda },\phi ,\varphi ,t;\varrho )\pm \beta \stackrel{̲}{v}(\mathsf{\Lambda },\phi ,\varphi ,t;\varrho )]& \hfill =[\Im {\stackrel{̲}{W}}_{\mathit{ȷ}}(\mathsf{\Lambda },\phi ,\varphi ;\varrho )\pm \beta {\stackrel{̲}{V}}_{\mathit{ȷ}}(\mathsf{\Lambda },\phi ,\varphi ;\varrho )].\hfill \end{array}\right\}\end{array}$$

(75)

3. 

$$\begin{array}{c}\hfill \left.\begin{array}{cc}\hfill R_D[{\partial }^{N\Im }/\partial t^{N\Im }\underline{w}(\mathsf{\Lambda },\phi ,\varphi ,t;\varrho )]& \hfill =\mathsf{\Gamma }(\mathit{ȷ}\Im +N\Im +1)/\mathsf{\Gamma }(\mathit{ȷ}\Im +1){\underline{W}}_{\mathit{ȷ}+N}(\mathsf{\Lambda },\phi ,\varphi ;\varrho ),\hfill \\ \hfill R_D[{\partial }^{N\Im }/\partial t^{N\Im }\stackrel{̲}{w}(\mathsf{\Lambda },\phi ,\varphi ,t;\varrho )]& \hfill =\mathsf{\Gamma }(\mathit{ȷ}\Im +N\Im +1)/\mathsf{\Gamma }(\mathit{ȷ}\Im +1){\stackrel{̲}{W}}_{\mathit{ȷ}+N}(\mathsf{\Lambda },\phi ,\varphi ;\varrho ).\hfill \end{array}\right\}\end{array}$$

(76)

4. 

$$\begin{array}{c}\hfill \left.\begin{array}{cc}\hfill R_D[{\partial }^{m+n+p+s}/\partial {\mathsf{\Lambda }}^m\partial {\phi }^n\partial {\mathsf{\Lambda }}^p\partial t^s\underline{w}(\mathsf{\Lambda },\phi ,\varphi ,t;\varrho )]& \hfill =(\mathit{ȷ}+s)!/\mathit{ȷ}!{\partial }^{m+n+p}/\partial {\mathsf{\Lambda }}^m\partial {\phi }^n\partial {\mathsf{\Lambda }}^p{\underline{W}}_{\mathit{ȷ}+s}(\mathsf{\Lambda },\phi ,\varphi ;\varrho )\hfill \\ \hfill R_D[{\partial }^{m+n+p+s}/\partial {\mathsf{\Lambda }}^m\partial {\phi }^n\partial {\mathsf{\Lambda }}^p\partial t^s\stackrel{̲}{w}(\mathsf{\Lambda },\phi ,\varphi ,t;\varrho )]& \hfill =(\mathit{ȷ}+s)!/\mathit{ȷ}!{\partial }^{m+n+p}/\partial {\mathsf{\Lambda }}^m\partial {\phi }^n\partial {\mathsf{\Lambda }}^p{\stackrel{̲}{W}}_{\mathit{ȷ}+s}(\mathsf{\Lambda },\phi ,\varphi ;\varrho ).\hfill \end{array}\right\}\end{array}$$

(77)

5. 

$$R_D\left[{\mathsf{\Lambda }}^m{\phi }^n{\mathsf{\Lambda }}^p{t}^q\right]=\left\{\begin{array}{cc}\hfill {\mathsf{\Lambda }}^m{\phi }^n{\mathsf{\Lambda }}^p,\hfill & \hfill \mathit{ȷ}=q\\ \hfill 0\hfill & \hfill otherwise.\end{array}\right.$$

6. 

$$R_D[exp\left(\lambda t\right)]=\frac{{\lambda }^{\mathit{ȷ}}}{\mathit{ȷ}!}.$$

7. 

$$R_D[sin(\Im \mathsf{\Lambda }+\beta \phi +\gamma \mathsf{\Lambda }+\omega t)]=\frac{w^{\mathit{ȷ}}}{\mathit{ȷ}!}sin\left(\frac{\pi \mathit{ȷ}}{2!}+\Im \mathsf{\Lambda }+\beta \phi +\gamma \mathsf{\Lambda }\right).$$

8. 

$$R_D[cos(\Im \mathsf{\Lambda }+\beta \phi +\gamma \mathsf{\Lambda }+\omega t)]=\frac{w^{\mathit{ȷ}}}{\mathit{ȷ}!}cos\left(\frac{\pi \mathit{ȷ}}{2!}+\Im \mathsf{\Lambda }+\beta \phi +\gamma \mathsf{\Lambda }\right).$$

4.2. Two-Dimensional Fuzzy Time-Fractional Telegraphic Equations

We consider the following two-dimensional fuzzy time-fractional telegraphic Equation (62) as

$$\begin{array}{c}\hfill \left.\begin{array}{cc}\hfill \frac{\mathsf{\Gamma }(\mathit{ȷ}\Im +2\Im +1)}{\mathsf{\Gamma }(\mathit{ȷ}\Im +1)}{\underline{W}}_{\mathit{ȷ}+2}(\mathsf{\Lambda },\phi ;\varrho )& \hfill +2p\frac{\mathsf{\Gamma }(\mathit{ȷ}\Im +\Im +1)}{\mathsf{\Gamma }(\mathit{ȷ}\Im +1)}{\underline{W}}_{\mathit{ȷ}+1}(\mathsf{\Lambda },\phi ;\varrho )+q^2{\underline{W}}_{\mathit{ȷ}}(\mathsf{\Lambda },\phi ;\varrho )\hfill \\ \hfill & \hfill =\frac{{\partial }^2}{\partial {\mathsf{\Lambda }}^2}{\underline{W}}_{\mathit{ȷ}}(\mathsf{\Lambda },\phi ;\varrho )+\frac{{\partial }^2}{\partial {\phi }^2}{\underline{W}}_{\mathit{ȷ}}(\mathsf{\Lambda },\phi ;\varrho )+R_D\left[f_1(\mathsf{\Lambda },\phi ,t)\right],\hfill \\ \hfill \frac{\mathsf{\Gamma }(\mathit{ȷ}\Im +2\Im +1)}{\mathsf{\Gamma }(\mathit{ȷ}\Im +1)}{\underline{H}}_{\mathit{ȷ}+2}(\mathsf{\Lambda },\phi ;\varrho )& \hfill +2p\frac{\mathsf{\Gamma }(\mathit{ȷ}\Im +\Im +1)}{\mathsf{\Gamma }(\mathit{ȷ}\Im +1)}{\underline{H}}_{\mathit{ȷ}+1}(\mathsf{\Lambda },\phi ;\varrho )+q^2{\underline{H}}_{\mathit{ȷ}}(\mathsf{\Lambda },\phi ;\varrho )\hfill \\ \hfill & \hfill =\frac{{\partial }^2}{\partial {\mathsf{\Lambda }}^2}{\underline{H}}_{\mathit{ȷ}}(\mathsf{\Lambda },\phi ;\varrho )+\frac{{\partial }^2}{\partial {\phi }^2}{\underline{H}}_{\mathit{ȷ}}(\mathsf{\Lambda },\phi ;\varrho )+R_D\left[f_1(\mathsf{\Lambda },\phi ,t)\right],\hfill \end{array}\right\}\end{array}$$

(78)

and

$$\begin{array}{c}\hfill \left.\begin{array}{cc}\hfill \frac{\mathsf{\Gamma }(\mathit{ȷ}\Im +2\Im +1)}{\mathsf{\Gamma }(\mathit{ȷ}\Im +1)}{\stackrel{̲}{W}}_{\mathit{ȷ}+2}(\mathsf{\Lambda },\phi ;\varrho )& \hfill +2p\frac{\mathsf{\Gamma }(\mathit{ȷ}\Im +\Im +1)}{\mathsf{\Gamma }(\mathit{ȷ}\Im +1)}{\stackrel{̲}{W}}_{\mathit{ȷ}+1}(\mathsf{\Lambda },\phi ;\varrho )+q^2{\stackrel{̲}{W}}_{\mathit{ȷ}}(\mathsf{\Lambda },\phi ;\varrho )\hfill \\ \hfill & \hfill =\frac{{\partial }^2}{\partial {\mathsf{\Lambda }}^2}{\stackrel{̲}{W}}_{\mathit{ȷ}}(\mathsf{\Lambda },\phi ;\varrho )+\frac{{\partial }^2}{\partial {\phi }^2}{\stackrel{̲}{W}}_{\mathit{ȷ}}(\mathsf{\Lambda },\phi ;\varrho )+R_D\left[f_1(\mathsf{\Lambda },\phi ,t)\right],\hfill \\ \hfill \frac{\mathsf{\Gamma }(\mathit{ȷ}\Im +2\Im +1)}{\mathsf{\Gamma }(\mathit{ȷ}\Im +1)}{\stackrel{̲}{H}}_{\mathit{ȷ}+2}(\mathsf{\Lambda },\phi ;\varrho )& \hfill +2p\frac{\mathsf{\Gamma }(\mathit{ȷ}\Im +\Im +1)}{\mathsf{\Gamma }(\mathit{ȷ}\Im +1)}{\stackrel{̲}{H}}_{\mathit{ȷ}+1}(\mathsf{\Lambda },\phi ;\varrho )+q^2{\stackrel{̲}{H}}_{\mathit{ȷ}}(\mathsf{\Lambda },\phi ;\varrho )\hfill \\ \hfill & \hfill =\frac{{\partial }^2}{\partial {\mathsf{\Lambda }}^2}{\stackrel{̲}{H}}_{\mathit{ȷ}}(\mathsf{\Lambda },\phi ;\varrho )+\frac{{\partial }^2}{\partial {\phi }^2}{\stackrel{̲}{H}}_{\mathit{ȷ}}(\mathsf{\Lambda },\phi ;\varrho )+R_D\left[f_1(\mathsf{\Lambda },\phi ,t)\right],\hfill \end{array}\right\}\end{array}$$

(79)

where $\mathit{ȷ}=2,3,4,\dots$

Putting the initial conditions (63), it easy to see that

$$\begin{array}{c}\hfill \left.\begin{array}{cc}\hfill {\underline{W}}_0(\mathsf{\Lambda },\phi ;\varrho )& \hfill ={\underline{\psi }}_1(\mathsf{\Lambda },\phi ;\varrho ),\hfill \\ \hfill {\underline{W}}_1(\mathsf{\Lambda },\phi ;\varrho )& \hfill ={\underline{\psi }}_2(\mathsf{\Lambda },\phi ;\varrho ),\hfill \\ \hfill {\underline{H}}_0(\mathsf{\Lambda },\phi ;\varrho )& \hfill ={\underline{\mathit{ȷ}}}_1(\mathsf{\Lambda },\phi ;\varrho ),\hfill \\ \hfill {\underline{H}}_1(\mathsf{\Lambda },\phi ;\varrho )& \hfill ={\underline{\mathit{ȷ}}}_2(\mathsf{\Lambda },\phi ;\varrho ),\hfill \end{array}\right\},(\mathsf{\Lambda },\phi )\in \mathsf{\Psi },\end{array}$$

(80)

and

$$\begin{array}{c}\hfill \left.\begin{array}{cc}\hfill {\stackrel{̲}{W}}_0(\mathsf{\Lambda },\phi ;\varrho )& \hfill ={\stackrel{̲}{\psi }}_1(\mathsf{\Lambda },\phi ;\varrho ),\hfill \\ \hfill {\stackrel{̲}{W}}_1(\mathsf{\Lambda },\phi ;\varrho )& \hfill ={\stackrel{̲}{\psi }}_2(\mathsf{\Lambda },\phi ;\varrho ),\hfill \\ \hfill {\stackrel{̲}{H}}_0(\mathsf{\Lambda },\phi ;\varrho )& \hfill ={\stackrel{̲}{\mathit{ȷ}}}_1(\mathsf{\Lambda },\phi ;\varrho ),\hfill \\ \hfill {\stackrel{̲}{H}}_1(\mathsf{\Lambda },\phi ;\varrho )& \hfill ={\stackrel{̲}{\mathit{ȷ}}}_2(\mathsf{\Lambda },\phi ;\varrho ),\hfill \end{array}\right\},(\mathsf{\Lambda },\phi )\in \mathsf{\Psi }.\end{array}$$

(81)

Using Equations (81) into (78), we obtain the values of ${\tilde{U}}_{\mathit{ȷ}}(\mathsf{\Lambda },\phi ),{\tilde{H}}_{\mathit{ȷ}}(\mathsf{\Lambda },\phi )$ where $\mathit{ȷ}=2,3,4,\dots$. Applying the differential inverse fuzzy reduced transform of ${\tilde{U}}_{\mathit{ȷ}}(\mathsf{\Lambda },\phi ),{\tilde{H}}_{\mathit{ȷ}}(\mathsf{\Lambda },\phi )$ where $\mathit{ȷ}=0,1,2,3,\dots ,$ we obtain the approximate solution for $\tilde{w}(\mathsf{\Lambda },\phi ,t)$ and $\tilde{h}(\mathsf{\Lambda },\phi ,t)$ as follows

$$\begin{array}{c}\hfill \left.\begin{array}{cc}\hfill \underline{w}(\mathsf{\Lambda },\phi ,t;\varrho )& \hfill =\sum _{\mathit{ȷ}=0}^{\infty }{\underline{W}}_{\mathit{ȷ}}(\mathsf{\Lambda },\phi ;\varrho )t^{\mathit{ȷ}\Im }\hfill \\ \hfill & \hfill ={\underline{W}}_0(\mathsf{\Lambda },\phi ;\varrho )+{\underline{W}}_1(\mathsf{\Lambda },\phi ;\varrho )t^{\Im }+{\underline{W}}_2(\mathsf{\Lambda },\phi ;\varrho )t^{2\Im }+{\underline{W}}_3(\mathsf{\Lambda },\phi ;\varrho )t^{3\Im }+\cdots ,\hfill \\ \hfill \underline{h}(\mathsf{\Lambda },\phi ,t;\varrho )& \hfill =\sum _{\mathit{ȷ}=0}^{\infty }{\underline{H}}_{\mathit{ȷ}}(\mathsf{\Lambda },\phi ;\varrho )t^{\mathit{ȷ}\Im }\hfill \\ \hfill & \hfill ={\underline{H}}_0(\mathsf{\Lambda },\phi ;\varrho )+{\underline{H}}_1(\mathsf{\Lambda },\phi ;\varrho )t^{\Im }+{\underline{H}}_2(\mathsf{\Lambda },\phi ;\varrho )t^{2\Im }+{\underline{H}}_3(\mathsf{\Lambda },\phi ;\varrho )t^{3\Im }+\cdots ,\hfill \end{array}\right\}\end{array}$$

(82)

and

$$\begin{array}{c}\hfill \left.\begin{array}{cc}\hfill \stackrel{̲}{w}(\mathsf{\Lambda },\phi ,t;\varrho )& \hfill =\sum _{\mathit{ȷ}=0}^{\infty }{\stackrel{̲}{W}}_{\mathit{ȷ}}(\mathsf{\Lambda },\phi ;\varrho )t^{\mathit{ȷ}\Im }\hfill \\ \hfill & \hfill ={\stackrel{̲}{W}}_0(\mathsf{\Lambda },\phi ;\varrho )+{\stackrel{̲}{W}}_1(\mathsf{\Lambda },\phi ;\varrho )t^{\Im }+{\stackrel{̲}{W}}_2(\mathsf{\Lambda },\phi ;\varrho )t^{2\Im }+{\stackrel{̲}{W}}_3(\mathsf{\Lambda },\phi ;\varrho )t^{3\Im }+\cdots ,\hfill \\ \hfill \stackrel{̲}{h}(\mathsf{\Lambda },\phi ,t;\varrho )& \hfill =\sum _{\mathit{ȷ}=0}^{\infty }{\stackrel{̲}{H}}_{\mathit{ȷ}}(\mathsf{\Lambda },\phi ;\varrho )t^{\mathit{ȷ}\Im }\hfill \\ \hfill & \hfill ={\stackrel{̲}{H}}_0(\mathsf{\Lambda },\phi ;\varrho )+{\stackrel{̲}{H}}_1(\mathsf{\Lambda },\phi ;\varrho )t^{\Im }+{\stackrel{̲}{H}}_2(\mathsf{\Lambda },\phi ;\varrho )t^{2\Im }+{\stackrel{̲}{H}}_3(\mathsf{\Lambda },\phi ;\varrho )t^{3\Im }+\cdots .\hfill \end{array}\right\}\end{array}$$

(83)

4.3. Three-Dimensional Fuzzy Time-Fractional Telegraphic Equations

Consider the following three-dimensional fuzzy time-fractional telegraphic Equation (64) as:

$$\begin{array}{c}\hfill \left.\begin{array}{cc}\hfill \frac{\mathsf{\Gamma }(\mathit{ȷ}\Im +2\Im +1)}{\mathsf{\Gamma }(\mathit{ȷ}\Im +1)}{\underline{W}}_{\mathit{ȷ}+2}(\mathsf{\Lambda },\phi ,\varphi ;\varrho )& \hfill +2p\frac{\mathsf{\Gamma }(\mathit{ȷ}\Im +\Im +1)}{\mathsf{\Gamma }(\mathit{ȷ}\Im +1)}{\underline{W}}_{\mathit{ȷ}+1}(\mathsf{\Lambda },\phi ,\varphi ;\varrho )+q^2{\underline{W}}_{\mathit{ȷ}}(\mathsf{\Lambda },\phi ,\varphi ;\varrho )\hfill \\ \hfill & \hfill =\frac{{\partial }^2}{\partial {\mathsf{\Lambda }}^2}{\underline{W}}_{\mathit{ȷ}}(\mathsf{\Lambda },\phi ,\varphi ;\varrho )+\frac{{\partial }^2}{\partial {\phi }^2}{\underline{W}}_{\mathit{ȷ}}(\mathsf{\Lambda },\phi ,\varphi ;\varrho )+\frac{{\partial }^2}{\partial {\mathsf{\Lambda }}^2}{\underline{W}}_{\mathit{ȷ}}(\mathsf{\Lambda },\phi ,\varphi ;\varrho )\hfill \\ \hfill & \hfill +R_D\left[f_1(\mathsf{\Lambda },\phi ,\varphi ,t)\right];\hfill \\ \hfill \frac{\mathsf{\Gamma }(\mathit{ȷ}\Im +2\Im +1)}{\mathsf{\Gamma }(\mathit{ȷ}\Im +1)}{\underline{H}}_{\mathit{ȷ}+2}(\mathsf{\Lambda },\phi ,\varphi ;\varrho )& \hfill +2p\frac{\mathsf{\Gamma }(\mathit{ȷ}\Im +\Im +1)}{\mathsf{\Gamma }(\mathit{ȷ}\Im +1)}{\underline{H}}_{\mathit{ȷ}+1}(\mathsf{\Lambda },\phi ,\varphi )+q^2{\underline{H}}_{\mathit{ȷ}}(\mathsf{\Lambda },\phi ,\varphi ;\varrho )\hfill \\ \hfill & \hfill =\frac{{\partial }^2}{\partial {\mathsf{\Lambda }}^2}{\underline{H}}_{\mathit{ȷ}}(\mathsf{\Lambda },\phi ,\varphi ;\varrho )+\frac{{\partial }^2}{\partial {\phi }^2}{\underline{H}}_{\mathit{ȷ}}(\mathsf{\Lambda },\phi ,\varphi ;\varrho )+\frac{{\partial }^2}{\partial {\mathsf{\Lambda }}^2}{\underline{H}}_{\mathit{ȷ}}(\mathsf{\Lambda },\phi ,\varphi ;\varrho )\hfill \\ \hfill & \hfill +R_D\left[f_2(\mathsf{\Lambda },\phi ,\varphi ,t)\right],\hfill \end{array}\right\}\end{array}$$

(84)

and

$$\begin{array}{c}\hfill \left.\begin{array}{cc}\hfill \frac{\mathsf{\Gamma }(\mathit{ȷ}\Im +2\Im +1)}{\mathsf{\Gamma }(\mathit{ȷ}\Im +1)}{\stackrel{̲}{W}}_{\mathit{ȷ}+2}(\mathsf{\Lambda },\phi ,\varphi ;\varrho )& \hfill +2p\frac{\mathsf{\Gamma }(\mathit{ȷ}\Im +\Im +1)}{\mathsf{\Gamma }(\mathit{ȷ}\Im +1)}{\stackrel{̲}{W}}_{\mathit{ȷ}+1}(\mathsf{\Lambda },\phi ,\varphi ;\varrho )+q^2{\stackrel{̲}{W}}_{\mathit{ȷ}}(\mathsf{\Lambda },\phi ,\varphi ;\varrho )\hfill \\ \hfill & \hfill =\frac{{\partial }^2}{\partial {\mathsf{\Lambda }}^2}{\stackrel{̲}{W}}_{\mathit{ȷ}}(\mathsf{\Lambda },\phi ,\varphi ;\varrho )+\frac{{\partial }^2}{\partial {\phi }^2}{\stackrel{̲}{W}}_{\mathit{ȷ}}(\mathsf{\Lambda },\phi ,\varphi ;\varrho )+\frac{{\partial }^2}{\partial {\mathsf{\Lambda }}^2}{\stackrel{̲}{W}}_{\mathit{ȷ}}(\mathsf{\Lambda },\phi ,\varphi ;\varrho )\hfill \\ \hfill & \hfill +R_D\left[f_1(\mathsf{\Lambda },\phi ,\varphi ,t)\right];\hfill \\ \hfill \frac{\mathsf{\Gamma }(\mathit{ȷ}\Im +2\Im +1)}{\mathsf{\Gamma }(\mathit{ȷ}\Im +1)}{\stackrel{̲}{H}}_{\mathit{ȷ}+2}(\mathsf{\Lambda },\phi ,\varphi ;\varrho )& \hfill +2p\frac{\mathsf{\Gamma }(\mathit{ȷ}\Im +\Im +1)}{\mathsf{\Gamma }(\mathit{ȷ}\Im +1)}{\stackrel{̲}{H}}_{\mathit{ȷ}+1}(\mathsf{\Lambda },\phi ,\varphi ;\varrho )+q^2{\stackrel{̲}{H}}_{\mathit{ȷ}}(\mathsf{\Lambda },\phi ,\varphi ;\varrho )\hfill \\ \hfill & \hfill =\frac{{\partial }^2}{\partial {\mathsf{\Lambda }}^2}{\stackrel{̲}{H}}_{\mathit{ȷ}}(\mathsf{\Lambda },\phi ,\varphi ;\varrho )+\frac{{\partial }^2}{\partial {\phi }^2}{\stackrel{̲}{H}}_{\mathit{ȷ}}(\mathsf{\Lambda },\phi ,\varphi ;\varrho )+\frac{{\partial }^2}{\partial {\mathsf{\Lambda }}^2}{\stackrel{̲}{H}}_{\mathit{ȷ}}(\mathsf{\Lambda },\phi ,\varphi ;\varrho )\hfill \\ \hfill & \hfill +R_D\left[f_2(\mathsf{\Lambda },\phi ,\varphi ,t)\right].\hfill \end{array}\right\}\end{array}$$

(85)

From the initial conditions (65), it follows that

$$\begin{array}{c}\hfill \left.\begin{array}{cc}\hfill \underline{W}(\mathsf{\Lambda },\phi ,\varphi ;\varrho )& \hfill ={\underline{\tau }}_1(\mathsf{\Lambda },\phi ,\varphi ;\varrho ),\hfill \\ \hfill {\underline{W}}_0(\mathsf{\Lambda },\phi ,\varphi ;\varrho )& \hfill ={\underline{\tau }}_2(\mathsf{\Lambda },\phi ,\varphi ;\varrho ),\hfill \\ \hfill \underline{H}(\mathsf{\Lambda },\phi ,\varphi ;\varrho )& \hfill ={\underline{\nu }}_1(\mathsf{\Lambda },\phi ,\varphi ;\varrho ),\hfill \\ \hfill {\underline{H}}_0(\mathsf{\Lambda },\phi ,\varphi ;\varrho )& \hfill ={\underline{\nu }}_2(\mathsf{\Lambda },\phi ,\varphi ;\varrho ),\hfill \end{array}\right\},(\mathsf{\Lambda },\phi ,\varphi )\in \mathsf{\Psi },\end{array}$$

(86)

and

$$\begin{array}{c}\hfill \left.\begin{array}{cc}\hfill \stackrel{̲}{W}(\mathsf{\Lambda },\phi ,\varphi ;\varrho )& \hfill ={\stackrel{̲}{\tau }}_1(\mathsf{\Lambda },\phi ,\varphi ;\varrho ),\hfill \\ \hfill {\stackrel{̲}{W}}_0(\mathsf{\Lambda },\phi ,\varphi ;\varrho )& \hfill ={\stackrel{̲}{\tau }}_2(\mathsf{\Lambda },\phi ,\varphi ;\varrho ),\hfill \\ \hfill \stackrel{̲}{H}(\mathsf{\Lambda },\phi ,\varphi ;\varrho )& \hfill ={\stackrel{̲}{\nu }}_1(\mathsf{\Lambda },\phi ,\varphi ;\varrho ),\hfill \\ \hfill {\stackrel{̲}{H}}_0(\mathsf{\Lambda },\phi ,\varphi ;\varrho )& \hfill ={\stackrel{̲}{\nu }}_2(\mathsf{\Lambda },\phi ,\varphi ;\varrho ),\hfill \end{array}\right\},(\mathsf{\Lambda },\phi ,\varphi )\in \mathsf{\Psi }.\end{array}$$

(87)

The approximate solution for $\tilde{w}(\mathsf{\Lambda },\phi ,\varphi ;\varrho )=[\underline{w}(\mathsf{\Lambda },\phi ,\varphi ;\varrho ),\stackrel{̲}{w}(\mathsf{\Lambda },\phi ,\varphi ;\varrho )]$ and $\tilde{h}(\mathsf{\Lambda },\phi ,\varphi ;\varrho )$ = $[\underline{h}(\mathsf{\Lambda },\phi ,\varphi ;\varrho ),\stackrel{̲}{h}(\mathsf{\Lambda },\phi ,\varphi ;\varrho )]$ is as follows

$$\begin{array}{c}\hfill \left.\begin{array}{cc}\hfill \underline{w}(\mathsf{\Lambda },\phi ,\varphi ,t;\varrho )& \hfill =\sum _{\mathit{ȷ}=0}^{\infty }{\underline{W}}_{\mathit{ȷ}}(\mathsf{\Lambda },\phi ,\varphi ;\varrho )t^{\mathit{ȷ}\Im }\hfill \\ & \hfill ={\underline{W}}_0(\mathsf{\Lambda },\phi ,\varphi ;\varrho )+{\underline{W}}_1(\mathsf{\Lambda },\phi ,\varphi ;\varrho )t^{\Im }+{\underline{W}}_2(\mathsf{\Lambda },\phi ,\varphi ;\varrho )t^{2\Im }+{\underline{W}}_3(\mathsf{\Lambda },\phi ,\varphi ;\varrho )t^{3\Im }+\dots ,\hfill \\ \hfill \underline{h}(\mathsf{\Lambda },\phi ,\varphi ,t;\varrho )& \hfill =\sum _{\mathit{ȷ}=0}^{\infty }{\underline{H}}_{\mathit{ȷ}}(\mathsf{\Lambda },\phi ,\varphi ;\varrho )t^{\mathit{ȷ}\Im }\hfill \\ \hfill & \hfill ={\underline{H}}_0(\mathsf{\Lambda },\phi ,\varphi ;\varrho )+{\underline{H}}_1(\mathsf{\Lambda },\phi ,\varphi ;\varrho )t^{\Im }+{\underline{H}}_2(\mathsf{\Lambda },\phi ,\varphi ;\varrho )t^{2\Im }+{\underline{H}}_3(\mathsf{\Lambda },\phi ,\varphi ;\varrho )t^{3\Im }+\dots ,\hfill \end{array}\right\}\end{array}$$

(88)

and

$$\begin{array}{c}\hfill \left.\begin{array}{cc}\hfill \stackrel{̲}{w}(\mathsf{\Lambda },\phi ,\varphi ,t;\varrho )& \hfill =\sum _{\mathit{ȷ}=0}^{\infty }{\stackrel{̲}{W}}_{\mathit{ȷ}}(\mathsf{\Lambda },\phi ,\varphi ;\varrho )t^{\mathit{ȷ}\Im }\hfill \\ & \hfill ={\stackrel{̲}{W}}_0(\mathsf{\Lambda },\phi ,\varphi ;\varrho )+{\stackrel{̲}{W}}_1(\mathsf{\Lambda },\phi ,\varphi ;\varrho )t^{\Im }+{\stackrel{̲}{W}}_2(\mathsf{\Lambda },\phi ,\varphi ;\varrho )t^{2\Im }+{\stackrel{̲}{W}}_3(\mathsf{\Lambda },\phi ,\varphi ;\varrho )t^{3\Im }+\dots ,\hfill \\ \hfill \stackrel{̲}{h}(\mathsf{\Lambda },\phi ,\varphi ,t;\varrho )& \hfill =\sum _{\mathit{ȷ}=0}^{\infty }{\stackrel{̲}{H}}_{\mathit{ȷ}}(\mathsf{\Lambda },\phi ,\varphi ;\varrho )t^{\mathit{ȷ}\Im }\hfill \\ \hfill & \hfill ={\stackrel{̲}{H}}_0(\mathsf{\Lambda },\phi ,\varphi ;\varrho )+{\stackrel{̲}{H}}_1(\mathsf{\Lambda },\phi ,\varphi ;\varrho )t^{\Im }+{\stackrel{̲}{H}}_2(\mathsf{\Lambda },\phi ,\varphi ;\varrho )t^{2\Im }+{\stackrel{̲}{H}}_3(\mathsf{\Lambda },\phi ,\varphi ;\varrho )t^{3\Im }+\dots \hfill \end{array}\right\}\end{array}$$

(89)

4.4. Applications and Results

In this part, we present the approximate solution of fuzzy time-fractional telegraphic equations via fuzzy RDTM.

Example 4.

We consider the following two-dimensional fuzzy linear time-fractional telegraphic equation

$$\frac{{\partial }^{2\Im }\tilde{w}}{\partial t^{2\Im }}\oplus 2\odot \frac{{\partial }^{\Im }\tilde{w}}{\partial t^{\Im }}\oplus \tilde{w}=\frac{{\partial }^2\tilde{w}}{\partial {\mathsf{\Lambda }}^2}\oplus \frac{{\partial }^2\tilde{w}}{\partial {\phi }^2},$$

(90)

under the initial conditions

$$\begin{array}{cc}\hfill \tilde{w}(\mathsf{\Lambda },\phi ,0)& \hfill =[{(1+2\varrho )}^{ı},{(5-2\varrho )}^{ı}]\odot exp(\mathsf{\Lambda }+\phi ),\hfill \\ \hfill \tilde{w}(\mathsf{\Lambda },\phi ,0)& \hfill =[{(1+2\varrho )}^{ı},{(5-2\varrho )}^{ı}]\odot -3exp(\mathsf{\Lambda }+\phi ),ı=1,2,3,\dots ,0\le \varrho \le 1.\hfill \end{array}$$

(91)

Using the fuzzy RDTM on (90), we obtain

$$\begin{array}{cc}\hfill & \hfill \frac{\mathsf{\Gamma }(\mathit{ȷ}\Im +2\Im +1)}{\mathsf{\Gamma }(\mathit{ȷ}\Im +1)}{\underline{W}}_{\mathit{ȷ}+2}(\mathsf{\Lambda },\phi ;\varrho )+2\frac{\mathsf{\Gamma }(\mathit{ȷ}\Im +\Im +1)}{\mathsf{\Gamma }(\mathit{ȷ}\Im +1)}{\underline{W}}_{\mathit{ȷ}+1}(\mathsf{\Lambda },\phi ;\varrho )\hfill \end{array}$$

$$\begin{array}{c}\hfill =\frac{{\partial }^2}{\partial {\mathsf{\Lambda }}^2}{\underline{W}}_{\mathit{ȷ}}(\mathsf{\Lambda },\phi ;\varrho )+\frac{{\partial }^2}{\partial {\phi }^2}{\underline{W}}_{\mathit{ȷ}}(\mathsf{\Lambda },\phi ;\varrho )-{\underline{W}}_{\mathit{ȷ}}(\mathsf{\Lambda },\phi ;\varrho ),\hfill \end{array}$$

(92)

$$\begin{array}{c}\hfill \frac{\mathsf{\Gamma }(\mathit{ȷ}\Im +2\Im +1)}{\mathsf{\Gamma }(\mathit{ȷ}\Im +1)}{\stackrel{̲}{W}}_{\mathit{ȷ}+2}(\mathsf{\Lambda },\phi ;\varrho )+2\frac{\mathsf{\Gamma }(\mathit{ȷ}\Im +\Im +1)}{\mathsf{\Gamma }(\mathit{ȷ}\Im +1)}{\stackrel{̲}{W}}_{\mathit{ȷ}+1}(\mathsf{\Lambda },\phi ;\varrho )\hfill \end{array}$$

$$\begin{array}{c}\hfill =\frac{{\partial }^2}{\partial {\mathsf{\Lambda }}^2}{\stackrel{̲}{W}}_{\mathit{ȷ}}(\mathsf{\Lambda },\phi ;\varrho )+\frac{{\partial }^2}{\partial {\phi }^2}{\stackrel{̲}{W}}_{\mathit{ȷ}}(\mathsf{\Lambda },\phi ;\varrho )-{\stackrel{̲}{W}}_{\mathit{ȷ}}(\mathsf{\Lambda },\phi ;\varrho ).\hfill \end{array}$$

(93)

From initial conditions (91), it follows that

$$\begin{array}{cc}\hfill {\underline{W}}_0(\mathsf{\Lambda },\phi ;\varrho )& \hfill ={(1+2\varrho )}^{ı}exp(\mathsf{\Lambda }+\phi ),{\underline{W}}_1(\mathsf{\Lambda },\phi ;\varrho )=-3{(1+2\varrho )}^{ı}exp(\mathsf{\Lambda }+\phi ),\hfill \end{array}$$

(94)

$$\begin{array}{cc}\hfill {\stackrel{̲}{W}}_0(\mathsf{\Lambda },\phi ;\varrho )& \hfill ={(5-2\varrho )}^{ı}exp(\mathsf{\Lambda }+\phi ),{\stackrel{̲}{W}}_1(\mathsf{\Lambda },\phi ;\varrho )=-3{(5-2\varrho )}^{ı}exp(\mathsf{\Lambda }+\phi ).\hfill \end{array}$$

(95)

Applying Equations (95) into (92), we obtain

$$\begin{array}{cc}\hfill {\underline{W}}_{\mathit{ȷ}}(\mathsf{\Lambda },\phi ;\varrho )& \hfill ={(1+2\varrho )}^{ı}\left[\frac{{(-3)}^{\mathit{ȷ}}}{\mathsf{\Gamma }\left(\frac{\mathit{ȷ}}{\zeta }+1\right)}\mathsf{\Gamma }\left(\frac{\zeta +1}{\zeta }\right)exp(\mathsf{\Lambda }+\phi )\right];\mathit{ȷ}\ge 2,\hfill \end{array}$$

(96)

$$\begin{array}{cc}\hfill {\stackrel{̲}{W}}_{\mathit{ȷ}}(\mathsf{\Lambda },\phi ;\varrho )& \hfill ={(5-2\varrho )}^{ı}\left[\frac{{(-3)}^{\mathit{ȷ}}}{\mathsf{\Gamma }\left(\frac{\mathit{ȷ}}{\zeta }+1\right)}\mathsf{\Gamma }\left(\frac{\zeta +1}{\zeta }\right)exp(\mathsf{\Lambda }+\phi )\right];\mathit{ȷ}\ge 2,\hfill \end{array}$$

(97)

where $\Im =\frac{1}{\zeta },\zeta >0.$

Utilizing the differential inverse fuzzy RDTM on ${\tilde{W}}_{\mathit{ȷ}}(\mathsf{\Lambda },\phi ;\varrho )$, we obtain

$$\begin{array}{cc}\hfill \underline{w}(\mathsf{\Lambda },\phi ,t;\varrho )& \hfill =\sum _{\mathit{ȷ}=0}^{\infty }{\underline{W}}_{\mathit{ȷ}}(\mathsf{\Lambda },\phi ;\varrho )t^{\mathit{ȷ}\Im }=\sum _{\mathit{ȷ}=0}^{\infty }{\underline{W}}_{\mathit{ȷ}}(\mathsf{\Lambda },\phi ;\varrho )t^{\frac{\mathit{ȷ}}{\zeta }}\hfill \\ \hfill & \hfill =\left[{\underline{W}}_0(\mathsf{\Lambda },\phi ;\varrho )+{\underline{W}}_1(\mathsf{\Lambda },\phi ;\varrho )t^{\frac{1}{\zeta }}+{\underline{W}}_2(\mathsf{\Lambda },\phi ;\varrho )t^{\frac{2}{\zeta }}+{\underline{W}}_3(\mathsf{\Lambda },\phi ;\varrho )t^{\frac{3}{\zeta }}+\dots \right],\hfill \\ \hfill & \hfill ={(1+2\varrho )}^{ı}\hfill \\ \hfill & \hfill \times \left[exp(\mathsf{\Lambda }+\phi )\left[1+(-3)t^{\frac{1}{\zeta }}+\mathsf{\Gamma }\left(\frac{\zeta +1}{\zeta }\right)\left[\frac{{(-3)}^2}{\mathsf{\Gamma }\left(\frac{2}{\zeta }+1\right)}{t}^{\frac{2}{\zeta }}+\frac{{(-3)}^3}{\mathsf{\Gamma }\left(\frac{3}{\zeta }+1\right)}{t}^{\frac{3}{\zeta }}+\dots \right]\right]\right],\hfill \end{array}$$

(98)

and

$$\begin{array}{cc}\hfill \stackrel{̲}{w}(\mathsf{\Lambda },\phi ,t;\varrho )& \hfill =\sum _{\mathit{ȷ}=0}^{\infty }{\stackrel{̲}{W}}_{\mathit{ȷ}}(\mathsf{\Lambda },\phi ;\varrho )t^{\mathit{ȷ}\Im }=\sum _{\mathit{ȷ}=0}^{\infty }{\stackrel{̲}{W}}_{\mathit{ȷ}}(\mathsf{\Lambda },\phi ;\varrho )t^{\frac{\mathit{ȷ}}{\zeta }}\hfill \\ \hfill & \hfill =\left[{\stackrel{̲}{W}}_0(\mathsf{\Lambda },\phi ;\varrho )+{\stackrel{̲}{W}}_1(\mathsf{\Lambda },\phi ;\varrho )t^{\frac{1}{\zeta }}+{\stackrel{̲}{W}}_2(\mathsf{\Lambda },\phi ;\varrho )t^{\frac{2}{\zeta }}+{\stackrel{̲}{W}}_3(\mathsf{\Lambda },\phi ;\varrho )t^{\frac{3}{\zeta }}+\dots \right],\hfill \\ \hfill & \hfill ={(5-2\varrho )}^{ı}\hfill \\ \hfill & \hfill \times \left[exp(\mathsf{\Lambda }+\phi )\left[1+(-3)t^{\frac{1}{\zeta }}+\mathsf{\Gamma }\left(\frac{\zeta +1}{\zeta }\right)\left[\frac{{(-3)}^2}{\mathsf{\Gamma }\left(\frac{2}{\zeta }+1\right)}{t}^{\frac{2}{\zeta }}+\frac{{(-3)}^3}{\mathsf{\Gamma }\left[\frac{3}{\zeta }+1\right)}{t}^{\frac{3}{\zeta }}+\dots \right]\right]\right].\hfill \end{array}$$

(99)

Thus, when $\zeta =1,$ i.e., $\Im =1$, it is easy to arrive at the exact solution:

$$\begin{array}{c}\hfill \tilde{w}(\mathsf{\Lambda },\phi ,t;\varrho )=[{(1+2\varrho )}^{ı},{(5-2\varrho )}^{ı}]\odot exp(\mathsf{\Lambda }+\phi -3t),0\le \varrho \le 1.\end{array}$$

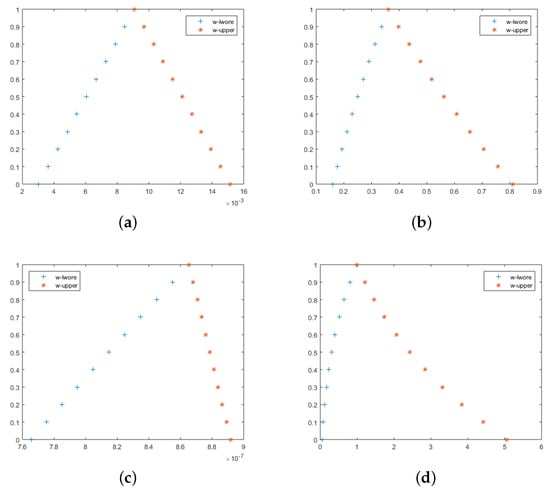
The fuzzy RDTM lower and upper solution of Equation (90) are demonstrated in Figure 2a, where $\mathsf{\Lambda }=0.0001,\phi =0.2,t=2,$ and $ı=1$ show the precision and compliance with the proposed theory.

Figure 2. The exact lower and upper solutions of Equations (90), (100), (110), and (118) at (a) $\mathsf{\Lambda }=0.0001,\phi =0.2,t=2,ı=1,$ (b) $\mathsf{\Lambda }=0.002,\phi =0.1,\varphi =0.6,t=3,ı=2,$ (c) $\mathsf{\Lambda }=0.01,\phi =0.03,t=7,ı=3,$ and (d) $\mathsf{\Lambda }=0.4,\phi =0.3,\varphi =0.8,t=4,ı=4,$ respectively.

Example 5.

Let us turn to consider the following three-dimensional fuzzy linear time-fractional telegraphic equation

$$\frac{{\partial }^{2\Im }\tilde{w}}{\partial t^{2\Im }}\oplus 2\odot \frac{{\partial }^{\Im }\tilde{w}}{\partial t^{\Im }}\oplus \tilde{w}=\frac{{\partial }^2\tilde{w}}{\partial {\mathsf{\Lambda }}^2}\oplus \frac{{\partial }^2\tilde{w}}{\partial {\phi }^2}\oplus \frac{{\partial }^2\tilde{w}}{\partial {\varphi }^2},$$

(100)

under the initial conditions

$$\begin{array}{cc}\hfill \tilde{w}(\mathsf{\Lambda },\phi ,\varphi ,0)& \hfill =[{(0.4+0.2\varrho )}^{ı},{(0.9-0.3\varrho )}^{ı}]\oplus sinh\left(\mathsf{\Lambda }\right)sinh\left(\phi \right)sinh\left(\varphi \right),\hfill \\ \hfill \tilde{w}(\mathsf{\Lambda },\phi ,\varphi ,0)& \hfill =[{(0.4+0.2\varrho )}^{ı},{(0.9-0.3\varrho )}^{ı}]\oplus -sinh\left(\mathsf{\Lambda }\right)sinh\left(\phi \right)sinh\left(\varphi \right),ı=1,2,3,\dots ,0\le \varrho \le 1.\hfill \end{array}$$

(101)

Using the fuzzy RDTM on (100), we have

$$\begin{array}{c}\hfill \frac{\mathsf{\Gamma }(\mathit{ȷ}\Im +2\Im +1)}{\mathsf{\Gamma }(\mathit{ȷ}\Im +1)}{\underline{W}}_{\mathit{ȷ}+2}(\mathsf{\Lambda },\phi ,\varphi ;\varrho )+2\frac{\mathsf{\Gamma }(\mathit{ȷ}\Im +\Im +1)}{\mathsf{\Gamma }(\mathit{ȷ}\Im +1)}{\underline{W}}_{\mathit{ȷ}+1}(\mathsf{\Lambda },\phi ,\varphi ;\varrho )\hfill \end{array}$$

$$\begin{array}{cc}\hfill & \hfill =\frac{{\partial }^2}{\partial {\mathsf{\Lambda }}^2}{\underline{W}}_{\mathit{ȷ}}(\mathsf{\Lambda },\phi ,\varphi ;\varrho )+\frac{{\partial }^2}{\partial {\phi }^2}{\underline{W}}_{\mathit{ȷ}}(\mathsf{\Lambda },\phi ,\varphi ;\varrho )+\frac{{\partial }^2}{\partial {\mathsf{\Lambda }}^2}{\underline{W}}_{\mathit{ȷ}}(\mathsf{\Lambda },\phi ,\varphi ;\varrho )-{\underline{W}}_{\mathit{ȷ}}(\mathsf{\Lambda },\phi ,\varphi ;\varrho ),\hfill \end{array}$$

(102)

$$\begin{array}{c}\hfill \frac{\mathsf{\Gamma }(\mathit{ȷ}\Im +2\Im +1)}{\mathsf{\Gamma }(\mathit{ȷ}\Im +1)}{\stackrel{̲}{W}}_{\mathit{ȷ}+2}(\mathsf{\Lambda },\phi ,\varphi ;\varrho )+2\frac{\mathsf{\Gamma }(\mathit{ȷ}\Im +\Im +1)}{\mathsf{\Gamma }(\mathit{ȷ}\Im +1)}{\stackrel{̲}{W}}_{\mathit{ȷ}+1}(\mathsf{\Lambda },\phi ,\varphi ;\varrho )\hfill \end{array}$$

$$\begin{array}{cc}\hfill & \hfill =\frac{{\partial }^2}{\partial {\mathsf{\Lambda }}^2}{\stackrel{̲}{W}}_{\mathit{ȷ}}(\mathsf{\Lambda },\phi ,\varphi ;\varrho )+\frac{{\partial }^2}{\partial {\phi }^2}{\stackrel{̲}{W}}_{\mathit{ȷ}}(\mathsf{\Lambda },\phi ,\varphi ;\varrho )+\frac{{\partial }^2}{\partial {\mathsf{\Lambda }}^2}{\stackrel{̲}{W}}_{\mathit{ȷ}}(\mathsf{\Lambda },\phi ,\varphi ;\varrho )-{\stackrel{̲}{W}}_{\mathit{ȷ}}(\mathsf{\Lambda },\phi ,\varphi ;\varrho ).\hfill \end{array}$$

(103)

Putting the initial conditions (100), it is easy to obtain

$$\begin{array}{c}\hfill \left.\begin{array}{cc}\hfill {\underline{W}}_0(\mathsf{\Lambda },\phi ,\varphi ;\varrho )& \hfill ={(0.4+0.2\varrho )}^{ı}+[sinh\left(\mathsf{\Lambda }\right)sinh\left(\phi \right)sinh\left(\varphi \right)],\hfill \\ \hfill {\underline{W}}_1(\mathsf{\Lambda },\phi ,\varphi ;\varrho )& \hfill ={(0.4+0.2\varrho )}^{ı}+[-sinh\left(\mathsf{\Lambda }\right)sinh\left(\phi \right)sinh\left(\varphi \right)],\hfill \end{array}\right\}\end{array}$$

(104)

$$\begin{array}{c}\hfill \left.\begin{array}{cc}\hfill {\stackrel{̲}{W}}_0(\mathsf{\Lambda },\phi ,\varphi ;\varrho )& \hfill ={(0.9-0.3\varrho )}^{ı}+[sinh\left(\mathsf{\Lambda }\right)sinh\left(\phi \right)sinh\left(\varphi \right)],\hfill \\ \hfill {\stackrel{̲}{W}}_1(\mathsf{\Lambda },\phi ,\varphi ;\varrho )& \hfill ={(0.9-0.3\varrho )}^{ı}+[-sinh\left(\mathsf{\Lambda }\right)sinh\left(\phi \right)sinh\left(\varphi \right)].\hfill \end{array}\right\}\end{array}$$

(105)

Putting (105) into (102), we obtain

$$\begin{array}{cc}\hfill {\underline{W}}_{\mathit{ȷ}}(\mathsf{\Lambda },\phi ,\varphi ;\varrho )& \hfill ={(0.4+0.2\varrho )}^{ı}+\left[\frac{{(-1)}^{\mathit{ȷ}}}{\mathsf{\Gamma }\left(\frac{\mathit{ȷ}}{\zeta }+1\right)}\mathsf{\Gamma }\left(\frac{\zeta +1}{\zeta }\right)sinh\left(\mathsf{\Lambda }\right)sinh\left(\phi \right)sinh\left(\varphi \right)\right];\mathit{ȷ}\ge 2,\hfill \end{array}$$

(106)

$$\begin{array}{cc}\hfill {\stackrel{̲}{W}}_{\mathit{ȷ}}(\mathsf{\Lambda },\phi ,\varphi ;\varrho )& \hfill ={(0.9-0.3\varrho )}^{ı}+\left[\frac{{(-1)}^{\mathit{ȷ}}}{\mathsf{\Gamma }\left(\frac{\mathit{ȷ}}{\zeta }+1\right)}\mathsf{\Gamma }\left(\frac{\zeta +1}{\zeta }\right)sinh\left(\mathsf{\Lambda }\right)sinh\left(\phi \right)sinh\left(\varphi \right)\right];\mathit{ȷ}\ge 2.\hfill \end{array}$$

(107)

Utilizing the fuzzy differential inverse RDTM on ${\tilde{W}}_{\mathit{ȷ}}(\mathsf{\Lambda },\phi ,\varphi ;\varrho )$, we obtain

$$\begin{array}{c}\hfill \left.\begin{array}{cc}\hfill & \hfill \underline{w}(\mathsf{\Lambda },\phi ,\varphi ,t;\varrho )=\sum _{\mathit{ȷ}=0}^{\infty }{\underline{W}}_{\mathit{ȷ}}(\mathsf{\Lambda },\phi ,\varphi ;\varrho )t^{\mathit{ȷ}\Im }=\sum _{\mathit{ȷ}=0}^{\infty }{\underline{W}}_{\mathit{ȷ}}(\mathsf{\Lambda },\phi ,\varphi ;\varrho )t^{\frac{\mathit{ȷ}}{\zeta }}\hfill \\ \hfill & \hfill =\left[{\underline{W}}_0(\mathsf{\Lambda },\phi ,\varphi ;\varrho )+{\underline{W}}_1(\mathsf{\Lambda },\phi ,\varphi ;\varrho )t^{\frac{1}{\zeta }}+{\underline{W}}_2(\mathsf{\Lambda },\phi ,\varphi ;\varrho )t^{\frac{2}{\zeta }}+{\underline{W}}_3(\mathsf{\Lambda },\phi ,\varphi ;\varrho )t^{\frac{3}{\zeta }}+\cdots \right]\hfill \\ \hfill & \hfill ={(0.4+0.2\varrho )}^{ı}+\left[sinh\left(\mathsf{\Lambda }\right)sinh\left(\phi \right)sinh\left(\varphi \right)\left[1+(-1)t^{\frac{1}{\zeta }}+\mathsf{\Gamma }\left(\frac{\zeta +1}{\zeta }\right)\left[\frac{{(-1)}^2}{\mathsf{\Gamma }\left(\frac{2}{\zeta }+1\right)}{t}^{\frac{2}{\zeta }}\right.\right.\right.\hfill \\ \hfill & \hfill \left.\left.\left.+\frac{{(-1)}^3}{\mathsf{\Gamma }\left(\frac{3}{\zeta }+1\right)}{t}^{\frac{3}{\zeta }}+\cdots \right]\right]\right],\hfill \end{array}\right\}\end{array}$$

(108)

and

$$\begin{array}{c}\hfill \left.\begin{array}{cc}\hfill & \hfill \stackrel{̲}{w}(\mathsf{\Lambda },\phi ,\varphi ,t;\varrho )=\sum _{\mathit{ȷ}=0}^{\infty }{\stackrel{̲}{W}}_{\mathit{ȷ}}(\mathsf{\Lambda },\phi ,\varphi ;\varrho )t^{\mathit{ȷ}\Im }=\sum _{\mathit{ȷ}=0}^{\infty }{\stackrel{̲}{W}}_{\mathit{ȷ}}(\mathsf{\Lambda },\phi ,\varphi ;\varrho )t^{\frac{\mathit{ȷ}}{\zeta }}\hfill \\ \hfill & \hfill =\left[{\stackrel{̲}{W}}_0(\mathsf{\Lambda },\phi ,\varphi ;\varrho )+{\stackrel{̲}{W}}_1(\mathsf{\Lambda },\phi ,\varphi ;\varrho )t^{\frac{1}{\zeta }}+{\stackrel{̲}{W}}_2(\mathsf{\Lambda },\phi ,\varphi ;\varrho )t^{\frac{2}{\zeta }}+{\stackrel{̲}{W}}_3(\mathsf{\Lambda },\phi ,\varphi ;\varrho )t^{\frac{3}{\zeta }}+\cdots \right]\hfill \\ \hfill & \hfill ={(0.9-0.3\varrho )}^{ı}+\left[sinh\left(\mathsf{\Lambda }\right)sinh\left(\phi \right)sinh\left(\varphi \right)\left[1+(-1)t^{\frac{1}{\zeta }}+\mathsf{\Gamma }\left(\frac{\zeta +1}{\lambda }\right)\left[\frac{{(-1)}^2}{\mathsf{\Gamma }\left(\frac{2}{\zeta }+1\right)}{t}^{\frac{2}{\lambda }}\right.\right.\right.\hfill \\ \hfill & \hfill \left.\left.\left.+\frac{{(-1)}^3}{\mathsf{\Gamma }\left(\frac{3}{\zeta }+1\right)}{t}^{\frac{3}{\zeta }}+\cdots \right]\right]\right].\hfill \end{array}\right\}\end{array}$$

(109)

Thus, when $\zeta =1,$ i.e., $\Im =1$, it is easy to arrive at the exact solution:

$$\begin{array}{c}\hfill \tilde{w}(\mathsf{\Lambda },\phi ,\varphi ,t;\varrho )=[{(0.4+0.2\varrho )}^{ı},{(0.9-0.3\varrho )}^{ı}]\oplus exp(-t)sinh\left(\mathsf{\Lambda }\right)sinh\left(\phi \right)sinh\left(\varphi \right),0\le \varrho \le 1.\end{array}$$

The fuzzy RDTM lower and upper solution of Equation (100) are demonstrated in Figure 2b, where $\mathsf{\Lambda }=0.002,\phi =0.1,\varphi =0.6,t=3,$ and $ı=2$ show the precision and compliance with the proposed theory.

Example 6.

Let us now consider the following two-dimensional nonlinear fuzzy time-fractional telegraphic equation

$$\frac{{\partial }^2\tilde{w}}{\partial {\mathsf{\Lambda }}^2}\oplus \frac{{\partial }^2\tilde{w}}{\partial {\phi }^2}=\frac{{\partial }^{2\Im }\tilde{w}}{\partial t^{2\Im }}\oplus 2\odot \frac{{\partial }^{\Im }\tilde{w}}{\partial t^{\Im }}\oplus {\tilde{w}}^2{\ominus }_{gH}exp(2(\mathsf{\Lambda }+\phi )-4t)+exp((\mathsf{\Lambda }+\phi )-2t),$$

(110)

under the initial conditions

$$\begin{array}{cc}\hfill \tilde{w}(\mathsf{\Lambda },\phi ,0)& \hfill =[{(0.96+0.04\varrho )}^{ı},{(1.01-0.01\varrho )}^{ı}]\odot exp(\mathsf{\Lambda }+\phi ),\hfill \\ \hfill {\tilde{w}}_t(\mathsf{\Lambda },\phi ,0)& \hfill =[{(0.96+0.04\varrho )}^{ı},{(1.01-0.01\varrho )}^{ı}]\odot -2exp(\mathsf{\Lambda }+\phi ),ı=1,2,3,\dots ,0\le \varrho \le 1.\hfill \end{array}$$

(111)

Using the fuzzy RDTM on (110), we have

$$\begin{array}{cc}\hfill & \hfill \frac{\mathsf{\Gamma }(\mathit{ȷ}\Im +2\Im +1)}{\mathsf{\Gamma }(\mathit{ȷ}\Im +1)}{\underline{W}}_{\mathit{ȷ}+2}(\mathsf{\Lambda },\phi ;\varrho )+2\frac{\mathsf{\Gamma }(\mathit{ȷ}\Im +\Im +1)}{\mathsf{\Gamma }(\mathit{ȷ}\Im +1)}{\underline{W}}_{\mathit{ȷ}+1}(\mathsf{\Lambda },\phi ;\varrho )=\frac{{\partial }^2}{\partial {\mathsf{\Lambda }}^2}{\underline{W}}_{\mathit{ȷ}}(\mathsf{\Lambda },\phi ;\varrho )+\frac{{\partial }^2}{\partial {\phi }^2}{\underline{W}}_{\mathit{ȷ}}(\mathsf{\Lambda },\phi ;\varrho )\hfill \end{array}$$

$$\begin{array}{cc}\hfill & \hfill -\sum _{\gamma =0}^{\mathit{ȷ}}{\underline{W}}_{\gamma }(\mathsf{\Lambda },\phi ;\varrho ){\underline{W}}_{\mathit{ȷ}-\gamma }(\mathsf{\Lambda },\phi ;\varrho )+exp\left(2(\mathsf{\Lambda }+\phi )\right)\left[\frac{{(-4)}^{\mathit{ȷ}}}{\mathit{ȷ}!}\right]-exp(\mathsf{\Lambda }+\phi )\left[\frac{{(-2)}^{\mathit{ȷ}}}{\mathit{ȷ}!}\right],\hfill \end{array}$$

(112)

$$\begin{array}{cc}\hfill & \hfill \frac{\mathsf{\Gamma }(\mathit{ȷ}\Im +2\Im +1)}{\mathsf{\Gamma }(\mathit{ȷ}\Im +1)}{\stackrel{̲}{W}}_{\mathit{ȷ}+2}(\mathsf{\Lambda },\phi ;\varrho )+2\frac{\mathsf{\Gamma }(\mathit{ȷ}\Im +\Im +1)}{\mathsf{\Gamma }(\mathit{ȷ}\Im +1)}{\stackrel{̲}{W}}_{\mathit{ȷ}+1}(\mathsf{\Lambda },\phi ;\varrho )=\frac{{\partial }^2}{\partial {\mathsf{\Lambda }}^2}{\stackrel{̲}{W}}_{\mathit{ȷ}}(\mathsf{\Lambda },\phi ;\varrho )+\frac{{\partial }^2}{\partial {\phi }^2}{\stackrel{̲}{W}}_{\mathit{ȷ}}(\mathsf{\Lambda },\phi ;\varrho )\hfill \end{array}$$

$$\begin{array}{cc}\hfill & \hfill -\sum _{\gamma =0}^{\mathit{ȷ}}{\stackrel{̲}{W}}_{\gamma }(\mathsf{\Lambda },\phi ;\varrho ){\stackrel{̲}{W}}_{\mathit{ȷ}-\gamma }(\mathsf{\Lambda },\phi ;\varrho )+exp\left(2(\mathsf{\Lambda }+\phi )\right)\left[\frac{{(-4)}^{\mathit{ȷ}}}{\mathit{ȷ}!}\right]-exp(\mathsf{\Lambda }+\phi )\left[\frac{{(-2)}^{\mathit{ȷ}}}{\mathit{ȷ}!}\right].\hfill \end{array}$$

(113)

Putting the initial conditions (111), we obtain

$$\begin{array}{c}\hfill \left.\begin{array}{cc}\hfill {\underline{W}}_0(\mathsf{\Lambda },\phi ;\varrho )& \hfill ={(0.96+0.04\varrho )}^{ı}exp(\mathsf{\Lambda }+\phi ),\hfill \\ \hfill {\underline{W}}_1(\mathsf{\Lambda },\phi ;\varrho )& \hfill =-2{(0.96+0.04\varrho )}^{ı}exp(\mathsf{\Lambda }+\phi ),\hfill \end{array}\right\},\end{array}$$

(114)

and

$$\begin{array}{c}\hfill \left.\begin{array}{cc}\hfill {\stackrel{̲}{W}}_0(\mathsf{\Lambda },\phi ;\varrho )& \hfill ={(1.01-0.01\varrho )}^{ı}exp(\mathsf{\Lambda }+\phi ),\hfill \\ \hfill {\stackrel{̲}{W}}_1(\mathsf{\Lambda },\phi ;\varrho )& \hfill =-2{(1.01-0.01\varrho )}^{ı}exp(\mathsf{\Lambda }+\phi ),\hfill \end{array}\right\}.\end{array}$$

(115)

From (115) into (112),

$$\begin{array}{cc}\hfill {\underline{W}}_{\mathit{ȷ}}(\mathsf{\Lambda },\phi ;\varrho )& \hfill ={(0.96+0.04\varrho )}^{ı}\left[\frac{{(-2)}^{\mathit{ȷ}}}{\mathsf{\Gamma }\left(\frac{\mathit{ȷ}}{\zeta }+1\right)}\mathsf{\Gamma }\left(\frac{\zeta +1}{\zeta }\right)exp(\mathsf{\Lambda }+\phi )\right];\mathit{ȷ}\ge 2,\hfill \end{array}$$

(116)

$$\begin{array}{cc}\hfill {\stackrel{̲}{W}}_{\mathit{ȷ}}(\mathsf{\Lambda },\phi ;\varrho )& \hfill ={(1.01-0.01\varrho )}^{ı}\left[\frac{{(-2)}^{\mathit{ȷ}}}{\mathsf{\Gamma }\left(\frac{\mathit{ȷ}}{\zeta }+1\right)}\mathsf{\Gamma }\left(\frac{\zeta +1}{\zeta }\right)exp(\mathsf{\Lambda }+\phi )\right];\mathit{ȷ}\ge 2.\hfill \end{array}$$

(117)

Similarly, using the differential inverse RDTM on ${\tilde{W}}_{\mathit{ȷ}}(\mathsf{\Lambda },\phi ;\varrho )$, when $\zeta =1,$ it is easy to arrive at the exact solution:

$$\begin{array}{c}\hfill \tilde{w}(\mathsf{\Lambda },\phi ,t;\varrho )=[{(0.96+0.04\varrho )}^{ı},{(1.01-0.01\varrho )}^{ı}]\odot exp((\mathsf{\Lambda }+\phi )-2t),0\le \varrho \le 1.\end{array}$$

The fuzzy RDTM lower and upper solution of Equation (110) are demonstrated in Figure 2c, where $\mathsf{\Lambda }=0.01,\phi =0.03,t=7,$ and $ı=3$ show the precision and compliance with the proposed theory.

Example 7.

Let us next consider the following three-dimensional nonlinear fuzzy time-fractional telegraphic equation

$$\frac{{\partial }^2\tilde{w}}{\partial {\mathsf{\Lambda }}^2}\oplus \frac{{\partial }^2\tilde{w}}{\partial {\phi }^2}\oplus \frac{{\partial }^2\tilde{w}}{\partial {\varphi }^2}=\frac{{\partial }^{2\Im }\tilde{w}}{\partial t^{2\Im }}\oplus 2\odot \frac{{\partial }^{\Im }\tilde{w}}{\partial t^{\Im }}\oplus {\tilde{w}}^2{\ominus }_{gH}exp(2(\mathsf{\Lambda }-\phi -\varphi )-4t)\oplus exp((\mathsf{\Lambda }-\phi -\varphi )-2t),$$

(118)

under the initial conditions

$$\begin{array}{cc}\hfill \tilde{w}(\mathsf{\Lambda },\phi ,\varphi ,0)& \hfill =[{(0.5+0.5\varrho )}^{ı},{(1.5-0.5\varrho )}^{ı}]{\ominus }_{gH}exp(\mathsf{\Lambda }-\phi -\varphi ),\hfill \\ \hfill {\tilde{w}}_t(\mathsf{\Lambda },\phi ,\varphi ,0)& \hfill =[{(0.5+0.5\varrho )}^{ı},{(1.5-0.5\varrho )}^{ı}]{\ominus }_{gH}-exp(\mathsf{\Lambda }-\phi -\varphi ),ı=1,2,3,\dots ,0\le \varrho \le 1.\hfill \end{array}$$

(119)

Using the fuzzy RDTM on (118), we obtain

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \hfill & \hfill \frac{\mathsf{\Gamma }(\mathit{ȷ}\Im +2\Im +1)}{\mathsf{\Gamma }(\mathit{ȷ}\Im +1)}{\underline{W}}_{\mathit{ȷ}+2}(\mathsf{\Lambda },\phi ,\varphi ;\varrho )+2\frac{\mathsf{\Gamma }(\mathit{ȷ}\Im +\Im +1)}{\mathsf{\Gamma }(\mathit{ȷ}\Im +1)}{\underline{W}}_{\mathit{ȷ}+1}(\mathsf{\Lambda },\phi ,\varphi ;\varrho )\hfill \\ \hfill \hfill & \hfill =\frac{{\partial }^2}{\partial {\mathsf{\Lambda }}^2}{\underline{W}}_{\mathit{ȷ}}(\mathsf{\Lambda },\phi ,\varphi ;\varrho )+\frac{{\partial }^2}{\partial {\phi }^2}{\underline{W}}_{\mathit{ȷ}}(\mathsf{\Lambda },\phi ,\varphi ;\varrho )+\frac{{\partial }^2}{\partial {\mathsf{\Lambda }}^2}{\underline{W}}_{\mathit{ȷ}}(\mathsf{\Lambda },\phi ,\varphi ;\varrho )\hfill \\ \hfill \hfill & \hfill -\sum _{\gamma =0}^{\mathit{ȷ}}{\underline{W}}_{\gamma }(\mathsf{\Lambda },\phi ,\varphi ;\varrho ){\underline{W}}_{\mathit{ȷ}-\gamma }(\mathsf{\Lambda },\phi ,\varphi ;\varrho )+exp\left(2(\mathsf{\Lambda }+\phi +\varphi )\right)\left[\frac{{(-4)}^{\mathit{ȷ}}}{\mathit{ȷ}!}\right]-exp(\mathsf{\Lambda }+\phi +\varphi )\left[\frac{{(-2)}^{\mathit{ȷ}}}{\mathit{ȷ}!}\right],\hfill \end{array}\end{array}$$

(120)

and

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \hfill & \hfill \frac{\mathsf{\Gamma }(\mathit{ȷ}\Im +2\Im +1)}{\mathsf{\Gamma }(\mathit{ȷ}\Im +1)}{\stackrel{̲}{W}}_{\mathit{ȷ}+2}(\mathsf{\Lambda },\phi ,\varphi ;\varrho )+2\frac{\mathsf{\Gamma }(\mathit{ȷ}\Im +\Im +1)}{\mathsf{\Gamma }(\mathit{ȷ}\Im +1)}{\stackrel{̲}{W}}_{\mathit{ȷ}+1}(\mathsf{\Lambda },\phi ,\varphi ;\varrho )\hfill \\ \hfill \hfill & \hfill =\frac{{\partial }^2}{\partial {\mathsf{\Lambda }}^2}{\stackrel{̲}{W}}_{\mathit{ȷ}}(\mathsf{\Lambda },\phi ,\varphi ;\varrho )+\frac{{\partial }^2}{\partial {\phi }^2}{\stackrel{̲}{W}}_{\mathit{ȷ}}(\mathsf{\Lambda },\phi ,\varphi ;\varrho )+\frac{{\partial }^2}{\partial {\mathsf{\Lambda }}^2}{\stackrel{̲}{W}}_{\mathit{ȷ}}(\mathsf{\Lambda },\phi ,\varphi ;\varrho )\hfill \\ \hfill \hfill & \hfill -\sum _{\gamma =0}^{\mathit{ȷ}}{\stackrel{̲}{W}}_{\gamma }(\mathsf{\Lambda },\phi ,\varphi ;\varrho ){\stackrel{̲}{W}}_{\mathit{ȷ}-\gamma }(\mathsf{\Lambda },\phi ,\varphi ;\varrho )+exp\left(2(\mathsf{\Lambda }+\phi +\varphi )\right)\left[\frac{{(-4)}^{\mathit{ȷ}}}{\mathit{ȷ}!}\right]-exp(\mathsf{\Lambda }+\phi +\varphi )\left[\frac{{(-2)}^{\mathit{ȷ}}}{\mathit{ȷ}!}\right].\hfill \end{array}\end{array}$$

(121)

From the initial conditions (119), it follows that

$$\begin{array}{c}\hfill \left.\begin{array}{cc}\hfill {\underline{W}}_0(\mathsf{\Lambda },\phi ,\varphi ;\varrho )& \hfill ={(0.5+0.5\varrho )}^{ı}-exp(\mathsf{\Lambda }-\phi -\varphi ),\hfill \\ \hfill {\underline{W}}_1(\mathsf{\Lambda },\phi ,\varphi ;\varrho )& \hfill ={(0.5+0.5\varrho )}^{ı}+exp(\mathsf{\Lambda }-\phi -\varphi ),\hfill \end{array}\right\}\end{array}$$

(122)

and

$$\begin{array}{c}\hfill \left.\begin{array}{cc}\hfill {\stackrel{̲}{W}}_0(\mathsf{\Lambda },\phi ,\varphi ;\varrho )& \hfill ={(1.5-0.5\varrho )}^{ı}-exp(\mathsf{\Lambda }-\phi -\varphi ),\hfill \\ \hfill {\stackrel{̲}{W}}_1(\mathsf{\Lambda },\phi ,\varphi ;\varrho )& \hfill ={(1.5-0.5\varrho )}^{ı}+exp(\mathsf{\Lambda }-\phi -\varphi ).\hfill \end{array}\right\}\end{array}$$

(123)

Putting (123) into (120), we have

$$\begin{array}{cc}\hfill {\underline{W}}_{\mathit{ȷ}}(\mathsf{\Lambda },\phi ,\varphi ;\varrho )& \hfill ={(0.5+0.5\varrho )}^{ı}-\left[\frac{{(-1)}^{\mathit{ȷ}}}{\mathsf{\Gamma }(\frac{\mathit{ȷ}}{\zeta }+1)}\mathsf{\Gamma }\left(\frac{\zeta +1}{\zeta }\right)exp(\mathsf{\Lambda }-\phi -\varphi )\right];\mathit{ȷ}\ge 2,\hfill \end{array}$$

(124)

$$\begin{array}{cc}\hfill {\stackrel{̲}{W}}_{\mathit{ȷ}}(\mathsf{\Lambda },\phi ,\varphi ;\varrho )& \hfill ={(1.5-0.5\varrho )}^{ı}-\left[\frac{{(-1)}^{\mathit{ȷ}}}{\mathsf{\Gamma }(\frac{\mathit{ȷ}}{\zeta }+1)}\mathsf{\Gamma }\left(\frac{\zeta +1}{\zeta }\right)exp(\mathsf{\Lambda }-\phi -\varphi )\right];\mathit{ȷ}\ge 2.\hfill \end{array}$$

(125)

Similarly, using the differential inverse RDTM on ${\tilde{W}}_{\mathit{ȷ}}(\mathsf{\Lambda },\phi ,\varphi ;\varrho )$, when $\Im =1$, it is easy to arrive at the exact solution:

$$\begin{array}{c}\hfill \tilde{w}(\mathsf{\Lambda },\phi ,\varphi ,t;\varrho )=[{(0.5+0.5\varrho )}^{ı},{(1.5-0.5\varrho )}^{ı}]{\ominus }_{gH}exp(\mathsf{\Lambda }-\phi -\varphi -t),0\le \varrho \le 1.\end{array}$$

The fuzzy RDTM lower and upper solution of Equation (118) are demonstrated in Figure 2d, where $\mathsf{\Lambda }=0.4,\phi =0.3,\varphi =0.8,t=4,$ and $ı=4$ show the precision and compliance with the proposed theory.

5. Fuzzy Time-Fractional Diffusion Equation

In the current section, let us present the definition of the fuzzy fractional VHPIM, which is utilized to solve the fuzzy fractional diffusion equation.

Assume that $f:R\to R,\mathsf{\Lambda }\to f\left(\mathsf{\Lambda }\right)$ is called the continuous function. Through the fractional Riemann–Liouville integral

$$\begin{array}{c}\hfill I_{\mathsf{\Lambda }}^{\Im }\tilde{f}\left(\mathsf{\Lambda }\right)=\frac{1}{\mathsf{\Gamma }(\Im )}{\int }_0^{\mathsf{\Lambda }}{(\mathsf{\Lambda }-\kappa )}^{\Im -1}f\left(\kappa \right)d\kappa ,\Im >0,\end{array}$$

(126)

the modified Riemann–Liouville derivative is given by

$$\begin{array}{c}\hfill D_{\mathsf{\Lambda }}^{\Im }\tilde{f}\left(\mathsf{\Lambda }\right)=\frac{1}{\mathsf{\Gamma }(ı-\Im )}\frac{d^n}{d{\mathsf{\Lambda }}^n}{\int }_0^{\mathsf{\Lambda }}{(\mathsf{\Lambda }-\kappa )}^{n-\Im }(f\left(\kappa \right)-f\left(0\right))d\kappa ,n\ge 1,n-1\le \Im <n.\end{array}$$

(127)

The formula for Jumarie’s fractional derivative of order ℑ is as follows:

$$\begin{array}{c}\hfill f^{(\Im )}=\underset{\epsilon \to 0}{lim}\frac{{\mathsf{\Delta }}^{\Im }f\left(\mathsf{\Lambda }\right)}{{\epsilon }^{\Im }},\end{array}$$

(128)

where

$$\begin{array}{c}\hfill {\mathsf{\Delta }}^{\Im }f\left(\mathsf{\Lambda }\right)={(Fw-1)}^{\Im }f\left(\mathsf{\Lambda }\right)=\sum _{\mathit{ȷ}=0}^{\infty }{(-1)}^{\mathit{ȷ}}\left(\begin{array}{c}\Im \\ \mathit{ȷ}\end{array}\right)f(\mathsf{\Lambda }+(\Im -\mathit{ȷ})\epsilon ),\end{array}$$

(129)

for $Fwf\left(\mathsf{\Lambda }\right)=f(\mathsf{\Lambda }+\epsilon ).$

The presented modified Riemann–Liouville derivative as given in (127) is strictly equivalent to (128), cf. [39,40]. The integral with respect to ${\left(d\mathsf{\Lambda }\right)}^{\Im }$ is given by

$$\begin{array}{c}\hfill d\phi =f\left(\mathsf{\Lambda }\right){\left(d\mathsf{\Lambda }\right)}^{\Im },\mathsf{\Lambda }\ge 0,\phi \left(0\right)=0,0<\Im \le 1.\end{array}$$

(130)

Suppose that $f\left(\mathsf{\Lambda }\right)$ is a continuous function, then the solution of (130) is given by

$$\begin{array}{c}\hfill \phi ={\int }_0^{\mathsf{\Lambda }}f\left(\kappa \right){\left(d\kappa \right)}^{\Im }=\Im {\int }_0^{\mathsf{\Lambda }}{(\mathsf{\Lambda }-\kappa )}^{\Im -1}f\left(\kappa \right)d\kappa ,0<\Im \le 1.\end{array}$$

(131)

Before recalling the fuzzy time-fractional diffusion equation, we introduced a few notations which will be utilized throughout this part. For order ℑ, we denote by $\frac{{\partial }^{\Im }}{\partial t^{\Im }}(·)$ the modified Riemann–Liouville derivative. The symbols ∇ and Δ denote the Hamilton and the Laplace operators, respectively. The expression $\mathsf{\Psi }=[0,L_1]\times [0,L_2]\times ···\times [0,L_d]$ stands for the spatial domain of the problem, d is the dimension of the space, $\mathsf{\Lambda }=({\ell }_1,{\ell }_2,{\ell }_3,\dots ,{\ell }_d)$, $\partial \mathsf{\Psi }$ denotes the boundary of $\mathsf{\Psi }$, $\tilde{w}(\mathsf{\Lambda },t)$ indicates the probability density fuzzy-valued function of locating a particle at $\mathsf{\Lambda }$ in time t. The letter D stands for the positive constant depending on the temperature, the friction coefficient, the universal gas constant, and the Avagadro constant. Moreover, $F\left(\mathsf{\Lambda }\right)$ is the external force.

Let us recall the fuzzy time-fractional diffusion equation given by the formula:

$$\frac{{\partial }^{\Im }\tilde{w}(\mathsf{\Lambda },t)}{\partial t^{\Im }}=D\mathsf{\Delta }\tilde{w}(\mathsf{\Lambda },t){\ominus }_{gH}\nabla ·(F\left(\mathsf{\Lambda }\right)\odot \tilde{w}(\mathsf{\Lambda },t)),0<\Im \le 1,D>0,$$

(132)

under the initial condition

$$\tilde{w}(\mathsf{\Lambda },0)=\tilde{\psi }\left(\mathsf{\Lambda }\right),\mathsf{\Lambda }\in \mathsf{\Psi },$$

(133)

as well as boundary condition

$$\tilde{w}(\mathsf{\Lambda },t)=\tilde{\psi }(\mathsf{\Lambda },t),\mathsf{\Lambda }\in \partial \mathsf{\Psi },t\ge 0.$$

(134)

From (132), it can be viewed as modeling the diffusion of a particle under the action of the external force $F\left(\mathsf{\Lambda }\right).$

5.1. Analysis of the Method

Here are the main steps of the fuzzy fractional variational homotopy perturbation iteration method:

Step 1${}^{\star }$. Let us say that a nonlinear equation, with two independent variables $\mathsf{\Lambda }$ and t, as follows:

$$D_t^{\Im }\tilde{w}(\mathsf{\Lambda },t)=\mathcal{L}\left(\tilde{w}(\mathsf{\Lambda },t)\right)\oplus \mathcal{N}\left(\tilde{w}(\mathsf{\Lambda },t)\right)\oplus \tilde{g}(\mathsf{\Lambda },t),$$

(135)

where $D_t^{\Im }(·)$ stands for the fuzzy Riemann–Liouville derivative, $\Im >0$, the symbols $\mathcal{N}$ and $\mathcal{L}$ stand for nonlinear and linear operators, respectively. We denote by $\tilde{g}(\mathsf{\Lambda },t)$ the fuzzy inhomogeneous term, and $\tilde{w}=\tilde{w}(\mathsf{\Lambda },t)$ is an unknown fuzzy-valued function.

Step 2${}^{\star }$. Let us construct the correct functional as follows:

$$\left.\begin{array}{cc}\hfill {\underline{w}}_{\mathit{ȷ}+1}(\mathsf{\Lambda },t;\varrho )& \hfill ={\underline{w}}_{\mathit{ȷ}}(\mathsf{\Lambda },t;\varrho )+J_t^{\Im }\left[\rho \left(\tau \right)\left(D_{\tau }^{\Im }{\underline{w}}_{\mathit{ȷ}}(\mathsf{\Lambda },\tau ;\varrho )-\mathcal{L}\left({\underline{w}}_{\mathit{ȷ}}(\mathsf{\Lambda },\tau ;\varrho )\right)\right.\right.\hfill \\ \hfill & \hfill \left.\left.-\mathcal{N}\left({\underline{w}}_{\mathit{ȷ}}(\mathsf{\Lambda },\tau ;\varrho )\right)-\underline{g}(\mathsf{\Lambda },\tau ;\varrho )\right)\right]\hfill \\ \hfill {\stackrel{̲}{w}}_{\mathit{ȷ}+1}(\mathsf{\Lambda },t;\varrho )& \hfill ={\stackrel{̲}{w}}_{\mathit{ȷ}}(\mathsf{\Lambda },t;\varrho )+J_t^{\Im }\left[\rho \left(\tau \right)\left(D_{\tau }^{\Im }{\stackrel{̲}{w}}_{\mathit{ȷ}}(\mathsf{\Lambda },\tau ;\varrho )-\mathcal{L}\left({\stackrel{̲}{w}}_{\mathit{ȷ}}(\mathsf{\Lambda },\tau ;\varrho )\right)\right.\right.\hfill \\ \hfill & \hfill \left.\left.-\mathcal{N}\left({\stackrel{̲}{w}}_{\mathit{ȷ}}(\mathsf{\Lambda },\tau ;\varrho )\right)-\stackrel{̲}{g}(\mathsf{\Lambda },\tau ;\varrho )\right)\right]\hfill \end{array}\right\},\mathit{ȷ}\ge 0,$$

whenever the letter $\rho$ appears, it refers to a general Lagrange multiplier that variational theory can ideally describe. The symbol $\mathit{ȷ}\ge 0$ means the ${\mathit{ȷ}}^{th}$ approximation, and the fuzzy-valued function ${\tilde{w}}_{\mathit{ȷ}}(\mathsf{\Lambda },\tau ;\varrho )=[{\underline{w}}_{\mathit{ȷ}}(\mathsf{\Lambda },\tau ;\varrho ),{\stackrel{̲}{w}}_{\mathit{ȷ}}(\mathsf{\Lambda },\tau ;\varrho )]$ is a restricted variant that corresponds to the formula

$$\begin{array}{c}\hfill \delta {\underline{w}}_{\mathit{ȷ}}(\mathsf{\Lambda },\tau ;\varrho )=\tilde{0},\delta {\stackrel{̲}{w}}_{\mathit{ȷ}}(\mathsf{\Lambda },\tau ;\varrho )=\tilde{0}.\end{array}$$

Step 3${}^{\star }$. Based on the fuzzy fractional VHPIM, let us derive the following iteration formula

$$\begin{array}{cc}\hfill \sum _{\mathit{ȷ}=0}^{\infty }{q}^{\mathit{ȷ}}{\underline{w}}_{\mathit{ȷ}}(\mathsf{\Lambda },t;\varrho )& \hfill ={\underline{w}}_0(\mathsf{\Lambda },t;\varrho )+q\left[\sum _{\mathit{ȷ}=0}^{\infty }{q}^{\mathit{ȷ}}{\underline{w}}_{\mathit{ȷ}}(\mathsf{\Lambda },t;\varrho )+J_t^{\Im }\left[\rho \left(\tau \right)\left(\sum _{\mathit{ȷ}=0}^{\infty }{q}^{\mathit{ȷ}}{D}_{\tau }^{\Im }{\underline{w}}_{\mathit{ȷ}}(\mathsf{\Lambda },\tau ;\varrho )\right.\right.\right.\hfill \\ \hfill & \hfill \left.\left.\left.-\sum _{\mathit{ȷ}=0}^{\infty }{q}^{\mathit{ȷ}}\mathcal{L}\left({\underline{w}}_{\mathit{ȷ}}(\mathsf{\Lambda },\tau ;\varrho )\right)-\sum _{\mathit{ȷ}=0}^{\infty }{q}^{\mathit{ȷ}}\mathcal{N}\left({\underline{w}}_{\mathit{ȷ}}(\mathsf{\Lambda },\tau ;\varrho )\right)-\underline{g}(\mathsf{\Lambda },\tau ;\varrho )\right)\right]\right],\hfill \end{array}$$

(136)

and

$$\begin{array}{cc}\hfill \sum _{\mathit{ȷ}=0}^{\infty }{q}^{\mathit{ȷ}}{\stackrel{̲}{w}}_{\mathit{ȷ}}(\mathsf{\Lambda },t;\varrho )& \hfill ={\stackrel{̲}{w}}_0(\mathsf{\Lambda },t;\varrho )+q\left[\sum _{\mathit{ȷ}=0}^{\infty }{q}^{\mathit{ȷ}}{\stackrel{̲}{w}}_{\mathit{ȷ}}(\mathsf{\Lambda },t;\varrho )+J_t^{\Im }\left[\rho \left(\tau \right)\left(\sum _{\mathit{ȷ}=0}^{\infty }{q}^{\mathit{ȷ}}{D}_{\tau }^{\Im }{\stackrel{̲}{w}}_{\mathit{ȷ}}(\mathsf{\Lambda },\tau ;\varrho )\right.\right.\right.\hfill \\ \hfill & \hfill \left.\left.\left.-\sum _{\mathit{ȷ}=0}^{\infty }{q}^{\mathit{ȷ}}\mathcal{L}\left({\stackrel{̲}{w}}_{\mathit{ȷ}}(\mathsf{\Lambda },\tau ;\varrho )\right)-\sum _{\mathit{ȷ}=0}^{\infty }{q}^{\mathit{ȷ}}\mathcal{N}\left({\stackrel{̲}{w}}_{\mathit{ȷ}}(\mathsf{\Lambda },\tau ;\varrho )\right)-\stackrel{̲}{g}(\mathsf{\Lambda },\tau ;\varrho )\right)\right]\right],\hfill \end{array}$$

(137)

where $q\in [0,1]$ stands for an imbedding parameter, and ${\tilde{w}}_0(\mathsf{\Lambda },t;\varrho )=[{\underline{w}}_0(\mathsf{\Lambda },t;\varrho ),{\stackrel{̲}{w}}_0(\mathsf{\Lambda },t;\varrho )]$ is the initial approximation of (135).

Step 4${}^{\star }$. In comparison to the coefficient of the same power of q in both hands of the formulas of Equations (136) and (137), we have $w_i(\mathsf{\Lambda },t;\varrho )$ for $i=0,1,2,3,\cdots$. For $q⟶1$ and using the fuzzy homotopy perturbation approach, we obtain

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \underline{w}(\mathsf{\Lambda },t;\varrho )& \hfill ={\underline{w}}_0(\mathsf{\Lambda },t;\varrho )+{\underline{w}}_1(\mathsf{\Lambda },t;\varrho )+\cdots \hfill \\ \hfill \stackrel{̲}{w}(\mathsf{\Lambda },t;\varrho )& \hfill ={\stackrel{̲}{w}}_0(\mathsf{\Lambda },t;\varrho )+{\stackrel{̲}{w}}_1(\mathsf{\Lambda },t;\varrho )+\cdots \hfill \end{array}\end{array}$$

(138)

5.2. Application of the Method

In this part, let us consider the correctness of the following functional for Equation (132), which we define as follows:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\underline{w}}_{n+1}(\mathsf{\Lambda },t;\varrho )\hfill & \hfill ={\underline{w}}_n(\mathsf{\Lambda },t;\varrho )+J_t^{\Im }\left[\rho \left(\tau \right)\left(\frac{{\partial }^{\Im }{\underline{w}}_n(\mathsf{\Lambda },\tau ;\varrho )}{\partial {\tau }^{\Im }}-\mathsf{\Delta }{\underline{w}}_n(\mathsf{\Lambda },\tau ;\varrho )+\nabla ·\left(F\left(\mathsf{\Lambda }\right){\underline{w}}_n(\mathsf{\Lambda },\tau ;\varrho )\right)\right)\right]\hfill \\ \hfill \hfill & \hfill ={\underline{w}}_n(\mathsf{\Lambda },t;\varrho )+\frac{1}{\mathsf{\Gamma }(\Im )}{\int }_0^t{(t-\tau )}^{\Im -1}\left[\rho \left(\tau \right)\left(\frac{{\partial }^{\Im }\underline{w}(\mathsf{\Lambda },t;\varrho )}{\partial {\tau }^{\Im }}\right.\right.\hfill \\ \hfill \hfill & \hfill \left.\left.-\mathsf{\Delta }{\underline{w}}_n(\mathsf{\Lambda },\tau ;\varrho )+\nabla ·\left(F\left(\mathsf{\Lambda }\right){\underline{w}}_n(\mathsf{\Lambda },\tau ;\varrho )\right)\right)\right]d\tau \hfill \\ \hfill \hfill & \hfill ={\underline{w}}_n(\mathsf{\Lambda },t;\varrho )+\frac{1}{\mathsf{\Gamma }(1+\Im )}{\int }_0^t\left[\rho \left(\tau \right)\left(\frac{{\partial }^{\Im }\underline{w}(\mathsf{\Lambda },t;\varrho )}{\partial {\tau }^{\Im }}\right.\right.\hfill \\ \hfill \hfill & \hfill \left.\left.-\mathsf{\Delta }{\underline{w}}_n(\mathsf{\Lambda },\tau ;\varrho )+\nabla ·\left(F\left(\mathsf{\Lambda }\right){\underline{w}}_n(\mathsf{\Lambda },\tau ;\varrho )\right)\right)\right]{\left(d\tau \right)}^{\Im },\hfill \end{array}\end{array}$$

(139)

and

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\stackrel{̲}{w}}_{n+1}(\mathsf{\Lambda },t;\varrho )\hfill & \hfill ={\stackrel{̲}{w}}_n(\mathsf{\Lambda },t;\varrho )+J_t^{\Im }\left[\rho \left(\tau \right)\left(\frac{{\partial }^{\Im }{\stackrel{̲}{w}}_n(\mathsf{\Lambda },\tau ;\varrho )}{\partial {\tau }^{\Im }}-\mathsf{\Delta }{\stackrel{̲}{w}}_n(\mathsf{\Lambda },\tau ;\varrho )+\nabla ·\left(F\left(\mathsf{\Lambda }\right){\stackrel{̲}{w}}_n(\mathsf{\Lambda },\tau ;\varrho )\right)\right)\right]\hfill \\ \hfill \hfill & \hfill ={\stackrel{̲}{w}}_n(\mathsf{\Lambda },t;\varrho )+\frac{1}{\mathsf{\Gamma }(\Im )}{\int }_0^t{(t-\tau )}^{\Im -1}\left[\rho \left(\tau \right)\left(\frac{{\partial }^{\Im }\stackrel{̲}{w}(\mathsf{\Lambda },t;\varrho )}{\partial {\tau }^{\Im }}\right.\right.\hfill \\ \hfill \hfill & \hfill \left.\left.-\mathsf{\Delta }{\stackrel{̲}{w}}_n(\mathsf{\Lambda },\tau ;\varrho )+\nabla ·\left(F\left(\mathsf{\Lambda }\right){\stackrel{̲}{w}}_n(\mathsf{\Lambda },\tau ;\varrho )\right)\right)\right]d\tau \hfill \\ \hfill \hfill & \hfill ={\stackrel{̲}{w}}_n(\mathsf{\Lambda },t;\varrho )+\frac{1}{\mathsf{\Gamma }(1+\Im )}{\int }_0^t\left[\rho \left(\tau \right)\left(\frac{{\partial }^{\Im }\stackrel{̲}{w}(\mathsf{\Lambda },t;\varrho )}{\partial {\tau }^{\Im }}\right.\right.\hfill \\ \hfill \hfill & \hfill \left.\left.-\mathsf{\Delta }{\stackrel{̲}{w}}_n(\mathsf{\Lambda },\tau ;\varrho )+\nabla ·\left(F\left(\mathsf{\Lambda }\right){\stackrel{̲}{w}}_n(\mathsf{\Lambda },\tau ;\varrho )\right)\right)\right]{\left(d\tau \right)}^{\Im },\hfill \end{array}\end{array}$$

(140)

where the expression $w_n(\mathsf{\Lambda },t;\varrho )=[{\underline{w}}_n(\mathsf{\Lambda },t;\varrho ),{\stackrel{̲}{w}}_n(\mathsf{\Lambda },t;\varrho )]$ denotes the restricted variation, which means $\delta {\underline{w}}_n(\mathsf{\Lambda },t;\varrho )=\tilde{0},\delta {\stackrel{̲}{w}}_n(\mathsf{\Lambda },t;\varrho )=\tilde{0}$, and $w_0(\mathsf{\Lambda },t;\varrho )=[{\underline{w}}_0(\mathsf{\Lambda },t;\varrho ),{\stackrel{̲}{w}}_0(\mathsf{\Lambda },t;\varrho )]$ is an initial approximation that must be chosen as suitable. The following can be utilized to find the fixed conditions:

$$\left.\begin{array}{cc}\hfill & \hfill {\rho }^{\Im }\left(\tau \right)=0,\tau \in [0,t],\hfill \\ \hfill & \hfill 1+\rho \left(\tau \right){\mid }_{\tau =t}=0.\hfill \end{array}\right\}$$

Hence, the Lagrange multiplier can be determined as $\rho =-1$. Utilizing Equations (139) and (140), we can formulate the iteration as follows:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \sum _{\mathit{ȷ}=0}^{\infty }{q}^{\mathit{ȷ}}{\underline{w}}_{\mathit{ȷ}}(\mathsf{\Lambda },t;\varrho )\hfill & \hfill ={\underline{w}}_0(\mathsf{\Lambda },t;\varrho )+q\left[\sum _{\mathit{ȷ}=0}^{\infty }{q}^{\mathit{ȷ}}{\underline{w}}_{\mathit{ȷ}}(\mathsf{\Lambda },t;\varrho )\right.\hfill \\ \hfill \hfill & \hfill -\frac{1}{\mathsf{\Gamma }(1+\Im )}{\int }_0^t\left(\sum _{\mathit{ȷ}=0}^{\infty }{q}^{\mathit{ȷ}}\frac{{\partial }^{\Im }{\underline{w}}_{\mathit{ȷ}}(\mathsf{\Lambda },\tau ;\varrho )}{\partial {\tau }^{\Im }}-\sum _{\mathit{ȷ}=0}^{\infty }{q}^{\mathit{ȷ}}▵{\underline{w}}_{\mathit{ȷ}}(\mathsf{\Lambda },\tau ;\varrho )\right.\hfill \\ \hfill \hfill & \hfill \left.\left.+\sum _{\mathit{ȷ}=0}^{\infty }{q}^{\mathit{ȷ}}\nabla ·(F\left(\mathsf{\Lambda }\right){\underline{w}}_{\mathit{ȷ}}(\mathsf{\Lambda },\tau ;\varrho )\right){\left(d\tau \right)}^{\Im }\right],0<\Im \le 1,\hfill \end{array}\end{array}$$

(141)

and

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \sum _{\mathit{ȷ}=0}^{\infty }{q}^{\mathit{ȷ}}{\stackrel{̲}{w}}_{\mathit{ȷ}}(\mathsf{\Lambda },t;\varrho )\hfill & \hfill ={\stackrel{̲}{w}}_0(\mathsf{\Lambda },t;\varrho )+q\left[\sum _{\mathit{ȷ}=0}^{\infty }{q}^{\mathit{ȷ}}{\stackrel{̲}{w}}_{\mathit{ȷ}}(\mathsf{\Lambda },t;\varrho )\right.\hfill \\ \hfill \hfill & \hfill -\frac{1}{\mathsf{\Gamma }(1+\Im )}{\int }_0^t\left(\sum _{\mathit{ȷ}=0}^{\infty }{q}^{\mathit{ȷ}}\frac{{\partial }^{\Im }{\stackrel{̲}{w}}_{\mathit{ȷ}}(\mathsf{\Lambda },\tau ;\varrho )}{\partial {\tau }^{\Im }}-\sum _{\mathit{ȷ}=0}^{\infty }{q}^{\mathit{ȷ}}▵{\stackrel{̲}{w}}_{\mathit{ȷ}}(\mathsf{\Lambda },\tau ;\varrho )\right.\hfill \\ \hfill \hfill & \hfill \left.\left.+\sum _{\mathit{ȷ}=0}^{\infty }{q}^{\mathit{ȷ}}\nabla ·(F\left(\mathsf{\Lambda }\right){\stackrel{̲}{w}}_{\mathit{ȷ}}(\mathsf{\Lambda },\tau ;\varrho )\right){\left(d\tau \right)}^{\Im }\right],0<\Im \le 1,\hfill \end{array}\end{array}$$

(142)

where ${\tilde{w}}_0(\mathsf{\Lambda },t;\varrho )$ is the initial approximate of Equation (132). In comparison to the coefficient of the same power of q in both hands of the above Equations (141) and (142), it is easy to obtain ${\tilde{w}}_i(\mathsf{\Lambda },t;\varrho )=[{\underline{w}}_i(\mathsf{\Lambda },t;\varrho ),{\stackrel{̲}{w}}_i(\mathsf{\Lambda },t;\varrho )]$, with $i=0,1,2,3,\cdots .$

Using the fuzzy homotopy perturbation method, we obtain

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \underline{w}(\mathsf{\Lambda },t;\varrho )& \hfill ={\underline{w}}_0(\mathsf{\Lambda },t;\varrho )+{\underline{w}}_1(\mathsf{\Lambda },t;\varrho )+{\underline{w}}_2(\mathsf{\Lambda },t;\varrho )+\cdots \hfill \\ \hfill \stackrel{̲}{w}(\mathsf{\Lambda },t;\varrho )& \hfill ={\stackrel{̲}{w}}_0(\mathsf{\Lambda },t;\varrho )+{\stackrel{̲}{w}}_1(\mathsf{\Lambda },t;\varrho )+{\stackrel{̲}{w}}_2(\mathsf{\Lambda },t;\varrho )+\cdots \hfill \end{array}\end{array}$$

(143)

5.3. Examples

We propose the different examples to illustrate the fuzzy fractional diffusion equation via fuzzy fractional VHPIM.

Now, let us discuss the fuzzy fractional diffusion equation in one dimension as the following:

Example 8.

Let us set $D=1,F\left(\mathsf{\Lambda }\right)=-1$ and $\mathsf{\Psi }=[0,1];$ then, Equation (132) can be written as

$$\begin{array}{c}\hfill \frac{{\partial }^{\Im }\tilde{w}(\mathsf{\Lambda },t)}{\partial t^{\Im }}=\frac{{\partial }^2\tilde{w}(\mathsf{\Lambda },t)}{\partial {\mathsf{\Lambda }}^2}\oplus \frac{\partial \tilde{w}(\mathsf{\Lambda },t)}{\partial \mathsf{\Lambda }},0<\Im \le 1,\end{array}$$

(144)

under the initial condition

$$\begin{array}{c}\hfill \tilde{w}(\mathsf{\Lambda },0)=[{(0.1+0.1\varrho )}^{ı},{(0.3-0.1\varrho )}^{ı}]\odot exp\left(\mathsf{\Lambda }\right),0\le \mathsf{\Lambda }\le 1,ı=1,2,3,\dots ,\end{array}$$

(145)

and the boundary conditions

$$\begin{array}{c}\hfill \tilde{w}(0,t)=E_{\Im }\left(2t^{\Im }\right),\tilde{w}(1,t)=e{E}_{\Im }\left(2t^{\Im }\right),t\ge 0.\end{array}$$

(146)

Putting the initial value ${\tilde{w}}_0(\mathsf{\Lambda },0)=\tilde{w}(\mathsf{\Lambda },0)=[{(0.1+0.1\varrho )}^{ı},{(0.3-0.1\varrho )}^{ı}]\odot exp\left(\mathsf{\Lambda }\right)$ into the iteration formulation (141) and (142), we obtain

$$\begin{array}{c}\hfill \left.\begin{array}{cc}\hfill q^0:{\underline{w}}_0(\mathsf{\Lambda },t;\varrho )& \hfill ={(0.1+0.1\varrho )}^{ı}exp\left(\mathsf{\Lambda }\right)\hfill \\ \hfill q^1:{\underline{w}}_1(\mathsf{\Lambda },t;\varrho )& \hfill =\frac{{(0.1+0.1\varrho )}^{ı}exp\left(\mathsf{\Lambda }\right)2t^{\Im }}{\mathsf{\Gamma }(1+\Im )},\hfill \\ \hfill q^2:{\underline{w}}_2(\mathsf{\Lambda },t;\varrho )& \hfill =\frac{{(0.1+0.1\varrho )}^{ı}exp\left(\mathsf{\Lambda }\right)2^2{t}^{2\Im }}{\mathsf{\Gamma }(1+2\Im )},\hfill \\ \hfill q^3:{\underline{w}}_3(\mathsf{\Lambda },t;\varrho )& \hfill =\frac{{(0.1+0.1\varrho )}^{ı}exp\left(\mathsf{\Lambda }\right)2^3{t}^{3\Im }}{\mathsf{\Gamma }(1+3\Im )},\hfill \\ \hfill ⋮\\ \hfill q^{\mathit{ȷ}}:{\underline{w}}_{\mathit{ȷ}}(\mathsf{\Lambda },t;\varrho )& \hfill =\frac{{(0.1+0.1\varrho )}^{ı}exp\left(\mathsf{\Lambda }\right)2^{\mathit{ȷ}}{t}^{\mathit{ȷ}\Im }}{\mathsf{\Gamma }(1+\mathit{ȷ}\Im )},\hfill \end{array}\right\}\end{array}$$

(147)

and

$$\begin{array}{c}\hfill \left.\begin{array}{cc}\hfill q^0:{\stackrel{̲}{w}}_0(\mathsf{\Lambda },t;\varrho )& \hfill ={(0.3-0.1\varrho )}^{ı}exp\left(\mathsf{\Lambda }\right)\hfill \\ \hfill q^1:{\stackrel{̲}{w}}_1(\mathsf{\Lambda },t;\varrho )& \hfill =\frac{{(0.3-0.1\varrho )}^{ı}exp\left(\mathsf{\Lambda }\right)2t^{\Im }}{\mathsf{\Gamma }(1+\Im )},\hfill \\ \hfill q^2:{\stackrel{̲}{w}}_2(\mathsf{\Lambda },t;\varrho )& \hfill =\frac{{(0.3-0.1\varrho )}^{ı}exp\left(\mathsf{\Lambda }\right)2^2{t}^{2\Im }}{\mathsf{\Gamma }(1+2\Im )},\hfill \\ \hfill q^3:{\stackrel{̲}{w}}_3(\mathsf{\Lambda },t;\varrho )& \hfill =\frac{{(0.3-0.1\varrho )}^{ı}exp\left(\mathsf{\Lambda }\right)2^3{t}^{3\Im }}{\mathsf{\Gamma }(1+3\Im )},\hfill \\ \hfill ⋮\\ \hfill q^{\mathit{ȷ}}:{\stackrel{̲}{w}}_{\mathit{ȷ}}(\mathsf{\Lambda },t;\varrho )& \hfill =\frac{{(0.3-0.1\varrho )}^{ı}exp\left(\mathsf{\Lambda }\right)2^{\mathit{ȷ}}{t}^{\mathit{ȷ}\Im }}{\mathsf{\Gamma }(1+\mathit{ȷ}\Im )}.\hfill \end{array}\right\}\end{array}$$

(148)

Therefore, the limit has a compact form, as demonstrated below:

$$\begin{array}{cc}\hfill \underline{w}(\mathsf{\Lambda },t;\varrho )& =\underset{n\to \infty }{lim}\sum _{\mathit{ȷ}=0}^n{\underline{w}}_{\mathit{ȷ}}(\mathsf{\Lambda },t;\varrho )\hfill \\ & ={(0.1+0.1\varrho )}^{ı}\left(\underset{n\to \infty }{lim}\sum _{\mathit{ȷ}=0}^n\frac{exp\left(\mathsf{\Lambda }\right)2^{\mathit{ȷ}}{t}^{\mathit{ȷ}\Im }}{\mathsf{\Gamma }(1+\mathit{ȷ}\Im )}\right),\hfill \end{array}$$

(149)

and

$$\begin{array}{cc}\hfill \stackrel{̲}{w}(\mathsf{\Lambda },t;\varrho )& =\underset{n\to \infty }{lim}\sum _{\mathit{ȷ}=0}^n{\stackrel{̲}{w}}_{\mathit{ȷ}}(\mathsf{\Lambda },t;\varrho )\hfill \\ & ={(0.3-0.1\varrho )}^{ı}\left(\underset{n\to \infty }{lim}\sum _{\mathit{ȷ}=0}^n\frac{exp\left(\mathsf{\Lambda }\right)2^{\mathit{ȷ}}{t}^{\mathit{ȷ}\Im }}{\mathsf{\Gamma }(1+\mathit{ȷ}\Im )}\right),\hfill \end{array}$$

(150)

The solution can be expressed in mathematical form as shown below:

$$\begin{array}{c}\hfill \tilde{w}(\mathsf{\Lambda },t;\varrho )=[{(0.1+0.1\varrho )}^{ı},{(0.3-0.1\varrho )}^{ı}]\odot exp\left(\mathsf{\Lambda }\right)E_{\Im }\left(2t^{\Im }\right),0\le \varrho \le 1.\end{array}$$

In the work of Osman et al. [41], the authors mentioned that for their method, the solution is convergent for $t=0.001$, but the issue of convergence of the fuzzy fractional VHPIM for large t is, in general, rather delicate. Therefore, we give the comparison for the VHPIM with Example $4.1$ in [41] and obtained that the solution for Example 8 using fuzzy fractional VHPIM in our current work shows convergence until time $t=254$. Hence, this shows that our method gives better results in comparison. Meanwhile, we have also compared the error terms between exact and approximate solutions in Example 8 for $\varrho$ between 0 and 1 in Table 1 for giving the clear solution for the $1D$ fuzzy fractional diffusion equation. Moreover, to present the solution in more depth, we plotted the solution in 3D as well, which can be seen in Figure 3b and Figure 4b.

Table 1. Table for the error term between exact solutions (ES) and approximate solutions (AS).

$\mathit{\varrho }$	Lower ES	Lower AS	Lower Error	Upper ES	Upper AS	Upper Error
0	9.0017	1.0376	7.9641	27.005	3.1128	23.892
0.1	9.9019	1.1414	8.7605	26.105	3.0091	23.096
0.2	10.802	1.2451	9.5569	25.205	2.9053	22.299
0.3	11.702	1.3489	10.353	24.305	2.8015	21.503
0.4	12.602	1.4527	11.15	23.404	2.6978	20.707
0.5	13.503	1.5564	11.946	22.504	2.594	19.91
0.6	14.403	1.6602	12.743	21.604	2.4903	19.114
0.7	15.303	1.7639	13.539	20.704	2.3865	18.317
0.8	16.203	1.8677	14.335	19.804	2.2827	17.521
0.9	17.103	1.9715	15.132	18.904	2.179	16.725
1	18.003	2.0752	15.928	18.003	2.0752	15.928

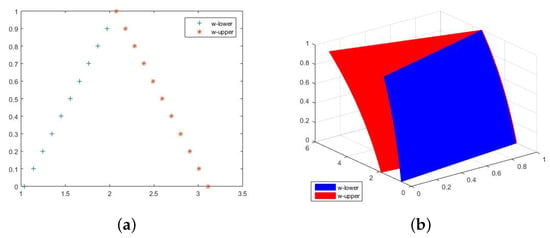
Figure 3. The approximate lower and upper solutions of Equation (144) at $\mathsf{\Lambda }=0.5,t=2,\Im =1/2,ı=1$. (a) 2D figure for the approximate solutions of one-dimensional fuzzy fractional diffusion equation of w in Example 8. (b) 3D figure for the approximate solutions of w in Example 8.

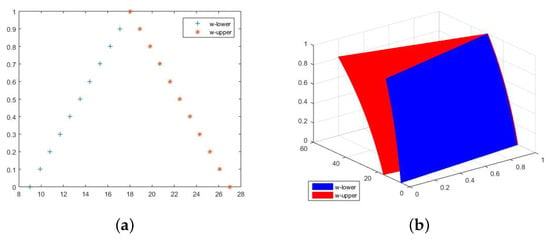
Figure 4. The exact lower and upper solutions of Equation (144) at $\mathsf{\Lambda }=0.5,t=2,\Im =1,ı=1$. (a) 2D figure for exact solutions of one-dimensional fuzzy fractional diffusion equation of w in Example 8. (b) 3D figure for the exact solutions of w in Example 8.

In Figure 3, we plotted $2D$ and $3D$ graphs of the approximation solution for $1D$ fuzzy FDE. Figure 3a shows that for $\mathsf{\Lambda }=0.5,\Im =1/2$ using $ı=1$ at $t=2$, the fuzzy FDE become bounded and closed. Moreover, the $\underline{w}$ represents increasing functions and $\stackrel{̲}{w}$ denotes the decreasing functions on the $\varrho$-level set of w. To discuss the concept of the $\varrho$-level set, it can be noted in Figure 3b that the $\varrho$-level set of the approximate solution for fuzzy FDE is bounded and closed for $t=2$, and $0\le \mathsf{\Lambda }\le 1$. Similarly, in Figure 4, we can observe the same explanation of $\varrho$—level set closedness and boundedness for Example 8.

In the next example, we consider a fuzzy fractional diffusion equation in two dimensions.

Example 9.

Let us assume $D=1,F(\mathsf{\Lambda },\phi )=-(\mathsf{\Lambda },\phi )$, and $\mathsf{\Psi }=[0,1]\times [0,1].$ Then, Equation (132)

$$\begin{array}{cc}\hfill \frac{{\partial }^{\Im }\tilde{w}(\mathsf{\Lambda },\phi ,t)}{\partial t^{\Im }}=& \frac{{\partial }^2\tilde{w}(\mathsf{\Lambda },\phi ,t)}{\partial {\mathsf{\Lambda }}^2}\oplus \frac{{\partial }^2\tilde{w}(\mathsf{\Lambda },\phi ,t)}{\partial {\phi }^2}\oplus \mathsf{\Lambda }\odot \frac{\partial \tilde{w}(\mathsf{\Lambda },\phi ,t)}{\partial \mathsf{\Lambda }}\oplus \phi \odot \frac{\partial \tilde{w}(\mathsf{\Lambda },\phi ,t)}{\partial \phi }\oplus 2\odot \tilde{w}(\mathsf{\Lambda },\phi ,t),\hfill \\ \hfill & 0<\Im \le 1,\mathsf{\Lambda }\ge 0,\phi \ge 0.\hfill \end{array}$$

(151)

under the initial condition

$$\begin{array}{c}\hfill \tilde{w}(\mathsf{\Lambda },\phi ,0)=[{(1+0.2\varrho )}^{ı},{(1.4-0.2\varrho )}^{ı}]\odot (\mathsf{\Lambda }+\phi ),0\le \mathsf{\Lambda },\phi \le 1,ı=1,2,3,\dots ,\end{array}$$

(152)

as well as the boundary conditions

$$\left\{\begin{array}{cc}\tilde{w}(0,\phi ,t)=\phi E_{\Im }\left(3t^{\Im }\right),\hfill & \hfill t\ge 0,\\ \tilde{w}(1,\phi ,t)=(1+\phi )E_{\Im }\left(3t^{\Im }\right),\hfill & \hfill t\ge 0,\\ \tilde{w}(\mathsf{\Lambda },0,t)=\mathsf{\Lambda }{E}_{\Im }\left(3t^{\Im }\right),\hfill & \hfill t\ge 0,\\ \tilde{w}(\mathsf{\Lambda },1,t)=(\mathsf{\Lambda }+1)E_{\Im }\left(3t^{\Im }\right),\hfill & \hfill t\ge 0.\end{array}\right.$$

(153)

Using the iteration Formulas (141) and (142), as well as the initial value ${\tilde{w}}_0(\mathsf{\Lambda },\phi ,t)=\tilde{w}(\mathsf{\Lambda },\phi ,0)=[{(1+0.2\varrho )}^{ı},{(1.4-0.2\varrho )}^{ı}]\oplus (\mathsf{\Lambda }+\phi ),$ we obtain

$$\begin{array}{c}\left.\begin{array}{cc}{q}^0:{\underline{w}}_0(\mathsf{\Lambda },\phi ,t;\varrho )\hfill & ={(1+0.2\varrho )}^{ı}(\mathsf{\Lambda }+\phi )\hfill \\ q^1:{\underline{w}}_1(\mathsf{\Lambda },\phi ,t;\varrho )\hfill & =\frac{{(1+0.2\varrho )}^{ı}(\mathsf{\Lambda }+\phi )3t^{\Im }}{\mathsf{\Gamma }(1+\Im )},\hfill \\ q^2:{\underline{w}}_2(\mathsf{\Lambda },\phi ,t;\varrho )\hfill & =\frac{{(1+0.2\varrho )}^{ı}(\mathsf{\Lambda }+\phi )3^2{t}^{2\Im }}{\mathsf{\Gamma }(1+2\Im )},\hfill \\ q^3:{\underline{w}}_3(\mathsf{\Lambda },\phi ,t;\varrho )\hfill & =\frac{{(1+0.2\varrho )}^{ı}(\mathsf{\Lambda }+\phi )3^3{t}^{3\Im }}{\mathsf{\Gamma }(1+3\Im )},\hfill \\ \hfill ⋮\\ q^{\mathit{ȷ}}:{\underline{w}}_{\mathit{ȷ}}(\mathsf{\Lambda },\phi ,t;\varrho )\hfill & =\frac{{(1+0.2\varrho )}^{ı}(\mathsf{\Lambda }+\phi )3^{\mathit{ȷ}}{t}^{\mathit{ȷ}\Im }}{\mathsf{\Gamma }(1+\mathit{ȷ}\Im )},\hfill \end{array}\right\}\hfill \end{array}$$

(154)

and

$$\begin{array}{c}\left.\begin{array}{cc}{q}^0:{\stackrel{̲}{w}}_0(\mathsf{\Lambda },\phi ,t;\varrho )\hfill & ={(1.4-0.2\varrho )}^{ı}(\mathsf{\Lambda }+\phi )\hfill \\ q^1:{\stackrel{̲}{w}}_1(\mathsf{\Lambda },\phi ,t;\varrho )\hfill & =\frac{{(1.4-0.2\varrho )}^{ı}(\mathsf{\Lambda }+\phi )3t^{\Im }}{\mathsf{\Gamma }(1+\Im )},\hfill \\ q^2:{\stackrel{̲}{w}}_2(\mathsf{\Lambda },\phi ,t;\varrho )\hfill & =\frac{{(1.4-0.2\varrho )}^{ı}(\mathsf{\Lambda }+\phi )3^2{t}^{2\Im }}{\mathsf{\Gamma }(1+2\Im )},\hfill \\ q^3:{\stackrel{̲}{w}}_3(\mathsf{\Lambda },\phi ,t;\varrho )\hfill & =\frac{{(1.4-0.2\varrho )}^{ı}(\mathsf{\Lambda }+\phi )3^3{t}^{3\Im }}{\mathsf{\Gamma }(1+3\Im )},\hfill \\ \hfill ⋮\\ q^{\mathit{ȷ}}:{\stackrel{̲}{w}}_{\mathit{ȷ}}(\mathsf{\Lambda },\phi ,t;\varrho )\hfill & =\frac{{(1.4-0.2\varrho )}^{ı}(\mathsf{\Lambda }+\phi )3^{\mathit{ȷ}}{t}^{\mathit{ȷ}\Im }}{\mathsf{\Gamma }(1+\mathit{ȷ}\Im )}.\hfill \end{array}\right\}\hfill \end{array}$$

(155)

Hence, the solution can be easily deduced as follows:

$$\begin{array}{c}\hfill \tilde{w}(\mathsf{\Lambda },\phi ,t;\varrho )=[{(1+0.2\varrho )}^{ı},{(1.4-0.2\varrho )}^{ı}]\odot (\mathsf{\Lambda }+\phi )E_{\Im }\left(3t^{\Im }\right),0\le \varrho \le 1.\end{array}$$

In the work of Osman et al. [41], the authors mentioned that for their method, the solution is convergent for $t=3$, but the issue of convergence of the fuzzy fractional VHPIM for large t is, in general, rather delicate. Therefore, we give the comparison for the VHPIM with Example $4.2$ in [41] and obtained the solution for Example 9 using fuzzy fractional VHPIM in our current work, which shows convergence until time $t=236$. Hence, this shows that our method gives better results in comparison. Meanwhile, we have also compared the error terms between exact and approximate solutions, which are fractional values of ℑ, in Example 9 for $\varrho$ between 0 and 1 in Table 2 for giving the clear solution for the 2D fuzzy fractional diffusion equation. Moreover, to present the solution in more depth, we plotted the solution in 3D as well, which can be seen in Figure 5b and Figure 6b.

Table 2. Table for the error term between exact solutions (ES) and approximate solutions (AS).

$\mathit{\varrho }$	Lower ES	Lower AS	Lower Error	Upper ES	Upper AS	Upper Error
0	4.5766 × 10${}^6$	7.5201 × 10${}^{24}$	−7.5201 × 10${}^{24}$	8.9702 × 10${}^6$	1.4739 × 10${}^{25}$	−1.4739 × 10${}^{25}$
0.1	4.7615 × 10${}^6$	7.8239 × 10${}^{24}$	−7.8239 × 10${}^{24}$	8.7157 × 10${}^6$	1.4321 × 10${}^{25}$	−1.4321 × 10${}^{25}$
0.2	4.9501 × 10${}^6$	8.1337 × 10${}^{24}$	−8.1337 × 10${}^{24}$	8.4649 × 10${}^6$	1.3909 × 10${}^{25}$	−1.3909 × 10${}^{25}$
0.3	5.1423 × 10${}^6$	8.4496 × 10${}^{24}$	−8.4496 × 10${}^{24}$	8.2178 × 10${}^6$	1.3503 × 10${}^{25}$	−1.3503 × 10${}^{25}$
0.4	5.3382 × 10${}^6$	8.7714 × 10${}^{24}$	−8.7714 × 10${}^{24}$	7.9743 × 10${}^6$	1.3103 × 10${}^{25}$	−1.3103 × 10${}^{25}$
0.5	5.5377 × 10${}^6$	9.0993 × 10${}^{24}$	−9.0993 × 10${}^{24}$	7.7345 × 10${}^6$	1.2709 × 10${}^{25}$	−1.2709 × 10${}^{25}$
0.6	5.7409 × 10${}^6$	9.4332 × 10${}^{24}$	−9.4332 × 10${}^{24}$	7.4983 × 10${}^6$	1.2321 × 10${}^{25}$	−1.2321 × 10${}^{25}$
0.7	5.9478 × 10${}^6$	9.7731 × 10${}^{24}$	−9.7731 × 10${}^{24}$	7.2658 × 10${}^6$	1.1939 × 10${}^{25}$	−1.1939 × 10${}^{25}$
0.8	6.1583 × 10${}^6$	1.0119 × 10${}^{25}$	−1.0119 × 10${}^{25}$	7.037 × 10${}^6$	1.1563 × 10${}^{25}$	−1.1563 × 10${}^{25}$
0.9	6.3725 × 10${}^6$	1.0471 × 10${}^{25}$	−1.0471 × 10${}^{25}$	6.8118 × 10${}^6$	1.1193 × 10${}^{25}$	−1.1193 × 10${}^{25}$
1	6.5903 × 10${}^6$	1.0829 × 10${}^{25}$	−1.0829 × 10${}^{25}$	6.5903 × 10${}^6$	1.0829 × 10${}^{25}$	−1.0829 × 10${}^{25}$

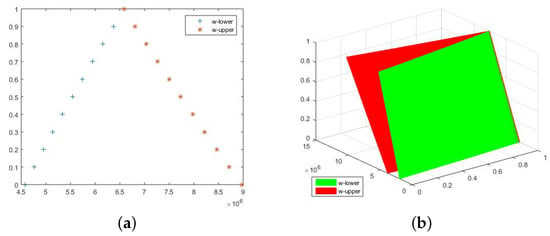
Figure 5. The exact lower and upper solutions of Equation (151) at $\mathsf{\Lambda }=0.6,\phi =0.8,t=5,\Im =1,ı=2$. (a) 2D figure for the exact solutions of two-dimensional fuzzy fractional diffusion equation of w in Example 9. (b) 3D figure for the exact solutions of w in Example 9.

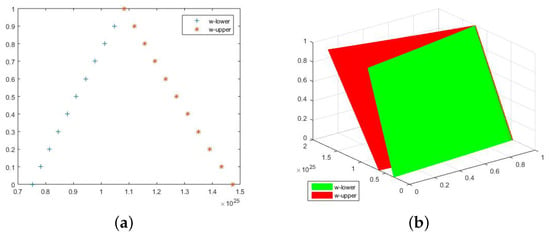
Figure 6. The approximate lower and upper solutions of Equation (151) at $\mathsf{\Lambda }=0.6,\phi =0.8,$$t=5,\Im =1/2,ı=2$. (a) 2D figure for the approximate solutions of two-dimensional fuzzy fractional diffusion equation of w in Example 9. (b) 3D figure for the approximate solutions of w in Example 9.

In Figure 5, we plotted $2D$ and $3D$ graphs of the $2D$ exact solution for fuzzy FDE. Figure 5a shows that for $\mathsf{\Lambda }=0.6,\phi =0.8,and\Im =1,$ using $ı=2,$ at $t=5$, the fuzzy FDE become bounded and closed. Moreover, the $\underline{w}$ shows increasing functions and $\stackrel{̲}{w}$ denotes the decreasing functions on the $\varrho$-level set of w. To discuss the concept of the $\varrho$-level set, Figure 5b illustrates that the $\varrho$-level set of fuzzy FDE is bounded and closed for $t=5$, and $0\le \phi \le 1$. Similarly, in Figure 6, we can observe the same explanation of $\varrho$-level set closedness and boundedness for Example 9.

In the next example, let us consider $D=1,F(\mathsf{\Lambda },\phi ,\varphi )=-(\mathsf{\Lambda },\phi ,\varphi ),\mathsf{\Psi }=[0,1]\times [0,1]\times [0,1];$ then, Equation (132) has the following:

Example 10.

Take into consideration the three-dimensional fuzzy fractional diffusion equation

$$\begin{array}{cc}\hfill \frac{{\partial }^{\Im }\tilde{w}(\mathsf{\Lambda },\phi ,\varphi ,t)}{\partial t^{\Im }}=& \mathsf{\Delta }\tilde{w}(\mathsf{\Lambda },\phi ,\varphi ,t)\oplus \mathsf{\Lambda }\odot \frac{\partial \tilde{w}(\mathsf{\Lambda },\phi ,\varphi ,t)}{\partial \mathsf{\Lambda }}\oplus \phi \odot \frac{\partial \tilde{w}(\mathsf{\Lambda },\phi ,\varphi ,t)}{\partial \phi }\oplus \varphi \odot \frac{\partial \tilde{w}(\mathsf{\Lambda },\phi ,\varphi ,t)}{\partial \varphi }\oplus 3\odot \tilde{w}(\mathsf{\Lambda },\phi ,\varphi ,t),\hfill \\ \hfill & 0<\Im \le 1,\mathsf{\Lambda }\ge 0,\phi \ge 0,\varphi \ge 0.\hfill \end{array}$$

(156)

under the initial conditions

$$\begin{array}{c}\hfill \tilde{w}(\mathsf{\Lambda },\phi ,\varphi ,0)=[{(0.2+0.1\varrho )}^{ı},{(0.4-0.1\varrho )}^{ı}]\odot {(\mathsf{\Lambda }+\phi +\varphi )}^2,0\le \mathsf{\Lambda },\phi ,\varphi \le 1,ı=1,2,3,\dots ,\end{array}$$

(157)

as well as the boundary conditions

$$\left\{\begin{array}{cc}\tilde{w}(0,\phi ,\varphi ,t)=(3+{(\phi +\varphi )}^2)E_{\Im }\left(5t^{\Im }\right)-3E_{\Im }\left(3t^{\Im }\right),\hfill & \hfill t\ge 0,\\ \tilde{w}(1,\phi ,\varphi ,t)=(3+{(1+\phi +\varphi )}^2)E_{\Im }\left(5t^{\Im }\right)-3E_{\Im }\left(3t^{\Im }\right),\hfill & \hfill t\ge 0,\\ \tilde{w}(\mathsf{\Lambda },0,\varphi ,t)=(3+{(\mathsf{\Lambda }+\varphi )}^2)E_{\Im }\left(5t^{\Im }\right)-3E_{\Im }\left(3t^{\Im }\right),\hfill & \hfill t\ge 0,\\ \tilde{w}(\mathsf{\Lambda },1,\varphi ,t)=(3+{(\mathsf{\Lambda }+1+\varphi )}^2)E_{\Im }\left(5t^{\Im }\right)-3E_{\Im }\left(3t^{\Im }\right),\hfill & \hfill t\ge 0,\\ \tilde{w}(\mathsf{\Lambda },\phi ,0,t)=(3+{(\mathsf{\Lambda }+\phi )}^2)E_{\Im }\left(5t^{\Im }\right)-3E_{\Im }\left(3t^{\Im }\right),\hfill & \hfill t\ge 0,\\ \tilde{w}(\mathsf{\Lambda },\phi ,1,t)=(3+{(\mathsf{\Lambda }+\phi +1)}^2)E_{\Im }\left(5t^{\Im }\right)-3E_{\Im }\left(3t^{\Im }\right),\hfill & \hfill t\ge 0.\end{array}\right.$$

(158)

Using the iteration Formulas (141) and (142), and plugging in the initial value ${\tilde{w}}_0(\mathsf{\Lambda },\phi ,\varphi ,t)=\tilde{w}(\mathsf{\Lambda },\phi ,\varphi ,0)=[{(0.2+0.1\varrho )}^{ı},{(0.4-0.1\varrho )}^{ı}]\odot {(\mathsf{\Lambda }+\phi +\varphi )}^2$, we obtain

$$\begin{array}{c}\left.\begin{array}{cc}{q}^0:{\underline{w}}_0(\mathsf{\Lambda },\phi ,\varphi ,t;\varrho )\hfill & ={(0.2+0.1\varrho )}^{ı}{(\mathsf{\Lambda }+\phi +\varphi )}^2\hfill \\ q^1:{\underline{w}}_1(\mathsf{\Lambda },\phi ,\varphi ,t;\varrho )\hfill & =\frac{{(0.2+0.1\varrho )}^{ı}(6+5{(\mathsf{\Lambda }+\phi +\varphi )}^2)t^{\Im }}{\mathsf{\Gamma }(1+\Im )},\hfill \\ q^2:{\underline{w}}_2(\mathsf{\Lambda },\phi ,\varphi ,t;\varrho )\hfill & =\frac{{(0.2+0.1\varrho )}^{ı}(48+25{(\mathsf{\Lambda }+\phi +\varphi )}^2)t^{2\Im }}{\mathsf{\Gamma }(1+2\Im )},\hfill \\ q^3:{\underline{w}}_3(\mathsf{\Lambda },\phi ,\varphi ,t;\varrho )\hfill & =\frac{{(0.2+0.1\varrho )}^{ı}(294+125{(\mathsf{\Lambda }+\phi +\varphi )}^2)t^{3\Im }}{\mathsf{\Gamma }(1+3\Im )},\hfill \\ \hfill ⋮\\ q^{\mathit{ȷ}}:{\underline{w}}_{\mathit{ȷ}}(\mathsf{\Lambda },\phi ,\varphi ,t;\varrho )\hfill & =\frac{{(0.2+0.1\varrho )}^{ı}(3(5^{\mathit{ȷ}}-3^{\mathit{ȷ}})+5^{\mathit{ȷ}}{(\mathsf{\Lambda }+\phi +\varphi )}^2)t^{\mathit{ȷ}\Im }}{\mathsf{\Gamma }(1+\mathit{ȷ}\Im )},\hfill \end{array}\right\}\hfill \end{array}$$

(159)

and

$$\begin{array}{c}\left.\begin{array}{cc}{q}^0:{\stackrel{̲}{w}}_0(\mathsf{\Lambda },\phi ,\varphi ,t;\varrho )\hfill & ={(0.4-0.1\varrho )}^{ı}{(\mathsf{\Lambda }+\phi +\varphi )}^2\hfill \\ q^1:{\stackrel{̲}{w}}_1(\mathsf{\Lambda },\phi ,\varphi ,t;\varrho )\hfill & =\frac{{(0.4-0.1\varrho )}^{ı}(6+5{(\mathsf{\Lambda }+\phi +\varphi )}^2)t^{\Im }}{\mathsf{\Gamma }(1+\Im )},\hfill \\ q^2:{\stackrel{̲}{w}}_2(\mathsf{\Lambda },\phi ,\varphi ,t;\varrho )\hfill & =\frac{{(0.4-0.1\varrho )}^{ı}(48+25{(\mathsf{\Lambda }+\phi +\varphi )}^2)t^{2\Im }}{\mathsf{\Gamma }(1+2\Im )},\hfill \\ q^3:{\stackrel{̲}{w}}_3(\mathsf{\Lambda },\phi ,\varphi ,t;\varrho )\hfill & =\frac{{(0.4-0.1\varrho )}^{ı}(294+125{(\mathsf{\Lambda }+\phi +\varphi )}^2)t^{3\Im }}{\mathsf{\Gamma }(1+3\Im )},\hfill \\ \hfill ⋮\\ q^{\mathit{ȷ}}:{\stackrel{̲}{w}}_{\mathit{ȷ}}(\mathsf{\Lambda },\phi ,\varphi ,t;\varrho )\hfill & =\frac{{(0.4-0.1\varrho )}^{ı}(3(5^{\mathit{ȷ}}-3^{\mathit{ȷ}})+5^{\mathit{ȷ}}{(\mathsf{\Lambda }+\phi +\varphi )}^2)t^{\mathit{ȷ}\Im }}{\mathsf{\Gamma }(1+\mathit{ȷ}\Im )}.\hfill \end{array}\right\}\hfill \end{array}$$

(160)

Hence, we obtain a compact form

$$\begin{array}{cc}\hfill \underline{w}(\mathsf{\Lambda },\phi ,\varphi ,t;\varrho )& \hfill ={(0.2+0.1\varrho )}^{ı}\left(\underset{n\to \infty }{lim}\sum _{\mathit{ȷ}=0}^n\frac{(3(5^{\mathit{ȷ}}-3^{\mathit{ȷ}})+5^{\mathit{ȷ}}{(\mathsf{\Lambda }+\phi +\varphi )}^2)t^{\mathit{ȷ}\Im }}{\mathsf{\Gamma }(1+\mathit{ȷ}\Im )}\right),\hfill \\ \hfill \stackrel{̲}{w}(\mathsf{\Lambda },\phi ,\varphi ,t;\varrho )& \hfill ={(0.4-0.1\varrho )}^{ı}\left(\underset{n\to \infty }{lim}\sum _{\mathit{ȷ}=0}^n\frac{(3(5^{\mathit{ȷ}}-3^{\mathit{ȷ}})+5^{\mathit{ȷ}}{(\mathsf{\Lambda }+\phi +\varphi )}^2)t^{\mathit{ȷ}\Im }}{\mathsf{\Gamma }(1+\mathit{ȷ}\Im )}\right).\hfill \end{array}$$

Thus, the following is the solution

$$\begin{array}{c}\hfill \tilde{w}(\mathsf{\Lambda },\phi ,\varphi ,t;\varrho )=[{(0.2+0.1\varrho )}^{ı},{(0.4-0.1\varrho )}^{ı}]\odot \left((3+{(\mathsf{\Lambda }+\phi +\varphi )}^2)E_{\Im }\left(5t^{\Im }\right)-3E_{\Im }\left(3t^{\Im }\right)\right),0\le \varrho \le 1.\end{array}$$

In the work of Osman et al. [41], the authors mentioned that for their method, the solution is convergent for $t=5$, but the issue of convergence of the fuzzy fractional VHPIM for large t is, in general, rather delicate. Therefore, we give the comparison for the VHPIM with Example $4.3$ in [41] and obtained that the solution for Example 10 using fuzzy fractional VHPIM in our current work shows convergence until time $t=141$. Hence, this shows that our method gives better results in comparison. Meanwhile, we have also compared the error terms between exact and approximate solutions for Example 10 for $\varrho$ between 0 and 1 in Table 3 for giving the clear solution for the 2D fuzzy fractional diffusion equation. Moreover, to present the solution in more depth, we plotted the solution in $3D$ as well, which can be seen in Figure 7b and Figure 8b.

Table 3. Table for the error term between exact solutions (ES) and approximate solutions (AS).

$\mathit{\varrho }$	Lower ES	Lower AS	Lower Error	Upper ES	Upper AS	Upper Error
0	1.5835 × 10${}^{13}$	2.0092 × 10${}^{131}$	−2.0092 × 10${}^{131}$	2.5336 × 10${}^{14}$	3.2147 × 10${}^{132}$	−3.2147 × 10${}^{132}$
0.1	1.9247 × 10${}^{13}$	2.4422 × 10${}^{131}$	−2.4422 × 10${}^{131}$	2.0636 × 10${}^{14}$	2.9051 × 10${}^{132}$	−2.9051 × 10${}^{132}$
0.2	2.3184 × 10${}^{13}$	2.9416 × 10${}^{131}$	−2.9416 × 10${}^{131}$	1.6623 × 10${}^{14}$	2.6184 × 10${}^{132}$	−2.6184 × 10${}^{132}$
0.3	2.7695 × 10${}^{13}$	3.5141 × 10${}^{131}$	−3.5141 × 10${}^{131}$	1.3225 × 10${}^{14}$	2.3535 × 10${}^{132}$	−2.3535 × 10${}^{132}$
0.4	3.2835 × 10${}^{13}$	4.1662 × 10${}^{131}$	−4.1662 × 10${}^{131}$	1.0377 × 10${}^{14}$	2.1092 × 10${}^{132}$	−2.1092 × 10${}^{132}$
0.5	3.8659 × 10${}^{13}$	4.9052 × 10${}^{131}$	−4.9052 × 10${}^{131}$	8.0163 × 10${}^{13}$	1.8844 × 10${}^{132}$	−1.8844 × 10${}^{132}$
0.6	4.5226 × 10${}^{13}$	5.7384 × 10${}^{131}$	−5.7384 × 10${}^{131}$	6.0831 × 10${}^{13}$	1.6781 × 10${}^{132}$	−1.6781 × 10${}^{132}$
0.7	5.2595 × 10${}^{13}$	6.6735 × 10${}^{131}$	−6.6735 × 10${}^{131}$	4.5226 × 10${}^{13}$	1.4892 × 10${}^{132}$	−1.4892 × 10${}^{132}$
0.8	6.0831 × 10${}^{13}$	7.7185 × 10${}^{131}$	−7.7185 × 10${}^{131}$	3.2835 × 10${}^{13}$	1.3167 × 10${}^{132}$	−1.3167 × 10${}^{132}$
0.9	6.9998 × 10${}^{13}$	8.8816 × 10${}^{131}$	−8.8816 × 10${}^{131}$	2.3184 × 10${}^{13}$	1.1597 × 10${}^{132}$	−1.1597 × 10${}^{132}$
1	8.0163 × 10${}^{13}$	1.0171 × 10${}^{132}$	−1.0171 × 10${}^{132}$	1.5835 × 10${}^{13}$	1.0171 × 10${}^{132}$	−1.0171 × 10${}^{132}$

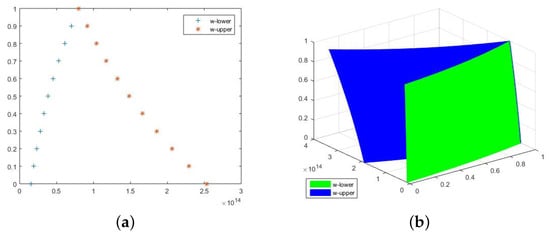
Figure 7. The exact lower and upper solutions of Equation (156) at $\mathsf{\Lambda }=0.9,\phi =0.5,\varphi =0.4,$$t=7,\Im =1,ı=4$. (a) 2D figure for the exact solutions of three-dimensional fuzzy fractional diffusion equation of w in Example 10. (b) 3D figure for the exact solutions of w in Example 10.

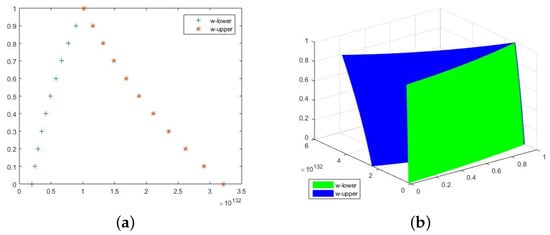
Figure 8. The approximate lower and upper solutions of Equation (156) at $\mathsf{\Lambda }=0.9,\phi =0.5,$$\varphi =0.4,t=7,\Im =1/2,ı=4$. (a) 2D figure for the approximate solutions of three-dimensional fuzzy fractional diffusion equation of w in Example 10. (b) 3D figure for the approximate solutions of w in Example 10.

In Figure 7, we plotted $2D$ and $3D$ graphs of the exact solution for $3D$ fuzzy FDE. Figure 7a shows that for $\mathsf{\Lambda }=0.9,\phi =0.5,\varphi =0.4,\Im =1$ using $ı=4,$ at $t=7$, the fuzzy FDE become bounded and closed. Moreover, the $\underline{w}$ sign shows increasing functions and $\stackrel{̲}{w}$ denotes the decreasing functions on the $\varrho$-level set of w. To discuss the concept of the $\varrho$-level set, Figure 7b illustrates that the $\varrho$-level set of fuzzy FDE is bounded and closed for $t=7$, and $0\le \phi \le 1$. Similarly, in Figure 8, we can observe the same explanation of $\varrho$-level set closedness and boundedness for Example 10.

6. Conclusions

This research introduced the comparative study of generalization DTM and fuzzy VIM for successful application to determine the approximate analytic solution of fuzzy fractional KdV, K(2,2), and mKdV equations. The primary advantage of the VIM is its rapid solution convergence. These numerical results conform its high level of precision. In addition, two-dimensional and three-dimensional approximation fuzzy time fractional telegraphic equations were established through the fuzzy RDTM instead using transformation, discretization, linearization, or restrictive assumption. Furthermore, the fuzzy VHPIM was presented and applied to solve the fuzzy fractional diffusion equation. The numerical analysis demonstrated that the fuzzy fractional VHPIM is an efficient technique for solving time-fractional diffusion problems by employing the initial conditions. Moreover, the boundary conditions can be used to justify the proposed solution that has been determined. The methods are investigated based on fuzzy fractional derivatives. Several examples put the proposed methods to the test. The solutions obtained by these four methods are illustrated in Figure 1, Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7 and Figure 8, showing the effectiveness and compliance with demonstrated theory and the potential to rely on these techniques without an exact solution. The analysis displayed that the proposed methods effectively obtain a solution for the fuzzy fractional partial differential equations.