Sharp Bounds of Hankel Determinant on Logarithmic Coefficients for Functions Starlike with Exponential Function

Abstract

Using the Lebedev–Milin inequalities, bounds on the logarithmic coefficients of an analytic function can be transferred to estimates on coefficients of the function itself and related functions. From this fact, the study of logarithmic-related problems of a certain subclass of univalent functions has attracted much attention in recent years. In our present investigation, a subclass of starlike functions ${\mathcal{S}}_e^{*}$ connected with the exponential mapping was considered. The main purpose of this article is to obtain the sharp estimates of the second Hankel determinant with the logarithmic coefficient as entry for this class.

1. Introduction and Definitions

There is a long history of study on univalent functions in geometric function theory. Suppose that $\mathcal{A}$ is the family of analytic functions defined in the open unit disc $\mathbb{D}:=\left\{z\in \mathbb{C}:\left|z\right|<1\right\}$ normalized by

$$f\left(z\right)=z+\sum _{l=2}^{\infty }{a}_l{z}^l.$$

(1)

Let $\mathcal{S}$ indicate the family of normalized univalent functions. By the $1/4$-theorem of Köebe, it is known that for each univalent function $f\in \mathcal{S}$, there exists an inverse function $f^{-1}$ defined at least on a disc of radius $1/4$ with Taylor’s series of the form

$$f^{-1}\left(w\right):=w+\sum _{n=2}^{\infty }{B}_n{w}^n,\left(\left|w\right|<1/4\right).$$

(2)

We say a function is bi-univalent in $\mathbb{D}$ if both f and $f^{-1}$ are univalent in $\mathbb{D}$.

The coefficient conjecture that $\left|a_n\right|\le n$ for $f\in \mathcal{S}$ proposed by Bieberbach [1] in 1916 has attracted many researchers to prove or disprove this result, until it was finally and solved by De Branges [2] in 1985. During this period, some important subclasses of univalent functions were introduced and investigated. The most well-known subfamilies are convex functions $\mathcal{K}$ and starlike functions ${\mathcal{S}}^{*}$, defined, respectively, by

$$\mathcal{K}:=\left\{f\in \mathcal{A}:\Re \left\{1+\frac{z{f}^{″}\left(z\right)}{f^{\prime }\left(z\right)}\right\}>0,z\in \mathbb{D}\right\}$$

(3)

and

$${\mathcal{S}}^{*}:=\left\{f\in \mathcal{A}:\Re \frac{z{f}^{\prime }\left(z\right)}{f\left(z\right)}>0,z\in \mathbb{D}\right\}.$$

(4)

Let $\alpha \in (0,1]$. If a function $f\in \mathcal{A}$ satisfies the condition

$$\left|arg\frac{z{f}^{\prime }\left(z\right)}{f\left(z\right)}\right|<\frac{\pi \alpha }{2},z\in \mathbb{D},$$

(5)

it is called strongly starlike of order $\alpha$. Moreover, we say a function $f\in \mathcal{A}$ is strongly convex of order $\alpha$ if

$$\left|arg\left(1+\frac{z{f}^{″}\left(z\right)}{f^{\prime }\left(z\right)}\right)\right|<\frac{\pi \alpha }{2},z\in \mathbb{D}.$$

(6)

For complex parameters ${\alpha }_1,\cdots ,{\alpha }_l$ and ${\beta }_1,\cdots ,{\beta }_m({\beta }_j\ne 0,-1,-2,\cdots ;j=1,2,\cdots ,m)$, the generalized hypergeometric function ${}_l{F}_m\left(z\right)({\alpha }_1,\cdots ,{\alpha }_l;{\beta }_1,\cdots ,{\beta }_m;z)$ is defined by

$${}_l{F}_m\left(z\right)({\alpha }_1,\cdots ,{\alpha }_l;{\beta }_1,\cdots ,{\beta }_m;z):=\sum _{n=0}^{\infty }\frac{{\left({\alpha }_1\right)}_n\cdots {\left({\alpha }_l\right)}_n}{{\left({\beta }_1\right)}_n\cdots {\left({\beta }_m\right)}_n}\frac{z^n}{n!}(l\le m+1;l,m\in {\mathbb{N}}_0:=\mathbb{N}\cup \left\{0\right\};z\in \mathbb{D}),$$

where $\mathbb{N}$ denotes the set of all positive integers, and ${\left(\lambda \right)}_k$ is the Pochhammer symbol defined by

$${\left(\lambda \right)}_n=\left\{\begin{array}{cc}1,\hfill & n=0,\\ \lambda (\lambda +1)(\lambda +2)\cdots (a+\lambda -1),\hfill & n\in \mathbb{N};\lambda \in \mathbb{C}.\end{array}\right.$$

In recent years, many subclasses of analytic univalent functions or bi-univalent functions associated with the generalized hypergeometric function have been introduced and studied; see, for example, [3,4,5,6,7,8].

The logarithmic coefficients ${\gamma }_n$ of $f\in \mathcal{S}$ play an important role in estimation theory. They are given by the below formula:

$$log\left(\frac{f\left(z\right)}{z}\right)=2\sum _{n=1}^{\infty }{\gamma }_n{z}^n=:F_f\left(z\right),z\in \mathbb{D}.$$

(7)

De Branges [2] obtained that for $n\ge 1,$

$$\sum _{l=1}^{n}l\left(n-l+1\right){\left|{\gamma }_n\right|}^2\le \sum _{l=1}^n\frac{n-l+1}{l},$$

(8)

and the equality holds if and only if f takes the form $\frac{z}{{\left(1-e^{i\theta }z\right)}^2}$ for some $\theta \in \mathbb{R}.$ Clearly, this inequality gives the famous Bieberbach–Robertson–Milin conjectures about Taylor coefficients of f belonging to $\mathcal{S}$ in its most general form. In 2005, Kayumov [9] solved Brennan’s conjecture for conformal mappings by considering the logarithmic coefficients. For $n\ge 3$, it seems to be a more difficult work on the logarithmic coefficients problem. It is noted that the inequality $\left|{\gamma }_n\right|\le \frac{1}{n}$ holds for $f\in {\mathcal{S}}^{*}$, but it does not hold for the full class $\mathcal{S}$, even in an order of magnitude (see [3]). For some significant work on studying logarithmic coefficients, see [10,11,12].

For the given functions $g_1,g_2\in \mathcal{A},$ the subordination between $g_1$ and $g_2$ (written as $g_1\prec g_2$) if an analytic function v appears in $\mathbb{D}$ comes with the restriction that $v\left(0\right)=0$ and $\left|v\left(z\right)\right|<1$ in such a manner that $f\left(z\right)=g\left(v\left(z\right)\right)$ holds. v is called a Schwarz function. Moreover, if $g_2$ in $\mathbb{D}$ is univalent, it is known that

$$g_1\left(z\right)\prec g_2\left(z\right),\left(z\in \mathbb{D}\right)$$

if and only if

$$g_1\left(0\right)=g_2\left(0\right)\mathrm{and}{g}_1\left(\mathbb{D}\right)\subset g_2\left(\mathbb{D}\right).$$

By employing the principle of subordination, Ma and Minda [13] considered a unified version of the class ${\mathcal{S}}^{*}\left(\varphi \right)$ in 1992 defined by

$${\mathcal{S}}^{*}\left(\varphi \right):=\left\{f\in \mathcal{A}:\frac{z{f}^{\prime }\left(z\right)}{f\left(z\right)}\prec \varphi \left(z\right),z\in \mathbb{D}\right\},$$

where $\varphi$ is a univalent function with ${\varphi }^{\prime }\left(0\right)>0$ and $\Re \varphi >0.$ Additionally, the region $\varphi \left(\mathbb{D}\right)$ is star-shaped about the point $\varphi \left(0\right)=1$ and is symmetric along the real-line axis. In the past few years, numerous sub-families of the collection $\mathcal{S}$ have been examined as particular choices of the class ${\mathcal{S}}^{*}\left(\varphi \right).$ For instance, if we choose $\varphi \left(z\right)=\frac{1+\left(1-2\xi \right)z}{1-z}$ with $0\le \xi <1$, then we achieve the class ${\mathcal{S}}^{*}\left(\xi \right):={\mathcal{S}}^{*}\left(\frac{1+\left(1-2\xi \right)z}{1-z}\right)$ of the starlike function family of order $\xi .$ It is noted that ${\mathcal{S}}^{*}:={\mathcal{S}}^{*}\left(\frac{1+z}{1-z}\right)$ is simply the familiar starlike function family. For more interesting related subclasses, see, for example, [14,15,16].

The Hankel determinant ${\mathcal{H}}_{q,n}\left(f\right)$ with $q,n\in \mathbb{N}$ for a function $f\in \mathcal{S}$ of the series form (1) was given by Pommerenke [17,18] as

$${\mathcal{H}}_{q,n}\left(f\right):=\left|\begin{array}{cccc}{a}_n\hfill & a_{n+1}\hfill & \dots \hfill & a_{n+q-1}\hfill \\ a_{n+1}\hfill & a_{n+2}\hfill & \dots \hfill & a_{n+q}\hfill \\ ⋮\hfill & ⋮\hfill & \dots \hfill & ⋮\hfill \\ a_{n+q-1}\hfill & a_{n+q}\hfill & \dots \hfill & a_{n+2q-2}\hfill \end{array}\right|.$$

In the literature, there are only a few references to the Hankel determinant for functions belonging to the general family of univalent functions. In [19], it was proved that $\left|{\mathcal{H}}_{2,n}\left(f\right)\right|\le \lambda \sqrt{n},$ where $f\in \mathcal{S}$ and $\lambda$ is an absolute constant. The challenge of finding the sharp limits of Hankel determinants in a particular family of functions drew the attention of numerous mathematicians. For example, the sharp bound of $\left|{\mathcal{H}}_{2,2}\left(f\right)\right|$ for the sub-families $\mathcal{K}$ and ${\mathcal{S}}^{*}$ were calculated by Janteng et al. [20,21]. It is quite clear from the formulas given in (10) that the calculation of $\left|{\mathcal{H}}_{3,1}\left(f\right)\right|$ is far more challenging compared with finding the bound of $\left|{\mathcal{H}}_{2,2}\left(f\right)\right|$. In [22], Babalola investigated the bounds of the third-order Hankel determinant for the families of $\mathcal{K}$ and ${\mathcal{S}}^{*}$. Later, several authors [23,24,25,26] obtained some interesting results on $\left|{\mathcal{H}}_{3,1}\left(f\right)\right|$ for certain sub-families of analytic and univalent functions. In recent years, some sharp bounds of the third-order Hankel determinant were obtained for several subclass of univalent functions. Kowalczyk et al. [27] and Lecko et al. [28] proved that

$$\left|{\mathcal{H}}_{3,1}\left(f\right)\right|\le \left\{\begin{array}{ccc}\frac{4}{135},\hfill & \mathrm{for}\hfill & f\in \mathcal{K},\hfill \\ \frac{1}{9},\hfill & \mathrm{for}\hfill & f\in {\mathcal{S}}^{*}\left(\frac{1}{2}\right),\hfill \end{array}\right.$$

where ${\mathcal{S}}^{*}\left(\frac{1}{2}\right)$ indicate the starlike functions family of order $\frac{1}{2}.$ For more contributions in this direction, see [29,30,31,32,33,34,35,36,37,38].

It seems a natural idea to generalize the Hankel determinant with logarithmic coefficients as entry. In [39,40], Kowalczyk et al. first introduced the Hankel determinant using logarithmic coefficients. Using the logarithmic coefficient as the element, we have

$${\mathcal{H}}_{q,n}\left(F_f/2\right)=\left|\begin{array}{cccc}{\gamma }_n\hfill & {\gamma }_{n+1}\hfill & \dots \hfill & {\gamma }_{n+q-1}\hfill \\ {\gamma }_{n+1}\hfill & {\gamma }_{n+2}\hfill & \dots \hfill & {\gamma }_{n+q}\hfill \\ ⋮\hfill & ⋮\hfill & \dots \hfill & ⋮\hfill \\ {\gamma }_{n+q-1}\hfill & {\gamma }_{n+q}\hfill & \dots \hfill & {\gamma }_{n+2q-2}\hfill \end{array}\right|.$$

(9)

In particular, it is noted that

$$\begin{array}{ccc}\hfill {\mathcal{H}}_{2,1}\left(F_f/2\right)& =& \left|\begin{array}{cc}{\gamma }_1\hfill & {\gamma }_2\hfill \\ {\gamma }_2\hfill & {\gamma }_3\hfill \end{array}\right|={\gamma }_1{\gamma }_3-{\gamma }_2^2,\hfill \\ \hfill {\mathcal{H}}_{2,2}\left(F_f/2\right)& =& \left|\begin{array}{cc}{\gamma }_2\hfill & {\gamma }_3\hfill \\ {\gamma }_3\hfill & {\gamma }_4\hfill \end{array}\right|={\gamma }_2{\gamma }_4-{\gamma }_3^2,\hfill \end{array}$$

If f is given by (1), then its logarithmic coefficients are given by

$$\begin{array}{ccc}\hfill {\gamma }_1& =& \frac{1}{2}{a}_2\hfill \end{array}$$

(10)

$$\begin{array}{ccc}\hfill {\gamma }_2& =& \frac{1}{2}\left(a_3-\frac{1}{2}{a}_2^2\right)\hfill \end{array}$$

(11)

$$\begin{array}{ccc}\hfill {\gamma }_3& =& \frac{1}{2}\left(a_4-a_2{a}_3+\frac{1}{3}{a}_2^3\right)\hfill \end{array}$$

(12)

$$\begin{array}{ccc}\hfill {\gamma }_4& =& \frac{1}{2}\left(a_5-a_2{a}_4+a_2^2{a}_3-\frac{1}{2}{a}_3^2-\frac{1}{4}{a}_2^4\right)\hfill \end{array}$$

(13)

Let $f_{\theta }\left(z\right):=e^{-i\theta }f\left(e^{i\theta }z\right),\theta \in \mathbb{R}$. It is observed that ${\mathcal{H}}_{2,1}\left(F_f/2\right)$ and ${\mathcal{H}}_{2,2}\left(F_f/2\right)$ are invariant under rotation since we have

$${\mathcal{H}}_{2,1}\left(F_{f_{\theta }}/2\right)=\frac{e^{4i\theta }}{4}\left(a_2{a}_4-a_3^2+\frac{1}{12}{a}_2^4\right)=e^{4i\theta }{\mathcal{H}}_{2,1}\left(F_f/2\right)$$

and

$$\begin{array}{ccc}\hfill {\mathcal{H}}_{2,2}\left(F_{f_{\theta }}/2\right)& =& e^{6i\theta }\left(\frac{1}{288}{a}_2^6-\frac{1}{48}{a}_3{a}_2^4-\frac{1}{24}{a}_2^3{a}_4+\frac{1}{16}{a}_3^2{a}_2^2-\frac{1}{8}{a}_5{a}_2^2+\frac{1}{4}{a}_3{a}_2{a}_4-\frac{1}{4}{a}_4^2+\frac{1}{4}{a}_3{a}_5-\frac{1}{8}{a}_3^3\right)\hfill \\ \hfill & =& e^{6i\theta }{\mathcal{H}}_{2,2}\left(F_f/2\right).\hfill \end{array}$$

In 2014, Mendiratta R. et al. [41] introduced a subclass of starlike functions defined by

$${\mathcal{S}}_e^{*}:=\left\{f\in \mathcal{S}:\frac{z{f}^{\prime }\left(z\right)}{f\left(z\right)}\prec e^z,z\in \mathbb{D}\right\}.$$

(14)

This class was later studied in [42] and generalized by Srivastava et al. [43], in which the authors determined the upper bound of the Hankel determinant. In 2019, Goel et al. [44] introduced a subclass of the starlike function ${\mathcal{S}}_{seg}^{*}$ defined by

$${\mathcal{S}}_{seg}^{*}:=\left\{f\in \mathcal{S}:\frac{z{f}^{\prime }\left(z\right)}{f\left(z\right)}\prec \frac{2}{1+e^{-z}},z\in \mathbb{D}\right\}.$$

The family ${\mathcal{S}}_{sin}^{*}$ of starlike functions characterised by the condition

$${\mathcal{S}}_{sin}^{*}:=\left\{f\in \mathcal{S}:\frac{z{f}^{\prime }\left(z\right)}{f\left(z\right)}\prec 1+sinz,z\in \mathbb{D}\right\}$$

was first investigated by Cho et al. [45]. In virtue of $sinz=\frac{e^{iz}-e^{-iz}}{2i}$, it is seen that the three function classes are associated with the exponential function. The exponential function $\phi \left(z\right)=e^z$ has a positive real part in $\mathbb{D}$ and an image domain $\phi \left(\mathbb{D}\right)=\left\{w\in \mathbb{C}:\left|log w\right|<1\right\}$ (see Figure 1). Let $\psi \left(z\right)=\frac{2}{1+e^{-z}}$. The function $\psi$ is called a modified sigmoid function. It maps $\mathbb{D}$ onto a domain ${\Delta }_{SG}:=\left\{w\in \mathbb{C}:\left|log\left(\frac{w}{2-w}\right)\right|<1\right\}$ (see Figure 2). Moreover, $\psi$ is convex and hence starlike with respect to $\psi \left(0\right)=1$. For $f\in {\mathcal{S}}_{sin}^{*}$, the quantity $\frac{z{f}^{\prime }\left(z\right)}{f\left(z\right)}$ lies in an eight-shaped region in the right-half plane.

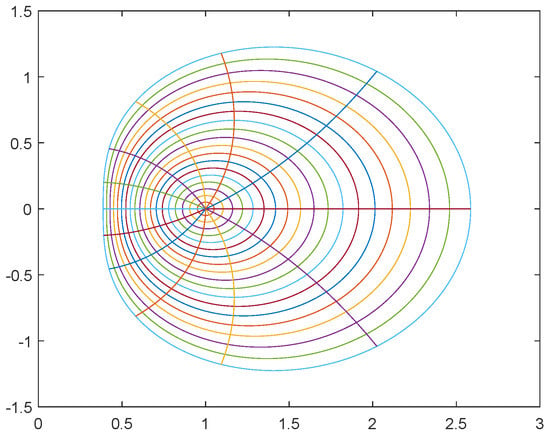
Figure 1. Image of $\mathbb{D}$ under $e^z$.

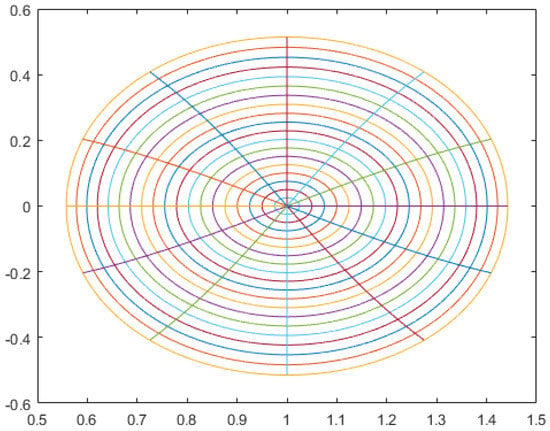
Figure 2. Image of $\mathbb{D}$ under $\frac{2}{1-e^{-z}}$.

Recently, Sevtap Sümer Eker et al. [46] obtained the sharp bounds for the second Hankel determinant of logarithmic coefficients for strongly starlike and strongly convex functions. In [47], the authors discussed the bounds of second Hankel determinants with logarithmic coefficients for the class ${\mathcal{S}}_{seg}^{*}$ and improved the estimation of the existing second Hankel determinant of logarithmic coefficients for the class ${\mathcal{S}}_{sin}^{*}$.

In the present article, our aim is to calculate sharp bounds of the Hankel determinants with logarithmic coefficients as entry for the class ${\mathcal{S}}_e^{*}$.

2. Main Results

A function $p\in \mathcal{P}$ if and only if $\Re p\left(z\right)\ge 0$ for $z\in \mathbb{D}$ with the series expansion

$$p\left(z\right)=1+\sum _{n=1}^{\infty }{c}_n{z}^n,z\in \mathbb{D}.$$

(15)

Lemma 1

(see [48]). Let $p\in \mathcal{P}$. Then, for some $x,\delta ,\rho \in \overline{\mathbb{D}}:=\left\{z\in \mathbb{C}:\left|z\right|\le 1\right\}$, we have

$$\begin{array}{ccc}\hfill 2c_2& =& c_1^2+\left(4-c_1^2\right)x,\hfill \end{array}$$

(16)

$$\begin{array}{ccc}\hfill 4c_3& =& c_1^3+2c_{1}x\left(4-c_1^2\right)-x^2{c}_1\left(4-c_1^2\right)+2\left(1-{\left|x\right|}^2\right)\left(4-c_1^2\right)\delta ,\hfill \\ \hfill 8c_4& =& c_1^4+x\left[c_1^2\left(x^2-3x+3\right)+4x\right](4-c_1^2)-4(4-c_1^2)(1-{\left|x\right|}^2)\hfill \end{array}$$

(17)

$$\begin{array}{ccc}& & \left[c_1(x-1)\delta +\overline{x}{\delta }^2-(1-{\left|\delta \right|}^2)\rho \right](4-c_1^2).\hfill \end{array}$$

(18)

Throughout this paper, in the following, we use $x,$ $\delta$ and $\rho$ to denote some complex number satisfying $\left|x\right|\le 1$, $\left|\delta \right|\le 1$ and $\left|\rho \right|\le 1$. Let $c_1=c$, $\left|x\right|=t$ and $\left|\rho \right|=y$ be real numbers that lie in the intervals $[0,2]$, $[0,1]$ and $[0,1]$, respectively.

Theorem 1.

Let $f\in {\mathcal{S}}_e^{*}$. Then,

$$\left|{\mathcal{H}}_{2,1}\left(F_f/2\right)\right|=\left|{\gamma }_1{\gamma }_3-{\gamma }_2^2\right|\le \frac{1}{16}.$$

(19)

The inequality is sharp.

Proof. 

Suppose that $f\in {\mathcal{S}}_e^{*}.$ From the definition, we know it can be written in the form of a Schwarz function as

$$\frac{z{f}^{\prime }\left(z\right)}{f\left(z\right)}=e^{w\left(z\right)},(z\in \mathbb{D}).$$

Define

$$p\left(z\right):=\frac{1+w\left(z\right)}{1-w\left(z\right)}=1+c_{1}z+c_2{z}^2+c_3{z}^3+c_4{z}^4+\cdots ,(z\in \mathbb{D}).$$

(20)

It follows that

$$\begin{array}{ccc}\hfill w\left(z\right)& =& \frac{1}{2}{c}_{1}z+\left(\frac{1}{2}{c}_2-\frac{1}{4}{c}_1^2\right)z^2+\left(\frac{1}{8}{c}_1^3-\frac{1}{2}{c}_1{c}_2+\frac{1}{2}{c}_3\right)z^3\hfill \\ & & +\left(\frac{1}{2}{c}_4-\frac{1}{2}{c}_1{c}_3-\frac{1}{4}{c}_2^2-\frac{1}{16}{c}_1^4+\frac{3}{8}{c}_1^2{c}_2\right)z^4+\cdots ,(z\in \mathbb{D}).\hfill \end{array}$$

(21)

Using (1), we obtain

$$\begin{array}{ccc}\hfill \frac{z{f}^{\prime }\left(z\right)}{f\left(z\right)}& =& 1+a_{2}z+\left(2a_3-a_2^2\right)z^2+\left(a_2^3-3a_2{a}_3+3a_4\right)z^3\hfill \\ & & +\left(4a_5-a_2^4+4a_2^2{a}_3-4a_2{a}_4-2a_3^2\right)z^4+\cdots ,(z\in \mathbb{D}).\hfill \end{array}$$

(22)

Using the series expansion of (21), we obtain

$$\begin{array}{ccc}\hfill e^{w\left(z\right)}& =& 1+\frac{1}{2}{c}_{1}z+\left(\frac{1}{2}{c}_2-\frac{1}{8}{c}_1^2\right)z^2+\left(-\frac{1}{4}{c}_1{c}_2+\frac{1}{48}{c}_1^3+\frac{1}{2}{c}_3\right)z^3\hfill \\ & & +\left(\frac{1}{348}{c}_1^4+\frac{1}{16}{c}_1^2{c}_2-\frac{1}{4}{c}_1{c}_3-\frac{1}{8}{c}_2^2+\frac{1}{2}{c}_4\right)z^4+\cdots ,(z\in \mathbb{D}).\hfill \end{array}$$

(23)

Now, comparing (22) and (23) leads to

$$\begin{array}{ccc}\hfill a_2& =& \frac{1}{2}{c}_1,\hfill \\ \hfill a_3& =& \frac{1}{4}{c}_2+\frac{1}{16}{c}_1^2,\hfill \\ \hfill a_4& =& \frac{1}{6}{c}_3-\frac{1}{288}{c}_1^3+\frac{1}{24}{c}_1{c}_2,\hfill \\ \hfill a_5& =& \frac{1}{1152}{c}_1^4-\frac{1}{96}{c}_1^2{c}_2+\frac{1}{48}{c}_1{c}_3+\frac{1}{8}{c}_4.\hfill \end{array}$$

From (10)–(13), we have

$$\begin{array}{ccc}\hfill {\gamma }_1& =& \frac{1}{4}{c}_1,\hfill \end{array}$$

(24)

$$\begin{array}{ccc}\hfill {\gamma }_2& =& \frac{1}{8}{c}_2-\frac{1}{32}{c}_1^2,\hfill \end{array}$$

(25)

$$\begin{array}{ccc}\hfill {\gamma }_3& =& \frac{1}{288}{c}_1^3-\frac{1}{24}{c}_1{c}_2+\frac{1}{12}{c}_3,\hfill \end{array}$$

(26)

$$\begin{array}{ccc}\hfill {\gamma }_4& =& \frac{1}{3072}{c}_1^4+\frac{1}{128}{c}_1^2{c}_2-\frac{1}{32}{c}_1{c}_3-\frac{1}{64}{c}_2^2+\frac{1}{16}{c}_4.\hfill \end{array}$$

(27)

From (24)–(26), we have

$$\left|{\gamma }_1{\gamma }_3-{\gamma }_2^2\right|=\frac{1}{9216}\left|-c_1^4-24c_1^2{c}_2+192c_1{c}_3-144c_2^2\right|.$$

Since ${\mathcal{H}}_{2,1}\left(F_f/2\right)$ is rotationally invariant, we may assume that $c_1=c\in [0,2]$. Using (16) and (17) to express $c_2$ and $c_3$ in terms of $c_1=c,$ we obtain

$$\begin{array}{ccc}\hfill \left|{\gamma }_1{\gamma }_3-{\gamma }_2^2\right|& =& \frac{1}{9216}\left|-c^4-48c^2{x}^2\left(4-c^2\right)-36x^2{\left(4-c^2\right)}^2+12x{c}^2\left(4-c^2\right)\right.\hfill \\ & & \left.+96c\left(1-{\left|x\right|}^2\right)\left(4-c^2\right)\delta \right|.\hfill \end{array}$$

By replacing $\left|\delta \right|\le 1$ and $\left|x\right|=t,$ it follows that

$$\begin{array}{ccc}\hfill \left|{\gamma }_1{\gamma }_3-{\gamma }_2^2\right|& \le & \frac{1}{9216}\left[c^4+48c^2{t}^2\left(4-c^2\right)+96c\left(1-t^2\right)\left(4-c^2\right)\right.\hfill \\ & & \left.+36t^2{\left(4-c^2\right)}^2+12c^{2}t\left(4-c^2\right)\right]=:\mathrm{\Omega }\left(c,t\right).\hfill \end{array}$$

Differentiating with respect to t, we have

$$\frac{\partial \mathrm{\Omega }\left(c,t\right)}{\partial t}=\frac{1}{9216}\times 12\left(4-c^2\right)\left(2t{c}^2-16tc+c^2+24t\right).$$

As $c\in [0,2]$, it is a simple exercise to show that $\frac{\partial \mathrm{\Omega }\left(c,t\right)}{\partial t}\ge 0$ for $t\in \left[0,1\right]$. Thus, we have $\mathrm{\Omega }\left(c,t\right)\le \mathrm{\Omega }\left(c,1\right).$ Putting $t=1$ gives

$$\left|{\gamma }_1{\gamma }_3-{\gamma }_2^2\right|\le \frac{1}{9216}\left[c^4+60c^2\left(4-c^2\right)+36{\left(4-c^2\right)}^2\right]=:\varpi \left(c\right).$$

Since ${\varpi }^{\prime }\left(c\right)\le 0$ for $c\in [0,2]$, we see that $\varpi \left(c\right)$ is a decreasing function, and it gives its maximum value at $c=0$. This yields

$$\left|{\mathcal{H}}_{2,2}\left(F_f/2\right)\right|\le \frac{576}{9216}=\frac{1}{16}.$$

Equality is determined using (10)–(12) and

$$f_1\left(z\right)=zexp\left({\int }_0^z\frac{e^{t^2}-1}{t}dt\right)=z+\frac{1}{2}{z}^3+\frac{1}{4}{z}^5+\cdots .$$

(28)

□

Theorem 2.

Let $f\in {\mathcal{S}}_e^{*}$. Then

$$\left|{\mathcal{H}}_{2,2}\left(F_f/2\right)\right|=\left|{\gamma }_2{\gamma }_4-{\gamma }_3^2\right|\le \frac{1}{36}.$$

This result is sharp.

Proof. 

As ${\mathcal{H}}_{2,2}\left(F_f/2\right)$ is rotation-invariant, we assume that $c_1=c\in \left[0,2\right]$. By using (24)–(27), we have

$$\begin{array}{ccc}\hfill \left|{\gamma }_2{\gamma }_4-{\gamma }_3^2\right|& =& \frac{1}{2654208}\left(-59c^6+228c^4{c}_2+1056c^3{c}_3-720c^2{c}_2^2-5184c^2{c}_4\right.\hfill \\ & & \left.+8064c{c}_2{c}_3-5184c_2^3+20736c_2{c}_4-18432c_3^2\right).\hfill \end{array}$$

(29)

Suppose that $u=4-c^2$. An application of Lemma 1 leads to

$$\begin{array}{ccc}\hfill \left|{\gamma }_2{\gamma }_4-{\gamma }_3^2\right|& =& \frac{1}{2654208}\left\{-5c^6+528c^{3}u\left(1-{\left|x\right|}^2\right)\delta -6c^{4}xu-828c^2{u}^2{x}^2\right.\hfill \\ & & -912c^4{x}^{2}u-288x^3{u}^2{c}^2+144x^4{u}^2{c}^2-4608u^2{\left(1-{\left|x\right|}^2\right)}^2{\delta }^2\hfill \\ & & +2592u{x}^2{c}^2+648c^{4}u{x}^3-648x^3{u}^3+5184u^2{x}^3-2592c^{3}u\left(1-{\left|x\right|}^2\right)x\delta \hfill \\ & & -2592c^{2}u\overline{x}\left(1-{\left|x\right|}^2\right){\delta }^2+2592c^{2}u\left(1-{\left|x\right|}^2\right)\left(1-{\left|\delta \right|}^2\right)\rho \hfill \\ & & -2016cx{u}^2\left(1-{\left|x\right|}^2\right)\delta -5184u^2{\left|x\right|}^2\left(1-{\left|x\right|}^2\right){\delta }^2\hfill \\ & & \left.-576c{u}^2{x}^2\left(1-{\left|x\right|}^2\right)\delta +5184u^{2}x\left(1-{\left|x\right|}^2\right)\left(1-{\left|\delta \right|}^2\right)\rho \right\}.\hfill \end{array}$$

Thus, we see that

$$\left|{\gamma }_2{\gamma }_4-{\gamma }_3^2\right|=\frac{1}{2654208}\left(v_1\left(c,x\right)+v_2\left(c,x\right)\delta +v_3\left(c,x\right){\delta }^2+\mathrm{\Phi }\left(c,x,\delta \right)\rho \right),$$

where

$$\begin{array}{ccc}\hfill v_1\left(c,x\right)& =& -6\left(4-c^2\right)x\left[6\left(4-c^2\right)x\left(-4x^2{c}^2-10x{c}^2+23c^2-72x\right)-108c^4{x}^2\right.\hfill \\ & & \left.+152c^{4}x+c^4-432x{c}^2\right]-5c^6,\hfill \\ \hfill v_2\left(c,x\right)& =& -48\left(4-c^2\right)\left(1-{\left|x\right|}^2\right)c\left[\left(12x^2+42x\right)\left(4-c^2\right)+54x{c}^2-11c^2\right],\hfill \\ \hfill v_3\left(c,x\right)& =& -288\left(4-c^2\right)\left(1-{\left|x\right|}^2\right)\left[\left(2{\left|x\right|}^2+16\right)\left(4-c^2\right)+9\overline{x}{c}^2\right],\hfill \\ \hfill \mathrm{\Phi }\left(c,x,\delta \right)& =& 2592\left(4-c^2\right)\left(1-{\left|x\right|}^2\right)\left(1-{\left|\delta \right|}^2\right)\left[2\left(4-c^2\right)x+c^2\right].\hfill \end{array}$$

Now, by utilizing $\left|\delta \right|=y,$$\left|x\right|=t$ and taking $\left|\rho \right|\le 1,$ we achieve

$$\begin{array}{ccc}\hfill \left|{\gamma }_2{\gamma }_4-{\gamma }_3^2\right|& \le & \frac{1}{2654208}\left(\left|v_1\left(c,t\right)\right|+\left|v_2\left(c,t\right)\right|y+\left|v_3\left(c,t\right)\right|y^2+\left|\mathrm{\Phi }\left(c,t,\delta \right)\right|\right),\hfill \\ & \le & \frac{1}{2654208}\left[H\left(c,t,y\right)\right].\hfill \end{array}$$

(30)

where

$$H\left(c,t,y\right)=h_1\left(c,t\right)+h_2\left(c,t\right)y+h_3\left(c,t\right)y^2+h_4\left(c,t\right)\left(1-y^2\right).$$

(31)

with

$$\begin{array}{ccc}\hfill h_1\left(c,t\right)& =& 6\left(4-c^2\right)t\left[6\left(4-c^2\right)t\left(4t^2{c}^2+10t{c}^2+23c^2+72t\right)+108c^4{t}^2\right.\hfill \\ & & \left.+152c^{4}t+c^4+432t{c}^2\right]+5c^6,\hfill \\ \hfill h_2\left(c,t\right)& =& 48\left(4-c^2\right)\left(1-t^2\right)c\left[\left(12t^2+42t\right)\left(4-c^2\right)+54t{c}^2+11c^2\right],\hfill \\ \hfill h_3\left(c,t\right)& =& 288\left(4-c^2\right)\left(1-t^2\right)\left[\left(2t^2+16\right)\left(4-c^2\right)+9t{c}^2\right],\hfill \\ \hfill h_4\left(c,t\right)& =& 2592\left(4-c^2\right)\left(1-t^2\right)\left[2\left(4-c^2\right)t+c^2\right].\hfill \end{array}$$

Let the closed cuboid be $\Delta :=\left[0,2\right]\times \left[0,1\right]\times \left[0,1\right].$ We have to achieve the points of maxima of $H(c,t,y)$ in $\Delta$. By observing that $H(0,0,1)=73728$, we know

$$\max H(c,t,y)\ge 73728,(c,t,y)\in \Delta .$$

(32)

Denote $m_0=73728$. In the following, we aim to prove that $\max H(c,t,y)=m_0$ for all $(c,t,y)\in \Delta$. To show this, we first prove that the global maximum value of $H(c,t,y)$ can be obtained on the face of $y=1$. On $t=1,$ $H\left(c,t,y\right)$ reduces to

$$q_1\left(c\right):=H\left(c,1,y\right)=-229c^6-4392c^4+10944c^2+41472,c\in \left(0,2\right).$$

(33)

Solving $q_1^{\prime }\left(c\right)=0,$ we obtain critical points $c=c_0=0$ and $c=c_1\approx 1.0694.$ Here, $c_0$ is the minimum points of $q_1.$ Thus, $q_1$ attains its maximum $47901.1108$ at $c_1$. Clearly, it is impossible for $H(c,t,y)$ to obtain its global maximum on the face of $t=1$. On $c=2,$ $H\left(c,t,y\right)$ reduces to

$$H\left(2,t,y\right)\equiv 320,t,y\in \left[0,1\right].$$

(34)

Obviously, the global maximal value of $H(c,t,y)$ also cannot be obtained on the face of $c=2$. In the following, we assume that $c<2$ and $t<1$.

I. Let $\left(c,t,y\right)\in \left[0,2\right)\times \left[0,1\right)\times \left(0,1\right).$ Now, to find points of maxima in $\Delta ,$ we take partial derivative of (31) with respect to y. Since

$$h_3(c,t)-h_4(c,t)=288\left(4-c^2\right)\left(1-t^2\right)(1-t)\left[\left(4-c^2\right)\left(16-2t\right)-9c^2\right],$$

(35)

it is easy to see that

$$\frac{\partial H}{\partial y}=h_2(c,t)+2\left[h_3(c,t)-h_4(c,t)\right]y=48\left(4-c^2\right)\left(1-t^2\right)M(c,t)y,$$

(36)

where

$$M(c,t)=6ct\left(2t+7\right)\left(4-c^2\right)+\left(54t+11\right)c^3+12(1-t)\left[\left(4-c^2\right)\left(16-2t\right)-9c^2\right].$$

(37)

Now, $\frac{\partial H}{\partial y}=0$ yields

$$y=\frac{6ct\left(4-c^2\right)\left(2t+7\right)+c^3\left(54t+11\right)}{12\left(1-t\right)\left[\left(4-c^2\right)\left(2t-16\right)+9c^2\right]}.$$

If $y_0$ is a critical point inside $\Delta ,$ then $y_0\in \left(0,1\right),$ which is possible only if

$$6ct\left(4-c^2\right)\left(2t+7\right)+c^3\left(54t+11\right)+12\left(1-t\right)\left(4-c^2\right)\left(16-2t\right)<108\left(1-t\right)c^2,$$

(38)

and

$$c^2>\frac{8\left(8-t\right)}{25-2t}=:h\left(t\right).$$

(39)

Then, we must obtain the solutions which satisfy both inequalities (38) and (39) for the existence of the critical points.

Since $h^{\prime }\left(t\right)<0$ for $\left(0,1\right),$ $h\left(t\right)$ is decreasing in $\left(0,1\right)$, hence, $c^2>\frac{56}{23}$. A simple exercise shows that (38) does not hold in this case for all values of $t\in \left[\frac{1}{2},1\right)$, and there is no critical point of H in $\left(0,2\right)\times \left(0,1\right)\times \left[\frac{1}{2},1\right).$ In fact, suppose that

$$\begin{array}{ccc}\hfill \mathrm{Y}(c,t):=& & 6ct\left(4-c^2\right)\left(2t+7\right)+c^3\left(54t+11\right)+12\left(1-t\right)\left(4-c^2\right)\left(16-2t\right)\hfill \\ & & -108\left(1-t\right)c^2.\hfill \end{array}$$

It is easily obtained that

$$\mathrm{Y}(c,t)\ge 672-276c^2+11c^3+6(-112+46c^2+9c^3)t=:L(c,t).$$

(40)

As it is observed that $L\left(c,\frac{1}{2}\right)\ge 0$ and $L\left(c,1\right)\ge 0$ for $c\in [0,2]$, we have

$$L(c,t)\ge \min \left\{L\left(c,\frac{1}{2}\right),L\left(c,1\right)\right\}\ge 0,(c,t)\in [0,2]\times \left[\frac{1}{2},1\right).$$

(41)

Combining (40) and (41), we see (38) is impossible to hold for all $t\in \left[\frac{1}{2},1\right)$. This is to say that there are no critical points of $H(c,t,y)$ satisfying $y\in (0,1)$ with $t\in \left[0,\frac{1}{2}\right)$.

For $t<\frac{1}{2}$, we will prove that all the critical points of $H(c,t,y)$ with $y\in (0,1)$ have a maximum value no larger than $m_0$. Suppose that $(\widehat{c},\widehat{t},\widehat{y})$ is a critical point of H and $\widehat{y}\in (0,1)$. To guarantee the inequalities (38) and (39) to be true simultaneously, we know that $\widehat{t}<\frac{1}{2}$. Using (39), it follows that ${\widehat{c}}^2>h\left(\frac{1}{2}\right)=\frac{5}{2}$. By noting that $1-t^2\le 1$ and $t<\frac{1}{2}$, it is not hard to observe that

$$h_1(c,t)\le h_1\left(c,\frac{1}{2}\right)=:{\kappa }_1\left(c\right)$$

(42)

and

$$h_j(c,t)\le \frac{4}{3}{h}_j\left(c,\frac{1}{2}\right)=:{\kappa }_j\left(c\right),j=2,3,4.$$

(43)

Hence, we obtain that

$$H(c,t,y)\le {\kappa }_1\left(c\right)+{\kappa }_2\left(c\right)y+{\kappa }_3\left(c\right)y^2+{\kappa }_4\left(c\right)\left(1-y^2\right)=:\mathrm{\Theta }(c,y).$$

(44)

A basic calculation shows that

$$\frac{{\partial }^2\mathrm{\Theta }(c,y)}{\partial y^2}=2\left[{\kappa }_3\left(c\right)-{\kappa }_4\left(c\right)\right]=3456\left(4-c^2\right)\left(5-2c^2\right)\le 0$$

(45)

for $c^2\in \left(\frac{5}{2},4\right]$. Thus, we know

$$\begin{array}{ccc}\hfill \frac{\partial \mathrm{\Theta }(c,y)}{\partial y}& \ge & \frac{\partial \mathrm{\Theta }(c,y)}{\partial y}{|}_{y=1}\hfill \\ & =& {\kappa }_2\left(c\right)+2\left[{\kappa }_3\left(c\right)-{\kappa }_4\left(c\right)\right]\hfill \\ & =& 48\left(4-c^2\right)\left(360+96c-150c^2+14c^3\right)\ge 0\hfill \end{array}$$

with $c\in \left(\sqrt{\frac{5}{2}},2\right]$. This leads to

$$\mathrm{\Theta }(c,y)\le {\kappa }_1\left(c\right)+{\kappa }_2\left(c\right)+{\kappa }_3\left(c\right):=\iota \left(c\right),c\in \left(\sqrt{\frac{5}{2}},2\right].$$

(46)

Now, a basic calculation shows that $\iota$ attains its maximum value $38095.55$ at $c\approx 1.5811399$. Therefore, we conclude that

$$H(\widehat{c},\widehat{t},\widehat{y})\le \mathrm{\Theta }(\widehat{c},\widehat{y})\le \iota \left(\widehat{c}\right)<m_0.$$

(47)

This implies that the global maximum value of $H(c,t,y)$ in $\Delta$ cannot be obtained with $y\in (0,1)$.

II. On the face of $y=0,$ we have

$$H(c,t,0)=h_1(c,t)+h_4(c,t)=:R_1(c,t)$$

(48)

and

$$H(c,t,1)=h_1(c,t)+h_2(c,t)+h_3(c,t)=:R_2(c,t).$$

(49)

It is noted that

$$R_2(c,t)-R_1(c,t)=h_2(c,t)+h_3(c,t)-h_4(c,t)=48\left(4-c^2\right)\left(1-t^2\right)N(c,t),$$

(50)

where

$$N(c,t)=12\left(4-c^2\right)(1+c)t^2+\left(-432+168c+162c^2+12c^3\right)t+384-150c^2+11c^3.$$

(51)

For $t>\frac{7}{10}$ and $c\ge 1$, it is found that

$$\begin{array}{ccc}\hfill \frac{\partial N(c,t)}{\partial t}& =& 24\left(4-c^2\right)(1+c)t-432+168c+162c^2+12c^3\hfill \\ & \ge & \frac{84}{5}\left(4-c^2\right)(1+c)-432+168c+162c^2+12c^3\hfill \\ & =& \frac{6}{5}\left(-304+196c+121c^2-4c^3\right)=:\varrho \left(c\right).\hfill \end{array}$$

As it is easy to see that ${\varrho }^{\prime }\left(c\right)>0$ for $c\in [1,2)$, we know that $\varrho$ attains its minimum value at $c=1$. Thus, we have

$$\varrho \left(c\right)\ge \varrho \left(1\right)=\frac{54}{5}>0,c\in [1,2).$$

(52)

It follows that $\frac{\partial N(c,t)}{\partial t}\ge 0$ for all $c\in [1,2)$. Therefore, we deduce that

$$N(c,t)\ge N\left(c,\frac{7}{10}\right)=\frac{1}{25}\left(2628+3528c-1062c^2+338c^3\right)\ge 0.$$

(53)

On the other hand, if $c>\frac{7}{10}$ and $c<1$, it is noted that $-432+168c+162c^2+12c^3\le 0$ and

$$\begin{array}{ccc}\hfill N(c,t)& \ge & 12\left(4-c^2\right)(1+c)t^2+384-150c^2+11c^3\hfill \\ & \ge & \frac{147}{25}\left(4-c^2\right)(1+c)+384-150c^2+11c^3\hfill \\ & =& \frac{1}{25}\left(10188+588c-3897c^2+128c^3\right)>0.\hfill \end{array}$$

Hence, we conclude that

$$N(c,t)\ge 0,(c,t)\in [0,2)\times \left(\frac{7}{10},1\right).$$

(54)

This implies that $R_2(c,t)\ge R_1(c,t)$ and

$$H(c,t,0)\le H(c,t,1),(c,t)\in [0,2)\times \left(\frac{7}{10},1\right).$$

(55)

Thus, we have

$$\max H(c,t,0)\le \max H(c,t,1),(c,t)\in [0,2]\times \left[\frac{7}{10},1\right].$$

(56)

For $t\le \frac{7}{10}$, it is observed that

$$h_1(c,t)\le h_1\left(c,\frac{7}{10}\right)=:{\tau }_1\left(c\right)$$

(57)

and

$$h_4(c,t)\le \frac{100}{51}{h}_4\left(c,\frac{7}{10}\right)=:{\tau }_2\left(c\right).$$

(58)

Then, it follows that

$$H(c,t,0)=h_1(c,t)+h_4(c,t)\le {\tau }_1\left(c\right)+{\tau }_2\left(c\right)=:{\tau }_3\left(c\right).$$

(59)

A basic calculation shows that ${\tau }_3$ attains its maximum value $72285.70$ at $c=0$. This means that

$$H(c,t,0)\le m_0\le maxH(c,t,1),(c,t)\in [0,2)\times \left[0,\frac{7}{10}\right].$$

(60)

Combining (56) and (60), the global optimal value of H is sure to be achieved on the face of $y=1$. Now, we only need to find points of maxima on the faces $y=1$ of $\Delta .$ On $y=1,$ it is clear that

$$H(c,t,1)=h_1(c,t)+h_2(c,t)+h_3(c,t)=:U(c,t).$$

(61)

We note that

$$\begin{array}{ccc}\hfill U(c,t)& & =5c^6+6\left(4-c^2\right)\left[88c^3+\left(c^2+432c+432\right)c^{2}t\right.\hfill \\ & & +\left.8\left(19c^2-11c+54\right)c^2{t}^2+108\left(c^2-4c-4\right)c^2{t}^3\right]\hfill \\ & & +36{\left(4-c^2\right)}^2\left[128+32ct+\left(23c^2+16c-112\right)t^2\right.\hfill \\ & & \left.+2\left(5c^2-16c+36\right)t^3+4\left(c^2-4c-4\right)t^4\right].\hfill \end{array}$$

As we see that $c^2-4c-4\le 0$, $5c^2-16c+36\ge 0$, $19c^2-11c+54\ge 0$ for $c\in [0,2]$ and $t^3\le t^2\le t$, it follows that

$$\begin{array}{ccc}\hfill U(c,t)& \le & 5c^6+6\left(4-c^2\right)\left[88c^3+\left(c^2+432c+432\right)c^{2}t+8\left(19c^2-11c+54\right)c^{2}t\right]\hfill \\ & & +36{\left(4-c^2\right)}^2\left[128+32ct+\left(23c^2+16c-112\right)t^2+2\left(5c^2-16c+36\right)t^2\right]\hfill \\ & =& 5c^6+6\left(4-c^2\right)\left[88c^3+\left(153c^4+344c^3+864c^2\right)t\right]\hfill \\ & & +36{\left(4-c^2\right)}^2\left[128+32ct+\left(33c^2-16c-40\right)t^2\right]=:V(c,t).\hfill \end{array}$$

In virtue of $t<1$, we deduce that

$$\begin{array}{ccc}\hfill V(c,t)& \le & 5c^6+6\left(4-c^2\right)\left(153c^4+432c^3+864c^2\right)\hfill \\ & & +36{\left(4-c^2\right)}^2\left[128+32ct+\left(33c^2-16c-40\right)t^2\right]=:W(c,t).\hfill \end{array}$$

Define

$$S(c,t):=128+32ct+\left(33c^2-16c-40\right)t^2,(c,t)\in [0,1)\times [0,1).$$

(62)

For $c<1$, it is easily noted that $33c^2-16c-40\le -23$ and

$$S(c,t)\le 128+32ct-23t^2=:T(c,t),(c,t)\in [0,1)\times [0,1).$$

(63)

It is seen that

$$t_0=\frac{16}{23}c\in [0,1);$$

(64)

thus, we have

$$T(c,t)\le \frac{4\times (-23)\times 128-1024c^2}{4\times (-23)}=128+\frac{256}{23}{c}^2\le 128+12c^2.$$

(65)

It follows that

$$\begin{array}{ccc}\hfill W(c,t)& \le & 5c^6+6\left(4-c^2\right)\left(153c^4+432c^3+864c^2\right)+36{\left(4-c^2\right)}^2\left(128+12c^2\right)\hfill \\ & =& -481c^6-2592c^5-360c^4+10368c^3-9216c^2+73728=:\chi \left(c\right)\hfill \end{array}$$

To prove that $\chi \left(c\right)\le 73728$ for $c\in [0,1)$, we need to show that

$$-481c^6-2592c^5-360c^4+10368c^3-9216c^2\le 0,$$

(66)

which is equivalent to

$$-481c^4-2592c^3-360c^2+10368c-9216\le 0.$$

(67)

Let

$$\vartheta \left(c\right):=-481c^4-2592c^3-360c^2+10368c-9216,c\in [0,1).$$

(68)

It is clear that

$$\vartheta \left(c\right)\le -481c^4-2592c^3+10368c-9216=:\widehat{\vartheta }\left(c\right).$$

(69)

Since ${\widehat{\vartheta }}^{\prime }\left(c\right)\ge 0$ for $c\in [0,1)$, thus, we know that $\widehat{\vartheta }\left(c\right)\le \widehat{\vartheta }\left(1\right)=-1921$. This implies that $\vartheta \left(c\right)\le 0$. Then we obtain that $\chi \left(c\right)\le 73728$ and thus $U(c,t)\le 73728$ for all $(c,t)\in [0,1)\times [0,1)$.

For $c\in [1,2)$, it is found that

$$\begin{array}{ccc}\hfill \frac{\partial V(c,t)}{\partial t}& =& 6(4-c^2)(153c^4+344c^3+864c^2)+36{(4-c^2)}^2\left[32c+2(33c^2-16c-120)t\right]\hfill \\ & \ge & 6(4-c^2)(153c^4+344c^3+864c^2)+36{(4-c^2)}^2(32c-23t)\hfill \\ & \ge & 6(4-c^2)(153c^4+344c^3+864c^2)+36{(4-c^2)}^2(32c-23)\hfill \\ & =& 6(4-c^2)\left(153c^4+152c^3+1002c^2+768c-552\right)\ge 0.\hfill \end{array}$$

Thus, we have

$$\begin{array}{ccc}\hfill V(c,t)& \le & V(c,1)\hfill \\ & =& 5c^6+6\left(4-c^2\right)\left(153c^4+432c^3+864c^2\right)+36{\left(4-c^2\right)}^2\left(33c^2+16c+88\right)\hfill \\ & =& 275c^6-2016c^5-7848c^4+5760c^3+14400c^2+9216c+50688=:\mu \left(c\right)\hfill \end{array}$$

In virtue of $\mu$ attaining its maximum $71992.07$ at $c\approx 1.179235$, we know $U(c,t)\le m_0$ for $(c,t)\in [1,2)\times [0,1)$. Thus, we claim that the maximum value of $U(c,t)$ is sure to exist in $(c,t)\in [0,1)\times [0,1)$ and hence has a maximum value no larger than $m_0$. Since $H(c,t,1)=U(c,t)$, and the global maximum value of H is sure to exist on the face $y=1$ of $\Delta$, we obtain that $H(c,t,y)\le m_0$ for $(c,x,y)\in \Delta$. From Equation (30), we can write

$$\left|{\gamma }_2{\gamma }_4-{\gamma }_3^2\right|\le \frac{m_0}{2654208}=\frac{73728}{2654208}=\frac{1}{36}.$$

If $f\in {\mathcal{S}}_e^{*},$ then the equality is determined by using (10)–(13) and

$$f_2\left(z\right)=zexp\left({\int }_0^z\frac{e^{\left(t^3\right)}-1}{t}dt\right)=z+\frac{1}{3}{z}^4+\frac{5}{36}{z}^7+\cdots .$$

(70)

This completes the proof. □

3. Conclusions

The Hankel determinants can be used in the study of singularities and power series with integral coefficients. Additionally, there are some of its applications in meromorphic functions in the literature. Therefore, to obtain the upper bounds of Hankel determinants for certain subclasses of univalent functions is an active topic in the field of geometric function theory. In the present work, we consider a family of starlike functions ${\mathcal{S}}_e^{*}$ connected with the exponential function. For functions in this class, we obtain some sharp results on the logarithmic coefficient-related problems. The method of proof is based on the well-known parametric formulas for initial coefficients in the Carathéodory class of functions. It was found that the logarithmic coefficients of functions can be transfered to obtain the bounds for the coefficients of a function and its inverse function. As the calculation of bounds on coefficients of the inverse function is often a more difficult task, our results on Hankel determinants with logarithmic coefficients seem to be of great significance. As the exponential function is a very special class of hypergeometric functions, this work may inspire some other investigations by considering univalent functions subordinated to a more general class. Additionally, it will be interesting if the sharp bounds of higher-order Hankel determinants can be obtained.