Controlled Parameter Estimation for The AR(1) Model with Stationary Gaussian Noise

Abstract

This paper deals with the maximum likelihood estimator for the parameter of first-order autoregressive models driven by the stationary Gaussian noises (Colored noise) together with an input. First, we will find the optimal input that maximizes the Fisher information, and then, with the method of the Laplace transform, both the asymptotic properties and the asymptotic design problem of the maximum likelihood estimator will be investigated. The results of the numerical simulation confirm the theoretical analysis and show that the proposed maximum likelihood estimator performs well in finite samples.

1. Introduction

The experiment design has been given a great deal of interest over the last decades from the early statistical literature [1,2,3,4] as well as in the engineering literature [5,6,7]. The classical approach for experiment design consists of two-step procedures: Maximize Fisher information under the energy constraint of the input and find an adaptive estimator that is asymptotically normal with an optimal convergence rate, and the variance achieves the inverse of this Fisher information, as presented in [8].

In the research of [9], the authors showed that real inputs exhibit long-range dependence: the behavior of a real process after a given time t depends on the entire history of the process up to time t, the classical examples are presented in finance [10,11,12], that is why the researchers considered controlled problems not only with white noise or standard Brownian motion, but also with fractional type noise such as the fractional Brownian motion [13,14]. The applications of fractional case can be seen in [15,16,17,18]. Let us take [13] for the example: The authors considered the controlled drift estimation problem in fractional Ornstein–Ulenbeck (FOU) process:

$$d{X}_t=-\vartheta X_{t}dt+u\left(t\right)dt+d{B}_t^H,\vartheta >0,t\in [0,T]$$

(1)

where $B_t^H$ is a fractional Brownian motion with a known Hurst parameter $H\in (0,1)$, whose covariance function is

$$\mathbf{E}\left(B_t^H{B}_s^H\right)=\frac{1}{2}(t^{2H}+s^{2H}{-|t-s|}^{2H}),s,t\in [0,T].$$

$u\left(t\right)$ is a deterministic function in a control space and $\vartheta$ is the unknown drift parameter. They have achieved the goal of the experiment design.

However, in the real world, we always try to deal with high-frequency or low-frequency data, but not with continuous ones, as presented in the previous example. So, can we find a discrete model which will be pretty close to (1)? To achieve this goal, we apply the Euler approximation with discrete time $t=\mathrm{\Delta },2\mathrm{\Delta },\cdots ,N\mathrm{\Delta }(=T)$ to $X_t$, then we have a time series:

$$X_{i\mathrm{\Delta }}=\beta X_{(i-1)\mathrm{\Delta }}+\mathrm{\Delta }u\left((i-1)\mathrm{\Delta }\right)+{\eta }_{i\mathrm{\Delta }}^H$$

(2)

where $\beta =1-\vartheta \mathrm{\Delta }$, ${\eta }_{i\mathrm{\Delta }}^H=B_{i\mathrm{\Delta }}^H-B_{(i-1)\mathrm{\Delta }}^H$ is a fractional Gaussian noise with distance $\mathrm{\Delta }$. When $\vartheta$ is a positive constant, we can take some special $\mathrm{\Delta }$ such that $\left|\beta \right|<1$ then the Equation (2) is a controlled AR(1) (Autoregressive model of order 1) process with fractional Gaussian noise. For simplicity, we rewrite this model with

$$X_n=\vartheta X_{n-1}+u\left(n\right)+{\xi }_n,0<\left|\vartheta \right|<1,X_0=0,$$

(3)

where $\xi =({\xi }_n,n\in \mathbb{Z})$ is the fractional Gaussian noise (fGn) with the covariance function defined in (20) (when the variance will not affect the final results, here we always suppose that it will be 1). In fact, according to [19] we can extend the noise $\xi =({\xi }_n,n\in \mathbb{Z})$ to the centered regular stationary Gaussian noise with

$${\int }_{-\pi }^{\pi }|log{f}_{\xi }\left(\lambda \right)|d\lambda <\infty ,$$

(4)

where $f_{\xi }\left(\lambda \right)$ is the spectral density of $\xi$. A similar change-point and Kalman–Bucy problem can be found in [20,21].

Now, let us return to the model (3), the same as the function $u\left(t\right)$ in (1), $u\left(n\right)$ denotes a deterministic function of $n\in \mathbb{Z}$. Obviously, when considering the problem of estimating the unknown parameter, $\vartheta$ with the observation data $X^{\left(N\right)}=\left(X_n,n=1,\cdots ,N\right)$, if $u\left(n\right)=0$, it has been solved in [19]. When $u\left(n\right)\in {\mathcal{U}}_N$– the control space defined in (17), Let us denote $L(\vartheta ,X^{\left(N\right)})$ the likelihood function for $\vartheta$, then the Fisher information can be written as

$${\mathcal{I}}_N(\vartheta ,u)=-{\mathbf{E}}_{\vartheta }\frac{{\partial }^2}{\partial {\vartheta }^2}lnL(\vartheta ,X^{\left(N\right)}).$$

Therefore, we denote

$${\mathcal{J}}_N\left(\vartheta \right)=\underset{u\in {\mathcal{U}}_N}{sup}{\mathcal{I}}_N(\vartheta ,u).$$

our main goal is to find a function, say, $\widehat{u}\in {\mathcal{U}}_N$ such that

$${\mathcal{I}}_N(\vartheta ,\widehat{u})={\mathcal{J}}_N\left(\vartheta \right)$$

and then with this $\widehat{u}$ we will find an adapted estimator ${\overline{\vartheta }}_N$ of the parameter $\vartheta$, which is asymptotically efficient in the sense that, for any compact set $\mathbb{K}=\left\{\vartheta \right|-1<\vartheta <1\}$,

$$\underset{\vartheta \in \mathbb{K}}{sup}{\mathcal{J}}_N\left(\vartheta \right){\mathbf{E}}_{\vartheta }{({\overline{\vartheta }}_N-\vartheta )}^2=1+o\left(1\right),$$

(5)

as $N\to \infty$.

In this paper, with the computation of the Laplace transform, we will find $\widehat{u}$ for the model (3) and we check that the Maximum Likelihood Estimator (MLE) satisfy (5).

Remark 1.

Here, we assume that the covariance structure of the noise ξ is known. In fact, if this covariance depends only on one parameter, for example, the Hurst parameter H of the fractional Gaussian noise presented in Section 4 we can estimate this parameter with the log-periodogram method [22] or with generalized quadratic variation [23] and study the plug-in estimator. All details can be found in [24].

Remark 2.

In this paper, we will not estimate the function $u\left(n\right)$, but we will simply find one function that maximizes Fisher information.

The organization of this paper is as follows. In Section 2, we give some basic results of regular stationary noise ${\xi }_n$, find the likelihood function, and the formula for Fisher information. Section 3 provides the main results of this paper, and Section 4 shows some simulation examples to show the performance of the proposed MLE. All proofs are collected in Appendix A.

2. Preliminaries and Notations

2.1. Stationary Gaussian Sequences

First of all, let us construct the connection between stationary Gaussian noise and the independent case. Suppose that the covariance of the stationary Gaussian process $\xi ={\left({\xi }_n\right)}_{n\ge 1}$ is defined by

$$\mathbf{E}{\xi }_m{\xi }_n=c(m,n)=\rho \left(\right|n-m\left|\right),\rho \left(0\right)=1.$$

(6)

when it is positive, then there exists an associated innovation sequence ${\left({\sigma }_n{\epsilon }_n\right)}_{n\ge 1}$ where ${\epsilon }_n\sim \mathcal{N}(0,1)$, $n\ge 1$ are independent, defined by the following relations:

$${\sigma }_1{\epsilon }_1={\xi }_1,{\sigma }_n{\epsilon }_n={\xi }_n-\mathbf{E}\left({\xi }_n\right|{\xi }_1,{\xi }_2,\cdots ,{\xi }_{n-1}),n\ge 2.$$

From the theorem of Normal Correlation (Theorem 13.1, [25]) that there exists a deterministic kernel $k=\left(k\right(n,m),n\ge 1,m\le n)$ such that $k(n,n)=1$ and

$${\sigma }_n{\epsilon }_n=\sum _{m=1}^{n}k(n,m){\xi }_m.$$

(7)

For $n\ge 1$, we will denote by ${\beta }_{n-1}$ the partial correlation coefficient

$${\beta }_{n-1}=-k(n,1).$$

(8)

As with the Levinson–Durbin algorithm (see [26]), we have the following relationship between $k(·,·)$, the covariance function $\rho (·)$ defined in (6), the sequence of partial correlation coefficients ${\left(\beta \right)}_{n\ge 1}$ and the variances of innovation ${\left({\sigma }_n^2\right)}_{n\ge 1}$:

$${\sigma }_n^2=\prod _{m=1}^{n-1}(1-{\beta }_m^2),n\ge 2,{\sigma }_1=1,$$

(9)

$$\sum _{m=1}^{n}k(n,m)\rho \left(m\right)={\beta }_n{\sigma }_n^2,$$

(10)

$$k(n+1,n+1-m)=k(n,n-m)-{\beta }_{n}k(n,m)$$

(11)

Since the covariance matrix of ${\xi }_n$ is positively defined, there also exists an inverse deterministic kernel $K=\left(K\right(n,m),n\ge 1,m\le n)$ such that

$${\xi }_n=\sum _{m=1}^{n}K(n,m){\sigma }_m{\epsilon }_m.$$

(12)

The relationship of the kernel k and K can be found in [19].

Remark 3.

It is worth mentioning that the condition (4) implies that

$$\sum _{n\ge 1}{\beta }_n^2<\infty .$$

This condition is theoretically verified for classical autoregressive-moving-average (ARMA) noises. To our knowledge, no explicit form of the partial autocorrelation coefficients for fractional Gaussian noise (fGn) is known, but because the explicit formula of the spectral density of fGn sequences has been exhibited in [27], condition (4) is fulfilled for any Hurst index $H\in (0,1)$. For very similar fractional autoregressive integrated moving average (fractional ARIMA) processes, it has been proven that ${\beta }_n=O\left(1\right)$ in [28].

2.2. Model Transformation

Let us define the process $Z=(Z_n,n\ge 1)$ so that

$$Z_n=\sum _{m=1}^{n}k(n,m)X_m,n\ge 1,$$

(13)

where $k(n,m)$ is the kernel defined in (7). Similar to (12), we have

$$X_n=\sum _{m=1}^{n}K(n,m)Z_m.$$

(14)

From the Equalities (13) and (14) the process $Z=(Z_n,n\ge 1)$ has the same filtration of $X=(X_n,n\ge 1)$. In the following parts, let the observation be $(Z_1,Z_2,\cdots ,Z_N)$. Actually, it was shown in [19] that the process Z can be considered as the first component of a 2-dimensional AR(1) process $\zeta =({\zeta }_n,n\ge 1)$, which is defined by:

$${\zeta }_n=\left(\begin{array}{c}{Z}_n\\ {\displaystyle \sum _{r=1}^{n-1}}{\beta }_r{Z}_r\end{array}\right).$$

It is not hard to obtain that ${\zeta }_n$ is a 2-dimensional Markov process, which satisfies the following equation:

$${\zeta }_n=A_{n-1}{\zeta }_{n-1}+bv\left(n\right)+b{\sigma }_n{ϵ}_n,n\ge 1,{\zeta }_0={\mathbf{0}}_{2\times 1},$$

(15)

with

$$A_n=\left(\begin{array}{cc}\vartheta & \vartheta {\beta }_n\\ {\beta }_n& 1\end{array}\right),b=\left(\begin{array}{c}1\\ 0\end{array}\right)$$

(16)

and ${ϵ}_n\sim \mathcal{N}(0,1)$ are independent. Following from the idea of [13] we will define the control space ${\mathcal{V}}_N$ of the function $v\left(n\right)$:

$${\mathcal{V}}_N=\left\{v\left(n\right)|\frac{1}{N}\sum _{n=1}^N{\left|\frac{v\left(n\right)}{{\sigma }_{n+1}}\right|}^2\le 1\right\}.$$

From the control space of ${\mathcal{V}}_N$ we can define that for the function $u\left(n\right)$:

$${\mathcal{U}}_N=\left\{u\left(n\right)|\frac{1}{N}{\displaystyle \sum _{n=1}^N}{\left|\frac{{\displaystyle \sum _{m=1}^n}k(n,m)u\left(m\right)}{{\sigma }_{n+1}}\right|}^2\le 1\right\},$$

(17)

where $|·|$ is just the absolute value.

2.3. Fisher Information

As we have interpreted, the observation will be the first component of the process $\zeta =({\zeta }_n,n\ge 1)$. Now, from Equation (15), it is easy to write the likelihood function $L(\vartheta ,X^{\left(N\right)})$, which depends on the function $v\left(n\right)$:

$$L(\vartheta ,X^{\left(N\right)})=\prod _{n=1}^N\frac{1}{\sqrt{2\pi {\sigma }_n^2}}exp\left(-\frac{1}{2}{\left(\frac{b^{{}^{*}}\left({\zeta }_n-A_{n-1}{\zeta }_{n-1}-bv\left(n\right)\right)}{{\sigma }_n}\right)}^2\right).$$

(18)

Consequently, Fisher information ${\mathcal{I}}_N(\vartheta ,v)$ can be written as

$${\mathcal{I}}_N(\vartheta ,v)=-{\mathbf{E}}_{\vartheta }\frac{{\partial }^2}{\partial {\vartheta }^2}lnL(\vartheta ,X^{\left(N\right)})={\mathbf{E}}_{\vartheta }\sum _{n=1}^{N-1}{\left(\frac{a_n^{*}{\zeta }_n}{{\sigma }_{n+1}}\right)}^2,$$

(19)

where $a_n=\left(\begin{array}{c}1\\ {\beta }_n\end{array}\right)$.

3. Main Results

In this part, we will present the main results of this paper. First of all, from the presentation of Fisher information (19), we have the following.

Theorem 1.

The asymptotical optimal input in the class of control ${\mathcal{U}}_T$ is $u_{opt}\left(n\right)={\displaystyle \sum _{m=1}^n}K(n,m){\sigma }_{m+1}$ for $0<\vartheta <1$ and $u_{opt}\left(n\right)={(-1)}^n{\displaystyle \sum _{m=1}^n}K(n,m){\sigma }_{m+1}$ or $u_{opt}\left(n\right)={(-1)}^{n+1}{\displaystyle \sum _{m=1}^n}K(n,m){\sigma }_{m+1}$ for $-1<\vartheta <0$. Furthermore,

$$\underset{N\to \infty }{lim}\frac{{\mathcal{J}}_N\left(\vartheta \right)}{N}=\mathcal{I}\left(\vartheta \right),$$

where $\mathcal{I}\left(\vartheta \right)=\frac{1}{1-{\vartheta }^2}+\frac{1}{{(1-\vartheta )}^2}$ for $0<\vartheta <1$ and $\mathcal{I}\left(\vartheta \right)=\frac{1}{1-{\vartheta }^2}+\frac{1}{{(1+\vartheta )}^2}$ for $-1<\vartheta <0$.

Remark 4.

Theorem 1 can be generalized to the AR(p) case with the norm of the Fisher information matrix, but this purpose is not as clear as AR(1), that is: when the Fisher information is larger, the error will be smaller. For this reason, we will illustrate only the result of the first order, but not of the order p.

From Theorem 1, since the optimal input does not depend on the unknown parameter $\vartheta$, we can consider ${\overline{\vartheta }}_N$ as the MLE ${\widehat{\vartheta }}_N$. The following theorem states that ${\widehat{\vartheta }}_N$ will reach the efficiency of (5).

Theorem 2.

With the optimal input $u_{opt}\left(n\right)$ defined in Theorem 1, for $0<\left|\vartheta \right|<1$, the MLE ${\widehat{\vartheta }}_N$ has the following properties:

• ${\widehat{\vartheta }}_N$ is strong consistency, that is, ${\widehat{\vartheta }}_N\stackrel{a.s.}{\to }\vartheta$ as $N\to \infty$.
• ${\widehat{\vartheta }}_N$ is uniformly consistent on compact $\mathbb{K}\subset \mathbb{R}$, i.e. for any $\nu >0$

  $$\underset{N\to \infty }{lim}\underset{\vartheta \in \mathbb{K}}{sup}{\mathbf{P}}_{\vartheta }^N\left\{\left|{\widehat{\vartheta }}_N-\vartheta \right|>\nu \right\}=0$$
• ${\widehat{\vartheta }}_N$ is uniformly on compacts asymptotically normal, i.e., as $N\to \infty$,

  $$\underset{N\to \infty }{lim}\underset{\vartheta \in \mathbb{K}}{sup}\left|{\mathbf{E}}_{\vartheta }f\left(\sqrt{N}\left({\widehat{\vartheta }}_N-\vartheta \right)-\mathbf{E}f\left(\xi \right)\right)\right|=0,\forall f\in {\mathcal{C}}_b,$$

  where ξ is a zero mean Gaussian random variable with variance ${\mathcal{I}}^{-1}\left(\vartheta \right)$ defined in Theorem 1. Moreover, we have the uniform on $\vartheta \in \mathbb{K}$ convergence of the moments: for any $q>0$,

  $$\underset{N\to \infty }{lim}\underset{\vartheta \in \mathbb{K}}{sup}\left|{\mathbf{E}}_{\vartheta }{\left|\sqrt{N}\left({\widehat{\vartheta }}_N-\vartheta \right)\right|}^q-\mathbf{E}{\left|\xi \right|}^q\right|=0.$$

Remark 5.

From Theorem 2, we can see that the asymptotical properties of the MLE do not depend on the structure of the noise, which is the same as described in [19].

4. Simulation Study

In this section, Monte-Carlo simulations are done just for the verification of the asymptotical normality of the MLE ${\widehat{\vartheta }}_N$ with different Gaussian noise such as AR(1), MA(1) and fractional Gaussian noise(fGn). When ${\beta }_n$ defined in (8) for the ARMA case is explicit, we can easily obtain the result of MLE, so here we just take the fGn as an example. In fact, the covariance function of fGn is

$$\rho \left(\right|n-m\left|\right)=\frac{1}{2}{\left(\right|m-n+1|}^{2H}{-2|m-n|}^{2H}{+|m-n-1|}^{2H}).$$

(20)

As presented in Remark 5, the asymptotical normality for the MLE does not depend on the structure of the stationary noise, which means it does not depend on the Hurst parameter H. So, different from [29] and other LSE methods, which have a change at $H=2/3$ or another point in the fractional case, we only need to verify the asymptotical normality with only one fixed H, and we take this value $H=0.65$. Here we compare the different $\vartheta =0.7$ and $\vartheta =-0.7$ in Figure 1 and Figure 2.

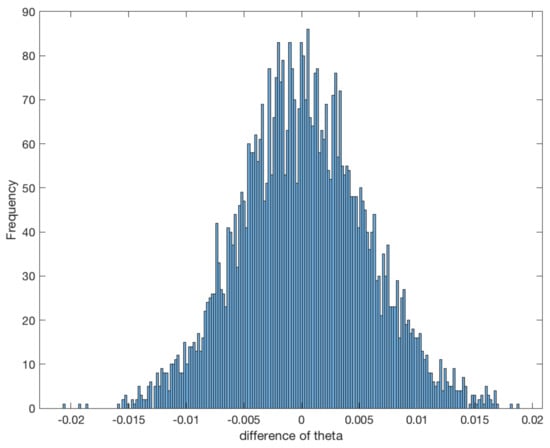
Figure 1. Histogram of the statistic $\mathrm{\Phi }(N,\vartheta ,X)$ with $\vartheta =-0.7$ and $N=4000$.

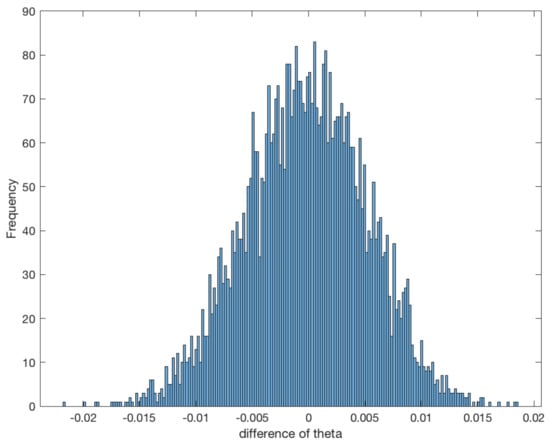
Figure 2. Histogram of the statistic $\mathrm{\Phi }(N,\vartheta ,X)$ with $\vartheta =0.7$ and $N=4000$.

Even if we have got the optimal input $u_{opt}\left(n\right)$ in Theorem 1, our simulation will not use the initial model (1) because obviously this $u_{opt}\left(n\right)$ is so complicated in the fractional case. We will compute our MLE with the transformation (15) with the corresponding $v_{opt}\left(n\right)={\sigma }_{n+1}$ using the method of Wood and Chan (see [30]) for the simulation of fractional Gaussian noise. All the simulations will be the same as presented in [19].

Remark 6.

From the two figures, we can see that the statistical error of the MLE is asymptotically normal, and we also have verified that the variance is nearly the same as the inverse of the Fisher information.

5. Conclusions

With the approximation of the controlled fractional Ornstein–Ulenbeck model in (1), we considered the optimal input problem in the AR(1) process driven by stationary Gaussian noise. We have found the controlled function, which maximizes the Fisher information, and with the Laplace Transform, we have proved the asymptotical normality of the MLE, whose asymptotical variance does not depend on the structure of the noise. Our future study will focus on the non-Gaussian case, such as the general fractional ARIMA, and so on.

Appendix A.1. Proof of Theorem 1

To prove Theorem 1, we separate the Fisher Information of (19) into two parts:

$$\begin{array}{ccc}\hfill {\mathcal{I}}_N(\vartheta ,v)& =& {\mathbf{E}}_{\vartheta }\sum _{n=1}^{N-1}{\left(\frac{a_n^{*}{\zeta }_n-a_n^{*}{\mathbf{E}}_{\vartheta }{\zeta }_n+a_n^{*}{\mathbf{E}}_{\vartheta }{\zeta }_n}{{\sigma }_{n+1}}\right)}^2\hfill \\ & =& {\mathbf{E}}_{\vartheta }\sum _{n=1}^{N-1}{\left(\frac{a_n^{*}({\zeta }_n-{\mathbf{E}}_{\vartheta }{\zeta }_n)}{{\sigma }_{n+1}}\right)}^2+\sum _{n=1}^{N-1}{\left(\frac{a_n^{*}{\mathbf{E}}_{\vartheta }{\zeta }_n}{{\sigma }_{n+1}}\right)}^2\hfill \\ & =& {\mathbf{E}}_{\vartheta }\sum _{n=1}^{N-1}{\left(\frac{a_n^{*}{\mathcal{P}}_n^{\vartheta }}{{\sigma }_{n+1}}\right)}^2+\sum _{n=1}^{N-1}{\left(\frac{a_n^{*}{\mathbf{E}}_{\vartheta }{\zeta }_n}{{\sigma }_{n+1}}\right)}^2\hfill \\ & =& {\mathcal{I}}_{1,N}\left(\vartheta \right)+{\mathcal{I}}_{2,N}(\vartheta ,v).\hfill \end{array}$$

where ${\mathcal{P}}_n^{\vartheta }$ satisfies the following equation:

$${\mathcal{P}}_n^{\vartheta }=A_{n-1}{\mathcal{P}}_{n-1}^{\vartheta }+b{\sigma }_n{ϵ}_n,{\mathcal{P}}_0^{\vartheta }={\mathbf{0}}_{2\times 1}.$$

Obviously, ${\mathcal{I}}_{1,N}\left(\vartheta \right)$ does not depend on $v\left(n\right)$. Thus, and as presented in [19], we have

$$\underset{N\to \infty }{lim}{\mathbf{E}}_{\vartheta }exp\left(-\frac{1}{2N}\sum _{n=1}^{N-1}\frac{{\left(a_n^{*}{\mathcal{P}}_n^{\vartheta }\right)}^2}{{\sigma }_{n+1}^2}\right)=exp\left(-\frac{1}{2}{\mathcal{I}}_1\left(\vartheta \right)\right)$$

and ${\mathcal{I}}_1\left(\vartheta \right)=\frac{1}{1-{\vartheta }^2}$ which can be deduced by (9) in [19].

A standard calculation yields

$$\underset{N\to \infty }{lim}\frac{{\mathcal{I}}_{1,N}\left(\vartheta \right)}{N}={\mathcal{I}}_1\left(\vartheta \right)=\frac{1}{1-{\vartheta }^2}.$$

(A1)

To compute ${\mathcal{I}}_{2,N}\left(\vartheta \right)$, let $s\left(n\right)=\frac{{\mathbf{E}}_{\vartheta }{\zeta }_n}{{\sigma }_{n+1}}$. Then, we can see that $s\left(n\right)$ satisfies the following equation:

$$s\left(n\right)=A_{n-1}s(n-1)\frac{{\sigma }_n}{{\sigma }_{n+1}}+bf\left(n\right),$$

(A2)

where $f\left(n\right)=\frac{v\left(n\right)}{{\sigma }_{n+1}}$ and it is bounded.

Note that ${\beta }_n\to 0$ and $\frac{{\sigma }_n}{{\sigma }_{n+1}}\to 1$, we assume that for $n=1,2,\cdots$, $\frac{{\sigma }_n}{{\sigma }_{n+1}}\le (1+\epsilon )$ and ${\beta }_n\le \epsilon$ for the sufficiently small positive constant $\epsilon$ and $(1+\epsilon )\vartheta <1$. Consequently, we can state the following result.

Lemma A1.

Let $Y=(Y_n,n\ge 1)$ be the 2-dimension vector, which satisfies the following equation:

$$Y_n=\left(\begin{array}{cc}\vartheta & 0\\ 0& 1\end{array}\right)Y_{n-1}+bf\left(n\right),Y\left(0\right)=y_0.$$

Then, we have

$$\underset{N\to \infty }{lim}\frac{1}{N}\left(\sum _{n=1}^N{\left(a_n^{*}s\left(n\right)\right)}^2-\sum _{n=1}^N{\left(b^{*}{Y}_n\right)}^2\right)=0.$$

Proof. 

For the sake of notational simplicity, we introduce a 2-dimensional vector $Y^{\prime }=(Y_n^{\prime },n\ge 1)$, which satisfies the following equation:

$$Y_n^{\prime }=A_{n-1}{Y}_{n-1}^{\prime }\frac{{\sigma }_n}{{\sigma }_{n+1}}+bf\left(n\right),Y_0^{\prime }=y_0^{\prime }.$$

In this situation, we have three comparisons. First, we compare $b^{*}(s\left(n\right)-Y_n^{\prime })\to 0$. A standard calculation implies that

$$\begin{array}{cc}\hfill s\left(n\right)-Y_n^{\prime }& =A_{n-1}s(n-1)\frac{{\sigma }_n}{{\sigma }_{n+1}}-A_{n-1}{Y}_{n-1}^{\prime }\frac{{\sigma }_n}{{\sigma }_{n+1}}\hfill \\ \hfill & =\left(\begin{array}{cc}\vartheta & \vartheta {\beta }_{n-1}\\ {\beta }_{n-1}& 1\end{array}\right)(s(n-1)-Y_{n-1}^{\prime })\frac{{\sigma }_n}{{\sigma }_{n+1}},\hfill \end{array}$$

since ${\beta }_n\to 0,\frac{{\sigma }_n}{{\sigma }_{n+1}}\to 1$, we have

$$b^{*}(s\left(n\right)-Y_n^{\prime })=\vartheta b^{*}(s(n-1)-Y_{n-1}^{\prime }),(n\to \infty )$$

which implies $b^{*}(s\left(n\right)-Y_n^{\prime })\to 0$.

Now, we compare $b^{*}{Y}_n-b^{*}{Y}_n^{\prime }$. A simple calculation shows that

$$Y_n-Y_n^{\prime }=\left(\begin{array}{cc}\vartheta & 0\\ 0& 1\end{array}\right)Y_{n-1}-A_{n-1}{Y}_{n-1}^{\prime }\frac{{\sigma }_n}{{\sigma }_{n+1}}$$

$n\to \infty$ on both sides of this equation, then we have

$$\underset{n\to \infty }{lim}(Y_n-Y_n^{\prime })=\left(\begin{array}{cc}\vartheta & 0\\ 0& 1\end{array}\right)\underset{n\to \infty }{lim}(Y_{n-1}-Y_{n-1}^{\prime })$$

which implies $b^{*}(Y_n^{\prime }-Y_n)\to 0$.

Finally, since ${\beta }_n\to 0$ and the component of $s\left(n\right)$ is bounded, we can easily obtain $a_n^{*}s\left(n\right)-b^{*}{Y}_n\to 0$, which demonstrates the proof. □

Now, we define $\alpha \left(n\right)=b^{*}{Y}_n$. Then $\alpha \left(n\right)=\vartheta \alpha (n-1)+f\left(n\right)$, where $f\left(n\right)$ is in the space of ${\mathcal{F}}_N=\left\{f\left(n\right)|\frac{1}{N}{\displaystyle \sum _{n=1}^N}{f}^2\left(n\right)\le 1\right\}$. Since the initial value $\alpha \left(0\right)$ will not change our result, we assume $\alpha \left(0\right)=0$ without loss of generality.

Let ${\mathcal{J}}_{2,N}\left(\vartheta \right)=\underset{v\in {\mathcal{V}}_N}{sup}{\mathcal{I}}_{2,N}(\vartheta ,v)$. Then, it is clear that

$$\underset{N\to \infty }{lim}\frac{{\mathcal{J}}_{2,N}\left(\vartheta \right)}{N-1}=\underset{N\to \infty }{lim}\frac{1}{N}\underset{f\in {\mathcal{F}}_N}{sup}\sum _{n=1}^N{\alpha }^2\left(n\right).$$

(A3)

Now to prove Theorem 1, we only need the following lemma.

Lemma A2.

As ${\mathcal{J}}_{2,N}\left(\vartheta \right)$ is presented in (A3), we have

$$\underset{N\to \infty }{lim}\frac{{\mathcal{J}}_{2,N}\left(\vartheta \right)}{N-1}={\mathcal{I}}_2\left(\vartheta \right),$$

(A4)

where ${\mathcal{I}}_2\left(\vartheta \right)=\frac{1}{{(1-\vartheta )}^2}$.

Proof. 

First of all, taking $f\left(n\right)=1$, then $\alpha \left(n\right)=\vartheta \alpha (n-1)+1$, we can conclude that

$$\alpha \left(n\right)=\frac{1-{\vartheta }^n}{1-\vartheta },{\alpha }^2\left(n\right)=\frac{{(1-{\vartheta }^n)}^2}{{(1-\vartheta )}^2}$$

we can easily abtain that

$$\underset{N\to \infty }{lim}\frac{1}{N}\sum _{n=1}^N{\alpha }^2\left(n\right)=\frac{1}{{(1-\vartheta )}^2}$$

It is easy to get the lower bound

$$\underset{N\to \infty }{lim}\frac{1}{N}\underset{f\in {\mathcal{F}}_N}{sup}\sum _{n=1}^N{\alpha }^2\left(n\right)\ge \frac{1}{{(1-\vartheta )}^2}.$$

Furthermore, a simple calculation shows that

$$\alpha \left(n\right)=\phi \left(n\right)\sum _{i=1}^n{\phi }^{-1}\left(i\right)f\left(i\right),n\ge 1,\alpha \left(0\right)=0,$$

where

$$\phi \left(n\right)=\vartheta \phi (n-1),\phi \left(0\right)=1.$$

Obviously, we can rewrite $\frac{1}{N}{\sum }_{n=1}^N{\alpha }^2\left(n\right)$ as

$$\frac{1}{N}\sum _{n=1}^N{\alpha }^2\left(n\right)=\sum _{n=1}^N\left(\phi \left(n\right)\sum _{i=1}^n{\phi }^{-1}\left(i\right)\frac{f\left(i\right)}{\sqrt{N}}\right)\left(\phi \left(n\right)\sum _{i=1}^n{\phi }^{-1}\left(i\right)\frac{f\left(i\right)}{\sqrt{N}}\right).$$

or

$$\frac{1}{N}\sum _{n=1}^N{\alpha }^2\left(n\right)=\sum _{i=1}^N\sum _{j=1}^N{F}_N(i,j)\frac{f\left(i\right)}{\sqrt{N}}\frac{f\left(j\right)}{\sqrt{N}},$$

where

$$F_N(i,j)=\sum _{\ell =i\bigvee j}^N\left(\phi (\ell ){\phi }^{-1}\left(i\right)\right)\left(\phi (\ell ){\phi }^{-1}\left(j\right)\right).$$

Let ${\varphi }_n={\phi }^{-1}\left(n\right){\displaystyle \sum _{\ell =n}^N}\phi (\ell ){ϵ}_{\ell }$ with ${ϵ}_{\ell }\sim \mathcal{N}(0,1)$ are independent. Then, we have

$$F_N(i,j)=\mathbf{E}\left({\varphi }_i{\varphi }_j\right)$$

and

$${\varphi }_{n-1}=\vartheta {\varphi }_n+{ϵ}_{n-1},{\varphi }_N=0.$$

Let us mention that $F_N(i,j)$ is a compact symmetric operator for fixed N. We should estimate the spectral gap (the first eigenvalue ${\nu }_1\left(N\right)$) of the operator. The estimation of the spectral gap is based on the Laplace transform of ${\displaystyle \sum _{i=1}^N}{\varphi }_i^2$, which is written as

$$L_N\left(a\right)={\mathbf{E}}_{\vartheta }exp\left(-\frac{a}{2}\sum _{i=1}^N{\varphi }_i^2\right),$$

for sufficiently small negative $a<0$. On the one hand, when $a>-\frac{2}{{\nu }_1\left(N\right)}$, $\varphi$ is a centered Gaussian process with a covariance operator $F_N$. Using Mercer’s theorem and Parseval’s identity, $L_T\left(a\right)$ can be represented by

$$L_N\left(a\right)=\prod _{i\ge 1}{(1+a{\nu }_i\left(N\right))}^{-1/2},$$

(A5)

where ${\nu }_i\left(N\right)$ is the sequence of positive eigenvalues of the covariance operator. A straightforward algebraic calculation shows the following.

$$L_N\left(a\right)={\left({\vartheta }^{N-1}{\mathrm{\Psi }}_N^1\right)}^{-1/2},$$

(A6)

where

$${\mathrm{\Psi }}_N=\left(\begin{array}{cc}1& 0\end{array}\right){\left(\begin{array}{cc}\frac{1}{\vartheta }& \frac{1}{\vartheta }\\ \frac{a}{\vartheta }& \frac{a}{\vartheta }+\vartheta \end{array}\right)}^{N-1}\left(\begin{array}{c}1\\ 0\end{array}\right).$$

For

$$\mathrm{\Delta }={\left(\frac{1+a}{\vartheta }+\vartheta \right)}^2-4\ge 0,$$

there exists two real eigenvalues ${\lambda }_2\ge 1,{\lambda }_1\le 1$ of the matrix

$$\left(\begin{array}{cc}\frac{1}{\vartheta }& \frac{1}{\vartheta }\\ \frac{a}{\vartheta }& \frac{a}{\vartheta }+\vartheta \end{array}\right).$$

Then, we can see that

$${\mathrm{\Psi }}_N=\left(\frac{{\lambda }_2^{N-1}-{\lambda }_1^{N-1}}{{\vartheta }^2}-\frac{{\lambda }_2^{N-2}-{\lambda }_1^{N-2}}{\vartheta }\right)\frac{\vartheta }{{\lambda }_2-{\lambda }_1}\ge 0.$$

That is to say for $\vartheta >0$ and for any $0>a\ge -{(1-\vartheta )}^2$, $L_N\left(a\right)\ge 0$. Thus, $\underset{N\to \infty }{lim}{\nu }_1\left(N\right)\le \frac{1}{{(1-\vartheta )}^2}$ and we complete the proof. □

Remark A1.

For $-1<\vartheta <0$, $\mathrm{\Delta }\ge 0$ means $\frac{1+a}{\vartheta }+\vartheta \le -2$ and $0>a\ge -{(1+\vartheta )}^2$. As a consequence, we have ${\nu }_1\left(N\right)\le \frac{1}{{(1+\vartheta )}^2}$.

Appendix A.2. Proof of Theorem 2

Let $v_{opt}\left(n\right)={\sigma }_{n+1}$ and ${\zeta }^o=({\zeta }_n^o,n\ge 1)$ be the process $\zeta$ with the function $v_{opt\left(n\right)}$. Then, we have

$${\zeta }_n^o=A_{n-1}{\zeta }_{n-1}^o+b{v}_{opt}\left(n\right)+b{\sigma }_n{ϵ}_n,{\zeta }_0={\mathbf{0}}_{2\times 1}$$

To estimate the parameter $\vartheta$ from observations ${\zeta }_1,{\zeta }_2,\cdots ,{\zeta }_N$, we can write the MLE of $\vartheta$ with the help of (18)

$${\widehat{\vartheta }}_N={\left(\sum _{n=1}^N{\left(\frac{a_n^{*}{\zeta }_n}{{\sigma }_{n+1}}\right)}^2\right)}^{-1}\left(\sum _{n=1}^N\frac{a_n^{*}{\zeta }_n{b}^{*}{\eta }_{n+1}}{{\sigma }_{n+1}^2}\right).$$

(A7)

where ${\eta }_n=\left(\begin{array}{c}{Z}_n-v\left(n\right)\\ 0\end{array}\right).$

A standard calculation yields

$${\widehat{\vartheta }}_N-\vartheta =\frac{M_N}{{⟨M⟩}_N},$$

where

$$M_N=\sum _{n=1}^N\frac{a_n^{*}{\zeta }_n}{{\sigma }_{n+1}}{ϵ}_{n+1},{⟨M⟩}_N=\sum _{n+1}^N{\left(\frac{a_n^{*}{\zeta }_n}{{\sigma }_{n+1}}\right)}^2.$$

The second and third conclusions on the asymptotic normality of Theorem 2 are crucially based on the asymptotical study of the Laplace transform

$${\mathcal{L}}_N^{\vartheta }\left(\frac{\mu }{N}\right)={\mathbf{E}}_{\vartheta }exp\left(-\frac{\mu }{2N}{⟨M⟩}_N\right),$$

for $N\to \infty$.

First, we can rewrite ${\mathcal{L}}_N^{\vartheta }\left(\frac{\mu }{N}\right)$ by the following formula:

$${\mathcal{L}}_N^{\vartheta }\left(\frac{\mu }{N}\right)={\mathbf{E}}_{\vartheta }exp\left(-\frac{1}{2}\sum _{n=1}^N{\zeta }_n^{*}{\mathcal{M}}_n{\zeta }_n\right),$$

where ${\mathcal{M}}_n=\frac{\mu }{N{\sigma }_{n+1}^2}{a}_n{a}_n*$.

As presented in [19] and using the Cameron–Martin formula [31], we have the following result.

Lemma A3.

For any N, the following equality holds:

$${\mathcal{L}}_N^{\vartheta }\left(\frac{\mu }{N}\right)=\prod _{n=1}^N{[det(\mathbf{Id}+\gamma (n,n){\mathcal{M}}_n)]}^{-1/2}exp\left(-\frac{1}{2}\sum _{n=1}^N{z}_n^{*}{\mathcal{M}}_n{(\mathbf{Id}+\gamma (n,n){\mathcal{M}}_n)}^{-1}{z}_n\right),$$

where $\left(\gamma \right(n,m),1\le m\le n)$ is the unique solution of the equation

$$\gamma (n,m)=\left[\prod _{r=m+1}^n{A}_{r-1}{(\mathbf{Id}+\gamma (r,r){\mathcal{M}}_r)}^{-1}\right]\gamma (m,m),$$

(A8)

and the function $\left(\gamma \right(n,n,n\ge 1\left)\right)$ is the solution of the Ricatti equation:

$$\gamma (n,n)=A_{n-1}{(\mathbf{Id}+\gamma (n-1,n-1){\mathcal{M}}_{n-1})}^{-1}\gamma (n-1,n-1)A_{n-1}^{*}+{\sigma }_n^{2}b{b}^{*}.$$

(A9)

It is worth mentioning that $(z_n,1\le n\le N)$ is the unique solution of the equation

$$z_n=m_n-\sum _{r=1}^{n-1}\gamma (n,r){[\mathbf{Id}+\gamma (r,r){\mathcal{M}}_r]}^{-1}{\mathcal{M}}_r{z}_r,z_0=m_0.$$

where $m_n=\mathbf{E}{\zeta }_n^o$.

With the explicit formula of the Laplace transform presented in Lemma A3, we have its asymptotical property.

Lemma A4.

Under the condition (4), for any $\mu \in \mathbb{R}$, we have

$$\underset{N\to \infty }{lim}{\mathcal{L}}_N^{\vartheta }\left(\frac{\mu }{N}\right)=exp\left(-\frac{\mu }{2}\mathcal{I}\left(\vartheta \right)\right)$$

(A10)

where $\mathcal{I}\left(\vartheta \right)=\frac{1}{1-{\vartheta }^2}+\frac{1}{{(1-\vartheta )}^2}$.

Proof. 

In [19], we have stated that

$$\underset{N\to \infty }{lim}\prod _{n=1}^N{[det(\mathbf{Id}+\gamma (n,n){\mathcal{M}}_n)]}^{-1/2}=exp(-\frac{1}{2}\frac{\mu }{1-{\vartheta }^2}).$$

(A11)

Since the component of $\gamma (n,n)$ is bounded, we have

$$\underset{N\to \infty }{lim}\mathbf{Id}+\gamma (n,n){\mathcal{M}}_n=\mathbf{Id}.$$

On the other hand,

$$\sum _{n=1}^N{m}_n^{*}{\mathcal{M}}_n{m}_n=\frac{\mu }{N}\sum _{n=1}^N{\left(\frac{a_n^{*}\mathbf{E}{\zeta }_n^0}{{\sigma }_{n+1}}\right)}^2⟶\frac{\mu }{{(1-\vartheta )}^2},N\to \infty .$$

(A12)

which was presented in the last part. Finally, notice

$$\sum _{r=1}^{n-1}\gamma (n,r){[\mathbf{Id}+\gamma (r,r){\mathcal{M}}_r]}^{-1}{\mathcal{M}}_r{z}_r=\sum _{r=1}^{n-1}\left[\prod _{\tau =r+1}^n{A}_{\tau -1}{(\mathbf{Id}+\gamma (\tau ,\tau ){\mathcal{M}}_{\tau })}^{-1}\right]{[\mathbf{Id}+\gamma (r,r){\mathcal{M}}_r]}^{-1}{\mathcal{M}}_r{z}_r$$

we have the following.

$$\underset{N\to \infty }{lim}\sum _{r=1}^{n-1}\gamma (n,r){[\mathbf{Id}+\gamma (r,r){\mathcal{M}}_r]}^{-1}{\mathcal{M}}_r{z}_r=0.$$

(A13)

Combining (A11) and (A12) and (A13), the Lemma A4 achieves. □

From this conclusion, it follows immediately that

$${\mathbf{P}}_{\vartheta }\underset{N\to \infty }{lim}\frac{1}{N}{⟨M⟩}_N=\mathcal{I}\left(\vartheta \right).$$

Furthermore, using the central limit theorem for martingale, we have

$$\frac{1}{\sqrt{N}}{M}_N⟹\mathcal{N}(0,\mathcal{I}\left(\vartheta \right)).$$

Consequently, the asymptotical part of Theorem 2 is obtained.

Strong consistency is immediate when we change $\frac{\mu }{N}$ with a positive proper constant $\mu$ in the Lemma A4 because the determinant part tends to 0 as presented in Section 5.2 of [19] and the extra part is bounded.