Abstract
Azacytidine is the only approved treatment for patients with higher-risk myelodysplastic syndromes (MDS); yet less than half of the patients will achieve a response, whereas the duration of response is highly heterogeneous and there are no predictors for response duration. The aim of this study is to estimate the patient’s time to loss of response (LoR) to azacytidine based on clinical measurements during treatment. To this end, a personalized prediction framework is proposed that estimates the LoR of a new patient using a patient similarity-based approach. Namely, the new patient’s clinical data—represented as a multivariate time series—are compared to a reference set of patients. The comparison uses distance metrics that quantify how similar two patients’ time series are, assuming patients with similar trajectories tend to have similar LoR. Then, the LoR of the new patient is predicted by averaging the outcomes of the most similar reference patients. The pipeline includes a data normalization strategy that centers each feature on its baseline value and scales it to highlight relative changes and distance metrics to quantify similarity. Both real-world and simulated data were utilized to evaluate the proposed methodology, employing the leave-one-out validation and the Mean Absolute Percentage Error (MAPE) to assess accuracy. The estimated MAPE was found to be 30.52% and 11.82% in the real-world and simulated dataset, respectively. The best and most robust predictions were achieved using the Euclidean distance metric and setting the number of most similar patients around three to five. This study proposes a personalized predictive approach for the LoR to azacitidine in the MDS clinical setting, demonstrating potential for a serviceable prediction of LoR and forming the foundation for further research.
1. Introduction
Myelodysplastic syndromes (MDS) are a heterogeneous group of hematologic disorders characterized by ineffective hematopoiesis, dysplasia of one or more cell lines, and a varying risk of progression to acute myeloid leukemia []. Several prognostic scoring systems have been developed over the years to stratify patients with MDS according to their risk of disease progression and overall survival. Among these, the Revised International Prognostic Scoring System (IPSS-R) remains the most widely used tool in clinical practice, with an IPSS-R score of 3.5 or higher being a practical threshold to define higher-risk disease [].
The therapeutic decision-making in MDS depends on several factors, including disease risk level, the patient’s age, comorbidities, performance status, and the molecular landscape of the disease. For patients with higher-risk MDS, as defined by the IPSS-R [,], two major treatment pathways are broadly recognized, curative intent via allogeneic hematopoietic stem cell transplantation (HSCT) and disease-modifying approaches, primarily using hypomethylating agents such as azacitidine []. The hypomethylating agents, primarily azacitidine and decitabine, are the cornerstone of treatment in higher-risk MDS. These agents act by targeting epigenetic dysregulation, a hallmark of MDS pathophysiology []. Despite its widespread use, the response to azacitidine is often partial and transient. Clinical trials and real-world studies have shown that only 40–50% of patients achieve a clinical response, including complete remission, hematologic improvement, or stable disease. Specifically, complete remission is achieved in only about 10–17% of patients, while hematologic improvement, such as transfusion independence or improved blood counts, is more common, occurring in 20–30% of cases [,]. The median duration of response is approximately 9–12 months, and eventually all patients develop resistance or lose response to the drug. According to the latest International Working Group (IWG) 2006 criteria, a hemoglobin drop of ≥1.5 g/dL or ≥50% decrement of maximum response levels of neutrophils or platelets signifies the loss of response (LoR) []. More importantly, even in responders, LoR typically occurs within 12 to 18 months, and treatment failure is nearly universal over time [,,].
In this context, a major clinical question arises, whether it is possible to identify early–ideally within the first two months of treatment–patients who will likely lose their response to azacitidine. Early prediction of treatment failure carries significant implications, both for therapeutic planning and for patient-centered care. From a clinical perspective, early identification of impending LoR to azacitidine is critical in deciding when a patient should undergo HSCT. HSCT is the only potentially curative therapy for MDS, but several issues must be considered when weighing the benefits and risks, with probably the most critical being the optimal timing of therapy []. Equally important is the patient’s perspective. A diagnosis of high-risk MDS entails life-altering decisions regarding employment, caregiving, long-term planning, and potentially relocating for transplantation. For many patients, uncertainty regarding the efficacy of treatment can be psychologically and practically debilitating. Providing an early, individualized prognosis can offer clarity and empower both patients and their families to make informed, proactive decisions about the course of care.
Despite the wide use of azacitidine, for more than two decades there are currently no widely accepted clinical or molecular predictive models of primary or secondary resistance to azacitidine []. This literature gap motivated this study, which aims to introduce a personalized approach using the early temporal clinical information of individual patients to estimate the LoR time. Personalized approaches that go beyond the typical static prediction at specific time points, such as the diagnosis, by employing dynamic modeling to exploit temporal patterns in patient data have also been proposed in another context by our group. Specifically, Moysiadis et al. [] proposed a personalized stepwise dynamic predictive algorithm (PSDPA) for patients with chronic lymphocytic leukemia (CLL). The PSDPA introduced an individualized score that evolves over each patient’s follow-up, effectively capturing disease kinetics. By comparing a new CLL patient’s score trajectory to a reference set of CLL patients’ score trajectories, the PSDPA predicts that patient’s time-to-first treatment at any given follow-up point [].
Herein, a customized framework is proposed that estimates the LoR of a patient in a personalized fashion, based on a reference patient pool. This framework leverages a normalization strategy that aims to highlight the relative changes in the observed clinical features and similarity metrics in order to identify reference patients whose initial clinical trajectories closely match those of a new patient. The underlying assumption is that patients exhibiting similar patterns of clinical evolution during the early months of treatment are likely to share comparable durations of therapeutic response. The methodological framework is shown in Figure 1. This approach was validated using both real-world clinical data and a larger set of simulated patients, designed to reflect realistic clinical variability.
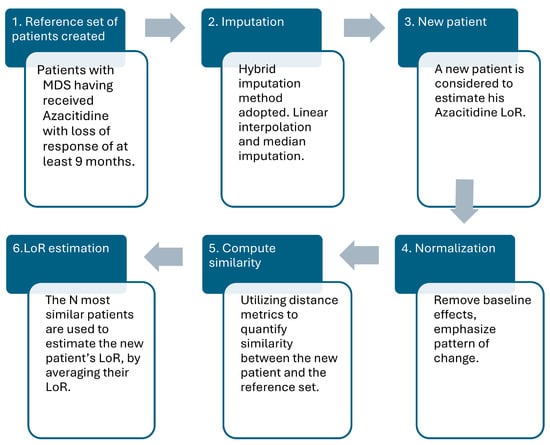
Figure 1.
The methodological framework of the study in six sequential steps, namely, (1) creation of the reference pool of patients, (2) imputation of the dataset, (3) introduction of a new patient, (4) employ normalization strategy, (5) compute similarity between patients, and (6) estimate the LoR time of the new patient.
2. Materials and Methods
The primary objective was to propose a customized prediction scheme that estimates the duration in months a patient with MDS will continue to benefit from azacitidine before losing therapeutic response. The follow-up of each patient is performed in one-month intervals, i.e., the timepoint at which the treatment is initiated, 1st month after the treatment initiated, 2nd month after the treatment initiated, etc. It was determined that using the first three timepoints–namely, within two months from treatment initiation–of clinical measurements provides a practical and medically relevant time window, referring to the set of consecutive timepoints used as a patient’s trajectory, for prediction. Although in real life situations treatment response is most commonly assessed after 4 cycles, discontinuation of azacitidine even before 4 cycles is not uncommon. Therefore, early prediction of azacitidine LoR is of particular importance to timely design of other therapeutic strategies. To explore prediction at the earliest meaningful stage, while still ensuring sufficient data for comparison are available, three timepoints were selected.
The prediction scheme employed in this study is based on patient similarity and draws conceptual inspiration from recommender systems. Traditionally used in domains such as e-commerce and media platforms, these systems are tools providing personalized suggestions by analyzing similarities in user preferences or behavior []. In healthcare, analogous systems—known as health recommender systems—offer personalized medical recommendations based on individual health profiles []. For instance, prior studies have utilized recommender-based models for disease prediction and clinical decision support in cardiac patients []. Just as recommender systems suggest items based on prior user behavior, in this framework, the idea is to take each new, prospectively followed patient, compare them to a reference set of already analyzed patients, and provide a personalized estimate of the LoR to azacitidine for the new patient. The proposed approach assumes that the early-recorded measurements for all patients are both temporally and clinically comparable, capturing the initial response to azacitidine therapy.
In summary, the underlying rationale of the proposed methodology is that patients who display similar early treatment responses are likely to experience similar treatment LoR. Reflecting on this assumption, the framework directly compares the timeseries of a new patient with the timeseries of patients that have been retrospectively analyzed (reference patients). By quantifying how similar the timeseries are—utilizing distance metrics—the most “similar” patients to the new patient in terms of their early treatment dynamics are identified and the estimation for the new patient is generated. This study was designed to exhibit the feasibility of the proposed methodology, utilizing both real and simulated data as pilot applications.
The proposed approach includes the following algorithmic steps (see also Figure 1):
- A reference patient cohort is created, including retrospectively analyzed patients diagnosed with MDS who have undergone azacitidine treatment and experience a LoR of at least 9 months.
- Each patient’s multivariate time series—represented by clinical measurements in monthly timepoints—is preprocessed to handle missingness through the imputation strategy adopted. For variables with low missingness, linear interpolation was used, while median imputation was used for variables with higher rates maintaining consistency.
- The target new patient’s first three timepoints, —where each represents the patient’s medical features for the first three timepoints–is introduced to estimate their LoR time utilizing the reference set of patients.
- Each patient’s first three timepoints window is normalized, as described in Section 2.4, to remove baseline effects and emphasize the pattern of change over time, transforming the time series to common scale independent of absolute values.
- The resulting normalized window of the new patient is flattened and compared with corresponding ones of the reference patients using distance metrics. The metrics used to quantify similarity are Euclidean distance, cosine similarity, and Dynamic Time Warping (DTW).
- The N closest matches (Top N) across all reference patients are obtained, and their known LoR times are averaged to derive the estimation for the new patient.
2.1. Real-World Dataset
To evaluate the effectiveness of the proposed methodological pipeline, a real-world patient dataset was used consisting of 18 fully anonymized patients diagnosed with MDS, each undergoing azacitidine treatment. The data for this study originated from patients at the University General Hospital of Alexandroupolis. The dataset refers to clinical information related to the routine clinical check-up and laboratory testing for each patient, consisting of 21 clinical variables (see Appendix A Table A1 for more details) at consecutive timepoints, starting at treatment initiation. MDS patients receiving azacitidine followed a monthly monitoring protocol; thus, these timepoints were observed at approximately one-month intervals. It was assumed that the distance between these consecutive timepoints was exactly one month. It is also important to note that not all variables were measured at every visit. To address any irregular attendance and missing values in measurements, a hybrid imputation technique was applied (described in Section 2.3). An inclusion criterion in this study was a patient to exhibit a minimum of nine timepoints for LoR. This decision ensured that each patient trajectory included sufficient information, especially since the predictive framework relied on a three timepoint window.
2.2. Simulated Dataset
To assess the proposed approach in a much larger sample size, 300 simulated patients were generated based on the real dataset. Each simulated patient was derived from a real patient by applying a controlled noise-augmentation process that introduced variability while preserving the clinical structure and trajectory. The aim was to create simulated data that retained medical realism and patient behavior under azacitidine treatment and yet was versatile enough to test the generalizability of the model.
For each timepoint—monthly measurement of medical variable—the corresponding values were perturbed using controlled noise to simulate inter-patient variability. Specifically, for each timepoint of every patient, each individual medical variable was modified by applying one of three noise levels—none, mild, or strong—with associated probabilities of 40%, 40%, and 20%, respectively. Mild deviations introduced random noise ±5% of the original value, while strong deviations applied noise of ±10%. This approach ensured that the numerical values varied across simulated patients while preserving the original temporal trends and clinical plausibility.
Subsequently, the addition of statistical noise was used for each variable separately. Two types of noise were applied; specifically, to each patient’s medical variable one of the perturbation methods was assigned at random to maintain diversity in how variability was applied. The types of noise used were Gaussian noise with a fixed standard deviation of σ = 0.05 to simulate continuous measurement variability and random scaling adjusting the overall amplitude of values by ±5%.
Lastly, the perturbation of the target variable, LoR, was implemented. As the LoR is a key variable in this study, it was also perturbed in a controlled manner. There was a 20% chance to retain the original LoR value, 40% to be shifted by ±1 and 40% to be shifted by ±2.
This distribution was designed to simulate realistic clinical variability, avoiding duplicate simulated patients while also providing different LoR. A fair distribution strategy ensured that each real patient contributed almost a similar number of simulated ones.
2.3. Imputation
To impute the observed missing values, a diverse range of imputation techniques was considered and evaluated to select the most suitable approach. Several methods were investigated, leading to linear interpolation, which emerged as the most consistent and best-performing imputation method overall. However, recognizing that some features in the dataset had more than 25% missingness in their time series, which exceeds the threshold where interpolation remains reliable, a hybrid imputation strategy was adopted. Features with up to 25% missing values were imputed using linear interpolation. For those exceeding this threshold, a median imputation strategy was used to minimize bias and avoid the propagation of artificial patterns that could distort patient trajectories. This hybrid approach balanced the need for fidelity in temporal data reconstruction with robustness.
2.4. Normalization
In the real-world dataset, patients presented different baseline values of clinical measurements due to individual physiology, comorbidities, or concurrent medications. If these raw values were compared directly, the resulting distances would reflect absolute differences rather than relative trends—obscuring the patterns that are most relevant to treatment response.
To address this, a custom normalization strategy was developed aiming to standardize each patient’s time series, remove baseline effects, emphasize the pattern of change during treatment, and allow trajectories from different patients to be directly comparable. The implemented normalization procedure works as follows.
The first value of each clinical measurement (azacitidine treatment initiation) is used as a baseline—treated as 0—and subtracted from all subsequent values. This shifts the entire series so that it begins at zero, and then the resulting series is divided by the maximum absolute deviation from the baseline to rescale the pattern within the range [−1, 1], with ±1 representing the maximum deviation:
where , denotes the length of the normalization window.
For calculation and consistency reasons, if a patient’s values are constant over the timepoint window (i.e., no deviation from baseline), the normalized output is a vector of zeros (see Equation (1)).
Using this approach, it was ensured that each time series starts at 0, the most extreme deviation was mapped to ±1, and the shape and relative dynamics of the variable were preserved. This normalization strategy ensured that patterns of change become both visually clear (see, for example, Figure A1) and easily comparable between patients, highlighting the relative changes in the time window. For the purpose of this analysis, the normalization takes place at the first three timepoint window, normalizing locally, to highlight early effects enabling direct comparison of the trajectories.
2.5. Distance Metrics
The performance of the proposed predictive framework depends fundamentally on quantifying patient similarity based on their treatment trajectories. To measure the similarity between patients in order to compare them, three widely recognized distance metrics were evaluated: Euclidean distance [], cosine similarity [] and Dynamic Time Warping []. Each distance metric was applied independently, directly to the flattened, normalized vectors representing the first three timepoints of each patient. The Euclidean distance measured the straightforward overall differences. The cosine similarity evaluated the directional alignment of patient trajectories and the DTW accommodated the temporal shifts between sequences. Evaluating these metrics independently during validation allowed the assessment of how each notion of similarity influenced the accuracy and robustness of the predictive framework.
2.5.1. Euclidean Distance
Euclidean distance is mathematically and conceptually the simplest, most commonly used, distance metric. It calculates the straight-line distance between two points in a multidimensional space []. Conceptually straightforward and computationally efficient, Euclidean distance effectively quantifies the overall magnitude of differences between patient trajectories, provided the data points are well aligned temporally. On the other hand, it is sensitive to scale differences of data and ignores temporal dynamics between points.
2.5.2. Cosine Similarity
Cosine similarity measures the angle between two vectors rather than their magnitude, emphasizing their directional alignment. It was chosen for this exact reason; it does not only measure the distance between two patients points but also considers if the patient’s values are dropping or not []. In clinical time series, cosine similarity is useful when the pattern or shape of a patient’s trajectory is more important than its absolute amplitude. The great advantage is that it captures directional trends and is less sensitive to absolute value shifts, while on the other hand, it can be misleading when magnitudes carry meaningful clinical information. To use this as a distance metric, it was converted into a dissimilarity score, namely:
2.5.3. Dynamic Time Warping
DTW is a well-established technique for comparing time series that may vary in speed or alignment. Unlike point-to-point distance measures such as the Euclidean distance, DTW allows for non-linear warping of the time axis, aligning two sequences in a way that minimizes the overall distance between them—even if they are out of phase []. This is particularly useful in medical time series, where different patients may exhibit similar trends at slightly different rates.
Mathematically, DTW computes the minimum cumulative distance path between two sequences by considering all possible alignments. A cost matrix is created between the two sequences, and dynamic programming is used to find the warping path that minimizes the total distance. Its advantage is that it handles temporal shifts and misalignments well, and it is effective for short, noisy clinical sequences [].
2.6. Cross-Validation and Evaluation Desing
To evaluate the performance of the proposed similarity-based prediction framework, a leave-one-out validation strategy was used. This approach ensured that the methodology was tested in a manner that closely mirrors its intended real-world use: predicting the outcome for a new patient based solely on the known outcomes of the reference patient’s set.
Specifically, for the real patients, the validation process followed the leave-one-out cross-validation approach, and for each iteration, all three distance metrics were utilized to explore the best performing one. The procedure was repeated for the N values ranging from 2 to 5; the rationale being to identify the local minimum in the error landscape, capturing the balance between underfitting—N too small—and excessive averaging—N too large. A maximum value of N = 5 was used to avoid averaging over a disproportionately large portion of the dataset. The same approach was adopted for the simulated dataset of the 300 patients, the difference being that N values ranged from 2 to 30, since the simulated dataset’s size was considerably larger, using the same rationale.
For each evaluation experiment run, a single patient from the dataset was held out and treated as the new patient. The rest of the dataset formed the reference pool for comparison. The new patient’s time series was normalized and compared to the reference patient’s using one of the distance metrics at a time. Then, the most similar patients were selected, and their known LoR values were averaged to produce the prediction for the held-out patient. This process was repeated for every patient in the dataset, ensuring each one serves exactly once as the unseen test case.
The accuracy of the predicted LoR values was assessed using the Mean Absolute Percentage Error (MAPE). This metric quantifies the average magnitude of error between predicted and actual values, expressed as a percentage of the actual value. It is defined as:
where represented the true LoR for a patient; represented the predicted LoR; and corresponded to the total number of patients.
When selecting performance metrics in prediction tasks, there is no golden standard; Mean Absolute Error (MAE) or Root Mean Squared Error are generally preferred to directly measure the magnitude of errors. Furthermore, MAE is more dependable when handling outliers []. The MAPE was chosen as the accuracy metric, as it is widely used in estimation tasks where the magnitude of the target variable varies []. Moreover, the errors are expressed in percentage terms, facilitating interpretation, which is especially useful in clinical settings for assessing over- or underestimation relative to the actual LoR. However, it can be sensitive to very small/large true values—small denominators—so patients with extremely short/long LoR durations or very high errors heavily impacted the resulted MAPE values. Considering this, adjusted MAPE error metrics were also utilized that considered only predictions within ±10 (adjusted MAPE@10) and ±5 months (adjusted MAPE@5) of the true value. This enabled a robust and realistic assessment of the model’s generalization ability across different distance metrics and parameter settings.
2.7. Software and Reproducibilty
All analyses were conducted using Python 3.10. The following libraries were utilized throughout the data preprocessing, modeling, and evaluation pipeline: numpy, pandas, scikit-learn, tqdm, scipy.spatial.distance, fastdtw, sklearn.metrics, matplotlib, and seaborn. To ensure full transparency and reproducibility, the complete analysis pipeline—including code and synthetic datasets—is publicly available on GitHub https://github.com/VantarakiS/MDS_LoR_Personalized_Prediction (accessed on 1 September 2025). User documentation accompanies the repository to facilitate replication and further exploration.
3. Results
3.1. Results on Real Patients
The methodology was first applied to the real-world cohort consisting of 18 patients. The dataset included one patient in the normal BMI range, eight patients in the overweight BMI category and eight patients in obesity class 1. The age at diagnosis ranged from 53.81 to 86.76 years, with a median of 70.29 years. Regarding the IPSS-R score, which reflects the patients’ disease risk, the scores spanned at diagnosis from 1.00 to 9.50, with a median value of 5.00. At the time of treatment initiation, all patients fulfilled criteria for higher-risk MDS (IPSS-R ≥ 3.5) [], and none of the patients that were classified as low-risk at diagnosis received treatment with azacitidine prior to risk progression (IPSS-R ≥ 3.5). Lastly, the LoR time ranged from 9 to 33 months with a median value of 15.69 months.
The analysis (see Figure 2) demonstrated that the Euclidean distance consistently achieved the lowest error. The cosine similarity followed closely, though it was slightly less stable. DTW, while conceptually appealing for time-series alignment, performed rather poorly compared to the other two selected distances. The MAPE decreased notably in the case of the Euclidean distance from Top N = 2 to Top N = 4, which indicated Top N = 4 as a local minimum for the prediction error–30.52% for Euclidean distance—and was therefore selected as the optimal configuration for further experiments in the real-world dataset. This local optimum reflected a trade-off between capturing sufficient information from the patient pool and avoiding dilution from dissimilar cases.
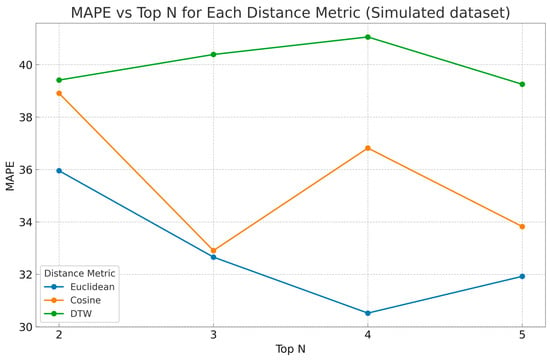
Figure 2.
The MAPE is illustrated across different Top N values for the real patient dataset LoR estimation. Each line represents one of the three distance metrics used to compute patient similarity: Euclidean distance (blue), cosine similarity (orange), and DTW (green).
Summarizing the performance across the three metrics and Top N values, in Figure 3a, the MAPE results highlight and reconfirm explicitly that Euclidean distance combined with Top N = 4 achieved the lowest estimation error (30.52%). As shown in the case of adjusted MAPE@10 (Figure 3b), the lowest error was observed for DTW at Top N = 2 (25.24%); however, DTW’s performance deteriorated with larger Ns, reaching a peak error of 36.62% at Top N = 4. Euclidean and cosine distance metrics demonstrated similar and more stable performance, with cosine achieving its lowest error of 26.23% at Top N = 5. In contrast, for adjusted MAPE@5 (Figure 3c), the results showed that the Euclidean distance outperformed the other metrics, achieving the lowest overall error of 11.46% at Top N = 5, and cosine similarity displayed variable results, performing well at Top N = 2 (12.30%) but showing degraded accuracy at Top N = 4. DTW remained relatively stable across Top N values in the adjusted MAPE@5 setting, although it never outperformed the other metrics.
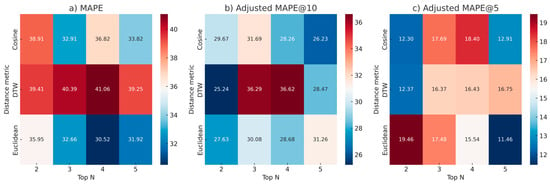
Figure 3.
Heatmaps visualizing MAPE and adjusted metrics across the three distance metrics and Top N values for LoR estimation using the real patient dataset. Each subfigure corresponds to a different evaluation metric: (a) overall MAPE, (b) adjusted MAPE@10, and (c) adjusted MAPE@5. Rows represent the three distance metrics—Euclidean distance, cosine similarity, and DTW—while columns show performance for Top N values from 2 to 5.
In Table 1, the similarity-based framework was used to estimate the loss of response for the 18 real patients. The Euclidean distance metric with Top N = 4 was selected since it showcased the best results during the analysis. Over half of the patients—10 out of 18—had prediction errors below 35%, indicating a generally stable estimation capacity, while some patients exhibited quite accurate predictions, showcasing the framework’s potential. The patients with LoR values that are rare for the dataset (e.g., P11 and P13) showcased the largest error values.

Table 1.
Estimation results of the proposed framework on real patients. For each patient (P1–P18), the table presents the actual observed time to LoR to azacitidine in months, the estimated LoR predicted by the framework, and the corresponding percentage error. The percentage error was calculated as .
3.2. Results on Simulated Dataset
The method was further validated using a simulated dataset of 300 patients, generated as controlled perturbations of the original real patients. The simulated patients were expected to maintain internal consistency due to them being noisy variations of real patients. This inherently promoted similarity within the dataset, which in turn influenced the performance of different similarity-based estimators.
As shown in the line plot of MAPE vs. Top N (Figure 4), the Euclidean and cosine distance consistently yielded the lowest prediction errors, especially within the range of Top N values from 2 to 15. Taking into account the whole range of Top N, Euclidean distance yielded the lowest errors overall, with cosine similarity following closely but showing slightly more variance in higher values of Top N, while DTW demonstrated the poorest performance. These results were anticipated given the results on real patients—retaining similar shape and magnitude. The best performing Top N seemed to be in the range of 2–5 approximately, as it is observed that for Top N values greater than 6–7, MAPE was increasing.
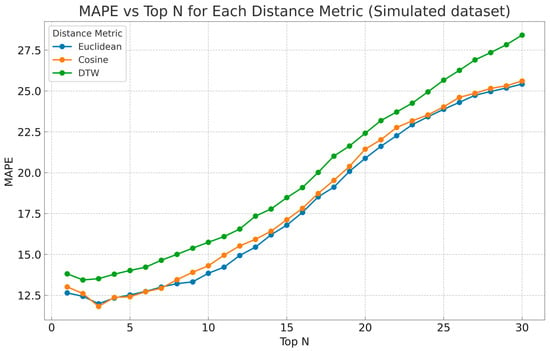
Figure 4.
The MAPE is plotted across the number of Top N and distance metrics—Euclidean distance (blue), cosine similarity (orange), and Dynamic Time Warping (green)—to assess best performing Ns.
To better understand the impact of Top N in the range of 2–5, three heatmaps were created (see Figure 5) for each distance metric showing MAPE as a function of Top N. Regarding MAPE (Figure 5a) the cosine and the Euclidean distance metrics achieved the best performance, with MAPE values remaining relatively stable around a mean of 12.31% across Top N in the range of 2–5. Cosine exhibited the lowest error at Top N = 3 (11.82%), while Euclidean yielded similar performance (11.98%). DTW, in contrast, showed the highest errors, increasing steadily to a peak of 14.02% at Top N = 5. In the adjusted MAPE@10 heatmap (Figure 5b), Euclidean distance outperformed the other metrics, achieving its lowest error of 11.03% at Top N = 2, suggesting strong generalization in this range of Top N values. Cosine similarity followed closely with 11.32% at Top N = 3, while the performance between Euclidean and cosine distance was comparable, with each metric occasionally surpassing the other across different N configurations. DTW once again showed the highest adjusted errors, peaking at 12.85% at Top N = 5. Finally, in the adjusted MAPE@5 heatmap (Figure 5c), cosine and Euclidean distance metrics both delivered optimal results, with Euclidean distance achieving the best score of 9.14% at Top N = 5, while both cosine and Euclidean showed consistent performance across all Top N values, maintaining errors with a mean of 9.59% and 9.48%, respectively. DTW remained the least effective metric across all windows, yet it achieved consistently good performance. Overall, these results reinforced the insight of Euclidean distance as the most robust and stable metric across different validation windows, while cosine similarity also demonstrated competitive performance, in some cases even better. DTW appeared to be the least effective approach.
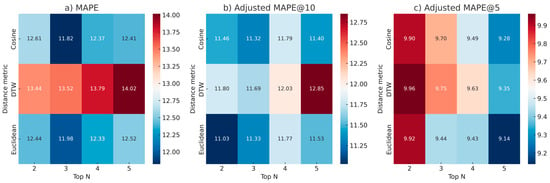
Figure 5.
Heatmaps visualizing MAPE and adjusted metrics across the three distance metrics and Top N values for LoR estimation using the simulated patient dataset. Each subfigure corresponds to a different evaluation metric: (a) overall MAPE, (b) adjusted MAPE@10, and (c) adjusted MAPE@5. Rows represent the three distance metrics—Euclidean distance, cosine similarity and DTW—while columns show performance for Top N values from 2 to 5.
From the results (Figure 5), it was concluded that the optimal configuration was using cosine distance, which closely overperformed Euclidean distance with Top N = 3 when considering the MAPE, while Top N = 2 and 5 were better choices for adjusted MAPE@10 and @5, respectively, when combined with Euclidean distance. Euclidean distance was the most robust distance metric across all evaluation metrics, with cosine similarity achieving comparable results. An important insight is that when every LoR time was well represented in the reference set, the patients were comparable with one another, showcasing better estimation with an overall error around 12% approximately. Another interesting insight is that the number of Top N remained approximately the same in both datasets—around Top N = 3–regardless of the simulated dataset’s much larger size.
4. Discussion
4.1. Summary of Findings
This study proposed a personalized prediction framework to estimate the LoR to azacitidine therapy in MDS patients using an instance-based, similarity-driven approach. Leveraging real-world longitudinal clinical data from 18 patients, along with 300 statistically simulated patients, this study sought to predict the treatment’s LoR early in the treatment timeline. The patient similarity was calculated using three distinct distance metrics–Euclidean distance, cosine similarity, and DTW—and a normalization approach was proposed that emphasized relative changes from baseline to ensure meaningful and accurate comparisons, with the final predictions derived by averaging the LoR of the N most similar patients.
The real patient dataset results underscored the importance of both the choice of distance metric and the tuning of Top N, suggesting that Euclidean distance, showcasing a MAPE of 30.52% (Figure 3a) when using Top N = 4, offered the most consistent and accurate performance under the current framework and dataset. Also, while Top N = 5 seemed to perform a little bit better for adjusted MAPE@5 (Figure 3c), the smoothing effect started to take effect due to the averaging of many patients. Thus, the line plot across Top N values (Figure 2) and heatmaps (Figure 3), summarizing performance metrics, reinforced the superiority of Euclidean distance, with Top N = 4 emerging as a consistent spot that minimized error across metrics without the fear of smoothing effects. Also, the results of Table 1 reinforced the clinical assumption that similar early treatment dynamics often predict similar response durations—but only when similar cases were present in the reference pool. The algorithm tended to underestimate LoR in long-responders and overestimate it in short-responders, probably due to them being rare instances in the dataset. In particular, there were cases of long-responders in which the absolute difference between the observed and estimated LoR was quite large, for example, patients #3, #7, and #13 exhibited an absolute difference of at least 10 months. Of note, all these three patients exhibited a quite long LoR to azacytidine with 28.85. 25.87, and 31.15 months, respectively. The estimated LoR was, respectively, 18.40, 13.59, and 20.09, showing that for these long-responders, the proposed framework did not produce a satisfactory prediction by underestimating their LoR. From a clinical perspective this magnitude of an error (±10 months) is clearly important, practically overshadowing the benefit of the proposed framework in aiding medical experts’ decisions. This is because the ability to efficiently estimate the LoR to azacitidine in higher-risk MDS directly influences the timing of subsequent therapeutic interventions. In addition, it is related to the patient’s own experience, specifically, awareness of whether azacitidine is likely to provide durable benefit may offer individuals and their families the opportunity to engage in informed conversations with their care team and to prepare for what lies ahead. Nevertheless, these results should be treated in the light of a pilot application of the proposed framework. Increasing the sample size of the real cohort, thus increasing the probability of patients with similar characteristics and disease course being present in the cohort, is expected to lead to improved outcomes.
This was partly supported by the observed results in the case of the simulation analysis. The simulated results, summarized in Figure 5, validated the methodological framework, supported the effectiveness of Euclidean and cosine distance, and suggested an optimal Top N in the range of 3 to 5. Specifically, the cosine distance combined with Top N =3 showed promising results with an MAPE of 11.82% (Figure 5a). These insights supported the framework’s potential, already demonstrated in the real patient estimation of LoR time, and underscored the importance of parameter selection in the estimation.
Overall, across both real and simulated datasets, the results consistently showed that Euclidean distance was overall more robust compared to other similarity metrics. The normalization strategy, which emphasized the relative change at treatment initiation, enhanced the effectiveness of Euclidean distance in comparing treatment trajectories, while despite DTW’s theoretical strengths in temporal alignment, it performed generally poorly. Cosine similarity showed comparable performance even surpassing Euclidean distance but not consistently. Analysis of the Top N parameter revealed that using 3 to 5 most similar patients produced the best performing results, a finding that was consistent across both real and simulated datasets. Smaller N values tended to work better with real patients, while the simulated dataset allowed slightly larger N values to maintain accuracy, especially when considering the adjusted metrics.
The use of adjusted metrics—adjusted MAPE@10 and adjusted MAPE@5—enabled a more focused assessment by attempting to exclude patients for whom the estimation did not perform well, likely due to poor representation in the reference set, which would otherwise distort the overall MAPE. These adjusted metrics highlighted how accurate the predictions were for the well-estimated cases, offering a clearer picture of the model’s potential when sufficient similarity existed. In real patients, over 80% of predictions fell within ±10 months of the true LoR, and nearly 50% within ±5 months, while for simulated patients, over 90% were within ±5 months regardless of the distance metric used. Especially as seen in Table 1, certain patient cases exhibited highly accurate estimations, demonstrating and underscoring the framework’s potential in estimating LoR.
In summary, this personalized prediction framework proved promising and effective at estimating LoR, highlighting its potential and viability. Within the performed analysis, the Euclidean distance emerged as the best-performing and most robust similarity metric, and the optimal Top N parameter for both datasets was around three to five regardless of size. All these insights support the perspective of the proposed methodology and the need for further research.
4.2. Limitations and Future Research
Several limitations must be acknowledged. First, the small size of the real-world patient cohort restricted the diversity of disease trajectories and response patterns in the reference patient set. As a result, there were patients whose LoR times were atypical compared to the overall distribution in the cohort, naturally leading to less accurate predictions. Even though our approach is instance-based and personalized, making such limitations less pronounced, the risks cannot be excluded. Another limitation stemmed from the choice of using only the first three timepoints for prediction. While this decision was purposefully made to prioritize early response estimation, it impacted the amount of information employed, potentially increasing the risk of error.
This work lays a step towards the personalized prediction of azacitidine LoR in higher-risk MDS patients. The purpose of the study was to propose a personalized prediction framework and demonstrate the framework’s potential and its auspicious strength in a clinical setting. Although the real patient cohort was limited; and the simulated patients inherently shared high similarity—potentially introducing overfitting—these experiments were designed as a pilot application to illustrate the methodology. A future research priority of our group is the expansion of the real-world patient dataset used in this study, aiming to further focus on the framework’s assessment, medical aspects and interpretations. To this end, non-temporal patient characteristics, such as the IPSS-R score, or patient comorbidities, could enable stratification of patients into clinically meaningful groups or enhance the distance computation by adding a “context-aware” dimension to the similarity metric. This integration would likely improve the prediction accuracy and clinical interpretability, representing a valuable and promising future direction.
Author Contributions
Conceptualization, S.V., D.K. and T.M.; methodology, S.V. and T.M.; software, S.V.; validation, D.K., K.L. and T.M.; formal analysis, S.V.; investigation, S.V. and D.K.; resources, D.K., T.S. and I.K.; data curation, S.V., D.K. and T.S.; writing—original draft preparation, S.V. and T.M.; writing—review and editing, D.K., T.S., K.L. and I.K.; visualization, S.V.; supervision, K.L., I.K. and T.M.; project administration, I.K. and T.M.; funding acquisition, I.K. and T.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
This study was approved by the Institutional Research Committee of the University Hospital of Alexandroupolis, Greece (18427/10-04-2023), on 14 June 2023.
Informed Consent Statement
Written informed consent was obtained from all subjects involved in the study.
Data Availability Statement
The simulated data are available on GitHub in the link: https://github.com/VantarakiS/MDS_LoR_Personalized_Prediction (accessed on 1 September 2025).
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| CLL | Chronic Lymphocytic Leukemia |
| HSCT | Hematopoietic Stem Cell Transplantation |
| IPSS-R | Revised International Prognostic Scoring System |
| LoR | Loss of Response |
| MAPE | Mean Absolute Percentage Error |
| MDS | Myelodysplastic Syndrome |
| PSDPA | Personalized Stepwise Dynamic Predictive Algorithm |
Appendix A
The list of the medical variables that were recorded during the patient’s follow-up are displayed in Table A1. These variables were used for any experiments and analysis for both real and simulated datasets.

Table A1.
List of medical variables measured during patients’ follow-up check-ups and laboratory tests. The variables were used as input to the framework to quantify similarity between patients.
Table A1.
List of medical variables measured during patients’ follow-up check-ups and laboratory tests. The variables were used as input to the framework to quantify similarity between patients.
| WBC (K/μL) | Hct | LDH |
| NEU (K/μL) | PLTs (K/μL) | Glob |
| Lymph (K/μL) | Glu | K |
| RBC | Ur | Na |
| MCV | UA | Ca |
| MCH | SGPT/ALT | P |
| Hb | γGT | CRP |
An example of a time series of the medical variables of patient P1 after the imputation and normalization steps were applied. To highlight the strength of the normalization strategy adopted, the normalization was applied using all the timepoints available in the time window T (as mentioned in Equation (1)).
Figure A1.
Time series of the medical variables from patient #1 after imputation and normalization were applied in the whole timeseries of the patient.
References
- Dotson, J.L.; Lebowicz, Y. Myelodysplastic Syndrome. In StatPearls; StatPearls Publishing: Treasure Island, FL, USA, 2025. [Google Scholar]
- Liapis, K.; Papadopoulos, V.; Vrachiolias, G.; Galanopoulos, A.G.; Papoutselis, M.; Papageorgiou, S.G.; Diamantopoulos, P.T.; Pappa, V.; Viniou, N.-A.; Kourakli, A.; et al. Refinement of Prognosis and the Effect of Azacitidine in Intermediate-Risk Myelodysplastic Syndromes. Blood Cancer J. 2021, 11, 30. [Google Scholar] [CrossRef]
- Greenberg, P.; Cox, C.; LeBeau, M.M.; Fenaux, P.; Morel, P.; Sanz, G.; Sanz, M.; Vallespi, T.; Hamblin, T.; Oscier, D.; et al. International Scoring System for Evaluating Prognosis in Myelodysplastic Syndromes. Blood 1997, 89, 2079–2088. [Google Scholar] [CrossRef]
- Greenberg, P.L.; Tuechler, H.; Schanz, J.; Sanz, G.; Garcia-Manero, G.; Solé, F.; Bennett, J.M.; Bowen, D.; Fenaux, P.; Dreyfus, F.; et al. Revised International Prognostic Scoring System for Myelodysplastic Syndromes. Blood 2012, 120, 2454–2465. [Google Scholar] [CrossRef] [PubMed]
- Jabbour, E.; Mathisen, M.S.; Garcia-Manero, G.; Champlin, R.; Popat, U.; Khouri, I.; Giralt, S.; Kadia, T.; Chen, J.; Pierce, S.; et al. Allogeneic Hematopoietic Stem Cell Transplantation versus Hypomethylating Agents in Patients with Myelodysplastic Syndrome: A Retrospective Case–Control Study. Am. J. Hematol. 2013, 88, 198–200. [Google Scholar] [CrossRef] [PubMed]
- Bewersdorf, J.P.; Zeidan, A.M. Management of Patients with Higher-Risk Myelodysplastic Syndromes after Failure of Hypomethylating Agents: What Is on the Horizon? Best Pract. Res. Clin. Haematol. 2021, 34, 101245. [Google Scholar] [CrossRef] [PubMed]
- Goetze, K. The Role of Azacitidine in the Management of Myelodysplastic Syndromes (MDS). Cancer Manag. Res. 2009, 2009, 119–130. [Google Scholar] [CrossRef]
- Vigil, C.E.; Martin-Santos, T.; Garcia-Manero, G. Safety and Efficacy of Azacitidine in Myelodysplastic Syndromes. Drug Des. Dev. Ther. 2010, 4, 221–229. [Google Scholar] [CrossRef] [PubMed]
- Cheson, B.D. Clinical Application and Proposal for Modification of the International Working Group (IWG) Response Criteria in Myelodysplasia. Blood 2006, 108, 419–425. [Google Scholar] [CrossRef] [PubMed]
- Fenaux, P.; Mufti, G.J.; Hellstrom-Lindberg, E.; Santini, V.; Finelli, C.; Giagounidis, A.; Schoch, R.; Gattermann, N.; Sanz, G.; List, A.; et al. Efficacy of Azacitidine Compared with That of Conventional Care Regimens in the Treatment of Higher-Risk Myelodysplastic Syndromes: A Randomised, Open-Label, Phase III Study. Lancet Oncol. 2009, 10, 223–232. [Google Scholar] [CrossRef] [PubMed]
- Silverman, L.R.; Demakos, E.P.; Peterson, B.L.; Kornblith, A.B.; Holland, J.C.; Odchimar-Reissig, R.; Stone, R.M.; Nelson, D.; Powell, B.L.; DeCastro, C.M.; et al. Randomized Controlled Trial of Azacitidine in Patients with the Myelodysplastic Syndrome: A Study of the Cancer and Leukemia Group B. J. Clin. Oncol. 2002, 20, 2429–2440. [Google Scholar] [CrossRef] [PubMed]
- Itzykson, R.; Thépot, S.; Quesnel, B.; Dreyfus, F.; Beyne-Rauzy, O.; Turlure, P.; Vey, N.; Recher, C.; Dartigeas, C.; Legros, L.; et al. Prognostic Factors for Response and Overall Survival in 282 Patients with Higher-Risk Myelodysplastic Syndromes Treated with Azacitidine. Blood 2011, 117, 403–411. [Google Scholar] [CrossRef] [PubMed]
- Tentori, C.A.; Gregorio, C.; Robin, M.; Gagelmann, N.; Gurnari, C.; Ball, S.; Caballero Berrocal, J.C.; Lanino, L.; D’Amico, S.; Spreafico, M.; et al. Clinical and Genomic-Based Decision Support System to Define the Optimal Timing of Allogeneic Hematopoietic Stem-Cell Transplantation in Patients with Myelodysplastic Syndromes. J. Clin. Oncol. 2024, 42, 2873–2886. [Google Scholar] [CrossRef] [PubMed]
- Sekeres, M.A.; Taylor, J. Diagnosis and Treatment of Myelodysplastic Syndromes: A Review. JAMA 2022, 328, 872–880. [Google Scholar] [CrossRef] [PubMed]
- Moysiadis, T.; Koparanis, D.; Liapis, K.; Ganopoulou, M.; Vrachiolias, G.; Katakis, I.; Moyssiadis, C.; Vizirianakis, I.S.; Angelis, L.; Fokianos, K.; et al. A Personalized Stepwise Dynamic Predictive Algorithm of the Time to First Treatment in Chronic Lymphocytic Leukemia. iScience 2023, 26, 107591. [Google Scholar] [CrossRef] [PubMed]
- Cai, Y.; Yu, F.; Kumar, M.; Gladney, R.; Mostafa, J. Health Recommender Systems Development, Usage, and Evaluation from 2010 to 2022: A Scoping Review. Int. J. Environ. Res. Public Health 2022, 19, 15115. [Google Scholar] [CrossRef] [PubMed]
- De Croon, R.; Van Houdt, L.; Htun, N.N.; Štiglic, G.; Vanden Abeele, V.; Verbert, K. Health Recommender Systems: Systematic Review. J. Med. Internet Res. 2021, 23, e18035. [Google Scholar] [CrossRef] [PubMed]
- Mustaqeem, A.; Anwar, S.M.; Khan, A.R.; Majid, M. A Statistical Analysis Based Recommender Model for Heart Disease Patients. Int. J. Med. Inform. 2017, 108, 134–145. [Google Scholar] [CrossRef] [PubMed]
- Liberti, L.; Lavor, C.; Maculan, N.; Mucherino, A. Euclidean Distance Geometry and Applications. SIAM Rev. 2014, 56, 3–69. [Google Scholar] [CrossRef]
- Begum, S.; Ahmed, M.U.; Funk, P.; Xiong, N.; von Schéele, B. Similarity of Medical Cases in Health Care Using Cosine Similarity and Ontology. In Proceedings of the Springer LNCS, 5th Workshop on CBR in the Health Sciences, ICCBR-07, Belfast, UK, 13–16 August 2007; pp. 263–272. [Google Scholar]
- Berndt, D.J.; Clifford, J. Using Dynamic Time Warping to Find Patterns in Time Series. In Proceedings of the AAAI Workshop ’94, New York, NY, USA, 26 April 1994; KDD Workshop. AAAI Press: Washington, DC, USA, 1994; pp. 359–370. [Google Scholar]
- Lahreche, A.; Boucheham, B. A Comparison Study of Dynamic Time Warpings Variants for Time Series Classification. Int. J. Inform. Appl. Math. 2021, 4, 56–71. [Google Scholar]
- Dumre, P.; Bhattarai, S.; Shashikala, H.K. Optimizing Linear Regression Models: A Comparative Study of Error Metrics. In Proceedings of the 2024 4th International Conference on Technological Advancements in Computational Sciences (ICTACS) IEEE, Tashkent, Uzbekistan, 13 November 2024; pp. 1856–1861. [Google Scholar]
- Kim, S.; Kim, H. A New Metric of Absolute Percentage Error for Intermittent Demand Forecasts. Int. J. Forecast. 2016, 32, 669–679. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).