Bridge Risk Index for Freight Corridor Resilience: A Non-Parametric Machine Learning and Threat Modeling Approach

Abstract

Bridges are critical nodes in freight networks, yet limited funding prevents agencies from maintaining all structures in good condition. This creates the need for a transparent and scalable method to identify which bridges pose the greatest risk to supply chain continuity. This study develops a bridge risk index using the threat–vulnerability–consequence (TVC) framework and validates its components with machine learning. Threat is defined as per-lane average daily traffic, vulnerability as effective bridge age (epoch), and consequence as detour distance, with traffic also contributing to disruption magnitude. The methodology applies log transformation and normalization to construct an interpretable multiplicative index, then classifies risk using Jenks natural breaks. The results show that epoch dominates vulnerability, detour distance amplifies consequence, and their interaction explains most of the risk variation. Specifically, effective age explains over three times more variation in bridge condition than any other attribute. The vulnerability–consequence interaction dominates with an R² = 0.98. The highest-risk bridges are concentrated in rural areas and near major freight gateways where detour options are limited. The proposed TVC index provides a transparent, data-driven decision-support tool that agencies can apply nationwide to prioritize investments, safeguard freight corridors, and strengthen supply chain resilience.

1. Introduction

Bridges are critical elements of highway networks and often act as bottlenecks on freight corridors. Trucks move more than 65% of U.S. freight by weight compared with 8% by rail and 3% by other modes [1]. This makes bridge reliability essential for supply chain continuity. Yet bridge owners face persistent funding shortfalls that limit their ability to keep all structures in good condition [2]. A practical way to rank bridges by the risk they pose to freight operations would help agencies target maintenance funds where they deliver the greatest resilience benefits. Such information would also enable trucking companies to identify lower-risk routes when planning logistics.

The goal of this paper is to develop a bridge risk index that quantifies threats to supply chain continuity. The methodology applies the threat–vulnerability–consequence (TVC) model institutionalized by the United States Department of Homeland Security, marking a progression from earlier additive formulas toward a more structured multiplicative formulation [3]. Analysts describe the TVC model as a sound philosophical decomposition that aligns with accepted risk analysis practices and informs resource prioritization [4]. This work defines the TVC model as the product of operational loading, structural vulnerability, and the cost of disruption. In this context, the model quantifies threat as the per-lane average daily traffic (ADT), vulnerability as the effective age (epoch) of the structure, and consequence as the detour distance. Together, these factors provide an interpretable and scalable representation of risk that aligns with the operational realities of freight movement.

The methodology integrates machine learning (ML) with risk modeling to identify the most predictive attributes of bridge vulnerability. The ML models are non-parametric and include extreme gradient boosting, random forest, and neural networks to ensure empirical rigor alongside interpretability. It then applies normalization, log transformation, and multiplicative aggregation to produce a risk index. The approach is validated across more than 83,000 National Highway System (NHS) bridges. The NHS is a critical subset of U.S. highways that serves as the backbone of freight movement [5]. Trucks, which carry the majority of national freight by tonnage and value, rely heavily on the NHS for efficient delivery. As freight corridors emerged on the system, the industry constructed hundreds of freight-only terminals on the NHS. Similarly, states constructed freight connectors to access hundreds of multimodal river and ocean ports [6]. Finally, for actionable interpretation, the methodology classified the risk indices into categories using Jenks natural breaks.

The contributions of this work are threefold. First, it introduces a transparent, supply chain-oriented risk index that can be computed nationwide with existing data. Second, it validates the vulnerability factor through non-parametric ML models. Third, it demonstrates how the index highlights geographic concentrations of high-risk bridges that threaten freight corridor continuity.

The remainder of the paper is organized as follows: Section 2 reviews the literature on bridge risk assessment and network resilience. Section 3 describes the methodology used to construct and validate the TVC index. Section 4 presents the results, including ML validation, regression analysis, and risk rankings. Section 5 discusses the implications and limitations of the findings, and Section 6 concludes with contributions and directions for future work.

2. Literature Review

Research on bridge and network risk has expanded across multiple domains. This expansion reflects the critical role of infrastructure in safety, mobility, and economic resilience. Prior studies have examined climate-driven deterioration, component-level vulnerability, hazard-specific risk models, and data-driven prediction of structural condition [7]. Others have focused on multi-risk frameworks and road network resilience to emphasize robustness, reliability, and recovery capacity. While these efforts have advanced the understanding of bridge performance and critical infrastructure protection, they often emphasize hazards or structural mechanics rather than supply chain continuity. This review synthesizes recent contributions across these themes. The synthesis positions the present work within the broader body of literature.

ML studies advanced predictive accuracy for condition states. Fard and Fard (2024) trained random forest (RF), extreme gradient boosting (XGB), and artificial neural network (ANN) models on large U.S. datasets [8]. They showed that historical data improved prediction accuracy for deck condition. Permutation importance highlighted age, traffic, and climate as key predictors. This reinforced the value of data-driven prioritization. Principi et al. (2025) proposed a fast neural-network screening to flag high-risk bridges from a small set of inputs that were easy to obtain. They demonstrated scalable triage on Italy’s highway network [9].

Broader risk and resilience analyses emphasized multi-risk and coupled systems. Li and Mostafavi (2025) created an index based on ML for post-disaster community risk and resilience [10]. They blended human actions, asset performance, and recovery features to map disparities after Hurricane Harvey. A systematic review by Nirandjan et al. (2024) compiled fragility and vulnerability curves for critical infrastructure across hazards and sectors [11]. They aimed to enable standardized input for hazard-risk assessments. Cao et al. (2025) extended Bayesian networks with multi-state fuzzy logic and expert confidence to infer bridge safety risks and identify critical nodes in causal chains [12]. Kammouh and Chahrour (2025) assembled indicator bundles spanning physical, operational, and social dimensions for transport resilience [13]. The work highlighted practical, indicator-based assessment paths.

Network-level literature focused on vulnerability, resilience, robustness, and reliability. Bibliometric reviews summarize methods and trends for road-network vulnerability and resilience. Bashir et al. (2025) noted varied metrics and modeling traditions [14]. Similarly, Santos and Bertoncini (2025) linked vulnerability to robustness and reliability for roads [15]. Nicholson et al. (2024) simulated spatially correlated failures to rank structural component importance under a hazard footprint. The simulation captured interdependence beyond independent-failure assumptions [16]. Doğaroğlu and Çalışkanelli (2025) defined link and node vulnerability indices using microsimulation to quantify and rebalance network vulnerability [17]. López et al. (2025) provided a reliability-based, component-level vulnerability assessment for steel truss bridges. They integrated finite element analysis (FEM) and uncertainty quantification to optimize inspections [18]. Arabi et al. (2024) reviewed multilayer transport networks and proposed equity-aware resilience metrics to guide inclusive resource allocation [19].

Hazard-specific applications illustrated method depth but had limited generality. In 2024, Ren et al. combined convolutional neural networks (CNNs) and conventional ML to predict driftwood accumulation and rainfall-driven bridge damage [20]. They aimed to link landslide susceptibility to bridge safety. Hazard-specific studies, such as seismic risk assessments, highlight the importance of earthquakes in certain regions [21]. Urban flood studies similarly quantify subsystem performance degradation and routing shifts under inundation [22]. Ansari et al. (2025) used a fuzzy synthetic approach to classify seismic damage with attention to ground conditions, span orientation, and proximity to fault rupture [23]. Han et al. (2025) synthesized lessons from historical failures and emphasized life-cycle management, preventive maintenance, and monitoring [24]. Beyond transport, analysis based on the Method Organized Systematic Analysis of Risk (MOSAR) for energy networks showed structured, scenario-driven critical infrastructure (CI) risk assessments to inform cross-sector practices [25]. Rodriguez et al. (2025) adapted a Quality Function Deployment (QFD) tool into a multi-risk deployment framework to assess preparedness in industrial facilities [26]. They aimed to add territorial prioritization and practical rating schemes.

Data and digital-twin advances promised richer, real-time risk forecasting but they increased complexity. Geng et al. (2025) proposed a digital twin framework with Bayesian networks to integrate inspection, traffic, and hydrologic data for life-cycle risk assessment across bridge networks [27]. They captured interdependencies across components, structures, and systems but required intensive data assimilation. Intini et al. (2025) modeled annual average daily traffic (AADT) exposure using public predictors to fill traffic-count gaps and support multi-risk frameworks [28]. They showed that using ML improved heavy-vehicle accuracy. Grieco et al. (2024) presented an index-based multi-hazard prioritization for large portfolios under limited knowledge [29]. They delivered rankings that were consistent with national guidelines. Papamichael et al. (2024) examined how transnational challenges and human decision biases shaped CI risk processes [30]. They highlighted the need for transparent, domain-aware methods.

Across these strands, the literature advanced climate-aware protocols, component reliability, ML-based condition prediction, multi-risk frameworks, and network vulnerability metrics. Yet three practical gaps persist in freight-corridor decision support:

• Freight-centric consequence is under-specified. Most studies emphasized hazard intensity, structural fragility, or community recovery. Fewer quantified the potential for daily supply chain disruption with simple, scalable measures such as detour distance that is a proxy for user cost and logistics delay [29].
• Operational threat exposure lacks a direct, routable metric in portfolio risk indices. Traffic is often ancillary, imputed, or used for mapping exposure rather than embedded as a multiplicative driver of risk at the structure level [28].
• Interpretable, nation-scale screenings are rare. Rich Bayesian/digital-twin or fuzzy frameworks offer depth but can be data-heavy. Many methods stop at component-reliability or hazard-specific scoring, limiting transferability to routine prioritization across an entire inventory [18].

This paper addresses those gaps with a transparent TVC risk index, aligned with federal guidelines in risk assessment, and designed for freight corridors. The methodology log-transforms and normalizes factors, multiplies them into a single interpretable score, and classifies the results with Jenks natural breaks for actionable mapping. The risk index design remains hazard-agnostic yet supply chain relevant. Hence, the proposed method enables consistent ranking across a national portfolio and provides direct linkage to routing and investment decisions.

3. Methodology

This study developed and validated a risk index for bridges through a structured data mining and modeling workflow. The methodology integrates data preparation, descriptive analysis, index construction, ML validation, and regression analysis. The workflow emphasizes interpretability while ensuring empirical rigor by combining established risk modeling concepts with non-parametric ML techniques. The foundation of the index is the TVC framework, which quantifies risk as the product of operational loading, structural vulnerability, and the disruption costs of rerouting freight. The design process, therefore, required variables that could represent each dimension in a transparent and scalable way.

Figure 1 provides an overview of this workflow.

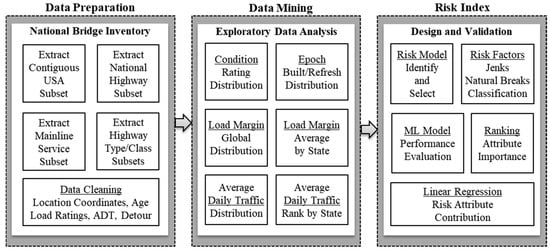
Figure 1. The workflow to develop and evaluate the bridge risk index.

It illustrates the sequence from raw data preparation to the development and validation of the final bridge risk index. The workflow proceeds in three stages. First, it filtered a large bridge inventory dataset and cleaned it to create a representative subset of highway bridges used for long-haul trucking. Second, descriptive analyses summarized the distributions of condition ratings, effective age, load margins, and traffic intensity. Third, it constructed the risk index through nonlinear transformations and normalizations of the TVC risk factors, and risk classification using Jenks natural breaks. The methodology also incorporated non-parametric ML models and regression analysis to validate the selection of vulnerability factors and quantify the relative contributions of threat, vulnerability, and consequence. The subsections that follow further describe each step in the workflow.

3.1. Data Preparation

This research utilized the National Bridge Inventory (NBI) database, annually updated by the Federal Highway Administration [31]. The NBI includes identification information, structural specifications, operational conditions, traffic loading, geometric data, functional descriptions, and inspection ratings for 624,193 U.S. bridges. The record for each structure contained 128 attributes or meta data. The ArcGIS online version included two more fields that provide corrected latitude and longitude coordinates.

Table 1 summarizes the data extraction, filtering, and cleaning of the NBI dataset to focus the analysis on contiguous United States (CONUS) bridges that support long-haul trucking. This focus maintains consistency where bridges form a connected freight network without the distortions of extreme detour distances or unique hazard regimes of islands. Hence, the data filtering first extracted CONUS bridges by removing records for Alaska, Hawaii, Puerto Rico, and the U.S. Virgin Islands. For replication, the item number listed in parentheses after the attribute description is the NBI data dictionary item number [32]. The next filter extracted records for bridges on the NHS. This filtering stage revealed that close to one-quarter (23.6%) of the CONUS bridges are on the NHS.

Table 1. Data Cleaning and Filtering.

Category	Attribute (Item Number)	Filter	Bridges
CONUS	State Code (1)	NOT IN (‘02’,‘15’,‘72’,‘78’)	618,495
NHS	Highway System (104)	IN (‘1’)	145,705
Mainline	Service Level (5C)	IN (‘1’)	126,043
Highway	Bridge Service (42A)	IN (‘1’)	111,304
Open	Open-Close (41)	IN (‘A’)	109,635
Road Class	Route Prefix (5B)	IN (‘1’,‘2’,‘3’,‘4’)	106,443
Latitude	LATDD	>0	106,443
Rated Load	Inventory Rating (66)	>0	106,126
Design Load	Design Load Capacity (31)	>0	101,761
ADT per Lane	ADT (29)/Lanes (28A)	>0	101,681
Detour	Detour Length (19)	>0	87,752
Epoch	2025—max [Built (27), Rec (106), Imp (97)]	>0	83,479

To focus on long-haul truck routes, the next filter stage extracted functional bridges on the mainline highways. These excluded ramps, bypasses, spurs, frontage roads, and other structures that do not support the main traffic load. The remaining filters then cleaned the data by removing records with missing or obvious erroneous data such as no geospatial coordinates, zero design load capacity, zero ADT, or zero detour distance.

The workflow defines the variable “epoch” as the years from the most recent defining event in the bridge’s life cycle. Hence, the epoch is the years since built, reconstructed, or improved, whichever is the most recent, to capture the “effective age” of the bridge. Subsequently, the filter removed records with an epoch of zero or negative years. The final cleaning step removed attributes and meta data that were irrelevant to the risk model development. These items included information such as bridge identification number, ownership, history, approach type, clearances, structures under the bridge, and navigational features. The final filtered and cleaned dataset had 83,479 records, each with 67 attributes and four meta data items.

3.2. Data Mining

To motivate the development of the risk index, the methodology first applies exploratory data analysis to key attributes of the cleaned bridge dataset. It examined five important factors: inspector-assigned condition ratings, the distribution of effective age (epoch), the distribution of load margin, ADT per lane, and detour distance. These descriptive statistics establish baseline patterns for structural condition, traffic demand, loading, and rerouting penalties. The subsections that follow provide more context for how each factor contributes to the threat, vulnerability, and consequence components of the TVC model.

3.2.1. Condition Rating

Table 2 summarizes the condition rating that inspectors assigned to the major structural sections of the bridge, namely the deck, sub-structure, and super-structure [33].

Table 2. Structural Rating.

Condition	Rating	Description
Excellent	9	Pristine condition—no deficiencies observed.
Very Good	8	No noteworthy deficiencies observed, other than cosmetic.
Good	7	Some minor issues that do not affect the structural performance.
Satisfactory	6	Some minor deterioration in the structural elements.
Fair	5	Some minor section loss or damage but the primary structural elements are sound.
Poor	4	Notable advancement in section loss, damage, or deterioration.
Serious	3	Section loss, damage, cracking, shearing, or other deterioration seriously affects the primary structural components.
Critical	2	The primary structural elements are in a state of advanced deterioration. The bridge should be closely monitored or closed until fixed.
Failing	1	Inspectors expect that the critical structural elements are about to fail or that obvious movement destabalized the structure. The bridge should be closed until fixed.
Failed	0	The bridge is beyond corrective action and cannot presently carry traffic.

To facilitate downstream ML models, the research workflow defined the categorical variable “Undamaged” to take on the label of “1” if the rating is 8 or 9 and zero otherwise. Hence, a label of “1” indicates that the structure has no deficiencies that require repair to support traffic. A label of “0” indicates that the structure does require some level of remediation as described by the rating levels from 0 to 7. Figure 2 plots the distribution of the lowest rating received for any portion of the bridge. The distribution indicates that there is a central tendency toward ratings from 5 to 7. This suggests that the majority of bridges on the NHS have some minor damage or deterioration that requires attention.

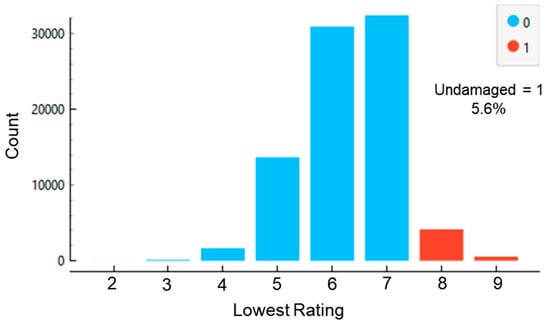
Figure 2. Lowest condition rating for the cleaned sample of bridges on the NHS.

3.2.2. Epoch Distribution

Figure 3 shows the distribution of the epoch as defined above in Table 1. The pattern aligns with intuition in that a larger number of the more recently built, reconstructed, or improved bridges are in the undamaged category. As expected, the undamaged category decreases steadily with the increasing epoch. Overall, only 5.6% of the bridges are in the undamaged category. The average and standard deviation of the epoch was 33.2 and 22.5 years, respectively.

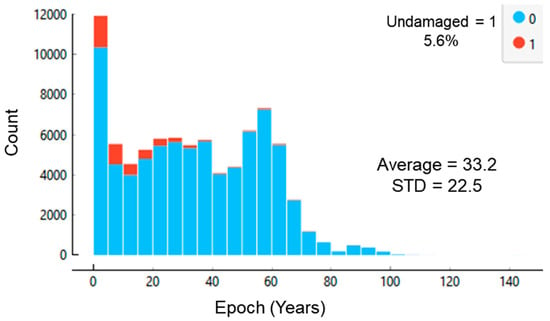
Figure 3. Distribution of bridge age, accounting for the most recent reconstruction or improvement.

Interestingly, epoch within the recent five years dominates the distribution. This outcome aligns with the U. S. Infrastructure Investment and Jobs Act passed in 2021. This is a federal law allocating $550 trillion to modernize the nation’s transportation infrastructure [34]. The distribution reveals that states of New York, Wisconsin, and Washington have been the most active among states within that distribution peak. This also aligns with the major bridge improvement programs and funding that those states recently established. For instance, New York established a five-year capital program of $200 million annually to fund bridge rehabilitation and replacement [35]. Wisconsin established their Local Bridge Improvement Assistance Program to supplement grants from the U. S. Bipartisan Infrastructure Law with local funding [36]. Washington State estimated that its Interstate Bridge Replacement Program will invest $7.5 billion [37].

3.2.3. Load Margin

The research workflow defines a load margin as the difference between the load capacity rating and the design load of the bridge. The NBI data attribute described as “inventory” rating (item 66) stores the bridge’s inspection rated capacity in metric tons. The NBI data attribute described as design load (item 31) is the weight of a live load for which the bridge was designed. The data are coded in weight categories as “H xx” where xx is the live load in tons, which the load margin calculation converted to metric tons [38]. Figure 4 plots the distribution of the load margin.

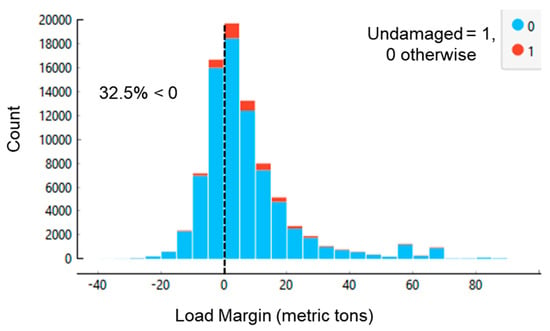
Figure 4. Distribution of the load margin.

The results reveal that nearly one-third (32.5%) of the bridges are rated for a load capacity that is below their design load. The distribution also shows a central tendency for the capacity ratings to be within 20 metric tons of the design load. For reference, most multi-axle trucks in the U.S. have a loaded maximum weight of 80,000 pounds, which is around 36.3 metric tons [39]. A deeper examination of the distribution also revealed that 6.6% of the bridges rated with positive load margin are in the undamaged category versus 3.6% of bridges rated with negative load margin. Hence, aligning with intuition, bridges rated with a positive load margin have more than 1.8 times those in the undamaged category than bridges rated with a negative load margin.

Figure 5 shows the rank of states by the percentage of state bridges rated below their design load. Figure 6 shows the same results on a map. It is evident that Tennessee, California, Oregon, New Mexico, and Georgia ranked in the top five. Figure 7 plots a ranking of the average load margin of bridges within a state. Figure 8 plots the same data on a map. It is evident that the states of Oregon, Tennessee, Wyoming, Texas, and New Mexico are among the top five states that have bridges rated with the lowest average load margin. This result aligns with the previous result of states having the highest percentage of bridges rated with a negative load margin. In contrast, the states of Arizona, Virginia, Maryland, Nevada, and Vermont are in the top five with bridges rated with the highest average load margins.

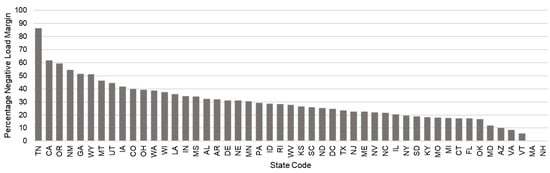
Figure 5. Rank of states by the percentage of state bridges rated below their design load, indicating where structural capacity most often falls short of design standards.

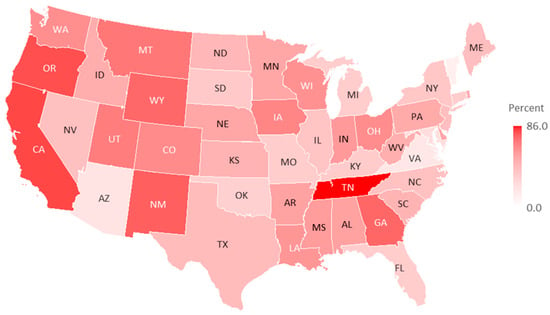
Figure 6. Choropleth state map of the percentage of state bridges rated below their design load, highlighting geographic patterns of structural underperformance.

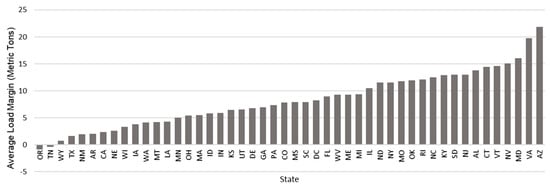
Figure 7. Rank of states by the average load margin of their bridges.

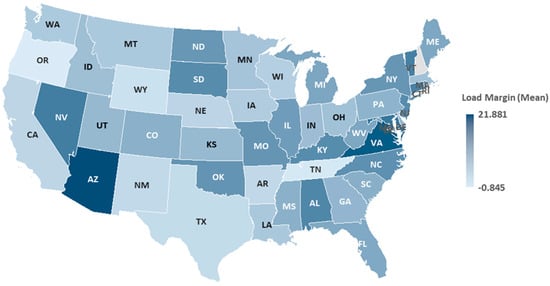
Figure 8. Choropleth state map of the average load margin (metric tons) of their bridges.

3.2.4. Average Daily Traffic

Figure 9a plots the ADT per lane distribution of the bridges analyzed. Overall, the average and standard deviation was 10,618 and 11,143, respectively.

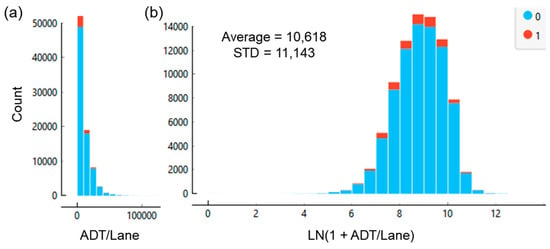
Figure 9. Distribution of (a) the per lane ADT, and (b) log transformed ADT/lane for bridges on the NHS.

The distribution is highly skewed, showing a strong tendency for most of the NHS highway bridges to carry less than 10,000 vehicles per lane. The central tendency within that category ranged from 2000 to 2800. Outliers carried between 20,000 and 60,000 vehicles per lane. Figure 9b shows the log-transformed distribution, which improved the ML performance downstream in the workflow.

Figure 10 shows the average ADT per lane for the subset of bridges on interstate routes. Figure 11 illustrates the same information on a map. The results indicate that Tennessee, Washington, D.C., Maryland, Florida, and Georgia rank in the top five among states. This aligns with the intuition that the eastern U.S. freight corridors and ports carry or generate much of that traffic. California is next in rank, which also aligns with intuition that the Western U.S. freight corridors and ports carry or generate some of the most traffic.

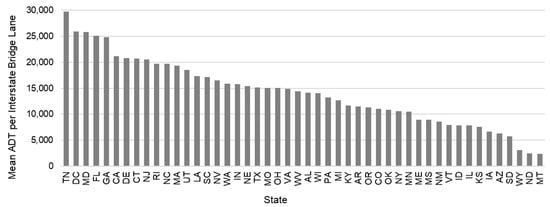
Figure 10. Rank of the average ADT/lane on interstate bridges in a state.

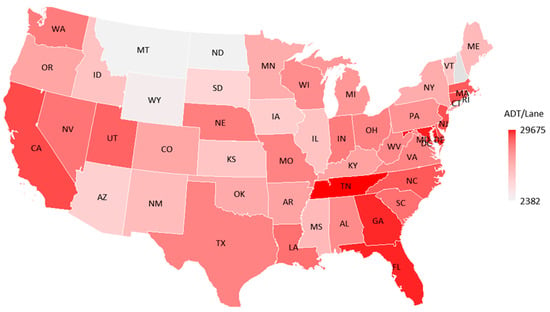
Figure 11. Choropleth state map of the average per lane ADT on interstate bridges.

3.2.5. Detour Distance

The distribution of the detour distance is highly skewed, as shown in Figure 12a. The average distance is just over 15 km, and the standard deviation is just over 34 km. Within the distribution peak, most of the detour distance is within three kilometers. Figure 12b shows the natural log transformation to reduce the skew, which improves the performance of ML algorithms downstream by rebalancing the data.

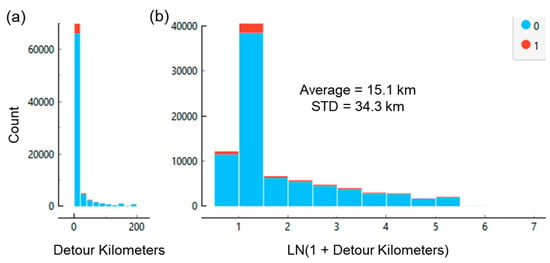
Figure 12. Distribution of (a) the detour distance, and (b) log transformed detour distance for bridges on the NHS.

3.3. Index Design and Validation

The following subsections explain the selection of key risk factors, the transformations and normalizations applied to ensure comparability, and the use of the Jenks method to classify the index into clear and interpretable clusters.

3.3.1. TVC Model

The TVC model is a product of threat (T), vulnerability (V), and consequence (C) factors as

$$\mathrm{Risk}=\mathrm{T} \times \mathrm{V} \times \mathrm{C}$$

(1)

to quantify a level of risk that aligns with the operational realities of freight corridors. The TVC framework is widely used in critical infrastructure protection because it captures the three essential dimensions of risk: the likelihood of stressors, the susceptibility of structures to deterioration, and the magnitude of impacts due to loss of functionality. Unlike purely probabilistic or reliability-based models, the TVC model emphasizes the integration of operational exposure and system consequences, making it well suited for transportation security and supply chain analysis. Alternative models such as Fault Tree Analysis, Failure Modes and Effects Analysis, or probabilistic risk assessment are valuable for component-level reliability studies. However, they often require detailed failure probability data that are not available at a network scale. The TVC model balances conceptual clarity with practical data availability, which enables consistent application across large bridge inventories.

In the TVC context, threat is defined as the operational loading intensity on a bridge. For freight corridors, ADT per lane captures the degree of stress imposed by vehicles, particularly long-haul trucks. Vulnerability reflects the structural condition of a bridge. ML models later confirm that the effective age of a bridge (epoch) has the highest power in predicting the condition rating. In the results section below, the ML models showed that effectively newer bridges strongly correlate with undamaged ratings, while older bridges correlate with various levels of deterioration. Consequence measures the disruption imposed on freight if a bridge becomes unusable. Hence, the detour distance captures the added cost of rerouting trucks. These costs are due to increased travel time, fuel consumption, and logistical inefficiencies. The ADT per lane is also a component of consequence. That is, bridges with higher per-lane traffic volumes face elevated risk of disruption because closures would affect more vehicles and critical freight flows. These costs reflect the supply chain perspective, where continuity of freight movement is paramount. Hence, the TVC framework ensures that the risk index remains transparent, scalable, and grounded in both security literature and practical freight logistics considerations.

To construct the risk index, the workflow first transformed and normalized each factor to ensure comparability across scales. The workflow log-transformed the threat and the consequence factors to reduce skewness and then normalized them to the [0, 1] range. The workflow normalized the vulnerability factor (epoch) without log transformation because its distribution was less skewed, and the interpretation would be more direct. The procedure then constructed the risk index as the product of these transformed and normalized factors as

$$z_i=\mathrm{N}{\left[\mathrm{L}\mathrm{N}\left(1+T\right)\right]}_0^1\times \mathrm{N}{\left[\mathrm{L}\mathrm{N}\left(1+V\right)\right]}_0^1\times \mathrm{N}{\left[\mathrm{L}\mathrm{N}\left(1+C\right)\right]}_0^1$$

(2)

where $\mathrm{N}{\left[x\right]}_0^1$ is the normalization function

$$\mathrm{N}{\left[x\right]}_0^1={\displaystyle \frac{x-\mathrm{m}\mathrm{i}\mathrm{n}\left(x\right)}{\max \left(x\right)-\mathrm{m}\mathrm{i}\mathrm{n}\left(x\right)}}$$

(3)

and LN is the natural logarithm.

3.3.2. Jenks Classification

The workflow used the Jenks natural breaks method to classify the TVC risk index into categories. The optimization method partitions data into classes that minimize variance within each class while maximizing variance between classes. The algorithm seeks to minimize the total within-class sum of squared deviations as

$$V_W=\sum _{j=1}^k\sum _{i\in C_j}{\left(x_i-\overline{x_j}\right)}^2$$

(4)

where k is the number of classes, C_j is the set of values in class j, $x_i$ is an observation, and $\overline{x_j}$ is the mean value of class j. At the same time, it maximizes the between-class variance as

$$V_B=\sum _{j=1}^k{n_j\left(\overline{x_j}-\overline{x}\right)}^2$$

(5)

where n_j is the number of observations in class j, and $\overline{x}$ is the global mean value. The objective is to maximize the goodness-of-variance fit (GVF):

$$GVF={\displaystyle \frac{V_T-V_W}{V_T}}$$

(6)

where

$$V_T=\sum _{i=1}^n{\left(x_i-\overline{x}\right)}^2$$

(7)

is the total variance. A GVF closer to 1 indicates stronger class separation. This method is well suited for skewed distributions, such as the TVC risk index, because it identifies natural groupings in the data rather than imposing equal intervals or quantiles.

3.4. ML Models

The workflow defines ‘undamaged’ as the target variable for the ML models. Attributes that best predict undamaged bridges are considered most relevant for the vulnerability component of the TVC model. The workflow applied six non-parametric models to rank the predictive power of attributes: extreme gradient boosting (XGB), random forest (RF), artificial neural network (ANN), logistic regression (LR), k-nearest neighbor (kNN), and support vector machine (SVM). Although more complex to implement and explain, non-parametric models are advantageous in that they do not assume strict functional forms. This flexibility allows them to capture nonlinear and complex relationships in bridge condition data. Parametric models, by contrast, require strong distributional assumptions that do not hold for infrastructure data.

XGB is an ensemble method that builds decision trees sequentially, with each tree correcting errors from the previous one [40]. The algorithm minimizes a loss function with regularization to prevent overfitting. The prediction is as follows:

$$\widehat{y_i}=\sum _{k=1}^K{f}_k\left(x_i\right),f_k\in \mathrm{F}$$

(8)

where $f_k$ are regression trees and $\mathrm{F}$ is the space of all possible trees. In all models, y_i and x_i represent the target values and the set of associated features, respectively, for record i in the dataset.

RF constructs many decision trees on bootstrapped samples and averages their predictions [41]. Each tree uses a random subset of features, which reduces correlation and variance. The prediction is as follows:

$$\widehat{y}={\displaystyle \frac{1}{T}}\sum _{t=1}^T{h}_t\left(x\right)$$

(9)

where $h_t$ is the prediction from tree t.

ANN uses layers of interconnected neurons to capture nonlinear relationships [40]. Each neuron applies an activation function to a weighted sum of inputs. The output is as follows:

$$\widehat{y}=\sigma \left(\sum _j{w}_j{x}_j+b\right)$$

(10)

where σ is the activation function, w_j are weights, and b is the bias.

Although often considered parametric, LR is included for its interpretability and to compare performance against the other non-parametric models [41]. LR estimates the probability that a bridge is undamaged using the logistic function

$$P\left(y=1|x\right)={\displaystyle \frac{1}{1+e^{-\left({\beta }_0+{\beta }_1{x}_1+\cdots +{\beta }_p{x}_p\right)}}}$$

(11)

where y is the binary target variable (undamaged or damaged), x₁, …, x_p are the predictor attributes, and ${\beta }_0$, ${\beta }_1$, ..., ${\beta }_p$ are the model coefficients.

kNN classifies a bridge based on the majority class among its k nearest neighbors in attribute space [41]. The decision rule is as follows:

$$\widehat{y}=\mathrm{mode}\left\{y_i:x_i\in N_k\left(x\right)\right\}$$

(12)

where $N_k\left(x\right)$ is the set of k nearest neighbors of x.

SVM finds the hyperplane that best separates undamaged and damaged bridges [40]. The objective is to maximize the margin between classes as follows:

$$\begin{gathered} \underset{w,b}{\min }{\displaystyle \frac{1}{2}}{‖w‖}^2 \\ \mathrm{subject} \mathrm{to}: y_i\left(w·x_i+b\right)\ge 1 \end{gathered}$$

(13)

These models are expected to perform differently on highly unbalanced data, which is the case in this dataset where less than 6% of bridges are undamaged. XGB and RF often perform well because they handle nonlinearity and class imbalance with sampling or weighting. ANN can capture complex patterns but may require resampling or cost-sensitive learning to avoid bias toward the majority class. LR provides baseline interpretability but typically struggles with unbalanced datasets. kNN is sensitive to imbalance because the class containing the majority of records dominates local neighborhoods. SVM can be effective due to the use of kernel functions but is sensitive to data with a noisy class boundary. Together, these models provide a comprehensive evaluation of attribute importance under unbalanced conditions to robustly and reliably identify the vulnerability factors.

3.5. Performance Evaluation

The workflow evaluates the performance of each model by using five metrics: classification accuracy (CA), F1-score, precision, recall, and the area under the curve (AUC). These metrics provide a balanced view of predictive ability, especially under unbalanced data [40]. CA measures the proportion of correctly classified bridges.

$$CA={\displaystyle \frac{TP+TN}{TP+TN+FP+FN}}$$

(14)

where TP is the number of true positives, TN the true negatives, FP the false positives, and FN the false negatives. However, CA can be misleading under unbalanced data. For example, a model that always predicts the target variable as the same value, e.g., the bridge is damaged, would achieve high accuracy but would fail to identify any undamaged bridges.

Precision (Pr), also called specificity, measures the fraction of correctly identified undamaged bridges among all bridges predicted as undamaged.

$$Pr={\displaystyle \frac{TP}{TP+FP}}$$

(15)

Recall (Rc), also called sensitivity, measures the fraction of undamaged bridges correctly identified by the model.

$$Rc={\displaystyle \frac{TP}{TP+FN}}$$

(16)

The F1-score is the harmonic mean of precision and recall. It balances both metrics, which is critical in unbalanced datasets.

$$F1=2\times {\displaystyle \frac{Pr\times Rc}{Pr+Rc}}$$

(17)

AUC measures the ability of the model to distinguish between undamaged and damaged bridges across different thresholds. It is calculated as the area under the receiver operating characteristic (ROC) curve as

$$AUC={\int }_0^1{\rho }_{TP}{\rho }_{FP}d\left({\rho }_{FP}\right)$$

(18)

where ${\rho }_{TP}$ is the true positive rate and ${\rho }_{TP}$ is the false positive rate. The models use a probability threshold to determine whether a bridge is classified as undamaged or damaged. By varying this threshold from 0 to 1, the AUC evaluates performance at every decision point. The ROC curve plots the true positive rate against the false positive rate for each threshold, and the AUC is the area under this curve. The ML procedures determined these rates through stratified k-fold cross-validation and hyperparameter tuning to maximize the AUC. This approach ensured robust and generalizable performance despite class imbalance.

Using the above metrics together ensured that model performance is not judged solely on overall accuracy. They emphasize the correct identification of the minority class, which is critical since less than 6% of bridges are undamaged. However, the evaluation emphasized AUC because it measures the model’s ability to distinguish between undamaged and damaged bridges across all thresholds. Unlike accuracy, AUC is not biased by class imbalance and provides a threshold-independent assessment. This ensures that the minority class of undamaged bridges is properly recognized.

3.6. Attribute Importance

The workflow used the permutation feature importance (PFI) method to assess the contribution of each attribute [42]. The PFI method measures the change in model performance, based on the AUC, when randomly shuffling the values of a single attribute while keeping all other attributes fixed. Intuitively, randomly shuffling an attribute effectively nullifies its contribution toward predicting the class of the target variable. Hence, if shuffling an attribute causes a large drop in performance, that attribute is considered important for prediction. Conversely, if the performance remains stable, the attribute has little influence. The model quantifies the importance of an attribute as

$$\Delta M=M_u-M_p$$

(19)

where $M_u$ is the model performance with unshuffled data and $M_p$ is the performance after permutation. Overall, the PFI is model-agnostic, simple to implement, and directly interprets the predictive power of attributes by quantifying their effect on classification outcomes.

3.7. Regression

To quantify the relative influence of threat, vulnerability, and consequence factors on the risk index, the workflow used an ordinary least squares (OLS) regression model with all pairwise combinations of the transformed and normalized factors. A regression model with the three pairwise terms as predictors was

$$z_i={\beta }_0+{\beta }_1\left(T_i{V}_i\right)+{\beta }_2\left(T_i{C}_i\right)+{\beta }_3\left(V_i{C}_i\right)+{ϵ}_i$$

(20)

where $z_i$ is the risk index for bridge i. Hence, the variables ${\beta }_1$, ${\beta }_2$, and ${\beta }_3$ are the estimated coefficients for the three pairwise factors. The variable ${\beta }_0$ is the estimated regression constant, and ${ϵ}_i$ is the error term. The estimated coefficients directly reflect the relative contributions of the underlying factors. For example, if ${\beta }_3$ (associated with VC) is larger than ${\beta }_1$ or ${\beta }_2$, it indicates that the combination of vulnerability and consequence explains more of the variation in the risk index, and therefore the threat factor contributes less.

The explanatory power of the model is measured by the coefficient of determination (R²) as

$$R^2=1-{\displaystyle \frac{\sum {\left(z_i-{\widehat{z}}_i\right)}^2}{\sum {\left(z_i-\overline{z}\right)}^2}}$$

(21)

where ${\widehat{z}}_i$ is the predicted value and $\overline{z}$ is the average value of the risk index. Higher R² values indicate stronger predictive ability.

The selection of this approach was due to its simplicity, transparency, and interpretability. As pairwise terms in the regression, one can assess the marginal contribution of each factor to the overall risk index without resorting to complex decomposition and less intuitive methods.

4. Results

The analysis produced results at three levels: attribute validation, index construction, and risk ranking. First, non-parametric ML models identified the most predictive attributes for bridge condition and confirmed the dominance of effective age (epoch) as the vulnerability factor. Second, regression analysis quantified the relative contributions of threat, vulnerability, and consequence, showing that vulnerability and detour distance explain most of the variation in the risk index. Finally, the workflow applied the constructed TVC index to bridges across the NHS to reveal geographic patterns and clusters of high-risk bridges. The following subsections present these results in detail.

4.1. Machine Learning

The ML models ranked bridge attributes by their predictive power for the target variable undamaged. Table 3 summarizes the attributes in descending order of importance, and Figure 13 shows the decrease in AUC after permuting each attribute. The variable epoch, which represents effective bridge age, dominated the rankings. The model performance was approximately 3.5 times more sensitive to removing the influence of epoch than to the next most important attribute, structural material type. This strong signal justified selecting epoch as the vulnerability factor in the TVC risk index.

Table 3. Bridge Attributes Ranked by their Predictive Power for Undamaged Condition Rating.

Attribute	Item	Description
Epoch		Defined in Table 2. Years since the most recent defining event in the life cycle.
STRUC_MAT	43A	Structure material type (concrete, steel, wood, etc.).
NOM_LD	66	Inventory rating. The nominal load for which inspectors rated the bridge.
Max_Span_L	48	Natural log of the meters of the maximum span length.
Spans_L	45	Natural log of the number of spans in the main unit.
ADT_Lane_L	29/28A	Average daily traffic per lane.
Width_L	52	Natural log of the meters of deck width.
STRUC_TYP	43B	Type of structure (slab, tee beam, truss, movable, etc.).
PARALLELS	101	Boolean variable indicating if the bridge has parallel structures/spans.
Detour_KM_L	19	Natural log of the kilometers of bypass or detour.
Rural	26	Boolean if functional class is at most 9.
TRAFFIC_DI	102	Direction of traffic on the same or parallel structure.
Lanes	28A	Number of lanes on the structure.

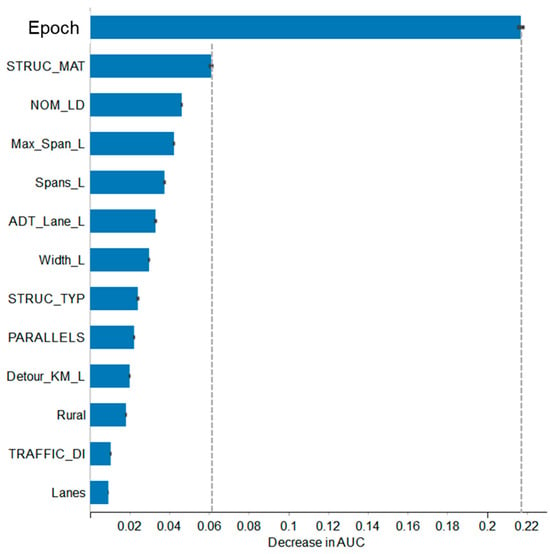
Figure 13. Feature importance in predicting bridge condition.

Several other attributes showed moderate influence, including structural material type, inventory load, maximum span length, number of spans, and ADT per lane. Attributes such as deck width, structure type, and detour distance had smaller effects. The lowest-ranked attributes, including traffic direction and number of lanes, contributed little to predictive performance. This confirms that age-related deterioration is the strongest predictor of undamaged bridges, while other attributes add only marginal value.

Table 4 reports the performance of the six ML models. XGB achieved the best performance with an AUC of 0.90, classification accuracy of 0.95, and F1-score of 0.93. RF and NN models followed closely, with AUC values of 0.86. LR also performed well with an AUC of 0.82, while kNN trailed at 0.75. The SVM performed poorly on this dataset, with an AUC of 0.57 and much lower classification accuracy.

Table 4. ML Model Performance.

Model	AUC	CA	F1	Pr	Rc
XGB	0.90	0.95	0.93	0.93	0.95
Random Forest	0.86	0.95	0.93	0.93	0.95
Neural Network	0.86	0.94	0.93	0.92	0.94
Logistic Regression	0.82	0.94	0.92	0.92	0.94
kNN	0.75	0.94	0.93	0.92	0.94
SVM	0.57	0.82	0.86	0.90	0.82

The consistently high classification accuracy across most models reflected the strong imbalance in the dataset, where undamaged bridges accounted for less than 6% of the population. The AUC and F1-score were therefore more reliable indicators of true performance. Among these, the tree-based ensemble models provided the most robust results. Together, these findings confirm that the effective bridge age (epoch) is the most critical vulnerability factor, and that the chosen ML framework reliably identified it.

4.2. OLS Regression

Figure 14 plots the instances of risk index predicted by the OLS regression against the constructed risk index and the best linear fit. The regression of the risk index on the three pairwise terms (TV, TC, and VC) produced a high coefficient of determination of R² = 0.98. This indicates that the three pairwise combinations together captured most of the variation in the constructed risk index.

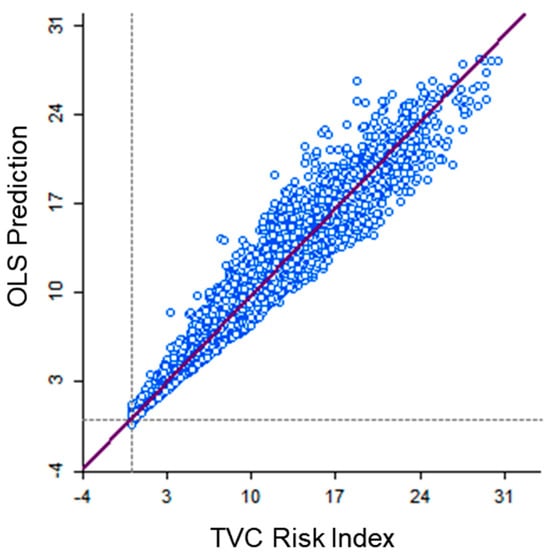
Figure 14. Instances of risk index predicted by the OLS regression against the constructed risk index and the best linear fit.

Table 5 summarizes the estimated coefficients for each pairwise combination. The t-statistic and the p-value indicate the probability that the estimated values are non-zero. The relative magnitudes of the regression coefficients provide insight into the contributions of the underlying factors. The coefficient for the VC term (${\beta }_3$) was the largest, followed by the coefficient for TV (${\beta }_1$). This result shows that the interaction of vulnerability and consequence explains the majority of the risk index. In contrast, terms containing threat contribute less to prediction once vulnerability and consequence are included.

Table 5. Fitted OLS Regression Model.

Variable	Coefficient	t-Statistic	p-Value
Constant	−0.38	−90.3	10−6
TV	3.1	139.9	10−6
TC	2.8	110.7	10−6
VC	52.8	1048.6	10−6

These findings indicate that bridge age and detour distance dominate the risk measure, while traffic intensity plays a secondary role. The results are consistent with the interpretation that supply chain disruption is more sensitive to structural deterioration and rerouting costs than to traffic loading alone.

4.3. Ranking Risks

Figure 15 ranks states by their average TVC risk index. Oklahoma has the highest average risk, followed by Nebraska, Oregon, Wyoming, and Montana. States with the lowest averages include South Carolina, Wisconsin, New York, and Massachusetts. Figure 16 maps these averages across states, where darker shades highlight higher average risk. The map shows a concentration of higher-risk states in the Great Plains and Mountain West. This result is intuitive because these rural regions combine older bridges, higher detour distances, and fewer redundancy options, which increase risk.

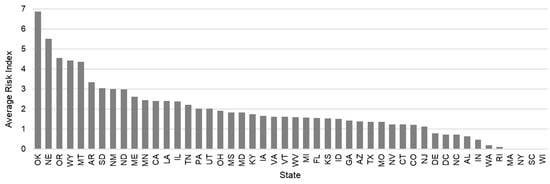
Figure 15. Rank of states by their average risk index.

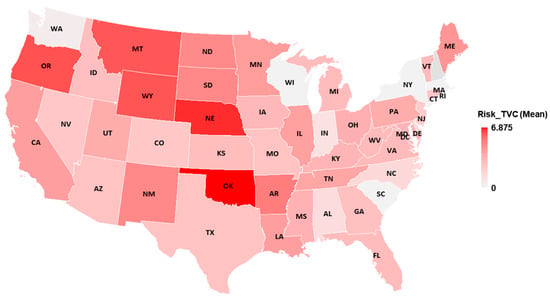
Figure 16. Choropleth state map of the average risk index.

Figure 17 presents the distribution of the TVC risk index using Jenks natural breaks into 10 intervals. Most bridges cluster at low-risk values, but a long tail extends toward extreme outliers. This confirms that while the majority of bridges present low supply chain risk, a small fraction represents disproportionately high vulnerabilities.

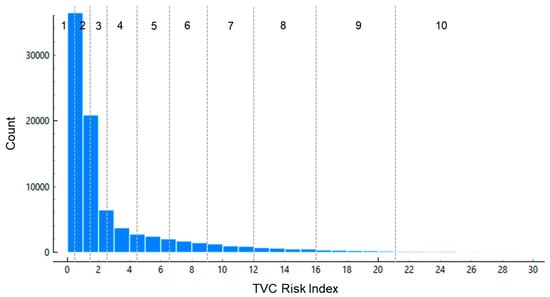
Figure 17. Distribution of the TVC risk index.

Figure 18 highlights bridges in the highest Jenks category, showing 292 outliers. The map uses k-means clustering to group these into five clusters. The outliers often appear near major cities, where dense NHS corridors converge. Many outliers also fall close to primary U.S. port areas, shown in orange. This overlap emphasizes how failures at these bridges would disrupt freight flows at strategic gateways, amplifying risks to supply chains.

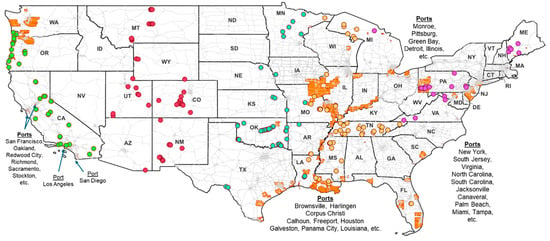
Figure 18. Bridges on the NHS within the outlier risk category of the Jenks-10 natural break.

Table 6 lists the top 20 bridges ranked by the risk index. The table includes the lowest rating (L), if it is in a rural location (R = 1), the detour distance (DD), the ADT per lane (ADL), and the latitude (LAT)/longitude (LON) coordinates of the structure. The average effective age of these bridges is 91 years. They carry an average of more than 5000 vehicles per lane per day, and detours average 170 km. Most are on major interstate or U.S. routes within the NHS. Several bridges in Oregon, Missouri, Tennessee, and Colorado dominate the top of the list, with risk index values approaching 30. Many of the Colorado bridges fall on Interstate 12A and share similar characteristics, highlighting clusters of high vulnerability.

Table 6. The Top 20 Bridges Based on the TVC Risk Index.

Route	State	Bridge ID	Epoch	ADL	DD	Risk	L	R	LAT	LON
101	OR	01172 009 32764	95	3700	199	30.34	6	1	42.4245	−124.4130
54	MO	5255	101	3137	153	29.80	5	1	37.8436	−94.5893
45	TN	55SR0050015	98	8013	101	29.38	6	1	35.2984	−88.6367
45	TN	55SR0050019	98	8013	101	29.38	7	1	35.3394	−88.6394
39	CA	53 0113	92	3679	199	29.35	7	0	34.1641	−117.8950
285	CO	G-13-G	88	5076	199	29.22	5	1	39.2773	−105.9250
23	MN	6073	101	2325	159	28.89	5	1	45.9515	−93.0719
30	PA	35921	86	7943	159	28.66	5	0	40.3265	−79.7112
24A	CO	I-12-AC	88	4322	199	28.64	6	1	38.8409	−106.0130
24A	CO	I-13-D	88	4322	199	28.64	5	1	38.8582	−105.9860
24A	CO	I-13-E	88	4322	199	28.64	7	1	38.8649	−105.9850
24A	CO	I-12-V	87	4322	199	28.31	5	1	38.8205	−106.0650
24A	CO	I-12-W	87	4322	199	28.31	5	1	38.8209	−106.0640
24A	CO	I-12-X	87	4322	199	28.31	5	1	38.8227	−106.0590
24A	CO	I-12-Y	87	4322	199	28.31	6	1	38.8258	−106.0530
54	MO	4886	98	5436	101	28.05	6	1	39.2596	−91.6450
101	OR	11817	80	7750	199	27.91	6	0	44.9983	−123.9950
19	VA	18855	92	4581	135	27.65	5	1	36.7484	−82.0537
11	TN	62SR0020003	94	6304	105	27.65	6	0	35.5974	−84.4648
101	OR	11927	80	6950	199	27.56	5	1	44.9127	−124.0050
AVG			91	5158	170	29	6

Together, these results show that high-risk bridges are not evenly distributed. They concentrate in specific states and along major freight corridors near ports. The combination of advanced age, heavy truck volumes, and long detour distances create localized but severe threats to supply chain continuity.

5. Discussions

The results demonstrate that a TVC-based index that is transparent can effectively capture how structural aging and rerouting costs dominate supply chain risk across the U.S. bridge network. The consistent identification of epoch as the strongest predictor validates the use of effective bridge age as the most representative vulnerability factor. Combined with detour distance, these attributes explain the majority of the variation in the risk index. This outcome supports this study’s goal to create a practical decision-support tool for freight corridor resilience.

The findings highlight how disruptions to supply chains are more sensitive to deterioration and rerouting penalties than to traffic intensity alone. This interpretation aligns with the operational reality that long detours and aging structures impose significant costs even when traffic volumes are moderate. By integrating per-lane ADT as both a loading factor and a multiplier of consequence, the model balances exposure and disruption in the risk ranking process.

This study advances the body of knowledge by translating the widely recognized TVC framework into a scalable and interpretable index tailored for freight infrastructure. Unlike hazard-specific or component-level assessments, this index generalizes across regions and hazards while remaining rooted in supply chain continuity. The ability to classify risk through Jenks natural breaks further enhances interpretability by identifying natural clusters of high-risk bridges and allowing agencies to prioritize clusters rather than isolated outliers.

When compared with related work, this approach extends beyond climate-focused protocols, seismic or flood-specific models, and digital-twin frameworks that require intensive data assimilation. It provides a middle ground that is both empirically validated through ML methods and is operationally simple to compute at scale. The explicit incorporation of detour distance as a proxy for user cost distinguishes this work from prior studies that emphasized hazard intensity or component fragility without addressing freight logistics implications.

This study focused on developing a transparent and scalable risk index using variables available in the NBI. While the approach captured key dimensions of supply chain disruption, several aspects were not within the scope of this effort. The index does not incorporate dynamic traffic variations, seasonal demand shifts, or real-time hazard exposure. Those factors may alter risk profiles in practice. The consequence term is represented by detour distance as a proxy for user cost, but it does not differentiate by commodity value, time sensitivity, or regional economic dependence. In addition, the analysis treated hazards in a hazard-agnostic manner rather than tailoring fragility relationships to specific threats such as floods, earthquakes, or extreme weather. These limitations suggest clear paths for future research. Extending the framework to include dynamic traffic data, hazard-specific fragility models, and commodity-sensitive consequence measures will enhance the precision of the risk index. Integrating multimodal supply chain flows and regional economic models would further strengthen its relevance for investment planning and resilience strategies. Such extensions will broaden the implications of this work while preserving its central value: a simple, interpretable, data-driven foundation for prioritizing bridges that matter most to freight continuity.

6. Conclusions

This study addressed the challenge of prioritizing bridge investments by developing a transparent and scalable risk index tailored to freight corridors. Bridges are indispensable to the U.S. supply chain, yet limited resources force agencies to make difficult decisions about which structures to repair or replace. By applying the threat–vulnerability–consequence (TVC) framework and validating its components with machine learning, the research provides a practical tool to identify which bridges pose the greatest disruption risk to freight movement. The conclusions connect directly to the goal of the study to support decision-making for both infrastructure managers and supply chain stakeholders.

The analysis showed that effective age (epoch) is the dominant vulnerability factor, while detour distance magnifies the consequence of bridge closures. Together, these factors explain most of the risk variation across the network. The index successfully identified clusters of high-risk bridges in rural regions and freight gateways where limited redundancy amplifies disruption potential. The results confirm that supply chain continuity is most sensitive to deterioration and rerouting costs rather than traffic intensity alone.

The contribution of this work is a practical and scalable decision-support tool for state and federal agencies. The TVC index can guide prioritization of maintenance investments, inform freight routing strategies, and support long-range infrastructure planning. The index offers consistent applicability across the national bridge inventory because it is hazard-agnostic and based on publicly available data. Beyond freight applications, the framework demonstrates how interpretable machine learning and risk modeling can be combined to derive actionable indices for critical infrastructure. This study acknowledged potential limitations in that the risk index is hazard-agnostic. Hence, future research could extend the framework by integrating hazard-specific fragility models to enhance precision while preserving interpretability. The TVC approach can be generalized to other asset classes where exposure, vulnerability, and consequence interact to drive operational risk.