Design-Assisted of Pitching Aerofoils through Enhanced Identification of Coherent Flow Structures
Abstract
1. Introduction
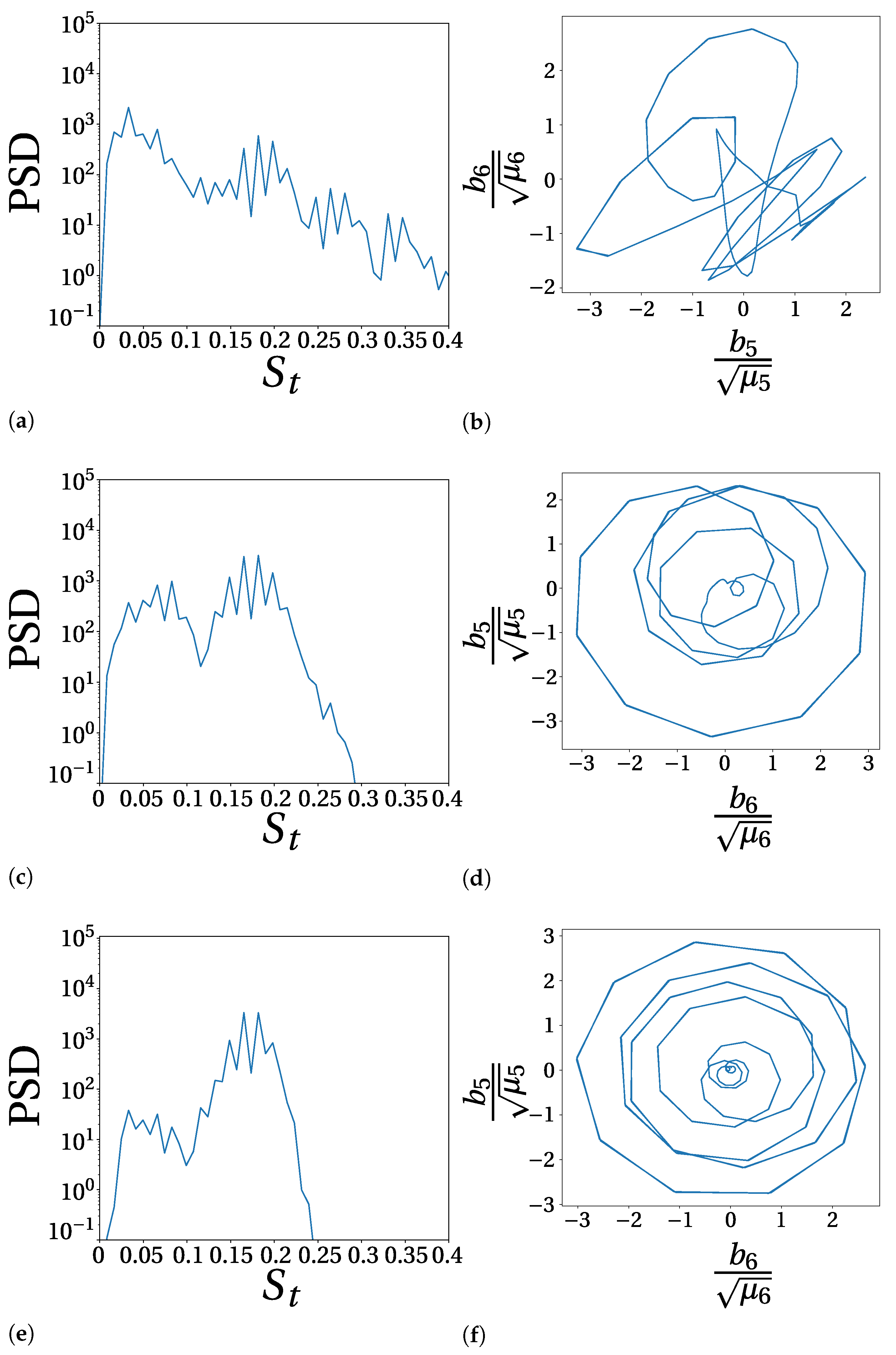
2. Spectral Proper Orthogonal Decomposition
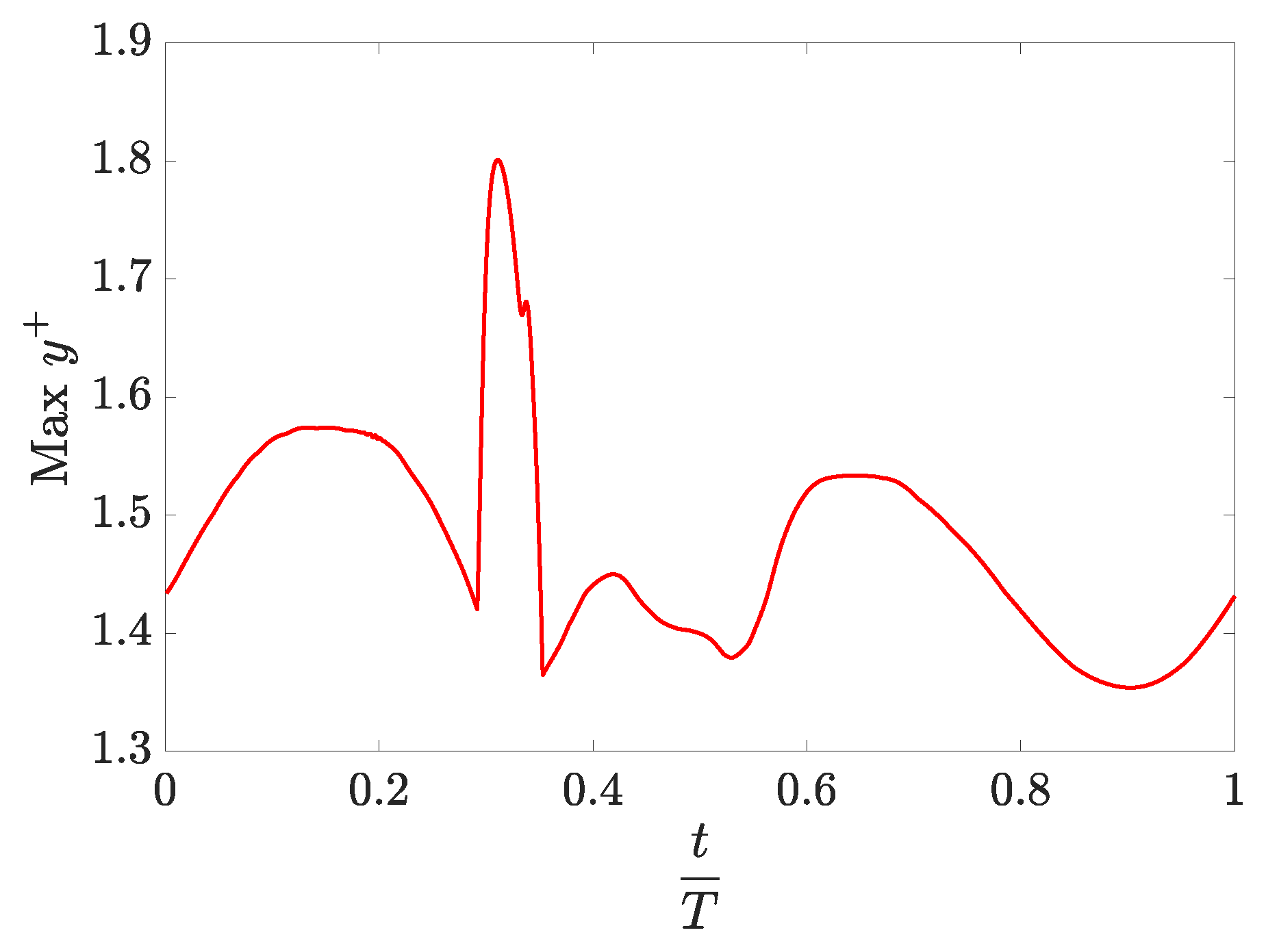
3. Computational Setup
4. Results and Discussion
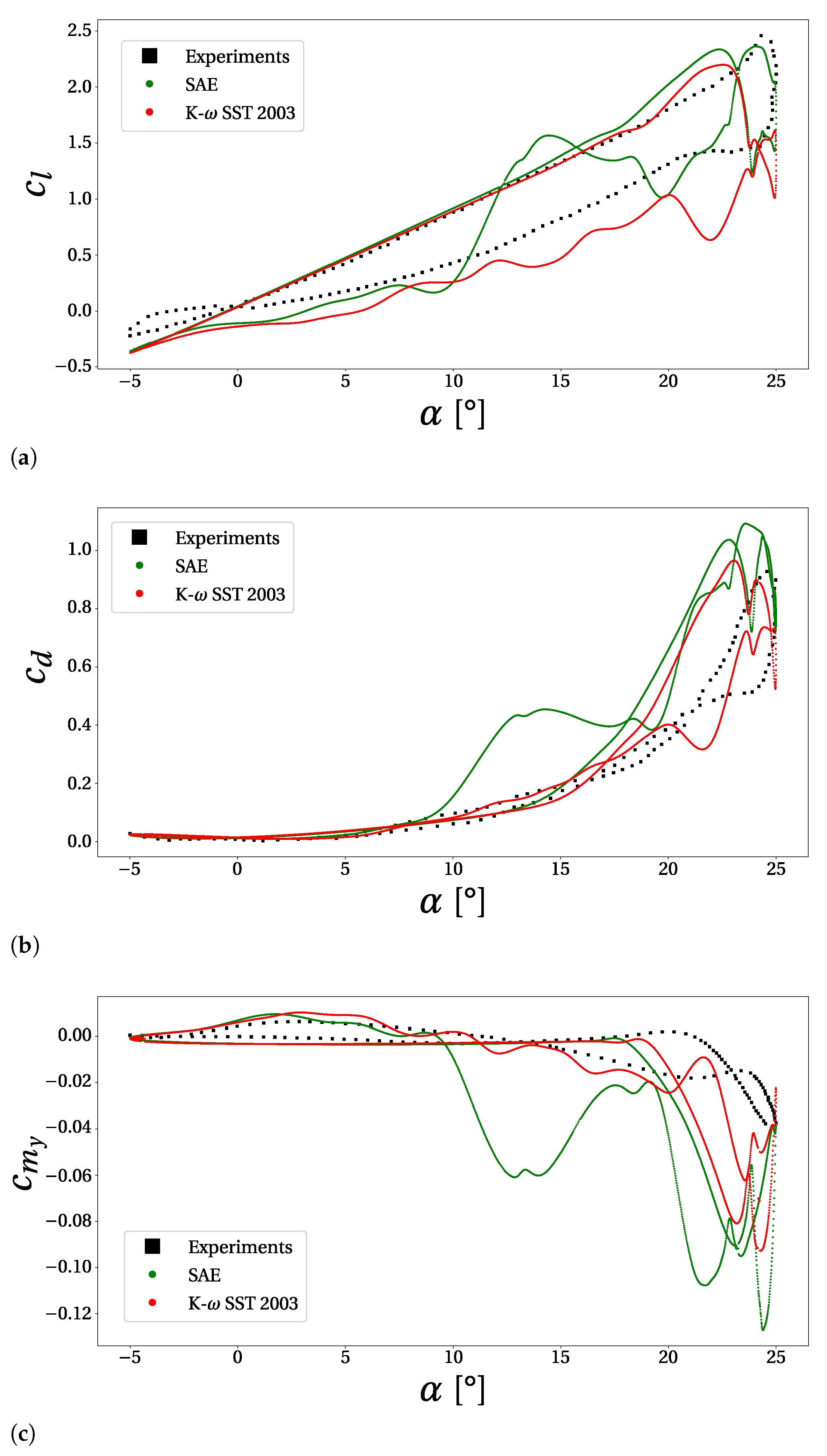
4.1. Simulation Results Compared to Experimental Setup
4.2. Simulation with Case Study Conditions
 follows the same trace until the steady-state angle of attack is reached (Figure 6a). Here, again, the slope of the curve briefly flattens
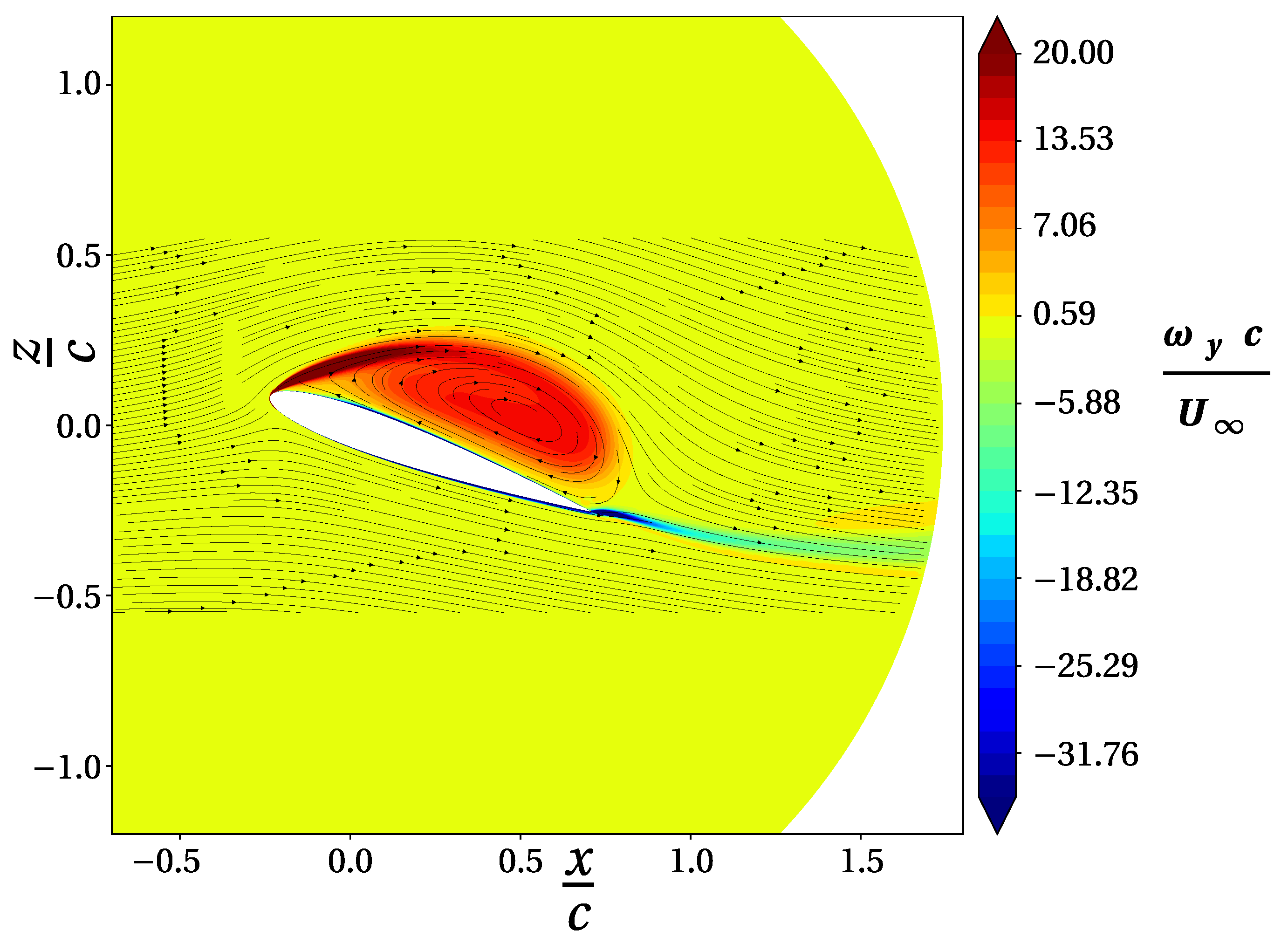
follows the same trace until the steady-state angle of attack is reached (Figure 6a). Here, again, the slope of the curve briefly flattens  before becoming even greater than in the linear trend. This condition also induces a drop of the moment curve (Figure 6c). The reason for this can be ascribed to the gradual thickening of the boundary layer that generates the leading edge vortex, whose low-pressure core travels down to the trailing edge throughout the motion. As it passes the centre of pressure of the aerofoil, the negative effect of the moment drastically increases. This process continues in full attachment conditions, which explains the protracted trend of the loads. After lift stall occurs, with the vortex shedding at
before becoming even greater than in the linear trend. This condition also induces a drop of the moment curve (Figure 6c). The reason for this can be ascribed to the gradual thickening of the boundary layer that generates the leading edge vortex, whose low-pressure core travels down to the trailing edge throughout the motion. As it passes the centre of pressure of the aerofoil, the negative effect of the moment drastically increases. This process continues in full attachment conditions, which explains the protracted trend of the loads. After lift stall occurs, with the vortex shedding at  , the load along the z axis shows an almost monotonic behaviour. Differently, the sudden formation of a trailing edge vortex affects both the drag (Figure 6b) and moment loads. The appearance of a trailing edge vortex is depicted by a second peak in the two plots
, the load along the z axis shows an almost monotonic behaviour. Differently, the sudden formation of a trailing edge vortex affects both the drag (Figure 6b) and moment loads. The appearance of a trailing edge vortex is depicted by a second peak in the two plots  and in particular, for the moment load, this value represents the maximum negative excursion. The concluding part of the upstroke phase is influenced by a brief re-attachment of the circulating flow. In fact, in the neighbourhood of the maximum incidence, the three aerodynamics coefficients show a rapid, though limited, excursion
and in particular, for the moment load, this value represents the maximum negative excursion. The concluding part of the upstroke phase is influenced by a brief re-attachment of the circulating flow. In fact, in the neighbourhood of the maximum incidence, the three aerodynamics coefficients show a rapid, though limited, excursion  . As can be seen from the flow distribution, this event is generated by a circulation bubble that extends over the whole aerofoil and has a low-pressure core located beyond the centre of pressure. The remainder of the flow evolution
. As can be seen from the flow distribution, this event is generated by a circulation bubble that extends over the whole aerofoil and has a low-pressure core located beyond the centre of pressure. The remainder of the flow evolution  develops with conditions typical of full detachment. Here, the small fluctuations seem to be mostly related to the numerics and not to the physics of the system.
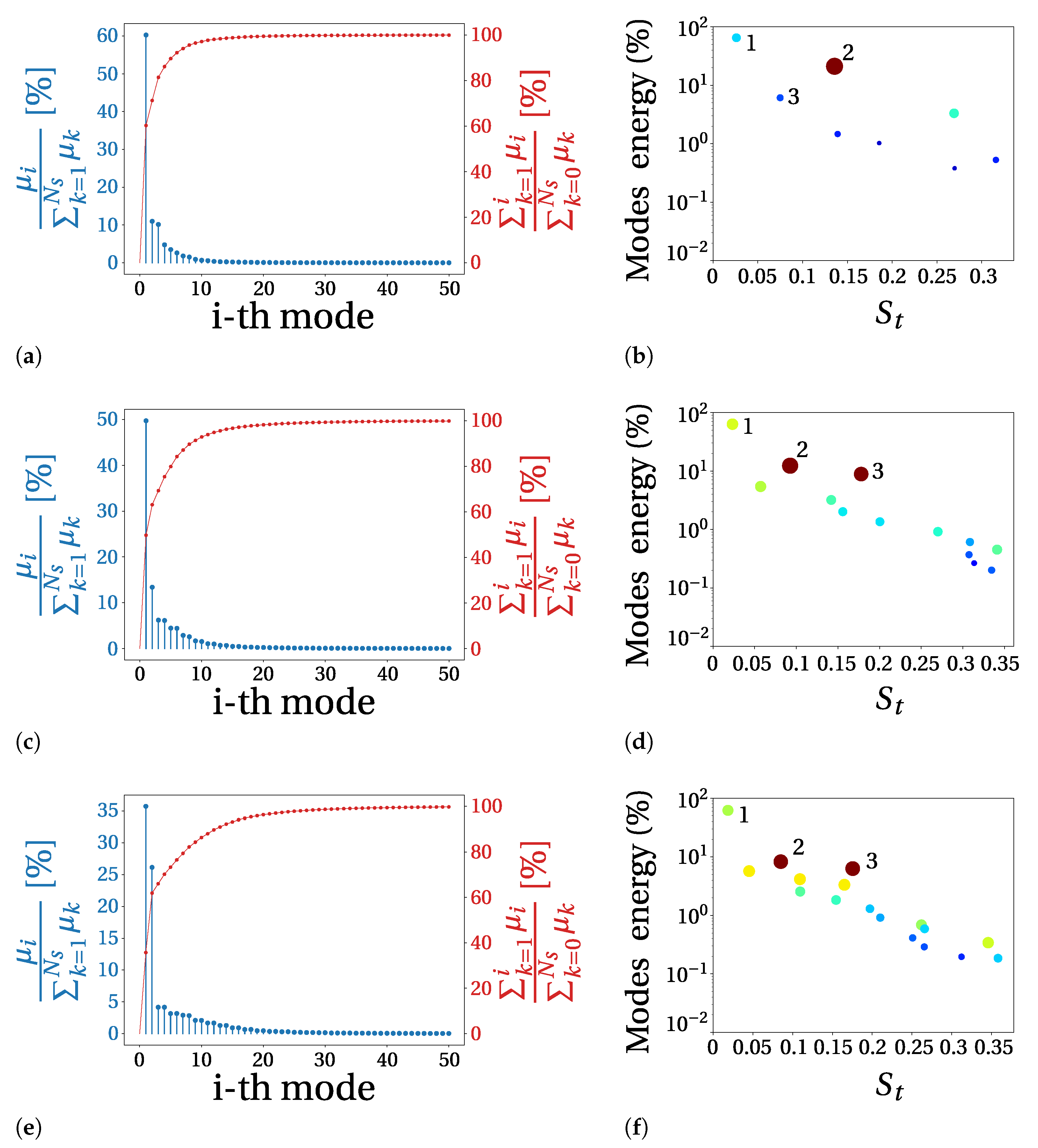
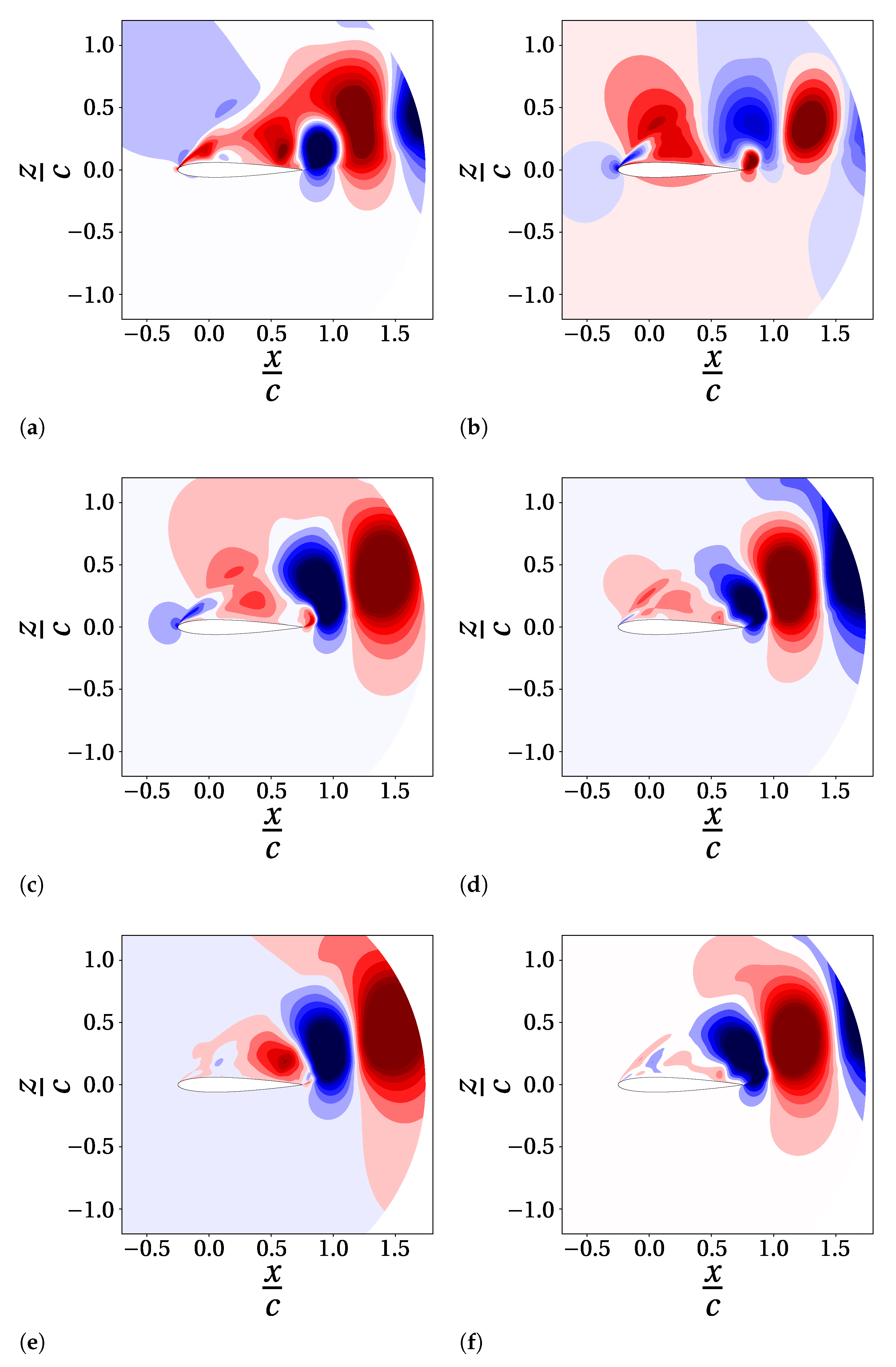
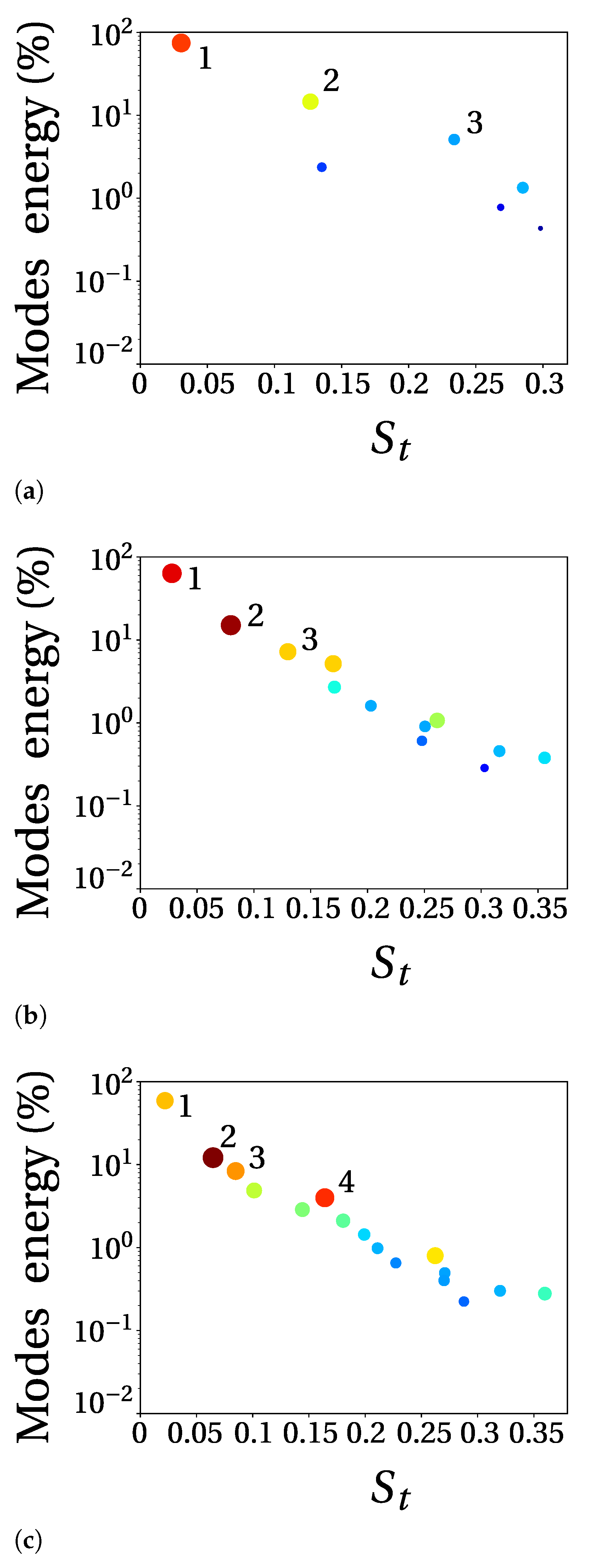
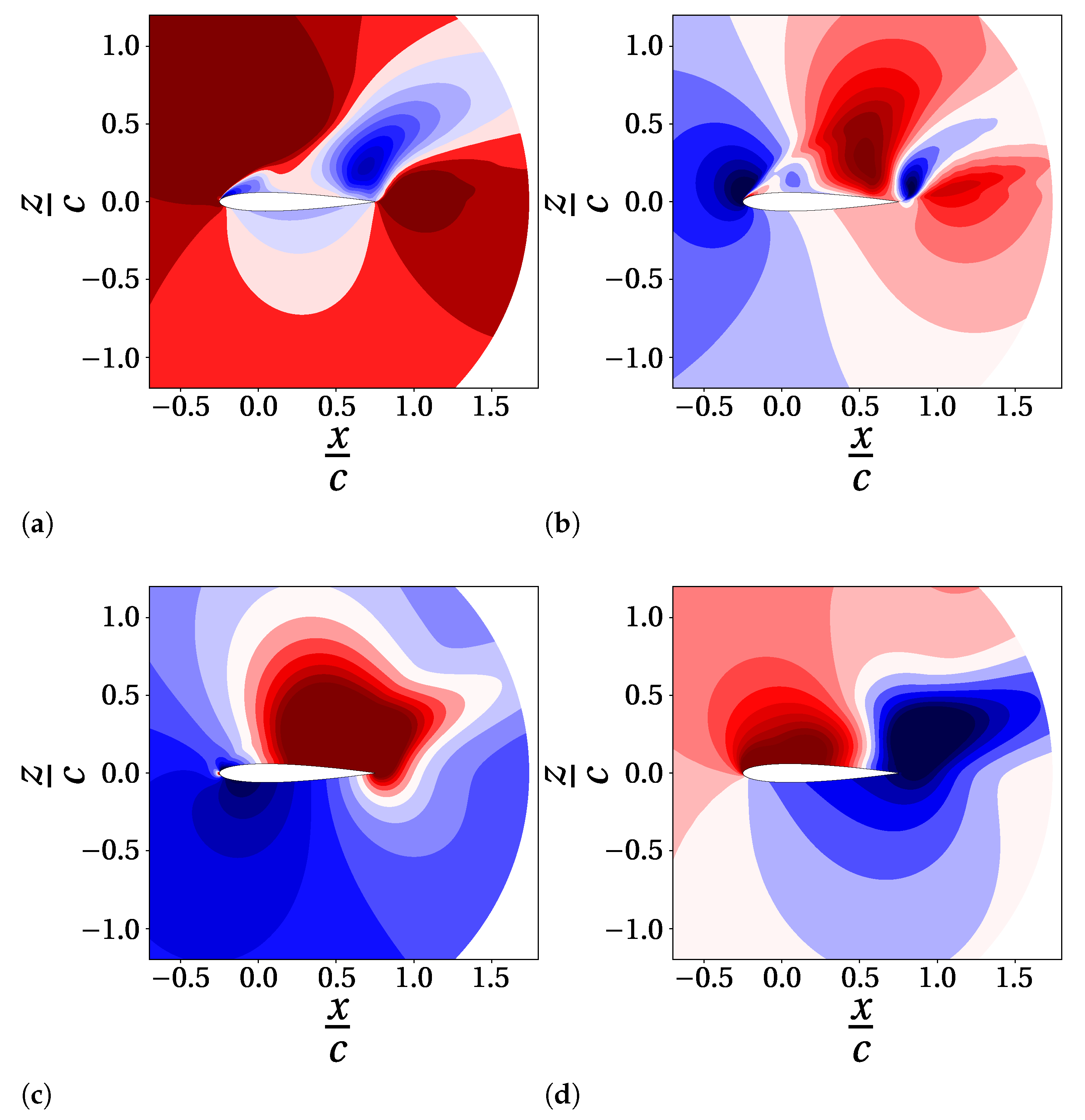
develops with conditions typical of full detachment. Here, the small fluctuations seem to be mostly related to the numerics and not to the physics of the system.4.3. Spectral Proper Orthogonal Decomposition
4.4. Comparison between Decompositions of Pressure and Velocity Field
4.5. Reconstruction of Aerodynamic Coefficients
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CFD | Computational Fluid Dynamics |
| DES | Detached Eddy Simulation |
| DFT | Discrete Fourier Transform |
| DLR | Deutsches Zentrum für Luft- und Raumfahrt |
| DMD | Dynamic Mode Decomposition |
| ILES | Implicit Large-Eddy Simulations |
| LES | Large-Eddy Simulations |
| MPI | Message Passing Interface |
| PIV | Particle Image Velocimetry |
| POD | Proper Orthogonal Decomposition |
| PSD | Power Spectral Density |
| SAE | Spalart-Allmaras with Edwards modification |
| SPOD | Spectral Proper Orthogonal Decomposition |
| SST | Shear Stress Model |
| URANS | Unsteady Reynolds-Averaged Navier-Stokes |
References
- Wen, G.; Gross, A. Numerical Investigation of Deep Dynamic Stall for a Helicopter Blade Section. AIAA J. 2018, 57, 1434–1451. [Google Scholar] [CrossRef]
- Conlisk, A.T. Modern helicopter rotor aerodynamics. Prog. Aerosp. Sci. 2001, 37, 419–476. [Google Scholar] [CrossRef]
- Leishman, J.G. Principles of Helicopter Aerodynamic; Cambridge Aerospace Series; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- Greenblatt, D.; Wygnanski, I. Dynamic Stall Control by Periodic Excitation, Part 1: NACA 0015 Parametric Study. J. Aircr. 2001, 38, 430–438. [Google Scholar] [CrossRef]
- Corke, T.C.; Thomas, F.O. Dynamic Stall in Pitching Airfoils: Aerodynamic Damping and Compressibility Effects. Annu. Rev. Fluid Mech. 2015, 47, 479–505. [Google Scholar] [CrossRef]
- Martin, J.M.; Empey, R.W.; McCroskey, W.J.; Caradonna, F.X. An Experimental Analysis of Dynamic Stall on an Oscillating Airfoil. J. Am. Helicopter Soc. 1974, 19, 26–32. [Google Scholar] [CrossRef]
- Carr, L.W.; McAlister, K.W.; McCroskey, W.J. Analysis of the Development of Dynamic Stall Based on Oscillating Airfoil Measurements; Technical Report TN D-8382; National Aeronautics and Space Administration: Moffett Field, CA, USA, 1977.
- McAlister, K.W.; Carr, L.W.; McCroskey, W.J. Dynamic Stall Experiments on the Naca 0012 Airfoil; Technical Report TP-1100; National Aeronautics and Space Administration: Moffett Field, CA, USA, 1978.
- McCroskey, W.J. The Phenomenon of Dynamic Stall; Technical Report TM-81264; National Aeronautics and Space Administration: Moffett Field, CA, USA, 1981.
- Leishman, J. Dynamic stall experiments on the NACA 23012 aerofoil. Exp. Fluids 1990, 9, 49–58. [Google Scholar] [CrossRef]
- Wernert, P.; Geissler, W.; Raffel, M.; Kompenhans, J. Experimental and numerical investigations of dynamic stall on a pitching airfoil. AIAA J. 1996, 34, 982–989. [Google Scholar] [CrossRef]
- Gerontakos, P. An Experimental Investigation of Flow Over an Oscillating Airfoil. Master’s Thesis, McGill University, Ottawa, ON, Canada, 2004. [Google Scholar]
- De Vanna, F.; Picano, F.; Benini, E. A sharp-interface immersed boundary method for moving objects in compressible viscous flows. Comput. Fluids 2020, 201, 104415. [Google Scholar] [CrossRef]
- De Vanna, F.; Picano, F.; Benini, E. An Immersed Boundary Method for Moving Objects in Compressible Flows. In ERCOFTAC Workshop Direct and Large Eddy Simulation; Springer: Berlin, Germany, 2019; pp. 291–296. [Google Scholar]
- De Vanna, F.; Picano, F.; Benini, E. Large-Eddy-Simulations of the unsteady behaviour of a Mach 5 hypersonic intake. In Proceedings of the AIAA Aerospace Sciences Meeting-AIAA Science and Technology Forum and Exposition, SciTech 2021, Virtual Event, 11–15 & 19–21 January 2021. [Google Scholar] [CrossRef]
- Spalart, P.; Allmaras, S. A One-Equation Turbulence Model for Aerodynamic Flows. AIAA 1992, 439. [Google Scholar] [CrossRef]
- Duraisamy, K.; McCroskey, W.J.; Baeder, J.D. Analysis of Wind Tunnel Wall Interference Effects on Subsonic Unsteady Airfoil Flows. J. Aircr. 2007, 44, 1683–1690. [Google Scholar] [CrossRef]
- Wang, Q.; Zhao, Q. Unsteady aerodynamic characteristics investigation of rotor airfoil under variational freestream velocity. Aerosp. Sci. Technol. 2016, 58, 82–91. [Google Scholar] [CrossRef]
- Schulz, K.W.; Kallinderis, Y. Unsteady Flow Structure Interaction for Incompressible Flows Using Deformable Hybrid Grids. J. Comput. Phys. 1998, 143, 569–597. [Google Scholar] [CrossRef]
- Nithiarasu, P.; Liu, C.B. An artificial compressibility based characteristic based split (CBS) scheme for steady and unsteady turbulent incompressible flows. Comput. Methods Appl. Mech. Eng. 2006, 195, 2961–2982. [Google Scholar] [CrossRef]
- Edwards, J.R.; Chandra, S. Comparison of eddy viscosity-transport turbulence models for three-dimensional, shock-separated flowfields. AIAA J. 1996, 34, 756–763. [Google Scholar] [CrossRef]
- Rung, T.; Bunge, U.; Schatz, M.; Thiele, F. Restatement of the Spalart-Allmaras Eddy-Viscosity Model in Strain-Adaptive Formulation. AIAA J. 2003, 41, 1396–1399. [Google Scholar] [CrossRef]
- Dwight, R.P.; Brezillon, J. Effect of Approximations of the Discrete Adjoint on Gradient-Based Optimization. AIAA J. 2006, 44, 3022–3031. [Google Scholar] [CrossRef]
- Richter, K.; Pape, A.; Knopp, T.; Costes, M.; Gleize, V.; Gardner, A. Improved Two-Dimensional Dynamic Stall Prediction with Structured and Hybrid Numerical Methods. J. Am. Helicopter Soc. 2011, 56, 1–2. [Google Scholar] [CrossRef]
- Singh, K.; Páscoa, J.C. Numerical Modelling of Stall and Post Stall Events of a Single Pitching Blade of a Cycloidal Rotor. J. Fluids Eng. 2019, 141. [Google Scholar] [CrossRef]
- Wang, S.; Ingham, D.B.; Ma, L.; Pourkashanian, M.; Tao, Z. Numerical investigations on dynamic stall of low Reynolds number flow around oscillating airfoils. Comput. Fluids 2010, 39, 1529–1541. [Google Scholar] [CrossRef]
- Wang, S.; Ingham, D.B.; Ma, L.; Pourkashanian, M.; Tao, Z. Turbulence modeling of deep dynamic stall at relatively low Reynolds number. J. Fluids Struct. 2012, 33, 191–209. [Google Scholar] [CrossRef]
- Kai, X.; Abbas, L.; Dongyang, C.; Fufeng, Y.; Xiaoting, R. Numerical Investigations on Dynamic Stall of a Pitching-Plunging Helicopter Blade Airfoil. Int. J. Mech. Mechatron. Eng. 2017, 11, 1639–1644. [Google Scholar]
- Marchetto, F.; Benini, E. Numerical Simulation of Harmonic Pitching Supercritical Airfoils Equipped with Movable Gurney Flaps. Int. Rev. Aerosp. Eng. (IREASE) 2019, 12, 109–122. [Google Scholar] [CrossRef]
- Fiedler, H.E. Coherent structures in turbulent flows. Prog. Aerosp. Sci. 1988, 25, 231–269. [Google Scholar] [CrossRef]
- Lumley, J.L. The structure of inhomogeneous turbulence. In Atmospheric Turbulence and Wave Propagation; Yaglom, A.M., Tatarski, V.I., Eds.; Nauka: Moscow, Russia, 1967; pp. 166–178. [Google Scholar]
- Aubry, N.; Holmes, P.; Lumley, J.L.; Stone, E. The dynamics of coherent structures in the wall region of a turbulent boundary layer. J. Fluid Mech. 1988, 192, 115–173. [Google Scholar] [CrossRef]
- Ribeiro, J.; Wolf, W. Identification of coherent structures in the flow past a NACA0012 airfoil via proper orthogonal decomposition. Phys. Fluids 2017, 29, 085104. [Google Scholar] [CrossRef]
- Cantwell, B.J. Organized Motion in Turbulent Flow. Annu. Rev. Fluid Mech. 1981, 13, 457–515. [Google Scholar] [CrossRef]
- Berkooz, G.; Holmes, P.J.; Lumley, J.L. The Proper Orthogonal Decomposition in the Analysis of Turbulent Flows. Annu. Rev. Fluid Mech. 1993, 25, 539–575. [Google Scholar] [CrossRef]
- Holmes, P.; Lumley, J.L.; Berkooz, G.; Rowley, C.W. Turbulence, Coherent Structures, Dynamical Systems and Symmetry, 2nd ed.; Cambridge Monographs on Mechanics, Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Sirovich, L. Turbulence and the dynamics of coherent structures. I-Coherent structures. Q. Appl. Math. 1987, 45, 561–571. [Google Scholar] [CrossRef]
- Sieber, M.; Paschereit, C.; Oberleithner, K. Spectral proper orthogonal decomposition. J. Fluid Mech. 2016, 792, 798–828. [Google Scholar] [CrossRef]
- Sieber, M.; Paschereit, C.; Oberleithner, K. Advanced Identification of Coherent Structures in Swirl-Stabilized Combustors. J. Eng. Gas Turbines Power 2016, 139, 021503. [Google Scholar] [CrossRef]
- Lückoff, F.; Sieber, M.; Paschereit, C.; Oberleithner, K. Characterization of Different Actuator Designs for the Control of the Precessing Vortex Core in a Swirl-Stabilized Combustor. J. Eng. Gas Turbines Power 2017, 140, 041503. [Google Scholar] [CrossRef]
- Ricciardi, T.; Wolf, W.; Speth, R. Acoustic Prediction of the LAGOON Landing Gear: Cavity Noise and Coherent Structures. AIAA J. 2018, 56. [Google Scholar] [CrossRef]
- Sieber, M.; Paschereit, C.; Oberleithner, K. On the nature of spectral proper orthogonal decomposition and related modal decompositions. arXiv 2017, arXiv:1712.08054. [Google Scholar]
- Lee, T.; Gerontakos, P. Investigation of flow over an oscillating airfoil. J. Fluid Mech. 2004, 512, 313–341. [Google Scholar] [CrossRef]
- DLR. TAU-Code User Guide: Release 2018.1.0; Institute of Aerodynamics and Flow Technology: Göttingen, Germany, 2018. [Google Scholar]
- Institute of Aerodynamics and Flow Technology. Technical Documentation of the DLR TAU-Code Release 2018.1.0.; Technical Report; Deutsches Zentrum für Luft- und Raumfahrt: Cologne (Köln), Germany, 2018. [Google Scholar]
- Spiering, F. Development of a Fully Automatic Chimera Hole Cutting Procedure in the DLR TAU Code. New Results in Numerical and Experimental Fluid Mechanics X; Dillmann, A., Heller, G., Krämer, E., Wagner, C., Breitsamter, C., Eds.; Springer International Publishing: Cham, Switzerland, 2016; pp. 585–595. [Google Scholar]
- Abbruzzese, G.; Gómez, M.; Cordero-Gracia, M. Unstructured 2D grid generation using overset-mesh cutting and single-mesh reconstruction. Aerosp. Sci. Technol. 2018, 78, 637–647. [Google Scholar] [CrossRef]
- Wang, Z.J.; Parthasarathy, V. A fully automated Chimera methodology for multiple moving body problems. Int. J. Numer. Methods Fluids 2000, 33, 919–938. [Google Scholar] [CrossRef]
- Schwamborn, D.; Gerhold, T.; Hannemann, V. On the Validation of the DLR-TAU Code. In New Results in Numerical and Experimental Fluid Mechanics II: Contributions to the 11th AG STAB/DGLR Symposium Berlin, Germany 1998; Vieweg+Teubner Verlag: Wiesbaden, Germany, 1999; pp. 426–433. [Google Scholar]
- Kroll, N.; Langer, S.; Schwöppe, A. The DLR flow solver TAU-Status and recent algorithmic developments. In Proceedings of the 52nd AIAA Aerospace Sciences Meeting-AIAA Science and Technology Forum and Exposition, SciTech 2014, Harbor, MD, USA, 13–17 January 2014. [Google Scholar]
- Stuermer, A. DLR TAU-Code uRANS Turbofan Modeling for Aircraft Aerodynamics Investigations. Aerospace 2019, 6, 121. [Google Scholar] [CrossRef]
- Carr, L.W.; Chandrasekhara, M.S. Compressibility effects on dynamic stall. Prog. Aerosp. Sci. 1996, 32, 523–573. [Google Scholar] [CrossRef]
- Welch, P. The use of fast Fourier transform for the estimation of power spectra: A method based on time averaging over short, modified periodograms. IEEE Trans. Audio Electroacoust. 1967, 15, 70–73. [Google Scholar] [CrossRef]
- Taira, K.; Brunton, S.L.; Dawson, S.T.M.; Rowley, C.W.; Colonius, T.; McKeon, B.J.; Schmidt, O.T.; Gordeyev, S.; Theofilis, V.; Ukeiley, L.S. Modal Analysis of Fluid Flows: An Overview. AIAA J. 2017, 55, 4013–4041. [Google Scholar] [CrossRef]




| Parameter | Symbol | Exp. Setup [12] | Case Study Setup |
|---|---|---|---|
| Mean angle of attack [] | 10 | 13.18 | |
| Pitch amplitude [] | 15 | 9.55 | |
| Reduced frequency | k | 0.1 | 0.135 |
| Pitching angular frequency [rad/s] | 18.67 | 275 | |
| Free stream velocity [m/s] | 14 | 152.73 | |
| Reynolds number | 1.35·105 | 1.57·106 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Avanzi, F.; De Vanna, F.; Ruan, Y.; Benini, E. Design-Assisted of Pitching Aerofoils through Enhanced Identification of Coherent Flow Structures. Designs 2021, 5, 11. https://doi.org/10.3390/designs5010011
Avanzi F, De Vanna F, Ruan Y, Benini E. Design-Assisted of Pitching Aerofoils through Enhanced Identification of Coherent Flow Structures. Designs. 2021; 5(1):11. https://doi.org/10.3390/designs5010011
Chicago/Turabian StyleAvanzi, Filippo, Francesco De Vanna, Yin Ruan, and Ernesto Benini. 2021. "Design-Assisted of Pitching Aerofoils through Enhanced Identification of Coherent Flow Structures" Designs 5, no. 1: 11. https://doi.org/10.3390/designs5010011
APA StyleAvanzi, F., De Vanna, F., Ruan, Y., & Benini, E. (2021). Design-Assisted of Pitching Aerofoils through Enhanced Identification of Coherent Flow Structures. Designs, 5(1), 11. https://doi.org/10.3390/designs5010011








