Abstract
With the implementation of China’s “dual carbon” strategy, the installed capacity of new energy has grown rapidly. Wind power and photovoltaic power have accounted for more than 40%, but the integration of power electronic apparatus into the grid has resulted in the manifestation of a system with “low inertia and weak damping”, which can easily lead to transient overvoltage problems at transmitters when high-voltage direct-current (HVDC) latching faults occur. Although a variety of dynamic reactive power optimization strategies have been proposed in the existing research, most of them are aimed at single equipment, and multi-reactive power source collaborative control schemes are lacking. In this paper, we innovatively establish a transient voltage analysis model for a new energy transmitter, derive the expression of overvoltage amplitude, and propose a method for the construction of a multi-reactive source collaborative optimization model, which can effectively suppress transient overvoltage through capacity and initial output configuration. We provide a new idea for the safe operation of a significant percentage of new energy grids. The case analysis shows that the co-optimization method outlined in this paper is an effective solution to suppress the transient overvoltage triggered by AC faults and has wide application value.
1. Introduction
With the in-depth promotion of the carbon peaking and carbon-neutral goal, China’s new energy installed capacity has shown quick growth. By the end of 2024, the total capacity of wind and photovoltaic energy that had been installed exceeded 1.2 billion kilowatts, accounting for more than 40% of the total energy supply. Connection of new energy power generation equipment to the grid is generally achieved through a power electronic interface, resulting in the system gradually showing “low inertia, weak damping” [1,2,3,4]. In UHV DC transmission scenarios with the occurrence of a DC blocking fault at the delivery end of the system, the instantaneous energy surplus will trigger a significant transient overvoltage phenomenon [5,6,7]. Actual operation data show that in a new energy base in northwest China, during the “8–15” big disturbance event in 2023, the local bus voltage instantaneously increased up to 1.35 pu, causing several converters to go off-grid protectively. The physical nature of this phenomenon lies in the fact that electronic power equipment cannot provide natural reactive power support during faults, as is possible with synchronous machines, but instead generates additional reactive power back-feeding due to control strategy switching. More seriously, the spatial and temporal distribution characteristics of new energy clusters lead to a long response delay with the traditional centralized voltage control strategy, and the transient overvoltage limit of 1.1 pu specified by the existing standard has been breached in several actual systems. Although this transient process lasts only a few hundred milliseconds, it is enough to trigger the protective device, incurring a risk of chain failure.
In an effort to address the overvoltage challenges posed by new energy and DC systems, scholars from both domestic and international backgrounds have undertaken a substantial amount of research pertaining to the analysis and mitigation of these issues [8,9,10,11,12,13,14,15]. In view of the increasingly severe problem of voltage stability in receiving grids, an optimization approach using dynamic reactive power for hybrid AC/DC power grids, taking into account the incorporation of new energy into a grid, was put forward in [16] to enhance voltage recovery capability following a fault.
To solve the issue of transient overvoltage caused by reactive power surplus in HVDC systems, reference [17] came up with an optimal reactive power control strategy based on multi-DC power modulation. It is capable of optimizing the distribution of the reactive power in special hybrid AC/DC systems to accurately control the grid voltage. Reference [18] introduces the gray wolf algorithm for the purpose of obtaining an optimal compromise solution for multi-objective reactive power optimization of transmission grids, and the performance of new energy units in terms of reactive power regulation is evaluated and utilized by taking network loss, voltage deviation, and static voltage stability margin as three object functions. Since most of the dynamic reactive power distribution lack an apportionment technique founded upon quantitative evaluation indices, a method for optimizing the allocation of dynamic reactive power is outlined in [19], which is based on the sensitivity of reactive power compensation.
To address the issues of the inaccurate response of current dynamic reactive power control schemes for various fault situations and the low operation efficiency of independent equipment, a strategy for coordinated and optimal control was proposed in [20], integrating a variety of dynamic reactive power sources for distinct fault traits. Authors [21] used the grid-based as well as grid-following control features of contemporary power electronic inverters to establish a model for the collaborative optimal configuration of reactive power equipment that is both grid-connected and grid-attached. A multi-time-scale collaborative allocation strategy was put forward. This strategy aims to solve the problem of the insufficient active support capacity of reactive power equipment, which is used for the purpose of suppressing short-term fluctuations in voltage within the power grid. To enhance the stability of the voltage in the power system with escalating levels of wind power infiltration and constant induction load, a robust, adaptive, multi-objective optimization model was put forward in [22] for a solution of the configuration issue of dynamic reactive power supply. A model with data-driven, two-stage, stochastic, dynamic, reactive power optimization was suggested in [23], managing the simultaneous operation of both discrete and continuous controllable devices whilst taking into account the variable output of DG.
In order to enable wind turbines to modulate momentary overvoltage, a superior voltage-reactive power control strategy was proposed [24], including voltage time-series prediction for reactive power control delay compensation and power command optimization. To solve the issue of transient overvoltage in the recovery stage after AC short-circuit faults, the specific expression of transient overvoltage is deduced in detail [25], and a method f optimizing the analytical control parameter is put forward for the reduction in the amplitude and recovery speed of fault overvoltage while under different short-circuit ratios.
To summarize, there is a substantial body of literature on the suppression of transient overvoltage in power systems. However, research related to the suppression of overvoltage triggered by the high proportion of power electronic devices is comparatively limited. A number of studies have indicated that a reduction in overvoltage can be achieved through the alteration of reactive power control strategies. However, these studies have been limited in their scope, as they have focused exclusively on individual devices rather than on the broader system. The extant literature on the subject is limited, and no analysis has yet been published that looks at the suppression of transient overvoltage in scenarios involving a large number of reactive power sources. The present study aims to address this issue by analyzing the transient voltage characteristics of different reactive power sources. The objective is to optimize the capacity and initial yield of each reactive power source within the system, with the transient overvoltage amplitude set as the optimization target. As demonstrated by example calculations, the proposed collaborative method for multiple reactive power sources has the capacity to effectively suppress transient overvoltage caused by renewable energy sources.
The primary innovations in this study are as follows:
- A transient voltage analysis model for the equivalent sending end of renewable energy was established, leading to a mathematical expression that was devised to demonstrate the amplitude of transient overvoltage caused by AC faults.
- A transient overvoltage optimization model for the new energy transmission end, coordinated with multiple reactive power sources, was established, achieving optimization of reactive power source capacity and initial output configuration.
The organizational structure of this document is as follows: The second section discusses the construction of the equivalent model for new energy sending ends; the third section provides a detailed derivation of the calculation of transient overvoltage at new energy-sending ends. The fourth section establishes a coordinated multi-reactive power source optimization model aimed at suppressing transient overvoltage at new energy sending ends; the fifth section validates and analyzes the proposed method. Finally, a summary of the work conducted in this study is presented.
2. Materials and Methods
2.1. Equivalent Models for New Energy Delivery Systems
To accurately analyze the reactive power exchange process at the converter station as well as the transient overvoltage at the converter bus during DC blocking faults on the renewable energy transmission end, it is necessary to simplify and establish an equivalent model of the actual renewable energy transmission-end system for theoretical analysis.
In Figure 1, Pac and Qac represent the active and reactive power outputs of the renewable energy source, respectively; j denotes an imaginary unit; Bc represents the susceptance value of the capacitor; Qc represents the reactive power supplied by the capacitor; Pd and Qd indicate the active and reactive powers absorbed by the DC system, respectively; Ud and Id are the DC line voltage and current, respectively.

Figure 1.
Equivalent model of renewable energy transmission-end system.
During normal operation of the DC transmission system, a reactive static capacitor power compensator is required to provide reactive power support equal to 0.5 times the transmitted active power. When a DC blocking fault occurs, the converter station is unable to consume the currently higher reactive power and thus feeds it back into the AC system. Let PdN denote the active rated DC power transmitted under normal conditions, and let dQ represent the quantity of reactive power fed from the converter station to the AC system.
- Unipolar closure: dQ = 0.25 .
- Bipolar blocking: dQ = 0.5 PdN.
In accordance with the DC quasi-steady-state model, if we ignore the power losses caused by the converter transformer and other factors, the relationships of various electrical quantities on the inverter side are calculated as follows:
In the formulas, Qac denotes the aggregate reactive power interaction between alternating current (AC) and direct current (DC); Qc is the reactive power produced by the compensation devices at the converter station; Qd is the reactive power consumed by the inverter-side converter; Pd refers to the direct-current transmission power, which corresponds to the total active power that is exchanged between AC and DC; Ud and Id represent the direct current voltage and current, respectively; φ is the power factor angle of the inverter-side converter; Ud0 is the no-load direct-current voltage; k is the transformation ratio of the converter transformer; γ is the commutation angle of the inverter-side converter; X is the equivalent commutation reactance on the inverter side; Bc is the equivalent susceptance of the reactive compensation device.
While a distant fault occurs in the power grid or during high-resistance grounding, the risk of transient voltage instability in the vicinity of the DC drop is negligible. Accordingly, the primary emphasis in this paper is on the analysis of critical faults occurring in the near field to the DC-receiving end. When a near-field fault causes the DC inverter-side converter to experience commutation failure, the upper and lower arms of the converter will conduct, resulting in a rapid drop in the DC voltage Ud. The arms’ instantaneous conduction will cause the DC current to increase rapidly and subsequently fall back to the vicinity of the limiting value under the effect of the VDCOL (Voltage Direct-Current Overload Limitation) mechanism. According to Equation (2), if the DC voltage Ud drops close to 0, the active power of the DC system will essentially be 0. From Equation (3), at this time, the reactive power Qd consumed by the converter is nearly 0. If the DC voltage Ud remains at a certain level, the DC current will cause the converter to consume reactive power. On the AC side, based on Equation (5), due to a significant voltage drop, the reactive power Qc generated by the reactive power devices at the converter station will be diminished to minuscule amounts, possibly even to 0. Therefore, during the commutation failure period under severe near-field faults, the overall reactive power interaction Qac between the AC and DC systems is quite small, primarily depending on the relative magnitudes of the reactive powers Qd and Qc.
2.2. Calculation of Transient Overvoltage of Converter Station Busbars
Assuming the power supply voltage of the AC system is Ue, the voltage drop across the AC-line impedance is divided into transverse voltage drop ∆Ue and longitudinal voltage drop δUe. The calculation formula for the converter bus voltage Up can be expressed as follows:
The expression for the vertical pressure drop is
The expression for the lateral pressure drop component is
In order to simplify the calculations, this study considers neglecting the transverse components with smaller voltage drops. In this case, the expression for the converter station bus voltage is
The above formula represents the calculation expression for the transient overvoltage of the busbar at the converter station when the DC generation is locked. The following will use this expression to construct the safe-operating constraints for transient overvoltage throughout the procedure of the new energy-sending system.
2.3. Optimization Model
2.3.1. Optimization Objective
The sending-end system of new energy includes thermal power units, wind power units, photovoltaic units, and energy storage stations, as well as reactive power compensation equipment such as phase shifters, SVGs, and static reactive power compensators. The present method aims to optimize the economic operation of the sending-end system throughout the year. Let the operating costs per kilowatt-hour of thermal power units, wind power units, photovoltaic units, and energy storage stations be denoted as Cf, Cw, Cp, and Ce, respectively, with their output capacities represented as Pfi, Pwi, Ppi, and Pei.
The expression for calculating the annual operating costs of the system is
In the formula, i represents the i-th hour, where 1 ≤ i ≤ 8760.
2.3.2. Constraints of the Multi-Active Power Source Optimization Model
This section will model various power supply models and reactive power compensation devices, establish relevant constraints, and further refine the multi-reactive source optimization model.
- (1)
- Thermal power unit
In the formula, is the flexibility modification coefficient for the thermal power unit; and represent the total capacity added and reduced by the thermal power unit at time t, respectively; is the total online capacity of the thermal power unit at time t; and are the shortest time intervals between the start-up and shutdown of the thermal power unit, respectively; is the minimum technical output coefficient of the thermal power unit before the flexibility modification; and represent the allowed upward and downward ramping power of thermal power unit I, respectively.
- (2)
- Wind power unit
The output of the wind turbine units must meet the upper and lower limit requirements.
In the equation, represents the upper limit of the power generation capacity of the wind turbine v at time t.
- (3)
- Photovoltaic unit
The output of the photovoltaic power generation unit must meet the upper- and-lower limit requirements.
In the equation, represents the upper limit of the power generation capacity of photovoltaic unit v at time t.
- (4)
- Energy storage unit
The main constraints on energy storage include three equations: energy conservation, upper and lower power limits, and charge–discharge conversion.
In the equation, represents the step size, with a model value of 1 h; is the minimum discharge coefficient set for considering energy storage lifespan, typically taken as 0.1.
- (5)
- Power supply security and consumption guarantee constraint
In the formula, and represent the target rate of electricity wastage and the target rate of electricity shortage, respectively; is the percentage coefficient of the load-shedding power at time t in relation to the maximum load.
- (6)
- Excitation generator output constraint
Capacity constraint:
Terminal voltage stability constraint:
Power angle constraint:
Thermal stability constraint:
Excitation current and electromotive force relationship:
- (7)
- Static var generator (SVG) output constraint
Capacity constraint:
Voltage-reactive power coupling constraint:
Dynamic response constraint:
Operating mode constraint:
- (8)
- Capacitor reactive power compensator
Due to the impact of the voltage magnitude of the reactive power compensation bus generated by the capacitor compensator, which is non-adjustable, the constraints on reactive power output are as follows:
The magnitude of the capacitor’s impedance is represented by Xc in the equation, and Up denotes the amplitude of the converter bus voltage.
- (9)
- Network transmission constraints:
In the equation, and represent the maximum and minimum powers that can be transmitted at grid node n, respectively.
In the equation, represents the voltage value at grid node n during time period t; and are, respectively, the permissible maximum and minimum voltages for the transmission of electrical energy at grid node n.
- (10)
- Transient overvoltage safety constraint
This constraint serves as the core constraint condition in the present method. In accordance with relevant regulations, the transient overvoltage peak value at the new energy delivery end shall not exceed 1.3 times the rated operating value. Therefore, the following constraint expression is provided:
- (11)
- Optimization analysis of steady-state reactive power output
At this point, the present study set up an equivalent simulation model for the new energy sending-end system, derives the expression for the transient overvoltage of the circulating bus, and combines various power output models, multi-reactive power source output models, as well as safety constraints for transient overvoltage to construct a comprehensive collaborative optimization model for multiple reactive power sources aimed at suppressing transient overvoltage in the new energy sending-end system.
Input the annual output data on renewable energy and the relevant parameters of each device into the model. By solving the aforementioned model, the steady-state reactive power output of each reactive source can be obtained:
2.3.3. Algorithm for Solving
The objective function of the model established in this paper is a bi-objective, nonlinear problem, which is addressed by introducing heuristic intelligent algorithms. Considering the solving speed and accuracy of this model, and to enhance the practicality and variability of its algorithms, a genetic algorithm integrated with a tabu search algorithm will be utilized to solve the optimization problem related to integrated energy system planning. The algorithm, along with its specific steps and implementation process, is described below.
- (1)
- Transient overvoltage safety constraint
In the process of genetic algorithms, the fitness function serves as the function for model optimization. In this model, the dual objective functions are to minimize annual investment costs and carbon emissions. To enhance the robustness of the algorithm, a penalty function is introduced, which increases the fitness function for solutions outside the constraints. The formula is as follows:
In the equation, is the penalty factor, and is a function related to inequality constraints. Its value is 0 when the x value is within the constraints; otherwise, the function value is greater than 0. Similarly, this applies to the equality constraint function of ; f(x) is the objective function; represents the model results.
- (2)
- Crossover operator
The essence of the crossover operator is the process of taking a segment of one chromosome and performing crossover exchange with segments from other chromosomes to form two new chromosomes. Through crossover, the search capability of the genetic algorithm is significantly enhanced.
- (3)
- TSM operator
In the newly improved algorithm, the TSM operator replaces the mutation operator originally used in the genetic algorithm with a tabu search algorithm, which is referred to as the TSM operator.
- (3-1) For each chromosome, by assessing the magnitude of its randomly generated number against the mutation probability, if mutation is necessary, the chromosome should be used as the initial value for the tabu search algorithm.
- (3-2) Set the length of the tabu list, define the movement rules and candidate solution set, provide the aspiration level, and determine whether the stopping criterion for the tabu search has been met. If so, return to step (3-1); otherwise, perform neighborhood search based on the strategy of tabu search, select a solution, and update the tabu list.
- (3-3) Proceed to the next step with the updated population.
- (4)
- Selection operator
The selecting operators choose the superior individuals to be passed on to the next generation using the formula as follows:
In the equation, represents the probability of an individual being selected; m denotes the population size; refers to the fitness of individual i.
Genetic algorithms seek optimal solutions through three genetic operators: selection, crossover, and mutation. As global search algorithms, they may not always yield the absolute optimal point due to certain limitations; however, the results are generally close to the optimal point, thus providing a satisfactory initial solution. Therefore, by embedding a tabu search algorithm, which has strong local search capabilities, into the genetic algorithm’s solving process, the tabu search algorithm can be converted into a mutation operator to enhance the local search capability of the genetic algorithm during global optimization.
3. Results
For the IEEE 39-node test system (Figure 2), the load at node 4 is converted to direct-current (DC) transmission power, making node 4 the DC converter bus. The DC power delivered by node 4 is 2000 MVA, the power loads at other nodes are adjusted accordingly, while all other parameters remain unchanged from the original parameters of the IEEE 9-node system. Relevant code was written via MATLAB 2025a platform and solved with the commercial software GUROBI 12.0.0.
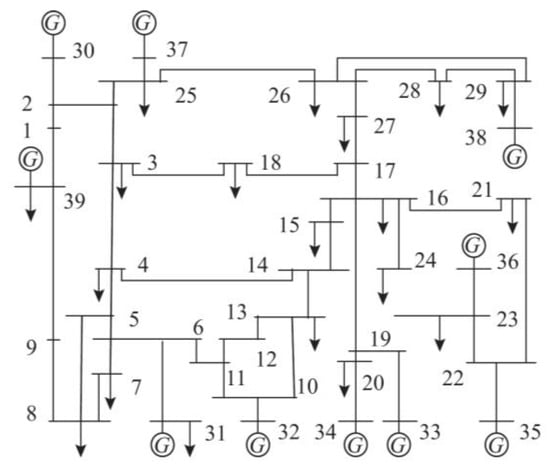
Figure 2.
Example topology.
According to the reactive power planning model proposed in this article, the reactive power planning results for a converter station configured with both capacitor bank (CB) and synchronous compensators, as well as for a configuration with only synchronous compensators, are shown in Table 1. Under the scheme that includes both capacitors and synchronous compensators, the optimal reactive power capacity of the capacitors is approximately 257 Mvar, while the optimal rated capacity of the synchronous compensators is about 432 Mvar, leading to an investment cost of CNY 85.47 million for reactive power devices. Conversely, under the scheme that includes only synchronous compensators (SC), the optimal rated capacity is 753 Mvar, resulting in a significantly higher investment cost of up to CNY 135.54 million. Based on the aforementioned reactive power planning results, the effective values of the transient voltages at the DC blocking moment for the converter bus were obtained using the proposed computational method based on secondary transient flow and electromagnetic transient simulation, as shown in Table 2. Additionally, Figure 3 illustrates the variation in the effective values of the line voltages at the converter bus for the IEEE 39-bus test system.

Table 1.
Results of reactive power planning.

Table 2.
Comparative analysis of transient voltage at converter bus.

Figure 3.
Transient voltage profiles with different reactive power sources.
At the same time, the computational results and the calculation time obtained by the joint time-domain simulation method are compared with the results of the method proposed in this paper, as shown in Table 3.

Table 3.
Comparative analysis of reactive power planning results.
According to Figure 3, it can be observed that the configuration mode in scenario 3 demonstrates the best suppression effect of transient overvoltage when only a phase-shifting device is configured. This is attributed to the fact that the reactive power emitted by the capacitor is proportional to the square of the voltage. The amplitude of the voltage and the reactive power generated by the capacitor mutually reinforce each other, leading to a detrimental impact on voltage stability.
Table 1 presents the planning results for the phase-shifting device and capacitors. In the case where SVG, synchronous phase-shifting devices, and capacitors coexist, the planning results obtained through this method are as shown in Table 4.

Table 4.
Reactive power source capacity allocation results.
In order to suppress the amplitude of transient overvoltage during system failures, it is necessary to reasonably allocate the initial outputs of each reactive power source. The initial outputs of each reactive power source after applying the optimization method presented in this paper, as well as the output curves during the transient process, are illustrated in the figure below.
According to Figure 4, before the fault occurs, each reactive power source outputs a constant reactive power, with the initial reactive power of the SVG, SVC, and capacitors being 321.2, 281.2, and 121.5 MVar, respectively. During an AC fault, the voltage experiences a process of first decreasing and then increasing. In the voltage drop phase, the reactive power generated by the SVG and SC rapidly increases to support the voltage, while the capacitors do not generate reactive power due to the voltage dropping to zero. In the subsequent voltage recovery phase following the fault, the reactive power generated by the SVG and SC gradually decreases to prevent the system voltage from becoming excessively high, while the reactive power generated by the capacitors also gradually recovers to its pre-fault level. In the following process, the reactive power output from each source progressively stabilizes.
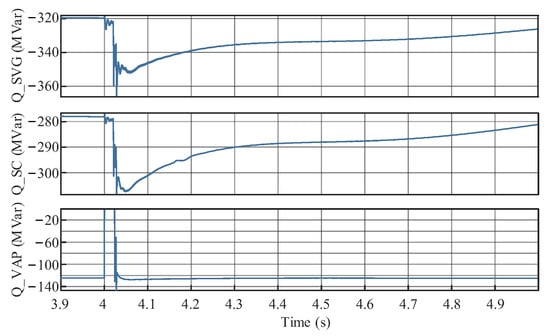
Figure 4.
Reactive power output curve.
According to the transient voltage curves before and after optimization in Figure 5, the use of the multi-reactive power source coordination method proposed in this paper effectively suppresses the transient overvoltage’s peak value, demonstrating the effectiveness of the method presented herein.

Figure 5.
Voltage transient characteristics before and after optimization.
To further verify the correctness of the method proposed in this paper, three-phase faults were set up at node 13 for overvoltage analysis. The transient voltage curves before and after the reactive power source optimization configuration are shown in Figure 6. The optimized transient overvoltage has been effectively suppressed. In addition, the maximum voltage drop after optimization is smaller than before optimization, which helps to improve the degree of voltage sag in faults. Therefore, the multi-reactive power source coordination and optimization method proposed in this paper can not only effectively improve transient overvoltage but also achieve voltage quality improvement through dynamic reactive power regulation.

Figure 6.
Transient overvoltage curve and reactive power output.
4. Discussion
The suppression of transient overvoltage has been achieved through the multi-reactive power source optimization configuration method proposed in this paper. The configuration principle of multiple reactive power sources is as follows: reactive power sources with slow regulation speed and large capacity can be configured for steady-state reactive voltage support, while those with slow regulation speed and small capacity can be used for transient voltage support. The mutual cooperation of the two can achieve long-term voltage stability in a system.
5. Conclusions
By establishing a dynamic response-matching model for SVG, CB, and SC, a hierarchical control architecture triggered by events is proposed. The SVG prioritizes responses to high-frequency voltage fluctuations within 5 ms, and the phase-shifting compensator achieves medium-frequency reactive power compensation at a 50 ms level through improved excitation control. The capacitor banks utilize a preset switching strategy for second-level adjustments. Simulation results indicate that this method reduces the transient overvoltage peak by 23% (from 1.35 to 1.05 pu), shortens the voltage recovery time to 0.8 s, enhances dynamic response efficiency by 40% compared to traditional strategies, and improves equipment utilization by 18%. The reactive power optimization method proposed in this paper can achieve the suppression of overvoltage generated in a grid connected to new energy with DC access. In weak power grids, this method can effectively enhance the safety level of transient voltage and contribute to reliable power supply in the grid.
A new energy inverter adaptive voltage-reactive power (V/Q) curve reconstruction technology has been developed, which dynamically relaxes the PQ operating boundaries during sudden voltage surges. Combined with a current phase angle optimization algorithm, this technology increases the upper limit of reactive power output by 35% (from 0.4 to 0.54 pu).
A three-level coordination mechanism of “transient—dynamic—stable” has been established, which is applicable to power grids of different structures. The static reactive power generator (SVG) and SC are combined to suppress the initial impact, the new energy unit participates in the mid-term dynamic regulation, and the capacitor bank realizes the precise control of the steady-state voltage.
Author Contributions
Conceptualization, Q.Z. and L.L.; methodology, X.W.; software, H.L.; validation, H.L. and Z.L.; formal analysis, D.Z.; investigation, L.L.; resources, Y.Q. and Z.L.; data curation, X.W.; writing—original draft preparation, Q.Z. and D.Z.; writing—review and editing, D.Z.; visualization, H.L.; supervision, Z.L.; project administration, Z.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by State Grid Shaanxi Electric Power Co., Ltd., grant number (SGSN0000DKJS2404793).
Data Availability Statement
The data presented in this study will be available when required.
Conflicts of Interest
Authors Qinglei Zhang, Lei Luo, and Xiaoping Wang were employed by State Grid Shaanxi Electric Power Co., LTD. Authors Dehai Zhang, Haibo Li, Zongxiang Lu, and Ying Qiao were employed by the Sichuan Energy Internet Research Institute, Tsinghua University. The funders had no role in the study design, data collection or analysis, decision to publish, or preparation of this manuscript.
References
- Ghoddami, H.; Yazdani, A. A Mitigation Strategy for Temporary Overvoltage Caused by Grid-Connected Photovoltaic Systems. IEEE Trans. Energy Convers. 2015, 30, 413–420. [Google Scholar] [CrossRef]
- Ibrahim, T.; Rubira, T.T.D.; Rosso, A.D.; Patel, M.; Guggilam, S.; Mohamed, A.A. Alternating Optimization Approach for Voltage-Secure Multi-Period Optimal Reactive Power Dispatch. IEEE Trans. Power Syst. 2022, 37, 3805–3816. [Google Scholar] [CrossRef]
- Chen, L.; Deng, Z.; Xu, X. Two-Stage Dynamic Reactive Power Dispatch Strategy in Distribution Network Considering the Reactive Power Regulation of Distributed Generations. IEEE Trans. Power Syst. 2019, 34, 1021–1032. [Google Scholar] [CrossRef]
- Liu, J.H.; Cheng, J.S. Online Voltage Security Enhancement Using Voltage Sensitivity-Based Coherent Reactive Power Control in Multi-Area Wind Power Generation Systems. IEEE Trans. Power Syst. 2021, 36, 2729–2732. [Google Scholar] [CrossRef]
- Li, Z.; Zhao, F.; Munk-Nielsen, S.; Geske, M.; Wang, X. Analysis and Mitigation of Transient Overvoltage and Voltage Imbalance in Submodule Capacitors for MMC-Based Grid Emulators. IEEE J. Emerg. Sel. Top. Power Electron. 2024, 12, 5735–5749. [Google Scholar] [CrossRef]
- Wang, Q.; Yao, L.; Xu, J.; Zheng, Y.; Li, W.; Wang, W. Steady-state Voltage Security-constrained Optimal Frequency Control for Weak HVDC Sending-end AC Power Systems. J. Mod. Power Syst. Clean Energy 2024, 12, 658–669. [Google Scholar] [CrossRef]
- Liu, X.; Huang, J.; Zheng, D.; Xin, H.; Bi, T. Analysis and Suppression for Temporary Overvoltage Considering Dynamic Interactions Between LCC-HVDC and Renewable Energy Plants. IEEE Trans. Sustain. Energy 2025, 16, 1849–1859. [Google Scholar] [CrossRef]
- Ding, T.; Liu, S.; Yuan, W.; Bie, Z.; Zeng, B. A Two-Stage Robust Reactive Power Optimization Considering Uncertain Wind Power Integration in Active Distribution Networks. IEEE Trans. Sustain. Energy 2016, 7, 301–311. [Google Scholar] [CrossRef]
- Yin, C.; Li, F. Reactive power control strategy for inhibiting transient overvoltage caused by commutation failure. IEEE Trans. Power Syst. 2021, 36, 4764–4777. [Google Scholar] [CrossRef]
- Pei, L.; Wang, T.; Wang, J.; Wang, Z. Transient overvoltage analysis of wind farm PCC caused by HVDC commutation failure under different faults. In Proceedings of the 2021 IEEE/IAS Industrial & Commercial Power System Asia, Chengdu, China, 18–21 July 2021. [Google Scholar]
- Xue, A.; Yue, L.; Zhang, J.H.; Cui, J.H. A new quantitative analysis method for overvoltage in sending end electric power system with UHVDC. IEEE Access 2020, 8, 145898–145908. [Google Scholar] [CrossRef]
- Xiao, H.; Duan, X.; Zhang, Y.; Li, Y. Analytically assessing the effect of strength on temporary overvoltage in hybrid multi-infeed HVDC systems. IEEE Trans. Power Electron. 2022, 37, 2480–2484. [Google Scholar] [CrossRef]
- Xie, Q.; Zheng, Z.; Xiao, X.; Huang, C.; Zheng, J.; Ren, J. Enhancing HVRT capability of DFIG-based wind farms using cooperative rotor-side SMES considering the blocking fault of LCC-HVDC system. CSEE J. Power Energy Syst. 2021, 7, 698–707. [Google Scholar]
- Yin, C.; Li, F. Analytical expression on transient overvoltage peak value of converter bus caused by DC faults. IEEE Trans. Power Syst. 2021, 36, 2741–2744. [Google Scholar] [CrossRef]
- Kim, Y.K.; Lee, G.S.; Kim, C.K.; Moon, S.I. An improved AC system strength measure for evaluation of power stability and temporary overvoltage in hybrid multi-infeed HVDC systems. IEEE Trans. Power Del. 2022, 37, 638–649. [Google Scholar] [CrossRef]
- Feng, N.; Feng, Y.; Su, Y.; Zhang, Y.; Niu, T. Dynamic Reactive Power Optimization Strategy for AC/DC Hybrid Power Grid Considering Different Wind Power Penetration Levels. IEEE Access 2024, 12, 187471–187482. [Google Scholar] [CrossRef]
- Miao, Y.; Cheng, H. An Optimal Reactive Power Control Strategy for UHVAC/DC Hybrid System in East China Grid. IEEE Trans. Smart Grid 2016, 7, 392–399. [Google Scholar] [CrossRef]
- Linlin, Y.; Lihua, Z.; Gaojun, M.; Feng, Z.; Wanxun, L. Research on Multi-Objective Reactive Power Optimization of Power Grid With High Proportion of New Energy. IEEE Access 2022, 10, 116443–116452. [Google Scholar] [CrossRef]
- Li, Y.; Guo, P.; Zhuang, W.; Li, Z.; Huo, C.; Zhang, J.; Yue, L.; Xue, A. A Dynamic Reactive Power Allocation Method for Sending-End Power System of the UHVDC Delivering Large Terminal of Renewable Energy. Math. Probl. Eng. 2023, 1, 9764844. [Google Scholar] [CrossRef]
- Xue, S.; Zeng, S.; Jia, Q.; Hu, X. Collaborative Optimization Allocation of Grid-Forming and Grid-Following Reactive Power Resources Considering Auxiliary Equipment Services. IEEE Access 2023, 11, 95840–95857. [Google Scholar] [CrossRef]
- Sun, S.; Yuan, Z.; Chen, D.; Li, Z.; Tang, X.; Song, Y.; Zhou, G. Research on Coordinated Control of Dynamic Reactive Power Sources of DC Blocking and Commutation Failure Transient Overvoltage in New Energy Transmission. Energies 2025, 18, 2349. [Google Scholar] [CrossRef]
- Chi, Y.; Tao, A.; Xu, X.; Wang, Q.; Zhou, N. An Adaptive Many-Objective Robust Optimization Model of Dynamic Reactive Power Sources for Voltage Stability Enhancement. J. Mod. Power Syst. Clean Energy 2023, 11, 1756–1769. [Google Scholar] [CrossRef]
- Ding, T.; Yang, Q.; Yang, Y.; Li, C.; Bie, Z.; Blaabjerg, F. A Data-Driven Stochastic Reactive Power Optimization Considering Uncertainties in Active Distribution Networks and Decomposition Method. IEEE Trans. Smart Grid 2018, 9, 4994–5004. [Google Scholar] [CrossRef]
- Pang, B.; Jin, X.; Zhang, Q.; Tang, Y.; Liao, K.; Yang, J.; He, Z. Transient ac overvoltage suppression orientated reactive power control of the wind turbine in the LCC-HVDC sending grid. CES Trans. Electr. Mach. Syst. 2024, 2, 152–161. [Google Scholar] [CrossRef]
- Tian, X.; Wu, S.; Wei, L.; Zhang, L.; Wang, N.; Zheng, Q. Analytical Analysis of The Mechanism and Mitigation Methods of Transient Overvoltage in Direct-Drive Wind Turbine Generators Connected to Weak Power System. IEEE Access 2025, 13, 23768–23781. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).