Skyrmion Crystal in Bilinear–Biquadratic–Bicubic Model on a Centrosymmetric Triangular Lattice
Abstract
1. Introduction
2. Model and Methods
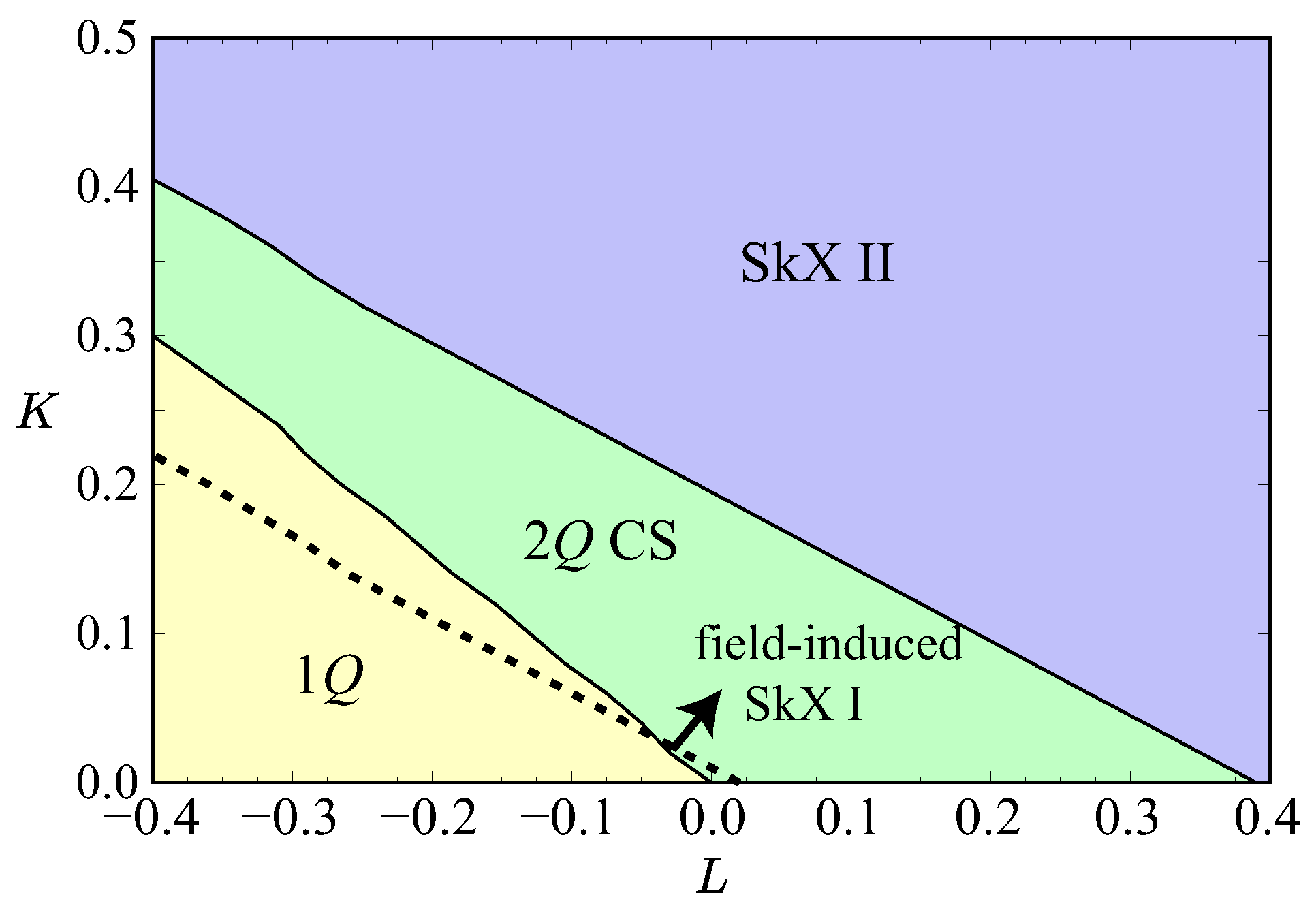
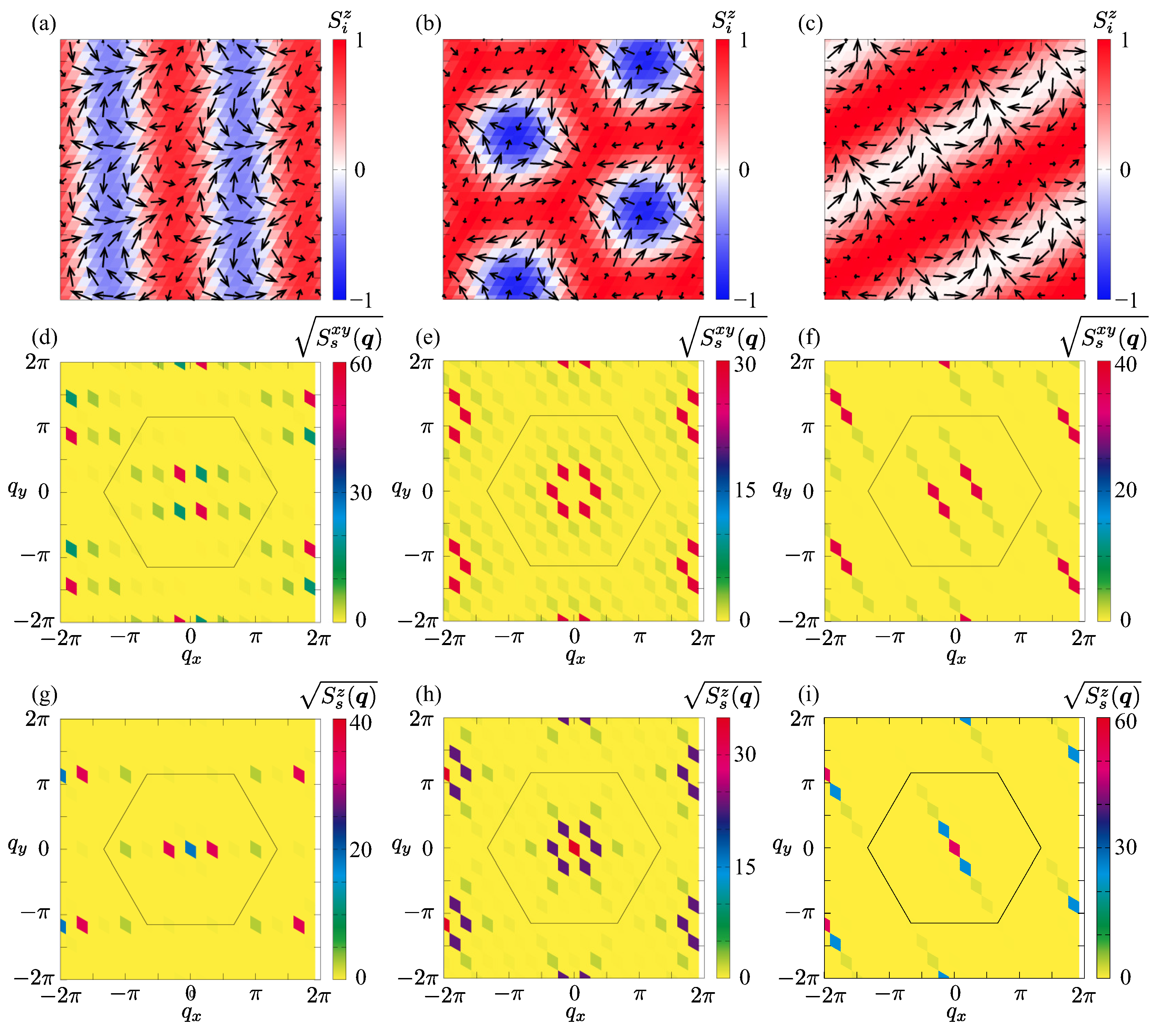
3. Results
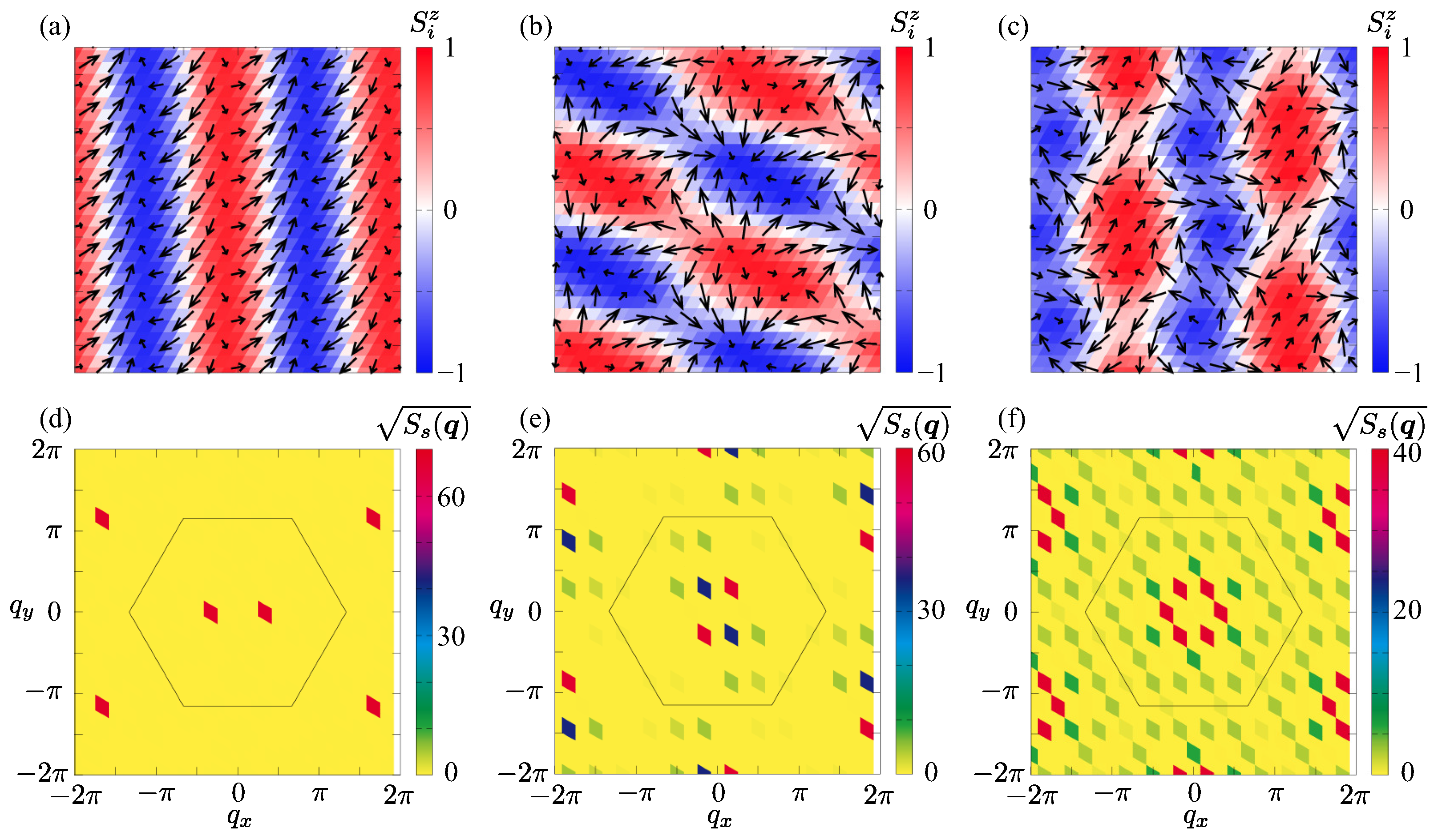
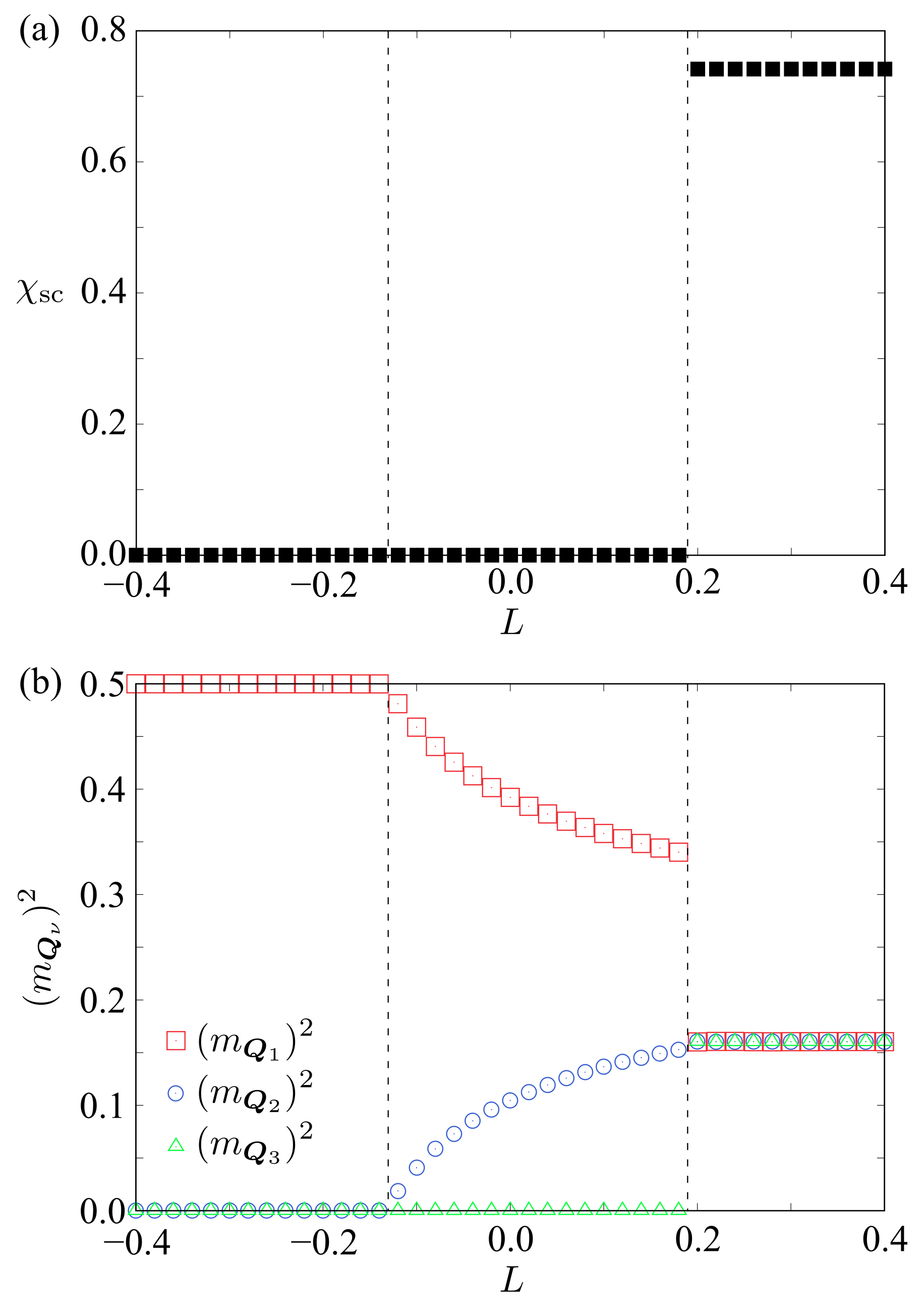
3.1. Zero Magnetic Field
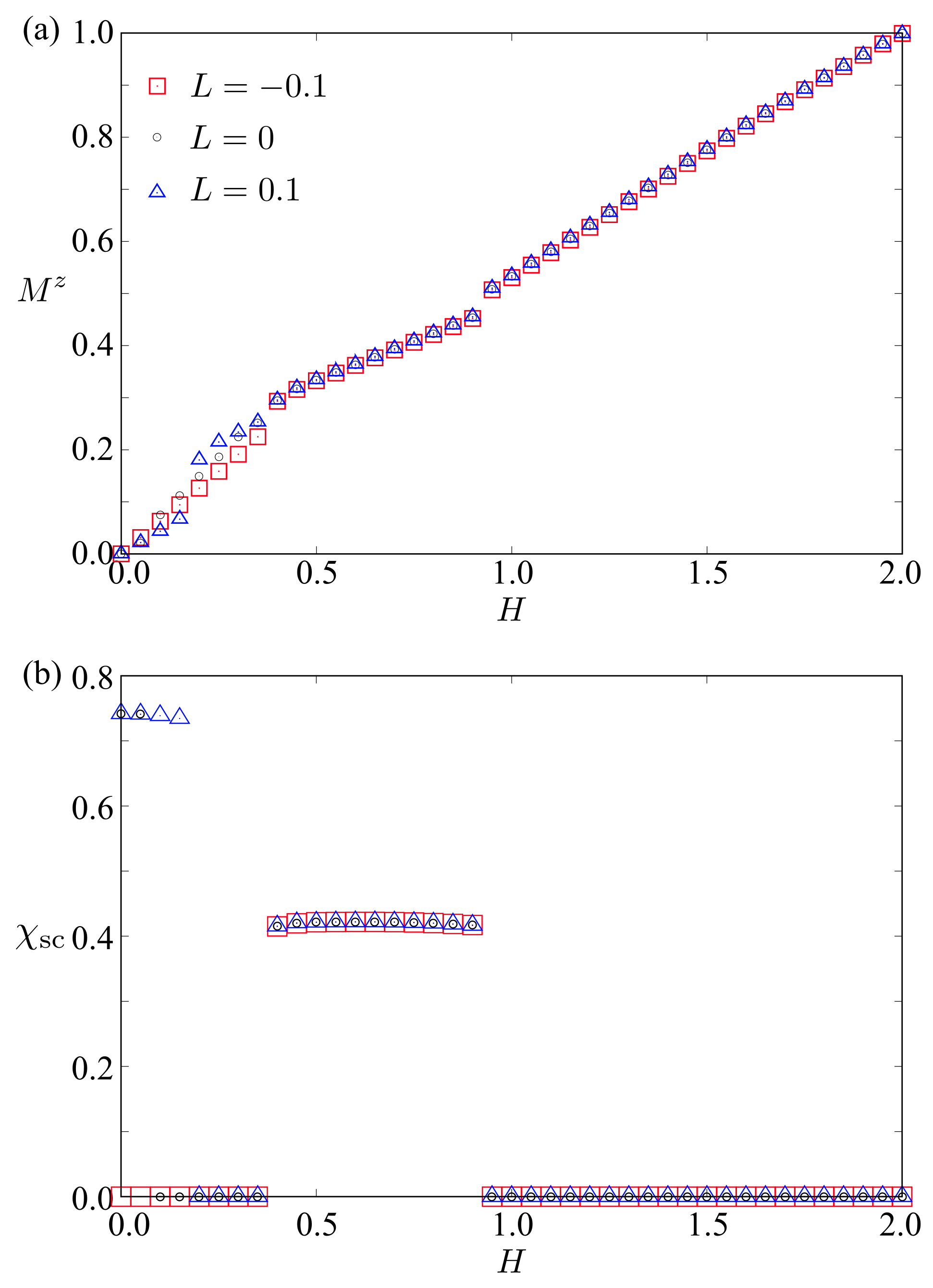
3.2. Finite Magnetic Fields
4. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Peierls, R.E. Quantum Theory of Solids; Number 23; Oxford University Press: Oxford, UK, 1955. [Google Scholar]
- Grüner, G. The dynamics of charge-density waves. Rev. Mod. Phys. 1988, 60, 1129–1181. [Google Scholar] [CrossRef]
- Grüner, G. The dynamics of spin-density waves. Rev. Mod. Phys. 1994, 66, 1–24. [Google Scholar] [CrossRef]
- Bak, P.; Lebech, B. “Triple-” Modulated Magnetic Structure and Critical Behavior of Neodymium. Phys. Rev. Lett. 1978, 40, 800–803. [Google Scholar] [CrossRef]
- McEwen, K.A.; Walker, M.B. Free-energy analysis of the single-q and double-q magnetic structures of neodymium. Phys. Rev. B 1986, 34, 1781–1783. [Google Scholar] [CrossRef] [PubMed]
- Zochowski, S.; McEwen, K. Thermal expansion study of the magnetic phase diagram of neodymium. J. Magn. Magn. Mater. 1986, 54, 515–516. [Google Scholar] [CrossRef]
- Forgan, E.; Rainford, B.; Lee, S.; Abell, J.; Bi, Y. The magnetic structure of CeAl2 is a non-chiral spiral. J. Phys. Condens. Matter 1990, 2, 10211. [Google Scholar] [CrossRef]
- Longfield, M.J.; Paixão, J.A.; Bernhoeft, N.; Lander, G.H. Resonant X-ray scattering from multi-k magnetic structures. Phys. Rev. B 2002, 66, 054417. [Google Scholar] [CrossRef]
- Bernhoeft, N.; Paixão, J.A.; Detlefs, C.; Wilkins, S.B.; Javorský, P.; Blackburn, E.; Lander, G.H. Resonant X-ray scattering from UAs0.8Se0.2: Multi-k configurations. Phys. Rev. B 2004, 69, 174415. [Google Scholar] [CrossRef]
- Stewart, J.; Ehlers, G.; Wills, A.; Bramwell, S.T.; Gardner, J. Phase transitions, partial disorder and multi-k structures in Gd2Ti2O7. J. Phys. Condens. Matter 2004, 16, L321. [Google Scholar] [CrossRef]
- Watson, D.; Forgan, E.M.; Nuttall, W.J.; Stirling, W.G.; Fort, D. High-resolution magnetic X-ray diffraction from neodymium. Phys. Rev. B 1996, 53, 726–730. [Google Scholar] [CrossRef] [PubMed]
- Harris, A.B.; Schweizer, J. Theoretical analysis of the double-q magnetic structure of CeAl2. Phys. Rev. B 2006, 74, 134411. [Google Scholar] [CrossRef]
- Martin, I.; Batista, C.D. Itinerant Electron-Driven Chiral Magnetic Ordering and Spontaneous Quantum Hall Effect in Triangular Lattice Models. Phys. Rev. Lett. 2008, 101, 156402. [Google Scholar] [CrossRef] [PubMed]
- Chern, G.W. Noncoplanar Magnetic Ordering Driven by Itinerant Electrons on the Pyrochlore Lattice. Phys. Rev. Lett. 2010, 105, 226403. [Google Scholar] [CrossRef] [PubMed]
- Venderbos, J.W.F.; Daghofer, M.; van den Brink, J.; Kumar, S. Switchable Quantum Anomalous Hall State in a Strongly Frustrated Lattice Magnet. Phys. Rev. Lett. 2012, 109, 166405. [Google Scholar] [CrossRef] [PubMed]
- Barros, K.; Venderbos, J.W.F.; Chern, G.W.; Batista, C.D. Exotic magnetic orderings in the kagome Kondo-lattice model. Phys. Rev. B 2014, 90, 245119. [Google Scholar] [CrossRef]
- Ghosh, S.; O’Brien, P.; Henley, C.L.; Lawler, M.J. Phase diagram of the Kondo lattice model on the kagome lattice. Phys. Rev. B 2016, 93, 024401. [Google Scholar] [CrossRef]
- Jiang, K.; Zhang, Y.; Zhou, S.; Wang, Z. Chiral Spin Density Wave Order on the Frustrated Honeycomb and Bilayer Triangle Lattice Hubbard Model at Half-Filling. Phys. Rev. Lett. 2015, 114, 216402. [Google Scholar] [CrossRef] [PubMed]
- Venderbos, J.W.F. Multi-Q hexagonal spin density waves and dynamically generated spin-orbit coupling: Time-reversal invariant analog of the chiral spin density wave. Phys. Rev. B 2016, 93, 115108. [Google Scholar] [CrossRef]
- Shahzad, M.; Sengupta, P. Noncollinear magnetic ordering in a frustrated magnet: Metallic regime and the role of frustration. Phys. Rev. B 2017, 96, 224402. [Google Scholar] [CrossRef]
- Akagi, Y.; Udagawa, M.; Motome, Y. Hidden Multiple-Spin Interactions as an Origin of Spin Scalar Chiral Order in Frustrated Kondo Lattice Models. Phys. Rev. Lett. 2012, 108, 096401. [Google Scholar] [CrossRef]
- Hayami, S.; Motome, Y. Multiple-Q instability by (d-2)-dimensional connections of Fermi surfaces. Phys. Rev. B 2014, 90, 060402(R). [Google Scholar] [CrossRef]
- Hayami, S.; Ozawa, R.; Motome, Y. Effective bilinear-biquadratic model for noncoplanar ordering in itinerant magnets. Phys. Rev. B 2017, 95, 224424. [Google Scholar] [CrossRef]
- Hayami, S.; Okubo, T.; Motome, Y. Phase shift in skyrmion crystals. Nat. Commun. 2021, 12, 6927. [Google Scholar] [CrossRef] [PubMed]
- Tokura, Y.; Yasuda, K.; Tsukazaki, A. Magnetic topological insulators. Nat. Rev. Phys. 2019, 1, 126–143. [Google Scholar] [CrossRef]
- Bernevig, B.A.; Felser, C.; Beidenkopf, H. Progress and prospects in magnetic topological materials. Nature 2022, 603, 41–51. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Y.; Li, S.; Liang, X.; Zhou, Y. Topological spin textures: Basic physics and devices. Adv. Mater. 2025, 37, 2312935. [Google Scholar] [CrossRef] [PubMed]
- Bogdanov, A.N.; Yablonskii, D.A. Thermodynamically stable “vortices” in magnetically ordered crystals: The mixed state of magnets. Sov. Phys. J. Exp. Theor. Phys. 1989, 68, 101. [Google Scholar]
- Bogdanov, A.; Hubert, A. Thermodynamically stable magnetic vortex states in magnetic crystals. J. Magn. Magn. Mater. 1994, 138, 255–269. [Google Scholar] [CrossRef]
- Rößler, U.K.; Bogdanov, A.N.; Pfleiderer, C. Spontaneous skyrmion ground states in magnetic metals. Nature 2006, 442, 797–801. [Google Scholar] [CrossRef] [PubMed]
- Nagaosa, N.; Tokura, Y. Topological properties and dynamics of magnetic skyrmions. Nat. Nanotechnol. 2013, 8, 899–911. [Google Scholar] [CrossRef] [PubMed]
- Loss, D.; Goldbart, P.M. Persistent currents from Berry’s phase in mesoscopic systems. Phys. Rev. B 1992, 45, 13544–13561. [Google Scholar] [CrossRef]
- Ye, J.; Kim, Y.B.; Millis, A.J.; Shraiman, B.I.; Majumdar, P.; Tešanović, Z. Berry Phase Theory of the Anomalous Hall Effect: Application to Colossal Magnetoresistance Manganites. Phys. Rev. Lett. 1999, 83, 3737–3740. [Google Scholar] [CrossRef]
- Ohgushi, K.; Murakami, S.; Nagaosa, N. Spin anisotropy and quantum Hall effect in the kagomé lattice: Chiral spin state based on a ferromagnet. Phys. Rev. B 2000, 62, R6065–R6068. [Google Scholar] [CrossRef]
- Taguchi, Y.; Oohara, Y.; Yoshizawa, H.; Nagaosa, N.; Tokura, Y. Spin chirality, Berry phase, and anomalous Hall effect in a frustrated ferromagnet. Science 2001, 291, 2573–2576. [Google Scholar] [CrossRef] [PubMed]
- Tatara, G.; Kawamura, H. Chirality-driven anomalous Hall effect in weak coupling regime. J. Phys. Soc. Jpn. 2002, 71, 2613–2616. [Google Scholar] [CrossRef]
- Machida, Y.; Nakatsuji, S.; Maeno, Y.; Tayama, T.; Sakakibara, T.; Onoda, S. Unconventional anomalous Hall effect enhanced by a noncoplanar spin texture in the frustrated Kondo lattice Pr2Ir2O7. Phys. Rev. Lett. 2007, 98, 057203. [Google Scholar] [CrossRef] [PubMed]
- Neubauer, A.; Pfleiderer, C.; Binz, B.; Rosch, A.; Ritz, R.; Niklowitz, P.G.; Böni, P. Topological Hall Effect in the A Phase of MnSi. Phys. Rev. Lett. 2009, 102, 186602. [Google Scholar] [CrossRef] [PubMed]
- Takatsu, H.; Yonezawa, S.; Fujimoto, S.; Maeno, Y. Unconventional anomalous Hall effect in the metallic triangular-lattice magnet PdCrO2. Phys. Rev. Lett. 2010, 105, 137201. [Google Scholar] [CrossRef] [PubMed]
- Ueland, B.; Miclea, C.; Kato, Y.; Ayala-Valenzuela, O.; McDonald, R.; Okazaki, R.; Tobash, P.; Torrez, M.; Ronning, F.; Movshovich, R.; et al. Controllable chirality-induced geometrical Hall effect in a frustrated highly correlated metal. Nat. Commun. 2012, 3, 1067. [Google Scholar] [CrossRef] [PubMed]
- Hamamoto, K.; Ezawa, M.; Nagaosa, N. Quantized topological Hall effect in skyrmion crystal. Phys. Rev. B 2015, 92, 115417. [Google Scholar] [CrossRef]
- Nakazawa, K.; Bibes, M.; Kohno, H. Topological Hall effect from strong to weak coupling. J. Phys. Soc. Jpn. 2018, 87, 033705. [Google Scholar] [CrossRef]
- Matsui, A.; Nomoto, T.; Arita, R. Skyrmion-size dependence of the topological Hall effect: A real-space calculation. Phys. Rev. B 2021, 104, 174432. [Google Scholar] [CrossRef]
- Gao, S.; Zaharko, O.; Tsurkan, V.; Su, Y.; White, J.S.; Tucker, G.S.; Roessli, B.; Bourdarot, F.; Sibille, R.; Chernyshov, D.; et al. Spiral spin-liquid and the emergence of a vortex-like state in MnSc2S4. Nat. Phys. 2017, 13, 157–161. [Google Scholar] [CrossRef]
- Gao, S.; Rosales, H.D.; Albarracín, F.A.G.; Tsurkan, V.; Kaur, G.; Fennell, T.; Steffens, P.; Boehm, M.; Čermák, P.; Schneidewind, A.; et al. Fractional antiferromagnetic skyrmion lattice induced by anisotropic couplings. Nature 2020, 586, 37–41. [Google Scholar] [CrossRef] [PubMed]
- Saha, S.R.; Sugawara, H.; Matsuda, T.D.; Sato, H.; Mallik, R.; Sampathkumaran, E.V. Magnetic anisotropy, first-order-like metamagnetic transitions, and large negative magnetoresistance in single-crystal Gd2PdSi3. Phys. Rev. B 1999, 60, 12162–12165. [Google Scholar] [CrossRef]
- Kurumaji, T.; Nakajima, T.; Hirschberger, M.; Kikkawa, A.; Yamasaki, Y.; Sagayama, H.; Nakao, H.; Taguchi, Y.; Arima, T.h.; Tokura, Y. Skyrmion lattice with a giant topological Hall effect in a frustrated triangular-lattice magnet. Science 2019, 365, 914–918. [Google Scholar] [CrossRef] [PubMed]
- Hirschberger, M.; Spitz, L.; Nomoto, T.; Kurumaji, T.; Gao, S.; Masell, J.; Nakajima, T.; Kikkawa, A.; Yamasaki, Y.; Sagayama, H.; et al. Topological Nernst Effect of the Two-Dimensional Skyrmion Lattice. Phys. Rev. Lett. 2020, 125, 076602. [Google Scholar] [CrossRef] [PubMed]
- Kumar, R.; Iyer, K.K.; Paulose, P.L.; Sampathkumaran, E.V. Magnetic and transport anomalies in R2RhSi3 (R = Gd, Tb, and Dy) resembling those of the exotic magnetic material Gd2PdSi3. Phys. Rev. B 2020, 101, 144440. [Google Scholar] [CrossRef]
- Spachmann, S.; Elghandour, A.; Frontzek, M.; Löser, W.; Klingeler, R. Magnetoelastic coupling and phases in the skyrmion lattice magnet Gd2PdSi3 discovered by high-resolution dilatometry. Phys. Rev. B 2021, 103, 184424. [Google Scholar] [CrossRef]
- Nakamura, S.; Kabeya, N.; Kobayashi, M.; Araki, K.; Katoh, K.; Ochiai, A. Spin trimer formation in the metallic compound Gd3Ru4Al12 with a distorted kagome lattice structure. Phys. Rev. B 2018, 98, 054410. [Google Scholar] [CrossRef]
- Hirschberger, M.; Nakajima, T.; Gao, S.; Peng, L.; Kikkawa, A.; Kurumaji, T.; Kriener, M.; Yamasaki, Y.; Sagayama, H.; Nakao, H.; et al. Skyrmion phase and competing magnetic orders on a breathing kagome lattice. Nat. Commun. 2019, 10, 5831. [Google Scholar] [CrossRef] [PubMed]
- Hirschberger, M.; Hayami, S.; Tokura, Y. Nanometric skyrmion lattice from anisotropic exchange interactions in a centrosymmetric host. New J. Phys. 2021, 23, 023039. [Google Scholar] [CrossRef]
- Nakamura, S. Magnetic anisotropies and skyrmion lattice related to magnetic quadrupole interactions of the RKKY mechanism in the frustrated spin-trimer system Gd3Ru4Al12 with a breathing kagome structure. Phys. Rev. B 2025, 111, 184433. [Google Scholar] [CrossRef]
- Khanh, N.D.; Nakajima, T.; Yu, X.; Gao, S.; Shibata, K.; Hirschberger, M.; Yamasaki, Y.; Sagayama, H.; Nakao, H.; Peng, L.; et al. Nanometric square skyrmion lattice in a centrosymmetric tetragonal magnet. Nat. Nanotechnol. 2020, 15, 444. [Google Scholar] [CrossRef] [PubMed]
- Khanh, N.D.; Nakajima, T.; Hayami, S.; Gao, S.; Yamasaki, Y.; Sagayama, H.; Nakao, H.; Takagi, R.; Motome, Y.; Tokura, Y.; et al. Zoology of Multiple-Q Spin Textures in a Centrosymmetric Tetragonal Magnet with Itinerant Electrons. Adv. Sci. 2022, 9, 2105452. [Google Scholar] [CrossRef] [PubMed]
- Matsuyama, N.; Nomura, T.; Imajo, S.; Nomoto, T.; Arita, R.; Sudo, K.; Kimata, M.; Khanh, N.D.; Takagi, R.; Tokura, Y.; et al. Quantum oscillations in the centrosymmetric skyrmion-hosting magnet GdRu2Si2. Phys. Rev. B 2023, 107, 104421. [Google Scholar] [CrossRef]
- Wood, G.D.A.; Khalyavin, D.D.; Mayoh, D.A.; Bouaziz, J.; Hall, A.E.; Holt, S.J.R.; Orlandi, F.; Manuel, P.; Blügel, S.; Staunton, J.B.; et al. Double-Q ground state with topological charge stripes in the centrosymmetric skyrmion candidate GdRu2Si2. Phys. Rev. B 2023, 107, L180402. [Google Scholar] [CrossRef]
- Eremeev, S.; Glazkova, D.; Poelchen, G.; Kraiker, A.; Ali, K.; Tarasov, A.V.; Schulz, S.; Kliemt, K.; Chulkov, E.V.; Stolyarov, V.; et al. Insight into the electronic structure of the centrosymmetric skyrmion magnet GdRu2Si2. Nanoscale Adv. 2023, 5, 6678–6687. [Google Scholar] [CrossRef] [PubMed]
- Nomoto, T.; Arita, R. Ab initio exploration of short-pitch skyrmion materials: Role of orbital frustration. J. Appl. Phys. 2023, 133, 150901. [Google Scholar] [CrossRef]
- Kakihana, M.; Aoki, D.; Nakamura, A.; Honda, F.; Nakashima, M.; Amako, Y.; Nakamura, S.; Sakakibara, T.; Hedo, M.; Nakama, T.; et al. Giant Hall resistivity and magnetoresistance in cubic chiral antiferromagnet EuPtSi. J. Phys. Soc. Jpn. 2018, 87, 023701. [Google Scholar] [CrossRef]
- Kaneko, K.; Frontzek, M.D.; Matsuda, M.; Nakao, A.; Munakata, K.; Ohhara, T.; Kakihana, M.; Haga, Y.; Hedo, M.; Nakama, T.; et al. Unique Helical Magnetic Order and Field-Induced Phase in Trillium Lattice Antiferromagnet EuPtSi. J. Phys. Soc. Jpn. 2019, 88, 013702. [Google Scholar] [CrossRef]
- Tabata, C.; Matsumura, T.; Nakao, H.; Michimura, S.; Kakihana, M.; Inami, T.; Kaneko, K.; Hedo, M.; Nakama, T.; Ōnuki, Y. Magnetic Field Induced Triple-q Magnetic Order in Trillium Lattice Antiferromagnet EuPtSi Studied by Resonant X-ray Scattering. J. Phys. Soc. Jpn. 2019, 88, 093704. [Google Scholar] [CrossRef]
- Kakihana, M.; Aoki, D.; Nakamura, A.; Honda, F.; Nakashima, M.; Amako, Y.; Takeuchi, T.; Harima, H.; Hedo, M.; Nakama, T.; et al. Unique Magnetic Phases in the Skyrmion Lattice and Fermi Surface Properties in Cubic Chiral Antiferromagnet EuPtSi. J. Phys. Soc. Jpn. 2019, 88, 094705. [Google Scholar] [CrossRef]
- Mishra, A.K.; Ganesan, V. A-phase, field-induced tricritical point, and universal magnetocaloric scaling in EuPtSi. Phys. Rev. B 2019, 100, 125113. [Google Scholar] [CrossRef]
- Takeuchi, T.; Kakihana, M.; Hedo, M.; Nakama, T.; Ōnuki, Y. Magnetic field versus temperature phase diagram for H‖[001] in the trillium lattice antiferromagnet EuPtSi. J. Phys. Soc. Jpn. 2019, 88, 053703. [Google Scholar] [CrossRef]
- Hayami, S.; Yambe, R. Field-Direction Sensitive Skyrmion Crystals in Cubic Chiral Systems: Implication to 4f-Electron Compound EuPtSi. J. Phys. Soc. Jpn. 2021, 90, 073705. [Google Scholar] [CrossRef]
- Matsumura, T.; Tabata, C.; Kaneko, K.; Nakao, H.; Kakihana, M.; Hedo, M.; Nakama, T.; Ōnuki, Y. Single helicity of the triple-q triangular skyrmion lattice state in the cubic chiral helimagnet EuPtSi. Phys. Rev. B 2024, 109, 174437. [Google Scholar] [CrossRef]
- Tanigaki, T.; Shibata, K.; Kanazawa, N.; Yu, X.; Onose, Y.; Park, H.S.; Shindo, D.; Tokura, Y. Real-space observation of short-period cubic lattice of skyrmions in MnGe. Nano Lett. 2015, 15, 5438–5442. [Google Scholar] [CrossRef] [PubMed]
- Kanazawa, N.; Seki, S.; Tokura, Y. Noncentrosymmetric magnets hosting magnetic skyrmions. Adv. Mater. 2017, 29, 1603227. [Google Scholar] [CrossRef] [PubMed]
- Fujishiro, Y.; Kanazawa, N.; Nakajima, T.; Yu, X.Z.; Ohishi, K.; Kawamura, Y.; Kakurai, K.; Arima, T.; Mitamura, H.; Miyake, A.; et al. Topological transitions among skyrmion-and hedgehog-lattice states in cubic chiral magnets. Nat. Commun. 2019, 10, 1059. [Google Scholar] [CrossRef] [PubMed]
- Kanazawa, N.; Kitaori, A.; White, J.S.; Ukleev, V.; Rønnow, H.M.; Tsukazaki, A.; Ichikawa, M.; Kawasaki, M.; Tokura, Y. Direct Observation of the Statics and Dynamics of Emergent Magnetic Monopoles in a Chiral Magnet. Phys. Rev. Lett. 2020, 125, 137202. [Google Scholar] [CrossRef] [PubMed]
- Ishiwata, S.; Tokunaga, M.; Kaneko, Y.; Okuyama, D.; Tokunaga, Y.; Wakimoto, S.; Kakurai, K.; Arima, T.; Taguchi, Y.; Tokura, Y. Versatile helimagnetic phases under magnetic fields in cubic perovskite SrFeO3. Phys. Rev. B 2011, 84, 054427. [Google Scholar] [CrossRef]
- Ishiwata, S.; Nakajima, T.; Kim, J.H.; Inosov, D.S.; Kanazawa, N.; White, J.S.; Gavilano, J.L.; Georgii, R.; Seemann, K.M.; Brandl, G.; et al. Emergent topological spin structures in the centrosymmetric cubic perovskite SrFeO3. Phys. Rev. B 2020, 101, 134406. [Google Scholar] [CrossRef]
- Rogge, P.C.; Green, R.J.; Sutarto, R.; May, S.J. Itinerancy-dependent noncollinear spin textures in SrFeO3, CaFeO3, and CaFeO3/SrFeO3 heterostructures probed via resonant X-ray scattering. Phys. Rev. Mater. 2019, 3, 084404. [Google Scholar] [CrossRef]
- Onose, M.; Takahashi, H.; Sagayama, H.; Yamasaki, Y.; Ishiwata, S. Complete phase diagram of Sr1-xLaxFeO3 with versatile magnetic and charge ordering. Phys. Rev. Mater. 2020, 4, 114420. [Google Scholar] [CrossRef]
- Dong, Y.; Kinoshita, Y.; Ochi, M.; Nakachi, R.; Higashinaka, R.; Hayami, S.; Wan, Y.; Arai, Y.; Huh, S.; Hashimoto, M.; et al. Pseudogap and Fermi arc induced by Fermi surface nesting in a centrosymmetric skyrmion magnet. Science 2025, 388, 624–630. [Google Scholar] [CrossRef] [PubMed]
- Grytsiuk, S.; Hanke, J.P.; Hoffmann, M.; Bouaziz, J.; Gomonay, O.; Bihlmayer, G.; Lounis, S.; Mokrousov, Y.; Blügel, S. Topological–chiral magnetic interactions driven by emergent orbital magnetism. Nat. Commun. 2020, 11, 511. [Google Scholar] [CrossRef] [PubMed]
- Bömerich, T.; Heinen, L.; Rosch, A. Skyrmion and tetarton lattices in twisted bilayer graphene. Phys. Rev. B 2020, 102, 100408. [Google Scholar] [CrossRef]
- Hayami, S. Multiple-Q magnetism by anisotropic bilinear-biquadratic interactions in momentum space. J. Magn. Magn. Mater. 2020, 513, 167181. [Google Scholar] [CrossRef]
- Stewart, G.R. Heavy-fermion systems. Rev. Mod. Phys. 1984, 56, 755–787. [Google Scholar] [CrossRef]
- Hewson, A.C. The Kondo Problem to Heavy Fermions (Cambridge Studies in Magnetism); Cambridge University Press: Oxford, UK, 1997. [Google Scholar]
- Stewart, G.R. Non-Fermi-liquid behavior in d- and f-electron metals. Rev. Mod. Phys. 2001, 73, 797–855. [Google Scholar] [CrossRef]
- Komarov, K.; Dzebisashvili, D. Effective indirect multi-site spin–spin interactions in the s–d (f) model. J. Magn. Magn. Mater. 2017, 440, 57–59. [Google Scholar] [CrossRef]
- Ruderman, M.A.; Kittel, C. Indirect Exchange Coupling of Nuclear Magnetic Moments by Conduction Electrons. Phys. Rev. 1954, 96, 99–102. [Google Scholar] [CrossRef]
- Kasuya, T. A Theory of Metallic Ferro- and Antiferromagnetism on Zener’s Model. Prog. Theor. Phys. 1956, 16, 45–57. [Google Scholar] [CrossRef]
- Yosida, K. Magnetic Properties of Cu-Mn Alloys. Phys. Rev. 1957, 106, 893–898. [Google Scholar] [CrossRef]
- Dzyaloshinsky, I. A thermodynamic theory of “weak” ferromagnetism of antiferromagnetics. J. Phys. Chem. Solids 1958, 4, 241–255. [Google Scholar] [CrossRef]
- Moriya, T. Anisotropic superexchange interaction and weak ferromagnetism. Phys. Rev. 1960, 120, 91. [Google Scholar] [CrossRef]
- Brinker, S.; dos Santos Dias, M.; Lounis, S. The chiral biquadratic pair interaction. New J. Phys. 2019, 21, 083015. [Google Scholar] [CrossRef]
- Lászlóffy, A.; Rózsa, L.; Palotás, K.; Udvardi, L.; Szunyogh, L. Magnetic structure of monatomic Fe chains on Re(0001): Emergence of chiral multispin interactions. Phys. Rev. B 2019, 99, 184430. [Google Scholar] [CrossRef]
- Mankovsky, S.; Polesya, S.; Ebert, H. Extension of the standard Heisenberg Hamiltonian to multispin exchange interactions. Phys. Rev. B 2020, 101, 174401. [Google Scholar] [CrossRef]
- Brinker, S.; dos Santos Dias, M.; Lounis, S. Prospecting chiral multisite interactions in prototypical magnetic systems. Phys. Rev. Res. 2020, 2, 033240. [Google Scholar] [CrossRef]
- Lounis, S. Multiple-scattering approach for multi-spin chiral magnetic interactions: Application to the one-and two-dimensional Rashba electron gas. New J. Phys. 2020, 22, 103003. [Google Scholar] [CrossRef]
- dos Santos Dias, M.; Brinker, S.; Lászlóffy, A.; Nyári, B.; Blügel, S.; Szunyogh, L.; Lounis, S. Proper and improper chiral magnetic interactions. Phys. Rev. B 2021, 103, L140408. [Google Scholar] [CrossRef]
- Binz, B.; Vishwanath, A.; Aji, V. Theory of the Helical Spin Crystal: A Candidate for the Partially Ordered State of MnSi. Phys. Rev. Lett. 2006, 96, 207202. [Google Scholar] [CrossRef] [PubMed]
- Binz, B.; Vishwanath, A. Theory of helical spin crystals: Phases, textures, and properties. Phys. Rev. B 2006, 74, 214408. [Google Scholar] [CrossRef]
- Park, J.H.; Han, J.H. Zero-temperature phases for chiral magnets in three dimensions. Phys. Rev. B 2011, 83, 184406. [Google Scholar] [CrossRef]
- Leonov, A.O.; Mostovoy, M. Multiply periodic states and isolated skyrmions in an anisotropic frustrated magnet. Nat. Commun. 2015, 6, 8275. [Google Scholar] [CrossRef] [PubMed]
- Janssen, L.; Andrade, E.C.; Vojta, M. Honeycomb-Lattice Heisenberg-Kitaev Model in a Magnetic Field: Spin Canting, Metamagnetism, and Vortex Crystals. Phys. Rev. Lett. 2016, 117, 277202. [Google Scholar] [CrossRef] [PubMed]
- Yambe, R.; Hayami, S. Effective spin model in momentum space: Toward a systematic understanding of multiple-Q instability by momentum-resolved anisotropic exchange interactions. Phys. Rev. B 2022, 106, 174437. [Google Scholar] [CrossRef]
- Hayami, S.; Yambe, R. Stabilization mechanisms of magnetic skyrmion crystal and multiple-Q states based on momentum-resolved spin interactions. Mater. Today Quantum 2024, 3, 100010. [Google Scholar] [CrossRef]
- Sharma, V.; Wang, Z.; Batista, C.D. Machine learning assisted derivation of minimal low-energy models for metallic magnets. NPJ Comput. Mater. 2023, 9, 192. [Google Scholar] [CrossRef]
- Hayami, S.; Kato, Y. Widely-sweeping magnetic field–temperature phase diagrams for skyrmion-hosting centrosymmetric tetragonal magnets. J. Magn. Magn. Mater. 2023, 571, 170547. [Google Scholar] [CrossRef]
- Takagi, R.; White, J.; Hayami, S.; Arita, R.; Honecker, D.; Rønnow, H.; Tokura, Y.; Seki, S. Multiple-q noncollinear magnetism in an itinerant hexagonal magnet. Sci. Adv. 2018, 4, eaau3402. [Google Scholar] [CrossRef] [PubMed]
- Berg, B.; Lüscher, M. Definition and statistical distributions of a topological number in the lattice O(3) σ-model. Nucl. Phys. B 1981, 190, 412–424. [Google Scholar] [CrossRef]
- Hayami, S.; Yambe, R. Degeneracy Lifting of Néel, Bloch, and Anti-Skyrmion Crystals in Centrosymmetric Tetragonal Systems. J. Phys. Soc. Jpn. 2020, 89, 103702. [Google Scholar] [CrossRef]
- Hayami, S.; Motome, Y. Noncoplanar multiple-Q spin textures by itinerant frustration: Effects of single-ion anisotropy and bond-dependent anisotropy. Phys. Rev. B 2021, 103, 054422. [Google Scholar] [CrossRef]
- Ozawa, R.; Hayami, S.; Motome, Y. Zero-Field Skyrmions with a High Topological Number in Itinerant Magnets. Phys. Rev. Lett. 2017, 118, 147205. [Google Scholar] [CrossRef] [PubMed]
- Hayami, S.; Motome, Y. Effect of magnetic anisotropy on skyrmions with a high topological number in itinerant magnets. Phys. Rev. B 2019, 99, 094420. [Google Scholar] [CrossRef]
- Amoroso, D.; Barone, P.; Picozzi, S. Spontaneous skyrmionic lattice from anisotropic symmetric exchange in a Ni-halide monolayer. Nat. Commun. 2020, 11, 5784. [Google Scholar] [CrossRef] [PubMed]
- Yambe, R.; Hayami, S. Skyrmion crystals in centrosymmetric itinerant magnets without horizontal mirror plane. Sci. Rep. 2021, 11, 11184. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Su, Y.; Lin, S.Z.; Batista, C.D. Meron, skyrmion, and vortex crystals in centrosymmetric tetragonal magnets. Phys. Rev. B 2021, 103, 104408. [Google Scholar] [CrossRef]
- Amoroso, D.; Barone, P.; Picozzi, S. Interplay between Single-Ion and Two-Ion Anisotropies in Frustrated 2D Semiconductors and Tuning of Magnetic Structures Topology. Nanomaterials 2021, 11, 1873. [Google Scholar] [CrossRef] [PubMed]
- Hayami, S. Multiple skyrmion crystal phases by itinerant frustration in centrosymmetric tetragonal magnets. J. Phys. Soc. Jpn. 2022, 91, 023705. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hayami, S. Skyrmion Crystal in Bilinear–Biquadratic–Bicubic Model on a Centrosymmetric Triangular Lattice. Condens. Matter 2025, 10, 39. https://doi.org/10.3390/condmat10030039
Hayami S. Skyrmion Crystal in Bilinear–Biquadratic–Bicubic Model on a Centrosymmetric Triangular Lattice. Condensed Matter. 2025; 10(3):39. https://doi.org/10.3390/condmat10030039
Chicago/Turabian StyleHayami, Satoru. 2025. "Skyrmion Crystal in Bilinear–Biquadratic–Bicubic Model on a Centrosymmetric Triangular Lattice" Condensed Matter 10, no. 3: 39. https://doi.org/10.3390/condmat10030039
APA StyleHayami, S. (2025). Skyrmion Crystal in Bilinear–Biquadratic–Bicubic Model on a Centrosymmetric Triangular Lattice. Condensed Matter, 10(3), 39. https://doi.org/10.3390/condmat10030039





