Optimized Flow Field Design with Dead-Zone Compensation for Enhanced Performance in Aqueous AgO-Al Batteries
Abstract
1. Introduction
2. Numerical Methods
2.1. Physical Model
2.2. Numerical Details
2.3. Post-Process Simulations
2.3.1. Pressure Drop
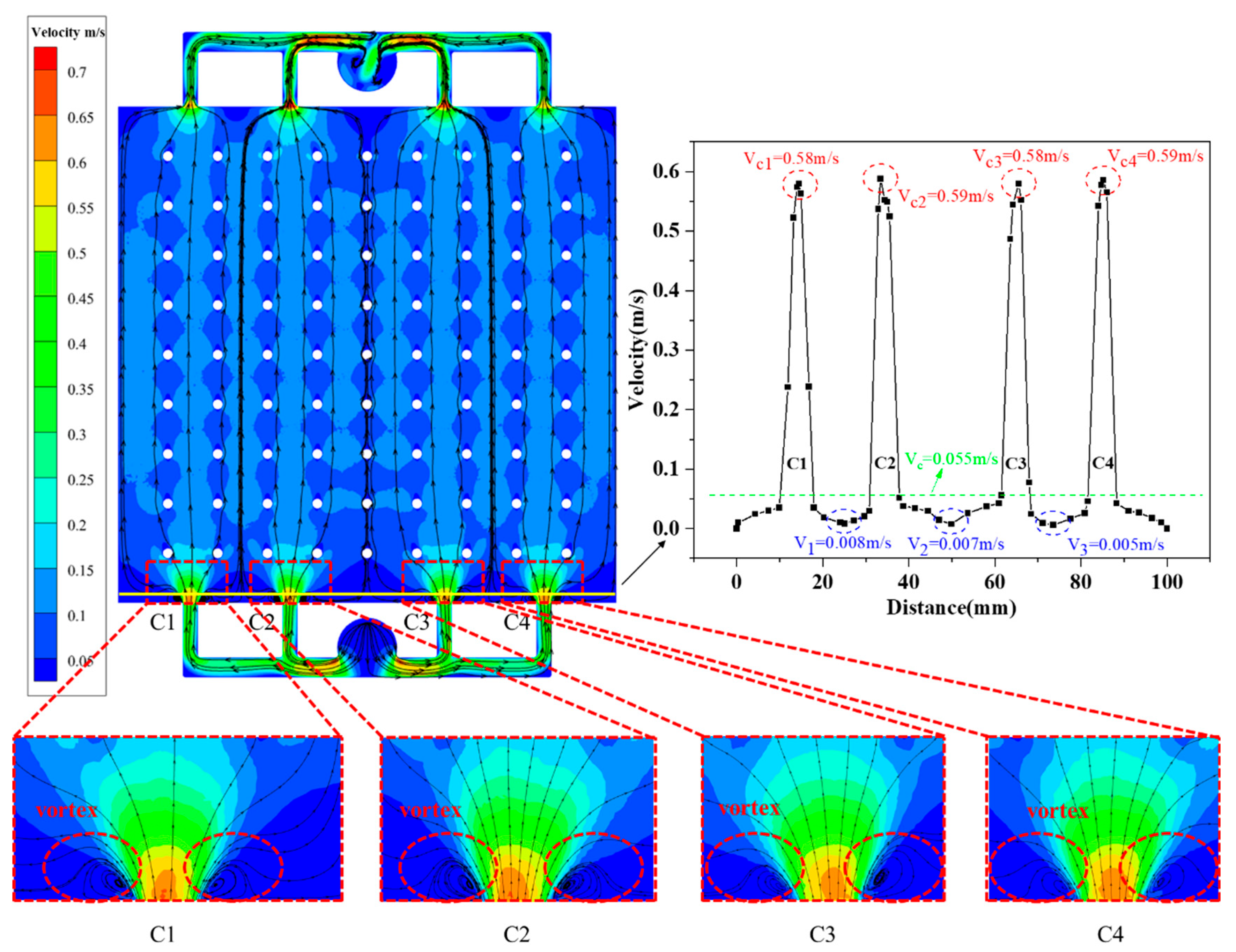
2.3.2. Ratio of the Dead-Zone Area
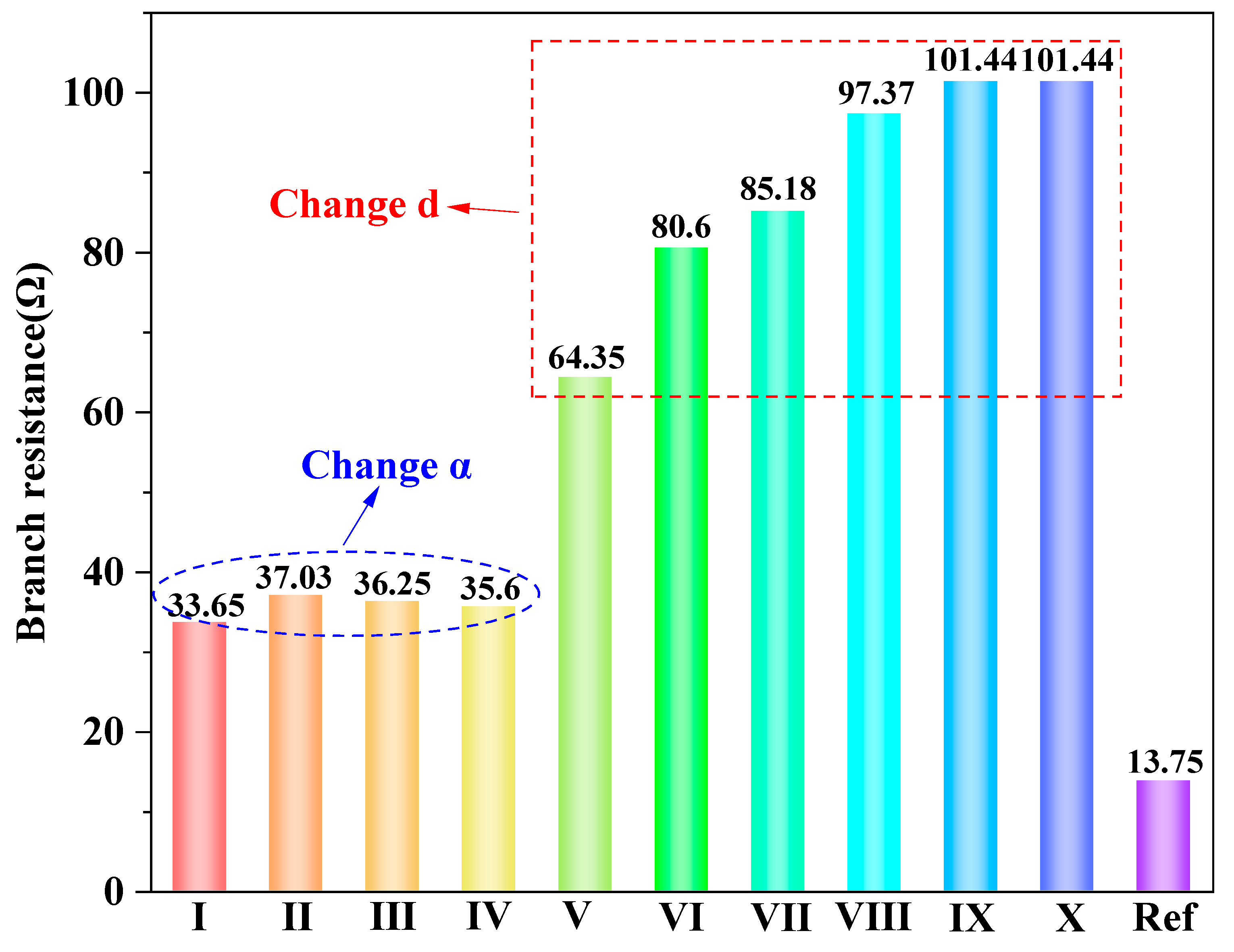
2.3.3. Branch Resistance
3. Experimental
3.1. Battery Setup
3.2. Battery Tests
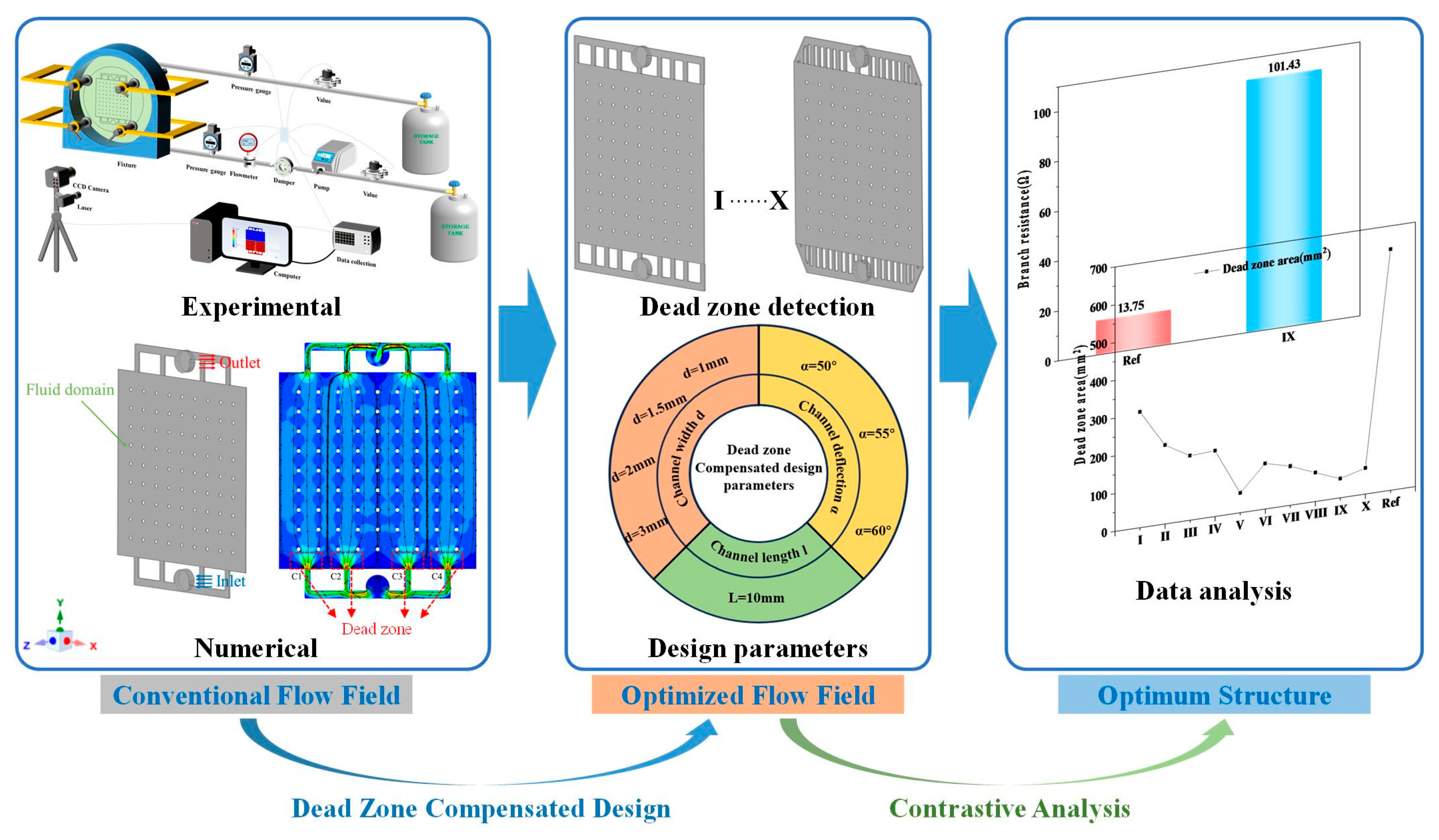
4. Results
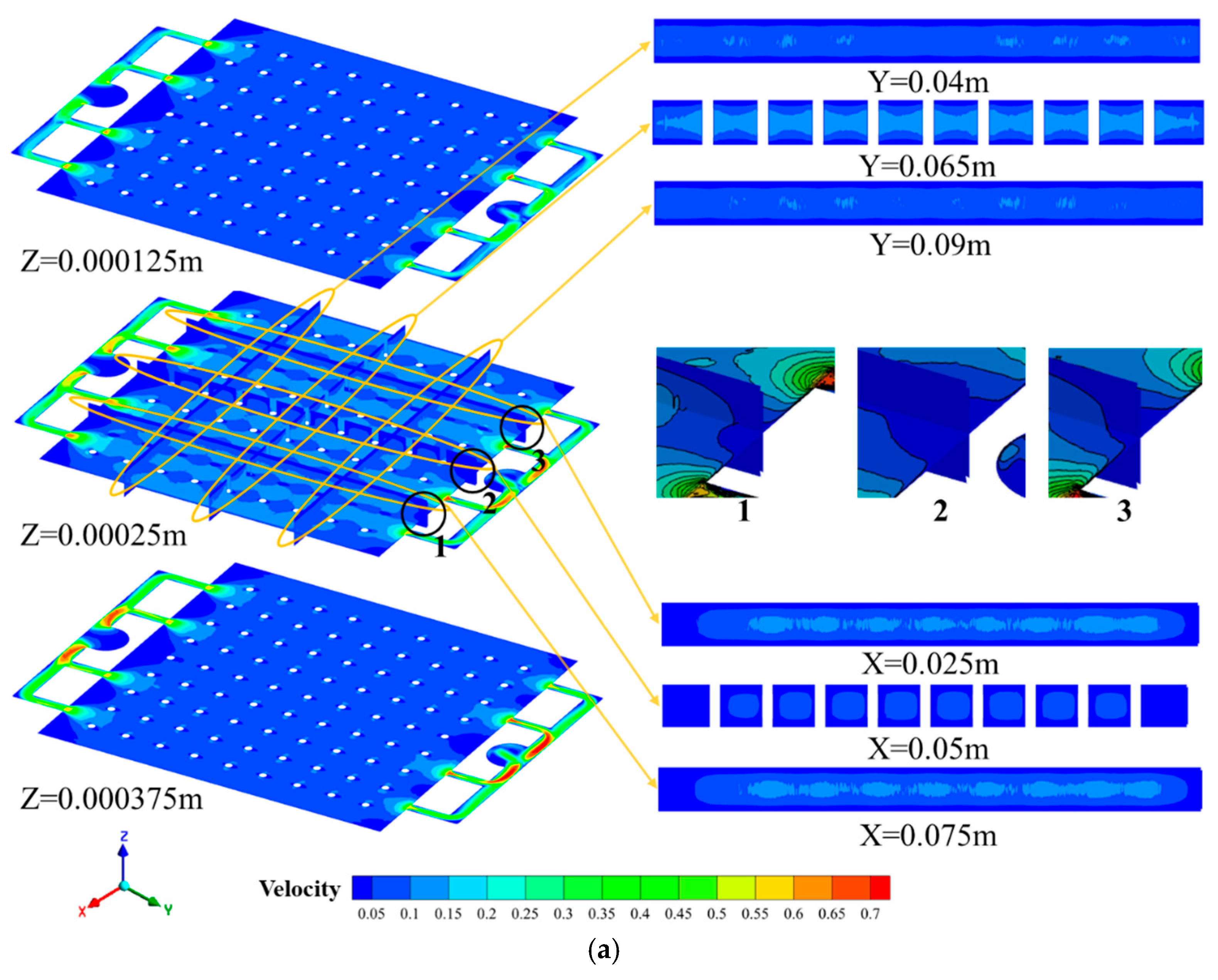
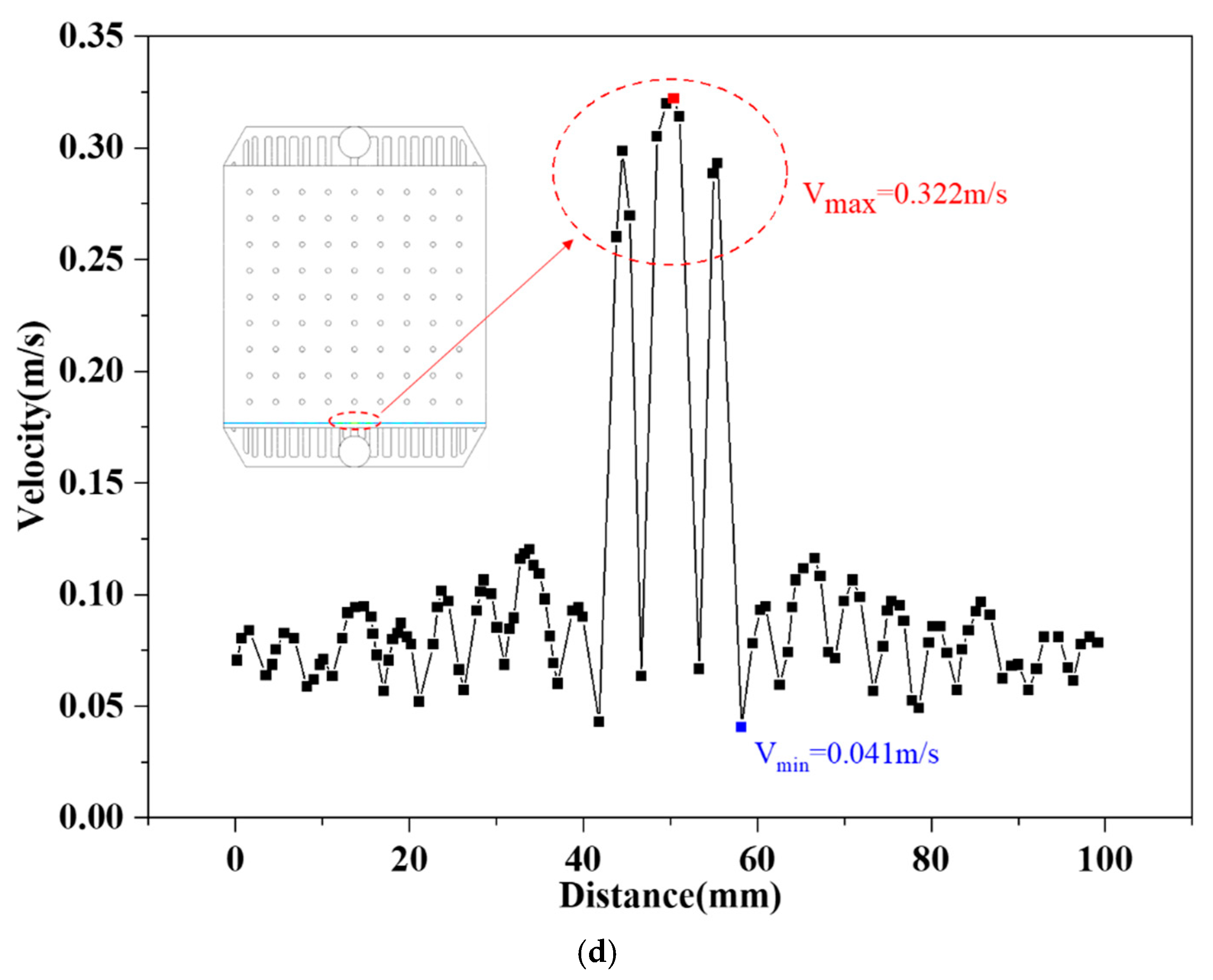
4.1. Simulations of Electrolyte Flow Field
4.2. Dead--Zone-Compensated Design
4.3. Effects of Channel Width and Angle
4.4. Branch Resistance Analyses
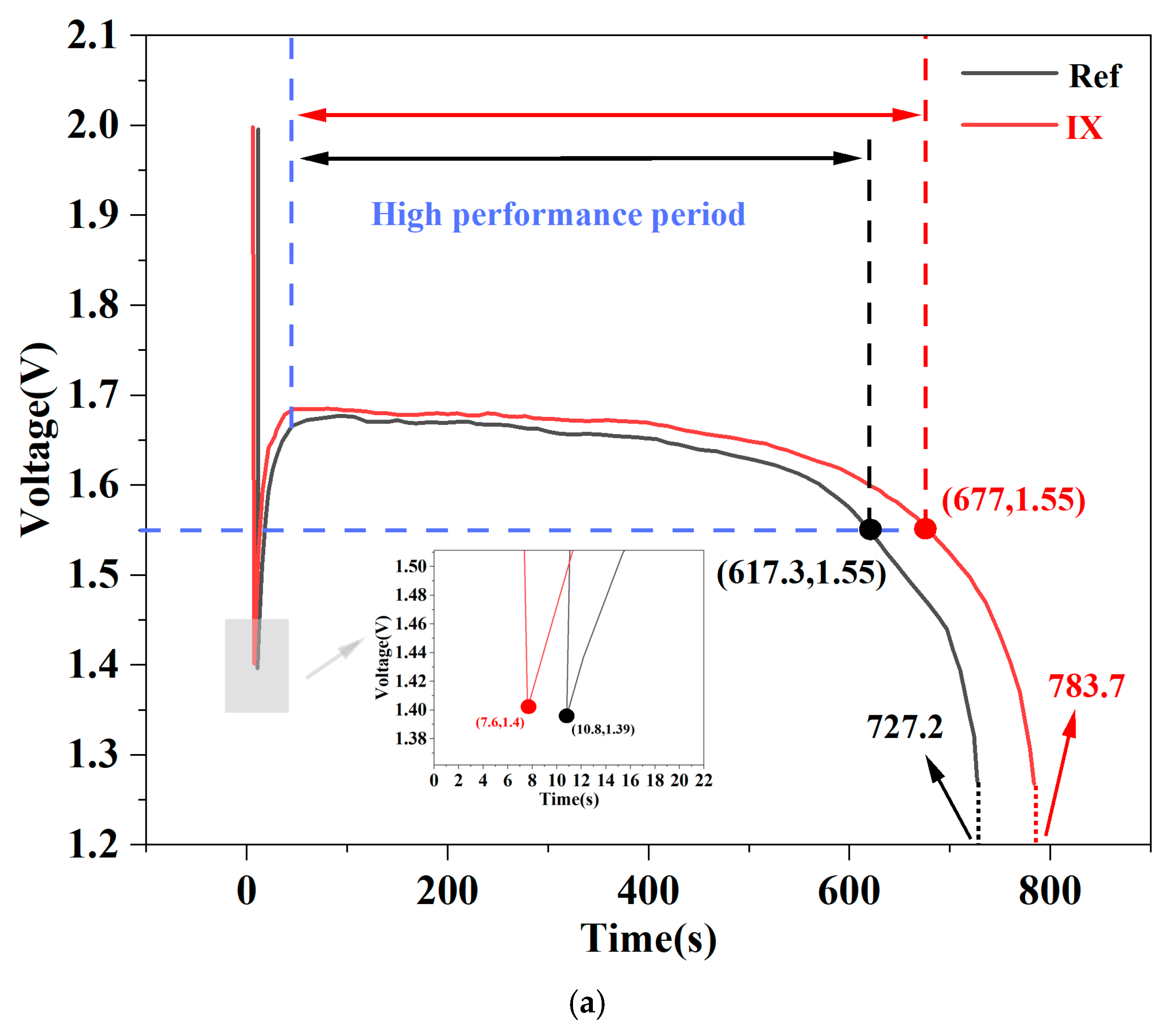
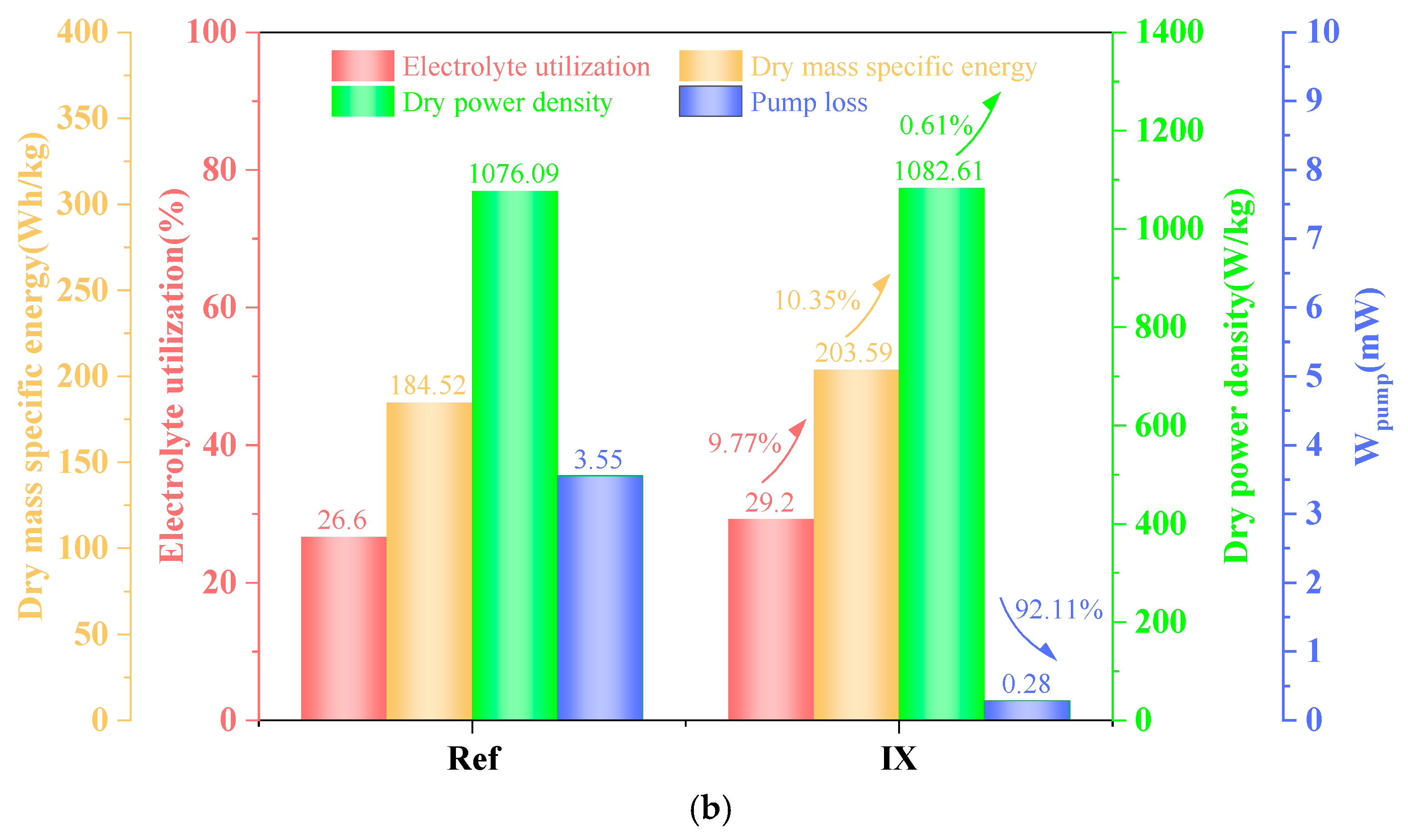
4.5. Performance of Aqueous AgO-Al Batteries with DZCD
5. Discussion
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| R | Radius of inlet and outlet, mm |
| h1 | Depth of reaction area, mm |
| h2 | Depth of flow channel at inlet and outlet, mm |
| L1 | Side length of reaction area, mm |
| d1 | Primary branch channel width, mm |
| d2 | Secondary branch channel width, mm |
| S1 | Branch channel spacing, mm |
| S2 | Branch channel spacing on both sides of the inlet/outlet, mm |
| L | Length of branch channel, mm |
| ΔP | Pressure drop, Pa |
| ADR | Dead-zone area ratio |
| AD | Dead-zone area, mm2 |
| At | Total reaction area, mm2 |
| AAR | Active-zone area ratio |
| AA | Active-zone area, mm2 |
| M | Mass of battery, kg |
| Wbattery | Power of battery, W |
| ΔP | Pressure drop, Pa |
| EM | Dry-mass-specific energy, Wh/kg |
| R | Branch resistance, Ω |
| Lm | Material length, m |
| S | Material cross-sectional area, m2 |
| EU | Electrolyte utilization |
| Qdischarge | Available discharge capacity, mAh·g−1 |
| Qtheory | Theoretical capacity of the electrode, 433 mAh·g−1 |
| Edischarge | Discharge energy, Wh |
| WM | Dry power density, W/kg |
| Wpump | Pump loss, mW·cm−2 |
| q | Flow rate, m3·s−1 |
| Greek symbols | |
| α | Deflection angle of flow channel, ° |
| ρ | Electrical resistivity, Ω·m |
| Subscripts | |
| in | Inlet |
| out | Outlet |
References
- Jeong, H.; Ahn, S.H.; Jo, C.S. Effects of chelating agent on the nanostructure of nickel hexacyanoferrate and its performance in seawater battery application. Chem. Eng. J. 2023, 465, 142834. [Google Scholar] [CrossRef]
- Chen, J.L.; Sun, L.; Wang, K.; Zhang, Y.H. Research and applications of rechargeable seawater battery. J. Energy Storage 2024, 76, 109659. [Google Scholar] [CrossRef]
- Park, M.; Ryu, J.; Wang, W.; Cho, J. Material design and engineering of next-generation flow-battery technologies. Nat. Rev. Mater. 2017, 2, 16080. [Google Scholar] [CrossRef]
- Wang, Z.Y.; Ren, J.Y.; Sun, J.; Guo, Z.X.; Wei, L.; Fan, X.Z.; Zhao, T.S. Characterizations and selections of electrodes with optimal performance for large-scale vanadium redox flow batteries through lab-scale experiments. J. Power Sources 2022, 549, 232094. [Google Scholar] [CrossRef]
- Houser, J.; Pezeshki, A.; Clement, J.; Aaron, D.; Mench, M.M. Architecture for improved mass transport and system performance in redox flow batteries. J. Power Sources 2017, 351, 96–105. [Google Scholar] [CrossRef]
- Ren, J.Y.; Wei, L.; Wang, Z.Y.; Yue, Q.L.; Liu, B.; Jia, G.C.; Fan, X.Z.; Zhao, T.S. An electrochemical-thermal coupled model for aqueous redox flow batteries. Int. J. Heat Mass Transf. 2022, 192, 122926. [Google Scholar] [CrossRef]
- Yue, M.; Yan, J.W.; Zhang, H.M.; Zheng, Q.; Li, X.F. The crucial role of parallel and interdigitated flow channels in a trapezoid flow battery. J. Power Sources 2021, 312, 230497. [Google Scholar] [CrossRef]
- Gundlapalli, R.; Jayanti, S. Effective splitting of serpentine flow field for applications in large-scale flow batteries. J. Power Sources 2021, 487, 229409. [Google Scholar] [CrossRef]
- Satola, B. Review-Bipolar Plates for the Vanadium Redox Flow Battery. J. Electrochem. Soc. 2021, 168, 060503. [Google Scholar] [CrossRef]
- Esan, O.C.; Shi, X.Y.; Pan, Z.F.; Huo, X.Y.; An, L.; Zhao, T.S. Modeling and simulation of flow batteries. Adv. Energy Mater. 2020, 10, 2000758. [Google Scholar] [CrossRef]
- Ke, X.; Prahl, J.M.; Alexander, J.I.D.; Wainright, J.S.; Zawodzinski, T.A.; Savinell, R.F. Rechargeable redox flow batteries: Flow fields, stacks and design considerations. Chem. Soc. Rev. 2018, 23, 8721–8743. [Google Scholar] [CrossRef] [PubMed]
- Gundlapalli, R.; Bhattarai, A.; Ranjan, R.; Ghimire, P.C.; Yeo, X.M.; Zainudin, N.A.B.; Wai, N.; Mahlendorf, F.; Jasincuk, A.; Thorsten, H. Characterization and scale-up of serpentine and interdigitated flow fields for application in commercial vanadium redox flow batteries. J. Power Sources 2022, 542, 231812. [Google Scholar] [CrossRef]
- Messaggi, M.; Gambaro, C.; Casalegno, A.; Zago, M. Development of innovative flow fields in a vanadium redox flow battery: Design of channel obstructions with the aid of 3D computational fluid dynamic model and experimental validation through locally-resolved polarization curves. J. Power Sources 2022, 526, 231155. [Google Scholar] [CrossRef]
- Zhang, B.W.; Lei, Y.; Bai, B.F.; Zhao, T.S. A two-dimensional model for the design of flow fields in vanadium redox flow batteries. Int. J. Heat Mass Transf. 2019, 135, 460–469. [Google Scholar] [CrossRef]
- Eifert, L.; Jusys, Z.; Behm, R.J.; Zeis, R. Side reactions and stability of pre-treated carbon felt electrodes for vanadium redox flow batteries: A DEMS study. Carbon 2020, 158, 580–587. [Google Scholar] [CrossRef]
- Ye, Q.; Zhang, Y.J.; Cheng, P.; Shao, Z.G. Effects of wettability and flow direction on gas retention and flow resistance of water flowing through carbon felts with thermally induced gas evolutions. Int. J. Heat Mass Transf. 2020, 156, 119911. [Google Scholar] [CrossRef]
- Aaron, D.S.; Liu, Q.; Tang, Z.; Grim, G.M.; Papandrew, A.B.; Turhan, A.; Zawodzinski, T.A.; Mench, M.M. Dramatic performance gains in vanadium redox flow batteries through modified cell architecture. J. Power Sources 2012, 206, 450–453. [Google Scholar] [CrossRef]
- Kumar, S.; Jayanti, S. Effect of flow field on the performance of an all-vanadium redox flow battery. J. Power Sources 2016, 307, 782–787. [Google Scholar] [CrossRef]
- Zheng, Q.; Xing, F.; Li, X.F.; Ning, G.L.; Zhang, H.M. Flow field design and optimization based on the mass transport polarization regulation in a flow-through type vanadium flow battery. J. Power Sources 2016, 324, 402–411. [Google Scholar] [CrossRef]
- Chen, J.Q.; Wang, B.G.; Lv, H.V. Numerical simulation and experiment on the electrolyte flow distribution for all vanadium redox flow battery. Adv. Mater. Res. 2011, 236–238, 604–607. [Google Scholar]
- Lisboa, K.M.; Marschewski, J.; Ebejer, N.; Ruch, P.; Cotta, R.M.; Michel, B.; Poulikakos, D. Mass transport enhancement in redox flow batteries with corrugated fluidic networks. J. Power Sources 2017, 359, 322–331. [Google Scholar] [CrossRef]
- Guo, Z.X.; Sun, J.; Wang, Z.Y.; Fan, X.Z.; Zhao, T.S. Numerical modeling of interdigitated flow fields for scaled-up redox flow batteries. Int. J. Heat Mass Transf. 2023, 201, 123548. [Google Scholar] [CrossRef]
- Sun, J.; Zheng, M.L.; Yang, Z.S.; Yu, Z.T. Flow field design pathways from lab-scale toward large-scale flow batteries. Energy 2019, 173, 637–646. [Google Scholar] [CrossRef]
- Sun, J.; Liu, B.C.; Zheng, M.L.; Luo, Y.S.; Yu, Z.T. Serpentine flow field with changing rib width for enhancing electrolyte penetration uniformity in redox flow batteries. J. Energy Storage 2022, 49, 104135. [Google Scholar] [CrossRef]
- Sun, J.; Zheng, M.L.; Luo, Y.S.; Yu, Z.T. Three-dimensional detached serpentine flow field design for redox flow batteries. J. Power Sources 2019, 428, 136–145. [Google Scholar] [CrossRef]
- Wang, Q.; Qu, Z.G.; Jiang, Z.Y.; Yang, W.W. Numerical study on vanadium redox flow battery performance with non-uniformly compressed electrode and serpentine flow field. Appl. Energy 2018, 220, 106–116. [Google Scholar] [CrossRef]
- Clement, J.T.; Zawodzinski, T.A.; Mench, M.M. Measurement of localized current distribution in a vanadium redox flow battery. ECS Trans. 2014, 58, 9–16. [Google Scholar] [CrossRef]
- Ertugrul, T.Y.; Clement, J.T.; Gandomi, Y.A.; Aaron, D.S.; Mench, M.M. In-situ current distribution and mass transport analysis via strip cell architecture for a vanadium redox flow battery. J. Power Sources 2019, 437, 226920. [Google Scholar] [CrossRef]
- Xu, Q.; Zhao, T.S.; Leung, P.K. Numerical investigations of flow field designs for vanadium redox flow batteries. Appl. Energy 2013, 105, 47–56. [Google Scholar] [CrossRef]
- Messaggi, M.; Canzi, P.; Mereu, R.; Baricci, A.; Inzoli, F.; Casalegno, A.; Zago, M. Analysis of flow field design on vanadium redox flow battery performance: Development of 3D computational fluid dynamic model and experimental validation. Appl. Energy 2018, 228, 1057–1070. [Google Scholar] [CrossRef]
- Xu, Q.; Zhao, T.S.; Zhang, C. Performance of a vanadium redox flow battery with and without flow fields. Electrochim. Acta 2014, 142, 61–67. [Google Scholar] [CrossRef]
- Ishitobi, H.; Saito, J.; Sugawara, S.; Oba, K.; Nakagawa, N. Visualized cell characteristics by a two-dimensional model of vanadium redox flow battery with interdigitated channel and thin active electrode. Electrochim. Acta 2019, 313, 513–522. [Google Scholar] [CrossRef]
- Lu, M.Y.; Deng, Y.M.; Yang, W.W.; Ye, M.; Jiao, Y.H.; Xu, Q. A novel rotary serpentine flow field with improved electrolyte penetration and species distribution for vanadium redox flow battery. Electrochim. Acta 2020, 361, 137089. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, P.F.; Yang, J.L.; Li, J.; Chu, F.M. Effect of variable cross-section electrode on the battery performance of all-vanadium redox flow battery. Int. J. Heat Mass Transf. 2023, 215, 124382. [Google Scholar] [CrossRef]
- Zeng, Y.K.; Li, F.H.; Lu, F.; Zhou, X.L.; Yuan, Y.P.; Cao, X.L.; Xiang, B. A hierarchical interdigitated flow field design for scale-up of high performance redox flow batteries. Appl. Energy 2019, 238, 435–441. [Google Scholar] [CrossRef]
- Pan, L.M.; Xie, J.Y.; Guo, J.C.; Wei, D.B.; Qi, H.H.; Rao, H.Y.; Leung, R.; Zeng, L.; Zhao, T.S.; Wei, L. In-plane gradient design of flow fields enables enhanced convections for redox flow batteries. Energy Adv. 2023, 2, 1973–2152. [Google Scholar] [CrossRef]
- Pan, L.M.; Sun, J.; Qi, H.H.; Han, M.S.; Dai, Q.X.; Xu, J.H.; Yao, S.X.; Li, Q.L.; Wei, L.; Zhao, T.S. Dead-zone-compensated design as general method of flow field optimization for redox flow batteries. Proc. Natl. Acad. Sci. USA 2023, 120, e2305572120. [Google Scholar] [CrossRef]
- Pan, L.M.; Sun, J.; Qi, H.H.; Han, M.S.; Chen, L.P.; Xu, J.H.; Wei, L.; Zhao, T.S. Along-flow-path gradient flow field enabling uniform distributions of reactants for redox flow batteries. J. Power Sources 2023, 570, 233012. [Google Scholar] [CrossRef]
- Su, R.H.; Wang, Z.M.; Cai, Y.H.; Ying, J.H.; Li, H.J.; Zhao, T.S.; Jiang, H.R. Scaling up flow fields from lab-scale to stack-scale for redox flow batteries. Chem. Eng. J. 2024, 486, 149946. [Google Scholar] [CrossRef]
- Sun, Y.; Lin, Y.X.; Wang, Q.L.; Yang, C.; Yin, W.; Wan, Z.M.; Qiu, T. Novel design and numerical investigation of a windward bend flow field for proton exchange membrane fuel cell. Energy 2024, 290, 130142. [Google Scholar] [CrossRef]
- Zhang, S.Y.; Lin, S.; Xu, H.T.; Liu, G.J.; Wang, K. Performance of proton exchange membrane fuel cells with honeycomb-like flow channel design. Energy 2022, 239, 122102. [Google Scholar] [CrossRef]
- Chen, P.Q.; Zheng, Q. Investigation on flow field optimization of seawater activated battery based on flow channel structure design. J. Energy Storage 2024, 84, 110798. [Google Scholar] [CrossRef]
- Chen, W.S.; Xiang, Q.J.; Li, Y.J.; Liu, Z.Q. On the mechanisms of pressure drop and viscous losses in hydrofoil tip-clearance flows. Energy 2023, 269, 126712. [Google Scholar] [CrossRef]
- Chen, P.Q.; Xiong, C.H.; Zheng, Q.; Ruan, M.; Xu, W.L. Numerical simulation and experimental investigation on the optimization of flow-guided structures for high-performance aqueous AgO-Al batteries. Int. J. Heat Mass Transf. 2024, 235, 126167. [Google Scholar] [CrossRef]
- Zhao, W.K.; Wang, L.J.; Zhang, Y.N.; Cao, X.Y.; Wang, W.; Liu, Y.; Li, B.X. Snow melting on a road unit as affected by thermal fluids in different embedded pipes. Sustain. Energy Technol. Assess. 2021, 46, 101221. [Google Scholar] [CrossRef]
- Zhao, W.K.; Zhang, Y.N.; Cao, X.Y.; Wang, L.J.; Li, B.X. Applied thermal process for a hydronic snow-melting system in the coldest provincial capital of China. Appl. Therm. Eng. 2023, 218, 119421. [Google Scholar] [CrossRef]
- He, X.H.; Li, Z.; Wang, Y.K.; Xu, W.L.; Zhang, Q.; Wang, X.Y.; Liu, H.; Yang, G.Z.; Zhang, H.T.; Song, J.M.; et al. A high-purity AgO cathode active material for high-performance aqueous AgO-Al batteries. J. Power Sources 2022, 551, 232151. [Google Scholar] [CrossRef]
- Guo, Z.X.; Ren, J.Y.; Sun, J.; Wang, Z.Y.; Wei, L.; Liu, B.; He, C.X.; Fan, X.Z.; Zhao, T.S. A split convection-enhanced flow field for stack-scale redox flow batteries . Chem. Eng. J. 2025, 511, 1161937. [Google Scholar] [CrossRef]
- Wan, S.B.; Jiang, H.R.; Guo, Z.X.; He, C.X.; Liang, X.W.; Djilali, N.; Zhao, T.S. Machine learning-assisted design of flow fields for redox flow batteries. Energy Environ. Sci. 2022, 7, 2874–2888. [Google Scholar] [CrossRef]
- Schweiss, R.; Pritzl, A.; Meiser, C. Parasitic hydrogen evolution at different carbon fiber electrodes in vanadium redox flow batteries. J. Electrochem. Soc. 2016, 163, A2089–A2094. [Google Scholar] [CrossRef]
- Shah, A.A.; Al-Fetlawi, H.; Walsh, F.C. Dynamic modelling of hydrogen evolution effects in the all vanadium redox flow battery. Electrochim. Acta 2010, 55, 1125–1139. [Google Scholar] [CrossRef]
- Al-Fetlawi, H.; Shah, A.A.; Walsh, F.C. Modelling the effects of oxygen evolution in the all-vanadium redox flow battery. Electrochim. Acta 2010, 55, 3192–3205. [Google Scholar] [CrossRef]
- Eifert, L.; Bevilacqua, N.; Köble, K.; Fahy, K.; Xiao, L.S.; Li, M.; Duan, K.J.; Bazylak, A.; Sui, P.C.; Zeis, R. Synchrotron X-ray radiography and tomography of vanadium redox flow batteries-cell design, electrolyte flow geometry, and gas bubble formation. Chem. Sustain. Energy Mater. (ChemSusChem) 2020, 13, 3154–3165. [Google Scholar] [CrossRef] [PubMed]
- Köble, K.; Eifert, L.; Bevilacqua, N.; Fahy, K.F.; Bazylak, A.; Zeis, R. Synchrotron X-ray radiography of vanadium redox flow batteries—Time and spatial resolved electrolyte flow in porous carbon electrodes. J. Power Sources 2021, 492, 229660. [Google Scholar] [CrossRef]
- He, X.H.; Wang, X.Y.; Zhang, Q.; Wang, Y.K.; Song, J.M.; Li, Z.; Li, H.X.; Wang, S.G.; Yu, K. In-situ synthesis AgO/AgNPs composite as binder-free cathode for high-performance aqueous AgO-Al batteries. J. Energy Storage 2024, 101, 113960. [Google Scholar] [CrossRef]
- Huang, Z.B.; Mu, A.L.; Wu, L.X.; Wang, H. Vanadium redox flow batteries: Flow field design and flow rate optimization. J. Energy Storage 2022, 45, 103526. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, P.; Zheng, Q.; Xiong, C.; Chen, J.; Wang, X.; Su, X.; Huang, L.; Li, P.; Xu, W.; Ruan, M. Optimized Flow Field Design with Dead-Zone Compensation for Enhanced Performance in Aqueous AgO-Al Batteries. Batteries 2025, 11, 237. https://doi.org/10.3390/batteries11070237
Chen P, Zheng Q, Xiong C, Chen J, Wang X, Su X, Huang L, Li P, Xu W, Ruan M. Optimized Flow Field Design with Dead-Zone Compensation for Enhanced Performance in Aqueous AgO-Al Batteries. Batteries. 2025; 11(7):237. https://doi.org/10.3390/batteries11070237
Chicago/Turabian StyleChen, Peiqiang, Qun Zheng, Chunhua Xiong, Jinmao Chen, Xudong Wang, Xing Su, Long Huang, Pan Li, Wanli Xu, and Man Ruan. 2025. "Optimized Flow Field Design with Dead-Zone Compensation for Enhanced Performance in Aqueous AgO-Al Batteries" Batteries 11, no. 7: 237. https://doi.org/10.3390/batteries11070237
APA StyleChen, P., Zheng, Q., Xiong, C., Chen, J., Wang, X., Su, X., Huang, L., Li, P., Xu, W., & Ruan, M. (2025). Optimized Flow Field Design with Dead-Zone Compensation for Enhanced Performance in Aqueous AgO-Al Batteries. Batteries, 11(7), 237. https://doi.org/10.3390/batteries11070237






