Impact of Temperature and Depth of Discharge on Commercial Nickel Manganese Oxide and Lithium Iron Phosphate Batteries After Three Years of Aging

Abstract

Accurate cell selection is primordial to ensure battery safety and longevity. Unfortunately, because of path dependence, finding out which cells are best adapted to a specific application is not straightforward and might require significant testing. This work provides the analysis of three years of aging, both cycling and calendar, for two batches of commercial cells of different chemistries. Using design of experiments and analysis of variance, this work showed that the impact of temperature and depth of discharge, both at the beginning and end of discharge, are chemistry dependent. Moreover, an analysis of the cells’ degradation modes also showcased different pathways depending on the positive electrode chemistry and the type of aging.

1. Introduction

Many applications are looking into transitioning to lithium-ion batteries; however, with multiple chemistries and sizing options available from many manufacturers, the choice of which battery to use for a particular application is not simple. This is especially true as the battery spec-sheets typically do not cover specific applications and often only relay some standard well-controlled results. Since battery degradation is path dependent [1,2], the specific conditions for a given application (current, pulsing, temperature, depth of discharge (DOD) at the beginning and the end of discharge, …) might drastically affect the safety and durability of the cells. This is because there exists a multitude of possible degradation mechanisms within a battery [3,4] that can be exacerbated or inhibited by different stress factors. As a result, every usage will lead to a unique mix of those mechanisms. While numerous aging studies are already available in the open literature [5], they might not cover the exact conditions the cells will experience under a different application. As a result, tailored battery testing might be necessary to select the best cell as, in some cases, the most aggressive cycling might not be the most damaging one [6]. Such testing could be overwhelming based on the number of variable parameters to account for and all their possible combinations.

An approach to reduce the complexity of representative cycle aging is to use design of experiments (DoE) [7,8], which provides a set of statistical tools to effectively plan and analyze experiments in order to assess cause and effect relationships. Introduced in the 1920s [9], they have since been used in many fields of engineering and science, including batteries, beginning in the early 2010s [10,11]. Since then, multiple studies have used them to study the influence of different parameters [10,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26], whether to optimize lifetime or charging conditions, to calibrate models [27,28,29], or for electrode optimization [30,31]. More details can be found in a review paper by Román-Ramírez and Marco [32]. Among the most notable studies on battery testing conditions, Prochazka et al. studied the impact of the state of charge (SOC), the delta SOC, and the temperature on lithium iron phosphate (LFP) and nickel aluminum cobalt oxide (NCA) cells [10]. Chu and al. investigated the impact of DOD, rate, cutoffs, and temperature on lithium cobalt oxide cells [12]; Su et al. added constant voltage (CV) time as well as cutoff and CV in discharge [23] for NCA cells. We studied the impact of vehicle-to-grid and calendar aging [17,18] on NCA cells and different frequency regulation schedules for grid-tied batteries with lithium–titanium oxide [16]. Saxena et al. looked into the impact of temperature, rate, cutoff, and DODs [15] without specifying any battery chemistry. Stadler et al. investigated the impact of temperature, charging power and charge cutoffs on two different type of nickel manganese cobalt oxide (NMC) cells, 622 and 111 [22]. Sandrucci et al. investigated the impact of initial SOC, C rate, rest time and DOD on Li-rich NMC cells [25]. Recently, Xiong et al. investigated the impact of temperature, crate, and cutoffs on LFP cells [26]. In terms of calendar aging, a study by Mathieu et al. investigated the impact of temperature and SOC on a blended NMC/lithium–manganese oxide cell [22].

In this work, we used DoEs to investigate cycle and calendar aging for two battery chemistries with different positive electrodes (PE): NMC 532 and a blend of LFP with a high voltage layered oxide. Both cells used a graphite negative electrode (NE). Based on the considered application, temperature, as well as the DOD at the beginning and end of discharge (BOD and EOD, respectively), were selected as the most relevant factors. DOD was used instead of SOC because it was calculated from the application rate and not from the maximum capacity [33]. According to Sadler [22], the temperature is expected to have the highest impact on capacity loss, with higher losses for higher DODs. They also noted that decreasing DOD_BOD decreased capacity loss. For the LFP cells, the study by Xiong et al. [26] is the most relevant and also indicated a higher impact for the temperature followed by DOD_BOD, then DOD_EOD. Looking into cycling studies without DoEs, a study by Preger et al. [34] showcased that LFP cells seems to cycle better than NMC cells and that the impact of DOD was greater on NMC cells, although Neuman et al. noted a bigger impact of DOD on LFP capacity loss and resistance increase [35]. For NMC cells, Park et al. and Gauthier et al. noted a DOD impact of capacity loss with discharge at lower DOD, accelerating the capacity loss [36,37]. Looking into calendar aging, a review from 2018 [38] summarized the impact of temperature and SOC on the chemistries of interest. It appeared that the capacity loss for the NMC cells had a combined effect of temperature and SOC, whereas the LFP cells were most sensitive to DOD in the region of interest for this work (0 to 80% DOD, 20 to 40 °C), with a limited combined effect of temperature and SOC. More recent work seemed to be mostly consistent with these observations [35,39,40,41]. It must be noted that while most of the literature focused on capacity loss and sometimes resistance, this work also investigated rate capability. In addition, the analysis will be pushed further with an investigation of the variations in degradation modes [4,42], namely the loss of lithium inventory (LLI), the losses of active material (LAMs) on the positive and negative electrodes (PE and NE, respectively), and on kinetic limitations.

2. Materials and Methods

2.1. Design of Experiments

For the cycle aging DoE, three factors were selected as part of the design: the temperature, the DOD at BOD, and the DOD at EOD. Since only two temperature chambers were available, two levels were considered for the experiments, 20 °C and 35 °C. Three levels were considered for the DOD_BOD (a proxy to the charge cut-off voltage), 0%, 3%, and 5%, and the DOD_EOD, 40%, 60%, and 80%. Based on this information, an optimal custom design was calculated using the Design Expert 13 software (Stat-Ease, Minneapolis, MN, USA) using an I-optimality to maximize prediction capability. More details on different DoEs and optimalities can be found in [8]. The calculated design contains twelve unique experiments, as shown in Figure 1a and

Table A1. Cycle aging DoE experiments.

Experiment #	Temperature (°C)	DODBOD (%)	DODEOD (%)
1	20	3	40
2	20	0	40
3	20	5	60
4	20	0	60
5	20	3	80
6	20	0	80
7	35	5	40
8	35	0	40
9	35	3	60
10	35	0	60
11	35	5	80
12	35	0	80

. For the calendar aging DoE, only two factors were considered, the temperature and the DOD, as shown in Figure 1b and

Table A2. Calendar aging DoE experiments.

Experiment #	Temperature (°C)	DOD (%)
1	20	80
2	40	80
3	35	60
4	27.5	40
5	40	40
6	35	20
7	20	0
8	40	0

. The temperatures were chosen to be 20, 27.5, 35, and 40 °C. This temperature range was selected as the most representative of the planned application for the cells. For the same reasons, the DOD range was set to be between 0 and 80%. The resulting optimal custom design, still with an I-optimality, consisted of 8 unique experiments, as shown in Figure 1b and Table A2. All DODs were calculated assuming discharges at 1/6th of the nominal power, which is the power level most relevant to the application.

The results of the experiments were analyzed using an analysis of variance (ANOVA). For each response, three types of models were considered: a linear model, a two-factor interaction (2FI) model, and a quadratic model. The 2FI model considers combined effects on top of the linear ones and the quadratic one the 2FI parameters plus the squared effects. The difference between these models is schematically represented in Figure A1. Model selection was based on three parameters in order: the p-value, the R² value, and the F-value. The p-value measures the probability of obtaining the observed results, assuming that the null hypothesis is true, with lower values indicating greater significance (the typical threshold for significance is 0.05). The R² is the coefficient of determination, which is the proportion of the variation that is predictable from the independent variables; the closer to one the better. The F value is the ratio of the between-group variance to the within-group variance; the larger, the better. E.g., an F-value of 10 indicates that there is a 1% chance that the observed variations are induced by noise. This drops to 0.01% for an F-value of 50. All these statistics were directly calculated by the Design Expert software.

For ease of comparison, all the results in this work will be presented as coded parameters. In the coded equation, each parameter variation is normalized between −1 and 1 to allow for a direct weight comparison. E.g. for the cycling DoE, the 20 °C temperature became −1 and the 35 °C one +1, 40% DOD_EOD was coded as 0, 60% as 0.5 and 80% as 1, and 0% DOD_BOD became 0, 3% became 0.2, and 5% became 1.

2.2. Electrochemical Testing

For this study, two batches of cells were obtained directly from their respective manufacturers. The first batch consisted of 165 cells with a graphite NE and an NMC532 PE. The second batch consisted of 190 cells with a graphite NE and a blended positive electrode with LFP and a high voltage phase. Since we were not allowed to disclose the make and model, all the data will be anonymized and only normalized values will be reported when weight, capacity, and resistance are involved.

All the electrochemical testing was performed on Bio-Logic BCS-815 testers (Claix, France). Each batch of cells was first subjected to an initial conditioning and characterization test (ICCT) similar to the one proposed in [43], beginning with some stabilization cycles at C/2 to ensure that the cell performance was stable, followed by C/5 and C/2 discharges with the manufacturer recommend charges and four hour relaxations, as shown in Figure A2. Based on the results of the ICCT and the analysis of the cell-to-cell variations, cells from each batch were selected for the two DoEs. Each of the main experiments for the cycle aging DoE had five replicates (60 cells for each chemistry). For the calendar aging DoE, all experiments had four replicates (36 cells per chemistry). In total, 96 cells of each chemistry were used for both DoEs. Each test started with a reference performance test (RPT) consisting of a conditioning cycle to fully charge the cells, then a cycle at C/25 and one at C/6, both with 4 h rests and residual capacity steps at C/50, following the guidelines in [43], as shown Figure A3. For the cycle aging DoE, and because the experiments could not be perfectly time-aligned due to the different DODs, the RPTs were performed at cycling temperature and repeated every 100 cycles. The cycle aging protocol for the cycle aging DoE was tailored to the application and consisted of constant power charges and discharges at 1/6th of the nominal power, without relaxations. For the calendar aging DoE, the RPT was performed at 20 °C every 3 months. For all the cycling experiments, the cutoffs were of 2.75V and 4.1V for the NMC cells and 2.5V and 3.8V for the LFP cells; however, it has to be noted that the first RPT for the LFP cells was incorrectly stopped at 3.7 V instead of 3.8 V for both DoEs.

3. Results

3.1. Cell-to-Cell Variations

Figure 2 presents the distributions of the main parameters gathered during the ICCT for the NMC cells (left column) and the LFP cells (right column). Complete statistics are provided in

Table A3. CtcV statistics summary.

	NMC		LFP
	Mean	Std	Mean	Std
As-received OCV (V)	3.982	0.017	3.751	0.010
As-received SOC (%)	84.0	1.6	99.2	0.2
Normalized capacity @ C/5 (Ah)	91.8	0.7	98.8	1.2
Normalized capacity @ C/2 (Ah)	91.3	0.8	98.0	1.3
Rate capability (QC/2/QC/5, %)	99.5	0.2	99.2	0.4
Specific resistance from C/5 (Ω·Ah)	233.5	12.5	107.3	27.0
Specific resistance from C/2 (Ω·Ah)	231.1	6.8	106.1	26.8
RCV C/5 BOD (V)	4.085	0.003	3.758	0.004
RCV C/5 EOD (V)	3.336	0.025	2.787	0.010
RCV C/2 BOD (V)	4.084	0.001	3.758	0.004
RCV C/2 EOD (V)	3.359	0.027	2.901	0.068
Capacity Ration from C/5 (%Qnom/%SOC)	1.03	0.00	0.99	0.01
Capacity Ration from C/2 (%Qnom/%SOC)	1.03	0.00	0.99	0.03
Normalized weight (%)	100.1	0.6	100.0	0.8

. The weight distributions, Figure 2a,b, are both centered on 100% of the weight reported on the spec sheets, with less than 1% deviation. The NMC weight distribution, Figure 2a, appeared almost normal, with a few cells having either a lower or higher weight than normal. The LFP cells’ weigh distribution, Figure 2b, looked multimodal with one mode around 99.5%, one around 100%, and a third one just below 101%.

Looking at the as received open-circuit voltages (OCVs), Figure 2c,d, the NMC ones are, unsurprisingly, higher than the one recorded for the LFP cells (3.392 V vs. 3.751), with similar standard deviations between 10 and 17 mV. It must be noted that although most NMC cells had as-received OCVs above 3.980 V, some of the cells had as-received OCVs up to 100 mV lower than others. For the LFP cells, the distribution looked more normal but some outliers with lower or higher as-received OCVs were also recorded.

The normalized capacities at C/5 (blue) and C/2 (red), Figure 2e,f, were found to be almost normal for both chemistries. For the NMC cells, the capacities were of 91.8% and 91.3% of the rated capacity, which were lower than expected and might indicate some calendar aging before shipment. For the LFP cells, values closer to 100% were recorded, with 98.8% for the C/5 discharges and 98.0% for the C/2s. The standard deviations were below 1% for the NMC cells but slightly above for the LFP ones. Since the difference between the C/5 and C/2 capacities was higher for the LFP cells, their average ratio (referred to as rate capability herein) was slightly lower than that of the NMC cells, Figure 2g,h, but still above 99%. The rate capabilities distribution for both chemistries appeared bimodal.

The last main parameter that was investigated was the specific resistance calculated from the IR drop at the beginning of the C/2 discharge [43], as shown in Figure 2i,j. For the NMC cells, the distribution is symmetric, with some cells having lower or higher resistance than normal and an overall as small standard deviation around the mean (6.8 mΩ·Ah). For the LFP cells, the mean resistance is more than twice as low (106 vs. 231 mΩ·Ah) but the distribution is skewed towards higher resistance, and the standard deviation is much higher (26.7 mΩ·Ah), with four cells having a significantly higher than average resistance.

Additional statistics are presented in Table A3, which includes the specific resistance calculated from the C/5 cycle, as well as the rest-cell voltages (RCVs) prior and after the discharges. The resistances calculated from C/5 were similar to the one calculated at C/2. The RCVs at BOD were all within 4 mV, independently of the rate and chemistry, but more variations were observed for the RCVs at EOD, with 25 mV variations for the NMC cells and up to 56 mV for the LFP cells. While these variations might appear significant, it is important to realize that the RCVs might be in a region where the OCVs vs. state of charge (SOC) curve is very steep and therefore corresponds to a small SOC spread. Inversely, a 4-mV variation on a voltage plateau might correspond to a large SOC spread.

In order to quantify the SOC spread associated with the variation in as-received OCVs and RCVs, the cells’ pseudo-OCV curves were calculated by averaging the C/25 charge and discharge curves for a representative cell of each batch, as shown in Figure A4. For the NMC cell, the C/25 charge and discharge are close together and the pseudo-OCV curve does not showcase specific regions of inaccuracy. By reporting the as-received OCVs on this curve, it can be determined that the cells were shipped at a high SOC (84%) and that their spread of more than 100 mV corresponds to a 13% spread in SOC. The cells RCVs were much closer together, with a spread of less than 1% at BOD and around 3% at EOD. For the LFP cells, there are much more pronounced differences between the C/25 charge and discharge and, as a result, the calculated pseudo-OCV has two regions where the SOC estimation might not be trustworthy. The first one is at high voltage between 88 and 95% SOC, where the additional high voltage phase is clearly visible. From the C/25 charge and discharge, it can be determined that this cell has a blended PE with around 10% of the high voltage phase, likely a nickel-based layered oxide. However, since the voltage response of the LFP and of this phase are completely separated, the high voltage phase is seeing all the current at the beginning of discharge and at the end of charge. As a result, the local current density is not the applied C/25 but around C/2.5 (100% of the current on 10% of the electrode) [44,45], which explains the additional polarization. The second area of concern was the 0 to 10% SOC region, where it seems that in charge the beginning of the graphite lithiation is missing. This is likely due to kinetic limitations on the PE at EOD, which lowers the potential of the electrode preventing the full delithiation of the graphite [46]. In any case, the spread of the as-received OCVs and BOD RCVs are in a region where the SOC estimation should be trustworthy. It can be determined that the cells were shipped almost fully charged (99.2% SOC) with a spread of around 1.5%. For the BOD RCVs, the spread was below 1%. The EOD RCVs unfortunately sit in a region where the pseudo-OCV curve is not accurate. Nonetheless, it can be estimated that the EOD RDVs at C/2 seemed to spread between 0 and 20% SOC, therefore the observed 56 mV is significant, with four cells having a much higher EOD SOC than others.

The SOC estimations also allowed the calculation of the capacity ration (QR), in %Qnom/%SOC because of the anonymization of the data, which is our third attribute to characterize cell-to-cell variations [43,47]. Using this capacity ration, the rate capability, the specific resistance, and the extent of the cell-to-cell variations can be plotted in three dimensions at the same scale for both cells, as shown in Figure 3a and Figure 3b, respectively, for the NMC and LFP cells. Using this representation, it can be observed that the overall cell-to-cell variations were smaller for the NMC cells but that, for both chemistries, most of the cells fell within 2σ around the mean. The biggest outliers were observed for the LFP cells, with four cells having a much higher resistance, which were the same cells with the much higher EOD RCVs.

Figure 3c,d presents the incremental capacity signature of all the cells at both C/5 in blue and C/2 in red. For the NMC cells, Figure 3c, the IC response is close for all the cells and what was expected for the chemistry with a shoulder at high voltage (A), a main peak (B), and small broad last peak (C) not visible at C/2. For the LFP cells, Figure 3d, the response is also the expected one with two main peaks (A and B) and a smaller peak at low voltage (C). Some small intensity is also present at high voltage because of the layered oxide (D). The C/5 data are consistent, but some C/2 discharges were noisy, especially the four cells with higher resistance (* on Figure 3d).

Based on the results of the cell-to-cell variations analysis, only NMC cells within 1.5σ and LFP cells within 1.75σ on all three attributes were selected for the two DoEs.

3.2. Cycle Aging DoE

Figure 4 presents the evolution of the normalized capacities, rate capabilities, and resistances as a function of the cycle number for the NMC and LFP cells. For ease of visualization, the cells tested at 20 °C are plotted in blue and the cells tested at 35 °C in red. The type of lines refers to the DOD_EOD and the symbol to the DOD_BOD. From Figure 4a,b, the spread of capacity loss ranges from 10% to close to 30% depending on the conditions. The cells tested at 20 °C up to low DODs_BOD (blue dotted lines) seemed to lose capacity the least, whereas all the cells tested at 35 °C experienced more capacity loss, especially for higher DODs_BOD. Looking at the rate capabilities, Figure 4c,d, it remained rather stable for the LFP cells. For the NMC cells, it increased a little at first then remained mostly stable at 20 °C, although it shows sign of decay for some conditions towards the end of the test. At 35 °C the rate capability started to degrade significantly after 2000 cycles. Values above one likely resulted from calibration issues or inaccuracies at lower currents.

Finally, the resistance for the NMC cells was multiplied by up to 2.5 in the worst case, Figure 4e, with a mostly linear increase for all experiments. The resistance seemed to increase less for the cells tested at 35 °C but some acceleration and variability started to be visible for some experiments towards the end of the tests for the same cells that experienced a lowering of the rate capability. For the LFP cells, the resistance seemed to increase more for the 35 °C experiments (up to ×4) and less for the 20 °C ones (<×2), as shown in Figure 4f.

Figure 5 presents the evolution of the IC signature for the cells with the least (top row) and most (bottom row) capacity loss for the NMC (left column) and LFP (right column) cells. For ease of visualization, peak movement was represented by colored arrows. For the NMC cells, it can be seen that, in the case of the least capacity loss, Figure 5a, the local minima in charge around 3.75 V between A and B moved towards higher voltages, the main peak B shrank from the lower voltages in charge and higher voltages in discharge, and the low voltage peak C broadened in discharge and moved towards higher voltages in charge. For the cells with the most capacity loss, Figure 5b, the evolution of the local minima is similar but peak B almost disappeared while moving towards higher voltages in charge, whereas peak C broadened in both charge and discharge while moving towards higher voltages. The IC evolution for all the other experiments sits in between and is provided in Figure A5 for C/25 and Figure A6 for C/6.

For the LFP cell with the least capacity loss, Figure 5c, the two main peaks A and B showcased a similar slight decrease in both charge and discharge while the low voltage peak C moved towards lower voltages. Looking at the high voltage phase and peak D, insert in Figure 5c, it remained quite stable but the intensity of its low voltage side increased. For the cell with the most capacity loss, Figure 5d, the peak A went down until disappearing while B only decreased a little. All peaks also seemed to move slightly towards lower voltages in charge. Finally, the high voltage front peak increased first before significantly decreasing, while the overall area decreased, insert in Figure 5d. The IC evolution for all the other experiments also sits in between and is provided in Figure A7 for C/25 and Figure A8 for C/6.

3.3. Calendar Aging DoE

Figure 6 presents the evolution of the normalized capacity, rate capability, and resistance for the calendar aging DoE on the NMC (left column) and LFP (right column) cells. Results were color coded for the temperature from dark blue (lowest temperatures) to light blue, green, then red (highest temperatures). The marker type indicates the resting DOD. In terms of capacity loss, the NMC cells lost about twice as much as the LFP cells, Figure 6a,b, with up to 25% loss for the highest temperature and lowest DOD compared to 10% for the LFP cells under the same conditions. For the rate capabilities, similar to what was observed for the cycle aging experiments, they increased first for the NMC cells before stabilizing, as shown in Figure 6c. It degraded only for the cells calendar aged at 40 °C and 0% DOD after more than two years of aging. The rate capabilities remained stable for all LFP cells, as shown in Figure 6d. For all experiments but the one aged at 40 °C and 0% DOD, where the resistance doubled for both chemistries, the resistance increases were below 50%, as shown in Figure 6e. For the LFP cells, the resistances even appear to remain stable or even decrease after 20 months of calendar aging, as shown in Figure 6f.

Looking at the variations in the voltage responses for the cells with the least and most capacity loss, Figure 7, for both chemistries, it can be seen that for NMC cells with the least capacity loss, Figure 7a, not much changed except a shift towards higher voltages. For the cells with the most capacity loss, Figure 7b, the changes are quite similar to the ones observed for the cycle aging experiments. The IC evolution for all the other experiments is provided in Figure A9. For the LFP cell with the lowest capacity loss, Figure 7c, the main LFP peak A broadened in charge, but no intensity change was observed in discharge. Peak B did not appear to change much, peak C moved slightly towards the lower voltages, and there was little impact of the high voltage phase other than its front peak increasing in charge. For the cell with the most capacity loss, Figure 7d, all the peaks seemed to move towards the lower voltages. In addition, peak A intensity went down in charge and discharge, with no significant intensity change on the other peaks. To the contrary of the NMC cells, this is quite different from what was observed for the cycle aging experiment. The IC evolutions for all the other experiments are provided in Figure A10.

4. Discussion

DoE Analysis

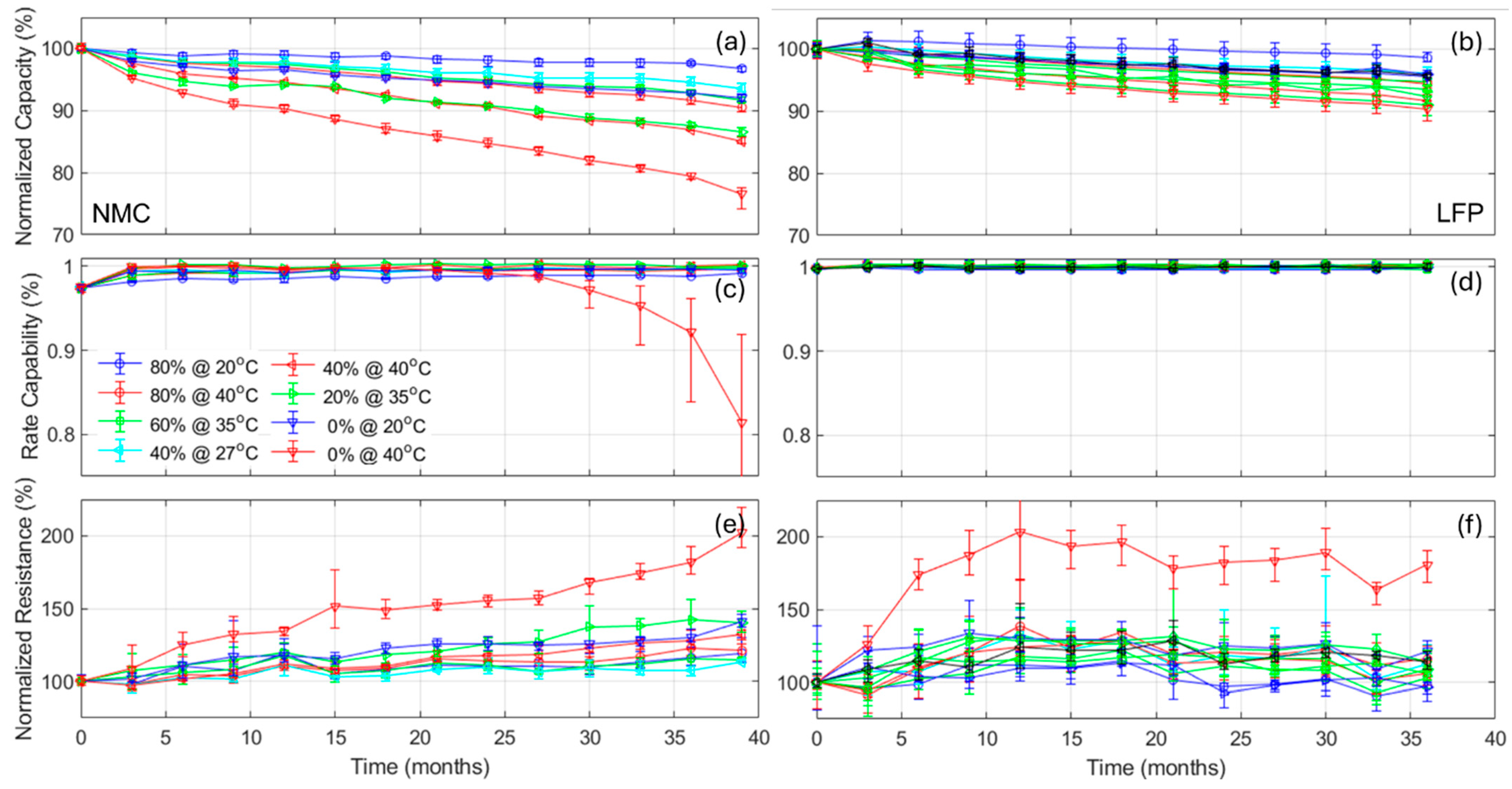
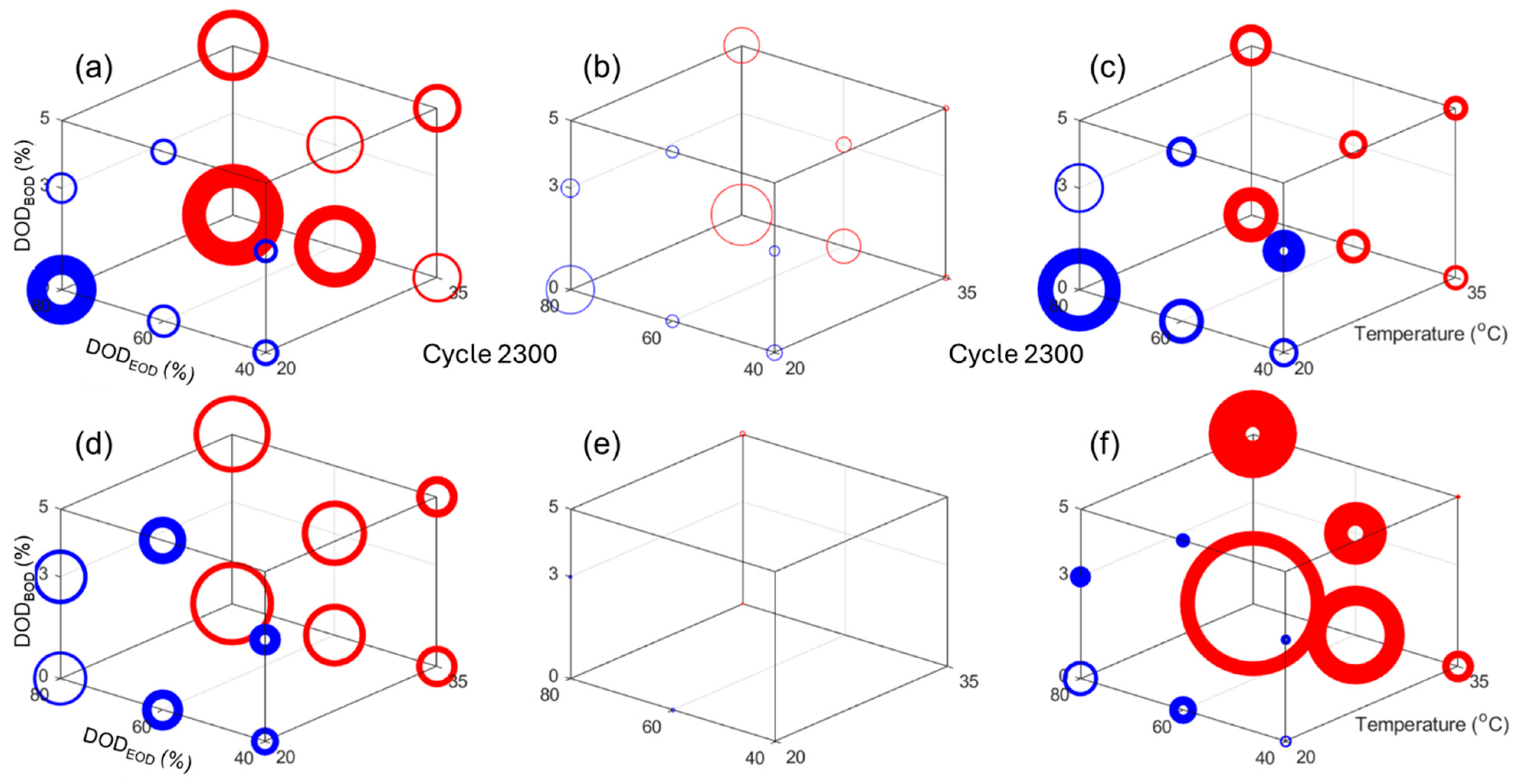
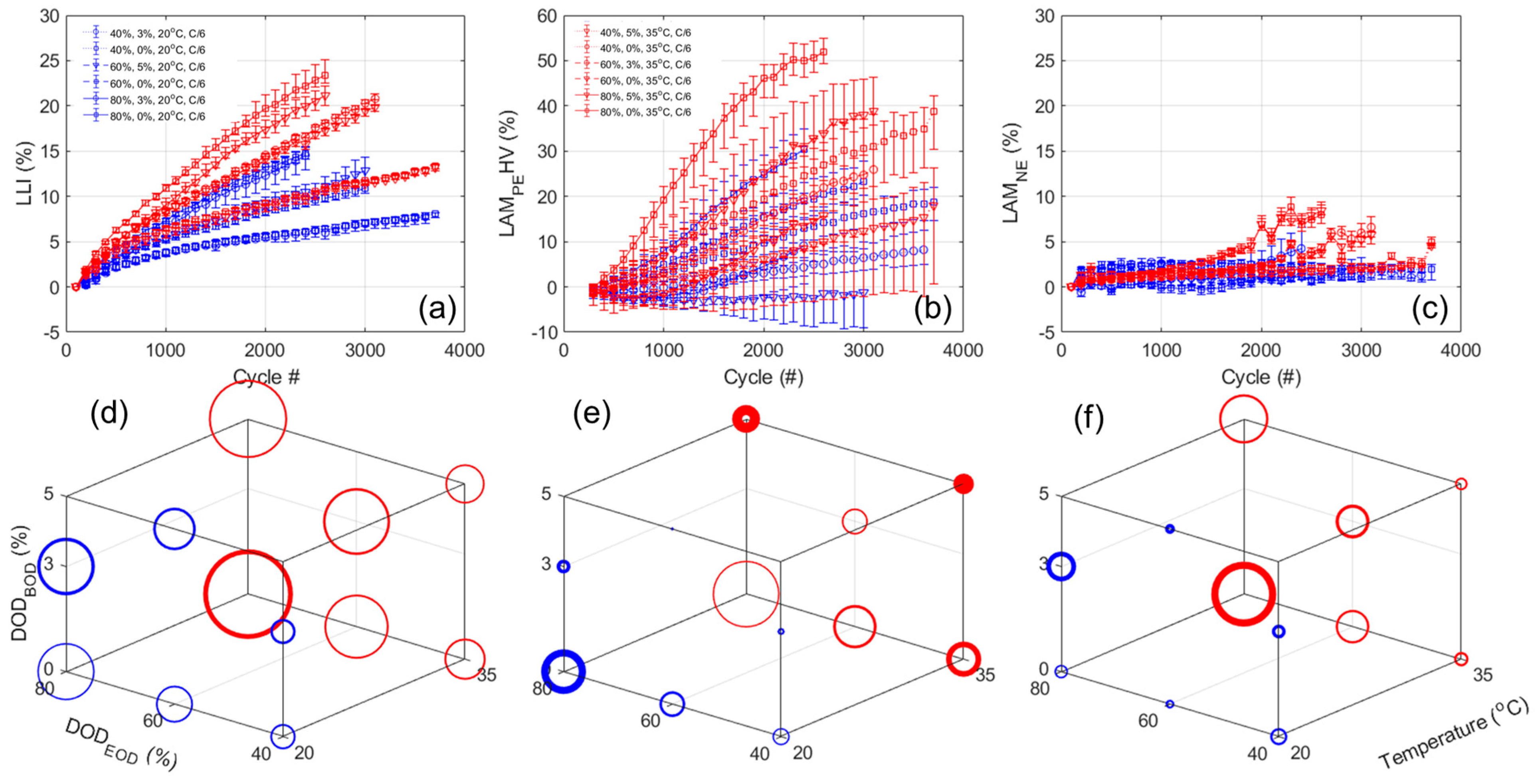
Because of the number of experiments, it is difficult to visualize the impact of the different DoE factors (temperature, DOD_EOD, and DOD_BOD) on the different responses in Figure 4. The impact is better visualized by using the 3D representation presented in Figure 1a. Figure 8 presents the impact of the design factors on (a, d) the capacity loss, (b, e) the rate capability deviation from 100%, and (c, f) the normalized resistance increased for cycle 2300, which is the highest common cycle between all the experiments for the NMC and LFP cells, respectively. In Figure 8, the circle size is proportional to the changes and the line width is proportional to the deviation within the replicates. The scale was also kept consistent between chemistries. Looking at the capacity loss, Figure 8a,d, there is a clear direct impact of temperature, a direct impact of the DOD_EOD, and the smallest impact seemed to be DOD_BOD, which is inverted (more loss for lower DODs_BOD). All impacts seemed slightly larger for the NMC cells, but overall they seem close. For the rate capabilities, Figure 8b,e, there was no change for the LFP cells, but for the NMC ones, the impacts seemed similar to the one observed on capacity losses. For the normalized resistances, Figure 8c,f, the impact order also seemed to be the same, but this time temperature affected the LFP cells much more than the NMC ones.

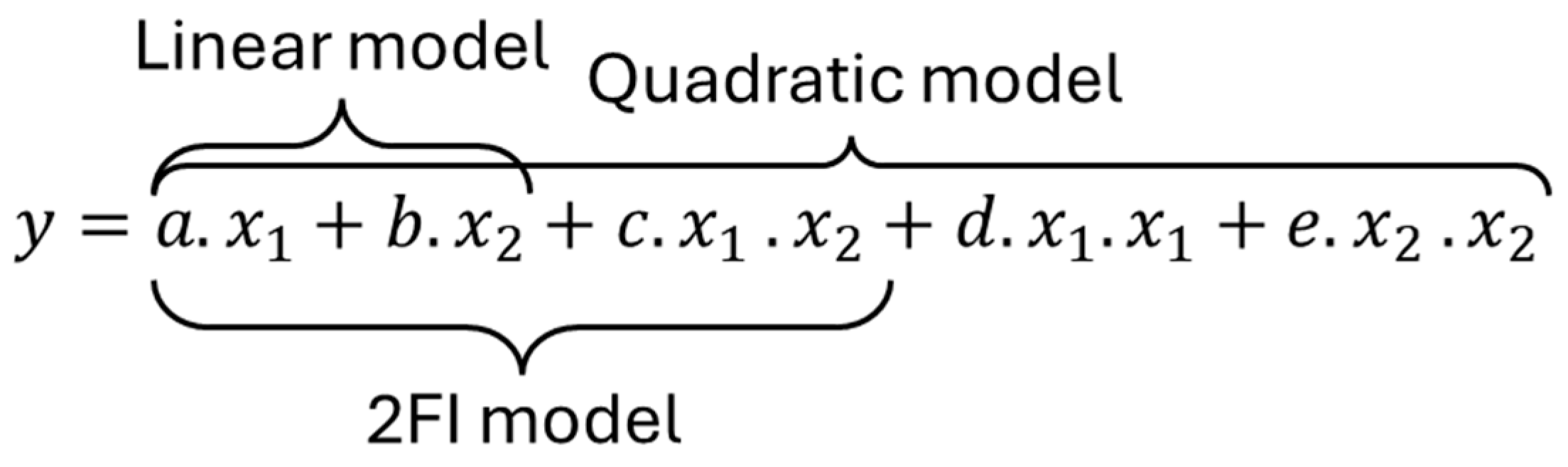
To quantify the impact of the different design parameters, the capacity, rate capability, and normalized resistance changes after 2300 cycles were analyzed using an ANOVA, of which the results are summarized in

Table A4. Summary of the coded parameter value for the capacity, RC, and R changes at cycle 2300. Parameters in italics indicate that their individual p-value was above 0.05.

	NMC			LFP
	Q	RC	R	Q	RC	R
Intersect	13.63	0.85	76.43	14.42		78.67
Temperature	4.84	0.15	−11.75	3.20		50.33
DODEOD	3.46	0.63	29.75	5.52		41.36
DODBOD	−1.90	−0.29	−11.38	−0.18		−35.52
T × DODEOD						40.35
T × DODBOD						−17.06
DODEOD × DODBOD						−36.96
R2	0.93	0.64	0.76	0.96	0.14	0.66
p-value	0.0001	0.01	0.002	0.0001	0.26	0.0077
F-value	50	7	13	89		39

. For the NMC cell, the best statistical metrics were obtained for a linear model where the p-values were the only ones below 0.05, and where the R²s were of 0.93, 0.64, and 0.76, respectively, for the capacity, rate capability, and resistance changes. The 2FI models offered slightly higher R² values (0.95, 0.77, and 0.86) but their p-values were above the threshold. For the LFP cells, the capacity loss could also be fitted best with a linear model, whereas the RC changes were not significant enough (p-value > 0.19), which was expected since negligible changes were observed. The normalized resistance changes were best fitted with a 2FI model with combined effects of the temperature and DODs (similar p-value but much higher R² and F).

Because of the coded variables, the weights for each parameter of the fitted equations can be compared directly. For the capacity loss, the impact of temperature was found to be larger for the NMC cells than for the LFP ones (4.84 vs. 3.20), whereas the opposite is true for the DODs_EOD (3.46 vs. 5.52), which is consistent with Neumann at al. [35]. The DODs_BOD had an inverse impact on both cells but they were only significant for the NMC cells (−1.90 vs. −0.18). Overall, this confirms the observations from Figure 7, and there were therefore differences in the impact of the three parameters depending on cell PE chemistry. The results for the LFP cells contradicts the observations by Xiong et al. [26] as the impact of DOD_EOD was larger than the one of temperature and DOD_BOD. This could be due to different additives in the electrolytes or to the different discharging schedule. For the results for the NMC cells, the impact ordering was consistent with the literature [22]. For the rate capability changes, the model for the LFP cell was not significant because the variations were negligeable, Figure 4, and, for the NMC cell, while the p-value for the model was overall below 0.05, the individual p-values for temperature and DOD_BOD were not significant. It therefore seemed that the DOD_EOD had the only significant impact on the changes of rate capability for the NMC cells. Finally, looking at the changes in normalized resistances, the results were also PE chemistry dependent. For the NMC cells, the biggest impact was for the DOD_EOD (29.75) with the temperature and DOD_BOD having similar inverse impacts (around −11). For the LFP cells, the highest impact was for the temperature (50.33), followed by the DOD_EOD (41.36), which was larger than the one for the NMC cell, as observed in Figure 8. The DODs_BOD also had a much more significant inverse impact (−35.52) on the LFP cells and there were also noteworthy combined effects (over 35 for temperature and DOD_EOD and between DODs, −17.06 for the temperature and DOD_BOD).

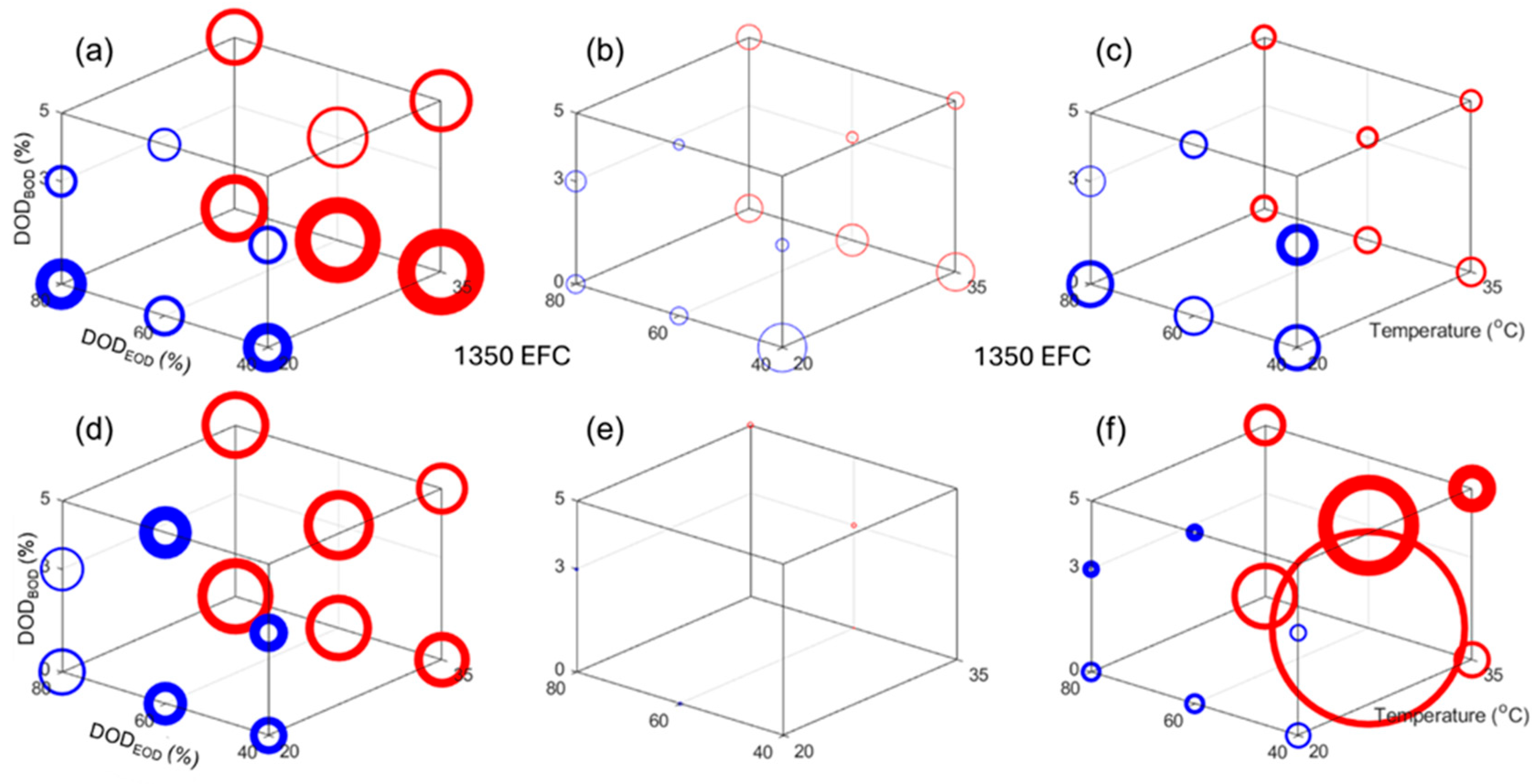
Because the cells cycled from different DODs_BOD and to different DODs_EOD, the cycle number might not be the best way to compare the results, and an equivalent full cycle scale (efc) allowed comparison of the results on a common exchanged capacity scale. The equivalent of Figure 8, but after 1350 efc instead of 2300 cycles, is provided in Figure A11. From this representation, it seemed that the impact of temperature remained, but that the impact of the DOD_EOD diminished. This was confirmed by the ANOVA analysis,

Table A5. Summary of the coded parameter value for the capacity, RC, and R changes after 1350 efc. Parameters in italics indicate that their individual p-value was above 0.05.

	NMC			LFP
	Q	RC	R	Q	RC	R
Intersect	14.70		66.29	14.48
Temperature	4.22		−13.86	3.23
DODEOD	−0.84		−1.86	2.39
DODBOD	−1.56		−10.87	−0.20
T × DODEOD
T × DODBOD
DODEOD × DODBOD
R2	0.69	0.21	0.11	0.94	0.24	−0.11
p-value	0.0001	0.19	0.008	0.0001	0.37	0.17
F-value	87		17	65

, that showed a lowering of the coded DOD_EOD parameter from 3.46 to −0.84 for the NMC capacity loss, from 29.75 to −1.86 for the NMC resistance increase, and from 5.52 to 2.39 for the LFP cell capacity loss. In all three cases, the other parameters were stable. All the other models (rate capability for both and resistance for LFP) were not significant because the variations were small and within cell-to-cell variations.

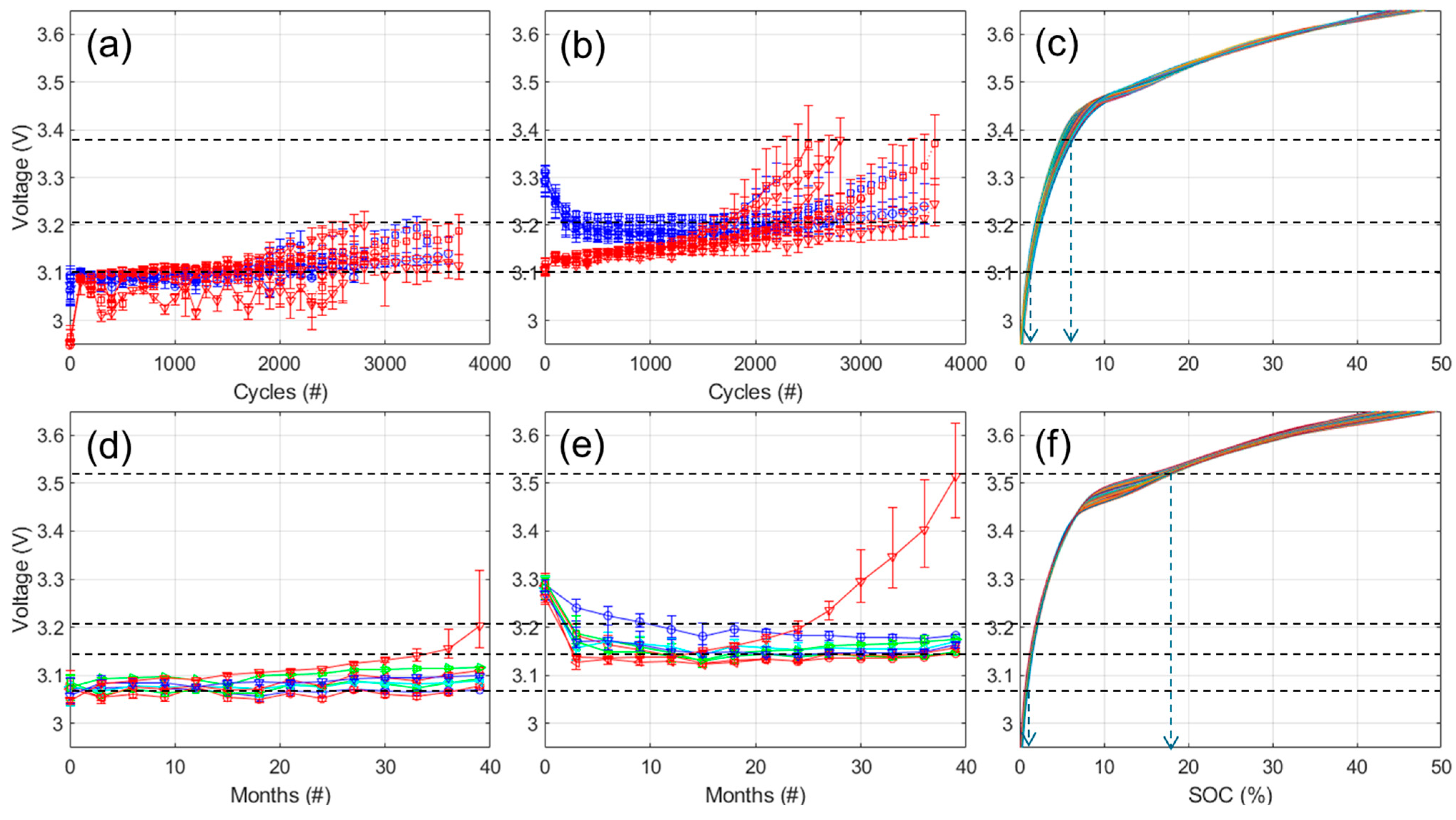
Figure 9 presents a similar visualization for the calendar aging experiments, where a similar impact of DOD on both chemistries can be seen, but a much larger impact of temperature on the NMC cells capacity loss can be observed, as shown in Figure 9a,d. For the rate capabilities, the only significant variation was observed for the NMC cells calendared aged at 40 °C and 0% DOD, as shown in Figure 9b. The normalized resistance increase, Figure 9c,f, seemed to be mild below 35 °C for the NMC cells and 40 °C for the LFP cells. Above those temperatures, the resistance increased more, with an additional impact of DOD, with the lower DODs increasing the degradation. The ANOVA analysis is presented in

Table A6. Summary of the coded parameter value for the capacity, RC, and R changes after 36 months of calendar aging. Parameters in italics indicate that their individual p-value was above 0.05.

	NMC			LFP
	Q	RC	R	Q	RC	R
Intersect	6.51		13.58	5.39
DOD	−4.29		−18.57	−1.97
Temperature	4.82		15.17	2.62
T × DOD	−1.87		−11.43
DOD2	1.30		25.61
Temperature2	1.79		−1.23
R2	1	0.23	0.99	0.92	−0.46	0.5
p-value	0.0009	0.17	0.02	0.0008	0.81	0.31
F-value	9200.00		104.00	40

. Sadly, the models for the rate capabilities and the LFP resistance increase were not significant. For NMC cells’ capacity loss, the best fit was obtained for a quadratic model (although the p-value for the linear one was also below 0.05), which showcased a similar impact but with opposite signs for the temperature and SOC (around 4.5). The combined and square effects were lower and around 1.5. For LFP cells; the best fit was obtained for a linear model with an impact close to twice as small than of the one observed for the NMC cells with a slightly larger impact of DOD (−1.97 versus 2.62). This is consistent with the literature [38], where NMC was shown to have significant combined effects, but not LFP, and where LFP’s DOD impact was larger than the temperature one. Lastly, for the NMC resistance, the best statistics were obtained for a quadratic model with a strong impact of the DOD (−18.57 and 25.61 squared). The temperature only had a significant impact non-squared values (15.17). The combined effect of DOD and temperature was the smallest (−11.43). This analysis confirmed the observations from Figure 9.

The results analysis can be pushed further with the quantification of the degradation modes [4,42], both thermodynamics, LLI and LAMs, and kinetic, rate degradation factor, and ohmic resistance increase, the latest being equivalent to the specific resistance increase and thus already covered. 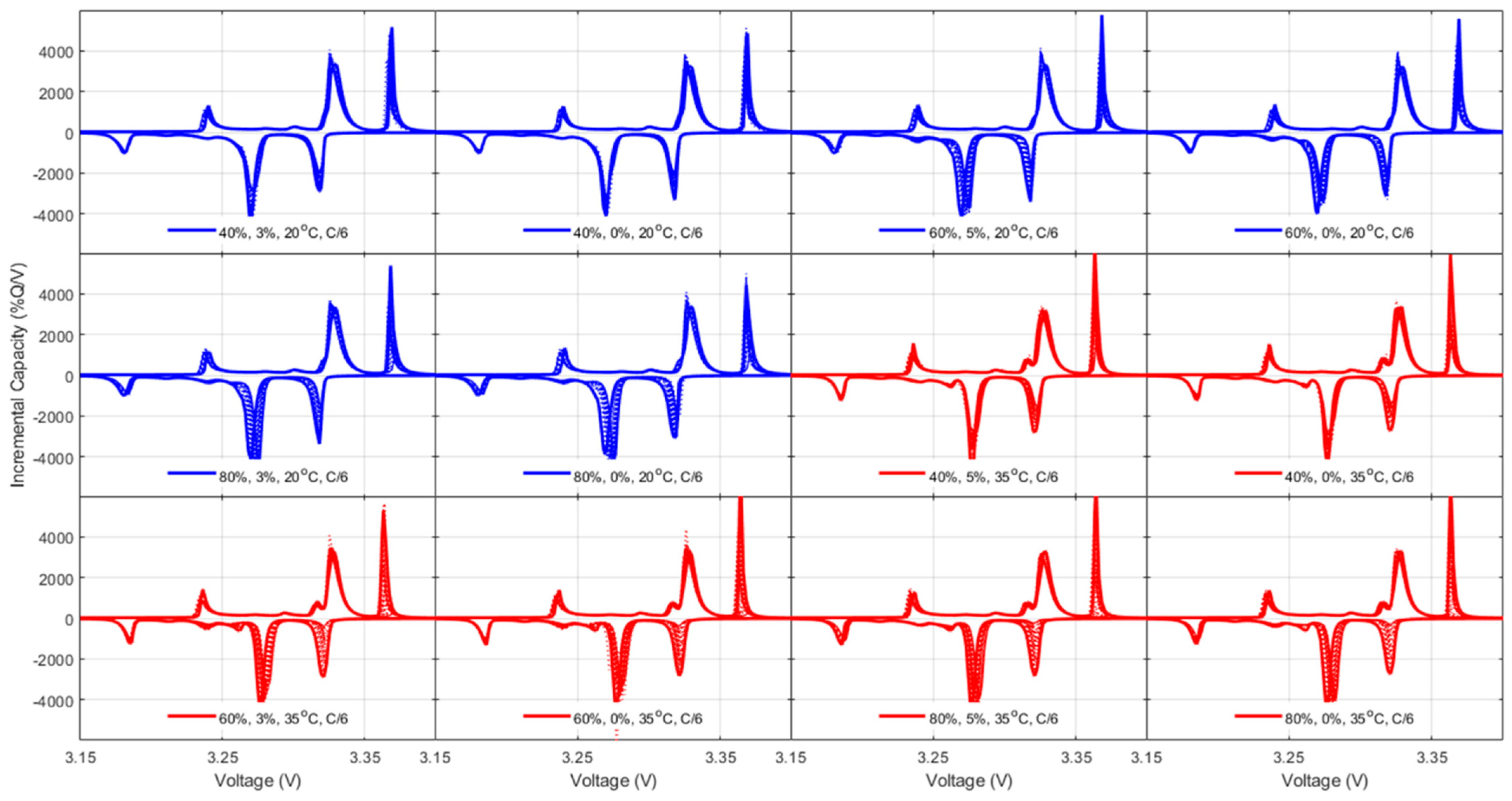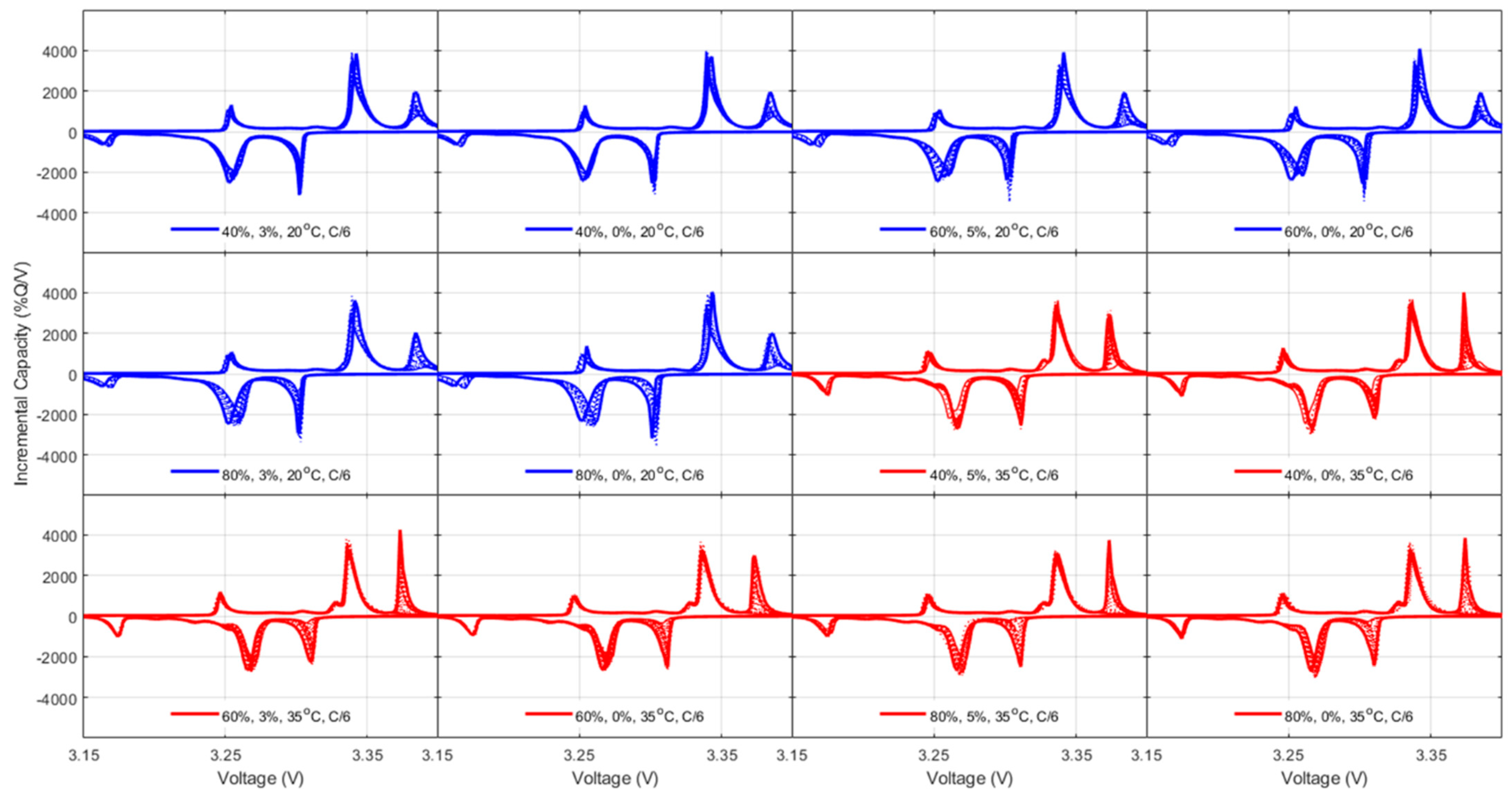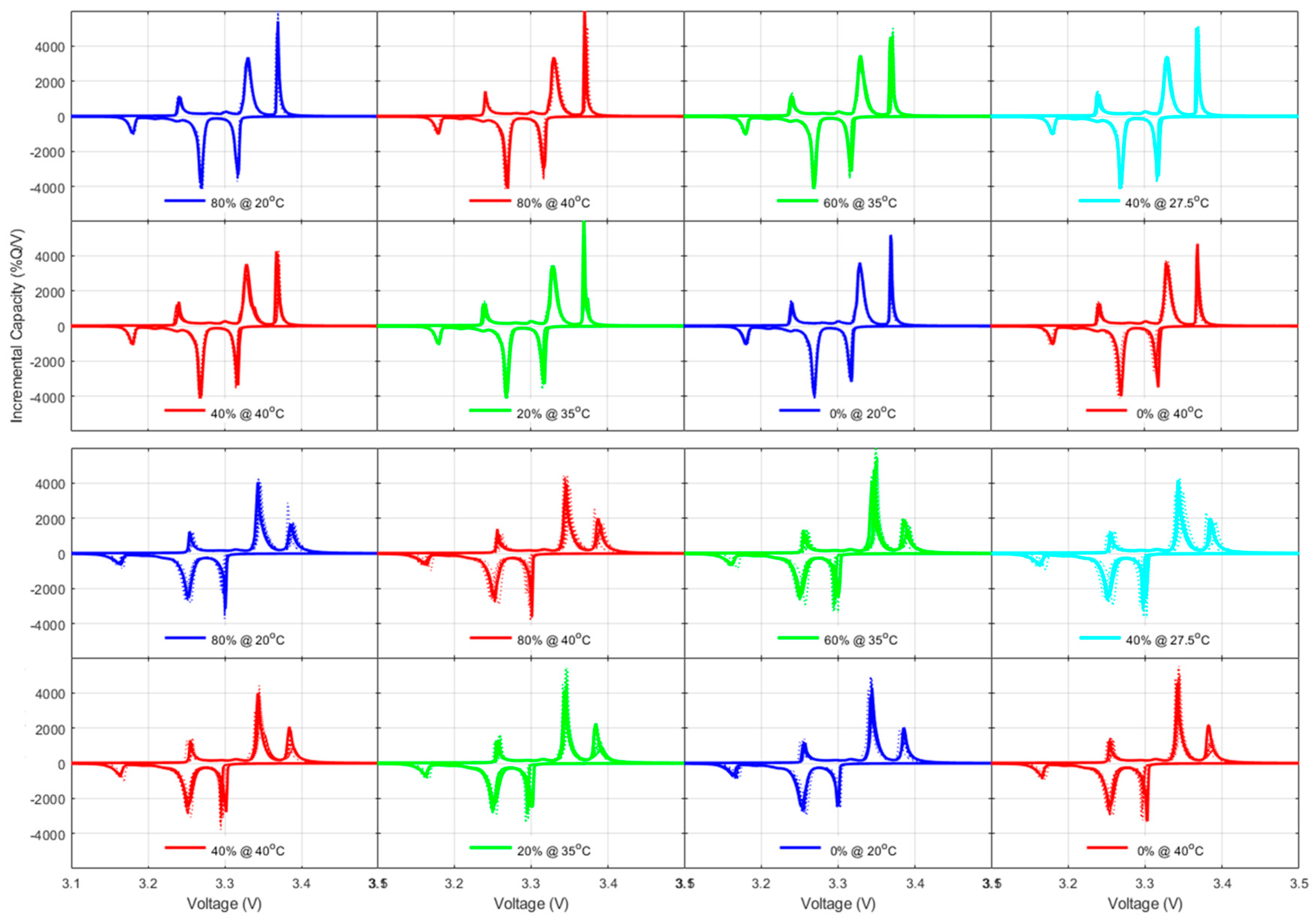For the thermodynamic ones, a closer analysis to the changes in the voltage response of the cells upon aging, Figure 5, Figure A5 and Figure A7 allowed quantification of the LLI and LAM_PE for the NMC cells and the LLI, LAM_NE, and LAM_PE on the high voltage phase for the LFP cells, following guidelines from the literature [48].

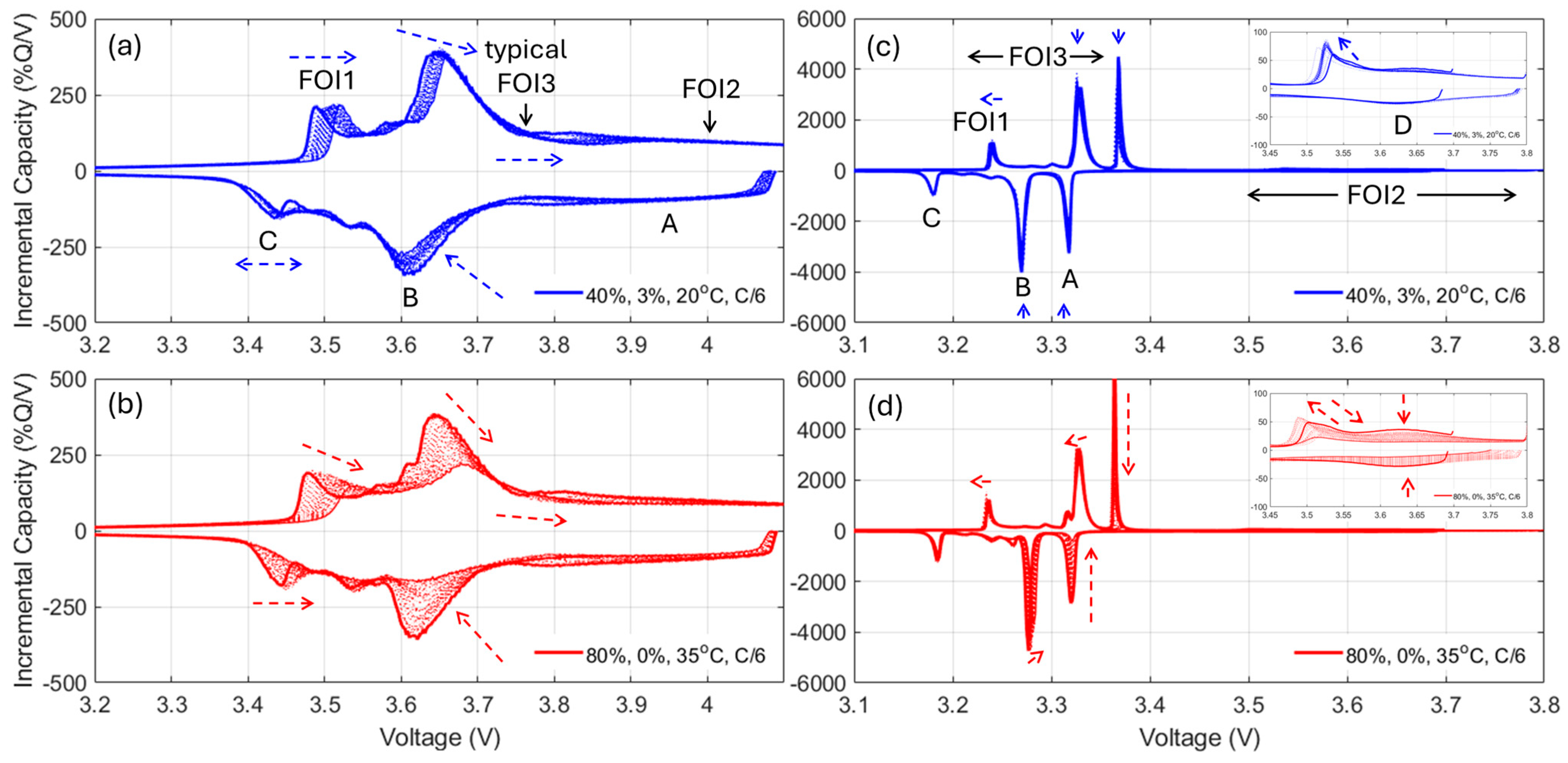
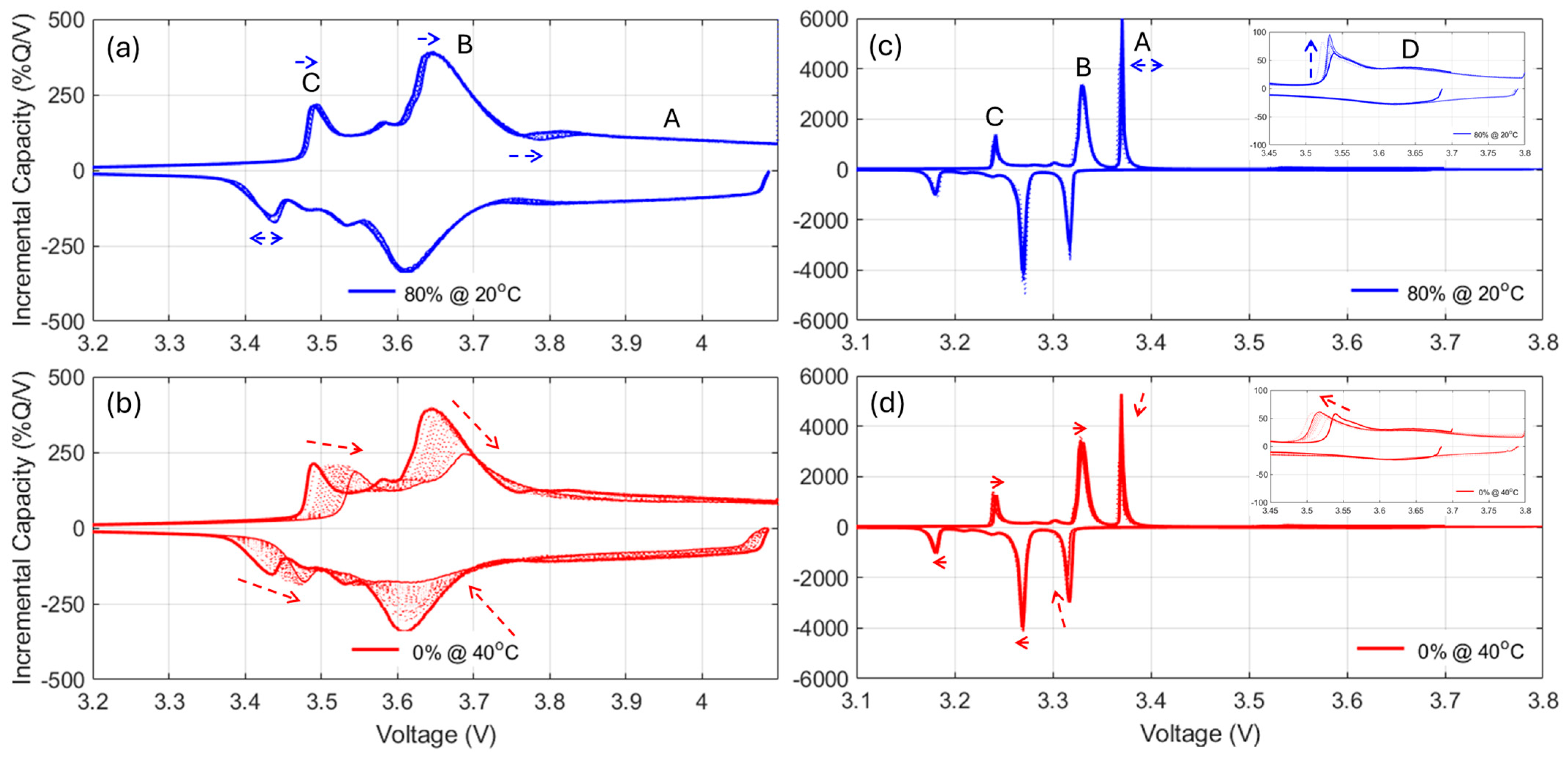
For the NMC cells, since FOI1 is always present and moving towards higher voltages, it can be concluded that the NE remained limiting at EOD [48]. Therefore, the capacity loss can only be imputable to the LLI. The LLI is thus directly proportional to the capacity loss with a ratio of about 0.9, assuming a 10% offset between the PE and the NE. For the NMC chemistry, the LAM_PE can be directly inferred from the changes of intensity of the high voltage shoulder (FOI2). The LAM_NE is much harder to decipher automatically, especially when kinetic limitations are present, since the usual FOI to use is the area between the beginning of charge and the local minima after the main peak (FOI3). In this work, unfortunately, this local minimum is not visible for most of the conditions, and the LAM_NE could not be deciphered using this method. 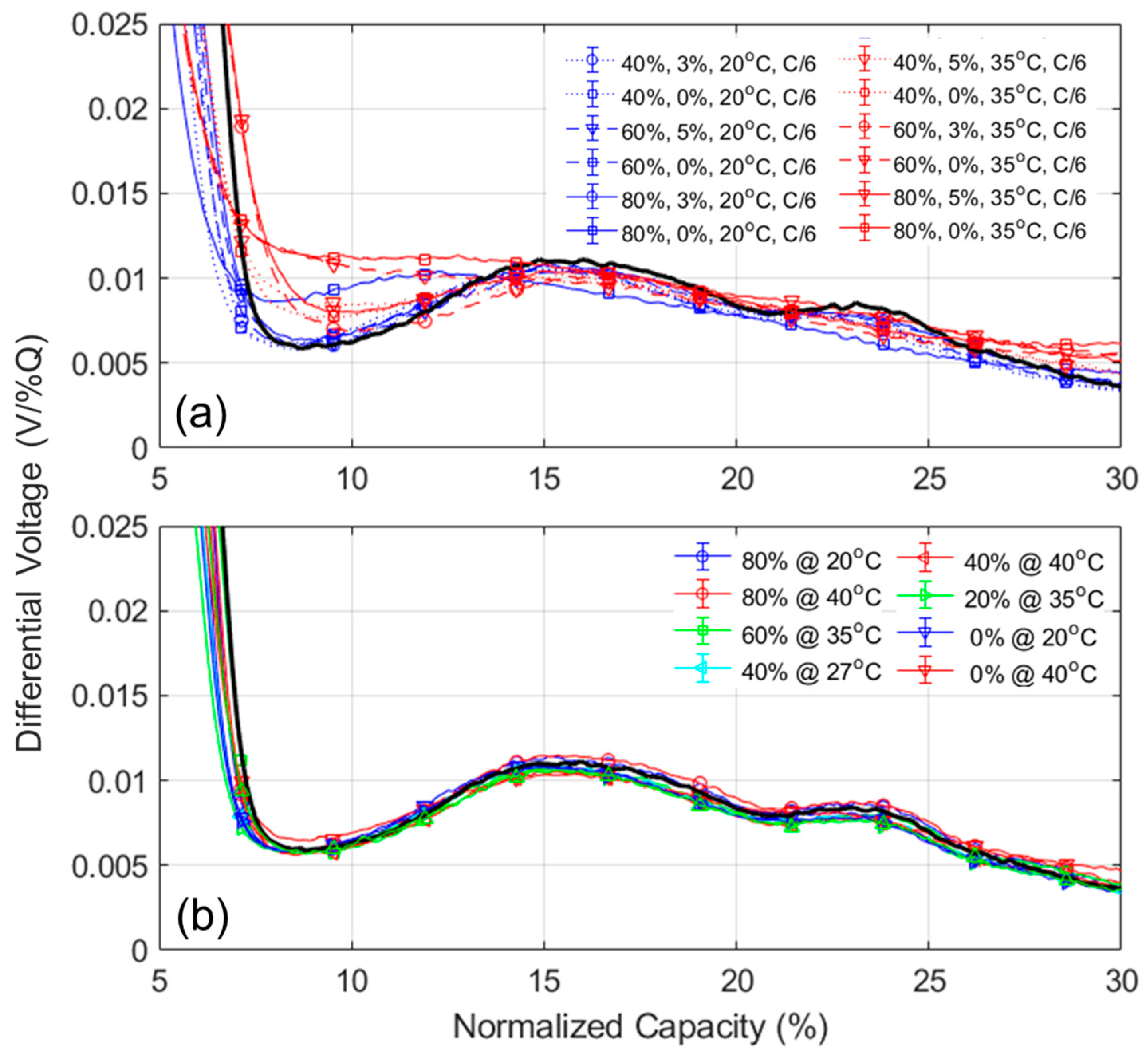A typical alternative solution is to investigate the other derivative of the voltage curve, the differential voltage (DV, dV/dQ = f(Q)), Figure A12, with the tracking of the capacity difference between the center graphitic peak and BOD or another low-capacity peak. Sadly, for the same reasons as for the IC method, this is not working when kinetic limitation occurs because the peak is broadened. Figure A12 showcased the DV variations for the most degraded cells for both the cycle aging (left column) and calendar aging (right column) at both 20 °C (top row) and 35 °C (bottom row). While the center peak is clearly marked initially, it quickly fades for most of the experiments, especially at 35 °C. A possible solution is to use a less desirable configuration and the capacity between the beginning of charge and the first of the low-capacity graphitic peaks, FOI4. As can be seen on Figure A12, this peak was not affected much by the kinetic limitations and remained clearly visible throughout most of the experiments.

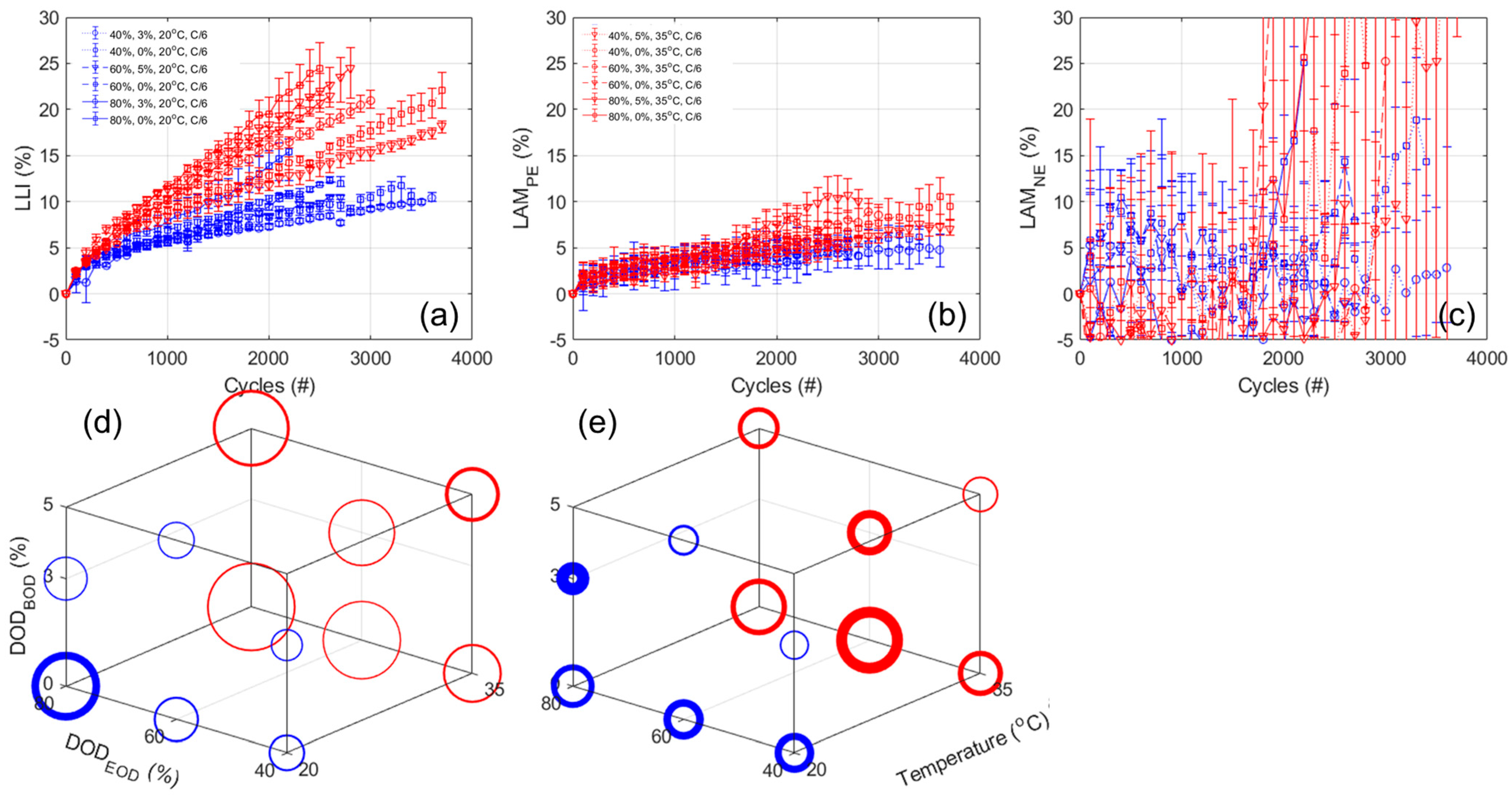
Figure 10a,b,c presents the evolution of the estimated LLI, LAM_PE, and LAM_NE, respectively, with Figure 10d,e displaying the 3D representation of the results after 2300 cycles for the LLI and LAM_PE. The results for the ANOVA analysis are provided in

Table A7. Summary of the coded parameter value for the LLI, LAM_PE, and LAM_NE after 1350 efc. Parameters in italics indicate that their individual p-value was above 0.05.

	NMC			LFP
	LLI	LAMPE	LAMNE	LLI	LAMPEHV	LAMNE
Intersect	13.54	6.28		12.70	15.81	3.36
Temperature	3.52	1.55		2.87	6.74	1.47
DODEOD	2.87	0.47		4.75	5.64	1.80
DODBOD	−1.45	−0.64		−0.25	−11.18	−0.21
T × DODEOD					2.67
T × DODBOD					−0.86
DODEOD × DODBOD					−5.43
R2	0.94	0.68		0.93	0.97	0.61
p-value	0.0001	0.0067		0.0001	0.012	0.01
F-value	66	9		95	60	7

. For the LLI, and unsurprisingly, the results are similar to the one observed for the capacity loss, with a bigger impact for temperature (3.52 from the ANOVA analysis), then the DOD_EOD (2.87), and finally a lower inverse impact for the DOD_BOD (−1.45). For the LAM_PE, there seems to be mostly an impact of temperature, which is confirmed by the ANOVA analysis (1.55, 0.47, and −0.64, respectively, for temperature, DOD_EOD, and DOD_BOD). From the LAM_NE, the automatic quantification is unfortunately very noisy, Figure 10c, and the variations between replicates cover the same range as the evolution with cycle. However, a closer look at the variations cell by cell, Figure A14a allowed the estimation that no significant LAM_NE was occurring for all but three cells, the one tested up to 60% and 80% DOD from 0% at 20 °C and the one tested up to 60% DOD from 0% at 35 °C, that likely experienced around 5% LAM_NE only starting to occur from the latest 600 cycles; however, a more precise quantification is not possible without significant modeling which was out of the scope of this work.

Concerning kinetic limitations, Figure 10 and Figure A12 showcased significant peak broadening. This is confirmed by an analysis of the RCVs at EOD, Figure A13a,b, that showed an increase with cycle number, especially for the higher rate. When compared to the pseudo-OCV curves calculated from each state of health, Figure A13c, this kinetic induced undercharge accounted for up to 5% capacity loss for the higher rate, which explains the lowering of the rate capability. Because the broadening is visible at the beginning of charge, it is likely induced by kinetic limitations on the NE because, while the NE is undergoing several phase transformations, the PE is only undergoing one, which should go fast initially, but a quantification without modeling is not possible.

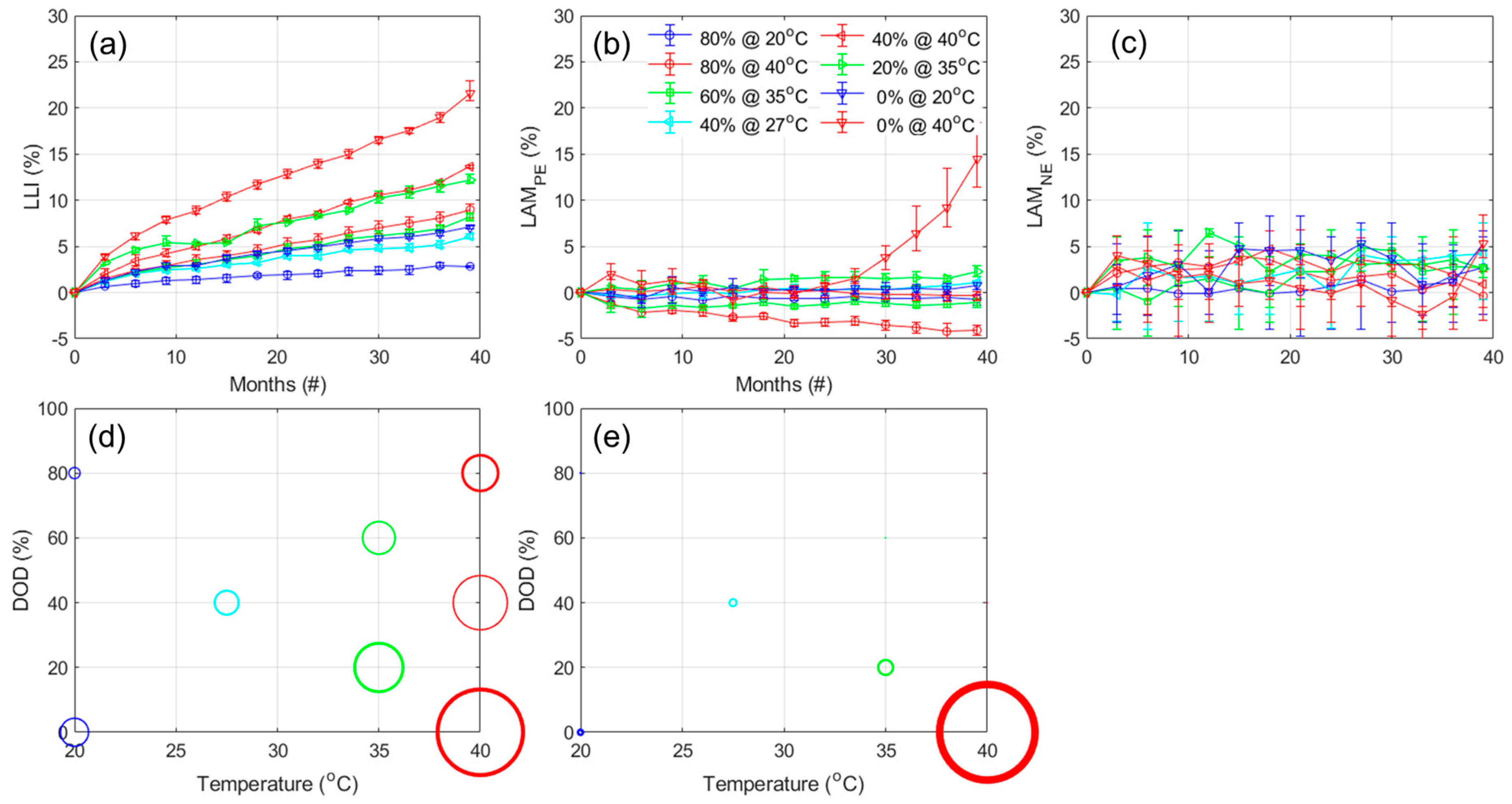
Figure 11 presents the results for the calendar aging experiment using the same representation for the NMC cells. For the LLI, similar to what was observed for the capacity loss, the cells calendar aged at higher temperatures experienced more degradation. The impact of temperature and DOD are close but of opposite sign (5.1 vs. −4.07, respectively). Looking into the LAM_PE, it appears limited for every experiment except the one where the cells were left fully charged at 40 °C, where the LAM_PE gradually increased to 15% in the last year of aging. The ANOVA analysis,

Table A8. Summary of the coded parameter value for the LLI, LAM_PE, and LAM_NE after changes 36 months of calendar aging. Parameters in italics indicate that their individual p-value was above 0.05.

	NMC			LFP
	LLI	LAMPE	LAMNE	LLI	LAMPEHV	LAMNE
Intersect	7.02	1.23		4.56
DOD	−4.07	−4.60		−1.67
Temperature	5.10	1.45		2.33
T × DOD	−2.01	−4.05
DOD2	1.54
Temperature2	1.54
R2	0.83	0.74		0.91	0.1	0.35
p-value	0.06	0.04		0.0009	0.32	0.14
F-value	119	8		39

, showcases that the main impacts were the one of the DOD and the combined one (−4.60 and −4.05, respectively), with a much lower one for the temperature (1.45), which was not significant. For the LAM_NE, the results were again too noisy for automatic analysis. Looking on a cell-by-cell basis, Figure A14b, there does not appear to be any LAM_NE for the calendar aging experiments. Moreover, no significant broadening of the peaks was observed whether in IC or DC, Figure 7 and Figure A14; therefore, there does not appear to be any significant kinetic limitations. This is confirmed by looking at the evolution of the RCVs, Figure A13c,d, which remained rather stable with the exception of the cells aged at 40% fully charged. In that case, the RCV increased but it is likely because of the high LAM_PE where the PE might have become limiting for the C/6 discharge. This is an example where the limiting electrode at EOD is changing with the rate. As such, the capacity loss is solely from the LLI at C/25 but entirely from the LAM_PE at C/6.

For the LFP cells, for the same reasons as for the NMC cells, the LLI can also be directly inferred from capacity loss, FOI1. Since the NE remained limiting at EOD, the LAM_NE can be directly calculated from the change of area between the beginning of charge and the end peak B (FOI2) [48]. For the PE, the LAM for LFP and the high-voltage layered oxide phase must be separated. Sadly, the LAM_LFP is not quantifiable because the voltage response is flat and because it is not limiting at BOD nor EOD. This was confirmed by verifying that the shape of peak C did not change, which implied that the discharges always stopped on the plateau and not in a region where the potential of LFP changed. The LAM_PEHV can be estimated for the changes in the area above 3.5 V where LFP cannot contribute any capacity (FOI2). Figure 12a,b,c presents the evolution of the LLI, LAM_PEHV, and LAM_NE, respectively, versus cycle number. Figure 12d–f presents their evolution in the 3D representation in the same order after 2300 cycles. The results for the ANOVA analysis are provided in Table A7. Just as for the NMC cells, the LLI variations are similar to the one of the capacity losses with a bigger impact of DOD_EOD (4.75), followed by temperature (2.87) and DOD_BOD (−0.25). For the LAM_PEHV, significant losses were estimated, with up to 50% for 35 °C experiments with low DOD_BOD. The ANOVA analysis indicated a significant impact of the DOD_BOD (−11.16), close to twice as big as the impact of temperature (6.74) and DOD_BOD (5.64). Some significant combined effects were also identified, especially between the DODs (−5.43). Interestingly, some conditions did not seem to introduce any loss and even a gain of active material (e.g., up to 60% DOD from 5% at 20 °C). This is likely induced by the impact of the LLI. Indeed, with the LLI, the NE is pushed towards higher SOC, therefore its potential towards EOC will increase. As a result, the PE cutoff potential will also increase to match the cutoff voltage and more of the HV phase will be used. Looking into the LAM_NE, it appeared quite limited (<3%) for all 20 °C experiments but seemed to accelerate for the 35 °C one after 1000 cycles (up to 10% in the worst case). The ANOVA analysis indicated a similar impact for the temperature and DOD_EOD (1.5 and 1.80) and almost no impact of the DOD_BOD (−0.21), without any combined effects. Finally, no kinetic limitations were observed on the voltage response of the cells nor on the evolution of the RCVs.

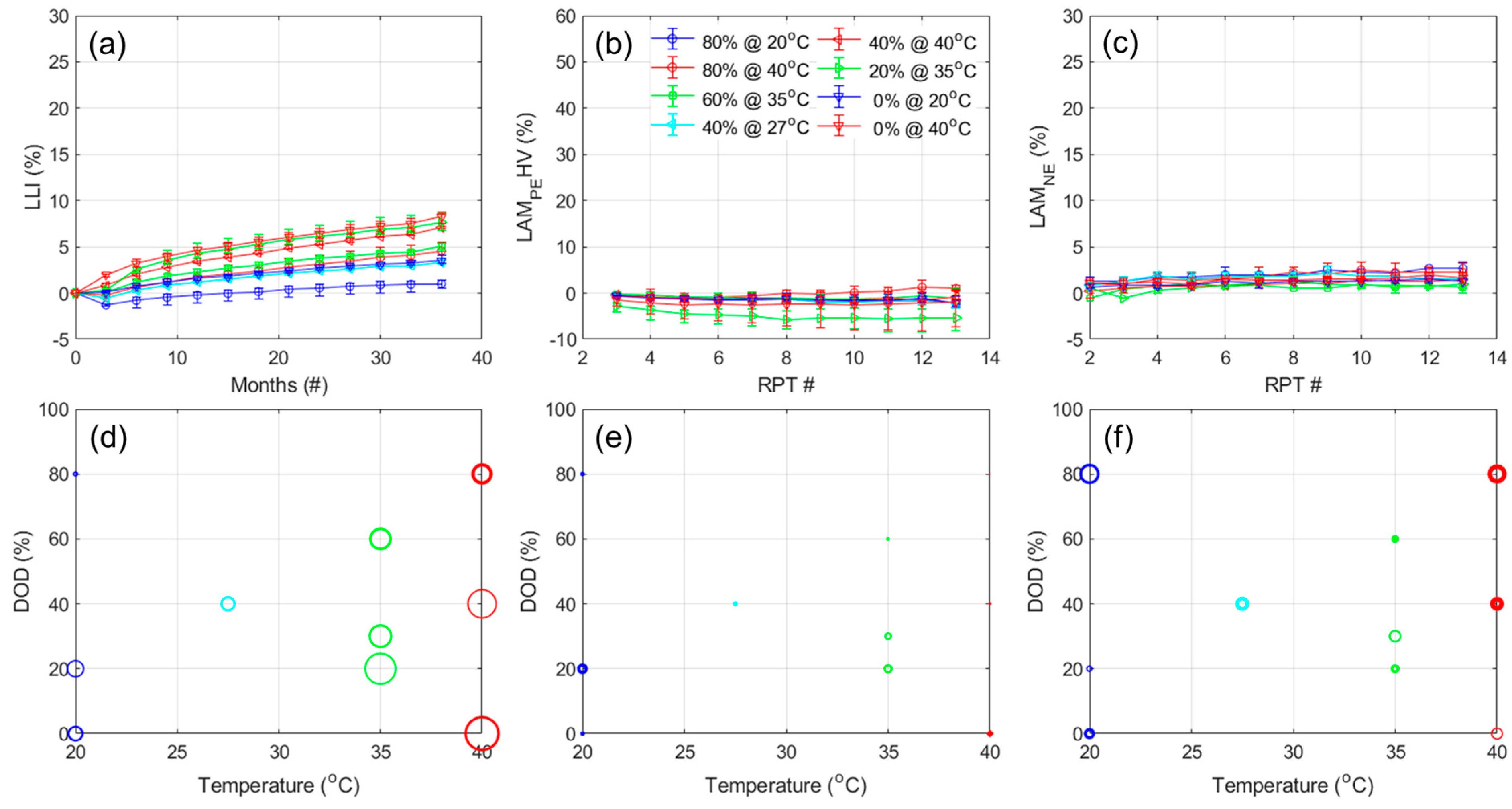
Figure 13 presents the results for the LFP calendar aging experiment. The results for the ANOVA analysis are provided in Table A8. The LLI evolution matched the capacity loss with a maximum below 10% after three years of calendar aging, fully charged at 40 °C. The biggest impact was the one of temperature (2.33) over DOD (−1.67). The LAM_PEHV seemed to mostly decrease with aging, likely for the same reason mentioned above. No statistically sound model was found to cover the observed variations (p-value > 0.36). The LAM_NE was really limited and stayed below 3% independently of the conditions. With all the values being close, no statistically significant model was found (p-value of 0.14 minimum). Finally, similar to the cycle aging experiment and the calendar one for the NMC cells, no significant kinetic limitations were detected.

5. Conclusions

This work tested two different commercial batteries of different chemistries, NMC532 and LFP, for more than three years under both cycle aging and calendar aging conditions. Investigating first the cell-to-cell variations, it was found that they were small, with all but four cells below 2σ around the mean, which were overall lower for the NMC cells.

The cycle aging experiment investigated the impact of temperature, DOD_EOD, and DOD_BOD. By using a design of experiments and an analysis of variance it was possible to quantify the impact of each factor. After 2300 cycles, while both cells lost about the same capacity, there was a 20% bigger impact of the temperature versus DOD_EOD on the NMC cells but the opposite for the LFP cells with a 65% larger impact of DOD_EOD over temperature. DOD_BOD, a proxy to the impact of the charge cut-off voltage, only had half the impact of the others on NMC cells capacity loss and almost no impact on the LFP cells. This was not the case for the resistance increase where DOD_BOD had the almost the same impact as temperature for the NMC cells, although it was almost three times smaller than the impact of DOD_EOD. For the LFP cells, it was also significant but the lowest of the three. The LFP cells’ resistance was much more sensitive to temperature than the NMC ones (more than four times higher effect of opposite sign as temperature reduced the resistance for the NMC cells). Investigating the degradation modes, the LLI was found to be proportional to the capacity loss for both cells. The LAM_PE was found to be around half of the LLI for the NMC cells with similar impacts. The LAM_NE was found to be limited for most cells other than the ones tested from 0% DOD_BOD along with significant kinetic limitations. For the LFP cells, the LAM_LFP could not be quantified but the LAM on the high voltage phase was found to be significant, especially for the low DOD_BOD and 30 °C. The LAM_NE was found to be small and mostly influenced by temperature and DOD_EOD.

In terms of calendar aging, it was found that the NMC cells lost about twice as much capacity than the LFP cells after three years. For the NMC cells, the impact of temperature and DOD was about the same, whereas the temperature had about a 25% higher impact on capacity loss than the DOD for the LFP cells. Looking at the resistance, the increase was limited for both chemistries, and mostly driven by DOD, but with a combined effect with temperature. In terms of degradation modes, no significant LAM_NE nor kinetic degradation were observed and the LLI remained proportional to the capacity loss for all the C/25 experiments and all but one of the experiments at C/6 for the NMC cells tested at 40 °C and 0% DOD, where the LAM_PE appeared to take over. For all the other experiments, the LAM_PE appeared limited.

Overall, both batches of cells performed well and only passed the 20% capacity loss mark after 1750 cycles under the worst conditions (highest temperature, highest DOD_EOD, and lowest DOD_BOD). Under more auspicious conditions, capacity losses around 10% were observed after three years of testing and up to more than 3500 cycles, which provided useful information for cell selection, as well as pack design and sizing towards the final application. If those cells are to be continuously used, their performance appears to be quite similar, but if long calendar aging periods are required, the LFP cells might be a better choice as the observed capacity losses were twice as small.