Abstract
This paper explores the stability and dynamics of a three-dimensional evaporating/condensing film while falling down a heated/cooled incline. Instead of using the Hertz–Knudsen–Langmuir relation, a more comprehensive phase-change boundary condition is employed. A nonlinear differential equation is derived based on the Benny-type equation, which takes into account gravity, energy transport, vapor recoil, effective pressure, and evaporation. The impact of effective pressure and vapor recoil on instability is studied using a linear stability analysis. The results show that spanwise perturbations can amplify the destabilizing effects of vapor recoil, leading to instability. Energy transport along the interface has almost no effect on the stability of the system, but it does influence the linear wave speed. Nonlinear evolution demonstrates that, in contrast to the vapor recoil effect, effective pressure can improve stability and delay film rupture. The self-similar solution demonstrates that the minimal film thickness decreases as and under the dominance of evaporation and vapor recoil, respectively.
1. Introduction
The evaporation/condensation of liquid films is ubiquitous in nature and technological systems with numerous applications, such as ice formation on aircraft wings, liquid films in mammalian lungs, heat exchanger design, and seawater desalination cooling systems [1,2,3,4]. As there exists a complex interaction of mechanisms, including vapor recoil, thermocapillarity, and van der Waals forces, several studies have revealed the importance of these factors’ effects on the stability of films [5,6,7,8]. A detailed review of long-scale models for evaporative thin films has been examined by Oron et al. [9], as well as by Craster and Matar [10] and Chattopadhyay et al. [11].
A number of theoretical studies targeted at describing these films and their potential to destabilize have been conducted to examine the issue of flat thin-film stability. The earliest stability studies focused on non-evaporating films falling down an inclined plane [12,13,14]. Yih [15,16] and Benjamin [17] demonstrated linear stability analyses of the falling thin-film model. Their findings suggested that this basic state is unstable in long-wavelength perturbations. Based on their works, Benney [18] derived an evolution equation for the film thickness, known as the Benny equation, and expanded the analysis of falling films into the nonlinear regime. After that, Williams and Davis [19] created a nonlinear stability model for which they carried out a numerical analysis for a finite perturbation. Comparing to the linear model, the results of their nonlinear model showed that the time to rupture was shortened and the needed perturbation wavelength was changed to one with a smaller value. These conclusions are supported by Sharma and Ruckenstein [20], who added Marangoni effects, and the stability of the film was found to be improved by the nonlinear effects associated with Marangoni motion. In recent studies, the understanding of interfacial phenomena at the microscopic level has been greatly enhanced by advanced experimental techniques. For instance, high-energy X-ray reflectivity measurements have provided significant insights into the hydrophobic gap at the water–octadecyl-trichlorosilane interface, showing the existence of a molecular-scale density deficit at the interface [21]. Similarly, investigations into the capillary wave dynamics of thin liquid polymer films have elucidated the behavior of liquid surfaces at nanometric thicknesses, contributing to our knowledge of surface tension and molecular interactions in confined systems [22].
In the context of liquid films, the Marangoni effect can play an important role in determining stability and flow behavior. Davis [6] examined Marangoni effects on thin-film stability, which mostly focused on thermocapillary effects. This analysis showed that hydrodynamic instabilities, which appear as 2D and 3D surface waves, are powered by heat gradients. The investigation of evaporating and condensing thin liquid films on a hot inclined plane by Bankhoff [23] demonstrated the impact of phase shift on thin-film stability. The findings of the study found that evaporation from the surface has a destabilizing effect, while condensation has the opposite influence, which was recently proved by [24]. Thus, thermocapillarity potentially becomes one of the most researched phenomena in fluid mechanics, which leads to variations in surface tension and can amplify the runaway effect as warmer liquid from the depression is dragged towards the cooler areas of the interface.
Sreenivasan and Lin [25] used the linear theory to study the onset of surface tension-driven stationary circulation in a thin-film flow down a heated incline. Their results were supported by Kelly et al. [26], who investigated the impact of a temperature-dependent surface tension with long-wavelength disturbances. While many studies have adopted a uniform heated plane [27,28,29], Scheid et al. [30] were more concerned with the instabilities of thin-film flow over a localized heater to determine the influence of the temperature from the inclined plane. Similarly, Gambaryan-Roisman [31] investigated how the non-uniformity of substrate thermal conductivity affected the hydrodynamics and heat transport in thin liquid films while taking surface tension, thermocapillarity, and evaporation into account. Recently, a two-dimensional flow of a thin film over a uniformly heated/cooled slippery inclined substrate was analyzed by Ding et al. [32] to capture the Marangoni effect. They employed a weighted-residual model and a Benney-type model for comparison, and they discovered that the weighted-residual model was more logical than the Benney-type model. To express a thin liquid film flow on a non-uniformly heated, slippery inclined plane, Ref. [33] developed a mathematical model within the framework of the long-wave approximation method.
As volatile processes significantly impact the thermal response of the system in actual circumstances, the Hertz–Knudsen–Langmuir relation was adopted by some researchers to describe the phase-change occurrence at the liquid–vapor interface [5,7,34,35,36,37,38,39]. This relationship is predicated on the idea that mass momentum and energy transfer are unrelated to evaporation and only affect the states of the liquid and vapor phases [40]. Burelbach et al. [5] provided a thorough explanation of how the pertinent equations were derived. As a result of the assumption that the ratios between the densities, viscosities, and thermal conductivities of gases and liquids are very tiny, there is significant simplification and the creation of so-called one-sided models [5]. Instead of applying the traditional Hertz–Knudsen–Langmuir relation, Shklyaev and Fried [41] revisited this problem and imposed the more general equations that Fried et al. [42,43] proposed for expressing the balance of configurational momentum at the liquid–vapor interface. They developed a nonlinear evolution equation determining film thickness, and two new terms were added to their model. One was known as the effective pressure accounting for the vapor recoil, , and the other was the energy transmission within the liquid–vapor interface, . The two terms were stabilized according to the results of a linear stability analysis.
Therefore, in order to discuss the behavior of an evaporation or condensation film under general boundary conditions in three dimensions, we draw on the research conducted by Shklyaev and Fried [41]. We aim to specifically look into how the stability of a system is impacted by spanwise perturbations, effective pressure, evaporation, and vapor recoil. The structure of this paper as follows. Utilizing the long-wave assumption, we develop the mathematical model in Section 2. The linear stability theory is employed to reveal the influences of effective pressure and energy transport along the interface on the stability of the system in Section 3. In Section 4, we investigate the nonlinear evolution of the evaporation/condensation film. A conclusion is made in Section 5.
2. Mathematical Formulation
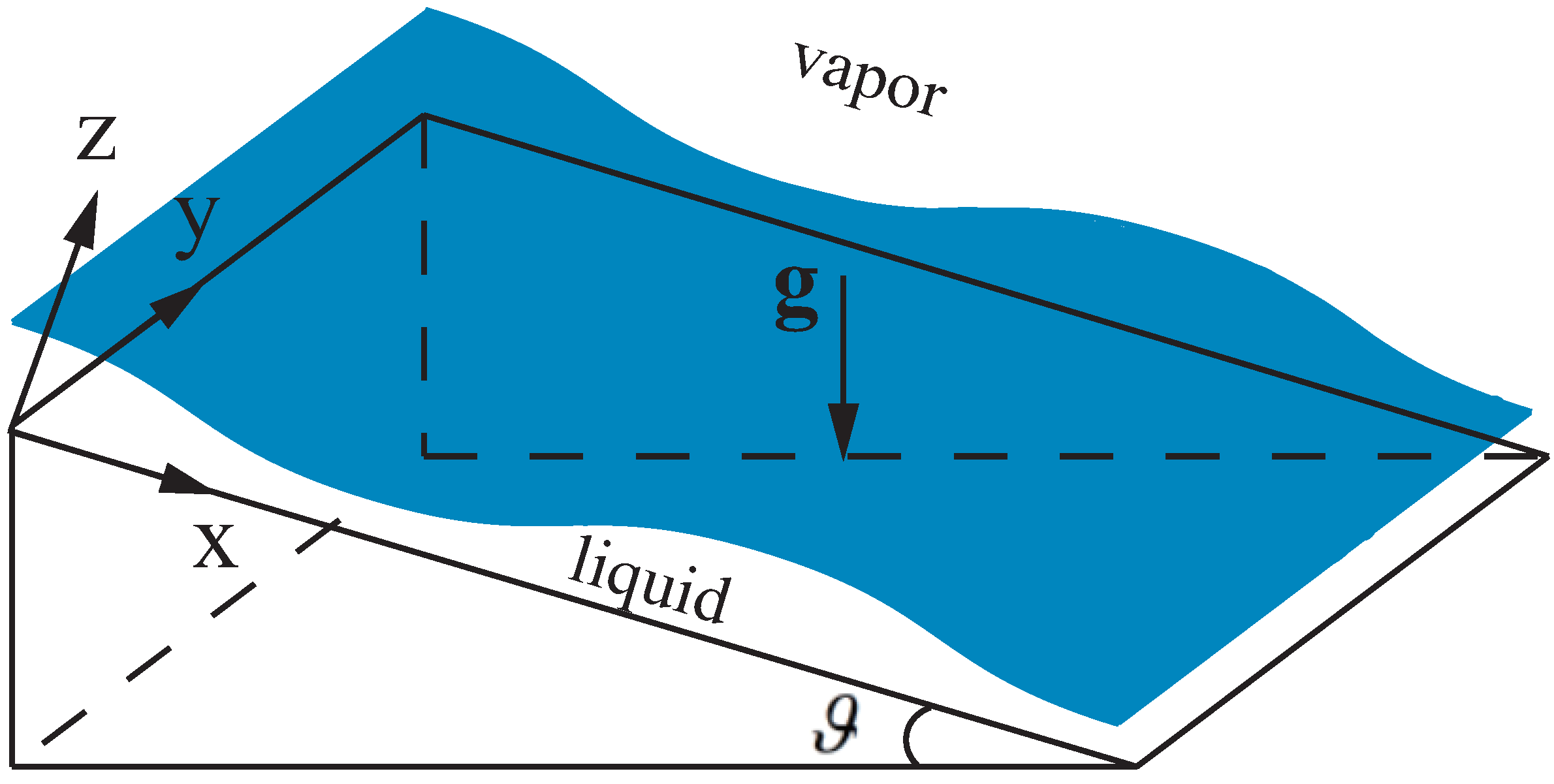
We examine the behavior of a three-dimensional incompressible fluid. It falls down along an inclined plane which is either heated or cooled, as depicted in Figure 1. The angle of inclination is denoted by . The physical properties of the fluid are characterized by its density, kinematic viscosity, and thermal conductivity, denoted by for the liquid phase and for the vapor phase. We assume that the physical properties of the vapor phase are significantly smaller than those of the liquid phase, which can be expressed mathematically as
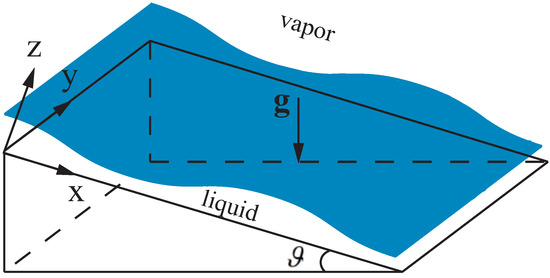
Figure 1.
Schematic of the system.
The dynamics of the liquid film are governed by the continuity equation, the momentum equation, and the energy equation, which can be written as
where is the velocity field and is the Hamilton operator. is the fluid density, p is the pressure, is the dynamic viscosity of fluid, is the gravitational acceleration, and t is time. The temperature and the thermal diffusivity are denoted by T and , respectively. These equations form the basis of numerical simulations and enable us to study the behavior of the liquid film under various conditions.
Here, we consider no slip, no penetration, and a constant temperature condition at the solid wall , which can be written as follows:
At the liquid–vapor phase interface , several conditions need to be satisfied, including mass flux conservation, stress balance, energy balance, and kinetic conditions. The mass flux conservation can be expressed as
where represents the velocity at the interface, is the velocity of the vapor, and is the unit normal vector to the interface.
For the purposes of this study, we assume that the surface tension is linearly dependent on the temperature T. Specifically, we use the following expression to model the temperature dependence of the surface tension:
where and are constants of the interfacial free-energy and entropy densities arising from ; represents the saturation temperature where the liquid and vapor phases are in thermodynamic equilibrium.
The stress balance of the interface conditions is
where is the stress tensor, is the identity tensor, is the surface gradient operator, and is the vapor recoil term, which describes the contribution of the momentum of the evaporating or condensing vapor to the overall momentum balance of the liquid–vapor interface. When the liquid is evaporating, it releases molecules of vapor into the surrounding gas. These vapor molecules have a certain momentum due to their thermal motion, and this momentum can cause a recoil effect on the liquid–vapor interface. Similarly, when vapor condenses back into the liquid, the momentum of the vapor molecules can cause a recoil effect on the interface in the opposite direction.
The energy balance at the liquid–vapor interface is expressed as
where is the curvature of the interface, L is the latent heat of phase change, and is the unit tangent vector on the interface. The left-hand side of the equation represents the energy flux at the interface due to interfacial shear and convection. Note that the term is much smaller than the term in the assumption of the long-wave model; thus, this term can be neglected in this paper [41]. On the right-hand side, the term represents the heat flux as conduction across the interface, while the term denotes the energy released or absorbed since phase change at the interface.
In order to describe the phase-change phenomenon, we utilize the equation proposed by Fried et al. [43]:
where is a modulus associated with the kinetics of attachment and detachment at the interface [41,43]. The term on the right-hand side of Equation (10) is defined as the effective pressure term. The kinetic energy term is much smaller than the other two terms, and is therefore negligible [41]. Wayner took a different approach and discussed the influence of pressure on the evaporating meniscus, where he did not consider the vapor recoil’s influence on the mass flux [44]. However, in the present work we consider the vapor recoil effect and use the model as described in Equation (10).
2.1. Nondimensionalization
We start by introducing the following scales: the initial mean thickness of the film, , , , , , as the length, velocity, time, pressure, temperature, and mass flux scales, respectively. Using these scales, we can nondimensionalize the system of Equations (2)–(10). The resulting nondimensional governing equations are
where , represents the direction of gravity, the Prandtl number is denoted as , is defined as the Reynolds number, and is the dimensionless temperature.
The dimensionless boundary condition at solid wall is
At the liquid–vapor interface, the boundary conditions can be written as
where is the density ratio; is the evaporation number. is the dimensionless surface tension. is the Crispation number, , which accounts for the thermal diffusion along the interface, and is the Marangoni number.
Thus, recall that the dimensionless phase-change condition at the interface becomes
where ; . characterizes how far the system is from thermodynamic equilibrium, and expresses the magnitude of the effective pressure.
The dimensionless form of the kinematic condition of the moving interface is
where , , and are the partial derivations of liquid film thickness h.
In this paper, , N, and are the three important dimensionless parameters that we will focus on to study the influences of the effective pressure, the interfacial energy transport, and the vapor recoil effect on the dynamics of the film.
2.2. Long-Wave Model
The long-wave model is a common simplification used to study the dynamics of thin liquid films in which the characteristic length scales of the system are much larger than the mean film thickness. In this model, the governing equations are derived by assuming that the perturbations in the film thickness, velocity, and temperature vary slowly in the streamwise and spanwise directions.
To derive the long-wave model for our system, we introduce the small parameter , where l is the characteristic length scale of the system. In this paper, we fix , which means that the characteristic length l is much larger than the mean film thickness , and this is a typical assumption for thin liquid films. Based on the long-wave assumption, we make the following transformation:
For ease of writing, we will omit the wave number symbol in the following statements.
We use the perturbation method to study each physical quantity of the system, assuming that the solution of the parameter follows a power law with respect to . We expand the variables in powers of as shown below:
Substituting Equations (22)–(27) into governing Equations (11)–(13) together with using boundary conditions (14)–(20), we can derive a set of long-wave equations that describe the dynamics of the liquid film with the leading order and first order in term . These equations involve the dimensionless parameters , , N, E, and S, which were defined in the previous section.
The leading orders of the system are
With the velocity and temperature boundary conditions at ,
and at ,
It is easy to obtain the solution of the following parameters:
The first orders of the system are
And the first-order boundary conditions at are
At the liquid–vapor interface, the first-order boundary conditions are
Integrating twice with respect to in Equation (44), while incorporating boundary conditions Equations (50) and (48), yields
We can also obtain that the velocity component in the y direction is
Note that to investigate the effects of these parameters we rescale the parameters as , which is shown in the above equations. The term was neglected due to its much smaller magnitude compared to the unity.
With the rescaling parameters, the integral form of kinematic condition Equation (20) can be written as
Substituting the velocity into the kinematic equation, we obtain the evolution equation of the film thickness :
where
and , with
where
The equation presented in Equation (56) is the same as the one given by Shklyaev and Fried [41] when and . Additionally, it is identical to the equation presented by Burelbach et al. [5] when .
The values of were originally proposed by Shklyaev and Fried and Wei et al. [41,45] for water, sodium and 1,2-Ethanediol. In this paper, we assume that the film thickness is macroscopic at about ∼ mm and that the system is primarily governed by hydrodynamic effects and heat transfer rather than intermolecular interactions. Thus, the Van der Waals force can be neglected, together with kg m−3, 10−4 N m−1K−1, 106 kg m−2s−1, (10−3∼1) K, (0.01∼0.1) Nm−1, (102∼103) K, (1∼10) Wm−1 K−1, (105∼106) J kg−1, and ∼10−6) m2s−1, where the evaporation and vapor recoil effects are the dominant factors. The value ranges of dimensionless parameters in this paper are as follows: ranges from to , is in the range , is in the range , is in the range , is in the range , the Prandtl number is fixed at , and the inclined angle is fixed at . The evaporation number E is in the range of . When E is positive, the system is evaporating. When , it is a nonvolatile film; otherwise, it is condensing. We discovered that the thermocapillary effect destabilizes the system.
3. Linear Stability Analysis
First, we conduct a linear stability analysis of the system. We consider a small perturbation of the base state of the system by using normal mode analysis. Specifically, the perturbation is expressed as , where and represent the streamwise and spanwise wavenumbers, respectively. is the complex growth rate; the real part represents the effective growth rate, which characterizes the rate where the perturbation either grows or decays in time; and the imaginary part is related to the wavespeed.
The base state of the system was investigated through the resolution of Equation (56), which is expressed as follows:
It should be noted that is a parameter that is used to define the base state of the system, which can change with time. The value of is usually chosen to be a specific value, while the value of t changes continuously as times progresses, and it is used to track the evolution of perturbation over time. Furthermore, Equation (67) demonstrates that an evaporating film will desiccate within a definite time frame of .
For the leading-order problem, the dispersion relationship was obtained:
We also tested the first-order dispersion relationship, and the growth rate is expressed in by ; the detailed expression is shown in Appendix A.
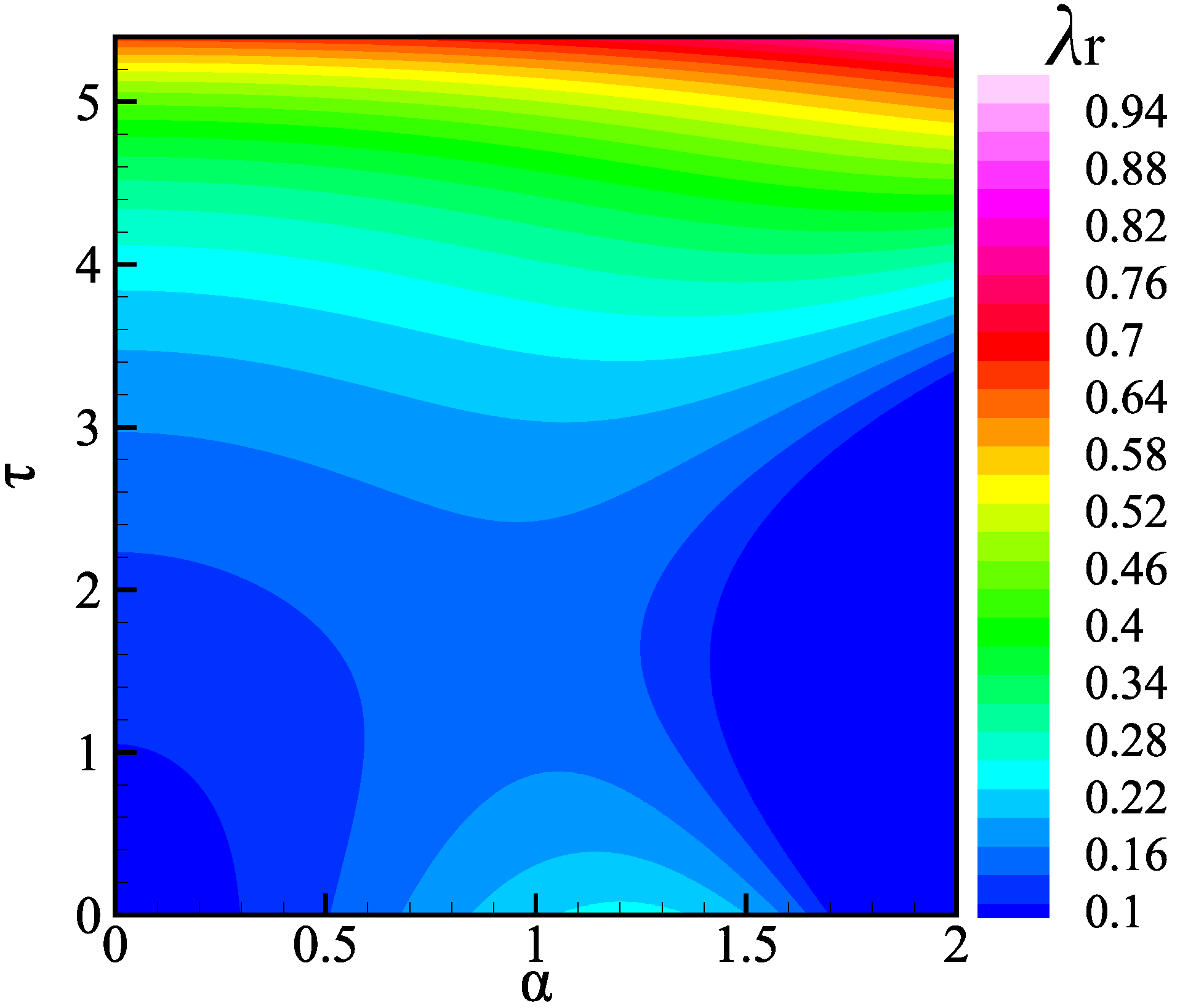
The contour plot in Figure 2 illustrates the variation in the first-order real growth rate with respect to the base-state time . It can be observed that the effective growth rate exhibits a saddle shape. As time progresses, the system experiences a sharp increase in growth rate, causing it to become highly unstable. This is attributed to the significant reduction in the liquid film thickness resulting from film evaporation within a limited time. The stability study following film rupture will not be further detailed since it has no practical relevance. In the subsequent analysis, we examine the scenario at the base-state time , i.e., .
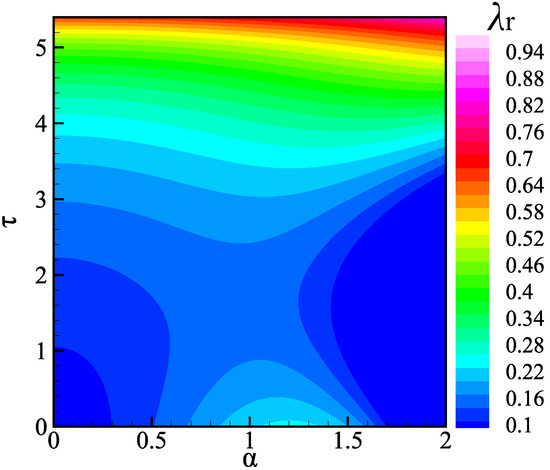
Figure 2.
Contour graph of effective growth rate with flow wave number and time . The other parameters are .
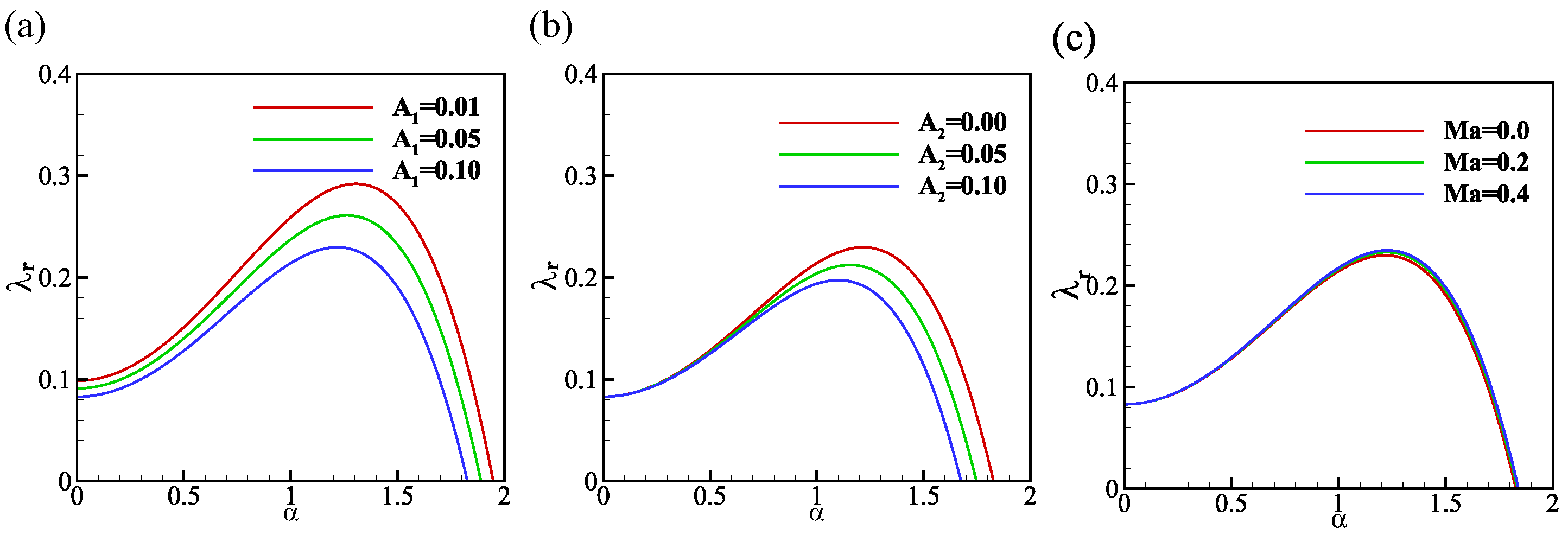
We first start the analysis by ignoring the spanwise influence, i.e., . The impact of parameter , which represents the distance of the system from thermodynamic equilibrium, is demonstrated in Figure 3a. It can be inferred that parameter plays a crucial role in determining the stability of the liquid film, where the real growth rate decreases as increases. Another important stability parameter, effective pressure , is depicted in Figure 3b. Both the growth rate and the critical wave number decrease with the increasing effective pressure, which is consistent with the analytical findings in Equation (68). However, at small wave numbers (i.e., ), stability is barely affected by effective pressure , since is proportional to the wave number in Equation (68). Extensive research has been conducted in previous studies regarding the Marangoni effect [32]. As shown in Figure 3c, it can be observed that within the given range of values, the destabilizing impact of the Marangoni effect is minimal. Thus, we will proceed with setting for the forthcoming studies.
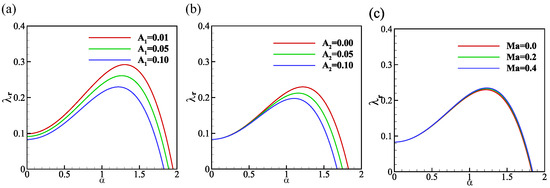
Figure 3.
The real growth rate versus the wavenumber for (a) , ; (b) , ; (c) , . The other parameters are .
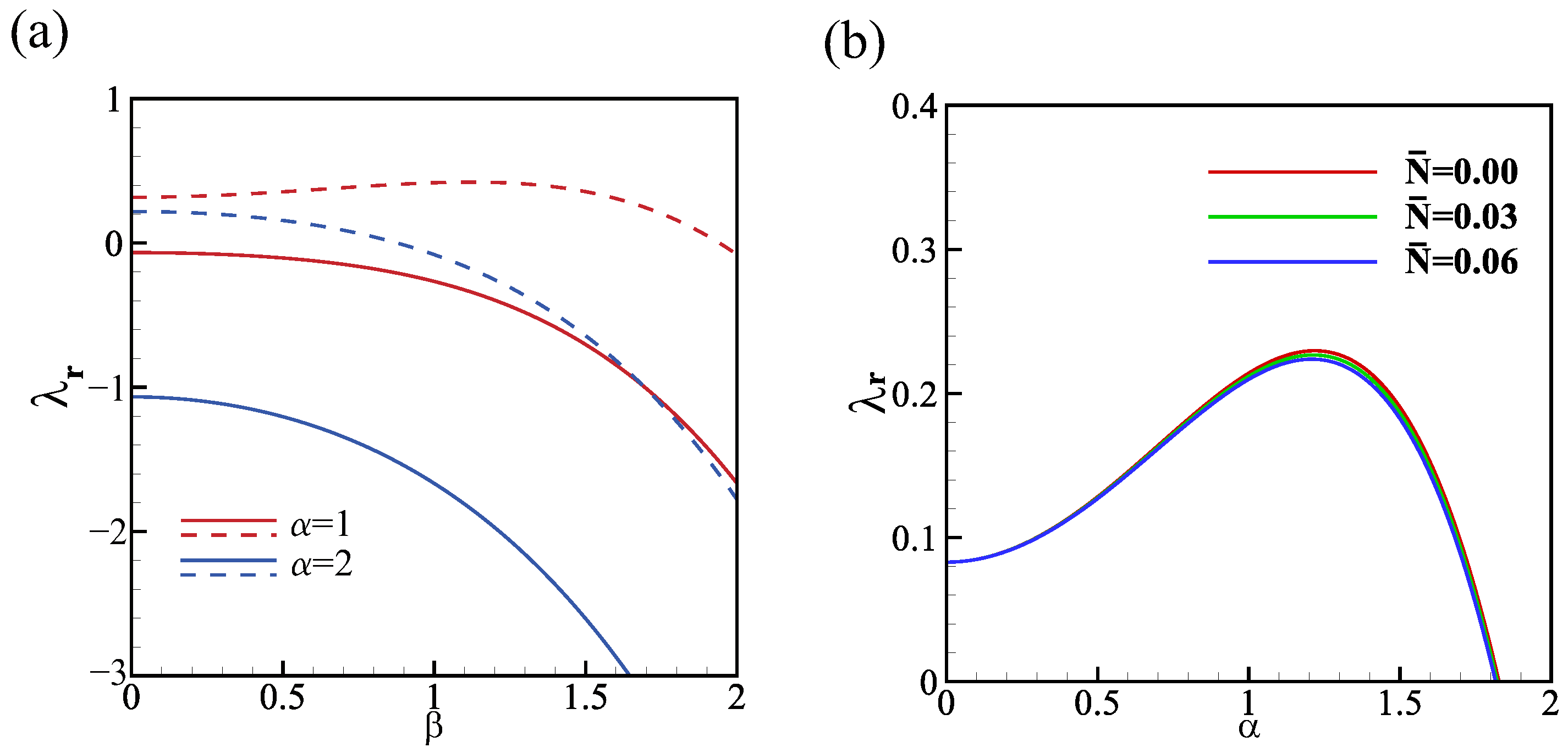
The influences of spanwise perturbation are illustrated in Figure 4a. We observe that spanwise perturbations always play a stabilizing role in the absence of gravity and evaporation (solid lines), as the maximum effective growth rate consistently decreases with an increase in . In fact, spanwise perturbations are typically considered stabilizing in linear stability analysis of a falling liquid film. This is because spanwise perturbations introduce cross-stream vorticity, which interacts with the streamwise vorticity generated by the primary instability to produce three-dimensional flow structures. These three-dimensional structures can enhance the stabilizing effect of viscosity and delay the onset of the primary instability. However, in the presence of film evaporation, as demonstrated by the dashed lines in Figure 4a, this stabilizing effect of spanwise perturbations does not hold true. Since the evaporation effect causes the film to become thinner, making it more susceptible to destabilizing mechanisms such as vapor recoil, the term in Equation (A7) can explain this phenomenon. Therefore, the stabilizing effect of spanwise perturbations is diminished in the presence of evaporation.
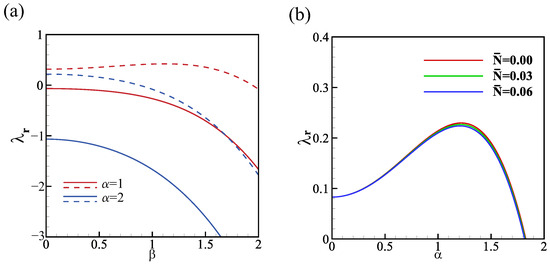
Figure 4.
(a) The real growth rate versus the wavenumber for ; solid lines: , and dashed lines: , . (b) The real growth rate versus the wavenumber for , , , . The other parameters are , , .
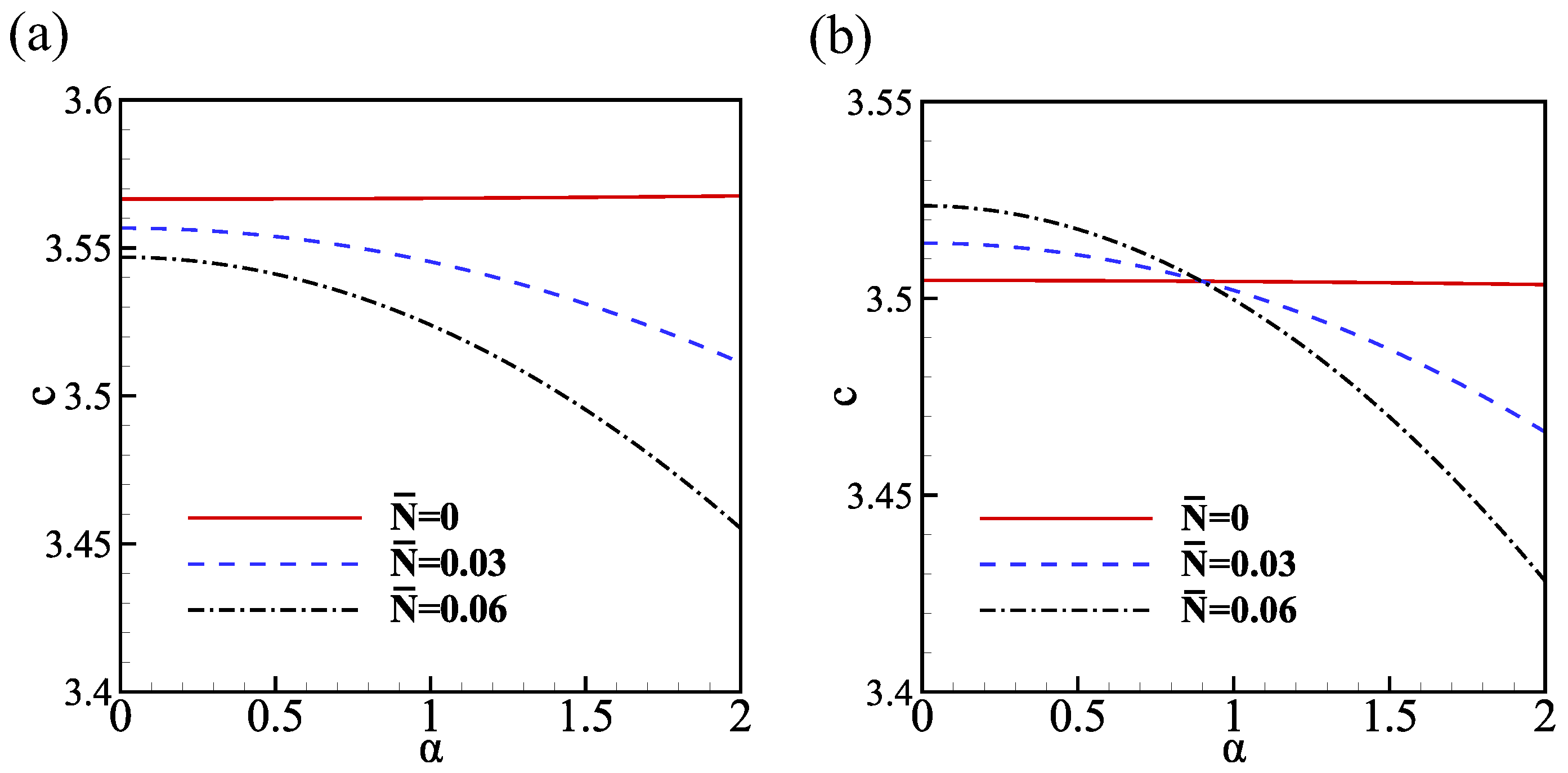
In the present work, surface energy transport has a negligible effect on stability, as shown in Figure 4b, as the parameter exists in the first-order part of the effective growth rate . However, the influence of energy transport on wave speed cannot be discounted, and Figure 5 provides insight into this effect. For an evaporating film , an increment in energy transport leads to an increase in wave speed, as shown in Figure 5a. In the case of a condensing film, rises when the wave speed increases at a small wave number, while it decreases at a large wave number, with the critical wave number being . These results suggest that surface energy transport may not have a significant impact on the stability of the film, but it can affect the wave speed and, hence, the dynamics of the system. Thus, it is important to consider these factors when studying the behavior of evaporating or condensing films.
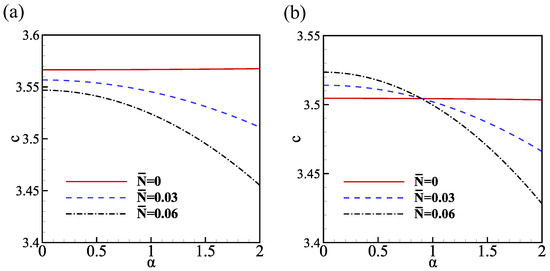
Figure 5.
The wave speed c versus wave number . (a) Evaporating film . (b) Condensing film . The other parameters are .
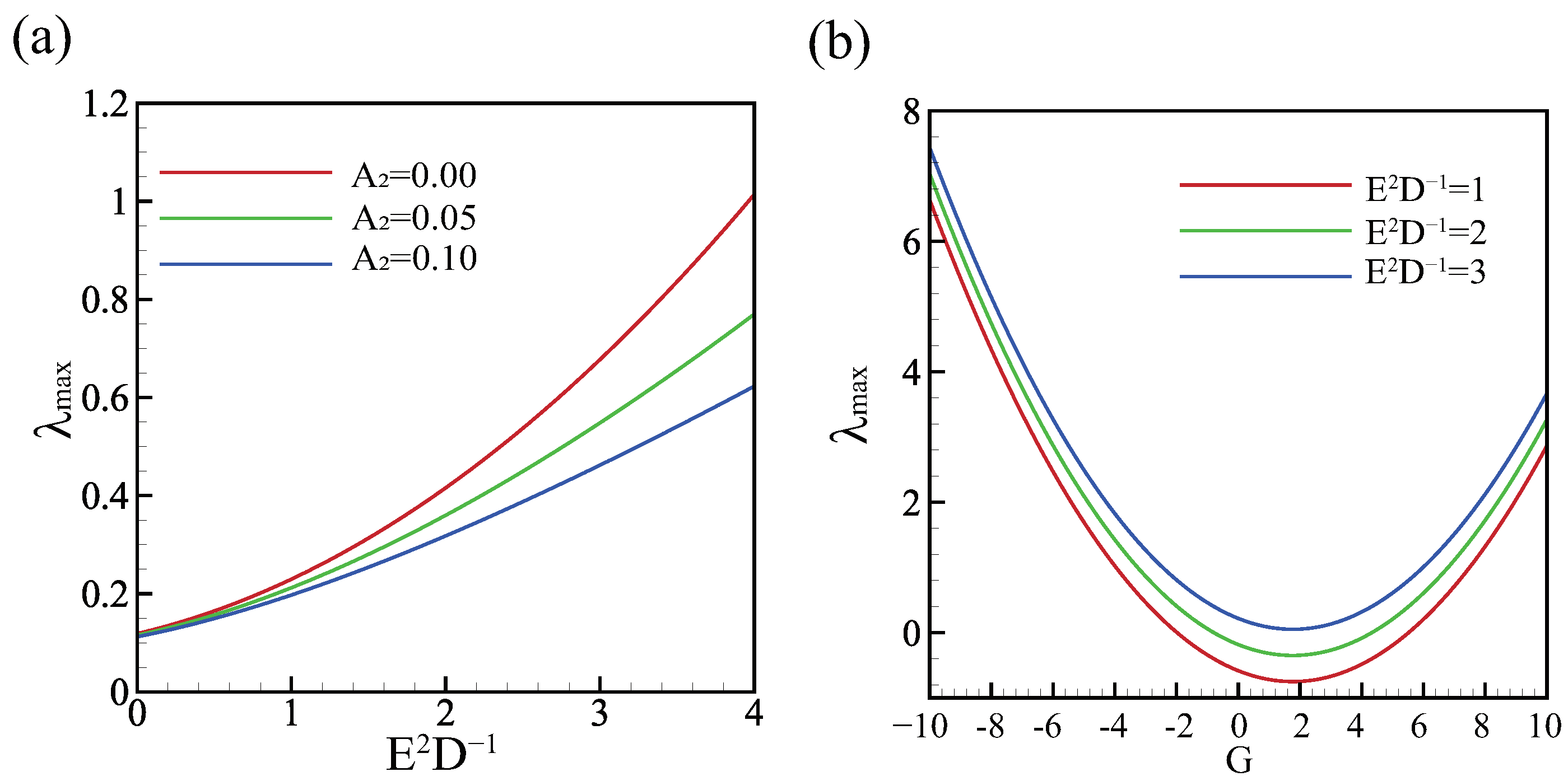
Figure 6 illustrates the destabilizing effects of vapor recoil and gravity on the system. Note that when , it represents an inverted liquid film. As observed in Figure 6a, increasing the vapor recoil effect can result in a higher maximum growth rate, whereas this instability can be mitigated by increasing the effective pressure coefficient . Moreover, the maximum real growth rate is relatively small under microgravity conditions. When the gravity increases, the maximum effective growth rate also increases. Under the same conditions, the inverted liquid film appears to be more unstable, as demonstrated by Figure 6b. It is noteworthy that a larger vapor recoil term leads to a larger maximum growth rate, indicating its destabilizing effect on the system. These findings show that both vapor recoil and gravity are critical factors affecting the stability of the system.
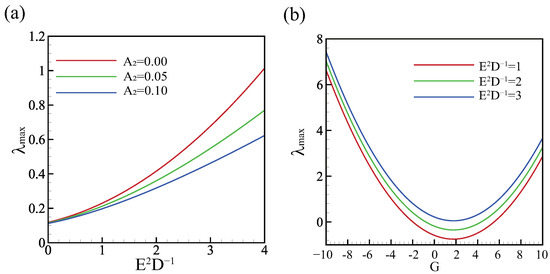
Figure 6.
(a) The max real growth rate versus the vapor recoil effect, . (b) The max real growth rate versus gravity, . The other parameters are .
4. Nonlinear Evolution
This section aims to provide insights into the nonlinear dynamical evolution of a uniform interface subjected to small finite disturbances. To perturb the interface, we introduce a harmonic wave:
Equation (56) subjected to periodic boundary conditions was solved numerically by using the Fourier spectral method. We assume that the solution of can be expanded by the Fourier series:
where are the time-dependent Fourier coefficients. and are the wave numbers in the x and y directions, respectively, where and are the lengths of the computational domain in the x and y directions. We chose the number of Fourier modes in the x direction to be and those in the y direction to be . Thus, there exist a total of Fourier modes, which is sufficient to ensure numerical accuracy.
To investigate the influence of evaporation and the vapor recoil effect, we first consider the quasi-equilibrium case where , which means the temperature is equal to its saturation value. We then focus specifically on the impact of evaporation and vapor recoil, by setting . With these assumptions, the evolution equation (Equation (56)) can be simplified as
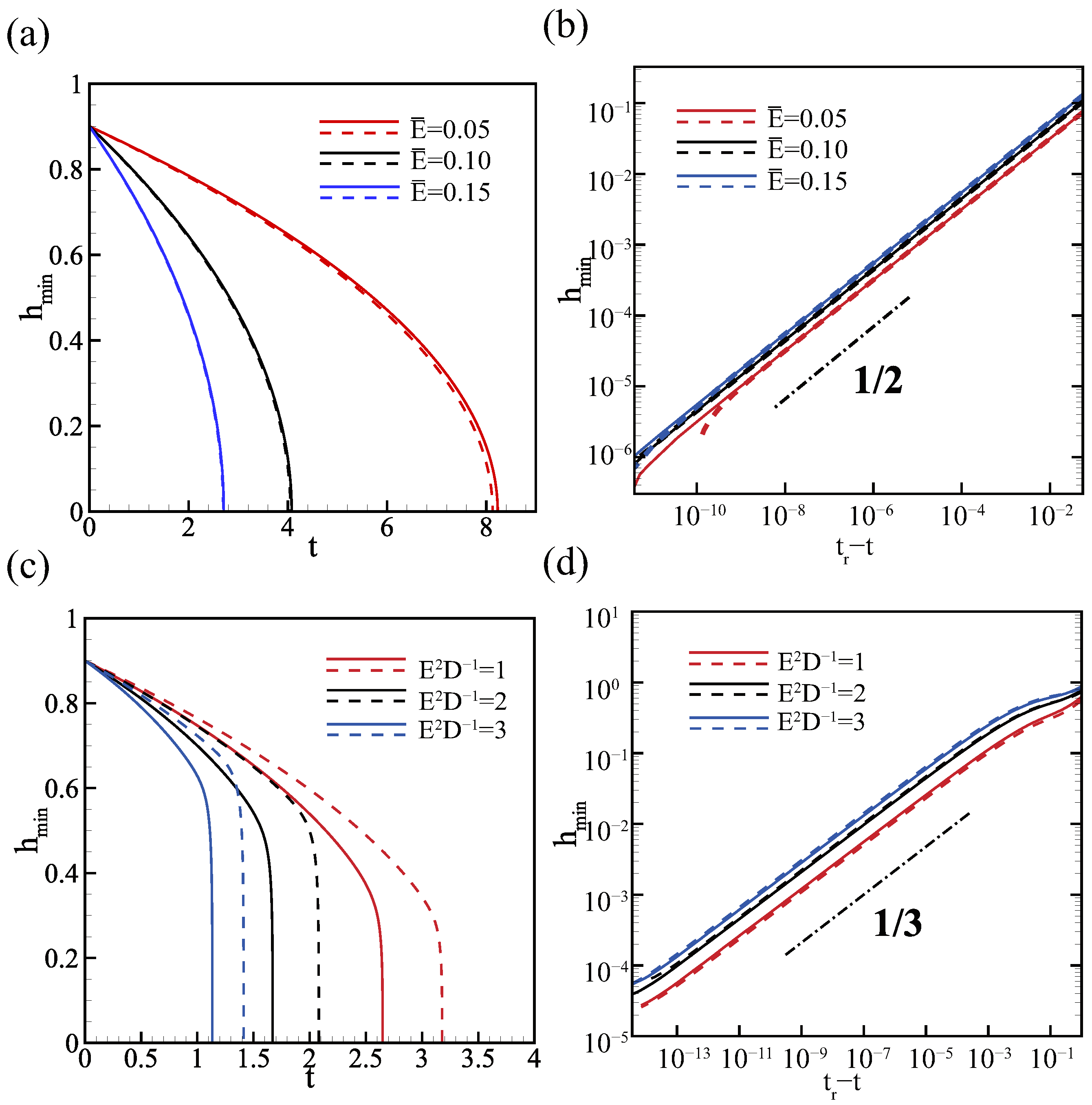
The spatiotemporal evolution in both 2D and 3D simulations revealed that an increase in the evaporation number and vapor recoil could accelerate the breakdown of the film, as shown in Figure 7a,c. Specifically, when evaporation is the dominant factor (Figure 7a), the system exhibits greater stability in the 3D cases. On the other hand, when vapor recoil is the determining element (Figure 7c), the system becomes more unstable in 3D, which is matched with the predictions of linear stability theory. The results indicate that the 3D disturbances exacerbate the vapor recoil effect.
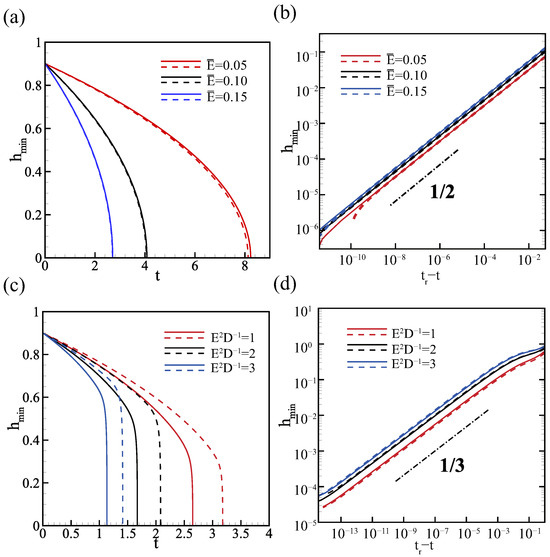
Figure 7.
The relationship between film thickness and time. The solid lines represent the results obtained in 3D, while the dashed lines represent the results obtained in 2D. (a,b) , (c,d). The other parameters are .
To gain a better understanding of the breakup process, we utilize a self-similar solution to extract the underlying scaling law:
where is the breakup time and is the breakup location. The order of each term in Equation (71) yields
When the evaporation plays an important role, balancing the terms , , and gives
This means the minimal film thickness reduces to , which is demonstrated in Figure 7b. When the vapor recoil effect is the dominant fact, balancing the terms of , , and gives
This indicates that the film will break down within a finite time, and the minimum thickness will thin as . The contribution under evaporation has a higher order, , than that under the vapor recoil effect, which gives . This implies that the scaling governing the breakdown process is not affected by the vapor recoil effect, and it is in line with the conclusion obtained by Wei and Duan [45].
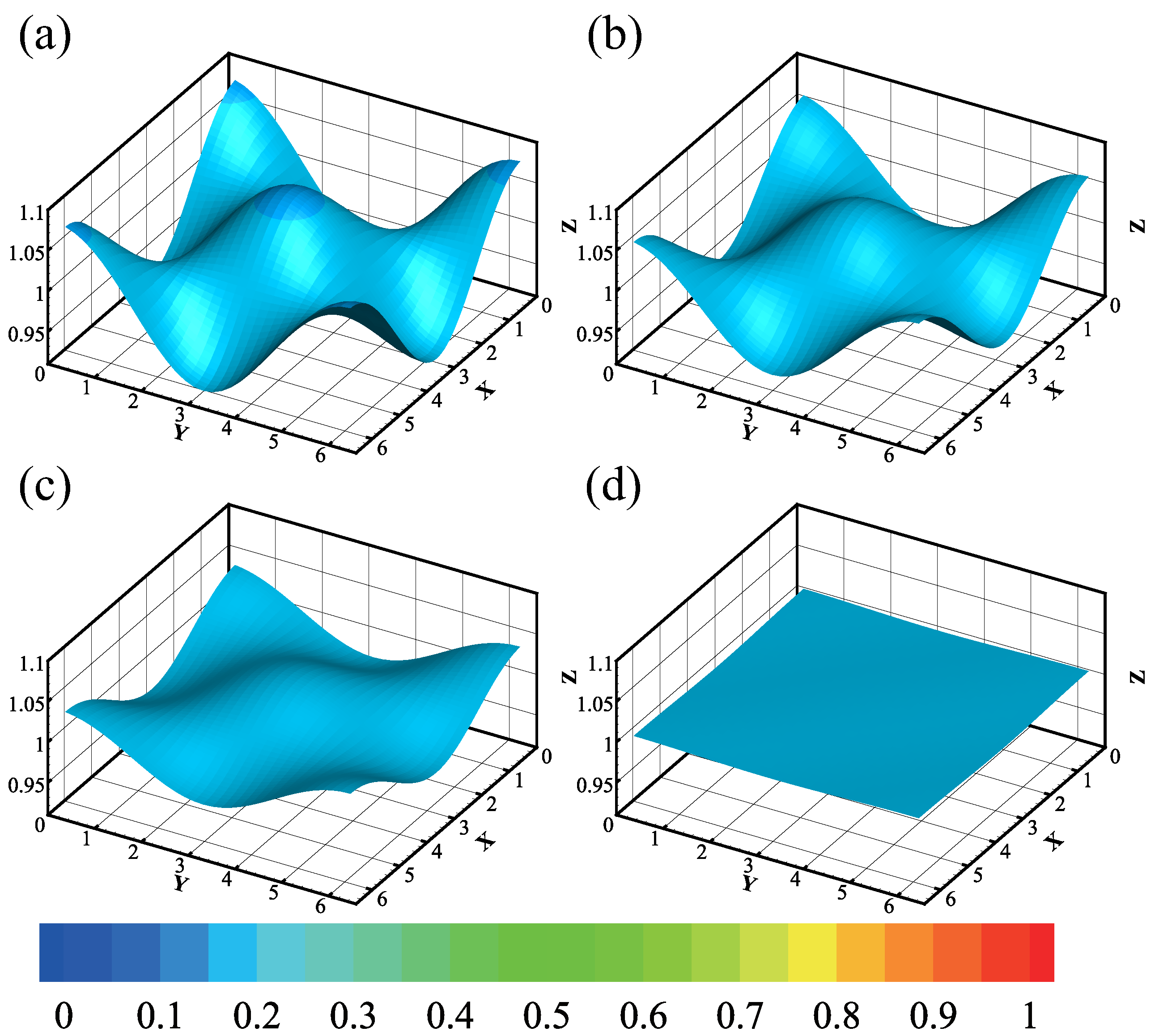
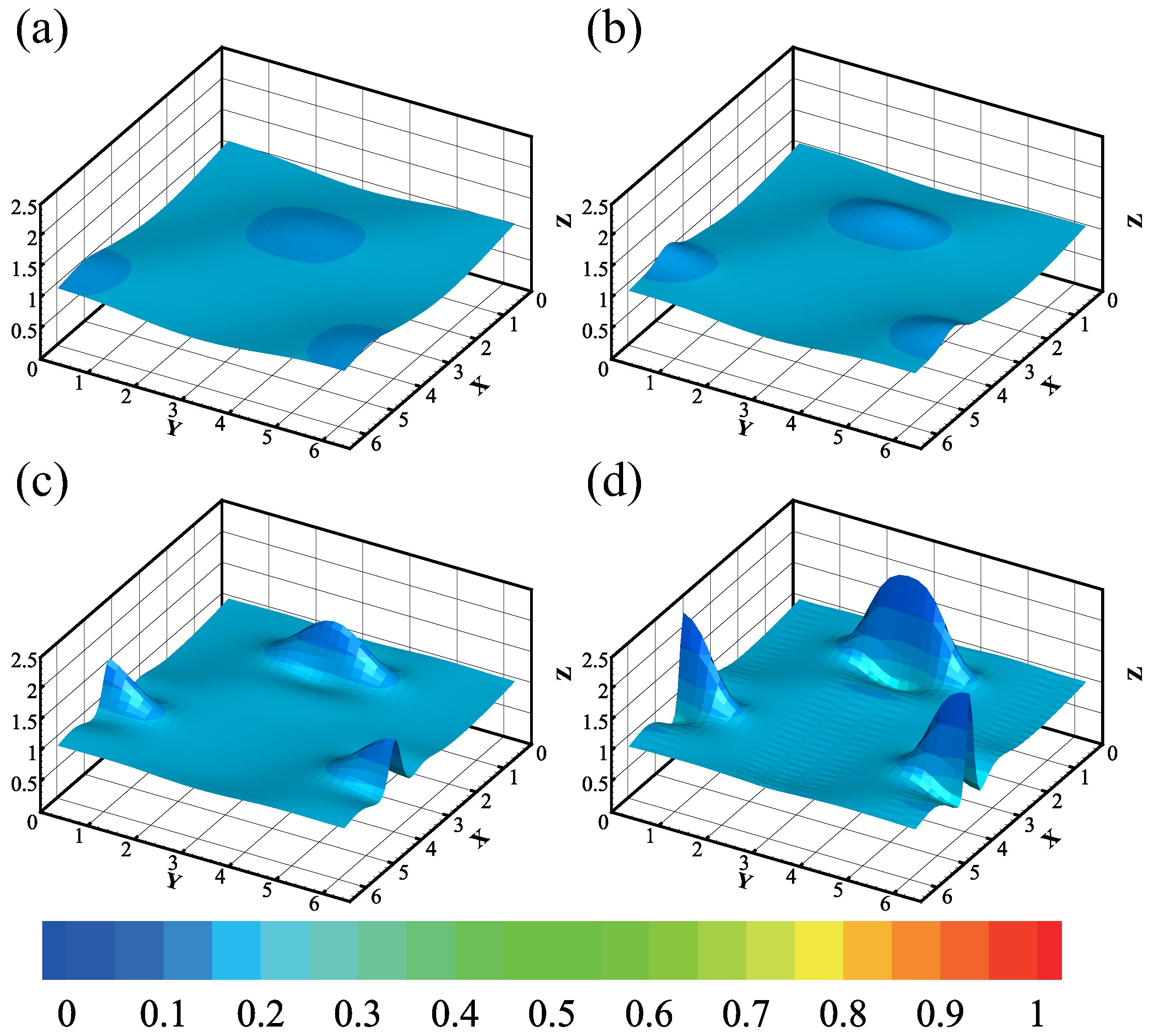
Figure 8 illustrates the behavior of a nonvolatile film () in zero gravity. The film’s initial state is a uniform thickness of , but it will be perturbed with a random amplitude of . Over time, the film surface becomes gradually stabilized, with the peaks and valleys decreasing in amplitude. Eventually, the film will reach a fully stable state where the surface is once again flat with . Since there are no external forces that could cause the film to become unstable in the absence of gravity and evaporation, this behavior is expected. Instead, any initial perturbations are simply damped out over time, leading to a fully stable state.
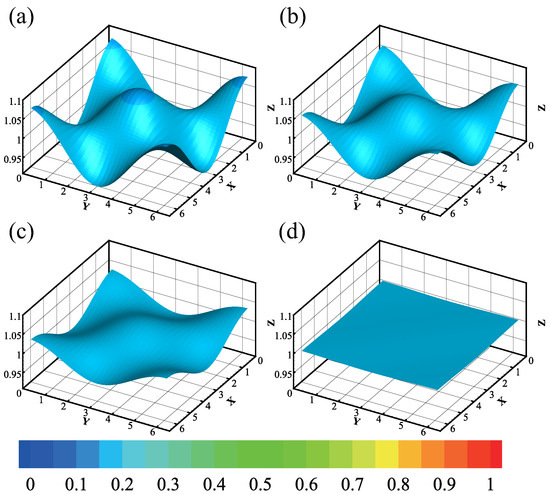
Figure 8.
The evolution of the nonvolatile film () at different times. The depth of the color represents the magnitude of the temperature. The parameters are . The consecutive snapshots correspond to (a) t = 0.97, (b) t = 2.07 s, (c) t = 4.19 s, (d) t = 15 s. The minimum and maximum of the interface are , respectively.
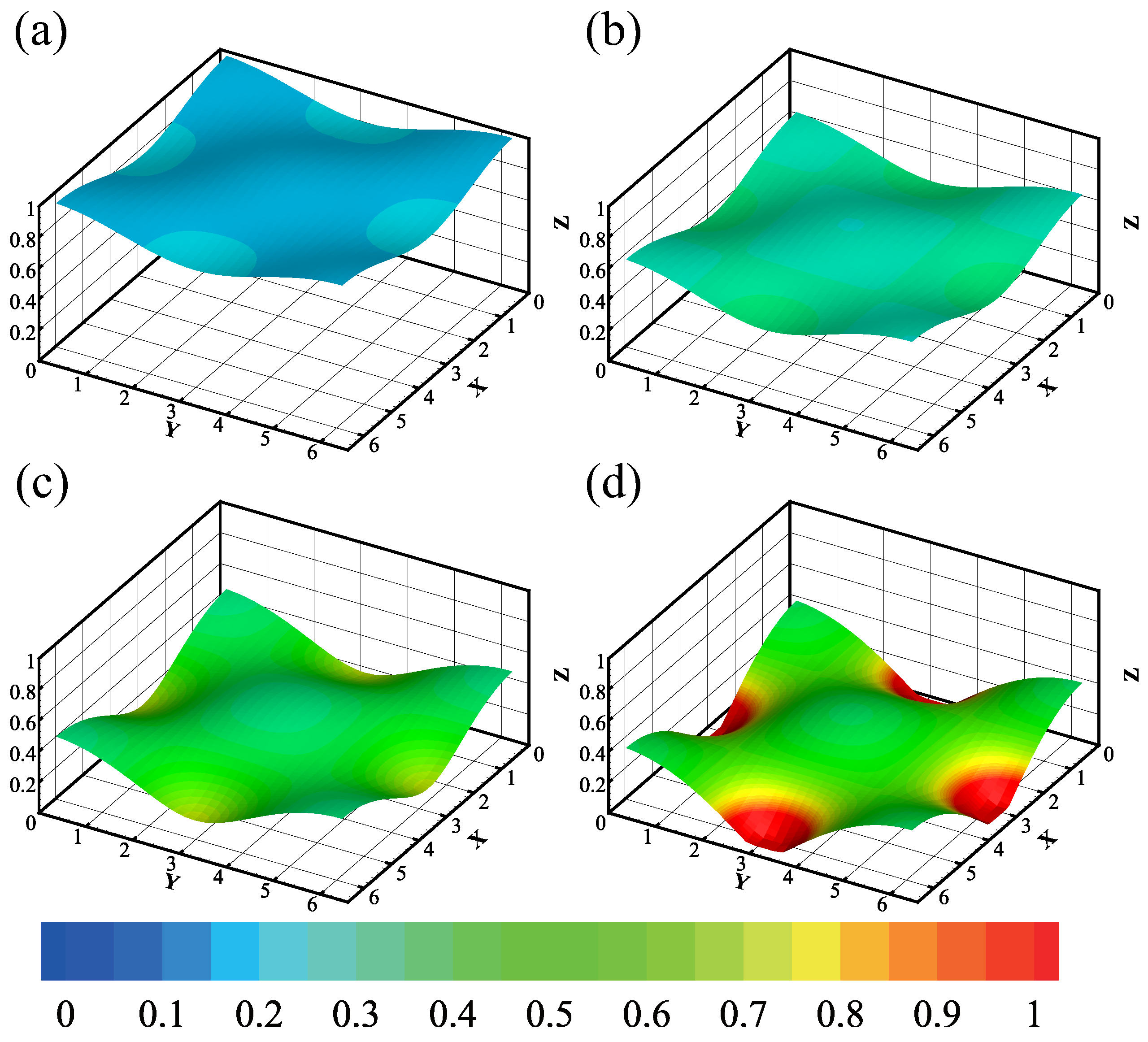
To study the impact of evaporation on a liquid film, we set the evaporation number to a fixed value of . Figure 9 demonstrates the gradual thinning of the film due to evaporation, with partial drying occurring around s. Additionally, the amplitude of the liquid film’s vibration steadily increases over time, indicating that the evaporation process significantly reduces the stability of the system.
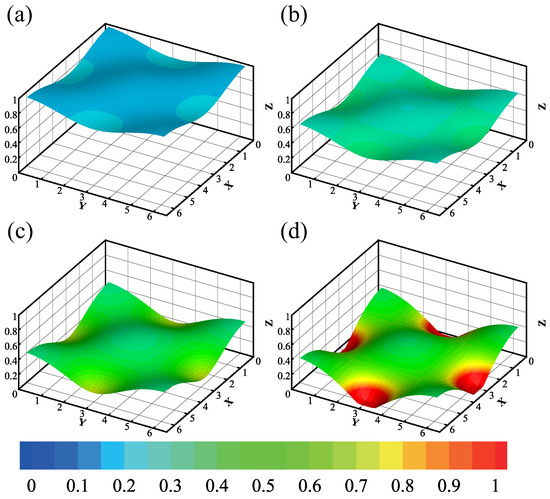
Figure 9.
The evolution of the evaporation film () at different times. The depth of the color represents the magnitude of the temperature. The parameters are , A1 = 0.1, A2 = 0, . The consecutive snapshots correspond to (a) t = 0.97 s, (b) t = 4.00 s, (c) t = 5.01 s, (d) t = 5.40 s. The minimum and maximum of the interface are , respectively.
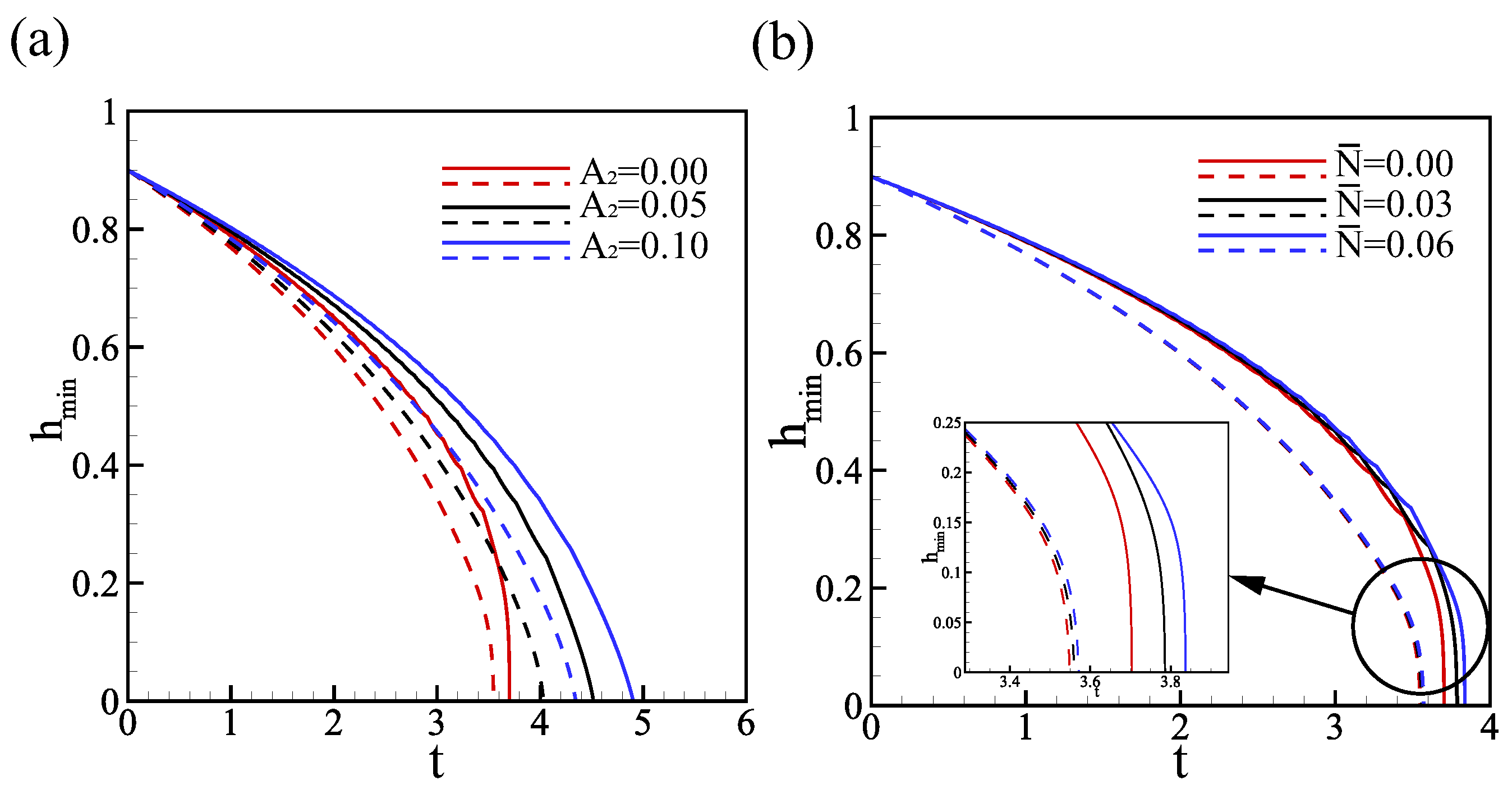
Figure 10a presents the influence of the effective pressure, which illustrates that the film develops slower for larger values of . This result is constant with the linear stability analysis that the system is stabilized as increases. However, when gravity is increased, the breakup time is delayed, which is contradicted by the prediction of the linear stability analysis. This different performance can be attributed to the nonlinear interactions between gravity and surface tension. As the film thickness decreases due to evaporation, the surface tension forces become more dominant, resulting in a more pronounced curvature of the free surface. This can amplify the effect of gravity and stabilize the film, which fails to achieve linear capture in the linear stability analysis. The delay in breakup time for larger gravity is consistent with the physical intuition that flow can enhance stability. The influence of energy transport on liquid film evolution is still small, especially in the case of microgravity, but overall, energy transport still has a small stabilizing effect, as shown in Figure 10b.
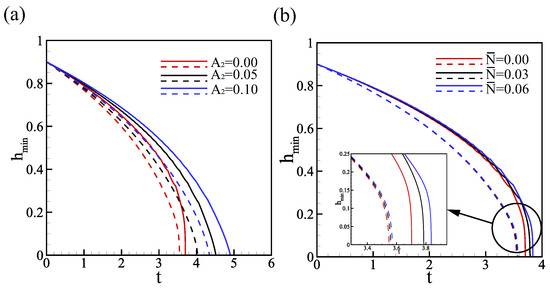
Figure 10.
Minimum thickness versus time t. Solid lines for , dashed lines for . (a) ; (b) . The other parameters are .
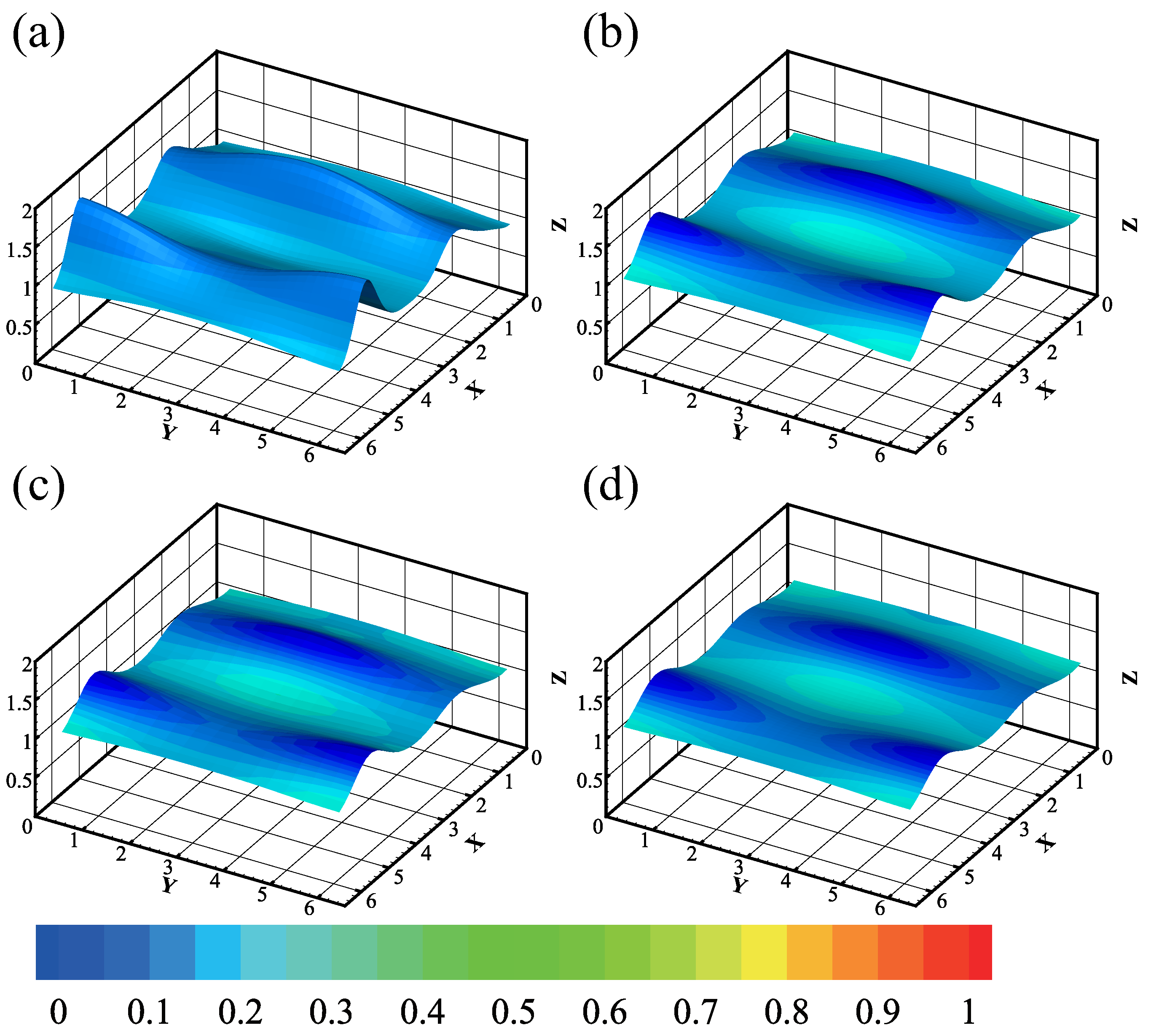
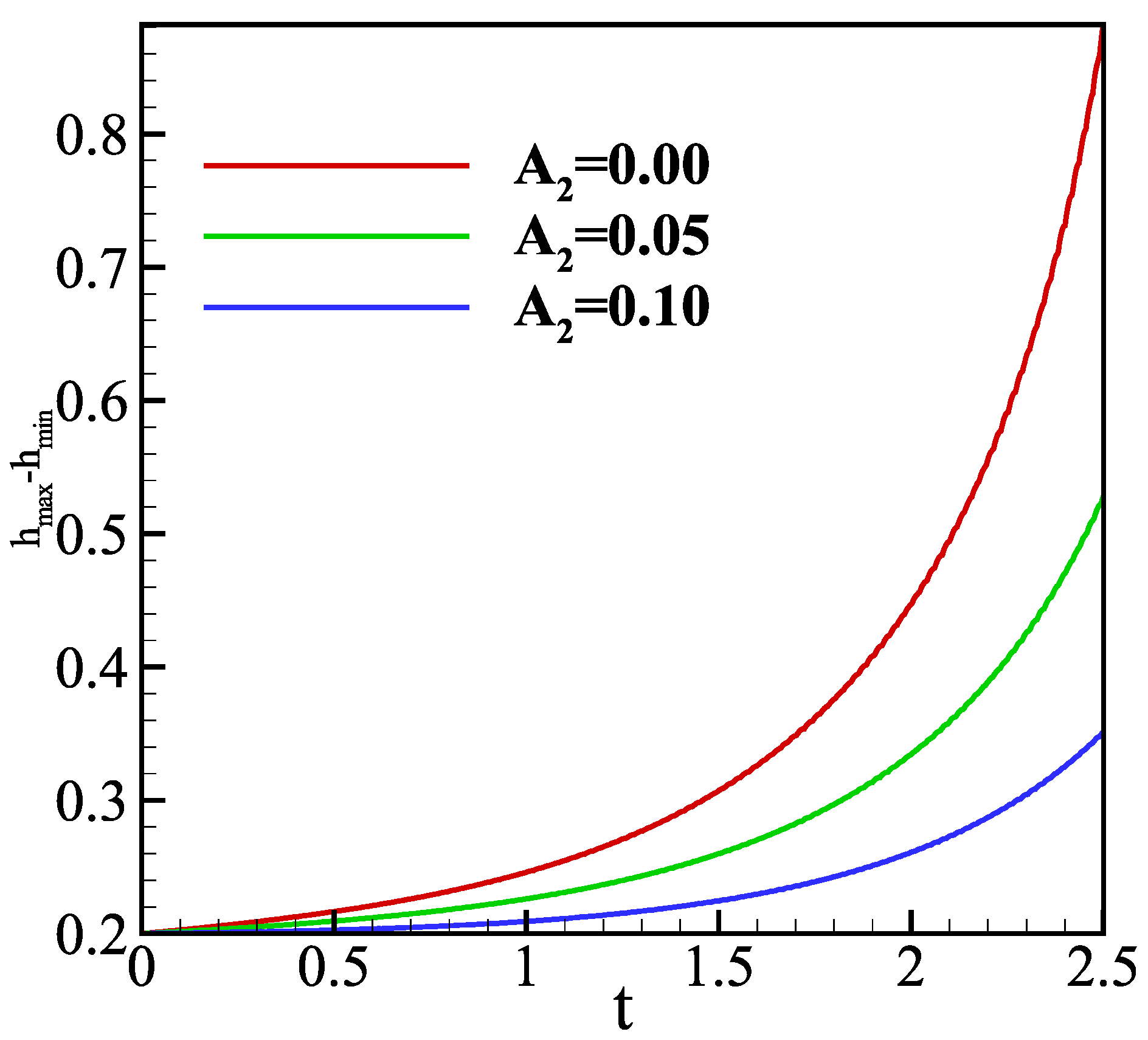
As shown in Figure 11, we investigate the evolution of a condensing film with while fixing the gravity at , which makes the film flow down in the x direction with a constant velocity. Moreover, at s, we notice that the film thickness decreases as increases. Figure 12 supports the conclusion by showing how the amplitude of film thickness reduces with an increase in , proving that the effect pressure acts as a stabilizing factor.
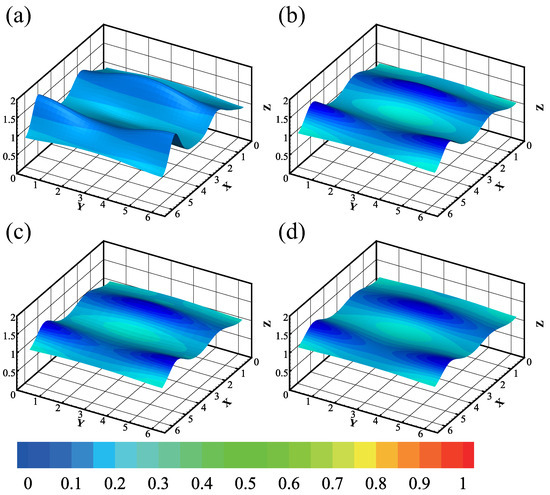
Figure 11.
The evolution of the condensing film () at s. The depth of the color represents the magnitude of the temperature. The parameters are , , , . The consecutive snapshots correspond to (a) , (b) , (c) , (d) . The minimum and maximum of the interface are , respectively.
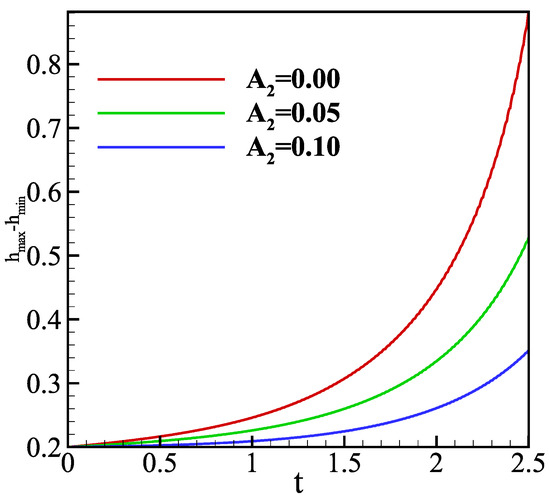
Figure 12.
The amplitude of film thickness versus time t. The parameters are .
In many practical situations, such as inkjet printing, the liquid is often deposited under a substrate, and the system is controlled by the Rayleigh–Taylor instability mechanism. Therefore, we investigated the performance of an inverted film as shown in Figure 13. It was observed that the film initially moves along the incline due to the force of gravity. At a certain point, a droplet appears on the film’s surface, which grows rapidly over a short period of time. The formation and growth of the droplet can be attributed to the destabilizing effect of gravity on the inverted film. Due to gravity, the thickness of the film varies along the incline, leading to non-uniform flow and the formation of a droplet. The layer thins as the droplet grows, causing an increase in the curvature of the droplet’s interface and accelerating its growth.
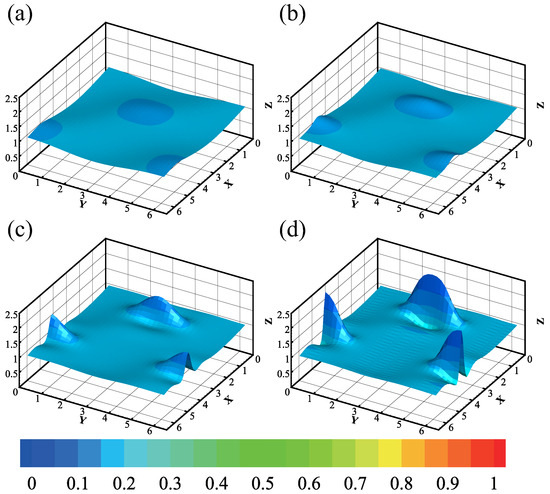
Figure 13.
The evolution of inverted liquid film. The depth of the color represents the magnitude of the temperature. The parameters are , , , , , The consecutive snapshots correspond to (a) t = 0.10 s, (b) t = 0.15 s, (c) t = 0.20 s, (d) t = 0.21 s. The minimum and maximum of the interface are , respectively.
5. Conclusions
This study set out to study a three-dimensional evaporating/condensing liquid film with a nonlinear evolution equation under the consideration of the balance of the configurational momentum at the liquid–vapor interface. We considered effect pressure, vapor recoil, and gravity especially and discussed the impact of complex interactions on both linear stability and fully nonlinear dynamics with a long-wave model. Two terms were introduced in our model. One was the effective pressure, , accounting for vapor recoil, , and the other was the energy transport along the interface, ( is the tangential component velocity at the liquid–vapor interface). The dimensionless parameter N accounts for the magnitude of the energy flux along the interface. The effect of the effective pressure and vapor recoil of the system on instability was studied using linear stability. The results indicate that the system is always stabilized by the effective pressure, whereas the vapour recoil effect acts to destabilize the system. Additionally, in this paper spanwise perturbation was considered as a stabilizing term in a three-dimensional nonvolatile film. However, the results demonstrate that vapour recoil reduces the stabilizing effect of spanwise perturbations in the presence of evaporation. For the influence of energy transport, while it had a very minor effect on the stability of the system, evaporation along the interface had an impact on the linear wave speed.
The nonlinear evolution of the nonvolatile, evaporating and condensing film falling down an inclined plane was examined using a Fourier spectral method, taking into account the influences of evaporation number, effective pressure, and vapor recoil. The nonlinear dynamics of the system reveal that effective pressure can enhance stability, thus delaying the rupture of an evaporating film. The study of the self-similar solution reveals that the minimal film thickness reduces as and under the dominance of evaporation and vapor recoil, respectively. The behavior of nonvolatile films under zero gravity was also discussed, showing signs of stabilization over time and reaching a fully stable state where the film surface is flat again.
Author Contributions
Conceptualization, Q.Y. and Z.D.; Data curation, R.H.; Formal analysis, W.J.; Funding acquisition, Q.Y. and Z.D.; Methodology, W.J.; Software, W.J.; Supervision, Z.D.; Writing—original draft, W.J.; Writing—review and editing, R.H. All authors have read and agreed to the published version of the manuscript.
Funding
The authors were supported by the State Key Laboratory of Aerodynamics, the National Key R&D Program of China, and the National Natural Science Foundation of China (Grant No. 12102109).
Data Availability Statement
The data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
Nomenclature
| Liquid (vapor) phase density | |
| Liquid (vapor) phase kinematic viscosity | |
| Liquid (vapor) phase thermal conductivity | |
| Velocity in x, y, z component, respectively | |
| () | Interface (vapor) velocity |
| t, | Time |
| p | Pressure |
| Liquid dynamic viscosity | |
| g | Acceleration of gravity |
| Thermal diffusivity | |
| ∇ | Hamilton operator |
| Surface gradient operator | |
| Slope angle | |
| h | Liquid film thickness |
| Unit normal vector | |
| Unit tangent vector | |
| Aspect ratio | |
| Complex growth rate | |
| , | Streamwise and spanwise wavenumbers |
| Surface tension | |
| Interfacial free-energy | |
| Entropy densities | |
| Stress tensor | |
| Identity tensor | |
| Interface modulus | |
| Dimensionless temperature | |
| Thermodynamic equilibrium parameter | |
| Effective pressure coefficient | |
| C | Crispation number |
| D | Density ratio |
| E | Evaporation number |
| G | Dimensionless gravity |
| J | Mass flux conservation |
| K | Mean curvature |
| L | Latent heat |
| Marangoni number | |
| N | Energy flux coefficient |
| T, , | Temperature, the wall temperature, the saturation temperature |
| Prandtl number | |
| S | Dimensionless surface tension |
Appendix A. The First-Order Growth Rate
Here, we provide the detailed expression of the first-order complex growth rate:
with
where
References
- Grotberg, J.B. Pulmonary flow and transport phenomena. Annu. Rev. Fluid Mech. 1994, 26, 529–571. [Google Scholar] [CrossRef]
- Goldstein, R.J. Film cooling. In Advances in Heat Transfer; Elsevier: Amsterdam, The Netherlands, 1971; Volume 7, pp. 321–379. [Google Scholar]
- Mu, X.; Yang, Y.; Shen, S.; Liang, G.; Gong, L. Experimental study of heat transfer characteristics for horizontal-tube falling film evaporation. In Heat Transfer Summer Conference; American Society of Mechanical Engineers: New York, NY, USA, 2012; Volume 44786, pp. 865–871. [Google Scholar]
- Dai, Z.; Zhang, Y.; Wang, S.; Nawaz, K.; Jacobi, A. Falling-film heat exchangers used in desalination systems: A review. Int. J. Heat Mass Transf. 2022, 185, 122407. [Google Scholar] [CrossRef]
- Burelbach, J.P.; Bankoff, S.G.; Davis, S.H. Nonlinear stability of evaporating/condensing liquid films. J. Fluid Mech. 1988, 195, 463. [Google Scholar] [CrossRef]
- Davis, S.H. Thermocapillary instabilities. Annu. Rev. Fluid Mech. 1987, 19, 403–435. [Google Scholar] [CrossRef]
- Joo, S.W.; Davis, S.H.; Bankoff, S.G. Long-wave instabilities of heated falling films: Two-dimensional theory of uniform layers. J. Fluid Mech. 1991, 230, 117–146. [Google Scholar] [CrossRef]
- Reisfeld, B.; Bankoff, S.G. Nonlinear stability of a heated thin liquid film with variable viscosity. Phys. Fluids Fluid Dyn. 1990, 2, 2066–2067. [Google Scholar] [CrossRef]
- Oron, A.; Davis, S.H.; Bankoff, S.G. Long-scale evolution of thin liquid films. Rev. Mod. Phys. 1997, 69, 931–980. [Google Scholar] [CrossRef]
- Craster, R.V.; Matar, O.K. Dynamics and stability of thin liquid films. Rev. Mod. Phys. 2009, 81, 1131. [Google Scholar] [CrossRef]
- Chattopadhyay, S.; Mukhopadhyay, A.; Barua, A. A review on hydrodynamical stability of thin film flowing along an inclined plane. J. Math. Sci. Model. 2019, 2, 133–142. [Google Scholar] [CrossRef]
- Sheludko, A. Thin liquid films. Adv. Colloid Interface Sci. 1967, 1, 391–464. [Google Scholar] [CrossRef]
- Ruckenstein, E.; Jain, R.K. Spontaneous rupture of thin liquid films. J. Chem. Soc. Faraday Trans. Mol. Chem. Phys. 1974, 7, 132–147. [Google Scholar] [CrossRef]
- Vrij, A. Possible mechanism for the spontaneous rupture of thin, free liquid films. Discuss. Faraday Soc. 1966, 42, 23–33. [Google Scholar] [CrossRef]
- Yih, C.-S. Stability of parallel laminar flow with a free surface. J. Appl.-Mech.-Trans. ASME 1954, 21, 281. [Google Scholar]
- Yih, C. Stability of liquid flow down an inclined plane. Phys. Fluids 1963, 6, 321–334. [Google Scholar] [CrossRef]
- Benjamin, T. Wave formation in laminar flow down an inclined plane. J. Fluid Mech. 1957, 2, 554–573. [Google Scholar] [CrossRef]
- Benney, D.J. Long waves on liquid films. J. Math. Phys. 1966, 45, 150–155. [Google Scholar] [CrossRef]
- Williams, M.B.; Davis, S.H. Nonlinear theory of film rupture. J. Colloid Interface Sci. 1982, 90, 220–228. [Google Scholar] [CrossRef]
- Sharma, A.; Ruckenstein, E. An analytical nonlinear theory of thin film rupture and its application to wetting films. J. Colloid Interface Sci. 1986, 113, 456–479. [Google Scholar] [CrossRef]
- Mezger, M.; Reichert, H.; Schöer, S.; Okasinski, J.; Schrxoxer, H.; Dosch, H.; Palms, D.; Ralston, J.; Honkimäi, V. High-resolution in situ X-ray study of the hydrophobic gap at the Octadecyl-Trichlorosilane Interface. Proc. Natl. Acad. Sci. USA 2006, 103, 401–404. [Google Scholar] [CrossRef]
- Lin, F.-Y.; Steffen, W. Capillary wave dynamics of thin liquid polymer films. J. Chem. Phys. 2014, 141, 104903. [Google Scholar] [CrossRef]
- Bankoff, S.G. Stability of liquid flow down a heated inclined plane. Int. J. Heat Mass Transf. 1971, 14, 377–385. [Google Scholar] [CrossRef]
- Abderrahmane, H.A. Stability of an evaporating and condensing liquid film flowing down an inclined plane. Energy Procedia 2017, 142, 3944–3949. [Google Scholar] [CrossRef]
- Sreenivasan, S.; Lin, S. Surface tension driven instability of a liquid film flow down a heated incline. Int. J. Heat Mass Transf. 1978, 21, 1517–1526. [Google Scholar] [CrossRef]
- Kelly, R.E.; Davis, S.H.; Goussis, D.A. On the instability of heated film flow with variable surface tension. Int. Heat Transf. Conf. 1986, 8, 1937–1942. [Google Scholar]
- Kalliadasis, S.; Demekhin, E.; Ruyer-Quil, C.; Velarde, M. Thermocapillary instability and wave formation on a film falling down a uniformly heated plane. J. Fluid Mech. 2003, 492, 303–338. [Google Scholar] [CrossRef]
- Thiele, U.; Knobloch, E. Thin liquid films on a slightly inclined heated plate. Phys. Nonlinear Phenom. 2004, 190, 213–248. [Google Scholar] [CrossRef]
- Mukhopadhyay, A.; Mukhopadhyay, S.; Mukhopadhyay, A. Instabilities of thin viscous liquid film flowing down a uniformly heated inclined plane. J. Heat Mass Transf. Res. 2016, 3, 77–87. [Google Scholar]
- Scheid, B.; Oron, A.; Colinet, P.; Thiele, U.; Legros, J.C. Nonlinear evolution of nonuniformly heated falling liquid films. Phys. Fluids 2002, 14, 4130–4151. [Google Scholar] [CrossRef]
- Gambaryan-Roisman, T. Marangoni convection, evaporation and interface deformation in liquid films on heated substrates with non-uniform thermal conductivity. Int. J. Heat Mass Transf. 2010, 53, 390–402. [Google Scholar] [CrossRef]
- Ding, Z. Falling liquid films on a slippery substrate with marangoni effects. Int. J. Heat Mass Transf. 2015, 90, 689–701. [Google Scholar] [CrossRef]
- Chattopadhyay, S.; Mukhopadhyay, A.; Barua, A.K.; Gaonkar, A.K. Thermocapillary instability on a film falling down a non-uniformly heated slippery incline. Int. J.-Non-Linear Mech. 2021, 133, 103718. [Google Scholar] [CrossRef]
- Moussy, C.; Lebon, G.; Margerit, J. Influence of evaporation on bénard-marangoni instability in a liquid-gas bilayer with a deformable interface. Eur. Phys. J.-Condens. Matter Complex Syst. 2004, 40, 327–335. [Google Scholar] [CrossRef]
- Liu, R.; Liu, Q. The convective instabilities in a liquid–vapor system with a non-equilibrium evaporation interface. Microgravity Sci. Technol. 2009, 21, 233–240. [Google Scholar] [CrossRef]
- Liu, R.; Kabov, O. Instabilities in a horizontal liquid layer in cocurrent gas flow with an evaporating interface. Phys. Rev. 2012, 85, 066305. [Google Scholar] [CrossRef] [PubMed]
- Palmer, H.J. The hydrodynamic stability of rapidly evaporating liquids at reduced pressure. J. Fluid Mech. 1976, 75, 487. [Google Scholar] [CrossRef]
- Kanatani, K. Interfacial instability induced by lateral vapor pressure fluctuation in bounded thin liquid-vapor layers. Phys. Fluids 2010, 22, 012101. [Google Scholar] [CrossRef]
- Kanatani, K.; Oron, A. Nonlinear dynamics of confined thin liquid-vapor bilayer systems with phase change. Phys. Fluids 2011, 23, 032102. [Google Scholar] [CrossRef]
- Cammenga, H.K. Evaporation mechanisms of liquids. Curr. Top. Mater. Sci. 1980, 5, 335–446. [Google Scholar]
- Shklyaev, O.E.; Fried, E. Stability of an evaporating thin liquid film. J. Fluid Mech. 2007, 584, 157–183. [Google Scholar] [CrossRef]
- Anderson, D.M.; Cermelli, P.; Fried, E.; Gurtin, M.E.; Mcfadden, G.B. General dynamical sharp-interface conditions for phase transformations in viscous heat-conducting fluids. J. Fluid Mech. 2007, 581, 323–370. [Google Scholar] [CrossRef]
- Fried, E.; Shen, A.Q.; Gurtin, M.E. Theory for solvent, momentum, and energy transfer between a surfactant solution and a vapor atmosphere. Phys. Rev. E 2006, 73, 061601. [Google Scholar] [CrossRef] [PubMed]
- Wayner, P.C. Intermolecular forces in phase-change heat transfer: 1998 kern award review. AIChE J. 1999, 45, 2055–2068. [Google Scholar] [CrossRef]
- Wei, T.; Duan, F. Interfacial stability and self-similar rupture of evaporating liquid layers under vapor recoil. Phys. Fluids 2016, 28, 124106. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).