Abstract
A Buckley–Leverett analysis with capillary pressure to model the oil displacement in fractal porous media is herein presented. The effective permeability for a non-Newtonian micellar fluid is calculated by a constitutive equation used to describe the rheological properties of a displacement fluid. The main assumption of this model involves a bundle of tortuous capillaries with a size distribution and tortuosity that follow fractal laws. The BMP model predicts two asymptotic (Newtonian) regions at low and high shear and a power-law region between the two Newtonian regions corresponding to a stress plateau. Both the stress at the wall and the fluidity are calculated using an imposed pressure gradient in order to determine the mobility of the solution. We analyze different mobility ratios to describe the behavior of the so-called self-destructive surfactants. Initially, the viscosity of the displacing fluid (micellar solution) is high; however, interactions with the porous media lead to a breakage process and degradation of the surfactant, producing low viscosity. This process is simulated by varying the applied pressure gradient. The resulting equation is of the reaction–diffusion type with various time scales; a shock profile develops in the convective time scale, as in the traditional Buckley-Leverett analysis, while at longer times diffusion effects begin to affect the profile. Predictions include shock profiles and compressive waves. These results may find application when selecting surfactants for enhanced oil recovery processes in oilfields.
1. Introduction
Chemical-enhanced oil recovery (CEOR) is a group of techniques for improving recovery factors at the tertiary stage of the oilfield life cycle using combinations of chemical additives [1]. Surfactant flooding is a tertiary oil recovery technique that has become a useful method over the past years for obtaining additional oil production in depleted reservoirs [2,3]. The mechanism of enhanced recovery involved in polymer flooding is based on decreasing the mobility difference between the displacing and displaced fluids in order to reduce fingering effects [4]. The surfactants used in these operations display shear dependence of viscosity, thixotropy, and elasticity, among other features [5]. In contact with the porous (reservoir) structure, the flow of non-Newtonian fluids is a function of the permeability obtained by direct measurement of pressure drop and flow rate using cylindrical cores from blocks of coherent porous or granular media. The permeability obtained using a Newtonian fluid and the pressure drop/flow rate relationships are linearly related, confirming that Stokes law applies at the pore scale. When the fluid is non-Newtonian, an equivalent of Darcy’s law to describe this flow musy be sought. The use of nonlinear constitutive equations aims to provide extensions of Darcy’s law to cover fluids with complex rheology [6]. At the pore scale, flow fields are strongly affected by elastic forces that cause the principal directions of the stress and strain rates to be non-parallel, as occurs with generalized Newtonian or thixotropic fluids. However, at the Darcy scale the functional over past history becomes relevant, as all complexities at the pore scale are considered in the functional.
Polymeric surfactants are macromolecules with hydrophobic and hydrophilic groups in their structural makeup; although they are polymers, their unique molecular features technically allow them to be defined as surfactants as well. Macrosurfactants, on the other hand, are of more complex molecular structure and mostly have high molecular weight. Polymeric surfactants have been proposed to reduce the number of chemical additive slugs used to implement chemical floods in oil reservoirs, as they offer operational simplicity and improve cost efficiency [4]. Polymer-free fluids based on viscoelastic surfactants have been developed to recover oil from subterranean formations. These fluids are characterized by the presence of large multi-molecular structures which provide the required high viscosity and viscoelastic properties [1]. One of the most important advantages of viscoelastic surfactants is that the multimolecular structures are broken by their interaction with produced formation fluids containing hydrocarbons. As a result, the displacing fluid can be easily removed from the propped structure. A new concept called “self-destructing” viscoelastic surfactants form large micellar structures; these have the advantage that the gel can become a low-viscosity fluid during backflow, as the individual surfactant molecules break down into oil- and water-soluble species. They can then be easily removed by back-flowing formation fluids [7,8]. These self-destructing surfactants have been the subject of research for a long time following the pioneering work of [9,10]. Depending on the rheology of these fluids, their viscosity is a function of the applied pressure gradient. Micellar solutions have a complex rheology that can be used to improve the flow of the displaced oil fluid. These surfactants exhibit pressure gradient-dependent properties, such as the presence of a shear stress plateau at a critical value of the pressure gradient. This means that at this critical stress level the flow rate increases dramatically, resulting in increased oil production. For higher pressure gradients, the shear-thinning properties of the fluid lead to viscosities even lower than those of the oil phase, up to the situation where water displaces oil [11,12].
We have previously modeled the rheology of micellar solutions, including surfactants with self-destructive properties [13]. As mentioned, the presence of a stress plateau signals the large decrease in viscosity observed in these micellar fluids at a critical pressure gradient. The modeling does not take into account the chemistry associated with the surfactant breakage process; instead, the viscosity drop is predicted by increasing the applied stress or pressure gradient. The important parameter in oil displacement by a micellar solution is the mobility ratio (i.e., the mobility of the oil phase divided by the mobility of the micellar solution, which is a non-Newtonian fluid) [14,15]. At low pressure gradients, the mobility of the surfactant solution is small, giving rise to a large mobility ratio; as a Newtonian fluid, the viscosity of the oil phase is constant. As the pressure gradient increases, the mobility of the surfactant solution increases, leading to a decrease in the mobility ratio. The limit of this decrease (a very small ratio) corresponds to the situation where the viscoelastic properties of the surfactant are destroyed and the resulting low viscosity system can be easily removed through a backflow operation [7].
The conventional methods based on Euclidean geometry and fractal geometry have shown evident advantages for addressing the complexity and multiple scales of porous media [16]. Fractal geometry has been successfully applied to characterize the structures of transport processes in porous media [17]. As far as permeability is concerned, a series of models for porous media aim to reproduce the relevant features of real porous media. The fractal geometry theory characterizes irregular or disordered objects such as sandstone pores and grains, and represents a useful tool for analysis of porous media [18,19]. Models usually relate structural parameters of porous media, such as fractal dimensions, tortuosity fractal dimensions, microstructural parameters, and porosity, to the rheological material functions. These models seek relationships among the average flow velocity, effective permeability, effective porosity, pressure gradient, and material constants [20].
In this work, a Buckley–Leverett analysis with capillary pressure to model the oil displacement in a porous medium is presented. The model involves a bundle of tortuous capillaries with a size distribution and tortuosity that follow fractal scaling laws. The displacement of oil by a micellar solution in a fractal porous medium is described by the Bautista–Manero–Puig (BMP) model [6,21]. This model of capillary pressure allows the different shock profiles that may be present in a real porous medium to be described. Here, we use the definition of the mobility ratio M as the mobility of the oil phase/mobility of the micellar solution. Elsewhere, the definition of mobility ratio is . In the discusion section, we provide an alternate interpretation using as the mobility ratio.
2. Rheological Equation of State
The BMP model is described by the following equations [21]:
where is the upper-convected derivative of the stress tensor, is the symmetric part of the rate of the strain tensor, is the fluidity (inverse of the shear viscosity ), is the zero-shear-rate fluidity, is the fluidity at high shear rates, is the shear modulus, is the structural characteristic time, and is a kinetic constant related to structure modification. The upper-convected derivative of the stress tensor is
where is the velocity gradient tensor. Equations (1) and (2) reduce to the upper-convected Maxwell model when . These equations express that the nonlinear viscoelastic processes contained in the Maxwell equation are coupled with an equation written in terms of the fluidity, which is itself a kinetic equation with a characteristic time related to structure formation and a destruction term related to structure modification with a kinetic constant proportional to the dissipation. Under simple shear flow, the above equations reduce to
where is the shear rate and the nonlinear terms in Equation (3) are not considered, which implies that the normal stresses generated under flow are negligible. In steady state, both Equations (4) and (5) can be reduced to provide
Equation (6) predicts shear-thinning behavior when , shear-thickening behavior when , and Newtonian behavior when . A plateau region is predicted in the limits of very low and very high shear rates, with a power-law behavior at the intermediate shear rates. In addition, a stress plateau is predicted when . This implies a constant stress in the limit as the shear rate approaches zero. An apparent yield is predicted for very small values of . The physical meaning of Equation (6) can be revealed if it is written in terms of the non-dimensional dissipation, as follows:
Upon increasing dissipation , while for decreasing dissipation . From Equation (6), the plateau stress can be calculated when in the region of very small shear rates. This results in
Equation (6) can be solved for by expressing the results in terms of the plateau stress to provide
The three independent parameters in Equation (9) can be evaluated from the flow curve itself in the form of the viscosity versus the shear rate. The fluidity at low strain rates (inverse viscosity) is extracted from the first Newtonian plateau at vanishing shear rates, and the fluidity at an infinite shear rate corresponds to the plateau at high shear rates. When the plateau stress is approached, the viscosity tends to a slope of in a log–log plot. The usual form from which the plateau stress is evaluated considers the plateau that is exhibited as the shear rate tends to zero in a plot of the log stress versus log shear rate. In this context, the model does not contain fitting parameters. We can calculate the fluidity at the plateau stress by setting ; this provides
According to the model presented here, the pores are considered as capillaries with different diameters. The change in capillary radius is taken into account by modifying the tortuosity along the flow trajectories, and several results are shown in which changes in tortuosity or fractal dimensions are considered. Although transient flow exists in a real porous medium (i.e., complex expansion–contraction trajectories), in this model the change in geometry which modifies trajectories is considered as a change in tortuosity and a change in fractal dimensions. In other words, following the averaging procedures considered in the present model, the overall flow may be considered steady; however, locally it is intrinsically unsteady. This transient state is taken into account by the variation in thew tortuosity or fractal dimensions of the porous medium in time scales shorter than that of the global averaged macroscopic flow.
2.1. Calculation of Mobility
The procedure to calculate the mobility in a complex fluid is outlined in (the appendix of reference [6]). A momentum balance on a differential element in cylindrical geometry leads to a relationship between the shear stress and the pressure gradient; in this case, the shear stress at wall in tortuous capillaries is provided by [22,23].
Following the fractal scaling method, the wall shear stress is [6]
where is the fractal dimension describing the tortuous length of the capillary. Darcy’s law may then be written in terms of the non-Newtonian mobility as follows:
where
As the capillaries in porous media are tortuous, the total shear stress in Equation (12) at all capillary walls is related to the fractal dimensions and , microstructual parameters, and pressure gradient (see [6]). The resulting effective permeability is
The Newtonian permeability may be obtained as a particular case when , (Poiseuille’s law), yielding
In straight capillaries, ; therefore, we can obtain
This equation agrees with those of the current literature for Newtonian fluids. We obtained an analytical result for the permeability provided can be calculated [6]. This may be achieved assuming that the fluidity in the pore/capillary attains a minimum in the center of the geometry and reaches a maximum at the walls, i.e.,
Accordingly, the fluidity attains its minimum at the capillary center , that is, , and its maximum at the walls , . The fluidity at the wall requires the calculation of the wall stress according to Equation (11). Thus, the final result is [6]
When , next to the capillary center, the permeability tends to the Newtonian constant value provided by Equation (16). Near the wall, tends to a maximum value and the permeability diminishes asymptotically to another constant value as a function of the maximum fluidity. By defining
Equation (19) can be expressed as
Clearly, within the limit the permeability is constant, providing
In straight capillaries ,
which agrees with Equation (17). The non-Newtonian fluid mobility in Equation (14) becomes
which reduces to the Newtonian mobility
where is the fluidity of the Newtonian fluid, while the mobility ratio becomes
In Equation (26), the ratio is
The limits of Equation (26) consider expressions at low and high stresses; in the low range, and . At the upper stress limit, , and hence
At the plateau stress,
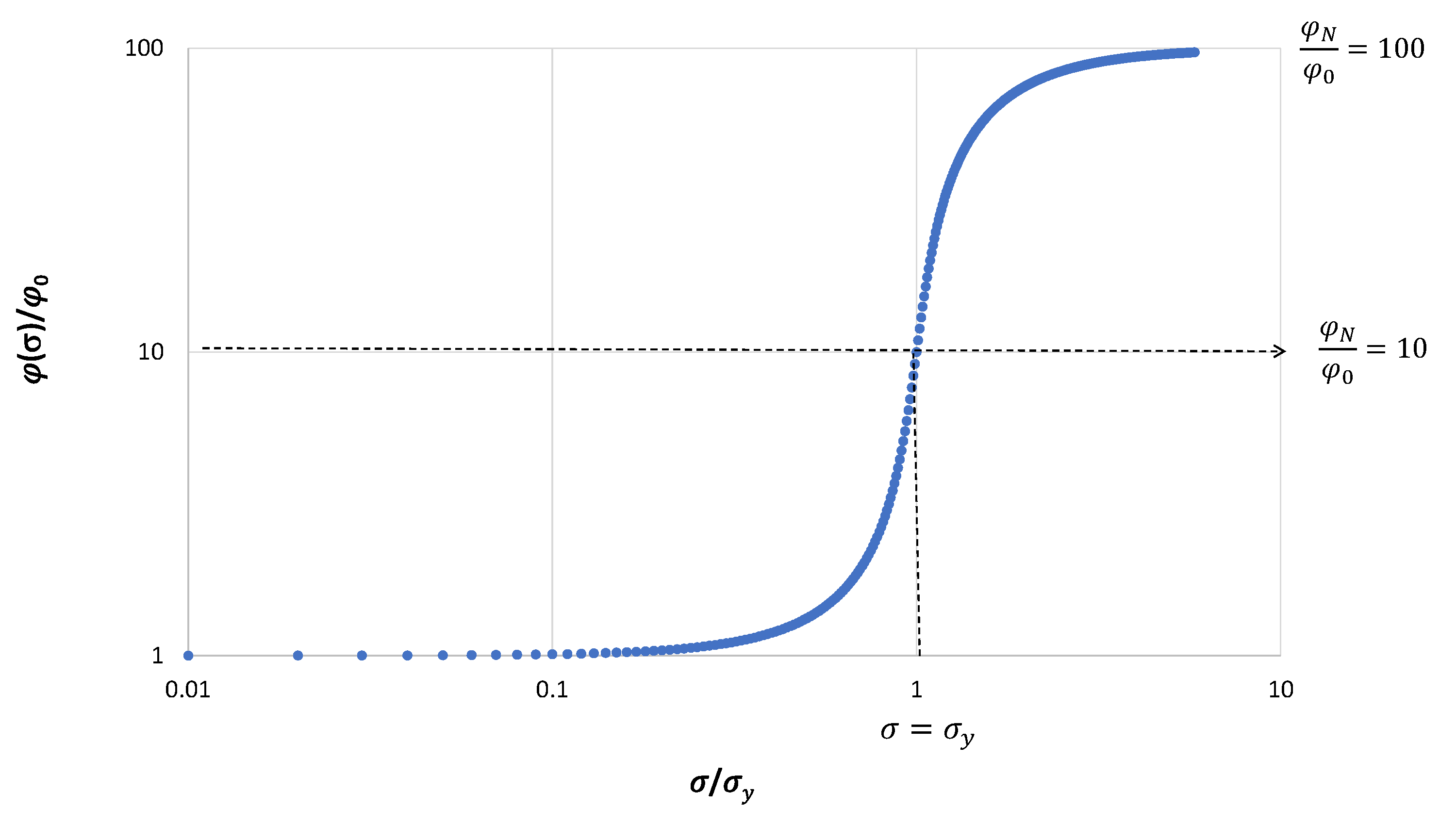
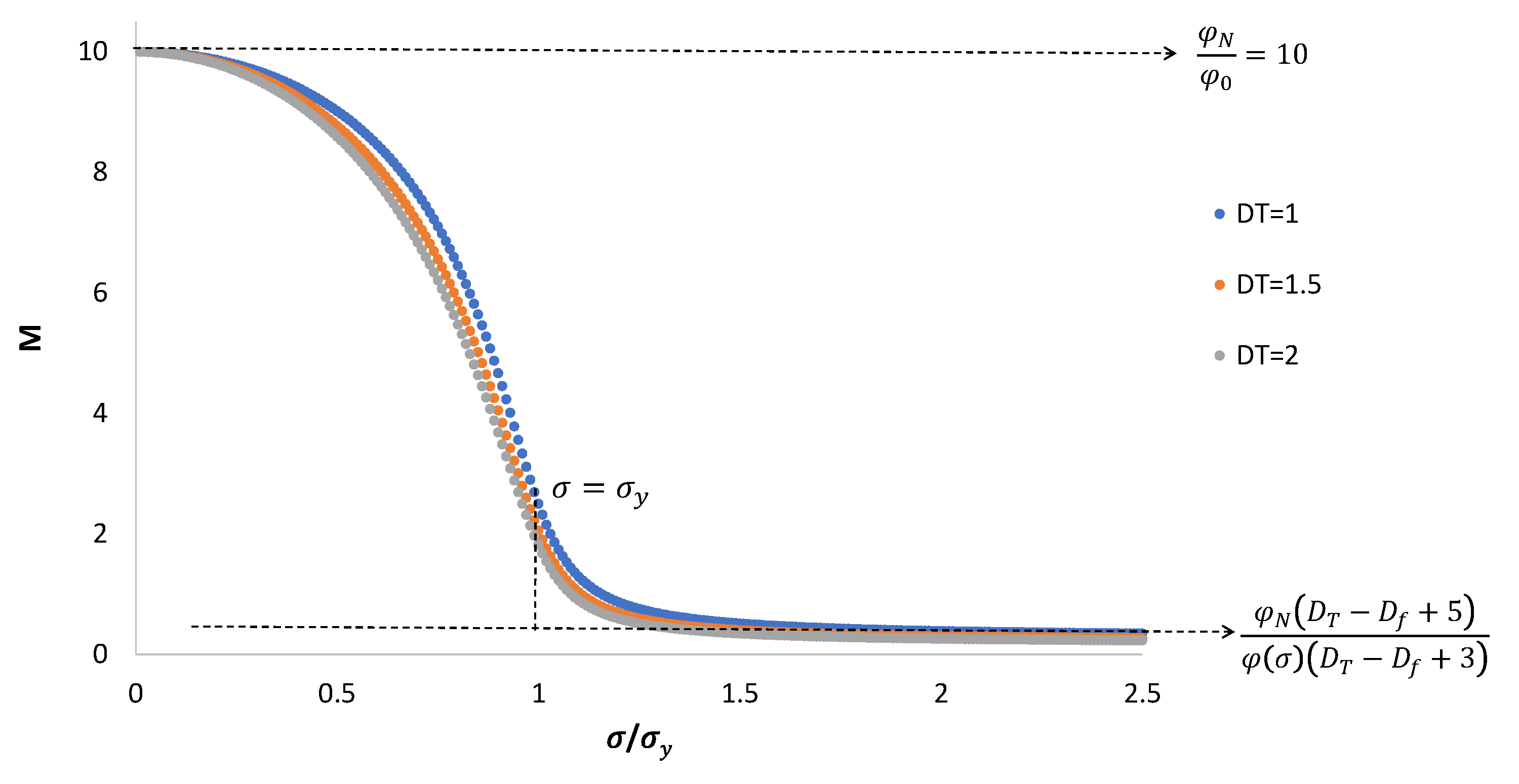
In Figure 1, a plot of the normalized fluidity as a function of the stress normalized by the yield stress is disclosed. We consider a Newtonian fluid with viscosity ten times smaller than that of the non-Newtonian fluid at small stresses. As the stress increases, the fluidity of the non-Newtonian fluid increases as well, overtaking that of the Newtonian fluid. In Figure 2, the mobility ratio is plotted with the applied stress.
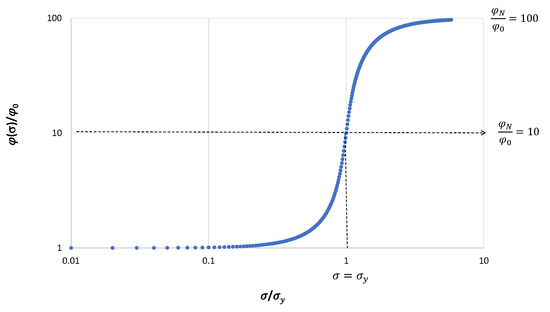
Figure 1.
Normalized fluidity as a function of the stress normalized by the plateau stress. When the normalized stress is equal to one, the fluidity is , which coincides with .
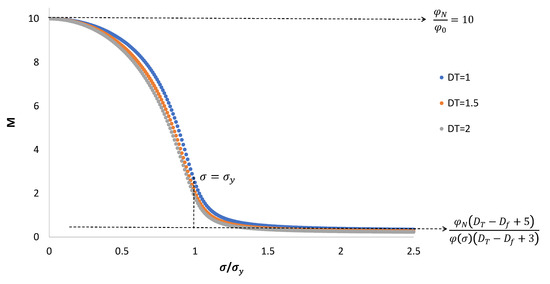
Figure 2.
Mobility ratio as a function of applied stress. For small stresses, the relative mobility is . For high stresses, the relative mobility is . At the plateau stress, . and the ratio is variable.
We define the following relative permeabilities:
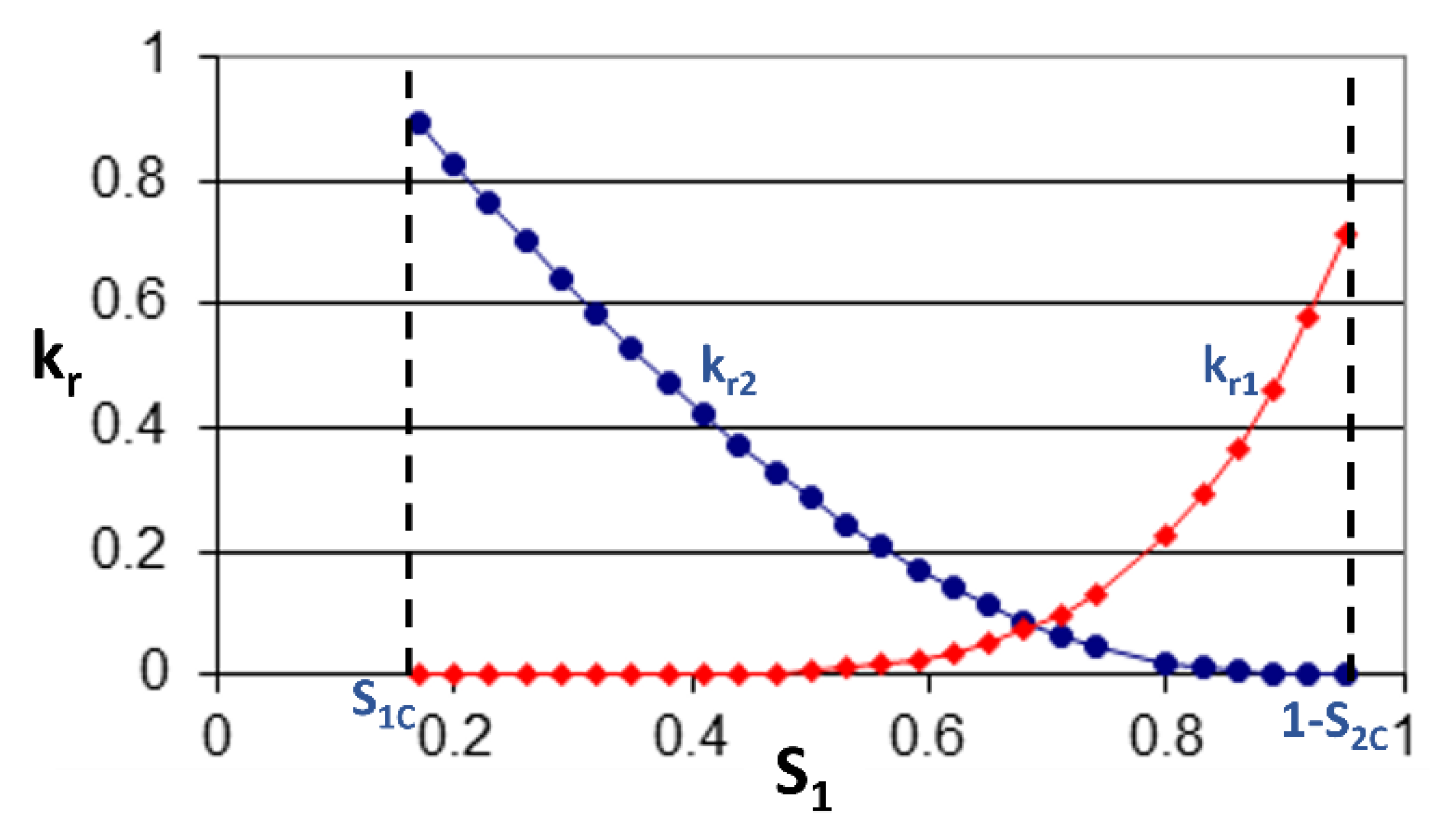
where is the relative permeability of fluid i and is the characteristic permeability of fluid i. Figure 3 shows the variation of the relative permeabilities as a function of the saturation.
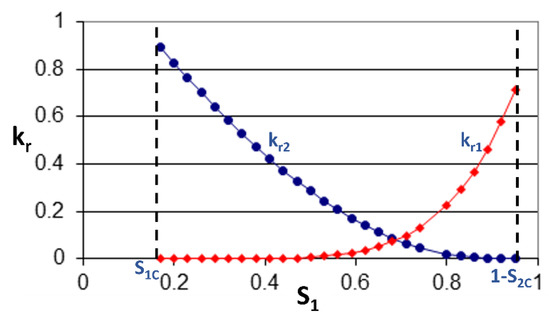
Figure 3.
Relative permeabilities of Fluids 1 and 2.
Saturation limits are for Fluid 1 such that is the maximum saturation of Fluid 1 and the minimum saturation of Fluid 2. Figure 3 shows that there is a quadratic dependence of the relative permeability on the saturation, and therefore the following relations represent this variation:
from the material balance for the two fluids, namely,
Upon substitution of the above equations for those of Darcy’s law for each fluid provides the following displacement velocities in the porous medium:
considering that the capillary pressure depends only on saturation
and the flow fractions are defined as follows:
where represents the sum of the flow rate fractions, as the flow area is the same for both fluids. Deriving Equation (37) with respect to x and solving for the pressure gradients in Equations (35) and (36), upon substitution we obtain
Using Equations (32) and (33) and the definition of the mobility ratio , we obtain
which can be expressed as
where
From the mass balance
the following equation is obtained:
2.1.1. The Buckley–Leverett Equation
Neglecting the capillary forces, Equation (46) reduces to
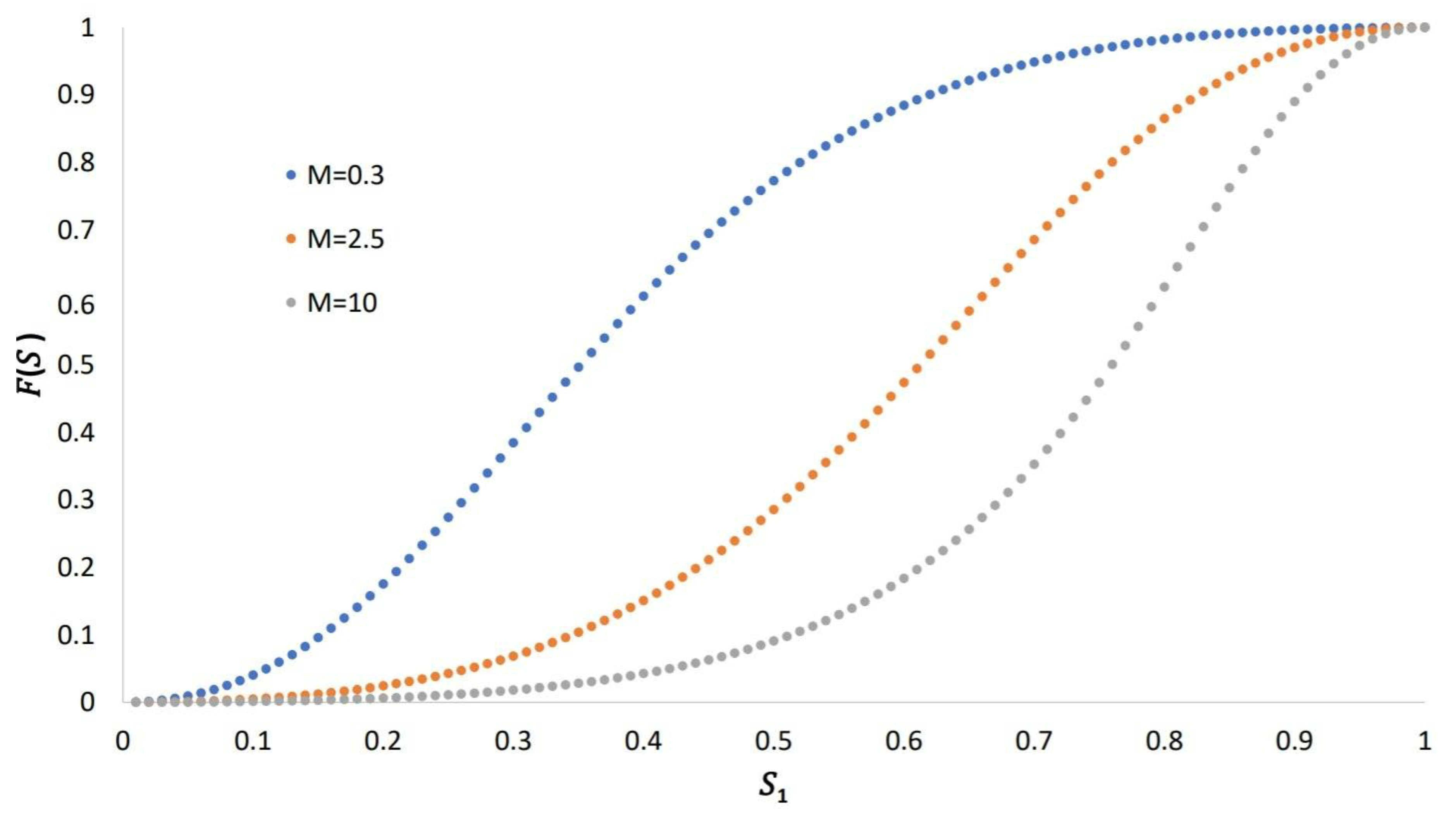
A plot of the flow fraction as a function of the saturation S for the three mobility ratios considering is shown in Figure 4.
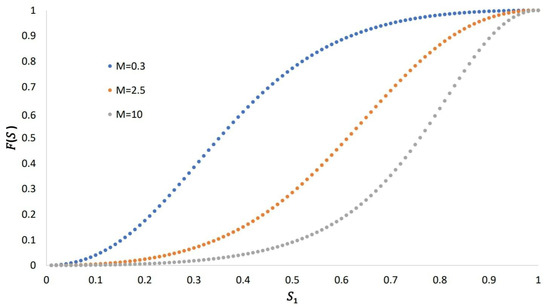
Figure 4.
The flow function F as a function of saturation for three mobility ratios.
Next, we make Equation (46) non-dimensional by defining the variables and . Dropping the sub-index, we can express Equation (46) as follows:
where S refers to the saturation of Fluid 1. Up to first order in the derivatives and small capillary pressure contributions, Equation (48) leads to
The Buckley–Leverett problem does not consider capillary effects:
The material derivative of S in one dimension is
Comparing Equations (50) and (51), we obtain
where
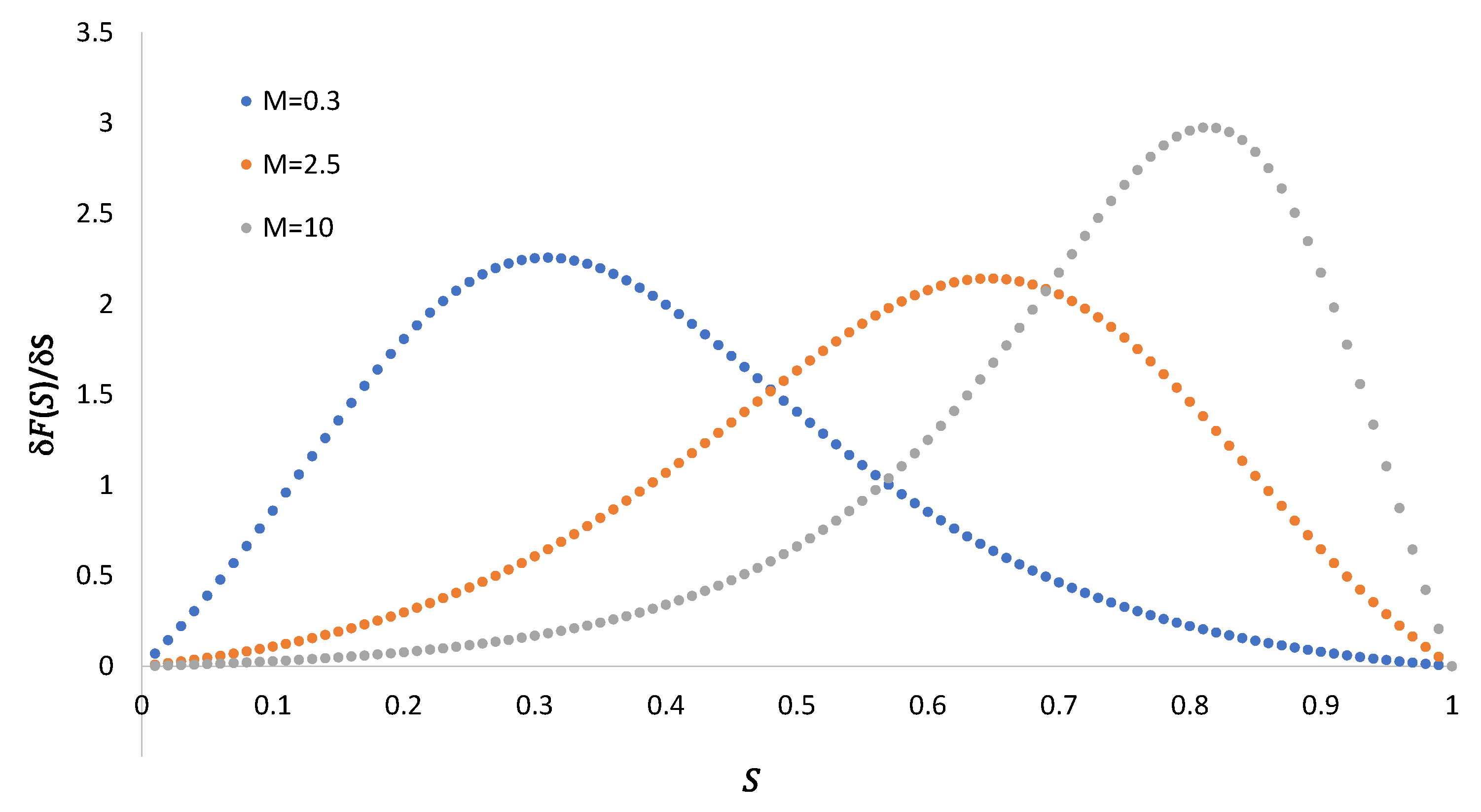
In Figure 5, we plot Equation (53) for the three mobility ratios.
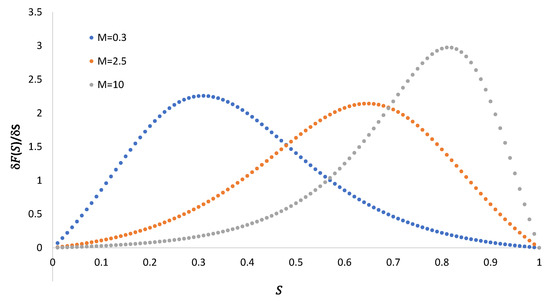
Figure 5.
The derivative of as a function of saturation for the three mobility ratios.
We can integrate Equation (52) as follows:
Because the function is not single-valued, the Buckley–Leverett analysis includes the calculation of the tangent to the flux function and the presence of a shock. The tangent condition reads
A unique root of Equation (55) is obtained, namely,
which is the abscise of the point of intersection of the tangent and the function . The slope of the tangent is found from the condition
and the mean saturation is found if , namely,
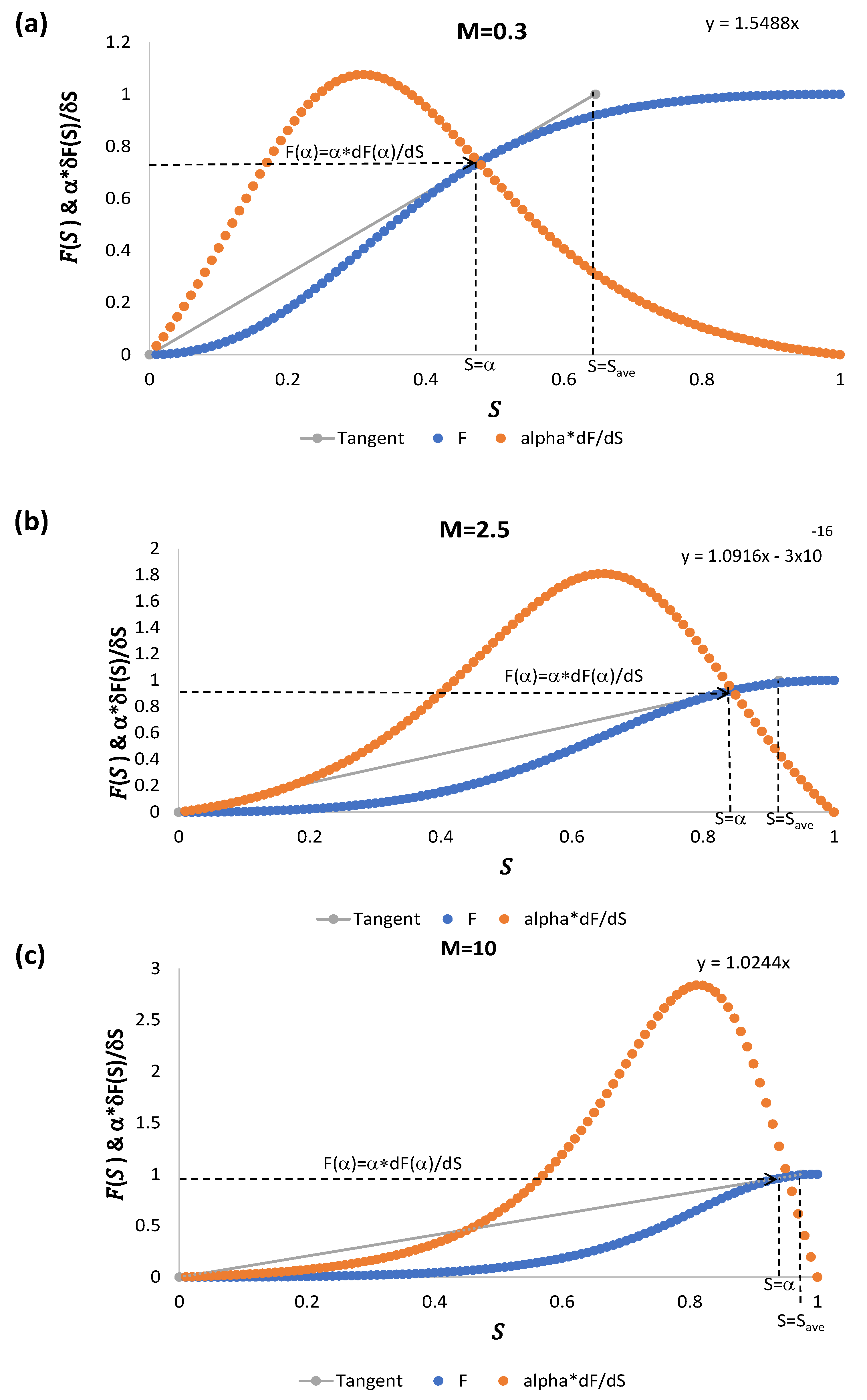
In Figure 6a–c, we plot the flux function and its derivative together with the tangent to locate the intersection point .
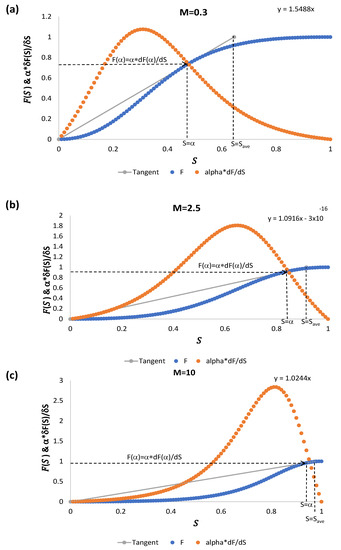
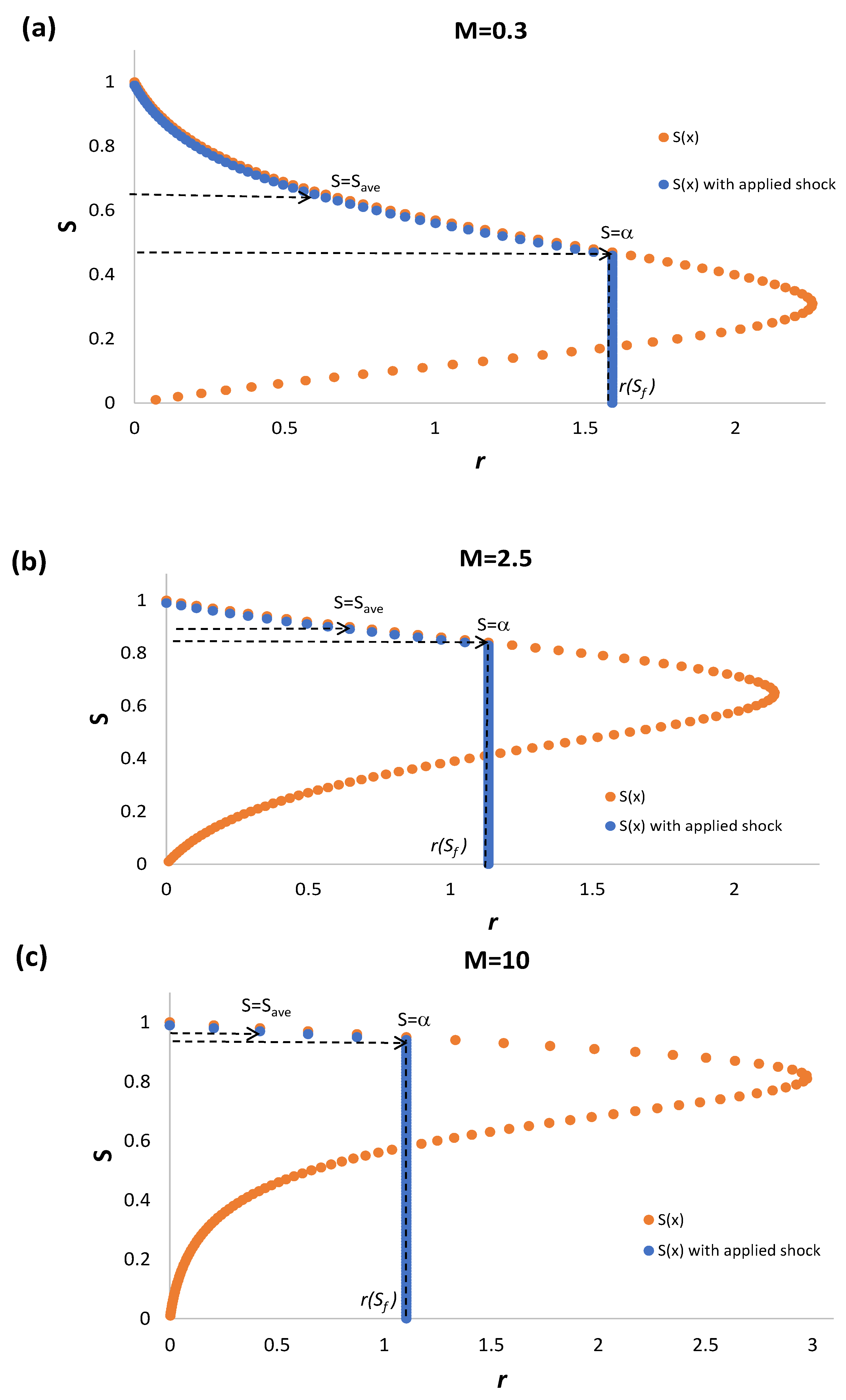
Figure 6.
The function and its derivative as functions of the saturation S for three mobility ratios (a) M = 0.3, (b) M = 2.5, and (c) M = 10. The tangent and point of intersection with abscise are also shown.
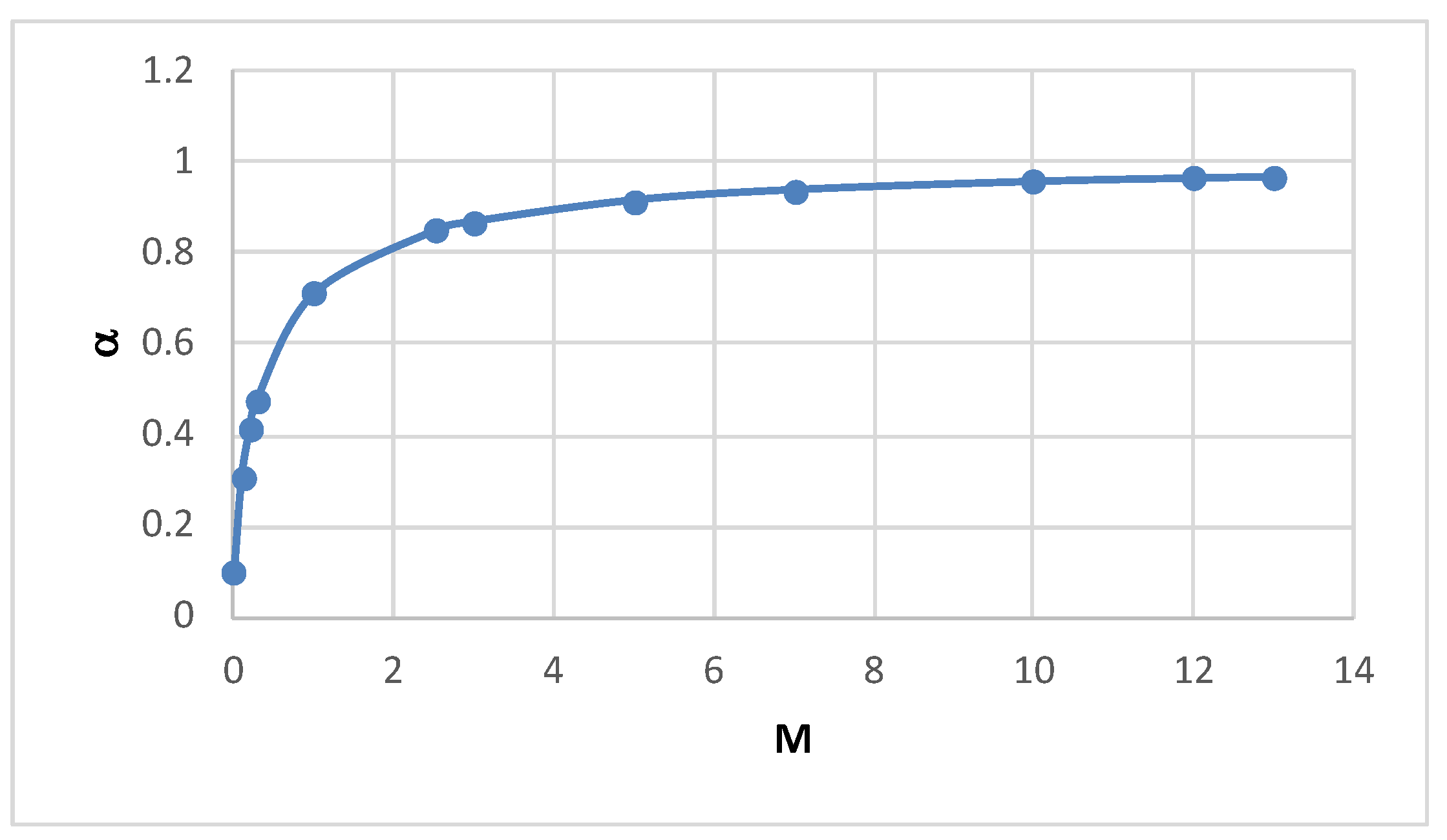
As the mobility ratio increases, the intersection point of the tangent and the function has ordinate approaching one as well as see Figure 7, and hence the slope tends to ; see Table 1.
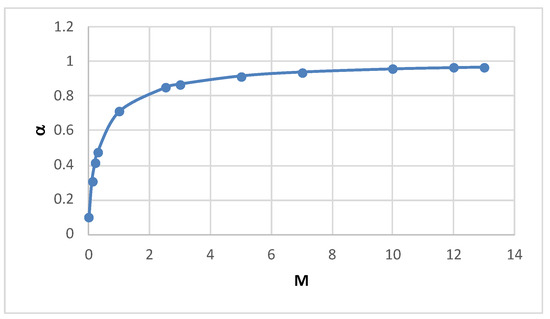
Figure 7.
The root as a function of the mobility ratio.

Table 1.
Mobility ratios with values and the corresponding average saturations and tangents.
In Figure 1 and Figure 2, it is clear that for low pressure gradients (namely, small stresses) the fluidity of the displacing fluid is small and the ratio of its fluidity with the fluidity of the Newtonian oil is large . The plateau stress of the micellar fluid coincides with that of the oil, with a mobility ratio around 2. For high pressure gradients, the fluidity of the non-Newtonian fluid is large (close to that of water), even larger than that of the oil. In this case the displacing action of the displacing fluid decreases, which is convenient for actual enhanced oil recovery operations. It is worth mentioning that the viscosity of the displacing fluid should be properly adjusted along with the applied pressure gradient in order to provide the optimal oil displacement. This is one of the advantages of a complex non-Newtonian fluid, which provides multiple options for actual oil operations.
The equal area criterion is used to specify the value at which the shock should occur, namely,
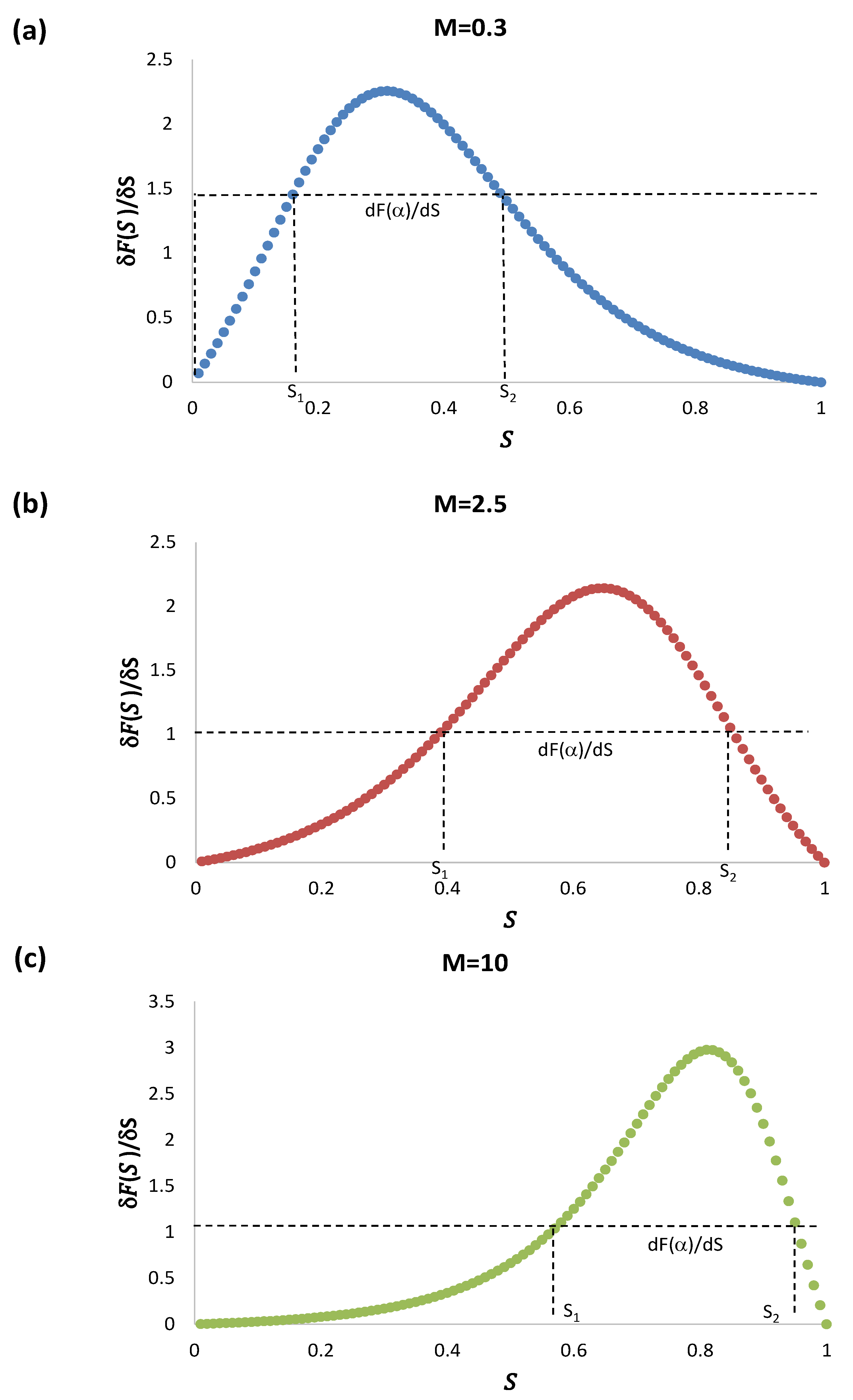
where denotes the ordinate at which the equal area criterion holds. Equation (59) is an illustration of the mean value theorem of integrals. In fact, if and , Equation (59) is satisfied. Therefore, the shock occurs at a value of the saturation equal to and ordinate , which is the speed of propagation according to Equation (52). In the Figure 8a–c, the saturation is plotted as a function of the propagation speed for the three mobilities.
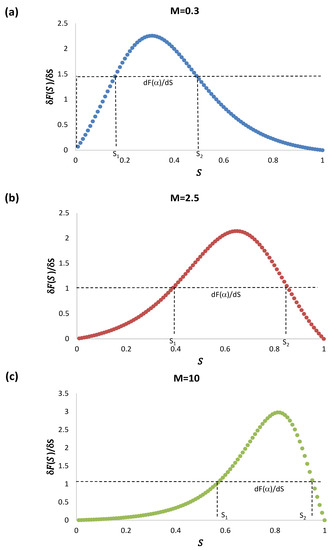
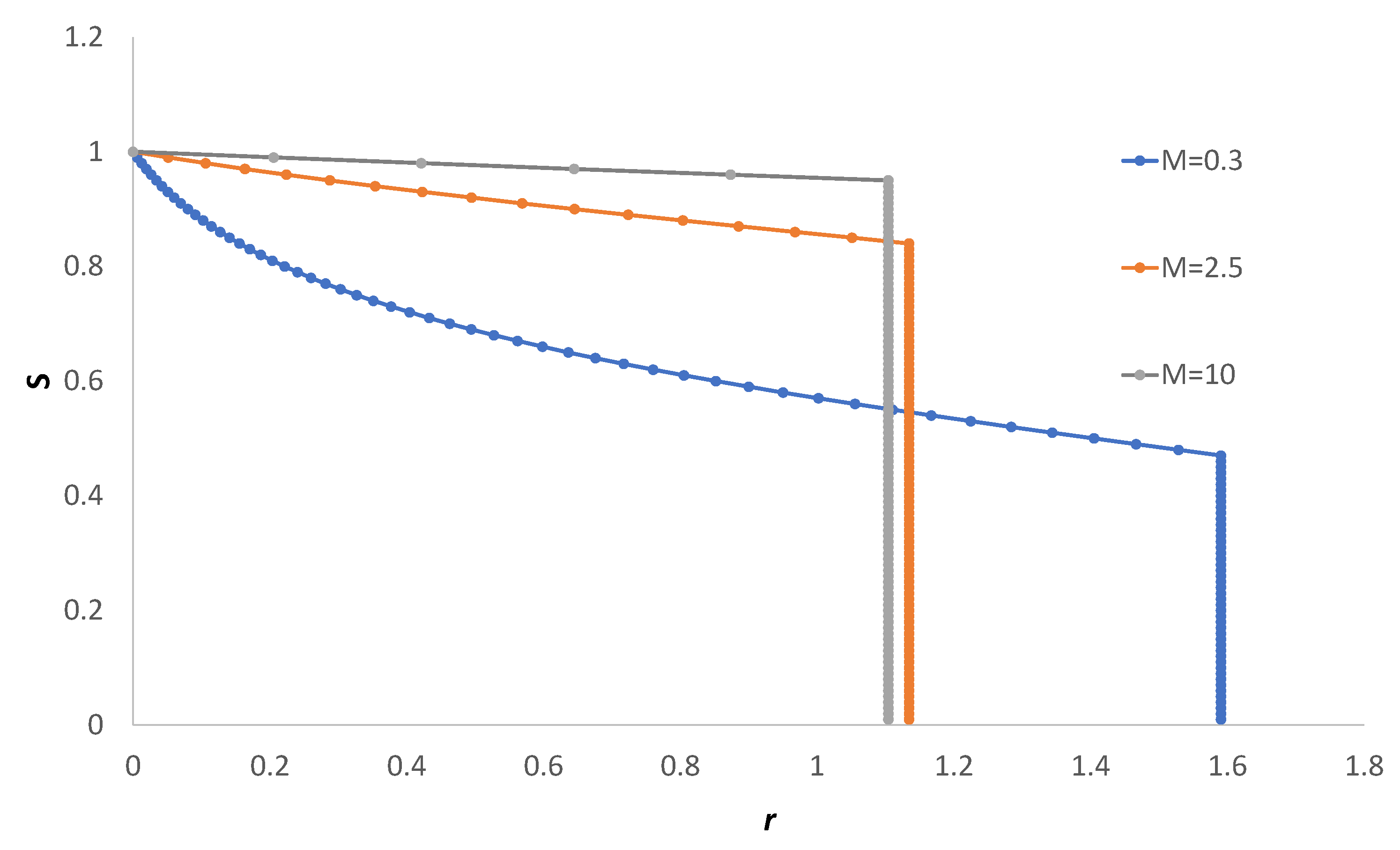
Figure 8.
The derivative as a function of the saturation for three different mobility ratios (a) M = 0.3, (b) M = 2.5, and (c) M = 10, illustrating the equal areas criterion. Here, denotes the ordinate at which the equal area criterion holds.
Figure 9a–c depict the speed of propagation of the shock profile as the mobility changes. The speed is higher as the mobility ratio decreases. This effect is expected, as the viscosity of the displacing non-Newtonian fluid is larger for . For higher pressure gradients the displacing fluid viscosity diminishes, allowing for larger propagation speeds. In Figure 10, the saturation is plotted with the propagation speed for the three fronts, exhibiting the effect of diminishing the viscosity of the non-Newtonian pushing fluid for large pressure gradients.
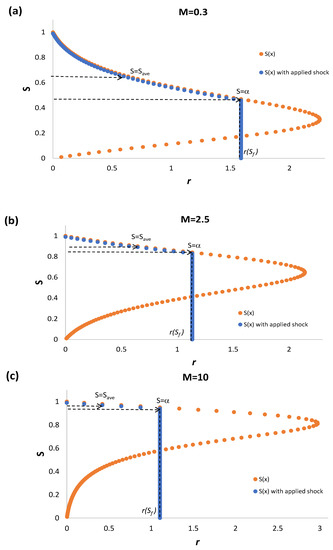
Figure 9.
Saturation as a function of propagation speed for three mobility ratios (a) M = 0.3, (b) M = 2.5, and (c) M = 10, illustrating the location of the shock.
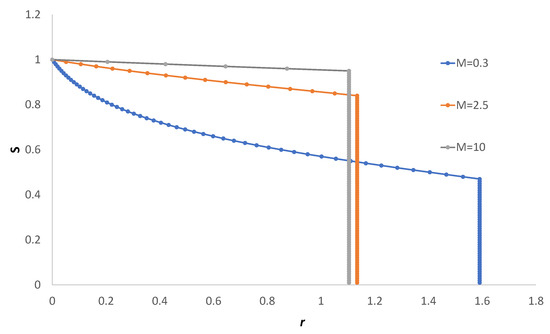
Figure 10.
The velocity of the propagation front for the three mobility ratios.
To further analyse the shock profiles, let be the saturation value to the left of the shock and let the value of the saturation to the right of the shock; moreover, let the boundary conditions be
The slope just before and after the shock corresponds to the Rankine–Hugoniot condition:
if . Applying the boundary conditions, we obtain
which corresponds to the tangent condition. Furthermore, applying the Oleinik entropy condition
if , and . Hence, the criterion of equal areas is sufficient to define the shock location according to the Oleinik criterion.
2.1.2. Capillary Pressure
Here, we consider the model by Hassanizadeh and Gray, in which the capillary pressure can be described according to the following expression:
where is the static capillary pressure and is a characteristic time. In this case, and considering that the capillary pressure in equilibrium is generally a decreasing function of saturation , Equation (46) becomes:
We discuss an extension to the B-L equation which includes the third-order mixed derivatives term and models the capillary pressure. Travelling wave solutions exist in the extended model. The speed of the shock, , and are related through the Rankine–Hugoniot (RH) condition Equation (62). Experiments in two-phase flow in porous media reveal complex infiltration profiles with overshoots (i.e., non-monotone profiles). Solutions with the second derivative term exist if , , and satisfy the RH and Oleinik entropy conditions. In the limit , traveling waves converge to the shock .
If , then a weak solution is composed of a rarefaction wave in the region where and a shock that spans the range . Focusing on the relation of and , we establish the existence of the function
where is defined through the equal area criterion
in such a way that Equation (66) may possess a shock wave solution in which
in which case is a bifurcation parameter when . For the case in which , the criterion is not fulfilled, and new types of shock waves are admissible.
With as defined above, we establish the existence of a function defined for such that Equation (66) has a travelling wave solution with if and only if .
The solution of Equation (66) for various cases is illustrated in the following plots; here, .
A Fortran numerical code was developed using the finite difference scheme proposed by [14]. This code was used to solve the model governing equation (see Equation (5.1) in [14]). With same parameters used by them, the computations were performed on the interval , with for the rarefaction and rarefaction-under-compressive shock solutions and in other cases. All solutions are shown at time and with . The numerical code was validated by comparing the cases reported by [14]. The results showed that the present code qualitatively reproduces the same results as shown in their figures.
3. Results
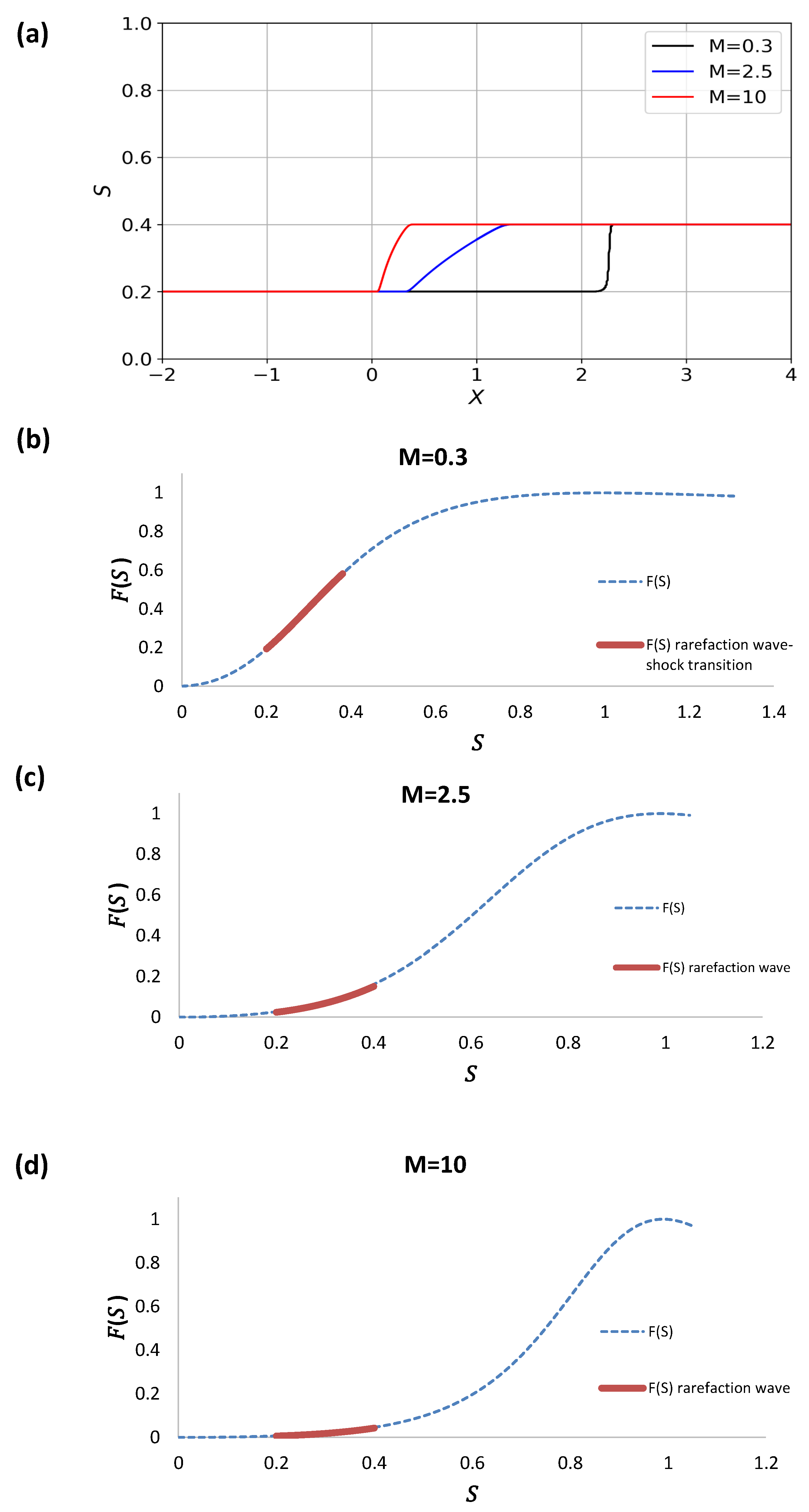
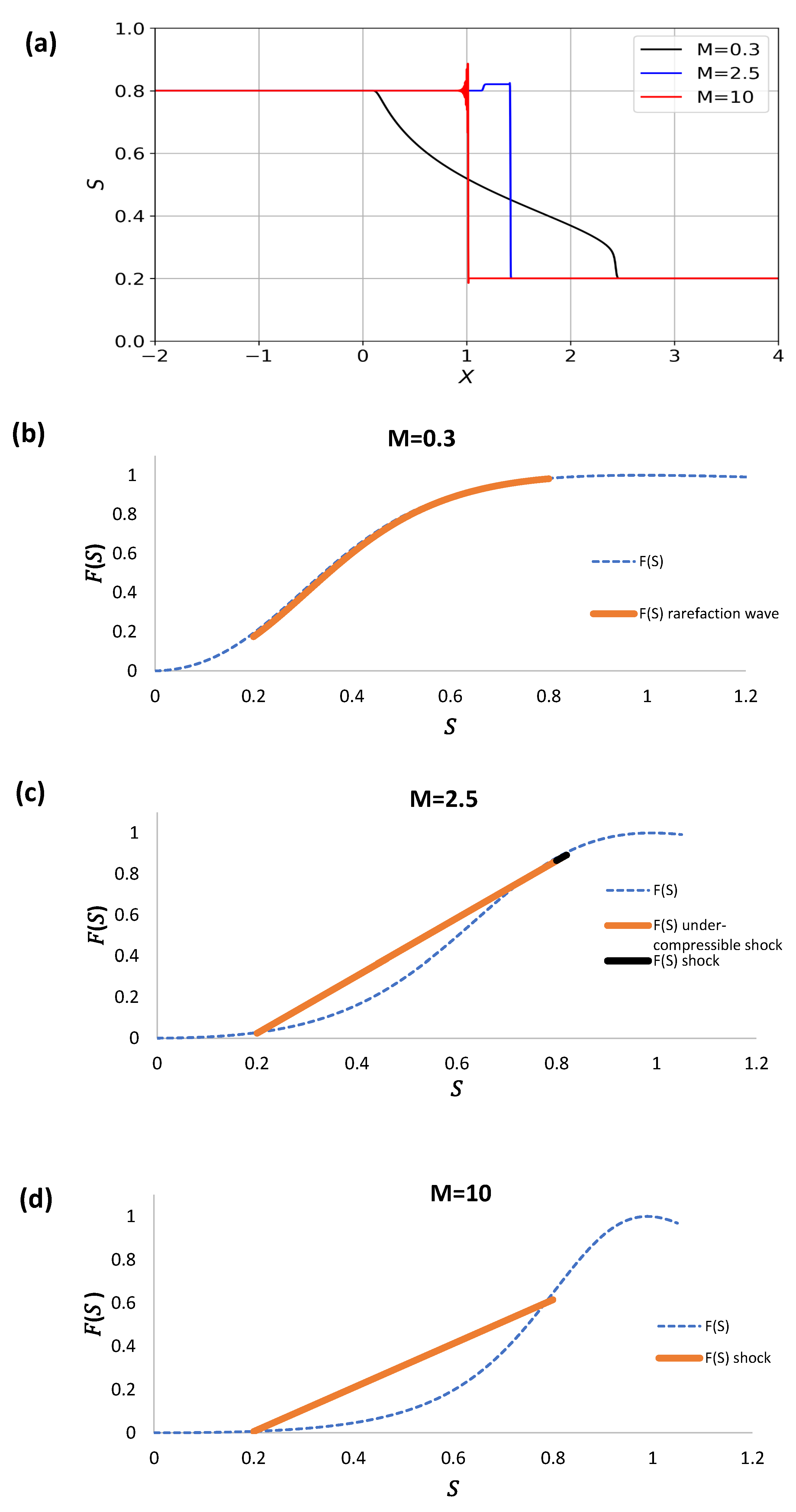
In Figure 11a–d we plot the first example, consisting of the case in which and , for the three mobility ratios . In Figure 11a rarefaction wave solutions are shown for high mobility ratios, becoming more shock-like as the ratio diminishes. The corresponding flux functions are illustrated in Figure 11b–d. It is clear that the front velocity increases as the mobility ratio decreases, as the slope of the curve between to increases from to . The fact that a near shock-like solution is apparent in Figure 11b indicates that the flux curve in this region is almost a straight line.
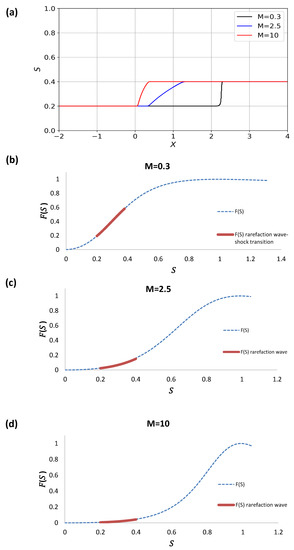
Figure 11.
(a) Rarefaction wave solution for , and . The corresponding flux functions for three different mobility ratios (b) M = 0.3, (c) M = 2.5, and (d) M = 10.
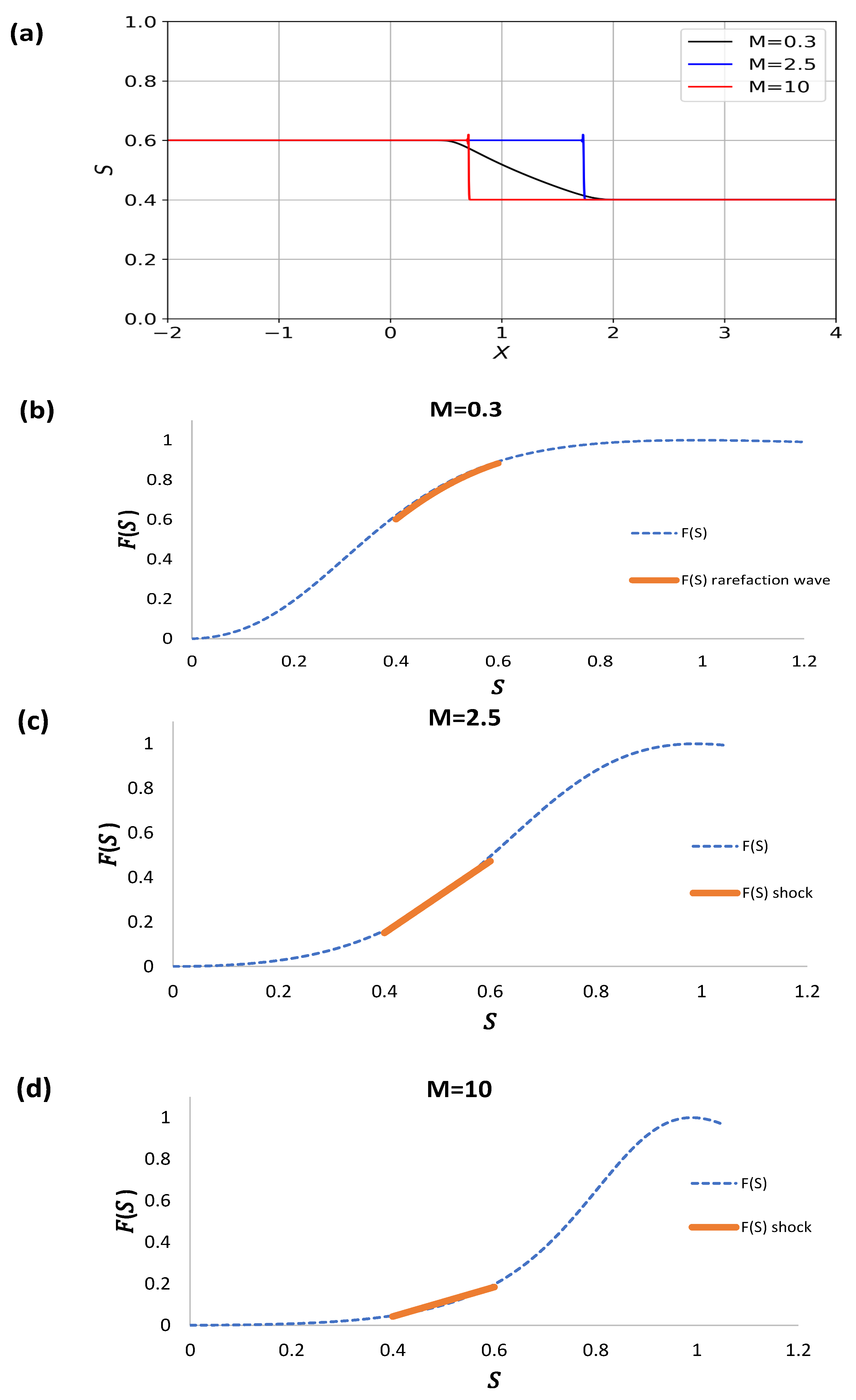
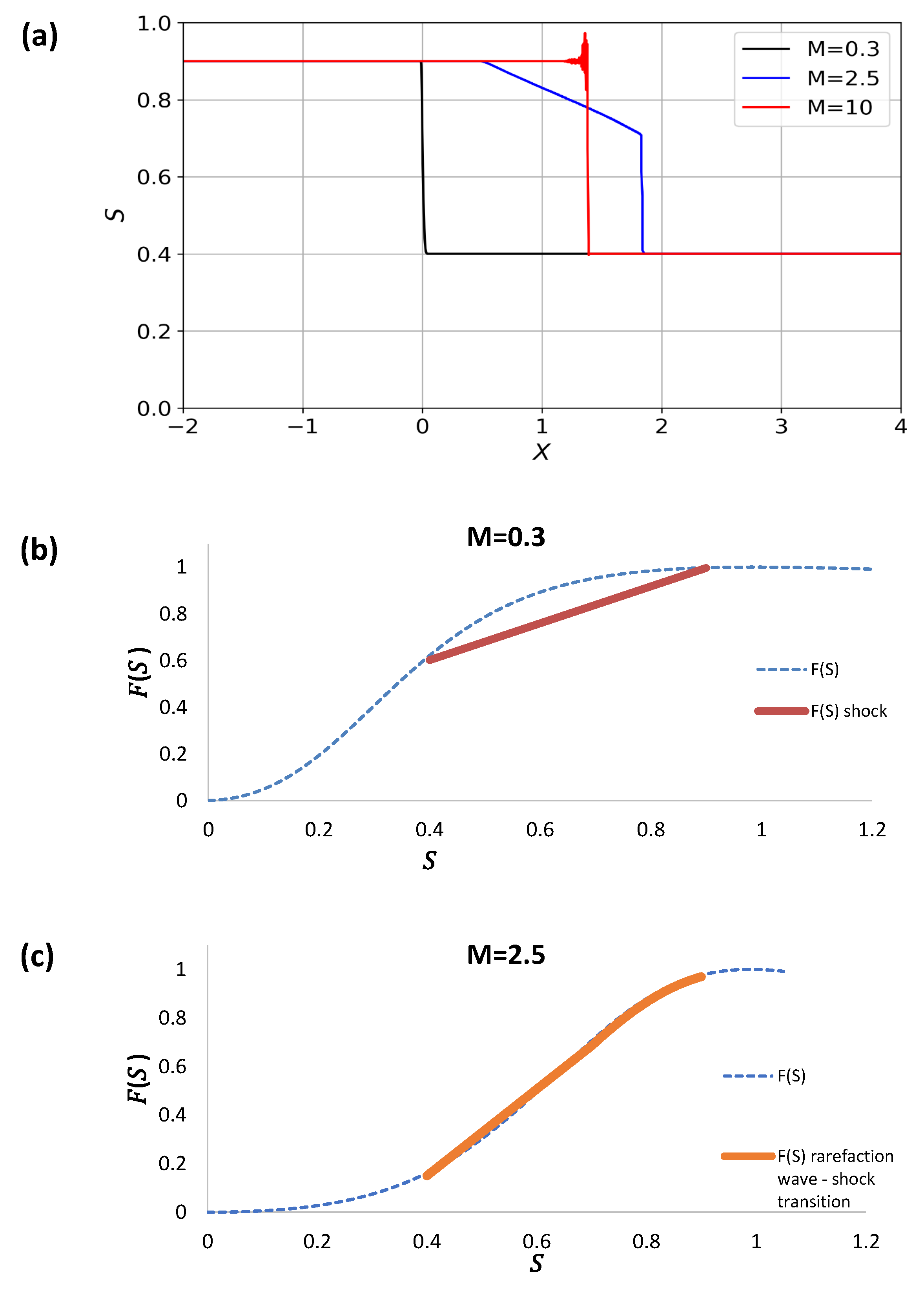
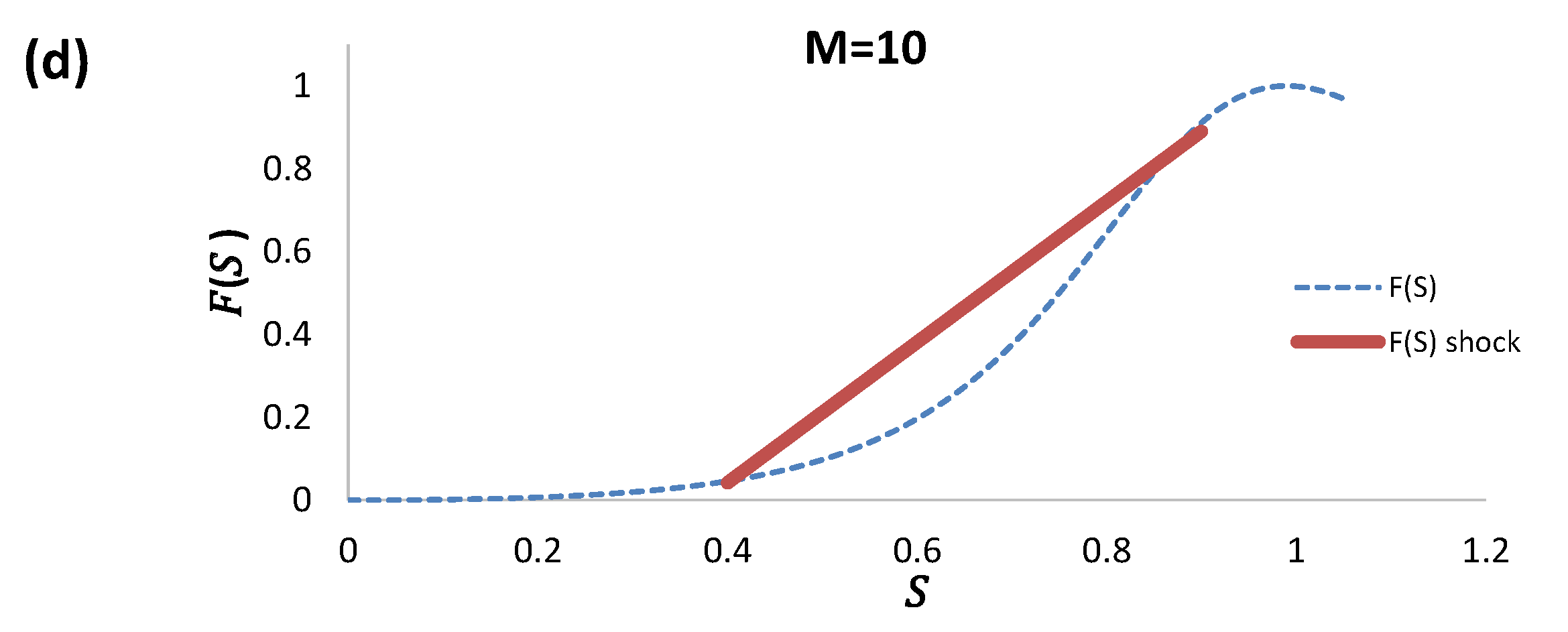
Figure 12a–d presents the solution for the three representative mobilities, from to . In Figure 12a, a rarefaction wave solution is apparent at a small mobility ratio. As the mobility ratio increases, the solutions now depict shocks appearing at a relatively high propagation velocity as well as at a lower velocity .
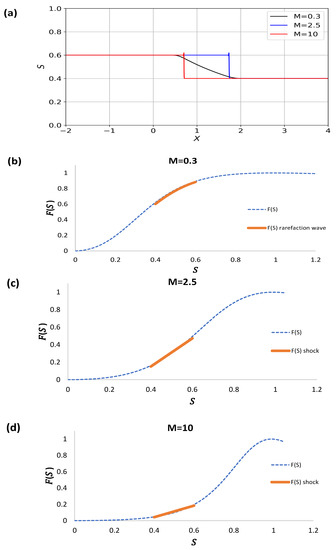
Figure 12.
(a) Rarefaction wave which evolves into to shocks as the mobility ratio diminishes for , and . (b) The rarefaction wave location in the upper region of the flux curve. (c,d) The shocks are represented by straight lines within the saturation interval .
A more complex situation is exhibited here, as a shock trailing the under-compressive shock for and is shown in Figure 13a–d.
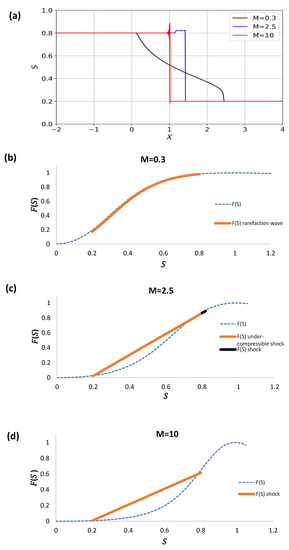
Figure 13.
(a) The rarefaction wave evolves into a shock trailing the under-compressible shock for and alternatively evolving into an under-compressive shock for . (b–d) The shock behaviour changes from a rarefaction wave at low mobility ratios into a small shock trailing an under-compressive shock at high mobility ratios.
For low mobility ratios, the rarefaction wave is represented in the flux curve in Figure 13b in the saturation interval . At intermediate mobility ratios there is a small shock from to trailing the large under-compressive shock from down to (Figure 13c). The propagation velocity of the first shock is smaller than that of the large shock, as represented in the flux curve by a small change in the slope of the black line with respect to the higher slope of the brown straight line. For large mobility ratios, oscillations followed by an under-compressible shock from down to are presented.
The last example exhibits two shock profiles at low and high mobility ratios, with an under-compressive wave trailing a shock in the intermediate mobilities. Figure 14a–d illustrates the saturation as a function of the propagation velocity (Figure 14a) and the corresponding flux curves for the three mobilities (Figure 14b–d). It is interesting that the smallest mobility ratio generates a shock at lower velocity than that of the high mobility ratio. The flux curve (Figure 14b) for describes a shock in the saturation interval , which is represented by a straight line with a slope corresponding to the abscise of the blue curve in Figure 14a. On the other hand, the flux curve for (Figure 14d) describes a shock in the same saturation interval, in this case represented by the straight line, except with larger slope. The oscillations above are due to the complex eigenvalues at , as referenced in [14]. The curves corresponding to the intermediate mobility ratio comprise a rarefaction wave from to trailing a shock profile from to . This behaviour may be described by a curve that follows the flux curve from to , trailing a straight line with the largest slope between down to , as illustrated in Figure 14c.
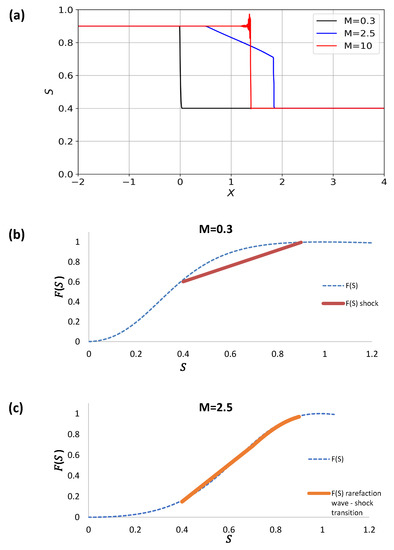
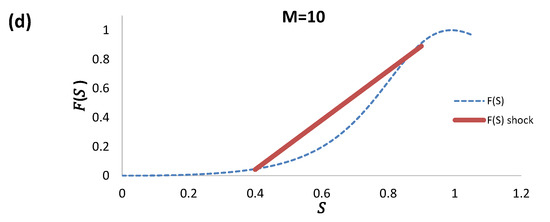
Figure 14.
(a) The undercompressive shock for , and . The corresponding flux functions for three different mobility ratios (b) M = 0.3, (c) M = 2.5, and (d) M = 10.
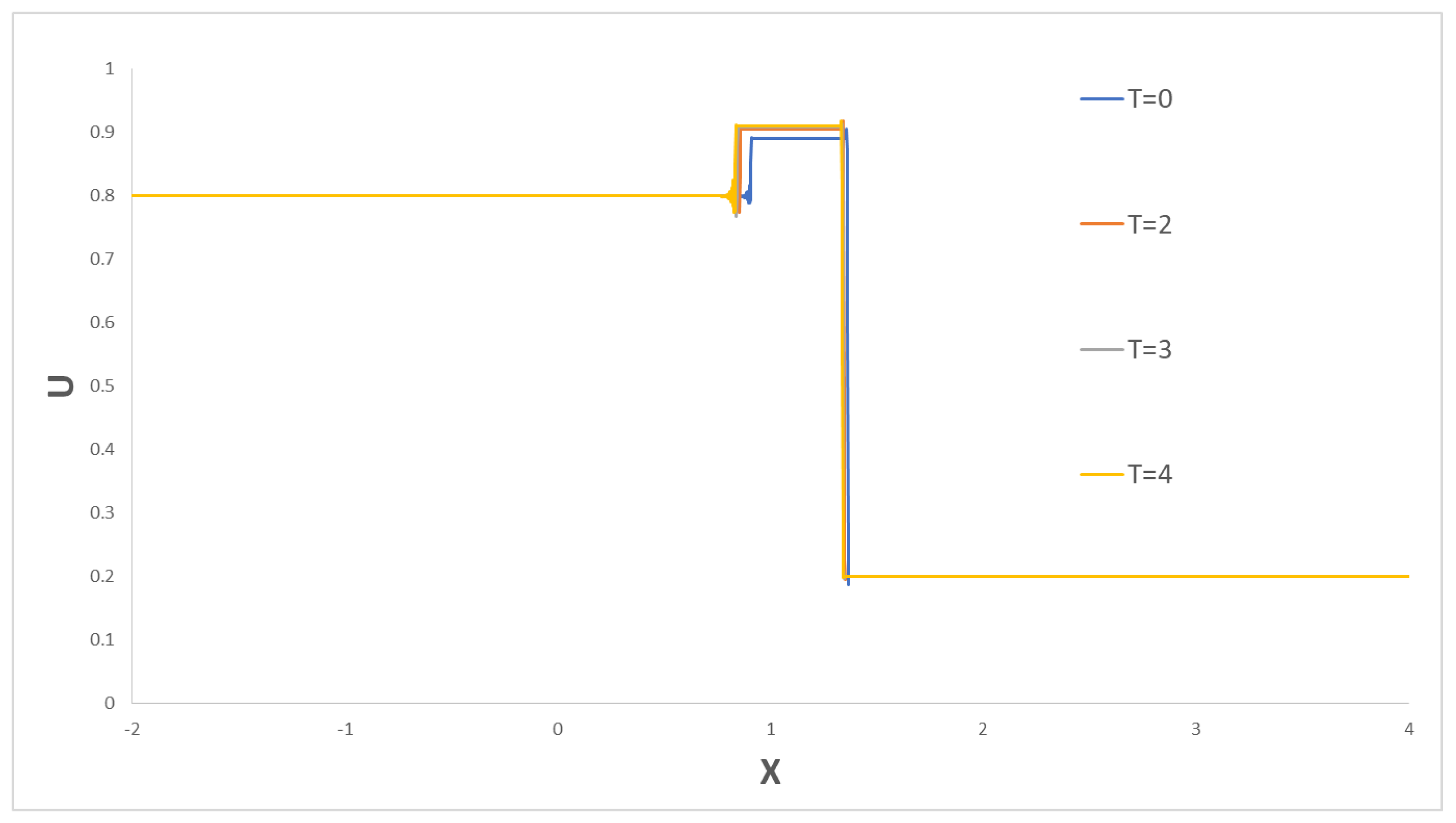
The influence of the characteristic time in Equation (66) on the shock pattern is small, as can be observed in Figure 15. The results presented here agree with the analytical solutions in [24]. Indeed, the shifting of the flux curve as the mobility ratio changes is reproduced. The shock propagation predictions agree with present results of our analysis as well.
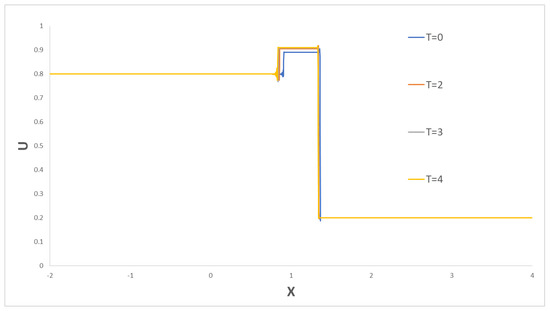
Figure 15.
Saturation as a function of velocity for various values of the characteristic times (the same example as that described in Figure 13a for ).
4. Discussion
Non-Newtonian fluids such as the micellar solution analysed here have variable viscosity that depends on the stress or pressure gradient. At low pressure gradients, the viscosity of these fluids is large, while upon increasing the pressure gradient the viscosity decreases. The viscosity drop can be quite large, in some cases more than two decades. In the process of oil displacement, the mobility ratio is one of the most important parameters, defined here as the mobility of the oil phase divided by the mobility of the non-Newtonian fluid. There are alternative definitions of the mobility ratio, namely, those that consider it as the mobility of the non-Newtonian fluid divided by the mobility of the oil phase. This definition, which according to the anonymous reviewer is conventional in the oil industry, is used to set a criterion that represents a favourable condition for ratios equal or lower than one, with ratios larger than one being unfavourable. The definition that we use here has been utilized previously in various references [14]. In fact, the presented results can be re-interpreted by substituting for M. In this context, the mobility ratio at low stresses in Figure 2 is small, corresponding to high viscosity (low fluidity) of the non-Newtonian fluid, which represents a favourable condition. An unfavourable condition is attained for mobility ratios larger than one, and this condition is found for stresses larger than the yield stress, corresponding to decreased viscosity of the non-Newtonian fluid. This is an important result, as the pressure gradient can be adjusted to conveniently provide mobility ratios. As shown in Figure 10, the curve with ( ) is now unfavourable, whereas the curves with and are favourable. Subsequently, in Figure 11, Figure 12, Figure 13 and Figure 14 we provide examples with various values of the saturations ( and ) for the examined mobility ratios. For mobility ratios larger than one, four examples (Figure 11b, Figure 12b, Figure 13b and Figure 14b) represent unfavourable conditions consists of fronts with rarefaction waves (Figure 12b and Figure 13b), rarefaction–shock transitions (Figure 11b), or retarded shocks (Figure 14b). These examples illustrate various situations for different regions along the flow curve for optimum oil displacement with low mobility ratios.
5. Conclusions
We performed a Buckley–Leverett analysis with capillary pressure to describe the flow patterns arising in the displacement of oil by a non-Newtonian micellar solution in a fractal porous medium. Although a number of upscaled and effective models can be used [24,25], our proposed approach provides a fast and simple description. The Darcian permeability for a Newtonian fluid generalizes to describe the flow of non-Newtonian fluids when the porous media has dimensions and tortuosity with a fractal structure. The micellar solution is a viscoelastic fluid in which the fluidity (inverse viscosity) varies with the applied pressure gradient. These ingredients provide expressions of the mobility ratio between the displacing fluid (the micellar solution) and the oil.
We use a constitutive equation for micellar fluids (the BMP model) to model the fluidity at a given shear stress or pressure gradient. This provides variations in the mobility ratio corresponding to the applied pressure gradient. Micellar solutions possess a complex rheology that can be used to improve the flow rates of the displaced oil fluid. In fact, these surfactants exhibit particular properties as the pressure gradient increases, such as the presence of a shear stress plateau at a critical value of the pressure gradient. This means that the flow rate increases drastically at this critical stress. These rheological properties allow the flow behavior to be mimicked in porous media of so-called self-destructive surfactants, which possess a high viscosity at the initial stage of the oil displacing process followed by degradation of their chemical structure, leading to a hydrophobic oil–affine structure and a hydrophilic molecule with affinity for water. The resulting solution has a small mobility ratio and low viscosity, and is easily removed from the formation.
The implementation of a Buckley–Leverett analysis with capillary pressure allows the different shock profiles that may be present in a real porous media to be described. Because the function is double-valued, the solution to this problem is to theoretically modify the plot by defining a saturation discontinuity at and then balancing the areas ahead of the front and below the curve. In other words, a discontinuity in S at a front location is needed to make the saturation distribution single-valued and to provide a material balance for fluid displacement.
With capillary pressure included, a variety of shock profiles and under-compressive waves are predicted. This discontinuity propagates as combinations of shock and rarefaction waves, suggesting the decomposition of the solutions of the general initial-value problems into combinations of traveling waves (approximating shocks) and smooth waves (approximating rarefaction waves).
It is worth mentioning that the viscosity of the displacing fluid and applied pressure gradient should be properly adjusted in order to provide the optimal oil displacement. This is one of the advantages of a complex non-Newtonian fluid, which provide multiple options for actual EOR operations.
Author Contributions
Conceptualization, O.M. and R.R.-C.; Software, R.O.V. and R.R.-C.; Validation, R.R.-C.; Formal analysis, O.M., R.R.-C. and M.T.; Investigation, R.O.V., R.R.-C., C.L.-G., E.R.-J., M.T. and O.M.; Writing – review and editing, C.L.-G., E.R.-J. and O.M.; Project administration, C.L.-G.; Funding acquisition, R.O.V. All authors have read and agreed to the published version of the manuscript.
Funding
R.O.V. would like to acknowledge the financial support of SIP-IPN 20221783.
Acknowledgments
OM gratefully acknowledges IN-100620 from DGAPA-UNAM for financial support. CL-G and ER-J thank the Mexican Institute of Petroleum’s project Y. 61127 for financial support and for permission to publish this paper. Martin Diaz-Viera of the Mexican Institute of Petroleum provided generous discussions and advice during the concluding stages of this work.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Afolabi, F.; Mahmood, S.M.; Yekeen, N.; Akbari, S.; Sharifigaliuk, H. Polymeric surfactants for enhanced oil recovery: A review of recent progress. J. Pet. Sci. Eng. 2022, 208, 109358. [Google Scholar] [CrossRef]
- Sheng, J. Status of Surfactant EOR Technology. Petroleum 2015, 79, 97–105. [Google Scholar] [CrossRef]
- Manrique, E.; Thomas, C.; Ravikiram, R.; Izadi, M.; Lantz, M.; Romero, J.; Alvarado, V. EOS: Current Status and Opportunities, 2010. In Proceedings of the SPE IOR Symposium, Tulsa, OK, USA, 24–28 April 2010. [Google Scholar]
- Raffa, P.; Broekhuis, A.A.; Picchioni, F. Polymeric surfactants for enhanced oil recovery: A review. J. Pet. Sci. Eng. 2016, 145, 723–733. [Google Scholar] [CrossRef]
- Ghannam, M.T.; Selim, M.Y.E.; Zekri, A.Y.; Esmail, N. Thixotropic Assessment of Some Enhanced Oil Recovery used Polymers. Int. J. Eng. Res. Technol. 2020, 9, 1683–1693. [Google Scholar] [CrossRef]
- Turcio, M.; Reyes, J.; Camacho, R.; Lira-Galeana, C.; Vargas, R.; Manero, O. Calculation of effective permeability for the BMP model in fractal porous media. J. Pet. Sci. Eng. 2013, 103, 51–60. [Google Scholar] [CrossRef]
- Othman, A.; AlSulaimani, M.; Aljawad, M.S.; Sangaru, S.S.; Kamal, M.S.; Mahmoud, M. The Synergetic Impact of Anionic, Cationic, and Neutral Polymers on VES Rheology at High-Temperature Environment. Polymers 2022, 14, 1145. [Google Scholar] [CrossRef] [PubMed]
- Holmberg, K. (Ed.) Novel Surfactants: Preparation, Applications, and Biodegradability; Dekker: New York, NY, USA, 1998. [Google Scholar]
- Lagerman, R.; Clancy, S.; Tanner, D.; Johnston, N.; Callian, B.; Friedli, F. Synthesis and performance of ester quaternary biodegradable softeners. J. Am. Oil Chem. Soc. 1994, 71, 97–100. [Google Scholar] [CrossRef]
- Wilk, K.A.; Bieniecki, A.; Burczyk, B.; Sokolowski, A. Synthesis and hydrolysis of chemodegradable cationic surfactants containing the 1,3-dioxolane moiety. J. Am. Oil Chem. Soc. 1994, 71, 81–85. [Google Scholar] [CrossRef]
- Wang, G.W.; Liu, Y.C.; Yuan, X.Y.; Lei, X.G.; Guo, Q.X. Preparation, Properties, and Applications of Vesicle-Forming Cleavable Surfactants with a 1,3-Dioxane Ring. J. Colloid Interface Sci. 1995, 173, 49–54. [Google Scholar] [CrossRef]
- West, C.A.; Sanchez, A.M.; Hanon-Aragon, K.A.; Salazar, I.C.; Menger, F.M. Preparation and characterization of a simple destructible surfactant. Tetrahedron Lett. 1996, 37, 9135–9138. [Google Scholar] [CrossRef]
- Manero, O.; Bautista, F.; Soltero, J.; Puig, J. Dynamics of worm-like micelles: The Cox-Merz rule. J. Non-Newton. Fluid Mech. 2002, 106, 1–15. [Google Scholar] [CrossRef]
- Spayd, K.; Shearer, M. The Buckley–Leverett Equation with Dynamic Capillary Pressure. SIAM J. Appl. Math. 2011, 71, 1088–1108. [Google Scholar] [CrossRef]
- Olajire, A.A. Review of ASP EOR (alkaline surfactant polymer enhanced oil recovery) technology in the petroleum industry: Prospects and challenges. Energy 2014, 77, 963–982. [Google Scholar] [CrossRef]
- Mandelbrot, B. The Fractal Geometry of Nature; Freeman: New York, NY, USA, 1982. [Google Scholar]
- Xu, P.; Mujumdar, A.S.; Sasmito, A.P.; Yu, B.M. Multiscale modeling of porous media. In Heat and Mass Transfer in Drying of Porous Media; Taylor and Francis: Oxfordshire, UK, 2019. [Google Scholar]
- Katz, A.J.; Thompson, A.H. Fractal Sandstone Pores: Implications for Conductivity and Pore Formation. Phys. Rev. Lett. 1985, 54, 1325–1328. [Google Scholar] [CrossRef] [PubMed]
- Wu, J.; Yu, B. A fractal resistance model for flow through porous media. Int. J. Heat Mass Transf. 2007, 50, 3925–3932. [Google Scholar] [CrossRef]
- Brambila, F. Fractal Analysis; IntechOpen: Rijeka, Croatia, 2017. [Google Scholar] [CrossRef]
- Bautista, F.; de Santos, J.; Puig, J.; Manero, O. Understanding thixotropic and antithixotropic behavior of viscoelastic micellar solutions and liquid crystalline dispersions. I. The model. J. Non-Newton. Fluid Mech. 1999, 80, 93–113. [Google Scholar] [CrossRef]
- Cavatorta, N.; Tonini, R.N. Dimensionless velocity profiles and parameter maps for non-Newtonian fluids. Int. Commun. Heat Mass Transf. 1987, 14, 359–369. [Google Scholar] [CrossRef]
- Li, Y.; Yu, B.; Chen, J.; Wang, C. Analysis of Permeability for Ellis Fluid Flow in Fractal Porous Media. Chem. Eng. Commun. 2008, 195, 1240–1256. [Google Scholar] [CrossRef]
- McWhorter, D.; Sunada, D. Exact Integral Solutions for Two-Phase Flow. Water Resour. Res. 1990, 26, 399–413. [Google Scholar] [CrossRef]
- Andersen, P.Ø; Nesvik, E.K.; Standnes, D.C. Analytical solutions for forced and spontaneous imbibition accounting for viscous coupling. J. Pet. Sci. Eng. 2020, 186, 106717. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).