A Novel BEM–FEM Scheme for the Interaction of Water Waves with Multiple Vertical Cylinders in the Presence of Currents
Abstract
1. Introduction
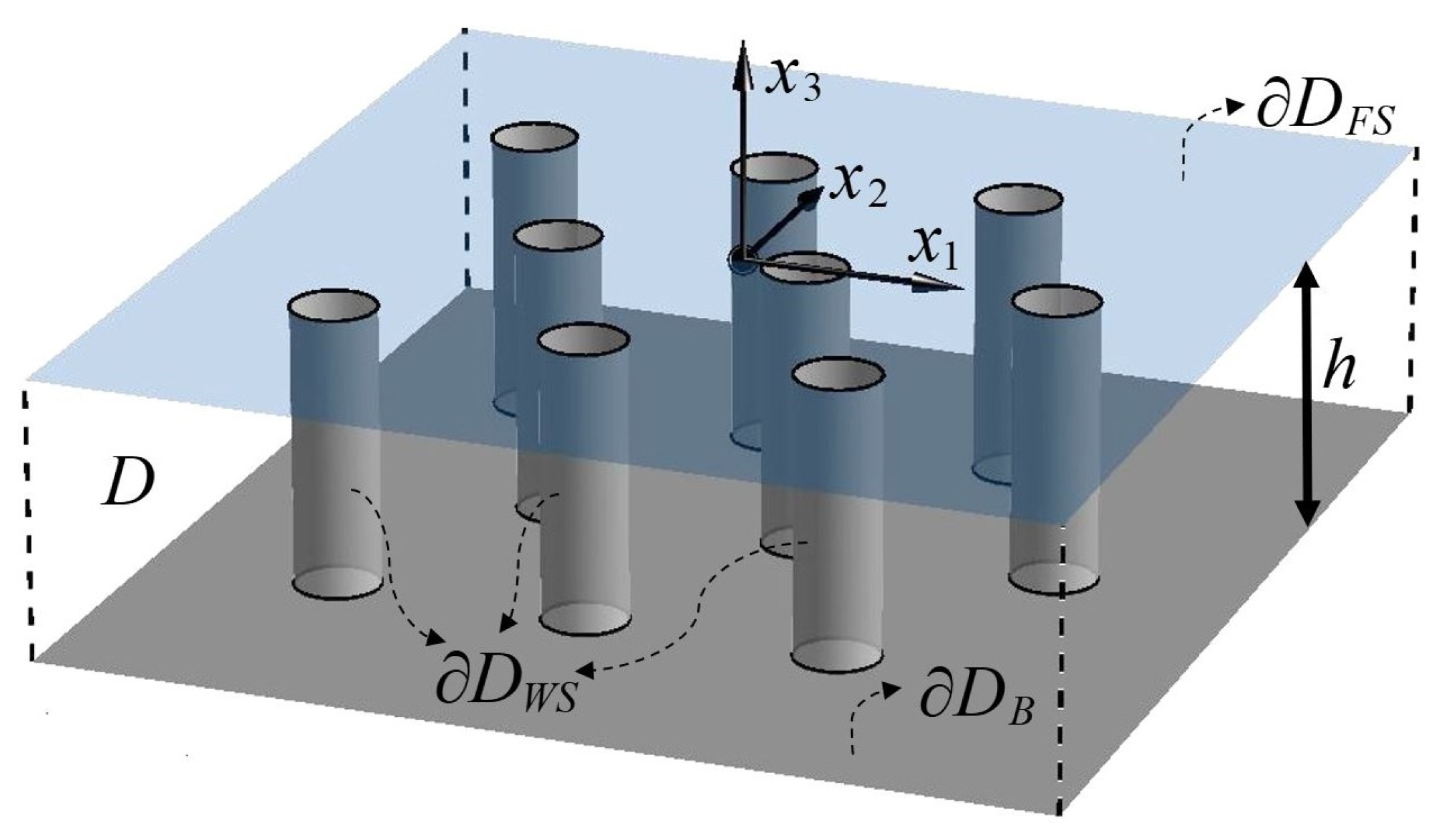
2. Mathematical Formulation of the 3D Problem
2.1. Formulation of the 3D Steady Current Flow Problem
2.2. The 3D BEM for the Steady Flow Problem
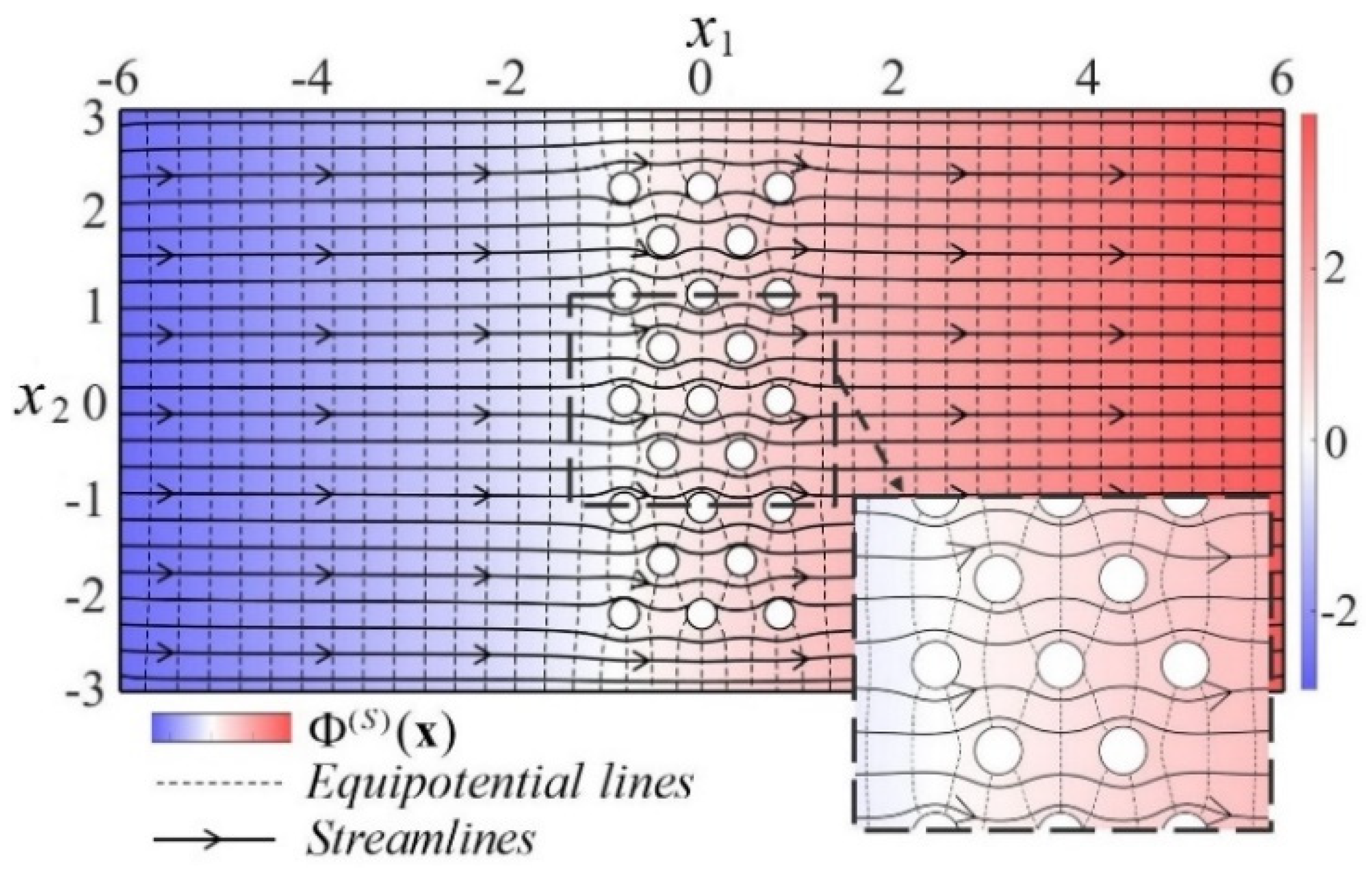
2.3. Resulting Steady Flow Fields
2.4. Formulation of the 3D Wave Problem
2.4.1. Implementation of the Absorbing Layer Technique
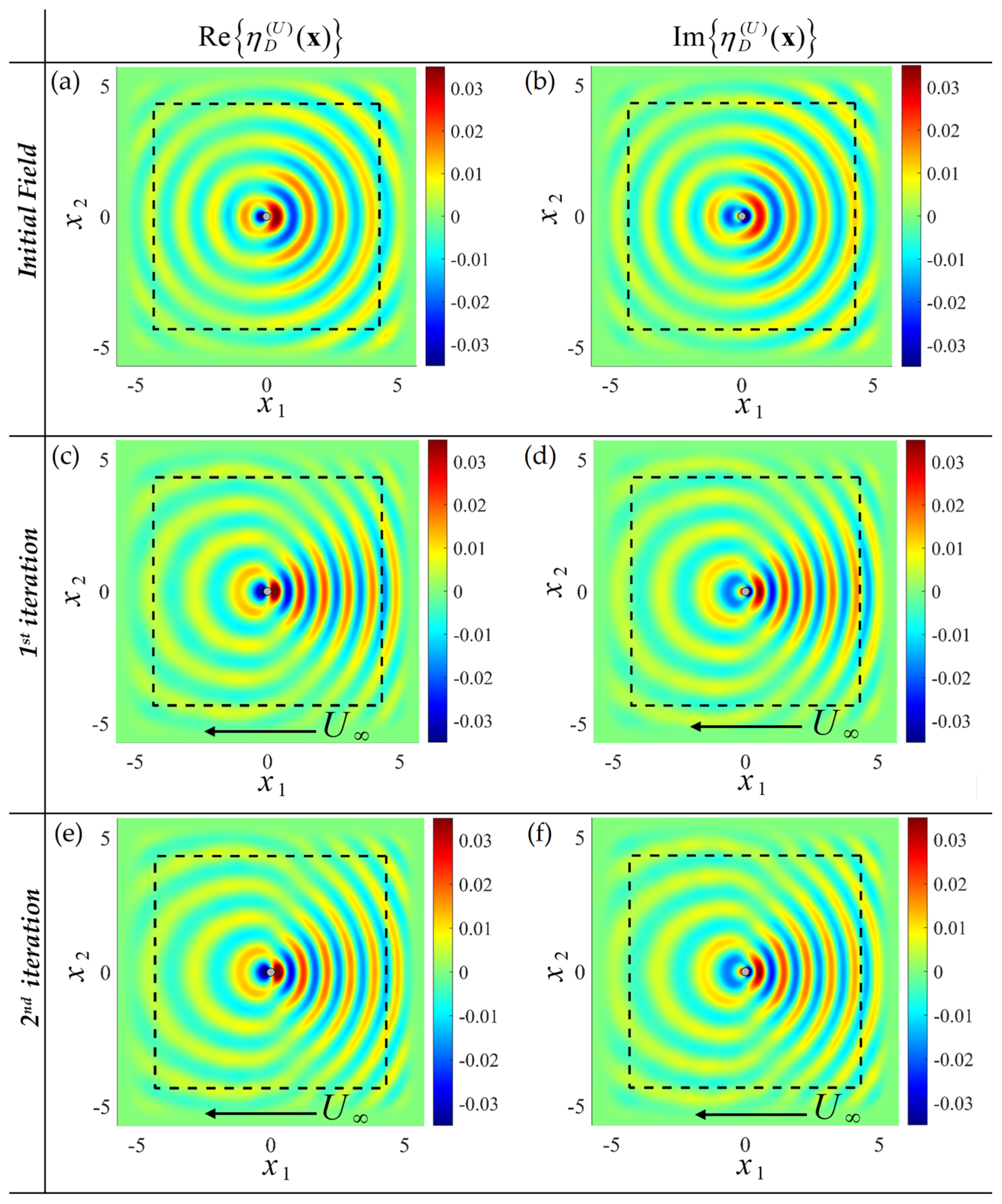
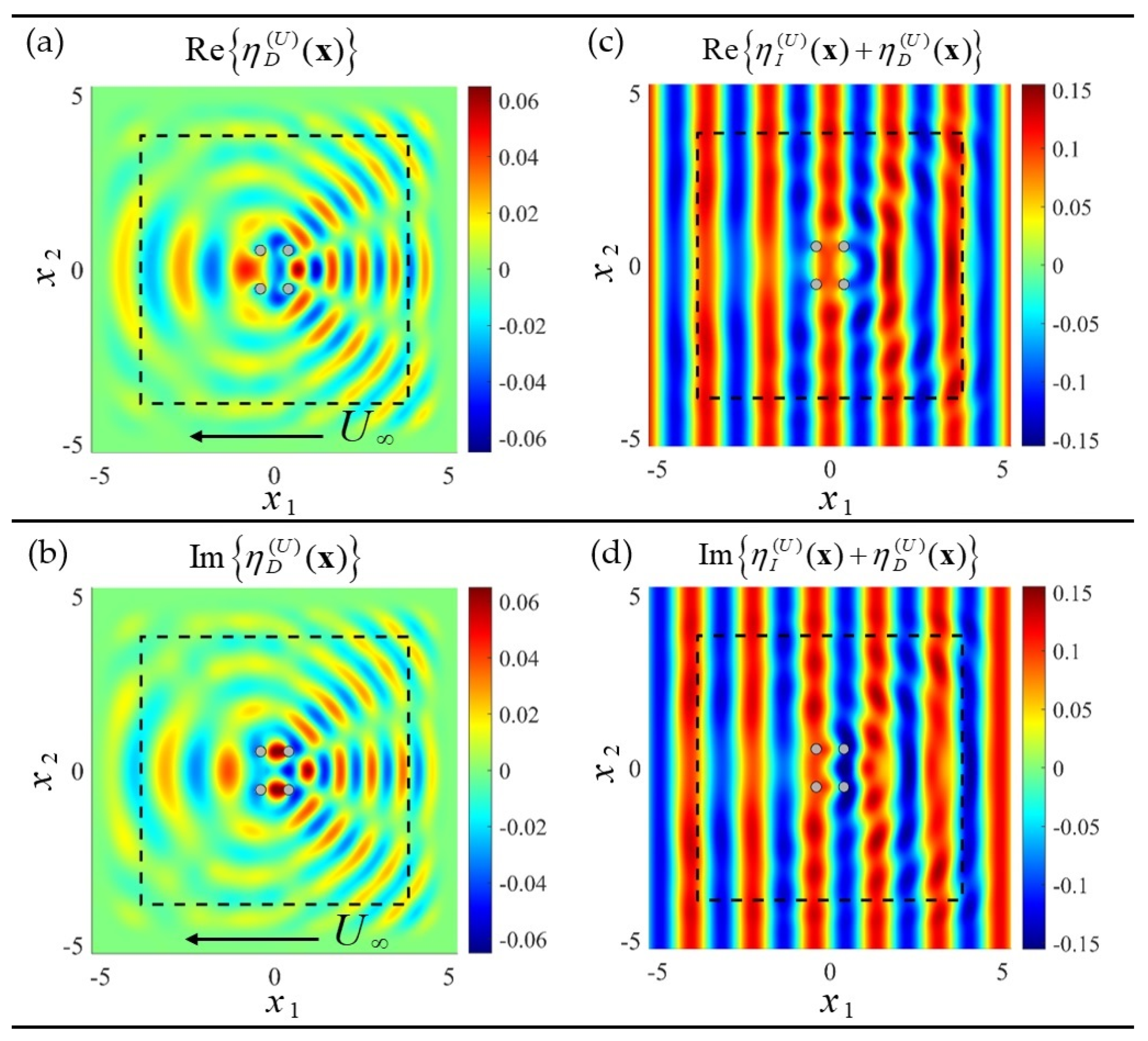
2.4.2. An Iterative Scheme for the Additional Scattering Effect Due to Current
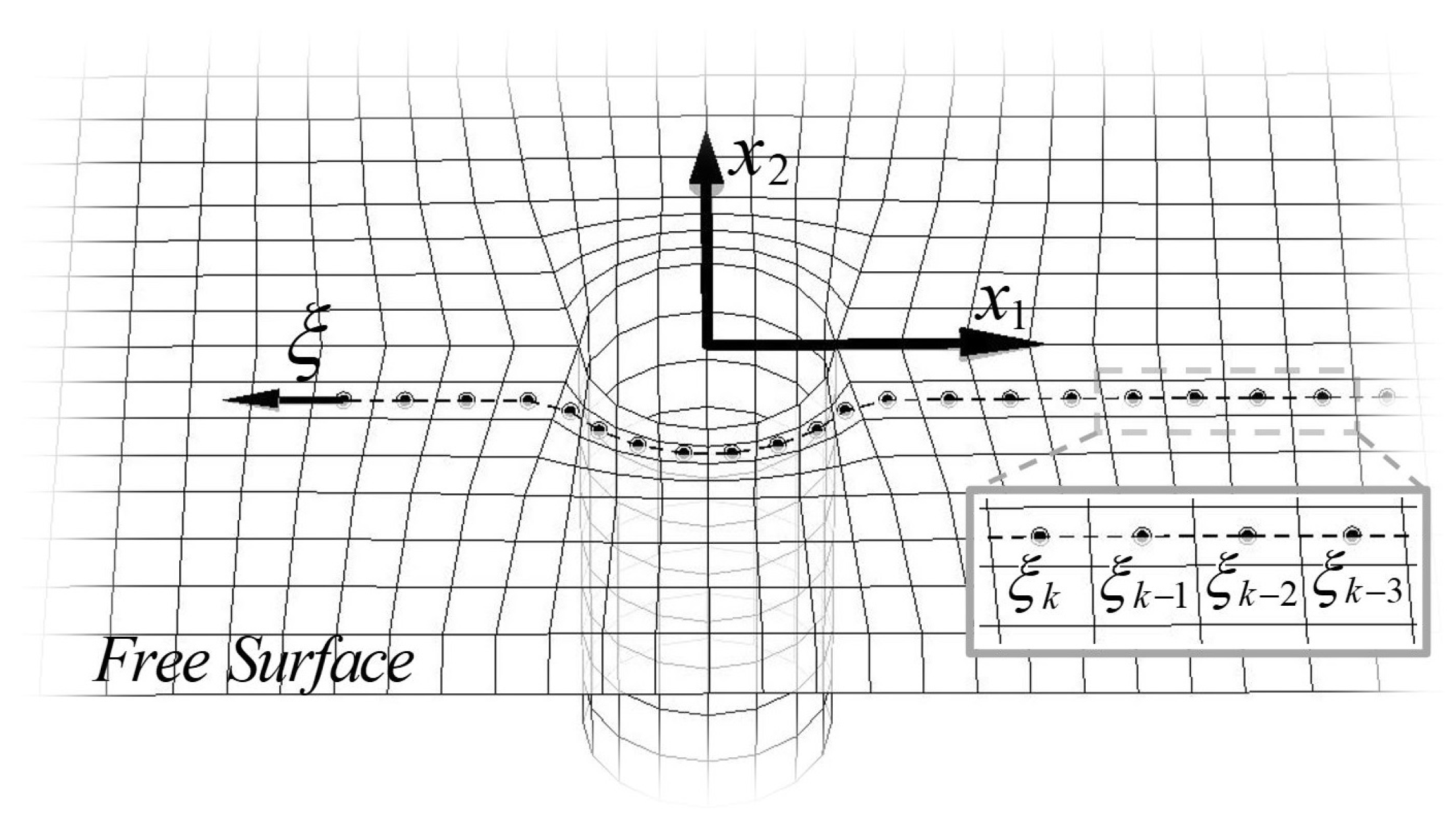
3. A Simplified 2D Formulation on the Horizontal Plane
3.1. Formulation of the Steady Current Problem
3.2. Formulation of the Wave Propagation Problem on the Horizontal Plane
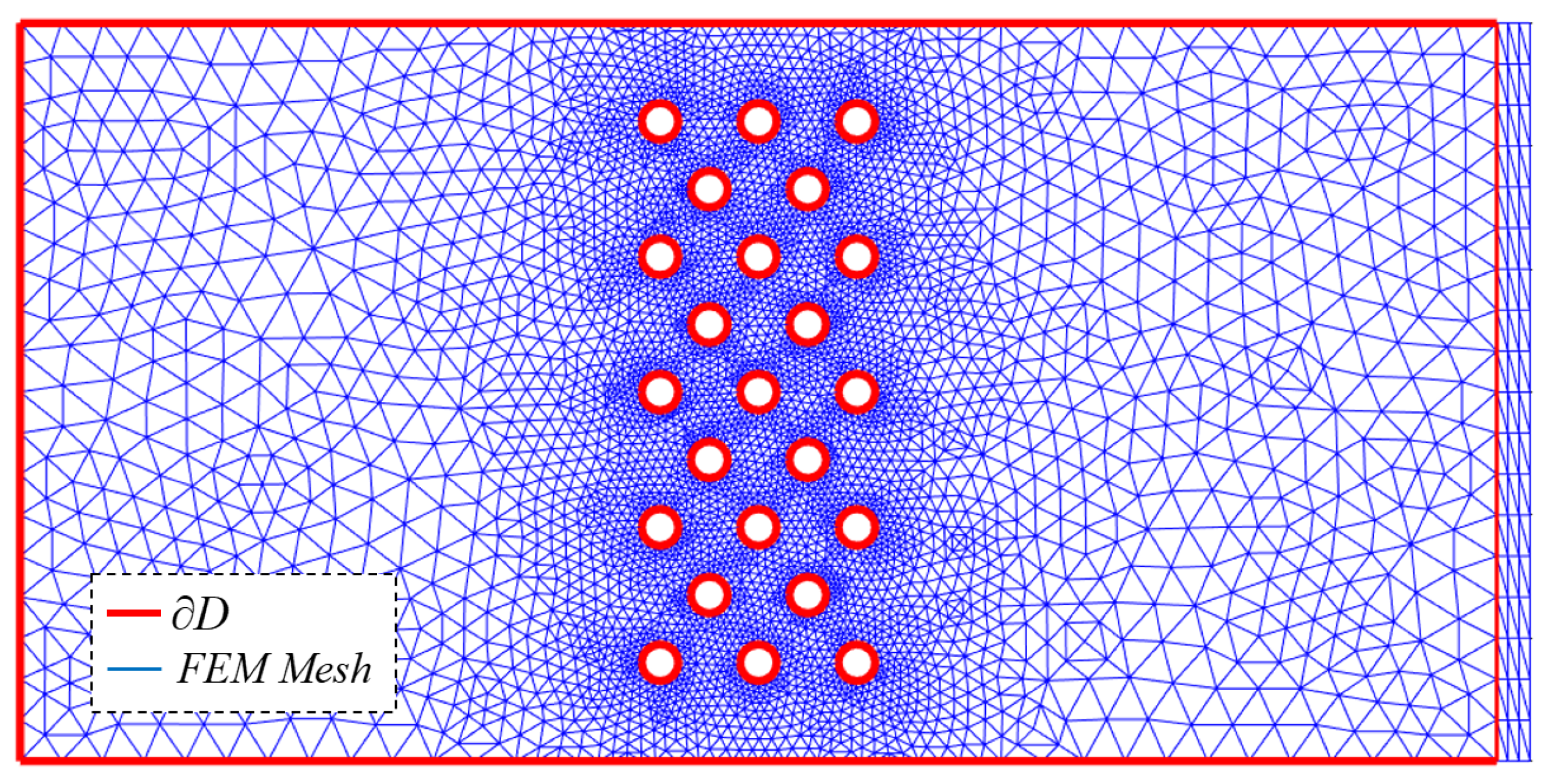
3.3. An FEM for the Wave Propagation–Scattering Problem
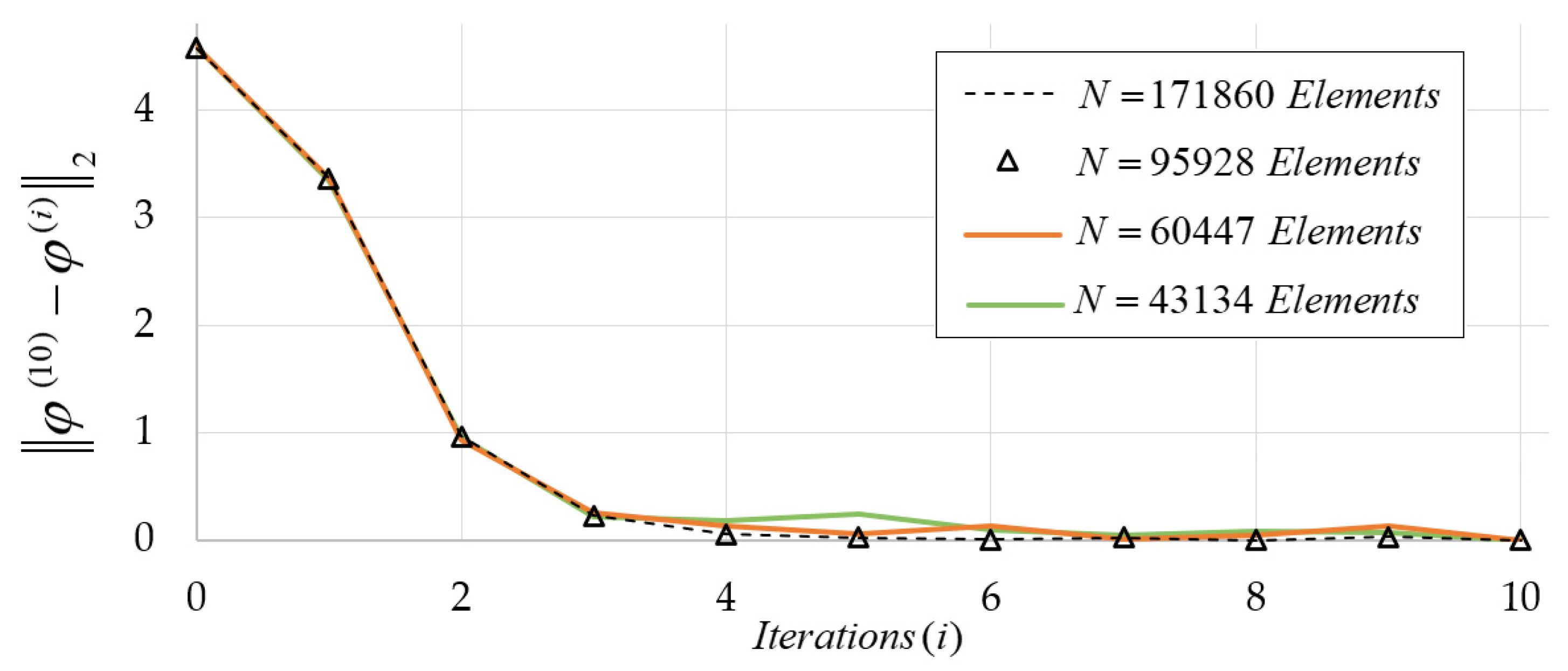
3.4. Iterative Scheme
4. Numerical Results
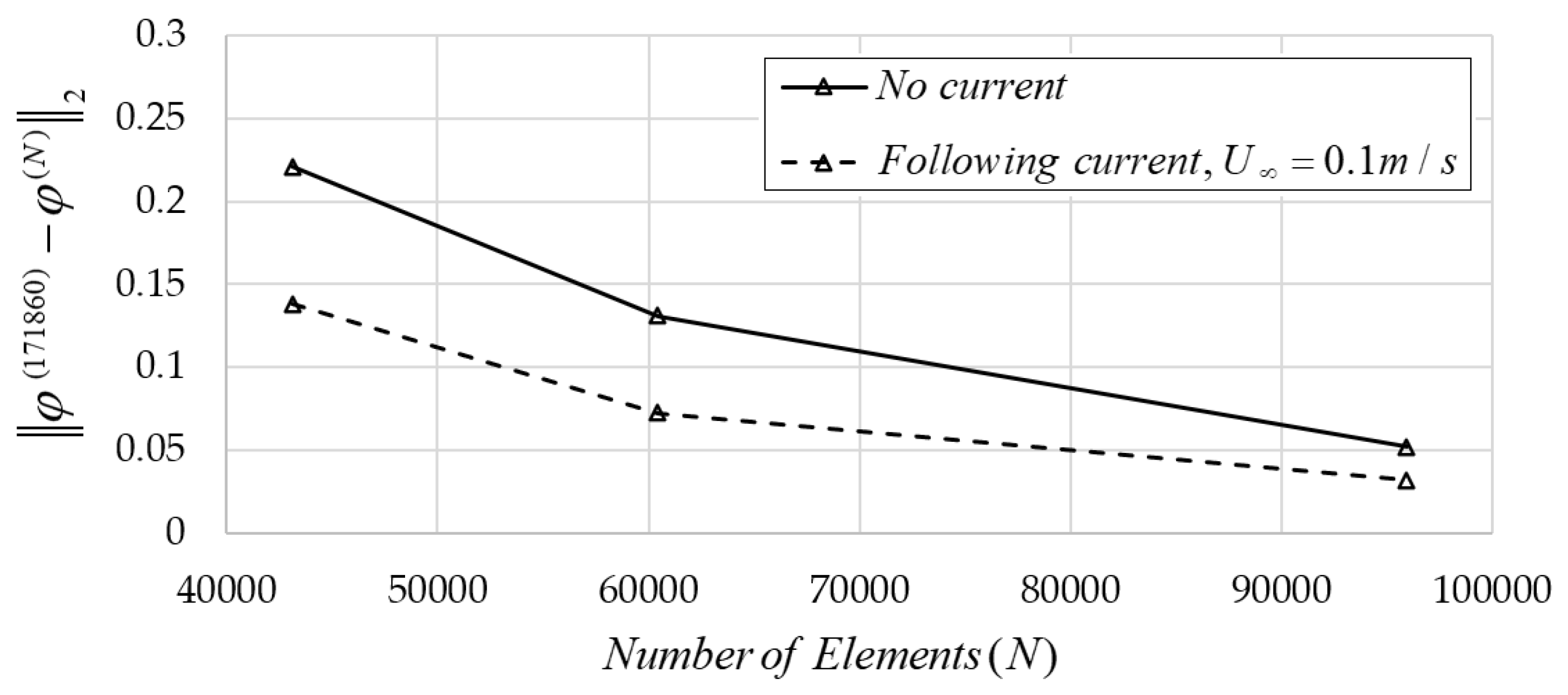
4.1. Verification of the FEM Scheme without Current
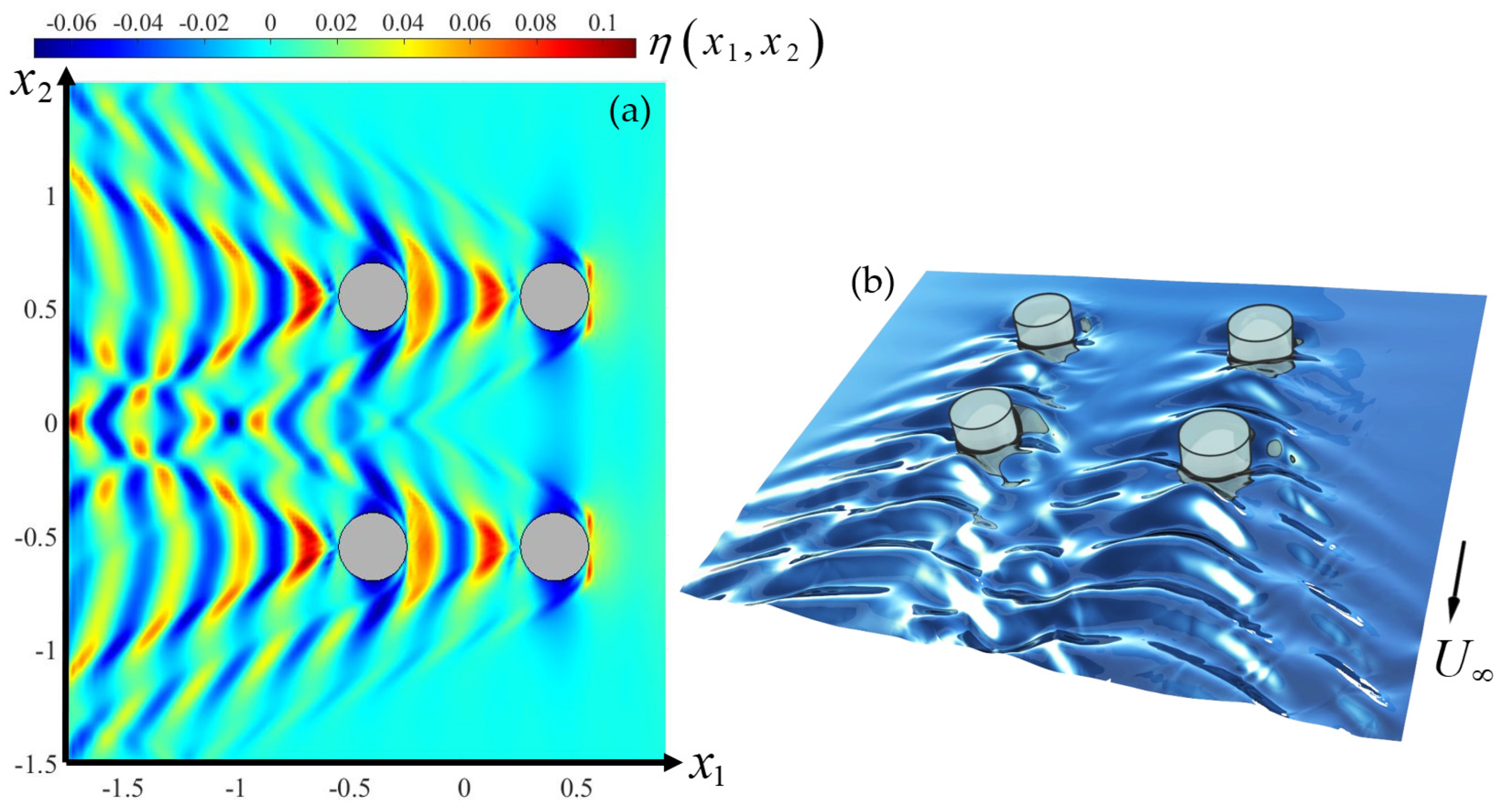
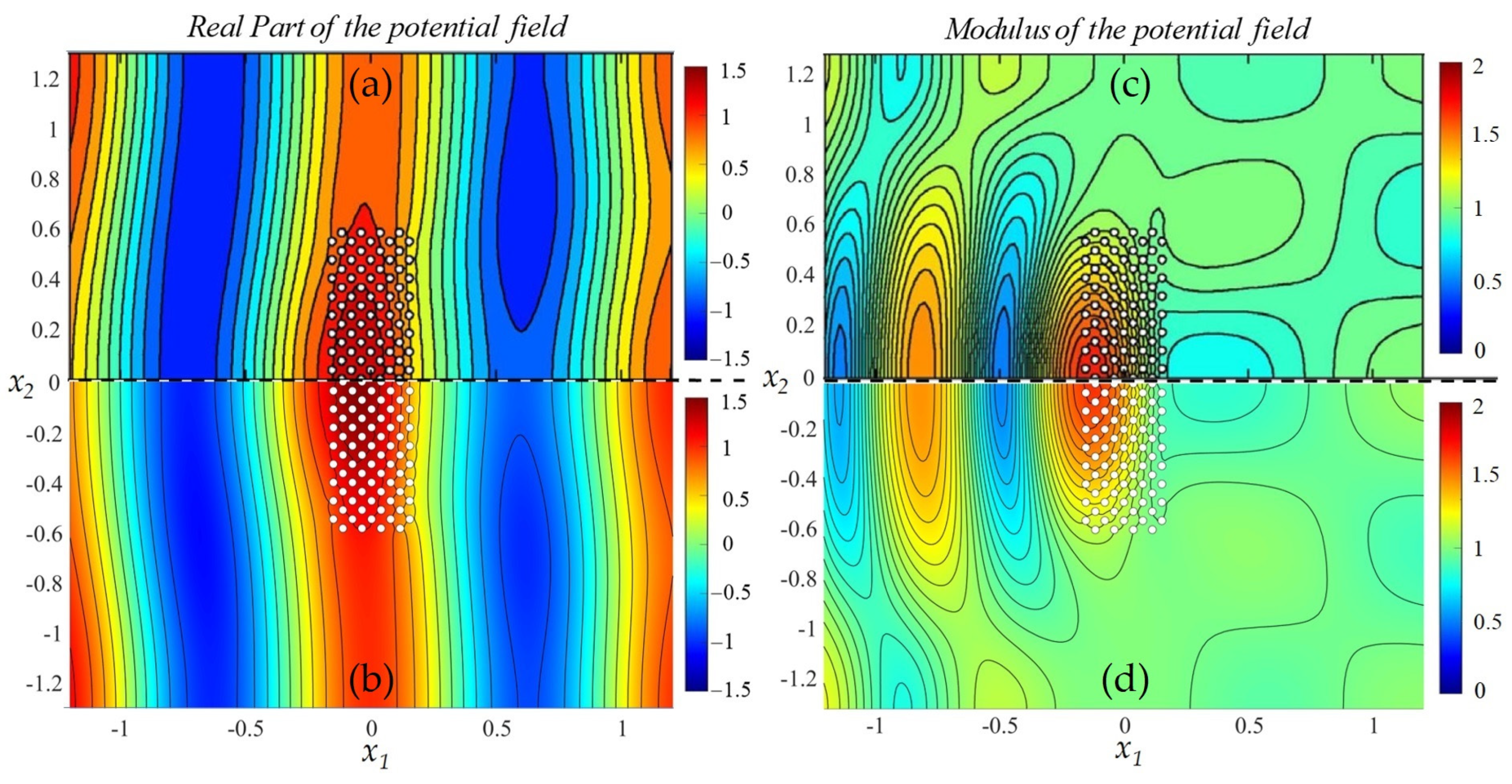
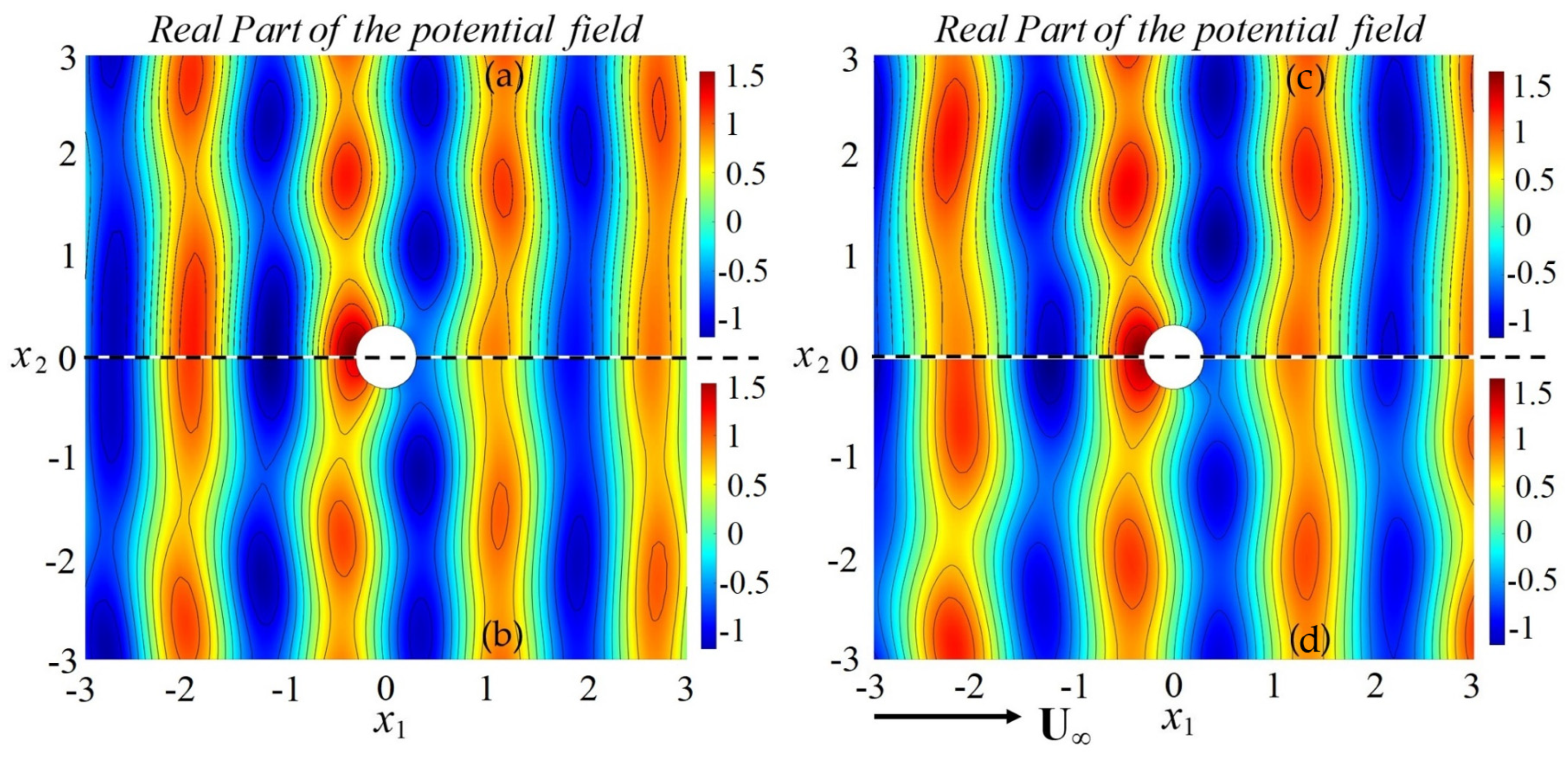
4.2. Verification of the Present FEM in the Case of Waves and Currents
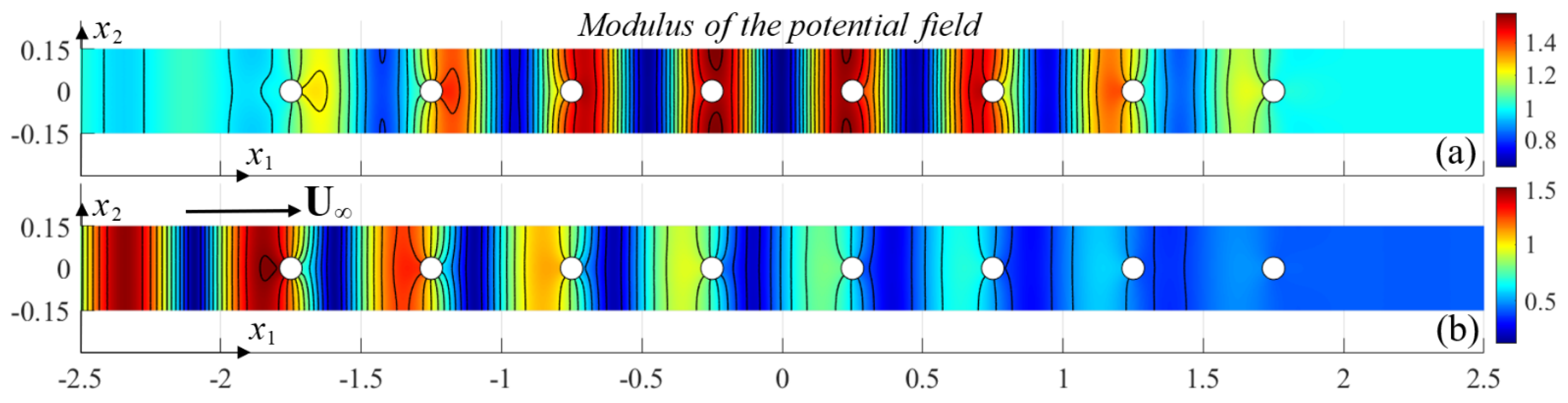
4.3. Resonances of Wave and Current Systems in the Case of a Line Array of Cylinders
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sulisz, W. Wave reflection and transmission at permeable breakwaters of arbitrary cross section. Coast. Eng. 1985, 9, 371–386. [Google Scholar] [CrossRef]
- Arnaud, G.; Rey, V.; Touboul, J.; Sous, D.; Molin, B.; Gouaud, F. Wave propagation through dense vertical cylinder arrays: Interference process and specific surface effects on damping. Appl. Ocean Res. 2017, 65, 229–337. [Google Scholar] [CrossRef]
- Belibassakis, K.A.; Gerostathis, T.P.; Athanassoulis, G.A. A coupled-mode model for water wave scattering by horizontal non-homogeneous current in general bottom topography. Appl. Ocean Res. 2011, 33, 384–397. [Google Scholar] [CrossRef]
- Belibassakis, K.; Arnaud, G.; Rey, V.; Touboul, J. Propagation and scattering of waves by dense arrays of impenetrable cylinders in a waveguide. Wave Motion 2018, 80, 1–19. [Google Scholar] [CrossRef]
- Molin, B.; Remy, F.; Arnaud, G.; Rey, V.; Touboul, J.; Sous, D. On the dispersion equation for linear waves traveling through or over dense arrays of vertical cylinders. Ocean Res. 2016, 61, 148–155. [Google Scholar] [CrossRef]
- Jamain, J.; Touboul, J.; Rey, V.; Belibassakis, K. Porosity Effects on the Dispersion Relation of Water Waves through Dense Array of Vertical Cylinders. J. Mar. Sci. Eng. 2020, 8, 960. [Google Scholar] [CrossRef]
- Li, Y.; Mei, C.C. Bragg scattering by a line array of small cylinders in a waveguide. Part 1. Linear aspects. J. Fluid Mech. 2007, 583, 161–187. [Google Scholar] [CrossRef]
- Linton, C.M.; Mclver, R. The scattering of water waves by an array of circular cylinders in a channel. J. Eng. Math. 1996, 30, 661–682. [Google Scholar] [CrossRef]
- Utsunomiya, T.; Eatock Taylor, R. Trapped modes around a row of circular cylinders in a channel. J. Fluid Mech. 1999, 386, 259–279. [Google Scholar] [CrossRef]
- Sumer, M.; Fredsoe, J. Hydrodynamics around Cylindrical Structures; Advanced Series on Ocean Engineering; World Scientific: Singapore, 1991; Volume 12. [Google Scholar]
- Ghadirian, A.; Vested, M.; Carstensen, S.; Christiensen, E.D.; Bredmose, H. Wave-current interaction effects on waves and their loads on a vertical cylinder. Coast. Eng. 2021, 165, 103832. [Google Scholar] [CrossRef]
- Thomas, G.P. Wave-current interactions: An experimental and numerical study. Part 1. Linear waves. J. Fluid Mech. 1981, 110, 457–474. [Google Scholar] [CrossRef]
- Belibassakis, K.A.; Athanassoulis, G.A.; Gerostathis, T. Directional wave spectrum transformation in the presence of strong depth and current inhomogeneities by means of coupled-mode model. Ocean Eng. 2014, 87, 84–96. [Google Scholar] [CrossRef]
- Noblesse, F. Alternative integral representations for the Green function of the theory of ship wave resistance. J. Eng. Math. 1981, 15, 241–265. [Google Scholar] [CrossRef]
- Katz, J.; Plotkin, A. Low Speed Aerodynamics; McGraw-Hill: New York, NY, USA, 2001. [Google Scholar]
- Belibassakis, K.A.; Kegkeroglou, A. A nonlinear BEM for the ship wave resistance. In Proceedings of the 18th International Congress of the International Maritime Association of the Mediterranean (IMAM2019), Varna, Bulgaria, 9–11 September 2019. [Google Scholar]
- Dawson, C.W. A practical computer method for solving ship-wave problems. In Proceedings of the 2nd International Conference on Numerical Ship Hydrodynamics, Los Angeles, CA, USA, 19–21 September 1977. [Google Scholar]
- Bonovas, M.; Belibassakis, K.; Rusu, E. Multi-DOF WEC Performance in Variable Bathymetry Regions Using a Hybrid 3D BEM and Optimization. Energies 2019, 12, 2108. [Google Scholar] [CrossRef]
- Kress, R. Linear Integral Equations; Springer: Berlin/Heidelberg, Germany, 1989. [Google Scholar]
- Karperaki, A.; Papathanasiou, T.K.; Belibassakis, K.A. An optimized parameter free PML FEM for wave scattering problems in the ocean and coastal environment. Ocean Eng. 2019, 179, 307–324. [Google Scholar] [CrossRef]
- Belibassakis, K.A.; Athanassoulis, G.A.; Gerostathis, T. A coupled-mode system for the refraction-diffraction of linear waves over steep three-dimensional topography. Appl. Ocean Res. 2001, 23, 319–336. [Google Scholar] [CrossRef]
- Belibassakis, K.; Touboul, J. A Nonlinear Coupled-Mode Model for Waves Propagating in Vertically Sheared Currents in Variable Bathymetry. Fluids 2019, 4, 61. [Google Scholar] [CrossRef]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Magkouris, A.; Belibassakis, K. A Novel BEM–FEM Scheme for the Interaction of Water Waves with Multiple Vertical Cylinders in the Presence of Currents. Fluids 2022, 7, 378. https://doi.org/10.3390/fluids7120378
Magkouris A, Belibassakis K. A Novel BEM–FEM Scheme for the Interaction of Water Waves with Multiple Vertical Cylinders in the Presence of Currents. Fluids. 2022; 7(12):378. https://doi.org/10.3390/fluids7120378
Chicago/Turabian StyleMagkouris, Alexandros, and Kostas Belibassakis. 2022. "A Novel BEM–FEM Scheme for the Interaction of Water Waves with Multiple Vertical Cylinders in the Presence of Currents" Fluids 7, no. 12: 378. https://doi.org/10.3390/fluids7120378
APA StyleMagkouris, A., & Belibassakis, K. (2022). A Novel BEM–FEM Scheme for the Interaction of Water Waves with Multiple Vertical Cylinders in the Presence of Currents. Fluids, 7(12), 378. https://doi.org/10.3390/fluids7120378





