Abstract
The bioconvection phenomenon, through the utilization of nanomaterials, has recently encountered significant technical and manufacturing applications. Bioconvection has various applications in bio-micro-systems due to the improvement it brings in mixing and mass transformation, which are crucial problems in several micro-systems. The present investigation aims to explore the bioconvection phenomenon in magneto-nanofluid flow via free convection along an inclined stretching sheet with useful characteristics of viscous dissipation, constant heat flux, solutal, and motile micro-organisms boundary conditions. The flow analysis is addressed based on the Buongiorno model with the integration of Brownian motion and thermophoresis diffusion effects. The governing flow equations are changed into ordinary differential equations by means of appropriate transformation; they were solved numerically using the Runge–Kutta–Fehlberg integration scheme shooting technique. The influence of all the sundry parameters is discussed for local skin friction coefficient, local Nusselt number, local Sherwood number, and local density of the motile micro-organisms number.
1. Introduction
The flow over a stretching surface is an important problem in many engineering processes with applications in industries such as extrusion, melt-spinning, hot rolling, wire drawing, glass fiber production, manufacture of plastic and rubber sheets; cooling of a large metallic plate in a bath, which may be an electrolyte, and others. In the industry, polymer sheets and filaments are manufactured by a continuous extrusion of the polymer from a die to a windup roller located at a finite distance. Crane [1] and Gupta and Gupta [2] analyzed the flow over a stretching surface with constant surface temperature, while Soundalgekar and Ramana [3] investigated the heat transfer through a continuous moving plate with variable temperature. Grubka and Bobba [4] analyzed the flow across a surface moving in a linear velocity with variable surface temperature. Modern evolution in nanotechnology encouraged the experts to direct their attention toward nanoparticle flow to promote multidisciplinary applications and thermal features. The appropriate utilization of nanoparticles significantly enhances the fundamental controls of the cooling processes and thermal performances. Choi [5] developed the primary concept of nanofluid and described a modern approach to enhance energy performance. Nanofluid is gained by combining the nanosized particles and base fluid. The thermal conductivity of nanofluid can be controlled by adjusting the concentration of nanoparticles and base fluid; this is because of the greater thermal conductivity of nanosized particles and lower thermal conductivity of base fluids. The concept of convective transmission in nanofluids considering these physical mechanisms has been widely reported [6,7,8,9,10].
The investigation into magnetic nanoparticles has various applications in physics and biomedical engineering. Magneto nanoparticles area group of nanoparticles that maneuver in the existence of a magnetic field. Magnetic nanoparticles have been examined by many scientists due to their multiple applications such as biomedicine, magnetic drug targeting, magnetic resonance imaging, and magneto nanoparticles to heal cancer and immunotherapy. Recent studies developed on magneto nanoparticles have exhibited increasing interest from investigators in recent years; see [11,12,13,14]. Hazarika et al. [15] studied the effects of thermophoresis and viscous dissipation of magneto nanofluid flow over a stretching permeable sheet. Narender et al. [16] presented a numerical investigation to examine the influence of viscous dissipation and chemical reaction on the heat and mass transfer of a magneto nanofluid past a radiative stretching sheet. Mansour et al. [17] investigated the heat transfer via MHD natural convection cooling of a localized heat source at the bottom wall of an enclosure filled with nanofluids. Khan et al. [18] considered the magnetized flow of tangent hyperbolic nanofluid over a stretchable sheet. Pourmehran et al. [19] considered the effects of buoyancy phenomenon and magnetic field on nanofluid flow and heat transfer over a vertical stretching sheet.
Bioconvection is a phenomenon that occurs during convection. Instability is caused by a self-propelled swimming micro-organism that is denser than cell fluid. Bio-convection processes have many applications in various industries and the medical field; they have been used in several micro-bio-systems such as enzyme biosensors, biotechnology, water treatment plants, and products including ethanol, hydrogen gas, biofuels, fertilizers, biodiesel, swimming class, subpopulations, and purified cultures. Mehryan et al. [20] studied the behavior of magneto nanofluid flow with motile gyrotactic micro-organisms past a nonlinear stretching sheet. Khan et al. [21] introduced a theoretical study on the nanofluid flow pasta bidirectional exponentially stretching sheet. Akbar and Khan [22] investigated the impacts of Brownian motion and thermophoresis on a nanofluid flow via magneto-free bioconvection over a stretching sheet containing gyrotactic micro-organisms. Hayat et al. [23] considered the magnetized flow of a nanofluid over a porous stretching surface with convective boundary conditions. Khan and Makinde [24] considered the magnetized flow with heat and mass transfer of a water-based nanofluid containing gyrotactic micro-organisms along a convectively heated stretching sheet. Khan et al. [25] examined the natural convection flow of a water-based nanofluid containing gyrotactic micro-organisms over a truncated cone with convective boundary conditions at the surface. Chamkha et al. [26] considered the effect of thermal radiation on the natural bioconvection flow of a nanofluid containing gyrotactic micro-organisms along a vertical flat plate. Hayat et al. [27] investigated the effect of magnetohydrodynamic on the boundary layer flow of a nanofluid containing gyrotactic micro-organisms in the presence of nonlinear thermal radiation. They showed that the velocity of fluid particles decays for a larger value of magnetic field parameter, motile micro-organisms density is an increasing function of thermophoresis parameter, and Brownian motion number and has an inverse relation with Peclet number. Ferdows et al. [28] investigated the magnetohydrodynamic flow of a dissipative nanofluid, including gyrotactic micro-organisms along an exponentially moving sheet.
Inspired by previously mentioned studies and discussion, the present investigation aims to analyze the magneto-free convective flow of a water-based nanofluid with gyrotactic micro-organism along an inclined stretching sheet with constant heat flux and viscous dissipation effect. This experiment has encouraged the current investigation and is particularly relevant to microbial fuel cells exploiting bioconvection and nanofluids. Similar solutions for the transport equations were obtained by using the Runge–Kutta–Fehlberg method coupled with a shooting technique. The effects of the emerging parameters on skin friction, the rate of heat transfer, and the rate of motile micro-organism transfer are analyzed numerically and discussed in detail using graphs.
2. Mathematical Formulation
A two-dimensional, steady, laminar, magneto-free bioconvection flow of a viscous, incompressible nanofluid containing gyrotactic micro-organisms over an inclined stretching sheet with an acute angle ϑ was considered. As shown in Figure 1, the x-direction moves along the leading edge of the inclined stretching sheet while y is normal to the flow. The flow analysis is addressed based on the Buongiorno model with the Brownian motion, thermophoresis diffusion effects and viscous dissipation phenomenon. The flow is also assumed to be in the x-direction, which moves along the surface in the upward direction, and the y-axis is normal to it. The velocity of the surface is assumed as u = U0x. The constant heat flux is qw, the nanoparticle volume fraction is Cw, and the density of motile micro-organisms is nw where the temperature, nanoparticle volume fraction, and density of motile micro-organisms far from the surface are T∞, C∞, n∞, respectively, where Cw> C∞ and nw>n∞. A magnetic field strength B0 is introduced to the normal direction of the flow. The nanoparticles suspension is assumed to be stable. We ignore the effect of nanoparticles on the swimming direction of micro-organisms and the velocity of swimming micro-organisms. Under these assumptions and using the Oberbeck–Boussinesq approximation, the governing equations related to conservation of mass, momentum, thermal energy, and micro-organisms can be written as:
where u and v are, respectively, the velocity components in the x- and y-direction; T, Tw and T∞ are the fluid temperature, the stretching sheet temperature, and the free stream temperature, respectively; while C, Cw, C∞, n, nw, and n∞ are the corresponding nanoparticle concentration and the micro-organism concentration, respectively. υ represents the viscosity of the nanofluid and micro-organisms, λ is the electrical conductivity, B0 is the magnetic field intensity, U0 is the stretching sheet parameter, g is the acceleration due to gravity, q is the constant heat flux per unit area, β the base fluid’s volumetric coefficient of thermal expansion, γ the micro-organism average volume, k is the thermal conductivity, α is the nanofluid thermal diffusivity, is the ratio of effective heat capacity among the nanoparticle material and base fluid; ρf, ρm, and ρp, respectively, represent the base fluid density, the micro-organism density, and the nanoparticle density; DB and DT are used for the coefficient of Brownian and thermophoretic diffusion, respectively; Dm is the micro-organism diffusivity, Wc is the utmost cell swimming speed, the subscript ∞ is used for equivalent values in the far field. The equations presented above are subject to the following boundary conditions:
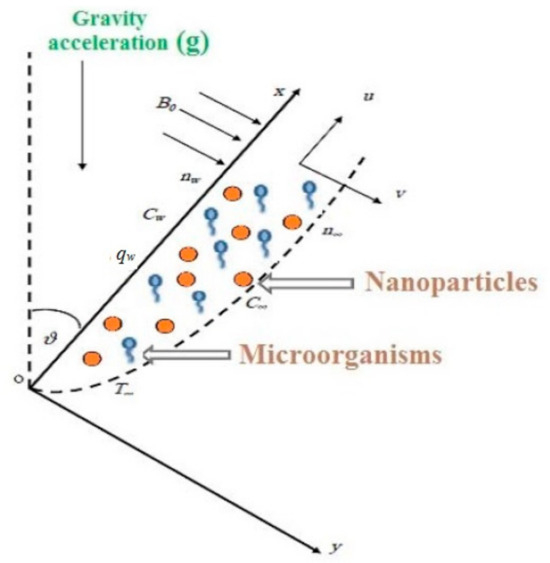
Figure 1.
Physical Model and coordinate system.
In this work we consider the case of constant heat flux and can define the following transformation:
where ψ is the function of stream represented as:
where dashes stand for differentiation in respect of η with boundary status as:
The dimensionless variables used in Equations (9)–(12) are defined as:
where Gr is the Grashof number, Pr is the Prandtl number, Le denotes the traditional Lewis number, Lb is the biconvection Lewis number, Nr represents the buoyancy ratio parameter, Pe represents the biconvection Peclet number, Rb is the biconvection Rayleigh number, Nt represents the thermophoresis parameter, Nb is the Brownian motion parameter, M represents the magnetic field parameter, Ec denotes the Eckert number, and σ is the bioconvection constant.
In practical applications, the physical properties of principal significance are local skin-friction coefficient Cf, local Nusselt number Nux, local Sherwood number Shx, and local density of the motile micro-organisms’ number Nnx. These can be defined as:
where
which can be obtained as:
3. Numerical Procedure
The set of Equations (9)–(12) under the boundary conditions (13) are coupled nonlinear boundary value problems (BVP) which are solved numerically using a shooting algorithm with a Runge–Kutta–Fehlberg integration scheme. This method involves transforming the equation into a set of initial value problems (IVP) containing unknown initial values that must be determined by approximation. The fourth order Runge–Kutta–Fehlberg iteration scheme is then employed to integrate the set of IVPs until the given boundary conditions are satisfied. We define the new variables as: and .
Equations (9) and (12) are then reduced to systems of first order differential equations as:
subject to the following initial conditions,
In the shooting method, the unknown initial conditions u1, u2, u3, and u4 in (22) are assumed and (18)–(21)are integrated numerically as an initial valued problem to a given terminal point. Presented here are 14 grid points used by taking the tolerance limit and the step size 0.001.
4. Results and Discussion
The current section deals with the graphical results of all the related parameters that arise in a governing flow problem. Assuming that the reference temperature is 300K, the corresponding realistic values for the physical parameters would be Pr = 6.8, M = Ec = Gr = Lb = Le = Pe = 1.0, Nb = Rb = 0.3, Nr = Nt =Nb = σ = 0.1, ϑ = 45°, depending on previously published research works, unless otherwise specified. For illustrated results, numerical values are plotted in Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9, Figure 10, Figure 11, Figure 12, Figure 13, Figure 14, Figure 15, Figure 16, Figure 17, Figure 18, Figure 19, Figure 20 and Figure 21 as well as a detailed discussion on the effects of the governing parameters, namely magnetic field parameter M, Eckert number Ec, Brownian motion number Nb, Lewis number Le, thermophoresis parameter Nt, bioconvection Peclet number Pe, buoyancy ratio parameter Nr, bioconvection Rayleigh number Rb, bioconvection Lewis number Lb, and bioconvection constant σ.
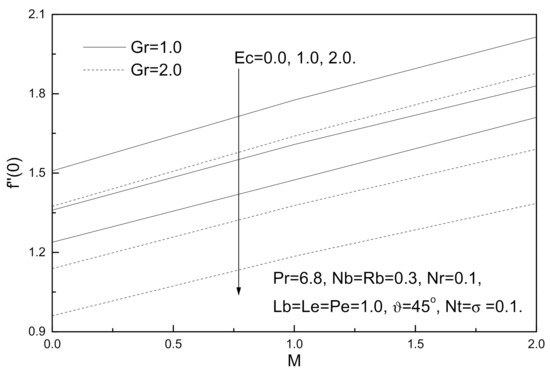
Figure 2.
Magnetic field parameter M, Eckert number Ec and Grashof number Gr effects on local skin friction coefficient.
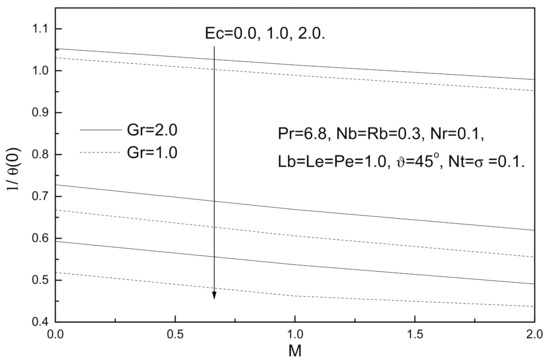
Figure 3.
Magnetic field parameter M, Eckert number Ec and Grashof number Greffects on local Nusselt number.
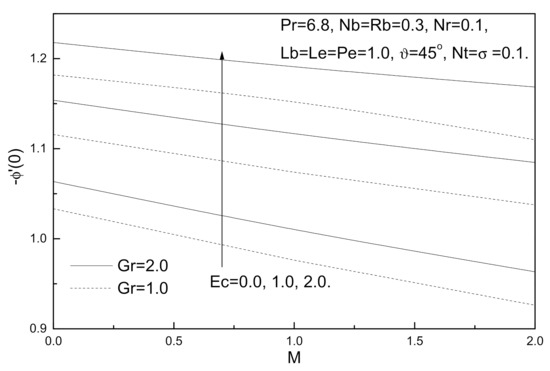
Figure 4.
Magnetic field parameter M, Eckert number Ec and Grashof number Greffects on local Sherwood number.
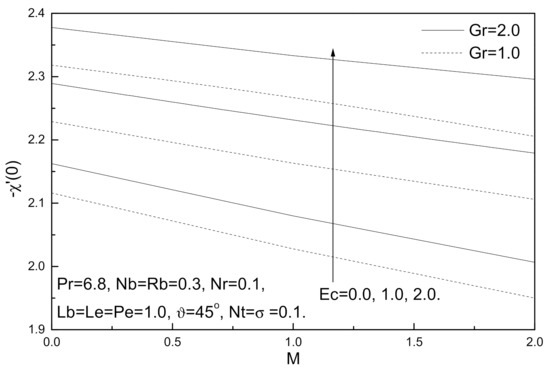
Figure 5.
Magnetic field parameter M, Eckert number Ec and Grashof number Gr effects on local density of the motile micro-organisms number.
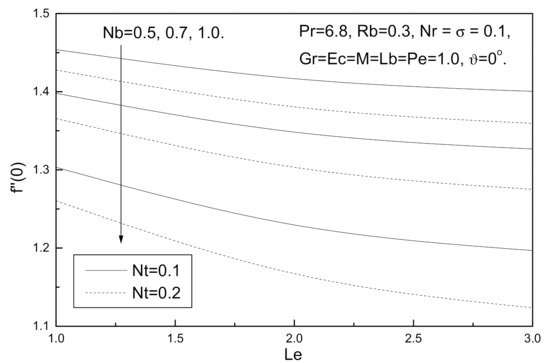
Figure 6.
Brownian motion number Nb, thermophoresis parameter Nt and Lewis number Le effects on local skin friction coefficient.
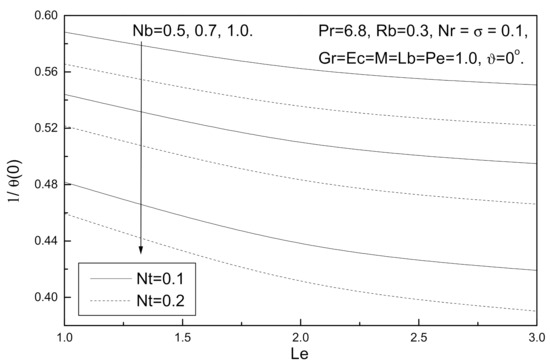
Figure 7.
Brownian motion number Nb, thermophoresis parameter Nt and Lewis number Le effects on local Nusselt number.

Figure 8.
Brownian motion number Nb, thermophoresis parameter Nt and Lewis number Le effects on local Sherwood number.
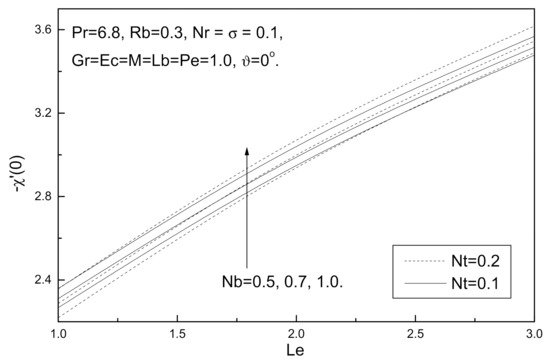
Figure 9.
Brownian motion number Nb, thermophoresis parameter Nt and Lewis number Le effects on local density of the motile micro-organisms number.
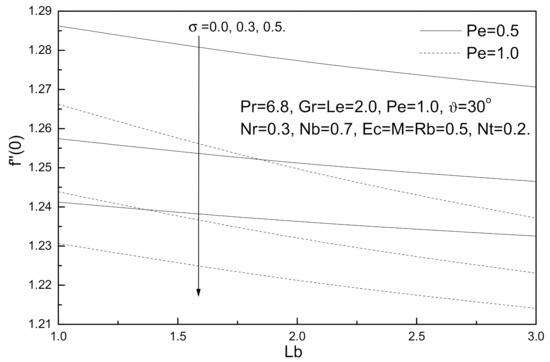
Figure 10.
Bioconvection Lewis number Lb, bioconvection constant σ and bioconvection Peclet number Pe effects on local skin friction coefficient.
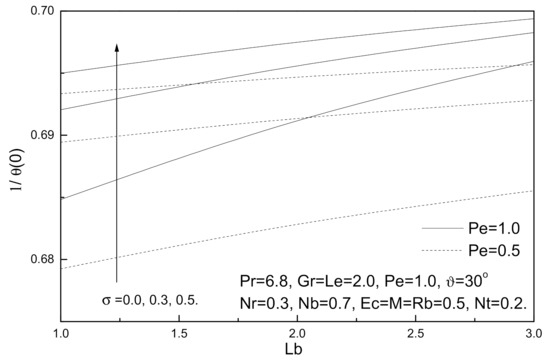
Figure 11.
Bioconvection Lewis number Lb, bioconvection constant σ and bioconvection Peclet number Pe effects on local Nusselt number.
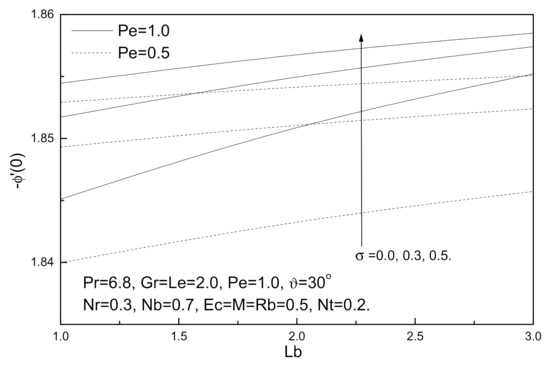
Figure 12.
Bioconvection Lewis number Lb, bioconvection constant σ and bioconvection Peclet number Pe effects on local Sherwood number.
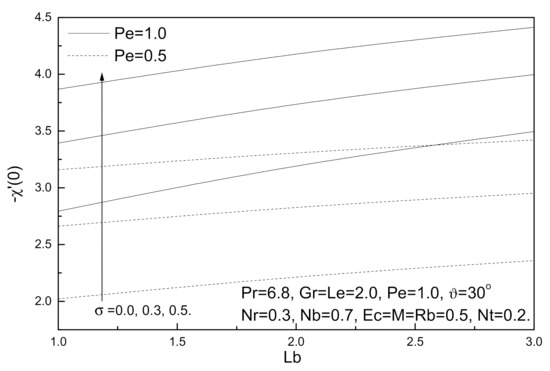
Figure 13.
Bioconvection Lewis number Lb, bioconvection constant σ and bioconvection Peclet number Pe effects on local density of the motile micro-organisms number.
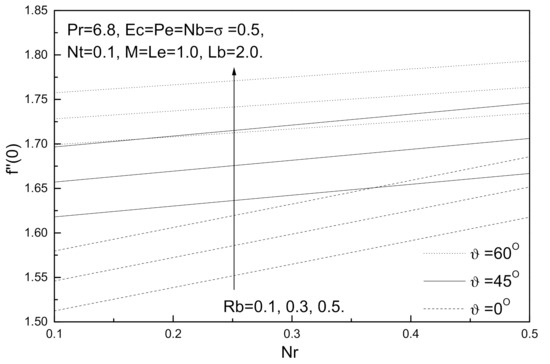
Figure 14.
Buoyancy ratio parameter Nr, bioconvection Rayleigh number Rb and Grashof number Gr effects on local skin friction coefficient.
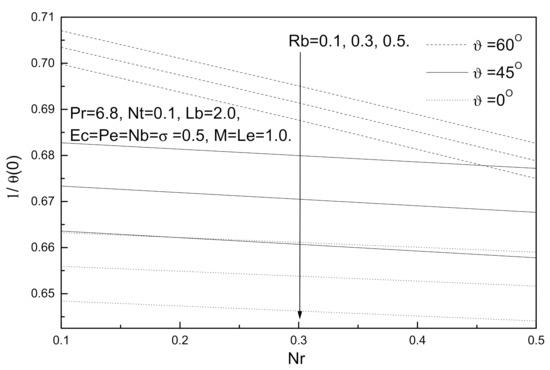
Figure 15.
Buoyancy ratio parameter Nr, bioconvection Rayleigh number Rb and Grashof number Gr effects on local Nusselt number.
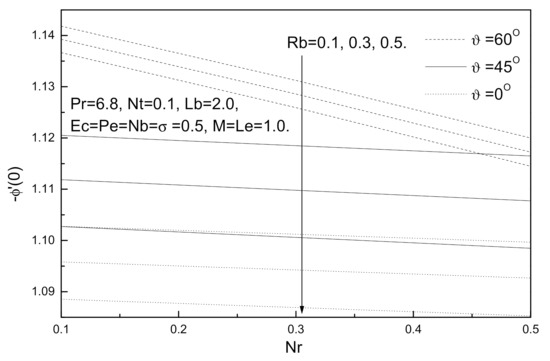
Figure 16.
Buoyancy ratio parameter Nr, bioconvection Rayleigh number Rb and Grashof number Gr effects on local Sherwood number.
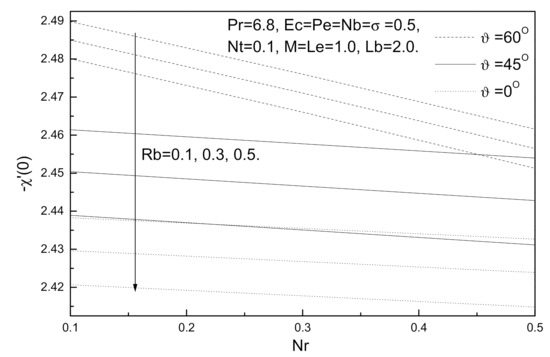
Figure 17.
Buoyancy ratio parameter Nr, bioconvection Rayleigh number Rb and Grashof number Gr effects on local density of the motile micro-organisms number.
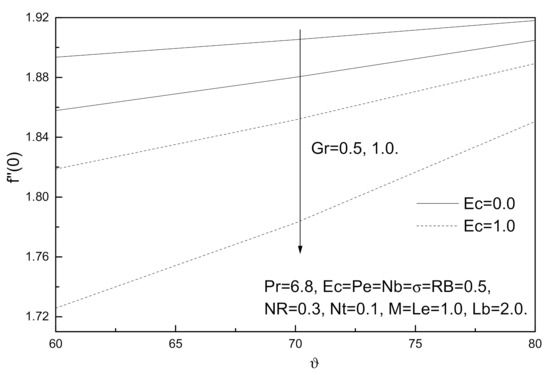
Figure 18.
Angle of inclination ϑ, Eckert number Ec and Grashof number Gr effects on local skin friction coefficient.
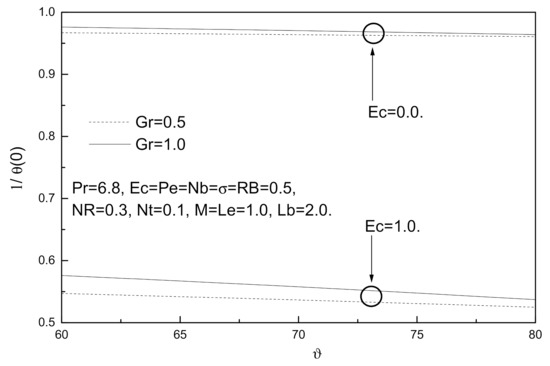
Figure 19.
Angle of inclination ϑ, Eckert number Ec and Grashof number Gr effects on local Nusselt number.
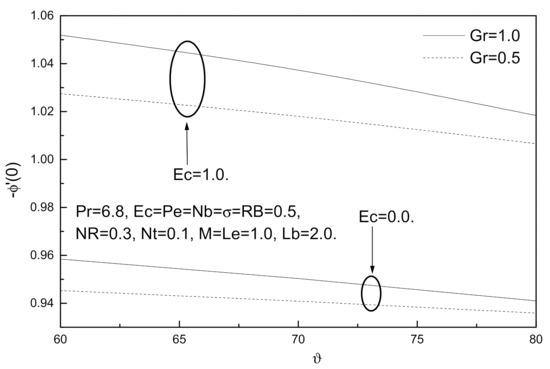
Figure 20.
Angle of inclination ϑ, Eckert number Ec and Grashof number Gr effects on local Sherwood number.
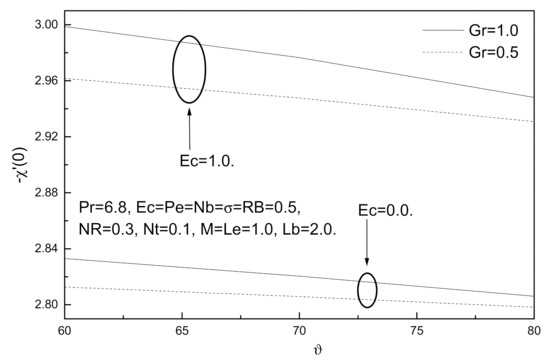
Figure 21.
Angle of inclination ϑ, Eckert number Ec and Grashof number Gr effects on local density of the motile micro-organisms number.
Figure 2, Figure 3, Figure 4 and Figure 5 display the effects of Grashof number Gr, magnetic field parameter M and Eckert number Ec on the local skin friction coefficient, local Nusselt number, local Sherwood number, and local density of the motile micro-organisms. It is clear from these figures that an augmentation in Grashof number Gr tends to minimize the local skin friction coefficient while maximizing the local Nusselt number, local Sherwood number, and local density of the motile micro-organisms. On the other hand, an increase in the value of Eckert number Ec reduces the local skin friction coefficient and local Nusselt number while both the local Sherwood number and local density of the motile micro-organisms decrease with this increase. By contrast, an increment in the magnetic field parameter M increases the local skin friction coefficient and decreases the local Nusselt number, local Sherwood number, and local density of the motile micro-organisms number due to the presence of Lorentz force which acts against the flow and resists the motion.
Figure 6, Figure 7, Figure 8 and Figure 9 illustrate the influence of Brownian motion number Nb, thermophoresis parameter Nt and Lewis number Le on local skin friction coefficient, local Nusselt number, local Sherwood number, and local density of the motile micro-organisms number. It is clear from these figures that an increase in the value of Brownian motion number Nb, thermophoresis parameter Nt and Lewis number Le reduce the local skin friction coefficient and local Nusselt number while local Sherwood number and local density of the motile micro-organisms demonstrate the opposite behavior with this increase.
Figure 10, Figure 11, Figure 12 and Figure 13 demonstrate the influence of local skin friction coefficient, local Nusselt number, local Sherwood number, and local density of the motile micro-organisms number for various values of bioconvection Lewis number Lb, bioconvection Peclet number Pe, and bioconvection constant σ; it is noted that for these parameters, bioconvection Lewis number Lb, bioconvection Peclet number Pe, and bioconvection constant σ have the same effects. With increasing bioconvection Lewis number Lb, bioconvection Peclet number Pe or bioconvection constant σ, local Nusselt number, local Sherwood number, and local density of the motile micro-organisms number increase, whereas the local skin friction coefficient decreases with these increases.
Figure 14, Figure 15, Figure 16 and Figure 17 illustrate the influence of buoyancy ratio parameter Nr, bioconvection Rayleigh number Rb, and the angle of inclination ϑ on the local skin friction coefficient, local Nusselt number, local Sherwood number, and local density of the motile micro-organisms number. The values of the angle of inclination ϑ (ranging from 0° to 60°), see Ref. [29], include ϑ =0°, which represents the vertical plate, and ϑ =90°, which represents the horizontal plate. It is clear from these figures that an augmentation in the angle of inclination ϑ has the same effect as Grashof number Gr, which tends to minimize the local skin friction coefficient while maximizing the local Nusselt number, local Sherwood number, and local density of the motile micro-organisms. It can be observed from these figures that an increase in the buoyancy ratio parameter Nr and bioconvection Rayleigh number Rb tends to decrease local Nusselt number, local Sherwood number, and local density of the motile micro-organisms number, whereas the local skin friction coefficient decreases.
The effect of viscous dissipation on the dimensionless local skin friction, Nusselt number, Sherwood number, and density number of the motile micro-organisms are shown in Figure 18, Figure 19, Figure 20 and Figure 21. It has been observed from these figures that the presence of viscous dissipation leads to a decrease in the rate of heat transfer and local Nusselt numbers as well as local skin friction because viscous dissipation (Eckert number Ec) works to raise the temperature of this fluid. On the other hand, the presence of viscous dissipation works to increase both the Sherwood number and density number of the motile micro-organisms.
5. Conclusions
The effect of viscous dissipation on magneto-free bioconvection flow of a water-based nanofluid containing gyrotactic micro-organisms over an inclined stretching sheet is investigated numerically. The governing equations were reduced to similar boundary layer equations using suitable transformations and then solved using the Runge–Kutta–Fehlberg numerical integration procedure in conjunction with shooting technique. The combined effects of all parameters governing the flow are shown graphically for the local skin friction coefficient, local Nusselt number, local Sherwood number, and local density of the motile micro-organisms number.
- It was found that an increase in the value of the Grashof number tends to minimize the local skin friction coefficient and maximize local Nusselt number, local Sherwood number, and local density of the motile micro-organisms.
- Increasing the value of the Eckert number reduces the local skin friction coefficient and local Nusselt number, whereas both the Sherwood number and the density of the motile micro-organisms decrease.
- An increment in the magnetic field parameter increases the skin friction coefficient and decreases the Nusselt and Sherwood numbers and local density of the motile micro-organisms number due to the presence of Lorentz force.
- An increase in the value of Brownian motion number, thermophoresis parameter, and Lewis number raise local Sherwood number and local density of the motile micro-organisms, whereas the local skin friction coefficient and local Nusselt number demonstrate the opposite behavior with this increase.
- An increase in the buoyancy ratio parameter and bioconvection Rayleigh number tend to decrease the local Nusselt number, local Sherwood number, and local density of the motile micro-organisms number, whereas the local skin friction coefficient decreases.
- As increments in the bioconvection Lewis number, bioconvection Peclet number or bioconvection constant, local Nusselt number, local Sherwood number, and local density of the motile micro-organisms number increase, the local skin friction coefficient decreases with these increases.
Author Contributions
All authors contributed equally. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Prince Sattam bin Abdulaziz University.
Data Availability Statement
Data available upon request.
Acknowledgments
The authors would like to thank Prince Sattam bin Abdulaziz University and the Deanship of Scientific Research at Prince Sattam bin Abdulaziz University for their continuous support and encouragement.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| b | Chemotaxis constant |
| B0 | Magnetic induction |
| C | Concentration |
| DB | Brownian diffusion coefficient |
| Dm | Thermophoresis diffusion coefficient |
| DT | Diffusivity of micro-organisms |
| Ec | Eckert number |
| f’ | Dimensionless velocity |
| g | Acceleration due to gravity |
| Gr | Grashof number |
| K | Thermal conductivity of fluid |
| Lb | Biconvection Lewis number |
| Le | Traditional Lewis number |
| M | Magnetic field parameter |
| N | Number density of motile micro-organisms |
| Nb | Brownian motion parameter |
| Nt | Thermophoresis parameter |
| Nr | Buoyancy ratio parameter |
| Pe | Biconvection Peclet number |
| Pr | Prandtl number |
| Rb | Biconvection Rayleigh number |
| Rex | Reynolds number |
| T | Temperature |
| u | Velocity component in x-direction |
| v | Velocity component in y-direction |
| Wc | The utmost cell swimming speed |
| x | Horizontal co-ordinate |
| y | Vertical co-ordinate |
| Greek symbols | |
| α | Thermal diffusivity of the fluid |
| β | Thermal expansion coefficient |
| γ | Micro-organism average volume |
| ϑ | Angle of inclination |
| τ | The ratio of effective heat capacity among the nanoparticle material and base fluid |
| τw | Shear stress coefficient |
| χ | Dimensionless density of motile micro-organisms |
| η | Dimensionless co-ordinate |
| λ | Electric conductivity of the fluid |
| μ | Dynamic viscosity |
| υ | Kinematic viscosity |
| θ | Dimensionless temperature |
| φ | Dimensionless concentration |
| Ψ | Stream function |
| ρ | Density of the fluid |
| ρf | base fluid density |
| ρ∞ | Micro-organism density |
| ρp | Nanoparticle density |
| σ | Bioconvection constant |
| Subscript | |
| w | Wall condition |
| ∞ | Ambient condition |
| Superscript | |
| ‘ | Differentiation with respect to η; |
References
- Crane, L.J. Flow past a stretching plane. Z. Angew. Math. Phys. 1970, 21, 645–647. [Google Scholar] [CrossRef]
- Gupta, P.S.; Gupta, A.S. Heat and mass transfer on a stretching sheet with suction or blowing. Can. J. Chem. Eng. 1977, 55, 744–746. [Google Scholar]
- Soundalgekar, V.M.; Murty, T.V.R. Heat transfer in flow past a continuous moving plate with variable temperature. Heat Mass Transf. 1980, 14, 91–93. [Google Scholar] [CrossRef]
- Grubka, L.J.; Bobba, K.M. Heat Transfer Characteristics of a Continuous, Stretching Surface with Variable Temperature. J. Heat Transf. 1985, 107, 248–250. [Google Scholar] [CrossRef]
- Choi, S. Enhancing thermal conductivity of fluids with nanoparticle. In Developments and Applications of Non-Newtonian Flows; ASME MD vol. 231 and FED vol. 66; Siginer, D.A., Wang, H.P., Eds.; ASME: New York, NY, USA, 1995; pp. 99–105. [Google Scholar]
- Tlili, I.; Nabwey, H.A.; Reddy, M.; Sandeep, N.; Pasupula, M. Effect of resistive heating on incessantly poignant thin needle in magnetohydrodynamic Sakiadis hybrid nanofluid. Ain Shams Eng. J. 2021, 12, 1025–1032. [Google Scholar] [CrossRef]
- El-Kabeir, S.M.M.; Chamkha, A.J.; Rashad, A.M. The Effect of Thermal Radiation on Non-Darcy Free Convection from a Vertical Cylinder Embedded in a Nanofluid Porous Media. J. Porous Media 2014, 17, 269–278. [Google Scholar] [CrossRef]
- Tlili, I.; Nabwey, H.A.; Samrat, S.P.; Sandeep, N. 3D MHD nonlinear radiative flow of CuO-MgO/methanol hybrid nanofluid beyond an irregular dimension surface with slip effect. Sci. Rep. 2020, 10, 9181. [Google Scholar] [CrossRef] [PubMed]
- Nabwey, H.A.; Boumazgour, M.; Rashad, A.M. Group method analysis of mixed convection stagnation-point flow of non-Newtonian nanofluid over a vertical stretching surface. Indian J. Phys. 2017, 91, 731–742. [Google Scholar] [CrossRef]
- Tlili, I.; Sandeep, N.; Reddy, M.G.; Nabwey, H.A. Effect of radiation on engine oil-TC4/NiCr mixture nanofluid flow over a revolving cone in mutable permeable medium. Ain Shams Eng. J. 2020, 11, 1255–1263. [Google Scholar] [CrossRef]
- Rashad, A. Impact of thermal radiation on MHD slip flow of a ferrofluid over a non-isothermal wedge. J. Magn. Magn. Mater. 2017, 422, 25–31. [Google Scholar] [CrossRef]
- Chamkha, A.J.; Rashad, A.M.; El-Zahar, E.R.; El-Mky, H.A. Analytical and Numerical Investigation of Fe3O4-Water Nanofluid Flow Over a Moveable Plane in A Parallel Stream With High Suction. Energies 2019, 12, 198. [Google Scholar] [CrossRef]
- Rashad, A.M.; Nabwey, H.A. Gyrotactic Mixed Bioconvection Flow of a Nanofluid Past a Circular Cylinder with Convective Boundary Condition. J. Taiwan Inst. Chem. Eng. 2019, 99, 9–17. [Google Scholar] [CrossRef]
- Nabwey, H.A.; Khan, W.A.; Rashad, A.M. Lie Group Analysis of Unsteady Flow of Kerosene/Cobalt Ferrofluid Past a Radiated Stretching Surface with Navier Slip and Convective Heating. Mathematics 2020, 8, 826. [Google Scholar] [CrossRef]
- Hazarika, S.; Ahmed, S.; Chamkha, A.J. Investigation of nanoparticles Cu, Ag and Fe3O4 on thermophoresis and viscous dissipation of MHD nanofluid over a stretching sheet in a porous regime: A numerical modeling. Math. Comput. Simul. 2021, 182, 819–837. [Google Scholar] [CrossRef]
- Narender, G.; Govardhan, K.; Sarma, G.S. Numerical Study of Radiative Magnetohydrodynamics Viscous Nanofluid Due to Convective Stretching Sheet with the Chemical Reaction Effect. Iraqi J. Sci. 2020, 61, 1733–1744. [Google Scholar] [CrossRef]
- Mansour, M.; Ahmed, S.E.; Rashad, A.M. MHD Natural Convection in a Square Enclosure using Nanofluid with the Influence of Thermal Boundary Conditions. J. Appl. Fluid Mech. 2016, 9, 2515–2525. [Google Scholar] [CrossRef]
- Khan, M.; Hussain, A.; Malik, M.; Salahuddin, T.; Khan, F. Boundary layer flow of MHD tangent hyperbolic nanofluid over a stretching sheet: A numerical investigation. Results Phys. 2017, 7, 2837–2844. [Google Scholar] [CrossRef]
- Pourmehran, O.; Rahimi-Gorji, M.; Ganji, D. Heat transfer and flow analysis of nanofluid flow induced by a stretching sheet in the presence of an external magnetic field. J. Taiwan Inst. Chem. Eng. 2016, 65, 162–171. [Google Scholar] [CrossRef]
- Mehryan, M.S.A.; Kashkooli, M.F.; Soltani, M.; Raahemifar, K. Fluid Flow and Heat Transfer Analysis of a Nanofluid Containing Motile Gyrotactic Micro-Organisms Passing a Nonlinear Stretching Vertical Sheet in the Presence of a Non-Uniform Magnetic Field; Numerical Approach. PLoS ONE 2016, 11, 0157598. [Google Scholar] [CrossRef]
- Khan, J.A.; Mustafa, M.; Hayat, T.; Alsaedi, A. Numerical study on three-dimensional flow of nanofluid past a convectively heated exponentially stretching sheet. Can. J. Phys. 2015, 93, 1131–1137. [Google Scholar] [CrossRef]
- Akbar, N.S.; Khan, Z. Magnetic field analysis in a suspension of gyrotactic microorganisms and nanoparticles over a stretching surface. J. Magn. Magn. Mater. 2016, 410, 72–80. [Google Scholar] [CrossRef]
- Hayat, T.; Imtiaz, M.; Alsaedi, A. Magnetohydrodynamic flow of nanofluid over permeable stretching sheet with convective boundary conditions. Therm. Sci. 2016, 20, 1835–1845. [Google Scholar] [CrossRef]
- Khan, W.A.; Makinde, O.D. MHD Nanofluid Bioconvection Due to Gyrotactic Microorganisms over a Convectively Heat Stretching Sheet. Int. J. Therm. Sci. 2014, 81, 118–124. [Google Scholar]
- Khan, W.A.; Rashad, A.M.; Abdou, M.M.M.; Tlili, I. Natural bioconvection flow of a nanofluid containing gyrotactic microorganisms about a truncated cone. Eur. J. Mech. B Fluids 2019, 75, 133–142. [Google Scholar] [CrossRef]
- Chamkha, A.; Rashad, A.M.; Kameswaran, P.K.; Abdou, M.M.M. Radiation Effects on Natural Bioconvection Flow of a Nanofluid Containing Gyrotactic Microorganisms Past a Vertical Plate with Streamwise Temperature Variation. J. Nanofluids 2017, 6, 587–595. [Google Scholar] [CrossRef]
- Hayat, T.; Bashir, Z.; Qayyum, S.; Alsaedi, A. Nonlinear radiative flow of nanofluid in presence of gyrotactic microorganisms and magnetohydro-dynamic. J. Numer. Methods Heat Fluid Flow 2019, 29, 3039–3055. [Google Scholar] [CrossRef]
- Ferdows, M.; Zaimi, K.; Rashad, A.M.; Nabwey, H.A. MHD Bioconvection Flow and Heat Transfer of Nanofluid through an Exponentially Stretchable Sheet. Symmetry 2020, 12, 692. [Google Scholar] [CrossRef]
- Ali, M.; Alim, A.; Alam, M.S. Similarity Solution of Heat and Mass Transfer Flow over an Inclined Stretching Sheet with Viscous Dissipation and Constant Heat Flux in Presence of Magnetic Field. Procedia Eng. 2015, 105, 557–569. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).