Abstract
Wall-thickness deformation is a critical indicator of fatigue risk in flexible risers exposed to vortex-induced vibration (VIV), especially under combined internal and external flow conditions. This study examines the spanwise evolution and distribution of wall-thickness deformation in a riser traversing air and water. The effects of external flow velocity, internal flow velocity, and internal fluid density on in-line (IL) and cross-flow (CF) wall deformation are systematically analyzed at characteristic positions. The results show that wall deformation exhibits strong spatial variability and media property dependence: IL deformation in the air-exposed segment is amplified under lock-in conditions due to lower damping, while the submerged segment experiences consistently larger deformation driven by added-mass effects. Internal flow influences wall-thickness response in a non-monotonic manner, and increased internal fluid density suppresses deformation while shifting the dominant frequency. These findings demonstrate that wall-thickness deformation is a sensitive and integrative response to fluid–structure interaction, offering a direct basis for identifying high-risk zones and improving fatigue-resistant design in deep-sea riser systems.
1. Introduction
1.1. Research Background and Engineering Significance
Flexible risers, owing to their excellent bending performance and adaptability to marine environments, have become critical components connecting offshore platforms to subsea oil and gas resources. In marine engineering, cross-flow currents often induce VIV through fluid–structure interaction (FSI) mechanisms. Under complex sea conditions, the combined effects of internal and external flows lead to multi-mode coupled vibration responses in the riser, which can significantly accelerate fatigue damage accumulation. This may eventually result in riser rupture; it can cause oil and gas leakage, economic losses, and severe marine environmental pollution.
Investigating the fluid–structure interaction mechanisms of VIV in flexible risers and uncovering the underlying excitation and fatigue damage patterns is of great scientific significance. Such studies can contribute to optimizing vibration-resistant design theories, developing reliable safety assessment methods, and enhancing the environmental adaptability of marine engineering equipment. Moreover, they provide essential technical support for environmental protection and risk management in offshore oil and gas development.
1.2. Progress of VIV Research on Flexible Risers
Due to the large aspect ratio and significant flexibility of marine risers, the influence of internal flow must be taken into account when analyzing VIV. In recent years, many researchers have conducted in-depth investigations into the dynamic characteristics of flexible risers.
Chaplin and King [1], as well as Zheng et al. [2,3], experimentally investigated the influence of external flow velocity, top tension, and boundary conditions on mode excitation and vibration amplitude. However, their investigations were primarily limited to single-external-flow scenarios. Franzini, Pesce, and colleagues [4] conducted model tests on long vertical flexible cylinders subjected to top-end displacement excitation to investigate their VIV behavior. Li et al. [5] performed combined wave-current tank experiments using fiber Bragg grating (FBG) sensing technology and found that the excitation water depth significantly influences the onset of lock-in, vibration frequency distribution, and amplitude characteristics of the riser’s dynamic response. Zhou et al. [6] investigated the vortex-induced vibration characteristics of deep-sea risers under bidirectional shear flow through scaled model experiments.
More recently, increasing attention has been given to the interaction between internal flow and flexible risers. Chen et al. [7,8,9] considered the fluid–structure coupling induced by internal flow and external shear currents in tensioned risers, employing empirical mode decomposition to identify model-free components and vibration modes. Duan et al. [10] analyzed the impact of internal flow velocity and fluid density on the VIV response using finite element modeling. Xie et al. [11] developed a nonlinear dynamic model to explore the effects of variable-density internal flow, highlighting the influence of pipe geometry. Martins et al. [12] and Meng et al. [13] numerically analyzed the effects of Reynolds number and internal flow-induced centrifugal forces on the vibration stability of risers. Zhu and Gao [14] used non-intrusive imaging to capture coupled flow-induced responses. Thorsen and Challabotla [15] numerically revealed that fatigue damage intensifies when the internal flow wavelength aligns with the riser’s dominant modal structure. Despite these advancements, the influence of internal flow—particularly variable-density effects—on the fatigue behavior of flexible risers under combined flow conditions remains insufficiently explored.
1.3. Objectives and Novelty of This Study
Most existing studies emphasize global displacement and dominant frequency, whereas fatigue damage accumulates through local strain range and cycle count. Wall-thickness deformation is kinematically tied to the hoop and axial strains at the pipe wall and thus reflects the stress state that governs crack initiation and growth. It is also highly sensitive to the surrounding medium and to the internal flow: the air–water segmentation modifies added mass and damping, through-flow changes inertia and energy dissipation, and variable-density internal fluids further rebalance excitation and structural response. Treating wall-thickness deformation as the response metric therefore provides a fatigue-relevant view that goes beyond global kinematics and motivates the present study.
We develop a three-dimensional two-way FSI model with an air–water segmented domain and moving-mesh RBF morphing. A controlled matrix of operating conditions varies the external velocity, the internal velocity, and the internal-fluid density one at a time. Spanwise monitoring in both in-line and cross-flow directions is used to quantify the evolution and distribution of wall-thickness deformation in the exposed and submerged segments.
This study introduces wall-thickness deformation as a primary response variable for flexible-riser VIV under combined internal–external flows, clarifies how external velocity, internal velocity, and internal-fluid density, respectively, amplify, phase-shift, or damp local deformation and establishes the engineering relevance of this metric for locating high-risk zones and informing fatigue-resistant design.
2. Numerical Methods
2.1. Fluid Governing Equations
For incompressible and viscous fluids, the energy conservation equation can be neglected since the energy conversion due to temperature variations is insignificant. For incompressible, isothermal two-phase flow, the governing equations comprise the continuity equation and the momentum equations [16].
The differential form of the continuity equation is given by:
The differential form of the momentum equations (i.e., the Navier–Stokes equations) is given as follows [17]:
In the above equation, i, j = 1, 2, 3 denote the three spatial dimensions. represents the mixture density of the fluid (kg/m3), defined as , where indicates the -th phase, is the volume fraction of phase , and is its corresponding density. is the mass-averaged velocity of the mixture (m/s), and denotes the Reynolds stress. is the dynamic viscosity. The volume of fluid (VOF) method is adopted to capture the liquid interface in the two-phase flow, where the phase volume fraction is used to describe the spatial distribution and properties of each phase [18].
The k–ε model is one of the most widely used two-equation turbulence models and has undergone numerous refinements over the years. The standard k–ε model, first proposed in 1974 [19], is governed by the following equations:
Here, denotes the turbulent kinetic energy; is the dynamic viscosity, is the turbulent (eddy) viscosity, and and are the turbulent Prandtl numbers for and , typically taken as 1.0 and 1.3, respectively. The empirical constants are , and . The Reynolds stress tensor is closed via the Boussinesq approximation [20],
where is the mean strain-rate tensor.
The unsteady RANS equations and the k–ε transport equations are advanced in time with a second-order implicit backward-difference formula. For any field ϕ,
A pressure-based predictor–corrector algorithm solves the momentum and pressure fields within each time step; the linear systems are handled by an algebraic multigrid preconditioner. For each step, we perform inner iterations until the scaled residuals of continuity, momentum, k, and ε drop by at least three orders of magnitude, and the maximum Courant number remains below unity. The time step Δt is fixed across a run and chosen from a preliminary sensitivity check to ensure temporal second-order convergence in the frequency and amplitude of the response. At each time level , the external two-phase RANS–VOF solver advances the mixture velocity, pressure, , , and the water volume fraction α. The internal solver advances single-phase velocity and pressure with the same k–ε variables. All transport equations use a second-order implicit BDF scheme with a pressure-based predictor–corrector; the volume-fraction advection uses bounded high-resolution fluxes. On the fluid–structure interface, the velocity is taken from the structural motion, and the resulting traction is returned to the structure. Mesh motion follows RBF morphing, gravity is included, and the air–water free surface is captured by α.
2.2. The Governing Equations of Solid Mechanics
The riser wall is treated as a three-dimensional, linear-elastic continuum. Neglecting thermal effects and assuming infinitesimal deformations, its motion obeys the Cauchy momentum equation [21,22]:
where is the solid density, u the displacement vector, and f is the body-force density.
The infinitesimal strain tensor is related to the displacement gradient by [23,24]
Isotropic Hooke’s law closes the system [25,26]:
with Lamé parameters obtained from the measured Young’s modulus E and Poisson’s ratio ν:
Both riser ends (z = 0, L) are fully clamped, enforcing u = 0 and ∂u/∂n = 0.
On the external surface, two-way coupling ensures displacement and traction continuity with the surrounding flow, whereas the internal surface is loaded by the inner-flow pressure and viscous shear.
A second-order implicit time integrator, combined with an RBF mesh-morphing algorithm, transfers the wall motion to the fluid mesh each step, maintaining cell quality for the maximum predicted deflection (<0.6% D). Structural (material) damping is neglected in this work, i.e., C = 0, consistent with the linear-elastic small-strain assumption. The semi-discrete form and time integration are presented in Section 2.3.
2.3. Flow–Structure Interaction Method
To represent the two-way coupling between the incompressible flow in Section 2.1 and the linearly elastic riser wall in Section 2.2, a partitioned FSI approach is adopted. Let and denote the fluid and solid domains, and the interface. The fluid velocity and pressure are and p, the solid displacement and velocity are and , and is the unit normal pointing from the solid to the fluid.
On the structural side, the finite-element semi-discrete equations read [27]:
where , and are the global mass, damping and stiffness matrices; represents the nodal displacements; is the external load vector; and is the fluid–structure interface traction mapped to the structural mesh.
In this study, structural (material) damping of the riser is neglected, i.e., C = 0, Equation (12) is used in its undamped form:
Structural time integration. The structural dynamics are advanced with a second-order implicit Newmark scheme with β = 1/4 and γ = 1/2. With C = 0, as in Equation (12a), the effective system is solved at each step using a consistent mass matrix, and the same time step Δt as the fluid solver is adopted to avoid time interpolation across the interface. This choice is unconditionally stable for the present linear-elastic case and proved sufficient to capture the response without introducing additional numerical damping.
The overall dissipation in the coupled problem is provided on the fluid side, through viscous effects represented by the turbulence closure in Section 2.1, and by the partitioned coupling at the fluid–solid interface, while the solid follows the linear-elastic, small-strain constitutive law of Section 2.2 without additional damping parameters. This modeling choice isolates the influence of the internal–external flow conditions on the response and avoids introducing non-essential calibration constants.
In the moving-mesh (ALE) frame used for coupling, the governing equations on the fluid side are written as
Equation (13) is written for the VOF mixture fields: the density and viscosity are the phase-averaged properties defined in Section 2.1, the mixture velocity is divergence-free for incompressible phases without phase change, and the interface is transported by the volume-fraction equation; this ALE form is therefore consistent with the two-phase RANS/VOF formulation. Where is the mesh velocity and is the viscous stress, with being the effective viscosity.
At the fluid–solid interface , the coupling conditions enforce kinematic and dynamic continuity together with mesh motion
where is the fluid Cauchy stress and is the solid stress.
The interface traction is consistently transferred to the structure as
with being the structural shape functions.
The interface coupling proceeds as follows. The structural velocity prescribes the Dirichlet boundary condition for the fluid at via (13). Accordingly, the structural Neumann load vector is assembled from both sides of the wall. Tractions from the external two-phase flow on the outer surface and from the internal single-phase flow on the inner surface are evaluated on their respective fluid interfaces, mapped to the structural interface, and added to the global load vector using the outward normal with respect to the solid. In the external domain, the stress uses the local phase properties provided by the VOF field, so air loads act on the exposed segment and water loads on the submerged segment. This completes the definition of the interface traction referred to in (15) and follows standard partitioned Dirichlet–Neumann coupling with surface-to-surface load transfer.
A staggered Dirichlet–Neumann iteration is performed at each time step to satisfy Equations (13)–(15). Given a predictor , the fluid problem is solved on with to obtain , which is then mapped through (14) to update the structural response in Equation (12). To enhance stability, Aitken under-relaxation is applied to the interface kinematics,
and the iteration proceeds until the relative change in interface traction or velocity falls below a prescribed tolerance [28]. The mesh motion is obtained from the RBF-based morphing described in Section 2.4, ensuring smooth propagation of the boundary displacement into the fluid interior while maintaining cell quality [29].
2.4. Dynamic Mesh Morphing Based on RBF Interpolation
In order to accommodate the interface motion produced by the structural response, the fluid mesh is updated at every time step using the RBF morphing technique. The structural solution provides the displacement u on the fluid–solid interface . A subset of interface and near-wall nodes is selected as control points, and their prescribed displacements are propagated to the whole fluid domain through an RBF interpolation, yielding a smooth mesh-displacement field . The mesh velocity is then obtained as and used in the ALE formulation of Section 2.3, where the interface conditions and are enforced on .
To enhance robustness under large interface excursions, a relaxation strategy is applied to the control-point updates, and the set of control nodes is adaptively thinned to avoid over-constraining the near-wall layers. The displacement field is constructed to preserve boundary-layer orthogonality and to smoothly decay towards the interior, which effectively mitigates skewness growth and prevents cell inversion in regions of strong curvature. This procedure maintains mesh quality throughout the simulation while preserving the boundary-layer resolution required by the turbulence closure. The resulting moving mesh enables accurate transfer of wall motion to the fluid solver without remeshing and has been verified to retain cell quality under the maximum predicted deflection reported in Section 2.2.
2.5. Grid Configuration and Simulation Domain Definition
The computational mesh consists of a combination of cut-cell grids and structured grids. Mesh refinement is applied to both the riser surface and the gas–liquid interface. In the XY plane, the refined mesh size is 0.05 m, and in the Z direction, it is 0.0025 m. Additional local refinement is performed around the riser, with a mesh size of 0.002 m in the XY plane and 0.006 m in the Z direction. The riser and the internal fluid domain are divided using structured layers with a total of 200 layers. The overall mesh consists of approximately 1.31 million cells. On the validation case, runs with 2Δt and 0.5Δt yield the same dominant frequency as the baseline. The doubled step gives a 14.3% deviation in peak-to-peak and RMS strain relative to the experiment, whereas the baseline and the halved step keep amplitude errors within 10%. Balancing accuracy and cost, we adopt Δt = 0.001 s for all simulations. The external computational domain is an incompressible air–water two-phase flow with gravity; along the span, the riser has an exposed segment in air and a submerged segment in water. The internal flow is single-phase liquid throughout with no gas entrainment or phase change.
The left boundary of the domain is defined as a velocity inlet, the right boundary as a pressure outlet, and the two lateral boundaries are set as symmetry planes. The top and bottom surfaces are treated as walls. The outer surface of the riser is also defined as a wall, with both ends of the riser constrained. Inside the riser, the top end is set as a velocity inlet and the bottom end as a pressure outlet; the inner wall is treated as a no-slip wall. The detailed parameters of the riser are listed in Table 1.

Table 1.
Riser parameters.
The geometric configuration and mesh refinement corresponding to the parameters listed in Table 1 are shown in Figure 1.
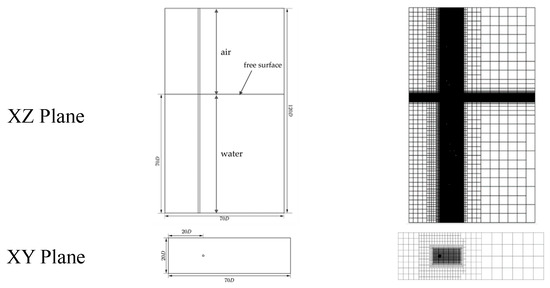
Figure 1.
Geometric model and mesh distribution.
3. Model Validation
Based on the internal and external flow experiments of flexible risers conducted by Guo [30], a numerical flume model was developed using the CFD software STAR-CCM+ ver2020. The experimental riser, representing a typical offshore platform riser, was modeled according to the motion capabilities of a towing device in a flume. The riser parameters are listed in Table 1. The computational domain was configured with the riser positioned 20D away from the outlet and lateral boundaries and the water depth set to 70D. The top and bottom ends of the riser were fixed to a steel frame, and two monitoring locations—Position 1 (Z/L = 0.583) and Position 2 (Z/L = 0.708)—were selected for validation.
The validation parameters were adopted from Guo’s experiment [30], which was conducted in the COE (China Ocean Engineering) Laboratory. In that experiment, a test platform was used to simulate combined internal and external flow conditions, and the dynamic responses of the riser under various internal flow velocities were measured. To ensure consistency and accuracy in the numerical validation, the same parameters were employed in this simulation. The CF strain time histories at Position 1 and Position 2 were extracted from the CFD results and compared against Guo’s experimental data to evaluate the validity of the numerical model.
In the model test, the measured strain in the CF direction consists of three components: the initial axial strain induced by the pretension, the variation in axial strain caused by different tension levels, and the bending strain due to hydrodynamic excitation. Therefore, the pure VIV strain at a given position z can be calculated as follows [31]:
where and are the strain measurements obtained from sensors and , respectively; represents the bending strain caused by VIV; and denotes the axial strain induced by tension.
Based on the comparison between the simulation validation results and the experimental data in Figure 2, quantitative indicators are reported to substantiate the agreement in both locations. At Position 1 the dominant frequency of both curves is about 7.2 Hz. The peak-to-peak strain is 181 µε for the simulation and 165 µε for the experiment, corresponding to a relative amplitude error of 9.6%. The RMS amplitudes are 120 µε and 110 µε, consistent with this error level. At Position 2 the dominant frequency is about 7.4 Hz. The peak-to-peak strain is 86 µε in the simulation and 80 µε in the experiment, giving a relative error of 7.5%, and the corresponding RMS values are 30.4 µε and 28.3 µε. These results show that frequency and amplitude agree well at both positions, with all amplitude errors within 10%.
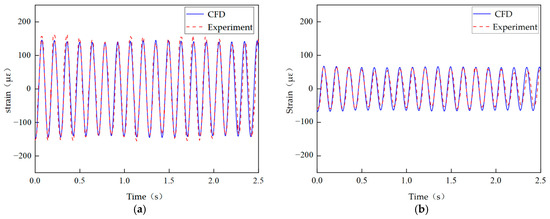
Figure 2.
Comparison of simulation and experimental strain results: solid lines represent simulation data, dashed lines represent experimental data. (a) Position 1 (Z/L = 0.583); (b) Position 2 (Z/L = 0.708).
To clarify the origin of the small residual differences, we note that they stem from mismatches between the numerical and physical boundary conditions and the inflow—such as inlet turbulence level in a recirculating flume, pump-induced low-frequency ripples, free-surface disturbances, and weak lateral gradients—together with experimental measurement uncertainty arising from sensor resolution and calibration drift, zero-strain referencing and pretension readout, and slight offsets of sensor locations from the nominal Z/L positions. Additional contributions come from geometric and material tolerances and support compliance; from modeling and discretization choices including the turbulence closure, mesh resolution and time stepping; and from the mapping between interface traction and velocity in the partitioned coupling. The finite reading resolution of the plotted curves also adds error. Collectively these factors explain the modest amplitude gap while the dominant frequency remains closely matched.
4. Results and Discussion
To isolate the role of each governing factor, the operating conditions in Table 2 were organized into three series. In Group A the external velocity Uo varies from 0.38 to 1.63 m/s, while the internal velocity is fixed at Ui = 0.25 m/s and the internal density at 998 kg/m3. This baseline Ui provides modest through-flow inertia without dominating the response; with d = 0.006 m and kinematic viscosity ν ≈ 1.0 × 10−6 m2/s, the internal Reynolds number is about 1.5×103, and the Uo range corresponds to Reo ≈ 3.8 × 103—1.6 × 104, which falls in the subcritical shedding regime and samples pre-lock-in, peak-response, and post-lock-in conditions. In Group B Uo is fixed at 0.38 m/s to keep the wake regime unchanged, and Ui increases from 0 to 2 m/s to probe through-flow effects from laminar to turbulent pipe conditions, with Rei rising to about 1.2 × 104. In Group C Uo = 0.38 m/s and Ui = 0.25 m/s are held constant, while the internal density varies from 0.675 to 2000 kg/m3 to bracket lightweight gas-lift at the low end and heavy brine or slurry transport at the high end. This one-parameter-at-a-time design keeps magnitudes within ranges widely reported for small-scale flexible-riser tests and enables clear attribution of the observed trends to Uo, Ui, or internal-fluid density.

Table 2.
Parameters of various working conditions.
Based on the operating conditions defined in Table 2, eleven monitoring sections were uniformly distributed along the riser length, covering the range Z/L = 0.083 to Z/L = 0.92, to characterize the riser’s dynamic response. Time-history displacement data in both the IL and CF directions were collected in real time. After the system reached a steady state, two complete vibration cycles were extracted for analysis. The displacement amplitudes in the IL and CF directions (denoted as X/D and Y/D, respectively), along with the corresponding nondimensional height Z/L, were used to reconstruct the three-dimensional motion trajectory of the riser. This data enabled a quantitative analysis of amplitude distribution, modal characteristics, and the evolution of vibration energy along the riser.
4.1. Modal Analysis and Motion Trajectory
Figure 3 shows how CF vibration envelopes respond to three governing parameters. In Group A (Figure 3a), raising Uo from 0.38 m/s (A1) to 1.63 m/s (A4) drives a clear modal escalation: the single-crest profile of A1 evolves into a five-crest waveform, and the peak amplitude rises from Y/D = 0.60 to Y/D = 0.90. This confirms that Uo controls both mode order and amplitude through enhanced vortex excitation. Group B (Figure 3b) fixes Uo at 0.38 m/s while increasing Ui from 0 to 2 m/s (B1–B4). The four curves almost coincide—apart from a slight mid-span swelling at Z/L = 0.55—indicating that through-flow mainly alters added mass and phase rather than overall magnitude. Group C (Figure 3c) keeps Ui = 0.25 m/s and raises density from 998 kg/m3 to 2000 kg/m3; the heavier fluid damps motion along the entire span, narrowing the envelope and lowering the peak amplitude by about 20%. Taken together, Uo amplifies and elevates modes, Ui adjusts phase distribution, and density provides global damping—offering complementary levers for CF mitigation in flexible-riser design.
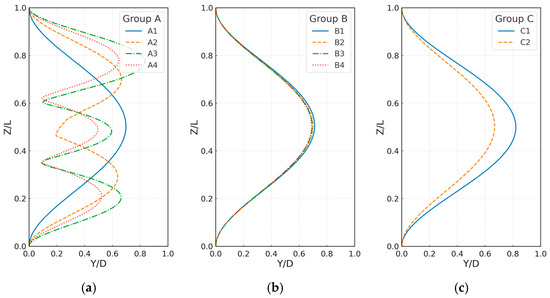
Figure 3.
Spanwise CF displacement envelopes (Y/D vs. Z/L) for (a) external-velocity cases A1–A4, (b) internal-velocity cases B1–B4, and (c) internal-density cases C1–C2.
Figure 4 depicts the IL displacement envelopes and corresponding 3D trajectories for the four representative cases A3, B1, B4, and C2. In Case A3 (Uo = 1.32 m/s, Ui = 0.25 m/s, density = 998 kg/m3), the IL envelope exhibits a five-crest profile, confirming that the resonance between vortex shedding and the structural natural frequency promotes a high-order modal response. The associated trajectory widens markedly in the mid-span region (Z/L ≈ 0.6) and tilts downstream, evidencing energy transfer from the external flow to the riser and the dominance of hydrodynamic inertial loading along the span.
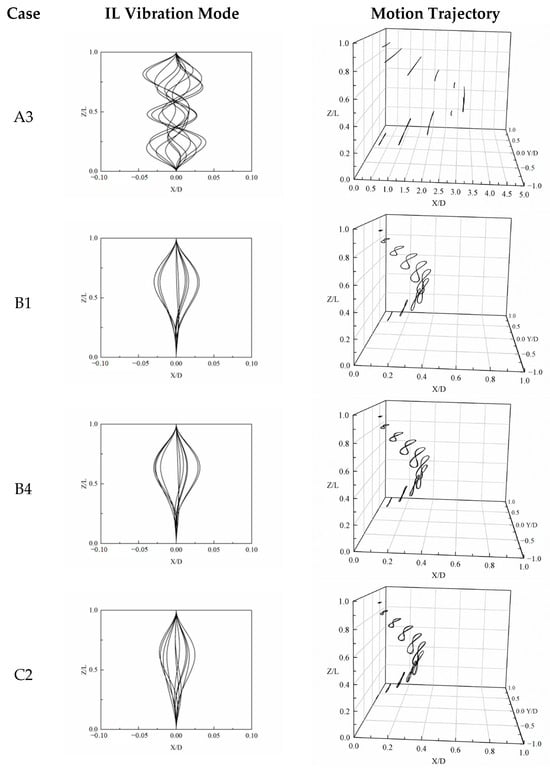
Figure 4.
IL mode shapes and three-dimensional trajectories for cases A3, B1, B4 and C2.
Case B1 (Uo = 0.38 m/s, Ui = 0 m/s) serves as the no-through-flow baseline. The IL mode remains first-order, with peak displacement confined to the upper half of the span, while the 3D path reduces to a slender figure eight. When Ui is increased to 2 m/s in Case B4, the IL amplitude rebounds, and the mode shape develops an additional inflection near Z/L ≈ 0.55. The trajectory correspondingly broadens, indicating that excessive internal velocity reverses the added-mass reduction observed at intermediate Ui and instead injects kinetic energy back into the IL direction.
Finally, Case C2 (Uo = 0.38 m/s, Ui = 0.25 m/s, density = 2000 kg/m3) exemplifies the damping effect of a heavy internal fluid. The entire IL envelope contracts by roughly 20% relative to the baseline, and the trajectory collapses into a narrow helix. This pronounced suppression confirms that density acts primarily through inertial damping, attenuating both modal escalation and spatial excursion.
Taken together, the four cases demonstrate that (i) Uo controls modal order and spatial energy distribution, (ii) Ui governs a non-monotonic transition that first suppresses and then re-amplifies IL motion, and (iii) density provides global damping that uniformly curtails amplitude and trajectory extent.
4.2. Flow Field and Spectral Analysis
Table 3 lists the dominant shedding frequency f and the corresponding Strouhal number St = f D/Uo for all ten test cases, whereas Figure 5 traces the variation in St with the three governing parameters. The coupled interpretation of these data sets clarifies the wake-excitation mechanisms that underlie the CF/IL responses discussed in Section 4.1.

Table 3.
Dominant frequency and Strouhal number for all cases.
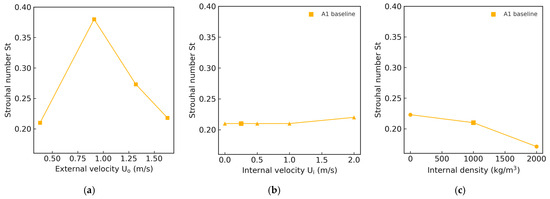
Figure 5.
Strouhal number St as a function of (a) external velocity Uo, (b) internal velocity Ui, and (c) internal-flow density. In panels (b,c), the square marker denotes the baseline case A1 (Uo = 0.38 m/s) for reference.
Increasing Uo from 0.38 m/s to 0.91 m/s drives St upward from 0.210 to 0.380 (Figure 5a), signifying a proportional increase in vortex-shedding frequency and a rapid concentration of spectral energy at the lock-in band. This peak marks the strongest wake–structure resonance within a narrow window; amplitudes grow rapidly toward this window and begin to roll off beyond, confirming that resonance between the wake and the structure is fully developed at St ≈ 0.38. Above this velocity, St falls back toward ≈ 0.22 (Cases A3–A4), indicating that the wake enters a higher-Re regime dominated by vortex pairing and broadband shedding; the redistributed energy reduces modal growth and explains the amplitude roll-off reported earlier. Comparable behavior has been observed in laboratory measurements on flexible risers [1,4], where amplitude envelopes and modal switching concentrate within a narrow lock-in window and weaken beyond it. These published data sets corroborate the present non-monotonic trend with increasing external velocity.
The non-monotonic trend is clarified by the local crest at Case A2: the cycle rate is highest there, while the wall-thickness deformation amplitude is not the largest. Fatigue depends on both how many cycles occur and how large the local strain range is. Case A2 is therefore a critical window, because a high cycle rate combines with a non-negligible local strain range and can rival or exceed the damage potential of neighboring cases that show larger deformation but lower frequency. This links the peak in St to fatigue significance and aligns with the present study’s focus on wall-thickness-based local strain range as a risk-relevant metric. The practical takeaway is to avoid long residence near Case A2 or mitigate it through added damping, higher internal-fluid density, or intensified monitoring at the identified hot spots.
When Ui is varied from 0 to 2 m/s, St remains nearly constant at 0.210 ± 0.010 (Figure 5b). Because Uo is fixed, the external wake frequency is dictated by the outer flow, and through-flow merely shifts added mass and phase. Consistent with prior studies, internal through-flow primarily adjusts effective inertia and damping, producing amplitude changes while exerting limited control over the dominant frequency; its influence further diminishes as the outer current strengthens [10]. This accounts for the non-monotonic—but low-frequency-bound—IL amplitudes in Figure 4: energy is neither injected nor removed from the wake, so structural response changes arise from hydrodynamic mass coupling rather than frequency modulation.
Raising the internal-flow density from 0.675 kg/m3 to 2000 kg/m3 lowers St from 0.223 to 0.171 (Figure 5c). The heavier fluid increases system inertia and viscous dissipation, weakening vortex formation and shifting the dominant frequency downward. The 20% contraction in IL amplitude for Case C2 (Figure 4) therefore reflects a broadband damping effect rather than a modal shift, demonstrating the efficiency of density-based mitigation. Reports on variable-density internal flow show that increased density or density fluctuations markedly modify VIV and fatigue accumulation in risers, supporting the damping-dominated interpretation and the downward shift in the response frequency observed here [11,15].
Figure 6 visualizes the instantaneous vorticity magnitude at Z/L = 0.50 for six representative cases and confirms the frequency-based interpretation given above. The snapshots are taken from the external domain at mid-span to illustrate the wake; internal-flow fields are not plotted. In the external-velocity series, the wake at Uo = 0.91 m/s (A2) presents compact, high-intensity vortex cores that match the St peak, whereas at Uo = 1.32 m/s (A3), the cores split and disperse, explaining the subsequent drop in St. In the internal-velocity series, the 2S pattern observed at Ui = 0 m/s (B1) is virtually unchanged at Ui = 2 m/s (B4), corroborating the near-constant St in Figure 5b. Finally, the internal-density series shows that increasing density from 0.675 kg/m3 (C1) to 2000 kg/m3 (C2) markedly weakens the vortex cores and narrows the wake, in line with the lower St and amplitude suppression reported for Case C2. Figure 7 complements this by showing the mid-span XZ free surface, delineating the air–water interface and confirming the exposed and submerged segments used in the analysis.
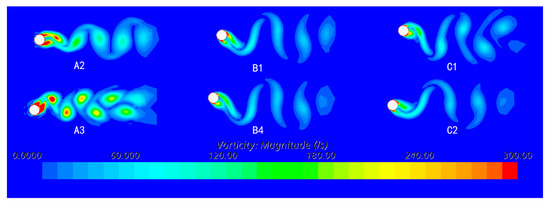
Figure 6.
Instantaneous vorticity magnitude at Z/L = 0.50 for cases A2, A3, B1, B4, C1 and C2 (common color scale 0–300/s).
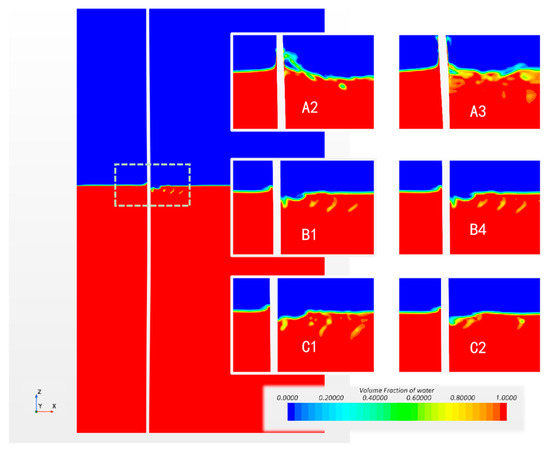
Figure 7.
External air–water free surface on the mid-span XZ plane visualized by water volume fraction (0–1).
In addition, Figure 8 shows the computed internal single-phase flow on cross-sections normal to the axis at Z/L = 0.50 for representative cases. These plots are included to document the internal boundary loading used in the coupling. The laminar-like structure of the internal velocity near the wall arises from viscous no-slip and boundary-layer development in pipe flow, whereas the bulk profile conforms to the imposed inlet condition through conservation of the mass flow rate.
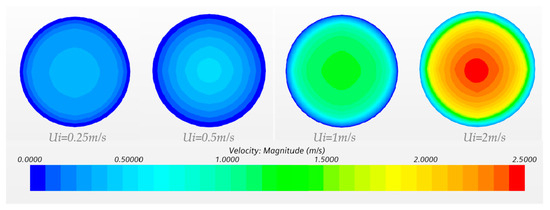
Figure 8.
Mid-span internal single-phase flow, common scale 0–2.5 m/s.
In summary, Uo governs modal escalation by concentrating spectral energy at high St, Ui alters the added-mass-induced phase without changing St, and internal density provides broadband damping that both lowers St and suppresses displacement.
4.3. Analysis of Pipe Wall Deformation
To further investigate the coupling mechanism between external flow velocity and local deformation of the riser, two representative monitoring sections were selected: one in the submerged segment at Z/L = 0.25 and the other in the air-exposed segment at Z/L = 0.75. At each section, the wall thickness deformation was measured at four key circumferential positions (a, b, c, and d), as shown in Figure 9, along both the CF and IL directions. Figure 9 provides a schematic diagram of these cross-sectional monitoring points (a–d), clearly indicating the positions selected for detailed deformation analysis. These points were strategically placed to effectively capture radial deformation characteristics around the riser’s circumference, enabling precise quantitative assessments at representative circumferential positions. By comparing the deformation at these four positions on the cross-section, the synergistic effect of medium properties and flow-induced excitation was revealed.
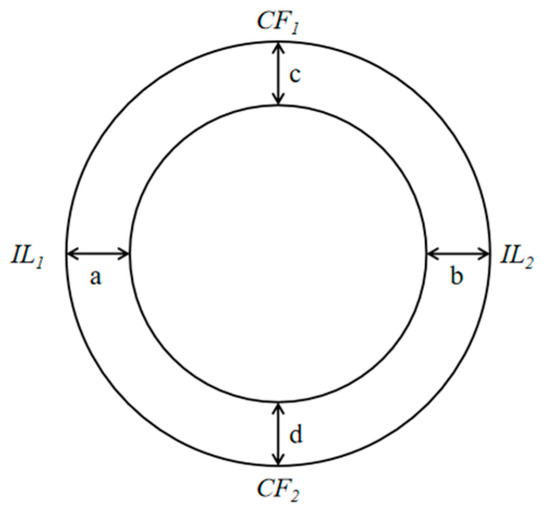
Figure 9.
Schematic diagram of cross-sectional monitoring points.
Figure 10 summarizes the maximum wall-thickness deformation under all investigated cases. Clearly, the external velocity (Uo) significantly impacts deformation magnitudes. Specifically, deformation sharply increases from 0.168 μm at 0.38 m/s (Case A1) to a peak of 1.773 μm at 1.32 m/s (Case A3), followed by a decline to 1.054 μm at the higher velocity of 1.63 m/s (Case A4). This non-monotonic deformation trend closely mirrors the variation in St observed earlier (Figure 5a), affirming that the maximum deformation corresponds to resonant excitation conditions.
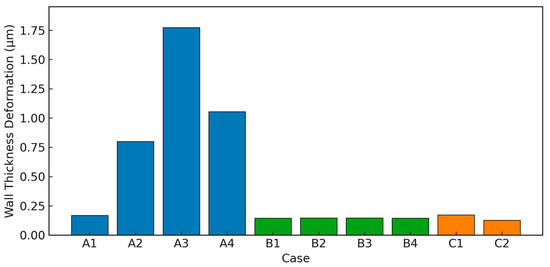
Figure 10.
Maximum Wall Thickness Deformation under Different Cases.
In contrast, internal velocity (Ui) variations in Cases B1–B4 have a negligible impact on deformation, remaining consistently around 0.145 μm. This observation corroborates previous spectral findings (Figure 5b) and vorticity analysis (Figure 6), further confirming that internal-flow velocity plays a minor role in modifying wall-thickness deformation.
Internal-flow density variations (Cases C1 and C2) demonstrate a clear damping effect. The deformation decreases notably from 0.173 μm (density = 0.675 kg/m3) to 0.128 μm (density = 2000 kg/m3), indicating a roughly 26% reduction. This outcome reinforces that higher internal density introduces considerable inertial damping, consistent with spectral (Figure 5c) and flow-field (Figure 6) analyses.
Figure 11 further illustrates the detailed time-history curves of wall-thickness deformation at the four selected cross-sectional monitoring points (a–d) for different external-flow cases and axial positions. Comparing subplots (a–b) and (c–d) (Case A2 vs. Case A3 at Z/L = 0.25 and 0.75), we observe substantial increases in deformation amplitude from Case A2 to resonant Case A3. This increase aligns with the maximum deformation values reported earlier (Figure 10), validating resonance-driven amplification effects.
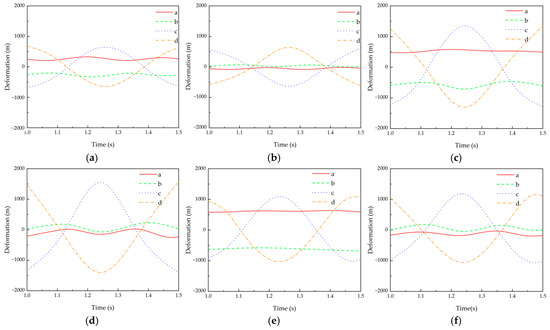
Figure 11.
Time-history curves of wall thickness deformation at four monitoring positions (a–d) under different external flow cases and axial positions: (a) Case A2 at Z/L = 0.25; (b) Case A2 at Z/L = 0.75; (c) Case A3 at Z/L = 0.25; (d) Case A3 at Z/L = 0.75; (e) Case A4 at Z/L = 0.25; (f) Case A4 at Z/L = 0.75.
Furthermore, subplots ((Figure 11e–f) highlight deformation trends for Case A4 at the same axial positions. Despite higher external velocity, deformation amplitudes at A4 are notably reduced compared to resonant Case A3, demonstrating the post-resonance reduction observed previously. Additionally, deformation magnitudes are consistently higher at Z/L = 0.75 compared to Z/L = 0.25 across all cases, indicating enhanced radial deformation towards the riser’s mid-span region.
Overall, these combined findings underline the governing influence of external flow velocity on wall-thickness deformation, especially around resonance conditions, while internal velocity exhibits minimal impact. Conversely, increased internal-flow density demonstrates a robust and effective damping mechanism, mitigating deformation and enhancing structural integrity. These results offer valuable insights for practical structural optimization and risk mitigation strategies in flexible riser design under complex internal and external flow conditions.
5. Conclusions
This study developed a three-dimensional, two-way FSI model with moving-mesh morphing to examine a flexible riser under combined internal and external flows with air–water segmentation, taking wall-thickness deformation as the primary response variable.
Across the external-velocity series, the response is non-monotonic. A narrow window of strong coupling exhibits the highest cycle rate, whereas the largest deformation occurs outside this window as wake–structure detuning grows. When the internal velocity varies at fixed external flow, the response frequency remains nearly unchanged, and the amplitude adjusts through added-mass and phase effects. Increasing internal-fluid density reduces deformation and shifts the dominant frequency downward, indicating stronger inertial damping. These patterns jointly clarify how medium segmentation and flow excitation shape localized pipe-wall deformation.
From an engineering viewpoint, fatigue risk depends on both cycle rate and the local strain range inferred from wall-thickness deformation. High-cycle-rate windows combined with non-negligible strain ranges are therefore critical for operation and monitoring. Practical levers include increasing structural or hydrodynamic damping, raising internal-fluid density, and tuning tension or boundary conditions to reduce local deformation; the spanwise deformation distributions reported here support such decisions.
For fatigue assessment, the reported wall-thickness deformation can be mapped to local hoop and axial strain ranges under the linear-elastic assumption and paired with the cycle rate inferred from the response frequency to rank hotspots along the span. These quantities are directly compatible with standard S–N or ε–N approaches and Miner’s rule, enabling life estimation without relying on global displacement or a single dominant frequency.
While these findings are actionable, the operating matrix remains limited. Future work will enrich the conditions to cover broader currents and transient or bidirectional flows, deepen the link between wall-thickness deformation and damage mechanisms, extend the model to multi-layer risers with realistic interfaces, and incorporate higher-fidelity turbulence modeling and uncertainty quantification to assess sensitivity across scales.
Author Contributions
Conceptualization, methodology, and writing—original draft, Z.S.; supervision and revision, J.L., D.W. and Y.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable. This work consists of computational simulations and analysis and does not involve human participants or animal subjects.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| CFD | Computational Fluid Dynamics |
| CF | Cross-Flow |
| IL | In-Line |
| COE | China Ocean Engineering Laboratory |
| FBG | Fiber Bragg Grating |
| FSI | Fluid–Structure Interaction |
| PMMA | Poly-Methyl Methacrylate |
| RBF | Radial Basis Function |
| VIV | Vortex-Induced Vibration |
| VOF | Volume of Fluid (VOF) method |
| RANS | Reynolds-Averaged Navier–Stokes |
References
- Chaplin, J.R.; King, R. Laboratory measurements of the vortex-induced vibrations of an untensioned catenary riser with high curvature. J. Fluids Struct. 2018, 79, 26–38. [Google Scholar] [CrossRef]
- Zheng, R.; Wang, C.; He, W.; Zhang, Z.; Ma, K.; Ren, M. The experimental study of dynamic response of marine riser under coupling effect of multiparameter. J. Mar. Sci. Eng. 2023, 11, 1787. [Google Scholar] [CrossRef]
- Zheng, R.; Wang, C.; He, W. Experimental study on dynamic response of marine riser under multi-parameter coupling action. Sci. Technol. Eng. 2023, 23, 9413–9422. (In Chinese) [Google Scholar]
- Franzini, G.R.; Pesce, C.P.; Goncalves, R.T.; Fujarra, A.L.C.; Mendes, P. An experimental investigation on concomitant vortex-induced vibration and axial top-motion excitation with a long flexible cylinder in vertical configuration. Ocean Eng. 2018, 156, 596–612. [Google Scholar] [CrossRef]
- Li, P.; Dong, Z.K.; Liu, Y.; Wang, Y.; Cong, A.J.; Guo, H.; Fu, Q. Experimental investigation on vortex-induced vibration of deep-sea risers at different excitation water depths. China Ocean Eng. 2021, 35, 215–227. [Google Scholar] [CrossRef]
- Zhou, W.W.; Duan, M.L.; Chen, R.Q.; Wang, S.; Li, H. Test study on vortex-induced vibration of deep-sea riser under bidirectional shear flow. J. Mar. Sci. Eng. 2022, 10, 1689. [Google Scholar] [CrossRef]
- Chen, Z.S.; Rhee, S.H. Effect of traveling wave on the vortex-induced vibration of a long flexible pipe. Appl. Ocean Res. 2019, 84, 122–132. [Google Scholar] [CrossRef]
- Chen, Z.S.; Liu, F.S.; Wang, L.P.; Liu, G.L. Empirical modeless decomposition and modal identification method for non-stationary vibration processes. Ocean Eng. 2016, 123, 291–302. [Google Scholar] [CrossRef]
- Chen, Z.S.; Kimm, W.J.; Xiong, C.B. Effect of upward internal flow on dynamics of riser model subject to shear current. China Ocean Eng. 2012, 26, 95–108. [Google Scholar] [CrossRef]
- Duan, J.; Zhou, J.; You, Y.; Wang, X. Effect of internal flow on vortex-induced vibration dynamics of a flexible mining riser in external shear current. Mar. Struct. 2021, 80, 103094. [Google Scholar] [CrossRef]
- Xie, W.; Xin, W.; Zhang, H. Influence of internal varying-density flow on the vibrations and fatigue damage of a top-tensioned riser undergoing vortex-induced vibrations. Appl. Ocean Res. 2021, 117, 102955. [Google Scholar] [CrossRef]
- Martins, F.A.C.; Avila, J.P.J. Three-dimensional CFD analysis of damping effects on vortex-induced vibrations of 2-DOF elastically-mounted circular cylinders. Mar. Struct. 2019, 65, 12–31. [Google Scholar] [CrossRef]
- Meng, S.; Song, S.; Che, C.; Zhang, W. Internal flow effect on the parametric instability of deep-water drilling risers. Ocean Eng. 2018, 149, 305–312. [Google Scholar] [CrossRef]
- Zhu, H.; Gao, Y.; Zhao, H. Coupling vibration response of a curved flexible riser under the combination of internal slug flow and external shear current. J. Fluids Struct. 2019, 91, 102724. [Google Scholar] [CrossRef]
- Thorsen, M.J.; Challabotla, N.R.; Sævik, S.; Nydal, O.J. A numerical study on vortex-induced vibrations and the effect of slurry density variations on fatigue of ocean mining risers. Ocean Eng. 2019, 174, 1–13. [Google Scholar] [CrossRef]
- Ishii, M.; Hibiki, T. Thermo-Fluid Dynamics of Two-Phase Flow, 2nd ed.; Springer: New York, NY, USA, 2011; pp. 43–52. [Google Scholar]
- Batchelor, G.K. An Introduction to Fluid Dynamics; Cambridge University Press: Cambridge, UK, 1967; pp. 2–28. [Google Scholar]
- Hirt, C.W.; Nichols, B.D. Volume of Fluid (VOF) Method for the Dynamics of Free Boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Launder, B.E.; Spalding, D.B. The Numerical Computation of Turbulent Flows. Comput. Methods Appl. Mech. Eng. 1974, 3, 269–289. [Google Scholar] [CrossRef]
- Pope, S.B. Turbulent Flows; Cambridge University Press: Cambridge, UK, 2000; pp. 72–75. [Google Scholar]
- Labropoulou, D.; Vafeas, P.; Dassios, G. Direct connection between Navier and spherical-harmonic kernels in elasticity. AIMS Math. 2023, 8, 3064–3082. [Google Scholar] [CrossRef]
- Schadt, F. Differential geometric formulation of the Cauchy–Navier equations. J. Elast. 2011, 104, 73–88. [Google Scholar]
- De Tommasi, D.; Marzano, S. Small strain and moderate rotation. J. Elast. 1993, 32, 37–50. [Google Scholar] [CrossRef]
- Soldatos, K.P. Small strain growth and the human nail. J. Elast. 2016, 124, 57–80. [Google Scholar] [CrossRef][Green Version]
- Xiao, H. On isotropic invariants of the elasticity tensor. J. Elast. 1997, 46, 115–149. [Google Scholar] [CrossRef]
- Adamov, A.A. Comparative analysis of the two-constant generalizations of Hooke’s law. J. Appl. Mech. Tech. Phys. 2001, 42, 890–897. [Google Scholar] [CrossRef]
- González, J.A.; Park, K.C. Three-field partitioned analysis of fluid–structure interaction problems with a consistent interface model. Comput. Methods Appl. Mech. Eng. 2023, 414, 116134. [Google Scholar] [CrossRef]
- Lorentzon, J.; Revstedt, J. On stability and relaxation techniques for partitioned fluid-structure interaction simulations. Eng. Rep. 2022, 4, e12514. [Google Scholar] [CrossRef]
- Li, Y.; Zhao, X.; Liu, Z.; Zhu, J. An efficient parallel mesh deformation technique based on spatially nested radial basis functions. Chin. J. Aeronaut. 2023, 36, 103–116. [Google Scholar]
- Guo, H.Y.; Lou, M. Effect of internal flow on vortex-induced vibration of risers. J. Fluids Struct. 2008, 24, 496–504. [Google Scholar] [CrossRef]
- Zou, L.; Huang, S.; Huera-Huarte, F. Separation of bending and axial strains in flexible risers subjected to vortex-induced vibrations. J. Fluids Struct. 2023, 117, 103565. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).