CFD-Based Transient Analysis for the Detection and Characterisation of Extended Partial Blockages in Pipes
Abstract
1. Introduction
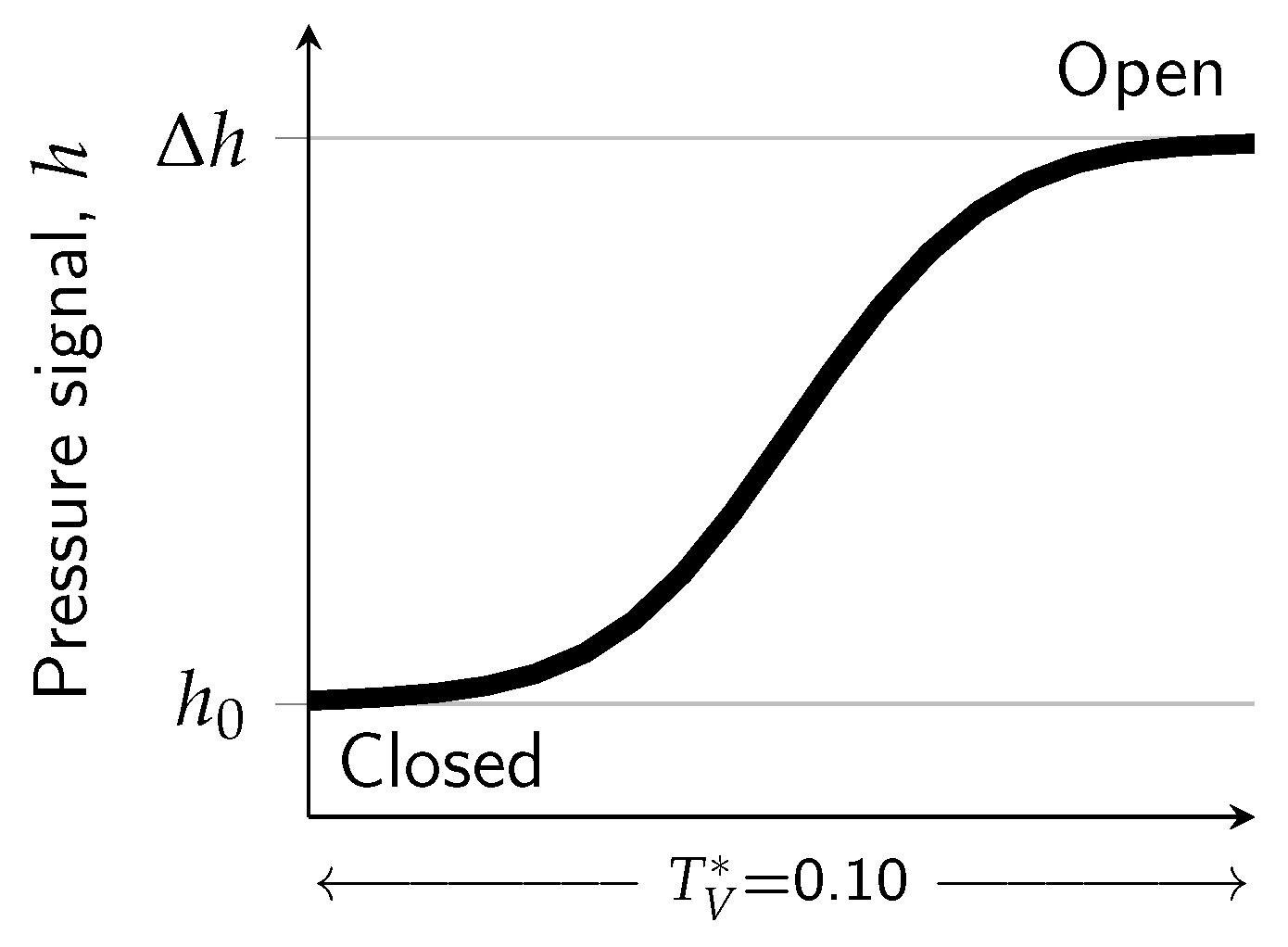
2. Materials and Methods
2.1. Computational Fluid Dynamics (CFD) Model
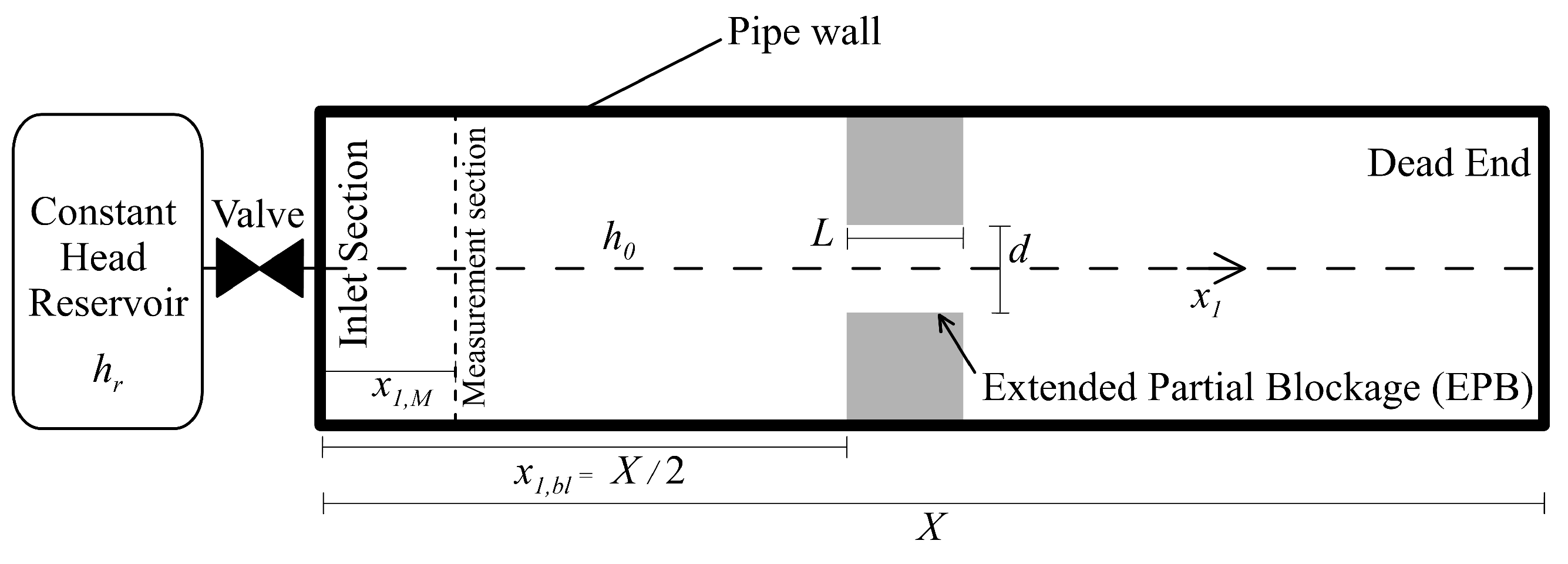
2.2. System Layout and Parameters
3. Results and Discussion
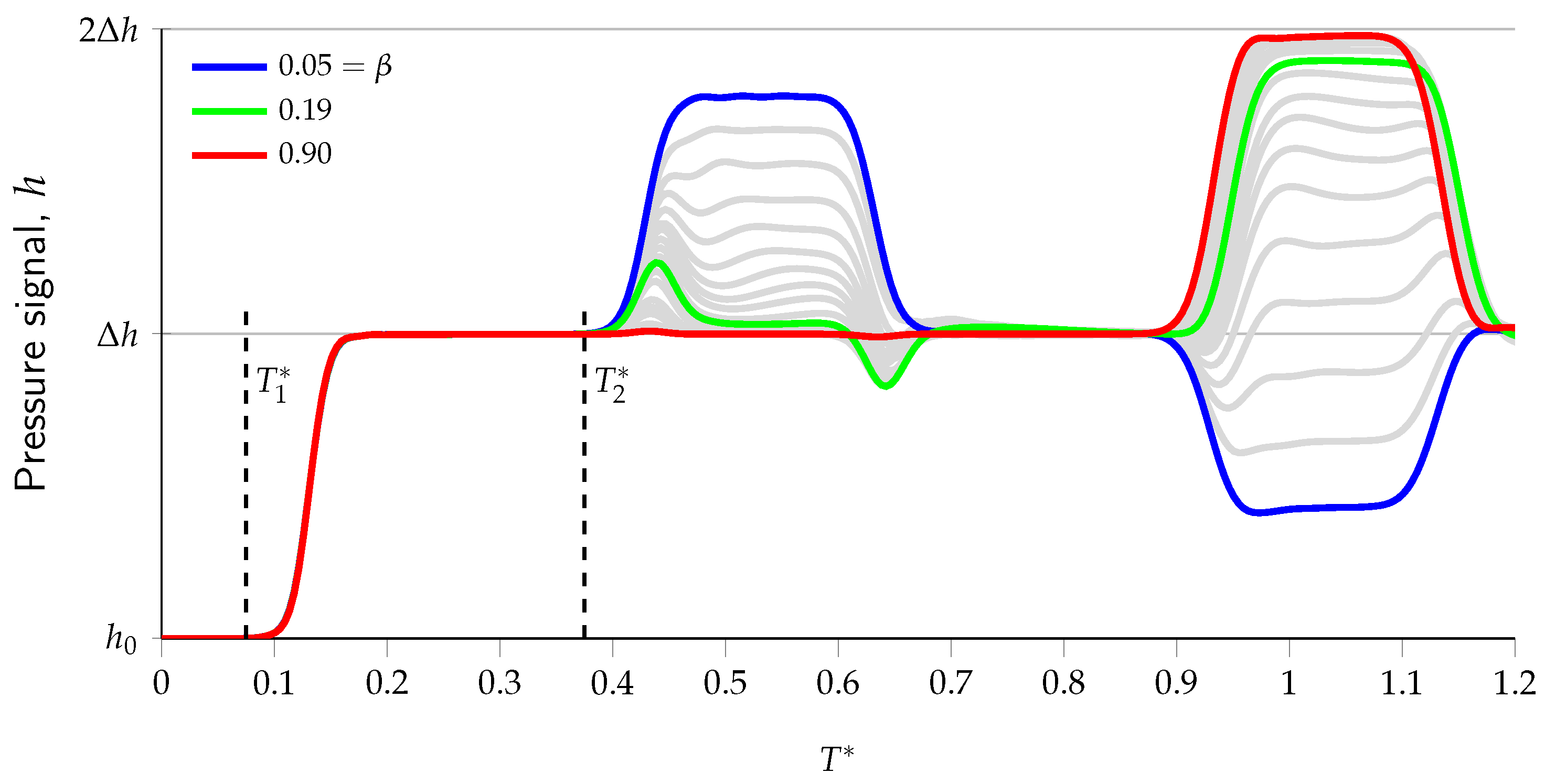
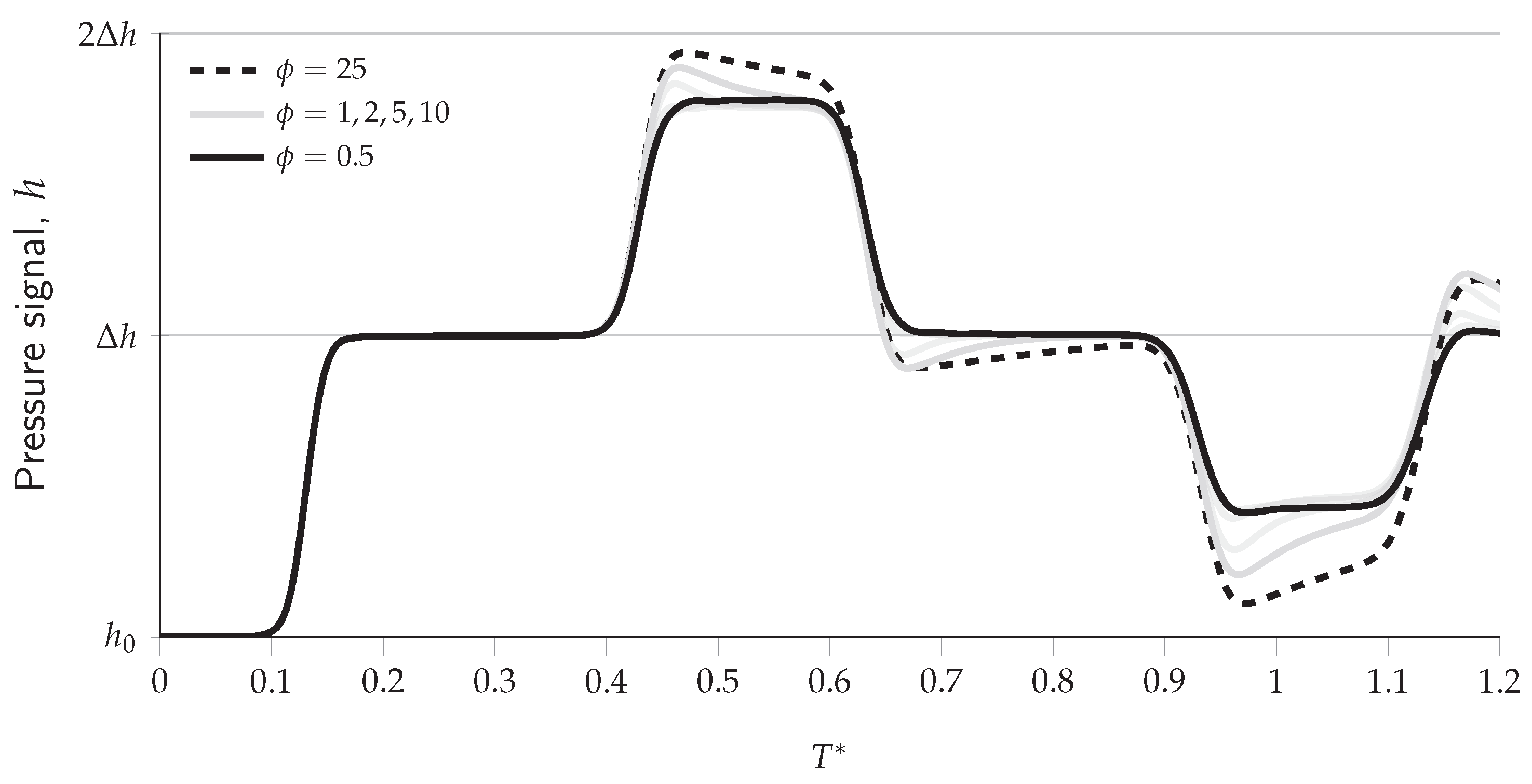
3.1. Role of EPB Severity in the Transient Response
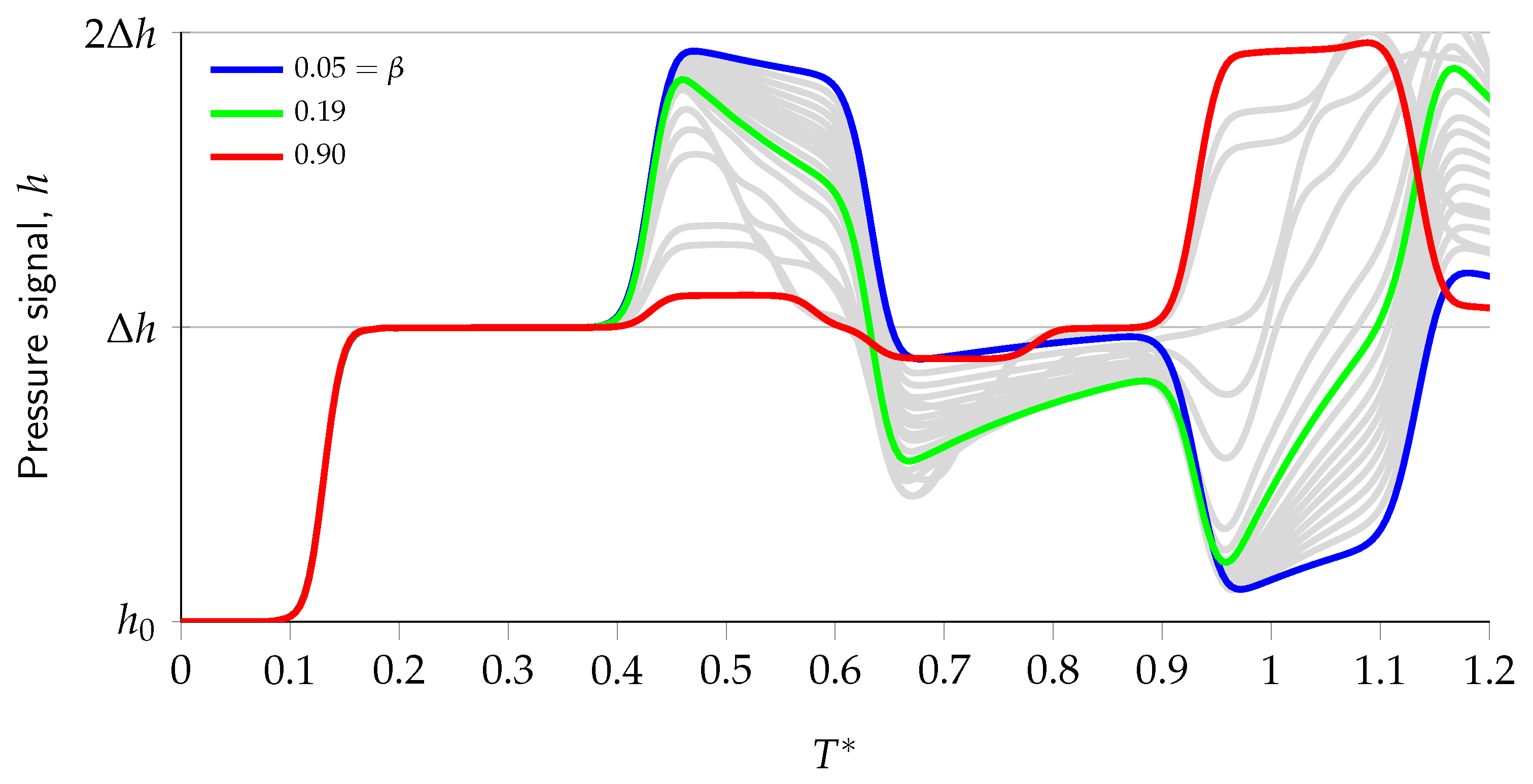
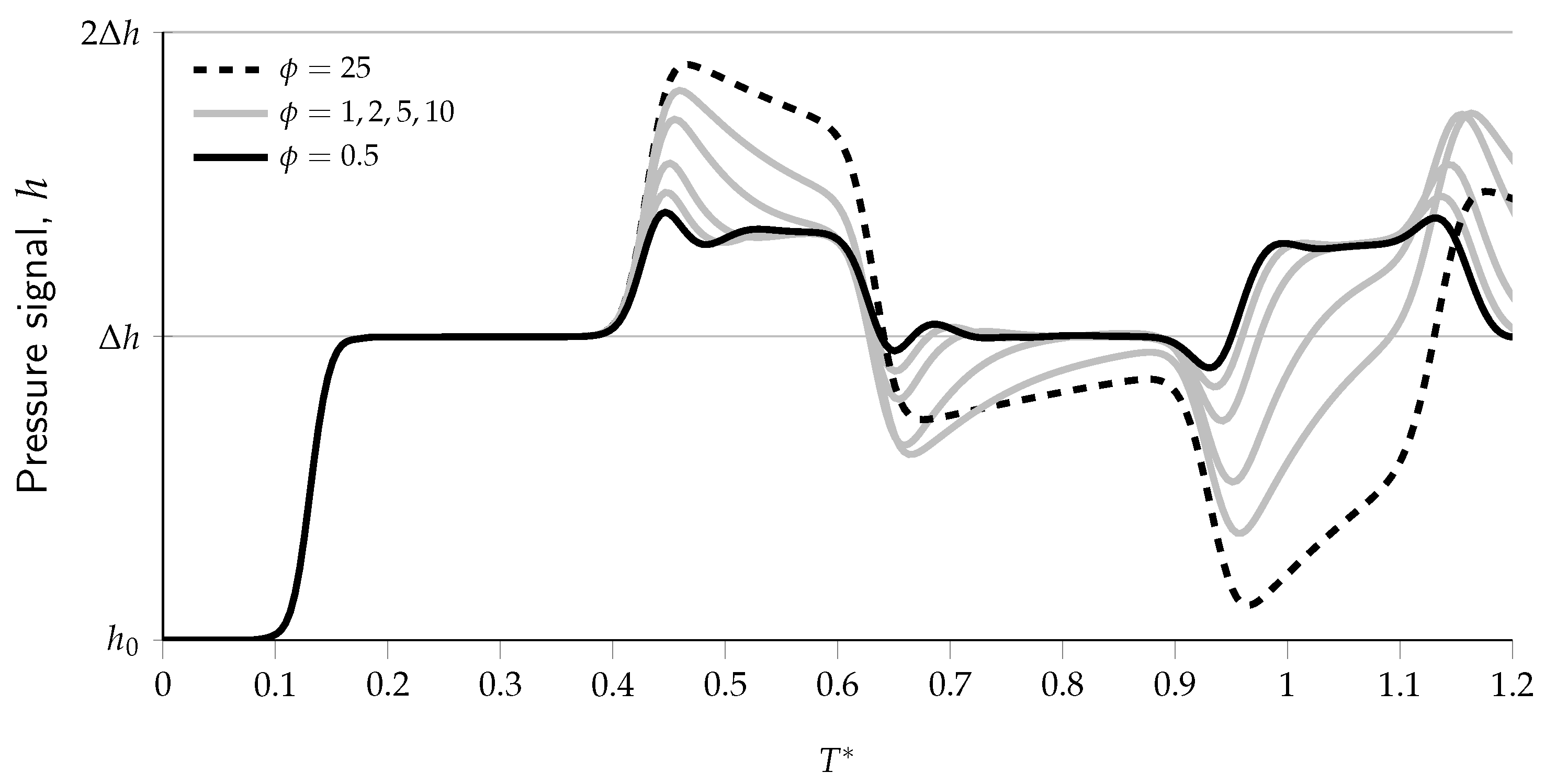
3.2. Role of EPB Length in the Transient Response
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Li, C.; Zhang, Y.; Jia, W.; Hu, X.; Song, S.; Yang, F. Blockage detection techniques for natural gas pipelines: A review. Gas Sci. Eng. 2024, 122, 205187. [Google Scholar] [CrossRef]
- Rosińska, W.; Jurasz, J.; Przestrzelska, K.; Wartalska, K.; Kaźmierczak, B. Climate change’s ripple effect on water supply systems and the water-energy nexus—A review. Water Resour. Ind. 2024, 32, 100266. [Google Scholar] [CrossRef]
- Fan, Q.; Zhan, J.; Hu, W.; Huang, Z. Effects of orifice size on the efficiency of a heaving oscillating water column. Eng. Appl. Comput. Fluid Mech. 2022, 16, 666–676. [Google Scholar] [CrossRef]
- Li, D.; Wang, C.; Ju, P.; Han, G.; Jin, D.; Wen, J. Effect of the number of orifice plate stages on cavitation characteristics. J. Phys. Conf. Ser. 2024, 2752, 012168. [Google Scholar] [CrossRef]
- Woolway, R.I.; Kraemer, B.M.; Lenters, J.D.; Merchant, C.J.; O’Reilly, C.M.; Sharma, S. Global lake responses to climate change. Nat. Rev. Earth Environ. 2020, 1, 388–403. [Google Scholar] [CrossRef]
- Bongioannini Cerlini, P.; Saraceni, M.; Silvestri, L.; Meniconi, S.; Brunone, B. Monitoring the water mass balance variability of small shallow lakes by an ERA5-Land reanalysis and water level measurement-based model. An application to the Trasimeno Lake, Italy. Atmosphere 2022, 13, 949. [Google Scholar] [CrossRef]
- Yakhot, V.; Bailey, S.C.C.; Smits, A.J. Scaling of global properties of turbulence and skin friction in pipe and channel flows. J. Fluid Mech. 2010, 652, 65–73. [Google Scholar] [CrossRef]
- Walski, T.; Chase, D.V.; Savic, D.; Grayman, W.; Beckwith, S.; Koelle, E. Advanced Water Distribution Modeling and Management; Haestad Press: Waterbury, CT, USA, 2003. [Google Scholar]
- Duan, H.F.; Lee, P.J.; Che, T.C.; Ghidaoui, M.S.; Karney, B.W.; Kolyshkin, A.A. The influence of non-uniform blockages on transient wave behavior and blockage detection in pressurized water pipelines. J. Hydro-Environ. Res. 2017, 17, 1–7. [Google Scholar] [CrossRef]
- Duan, H.F.; Lee, P.J.; Kashima, A.; Lu, J.; Ghidaoui, M.S.; Tung, Y.K. Extended blockage detection in pipes using the system frequency response: Analytical analysis and experimental verification. J. Hydraul. Eng. 2013, 139, 763–771. [Google Scholar] [CrossRef]
- Olajire, A.A. Review of wax deposition in subsea oil pipeline systems and mitigation technologies in the petroleum industry. Chem. Eng. J. Adv. 2021, 6, 100104. [Google Scholar] [CrossRef]
- Duan, X.; Shi, B.; Wang, J.; Song, S.; Liu, H.; Li, X.; Chen, Y.; Liao, Q.; Gong, J.; Chen, S.; et al. Simulation of the hydrate blockage process in a water-dominated system via the CFD-DEM method. J. Nat. Gas Sci. Eng. 2021, 96, 104241. [Google Scholar] [CrossRef]
- Duan, X.; Shi, B.; Ruan, C.; Jia, J.; Song, S.; Liao, Q.; Chen, Y.; Chen, S.; Wang, J.; Yao, H.; et al. Quantitative assessment of hydrate blockage risk in pipelines based on reliability theory. J. Nat. Gas Sci. Eng. 2022, 98, 104345. [Google Scholar] [CrossRef]
- Escarameia, M. Air Problems in Pipelines—A Design Manual; HR Wallingford Ltd.: Oxford, UK, 2005; p. 49. [Google Scholar]
- Mays, L.W. Water Distribution Systems Handbook; Mays, L.W., Ed.; McGraw-Hill: New York, NY, USA, 2000. [Google Scholar]
- Boulos, P.; Lansey, K.; Karney, B. Comprehensive Water Distribution Systems Analysis Handbook for Engineers and Planners, 2nd ed.; MWH Soft: Pasadena, CA, USA, 2006. [Google Scholar]
- Soini, S.; Koskinen, K.; Vilenius, M.; Puhakka, J. Effects of fluid-flow velocity and water quality on planktonic and sessile microbial growth in water hydraulic system. Water Res. 2002, 36, 3812–3820. [Google Scholar] [CrossRef] [PubMed]
- Likitha, J.; Savitha, M.; Karthik, M.; Kavya, P.; Usha, G. CFD analysis on different shapes of concentric orifice plate for turbulent flow. Int. J. Eng. Res. Technol. 2018, 7, 421–426. [Google Scholar]
- Zain, R.; Terry, A.; Dahing, N.S.; Yusoff, N.; Yahya, R.; Dahing, L.N.S.; Rahman, M.; Mustapha, I.; Hassan, N.; Chik, E.; et al. Technical aspect on procedure of gamma-ray pipeline inspection. In Proceedings of the Nuclear Technical Convention 2015 (NTC 2015), Bangi, Malaysia, 3–5 November 2015; pp. 1–5. [Google Scholar]
- Rogers, L. Pipeline blockage location by strain measurement using a ROV. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 1–4 May 1995. [Google Scholar] [CrossRef]
- Qunli, W. Reconstruction of blockage in a duct from single spectrum. Appl. Acoust. 1994, 41, 229–236. [Google Scholar] [CrossRef]
- Qunli, W.; Fricke, F. Estimation of blockage dimensions in a duct using measured eigenfrequency shifts. J. Sound Vib. 1989, 133, 289–301. [Google Scholar] [CrossRef]
- Brunone, B.; Capponi, C.; Meniconi, S. Design criteria and performance analysis of a smart portable device for leak detection in water transmission mains. Measurement 2021, 183, 109844. [Google Scholar] [CrossRef]
- Meniconi, S.; Brunone, B.; Tirello, L.; Rubin, A.; Cifrodelli, M.; Capponi, C. Transient tests for checking the Trieste subsea pipeline: Toward field tests. J. Mar. Sci. Eng. 2024, 12, 374. [Google Scholar] [CrossRef]
- Meniconi, S.; Brunone, B.; Tirello, L.; Rubin, A.; Cifrodelli, M.; Capponi, C. Transient tests for checking the Trieste subsea pipeline: Diving into fault detection. J. Mar. Sci. Eng. 2024, 12, 391. [Google Scholar] [CrossRef]
- Kim, S. Inverse transient analysis for a branched pipeline system with leakage and blockage using impedance method. Procedia Eng. 2014, 89, 1350–1357. [Google Scholar] [CrossRef]
- Kim, D.S.; Shin, S.; Choi, G.B.; Jang, K.H.; Suh, J.C.; Lee, J.M. Diagnosis of partial blockage in water pipeline using support vector machine with fault-characteristic peaks in frequency domain. Can. J. Civ. Eng. 2017, 44, 707–714. [Google Scholar] [CrossRef]
- Mohapatra, P.K.; Chaudhry, M.H. Frequency responses of single and multiple partial pipeline blockages. J. Hydraul. Res. 2011, 49, 263–266. [Google Scholar] [CrossRef]
- Guo, X.; Zhao, L.; Cao, Z.; Deng, J. The development and application of transient-based leak detection methods in pressurized liquid pipelines: A review. Measurement 2025, 257, 118867. [Google Scholar] [CrossRef]
- Ayati, A.H.; Haghighi, A.; Lee, P.J. Statistical review of major standpoints in hydraulic transient-based leak detection. J. Hydraul. Struct. 2019, 5, 1–26. [Google Scholar] [CrossRef]
- Colombo, A.F.; Lee, P.; Karney, B.W. A selective literature review of transient-based leak detection methods. J. Hydro-Environ. Res. 2009, 2, 212–227. [Google Scholar] [CrossRef]
- Xu, X.; Karney, B. An overview of transient fault detection techniques. In Modeling and Monitoring of Pipelines and Networks: Advanced Tools for Automatic Monitoring and Supervision of Pipelines; Verde, C., Torres, L., Eds.; Applied Condition Monitoring; Springer International Publishing: Berlin/Heidelberg, Germany, 2017; pp. 13–37. [Google Scholar] [CrossRef]
- Brunone, B.; Ferrante, M.; Meniconi, S. Discussion of “Detection of partial blockage in single pipelines” by P. K. Mohapatra, M. H. Chaudhry, A. A. Kassem, and J. Moloo. J. Hydraul. Eng. 2008, 134, 872–874. [Google Scholar] [CrossRef]
- Martins, N.M.C.; Covas, D.I.C.; Brunone, B.; Meniconi, S.; Capponi, C. Transient response of discrete partial blockages in laminar pressurized flow: Insights into pressure and velocity variations by Computational Fluid Dynamics. Phys. Fluids 2024, 36, 106112. [Google Scholar] [CrossRef]
- Jasak, H. OpenFOAM: Open Source CFD in Research and Industry. Technical Report, International Workshop on Coupled Methods in Numerical Dynamics, 2009. Available online: https://openfoam.org (accessed on 1 January 2025).
- Weller, H.G.; Tabor, G.; Jasak, H.; Fureby, C. A tensorial approach to computational continuum mechanics using object-oriented techniques. Comput. Phys. 1998, 12, 620–631. [Google Scholar] [CrossRef]
- Yang, L.; Fu, H.; Liang, H.; Wang, Y.; Han, G.; Ling, K. Detection of pipeline blockage using lab experiment and computational fluid dynamic simulation. J. Pet. Sci. Eng. 2019, 183, 106421. [Google Scholar] [CrossRef]
- Denton, J.D.; Dawes, W.N. Computational Fluid Dynamics for turbomachinery design. Proc. Inst. Mech. Eng. Part J. Mech. Eng. Sci. 1998, 213, 107–124. [Google Scholar] [CrossRef]
- Fay, J.A. Introduction to Fluid Mechanics; MIT Press: London, UK, 1994. [Google Scholar]
- White, F.M. Viscous Fluid Flow, 2nd ed.; McGraw-Hill: Columbus, OH, USA, 1991. [Google Scholar]
- Martins, N.M.C.; Covas, D.I.C.; Meniconi, S.; Capponi, C.; Brunone, B. Hydrodynamics of laminar pipe flow through an extended partial blockage by CFD. J. Hydroinform. 2023, 25, 2268–2280. [Google Scholar] [CrossRef]
- Martins, N.M.C.; Covas, D.I.C.; Capponi, C.; Meniconi, S.; Brunone, B. Unified approach for damping rate of transient laminar flow: Experiments, Computational Fluid Dynamics, one-dimensional, and global models. J. Fluids Eng. 2024, 146, 1–32. [Google Scholar] [CrossRef]
- Chaudhry, M.H. Applied Hydraulic Transients, 3rd ed.; Springer: New York, NY, USA, 2014. [Google Scholar] [CrossRef]
- Acharya, S.; Baliga, B.R.; Karki, K.; Murthy, J.Y.; Prakash, C.; Vanka, S.P. Pressure-Based Finite-Volume Methods in Computational Fluid Dynamics. J. Heat Transf. 2007, 129, 407–424. [Google Scholar] [CrossRef]
- Ushakova, O.V. Advances in Grid Generation; Nova Science Publishers Inc.: Hauppauge, NY, USA, 2007. [Google Scholar]
- Martins, N.M.C.; Carriço, N.J.G.; Ramos, H.M.; Covas, D.I.C. Velocity distribution in pressurized pipe flow using CFD: Accuracy and mesh analysis. Comput. Fluids 2014, 105, 218–230. [Google Scholar] [CrossRef]
- Oh, H.W. Applied Computational Fluid Dynamics; IntechOpen: London, UK, 2012. [Google Scholar]
- Zampaglione, D. Sul moto di una corrente laminare attraverso diaframmi. L’Energia Elettr. 1969, 66, 821–828. (In Italian) [Google Scholar]
- Johansen, F.C. Flow through pipe orifices at low Reynolds numbers. Proc. R. Soc. London Ser. 1997, 126, 231–245. [Google Scholar] [CrossRef]
- Hasegawa, T.; Suganuma, M.; Watanabe, H. Anomaly of excess pressure drops of the flow through very small orifices. Phys. Fluids 1997, 9, 1–3. [Google Scholar] [CrossRef]
- Sahin, B.; Ceyhan, H. Numerical and experimental analysis of laminar flow through square-edged orifice with variable thickness. Trans. Inst. Meas. Control 1996, 18, 166–174. [Google Scholar] [CrossRef]
- Jankowski, T.A.; Schmierer, E.N.; Prenger, F.C.; Ashworth, S.P. A series pressure drop representation for flow through orifice tubes. J. Fluids Eng. 2008, 130, 1–7. [Google Scholar] [CrossRef]
- Kiljanski, T. Discharge coefficient for free jets from orifices at low Reynolds number. J. Fluids Eng. 1993, 115, 778–781. [Google Scholar] [CrossRef]
- Alvi, S.H.; Sridharan, K.; Lakshmana Rao, N.S. Loss characteristics of orifices and nozzles. J. Fluids Eng. 1978, 100, 299–307. [Google Scholar] [CrossRef]
- Martins, N.M.C.; Covas, D.I.C.; Meniconi, S.; Capponi, C.; Brunone, B. Characterisation of low-Reynolds number flow through an orifice: CFD results vs. laboratory data. J. Hydroinform. 2021, 23, 709–723. [Google Scholar] [CrossRef]
- Martins, N.M.C.; Brunone, B.; Meniconi, S.; Ramos, H.M.; Covas, D.I.C. CFD and 1D approaches for the unsteady friction analysis of low Reynolds number turbulent flows. J. Hydraul. Eng. 2017, 143, 04017050. [Google Scholar] [CrossRef]
- Brunone, B.; Maietta, F.; Capponi, C.; Duan, H.F.; Meniconi, S. Detection of partial blockages in pressurized pipes by transient tests: A review of the physical experiments. Fluids 2023, 8, 19. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Martins, N.M.C.; Covas, D.I.C.; Brunone, B.; Meniconi, S.; Capponi, C. CFD-Based Transient Analysis for the Detection and Characterisation of Extended Partial Blockages in Pipes. Fluids 2025, 10, 291. https://doi.org/10.3390/fluids10110291
Martins NMC, Covas DIC, Brunone B, Meniconi S, Capponi C. CFD-Based Transient Analysis for the Detection and Characterisation of Extended Partial Blockages in Pipes. Fluids. 2025; 10(11):291. https://doi.org/10.3390/fluids10110291
Chicago/Turabian StyleMartins, Nuno M. C., Dídia I. C. Covas, Bruno Brunone, Silvia Meniconi, and Caterina Capponi. 2025. "CFD-Based Transient Analysis for the Detection and Characterisation of Extended Partial Blockages in Pipes" Fluids 10, no. 11: 291. https://doi.org/10.3390/fluids10110291
APA StyleMartins, N. M. C., Covas, D. I. C., Brunone, B., Meniconi, S., & Capponi, C. (2025). CFD-Based Transient Analysis for the Detection and Characterisation of Extended Partial Blockages in Pipes. Fluids, 10(11), 291. https://doi.org/10.3390/fluids10110291








