Abstract
The mechanical stability of carbon aerogels, particularly their thermal insulation performance, is closely linked to their elastic modulus. This property plays a crucial role in determining the material’s overall mechanical stability. The objective of this study is to enhance the accuracy of elastic modulus predictions for carbon aerogels using a power-scaling model. By setting the prefactor of the Gibson and Ashby equation to 1.0, accurate predictions of the elastic modulus can be achieved if the correct scaling exponent is determined. Twelve sets of experimental data were used to fit the power-scaling model, revealing that the scaling exponent for the elastic modulus of carbon aerogels typically falls between 2.2 and 3.0. This range is narrower than the 2.0 to 4.0 range reported in the literature, with a median value of 2.6 providing reliable predictions. Additionally, a relationship between the solid thermal conductivity and the elastic modulus of carbon aerogels was established using a thermal conduction model. The study also examined the elastic modulus of carbon nanotube and graphene aerogels—both allotropes of carbon aerogel. By fitting experimental data into the power-scaling model, the scaling exponents for carbon nanotube aerogels and graphene aerogels were found to range from 2.7 to 3.5 and 2.7 to 3.7, respectively. Median exponent values of 3.1 and 3.2 were identified as optimal for predicting the elastic moduli of carbon nanotube and graphene aerogels.
1. Introduction
Like silica aerogels, carbon aerogels also exhibit low density, large specific surface area and high porosity, and their particular physical and chemical properties also make them multifunctional materials for many applications, such as electrochemistry, energy storage, adsorption, thermal insulation, catalysis, and medical treatment [1,2,3]. Among these usages, carbon aerogels are very worthy as super thermal insulation materials due to their low thermal conductivity and good thermal stability under non-oxidizing environments [4,5,6]. The low thermal conductivity of carbon aerogels can be attributed to its special nanoporous structure displaying a complex three-dimensional network skeleton consisting of random interconnected carbon nanoparticles, which can significantly suppress thermal conduction via the gas and solid phases of the material [7,8]. However, this structure cannot bond the carbon nanoparticles effectively, and results in poor mechanical properties, such as elastic modulus, compress strength, yield strength, and toughness [8,9,10]. Therefore, when carbon aerogels are used as thermal insulation material, analyses of the overall performance of the insulation material should consider both the thermal conductivity and mechanical properties, and the mechanical stability is the foundation for the non-failure of the thermal insulation material.
Many studies have focused on the heat-transfer mechanism in aerogels. Theoretical studies, experimental tests, and numerical simulations of thermal conductivity have been carried out, and accurate theoretical models of heat transfer in aerogels have been established, which can achieve optimal designs of the material and improve the performance of the thermal insulation [7,8,11,12,13,14]. To ensure the mechanical stability of aerogels, extensive efforts were devoted to investigating the mechanical properties to strengthen the mechanical stability of the aerogels, such as elastic modulus, compressive strength, yield strength, sound velocity, stiffness [3,5,8,15,16,17,18,19].
The elastic modulus of carbon aerogels reflects the ability of the resistance of the material to the elastic deformation, which is one of the most concerned mechanical properties when high stress concentration occurs in the material. Most of the above studies on the elastic modulus of carbon aerogels were experimental tests and numerical simulations, and the obtained elastic modulus data were relatively scattered, which cannot match the theoretical models well and cannot help in obtaining accurate predictions. Due to the convenience and simple calculation, the power-scaling model of porous material, which was proposed by Gibson and Ashby [20] in 1982, has been frequently used for calculating the mechanical properties of the aerogels, and can be used to predict many properties, such as elastic moduli, sound velocity, yield strength, collapse strength, and even thermal and electric conductivity [21]. However, for the elastic modulus of carbon aerogels, the scaling exponent in Gibson and Ashby’s formula is often distributed in a wide range, and may lead to significant deviations among the predictions. The wide range of the scaling exponent of the elastic modulus for carbon aerogels may be attributed to the following factors: (1) different ratios of sp2 to sp3 hybridized bonds in amorphous carbon lead to different properties under the same density [22,23,24], and (2) due to the brittleness of carbon aerogels, the mechanical experiment may easily cause damage to the material, which will result in fluctuations in the tests of the elastic modulus. Therefore, it is necessary to obtain an accurate scaling exponent as well as a narrow distribution range to improve the prediction accuracy of the power-scaling model, and finally provide theoretical guidance for the design of mechanical properties of carbon aerogels.
The aim of this work is to narrow the scaling exponent range of the carbon aerogel elastic modulus, and then improve the prediction accuracy of the power-scaling model. In this study, the scaling exponent range of the carbon aerogel elastic modulus is obtained by the fittings of the experimental data, and the data are employed in two ways: (1) we directly cite open experimental data in the literature (mechanical experiments), which may contain some “destructive” factors, and (2) indirectly convert from the experimental values of the thermal conductivity, where the conversion method can be regarded as a “non-destructive” test method for the aerogel elastic modulus proposed in the authors’ previous work [25]. By comparing and analyzing the results of the two groups of data, we can obtain the expected results. In addition, carbon nanotube and graphene are the two most interesting carbon allotropes, and the corresponding aerogels named carbon nanotube aerogel and graphene aerogel also belong to the class of the carbon aerogels, so the elastic modulus of these two types of carbon aerogels will be also discussed in this study. For convenience, the carbon aerogel in this study specially denotes the traditional aerogel, i.e., amorphous porous material of carbon particle assembly.
2. Results and Discussion
2.1. Validation of Thermal Conduction Model of Elastic Modulus of Carbon Aerogels
In this section, three groups of available data of carbon aerogels are employed to validate the thermal conduction model of elastic modulus. The first case is to examine Equation (5) by the data of the “R/C = 200” carbon aerogels in Ref. [26]. Figure 1a shows the measured data of the effective thermal conductivity (solid symbols) and the solid thermal conductivity (open symbols) of the carbon aerogels, where the solid thermal conductivity as the input parameter of Equation (5) was extracted from the effective thermal conductivity by the heat transfer model of Equation (6).
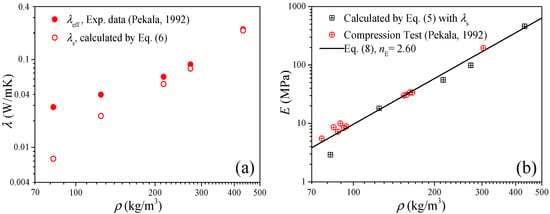
Figure 1.
Validation of the thermal conduction model of the elastic modulus of Equation (5). (a) Thermal conductivity as the input parameters. (b) Elastic modulus as the results (room temperature).
Figure 1b shows the comparison between the experimental data and the predictions of Equation (5), and good agreements can be observed as ρ > 120 kg/m3. For ρ < 100 kg/m3, we can find some large deviations between the experimental data and predictions from Equation (5), and these deviations may be attributed to two factors: (1) for low-density aerogels, the compression test may easily cause some damage to the material, which will lead to a few test fluctuations; and (2) since the elastic modulus depends on the bulk sound velocity and density, for low-density carbon aerogel (atmospheric pressure), the air density will be not neglected compared with the carbon aerogel, and the sound velocity is lower than that of the air (about 340 m/s); therefore, the elasticity of the air will have a certain impact on the elasticity test [27]. In addition, the solid line in Figure 1b is fitted by Equation (8) based on the experimental data and predictions (discussed in Section 2.2), and under the guidance of this straight line, we can believe that the solid thermal conductivity can obtain accurate predictions for the elastic modulus of the carbon aerogels.
The second example is to validate Equation (4) with the data of low-density and high-density carbon aerogels published in Refs. [5,28], respectively. In this case, the elastic modulus is the input parameter, and the solid thermal conductivity will be the prediction results. The experimental data of the carbon aerogel elastic modulus are revisited as shown in Figure 2a. Figure 2b shows the comparison between the experimental data of the solid thermal conductivity and the calculations of Equation (4), where the experimental data were extracted from the measured effective thermal conductivity by the heat-transfer model of Equation (6). For low-density carbon aerogels, good agreements exist under ρ > 100 kg/m3, and the deviation increases as the density decreases. For high-density carbon aerogels, the predictions agree well with the experimental data.
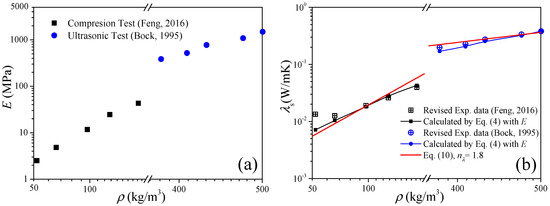
Figure 2.
Validation of the thermal conduction model of elastic modulus of Equation (4). (a) Elastic modulus as the input parameter. (b) Solid thermal conductivity as the results (room temperature).
From the above two validation examples of Equations (4) and (5), we can conclude that the thermal conduction model of the elastic modulus is suitable for the calculation of the solid thermal conductivity and elastic modulus of carbon aerogels, which is expected to be an alternative test method for the elastic modulus of high-density fragile aerogels.
2.2. Power-Scaling Model of Elastic Modulus of Carbon Aerogels
The power-scaling model is a highly favored model to predict the physical properties of the porous material due to its simple form and convenience of calculation, and in this section we focus on the power-scaling exponent (i.e., nE in Equation (8)) distribution interval as well as its median value by analysis of the available data of the elastic modulus of carbon aerogels. Figure 3a shows the open data [26,29,30,31,32] of the thermal conductivity of carbon aerogels, in which the data of the solid thermal conductivity (λs) were extracted from the experimental data of the effective thermal conductivity (λeff) by the heat-transfer model of Equation (6). Figure 3b shows the elastic modulus converted from the solid thermal conductivity by Equation (5). In the log–log coordinates, the elastic modulus increases approximately linearly with the increase in the density, and this indicates the power exponential function of Equation (8) can definitely describe the relation between the elastic modulus and the solid thermal conductivity. By fitting the data, the upper and lower limits as well as the median value of the exponent can be obtained, i.e., nE ∈ [2.3, 2.95] with an arithmetic mean value of 2.625.
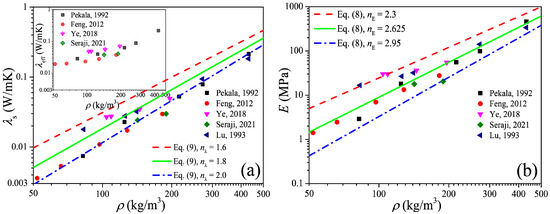
Figure 3.
Elastic modulus of carbon aerogels converted from experimental thermal conductivity. (a) Thermal conductivity. (b) Elastic modulus.
Figure 4 shows the measured data of the elastic modulus of the carbon aerogels in the literature [1,5,8,28,33,34,35], and an approximated linear relation between the elastic modulus and density can also be observed in the log–log coordinates. Fitting the data in Figure 4 as the form of Equation (8), we can obtain nE ∈ [2.2, 3.0] with a mean value of 2.6, of which the distribution interval as well as the median value is very close to that obtained from Figure 3b. According to Figure 3b and Figure 4, we can conclude that the elastic modulus of carbon aerogels is mostly distributed in the range of E0(ρ/ρ0)3.0 ≤ E ≤ E0(ρ/ρ0)2.2, and the relation of E = E0(ρ/ρ0)2.6 can be used to estimate the elastic modulus for most carbon aerogels, such as the good predictions in Figure 1b.
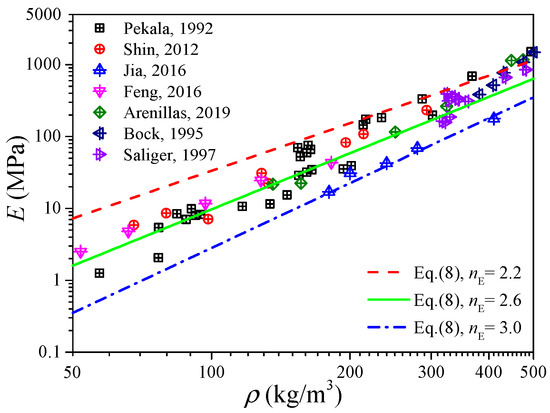
Figure 4.
Experimental elastic modulus of carbon aerogel.
2.3. Relation of Solid Thermal Conductivity and Elastic Modulus of Carbon Aerogels
To validate Equation (10), we substitute the median value of nE = 2.6 obtained in Section 2.2 into Equation (10), and we have nλ = 1.8. In Figure 1b and Figure 2b, good predictions also can be observed when ρ > 100 kg/m3, which is consistent with the results in Section 2.1. Furthermore, substituting nE ∈ [2.2, 3.0] into Equation (10), we can obtain nλ ∈ [1.6, 2.0], and in Figure 3a we can see that most of the experimental data of solid thermal conductivity are distributed between the predictions of λ0(ρ/ρ0)2.0 and λ0(ρ/ρ0)1.6, which also indicates that Equation (10) reflects the relationship between the elastic modulus and solid thermal conductivity of carbon aerogels and can be used to accurately predict the solid thermal conductivity of carbon aerogels.
2.4. Elastic Modulus of Carbon Nanotube Aerogels and Graphene Aerogels
Carbon nanotube aerogel (CNTA) and graphene aerogel (GA) are the two most interesting carbon-based aerogels due to their good electrical conductivity and their having superior mechanical properties to those of the traditional carbon aerogel (CA). The structure of CNTA or GA presents a three-dimensional network of CNTs or graphene instead of an amorphous assembly network consisting of carbon nanoparticles, and the primary CNT or graphene unit with crystalline nature enhances the mechanical properties of the network significantly compared with CA [2,3]. In this section, we focus on obtaining a scaling model as the form of Equation (8) for accurately predicting the elastic modulus of CNTA and GA. Similar to Section 2.2, the scaling exponent interval of CNTA and GA will also be derived by an analysis of available data in the literature, and then the median value of the upper and lower limits will be regarded as the value of the scaling exponent in Equation (8).
Since the carbon nanotube can be viewed as a graphene sheet coiled into seamless tubes, and also their values of mechanical properties are very close (see Table 1), the CNTA and GA can be regarded as a class of materials from the view of elastic modulus predictions by Equation (8). Figure 5 shows the experimental data of the elastic modulus of the CNTA and GA in the literature [33,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50], and the reference index is shown in Figure 6. By fitting the data in the form of Equation (8), like the CA, both the CNTA and GA present a linear relation between the density and elastic modulus in the log to log coordinates, and this proves that the power-scaling model also can be applicable to CNTA and GA. The relations of E = E0(ρ/ρ0)3.1 and E = E0(ρ/ρ0)3.2 may help us to predict the elastic modulus for the CNTA and GA, respectively.

Table 1.
Bulk properties for prediction of elastic modulus of carbon-based aerogels.
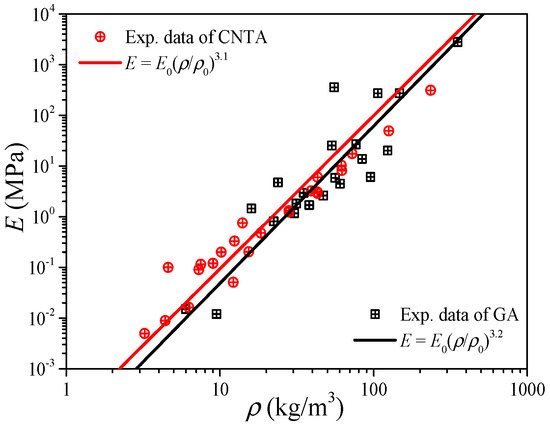
Figure 5.
Elastic modulus of carbon-based aerogel.
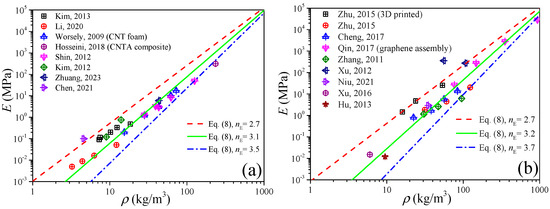
Figure 6.
Elastic modulus of CNTA and GA. (a) CNTA. (b) GA.
If from the perspective of material dimension, CNT is the one-dimensional material while graphene is the two-dimensional material, we still need to distinguish them. Figure 6a,b plot the elastic modulus of CNTA and GA, respectively. In Figure 6a, we can obtain that the exponent of CNTA is nE ∈ [2.7, 3.5], i.e., E0(ρ/ρ0)3.5 ≤ E ≤ E0(ρ/ρ0)2.7, while in Figure 6b we can observe that the elastic modulus of GA is distributed in the range of E0(ρ/ρ0)3.7 ≤ E ≤ E0(ρ/ρ0)2.7.
In addition, for low density, the predictions in Figure 6 are in good agreement with the experimental data, which is different from the deviations in Figure 1 and Figure 2, and this is because the bulk sound velocity of CNT and graphene is much higher than that of air, and under this condition the density effect will be less important than that of the sound velocity.
3. Conclusions
In this study, we investigated the elastic modulus of the carbon-based aerogels, and focused on improving the prediction accuracy of the power-scaling model for the elastic modulus of carbon-based aerogels. We set the prefactor of the Gibson and Ashby equation as C = 1.0, and then the key to improving the accuracy lies in obtaining an accurate exponent. Available experimental data in the literature were employed to fit relations as the form of the power-scaling model, and the exponent of carbon aerogels is mostly distributed in the range from 2.2 to 3.0, which is much narrower that the range of 2.0–4.0 reported in the literature. The median value of 2.6 was recommended as the exponent of the power-scaling model to predict the elastic modulus of carbon aerogels. The thermal conduction model of the elastic modulus of silica aerogels was also employed to predict the carbon aerogel elastic modulus, and the predictions agreed well with the experimental data, which proved that the thermal conduction model of elastic modulus is also suitable for the calculation of the solid thermal conductivity and elastic modulus of carbon aerogels. The relation between the solid thermal conductivity and elastic modulus of carbon aerogels was established in the form of a power-scaling model, and the exponents of solid thermal conductivity and elastic modulus can be expressed as nλ = (nE + 1)/2. The elastic modulus of the carbon nanotube and graphene aerogels as two allotropes of carbon aerogel was also discussed. Similar to the carbon aerogels, we still prefer the power-scaling model of the elastic modulus. The distribution intervals of carbon nanotube aerogels and graphene aerogels were about [2.7, 3.5] and [2.7, 3.7] fitted from the open experimental data, and the median values of 3.1 and 3.2 are recommended as the exponents in the scaling model to calculate the elastic modulus of the two types of carbon-based aerogels, respectively.
4. Materials and Methods
4.1. Definition of Elastic Modulus
Elastic moduli of solid materials include Yang’s modulus (E), shear modulus (G), and bulk modulus (K). In this study, the elastic modulus specifically refers to Young’s modulus, since the shear modulus and the bulk modulus can be deduced from Yang’s modulus [51]. The definition of E is the slope of the stress–strain curve in the elastic deformation during the mechanical tensile or compression test, i.e., σ = E·ε, where σ is the stress, and ε the elastic strain in the direction of principal stress. Due to the brittleness of the carbon aerogel, the elastic modulus is mostly measured by the mechanical compression test.
4.2. Elastic Mechanical Model of Elastic Modulus
Due to the high brittleness of carbon aerogels, the mechanical compression test of the elastic modulus may easily lead to some damage to the structure of the material, and thus large measurement errors may be brought in. An alternative method is to measure the sound velocity in the material, and then use the elastic mechanical model to calculate the elastic modulus, expressed by [52],
where vl is the longitudinal sound velocity, vt is the transverse sound velocity, ρ is the density, and μ is the Poisson’s ratio of the material. The sound velocity in aerogels can be measured by the ultrasonic echo method and the Brillouin scattering method [51].
4.3. Thermal Conduction Model of Elastic Modulus
According to the author’s previous work [25], the bridge between the elastic modulus and solid thermal conductivity of the silica aerogel is the sound velocity, and combining the scaling sound velocity model of the solid thermal conductivity [53],
with the elastic mechanical model Equations (1) and (2), we yield
and
where v is the average sound velocity approximated by v = 1/3vl + 2/3vt, v0 is the average sound velocity in the dense solid, λ0 is the thermal conductivity of the aerogel solid backbone (~the bulk value of the dense solid), and λs is the solid thermal conductivity which is the contribution of the thermal conductivity of the aerogel solid backbone to the effective thermal conductivity of the aerogel. Note that Equations (4) and (5) are the inverse operations between the elastic modulus and solid thermal conductivity. The solid thermal conductivity can be obtained by subtracting the gaseous thermal conductivity (λg), radiative thermal conductivity (λr), and coupling thermal conductivity (λc) from the effective thermal conductivity (λeff) of the aerogel [7],
where λeff can be directly measured by the thermal conductivity equipment, and λg, λc, and λr can be calculated by the heat transfer models. The gaseous thermal conductivity approximates to λg ≈ Cλg,free/(1 + 2βΛg/D), where λg,free is the thermal conductivity of the gas in free space, Λg is the mean free path of the gas molecules filled in the aerogel, D is the mean pore diameter of the aerogel (for carbon aerogels, D ≈ 333 exp(−ρ/86.8) + 37 fitted from the experimental data in Ref. [29]), β is a gas-dependent coefficient with β = 1.55 for air, and C is a correction coefficient with the consideration of the non-uniform pore size distribution effect, which is often in the range of 1.1–1.2 and one can use C = 1.15 for simple calculations. The coupling thermal conductivity can be accurately calculated by λc = 2/3λg when λ0 >> λg, such as silica aerogel, carbon aerogel, and alumina aerogel. The radiative thermal conductivity is as the functions of the density and temperature described by the photon-diffusion model, i.e., λg = 16σBT3/(3ρes), where σB is the Stefan–Boltzmann constant, and es is the specific Rossland mean extinction coefficient (for carbon aerogels, es ≈ 146 m3/kg [54]). Note that once the effective thermal conductivity of the aerogel is measured in a vacuum (p < 10 Pa) and at room temperature, the measured result can be regarded as the solid thermal conductivity. Although the thermal conduction model of elastic modulus was proposed based on the structure of silica aerogel, i.e., amorphous porous structure of silica particle assembly, it is still applicable to the traditional carbon aerogel due to its amorphous particle assembly porous structure, and the validation is described in Section 2.1.
4.4. Power-Scaling Model of Elastic Modulus of Porous Material
The power-scaling model of porous material was proposed by Gibson and Ashby in 1982 [20], and has been widely used to estimate many properties of porous materials due to its simple expression, given by,
where C is a constant (prefactor), ρ is the density of the porous material, x is the expected physical property, and subscript “0” denotes the bulk value of the dense solid. Equation (7) was proposed based on the foam structure modeling, and is applicable to the relative density of 0.01–1.0 [20], but it has also been proved to be applicable to amorphous porous carbon-based aerogels [36,48]. For the elastic modulus, when the density of the carbon aerogel approaches that of the dense carbon solid in theory, i.e., ρ/ρ0 = 1, which can be regarded as the boundary condition of Equation (7), we can believe that the elastic modulus of the aerogel is equal to the bulk value. Then, we can obtain C = 1.0 in Equation (7) and the elastic modulus can be written as
where nE is the power-scaling exponent of the elastic modulus which ranges from 2–4 for aerogels [51]. Note that, once the density of the aerogel is too low to neglect the effect of the air elasticity on the elastic modulus, we would obtain E > 0 and C ≠ 1 under the condition of ñ = 0. In the present study, C = 1 can be used for carbon aerogel under ñ > 100 kg/m3 as observed in Figure 1 and Figure 2. For CNTA and GA, the bulk sound velocity of CNT and graphene is much higher than that of the air, and under this condition the density effect will be less important than that of the sound velocity, so C = 1 can also be used for CNTA and GA, which is also proved in Refs. [36,48]. In addition, the range of nE is relatively wide, and this is not conducive to obtaining accurate predictions for the elastic modulus of carbon aerogels. For this reason, we prefer to narrow the range of the nE based on the analysis of the open data in the literature, and then take a reasonable mean value to obtain more accurate predictions.
4.5. Power-Scaling Model of Solid Thermal Conductivity of Carbon Aerogels
As mentioned in Section 4.3, the elastic modulus and solid thermal conductivity of aerogels can be predicted from each other under a given density. Once we obtain the scaling model of the elastic modulus of carbon aerogels, we also expect a scaling model to simplify the calculations of the solid thermal conductivity of carbon aerogels, and the scaling model based on the expression of Equation (7) can be written as below,
where nλ is the scaling exponent of the solid thermal conductivity of carbon aerogels. The parameter nλ can be deduced from nE by solving Equations (5), (8), and (9), and the simple derivation process is as follows: (1) Equations (5), (8), and (9) can be regarded as , , and , respectively; (2) making Equation (5) equal to Equation (8), we can obtain ; and (3) comparing with , the scaling exponent nλ can be expressed as,
4.6. Bulk Properties of Carbon Allotropes
Before the calculations of the carbon aerogel elastic modulus, the bulk properties of the dense carbon are necessary according to Equations (4), (5), and (8). In this work, the properties of amorphous carbon, single wall carbon nanotube, and monolayer graphene are used for the bulk values of the carbon aerogel, carbon nanotube aerogel, and graphene aerogel, respectively, and the related properties under room temperature are listed in Table 1. Note that, (1) for amorphous carbon, the values of density and thermal conductivity are taken from graphite [55], the elastic modulus adopts the value of glassy carbon [56], the average sound velocity is cited from Ref. [57], and the values of the longitude and transverse sound velocity are calculated by v = 1/3vl + 2/3vt with the approximation of vt ≈ 0.6vl; (2) for carbon nanotube, the value of the density takes the isolated single wall carbon nanotube [58], the elastic modulus is cited from Ref. [59], the thermal conductivity is from Ref. [60], and the sound velocities are the theoretical calculations in Ref. [61]; and (3) for the graphene, the elastic modulus and density are taken from Ref. [36], the thermal conductivity is from Ref. [62], and the sound velocities are the experimental data published in Ref. [63].
Author Contributions
Conceptualization, C.B.; methodology, C.B.; validation, M.Y., X.Y. and Y.Z.; writing—original draft preparation, C.B., K.Y. and Y.L.; writing—review and editing, C.B., M.Y., X.Y., K.Y., Y.L., Y.Z., J.Z. and M.D.; visualization, M.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Natural Science Basic Research Program of Shaanxi of China (Program No. 2024JC-YBMS-449), State Administration for Market Regulation Research Project of China (No. 2022MK165 and 2024MK174), the Postdoctoral Fellowship Program of CPSF of China (No. GZC20232066), Xi’an Science and Technology Plan Project of China (No. 24ZDCYISGG0045 and 24GXFW0038), and Shaanxi Province Technology Innovation Guidance Program of China (No. 2024QCY-KXJ-019), and Guangdong Basic and Applied Basic Research Foundation (No. 2024A1515011379 and 2023A1515110613).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding authors.
Conflicts of Interest
Ying Zhang was employed by the Xi’an Bright Laser Technologies Co., Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Pekala, R.W.; Alviso, C.T.; LeMay, J.D. Organic aerogels: Microstructural dependence of mechanical properties in compression. J. Non-Cryst. Solids 1990, 125, 67–75. [Google Scholar] [CrossRef]
- Worsley, M.A.; Baumann, T.F. Carbon Aerogels. In Handbook of Sol-Gel Science and Technology; Klein, L., Aparicio, M., Jitianu, A., Eds.; Springer International Publishing: Geneva, Switzerland, 2016; pp. 1–36. [Google Scholar]
- Aegerter, M.A.; Leventis, N.; Koebel, M.; Steiner, S.A., III. Springer Handbook of Aerogels; Series Springer Handbooks; Springer Nature Switzerland AG: Geneva, Switzerland, 2023; pp. 919–986. [Google Scholar]
- Wiener, M.; Reichenauer, G.; Braxmeier, S.; Hemberger, F.; Ebert, H.P. Carbon aerogel-based high-temperature thermal insulation. Int. J. Thermophys. 2009, 30, 1372–1385. [Google Scholar] [CrossRef]
- Feng, J.; Jiang, Y.G.; Feng, J.Z. Aerogel Material for Highly Efficient Thermal Insulation; China Science Press: Beijing, China, 2016; pp. 144–172. (In Chinese) [Google Scholar]
- Hu, L.; He, R.; Lei, H.; Fang, D. Carbon aerogel for insulation applications: A review. Int. J. Thermophys. 2019, 40, 1–25. [Google Scholar] [CrossRef]
- Tang, G.H.; Bi, C.; Zhao, Y.; Tao, W.Q. Thermal transport in nano-porous insulation of aerogel: Factors, models and outlook. Energy 2015, 90, 701–721. [Google Scholar] [CrossRef]
- Arenillas, A.; Menéndez, J.A.; Reichenauer, G.; Celzard, A.; Fierro, V.; Maldonado Hodar, F.J.; Bailόn-Garcia, E.; Job, N. Properties of carbon aerogels and their organic precursors. In Organic and Carbon Gels: From Laboratory Synthesis to Applications; Springer: Geneva, Switzerland, 2019; pp. 87–121. [Google Scholar]
- Araby, S.; Qiu, A.; Wang, R.; Zhao, Z.; Wang, C.H.; Ma, J. Aerogels based on carbon nanomaterials. J. Mater. Sci. 2016, 51, 9157–9189. [Google Scholar] [CrossRef]
- Patil, S.P.; Parale, V.G.; Park, H.H.; Markert, B. Mechanical modeling and simulation of aerogels: A review. Ceram. Int. 2021, 47, 2981–2998. [Google Scholar] [CrossRef]
- He, Y.L.; Xie, T. Advances of thermal conductivity models of nanoscale silica aerogel insulation material. Appl. Therm. Eng. 2015, 81, 28–50. [Google Scholar] [CrossRef]
- Zhu, C.Y.; Xu, H.B.; Zhao, X.P.; Gong, L. A review on heat transfer in nanoporous silica aerogel insulation materials and its modeling. Energy Storage Sav. 2022, 1, 217–240. [Google Scholar] [CrossRef]
- Lou, F.; Dong, S.; Zhu, K.; Chen, X.; Ma, Y. Thermal insulation performance of aerogel nano-porous materials: Characterization and test methods. Gels 2023, 9, 220. [Google Scholar] [CrossRef]
- Wang, C.; Bai, L.; Xu, H.; Qin, S.; Li, Y.; Zhang, G. A review of high-temperature aerogels: Composition, mechanisms, and properties. Gels 2024, 10, 286. [Google Scholar] [CrossRef]
- Lee, J.H.; Park, S.J. Recent advances in preparations and applications of carbon aerogels: A review. Carbon 2020, 163, 1–18. [Google Scholar] [CrossRef]
- Hsieh, T.H.; Huang, Y.S. The mechanical properties and delamination of carbon fiber-reinforced polymer laminates modified with carbon aerogel. J. Mater. Sci. 2017, 52, 3520–3534. [Google Scholar] [CrossRef]
- Yang, J.; Li, S.; Luo, Y.; Yan, L.; Wang, F. Compressive properties and fracture behavior of ceramic fiber-reinforced carbon aerogel under quasi-static and dynamic loading. Carbon 2011, 49, 1542–1549. [Google Scholar] [CrossRef]
- Li, L.; Feng, J.; Liu, F.; Li, L.; Jiang, Y.; Feng, J. Mechanical and thermal insulation properties of carbon fibre-reinforced carbon aerogel composites. Adv. Appl. Ceram. 2022, 121, 222–230. [Google Scholar] [CrossRef]
- Guo, F.; Yang, C.; Xu, Z.; Gao, C. Progress and perspective in mechanically robust carbon aerogels. J. Appl. Phys. 2022, 131, 110904. [Google Scholar] [CrossRef]
- Gibson, I.J.; Ashby, M.F. The mechanics of three-dimensional cellular materials. Proc. R. Soc. Lond. A Math. Phys. Sci. 1982, 382, 43–59. [Google Scholar]
- Abueidda, D.W.; Al-Rub, R.K.A.; Dalaq, A.S.; Lee, D.W.; Khan, K.A.; Jasiuk, I. Effective conductivities and elastic moduli of novel foams with triply periodic minimal surfaces. Mech. Mater. 2016, 95, 102–115. [Google Scholar] [CrossRef]
- Robertson, J. Amorphous carbon. Adv. Phys. 1986, 35, 317–374. [Google Scholar] [CrossRef]
- Uskoković, V. A historical review of glassy carbon: Synthesis, structure, properties and applications. Carbon Trends 2021, 5, 100116. [Google Scholar] [CrossRef]
- Giri, A.; Dionne, C.J.; Hopkins, P.E. Atomic coordination dictates vibrational characteristics and thermal conductivity in amorphous carbon. npj Comput. Mater. 2022, 8, 55. [Google Scholar] [CrossRef]
- Bi, C.; Tang, G.H.; He, C.B.; Yang, X.; Lu, Y. Elastic modulus prediction based on thermal conductivity for silica aerogels and fiber reinforced composites. Ceram. Int. 2022, 48, 6691–6697. [Google Scholar] [CrossRef]
- Pekala, R.W.; Alviso, C.T. Carbon aerogels and xerogels. MRS Online Proc. Libr. 1992, 270, 3–14. [Google Scholar] [CrossRef]
- Groβ, J.; Schlief, T.; Fricke, J. Ultrasonic evaluation of elastic properties of silica aerogel. Mater. Sci. Eng. A 1993, 168, 235–238. [Google Scholar] [CrossRef]
- Bock, V.; Nilsson, O.; Blumm, J.; Frike, J. Thermal properties of carbon aerogels. J. Non-Cryst. Solids 1995, 182, 233–239. [Google Scholar] [CrossRef]
- Lu, X.; Nilsson, O.; Fricke, J.; Pekala, R.W. Thermal and electrical conductivity of monolithic carbon aerogels. J. Appl. Phys. 1993, 73, 581–584. [Google Scholar] [CrossRef]
- Feng, J.; Feng, J.; Zhang, C. Thermal conductivity of low density carbon aerogels. J. Porous Mater. 2012, 19, 551–556. [Google Scholar] [CrossRef]
- Ye, C.; Zhang, R.; An, Z.; Wang, B. A machinable carbon aerogel conposite with a low thermal conductivity and enhanced mechnical properties. Adv. Appl. Ceram. 2018, 117, 468–475. [Google Scholar] [CrossRef]
- Seraji, M.M.; Arefazar, A. Thermal ablation-insulation performance, microstructural, and mechanical properties of carbon aerogel based lightweight heat shielding composites. Polym. Eng. Sci. 2021, 61, 1338–1352. [Google Scholar] [CrossRef]
- Shin, S.; Kucheyev, S.O.; Worsley, M.A.; Hamza, A.V. Mechanical deformation of carbon-nanotube-based aerogels. Carbon 2012, 50, 5340–5350. [Google Scholar] [CrossRef]
- Jia, X.; Dai, B.; Zhu, Z.; Wang, J.; Qiao, W.; Long, D.; Ling, L. Strong and machinable carbon aerogel monoliths with low thermal coductivity prepared via ambient pressure drying. Carbon 2016, 108, 551–560. [Google Scholar] [CrossRef]
- Saliger, R.; Bock, V.; Petricevic, R.; Tillostson, T.; Geis, S.; Fricke, J. Carbon aerogels from dilute catalysis of resorcinol with formaldehyde. J. Non-Cryst. Solids 1997, 221, 144–150. [Google Scholar] [CrossRef]
- Qin, Z.; Jung, G.S.; Kang, M.J.; Buehler, M.J. The mechnaics and design of a lightweihgt three-dimensional graphene assembly. Sci. Adv. 2017, 3, e1601536. [Google Scholar] [CrossRef]
- Kim, K.H.; Oh, Y.; Islam, M.F. Mechanical and thermal management characteristics of ultrahigh surface area single-walled carbon nanotube aerogels. Adv. Funct. Mater. 2013, 23, 377–383. [Google Scholar] [CrossRef]
- Li, M.; Gong, Q.; Cao, P.; Wang, H.; Qiao, J.; Yu, Y.; Lu, W.; Di, J.; Zhang, Z.; Zheng, L.; et al. Rational and wide-range tuning of CNT aerogel conductors with multifunctionalities. Nanoscale 2020, 12, 13771–13780. [Google Scholar] [CrossRef] [PubMed]
- Worsely, M.A.; Kucheyev, S.O.; Satcher, J.H.; Hamza, A.V.; Baaumann, T.F. Mechanically robust and electrically conductive carbon nanotube foams. Appl. Phys. Lett. 2009, 94, 073115. [Google Scholar] [CrossRef]
- Kim, K.H.; Oh, Y.; Islam, M.F. Graphene coating makes carbon nanotube aerogels superelastic and resistant to fatigue. Nat. Nanotechnol. 2012, 7, 562–566. [Google Scholar] [CrossRef]
- Zhuang, L.; Lu, D.; Zhang, J.; Guo, P.; Su, L.; Qin, Y.; Zhang, P.; Xu, L.; Niu, M.; Peng, K.; et al. Highly cross-linked carbon tube aerogels with enhanced elasticity and fatigue resistance. Nat. Commun. 2023, 14, 3178. [Google Scholar] [CrossRef]
- Chen, Y.W.; Zhan, H.; Wang, J.N. A direct foaming approach for carbon nanotube aerogels with ultra-low thermal conductivity and high mechanical stability. Nanoscale 2021, 13, 11878–11886. [Google Scholar] [CrossRef]
- Hosseini, H.; Kokabi, M.; Mousavi, S.M. Conductive bacterial cellulose/multiwall carbon nanotubes nanocomposite aerogel as a potentially flexible lightweight strain sensor. Carbohydr. Polym. 2018, 201, 228–235. [Google Scholar] [CrossRef]
- Zhu, C.; Han, Y.J.; Duoss, E.B.; Golobic, A.M.; Kuntz, J.D.; Spadaccini, C.M.; Worsley, M.A. Highly compressible 3D periodic graphene aerogel microlattices. Nat. Commun. 2015, 6, 6962. [Google Scholar] [CrossRef]
- Cheng, Y.; Zhou, S.; Hu, P.; Zhao, G.; Li, Y.; Zhang, X.; Han, W. Enhanced mechanical, thermal, and electric properties of graphene aerogel via supercritical ethanol drying and high-temperature thermal reduction. Sci. Rep. 2017, 7, 1439. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Sui, Z.; Xu, B.; Yue, S.; Luo, Y.; Zhan, W.; Liu, B. Mechanically strong and highly conductive graphene aerogel and its use as electrodes for electrochemical power sources. J. Mater. Chem. 2011, 21, 6494–6497. [Google Scholar] [CrossRef]
- Xu, Z.; Zhang, Y.; Li, P.; Gao, C. Strong, conductive, lightweight, neat graphene aerogel fibers with aligned pores. ACS Nano 2012, 6, 7103–7113. [Google Scholar] [CrossRef] [PubMed]
- Niu, L.; Xie, J.; Chen, P.; Li, G.; Zhang, X. Quasi-static compression properties of graphene aerogel. Diam. Relat. Mater. 2021, 111, 108225. [Google Scholar] [CrossRef]
- Xu, X.; Zhang, Q.; Yu, Y.; Chen, W.; Hu, H.; Li, H. Naturally dried graphene aerogels with superelasticity and tunable Poisson’s ratio. Adv. Mater. 2016, 28, 9223–9230. [Google Scholar] [CrossRef]
- Hu, H.; Zhao, Z.; Wan, W.; Gogotsi, Y.; Qiu, J. Ultralight and highly compressible graphene aerogels. Adv. Mater. 2013, 25, 2219–2223. [Google Scholar] [CrossRef]
- Woignier, T.; Primera, J.; Alaoui, A.; Despetis, F.; Calas-Etienne, S.; Faivre, A.; Duffours, L.; Levelut, C.; Etienne, P. Techniques for characterizing the mechanical properties of aerogels. J. Sol-Gel Sci. Technol. 2020, 93, 6–27. [Google Scholar] [CrossRef]
- Ensminger, D. Ultrasonic: Fundamentals, Technology, Applications; Marcel Dekker: New York, NY, USA, 1988. [Google Scholar]
- Nilsson, O.; Rüschenpöhler, G.; Gross, J.; Fricke, J. Correlation between thermal conductivity and elasto-mechanical properties of compressed porous media. High Temp. High Press. 1989, 21, 267–274. [Google Scholar]
- Feng, J.; Feng, J.; Jiang, Y.G.; Zhang, C.R. Ultralow density carbon aerogels with low thermal conductivity up to 2000 °C. Mater. Lett. 2011, 65, 3454–3456. [Google Scholar] [CrossRef]
- Holman, J.P. Heat Transfer, 10th ed.; China Machine Press: Beijing, China, 2011; p. 509. [Google Scholar]
- Manoharan, M.P.; Lee, H.; Rajagopalan, R.; Foley, H.C.; Haque, M.A. Elastic properties of 4-6 nm-thick glassy carbon thin films. Nanoscale Res. Lett. 2010, 5, 14–19. [Google Scholar] [CrossRef]
- Hrubesh, L.W.; Pekala, R.W. Thermal properties of organic and inorganic aerogels. J. Mater. Res. 1994, 9, 731–738. [Google Scholar] [CrossRef]
- Lu, Q.; Keskar, G.; Ciocan, R.; Rao, R.; Mathur, R.B.; Rao, A.M.; Larcom, L.L. Determination of carbon nanotube density by gradient sedimentation. J. Phys. Chem. B 2006, 110, 24371–24376. [Google Scholar] [CrossRef]
- Lu, J.P. Elastic properties of carbon nanotubes and nanoropes. Phys. Rev. Lett. 1997, 79, 1297–1300. [Google Scholar] [CrossRef]
- Han, Z.; Fina, A. Thermal conductivity of carbon nanotubes and their polymer nanocomposites: A review. Prog. Polym. Sci. 2011, 36, 914–944. [Google Scholar] [CrossRef]
- Saito, R.; Takeya, T.; Kimura, T.; Dresselhaus, G.; Dresselhaus, M. Raman intensity of single-wall carbon nanotubes. Phys. Rev. B 1998, 57, 4145. [Google Scholar] [CrossRef]
- Balandin, A.A.; Ghosh, S.; Bao, W.; Calizo, I.; Teweldebrhan, D.; Miao, F.; Lau, C.N. Superior thermal conductivity of single-layer graphene. Nano Lett. 2008, 8, 902–907. [Google Scholar] [CrossRef]
- Cong, X.; Li, Q.Q.; Zhang, X.; Lin, M.L.; Wu, J.B.; Liu, X.L.; Venezuela, P.; Tan, P.H. Probing the acoustic phonon dispersion and sound velocity of graphene by Raman spectroscopy. Carbon 2019, 149, 19–24. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).