Probabilistic Forecast for Real-Time Control of Rainwater Pollutant Loads in Urban Environments

Abstract

Advanced wastewater management systems are necessary to effectively direct severely contaminated initial rainwater runoff to the treatment facility only when pollutant concentrations are elevated during the initial flush event, thereby reducing the risk of water pollution caused by urban drainage systems. This necessitates the implementation of intelligent decision-making systems, forecasting, and monitoring. However, conventional “deterministic” forecasts are inadequate for making informed decisions in the presence of uncertainty regarding future values, despite the fact that a variety of modeling techniques have been employed to predict total suspended solids at specific locations. The literature contains a number of “probabilistic” forecasting approaches that take into account uncertainty. Among them, this paper proposes the Model Conditional Processor (MCP), which is well-known in hydrological, hydraulic, and climatological fields, to forecast the predictive probability density of total suspended solids based on one or more deterministic predictions. This is intended to address the issue. The decision to divert the first flush is subsequently guided by the predictive density and probabilistic thresholds. The effective implementation of the MCP approach is demonstrated in a real case study that is part of the USGS’s extensive and long-term stormwater monitoring initiative, based on observations of a real stormwater drainage system. The results obtained confirm that probabilistic approaches are suitable instruments for enhancing decision-making.

1. Introduction

The control of rainwater runoff in urban areas is a critical and complex issue. The development status of metropolitan regions, influenced by centuries of urbanization, does not always allow for the construction of a single reservoir to manage rainwater runoff. In this case, rainwater will be collected at a number of smaller reservoirs spread across the metropolitan basin. Flood control volumes in densely populated metropolitan basins can be increased by optimizing drainage network capacity through proper operation of movable gates, resulting in higher sewer collector fill levels. As a result, reservoir volumes must be effectively utilized by intelligent automated regulatory systems controlled by Real Time Control (RTC) devices.

To reduce the risk of water pollution caused by urban drainage systems, intelligent wastewater management systems are required that can intercept rainwater flow and direct it to a treatment facility only when pollutant concentrations are high during the initial flush phenomenon. Once the first flush phenomenon has passed, the need to completely intercept drained flow is no longer necessary, as the rainfall pollutant flow rate decreases to concentrations suitable for discharge into water bodies. In this case, intercepting drained flow becomes increasingly impractical because the concentration of pollutants has been reduced to a level that poses a similar risk of washout. When excessively diluted wastewater enters the treatment cycle, bacterial colonies in biological reactors may be washed away. As a result, following the initial flush, it would be beneficial for the Combined Sewer Overflow (CSO) system to release the total flow rate, completely bypassing the treatment facility. This necessitates a flow divider with adaptable hydraulic characteristics that can adjust to various operational conditions, also known as a smart flow divider. The urban drainage network must include a complex system consisting of three components:

• a qualitative and quantitative monitoring system for wet-weather flow delivered to the divider;
• a discharge outlet that can be adjusted for flow;
• volumes of detention.

Because flow rate division is determined by the qualitative and quantitative characteristics of the discharged wet-weather flow, a specialized system for high-frequency flow rate and pollutant load measurement must be installed near the divider. The flood divider will be activated once the monitoring system has collected data and processed it using the predictive model.

In contrast to the traditional approach of building spillways with hydraulic structures that ensure a nearly uniform flow rate to the treatment facility regardless of wastewater concentration (e.g., lateral spillways, frontal diverters, and bottom openings), the rainstorm flood spillway for the smart device must be adjustable to account for variations in the partitioning ratio based on operational scenarios.

The CSO system must be controlled by electromechanical equipment, which includes adjustable gates and a smart device that controls a buffering capacity to temporarily retain intercepted volumes of rainwater flows, preventing them from being delivered to the receiving water body during peak pollution loads.

It is, in fact, mandatory to guarantee that the flow rate is delivered to the treatment plant in accordance with the regulatory constraints, which include the regulatory threshold values for the concentrations of pollutants in discharges into water bodies and for the inflow rates of treatment plants.

It is common practice to use the “deterministic” decision approach to determine when to intercept rainwater flow and direct it to a treatment facility, comparing a single predicted value (usually the expected value) to a pre-established pollutant load value, without taking into account that, whereas this threshold value is a fixed, well-defined quantity, the forecasted value is an uncertain quantity. Comparing the predefined threshold value to the forecast entails assuming that the forecast is also a real quantity free of errors, whereas it is extremely unlikely that a prediction will ever coincide with a future real occurrence. This is why, as advocated by decision theory, when dealing with uncertain events, we propose using “probabilistic” decision-making approaches that consider the probability of all potential future outcomes [1,2,3]. This work creates classical-type predictions using either multivariate regression or artificial neural networks (ANN). Data-driven approaches, including those based on artificial networks, are increasingly used for modeling natural phenomena or specifically water quality for management strategies, as in [4], which implements Nonlinear Auto-Regressive models with eXogenous inputs (NARX) for assessment of Total Suspended Solids (TSS) concentration for different combinations of explanatory parameters, or in [5], which applies machine learning to improve sediment and nutrient first-flush prediction.

Given these prediction results, the Model Conditional Processor (MCP) [6], one of many available probabilistic post-processors, is used to convert them into the entire predictive probability distribution of the unknown future real occurrence, conditional on the “deterministic” forecasts of one or more independent models, after training on a set of historical data with known model forecasts and observed values. The evaluation of predictive probability density is required for probabilistic decision approaches, such as the Bayesian decision approach, because the use of a density function allows the probability of exceeding a threshold, or the expected value of benefits (or risks) to be estimated and traded off during the decision-making process [7,8]. This method can be used to determine when to divert polluted rainwater to the treatment plant, as previously described.

Probabilistic approaches have been shown to be effective tools for stormwater management in real-time control (RTC) systems in urban catchments [9,10]. RTC systems, when activated quickly by an effective predictive model, can reduce sewer overflows by preventing maximum polluting loads [11,12] from discharging into receiving bodies, lowering pollution risks. Combining stormwater storage tanks and RTC inflows can significantly reduce pollutant loads discharged into receiving water bodies, making it a valuable technique in Sustainable Urban Drainage Systems for flood risk reduction and water quality management [13,14]. Modeling and managing urban stormwater runoff quality, as well as implementing best management practices, are critical components of complying with local regulatory requirements [15].

The proposed MCP approach is used in this paper to predict the probability distribution of incoming TSS polluting loads based on surrogate parameter measurements (turbidity and flow rate), and it was tested on a real-world urban catchment in southeastern Virginia monitored by the United States Geological Survey. Section 2 goes over materials and methods, including forecasting models and the MCP probabilistic decision-making approach. The case study and results are presented in Section 3, followed by the conclusions in Section 4.

2. Materials and Methods

Traditional water quality monitoring programs rely on collecting water samples at infrequent intervals because polluting substance analyses are costly and complex [16,17]. As a result, it is impossible to fully understand the long-term spread of polluting loads carried by urban drainage systems. This obstacle can be overcome by using “surrogate” measurements, which are typically detected by multi-parametric probes that can be used in real time [18]. Surrogate measures allow high-frequency measures to be converted into “classic” water quality parameters, which are commonly used by regulators to limit pollutant dumping into bodies of water. Water level, flow, pH, specific conductance, dissolved oxygen, and turbidity are some of the variables commonly measured in situ.

In the literature, various conversion models have been studied, generally regression formulas, which, for example, predict Total Suspended Solids, Total Phosphorus, or Chemical Oxygen Demand through the measurement of turbidity [19,20], or dissolved solids and nutrients starting from specific conductance [21]. It should be specified that these relationships have a site-specific nature because multiple factors (hydrological, climatic, morphologic, traffic density, etc.) affect the quality [22,23] and complexity [24] of storm runoff; for this reason, an initial phase of traditional sampling is always necessary in order to calibrate the conversion models.

Rather than recalibrations, the surrogate parameter monitoring system requires periodic interventions and cleaning of the probes submerged in the wastewater flow. This is to keep the measurement from being influenced by the formation of a biological membrane, which would lead to its interpretation as a traditional pollution parameter. In fact, the latter’s measurement undergoes a complete transformation upon the formation of the biological film, making recalibration unnecessary

In this study, turbidity (T) and flow (Q) values were demonstrated to be effective surrogate variables to predict the total suspended solids (TSS) load, an important parameter for characterizing water quality and polluting loads, to which the technical standards for defining the admissibility thresholds for treated wastewater refer (e.g., legislative decree of the Italian Government n.152/2006; Directive (EU) 2024/3019 of the European Parliament and of the Council). In fact, the TSS parameter has gained widespread recognition as a common pollutant measure and primary indicator in urban stormwater runoff, making it an important parameter for assessing stormwater quality [25]. Furthermore, TSS loads have a significant impact on the accumulation and transportation of major potentially harmful substances like heavy metals, hydrocarbons, and nutrients [26]. As a result, while peak TSS volume does not coincide with peak concentration, it remains an important water quality parameter that is widely used in this research field [27]. A probabilistic water quality surrogate forecasting approach is proposed as a useful tool for decision-makers to protect receiving bodies from large pollutant loads that occur early in rainstorms (first flush phenomenon). The term “surrogate” is commonly used in urban water quality literature to refer to the variables that will be measured instead of the variable of interest. For example, as previously stated, turbidity (T) and flow values (Q) are useful surrogate variables for predicting TSS.

It will be demonstrated that the proposed approach predicts the pollution peak, making it an effective tool for the management of detention basins serving the drainage network if implemented in an RTC system. The proposed approach involves three steps:

• The first step converts the chosen surrogate variables into the expected value of TSS load, which was assumed to be a quality parameter representing stormwater pollution. The conversion performed in this step is also a deterministic forecast, as we obtain a future TSS load value directly from the most recent surrogate parameter values.
• The second step uses the observed time series to convert the output of a single model or multiple models in parallel into a probabilistic forecast using the Model Conditional Processor (MCP).
• The third and final step employs the conditional probability density function, obtained through the MCP approach, to establish a probability threshold mechanism by comparing the estimated probability of exceeding a TSS load threshold value to the allowed probability.

Before implementing the three-step approach, a preliminary issue must be resolved. Indeed, to obtain an effective prediction of the pollution phenomenon, it is necessary to first identify the surrogate variables (such as flow, turbidity, specific conductance, pH, etc.) to be used to predict a parameter commonly used to characterize the pollution state of a water body. Also, for the last parameter, it is necessary to identify a classic pollution target parameter (e.g., TSS, BOD5, COD) that can be predicted on the basis of the measurement of some surrogate parameters. In the following case study, the TSS was taken into consideration, as this parameter has been shown to be effective for modelling the drainage water quality of the analyzed urban catchment.

The relationship between the surrogate and actual parameters of the drainage water is site-specific [28,29]; therefore, the chosen quality variables and the correlation equations could change with the case studies, but the proposed methodology continues to be appropriate.

2.1. The Used Forecasting Models

The first step, forecasting the expected value of the decision variable (in this case TSS), can be done using a variety of approaches. This study used two types of surrogate variable-based models:

A multivariate regression model.

An ensemble of ten artificial neural networks (ANNs).

Both forecasting models estimate TSS load using the best-proven combination of stormwater surrogate parameters from qualitative and quantitative variables. The following models were developed through a trial-and-error approach that examined various combinations of available surrogate parameters (e.g., water temperature, discharge, water depth, specific conductance, and turbidity). The goal was to find the most significant minimal combination of surrogate measurements. Indeed, this approach excluded surrogate parameters that did not make a significant contribution, focusing the models on the key variables for prediction, namely turbidity and flow rate.

2.1.1. Multivariate Linear Regression

The pollutant load can be represented through a multivariate regression function based on the surrogate water quality parameters. By designating the instantaneous polluting load $y$ as the dependent variable and a collection of $s$ surrogate variables as $x_i$, where $i \in \{1, \dots , s\}$, a multivariate regression model can be established.

To facilitate the decision to detain/divert to the water body the flow, it is necessary to predict $y_{t_0+1∆t}$, the present value of $y$, at least one time step ahead. This requires $n$ previous values of the surrogate variables $x_i$, specifically $x_{i,t_0-j∆t}$, where $j\in \{0, \dots , n_i\}$, with $n_i$ representing the number of prior time steps utilized for each surrogate variable. The forecasted target variable ${\widehat{y}}_{t_0+1∆t}$ is subsequently defined by the traditional relationship:

$${\widehat{y}}_{t_0+1∆t} = a_0 +{\sum }_{i=1}^s{\sum }_{j=0}^{n_i}{a}_{i,j}{x}_{i,t_0-j∆t}$$

(1)

where $a_0$ and $a_{i,k}$ are the coefficients of the multivariate regression equation.

Generally, the variables $y$ and $x_i$ are not normally distributed, whereas the properties of linear multivariate regression, particularly its minimum variance, are defined for normally distributed variables. Consequently, it is advisable to transform the original variables $y$ and $x_i$ into the normal space utilizing one of the methodologies discussed in Section Transformation into the Normal Space: The Probability Matching Approach before executing the multivariate linear regression.

Let η and ξᵢ denote the standardized normal variables of $y$ and $xᵢ$ in the normal space, and let $\widehat{\eta }$ represent the predicted value. Equation (1) becomes:

$${\widehat{\eta }}_{t_0+1∆t} = {\alpha }_0 +{\sum }_{i=1}^s{\sum }_{j=0}^{n_i}{\alpha }_{i,j}{\xi }_{i,t_0-j∆t}$$

(2)

where ${\alpha }_0$ and ${\alpha }_{i,j}$ are the coefficients of the multivariate regression equation in the Normal space.

2.1.2. The Artificial Neural Network Approach

Artificial neural networks (ANNs) have recently received a lot of attention in the environmental field due to their excellent self-learning capabilities and high accuracy in mapping complex nonlinear relationships [30,31]. ANNs are thus popular machine learning techniques that mimic the learning mechanism found in biological organisms. This biological mechanism is simulated using artificial neural networks, which contain computation units known as neurons. Weights connect neurons to each other in the same way that synaptic connections do in biological organisms [31].

The weights are determined iteratively during the network’s learning process by providing training data that includes examples of input-output pairs for the function to be learned.

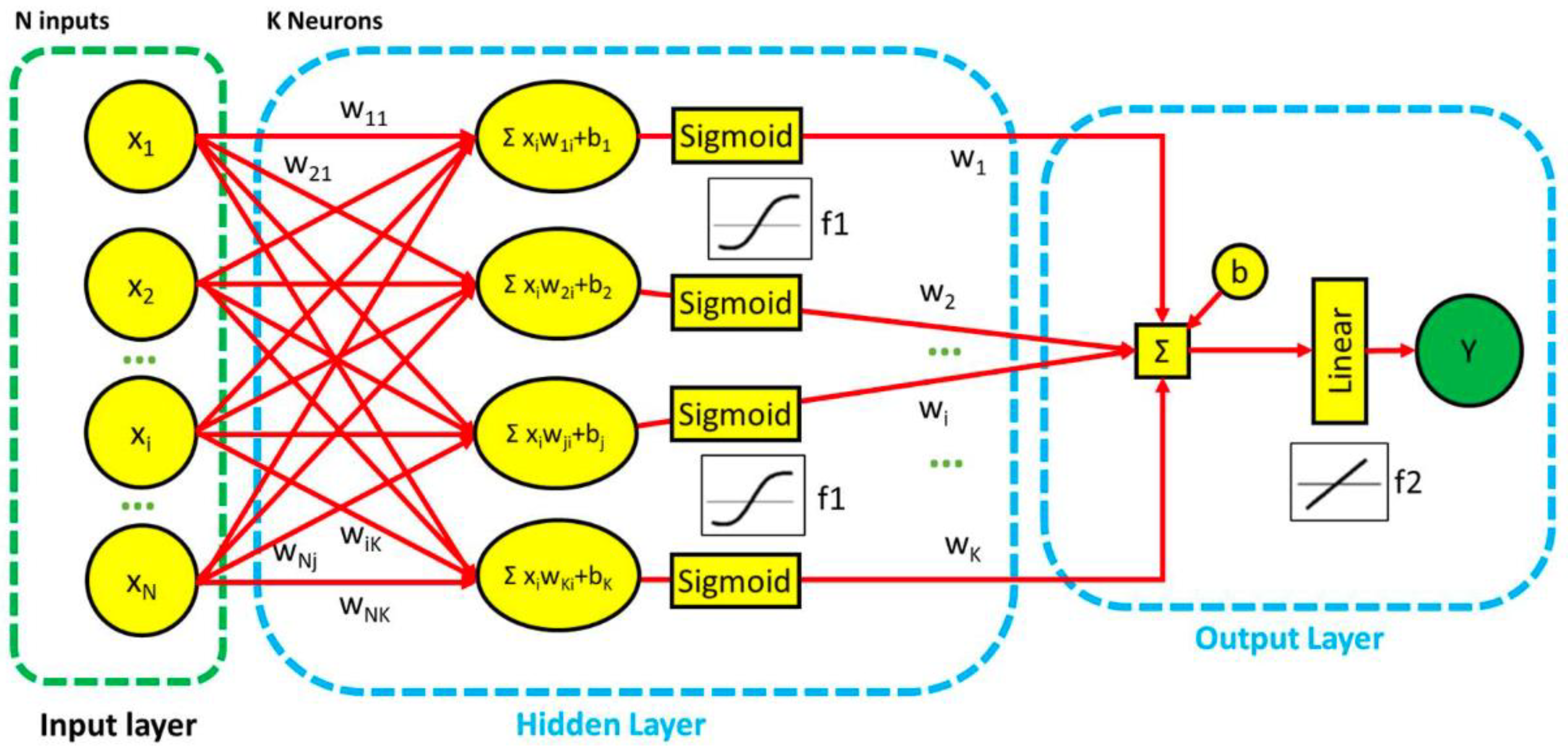
A Feed Forward Neural Network is a simple architecture that uses ANNs for a variety of tasks, including regression. It is made up of several components, each of which serves a distinct purpose:

• Input layer: this layer accepts raw data, with each neuron representing an input feature or parameter.
• Hidden layer(s): hidden layers, such as sigmoid neurons, are located between input and output layers. These layers extract intricate patterns and characteristics from the input data.
• Output layer: the output layer is responsible for the network’s final prediction, which is frequently achieved through the use of linear neurons in regression tasks.
• Activation Functions (Sigmoid and Linear): Neurons in the hidden layers use activation functions such as the sigmoid function, which introduces nonlinearity. Meanwhile, linear neurons in the output layer generate continuous-valued outputs appropriate for regression.

The network generates its output through a combination of weighted connections and biases. Each connection weight represents the strength of the relationship between neurons, whereas the bias adds an extra shift to the neuron input. The weights are determined iteratively during the network’s learning process by providing training data that includes examples of input-output pairs for the function to be learned. During training, these weights and biases are adjusted to improve the network’s performance in mapping multiple input parameters to continuous output values. The network structure employed in this study is represented in Figure 1, where one can observe the previously described elements constituting a Feed-Forward Neural Network.

Figure 1. Architecture of a Feed-Forward Neural Network.

2.2. The Probabilistic Decision-Making Approach

As previously stated, decision theory, specifically Bayesian decision theory [32,33,34], employs comprehensive predictive density information for “probabilistic” decision-making in the context of uncertain decision variables, rather than simply comparing actual quantities, such as predetermined thresholds, with uncertain quantities, such as forecasted values, as is done in “deterministic” methods.

Probabilistic decision-making approaches necessitate the estimation of the overall predictive density for decision-making operations aimed at managing and controlling the inflow of polluting loads into receiving water bodies. Indeed, understanding the probability distribution of the future load inflow amount can help you make more sound and appropriate decisions about managing the first flush phenomenon. The classical threshold, based on real-world values, should not be compared to a model forecast. The reason for this is that the threshold value is a real, well-defined value that is typically imposed by technical regulations, whereas the forecast is a virtual and error-prone image of what will actually occur, and one should never compare predefined real-world quantities with random ones. The best approach is to translate the threshold into the probability of exceeding it. In practice, the decision is made not because the expected predicted value exceeds the threshold value, but because the probability of a future value exceeding the threshold is greater than a pre-established probability value reflecting the decision maker’s acceptable level of hazard.

Accordingly, in our case, the decision on whether to divert the regular rainwater storm flow can be made based solely on the probability that the total pollutant loads will exceed a pre-established pollution value. This means that the probabilistic approach would need to estimate the entire probability distribution of the $y_{t_0+j∆t}$ future quantity value, where $t_0$ is the present time and $j$ is the number of time steps with which we make the prediction. Unfortunately, not knowing the future, $f\left(y_{t_0+j∆t}\right)$, the probability distribution encapsulating all the information on the future event, is unknown to us at time $t_0$. We then look for an approximation of this probability distribution based on our present information, and in particular on the forecasts made with one or several forecasting models [35], which we will indicate as ${\widehat{y}}_{m,t_0+j∆\mathrm{t}}$, with $m\in \{1, \dots , M\}$ where M is the number of forecasting models used. This approximation is $f\left(y_{t_0+j∆\mathrm{t}}|{\widehat{y}}_{m,t_0+j∆\mathrm{t}}\right)$, namely the probability distribution of the future value conditional on the models’ forecasts, which is usually called the “predictive probability density”, or just the “predictive density”.

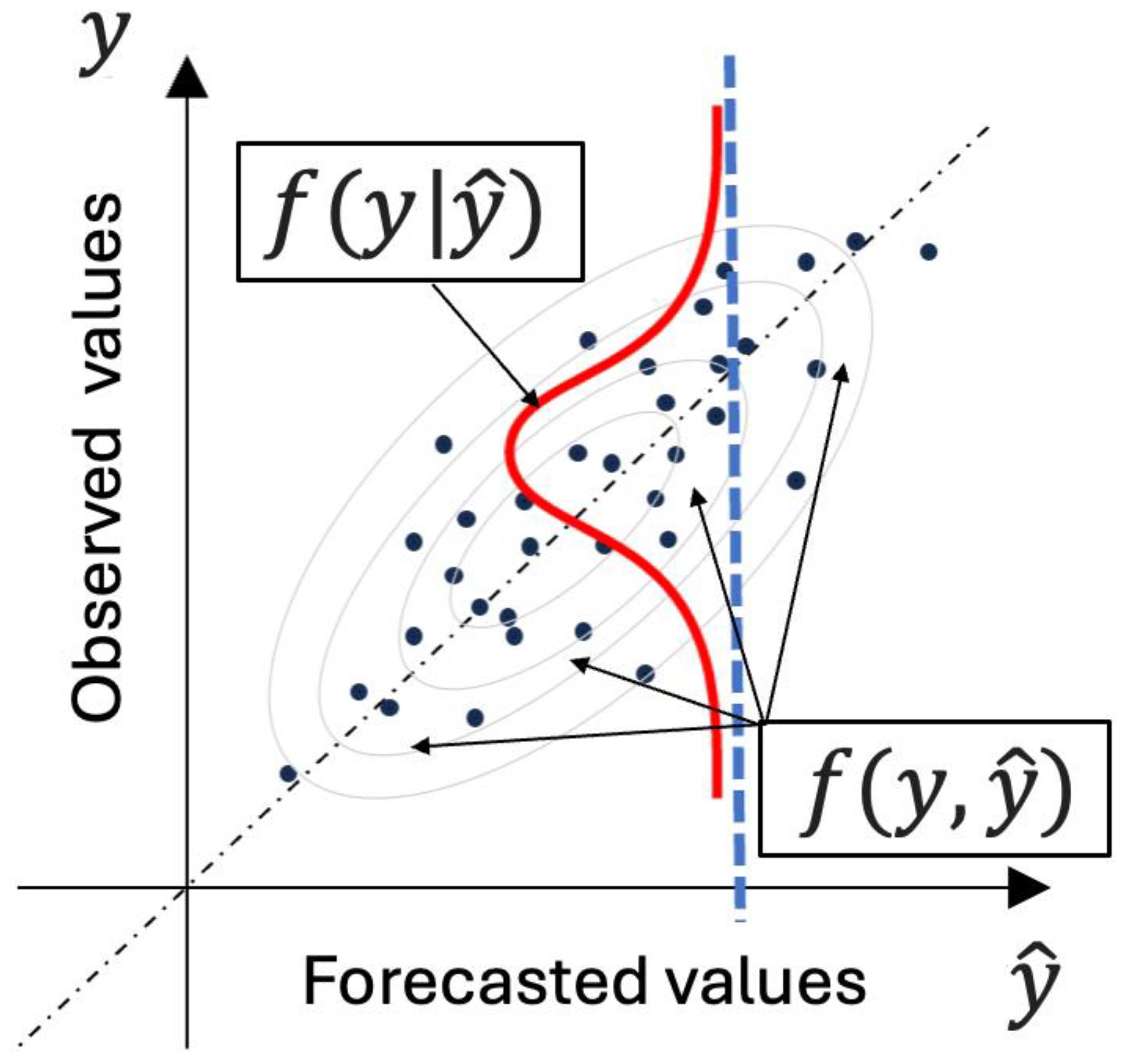
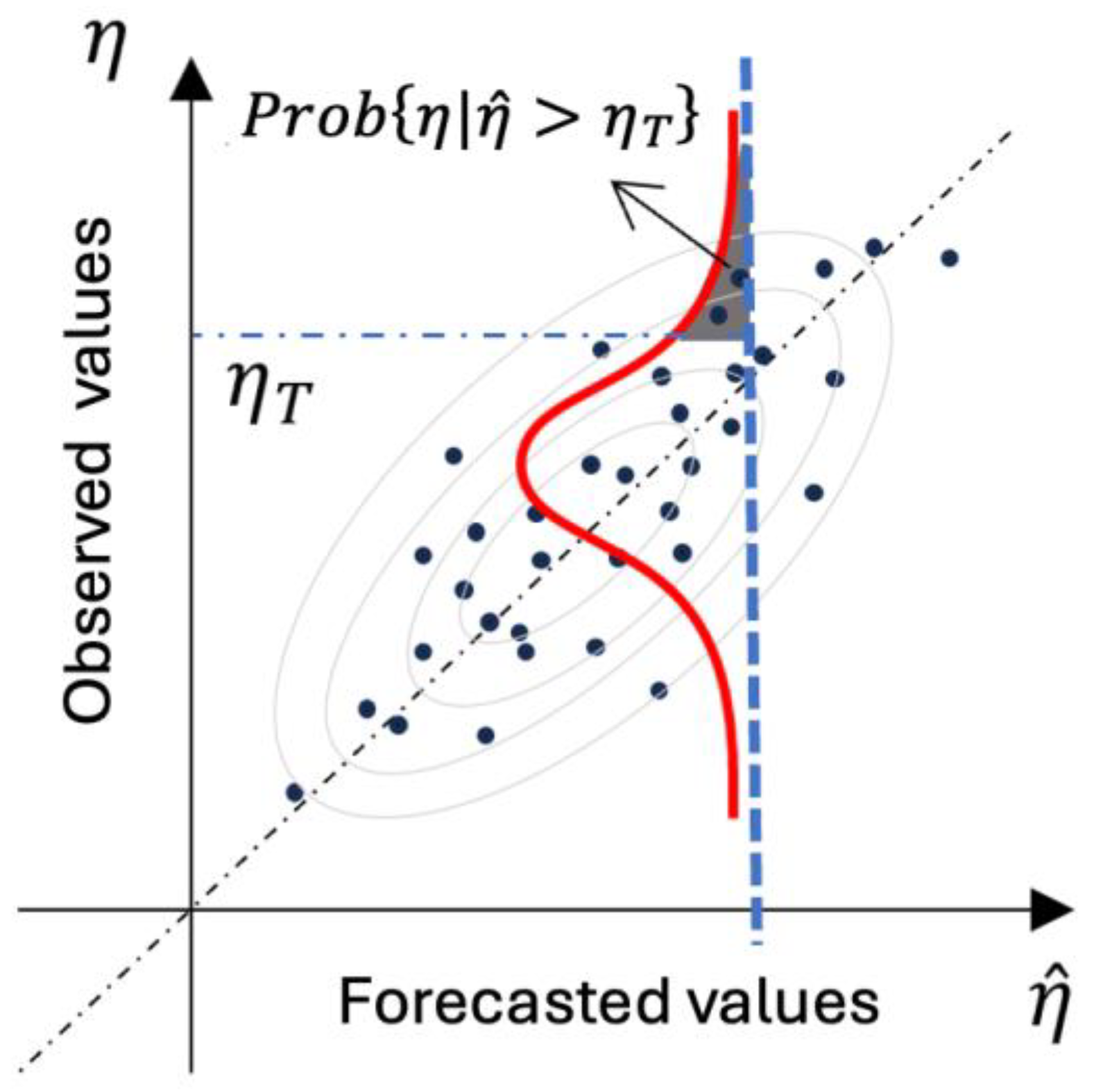
Let us clarify this concept of the “predictive density” using the following Figure 2, where the observed value $y$ is plotted as a function of its forecast $\widehat{y}$. The cloud of black dots, in the case of a single model forecast, represents the shape of $f\left(y,\widehat{y}\right),$ the joint distribution of observations and forecasts, as outlined by the grey ellipses. If we know a forecast value, we can then cut this joint distribution and renormalize it to obtain $f\left(y|\widehat{y}\right)=f(y,\widehat{y})/f\left(\widehat{y}\right)$, the probability distribution of $y$ conditional on the known forecasted value $\widehat{y}$ (red in Figure 2). This concept can be generalized and extended to multiple models [36] and to ensemble forecasts [37] to become a flexible tool used in decision-making schemes. Please note that our interest is fully concentrated on the probability distribution of the true event $f\left(y\right)$, not on that of the model forecasts $f\left(\widehat{y}\right)$, because it will be the outcome of $y$, not of $\widehat{y}$, that will impact our decision.

Figure 2. The representation of the predictive density, namely the density of a future observed quantity $y$ conditional upon its forecast $\widehat{y}$. The cloud of dots and the thin grey elliptical contour lines show the joint density $f\left(y,\widehat{y}\right).$ The predictive conditional density $f\left(y|\widehat{y}\right)$ is then represented by the red bell-shaped curve.

Several approaches to assessing and estimating the predictive probability density can be found in the literature. Numerous uncertainty post-processors are currently accessible in the meteorological, hydrological, and hydraulic literature. All these post-processors utilize the observed and predicted values to ascertain the predictive density of the future unknown quantity, contingent upon the forecasted value.

Multiple linear regression methods, referred to as Model Output Statistics (MOS), were likely the initial techniques employed in meteorological applications [38,39] as an uncertainty post-processor. Post-processing techniques have been widely used in economics, with Bayesian prediction and decision tools being popular for a long time [40].

Since its introduction by Raftery [41], Bayesian Model Averaging (BMA) has seen widespread use in meteorology [42] and hydrology [43]. However, Krzysztofowicz [35] made significant contributions to the application of uncertainty post-processors in hydrological contexts.

The Hydrological Uncertainty Processor (HUP), in conjunction with the Input Uncertainty Processor (IUP), resulted in the development of the Bayesian Forecasting System. Gneiting et al. [44] introduced EMOS, a variant of MOS for ensemble management.

Koenker [45] introduced the Quantile Regression approach, which has since been used by a variety of authors [46,47]. Todini [6] introduced the Model Conditional Processor (MCP), which can produce equivalent results more efficiently than BFS [48]. It was later adapted for multi-model and multi-temporal methodologies [49] and extended to accommodate ensemble predictions [37].

Recently, the European Centre for Medium-Range Weather Forecasts (ECMWF) retained both MCP and EMOS to post-process the European Flood Awareness System (EFAS) forecasts [50,51].

2.3. The Model Conditional Processor

The Model Conditional Processor computes the conditional probability distribution of the future event to be observed based on the models’ forecasts by projecting observations and forecasts into the Normal space. This concept was first proposed by Krzysztofowicz [35] when he created the Bayesian Forecasting System (BFS) and later used by Todini [6] to simplify the direct derivation of multidimensional joint and conditional distributions. The issue is that very few multivariate joint distributions are known and analytically tractable, and the marginal distributions of observations and forecasts are rarely normal. The Copula approach [52] can be used to solve simple bivariate problems (for example, one decision variable and one forecast), but it becomes impractical when the problem’s dimensionality increases, such as when the problem includes multiple decision variables and forecasts. This is why, by projecting the variables into the normal space, a much simpler problem can be solved.

As given in [53] (theorems 3.2.3 and 3.2.4, page 63) given a real-valued normally distributed random vector $\mathsf{\vartheta }\approx N\left\{{\mathsf{\mu }}_{\mathsf{\vartheta }},{\mathsf{\Sigma }}_{\mathsf{\vartheta }\mathsf{\vartheta }}\right\}$, with mean ${\mathsf{\mu }}_{\mathsf{\vartheta }}$ and variance-covariance matrix ${\mathsf{\Sigma }}_{\mathsf{\vartheta }\mathsf{\vartheta }}$ is partitioned into two vectors $\mathsf{\vartheta }=\left[\begin{array}{c}\mathsf{\eta }\\ \widehat{\mathsf{\eta }}\end{array}\right]$ respectively, of sizes $n_{\mathsf{\eta }}$ and $n_{\widehat{\mathsf{\eta }}}$, with the two partitions normally distributed, i.e., $\mathsf{\eta }\approx N\left\{{\mathsf{\mu }}_{\mathsf{\eta }},{\mathsf{\Sigma }}_{\mathsf{\eta }\mathsf{\eta }}\right\}$, and $\widehat{\mathsf{\eta }}\approx N\left\{{\mathsf{\mu }}_{\widehat{\mathsf{\eta }}},{\mathsf{\Sigma }}_{\widehat{\mathsf{\eta }}\widehat{\mathsf{\eta }}}\right\}$, then the mean can be written as ${\mathsf{\mu }}_{\mathsf{\vartheta }}=\left[\begin{array}{c}{\mathsf{\mu }}_{\mathsf{\eta }}\\ {\mathsf{\mu }}_{\widehat{\mathsf{\eta }}}\end{array}\right]$ and the variance-covariance matrix as ${\mathsf{\Sigma }}_{\mathsf{\vartheta }\mathsf{\vartheta }}=\left[\begin{array}{cc}{\mathsf{\Sigma }}_{\mathsf{\eta }\mathsf{\eta }}& {\mathsf{\Sigma }}_{\mathsf{\eta }\widehat{\mathsf{\eta }}}\\ {\mathsf{\Sigma }}_{\widehat{\mathsf{\eta }}\mathsf{\eta }}& {\mathsf{\Sigma }}_{\widehat{\mathsf{\eta }}\widehat{\mathsf{\eta }}}\end{array}\right]$.

Under these conditions, the probability distribution of $\mathsf{\eta }$ conditional upon $\widehat{\mathsf{\eta }}$ can be derived as $f\left\{\mathsf{\eta }|\widehat{\mathsf{\eta }}\right\}=N\left\{{\mathsf{\mu }}_{\mathsf{\eta }|\widehat{\mathsf{\eta }}},{\mathsf{\Sigma }}_{\mathsf{\eta }\mathsf{\eta }|\widehat{\mathsf{\eta }}}\right\}$, with

$${\mathsf{\mu }}_{\mathsf{\eta }|\widehat{\mathsf{\eta }}}={\mathsf{\mu }}_{\mathsf{\eta }}+{\mathsf{\Sigma }}_{\mathsf{\eta }\widehat{\mathsf{\eta }}}{\mathsf{\Sigma }}_{\widehat{\mathsf{\eta }}\widehat{\mathsf{\eta }}}^{-1}\left(\widehat{\mathsf{\eta }}-{\mathsf{\mu }}_{\widehat{\mathsf{\eta }}}\right)$$

(3)

and

$${\mathsf{\Sigma }}_{\mathsf{\eta }\mathsf{\eta }|\widehat{\mathsf{\eta }}}={\mathsf{\Sigma }}_{\mathsf{\eta }\mathsf{\eta }}-{\mathsf{\Sigma }}_{\mathsf{\eta }\widehat{\mathsf{\eta }}}{\mathsf{\Sigma }}_{\widehat{\mathsf{\eta }}\widehat{\mathsf{\eta }}}^{-1}{\mathsf{\Sigma }}_{\widehat{\mathsf{\eta }}\mathsf{\eta }}$$

(4)

The essence of the Model Conditional Processor is nothing other than

• transforming the observations $\mathbf{y}$ and their forecasts $\widehat{\mathbf{y}}$ into the normal space by probability matching to get the normally distributed variables, $\mathsf{\eta }$ and $\widehat{\mathsf{\eta }}$
• estimating the conditional mean ${\mathsf{\mu }}_{\mathsf{\eta }|\widehat{\mathsf{\eta }}}$ and the conditional variance-covariance matrix ${\mathsf{\Sigma }}_{\mathsf{\eta }\mathsf{\eta }|\widehat{\mathsf{\eta }}}$
• retransforming back into the real space the resulting predictive densities, using the reverse distribution matching process to get $f\left\{\mathbf{y}|\widehat{\mathbf{y}}\right\}$

Equations (3) and (4) are vector/matrix equations. When dealing with single output forecasts, as in the present case, ${\mathsf{\mu }}_{\mathsf{\eta }|\widehat{\mathsf{\eta }}}$ and ${\mathsf{\Sigma }}_{\mathsf{\eta }\mathsf{\eta }|\widehat{\mathsf{\eta }}}$ reduce to the scalar quantities ${\mu }_{\eta |\widehat{\mathsf{\eta }}}$, and ${\sigma }_{\eta |\widehat{\mathsf{\eta }}}^2$.

Transformation into the Normal Space: The Probability Matching Approach

Krzysztofowicz [35] and Todini [6] proposed developing a processor based on converting observations and model predictions into a Normal space using the Normal Quantile Transform (NQT) (Van der Waerden) [54,55,56], a non-parametric probability matching technique, to derive the joint distribution and predictive conditional distribution for a manageable multivariate distribution. One could also perform the transformation parametrically, but this requires fitting a probability distribution to both observations and predictions. Instead, the NQT is applied using the probability of an ordered sample whose expected value corresponds to the Weibull plotting position. In other words, the cumulative probability of the $k^{th}$ value in an ordered sample of $N$ observations is $Prob\left(y_k\right)=k/(N+1)$.

The transformed value in the normal space will then be the $N\left(\mathrm{0,1}\right)$ variable ${ \eta }_k$ with associated probability $Prob\left({\eta }_k\right)=Prob\left(y_k\right)=k/(N+1)$.

After the results are obtained, one can return to the real space by the reverse process. A simple way is to sample at each timestep the obtained predictive density $N\left({\mu }_{\eta |\widehat{\mathsf{\eta }}},{\sigma }_{\eta |\widehat{\mathsf{\eta }}}^2\right).$ The resulting ensemble of values ${\eta }_i$, $i\in 1, \dots , M$ is retransferred to the real space by estimating the probability of each member on the $N\left(\mathrm{0,1}\right)$ distribution to obtain the probability of ${\eta }_i$, $Prob\left({\eta }_i\right)$, and the corresponding image in the original space $y_i$, by matching the probability $Prob\left(y_i\right)=Prob\left({\eta }_i\right)$.

If $y_i$ falls within the range of observations, given $Prob\left(y\right)$, one finds $y_i$ by interpolating among the historical record values.

However, future occurrences and predictions may occur outside of the observational range, necessitating the estimation of values associated with extremely high or low probabilities during the conversion to and from normal space, respectively.

While a specific distribution model for tails is required in non-parametric methods, such as the NQT approach, it may also be required in parametric methods, as the probability distributions chosen typically provide optimal fits in the central region but may not adequately represent the tails.

To represent the tails of the distributions for probability quantiles smaller than $Prob\left\{y_i\right\}<1/(N+1)=p_{low}$ or larger than $Prob\left\{y_i\right\}>N/\left(N+1\right)=p_{high}$ the following models have been used, respectively, for the lower and the upper tails:

$$\left\{\begin{array}{c}{y}_i=y_{low}\left[{\displaystyle \frac{Prob\left\{y_i\right\}}{p_{low}}}\right] if Prob\left\{y_i\right\}<p_{low }\\ y_i=\left[{\displaystyle \frac{1}{\alpha +\beta Prob\left\{y_i\right\}}}\right] if Prob\left\{y_i\right\}>p_{high}\end{array}\right.$$

(5)

with $y_{low}$ the lowest value in the observed record.

In any case, it’s important to note that all information about the conversion to normal space, including the back conversion to real space, is entirely contained in the observed data set, whether using parametric or non-parametric conversion, such as NQT.

In other words, even when converting the data used for validation in both directions, the distribution of the historical data is only used to assign the data a probability of being converted to the normal space and vice versa.

2.4. The Probabilistic Evaluation Criteria

2.4.1. The Test on the Predictive Probability Distribution

Given that the purpose of using an uncertainty processor is to identify the predictive probability distribution, it is necessary to conduct a probability distribution acceptability test.

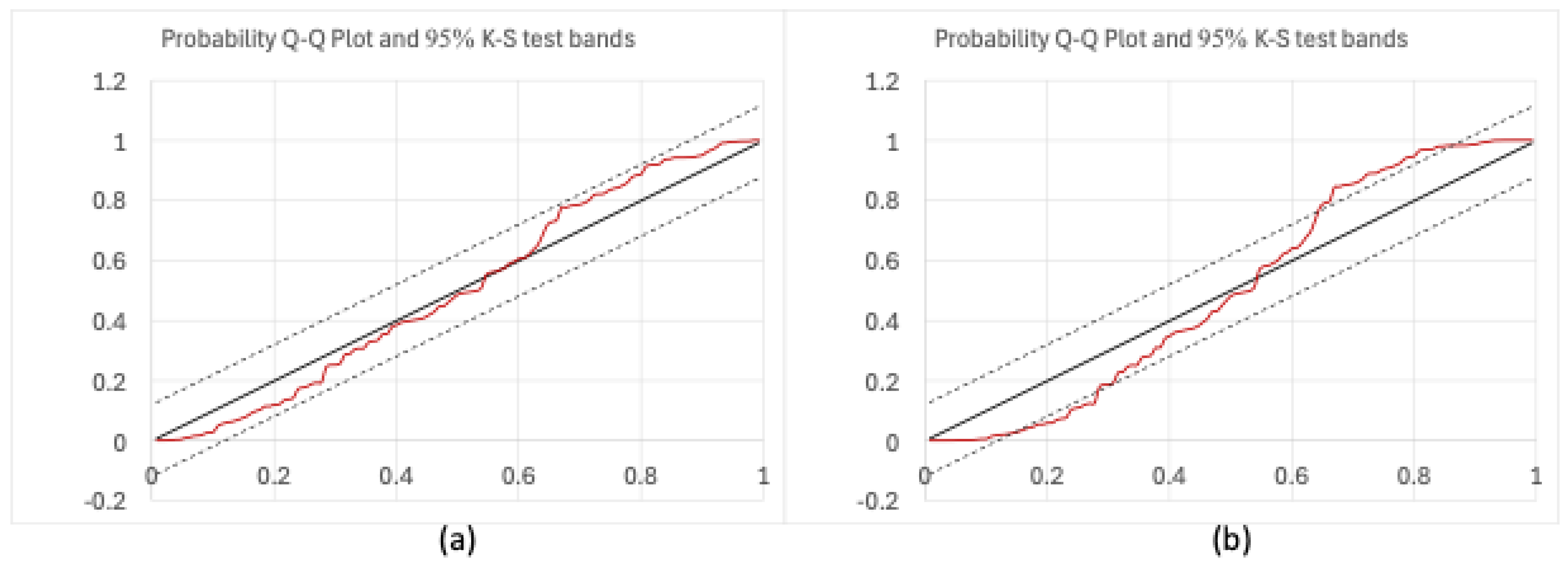
To assess the acceptability of the estimated predictive probability density [40,57], instead of using the traditional Kolmogorov–Smirnov (K-S) test, a probability plot with a histogram representation of the quantiles is recommended. The probability plot, also known as the Q-Q plot [58], compares the cumulative distribution of standardized prediction error values to their empirical cumulative distribution function (Figure 3).

Figure 3. Examples of probability Q-Q plots. The red line represents the Q-Q plot, which should approach the perfect match provided by the solid black line, whereas the dashed black lines represent the associated K-S test bands at a 95% probability level. (a) The correct probability distribution hypothesis is accepted; (b) it is rejected.

The shape of the resulting curve indicates whether the estimated predictive probabilities have an approximately uniform distribution, as expected. In other words, given that the distribution of the standardized prediction error ${\epsilon }_{t_0+1∆t}={\widehat{y}}_{t_0+1∆t}-y_{t_0+1∆t}$ is, as expected, N(0, 1), the probability distribution of the estimated $Prob\left\{{\epsilon }_{t_0+1∆t}\right\}$ must approximately plot as a uniform distribution U(0, 1) against the empirical cumulative distribution function (specifically $k/(N+1)$, with $k=1, \dots , N$) of an ordered sample. In such instances, the points ought to be situated near the bisector of the diagram. Confidence bands can also be represented on the same graph to facilitate a more formal assessment of uniformity. The Kolmogorov–Smirnov limiting bands consist of two straight lines, parallel to the bisector and positioned at a distance of $K_{\alpha }/\surd n$ from it, where $K_{\alpha }$ is a coefficient contingent upon the significance level of the test $\alpha$ (e.g., $K_{0.05}=1.358$). As shown in Figure 3, the test is deemed successful when the curves remain within these confidence bands.

2.4.2. The Evaluation of Decision Effectiveness

This work evaluates the performance of the proposed approach by demonstrating that the use of a probabilistic forecast improves the effectiveness of subsequent decisions when compared to classical deterministic decision-making approaches.

The evaluation is carried out using contingency matrices and the estimation of synthetic indices, which are widely used in the hydrological field [59,60]. The contingency table represents statistical classification accuracy, with each column containing predicted values and each row containing actual values. For binary variables (e.g., true or false), the table cells will contain Hits (a), False alarms (b), Misses (c), and Correct rejections (d), as shown in Table 1.

Table 1. Contingency matrix with two outcomes (true or false).

		Forecasts
		True	False
Observations	True	a (Hits)	c (Misses)
	False	b (False Alarms)	d (Correct Rejections)

As per Table 1, a hit means that the event, which actually occurred, was correctly anticipated by the decision maker; a false alarm means that the event, which did not occur, was instead assumed to occur by the decision maker; a miss means that the event, which actually occurred, was not anticipated by the decision maker; and a correct rejection means that the event, which did not occur, was correctly anticipated as such by the decision maker.

Following these definitions, it is possible to calculate the Proportion Correct index (PC), the Probability Of Detection (POD), the False Alarm Ratio (FAR), and the Critical Success Index (CSI), which are the typical indices used to assess the quality of decisions and at the same time the quality of the forecasts that generated them. The definition of these indices is provided in Equations (6)–(9) below.

$$PC \left(Proportion Correct index\right)={\displaystyle \frac{a+d}{a+b+c+d}}$$

(6)

$$POD \left(Probability Of Detection\right)={\displaystyle \frac{a}{a+c}}$$

(7)

$$FAR \left(False Alarm Ratio\right)={\displaystyle \frac{b}{a+b}}$$

(8)

$$CSI \left(Critical Success Index\right)={\displaystyle \frac{a}{a+b+c}}$$

(9)

A better predictive model has higher PC, POD, and CSI values, as well as a lower FAR value.

3. Application to a Real Urban Stormwater Drainage System

3.1. Description of the Case Study

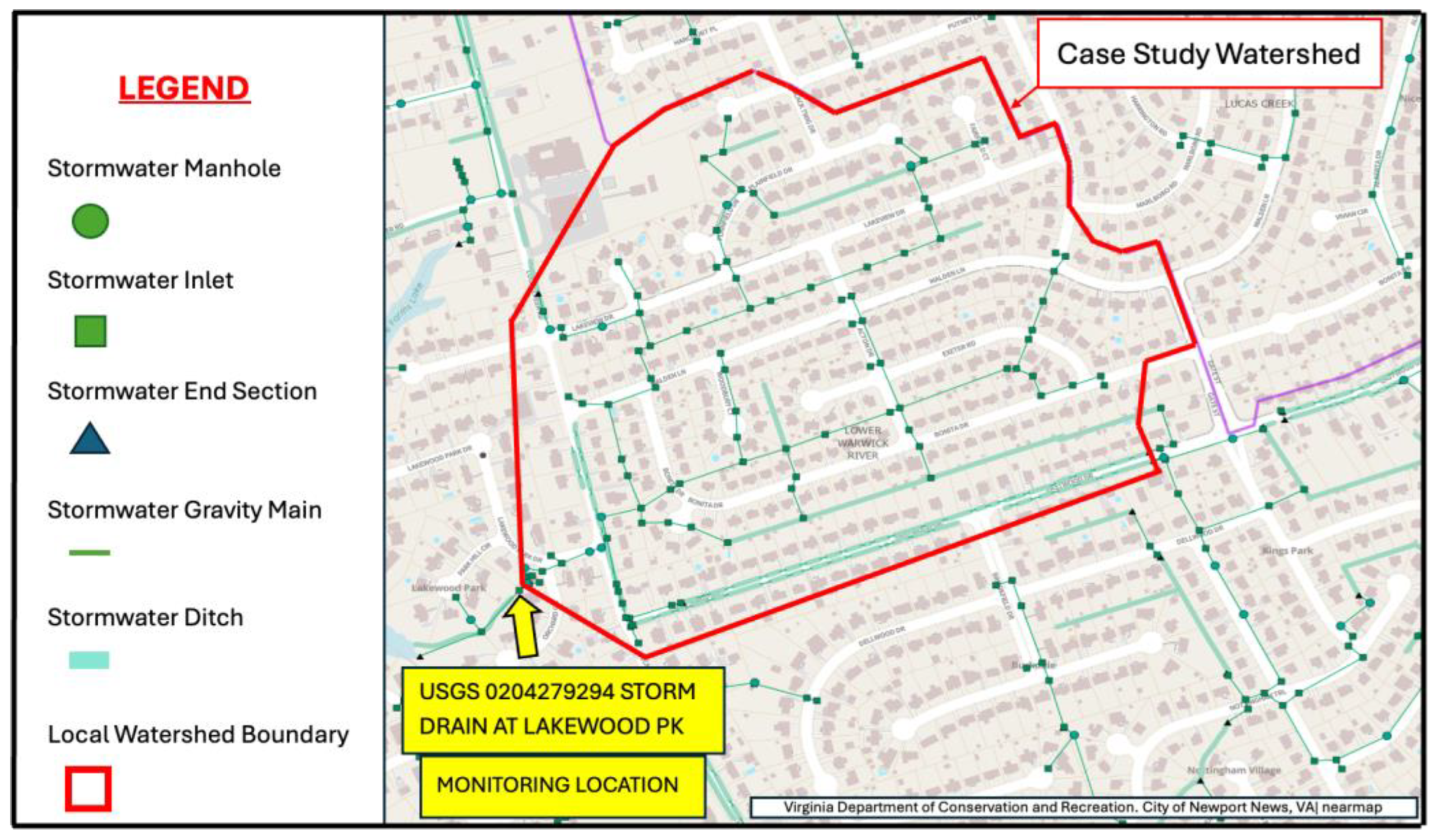
The analyzed time series were detected from an actual stormwater drainage system as part of a broad and long-term Virginia and West Virginia Water Science Center stormwater monitoring program of the United States Geological Survey (USGS) in collaboration with the Hampton Roads Sanitation District and the Hampton Roads Planning District Commission [61].

The case study focuses on the “Lucas Creek” monitoring site, which is located in Newport News, Hampton Roads. The monitoring system is integrated into a concrete stormwater pipe that serves a small urban catchment. This latter is comprised entirely of single-family residential land use and covers 39.6 hectares. The watershed’s impervious surfaces cover 21.4 hectares (52.9% of the urban catchment), while turf grass (lawns) covers 9.05 hectares (22.4% of the urban catchment), and tree canopy over turf grass covers 9.43 hectares (23.3% of the urban catchment). The remaining area is occupied by mixed open spaces.

Depending on the amount of rainfall and the initial conditions, the lag time between the hyetograph centroid and the hydrograph centroid at the Lukas Creek urban catchment’s outlet usually varies between 25 and 1 h [62], while the hydrograph’s estimated time to peak is approximately 45 min.

3.2. The Available Dataset

The Lucas Creek monitoring site shown in Figure 4, also known as “Storm Drain at Lakewood Pk” (USGS code: 0204279294), has both continuous and discrete data available. Continuous data includes water temperature, discharge, water depth, specific conductance (at 25 °C), and turbidity. Real-time USGS water-quality and flow data are collected at a high frequency, with one measurement every 5 min. Discrete data is represented by the measurement of different quality parameters derived from individual water samples, such as TSS.

Figure 4. “Lucas Creek” urban stormwater catchment, located in the city of Newport News in the Hampton Roads region, Virginia, USA.

The automated samplers are set to trigger (i.e., collect a sample) each time the water level in the storm drain exceeds the water level threshold, which is a unique height for each site. The sampler algorithm also checks when the last sample was taken—the time from the previous sample must exceed 15 min; this way, samples across the storm hydrograph are spaced out (Porter, personal communication).

Water quality data from the “Lucas Creek” study site and related processing have been published in a data release relating to a preliminary comprehensive report on stormwater quantity and quality in the urban watersheds of Hampton Roads for the period 2016–2020 [62,63]. Compared to the published data, further samplings that took place in 2021 and 2022 have been added here in order to expand the database for the calibration and validation of the models. For this work, the search for the best surrogate parameters for estimating the TSS load, among all the available parameters, has been extensively investigated, showing that they can be represented by flow and turbidity, confirming the parameters already assumed by Porter [62] for the same site examined. Temperature and specific conductance were found to be irrelevant for assessing TSS load. Furthermore, recent technical literature has shown that the turbidity parameter is effective in modeling water pollution phenomena [64].

Furthermore, only observations in rainy weather and with no missing values were used in the calculations. As previously stated, there are two types of differently structured data. The TSS concentration data are not temporally continuous but rather reflect intermittent sampling in rainy weather and subsequent laboratory analyses. TSS represents the variable to be forecasted (once converted into a polluting load); flow (Q) and turbidity (T) data are recorded continuously with a 5-min time step. Flow and turbidity serve as explanatory variables for estimating TSS load in real-time, making it easier to measure. In fact, it is necessary to obtain an estimate of the polluting load at compatible times in order to provide timely information for the implementation of pollution control measures. To split data for calibration and validation tasks, the overall dataset was divided in a 60/40% ratio while preserving the temporal sequence of the data.

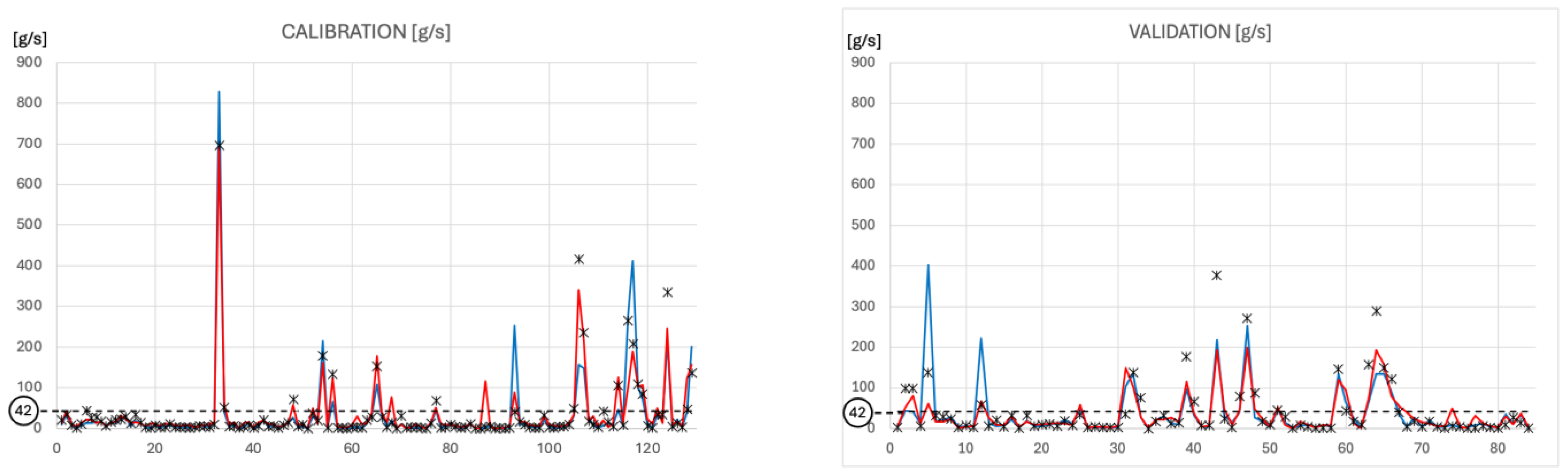
Therefore, 129 data of TSS load and the corresponding turbidity (T) and flow (Q) values of the four previous 5 min time steps were used in the model calibration process, and 84 data of TSS load and corresponding turbidity (T) and flow (Q) values of the four previous 5 min time steps were used for their validation.

3.3. The Deterministic and Probabilistic Thresholds

In this study, a TSS polluting load threshold of $42 \mathrm{g}/\mathrm{s}$ was used (about $8000 \mathrm{l}\mathrm{b}/\mathrm{d}$), a value supported by the analysis of historical data. In fact, it was noted that already when the concentration is 42 g/s, the TSS concentration frequently exceeds the Italian regulatory limit of 35 mg/L. It should be noted that the threshold value for pollutant loads is case-specific, as it is contingent upon the sewer channel being analyzed and expresses the safety margins that decision makers wish to adopt.

Anyway, given that the scope of this work is to demonstrate the superiority of the probabilistic approach against the deterministic one, the choice of a specific value, such as $42 \mathrm{g}/\mathrm{s}$, does not prevent generalizing results.

In the case of the deterministic decision-making approach, contingency tables were evaluated by comparing the multivariate regression and average ANN forecasts of the polluting load to the pre-established threshold value of 42 g/s.

In the probabilistic decision-making approach, contingency tables were evaluated by comparing the “probability” of exceeding the TSS load value threshold of 42 g/s, estimated using the predictive density, to a set of pre-established probability threshold levels ranging from 40% to 70%.

The most appropriate probabilistic threshold value was then determined by analyzing the effects of decisions made at different probability levels using classical decision assessment indices such as the Proportion Correct Index (PC), Probability of Detections (POD), False Alarm Ratio (FAR), and Critical Success Index (CSI).

3.4. Deterministic Forecast Models

The forecasting models were created to predict the expected value of the TSS load at the next 5-min time step using the flow and turbidity data from the previous four time steps (20 min). The time step was chosen based on the USGS monitoring system’s acquisition frequency; however, it corresponds to the urban catchment’s concentration time [62].

The time step corresponds to the operating times of an automatic electromechanical gate or other hydraulic regulation device controlled remotely by an RTC system.

3.4.1. The Multivariate Regression Model

The chosen surrogate parameters, turbidity and flow ($s = 2$), recorded in the four previous time intervals Δt ($n_1, n_2 = 4$) were used to estimate the TSS load at the future step using Equation (1).

Following Equations (3) and (4), the multivariate regressive model has been set up by converting all the observations, sampled with a Δt equal to 5 min, in the normal space, by means of the NQT. The resulting regression coefficient values are given in Table 2.

Table 2. Coefficient values of Equation (2) obtained using the multivariate regression in normal space.

Coefficient	Value
α0	0.01
α11	1.29
α12	−0.57
α13	−0.03
α14	0.01
α21	0.28
α22	0.07
α23	0.08
α24	−0.14

The obtained results in the normal space were then re-converted into the real space, and a model of the tail of the distribution of the TSS load measurements was developed, with parameters $\alpha$ and $\beta$ of Equation (5) resulting in $\alpha =5.33 {\times 10}^{-4} \mathrm{s}/\mathrm{g}$ and $\beta =5.31 \times {10}^{-4} \mathrm{s}/\mathrm{g}$.

3.4.2. The ANN Models

Training a neural network to generalize well to new data is a difficult task, particularly when dealing with noisy data or a small dataset. This challenge is made all the more difficult by the scarcity of available data. To address the common issue known as “overfitting” in machine learning, the training process was repeated multiple times, resulting in ten distinct neural network models. This method entails training multiple neural networks and averaging their output to improve generalization. In machine learning, the process of creating multiple models and combining them is known as ensemble averaging [65]. Each ANN model was constructed using only the calibration data as input to the training algorithm. This approach ensures that the validation database remains distinct from the training process of each neural network, allowing for an independent evaluation of the model’s performance. Furthermore, the training algorithm was configured with a random 70/30% split of the calibration data for training and validation and a hidden layer containing 5 neurons. Only neural networks with a Pearson correlation coefficient greater than 0.9 on the calibration database were selected.

3.4.3. Summary of Deterministic Model Results

As displayed in Table 3, for the multivariate regression calibration period, the coefficient of determination (R²) was 0.95 in the normal space while it was only 0.81 when returning to the real values. These values decrease to 0.67 and 0.56, respectively, over the validation period.

Table 3. Summary of R² values for the forecasting performances of the multivariate regression and the mean of the ten ANN models’ ensemble.

	Coefficient of Determination (R2)
	Normal Space		Real Space
	Calibration	Validation	Calibration	Validation
Multivarate Regression	0.95	0.81	0.67	0.56
ANN Mean of 10	Not Available	Not Available	0.92	0.79

The forecast resulting from the averaging of the 10 distinct ANN models is directly done in the real space and provides R² = 0.92 in calibration and R² = 0.79 in the validation period. The ANN approach clearly outperforms the multivariate regression in the real space.

Figure 5 compares the results of predictions based on the multivariate regression (the blue solid line) and the ensemble mean of the ten ANN models (the red solid line) with the observed values (black crosses). It is interesting to note that both in the calibration and in the verification period, several events with high TSS values occur.

Figure 5. Plots of the multivariate regression predictions of TSS load (in blue solid line), of the mean of the ten ANN models ensemble (in red solid line), and of the observations (black crosses) for the calibration and the validation periods; the black dashed line represents the decision threshold value of 42 g/s.

3.5. Probabilistic Forecast Approach

The predictions from the ten ANN models were converted into the normal space using the NQT, with all other transformed values, including observations and predictions from the multivariate regression, already available. The model for the upper tail of the observed TSS load is the same one established within the framework of multivariate regression (Section Transformation into the Normal Space: The Probability Matching Approach).

The probabilistic forecast is then formulated by marginalizing with respect to the conditioning variables the twelve-variate normal joint probability distribution encompassing the observed TSS load value, the multivariate regression forecast, and the complete ensemble of the ten ANN models’ forecasts, as delineated in Equations (3) and (4).

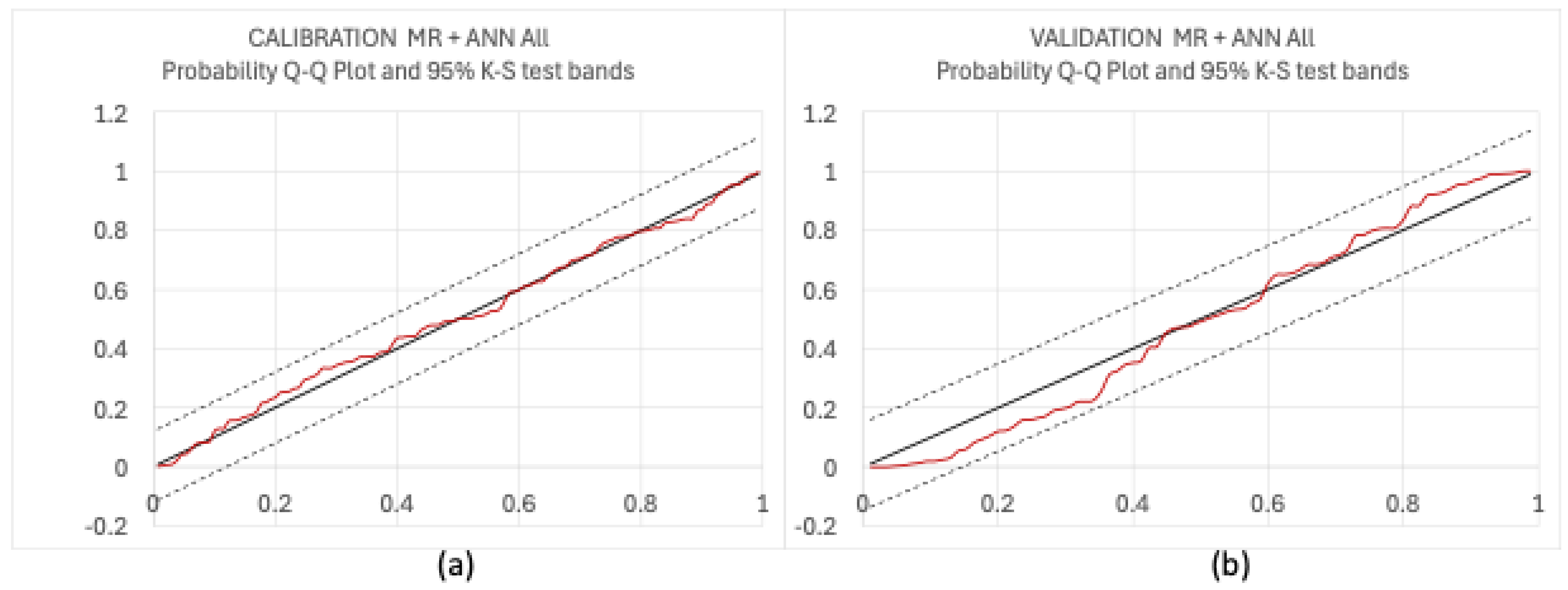
To validate the approach, we then use the KS test in the form of a Q-Q plot as discussed in Section Transformation into the Normal Space: The Probability Matching Approach.

From Figure 6, it is clear that the test is passed, at the 95% level, for both the calibration and the validation periods.

Figure 6. Q-Q plots of the estimated predictive densities of TSS load (red line) together with the 95% level limiting bands of the KS test (black dashed lines). Both predictive densities for the calibration and the verification periods passed the test and can be accepted.

3.6. Decision-Making Performance Assessment

In the deterministic forecast case, the decision to divert the flow is based on a comparison of the prediction to a predetermined threshold.

If, at any time interval, the predicted value $\widehat{y}$ exceeds the threshold value ${\widehat{y}}_T$, namely $\widehat{y}>y_T=42 \mathrm{g}/\mathrm{s}$, the flow is diverted. There is no action taken otherwise.

In the case of probabilistic forecasts, returning to real space is not strictly required for making probability-based decisions because the probability remains the same in both spaces. It is sufficient to convert the threshold value to its corresponding value in the standard normal space.

The probability, derived from the ordered sample, of an event less than or equal to the threshold value of $42 \mathrm{g}/\mathrm{s}$ is $Prob \left\{y\le y_T=42 \mathrm{g}/\mathrm{s}\right\}=0.8453$. According to this probability value, the threshold value $y_T$ corresponds to the $N\left(\mathrm{0,1}\right)$ variable ${\eta }_T=1.0166$ in the Gaussian domain.

The conditional probability of an event overtopping the threshold, $Prob\left\{\eta |\widehat{\eta }>{\eta }_T\right\}$, is then estimated at each time step based on the resulting predictive density $N({\mu }_{\eta |\widehat{\mathit{\eta }}},{\sigma }_{\eta |\widehat{\mathit{\eta }}}^2)$, as illustrated in Figure 7 and this value is compared to a chosen probability threshold value.

Figure 7. Decision-making in the normal space using the conditional predictive distribution shown in Figure 2 and discussed in Section 2.2. If $Prob\left\{\eta |\widehat{\eta }>{\eta }_T=1.0166\right\}$, represented by the grey shaded area, is larger than a prescribed probability level, the flow is diverted; otherwise, no action is taken.

Results obtained using several probability threshold values showed that the best decision-making probability threshold value is 42%. In other words, when the probability of overtopping the limiting value $Prob\left\{\eta |\widehat{\eta }>{\eta }_T\right\}$ is greater than $0.42$, then the decision is to divert the flow. No action is taken otherwise.

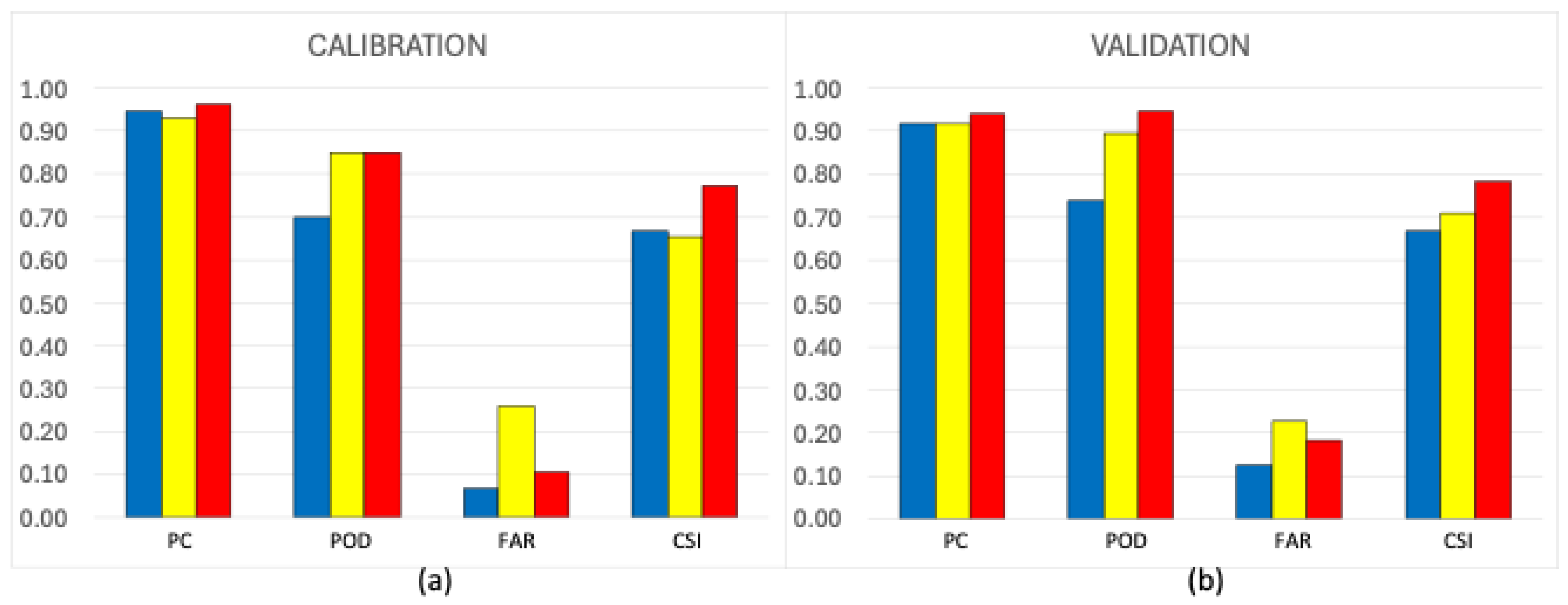
Figure 8 summarizes the decision-making results for the calibration (a) and validation (b) periods. The probabilistic combination of the multivariate regression and the ensemble of the ten ANN forecasts (in red) outperforms both deterministic decision-making approaches, based either on the multivariate regression prediction (in blue) or on the mean of the ensemble of ten ANN models (in yellow).

Figure 8. Summary of decision-making results for the calibration (a) and validation (b) periods. In blue, the results for deterministic decisions based on the multivariate regression forecast; in yellow are those for deterministic decisions based on the mean of the ten ANN models’ forecasts; and in red are the results based on the probabilistic combination of the multivariate regression and the ensemble of the ANN forecasts.

Table 4 and Table 5 provide the same results as Figure 8 in tabular form, with the best results shown in red.

Table 4. Summary of decision-making results for the calibration period in tabular form. Best values are marked in red.

Calibration		PC	POD	FAR	CSI
Deterministic	MR	0.95	0.70	0.07	0.67
	ANN Mean	0.93	0.85	0.26	0.65
Probabilistic Prob = 0.42	MR + ANN All	0.96	0.85	0.11	0.77

Table 5. Summary of decision-making results for the validation period in tabular form. Best values are marked in red.

Validation		PC	POD	FAR	CSI
Deterministic	MR	0.92	0.74	0.13	0.67
	ANN Mean	0.92	0.89	0.23	0.71
Probabilistic Prob = 0.42	MR + ANN All	0.94	0.95	0.18	0.78

Apart from FAR, which produces the best results in multivariate regression, the probabilistic decision-making method clearly improves all other indices.

In this case, the decision maker will benefit from higher values for POD, which assesses the ability to detect significant pollution events, and PC, which assesses the capacity to identify both high pollution occurrences and more acceptable situations determining flow diversion cessation. This is exactly what the probabilistic approach is demonstrated to improve. It is particularly noteworthy that, in the validation case, the probabilistic approach accounts for more than 50% of the events not detected by the deterministic approach, i.e., the POD uplift is ${\displaystyle \frac{0.95-0.89}{1.00-0.89}}\times 100\cong 54\%$. This is significant in making critical decisions.

4. Conclusions

This paper exemplifies the ease of transitioning from the use of deterministic model predictions that disregard uncertainty to the facilitation of decisions based on probabilistic assessments, as recommended by Decision Theory, which posits that uncertainty must be taken into account when making decisions about potential outcomes. Formally, this uncertainty is represented by probability distributions that are rather diffuse. Predictive models should not be regarded as tools that provide “information” about future outcomes, but rather as valuable insights that are used to assess and reduce our uncertainty, rather than as estimates of future outcomes that are directly used in the decision process. The function of models is subsequently transformed from merely representing future reality, as is often assumed, to primarily reducing uncertainty by gradually narrowing the prediction distribution around its mean value based on the information they provide.

The probabilistic approach is here founded on two classical types of models: artificial neural networks (ANNs) and multivariate linear regression. We contrast the results of their deterministic decision-making process with a probabilistic decision-making framework that employs their predictions to establish the predictive distribution, mitigate uncertainty, and, as a result, enhance the robustness of the decision-making process.

The potential of probabilistic forecasting in the real-time control of urban catchments, where pollution loads must be managed and mitigated in real time, has been described, illustrating how this potential can be realized in a case study that involves the control of “first flush” urban rainwater pollution. The Total Suspended Solids (TSS) decision variable is forecasted on the basis of real-time turbidity and flow data, and the deterministic and probabilistic forecasts are compared using metrics that are associated with exceeding a critical water quality threshold. The results obtained indicate that the proposed probabilistic decision-making methodology is robust, as decisions are enhanced not only during calibration but also, and particularly, during validation. In particular, the probability of detecting a polluting event (POD) increased by over 50% for probabilistic forecasting during the validation period in comparison to deterministic forecasting, suggesting a substantial performance improvement.

As a result, it is clear that all necessary conditions are present to establish an urban runoff control system that is based on probabilistic forecasting. This system will be capable of detecting and diverting highly contaminated runoff, thereby enabling the restoration of normal operational conditions after the transitory polluting events have subsided.

The validity of the case study under investigation can be questioned in several respects, including the use of total suspended solids volume as a decision variable, which is problematic due to the discrepancy between the volume of total suspended solids and their concentration. In order to obtain more comprehensive indications, it would also be desirable to apply the deterministic modeling approach to a broader range of cases in the future, as the morphometric characteristics of the basin are believed to significantly influence the hydrograph and the pollution graph, as well as the functional relationship between classical and surrogate pollution parameters. Nevertheless, the significance of this work and its results, which were obtained under the same conditions for deterministic and probabilistic forecasts, is not compromised by these factors. The implementation of more representative and high-performing forecasting models will not only result in improved deterministic forecasts but also in the enhancement of the probabilistic forecasts that are conditional on the deterministic ones.