Modeling of Temperature and Moisture Dynamics in Corn Storage Silos with and Without Aeration Periods in Three Dimensions
Abstract
1. Introduction
2. Materials and Methods
2.1. Mathematical Model
2.2. Boundary Conditions for the Transfer
2.3. Boundary Conditions for the Aeration Process
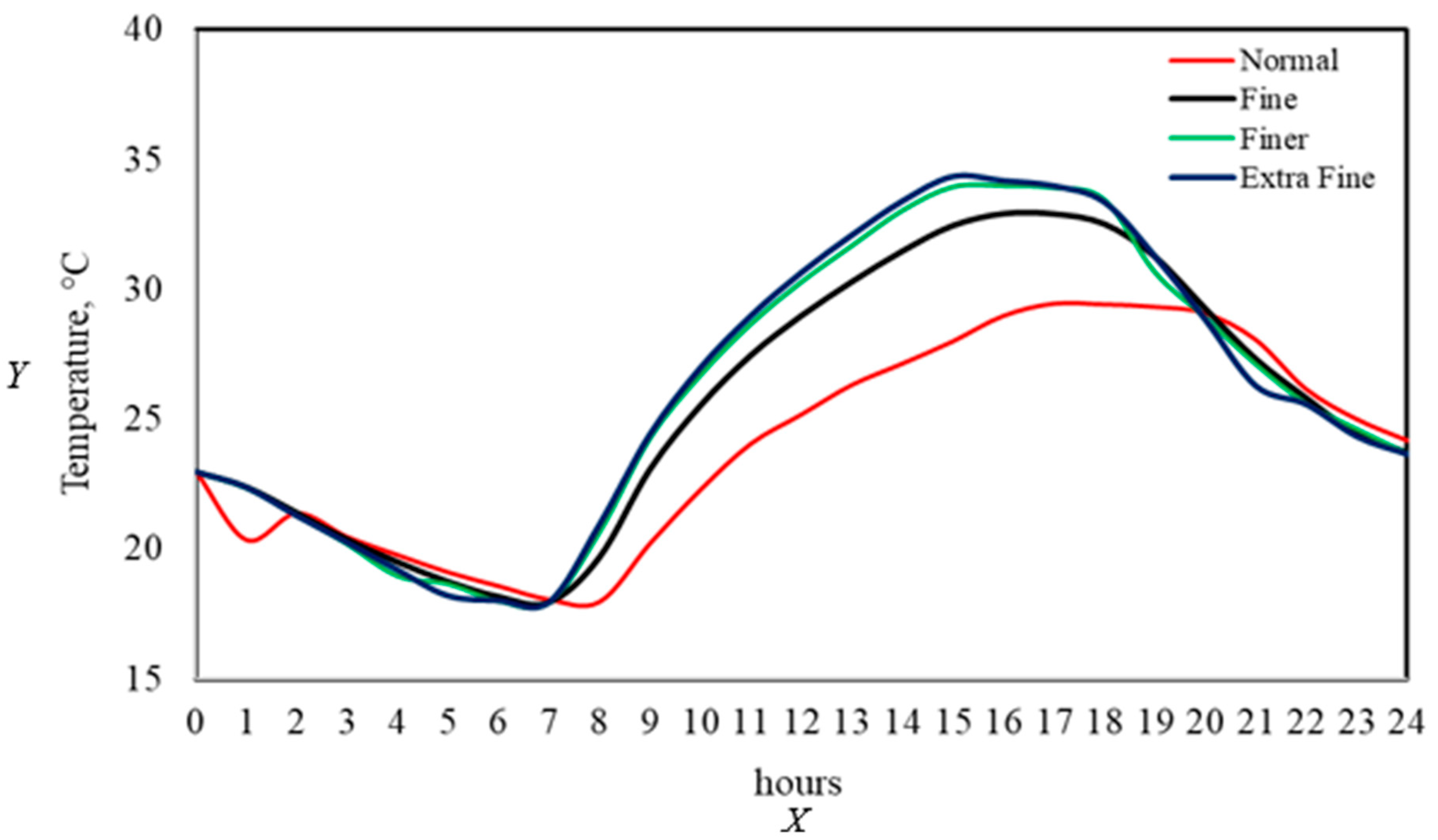
2.4. Numerical Solution
3. Results
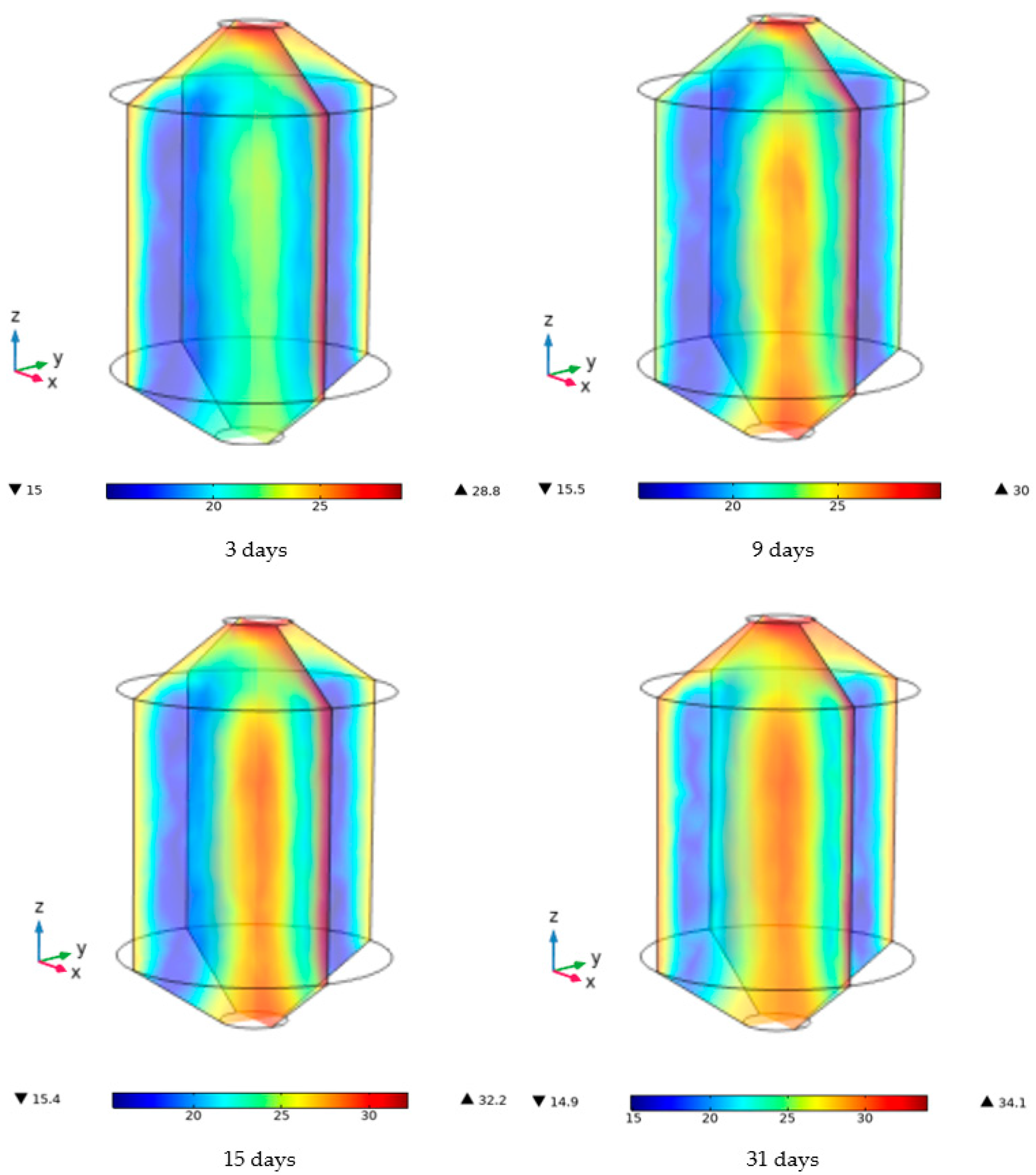
3.1. Temperature Distribution in January Without Aeration
3.2. Temperature Distribution in May Without Aeration
3.3. Silo with Aeration
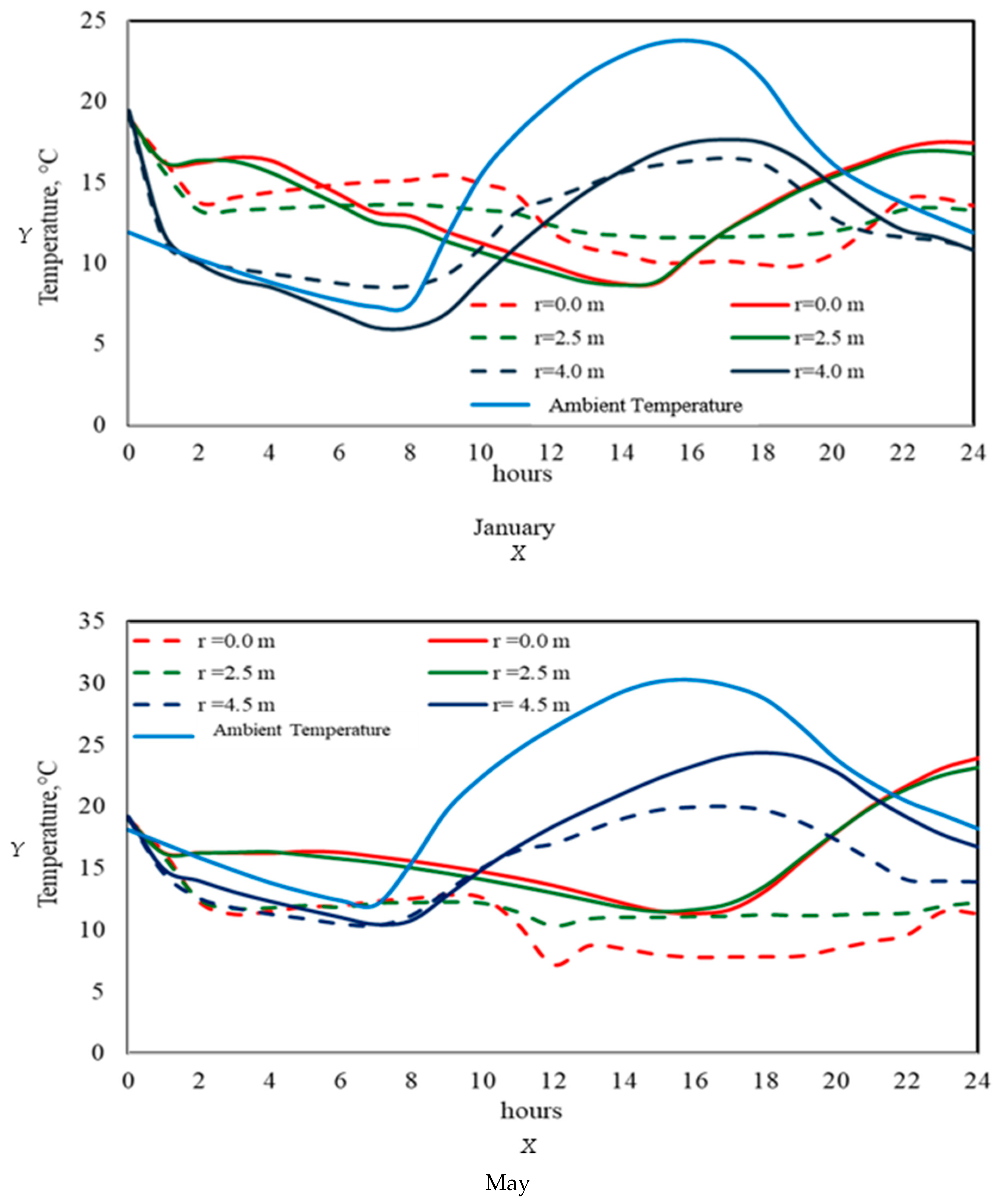
3.4. Temperature Distribution in January with Aeration
3.5. Temperature Distribution in May with Aeration
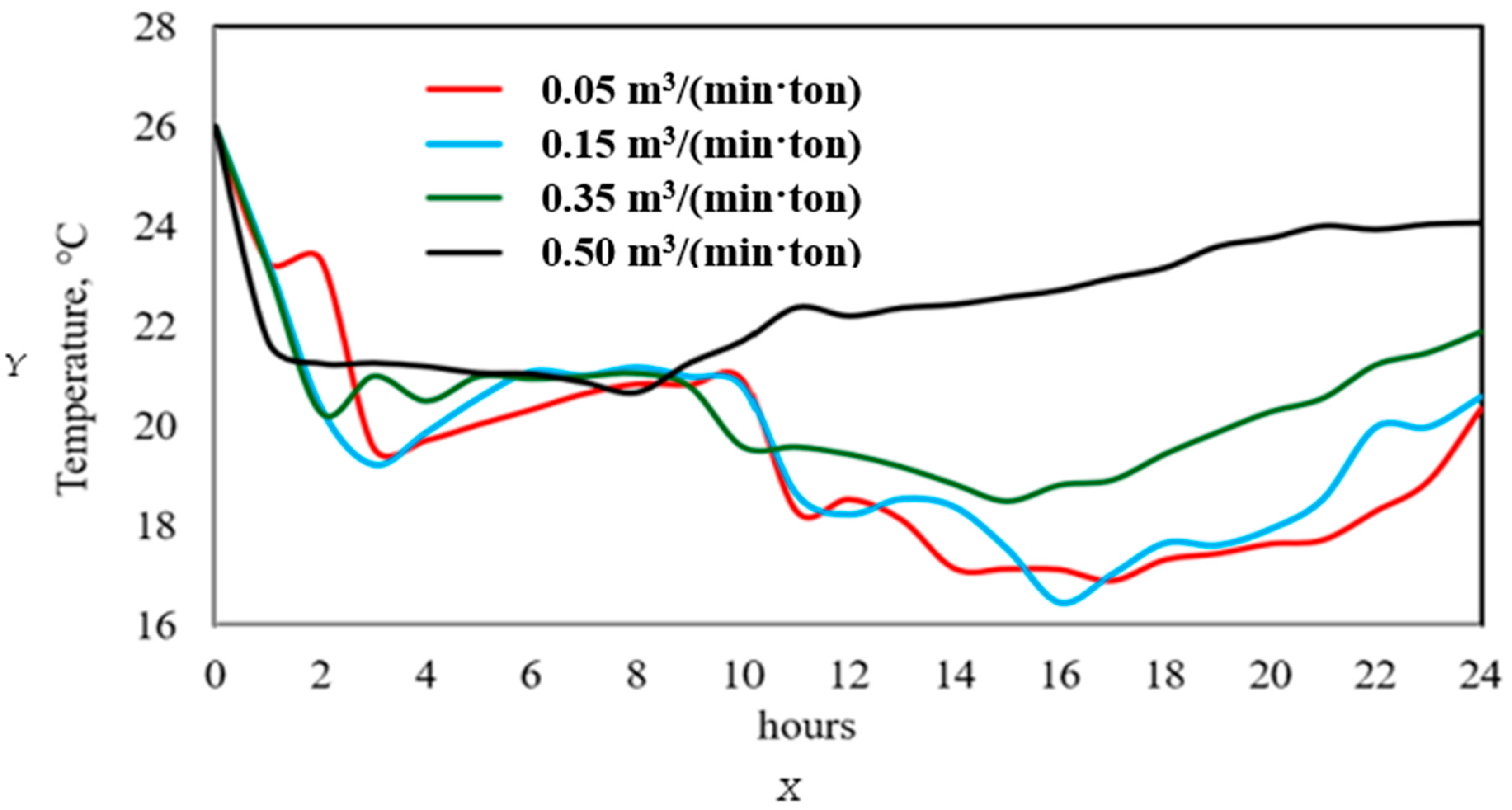
3.6. Effect of Airflow on Temperature Reduction in May
3.7. Radial and Axial Temperature Profiles with and Without Airation Periods
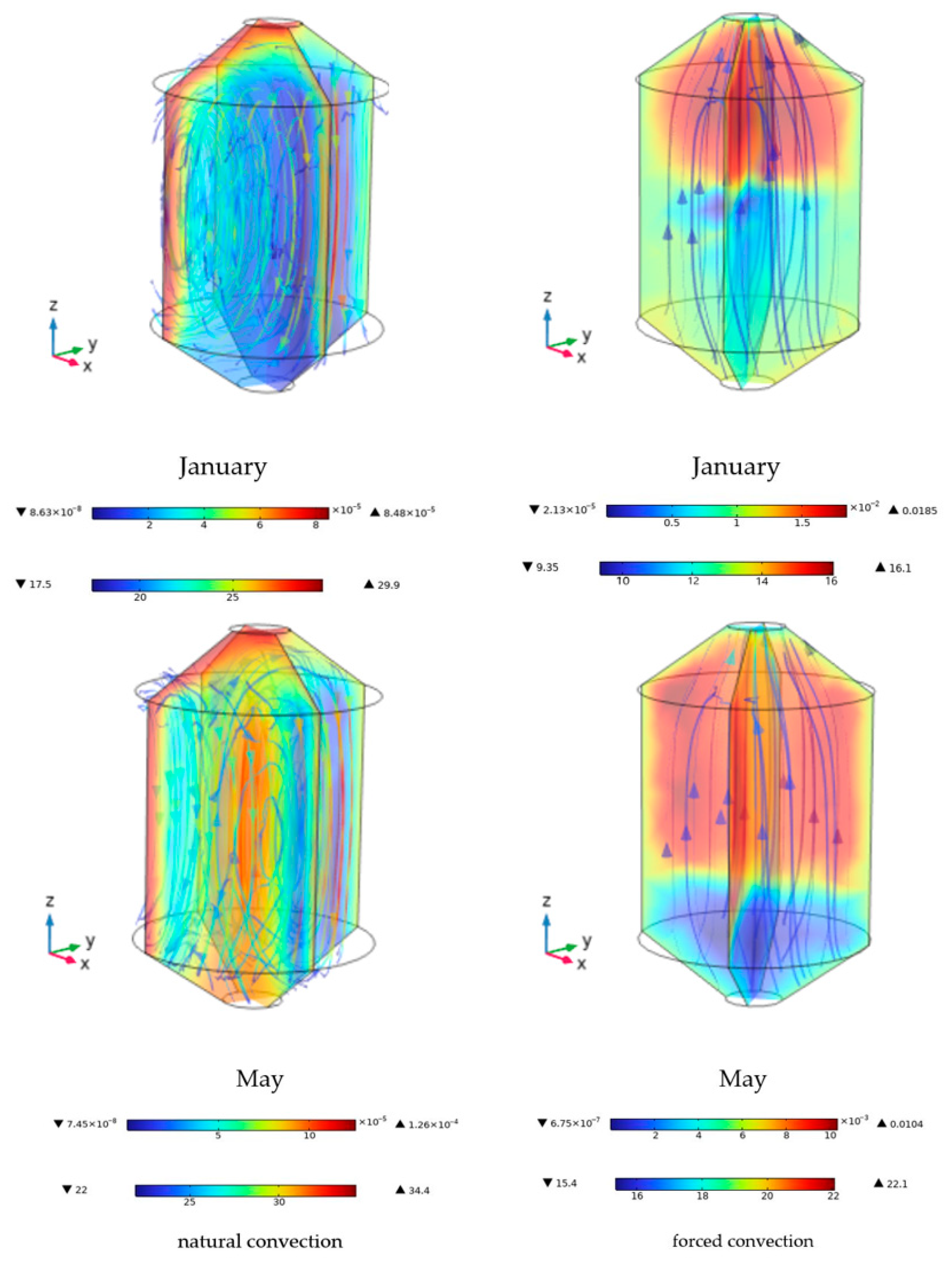
3.8. Effect of Natural and Forced Convection on Temperature Distribution
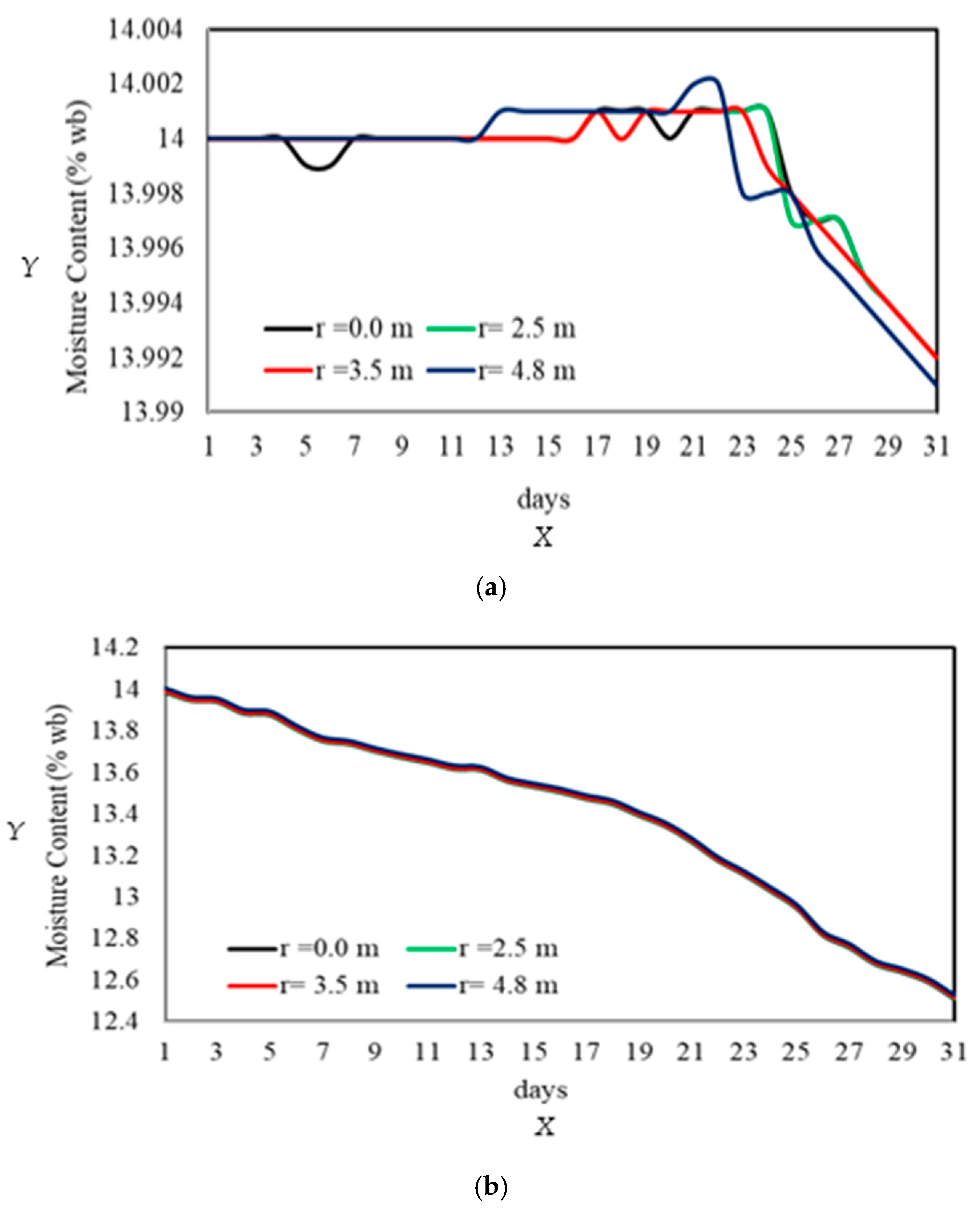
3.9. Thermal Response of Stored Grain During Accumulated Aeration Periods
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| List of Symbols | |
| absorptivity of galvanized steel | |
| grain-air interfacial, m2/m3 | |
| water activity, dimensionless | |
| concentration of grain moisture, kg/m3 | |
| moisture concentration of the air | |
| concentration of water vapor, kg/m3 | |
| specific heat, J/kg °C | |
| scalar diffusivity, m2/s | |
| function of the coordinates | |
| solar radiation incident on the silo surface, W/m2 | |
| acceleration of gravity, m/s2 | |
| heat transfer coefficient, W/ m2 °C | |
| convective heat transfer coefficient | |
| molecular mass of water | |
| molecular mass of air | |
| average molecular mass | |
| Effective thermal conductivity, W/m °C | |
| thermal conductivity of the silo, W/m °C | |
| mass transfer coefficient, m/s | |
| height of the cavity, m | |
| normal direction | |
| air pressure, mmHg | |
| volumetric generation of water by respiration, kg/m3 s | |
| vapor pressure, mmHg | |
| volumetric heat of respiration of cereal grain, J/m3 s | |
| radius of the cavity, m | |
| r, θ, z | cylindrical coordinates, m |
| time, hours | |
| fluid temperature, °C | |
| initial temperature of the grain, °C | |
| ambient temperature, °C | |
| sky temperature, °C | |
| average air velocity | |
| moisture of the grain on a dry basis, kg H2O/kg dry grain | |
| moisture of the grain on a wet basis, kg H2O/kg wet grain | |
| ambient moisture content | |
| x, y, z | Cartesian coordinates |
| X0 | Initial moisture content, kg H2O/kg dry grain |
| Absolute humidity of the air, kg H2O/kg dry air | |
| Y0 | Initial absolute moisture, kgH2O/kg dry air |
| Yi | Absolute humidity of air in the grain-air interface, kg H2O/kg dry air |
| Greek Symbols | |
| volumetric coefficient of thermal expansion, K−1 | |
| volumetric coefficient of mass expansion, m3/kg | |
| γ | continuous phase |
| ε | porosity |
| permeability, m2 | |
| ᴦ | boundary of the calculation domain |
| sky emissivity | |
| steel emissivity | |
| latent heat of vaporization of water, J/kg | |
| fluid viscosity, kg/m s | |
| density of dry air, kg/m3 | |
| density of the continuous phase, kg/m3 | |
| σ | Stefan-Boltzmann constant, W/m2 K4 |
| ω | discontinuous phase |
| Abbreviations | |
| CFD | computational fluid dynamics |
| FEM | finite element method |
| FEV | finite volume method |
| NEB | number of boundary elements |
| PDEs | partial differential equations |
| RH% | relative humidity % |
| wb | wet basis (moisture content) |
Appendix A. Model Validation

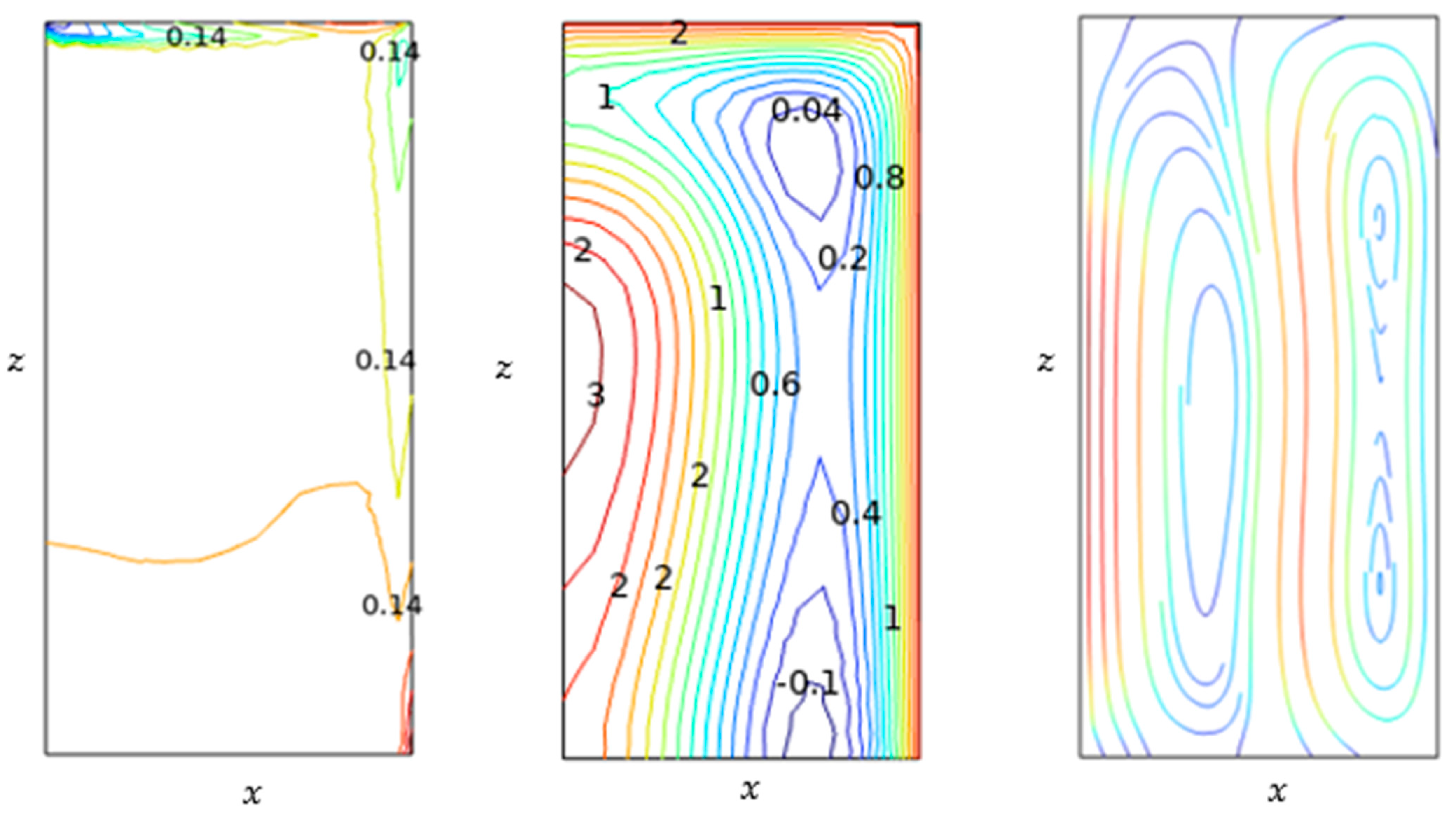
References
- Navarro, S.; Noyes, R.; Armitage, D.; Maier, D.E. Objectives of Aeration. In The Mechanics and Physics of Modern Grain Aeration Management; CRC Press: Boca Raton, FL, USA, 2001; pp. 25–58. [Google Scholar] [CrossRef]
- Casada, N.M.E.; Arthur, N.F.H.; Akdogan, N.H. Temperature Monitoring and Aeration Strategies for Stored Wheat in the Central Plains. In Proceedings of the 2002 ASAE Annual Meeting, Chicago, IL, USA, 28–31 July 2002. [Google Scholar] [CrossRef]
- Babangida, L.Y.; Yong, H. Design, Development and Techniques for Controlling Grains Post-Harvest Losses with Metal Silo for Small and Medium Scale Farmers. Afr. J. Biotechnol. 2011, 10, 14552–14561. [Google Scholar] [CrossRef]
- Rosentrater, K.A. Storage of Cereal Grains and Their Products, 5th ed.; Woodhead Publishing: London, UK, 2022. [Google Scholar] [CrossRef]
- Thorpe, G. Modelling Ecosystems in Ventilated Conical Bottomed Farm Grain Silos. Ecol. Model. 1997, 94, 255–286. [Google Scholar] [CrossRef]
- Lawrence, N.J.; Maier, N.D.E.; Stroshine, N.R.L. Three-Dimensional Transient Heat, Mass, Momentum, and Species Transfer in the Stored Grain Ecosystem: Part II. Model Validation. Trans. ASABE 2013, 56, 189–201. [Google Scholar] [CrossRef]
- Wu, Y.; Wu, W.; Chen, K.; Zhang, J.; Liu, Z.; Zhang, Y. Progress and Prospective in the Development of Stored Grain Ecosystems in China: From Composition, Structure, and Smart Construction to Wisdom Methodology. Agriculture 2023, 13, 1724. [Google Scholar] [CrossRef]
- Frisvad, J.C. Mycotoxins in Grain, Compounds Other than Aflatoxin. Trends Food Sci. Technol. 1994, 5, 235–236. [Google Scholar] [CrossRef]
- Madhukar, P.; Pandey, L.M.; Dixit, U.S. Post-harvest Grain Storage: Methods, Factors, and Eco-friendly Solutions. Food Control. 2025, 174, 111236. [Google Scholar] [CrossRef]
- Sutton, A.O.; Strickland, D.; Norris, D.R. Food Storage in a Changing World: Implications of Climate Change for Food-Caching Species. Clim. Change Responses 2016, 3, 12. [Google Scholar] [CrossRef]
- Lawrence, N.J.; Maier, N.D.E.; Stroshine, N.R.L. Three-Dimensional Transient Heat, Mass, Momentum, and Species Transfer in the Stored Grain Ecosystem: Part I. Model Development and Evaluation. Trans. ASABE 2013, 56, 179–188. [Google Scholar] [CrossRef]
- Chang, N.C.S.; Converse, N.H.H.; Steele, N.J.L. Modeling of Temperature of Grain During Storage with Aeration. Trans. ASAE 1993, 36, 509–519. [Google Scholar] [CrossRef]
- Balzi, U.; Gastón, A.; Abalone, R. Efecto de la Convección Natural en la Distribución de Temperatura y Migración de Humedad en Granos Almacenados en Silos. Asoc. Argent. Mec. Comput. 2009, XXVII, 10–13. [Google Scholar]
- Novoa-Muñoz, F. Simulation of the Temperature of Barley During its Storage in Cylindrical Silos. Math. Comput. Simul. 2018, 157, 1–14. [Google Scholar] [CrossRef]
- Wang, D.; Liu, K.; Zhang, X. Modeling of a Three-Dimensional Dynamic Thermal Field Under Grid-Based Sensor Networks in Grain Storage. IISE Trans. 2018, 51, 531–546. [Google Scholar] [CrossRef]
- Andrade, N.E.T.; Couto, N.S.M.; Queiroz, N.D.M.; Faroni, N.L.R.A.; De Sousa Damasceno, N.G. Three-Dimensional Simulation of the Temperature Variation in Corn Stored in Metallic Bin. In Proceedings of the 2002 ASAE Annual Meeting, Chicago, IL, USA, 28–31 July 2002. [Google Scholar] [CrossRef]
- Lawrence, J.; Maier, D.E. Three-Dimensional Airflow Distribution in a Maize Silo with Peaked, Levelled, and Cored Grain Mass Configurations. Biosyst. Eng. 2011, 110, 321–329. [Google Scholar] [CrossRef]
- Panigrahi, S.S.; Singh, C.B.; Fielke, J. CFD Modelling of Physical Velocity and Anisotropic Resistance Components in a Peaked Stored Grain with Aeration Ducting Systems. Comput. Electron. Agric. 2020, 179, 105820. [Google Scholar] [CrossRef]
- Montross, N.M.D.; Maier, N.D.E.; Haghighi, N.K. Validation of a Finite Element Stored Grain Ecosystem Model. Trans. ASAE 2002, 45, 1465. [Google Scholar] [CrossRef]
- Lawrence, N.J.; Maier, N.D.E. Aeration Strategy Simulations for Wheat Storage in the Sub-Tropical Region of North India. Trans. ASABE 2011, 54, 1395–1405. [Google Scholar] [CrossRef]
- Barreto, A.A.; Abalone, R.; Gastón, A. Mathematical Modelling of Momentum, Heat, and Mass Transfer in Grains Stored in Silos: Part II: Model Application. Lat. Am. Appl. Res. 2013, 43, 385–391. [Google Scholar]
- Zheng, D.; Li, L.; Chen, G.; Zhou, Y.; Liu, K. Numerical Study of Low-Temperature Ventilation Drying in a Wheat Grain Silo Considering Non-Uniform Porosity Distribution. Appl. Sci. 2023, 14, 96. [Google Scholar] [CrossRef]
- Araujo, M.E.V.; Barbosa, E.G.; Martins, M.A.; Corrêa, P.C.; Barbosa, E.G.; Araújo, R.S.L.; Gomes, F.A. CFD Analysis of Different Aeration Ducts on Temperature and Airflow in Stored Maize. J. Agric. Sci. 2019, 11, 301. [Google Scholar] [CrossRef]
- Iguaz, A.; Arroqui, C.; Esnoz, A.; VíRseda, P. Modelling and Simulation of Heat Transfer in Stored Rough Rice with Aeration. Biosyst. Eng. 2004, 89, 69–77. [Google Scholar] [CrossRef]
- De Carvalho Lopes, D.; Martins, J.H.; Filho, A.F.L.; De Castro Melo, E.; De Barros Monteiro, P.M.; De Queiroz, D.M. Aeration Strategy for Controlling Grain Storage Based on Simulation and on Real Data Acquisition. Comput. Electron. Agric. 2008, 63, 140–146. [Google Scholar] [CrossRef]
- Jian, F.; Jayas, D.S.; White, N.D. Temperature Fluctuations and Moisture Migration in Wheat Stored for 15 Months in a Metal Silo in Canada. J. Stored Prod. Res. 2008, 45, 82–90. [Google Scholar] [CrossRef]
- Khatchatourian, O.; De Oliveira, F. Mathematical Modelling of Airflow and Thermal State in Large Aerated Grain Storage. Biosyst. Eng. 2006, 95, 159–169. [Google Scholar] [CrossRef]
- Jiménez-Islas, H.; Navarrete-Bolaños, J.L.; Botello-Álvarez, E. Numerical Study of the Natural Convection of Heat and 2-D Mass of Grain Stored in Cylindrical Silos. Agrociencia 2004, 38, 325–342. [Google Scholar]
- Molina-Herrera, F.I.; Quemada-Villagómez, L.I.; Calderón-Ramírez, M.; Martínez-González, G.M.; Jiménez-Islas, H. Modeling Temperature and Moisture Dynamics in Corn Storage Silos: A Comparative 2D and 3D Approach. Modelling 2025, 6, 7. [Google Scholar] [CrossRef]
- Valle, F.J.M.; Gastón, A.; Abalone, R.M.; De la Torre, D.A.; Castellari, C.C.; Bartosik, R.E. Study and Modelling the Respiration of Corn Seeds (Zea mays L.) During Hermetic Storage. Biosyst. Eng. 2021, 208, 45–57. [Google Scholar] [CrossRef]
- Quemada-Villagómez, L.I.; Molina-Herrera, F.I.; Carrera-Rodríguez, M.; Calderón-Ramírez, M.; Martínez-González, G.M.; Navarrete-Bolaños, J.L.; Jiménez-Islas, H. Numerical Study to Predict Temperature and Moisture Profiles in Unventilated Grain Silos at Prolonged Time Periods. Int. J. Thermophys. 2020, 41, 52. [Google Scholar] [CrossRef]
- Khankari, N.K.K.; Morey, N.R.V.; Patankar, N.S.V. Application of a Numerical Model for Prediction of Moisture Migration in Stored Grain. Trans. ASAE 1995, 38, 1789–1804. [Google Scholar] [CrossRef]
- Jiang, N.S.; Jofriet, N.J.C. Finite Element Prediction of Silage Temperatures in Tower Silos. Trans. ASAE 1987, 30, 1744–1750. [Google Scholar] [CrossRef]
- Jofriet, J.C.; Jiang, S.; Tang, S.W. Finite Element Prediction of Temperature Gradients in Walls of Cylindrical Concrete Storage Structures. Can. J. Civ. Eng. 1991, 18, 12–19. [Google Scholar] [CrossRef]
- Abalone, R.; Gastón, A.; Cassinera, R.; Lara, M. Modelización de la Distribución de la Temperatura y Humedad en Granos Almacenados en Silos. Mecánica Comput. Asoc. Argent. 2006, XXV, 233–247. [Google Scholar]
- Dick, E. Introduction to Finite Volume Methods in Computational Fluid Dynamics. In Computational Fluid Dynamics; Springer: Berlin/Heidelberg, Germany, 2008; pp. 275–301. [Google Scholar] [CrossRef]
- Moukalled, F.; Mangani, L.; Darwish, M. The Finite Volume Method in Computational Fluid Dynamics; Fluid Mechanics and Its Applications; Springer: Cham, Switzerland, 2015. [Google Scholar] [CrossRef]
- Carrera-Rodríguez, M.; Martínez-González, G.M.; Navarrete-Bolaños, J.L.; Botello-Álvarez, J.E.; Rico-Martínez, R.; Jiménez-Islas, H. Transient Numerical Study of the Effect of Ambient Temperature on 2-D Cereal Grain Storage in Cylindrical Silos. J. Stored Prod. Res. 2011, 47, 106–122. [Google Scholar] [CrossRef]
- Markowski, M.; Bialobrzewski, I.; Bowszys, J.; Suchecki, S. Simulation of Temperature Distribution in Stored Wheat Without Aeration. Dry. Technol. 2007, 25, 1527–1536. [Google Scholar] [CrossRef]
- Alagusundaram, N.K.; Jayas, N.D.S.; White, N.N.D.G.; Muir, N.W.E. Three-Dimensional, Finite Element, Heat Transfer Model of Temperature Distribution in Grain Storage Bins. Trans. ASAE 1990, 33, 577–584. [Google Scholar] [CrossRef]
- Trombete, F.M.; De Ávila Moraes, D.; Porto, Y.D.; Santos, T.B.; Direito, G.M.; Fraga, M.E.; Saldanha, T. Determination of Aflatoxins in Wheat and Wheat By-Products Intended for Human Consumption, Marketed in Rio de Janeiro, Brazil. J. Food Nutr. Res. 2014, 2, 671–674. [Google Scholar] [CrossRef]
- Arlindo, M.A.; Ivano, A.D.; Antonio, C.B.N.; Beethoven, G.X.A.; Guiliano, R.A.; Mateus, M.S. Development of an Automated System of Aeration for Grain Storage. Afr. J. Agric. Res. 2016, 11, 4293–4303. [Google Scholar] [CrossRef]
- Lopes, D.d.C.; Neto, A.J.S.; Júnior, R.V. Comparison of Equilibrium Models for Grain Aeration. J. Stored Prod. Res. 2014, 60, 11–18. [Google Scholar] [CrossRef]
- Mirko, B.; Ljiljana, B.; Milivoj, R.; Ivan, P.; Zoran, S. Air Velocity Distribution During the Grain Aeration in Silo. DOAJ 2015, 19, 123–126. Available online: https://doaj.org/article/88d812723fc347d0a57f366620506fa4 (accessed on 5 November 2024).
- Khankari, N.K.K.; Morey, N.R.V.; Patankar, N.S.V. Mathematical Model for Moisture Diffusion in Stored Grain Due to Temperature Gradients. Trans. ASAE 1994, 37, 1591–1604. [Google Scholar] [CrossRef]

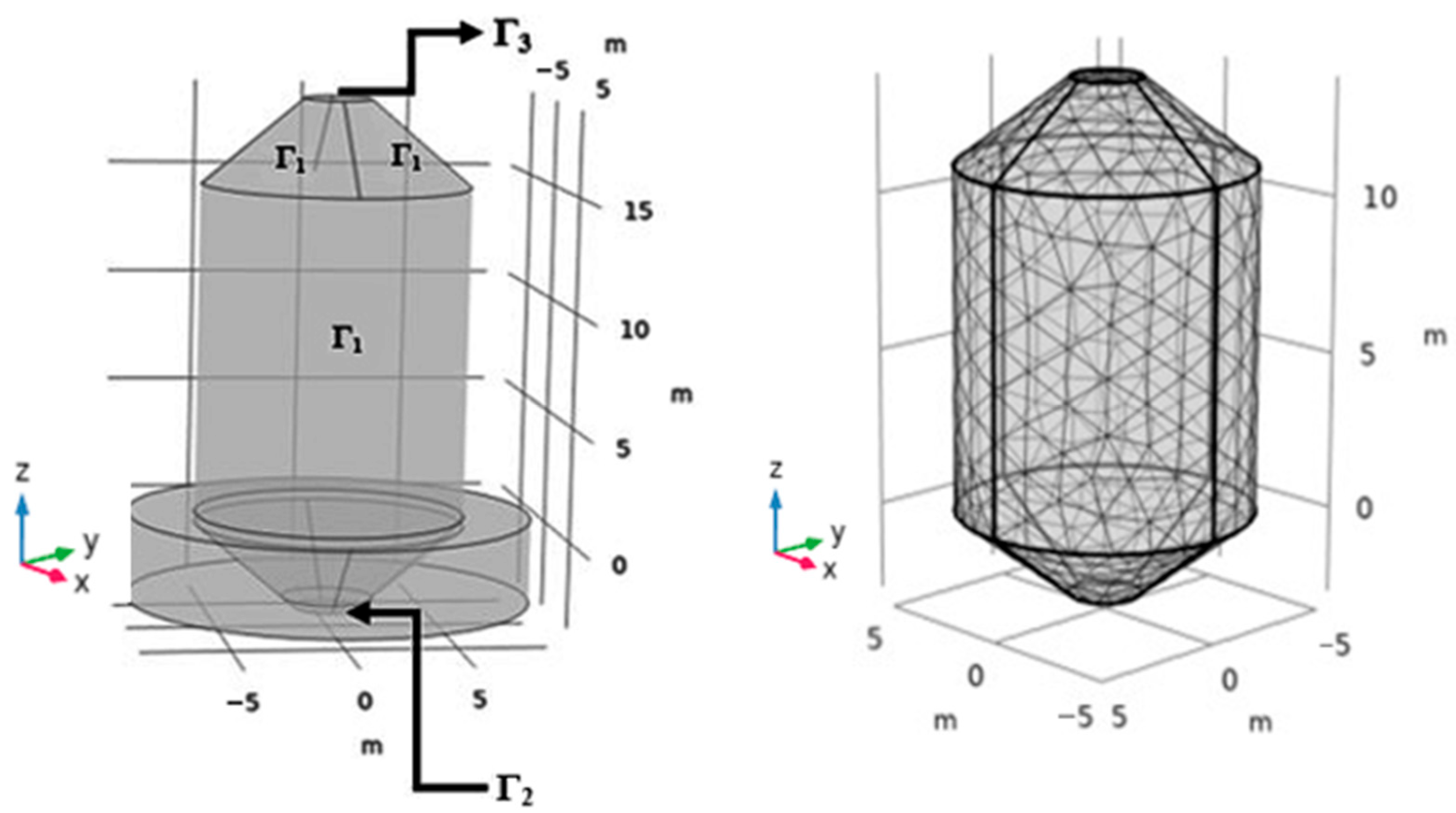








| Variable | Symbol |
|---|---|
| Specific heat | |
| Fluid density | |
| Grain density | |
| Air velocity | |
| Temperature | |
| Moisture content in the air | |
| Moisture content in the grain | |
| Diffusivity of water in air | |
| Diffusivity of water in the grain | |
| Effective thermal conductivity | |
| Grain-air interface | |
| Absolute humidity grain-air interface | |
| Mass transfer coefficient | |
| Fluid viscosity | |
| Permeability |
| Boussinesq approximation | ||
| Respiration heat | ||
| Water generation | ||
| Sorption isotherm | ||
| Water vapor pressure | ||
| Equilibrium moisture at the interface |
| Variable | Symbol |
|---|---|
| Reference concentration | |
| Water activity | |
| Molecular mass of water | |
| Molecular mass of air | |
| Average molecular mass | |
| Volumetric generation of water by respiration | |
| Vapor Pressure | |
| Universal gas constant | R |
| Volumetric heat of respiration of cereal grain | |
| Reference temperature | |
| volumetric coefficient of thermal expansion, | |
| volumetric coefficient of mass expansion |
| Parameters | Value | |
|---|---|---|
| Corn parameters a | Initial moisture content of corn Initial temperature Density Specific heat Thermal conductivity Effective thermal conductivity Permeability Porosity | 14.5% 20 °C 760 kg/m3 1780 kJ/kg K 0.13 W/m K 0.089W/m K 3.5 × 10−9 m2 0.38 |
| Air parameters a | Reference temperature Specific heat Thermal conductivity Viscosity Heat transfer coefficient Mass transfer coefficient Interfacial area Relative humidity (%) | 25 °C 972.92 kJ/kg K 0.023697 W/m K 1.7810−5 Pa s 15 W/m2 K 1.00 × 10−4 m/s 760 m2/m3 50 |
| Parameters for the Thermal Model | |
|---|---|
| Convective heat transfer coefficient Sky temperature # Sky emissivity # Steel emissivity # Steel absorptivity # Stefan-Boltzmann constant | σ = 5.670374419 × 10−8 W m−2 K−4 |
| Parameters for the mass transfer model | |
| Water diffusivity in air * Water diffusivity in corn Mass transfer coefficient * Particle diameter Interfacial area * | 2.437 × 10−5 m2/s 2.8766 × 10−11 m2/s 1.00 × 10−4 m/s 0.005 m 744 m2/m3 |
| Without Aeration | With Aeration | Without Aeration | With Aeration | ||||
|---|---|---|---|---|---|---|---|
| Mesh Size | NEB | Tmax °C | Tmin °C | Tmax °C | Tmin °C | Computation Time (min) | Computation Time (min) |
| Normal Fine Finer Extra Fine | 1813 3031 5938 14,729 | 29.457 32.915 34.014 34.347 | 17.953 17.948 17.966 17.960 | 18.984 18.983 19.064 19.072 | 15.654 16.046 16.236 16.248 | 14.58 18.37 45.26 68.58 | 11.29 14.54 33.30 57.40 |
| Insect | Optimal Temperature (°C) | Optimal Relative Humidity (%) |
|---|---|---|
| Maize weevil Indian meal moth Grain beetle Saw-toothed grain beetle Lesser grain borer Larger grain borer Dust mite | 25–30 30–35 20–25 20–25 18–28 20–35 25–30 | 85–99 80–95 78–85 75–90 70–85 80–90 85–95 |
| Fungus | Optimal Temperature (°C) | Optimal Relative Humidity (%) |
|---|---|---|
| Aspergillus flavus Aspergillus niger Penicillium spp. Fusarium spp. Cladosporium spp. Rhizopus spp. Mucor spp. | 25–30 30–35 20–25 20–25 18–28 20–30 25–30 | 85–99 80–95 78–85 78–90 70–85 80–90 85–95 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Molina-Herrera, F.I.; Jiménez-Islas, H.; Sandoval-Hernández, M.A.; Maldonado-Sierra, N.E.; Domínguez Campos, C.; Jarquín Enríquez, L.; Mondragón Rojas, F.J.; Flores-Martínez, N.L. Modeling of Temperature and Moisture Dynamics in Corn Storage Silos with and Without Aeration Periods in Three Dimensions. ChemEngineering 2025, 9, 89. https://doi.org/10.3390/chemengineering9040089
Molina-Herrera FI, Jiménez-Islas H, Sandoval-Hernández MA, Maldonado-Sierra NE, Domínguez Campos C, Jarquín Enríquez L, Mondragón Rojas FJ, Flores-Martínez NL. Modeling of Temperature and Moisture Dynamics in Corn Storage Silos with and Without Aeration Periods in Three Dimensions. ChemEngineering. 2025; 9(4):89. https://doi.org/10.3390/chemengineering9040089
Chicago/Turabian StyleMolina-Herrera, F. I., H. Jiménez-Islas, M. A. Sandoval-Hernández, N. E. Maldonado-Sierra, C. Domínguez Campos, L. Jarquín Enríquez, F. J. Mondragón Rojas, and N. L. Flores-Martínez. 2025. "Modeling of Temperature and Moisture Dynamics in Corn Storage Silos with and Without Aeration Periods in Three Dimensions" ChemEngineering 9, no. 4: 89. https://doi.org/10.3390/chemengineering9040089
APA StyleMolina-Herrera, F. I., Jiménez-Islas, H., Sandoval-Hernández, M. A., Maldonado-Sierra, N. E., Domínguez Campos, C., Jarquín Enríquez, L., Mondragón Rojas, F. J., & Flores-Martínez, N. L. (2025). Modeling of Temperature and Moisture Dynamics in Corn Storage Silos with and Without Aeration Periods in Three Dimensions. ChemEngineering, 9(4), 89. https://doi.org/10.3390/chemengineering9040089







