Abstract
Deep reinforcement learning has been extensively applied for resource allocation in elastic optical networks. However, many studies focus on link-level state analysis and rarely discuss the influence between links, which may affect the performance of allocation algorithms. In this paper, we propose a multi-link fragmentation deep reinforcement learning-based routing and spectrum allocation algorithm (MFDRL-RSA). We number the links using a breadth-first numbering algorithm. Based on the numbering results, high-frequency links are selected to construct the network state matrix that reflects the resource distribution. According to the state matrix, we calculate a multi-link fragmentation degree, quantifying resource fragmentation within a representative subset of network. The MFDRL-RSA algorithm enhances the accuracy of the agent’s decision-making by incorporating it into the reward function, thereby improving its performance in routing decisions, which contributes to the overall allocation performance. Simulation results show that MFDRL-RSA achieves lower blocking rates compared to the reference algorithms, with reductions of 16.34%, 13.01%, and 7.42% in the NSFNET network and 19.33%, 15.17%, and 9.95% in the Cost-239 network. It also improves spectrum utilization by 12.28%, 9.83%, and 6.32% in NSFNET and by 13.92%, 11.55%, and 8.26% in Cost-239.
1. Introduction
Elastic optical networks (EONs) have been extensively adopted in optical communication networks due to the flexibility in resource allocation [1]. As the utilization of EONs continues to increase, optimizing network performance has become a primary concern. routing and spectrum allocation (RSA) are critical in enhancing network efficiency. The RSA process can result in spectrum fragmentation arising due to allocation constraints, leading to the underutilization of spectrum, which causes resource wastage and service blocking [2,3,4]. Consequently, addressing spectrum fragmentation has become a key area of research in RSA optimization. In the last decade, many heuristic algorithms have been developed to address the RSA problem. And in recent years, significant growth has been seen in applying deep reinforcement learning (DRL) to network optimization problems, which has been primarily driven by advancements in artificial intelligence technologies [5,6,7,8]. DRL learns optimal strategies from historical and real-time network data without predefined rules. Compared to heuristic-based algorithms, DRL has demonstrated superior adaptability, flexibility, and efficiency, which can effectively address the evolving demands of networks and complex resource allocation challenges [9,10]. As a result, DRL has become a powerful tool for solving the RSA problem in EONs, with great potential for future research and practical use [11]. However, current DRL-based allocation algorithms face issues such as reward convergence to fixed values and poorly designed rewards that overlook interdependence among network links, leading to insufficient guidance for the agent.
To optimize the reward function of DRL, we proposed an MFDRL-RSA algorithm. This algorithm introduces a multi-link fragmentation degree into the reward function, aiming to help the agent focus on the heavily utilized parts of the network when making routing allocation decisions, rather than just the current candidate path. The innovations of MFRDL-RSA algorithm are as follows:
- Unlike other studies that evaluate spectrum fragmentation only on the links within the current candidate path, the MFDRL-RSA algorithm focusses on multiple links along different paths. Since spectrum fragmentation of links can influence each other, focusing on the candidate path may ignore the impact of allocation decisions on subsequent requests. In contrast, the multi-link fragmentation degree offers a more holistic and effective assessment of global allocation.
- We propose a breadth-first numbering (BFN) algorithm to ensure that the network state matrix constructed based on link numbering can represent the connectivity of links. This is crucial for correlating the multi-link fragmentation degree in the MFDRL-RSA algorithm with the distribution of network resource.
Simulation results show that in the NSFNET network, MFDRL-RSA reduces the blocking rate by 16.34%, 13.01%, and 7.42% and improves spectrum utilization by 12.28%, 9.83%, and 6.32% compared to KSP-FF, DeepRMSA, and DeepSF-PCE, respectively. In the Cost-239 network, it achieves greater improvements, with blocking rate reductions of 19.33%, 15.17%, and 9.95% and spectrum utilization improvements of 13.92%, 11.55%, and 8.26%, respectively. These findings underscore the efficacy of the MFDRL-RSA algorithm in enhancing the efficiency of EONs. Building upon the performance improvements already achieved by the basic DRL algorithm, MFDRL-RSA further reduces network blocking, positioning it as a promising solution for future optimization challenges.
2. Related Work
For the RSA problem in EONs, numerous heuristic algorithms have been proposed in past decades. For example, [12] proposed an adjustable defragmentation algorithm that uses the golden metric to guide selective rerouting. By combining heuristic and meta-heuristic strategies, it effectively reduces spectral fragmentation and blocking probability. And [13] proposed a service-driven fragmentation-aware scheme that reduces fragmentation during RSA by considering both the path and neighboring links. Using a new service-driven fragmentation metric with contiguous available resource separation degree, which also improves spectrum utilization. However, despite their performance benefits, such heuristic-based approaches typically rely on fixed rules or handcrafted metrics, which limit their adaptability in dynamic conditions. They struggle to generalize across varying traffic patterns or topological changes, reducing their effectiveness in real deployments where conditions evolve rapidly.
In recent years, DRL has developed rapidly and has been increasingly applied to resource allocation problems in EONs. For example, [14] proposed DeepRMSA, a DRL-based framework that, for the first time, demonstrated the effectiveness of applying DRL to solve the RSA problem. Compared with traditional methods, it achieved a significant reduction in blocking rate. In [15], an RMSA algorithm was introduced, which is based on deep Q-networks and incorporates prioritized experience replay, aiming to enhance the performance of dynamic spectrum allocation. However, these approaches adopt fixed-form reward functions, which offer limited capability to reflect the agent’s decision-making behavior and its impact on the overall network state.
To overcome this limitation, recent studies have focused on optimizing reward function design by embedding richer environmental feedback, enabling agents to learn more effective and adaptive strategies. In [16], a DRL-based framework was proposed with four reward functions to guide agent behavior: Reward1 encourages using available bands, Reward2 promotes compact spectrum, Reward3 combines both, and Reward4 reduces fragmentation. These designs helped lower network blocking rates. In [17], a DRL-based path computation engine was proposed. Its reward function was designed to encourage allocations that reduce future fragmentation by incorporating the change in Shannon entropy before and after allocation, which effectively helped lower the blocking rates. In [18], a DRL-assisted reoptimization framework was proposed to determine the optimal timing for reconfiguration. A Q learning agent was employed, with a reward function that balances request acceptance probability and reconfiguration cost, effectively suppressing spectrum defragmentation. In [19], the DRL algorithm introduced a proactive defragmentation strategy that integrates spectrum entropy and residual spectrum space into the reward function. This design helps the agent reduce fragmentation and blocking rate while controlling reconfiguration overhead. In [20], the author proposed an end-to-end DRL framework for joint routing and spectrum assignment. Its reward function is designed to implicitly capture spectrum fragmentation, guiding the agent toward more spectrum-efficient and defragmented resource allocations under dynamic traffic conditions. In [21], the authors proposed a heuristic reward-based DRL framework for RMSA in EONs. The reward function incorporates spectrum fragmentation level, quantified by two specific metrics. This encourages the agent to select actions that minimize fragmentation, thereby reducing blocking rate. Finally, [22] presented a DRL algorithm which incorporates quality-of-transmission awareness into reward design, guiding the agent to select feasible light paths and avoid low-quality routes, improving learning efficiency and overall network performance. These studies collectively demonstrate that embedding environment information into the reward function can significantly improve learning performance. Nevertheless, they still rely primarily on single-path information, lacking a holistic view of the network state. This limits the reward function’s ability to provide accurate and comprehensive feedback, thereby constraining the generalizability and optimality of the policies. Therefore, to address these limitations, we propose the MFDRL-RSA algorithm.
3. Multi-Link Fragmentation Deep Reinforcement Learning-Based Routing, Modulation, and Spectrum Allocation Algorithm
3.1. Problem Formulation
The EONs topology is modeled as a graph , where and represent the sets of nodes and fiber links, respectively. The request is modeled as , where is the source node, is the end node, is the data rate requirement, and is the request duration. When a new request arrives, the selection of a path is initiated. This selection is made from a pre-calculated set of K-shortest candidate paths, as determined by the shortest routing algorithm. The selection of the modulation level is then made based on the selected path’s length and the values presented in Table 1 [13].

Table 1.
Transmission reach for different modulation formats.
The number of required frequency slots (FSs) is calculated using Equation (1) [3]:
where is employed to denote the guard band, and represents the modulation level. The FS that satisfies the spectrum allocation constraints and specified number are allocated on each link of the selected path. The constraints include spectrum contiguity (the allocated FSs must be continuous on each link) and continuity (allocated FSs must be the same in all links along the selected path). In the event of a successful allocation, the request is accepted; otherwise, it is blocked.
3.2. Environment Perception Information State
An appropriate environment perception information state is critical for DRL to solve the RSA problem [9]. The environment perception information state is defined as shown in Equation (2):
The environment perception information state space is structured as a matrix with dimensions and incorporates information about the request and the candidate paths. The vectors and are binary vectors of length , encoding the presence 1 or absence 0 of each node in the network as the source and end nodes, respectively. The represents the request’s duration and occupies one element in the vector. denotes the starting index of the first available FS on the k- path, and denotes its length. denotes the number of FS required on the k- path. and denote the total and mean number of available FS on the k- path, respectively.
3.3. Action
The DRL agent continuously interacts with the environment, formulating strategies and executing actions. The action space is defined as shown in Equation (3). It is structured as a matrix with dimensions of [14]. The DRL agent is responsible for selecting one path from candidate paths, focusing only on optimizing routing decisions, while spectrum allocation is handled using the first-fit (FF) strategy [23], which assigns the first contiguous set of free FS that can accommodate the request.
3.4. Reward
Most approaches to optimizing DRL-based allocation algorithms are limited in their consideration of the state of single paths, neglecting the interdependencies between different links in the network and lacking a comprehensive assessment of the overall resource state. Consequently, these methods provide incomplete and imprecise evaluations of the agent’s decisions. Therefore, in the MFDRL-RSA algorithm, we propose a multi-link fragmentation degree, which aims to offer a more thorough evaluation of resource distribution within a representative subset of network, thereby improving the agent’s learning processes. The multi-link fragmentation degree is calculated based on the network state matrix, with the important caveat that the neighboring links in the network state matrix must be connected in the topology to ensure the reliability of the fragmentation degree calculation. Hence, the links must be sorted in a specific order. The traversing adjacency matrix (TAM) algorithm [24] is a widely adopted method that performs link sorting by sequentially traversing the network’s adjacency matrix. However, TAM sorts links based on the order of nodes, without considering the connectivity between links. To address this limitation, we propose a BFN algorithm, which is inspired by the breadth-first search (BFS) algorithm. BFS explores graph structures layer by layer, preserving the proximity relationships between nodes [25,26]. Building on this principle, BFN assigns link numbers by considering topological connectivity, ensuring that links with adjacent numbers are connected with each other.
The process of TAM is as follows: first, the adjacency matrix of the nodes is constructed, and then each row of the matrix is traversed sequentially. In the first row, the links between node 1 and node 2, and between node 1 and node 6 are visited in order. They are assigned as “Link 1” and “Link 2”, respectively. Then, in the second row, the links between node 2 and node 4, and between node 2 and node 5, are visited in order. They are assigned as “Link 3” and “Link 4”, respectively. This process continues in the same manner until all links are numbered. In Figure 1a,b, the results of the TAM algorithm show that Link 2 and Link 3 are assigned adjacent numbers but not connected; the same issue occurs with Link 4 and Link 5. Therefore, we propose the BFN algorithm, and the numbering process is as follows: first, node 1 is selected as the source node, and all connected links are assigned a numerical identifier. The link between nodes 1 and 6 is numbered as “Link 1”, and between nodes 1 and 2, it is numbered as “Link 2”. This is because node 2 has 3 adjacent links while node 6 has only two. Subsequently, node 2 is designated as the new source node, and the process is repeated until all links are numbered. Unlike TAM, the results of the BFN algorithm in Figure 1a,c demonstrate that all links with adjacent numbers are connected with each other. Algorithm 1 specifically illustrates the working procedure of the BFN algorithm, including topology traversal, variable initialization, link numbering, and iterative updates.
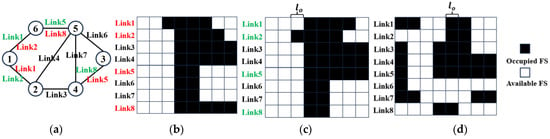
Figure 1.
Illustration of the network states under different numbering algorithms and at different conditions. (a) Six-node network topology. (b) Illustration of the network state matrix of TAM. (c) Illustration of the network state matrix of BFN. (d) Illustration of the network state matrix of BFN, with different FS occupation from (c). Red and green links indicate the different link numbering results between the TAM and BFN algorithms, and black links indicate the parts that are the same.
| Algorithm 1: Breadth-first numbering |
| 1.; |
| 2. ; |
| 3. ; |
| 4. do |
| 5.; |
| 6. do |
| 7. then |
| 8. ; |
| 9. end |
| 10. based on the number of adjacent links at the other end node; |
| 11. do |
| 12. as numbered; |
| 13. ; |
| 14. end |
| 15. ; |
| 16.end |
The change in the area-to-perimeter ratio is utilized to the degree of multilink fragmentation in the network state matrix. The matrix element is accomplished by calculating the ratio of free FS adjacent to occupied FS to the total number of occupied FS, thereby indicating the distribution of resources across the network. The resultant fragmentation degree is then normalized to ensure the stability of the reinforcement learning agent during training, as depicted in Equation (4):
where represents the number of occupied FSs, and represents the number of unoccupied FSs that are “adjacent” to the occupied FSs (adjacent FS on the same link and same FS on adjacent links are considered as “adjacent”; i.e., one FS has four “adjacent” FSs). represents the maximum value that can take, which occurs when all four adjacent FSs of every occupied FS in the network are free. In this case, . represents the minimum value that can take, which occurs when no resources in the network have been occupied. In this case, . Figure 1c,d show the network state matrices with the same number of FSs under different distributions. According to the Equation (4), for the Figure 1c: . And for Figure 1d: . Compared to Figure 1d, the distribution of occupied FSs in Figure 1c is more uniform, with less segmentation of available FSs. It can be observed that when the total number of occupied FSs is the same, the larger the value, the greater resource availability.
Based on this, the reward function is designed as shown in Equation (5):
Here, “success” means that the routing path selected by the agent led to a feasible spectrum allocation using the FF strategy, and the request was accepted. In this case, reward is fed back. “Blocking” means that no spectrum could be found along the selected path, resulting in request rejection. In this case, a reward of −1 is returned.
3.5. Training
In this paper, we adopt the asynchronous advantage actor-critic (A3C) algorithm, a multi-threaded variant of the actor-critic (AC) method [27]. The algorithm trains multiple AC networks in the environment and periodically updates the training parameters of each local network to the global AC network [28]. The agent aims to learn the optimal routing strategy that maximizes the accumulated discounted reward. During the agent’s training, each round stores the training results in an experienced pool. When the pool contains samples, the is calculated. is the discounted sum of future rewards starting from time step . Equation (6) shows the calculation of [29]:
where is the discount factor.
In each local AC network of the multi-thread, there is a policy network and a value network . Here, represents the network parameters of the policy network, and represents the network parameters of the value network. When the agent receives the reward feedback, it updates the global network parameters through gradient updating. Equations (7) and (8) show how it works [30]:
where and denote the parameters of the global network. denotes the extent to which the output action exceeds the expected average level. The policy entropy is used to enhance the agent’s ability to explore the environment, where denotes the regularization strength of the policy entropy.
Algorithm 2 shows the basic training process of the MFDRL-RSA algorithm presented in this paper. Upon receiving a novel request, the system determines whether the experience pool is vacant. If it is, and this constitutes the initial request, the local network parameters are synchronized with the global network parameters. Then, the agent engages with the environment to procure environment perception information state and selects actions based on the prevailing policy.
Executing these actions generates samples containing environment perception information state, action, reward, and other relevant information, which are then stored in the experience pool. Once the experience pool accumulates 2N-1 samples, the model is trained using the first samples from the experience pool. Calculating the cumulative discounted reward updates the global network parameters. This step ensures the agent continuously learns an optimized routing strategy, effectively reducing the blocking rate when combined with FF spectrum allocation.
| Algorithm 2: Training process of MFDRL-RSA algorithm |
| 1.; |
| 2.for every request do |
| 3. then |
| 4.; |
| 5.; |
| 6.; |
| 7. ; |
| 8. ; |
| 9. then |
| 10. do |
| 11. ; |
| 12. end |
| 13. ; |
| 14. ; |
| 15.end |
In summary, the MFDRL-RSA algorithm continuously updates and optimizes its model through the training process above. During training, the A3C agent leverages a fragmentation-aware reward function to perceive the current distribution of network resources in real time, enabling timely feedback and ongoing policy adjustment. The model interacts continuously with the environment, observes the spectrum allocation results produced by the fixed FF policy for each routing decision, and gradually improves its routing strategy through repeated experience. This allows the model to naturally adapt to the dynamic state of the network without requiring explicit environmental modeling. As the spectrum usage and fragmentation changes with traffic patterns, the agent updates its routing policy to maintain effective and flexible allocation decisions under dynamic conditions.
4. Simulation and Analysis
4.1. Simulation Setup
In this paper, the 14-node NSFNET [31] and 11-node Cost-239 [32] networks are selected for simulation (see Figure 2a,b). Each optical fiber link is equipped with 320 FSs; each FS is 12.5 . Requests are generated according to the Poisson process, with an average arrival rate and service duration following Poisson distribution with parameter and exponential distribution with parameter , respectively. Thus, the traffic load is λ/μ Erlang. The bandwidth demand for each request is uniformly distributed between 25 and 100 . The neural network in the AC network consists of five hidden layers, each with 128 neurons. The ReLU activation function is used for hidden layers, and the Adam optimizer is employed for training. The batch size is set to 200. The number of candidate paths is set to 5. The discount factor and the entropy regularization coefficient are set to 0.95 and 0.01, respectively. The exploration rate starts at 1 and is gradually decayed by . The minimum value is 0.05. A total of 500 training episodes are performed, each consisting of 10,000 connection requests.
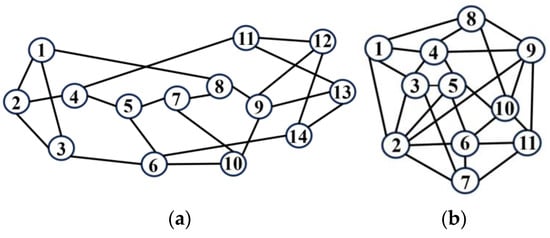
Figure 2.
Network topology in simulations. (a) NSFNET topology, (b) Cost-239 topology.
4.2. Simulation Result
In this section, the simulation results are presented to evaluate the performance of the MFDRL-RSA. Two metrics are used for the assessment: blocking rate and spectrum resource utilization. The blocking rate is defined as the ratio of the number of blocked requests to the total number of requests processed, while the spectrum resource utilization is defined as the ratio of occupied FSs to the total available FSs across all links in the network. These two metrics are commonly used to evaluate the effectiveness of RSA algorithms. A lower blocking rate indicates that the algorithm can successfully accommodate more requests. And a higher spectrum utilization implies that the algorithm can make more efficient use of available FSs, reducing spectrum waste caused by fragmentation.
The substantial volume of link state data implicated in the fragmentation calculation can potentially lead to prolonged training times for the model. To address this, we analyze the computational complexity of the fragmentation degree calculation defined in Equation (4), which measures the ratio of adjacent free FSs to occupied FSs across a set of links. Specifically, for each occupied FS, we traverse up to four adjacent FS positions to determine whether they are free. This results in a per-slot complexity of . Let denote the total number of links in the network and denote the number of FSs per link. Then, the total number of slot positions is , and in the worst case where most FSs are occupied, the overall complexity of calculating the fragmentation degree over all links is , simplified as assuming is constant. To reduce the computational burden, we propose using high-frequency links that appear more often in k shortest paths between node pairs. For the NSFNET topology, the 11 links (out of 22 total) that emerge with a frequency that exceeds the mean are designed as high-frequency links. Let denote the number of high-frequency links. The complexity of the fragmentation calculation under this approach becomes and, since , it is approximately , effectively reducing the computation cost.
The training results for the link statistic cases described above are presented in Figure 3. KSP-FF (k shortest path and first-fit) is a widely used heuristic algorithm for RSA in EONs [33]. Compared to it, the MFDRL-RSA algorithm achieves a lower blocking rate in both link statistic cases. MF-RSA is a heuristic algorithm developed based on the fragmentation degree proposed in this paper. In MF-RSA, for each request, the state matrix is constructed based on all links. The fragmentation degree of each feasible allocation is then calculated using the proposed equation, and the option with the highest value is selected for spectrum allocation. MFDRL-RSA-WA (short for MFDRL-RSA with all links) and MFDRL-RSA-WHF (short for MFDRL-RSA with high-frequency links) are two variants of the MFDRL-RSA algorithm that differ in how they calculate the multi-link fragmentation degree. MFDRL-RSA-WA computes fragmentation based on all links, and MFDRL-RSA-WHF focuses only on high-frequency links.
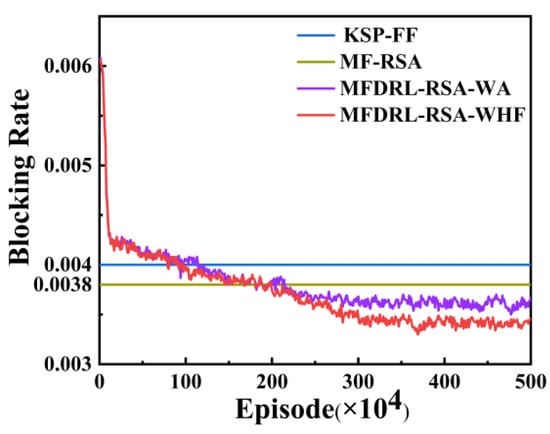
Figure 3.
Blocking rate of KSP-FF, MF-RSA, and MFDRL-RSA algorithms with different link statistic cases in NSFNET.
The results demonstrate that the algorithm incorporating fragmentation degree into the reward function of DRL achieves a lower blocking rate than the MF-RSA. Specifically, the MFDRL-RSA-WA algorithm using all links achieves an average blocking rate reduction of 5.15%, while the MFDRL-RSA-WHF algorithm using high-frequency links achieves an average reduction of 9.14%. This is because the fragmentation degree we designed is mainly calculated based on the resource status of a subset of links in the network. During the processing of each request, if the links involved are not within the scope of the state matrix, the allocation decision will not directly affect the value of the fragmentation degree. As a result, the metric fails to provide meaningful guidance. However, heuristic metrics are usually expected to clearly indicate the quality of different allocation options during each request, thus guiding decision-making. The fragmentation degree cannot fulfill this need, so it is not suitable for heuristic algorithms.
With adaptive learning capability, DRL can learn the latent information embedded in the fragmentation degree during training, thereby developing more effective routing strategies to reduce network fragmentation. As a result, the MFDRL-RSA algorithm successfully leverages the characteristics and advantages of DRL. Meanwhile, the blocking rate is demonstrably lower for the high-frequency link case than the all-links case, with an average reduction of approximately 5.31%. In the all-links case, the low-occupancy links increase the reward for decision. This distorts the multi-link fragmentation degree, thereby affecting the agent’s decision optimization. In contrast, the multi-link fragmentation degree in cases of a high-frequency link is more accurate. This is due to the selection of high-frequency links, which are key to determining whether a request is accepted or rejected, thereby providing the agent with more meaningful guidance for decision optimization. The fragmentation degree calculations in the following simulations are based on high-frequency links, which both accelerate the training process and enhance performance through a better-informed reward signal.
Figure 4 and Figure 5 show the blocking rate variation in different algorithms in the NSFNET and Cost-239 network environments when the traffic load is 250 Erlang. The blocking rate is calculated for every 10,000 request arrivals, and the entire training process consists of 500 episodes. It can be observed that in both network environments, the MFDRL-RSA, DeepSF-PCE, and DeepRMSA algorithms progressively converge to a stable performance as training advances. DeepRMSA is a widely referenced DRL-based allocation algorithm characterized by a simple reward function where a successful request receives a reward of 1, while a failed one receives −1 [14]. Compared to heuristic algorithms, DeepRMSA has been proven to more effectively reduce network blocking and enhance transmission performance, making it a fundamental benchmark in DRL resource allocation research. DeepSF-PCE is a fragmentation-aware DRL-based RMSA algorithm that enhances the reward function by incorporating Shannon entropy-based fragmentation metrics [17]. Compared to MFDRL-RSA, which constructs the network state matrix and computes the muti-link fragmentation degree based on representative links, DeepSF-PCE focuses only on the links within the current candidate path. This comparison highlights the advantage of the multi-link fragmentation degree, which provides a more holistic assessment of global allocation. Specifically, in the NSFNET network environment, the MFDRL-RSA algorithm reduces the blocking rate by 14.93% compared to the KSP-FF algorithm, by 12.11% compared to the DeepRMSA algorithm, and by 6.92% compared to the DeepSF-PCE algorithm. In the Cost-239 network environment, the MFDRL-RSA algorithm’s blocking rate is reduced by 18.11% compared to the KSP-FF algorithm, by 13.45% compared to the DeepRMSA algorithm, and by 9.27% compared to the DeepSF-PCE algorithm. Furthermore, the MFDRL-RSA algorithm has demonstrated remarkable adaptability across network environments, significantly enhancing transmission performance in NSFNET and Cost-239. Its superior capability highlights the potential to boost operational efficiency and service quality in EONs.
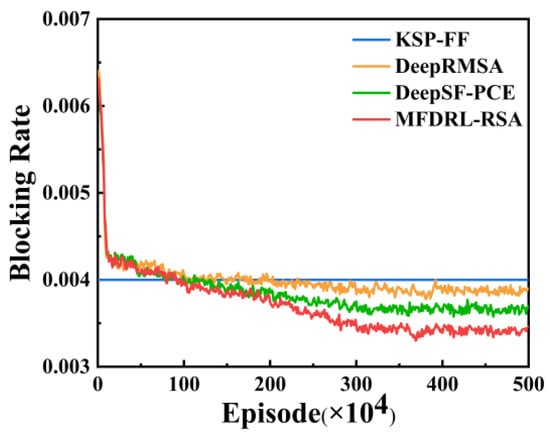
Figure 4.
Blocking rate of KSP-FF, DeepRMSA, DeepSF-PCE, and MFDRL-RSA in NSFNET.
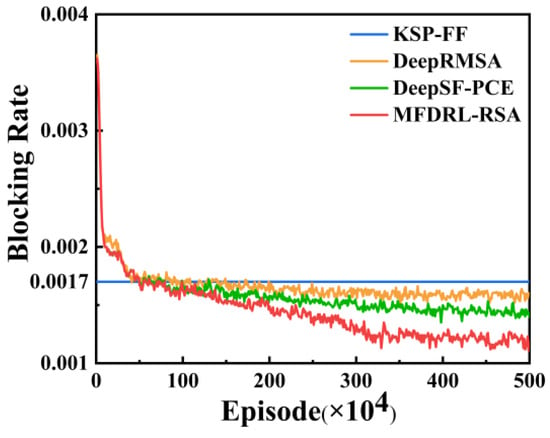
Figure 5.
Blocking rate of KSP-FF, DeepRMSA, DeepSF-PCE, and MFDRL-RSA in Cost-239.
Figure 6 and Figure 7, respectively, show the blocking rate and spectrum resource utilization results of different algorithms under different load conditions in the NSFNET network. The figures illustrate that as the network load increases, the blocking rate of all four algorithms rises. An increase in network load results in a higher utilization of spectrum resources, rendering it increasingly challenging to identify available free spectrum for subsequent service connections. In the NSFNET network, the blocking rate of the MFDRL-RSA algorithm is lower than that of the KSP-FF, DeepRMSA, and DeepSF-PCE algorithms. The blocking rate of the MFDRL-RSA algorithm is, on average, 16.34% lower than that of the KSP-FF algorithm, 13.01% lower than that of the DeepRMSA algorithm, and 7.42% lower than that of the DeepSF-PCE algorithm. The spectrum resource utilization by the MFDRL-RSA algorithm is higher than that of the KSP-FF, DeepRMSA, and DeepSF-PCE algorithms. Specifically, the resource utilization of the MFDRL-RSA algorithm is, on average, 12.28% higher than that of the KSP-FF algorithm, 9.83% higher than that of the DeepRMSA algorithm, and 6.32% higher than that of the DeepSF-PCE algorithm. The findings demonstrate the efficacy of the MFDRL-RSA algorithm in varying load conditions, outperforming reference approaches in reducing network blocking and improving resource utilization.
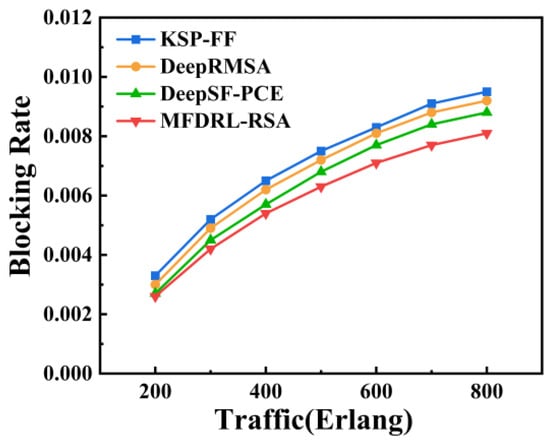
Figure 6.
Blocking rate of KSP-FF, DeepRMSA, DeepSF-PCE, and MFDRL-RSA under different traffic loads in NSFNET.
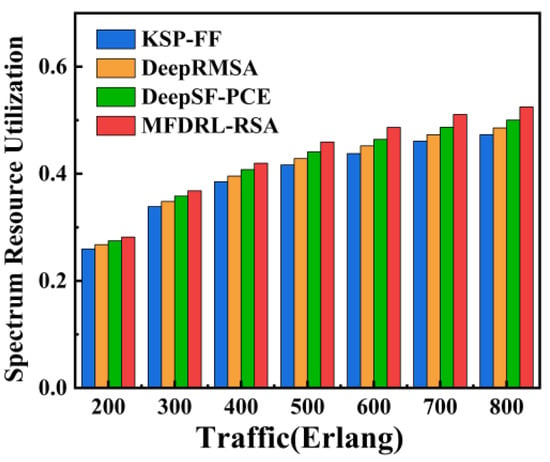
Figure 7.
Spectrum resource utilization of KSP-FF, DeepRMSA, DeepSF-PCE, and MFDRL-RSA under different traffic loads in NSFNET.
Figure 8 and Figure 9 illustrate the blocking rate and spectrum resource utilization of the algorithms under varying load conditions in the Cost-239 network. As network load increases, the blocking rate and spectrum resource utilization of all algorithms rise accordingly. In the Cost-239 network, the MFDRL-RSA algorithm achieves an average blocking rate that is 19.33% lower than that of the KSP-FF algorithm, 15.17% lower than that of the DeepRMSA algorithm, and 9.95% lower than that of the DeepSF-PCE algorithm. Additionally, the spectrum resource utilization of the MFDRL-RSA algorithm surpasses that of KSP-FF, DeepRMSA, and DeepSF-PCE. On average, MFDRL-RSA improves spectrum utilization by 13.92% over KSP-FF, 11.55% over DeepRMSA, and 8.26% over DeepSF-PCE. These results further confirm the effectiveness of the MFDRL-RSA algorithm under varying load conditions in different networks.
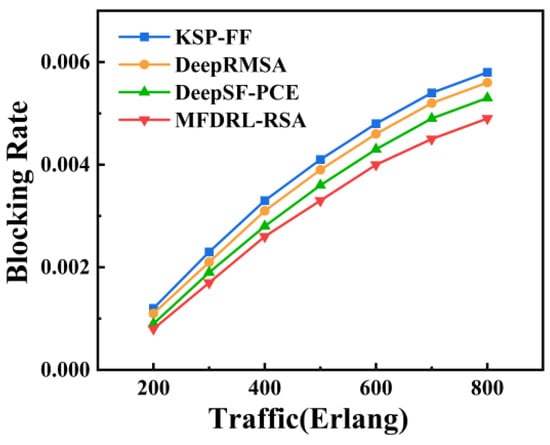
Figure 8.
Blocking rate of KSP-FF, DeepRMSA, DeepSF-PCE, and MFDRL-RSA under different traffic loads in Cost-239.
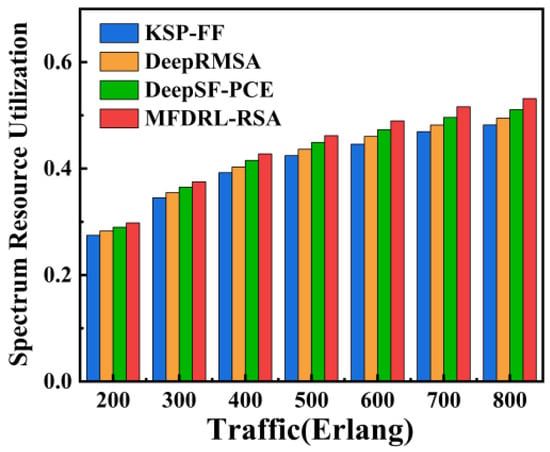
Figure 9.
Spectrum resource utilization of KSP-FF, DeepRMSA, DeepSF-PCE, and MFDRL-RSA under different traffic loads in Cost-239.
It is noteworthy that within the Cost-239 network, which is distinguished by a more significant number of links and an elevated level of environmental complexity, MFDRL-RSA exhibits a marked superiority in terms of optimization outcomes, achieving a more substantial reduction in blocking rates and a greater improvement in spectrum resource utilization compared to its performance in the NSFNET environment. This finding underscores the potential of MFDRL-RSA in enhancing transmission performance within complex network environments. The simulation results confirm the effectiveness of MFDRL-RSA in improving DRL-based routing decisions through a reward design with the multi-link fragmentation degree. This refinement allows the model to capture the network state better, leading to more informed routing decision-making. The efficacy of the MFDRL-RSA algorithm in comparison to other DRL-based resource allocation algorithms is demonstrated by its ability to reduce network blocking and enhance resource utilization.
5. Conclusions
This paper proposes MFDRL-RSA, an improved DRL-based routing algorithm for RSA problems that addresses the lack of global network awareness in existing methods. It introduces a multi-link fragmentation degree to evaluate resource distribution within a representative subset of a network. A novel BFN algorithm is used to preserve link adjacency in the network state matrix. To reduce computation, only high-frequency links are considered in fragmentation calculation, which improves training efficiency and lowers blocking rates compared to using all links. This fragmentation metric is integrated into the reward function, guiding the agent toward routing decisions that minimize fragmentation, with spectrum allocated using the FF strategy.
Simulation results show that MFDRL-RSA achieves lower blocking rates than KSP-FF, DeepRMSA, and DeepSF-PCE under identical load conditions in both NSFNET and Cost-239 networks and maintains consistent superiority under varying traffic loads. Specifically, it reduces average blocking rates by 16.34% and 19.33% compared to KSP-FF, by 13.01% and 15.17% compared to DeepRMSA, and by 7.42% and 9.95% compared to DeepSF-PCE, in NSFNET and Cost-239, respectively. In terms of spectrum utilization, MFDRL-RSA improves by 12.28% and 13.92% over KSP-FF, by 9.83% and 11.55% over DeepRMSA, and by 6.32% and 8.26% over DeepSF-PCE in the same networks. The gains are more pronounced in the more complex Cost-239 network. These results confirm that MFDRL-RSA is a practical solution for solving RSA problems in dynamic EONs.
Although MFDRL-RSA has shown promising results, several aspects remain to be explored. First, we did not consider the real deployment of the algorithm. In real networks, decision delay may cause degraded service. Thus, we plan to evaluate the decision time of MFDRL-RSA under the same hardware and compare it with other approaches. We will assess training time to discuss if the performance gain justifies the cost. Additionally, the model’s generalization is unexplored. Since real environments vary, we will test generalization by training on one topology, testing on others, and evaluating performance under different traffic patterns like bursty or non-Poisson arrivals.
Author Contributions
Conceptualization, J.J. and Y.S.; methodology, J.J. and Y.S.; software, J.J., Y.S. and T.S.; validation, J.J. and Y.S.; formal analysis, J.J., J.C. and Y.S.; investigation, J.J. and Y.S.; resources, J.J., J.C. and T.S.; data curation, J.J. and Y.S.; writing—original draft preparation, J.J. and Y.S.; writing—review and editing, J.J. and Y.S.; visualization, J.J. and Y.S.; supervision, J.J., J.C. and T.S.; project administration, J.J., J.C. and T.S.; funding acquisition, J.J. and T.S. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported in part by the National Natural Science Foundation of China (62401428), Natural Science Basic Program of Shaanxi (2024JC-YBQN-0714) and the Fundamental Research Funds for the Central Universities (ZYTS25040).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
There are no relevant datasets presented in this article. Data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| MFDRL-RSA | Multi-link fragmentation deep reinforcement learning-based routing and spectrum allocation algorithm |
| EONs | Elastic optical networks |
| RSA | Routing and spectrum allocation |
| DRL | Deep reinforcement learning |
| BFN | Breadth-first numbering |
| FS | Frequency slot |
| TAM | Traversing the adjacency matrix |
| AC | Actor-critic |
| KSP-FF | k shortest path and first-fit |
| FF | First-fit |
References
- Kumar, K.S.; Kalaivani, S.; Ibrahim, S.P.S.; Swathi, G. Traffic and fragmentation aware algorithm for routing and spectrum assignment in Elastic Optical Network (EON). Opt. Fiber Technol. 2023, 81, 103480. [Google Scholar] [CrossRef]
- Lechowicz, P.; Tornatore, M.; Włodarczyk, A.; Walkowiak, K. Fragmentation metrics and fragmentation-aware algorithm for spectrally/spatially flexible optical networks. J. Opt. Commun. Netw. 2020, 12, 133–145. [Google Scholar] [CrossRef]
- Kitsuwan, N.; Akaki, K.; Pavarangkoon, P.; Nag, A. Spectrum allocation scheme considering spectrum slicing in elastic optical networks. J. Opt. Commun. Netw. 2021, 13, 169–181. [Google Scholar] [CrossRef]
- Mandloi, A. Routing and dynamic core allocation with fragmentation optimization in EON-SDM. Opt. Fiber Technol. 2024, 83, 103658. [Google Scholar]
- Mei, J.; Wang, X.; Zheng, K.; Boudreau, G.; Bin Sediq, A.; Abou-Zeid, H. Intelligent radio access network slicing for service provisioning in 6G: A hierarchical deep reinforcement learning approach. IEEE Trans. Commun. 2021, 69, 6063–6078. [Google Scholar] [CrossRef]
- He, Q.; Wang, Y.; Wang, X.; Xu, W.; Li, F.; Yang, K.; Ma, L. Routing optimization with deep reinforcement learning in knowledge defined networking. IEEE Trans. Mob. Comput. 2023, 23, 1444–1455. [Google Scholar] [CrossRef]
- Qureshi, K.I.; Lu, B.; Lu, C.; Lodhi, M.A.; Wang, L. Multi-agent DRL for Air-to-Ground Communication Planning in UAV-enabled IoT Networks. Sensors 2024, 24, 6535. [Google Scholar] [CrossRef]
- Wang, S.; Yuen, C.; Ni, W.; Guan, Y.L.; Lv, T. Multiagent deep reinforcement learning for cost- and delay-sensitive virtual network function placement and routing. IEEE Trans. Commun. 2022, 70, 5208–5224. [Google Scholar] [CrossRef]
- Hernández-Chulde, C.; Casellas, R.; Martínez, R.; Vilalta, R.; Muñoz, R. Experimental evaluation of a latency-aware routing and spectrum assignment mechanism based on deep reinforcement learning. J. Opt. Commun. Netw. 2023, 15, 925–937. [Google Scholar] [CrossRef]
- Xu, L.; Huang, Y.C.; Xue, Y.; Hu, X. Hierarchical reinforcement learning in multi-domain elastic optical networks to realize joint RMSA. J. Lightw. Technol. 2023, 41, 2276–2288. [Google Scholar] [CrossRef]
- Tanaka, T.; Shimoda, M. Pre-and post-processing techniques for reinforcement-learning-based routing and spectrum assignment in elastic optical networks. J. Opt. Commun. Netw. 2023, 15, 1019–1029. [Google Scholar] [CrossRef]
- Khorasani, Y.; Rahbar, A.G.; Alizadeh, B. A novel adjustable defragmentation algorithm in elastic optical networks. Opt. Fiber Technol. 2024, 82, 103615. [Google Scholar] [CrossRef]
- Bao, B.; Yang, H.; Yao, Q.; Yu, A.; Chatterjee, B.C.; Oki, E.; Zhang, J. SDFA: A service-driven fragmentation-aware resource allocation in elastic optical networks. IEEE Trans. Netw. Serv. Manag. 2021, 19, 353–365. [Google Scholar] [CrossRef]
- Chen, X.; Li, B.; Proietti, R.; Lu, H.; Zhu, Z.; Ben Yoo, S.J. DeepRMSA: A deep reinforcement learning framework for routing, modulation and spectrum assignment in elastic optical networks. J. Lightw. Technol. 2019, 37, 4155–4163. [Google Scholar] [CrossRef]
- Yan, W.; Li, X.; Ding, Y.; He, J.; Cai, B. DQN with prioritized experience replay algorithm for reducing network blocking rate in elastic optical networks. Opt. Fiber Technol. 2024, 82, 103625. [Google Scholar] [CrossRef]
- Gonzalez, M.; Condon, F.; Morales, P.; He, J.; Cai, B. Improving multi-band elastic optical networks performance using behavior induction on deep reinforcement learning. In Proceedings of the 2022 IEEE Latin-American Conference on Communications (LATINCOM), Rio de Janeiro, Brazil, 30 November–2 December 2022; Volume 1, pp. 1–6. [Google Scholar]
- Errea, J.; Djon, D.; Tran, H.Q.; Verchere, D.; Ksentini, A. Deep reinforcement learning-aided fragmentation-aware RMSA path computation engine for open disaggregated transport networks. In Proceedings of the 2023 International Conference on Optical Network Design and Modeling (ONDM), Coimbra, Portugal, 8–11 May 2023; Volume 1, pp. 1–3. [Google Scholar]
- Johari, S.S.; Taeb, S.; Shahriar, N.; Chowdhury, S.R.; Tornatore, M.; Boutaba, R.; Mitra, J.; Hemmati, M. DRL-assisted reoptimization of network slice embedding on EON-enabled transport networks. IEEE Trans. Netw. Serv. Manag. 2023, 20, 800–814. [Google Scholar] [CrossRef]
- Etezadi, E.; Natalino, C.; Diaz, R.; Lindgren, A.; Melin, S.; Wosinska, L.; Monti, P.; Furdek, M. Deep reinforcement learning for proactive spectrum defragmentation in elastic optical networks. J. Opt. Commun. Netw. 2023, 15, E86–E96. [Google Scholar] [CrossRef]
- Shimoda, M.; Tanaka, T. Mask RSA: End-to-end reinforcement learning-based routing and spectrum assignment. In Proceedings of the European Conference on Optical Communication (ECOC), Bordeaux, France, 13–16 September 2021. [Google Scholar]
- Tang, B.; Huang, Y.C.; Xue, Y.; Song, H.; Xu, Z. Heuristic reward design for deep reinforcement learning-based routing, modulation and spectrum assignment of elastic optical networks. IEEE Commun. Lett. 2022, 26, 2675–2679. [Google Scholar] [CrossRef]
- Asiri, A.; Wang, B. Deep Reinforcement Learning for QoT-Aware Routing, Modulation, and Spectrum Assignment in Elastic Optical Networks. J. Lightw. Technol. 2025, 43, 42–60. [Google Scholar] [CrossRef]
- Wang, Y.; Cao, X.; Pan, Y. A study of the routing and spectrum allocation in spectrum-sliced elastic optical path networks. In Proceedings of the 2011 Proceedings IEEE Infocom, Shanghai, China, 10–15 April 2011; Volume 1, pp. 1503–1511. [Google Scholar]
- Zhang, C.; Wang, P. Fuzzy logic system assisted sensing resource allocation for optical fiber sensing and communication integrated network. Sensors 2022, 22, 7708. [Google Scholar] [CrossRef]
- Chen, X.; Xu, Z.; Wu, Y.; Wu, Q. Heuristic algorithms for reliability estimation based on breadth-first search of a grid tree. Reliab. Eng. Syst. Saf. 2023, 232, 109083. [Google Scholar] [CrossRef]
- Liao, J.; Zhao, J.; Gao, F.; Li, G.Y. Deep learning aided low complex breadth-first tree search for MIMO detection. IEEE Trans. Wirel. Commun. 2023, 23, 6266–6278. [Google Scholar] [CrossRef]
- Zhou, C.; Huang, B.; Hassan, H.; Fränti, P. Attention-based advantage actor-critic algorithm with prioritized experience replay for complex 2-D robotic motion planning. J. Intell. Manuf. 2023, 34, 151–180. [Google Scholar] [CrossRef]
- Wang, H.; Gao, W.; Wang, Z.; Zhang, K.; Ren, J.; Deng, L.; He, S. Research on Obstacle Avoidance Planning for UUV Based on A3C Algorithm. J. Mar. Sci. Eng. 2023, 12, 63. [Google Scholar] [CrossRef]
- Wang, S.; Song, R.; Zheng, X.; Huang, W.; Liu, H. A3C-R: A QoS-oriented energy-saving routing algorithm for software-defined networks. Future Internet 2025, 17, 158. [Google Scholar] [CrossRef]
- Labao, A.B.; Martija, M.A.M.; Naval, P.C. A3C-GS: Adaptive moment gradient sharing with locks for asynchronous actor–critic agents. IEEE Trans. Neural Netw. Learn. Syst. 2020, 32, 1162–1176. [Google Scholar] [CrossRef]
- National Science Foundation. NSFNET: The Birth of the Commercial Internet. Available online: https://www.nsf.gov/impacts/internet (accessed on 3 June 2025).
- SNDlib—Survivable Network Design Library. Cost239 Topology. Available online: https://sndlib.zib.de/network.jsp?topology=cost239 (accessed on 3 June 2025).
- Vincent, R.J.; Ives, D.J.; Savory, S.J. Scalable capacity estimation for nonlinear elastic all-optical core networks. J. Light. Technol. 2019, 37, 5380–5391. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).