Secret Key Agreement for SISO Visible Light Communication Systems

Abstract

This paper studies the use of secret key agreement for single-input single-output (SISO) visible light communication (VLC) systems. Specifically, we put forward a scheme for secret key generation and analyze the secret key rate in SISO VLC systems. First, we derive the secret key capacity bounds. Then, we analyze the achievable secret key rate distribution versus the illegal receiver’s location when the legal receiver’s location is fixed. Meanwhile, we deduce the average secret key capacity using random geometry knowledge when all the receivers’ positions are unknown. We also analyze the impact of employing a protected zone on the average secret key capacity and observe that a protected zone can obviously improve the secret performance. Finally, simulations are presented to verify the theoretical analysis.

1. Introduction

With the development of the Internet of Things (IoT), communication technology is facing new challenges. Traditional radio frequency (RF) resources cannot fully meet the needs of data transmission, requiring us to explore new spectrum resources. VLC has become a candidate technology for 6G mobile communication due to its advantages such as an ultrawide spectrum, high speed, and implementation of illumination and communication simultaneously. Since the light propagates along a straight line, VLC provides better signal confinement and higher security compared to traditional RF communication systems. Nevertheless, because it is inherently of a broadcast nature, information can be eavesdropped by unintended users located within the same light emitting diode (LED) lighting area. Consequently, the security of the VLC system is a critical challenge that needs to be addressed.

Physical layer security, as a technology that combines security and communication, has become an effective supplement to traditional network security encryption methods. There are two types of physical layer security methods [1]: one type is commonly known as keyless security, which is based on the wiretap channel model [2] and assumes that the eavesdropped channel is a degraded channel of the legitimate receiver. In recent years, much work has investigated keyless security [3,4,5,6,7,8] in VLC networks. The other type is secret key agreement, which focuses on generating secret keys from common randomness via public discussion [1,9,10]. In [9], Maurer first proposed the scheme that the legitimate parties generate a key over a public and error-free feedback channel, with the eavesdropper having no information on the key. Then, in [10], Ahlswede gave and proved the achievable secret key rates and the secret key capacity of the source-type model and channel-type model for secret key agreement. Maurer and Wolf subsequently extended the analysis of secure shared keys in the presence of active eavesdroppers in [11,12,13] .

Hershey first proposed utilizing wireless channel characteristics for secure key communication in [14]. Following more than 20 years of extensive research and technological advancement, secret key agreement mechanisms have been effectively implemented across various wireless communication systems including but not limited to RF networks [15,16], optical fiber networks [17], and underwater acoustic channels [18]. In some fields of the Optical Industrial Internet of Things (OIIoT), where RF communication is impractical and there is a demand high confidentiality, such as military-industrial manufacturing, the nuclear energy industry, and smart healthcare, the physical layer secret key mechanism emerges as a promising option for lightweight standalone secrecy solutions.

Current investigations in secret key agreement security predominantly concentrate on two key dimensions: (i) theoretical analysis of secret key capacity [19,20] and (ii) strategies for secret key distillation [16,21]. The secret key capacity analysis, which determines the fundamental limits of secret key generation performance, can provide guidance for actual key generation technology [1,22]. This paper focuses on the analysis of secret key capacity in VLC networks.

Although secret key capacity has been widely studied in the RF field, the developed theory cannot be directly applied to VLC scenarios. Due to the amplitude constraints of transmitted signals, it becomes more complex in VLC systems. To the best of our knowledge, only [23] has investigated the performance of secret key agreement in VLC systems with amplitude-constrained transmitted signals. In [23], the author studied secret key generation for multiple-input single-output (MISO) VLC networks. Specifically, the author obtained the analytical bounds of secret key capacity and proposed a beamforming method for secret key improvement. However, in the process of deriving the bounds on secret key capacity, the author scaled the secret key capacity to the secrecy capacity, as demonstrated in the proof of proposition 1 in [23]. Beyond [23], Alresheedi, M.T. et al. [24,25] investigated secret key generation from the bipolar optical orthogonal frequency division multiplexing (OFDM) samples. Nevertheless, this approach does not directly utilize the transmitted optical signal as the secret key source.

In this paper, we study the secret key agreement for SISO VLC systems. Specifically, we derive the analytical bounds on secret key capacity and the achievable secret key rate in some typical VLC scenarios. The major contributions of this work are summarized as follows.

• We analyze a secret key agreement scheme in SISO VLC systems, explore the secret key rate performance, and derive the analytic expressions of bounds on secrecy key capacity.
• Based on the lower bound of secret key capacity, we consider the situation in which all receivers’ positions are unknown and uniformly distributed within the designated range. We analyze the average secret key capacity and discuss the improvement of the secret performance by employing a protected zone.
• Furthermore, we numerically analyze the distribution of the achievable secret key rate in a typical indoor VLC scenario, where the legitimate receiver is positioned at the center of the receiving plane and an eavesdropper is located at any position on the receiving plane or on the window.
• Simulations are also presented to validate the theoretical analysis of the average secret key capacity and demonstrate the improved secrecy performance by introducing a protected zone.

The rest of this paper is arranged as follows. The system model of SISO VLC communication and the secret key background are presented in Section 2. The secret key capacity bounds are studied in Section 3. Then, we derive the average secret key capacity with randomly distributed terminals in Section 4. The numerical investigations and their implications are presented in Section 5 and Section 6, respectively. Finally, this article is summarized in Section 7.

2. System Model

Depending on the origin of randomness, secret key agreement is categorized into two fundamental models: the source-type model, in which all terminals share the correlated source observations, and channel-type model, in which one terminal transmits random symbols to others via a broadcast channel. Here, we consider the channel-type model as shown in Figure 1, where Alice is a transmitter, Bob is a legitimate receiver, and Eve is an eavesdropper. Alice and Bob intend to agree on common secret keys from the transmitted optical signal via public discussion. Alice is equipped with a single LED fixture, while both the legitimate receiver and the eavesdropper are equipped with a photo-diode (PD). The signals at the receivers can be described as

$$\begin{array}{cc}\hfill y_B& =h_{B}x+n_B\hfill \end{array}$$

(1)

$$\begin{array}{cc}\hfill y_E& =h_{E}x+n_E\hfill \end{array}$$

(2)

where x is the transmitted signal from the transmitter. $n_B\sim (0,{\sigma }_B^2)$ and $n_E\sim (0,{\sigma }_E^2)$ are zero-mean AWGN samples at the receivers. Considering that Bob and Eve are in the same environment, we can assume that the noise power is the same, i.e., ${\sigma }_B^2={\sigma }_E^2={\sigma }^2$. $h_B$ and $h_E$ represent the VLC channel gains from Alice to Bob and from Alice to Eve, respectively. The details of the channel gain will be discussed later.

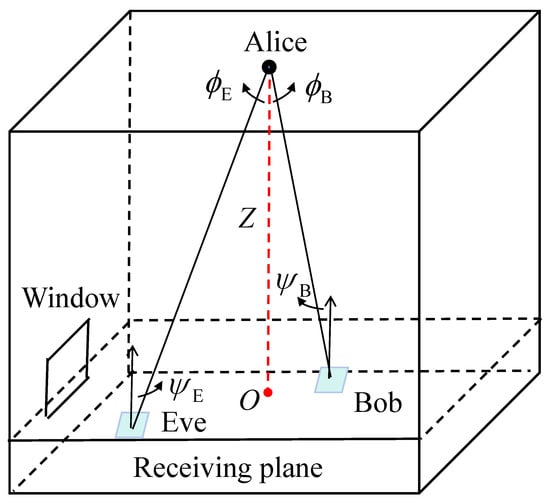
Figure 1. A SISO VLC system for secret key agreement.

Because of the inherent dynamic limitations of LED, the modulating signal must satisfy certain amplitude constraints to avoid clipping distortion. The transmitted signal must be subject to the constraint of peak amplitude in VLC systems:

$$\left|x\right|\le A$$

(3)

where A is the optical peak power of the LED.

2.1. The VLC Channel Gain

The channel gain from one transmitter to one receiver can be modeled as [26]

$$h=\left\{\begin{array}{cc}{\displaystyle \frac{(m+1)A_r}{2\pi d^2}}{\cos }^m\left(\varphi \right)\cos \left(\psi \right),\hfill & 0\le \psi \le {\psi }_{\mathrm{fov}}\hfill \\ 0,\hfill & \psi >{\psi }_{\mathrm{fov}}\hfill \end{array}\right.$$

(4)

where $m={\displaystyle \frac{-\ln 2}{\ln \left(\cos {\varphi }_{\frac{1}{2}}\right)}}$ denotes the mode order of the Lambertian emission, ${\varphi }_{{\displaystyle \frac{1}{2}}}$ denotes the half-power angle of the LED, d denotes the distance from the transmitter to the receiver, $\varphi$ denotes the angle between the emission light and the normal vector of the transmitter, $\psi$ denotes the angle between the incident light and the normal vector of the receiver, ${\psi }_{\mathrm{fov}}$ is the field-of-view (FOV) at the receiver, and $A_r$ denotes the effective area of the PD and can be expressed as [26]

$$A_r={\displaystyle \frac{n^2}{{\sin }^2\left({\psi }_{\mathrm{fov}}\right)}}{A}_{PD}$$

(5)

where n is the refractive index of the optical concentrator and $A_{PD}$ denotes the physical area of the PD.

2.2. Secret Key Agreement and Secret Key Capacity

Alice and Bob intend to establish a secret key for secure communication, and thus they need to employ a secret key agreement strategy which contains the following four steps. First, Alice transmits random signals, and Bob receives the correlated signals. Second, Alice and Bob quantize their correlated observations into random sequences. Then, in order to obtain a common random sequence, they exchange messages over a public and error-free channel, which can be observed by Eve. Last, using a hash function for privacy amplification, the two partners reach the secret key, which is entirely hidden from Eve.

Ahlswede gave and proved the achievable secret key rates of source-type models and channel-type models. The maximum achievable secret key rate is defined as the secret key capacity. The secret key capacity is given as [10]

$$\begin{array}{c}\hfill \begin{array}{c}\hfill \max \left[I\left(X;Y_B\right)-I\left(Y_B;Y_E\right),I\left(X;Y_E\right)-I\left(Y_B;Y_E\right)\right]\le C_{SK}\le \min \left[I\left(X;Y_B\right),I\left(X;Y_B\mid Y_E\right)\right]\end{array}\end{array}$$

(6)

When $Y_B\to X\to Y_E$ forms a Markov chain, $Y_B$ is independent of $Y_E$ if given X, and it follows that [1]

$$I\left(X;Y_B\mid Y_E\right)=I\left(X;Y_B\right)-I\left(Y_B;Y_E\right)$$

(7)

Then, we can rewrite the secret key capacity as

$$C_{SK}=\underset{p_x}{\max }\left(I\left(X;Y_B,Y_E\right)-I\left(X;Y_E\right)\right)$$

(8)

where ${\left\{p_x\right\}}_{x\in X}$ is a probability distribution over the finite set X, and x is subject to $\left|x\right|\le A$ for a VLC network.

3. Bounds on Secret Key Capacity

Following the approach adopted in [27], considering a sufficient statistic keeping mutual information unchanged [28], we can replace $I\left(X;Y_B,Y_E\right)$ with an equivalent channel capacity $I\left(X;Y_{BE}\right)$, and it follows that

$$I\left(X;Y_{BE}\right)=I\left(X;X+N_{BE}\right)$$

(9)

where $N_{BE}$ is the equivalent Gaussian noise with a variance ${\sigma }_{BE}^2$, and the relationship between ${\sigma }_{BE}^2$ and ${\sigma }_B^2$, ${\sigma }_E^2$ can be expressed as

$${\displaystyle \frac{1}{{\sigma }_{BE}^2}}={\displaystyle \frac{h_B^2}{{\sigma }_B^2}}+{\displaystyle \frac{h_E^2}{{\sigma }_E^2}}$$

(10)

Then, we can rewrite the secret key capacity as

$$C_{SK}=\underset{p_x}{\max }\left(I\left(X;Y_{BE}\right)-I\left(X;Y_E\right)\right)$$

(11)

Due to the amplitude constraints of x, the optimization of (11) is complex and only numerical results of the secret key capacity can be derived. Nevertheless, we know that the closed-form expression is important in order to assess the achievable secret key rate and extract secret key. So, in the next part, we focus on analyzing the closed-form bounds on secret key capacity.

From (11), we can see that the secret key capacity is transformed into an equivalent secrecy capacity of the eavesdropper channel, so we can use a similar approach as in [5] to derive the bounds on secret key capacity. However, we need to note that secret key capacity and secrecy capacity are different conceptions. In addition, because the mutual information of the equivalent channel is different, the bounds results must be different.

Using the similar approach to [5], we can derive the lower bound on secret key capacity. The details are discussed in the following.

3.1. Lower Bound

With the peak amplitude constraint, based on (11), we can verify that the following secret key rate is achievable, so it can be taken as a lower bound of secret key capacity for SISO VLC systems. The process follows as

$$\begin{array}{cc}\hfill C_{SK}& =\underset{p_X}{\max }\left(I\left(X;Y_{BE}\right)-I\left(X;Y_E\right)\right)\hfill \\ \hfill & =\underset{p_X}{\max }(h\left(Y_{BE}\right)-h\left(N_{BE}\right)-h\left(Y_E\right)+h\left(N_E\right))\hfill \\ \hfill & \stackrel{\left(\mathrm{a}\right)}{\ge }\underset{p_X}{\max }({\displaystyle \frac{1}{2}}\log (e^{2h\left(X\right))}+e^{2h\left(N_{BE}\right)})-h\left(N_{BE}\right)\hfill \\ \hfill & -{\displaystyle \frac{1}{2}}\log \left(2\pi e\mathrm{var}\left(Y_E\right)\right)+h\left(N_E\right))\hfill \\ \hfill & =\underset{p_X}{\max }({\displaystyle \frac{1}{2}}\log (1+{\displaystyle \frac{e^{2h\left(X\right)}}{2\pi e{\sigma }_{BE}^2}})-{\displaystyle \frac{1}{2}}\log (1+{\displaystyle \frac{\mathrm{var}(h_{E}X+N_E)}{{\sigma }_E^2}})\hfill \\ \hfill & \stackrel{\left(\mathrm{b}\right)}{\ge }{\displaystyle \frac{1}{2}}\log ({\displaystyle \frac{6h_B^2{A}^2+6h_E^2{A}^2+3\pi e{\sigma }^2}{\pi e{h}_E^2{A}^2+3\pi e{\sigma }^2}})\hfill \end{array}$$

(12)

where inequality (a) follows from the lower bound for $h\left(Y_{BE}\right)$ using the entropy-power inequality $h\left(Y_{BE}\right)\ge {\displaystyle \frac{1}{2}}\log (1+{\displaystyle \frac{e^{2h\left(X\right)}}{2\pi e{\sigma }_{BE}^2}})$ and the upper bound for $h\left(Y_E\right)$ using $h\left(Y_E\right)\le {\displaystyle \frac{1}{2}}\log \left(2\pi e\mathrm{var}\left(Y_E\right)\right)$. Inequality (b) is obtained by choosing a uniform distribution for $p_X$ instead of the maximization.

$$C_{SK}^d=\left\{\begin{array}{cc}{\displaystyle \frac{1}{2}}\log ({\displaystyle \frac{6h_B^2{A}^2+6h_E^2{A}^2+3\pi e{\sigma }^2}{\pi e{h}_E^2{A}^2+3\pi e{\sigma }^2}}),\hfill & \mathrm{if}\lambda h_B^2\ge h_E^2\hfill \\ 0,\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

(13)

where $\lambda ={\displaystyle \frac{6}{\pi e-6}}$ is about 2.3625. From this expression, we find that the lower bound of the secret key capacity is bigger than that of the secrecy capacity in the same situation [5] (Equation (10)). In particular, we can see that even if Bob’s channel is worse than that of Eve, a nonzero secret key rate can still be achieved. This means that we can secure message by using secret key agreement in this situation, because the classical eavesdropping encoding methods do not work.

3.2. Upper Bound

If we relax the peak power constraint $\left|x\right|\le A$ to the average power constraint $E\left\{X^2\right\}\le A^2$, an upper bound can be concluded as follows:

$$C_{SK}\le {\displaystyle \frac{1}{2}}\log ({\displaystyle \frac{1+A^2(\frac{h_B^2}{{\sigma }_B^2}+\frac{h_E^2}{{\sigma }_E^2})}{1+A^2\frac{h_E^2}{{\sigma }_E^2}}})={\displaystyle \frac{1}{2}}\log ({\displaystyle \frac{h_B^2{A}^2+h_E^2{A}^2+{\sigma }^2}{h_E^2{A}^2+{\sigma }^2}})=C_{SK}^u$$

(14)

It can be seen that $C_{SK}^u$ is always positive, no matter whether the condition of Bob’s channel is better or worse than that of Eve. This result is consistent with Equation (17) of [27] and half of the upper bound on secret key capacity in [23].

Figure 2 shows the secret key capacity bounds of Equations (13) and (14). We take $h_B^2/h_E^2=1,10,100$, and 1000, which include the channel situations for a common indoor VLC communication environment. We can see that the lower and upper bounds of the secret key capacity exhibit a trend similar to that of the secrecy capacity reported in [5], albeit with significantly higher values. It is shown that the upper and lower bounds are tight at both asymptotically low and high SNR levels. Given that typical indoor VLC environments can provide at least 40 dB of receiver SNR, these bounds are particularly relevant in practical scenarios.

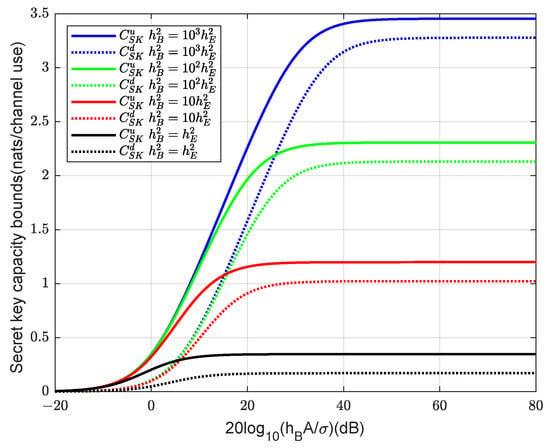
Figure 2. Secret key capacity bounds of the SISO VLC system.

4. Secret Key Rate with Randomly Distributed Terminals

In the previous section, all the receivers’ positions are assumed to be known; however, this is applicable only in some scenarios. Next, we will investigate the secret key performance when all the receivers’ CSI are unknown.

We still consider a scenario with one legitimate receiver and one eavesdropper, but considering that the receivers are usually deployed randomly and uniformly, we will model the scenario as all the terminals are uniformly positioned and analyze the average secret key capacity using the stochastic geometry in [29,30]. To improve the secret key performance, we will introduce a protected zone. This introduction is reasonable in a VLC scenario because the eavesdropper cannot be too close to the transmitter, subject to the restrictions imposed by the transmitter. Furthermore, we analyze the improvement of average secret key capacity by employing the protected zone.

The LED is fixed on the ceiling directly above the central point O. Because the illumination area of the LED on the receiving plane is circular, in this section, we will model the receiving plane as as a circular region with a central point O and a radius D. Bob is uniformly distributed within the receiving plane, so the probability density function (PDF) of Bob’s position is

$$f_{Bob}={\displaystyle \frac{1}{\pi D^2}}$$

(15)

The protected zone is also geometrically modeled as a circular region with the same central point O and a radius P ($P<D$). Eve is uniformly distributed in the receiving plane but outside of the protected zone. The probability density function (PDF) of Bob’s position is

$$f_{Eve}={\displaystyle \frac{1}{\pi (D^2-P^2)}}$$

(16)

Without loss of generality, it can be assumed that the normal direction of the PD is perpendicular to the receiving plane, so $\cos \varphi =\cos \psi ={\displaystyle \frac{Z}{\sqrt{Z^2+r_i^2}}}$, Z is the vertical distance between the receiver plane and the ceiling, while $r_i$ ($i=BorE$)) represents the distance from Bob or Eve to point O. Then, we can rewrite the channel gain as

$$h_i={\displaystyle \frac{A_{r}RT{Z}^{m+1}(m+1)}{2\pi {(Z^2+r_i^2)}^{\frac{m+3}{2}}}}=K{(Z^2+r_i^2)}^{-{\displaystyle \frac{m+3}{2}}}$$

(17)

where $K={\displaystyle \frac{A_{r}RT{Z}^{m+1}(m+1)}{2\pi }}$.

Based on (15), the cumulative distribution function (CDF) and the PDF of $r_B$ can be deduced as

$$\begin{array}{cc}\hfill F_{r_B}& ={\displaystyle \frac{r_B^2}{D^2}}\hfill \end{array}$$

(18)

$$\begin{array}{cc}\hfill f_{r_B}& ={\displaystyle \frac{2r_B}{D^2}}\hfill \end{array}$$

(19)

According to (17)–(19), the PDF of $h_B^2$ can be obtained as [31]

$$\begin{array}{cc}\hfill f_{h_B^2}\left(x\right)& =f_{r_B}\left(\sqrt{{\left({\displaystyle \frac{x}{K^2}}\right)}^{{\displaystyle \frac{-1}{m+3}}}-Z^2}\right)\times {\displaystyle \frac{\mathrm{d}}{\mathrm{d}x}}\left(\sqrt{{\left({\displaystyle \frac{x}{K^2}}\right)}^{{\displaystyle \frac{-1}{m+3}}}-Z^2}\right)\hfill \\ \hfill & =K^{{\displaystyle \frac{2}{m+3}}}{\displaystyle \frac{x^{-\frac{m+4}{m+3}}}{(m+3)D^2}},v_{\min }\le x\le v_{\max }\hfill \end{array}$$

(20)

Based on (16), the CDF and PDF of $r_E$ can be similarly derived as $F_{r_E}={\displaystyle \frac{r_E^2-P^2}{D^2-P^2}}$ and $f_{r_E}={\displaystyle \frac{2r_E}{D^2-P^2}}$. Using the same method of obtaining (20), we can derive the PDF of $h_E^2$

$$f_{h_E^2}\left(y\right)=K^{{\displaystyle \frac{2}{m+3}}}{\displaystyle \frac{y^{-\frac{m+4}{m+3}}}{(m+3)(D^2-P^2)}},v_{\min }\le y\le v_{\mathrm{mid}}$$

(21)

where $v_{\min }$, $v_{\mathrm{mid}}$ and $v_{\max }$ in (20) and (21) are given as

$$\begin{array}{cc}\hfill v_{\min }& =K^2{(Z^2+D^2)}^{-(m+3)}\hfill \end{array}$$

(22)

$$\begin{array}{cc}\hfill v_{\mathrm{mid}}& =K^2{(Z^2+P^2)}^{-(m+3)}\hfill \end{array}$$

(23)

$$\begin{array}{cc}\hfill v_{\max }& =K^2{Z}^{-(2m+6)}\hfill \end{array}$$

(24)

From the lower bound (13), we can deduce the average secret key capacity for the random VLC network as

$${\overline{C}}_{SK}^d=\left\{\begin{array}{cc}{\int }_{v_{\min }}^{v_{\max }}f\left(x\right)dx{\int }_{v_{\min }}^{v_{\mathrm{mid}}}{C}_{SK}^{d}f\left(y\right)dy,\hfill & \mathrm{if}\lambda \ge {\displaystyle \frac{v_{\mathrm{mid}}}{v_{\min }}}\hfill \\ {\int }_{v_{\min }}^{{\displaystyle \frac{v_{\mathrm{mid}}}{\lambda }}}f\left(x\right)dx{\int }_{v_{\min }}^{\lambda x}{C}_{SK}^{d}f\left(y\right)dy+\hfill \\ {\int }_{{\displaystyle \frac{v_{\mathrm{mid}}}{\lambda }}}^{v_{\max }}f\left(x\right)dx{\int }_{v_{\min }}^{v_{\mathrm{mid}}}{C}_{SK}^{d}f\left(y\right)dy\hfill & \mathrm{if}\lambda \le {\displaystyle \frac{v_{\mathrm{mid}}}{v_{\min }}}\hfill \end{array}\right.$$

(25)

5. Simulation Results

To verify the analytical results of the previous sections, we provide numerical simulation results in this section. The main parameters used in this paper are the same as those provided in [5] and are shown in Table 1. The room dimensions are $5\times 5\times 3$${\mathrm{m}}^3$, and the distance from the receiving plane to the room ground is $0.85$ m. The average electrical noise power is ${\sigma }^2=-98.82$ dBm. We take the center of the room floor as the coordinate origin (0, 0, 0), so the coordinate of the receiving plane center O is (0, 0, 0.85). The LED is fixed at the ceiling and the coordinate of it is (0, 0, 3). There is a window in the room, the area of which is $x=-2.5\mathrm{m}$, $-0.5\mathrm{m}\le y\le 0.5\mathrm{m}$, $0.5\mathrm{m}\le z\le 1.5\mathrm{m}$.

Table 1. VLC network simulation parameters.

Parameter	Value
Room dimensions	$5\times 5\times 3$${\mathrm{m}}^3$
Height of receivers	$0.85$ m
Semi-angle ${\varphi }_{{\displaystyle \frac{1}{2}}}$	${60}^{\circ }$
Receiver FOV ${\psi }_{\mathrm{fov}}$	${60}^{\circ }$
The physical area of PD $A_{\mathrm{PD}}$	1 ${\mathrm{cm}}^2$
Lens refractive index n	$1.5$
Noise variance ${\sigma }^2$	−98.82 dBm

5.1. Eve’s Known CSI

Figure 3 presents the achievable secret key rate $C_{SK}^d$ (see (13)) against the location of the eavesdropper on the receiving plane. Bob is located at the center $O(0,0,0.85)$ of the receiving plane, the optical power of the LED is 1 W, and the average electrical noise power is $-98.82$ dBm. The figure demonstrates several interesting phenomena. First, the further away Eve is from Bob, the larger the achievable secret key rate is, especially when Eve moves into the corner, when it reaches to a maximum secret key rate of 2.44 nats per channel use. Furthermore, even in the worst-case scenario where Eve occupies the central position (with channel conditions matching Bob’s), it still yields a positive achievable secret key rate of 0.17 nats per channel use as theoretically anticipated (see (13)), which demonstrates the robustness of the secret key scheme.

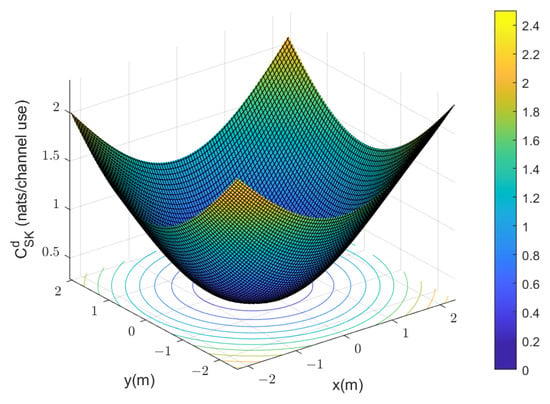
Figure 3. Achievable secret key rate $C_{SK}^d$ versus the location of Eve on the receiving plane. Bob is at $(0,0,0.85)$.

Figure 4 presents the distribution of the achievable secret key rate $C_{SK}^d$ versus Eve’s location in relation to the window, while Bob is still located at $O(0,0,0.85)$. As illustrated in Figure 4, we can achieve a secret key rate of at least 1.28 nats for every channel use. In addition, if the Z-axis coordinate of Eve in relation to the window exceeds 1.6 m, due to the limitation of FOV, Eve cannot receive the LED signals and the secret key rate can reach to communication rate.

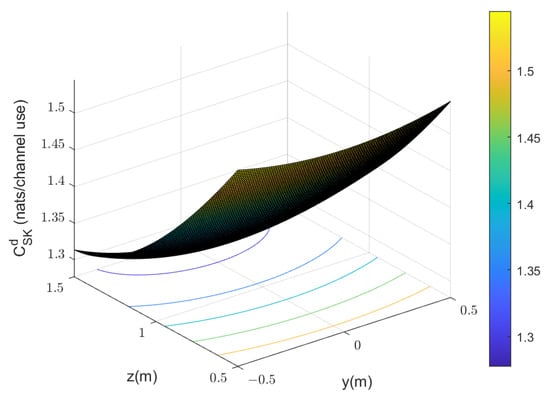
Figure 4. Achievable secret key rate $C_{SK}^d$ versus the location of Eve in relation to the window. Bob is at $(0,0,0.85)$.

5.2. Randomly Distributed Terminals

Figure 5 presents the average secret key capacity ${\overline{C}}_{SK}^d$ versus the square of the amplitude constraint $A^2$ for different values of P (P is the radius of the the protected zone), when $D=2.5$ m and ${\sigma }^2=-98.82$ dBm. We obtain the simulation results by running ${10}^5$ Monte-Carlo experiments. As shown in Figure 5, ${\overline{C}}_{SK}^d$ first increases and then tends to stabilize with the increase in $A^2$. Moreover, as the radius P of the protected zone increases, the average secret key capacity increases dramatically; this is because the equivalent distance from Eve to Alice is further than from Bob to Alice. Therefore, we can conclude that introducing a protected zone is an effective transmission strategy to improve secret key performance. Of course, we need to have a tradeoff between the secrecy performance and the complexity of the systems in the actual system design.

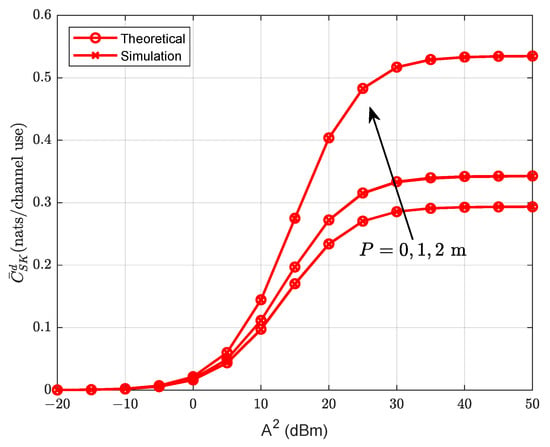
Figure 5. Average secret key capacity ${\overline{C}}_{SK}^d$ versus the square of the amplitude constraint $A^2$ for different P values when $D=2.5$ m and ${\sigma }^2=-98.82$ dBm.

6. Discussion

In this paper, we propose a novel secret key generation scheme for SISO VLC systems and establish both lower and upper bounds for the secret key capacity. Through numerical simulations, we demonstrate three critical phenomena: (i) The spatial dependency of the physical layer secret key in VLC systems is observed, which can also be found in keyless security research [5,32]. (ii) The robustness of our secret key scheme is observed, as even when the eavesdropper’s channel quality is comparable to that of the legitimate receiver, a non-negative achievable secret key rate can still be guaranteed. This is consistent with research [1,9], but the keyless method does not work in this situation [2]. (iii) Enhanced security effectiveness is achieved through protected zone implementation [30]. We notice that, for the case of a SISO VLC system, the secret key rate is finite; this motivates future exploration of multi-transmitter or multi-eavesdropper scenarios and security-enhancing technologies such as reconfigurable intelligent surfaces (RIS) [33]. We believe that this work can provide valuable knowledge about physical layer security in VLC networks and provide a reference for further work on the subject.

7. Conclusions

We have studied the use of secret key agreement for SISO VLC systems and established the analytical bounds on secret key capacity. On the base of the lower bound, we numerically analyzed the achievable secret key rate distribution when the legitimate receiver’s position is fixed and the eavesdropper is located at different positions in a room. Furthermore, considering the random and uniform distribution of the receivers’ locations, we deduced the average secret key capacity using stochastic geometric modeling and established a protected zone to improve the secret key capacity. The derived results can provide a theoretical foundation for extracting physical layer secret keys in SISO VLC systems and further theoretical research. In our future work, we will explore the use of secret key agreement in MISO VLC scenarios and design some schemes to enhance the secret key capacity.