Supercontinuum Generation in Suspended Core Fibers Based on Intelligent Algorithms
Abstract
1. Introduction
2. Basic Principles
2.1. Design of Ge20Sb15Se65 Suspended-Core Fiber
2.2. Analysis of the Theoretical Foundations of Supercontinuum Generation
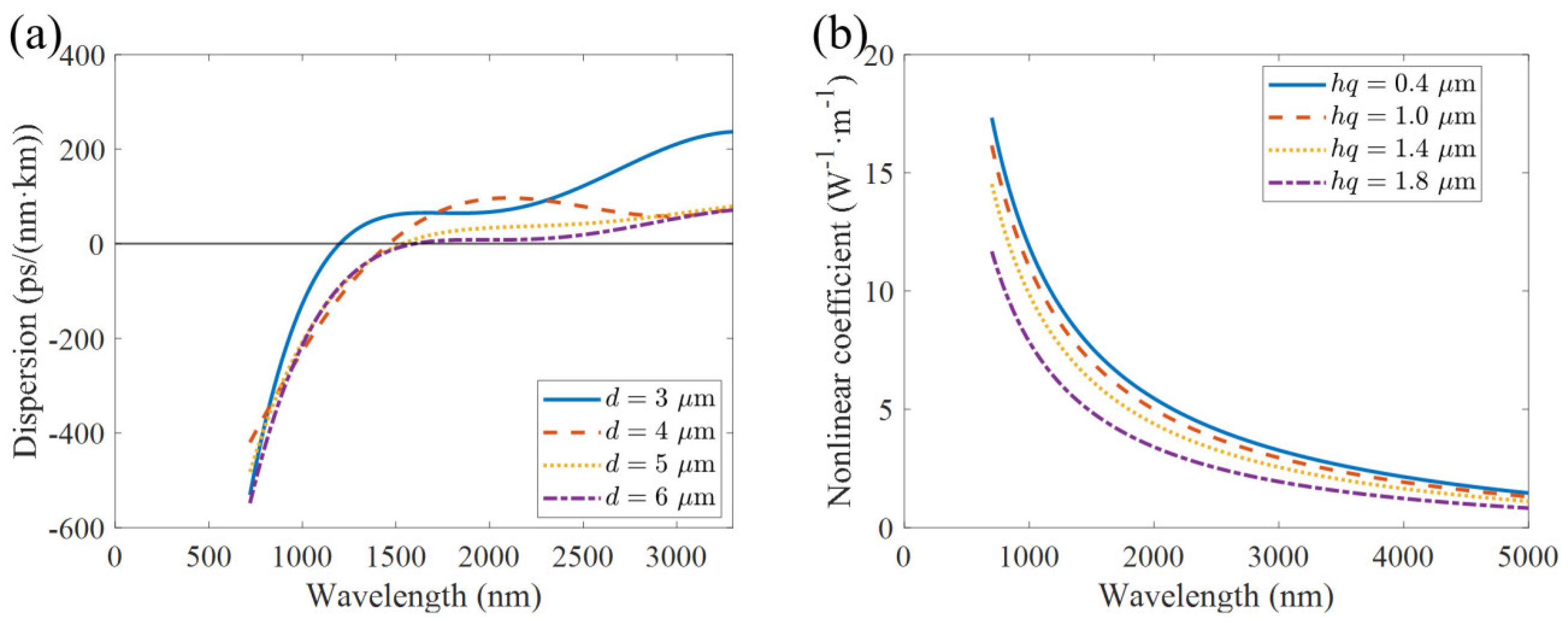
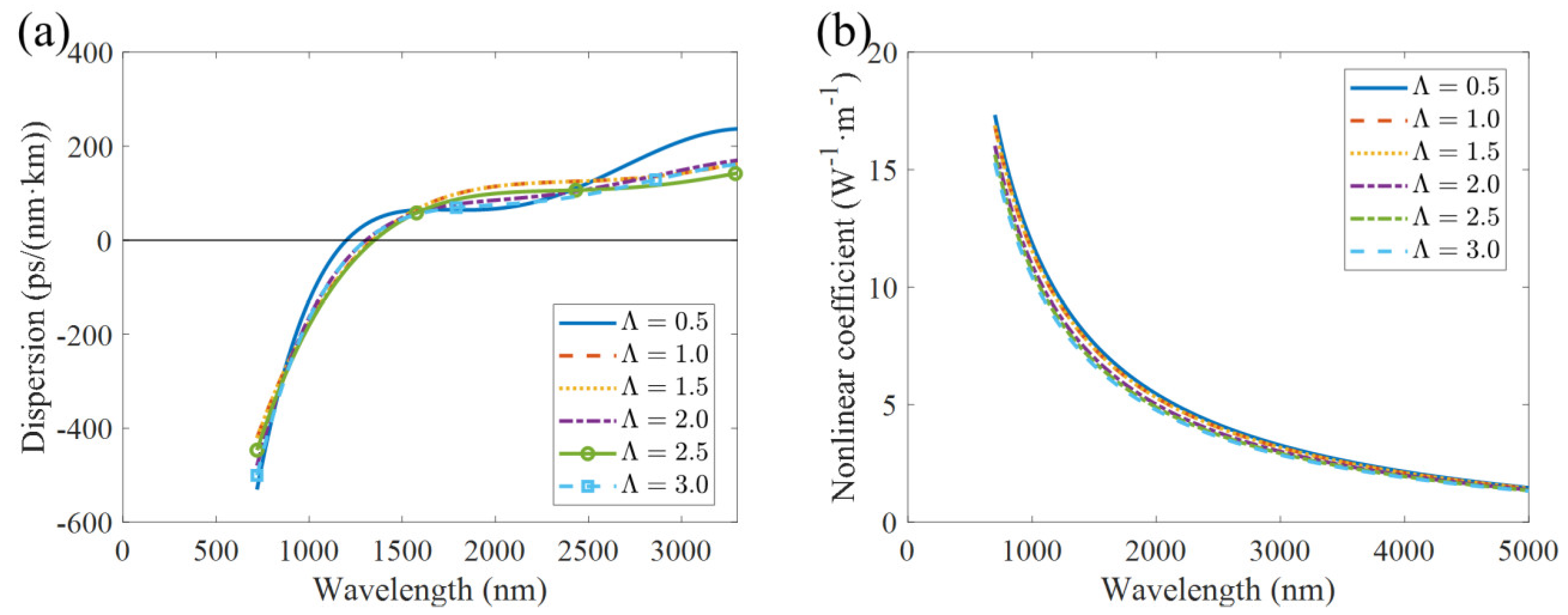
2.3. Effect of Fiber Structural Parameters on Dispersion and Nonlinearity
3. Neural Networks and Optimization Algorithms
3.1. Optimization Algorithms
3.2. Comparison of Different Optimization Algorithms
4. Analysis and Discussion
4.1. Performance Analysis of Optimized Fiber Structure
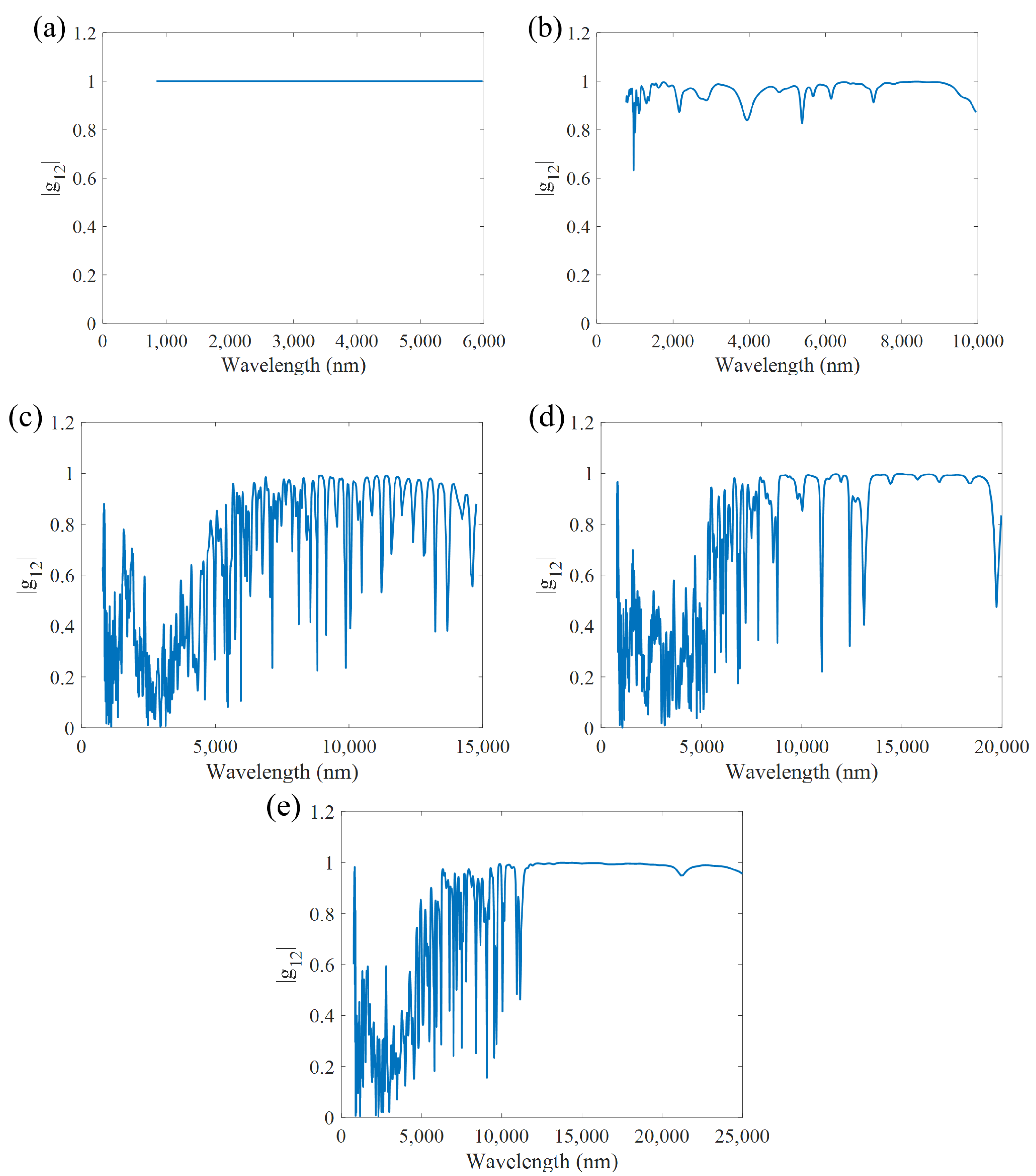
4.2. Analysis of Supercontinuum Coherence
4.3. Fiber Fabrication Tolerance Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Alfano, R.R.; Shapiro, S.L. Emission in the region 4000 to 7000 Å via four-photon coupling in glass. Phys. Rev. Lett. 1970, 24, 584–587. [Google Scholar] [CrossRef]
- Lin, C.; Stolen, R.H.; Jain, R.K. Group velocity matching in optical fibers. Opt. Lett. 1977, 1, 205–207. [Google Scholar] [CrossRef] [PubMed]
- Takushima, Y.; Futami, F.; Kikuchi, K. Generation of over 140-nm-wide super-continuum from a normal dispersion fiber by using a mode-locked semiconductor laser source. IEEE Photon. Technol. Lett. 1998, 10, 1560–1562. [Google Scholar] [CrossRef]
- Bartula, R.J.; Hagen, C.L.; Walewski, J.W.; Sanders, S.T. Generation of pulsed ultra-violet and mid-infrared supercontinua in standard single-mode fiber. In Laser Applications to Chemical, Security and Environmental Analysis; Optica Publishing Group: Incline Village, NV, USA, 2006; p. ThB2. [Google Scholar]
- Wang, Y.Y.; Zhang, N.; Zhang, P.Q. Broadband and coherent supercontinuum generation in all-normal-dispersion double-clad Ge-As-Se-Te fiber taper. Chin. J. Lasers 2022, 49, 0101010. [Google Scholar]
- Jia, Z.; Yao, C.; Li, Z.; Jia, S.; Zhao, Z.; Wei, Q.; Qin, G. High power mid-infrared supercontinuum light sources based on fluorotellurite glass fibers. Infrared Laser Eng. 2018, 47, 0803004. [Google Scholar]
- Yang, L.; Li, Y.; Zhang, B.; Wu, T.; Zhao, Y.; Hou, J. 30-W supercontinuum generation based on ZBLAN fiber in an all-fiber configuration. Photon. Res. 2019, 7, 1061–1065. [Google Scholar] [CrossRef]
- Karim, M.; Ahmad, H.; Ghosh, S.; Rahman, B. Mid-infrared supercontinuum generation using As2Se3 photonic crystal fiber and the impact of higher-order dispersion parameters on its supercontinuum bandwidth. Opt. Fiber Technol. 2018, 45, 255–266. [Google Scholar] [CrossRef]
- Medjouri, A.; Abed, D.; Becer, Z. Numerical investigation of a broadband coherent supercontinuum generation in Ga8Sb32S60 chalcogenide photonic crystal fiber with all-normal dispersion. Opto-Electron. Rev. 2019, 27, 1–9. [Google Scholar] [CrossRef]
- Madeikis, K.; Dansette, P.-M.; Bartulevičius, T.; Veselis, L.; Jutas, R.; Eremchev, M.; Danilevičius, R.; Girdauskas, V.; Michailovas, A. Investigation of materials for supercontinuum generation for subsequent nonlinear parametrical and Raman amplification at 1 MHz repetition rate. Opt. Laser Technol. 2021, 143, 107373. [Google Scholar] [CrossRef]
- Islam, A.M.T.U.; Ahmad, R.; Hossen, I.; Kabir, M.R.; Bishwas, M.S.; Faruque, O. Wideband mid-infrared supercontinuum generation in chloroform filled suspended core fiber. In Proceedings of the 2020 2nd International Conference on Sustainable Technologies for Industry 4.0 (STI), Dhaka, Bangladesh, 19–20 December 2020; pp. 1–4. [Google Scholar]
- Jiao, K.; Wang, X.G.; Liang, X.; Bai, S.; Zhao, Z.; Wang, X.; Zhang, P.; Dai, S.; Nie, Q.; Wang, R. Single-mode suspended large-core chalcohalide fiber with a low zero-dispersion wavelength for Supercontinuum generation. Opt. Express 2021, 30, 641–649. [Google Scholar] [CrossRef] [PubMed]
- Chugh, S.; Gulistan, A.; Ghosh, S.; Rahman, B.M.A. Machine learning approach for computing optical properties of a photonic crystal fiber. Opt. Express 2019, 27, 36414–36425. [Google Scholar] [CrossRef] [PubMed]
- Xiao, F.; Huang, W.; Yu, H.; Song, B. Predicting optical properties of different photonic crystal fibers from 2D structural images using convolutional neural network and transfer learning. Opt. Commun. 2024, 558, 130363. [Google Scholar] [CrossRef]
- Wei, W.H. Structural, thermal and optical properties and transition threshold in Ge-Sb-Se glassy system. J. Non-Cryst. Solids 2020, 536, 119991. [Google Scholar] [CrossRef]
- Amiri, I.; Khalek, A.; Chakma, S.; Paul, B.K.; Ahmed, K.; Dhasarathan, V.; Rajan, M.M. Design of Ge20Sb15Se65 embedded rectangular slotted quasi photonic crystal fiber for higher nonlinearity applications. Optik 2019, 184, 63–69. [Google Scholar] [CrossRef]
- Han, X.; You, C.; Dai, S.; Zhang, P.; Wang, Y.; Guo, F.; Xu, D.; Luo, B.; Xu, P.; Wang, X. Mid-infrared supercontinuum generation in a three-hole Ge20Sb15Se65 chalcogenide suspended-core fiber. Opt. Fiber Technol. 2017, 34, 74–79. [Google Scholar] [CrossRef]
- Shahriar, T.R.; Islam, O.; Tahmid, I.; Alam, Z.; Alam, M.S. Highly coherent supercontinuum generation in circular lattice photonic crystal fibers using low-power pulses. Optik 2023, 272, 170258. [Google Scholar] [CrossRef]
- Abdel-Basset, M.; Mohamed, R.; Jameel, M.; Abouhawwash, M. Nutcracker optimizer: A novel nature-inspired metaheuristic algorithm for global optimization and engineering design problems. Knowl.-Based Syst. 2023, 262, 110248. [Google Scholar] [CrossRef]
- John, H. Holland. Genetic algorithms. Sci. Am. 1992, 267, 66–73. [Google Scholar]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar]







| Parameters | Minimum Limit | Maximum Limit |
|---|---|---|
| hq | 0.4 µm | 1.8 µm |
| d | 3 µm | 6 µm |
| Λ | 0.5 µm | 2.9 µm |
| flength | 0.03 m | 0.1 m |
| P | 100 W | 1000 W |
| FWHM | 0.03 ps | 0.06 ps |
| C | −6 | 6 |
| Maximµm Spectral Bandwidth/µm | Coefficient of Variation (CV/%) | hq/µm | d/µm | Λ/µm | flength/m | P/W | FWHM/ps | C |
|---|---|---|---|---|---|---|---|---|
| 25 | 43.66 | 1.22 | 3.34 | 1.57 | 0.06 | 1000 | 0.046 | −0.94 |
| 20 | 52.52 | 0.84 | 3.22 | 2.90 | 0.08 | 873 | 0.035 | −0.44 |
| 15 | 55.85 | 0.68 | 5.85 | 1.70 | 0.06 | 861 | 0.06 | 1.40 |
| 10 | 62.12 | 1 | 5.36 | 0.60 | 0.05 | 500 | 0.06 | 3.63 |
| 6 | 66.20 | 0.55 | 4.67 | 1.08 | 0.03 | 176 | 0.05 | 2.63 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jing, M.; Ning, T. Supercontinuum Generation in Suspended Core Fibers Based on Intelligent Algorithms. Photonics 2025, 12, 497. https://doi.org/10.3390/photonics12050497
Jing M, Ning T. Supercontinuum Generation in Suspended Core Fibers Based on Intelligent Algorithms. Photonics. 2025; 12(5):497. https://doi.org/10.3390/photonics12050497
Chicago/Turabian StyleJing, Meiqian, and Tigang Ning. 2025. "Supercontinuum Generation in Suspended Core Fibers Based on Intelligent Algorithms" Photonics 12, no. 5: 497. https://doi.org/10.3390/photonics12050497
APA StyleJing, M., & Ning, T. (2025). Supercontinuum Generation in Suspended Core Fibers Based on Intelligent Algorithms. Photonics, 12(5), 497. https://doi.org/10.3390/photonics12050497




