A Heuristic Time-Domain Raman Forward Solver for Photon Migration in a Two-Layer Diffusive Medium

Abstract

An analytical heuristic model has been developed to describe the time-domain reflectance Raman signal in a two-layer diffusive medium. The model is based on the solution of two coupled diffusion equations at the excitation and emission wavelengths, respectively. The accuracy of the model is verified by comparison with the results of Monte Carlo simulations. This solver correctly accounts for the Raman emitters within the layers and the full wavelength dependence of the optical properties of the layers. The computational efficiency of the solver is compatible with the requirements of rapid reconstructions of Raman spectra from time-domain Raman measurements acquired for a large number of different wavelengths.

1. Introduction

Diffuse Raman spectroscopy (DIRS) [1,2,3,4,5,6,7,8] merges and incorporates the high chemical specificity of Raman spectroscopy [9,10] with in-depth or bulk analysis of Diffuse Optics to probe highly diffusive media [11,12]. Among different DIRS approaches, time-domain diffuse Raman spectroscopy (TD-DIRS) explores diffusive media exploiting the photon time of flight, which encodes the mean visited depth [13,14,15,16,17]. TD-DIRS extends the use of time gates, initially sought for fluorescence suppression [18,19,20] to encompass depth discrimination. The interpretation of time-domain diffuse Raman spectroscopy relies on the availability of a model capable of describing the migration of photons in the media of interest. Therefore, accurate modeling of light propagation is essential for this technique for the correct recovery of Raman spectra from the investigated medium [17,21]. Spontaneous Raman scattering in the TD in highly diffusive media can be computationally evaluated by three main approaches: stochastic forward solvers based on Monte Carlo (MC) simulations [11,21], analytical heuristic solutions of the Raman interactions [11,17,21], and rigorous analytical solutions of the diffusion equation (DE) [11,17,21]. Monte Carlo simulations can be performed for any geometry and have been exploited in the forward modeling of continuous-wave (CW) diffuse Raman propagation [22], yet they are computationally expensive, and their use for the inverse problem is more challenging, particularly for the TD. In contrast, exact analytical forward solvers are significantly faster; however, their availability is limited to homogeneous geometries [11,21]. We address photon migration in a two-layer medium using MC simulations and a heuristic analytical model that offers significant advantages compared to the existing one [17]. The layered geometry is of great interest in the field of tissue optics. Indeed, it represents the architecture of many tissues, such as the fat layer overlying muscle tissue, the extra-cerebral tissue over the brain, or the thorax over the lungs. The MC results serve as a reference for verifying the analytical model.

2. Theory

The usual approach used to obtain solutions for the Raman signal in diffusive media across any geometry involves two coupled diffusion equations [11,17,21], one at the excitation wavelength ($\lambda$) for the fluence rate $\Phi \left(\mathbf{r},t\right)$, describing the energy distribution of the excitation light, and one at the emission wavelength (${\lambda }_{\mathrm{e}}$) for the Raman fluence rate ${\Phi }_{\mathrm{eR}}\left(\mathbf{r},t\right)$, describing the energy distribution of the Raman emitted light [11,17,21]. In this scheme, the product of the Raman scattering coefficient ${\mu }_{\mathrm{sR}}$ (probability per unit path length to have Raman scattering [11,21]), where $\Phi \left(\mathbf{r},t\right)$ is the source term of the second DE generating the sought-for Raman solution ${\Phi }_{\mathrm{eR}}\left(\mathbf{r},t\right)$. Computing the TD Raman fluence signal, ${\Phi }_{\mathrm{eR}}$, according to the mentioned scheme, implies the evaluation of the following integral of Green’s function (for the details of the procedure, see Refs. [11,17,21]):

$$\begin{array}{c}{\Phi }_{\mathrm{eR}}\left(\mathbf{r},t,{\lambda }_e\right)=\underset{0}{\overset{t}{\int }}\underset{V^{\prime }}{\int }{\mu }_{\mathrm{sR}}({\mathbf{r}}^{\prime },\lambda \to {\lambda }_e){\Phi }_{\mathrm{G}}({\mathbf{r}}^{\prime },t^{\prime },\lambda )\times {\Phi }_{\mathrm{Ge}}({\mathbf{r}}^{\prime },\mathbf{r},t,t^{\prime },{\lambda }_{\mathrm{e}})\mathrm{d}{\mathbf{r}}^{\prime }\mathrm{d}{t}^{\prime },\end{array}$$

(1)

where ${\Phi }_{\mathrm{G}}$ and ${\Phi }_{\mathrm{Ge}}$ are Green’s functions for the two-layer medium at $\lambda$ and ${\lambda }_{\mathrm{e}}$ [11], respectively, and $V^{\prime }$ denotes the volume of the medium. The solution of Equation (1) is obtained, assuming that only single-scattering Raman events contribute to the signal. The evaluation of this integral can be computationally expensive in terms of computing time, with the risk of obtaining a model whose computation speed is not sufficiently high for applying the model in the inverse reconstructions of Raman spectra. For this reason, we opted for a heuristic approach.

From now on, the quantities without a suffix are related to $\lambda$, and the quantities with suffix “e” refer to ${\lambda }_e$. A two-layer cylinder (see Figure 1a) of radius L and thicknesses $s_1$ and $s_2$ is considered for the first and second layer, respectively. At $\lambda$, we identify the absorption coefficients ${\mu }_{\mathrm{a}1}$ and ${\mu }_{\mathrm{a}2}$; the reduced scattering coefficients ${\mu }_{\mathrm{s}1}^{\prime }$ and ${\mu }_{\mathrm{s}2}^{\prime }$; the Raman scattering coefficients ${\mu }_{\mathrm{s}\mathrm{R}1}$ and ${\mu }_{\mathrm{s}\mathrm{R}2}$; and the refractive indices $n_1$ and $n_2$ in the first and second layer, respectively. Similarly, the symbols ${\mu }_{\mathrm{a}1\mathrm{e}}$, ${\mu }_{\mathrm{a}2\mathrm{e}}$, ${\mu }_{\mathrm{s}1\mathrm{e}}^{\prime }$, ${\mu }_{\mathrm{s}2\mathrm{e}}^{\prime }$, $n_{1\mathrm{e}}$, and $n_{2\mathrm{e}}$ indicate the optical properties at ${\lambda }_{\mathrm{e}}$.

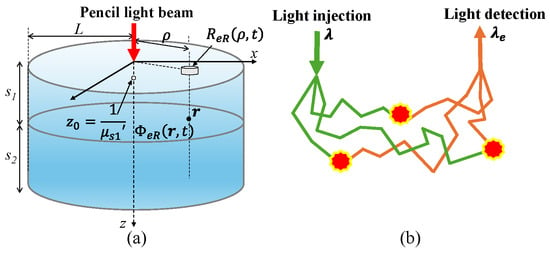
Figure 1. (a) Schematic of a two-layer cylinder illuminated by a pencil beam source with the representation of some symbols used in the Theory section. (b) Schematic of some trajectories resulting from light injected at $\lambda$, which, after interacting with the Raman scatterers, are converted into the emission wavelength ${\lambda }_{\mathrm{e}}$ due to Raman scattering and finally collected at the detector site.

We started from a previous heuristic approach proposed by Šušnjar et al. [17] that, by exploiting the typical low values of ${\mu }_{\mathrm{s}\mathrm{R}1}$ and ${\mu }_{\mathrm{s}\mathrm{R}2}$, usually lower than ${10}^{-6}$ mm⁻¹, expands the emitted fluence in a Taylor series up to its first-order approximation. According to this method, the TD Raman fluence signal at ${\lambda }_e$, ${\Phi }_{\mathrm{e}\mathrm{R}0}$, in a two-layer cylinder can be written, under the hypothesis that the optical properties of the medium are the same at $\lambda$ and ${\lambda }_e$, as follows: [17]

$$\begin{array}{c}{\Phi }_{\mathrm{e}\mathrm{R}0}(\mathbf{r},{\mu }_{\mathrm{a}1\mathrm{e}},{\mu }_{\mathrm{s}1\mathrm{e}}^{\prime },{\mu }_{\mathrm{a}2\mathrm{e}},{\mu }_{\mathrm{s}2\mathrm{e}}^{\prime },t,{\lambda }_e)\approx {\Phi }_{\lambda }(\mathbf{r},{\mu }_{\mathrm{a}1},{\mu }_{\mathrm{s}1}^{\prime },{\mu }_{\mathrm{a}2},{\mu }_{\mathrm{s}2}^{\prime },t,\lambda )\hfill \\ \times \left[{\mu }_{\mathrm{s}\mathrm{R}1}(\lambda \to {\lambda }_e)v_1⟨t_1⟩\left(t\right)+{\mu }_{\mathrm{s}\mathrm{R}2}(\lambda \to {\lambda }_e)v_2⟨t_2⟩\left(t\right)\right],\hfill \end{array}$$

(2)

with ${\Phi }_{\lambda }$ as the fluence rate in the two-layer medium at $\lambda$ [11], $⟨t_1⟩\left(t\right)$ and $⟨t_2⟩\left(t\right)$ as the average times spent by detected light at t in the first and second layer, respectively, and $v_1$ and $v_2$ as the speed of light in the layers. About $⟨t_1⟩\left(t\right)$ and $⟨t_2⟩\left(t\right)$, according to known properties of the Radiative Transfer Equation (RTE) arising from the microscopic Beer–Lambert–Bouguer law, they can be expressed as [11,23]

$$\begin{array}{c}{⟨t_i⟩}_{i=1,2}\left(t\right)=-{\displaystyle \frac{1}{v_i\Phi (\mathbf{r},{\mu }_{\mathrm{a}1},{\mu }_{\mathrm{s}1}^{\prime },{\mu }_{\mathrm{a}2},{\mu }_{\mathrm{s}2}^{\prime },t,\lambda )}}{\displaystyle \frac{\partial {\Phi }_{\lambda }(\mathbf{r},{\mu }_{\mathrm{a}1},{\mu }_{\mathrm{s}1}^{\prime },{\mu }_{\mathrm{a}2},{\mu }_{\mathrm{s}2}^{\prime },t,\lambda )}{\partial {\mu }_{\mathrm{ai}}}},\hfill \end{array}$$

(3)

with $⟨t_1⟩\left(t\right)+⟨t_2⟩\left(t\right)=t$. The second term of Equation (2) is the probability, $P(\lambda \to {\lambda }_e,t)$, to have Raman-generated photons from the two layers, subsequently detected at time t, i.e.,

$$\begin{array}{c}P(\lambda \to {\lambda }_{\mathrm{e}},t)={\mu }_{\mathrm{s}\mathrm{R}1}(\lambda \to {\lambda }_{\mathrm{e}})v_1⟨t_1⟩\left(t\right)+{\mu }_{\mathrm{s}\mathrm{R}2}(\lambda \to {\lambda }_{\mathrm{e}})v_2⟨t_2⟩\left(t\right).\hfill \end{array}$$

(4)

Equation (2) does not account for the dependence of the optical properties on ${\lambda }_e$ that actually influence the Raman signal emerging from the medium. We denote this model as “Model 0”.

In the more general case, ${\Phi }_{\mathrm{eR}}$ depends on both the optical properties at $\lambda$ and ${\lambda }_e$, since the propagation of photons received at ${\lambda }_e$ consists of two different parts, i.e., two phases of propagation: An initial photon propagation at $\lambda$ and a second propagation at ${\lambda }_{\mathrm{e}}$ (see Figure 1b). In principle, we know how to describe these two separated kinds of propagation; however, the challenging point is to establish how to combine them to obtain ${\Phi }_{\mathrm{eR}}$. In this work, we heuristically assume that the detected Raman signal is determined on average through a combination of photon propagation at $\lambda$ and ${\lambda }_{\mathrm{e}}$, i.e., one half at $\lambda$ and one half at ${\lambda }_{\mathrm{e}}$. This hypothesis is well verified when the diffusion conditions of light propagation hold and when the variation in optical properties between $\lambda$ and ${\lambda }_e$ is sufficiently low to have a similar propagation at $\lambda$ and ${\lambda }_e$ and thus a similar probability of having photons at these two wavelengths. Under these conditions, we have that the propagation of light is well randomized also in wavelength, so we have the same probability of finding photons at both wavelengths. Consequently, according to the above assumption, we can heuristically express the Raman fluence at ${\lambda }_{\mathrm{e}}$, ${\Phi }_{\mathrm{e}\mathrm{R}1}$, as

$$\begin{array}{c}{\Phi }_{\mathrm{e}\mathrm{R}1}(\mathbf{r},t,\dots ,\lambda ,{\lambda }_{\mathrm{e}})\approx P(\lambda \to {\lambda }_{\mathrm{e}},t){\displaystyle \frac{\left[{\Phi }_{\lambda }(\mathbf{r},{\mu }_{\mathrm{a}1},{\mu }_{\mathrm{s}1}^{\prime },{\mu }_{\mathrm{a}2},{\mu }_{\mathrm{s}2}^{\prime },t)+{\Phi }_{{\lambda }_{\mathrm{e}}}(\mathbf{r},{\mu }_{\mathrm{a}1\mathrm{e}},{\mu }_{\mathrm{s}1\mathrm{e}}^{\prime },{\mu }_{\mathrm{a}2\mathrm{e}},{\mu }_{\mathrm{s}2\mathrm{e}}^{\prime },t)\right]}{2}},\end{array}$$

(5)

where ${\Phi }_{\lambda }$ and ${\Phi }_{{\lambda }_e}$ are, respectively, the photon fluence rate at $\lambda$ and ${\lambda }_e$. We denote this improved model as “Model 1”. Unlike “Model 0”, which ignores ${\lambda }_e$ dependence, “Model 1” heuristically integrates both $\lambda$ and ${\lambda }_e$ propagation, as validated against MC simulations in the next section. The time-domain Raman signal received in reflectance configuration, $R_{\mathrm{e}\mathrm{R}1}$, from the two-layer medium (Figure 1) illuminated by a pulse source can thus be obtained as [11,17,21]

$$R_{\mathrm{e}\mathrm{R}1}(\rho ,t)={\displaystyle \frac{{\Phi }_{\mathrm{e}\mathrm{R}1}\left(\rho ,z=0,t\right)}{2A}},$$

(6)

with A being a coefficient related to the Fresnel reflection coefficient [11,23]. Alternatively, $R_{\mathrm{e}\mathrm{R}1}$ can also be calculated by Fick’s law [11,23]. Actually, there are only slight differences between the two ways of calculating the photon flux [11,21], which are of little interest in this context; therefore, in this work, we used Equation (6). The superiority of “Model 1” over “Model 0” is shown through a comparison with the results of the MC simulations in the next section.

The results presented in this work concern a unitary Dirac $\delta$ pulse pencil beam source incident perpendicularly on the medium, as shown in Figure 1. This kind of source can be accurately modeled as an isotropic point source of unitary strength, $\delta (\mathbf{r}-{\mathbf{r}}_{\mathrm{s}})\delta \left(t\right)$, placed at one transport mean free path from the injection point, i.e., at ${\mathbf{r}}_{\mathrm{s}}=(0,0,1/{\mu }_{\mathrm{s}}^{\prime })$ [11,23], and this is used to obtain the solutions of “Model 0” and “Model 1”. For details on this point, see [11].

3. Results: Comparison Models vs. Monte Carlo Simulations

The MC results were obtained by extending a previously developed code for simulating Raman propagation through a homogeneous medium to the case of a two-layer geometry [21,24]. The values of the optical properties selected for the comparison models vs. MC simulations were among those typical of various biological tissues. However, it is worth emphasizing that the particular values chosen do not affect the conclusions of this work. The considered geometric dimensions of the medium were large enough to have negligible boundary effects from the finite lateral dimension ($L\gg \rho$) and longitudinal dimension ($s_1+s_2\gg \rho$) as in most in vivo experiments on biological tissues. For this purpose, in all the comparisons in the figures, we had $s_1=15$ mm, $s_2=80$ mm, $L=80$ mm, and a maximum $\rho$ equal to 20 mm. Further, the refractive index of the layers was the same at both wavelengths, $n_1=n_2=n_{1e}=n_{2e}=1.4$, and the refractive index of the external medium was 1. The Raman scattering coefficients in the two layers were different in all comparisons made and were equal to ${\mu }_{\mathrm{s}\mathrm{R}1}={10}^{-5}$ mm⁻¹ and ${\mu }_{\mathrm{s}\mathrm{R}2}=2·{10}^{-5}$ mm⁻¹, small enough to ensure the usability of the models and a realistic scenario. The optical and geometrical properties considered in the comparisons are summarized in Table 1.

Table 1. Optical and geometrical properties of analyzed cases.

Properties	“Case 1”	“Case 2”	“Case 3”	“Case 4”
${\mu }_{\mathrm{a}1}$ (mm−1)	0.004	0.004	0.004	0.005
${\mu }_{\mathrm{a}2}$ (mm−1)	0.01	0.01	0.01	0.001
${\mu }_{\mathrm{s}1}^{\prime }$ (mm−1)	1	1	1	1
${\mu }_{\mathrm{s}2}^{\prime }$ (mm−1)	0.5	0.5	2	0.5
${\mu }_{\mathrm{R}1}$ (mm−1)	${10}^{-5}$	${10}^{-5}$	${10}^{-5}$	${10}^{-5}$
${\mu }_{\mathrm{R}2}$ (mm−1)	$2·{10}^{-5}$	$2·{10}^{-5}$	$2·{10}^{-5}$	$2·{10}^{-5}$
${\mu }_{\mathrm{a}1\mathrm{e}}$ (mm−1)	0.0052	0.006	0.006	0.0065
${\mu }_{\mathrm{a}2\mathrm{e}}$ (mm−1)	0.013	0.015	0.015	0.0013
${\mu }_{\mathrm{s}1\mathrm{e}}^{\prime }$ (mm−1)	0.9	0.9	0.9	0.9
${\mu }_{\mathrm{s}2\mathrm{e}}^{\prime }$ (mm−1)	0.45	0.45	1.8	0.45
$s_1$ (mm)	15	15	15	15
$s_2$ (mm)	80	80	80	80
L (mm)	80	80	80	80

In Figure 2, Figure 3, Figure 4 and Figure 5, the TD Raman reflectance calculated with the two models is compared to the MC results for four cases according to Table 1.

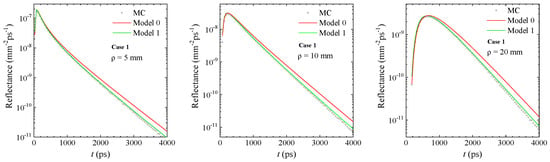
Figure 2. Comparison between models and MC results: Case 1. This case pertains to values of the optical properties typical of muscle with a subcutaneous fat layer, which is a configuration largely used to measure tissue oxygenation with near-infrared oximeters.

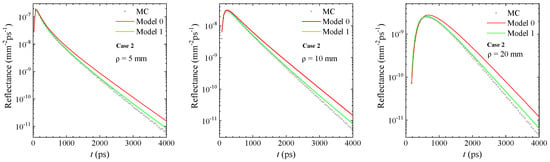
Figure 3. Comparison between models and MC results: Case 2. The same as Case 1, but for a larger variation in absorption at emission wavelength in both layers (see Table 1).

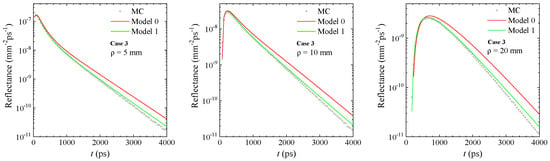
Figure 4. Comparison between models and MC results: Case 3. This case aims to test the model when ${\mu }_{\mathrm{s}1}^{\prime }<{\mu }_{\mathrm{s}2}^{\prime }$, typical for instances of thorax in the lungs [25]. Other representative cases of this situation can also be found in breast and muscle tissue [12] when the analysis is performed at low wavelengths (lower than 700 nm).

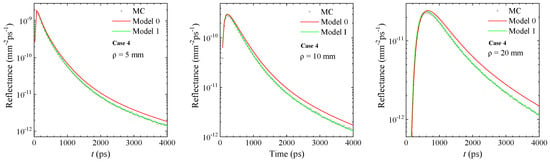
Figure 5. Comparison between models and MC results: Case 4. This case aims to address a situation where ${\mu }_{\mathrm{a}1}>{\mu }_{\mathrm{a}2}$ and thus complete the scenarios of the previous cases.

These comparisons intend to show the performances of the models to account for the variation in the optical properties of the two-layer medium between $\lambda$ and ${\lambda }_e$ and of the different Raman scattering coefficients in the two layers at $\lambda$. In Figure 2 and Figure 3, the considered optical properties at $\lambda$ were typical of muscle with a subcutaneous fat layer and the first layer thickness used (15 mm) can be a typical value for the fat layer. At ${\lambda }_e>\lambda$, a reduction in scattering of 10% was assumed in the layers, as well as increases in absorption of 30% (Figure 2) and 50% (Figure 3). The difference in accuracy between the two models is evident at both short and long distances, particularly at late times. In these two figures, the improvement of “Model 1” over “Model 0” is largely evident. However, given its heuristic nature, “Model 1” is also notably lacking at late times. Figure 4 shows results similar to those of Figure 3; however, they refer to a higher scattering in the second layer ${\mu }_{\mathrm{s}2}^{\prime }=2$ mm⁻¹, which can be linked to in vivo measurements of the chest, above the lungs [25]. The different combination of scattering does not alter the quality of the comparison between models and MC results, which are shown to be very close to that observed above. This confirms that the two-layer solution of “Model 1” can correctly account for the dependence of the Raman signal from the optical properties at $\lambda$ and ${\lambda }_e$, which is missing in “Model 0”.

In Figure 5, we finally have a case with absorption in the first layer being higher than in the second layer, for which the “Model 1” almost matches the MC results. Similar results were obtained for other values of $\rho$, such as 15 mm, and of $s_1$, such as 5 and 10 mm.

The proposed “Model 1” performs robustly but exhibits reduced accuracy at late times. It can be seen that the reduced accuracy at late times increases with the increase in the difference of optical properties at $\lambda$ and ${\lambda }_e$, as can be visually seen by comparing the results of Case 1 and Case 2. We can argue that the difference in the optical properties at $\lambda$ and ${\lambda }_e$ influences the validity of the hypothesis employed to obtain “Model 1”, i.e., Equation (5). To understand and explain this fact, we must go back to the hypothesis on which it is based, i.e., on the heuristic assumption of Equation (5). The validity of this hypothesis is strictly subordinate to having an average generation time for each Raman signal detected at time t, $⟨t_g⟩\left(t\right)$, equal to $t/2$. Under this condition, half of the light propagation of the detected Raman signal is determined with the optical properties at $\lambda$ and the other half with the optical properties at ${\lambda }_e$, and this is what Equation (5) synthetically expresses. In reality, this is only an approximation, whose validity depends on the optical properties of the two layers at $\lambda$ and ${\lambda }_e$. It is also important to point out that “Model 1” can only be used for sufficiently low values of ${\mu }_{\mathrm{s}\mathrm{R}1}$ and ${\mu }_{\mathrm{s}\mathrm{R}2}$, which is naturally satisfied since the spontaneous Raman scattering coefficient is usually lower than ${10}^{-6}$ mm⁻¹. The MC results have shown that for ${\mu }_{\mathrm{s}\mathrm{R}1},{\mu }_{\mathrm{s}\mathrm{R}2}\le {10}^{-4}$ mm⁻¹, the condition for representing the Raman fluence rate as a first-order approximation is well verified.

4. Discussion

To better understand the validity of the heuristic approximation underlying “Model 1”, in Figure 6, by means of MC simulations, the average generation time of the emitted Raman photons $⟨t_g⟩\left(t\right)$ is plotted as a function of time, along with the behavior hypothesized by the model for Cases 1, 2 and 4. The figure highlights that the heuristic hypothesis of “Model 1” holds exactly at early times, while at later times, a clear deviation emerges between the expected behavior $t/2$ and the actual behavior from the MC simulations.

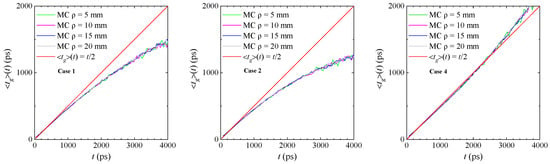
Figure 6. Average generation time of the emitted Raman photons calculated with MC simulations versus the detection time t for cases 1, 2, and 4 along with the assumed $⟨t_g⟩\left(t\right)$ by “Model 1”.

Furthermore, a direct correlation exists between the model’s accuracy and the deviation, at each detection time t, in the model assumption $⟨t_g⟩\left(t\right)=t/2$ from the actual $⟨t_g⟩\left(t\right)$ obtained from MC simulations. For instance, in Case 2, where larger discrepancies arise between “Model 1” and MC simulations at late times (Figure 3), we also observe greater deviations between MC-derived $⟨t_g⟩\left(t\right)$ and $t/2$. On the contrary, in Case 4 (Figure 5), where “Model 1” closely matches MC simulations even at late times, the differences between the MC-derived $⟨t_g⟩\left(t\right)$ and $t/2$ remain small. More importantly, the results of the figure confirm the previous observation that the validity of the hypothesis $⟨t_g⟩\left(t\right)=t/2$ depends on the difference in the optical properties between $\lambda$ and ${\lambda }_e$. In fact, Case 2, which has a larger absorption difference (between $\lambda$ and ${\lambda }_e$), shows a larger deviation from the hypothesis made compared to Cases 1 and 4, which have a lower absorption difference.

These observations clarify the underlying effect and suggest a viable approach for model improvement: implementing a late-time correction to “Model 1” proportional to the deviation in the actual $⟨t_g⟩\left(t\right)$ from $t/2$. It is also very important to note that this behavior is independent of the source–detector distance $\rho$ considered, as we see in Figure 6. This result is in agreement with the features of the proposed model and with what we can reasonably expect from the migration of photons through a layered medium. In fact, $⟨t_g⟩\left(t\right)$ depends on the two probability terms of having Raman-generated photons in the two layers, i.e., ${\mu }_{\mathrm{s}\mathrm{R}1}{v}_1⟨t_1⟩\left(t\right)$ and ${\mu }_{\mathrm{s}\mathrm{R}2}{v}_2⟨t_2⟩\left(t\right)$. Previous studies have shown that in the diffusive regime and in a two-layer medium, $⟨t_1⟩\left(t\right)$ and $⟨t_2⟩\left(t\right)$ weakly depend on $\rho$ [26]; thus, the results of Figure 6 fall completely within this frame.

Finally, we utilized the MC simulation values of $⟨t_g⟩\left(t\right)$ to refine and implement the final version of our proposed model. Figure 7 presents the recalculated comparison of Case 2, where “Model 1” now incorporates the exact generation time $⟨t_g⟩\left(t\right)$ obtained from MC simulations instead of using the $t/2$ approximation, denoted as “Model 2”. This approach effectively calculates the Raman fluence rate at ${\lambda }_e$, ${\Phi }_{\mathrm{e}\mathrm{R}2}$, using the fractions of time t spent by the detected photons at ${\lambda }_e$ in their previous propagation, respectively, at $\lambda$ and ${\lambda }_e$, as

$$\begin{array}{c}{\Phi }_{\mathrm{e}\mathrm{R}2}(\mathbf{r},t,\dots ,\lambda ,{\lambda }_{\mathrm{e}})\approx P(\lambda \to {\lambda }_{\mathrm{e}},t)\left[{\Phi }_{\lambda }(\mathbf{r},\dots ,t){\displaystyle \frac{⟨t_g⟩\left(t\right)}{t}}+{\Phi }_{{\lambda }_{\mathrm{e}}}(\mathbf{r},\dots ,t)\left(1-{\displaystyle \frac{⟨t_g⟩\left(t\right)}{t}}\right)\right].\end{array}$$

(7)

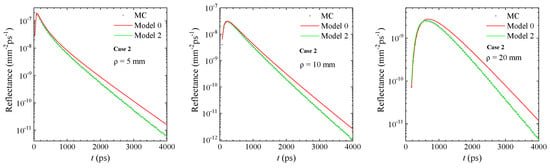
Figure 7. Comparison for Case 2, where “Model 1” is replaced with “Model 2” (Equation (7)), obtained with generation time $⟨t_g⟩\left(t\right)$ given by the actual values obtained from the MC simulations.

The results in Figure 7 obtained using Equation (7) demonstrate that the late-time discrepancy between the model and MC simulations is completely resolved with this correction. It is also important to emphasize how the agreement between the model and MC results remains surprisingly good for the distance of $\rho =5$ mm as well, for which one could expect a lower performance from the DE. This is because in the time-domain, what really matters in the validity of the diffusion approximation is only the observation time rather than the distance from the source. The same approach used here to generate the data of Figure 7 works exceptionally well for all other studied cases, confirming that Equation (7) provides a complete and optimal description of Raman light propagation through a layered diffusive medium. In the future, we aim to derive an analytical expression for $⟨t_g⟩\left(t\right)$ as the final step in refining “Model 2”. However, it is worth noting that evaluating $⟨t_g⟩\left(t\right)$ via MC simulations is both fast and straightforward, as it can be obtained using an arbitrarily large detector, since $⟨t_g⟩\left(t\right)$ is independent of the source–detector distance $\rho$.

The proposed solver “Model 1” for the Raman TD signal (5) is, in terms of computational cost, approximately equivalent to computing the DE solution twice for a two-layer medium used to obtain the solution of Equation (5) [11,27] and thus about twice “Model 0”, which was already used in the inverse reconstruction of Raman spectra [17], thus demonstrating its suitability for this purpose. For a better overview of the performance of the different models shown in the previous figures, in Table 2, we report the main characteristics of each model for approximation and calculation times. The computation time of “Model 1”, since it includes the calculation of the two-layer DE solution at both $\lambda$ and ${\lambda }_e$, is roughly twice the computation time of “Model 0”, and for a whole temporal profile, it is about 1 s with a CPU Intel i7-12650h. The computation time to reproduce the same temporal profiles with MC simulations is about 280 times larger using an NVIDIA GEFORCE RTX3080 Ti 12Gb. “Model 2”, compared to “Model 1”, requires further evaluation of the prior information on $⟨t_g⟩\left(t\right)$, which is achieved through a single MC simulation. By exploiting the fact that in the diffusive regime, $⟨t_g⟩\left(t\right)$ is independent of the source–detector distance $\rho$, we can run the MC simulation with a very large detector and a few thousands of trajectories are enough for a reasonable estimate of $⟨t_g⟩\left(t\right)$. So, calculating this information is very fast. For this reason, the computation time of “Model 2” is of the order of a few seconds compared to “Model 1”.

Table 2. Summary of the main approximations and performances of “Model 0”, “Model 1”, and “Model 2”. The computation time was evaluated with a PC with a CPU Intel i7-12650h.

Characteristics	“Model 0”	“Model 1”	“Model 2”
Kind of Theory	Heuristic, DE	Heuristic, DE	Heuristic, DE
Optical Properties $\lambda$	Accounted	Accounted	Accounted
Optical Properties ${\lambda }_e$	Not included	Accounted	Accounted
$⟨t_g⟩\left(t\right)$	Not included	$t/2$	Exact
Computation time per simulation	≈350 ms	≈1 s	Similar to “Model 1”

The modeling proposed here for the TD Raman signal also has some implications for applications involving fluorescence, both for steady state and TD sources, given the high similarities between the two phenomena. It is also straightforward to implement this kind of model for fluorescence calculations in the TD by replacing the Raman scattering coefficients with the fluorescence absorption coefficients and introducing the related decay time of the fluorophores. Thus, given the order of magnitude of the absorption term in fluorescence, which is usually much higher than the usual values of the Raman scattering coefficient, the same approximations for Raman may not be valid for fluorescence emission. Thus, we may expect that the Taylor expansion to the first order is not enough to obtain a correct representation of the signal. In the case of fluorescence, it may therefore be necessary to introduce higher-order terms to represent the probability $P(\lambda \to {\lambda }_e,t)$ in Equation (5). The complete expression of $P(\lambda \to {\lambda }_e,t)$ is as follows [17]:

$$\begin{array}{c}\hfill P(\lambda \to {\lambda }_e,t)=\underset{0}{\overset{t}{\int }}g\left(t_1\right)\left(1-{\mathrm{e}}^{-{\mu }_{\mathrm{s}\mathrm{R}1}{v}_1{t}_1-{\mu }_{\mathrm{s}\mathrm{R}2}{v}_2{t}_2}\right)\mathrm{d}{t}_1,\end{array}$$

(8)

with $g\left(t_1\right)$ as the probability density function of the photons spending a time duration of $t_1$ in the first layer. For the fluorescence calculation, coefficients ${\mu }_{\mathrm{s}\mathrm{R}1}$ and ${\mu }_{\mathrm{s}\mathrm{R}2}$ must be replaced with the correspondent absorption coefficients of the fluorophores in the layers and the quantum efficiency of the fluorophores should also be included [11,21]. The present “Model 1” and “Model 2” are obtained by expanding the exponential obtained for $P(\lambda \to {\lambda }_e,t)$ (Equation (8)) to the first order. For fluorescence calculations, one might consequently suggest deriving a second-order expression, which can be obtained by expanding the exponential term in the integral of Equation (8) up to the second order. The implementation of this part of the modeling is beyond the scope of this work. As for the use of the presented “Model 1” for fluorescence calculations, this is possible as long as the value of the absorption coefficient of the fluorophore is lower than ${10}^{-3}$ mm⁻¹.

The described models pertain to a pencil light beam impinging over the considered medium. In most cases, this is enough to describe real laser sources. The working hypothesis for a real beam would be that it is spatially incoherent and that scattering from one pencil beam will not coherently interfere with that from another pencil beam. This assumption is well justified in a regime of multiple scatterings due to the effects of scattering events (for some insights into a real beam source, see Equation 5.57 in Section 5.3.1 of [11]).

5. Conclusions

In conclusion, we developed a time-domain heuristic forward solver for calculating the Raman signal emerging from a two-layer medium (“Model 1”). This represents a significant advancement over existing methods, as it accounts for the full dependence of the Raman signal on the optical properties of the two-layer medium at both excitation and emission wavelengths, while in the previous “Model 0”, the dependence of the Raman solution on ${\lambda }_e$ had been completely neglected. The solver was validated against Monte Carlo simulations, demonstrating good accuracy. However, its heuristic nature reduces accuracy at later times. We investigated this effect and traced it to the underlying heuristic hypothesis, which assumes that photon propagation is determined on average through an equal combination at excitation and emission wavelengths. Our analysis reveals that this hypothesis is directly linked to the average generation time, $⟨t_g⟩\left(t\right)$, which the model approximates as $t/2$. By calculating the true value of $⟨t_g⟩\left(t\right)$ and quantifying its deviation from $t/2$, as realized in Equation (7), the model obtained becomes almost exact within the diffusion approximation (see Figure 7). This finding opens the way toward a final development of the proposed model with which the main cause of approximation is eliminated. From this perspective, an analytical expression for $⟨t_g⟩\left(t\right)$ is still missing, which could be the focus of future work on the subject. However, the calculation of this term via Monte Carlo simulations is very fast with a few thousands of received trajectories, and furthermore, this information could also be conveniently stored in a separate file as a lookup table for typical values of optical properties expected in biological tissue. This approach can already offer a nearly exact model of the Raman signal emerging from a bi-layer medium within the diffusion approximation (“Model 2”), with a computation time comparable to that of “Model 1”.