Harmonics-Assisted 50-Fold Optical Phase Amplification with a Self-Mixing Thin-Slice Nd:GdVO₄ Laser with Wide-Aperture Laser-Diode Pumping

Abstract

Harmonic-assisted phase amplification was investigated in a 300-µm-thick Nd:GdVO₄ laser with coated end mirrors in the self-mixing interference scheme. The key event is the self-induced hybrid skew cosh Gaussian (abbreviated as skew ch-G)-type transverse mode oscillation in a thin-slice solid-state laser with wide-aperture laser-diode pumping. The present hybrid skew-chG mode was proved to be formed by the locking of nearly frequency-degenerate TEM₀₀ and annular fields. The resultant modal-interference-induced gain modulation at the beat frequency between the two modal fields, which is far above the relaxation oscillation frequency, increased the experimental self-mixing modulation bandwidth accordingly. Fifty-fold phase amplification was achieved in a strong optical feedback regime.

1. Introduction

Kogelnik and Li published a monumental work on optical resonators based on the principles of optics in which they found that Hermite–Gaussian modes form in Fabry–Perot optical cavities as stable orthogonal transverse eigenmodes [1]. Then, the so-called transverse effect has appeared as spontaneous pattern formations in nonlinear optics and lasers which featured rolls, hexagons and vortices by various nonlinearities [2,3,4]. Various nonlinear patterns in optics have been investigated in wide-aperture lasers including vertical cavity semiconductor lasers [5,6,7,8]. Additionally, thin-slice solid-state lasers with coated end mirrors (abbreviated as TS³Ls), have been studied in a different context related to the spatiotemporal dynamics of transverse modes in Fabry–Perot microcavities. The Fresnel number of a thin-platelet TS³L cavity, NF = a²/$l{\lambda }_l$ (a: aperture radius, $l$: optical cavity length, ${\lambda }_l$: lasing wavelength), is on the order of 10²–10³ larger than those of conventional cavities. Large-cavity Fresnel numbers enable lasing in a variety of transverse modes depending on the shape and spot size of the pump beam, i.e., by controlling the gain and thermally induced refractive index confinements of the lasing transverse modes as well as the actuated saturation type of optical nonlinearities inherent to TS³Ls [9].

In addition to a variety of pump-profile dependent lasing transverse mode formations, the self-mixing interference effect in TS³Ls between the lasing field, $E_l$ and the weak optical field from the target, $E_s$, has been recognized as being a simple self-aligned, cost-effective optical sensing technique that does not use sophisticated optical interferometers and highly sensitive electronics, in which a laser acts as a high-efficiency mixer oscillator and a shot-noise-limited quantum detector [10,11,12]. The effective self-mixing modulation index is given by m_e = 2ηK (η = $\left|E_s\right.$/$\left.E_l\right|$: amplitude feedback ratio, K = τ/τ_p: fluorescence-to-photon lifetime ratio) and the power spectral intensity of the detected electrical self-mixing signal is proportional to m_e² [13]. TS³Ls with large lifetime ratios have been used to make versatile self-mixing metrology systems with extreme sensitivity [10].

On the other hand, amplifying the relative phase change between two light fields becomes attractive to improve the measurement resolution of the physical quantity causing this change. Phase amplification using a many-body entangled state (NOON state) is a well-known method in quantum optics [14,15,16,17,18]; nevertheless, the preparation process for a high-number NOON state is difficult and sensitive to optical loss, and the experimental highest phase amplification in NOON states is about 10. In optics, harmonics-assisted phase optical phase amplification has been demonstrated, where the relative phase difference between two polarization modes in a polarized interferometer is amplified coherently four times with cascaded second-harmonic generation processes [19]. Most recently, the optical-feedback-induced intracavity harmonics generation effect has been demonstrated to amplify the phase change 11 times. Furthermore, the 20th intracavity harmonic was generated by increasing the reinjected photon number, indicating that 20-time phase amplification is attainable. The proposed method has a prospect for precision measurement applications [20].

On the basis of the above background, we examined ways of forming the lasing transverse mode inherent to TS³Ls with wide-aperture LD pumping and their application to highly sensitive phase amplification by self-mixing modulation. In this paper, we describe skew-chG mode oscillations in a 300-μm-thick Nd:GdVO₄ laser with wide-aperture LD pumping for the first time, where an annular transverse field surrounding the central Gaussian field appears with increasing pump power by controlling the pump-beam diameter. A physical interpretation for the appearance of the annular lasing field is given in terms of the additional gain that appears around the preceding TEM₀₀ mode resulting from the transverse spatial hole burning effect of population inversions with wide-aperture pumping. The phase locking of nearly frequency-degenerate TEM₀₀ and annular fields is shown to form a hybrid type of skew-chG mode. Harmonic-assisted phase amplifications in such a hybrid skew-chG laser operation were demonstrated in the self-mixing laser Doppler velocimetry scheme as well as in the frequency-shifted optical feedback scheme using acousto-optic modulators (AOMs), and 50-fold phase amplification has been achieved.

2. Self-Induced Skew-Cosh Gaussian Mode Laser Oscillation

2.1. Wide-Aperture LD Pumping and Slope Efficiency

The experimental setup with an Nd:GdVO₄ laser is shown in Figure 1. A nearly collimated lasing beam from a laser diode (wavelength: 808 nm) was passed through an anamorphic prism pair to transform the elliptical beam into a circular one that was focused onto a 300 μm-thick laser crystal. One end surface was coated to be transmissive at the laser-diode pump wavelength of λ_p = 808 nm and highly reflective (R₁ = 99.9%) at the lasing wavelength of λ_l = 1063 nm. The other surface was coated to be R₂ = 99% at 1063 nm. Linearly polarized single longitudinal-mode emissions along the b-axis were observed in the entire pump power region, reflecting the fluorescence anisotropy. The pump-beam spot size, w_p, was changed by shifting the laser crystal along the z-axis, as depicted in Figure 1.

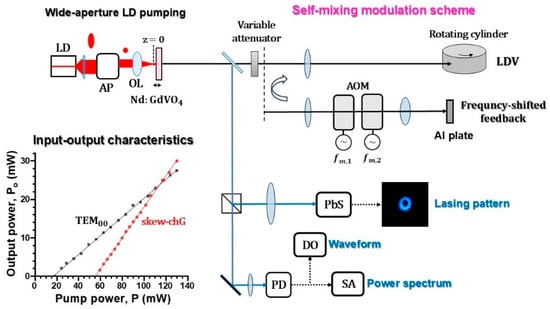
Figure 1. Experimental apparatus of a thin-slice Nd:GdVO₄ laser with LD pumping for harmonics-assisted phase amplification. Input–output characteristics for different pump spot sizes, i.e., mode-matching w_p $\cong$ w_o and wide-aperture pumping, w_p > w_o, where w_o is the lasing spot size. AP: anamorphic prism pair, OL: objective lens, VA: variable optical attenuator, AOM: acousto-optic modulator, PD: photo-diode, DO: digital oscilloscope (Tektronix TDS 3052, Tokyo, Japan, DC–500 MHz), SA: spectrum analyzer (Tektronix 2712, Tokyo, Japan, 9 kHz–18 GHz).

The pump spot size, w_p, increased as the laser crystal was shifted away from the pump-beam focus along the z-axis (i.e., z > 0). The pump spot size varied from w_p = 20 µm (z = 0) to 85 µm (z = 2.5 mm). A pure TEM₀₀ mode oscillation was obtained at the threshold pump power, Pth = 20 mW, at w_p = 20 µm (z = 0), where the lasing spot size was measured to be w_o = 30 µm and the slope efficiency was η_s = 24% as depicted by black in the input–output characteristics in Figure 1. As w_p increased, the threshold pump power gradually increased, and the resultant lasing transverse mode exhibited a structural change in the near-field pattern. The slope efficiency increased to η_s = 40% regardless of the increase in threshold pump power to Pth = 56 mW for wide-aperture pumping at w_p = 70 µm as depicted by red in the input–output characteristics due to the increase in the lasing mode volume as will be discussed in the following Section 2 and Section 3.

The harmonics-assisted phase amplification was examined in two ways. One was self-mixing laser Doppler velocimetry by focusing the output beam onto a rotating Al cylinder by a 15 cm focal-length lens placed 30 cm apart from the laser and the cylinder surface, where the laser was modulated at the Doppler-shift frequency, f_M = f_D = 2v/${\lambda }_l$ (v: velocity along the laser axis). The other mixing modulation was performed using a pair of PbMoO₄ acoustic-optic modulators (AOMs; center frequency = 80 MHz) whose self-mixing modulation frequency is given by f_M = 2(f_m,1−f_m,2) depicted in Figure 1.

2.2. Lasing Beam Profiles

Near- and far-field lasing patterns were measured using a PbS photo-conductive image sensor (Hamamatsu Photonics, C1000, Tokyo, Japan) followed by a TV monitor and an intensity profiler. Typical results are shown in Figure 2 with increasing the pump power for a wide-aperture pumping of w_p = 70 µm.

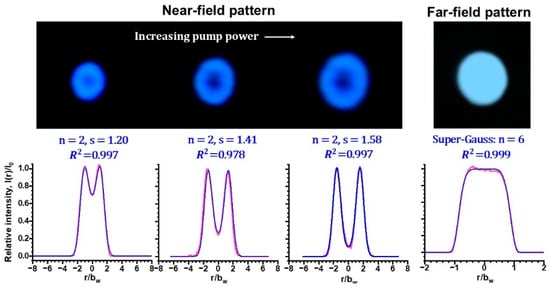
Figure 2. Pump-dependent lasing near- and far-field patterns of a thin-slice Nd:GdVO₄ laser with wide-aperture LD pumping. See Supplementary Materials S1 (near-field) and S2 (far-field). Pink and blue lines indicate experimental profiles and fitted profiles, respectively.

As can be seen in the video, the pure TEM₀₀ mode appearing near the threshold pump power exhibited successive structural changes and the annular part increased with increasing pump power. It is noteworthy that the near-field intensity patterns in the present laser with wide-aperture pumping are approximated by the following skew cosh Gaussian (skew-chG) mode profile, where $I\left(r\right)={\left|E\left(r\right)\right|}^2$:

$$E\left(r\right)=E\left(0\right){cosh}^n\left({\displaystyle \frac{rs}{b_w}}\right)\exp \left[-{\left({\displaystyle \frac{r}{b_w}}\right)}^2\right],$$

(1)

while the far-field patterns exhibited super-Gaussian-type intensity distributions of order p:

$$I\left(r\right)=I_0\left(0\right)\exp \left(-2{\left|{\displaystyle \frac{r}{b_w}}\right|}^p\right)$$

(2)

Here, n is the order of skewness, and s and b_w are the skewness parameter and the beam width [21]. Radial intensity profiles and fitting curves are shown on the lower row of Figure 2 by pink and blue, respectively, where the coefficient of determination is as high as R² $>$ 0.98.

2.3. Transverse Spatial Hole-Burning of Population Inversions

The spot sizes at the input and output mirrors, w₁ and w₂, and the effective focal length of the thermal lens, f_T, depicted in Figure 3a are given by [1]

$$w_i^2=\left({\displaystyle \frac{{\lambda n}_{0}l}{g_i}}\right)\sqrt{{\displaystyle \frac{g_1{g}_2}{1-g_1{g}_2}},} i=1, 2$$

(3)

$${\displaystyle \frac{1}{f_T}}=\left({\displaystyle \frac{lA}{2K_T}}\right)\left[\left({\displaystyle \frac{dn}{dT}}\right)+\alpha \left(n_0-1\right)\right]$$

(4)

Here, $g_1=1-{\displaystyle \frac{n_0}{{2f}_T}}, g_2=1,$l is the effective thickness of the thermally induced lens, while A is the heat-generated per unit volume and time, K_T is the thermal conductivity, dn/dT is the thermal-optic coefficient of the refractive index, a is the coefficient of thermal expansion, and n₀ is the refractive index of Nd:GdVO₄. Here, since A increased as the pump power increased, the focal length was considered to decrease and the lasing beam spot size decreased accordingly.

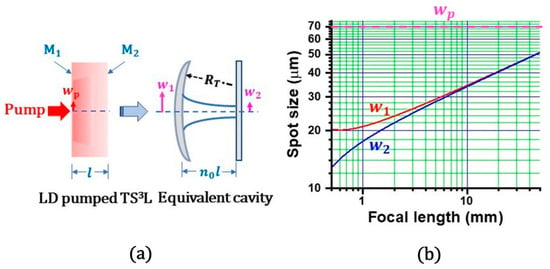
Figure 3. (a) Thermally formed laser cavity. (b) Calculated spot sizes at the crystal for the TEM₀₀ mode that arises from the thermal lens effect.

The TEM₀₀ spot sizes, w_1,2, were calculated using Equations (3) and (4) and the thermal constants of Nd:GdVO₄, K_T = 11.7 W/mK, dn/dT = 4.7 × 10⁻⁶/K, α = 1.5 × 10⁻⁶/K and n₀ = 1.972. They are plotted in Figure 3b, together with the average pump beam spot size, w_p = 70 µm. This figure indicates that wide-aperture pumping, i.e., w_p > w_o, is established for the case shown in Figure 2. In fact, the pure TEM₀₀ lasing mode spot sizes at the crystal near the threshold pump power are estimated to be 45~50 µm and agree with the lasing spot size, w_o = 47 µm, which was measured by the intensity profiler connected to the PbS phototube. The divergence angle was measured to be $\theta =7.56$mrad, implying the beam quality factor of M² = 1.05.

Next, let us consider the transverse spatial hole-burning effect of population inversions. The pump rate of excited atoms and decreasing rate of excited atoms by lasing photons through stimulated emission are given by σ_pI_p/hν_p and σ_eI_cir/hν_o, respectively. Here, I_p and I_cir denote the pump light and circulating lasing intensities within the cavity, n_p and n_o are pump and lasing light frequencies, whereas ν_p and ν_o are, respectively, emission and absorption cross sections. Assuming w_p = 70 µm, w_o = 47 µm, and spectroscopic data for Nd:GdVO₄: τ = 90 μs, σ_e = 7.6 $\times$ 10⁻¹⁹ cm² and σ_p = 4.9 $\times$ 10⁻¹⁹ cm², the calculated radial profiles related to the lasing intensity and population inversions are shown in Figure 4a–c, where

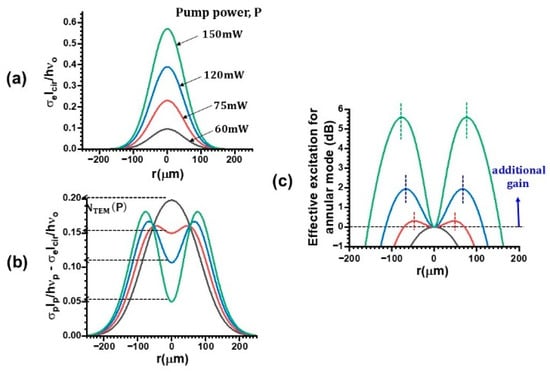
Figure 4. (a) Relative pump-dependent circulating photon emission rate of TEM₀₀ mode. (b) Relative atom excitation rate in the presence of TEM₀₀ mode. (c) Effective atom excitation for annular fields. Pump power in (b,c) is indicated by the same color as (a).

1.

The pump-dependent intracavity circulating photon emission rate of the proceeding TEM₀₀ mode, which is given by I_cir = I_s (I/Ith − 1) $\cong \mathrm{P}$_o/(πw_o²)ln(−R₂), where I_s = hν_o/σ_eτ is the emission saturation intensity, Ith is the threshold pump intensity and P_o is TEM₀₀ pump-dependent output power component as estimated from the input–output characteristics in Figure 1 and the weighting number for a TEM₀₀ field.

2.

The remaining atom excitation rate (i.e., remaining population inversions) in the presence of the preceding TEM₀₀ mode for various pump intensities.

3.

The effective atom excitation rate for the annular region defined as the hole depth, 10log(N_r/N_TEM), where N_r is the remaining atom excitation rate in Figure 4b.

As the pump power increases, depletion of the population inversion (i.e., transverse spatial hole burning) takes place. Here, the spatial integral of the remaining population in the version, V = $\iiint \mathrm{N}(\mathrm{x},\mathrm{y},\mathrm{z})$ dv, was found to coincide with the threshold value for I_cir = 0 for all pump powers within a 3% error. This strongly implies that the population inversion density is kept at the threshold value under the lasing condition for the preceding TEM₀₀ mode obeying laser theory. Meanwhile, the remaining population inversion shown in Figure 4b is expected to give an additional effective gain for annular mode to coexist with TEM₀₀ mode with increasing the pump power so that almost all the population inversion contributes to lasing by wide-aperture pumping. The effective excitation for the annular mode gain spreads outward, featuring a skewness with increasing pump power as shown in Figure 4c for the wide-aperture pumping, w_p > w_o, and a skewed annular-type of amplification is expected for lasing fields around the preceding TEM₀₀ mode via the gain guiding effect [22]. Here, the lasing mode volume increases and the higher slope efficiency is brought about in comparison with the TEM₀₀ mode as shown in Figure 1.

On the other hand, the population-inversion-dependent refractive index variation, $∆n$, can be expressed as [23,24]

$$∆n=\left({\displaystyle \frac{2\pi }{n_0}}\right)f_L^2{N}_e∆\alpha ,$$

(5)

Here, f_L = (n₀² + 2)/3 is the Lorentz local-field correction factor, N_e denotes the excited-state ion population and $∆\alpha$= α_e−α_g is the difference in the polarizability of active ions in the metastable and ground states. Usually, N_e is, to first order, proportional to the pump intensity, N_e ≈ N_T(I_p/I_s,a), where N_T is the terminal-state ion population, and I_s,a = hc/λ_pσ_pτ is the absorption saturation intensity at the excitation wavelength, λ_p. Since N_e is proportional to I_P, Equation (5) can be written in terms of the pump-intensity-dependent refractive index change, $∆$n = n₂′I_P: [23,24]

$$n_2’=\left({\displaystyle \frac{2\pi }{n_0}}\right)f_L^2{N}_T∆\alpha /I_{s,a},$$

(6)

For Nd:GdVO₄ crystals, the value of $∆\alpha$ is unknown, but the annular emission is expected to join with the pure Gaussian emission (which obeys Equations (3) and (4)) because of the pronounced modal gain G ($I_p$) resulting from gain guiding and refractive index confinement with wide-aperture pumping, i.e., w_p $>$ w_o, in accordance with Figure 4c and Equation (6).

It should be noted that the near-field intensity profile observed at P = 120 mW, which is fitted well by the skew-chG mode given by Equation (1) with R² = 0.978 in Figure 2, is theoretically reconstructed as shown in Figure 5a if we assume the phase locking of two nearly frequency-degenerate TEM₀₀ and annular fields, namely E_g and E_a, in the form of E_g + irE_a, where r is the weighting number for field amplitude and i implies the relative phase of π/2, which will be discussed in the next section. A skewed intensity profile reflecting the skewed gain profile in Figure 4c with respect to the gain peak is apparent for the annular mode. In fact, the peak gain determined from the amplitude ratio of two fields at P = 120 mW shown in Figure 5a is 2.07 dB, and it coincides well with 1.94 dB evaluated from Figure 4c. Theoretical reconstructions of modified skew-chG patterns for different pump powers in Figure 2 assuming the locking of TEM₀₀ and annular modes are shown in Figure 5b and Figure 5c, respectively. As for Figure 5b at P = 150 mW, the peak gain is 5.3 dB and it coincides with 5.6 dB evaluated from Figure 4c. Harmonics-assisted phase amplifications in the following section, which stem from the phase locking of two modes, were successfully achieved in the pump power region, 70 mW$\le p\le$160 mW.

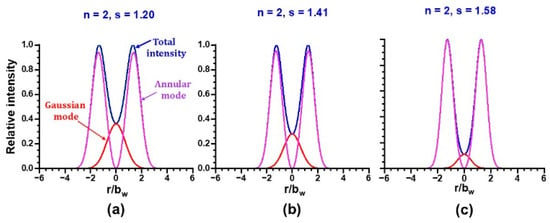
Figure 5. Reconstruction of the observed modified skew ch-G profile shown in Figure 2 by assuming the phase locking of the nearly frequency-degenerate Gaussian modal field and the annular field with the fixed relative phase of π/2.

3. Self-Mixing Modulation in Modified Skew Cosh Gaussian Mode Laser

3.1. Phase Amplification in Weak Feedback Regime

In this section, we address the key issue in the nonlinear dynamics of such modified skew-chG mode lasers subjected to self-mixing interference modulations by employing two methods, self-mixing laser Doppler velocimetry and frequency-shifted feedback using acousto-optic modulators, as shown in Figure 1. Here, self-mixing interference metrology works through the intensity modulation effect of a laser due to interference between the lasing and feedback fields. In short, the self-mixing laser acts both as a mixer–oscillator and highly sensitive detector of the signal from the target. The resultant optical sensitivity has been shown to be enhanced in proportion to the fluorescence-to-photon lifetime ratio, K = τ/τ_p, which reaches an order of 10⁵–10⁶ in state-of-the art TS³Ls. The photon lifetime in the present Nd:GdVO₄ laser was determined by measuring the dependence of the relaxation oscillation on the excess pump rate: f_RO = (1/2π)$[\sqrt{(w-1)/\tau {\tau }_p}$, w = P/Pth, as shown in Figure 6a. Assuming τ = 90 μs, τ_p of 20 ps was attained, yielding K = 4.5 × 10⁶.

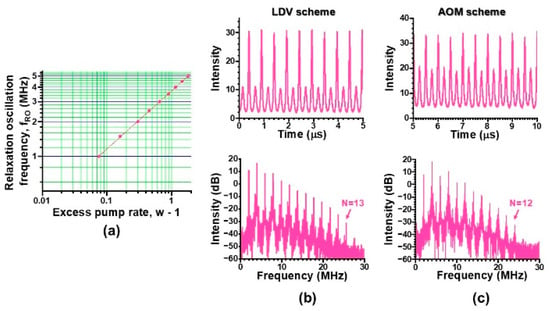
Figure 6. (a) Dependence of f_RO on the excess pump rate, w–1. (b,c) Waveforms and corresponding power spectra under the weak feedback regime, where f_M = f_RO/2 = 2 MHz. Pump power, P = 120 mW.

The effective self-mixing modulation index is given by m_e = 2mK, where m = E_s/E_o is the field amplitude feedback ratio. The resultant power spectrum intensity of the detected electrical signal is enhanced in proportion to m_e²$\propto$K² [10]. The experimentally determined large lifetime ratio of the present Nd:GdVO₄ laser of K = 4.5 × 10⁶ is expected to greatly pronounce phase amplification phenomena accompanied by the enhanced subharmonic resonance effect as shown hereafter.

Self-mixing interference effects in the modified skew ch-G laser subjected to subharmonic modulations, f_M = f_RO/2, have been found to depend critically on the feedback ratio from the target. In the case of the self-mixing laser Doppler velocimetry scheme in Figure 1, the effective intensity feedback ratio from the same rotating Al cylinder for the pure TEM₀₀ operation was estimated to be R₀ = −94 dB from the correspondence between the experimental and numerically reproduced power spectral intensities of the Doppler signal at f_D [13]. The basic idea of subharmonic resonance effect caused by the modulation at f_M = f_RO/2, which induced a quasi-period-2 modulation resembling that in Figure 6c, was reported in the self-mixing TS³L Doppler velocimetry scheme in 1979 [10].

By inserting a variable attenuator with a roundtrip attenuation of T_A $\cong$ 9 dB in Figure 1, the deep period-2 modulation took place as shown in Figure 6b. In this case, the overall feedback ratio is $R_T=R_0-T_A=-103 \mathrm{d}\mathrm{B}.$ The similar periodic-2 modulation was achieved in the AOM scheme as shown in Figure 6c by controlling the feedback condition from the Al plate in Figure 1 similarly to the LDV scheme mentioned above. Power spectrum was obtained by averaging 100 power spectra measured at intervals of the update, 160 μs, for both cases.

Period-2 pulsations inherent to phase amplification are considered to appear through coherent superposition of N harmonic waves. Harmonic waves up to N = 13 and 12 were obtained by filtering the original time series shown in the upper inset with a bandwidth of 100 kHz. The phases of the Nth-harmonic waves coincided with that of the fundamental wave every N periods. There are excellent phase correlations up to N = 13 and 12 in both self-mixing feedback schemes. Figure 7a shows the original and reconstructed LDV signal, which is the summation of harmonic waves up to N = 13 in the self-mixing LVD scheme. The excellent amplitude and phase correlations with R² = 0.997 are obvious, as expected. The excellent correlation was also obtained for the AOM feedback scheme.

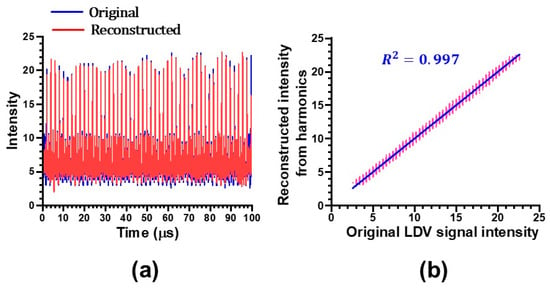
Figure 7. (a) Original and reconstructed self-mixing LDV signals. (b) Correlation plots indicating R² = 0.997.

These phase-synchronized waveforms shown in Figure 8a,b were theoretically reproduced by the following Equation (7) derived from dynamic equation [20] as shown in Figure 8a’,b’:

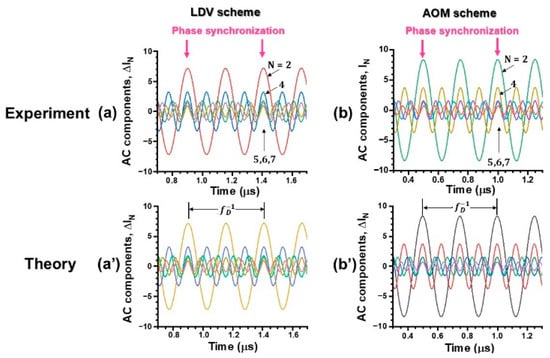
Figure 8. (a,b) Example harmonic waves for LDV and AOM self-mixing schemes, which were obtained experimentally. Theoretical harmonic waves, assuming Δ$\phi - {\phi }_0$= 1.601 for (a’) and 1.505 for (b’).

$$\Delta {\mathrm{I}}_{\mathrm{N}}/\mathrm{I} \propto {\mathrm{C}}_{\mathrm{N} \mathrm{COS}}[\mathrm{N} (2\pi {\mathrm{f}}_{\mathrm{M}}\mathrm{t}- {\phi }_0)+\mathrm{N}\Delta \phi ]$$

(7)

Here, ΔI_N is the intensity modulation (i.e., AC component) of the N-th harmonic component, Δ$\phi$ is the relative phase change between the two arms in the self-mixing laser interferometer, ${\phi }_0$ is the initial fixed phase of the system, C_N represents the intensity output coefficient of the N-th harmonic, which is related to the feedback induced gain and the cavity loss for harmonic waves.

Therefore, the observed phase-synchronization of all subharmonic waves with the fundamental wave is the direct experimental evidence supporting Tian and Tan’s assertion based on the analysis with the lock-in amplifier. They demodulated Δ$\phi$ through the lock-in amplifier and proved that the dependence on NΔφ instead of Δ$\phi$ allows us to achieve phase super-resolution measurement of Δ$\phi$, because the phase oscillation is N times faster than the original phase change and the unwrapped phase change Δφ_u is linearly proportional to the optical path change ΔL as Δφ_u = N(2π/λ_l)ΔL [20]. They achieved phase amplification up to N = 11 harmonics by using a 0.75 mm-thick Nd:YVO₄ TS³L which was modulated at subharmonic resonance frequency, f_M = f_RO/2 $\cong$2 MHz. In our case, the maximum deviation from the perfect phase-synchronization depicted in the lower part of Figure 8 was evaluated to be 1% for both feedback schemes.

We performed experiments at f_M = f_RO/2 = 0.483 MHz by decreasing the pump power to P = 62 mW. Results are shown in Figure 9, featuring (a) period-2 waveform, (b) corresponding power spectrum and (c) Poincare map. The phase synchronization up to N = 19 was achieved with SNR $\cong$ 5 dB at 9.18 MHz.

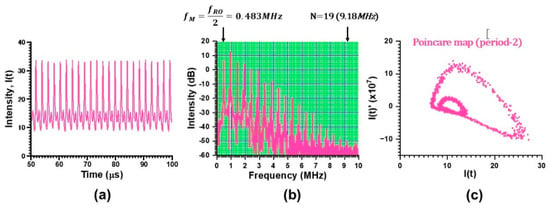
Figure 9. Phase synchronization up to N = 19 harmonics. P = 62 mW. (a) LDV signal waveform, (b) power spectrum, (c) Poincare map corresponding to the period-2 total output waveform.

3.2. Phase Amplification in Intermediate Feedback Regime

The additional gain shown in Figure 4c as well as the pump-intensity-dependent refractive index given by Equation (6), which are determined by the thermal lens effect, i.e., Equations (3) and (4), excite the annular mode around the preceding TEM₀₀ mode. The refractive index (equivalently, laser cavity length) for the annular mode increases with increasing the pump power, and the lasing frequency is expected to be shifted slightly from that of the central TEM₀₀ mode accordingly. With increasing a feedback ratio, the modal output waveform was strongly modified, while the self-mixing total output waveform exhibited the period-2 type of waveform, where self-mixing modulation originating from the two fields in Figure 5b in the skew-chG profile are coupled nonlinearly as will be discussed hereafter.

An example output waveform obtained by the self-mixing LDV scheme and the corresponding power spectrum obtained at f_M = f_RO/2 = 2 MHz are shown in Figure 10a, at a round-trip attenuation of T_A $\cong$ 6 dB ($R_T=-100 \mathrm{d}\mathrm{B})$ i.e., intermediated feedback regime. The power spectrum has a secondary peak around 24 MHz whose envelope has a Gaussian profile as will be discussed again later in Section 4. The enlarged peculiar total output waveform is shown at the top of Figure 10b, where the higher frequency component seems to be superimposed on the period-2 pulsation. To clarify such a higher frequency component, total output waveforms filtered below and above 17 MHz are shown in the middle of Figure 10b, where the total output in the lower-frequency band, I_L(t), exhibits a period-2-like periodic waveform reflecting the self-mixing modulation due to the coexisting transverse modes, whereas the total output in the higher-frequency band exhibits periodic oscillations at Δν_B = 24 MHz, whose envelope is modulated at f_M, as shown by the blue waveform.

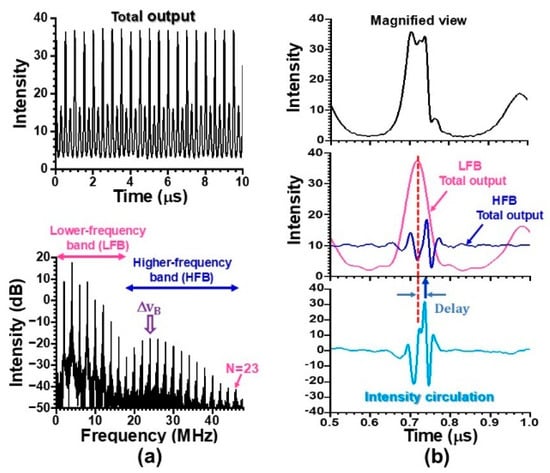
Figure 10. Response of skew ch-G laser subjected to self-mixing LDV (a). The total output in the lower- and higher-frequency band is shown in the middle plot in (b) P = 120 mW.

In the present experiment, the gain (stimulated emission) modulation is considered to be brought about at a beat frequency, Δν_B, through modal interference of phase-locked transverse modal fields corresponding to Figure 5 in the form of $B{N}_0\left(\iint {\tilde{E}}_g{\tilde{E}}_a^{*}dxdy+c.c\right)$, where ${\tilde{E}}_g$ and ${\tilde{E}}_a$ are the preceding TEM₀₀ field and the self-excited disturbing annular field, where B is the stimulated emission coefficient and N₀ is the population inversion density. Instead of the complete transverse mode locking, the present “hybrid” skew ch-G lasing pattern is formed of nearly frequency-degenerated TEM₀₀ and annular fields with the fixed relative phase of π/2 as discussed in Section 2.3, where the laser is modulated by coherent higher-frequency beat note at Δν_B >> f_M. Then, the coherent beat note might suffer the self-mixing modulation at f_M << Δν_B as well with increasing the feedback ratio. As a result, the power spectral components separated by f_M are considered to arise around Δν_B and form the higher-frequency band, where the harmonic resonance of Δν_B/f_M = 12 is established among the coexisting modal fields.

To clarify the interplay between these frequency bands, we carried out statistical analyses on total output waveforms belonging to the lower- and higher-frequency bands, i.e., I_L(t) and I_H(t), based on the observable quantity of intensity circulation given by [25]:

$$I_{L,H} = I_{L\to H}-I_{H\to L} = I_L\left(t\right){\dot{I}}_H\left(t\right)-{\dot{I}}_L\left(t\right)I_H\left(t\right).$$

(8)

The calculated intensity circulation is shown at the bottom plot of Figure 10b. Here, it can be seen that I_H(t) and I_L,H (t) are correlated, and I_H(t) exhibits peaks in accordance with the intensity transfer from the lower to higher-frequency band, i.e., I_L,H (t) > 0, as depicted by the blue upper arrow. This implies that the intensity transfer occurs from the lower to the higher band just after the strong peak of lower-frequency band indicated by the dashed line appears in I_L(t) and the total intensity I_H(t) reaches the maximum value within the periodic bursts at Δν_B.

Next, we examined the phase relationships among coexisting periodic waveforms of different harmonics within the lower- and higher-frequency bands in detail. The phases of the N-th harmonic waves in the higher-frequency band shown in Figure 11a are synchronized as well, obeying Equation (7). Meanwhile, harmonics belonging to the higher-frequency band exhibited antiphase dynamics against harmonics in the lower-frequency band, as shown by red dashed lines in Figure 11b,c, which parallel the middle inset of Figure 10b, where only the fundamental wave at 2 MHz in the low-frequency band is shown by red waveform for brevity.

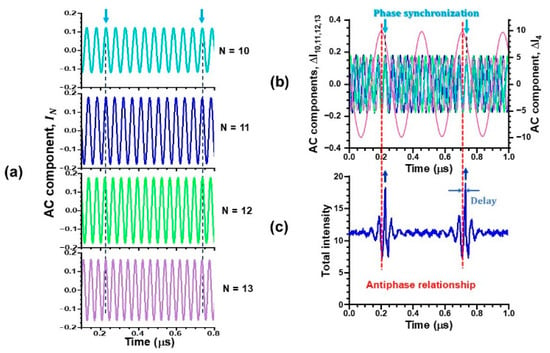
Figure 11. (a) Phase synchronization among harmonics in the higher-frequency band. (b) Phase relationship between harmonics in the higher-frequency band and the fundamental wave at 2 MHz in the lower frequency band depicted in red. (c) Total intensity waveform belonging to the higher-frequency band exhibiting antiphase dynamics against the lower frequency band. P = 120 mW.

After quite a short time delay depicted in Figure 11b, the phase synchronization is established among harmonic waves in the higher-frequency band as indicated by the light blue arrows in the same way as Figure 10b. In other words, the gain transfer from the lower to the higher frequency band corresponding to the intensity transfer, as depicted by the blue arrows at the bottom of Figure 10b, triggers the phase synchronization among all the harmonics in the higher-frequency band after a slight time delay on the order of 1/(2Δν_B). Consequently, the harmonic waves in both frequency bands obey Equation (7) via a slight time delay indicating the subharmonic resonance of f_M = Δν_B/12 in this case.

Similar nonlinear dynamics leading to the peculiar phase synchronization illustrated in the self-mixing laser Doppler velocimetry shown in Figure 10 and Figure 11 were produced by the frequency-shifted AOM feedback scheme as shown in Figure 12.

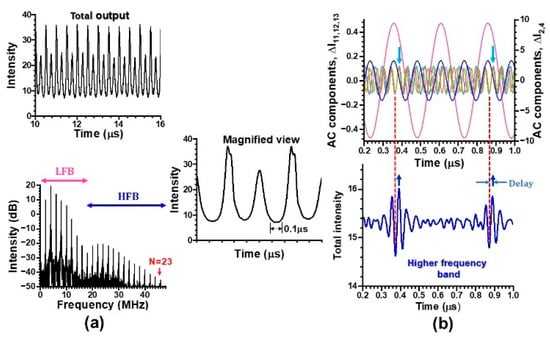
Figure 12. Subharmonic resonance observed in the AOM feedback scheme. (a) Oscillation wave form together with a magnified view and the corresponding power spectrum. (b) Typical waveforms of the N-th harmonics and their phase relations with the total intensity waveform belonging to the higher frequency band. P = 120 mW.

3.3. Phase Amplification in Strong Feedback Regime

When the feedback was increased further, T_A $\cong$3 dB ($\mathrm{i}.\mathrm{e}.,R_T=-97 \mathrm{d}\mathrm{B})$ self-mixing signals exhibited more complicated behavior, featuring low-frequency envelope modulations. An example result obtained for f_M = f_RO/2 = 2 MHz in the AOM feedback scheme is shown in Figure 13.

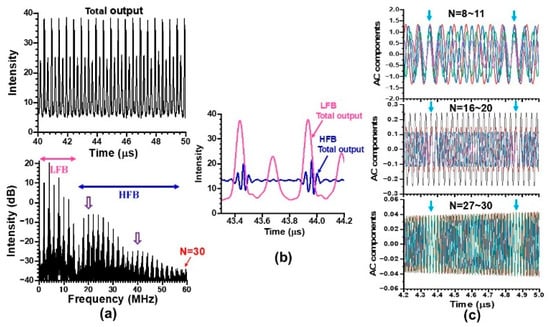
Figure 13. (a) Self-mixing modulation waveform and the corresponding power spectrum in a strong feedback regime. (b) Magnified view of outputs in low- and high-frequency bands. (c) Phase-locking among harmonics up to N = 30. P = 120 mW.

Here, the coherent beat frequency Δν_B between nearly frequency-degenerate transverse modes, TEM₀₀ and the outer ring, was shifted downward to 20 MHz and its harmonic peak appears at 40 MHz accordingly in the power spectrum. Despite such a nonlinear effect associated with increased feedback, harmonics-assisted phase amplifications up to N = 30 were achieved as shown in Figure 13c.

Finally, let us show a fifty-fold phase amplification observed by removing VA (i.e., ${\eta }_T=-94 \mathrm{d}\mathrm{B}$) in LDV as well as AOM feedback schemes. Results in the frequency-shifted feedback scheme are shown in Figure 14, where the pump power was decreased to P = 75 mW and the modulation frequency was set as f_M = f_RO/2 = 1 MHz. In this case, the lasing profile approached TEM₀₀ as shown in Figure 2 and the second peak Δν_B was shifted downward, where harmonics up to 3Δν_B $\cong$38 MHz appeared. The phase amplification up to N = 50 and essentially the same nonlinear dynamics as Figure 10, Figure 11, Figure 12 and Figure 13 were observed.

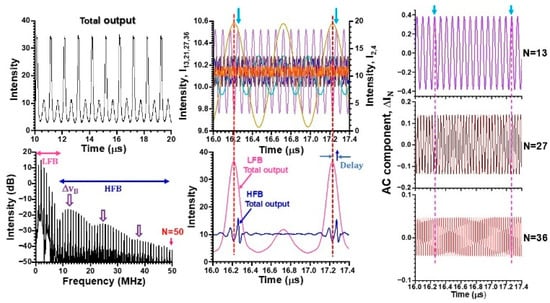
Figure 14. Fifty-fold phase amplification with the decreased pump power in the absence of VA in the AOM feedback scheme. f_M = f_RO/2 = 1 MHz. P = 75 mW.

Figure 11 and Figure 12 suggest that the coherent beat wave frequency, Dn_B, decreases with decreasing the pump power toward a TEM₀₀ mode oscillation at the threshold pump power. The degree of phase amplification by the subharmonic modulation at f_M = f_RO/2 = 1 MHz in the strong feedback regime is enhanced from N = 30 to 50 accordingly.

The correlation between original and reconstructed signal was found to be lowered as compared with that in the weak feedback regime shown in Figure 7; however, the coefficient of determination was confirmed to be kept R² > 0.93 even in the strong feedback regime by repeated experiments.

Finally, in this section, it should be noted that the power spectrum in the strong feedback regime extends far above the relaxation oscillation frequency, f_RO, in our hybrid skew cosh Gaussian laser system subjected to self-mixing modulation at f_M = f_RO/2 contrary to the usual modulation dynamics, where frequency components decrease rapidly above the relaxation oscillation frequency due to the inherent characteristic of lasers in a weak-feedback regime [26].

3.4. Overview of Nonlinear Dynamics of Hybrid Skew ch-G Mode Subjected to Subharmonic Self-Mixing Modulation

The formation of hybrid skew ch-G mode by wide-aperture pumping, w_p > w_o, is the core physics leading to 50-fold phase amplification. Here, we present an overview of our physical picture explained so far.

As the preceding TEM₀₀ lasing mode with w_o appears just above the threshold, the central part of population inversions is decreased. Then, population inversions remain around the central part through the “transverse” hole-burning due to the wide-aperture pumping as depicted in Figure 4. With increasing pump power, the hole-depth increases accordingly. As compared with the usual spatial hole-burning along the “longitudinal” direction, which results in multi-longitudinal oscillations, the transverse hole-burning is considered to occur more easily because of the relatively small spatial diffusion of population inversions across the pump beam.

As a result, the annular mode tends to join in the preceding TEM₀₀ mode through a “gain guiding effect” with increasing the pump power as shown in Figure 5. Assuming population-inversion-dependent refractive index variation, central and outer ring modes are expected to coexist in slightly different oscillation frequencies.

Meanwhile, the coherent beat wave appears around 20 MHz and its harmonics through the phase-locking are among nearly frequency-degenerate transverse modes, leading to N-fold phase amplifications up to N = 50 by the self-mixing modulation involving a coherent beat wave between phase-locked transverse modes with increased feedback regimes as shown in Figure 11, Figure 12, Figure 13 and Figure 14.

Finally, note that the phase amplification has been confirmed to be robust against environmental as well as pump power fluctuations.

4. Statistical Properties of Collective Dynamics in Lower- and Higher-Frequency Bands

The small-signal modulation bandwidth beyond the relaxation oscillation frequency was studied in the context of a monolithic twin-ridge laterally coupled diode laser, where single- and double-lobed lasing modes coexist with split lasing frequencies [27]. The study experimentally showed that these modes exhibit mode locking, and a lateral coupling resonance frequency arises above the relaxation oscillation frequency, similarly to our hybrid skew-chG mode operation involving two transverse lasing fields.

The significant dependence of the self-mixing subharmonic modulation effect on the feedback coefficient in the skew ch-G mode laser described in Section 3 can be interpreted in terms of the lateral coupling of Gaussian and annular fields within the laser. An example intensity power spectrum in the free-running condition, which follows the predictions of small signal analysis over a wide frequency range beyond the relaxation oscillation frequency [28], is shown in Figure 15a.

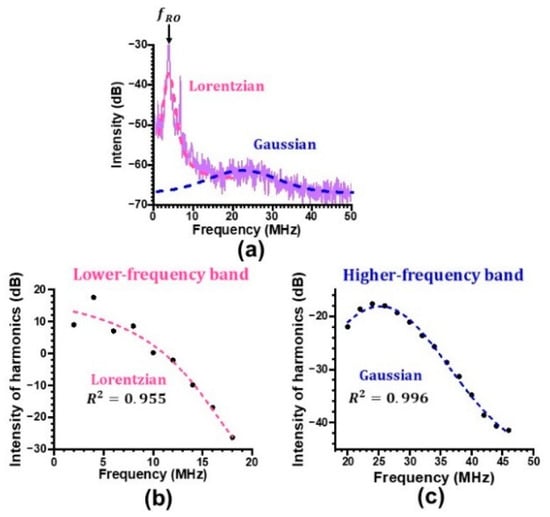
Figure 15. (a) Power spectrum in skew ch-G operation under the free-running condition. (b,c) Power spectral intensity of harmonics in the intermediate feedback regime. P =120 mW.

The power spectrum in skew ch-G operation under the free-running condition shown in Figure 15 is fitted by a Lorentzian profile in the lower frequency band around the relaxation oscillation frequency, f_RO, as expected in usual lasers and a Gaussian profile in the higher frequency band, which denotes the coherent beat note, Δν_B, resulting from phase locking among nearly frequency-degenerate transverse modes. This spectral nature seems to be inherited by the harmonics-assisted phase amplification in the intermediate feedback regime, as shown in Figure 10a, where the power spectral intensity of harmonics in the lower frequency band obeys a Lorentzian distribution while that in the higher frequency band follows a Gaussian distribution as indicated in Figure 15b,c. In the case of pure TEM₀₀ mode operations, only a noise-driven Lorentzian spectrum was observed.

The peak forming the higher-frequency band might be directly related to the lateral-coupling resonance frequency Δν_B around the coherent beat frequency between the TEM₀₀ and annular modal fields. Indeed, the broad Gaussian peak around Δν_B decreased in intensity when the pump power was decreased so that the lasing pattern approached the pure TEM₀₀ mode oscillation.

Finally, it is interesting to note that there is a non-trivial correlation between the histogram and power spectra in the present hybrid skew cosh Gauss mode laser system. Figure 16 shows the histograms (i.e., intensity probability distribution) of the output waveforms in the lower and higher frequency bands in the case of an intermediate feedback regime shown in Figure 10. They are fitted quite well by Lorentzian and Gaussian distributions, respectively, and exhibit a strong correlation with the power spectra shown in Figure 15b,c. The power spectral nature shown in Figure 15a with lateral-coupling resonance of coexisting transverse modes seems to play a crucial role in organizing collective dynamics.

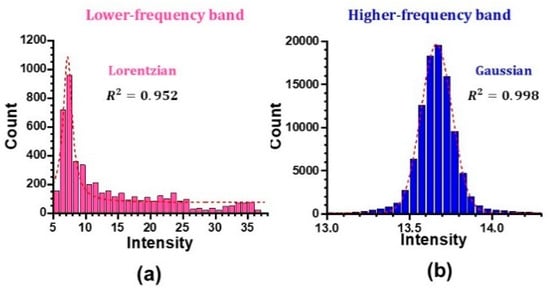
Figure 16. Histogram for total output intensity in (a) lower-frequency band and (b) higher-frequency band in the intermediate feedback regime. P = 120 mW, f_M = f_RO/2= 2 MHz.

The same histogram nature was also established for Figure 13 and Figure 14 in the strong feedback regime, i.e., Lorentzian for the lower-frequency band total intensity and Gaussian for the higher-frequency band total intensity as shown in Figure 17, which corresponds to Figure 13.

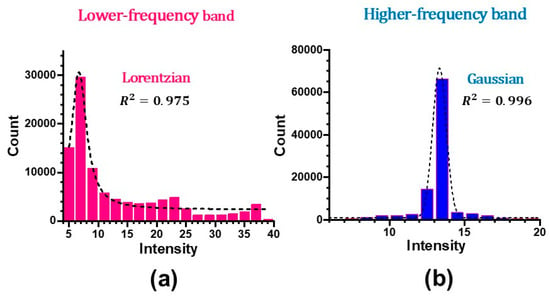
Figure 17. Histogram for total output intensity in (a) the lower-frequency band and (b) the higher-frequency band in the strong feedback regime. P = 120 mW, f_M = f_RO/2 = 2 MHz.

5. Summary and Discussion

The hybrid skew cosh Gaussian mode laser oscillation with a large slope efficiency of 40%, that makes use of most of the population inversions in the lateral direction, was demonstrated for the first time in a thin-slice solid-state laser with wide-aperture laser-diode pumping using a 300 µm-thick Nd:GdVO₄ crystal with coated end mirrors. The large fluorescence-to-photon lifetime ratio of K = 4.5 × 10⁶ enabled us to perform highly sensitive self-mixing modulation experiments, where the measured power spectrum intensity of the detected electrical signal is enhanced in proportion to K².

The hybrid skew-chG mode laser was proved to be formed by the locking of nearly frequency-degenerate TEM₀₀ and surrounding annular modal fields. The modal-interference-induced gain modulation took place around the beat frequency between modal fields featuring its higher harmonics with increasing the feedback ratio. Such a lateral-mode coupling resonance effect increased the frequency bandwidth beyond the relaxation oscillation frequency for harmonics-assisted phase amplifications, which are brought about by subharmonic modulation at f_M = f_RO/2 (f_RO: relaxation oscillation frequency), leading to fifty-fold phase amplification, N = 50.

The observed phenomenon is capable of the phase super-resolution measurement in real time by employing the phase-sensitive detection with a lock-in amplifier, since the phase oscillation is N times faster than the original phase change, and the unwrapped phase change against the optical path change becomes N times the original one. A proposed scheme employing the AOM frequency-shifter is shown in Figure 18. Generally, dynamic changes in any basic physical quantities can be converted to the detection of the phase change in light, including displacement, angle, etc. We believe that harmonic-assisted phase amplifications in the hybrid skew-chG laser, possessing the order-of-magnitude higher optical sensitivity than a state-of-the art self-mixing laser, resulting from the large K value accompanied by subharmonic resonance effect, would provide super-resolution optical metrologies. The present system is expected to respond to an extremely weak feedback light from a non-cooperative target, e.g., single-photon order per feedback modulation period.

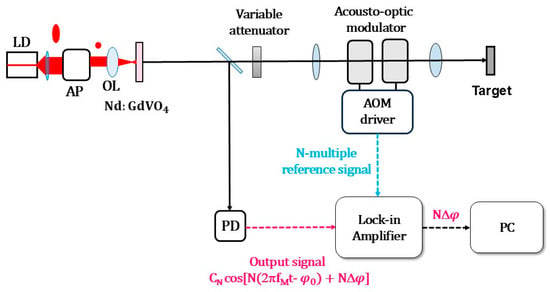
Figure 18. Real-time self-mixing laser metrology scheme with phase amplification. PD: photo-diode, PC: personal computer.