Abstract
Efficient and scalable quantum key scheduling remains a critical challenge in trusted-relay Quantum Key Distribution (QKD) networks due to imbalanced key resource utilization, dynamic key consumption, and topology-induced congestion. This paper presents a Q-learning-based adaptive routing framework designed to optimize quantum key delivery in dynamic QKD networks. The model formulates routing as a Markov Decision Process, with a compact state representation that combines the current node, destination node, and discretized key occupancy levels. The reward function is designed to jointly penalize resource imbalance and rapid key depletion while promoting traversal through links with sustainable key generation, guiding the agent toward balanced and congestion-aware decisions. Simulation results demonstrate that the Q-learning scheduler outperforms non-adaptive baseline algorithms, achieving an average distribution time of approximately 100 s compared with 170–590 s for the baseline algorithms, a throughput of 61 keys/s compared with 32–55 keys/s, and a failure ratio limited to 0–0.1, demonstrating superior scalability, congestion resilience, and resource-efficient decision-making in dynamic QKD networks.
1. Introduction
With the widespread deployment of 5G network and the ongoing development of 6G technologies, communication systems are advancing toward higher data rates, lower latency, and stronger security. In light of the growing severity of information security challenges in future mobile communications, quantum communication—particularly Quantum Key Distribution (QKD)—has emerged as a pivotal technology for enabling next-generation secure networks [1,2]. QKD, grounded in the no-cloning theorem and Heisenberg’s uncertainty principle, allows for theoretically unconditional secure key exchange, ensuring absolute confidentiality of shared keys between communication parties [3,4]. QKD demonstrates strong potential for applications in high-security domains, including military communications [5], financial data protection [6], and confidential government communications [7].
As QKD network technology matures, its architecture is evolving from simple point-to-point links to more complex topologies supporting multi-hop routing, multi-user access, and concurrent services. Currently, QKD network architectures can be broadly categorized into three types: optical node-based, quantum node-based, and trusted-relay node-based [8]. Optical and quantum node networks generate point-to-point quantum keys by establishing temporary quantum channels between users on demand. While these approaches support multi-user and long-distance key distribution in principle, they are constrained by signal attenuation and the immaturity of critical technologies such as quantum memory. As a result, optical node QKD networks are mainly suited for local-area applications, and quantum node QKD network remain in the experimental stage. In contrast, trusted-relay QKD networks perform key relaying at the upper layer of quantum key generation, enabling multi-user, long-distance key distribution via hop-by-hop forwarding. Due to its relative technological maturity and scalability, this architecture has become the most practical approach for current large-scale QKD network deployments [9].
At the current stage of development, a critical challenge facing trusted-relay QKD networks is efficient scheduling and stable transmission of key resources through appropriate routing strategies under complex physical conditions and limited resources. Unlike traditional communication networks that primarily optimize metrics such as latency and bandwidth, the performance of QKD links is fundamentally governed by physical-layer factors. These factors result in inherently low key generation rates, pronounced spatial heterogeneity, and significant temporal variability [10]. Consequently, resource management in such network faces challenges that can be broadly categorized into the following three aspects:
- Quantum key generation is fundamentally constrained by physical factors such as quantum bit error rate (QBER) and channel attenuation, leading to substantial heterogeneity in link performance. Links with insufficient availability are unable to sustain frequent transmissions, which can cause local key pool exhaustion and disrupt services.
- Key demand is tightly coupled with dynamic traffic patterns and often exhibits unpredictable and bursty behavior. During traffic surges or directional load concentrations, key resources on specific paths can be rapidly exhausted. In addition, imbalanced path selection and uneven request distribution may cause localized link overuse, leading to resource bottlenecks and reduced transmission efficiency.
- Existing routing strategies, such as shortest-path-first and maximum residual key, rely on static or instantaneous network states without modeling key pool dynamics. This limits their adaptability to resource fluctuations, leading to greater key transmission failures and degraded network performance. Routing in QKD networks must intelligently adapt to dynamic conditions, integrating key generation, consumption, and control feedback to ensure efficient and reliable key delivery.
The primary contributions of this paper are summarized as follows:
- 1.
- We propose a resource-aware key scheduling framework for trusted-relay QKD networks that integrates real-time link state monitoring, online Q-Learning–based adaptive routing, and multidimensional path feasibility verification to ensure dynamic congestion avoidance and stable key distribution under time-varying traffic and network conditions.
- 2.
- We constructed a discrete-time model to characterize key dynamics, where the normalized occupancy ratio was uniformly discretized into states, and the action space was defined by adjacent neighbor sets. A composite reward function, integrating occupancy deviation, consumption penalty, and generation incentive, enabled adaptive balancing between network load and key resource replenishment.
- 3.
- The simulation results demonstrate that the proposed method substantially enhances trusted-relay QKD network performance by improving transmission efficiency, optimizing resource utilization, and effectively mitigating congestion to ensure robust stability under high-load conditions.
The remainder of this paper is organized as follows. Section 2 reviews related work, followed by the presentation of the system model and problem formulation in Section 3. Section 4 reports the simulation results and provides a comprehensive performance discussion, before the paper concludes with key insights and future directions in Section 5.
2. Related Work
With the continuous expansion of trusted-relay QKD networks, the demand for efficient quantum key resource allocation and stable service delivery have increased significantly. Integrating efficient and adaptive routing algorithms has become essential for achieving balanced load distribution and improving overall network service capacity. To support ongoing research and practical deployment of trusted-relay QKD network, a variety of routing algorithms have been proposed.
The Open Shortest Path First (OSPF) protocol, a classical link state routing mechanism, was first applied in the experimental DARPA QKD network [11]. Building on this foundation, the SECOQC project modified OSPF to address the specific demand of relay path selection in QKD network [12]. The Tokyo QKD network adopted a hybrid routing strategy combining static and dynamic elements. Despite its limited scale and relatively simple dynamic algorithms, it effectively coordinated data and key transmission by incorporating link quality and key generation rate into node configurations [13]. In a larger deployment, the Beijing–Shanghai QKD backbone implemented an enhanced OSPF protocol, integrating real-time metrics such as key generation rate, link reliability, and relay node security to improve path selection adaptability [14]. As network architectures and service demand become more complex, recent efforts have focused on advanced dynamic routing strategies. For example, Bi et al. [15] proposed an environment-sensitive algorithm that balances key generation and traffic load across diverse topologies. Yu et al. [16] further introduced a hierarchical routing framework that integrates OSPF with quantum key management, significantly enhancing scalability and robustness.
To enhance key-awareness in routing, reference [17] incorporated the effective key volume of each link into OSPF-based path computation. Expanding on this, ref. [18] jointly considered both the current key pool size and the key generation rate, enabling more precise and dynamic resource scheduling. To mitigate key exhaustion at bottleneck links, ref. [19] introduced a hierarchical routing-based path optimization method to enhance transmission flexibility and overall performance. Reference [20] selected optimal routes using a combined metric of physical distance and key availability, while reference [21] incorporated controlled randomness to increase path diversity and robustness. Reference [22] developed a multifactor link cost model in conjunction with a key-aware routing strategy, significantly improving the key exchange success ratio. Within the realm of multipath routing, Han et al. [23] designed a multi-user routing algorithm aimed at optimizing quality of service (QoS) in optical QKD networks. Reference [24] presented a dynamic routing scheme comprising a Hello protocol, routing algorithm, and link state update mechanism to adapt to evolving network conditions. Furthermore, reference [25] implemented a node labeling strategy for multipath selection, effectively preventing routing loops and node conflicts, thus ensuring routing stability and efficiency.
Given the structural similarities between trusted-relay QKD networks and Wireless Ad Hoc Networks (WANETs)—notably their dynamic topologies—several studies have adapted classical WANET routing protocols to address frequent link state changes in QKD scenarios [26,27]. In quantum key distribution over Optical Networks (QKD-ON), joint routing, wavelength, and time-slot assignment (Routing and Wavelength Assignment/Routing and Resource Assignment, RWA/RRA) poses significant complexity beyond that of traditional optical networks [28,29]. To cope with this, key-on-demand strategies based on software-defined optical networks and key pool mechanisms were introduced for adaptive resource management [30]. Time scheduling models have also been developed to coordinate provisioning across domains [31], while heuristic RWA/RRA algorithms using enhanced node structures and auxiliary graphs help minimize key waste and avoid untrusted relays [32]. For secure multicast, distributed subkey relay trees have been designed to support efficient delivery of one to many keys [33]. Research on routing protocols for QKD networks has also been conducted from various perspectives, including adaptation to different types of QKD networks [34,35], enhancement of security [36], and suppression of crosstalk [37]. In this context, ref. [38] demonstrates an experimental B92 protocol for quantum key distribution path verification, while [39] proposes a hybrid QKD framework that dynamically selects protocols to optimize end-to-end key distribution routing security and efficiency.
Despite progress, key challenges remain in QKD routing. Most protocols rely on instantaneous link states and fixed cost functions, limiting foresight and adaptability, while resource allocation often prioritizes short-term gains over long-term efficiency. Machine Learning/Reinforcement Learning (ML/RL) techniques have been applied at various levels: ref. [40] optimized optical path routing and resource allocation in QKD networks with fixed topologies using deep reinforcement learning (DRL); ref. [41] combined autoencoders with the Cascade protocol to predict the QBER and key rates; ref. [42] proposed OptiNode for trusted node placement. These approaches primarily focus on performance or topology, without explicitly modeling the consumable and dynamically generated nature of QKD keys.
In contrast, our method uses online Q-learning with real-time key pool states to guide routing decisions that account for consumable resources, time-varying availability, and QKD-specific security requirements. Unlike classical ML/RL routing methods that assume reusable resources [43,44], our approach integrates both resource- and security-aware constraints. DRL has been shown to efficiently manage high-dimensional states, adapt to real-time dynamics, and optimize resource allocation and traffic scheduling in communication networks [45,46,47]. Future work could further integrate DRL with key pool dynamics to enable intelligent, scalable, and secure QKD routing.
3. System Model and Problem Formulation
To address the challenges of uneven resource distribution and dynamically changing key consumption in trusted relay QKD network, we propose a Q-learning-based key scheduling framework for adaptive and resource-aware path selection. As shown in Figure 1, the framework comprises three key modules. The Neighbor State Awareness Module continuously monitors adjacent links, extracting critical features such as key occupancy rate, deviation from ideal balance, consumption rate, and generation capability, constructing a comprehensive state representation. The episodic online Q-learning framework enables each routing request to evaluate the current policy and update the Q-table based on immediate rewards. Serving as the core decision engine, the Online Q-learning scheduler uses a reward function to balance resource uniformity and consumption efficiency, penalizing over-concentration and rapid depletion while promoting stable replenishment. The Routing and Validation module then generates trusted relay paths from the learned policies, ensuring topology compliance and efficient and stable key distribution. Although keys can be generated in parallel across links, our framework applies sequential, hop-by-hop forwarding decisions at the strategy level based on local and adjacent link states, ensuring balanced resource usage, bottleneck avoidance, and stable key distribution. The appendix, which presents the QKD Network Architecture (Figure A1) and the Relay Routing Mechanism in QKD Networks(Figure A2), provides the foundational knowledge framework underpinning this study.
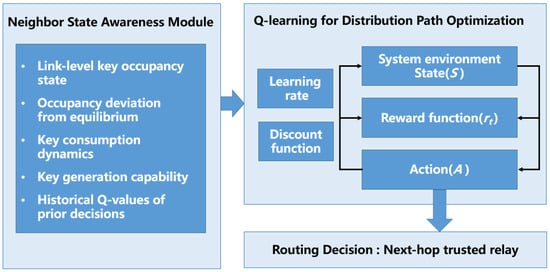
Figure 1.
Resource-aware Q-learning-based routing framework continuously monitors link states, updates routing policies via Q-learning based on observed rewards, and generates validated paths that ensure efficient and balanced key distribution.
3.1. QKDN Model and Constraints
3.1.1. Network Topology Model
In this study, the trusted-relay QKD network is modeled as an undirected graph , where the vertex set represents the trusted-relay nodes within the network. Each node is equipped with QKD devices as well as key management (KM) modules, enabling it to generate keys locally via physical quantum channels, store these keys, and securely forward keys to neighboring nodes through the key management layer.
The edge set E consists of key management links , which represent logical secure key relay channels between nodes and . These links serve as the backbone for multi-hop key forwarding and distribution within the trusted relay architecture. It should be noted that each key management link is supported by underlying physical quantum links that enable raw key generation between adjacent nodes. Edges in the graph correspond to the logical connections used for key relay rather than the physical quantum channels themselves.
To accurately characterize the operational attributes of each key management link, two key parameters are defined for every : the key transmission rate limit and the key pool size . Specifically, denotes the maximum rate at which quantum keys can be distributed through link , while represents the maximum size of the key pool between adjacent nodes.
3.1.2. Quantum Key Pool Model
Each link in the trusted-relay QKD network is associated with a key pool , which stores the quantum keys shared between adjacent nodes and . This key pool supports key generation, storage and consumption and dynamically reflects the availability of key resources on the corresponding link. The key pool is bidirectionally symmetric, i.e., for any node pair and , the shared key pool satisfies . The state of the key pool on link at time t is defined as a triplet:
where denotes the amount of remaining usable keys; represents the key generation rate; and represents the key consumption rate.
To ensure system stability and prevent the key pool from exceeding its maximum size, the key pool evolves over discrete time steps of duration according to the following update rule:
where the inner max ensures that the remaining usable keys cannot be negative. This formulation guarantees that the number of available keys remains within the allowed limits, thereby enabling dynamic control over key resources and supporting the sustainable operation of the QKD network.
3.1.3. Routing Constraints
The quantum key distribution task is defined as a triplet , where the source node intends to transmit quantum keys to the destination node with a transmission demand of R. To ensure the feasibility of key transmission and efficient allocation of network resources, the selected routing path must satisfy the following constraints.
- 1.
- Connectivity constraint: For any pair of adjacent nodes along the routing path, a key management link must exist to guarantee topological continuity.
- 2.
- Key transmission rate constraint: At any time t, for each link , the cumulative key transmission rate of all active tasks traversing this link must not exceed :where denotes the instantaneous key transmission rate of task on link at time t.
- 3.
- Key pool size constraint: To ensure path viability, all links must maintain a positive key pool size at time t, satisfyingwhere represents the path from source node s to destination node d.
3.1.4. Evaluation Metrics and Definitions
- 1.
- Average Key Distribution Time: quantifies the mean time required to deliver successfully distributed quantum keys during a single simulation cycle. It reflects the overall efficiency of routing and scheduling strategies in dynamic trusted-relay QKD networks. The total delivery time for the k-th distribution is defined asThe queuing delay, driven by total key volume and effective path key transmission rate, reflects network load and dominates variations in , while fixed transmission and random perturbation delays capture link characteristics and environmental fluctuations:where is the total keys delivered in the k-th trial, the path’s effective key transmission rate, the fixed propagation delay, and a small random perturbation capturing minor link fluctuations or transient rerouting; the average delivery time over K trials is then
- 2.
- Maximum Key Utilization: The highest utilization among active links at the moment of path selection:This metric captures the link that is most critically depleted in terms of key pool size. A value of indicates severe congestion and highlights the need for dynamic rerouting or pool scaling. E is the set of all links in the network, with denoting the total number of links. The active link set is defined aswhich includes links that are not fully occupied and thus can contribute to further key distribution. For any active link , the instantaneous utilization is defined aswhere denotes the current key pool size on link at the time of path selection. is the maximum key pool size of link .
- 3.
- Proportion of Over-Threshold Key Resource Links: Given a utilization threshold , the over-threshold link set includes all links whose utilization exceeds :where denotes the utilization of link at the time of path selection. The ratio quantifies the fraction of links that are potentially congested, providing an indicator of network-wide resource stress.
- 4.
- Network Throughput: The network throughput quantifies the efficiency of key distribution by measuring the total number of quantum keys successfully delivered per unit time across all links. It reflects the effectiveness of routing and key management strategies and provides insight into the trade-off between performance and congestion. Let denote the total number of keys successfully transmitted during a single distribution task, and the corresponding duration. The network throughput is then given by
- 5.
- Key Distribution Failure Ratio: This metric quantifies the fraction of failed key distribution attempts:where is the number of successful key transmissions and is the total number of key distribution attempts. serves as a direct indicator of the reliability and effectiveness of the routing strategy. Failures may result from key pool depletion, disconnected topologies, insufficient path length, or suboptimal routing decisions.
3.2. Online Q-Learning Model Design
3.2.1. State Space Definition
The agent’s state representation captures both routing information and the dynamic status of key resource utilization. Based on this, the state space is formally defined as
where denotes the current node of the quantum key at time t, and represents the destination node for the key distribution task. The set V includes all trusted-relay nodes in the network. represents the agent’s perception of the status of key resources on the link , which is a crucial input to decision-making as it reflects the degree of resource contention after normalization and discretization.
To accommodate the discrete nature of the Q-learning model, the continuous key pool size is discretized as follows.
- 1.
- Normalization: Given the known maximum size of the key pool on each link , the remaining key amount is first normalized into a key occupancy ratio:
- 2.
- Interval Partitioning: The range of occupancy ratios is uniformly divided into M intervals of equal width , forming a discrete set of states:
- 3.
- State Mapping: The continuous occupancy ratio is mapped to a discrete state label using
3.2.2. Action Space Definition
For an agent currently located at node , its set of possible actions is constrained by the set of neighboring nodes. The neighbor set is formally defined as
where A(i) represents all directly connected adjacent nodes to which the quantum key can be forwarded from node . Therefore, the agent’s action space at time t is defined as
where the action denotes the agent’s decision to transmit the quantum key from its current node to one of its neighboring nodes. The action space characterizes all feasible and permissible movements available to the agent at a given decision point.
3.2.3. Reward Function Design
In Q-learning-based routing, the reward function should comprehensively account for link resource utilization, key consumption, and replenishment dynamics to ensure balanced allocation, alleviate congestion, and mitigate the risk of key exhaustion. To this end, a reward function is constructed based on the effectiveness of quantum key resource usage, defined as
where denotes the key occupancy ratio on link at time t, while represents the predefined ideal occupancy ratio. The absolute deviation serves as a penalty for imbalance in resource distribution.
The term represents the instantaneous key consumption rate, penalizing links with rapid key depletion, while denotes the key generation rate, incentivizing routing through links with sustainable key supply. Together, they capture the dynamic consumption and replenishment of the key pool, essential for efficient resource utilization. The hyperparameters , , and tune the relative influence of each component in the reward. By combining positive and negative incentives, this reward structure discourages resource imbalance while promoting link selection that ensures adequate key availability and moderate usage.
3.2.4. Policy and Update Mechanism
In the Q-learning framework tailored for quantum key distribution routing, the core quantity is the action-value function , which represents the expected cumulative reward obtained by taking action a in state s and subsequently following the optimal policy . Formally, the optimal Q-function satisfies
where denotes the immediate reward, is the discount factor, and is the optimal policy. The Q-function guides the agent’s decision-making by prioritizing actions that maximize long-term rewards.
Within this framework, the environment is designed to simulate the dynamic evolution of key pools on all links after each action. This real-time feedback mechanism ensures that the agent consistently perceives key resource availability, enabling context-aware routing decisions. To balance exploration and exploitation, a temporal-difference (TD) learning approach with an -greedy policy is employed. The behavior policy is defined as
where denotes the exploration rate, and is the number of feasible actions in state s. This strategy ensures sufficient exploration during early training while enabling convergence to the optimal policy as learning progresses. The Q-values are updated online according to the TD-maximization rule:
where is the learning rate. The reward jointly considers key consumption, generation, and occupancy balance. Guided by a task-specific reward model aligned with resource efficiency, the agent progressively acquires optimal routing strategies through interaction with the dynamic QKD environment. The detailed training procedure is summarized in Algorithm 1, in which, at each hop, the agent selects an action, observes the reward, updates the Q-table, and proceeds to the next state.
| Algorithm 1 Episodic online Q-Learning for key scheduling. |
|
Q-learning incurs a training cost of , where is the number of training episodes, L the path length, and the average node degree. Once trained, its per-path routing complexity reduces to , which is generally lower than the cost of Dijkstra-based algorithms, reflecting significant training overhead but low per-decision computation suitable for real-time routing in large network. In this context (Figure 2), the end-to-end quantum key routing process is structured into four tightly integrated phases—Initialization, Local State Perception, Path Decision & Value Update, and Feasibility Verification & Feedback—which together form a closed-loop optimization cycle, where the virtual key channels represent abstracted logical links modeling resource availability and key generation/consumption for adaptive routing evaluation. During live operation, each routing decision triggers an immediate Q-table update, and this cycle continues iteratively until the policy converges.
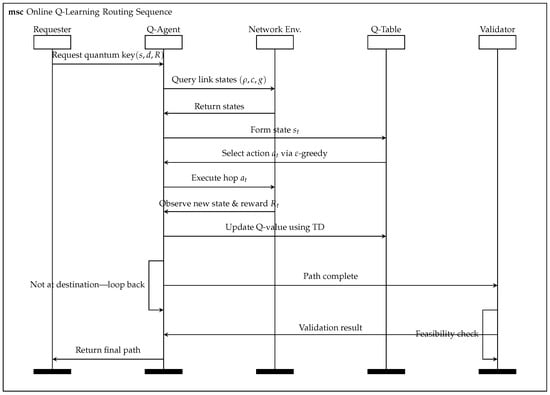
Figure 2.
Sequence diagram of online Q-learning routing and feedback loop: Upon receiving a quantum key distribution request, the Q-Agent queries adjacent link states, selects the next-hop action via -greedy Q-learning, executes the hop, and updates the Q-value using temporal-difference (TD) learning. The Validator then verifies path feasibility and returns the validated path, forming a continuous perception–decision–execution–feedback loop that enables dynamic, adaptive, and foresighted routing.
4. Results and Performance Discussion
4.1. Simulation Setting
4.1.1. Simulation Parameters
We develop a modular simulation framework based on QKDNetSim (NS-3.41) to model quantum key management and routing in dynamic trusted-relay QKD networks. Simulations are conducted on Ubuntu 22.04 with an Intel i7 CPU and 128 GB RAM, and algorithms are implemented in Python 3.9 via Anaconda 3.2.0.
Training and evaluation are performed on Barabási–Albert (BA) networks of 50–200 nodes (Figure 3). This scale-free topology captures the heterogeneity and hub-centric structure typical of real communication networks, where highly connected nodes form potential congestion points, providing a challenging environment for adaptive routing. Each edge represents a virtual key channel, characterized by static attributes (initial key pool and consumption/generation rates) and dynamic properties reflecting network variability.
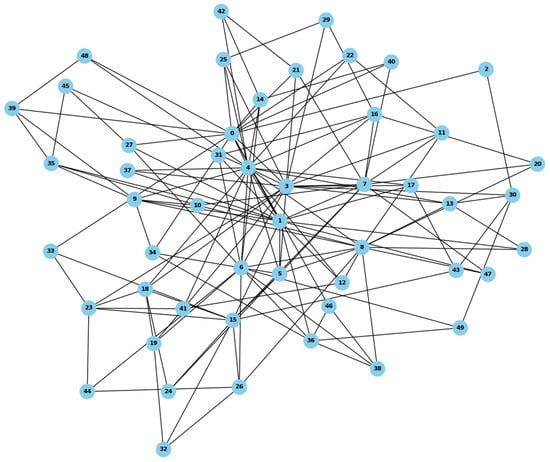
Figure 3.
Hub-centric BA network for evaluating adaptive QKD routing.
Table 1 summarizes the core network and experimental parameters. Network parameters—including node degree, key generation rates, key pool sizes, and initial key consumption rates—are configured to reflect practical QKD constraints. Overload thresholds and ideal key pool utilization ratios guide routing and load balancing, while traffic fluctuations, link drift, per-hop delays, transmission jitter, and probabilistic link failures evaluate algorithmic resilience. Simulations proceed in discrete time steps, with each episode representing a full key distribution cycle.

Table 1.
Network and experimental parameters with descriptions.
Table 2 presents Q-learning hyperparameters across training phases. The exploration rate decreases from high to low to shift from broad exploration to policy exploitation, while the learning rate diminishes to stabilize convergence. Weights , , and are adjusted to balance load, penalties, and quality rewards, guiding the agent from general learning to fine-tuned optimization. The discount factor increases to emphasize long-term rewards, enabling progressive learning of effective routing strategies in dynamic networks.

Table 2.
Q-learning hyperparameter settings across training phases.
Each episode spans 150 time steps, with 50 episodes totaling 7500 s of virtual time. Each network configuration is simulated 30 times to reduce stochastic variability, ensuring statistically reliable metrics for reward convergence, key distribution time, key utilization, and failure ratio, while reflecting the algorithm’s adaptability in dynamic QKD network.
4.1.2. Benchmark Methods
To evaluate the proposed QKD routing scheme, three representative baseline algorithms are considered, OSPF (Open Shortest Path First), CAD (Congestion-Aware Dijkstra), and RAKP (Residual-Adaptive Key Provisioning), covering routing strategies from topology-driven to local and global resource-aware methods. In this study, CAD is introduced as a congestion-aware extension of Dijkstra, while RAKP is adopted from prior work [48].
OSPF is a classical shortest-path protocol that assigns uniform cost (typically 1) to each link and selects paths minimizing total hop count. It relies solely on network topology and ignores key resources.
CAD incorporates local congestion awareness into Dijkstra’s algorithm. For each link , the weight is defined as
where denotes the residual key pool size and is a small constant to avoid singularities. Paths are chosen to minimize cumulative weight, favoring links with higher residual key pool size. CAD performs local optimization, considering only the current path’s link states.
RAKP is a global key provisioning. For each link , the residual ratio is
where is the maximum key pool size and is the currently allocated key volume. During each allocation round, links are proportionally allocated keys based on , and RAKP continuously adapts to global network dynamics.
4.2. Experimental Results and Analysis
4.2.1. Reward Convergence Analysis
The training rewards exhibit a clear exploration–convergence pattern (Figure 4). In the initial phase (Ep.1–5), high exploration leads to large fluctuations and predominantly negative rewards ( to ), as the agent explores randomly without an effective policy. During the intermediate phase (Ep.6–15), decreasing and adaptive learning rate drive rewards toward 0, reflecting the agent’s emerging ability to balance load and key resource utilization. In the later phase (Ep.16–30), rewards stabilize around with minor fluctuations (), indicating that the Q-learning policy has largely converged and maintains stable performance despite link perturbations.
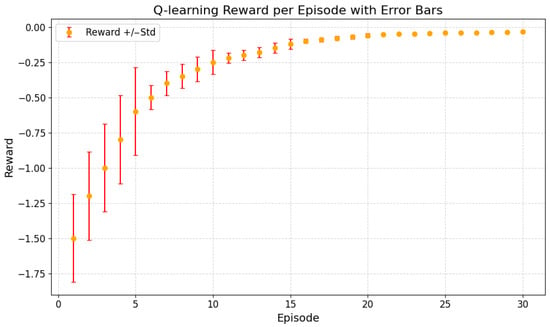
Figure 4.
Reward Convergence Analysis: Q-learning rewards evolve from large initial fluctuations to gradual improvement and finally stabilize, reflecting policy learning and convergence.
4.2.2. Total Quantum Key Volume: Performance Variation
This section systematically compares QKD routing algorithms under varying key volumes, considering average distribution time, maximum key utilization, failure ratio, and network throughput. The results reveal how network constraints interact with algorithmic design. Q-learning consistently achieves high throughput and low failure ratios by anticipating congestion and dynamically balancing load. In contrast, RAKP and CAD incur higher distribution time and failures due to reactive or localized strategies, while OSPF, insensitive to load, exhibits the highest utilization and failure accumulation.
As shown in Figure 5, the evolution of key distribution performance reflects congestion dynamics and algorithmic adaptation. Q-learning maintains low distribution times and moderate key utilization at low key volumes, exploiting underutilized links and avoiding nascent bottlenecks. As key volume increases, distribution time rises to 28–31 s and maximum utilization reaches 0.92, showing that even adaptive policies are limited by finite link key pool size. RAKP reacts slower to changing conditions, leading to higher delays (37–43 s) and utilization (0.93–0.96), while CAD, constrained by local information, suffers accelerated congestion at critical nodes (37–49 s, 0.945–0.985). OSPF consistently overloads frequently used links (33–54 s, 0.995).
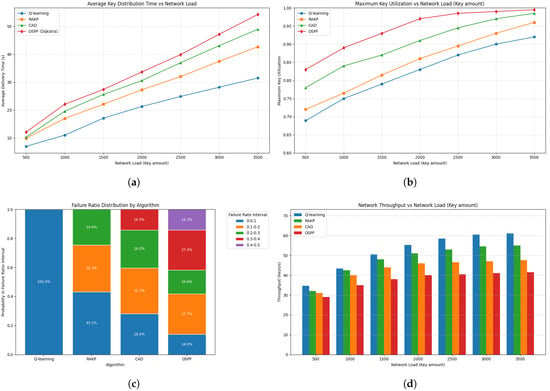
Figure 5.
Variation in total quantum key amount on key distribution performance, link utilization, failure ratios, and network throughput. (a) Impact of total quantum key amount on average key distribution time: Q-learning shows the lowest and slowest growth in delivery time, RAKP and CAD perform moderately, while OSPF exhibits the steepest increase. (b) Impact of total quantum key amount on maximum link utilization: Q-learning achieves the most balanced utilization, RAKP and CAD show moderate growth, while OSPF suffers from potential bottlenecks under high load. (c) Distribution of failure ratios: Q-learning failure ratios are primarily concentrated in the 0–0.1 interval. (d) Impact of total quantum key amount on network throughput: Q-learning achieves the highest throughput, followed by RAKP, CAD, and OSPF.
Failure ratio distributions further illustrate algorithmic foresight. Q-learning confines nearly all failures to 0–, reflecting proactive path selection. RAKP exhibits 57% of failures in – due to delayed global adjustments, while CAD shows 14% in –, highlighting the impact of local decisions at bottlenecks. OSPF reaches 14% in –, consistent with unbalanced traffic accumulation. Throughput trends (Q-learning 34.6–61 keys/s, RAKP/CAD 32–55 keys/s, and OSPF 29–41 keys/s) reflect the combined effects of adaptive load balancing and link saturation. Despite rising failure ratios, heterogeneous link utilization ensures continued key delivery, while marginal key pool size constraints gradually slow throughput growth and induce longer queues and localized failures.
4.2.3. Single-Node Key Transmission Rate: Performance Variation
This section presents a detailed comparison of QKD routing algorithms across varying single-node key transmission rates, highlighting the coupled behavior of average distribution time (), over-threshold link ratio (), and failure ratio (). These interdependent trends reflect the combined influence of algorithmic adaptation, cumulative multi-hop effects, and the hub-centric structure of BA topologies.
As shown in Figure 6, Q-learning consistently outperforms other algorithms under varying key rates by dynamically learning optimal paths and balancing network load. At low rates, initial exploration leads to moderate delays () and minimal overload (), as the agent gradually discovers efficient paths. RAKP, CAD, and OSPF exhibit higher delays and slightly increased overload, reflecting limited adaptivity or load-insensitive routing that cannot fully exploit underutilized links. As key rates increase, Q-learning maintains moderate delay growth and low failure ratio by proactively avoiding emerging bottlenecks and distributing traffic across less congested links. In contrast, RAKP and CAD experience higher delays and failures due to partial or local adaptivity, while OSPF suffers sharp escalations (delays up to and a substantial fraction of failures in the 0.6–0.8 range), illustrating the vulnerability of non-adaptive strategies to multi-hop congestion and saturation of core links.
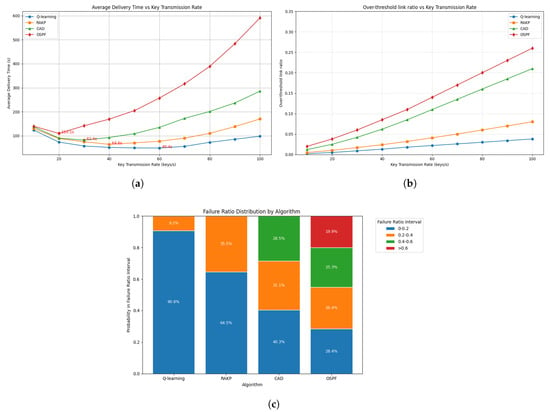
Figure 6.
Variation in single-node key transmission rates on key distribution performance, over-threshold link ratio, and failure ratio. (a) Impact of single-node key transmission rates on average key distribution time: Time decreases at low rates due to better link utilization, reaches a minimum at moderate rates, and rises at high rates from congestion, with Q-learning achieving the lowest and most stable delay. (b) Impact of single-node key transmission rates on over-threshold link ratio: The proportion of over-threshold links increases with key rates, reflecting rising congestion, with Q-learning maintaining the lowest ratio and more balanced load compared to RAKP, CAD, and OSPF. (c) Distribution of failure ratios: Q-learning failure ratios are primarily concentrated in the 0–0.2 interval.
Network performance exhibits nonlinear trends with increasing single-node key transmission rates, reflecting cumulative multi-hop effects as minor link overloads propagate. At low key rates, Q-learning exhibits a U-shaped delay due to queue initialization and exploration. As the key rate increases, CAD and OSPF experience sharp rises in average delay and failure ratio, whereas Q-learning consistently maintains lower latency. Extreme OSPF degradation highlights the limitations of topology-driven routing in hub-centric BA networks. These patterns arise from the interplay of algorithmic adaptability—Q-learning dynamically mitigates bottlenecks, RAKP partially optimizes paths, CAD struggles under congestion, and OSPF remains non-adaptive—and topology-induced hub congestion.
4.2.4. Network Scale: Performance Variation
The network size strongly affects QKD performance, impacting average distribution time and failure ratio. As the network expands from 50 to 200 nodes, longer paths, increased topology complexity, and intensified link contention naturally lead to higher distribution delays and elevated failure probabilities. These metrics jointly reflect the network’s capacity to balance load, mitigate congestion, and sustain reliable key delivery.
As shown in Figure 7, analysis under increasing node counts reveals distinct algorithmic patterns. Q-learning shows the slowest growth in distribution time (44 → 60 s) and failure ratio (0.056 → 0.086), benefiting from global load awareness and online learning that disperse traffic and prevent bottlenecks. RAKP exhibits moderate increases (50.5 → 85 s, 0.082 → 0.170), with mid-node acceleration followed by high-node stabilization, reflecting its residual-ratio allocation that mitigates local congestion while preserving balance. CAD incurs higher delays (57.5 → 105 s) and sharper failure growth (0.165 → 0.310) as its local congestion-aware routing accumulates bottlenecks with scale. OSPF performs worst, with delay increasing (65.5 → 123 s) and failure ratio rising (0.246 → 0.350), as its load-unaware shortest-path routing leads to escalating congestion and limited capacity for load balancing compared with adaptive strategies.
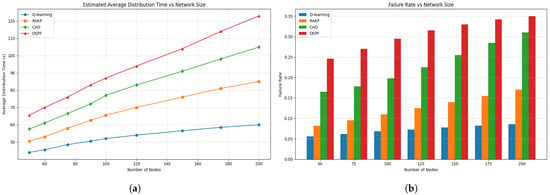
Figure 7.
Variation in network scale on key distribution performance and failure ratio. (a) Impact of network scale on average key distribution time: Time rises with node count due to longer paths and link contention, with Q-learning increasing slowest, RAKP moderate, CAD higher, and OSPF steepest. (b) Impact of network scale on failure ratio: Higher node counts increase path length and link contention, raising failure ratios, with Q-learning most resilient, RAKP moderate, CAD pronounced, and OSPF most severe.
Cross-comparison shows that node expansion amplifies path length, contention, and blocking probability, thereby magnifying algorithmic differences. Adaptive strategies such as Q-learning, with global load awareness, and RAKP, with residual-ratio allocation, effectively redistribute traffic to contain delay and failure growth. In contrast, CAD accumulates congestion due to reliance on local remaining-key information, while OSPF suffers persistent overload under shortest-path routing. Thus, scaling not only increases delay and failure but also highlights each algorithm’s efficiency in load balancing and congestion resilience.
Q-learning for QKD routing has low online computational complexity, as decisions depend only on the current node and path length, while offline training is more demanding due to the size of the state–action space and number of training episodes. The algorithm scales well in moderately sized or highly connected networks through adaptive load balancing, but in extremely large-scale or ultra-dense networks, performance may be limited by state-space growth, memory requirements, and restricted generalization, potentially requiring hierarchical or function-approximated reinforcement learning.
4.2.5. Link Failure Probability: Performance Variation
This section examines how increasing link failure probability affects QKD network performance, highlighting its substantial impact on average key distribution time and failure ratio, with algorithmic performance gaps widening at higher failure probabilities.
As shown in Figure 8, with increasing link failure probability, both distribution time and failure ratio exhibit coherent yet differentiated trends across algorithms. Q-learning exhibits the slowest growth in average delay, rising from 43.4 s to 85.0 s. Its failure ratio remains low and stable at low link failure probabilities due to proactive avoidance of sparse failures and local congestion but increases to 0.244 at higher probabilities as network constraints become unavoidable. RAKP maintains moderate performance (49.97 → 69.12 s) at low to medium link failure probability, but under higher probabilities, delay surges to 103.94 s and failures (0.082 → 0.372) accelerate as local bottlenecks emerge. CAD initially behaves like RAKP but proves more congestion-sensitive, with delay expanding from 57.46 to 134.34 s and failure ratio from 0.165 to 0.517, reflecting its lack of global load balancing. OSPF, constrained by shortest-path routing, consistently performs worst: distribution time escalates to 184.21 s and failure ratio from 0.246 to 0.670, as it cannot reroute around congested or failed links.
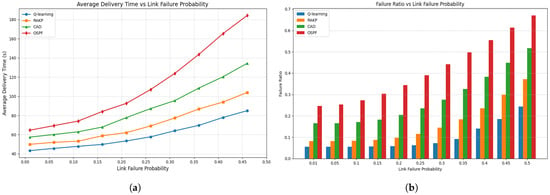
Figure 8.
Variation in link failure probability on key distribution performance and failure ratio. (a) Average key distribution time rises with increasing link failure probability, with Q-learning consistently exhibiting the lowest delays across the range. (b) Impact of link failure probability on key distribution reliability: Failure ratio increases with rising link failures, with Q-learning remaining most resilient, followed by RAKP, CAD, and OSPF.
At low link failure probabilities, abundant path availability allows global optimization algorithms (Q-learning and RAKP) to fully exploit network resources, resulting in distribution time and failure curves that increase slowly and remain relatively low. As link failure probabilities increase, path scarcity and congestion bottlenecks disproportionately affect local and non-adaptive strategies, amplifying algorithmic differences. The observed nonlinear growth and widening algorithmic differences reflect the interplay of path availability, congestion dynamics, and algorithmic design. At high link failure probabilities, performance gaps stabilize as network resources become saturated, with Q-learning mitigating degradation through dynamic path selection and load balancing.
5. Conclusions
This paper presents a novel Q-learning-based key scheduling framework designed for trusted-relay QKD networks, addressing the challenges posed by dynamic key consumption and heterogeneous resource allocation. The proposed framework comprises three integral components: a Neighbor State Awareness Module that provides comprehensive monitoring of adjacent link parameters; an Online Q-learning Scheduler that adaptively optimizes resource utilization through a rigorously defined reward function; and a Routing and Validation Module that guarantees feasible and resource-aware path selection under network constraints.
The episodic online learning paradigm enables real-time, fine-grained policy updates, ensuring balanced key pool utilization, preventing resource over-concentration, and maintaining stable replenishment. Simulation results demonstrate that Q-learning consistently outperforms RAKP, CAD, and OSPF across dynamic QKD network. Under total key volume variation, it limits failure ratios to 0–0.1 and achieves 61 keys/s throughput; when varying the single-node key transmission rate, average distribution time remains around 100 s with only 3.8% over-threshold links, indicating effective congestion mitigation; with increasing network scale, it sustains the lowest failure ratios; and under higher link failure probabilities, distribution time stays below 85 s, reflecting robust load balancing, adaptability, and efficiency. Future work could integrate reinforcement learning, graph neural networks, and hybrid optimization strategies to enable scalable, self-adaptive QKD network that optimize reliability, efficiency, and quantum resource utilization in ultra-large, heterogeneous, and dynamic environments.
Author Contributions
Conceptualization, Y.H.; methodology, Y.H.; software, Y.H.; validation, Y.H., Y.X. and W.G.; formal analysis, Y.H.; investigation, Y.H. and Y.X.; resources, Y.H.; data curation, Y.H.; writing—original draft preparation, Y.H.; writing—review and editing, Y.H.; visualization, Y.H.; supervision, J.T.; project administration, Y.X. and J.T.; funding acquisition, J.T. and W.G. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by Innovation Program for Quantum Science and Technology (2021ZD0301300).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A
Appendix A.1. QKD Network Architecture
The trusted-relay QKD network comprises quantum key distribution links, key management (KM) links, and trusted QKD nodes. Each node integrates a quantum transmitter (QKD-Tx), receiver (QKD-Rx), and key management module. The quantum layer consists of point-to-point QKD device pairs that independently generate keys, which are then relayed through KM modules and links. The key management layer handles key distribution and interconnection across arbitrary node pairs within the QKD network. Above these, the control layer coordinates network elements via distributed controllers, while the management layer oversees global monitoring and administrative tasks. Finally, keys are delivered to cryptographic applications within the service layer of the user network by the KM nodes. Figure A1, based on the ITU-T Y.3800 standard [2], depicts the reference architecture and core components of both the QKD and user network.
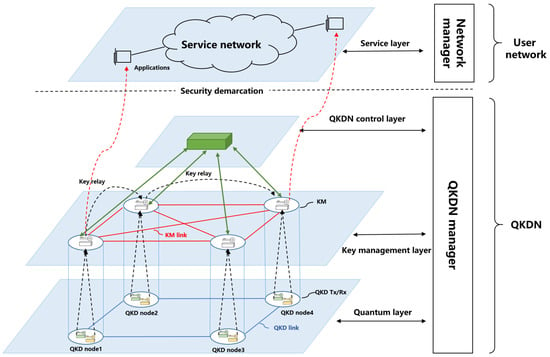
Figure A1.
QKD network architecture: The trusted-relay QKD network consists of a quantum layer generating keys, a key management layer handling distribution and relay, a control/management layer coordinating the network, and a service layer delivering keys to applications. The Q-learning algorithm deployed at the key management layer dynamically selects relay paths to optimize distribution, balance resources, and adapt to network changes.
In typical operations, cryptographic applications in the service layer initiate key requests to nearby KM nodes. These nodes verify local availability and, if sufficient keys exist, provision them directly to the application. Otherwise, a relay process is triggered. KM nodes cooperate with controllers to compute relay paths under the supervision of the manager, which continuously monitors network conditions. Keys are securely relayed across intermediate KM nodes along the selected path and finally delivered in a standardized format to the requesting application, ensuring secure, end-to-end key provisioning.
Appendix A.2. Relay Routing Mechanism in QKD Network
The trusted relay process of quantum key distribution, guided by routing algorithms, is illustrated in Figure A2 and consists of four steps, where the relay is performed using one-time pad (OTP) encryption to guarantee unconditional security. Future extensions could include multi-path parallel forwarding with end-to-end key aggregation, or hierarchical/multi-agent reinforcement learning to explicitly model multi-segment aggregation.
- 1.
- In the initialization phase, the source node Alice (node 1) identifies relay nodes within its communication range. Utilizing a classical network routing discovery protocol, responses are collected from various nodes. All responding nodes are included in the candidate set for the next-hop relay nodes, thereby initializing the routing algorithm.
- 2.
- According to the routing algorithm, Alice (node 1) generates a global key (communication key) and simultaneously negotiates a local key with node 2 based on the BB84 quantum key distribution protocol. The global key is sequentially forwarded by trusted-relay nodes. In the example shown in Figure 1, node 2 is selected to relay the global key .
- 3.
- Under frequently changing network topologies, the routing algorithm dynamically senses the availability of key resources within the network to select candidate relay nodes, ensuring efficient key distribution. A detailed description of this algorithm is provided in Section 4.
- 4.
- Node 1 and node 2 share the local key . Node 2 receives the encrypted message from node1 and decrypts it using the shared key to recover . Concurrently, node 2 negotiates a local key with node 4 and encrypts the transmission as .
In this example, node 4 serves as the destination Bob. Generally, in network with multiple relay nodes, the relay process repeats steps 2, 3, and 4 until the destination node obtains the global key . At this point, both Alice and Bob possess the global key , enabling secure communication.
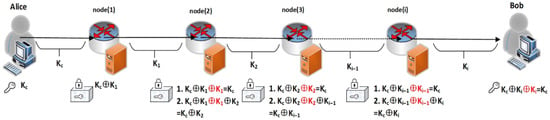
Figure A2.
Relay routing mechanism in QKD network: The trusted-relay QKD process uses one-time pad encryption to securely forward a global key from the source to the destination through multiple relay nodes, with routing algorithms dynamically selecting next-hop nodes and negotiating local keys at each hop to ensure efficient and secure key distribution.
References
- Zeydan, E.; De Alwis, C.; Khan, R.; Turk, Y.; Aydeger, A.; Gadekallu, T.R.; Liyanage, M. Quantum technologies for beyond 5G and 6G networks: Applications, opportunities, and challenges. arXiv 2025, arXiv:2504.17133. [Google Scholar] [CrossRef]
- ITU-T Y.3800; Overview of Quantum Key Distribution. ITU: Geneva, Switzerland, 2019.
- Wootters, W.K.; Zurek, W.H. A single quantum cannot be cloned. Nature 1982, 299, 802–803. [Google Scholar] [CrossRef]
- Ekert, A.K. Quantum cryptography based on Bell’s theorem. Phys. Rev. Lett. 1991, 67, 661. [Google Scholar] [CrossRef] [PubMed]
- Krelina, M. Quantum technology for military applications. EPJ Quantum Technol. 2021, 8, 24. [Google Scholar] [CrossRef]
- Liang, Q. Employing quantum key distribution for enhancing network security. In Proceedings of the 2023 International Conference on Image, Algorithms and Artificial Intelligence (ICIAAI 2023), Singapore, 11–13 August 2023; Atlantis Press: Dordrecht, The Netherlands, 2023; pp. 518–526. [Google Scholar]
- Sahu, S.K.; Mazumdar, K. State-of-the-art analysis of quantum cryptography: Applications and future prospects. Front. Phys. 2024, 12, 1456491. [Google Scholar] [CrossRef]
- Tsai, C.W.; Yang, C.W.; Lin, J.; Chang, Y.C.; Chang, R.S. Quantum key distribution networks: Challenges and future research issues in security. Appl. Sci. 2021, 11, 3767. [Google Scholar] [CrossRef]
- Yu, X.; Liu, Y.; Zou, X.; Cao, Y.; Zhao, Y.; Nag, A.; Zhang, J. Secret-key provisioning with collaborative routing in partially-trusted-relay-based quantum-key-distribution-secured optical networks. J. Light. Technol. 2022, 40, 3530–3545. [Google Scholar] [CrossRef]
- Zhou, H.; Lv, K.; Huang, L.; Ma, X. Quantum network: Security assessment and key management. IEEE/ACM Trans. Netw. 2022, 30, 1328–1339. [Google Scholar] [CrossRef]
- Elliott, C.; Colvin, A.; Pearson, D.; Pikalo, O.; Schlafer, J.; Yeh, H. Current status of the DARPA quantum network. In Proceedings of the Quantum Information and Computation III, Orlando, FL, USA, 29–30 March 2005; SPIE: Bellingham, WA, USA, 2005; Volume 5815, pp. 138–149. [Google Scholar]
- Peev, M.; Pacher, C.; Alléaume, R.; Barreiro, C.; Bouda, J.; Boxleitner, W.; Debuisschert, T.; Diamanti, E.; Dianati, M.; Dynes, J.F.; et al. The SECOQC quantum key distribution network in Vienna. New J. Phys. 2009, 11, 075001. [Google Scholar] [CrossRef]
- Sasaki, M.; Fujiwara, M.; Ishizuka, H.; Klaus, W.; Wakui, K.; Takeoka, M.; Miki, S.; Yamashita, T.; Wang, Z.; Tanaka, A.; et al. Field test of quantum key distribution in the Tokyo QKD Network. Opt. Express 2011, 19, 10387–10409. [Google Scholar] [CrossRef]
- Chen, Y.A.; Zhang, Q.; Chen, T.Y.; Cai, W.Q.; Liao, S.K.; Zhang, J.; Chen, K.; Yin, J.; Ren, J.-G.; Chen, Z.; et al. An integrated space-to-ground quantum communication network over 4,600 kilometres. Nature 2021, 589, 214–219. [Google Scholar] [CrossRef] [PubMed]
- Bi, L.; Miao, M.; Di, X. A dynamic-routing algorithm based on a virtual quantum key distribution network. Appl. Sci. 2023, 13, 8690. [Google Scholar] [CrossRef]
- Yu, J.; Qiu, S.; Yang, T. Optimization of hierarchical routing and resource allocation for power communication networks with QKD. J. Light. Technol. 2023, 42, 504–512. [Google Scholar] [CrossRef]
- Tanizawa, Y.; Takahashi, R.; Dixon, A.R. A routing method designed for a quantum key distribution network. In Proceedings of the 2016 Eighth International Conference on Ubiquitous and Future Networks (ICUFN), Vienna, Austria, 5–8 July 2016; pp. 208–214. [Google Scholar]
- Han, W.; Wu, X.; Zhu, Y.; Zhou, X.; Xu, C. QKD network routing research based on trust relay. J. Mil. Commun. Technol. 2013, 34, 43–48. [Google Scholar]
- Ma, C.; Guo, Y.; Su, J.; Yang, C. Hierarchical routing scheme on wide-area quantum key distribution network. In Proceedings of the 2016 2nd IEEE International Conference on Computer and Communications (ICCC), Chengdu, China, 14–17 October 2016; pp. 2009–2014. [Google Scholar]
- Zhang, H.; Quan, D.; Zhu, C.; Li, Z. A quantum cryptography communication network based on software defined network. ITM Web Conf. 2018, 17, 01008. [Google Scholar] [CrossRef]
- Li, M.; Quan, D.; Zhu, C. Stochastic routing in quantum cryptography communication network based on cognitive resources. In Proceedings of the 2016 8th International Conference on Wireless Communications & Signal Processing (WCSP), Yangzhou, China, 13–15 October 2016; pp. 1–4. [Google Scholar]
- Yang, C.; Zhang, H.; Su, J. Quantum key distribution network: Optimal secret-key-aware routing method for trust relaying. China Commun. 2018, 15, 33–45. [Google Scholar] [CrossRef]
- Han, Q.; Yu, L.; Zheng, W.; Cheng, N.; Niu, X. A novel QKD network routing algorithm based on optical-path-switching. J. Inf. Hiding Multim. Signal Process. 2014, 5, 13–19. [Google Scholar]
- Yang, C.; Zhang, H.; Su, J. The QKD network: Model and routing scheme. J. Mod. Opt. 2017, 64, 2350–2362. [Google Scholar] [CrossRef]
- Ma, C.; Guo, Y.; Su, J. A multiple paths scheme with labels for key distribution on quantum key distribution network. In Proceedings of the 2017 IEEE 2nd Advanced Information Technology, Electronic and Automation Control Conference (IAEAC), Chongqing, China, 25–26 March 2017; pp. 2513–2517. [Google Scholar]
- Mehic, M.; Maurhart, O.; Rass, S.; Voznak, M. Implementation of quantum key distribution network simulation module in the network simulator NS-3. Quantum Inf. Process. 2017, 16, 253. [Google Scholar] [CrossRef]
- Yao, J.; Wang, Y.; Li, Q.; Mao, H.; El-Latif, A.A.A.; Chen, N. An efficient routing protocol for quantum key distribution networks. Entropy 2022, 24, 911. [Google Scholar] [CrossRef]
- Cao, Y.; Zhao, Y.; Yu, X.; Wu, Y. Resource assignment strategy in optical networks integrated with quantum key distribution. J. Opt. Commun. Netw. 2017, 9, 995–1004. [Google Scholar] [CrossRef]
- Zhao, Y.; Cao, Y.; Wang, W.; Wang, H.; Yu, X.; Zhang, J.; Tornatore, M.; Wu, Y.; Mukherjee, B. Resource allocation in optical networks secured by quantum key distribution. IEEE Commun. Mag. 2018, 56, 130–137. [Google Scholar] [CrossRef]
- Cao, Y.; Zhao, Y.; Colman-Meixner, C.; Yu, X.; Zhang, J. Key on demand (KoD) for software-defined optical networks secured by quantum key distribution (QKD). Opt. Express 2017, 25, 26453–26467. [Google Scholar] [CrossRef]
- Cao, Y.; Zhao, Y.; Wu, Y.; Yu, X.; Zhang, J. Time-scheduled quantum key distribution (QKD) over WDM networks. J. Light. Technol. 2018, 36, 3382–3395. [Google Scholar] [CrossRef]
- Dong, K.; Zhao, Y.; Yu, X.; Nag, A.; Zhang, J. Auxiliary graph based routing, wavelength, and time-slot assignment in metro quantum optical networks with a novel node structure. Opt. Express 2020, 28, 5936–5952. [Google Scholar] [CrossRef]
- Dong, K.; Zhao, Y.; Nag, A.; Yu, X.; Zhang, J. Distributed subkey-relay-tree-based secure multicast scheme in quantum data center networks. Opt. Eng. 2020, 59, 065102. [Google Scholar] [CrossRef]
- Zou, X.; Yu, X.; Zhao, Y.; Nag, A.; Zhang, J. Collaborative routing in partially-trusted relay based quantum key distribution optical networks. In Proceedings of the 2020 Optical Fiber Communications Conference and Exhibition (OFC), San Diego, CA, USA, 8–12 March 2020; pp. 1–3. [Google Scholar]
- Amer, O.; Krawec, W.O.; Wang, B. Efficient routing for quantum key distribution networks. In Proceedings of the 2020 IEEE International Conference on Quantum Computing and Engineering (QCE), Denver, CO, USA, 12–16 October 2020; pp. 137–147. [Google Scholar]
- Yu, X.; Liu, X.; Liu, Y.; Nag, A.; Zou, X.; Zhao, Y.; Zhang, J. Multi-path-based quasi-real-time key provisioning in quantum-key-distribution enabled optical networks (QKD-ON). Opt. Express 2021, 29, 21225–21239. [Google Scholar] [CrossRef]
- Li, S.; Yu, X.; Zhao, Y.; Wang, H.; Zhou, X.; Zhang, J. Routing and wavelength allocation in spatial division multiplexing based quantum key distribution optical networks. In Proceedings of the 2020 International Conference on Computing, Networking and Communications (ICNC), Big Island, HI, USA, 17–20 February 2020; pp. 268–272. [Google Scholar]
- Gandelman, S.P.; Maslennikov, A.; Rozenman, G.G. Hands-On Quantum Cryptography: Experimentation with the B92 Protocol Using Pulsed Lasers. Photonics 2025, 12, 220. [Google Scholar] [CrossRef]
- Dehingia, K.; Dutta, N. Hybrid Quantum Key Distribution Framework: Integrating BB84, B92, E91, and GHZ Protocols for Enhanced Cryptographic Security. Concurr. Comput. Pract. Exp. 2025, 37, e70221. [Google Scholar] [CrossRef]
- Sharma, P.; Gupta, S.; Bhatia, V.; Prakash, S. Deep reinforcement learning-based routing and resource assignment in quantum key distribution-secured optical networks. IET Quantum Commun. 2023, 4, 136–145. [Google Scholar] [CrossRef]
- Al-Mohammed, H.A.; Al-Kuwari, S.; Kuniyil, H.; Farouk, A. Towards Scalable Quantum Key Distribution: A Machine Learning-Based Cascade Protocol Approach. arXiv 2024, arXiv:2409.08038. [Google Scholar] [CrossRef]
- Horoschenkoff, P.; Rödiger, J.; Kegreiß, S. OptiNode: A ML Algorithm for Optimal Trusted Node Positioning in QKD Networks. In Proceedings of the 2025 International Conference on Optical Network Design and Modeling (ONDM), Pisa, Italy, 6–9 May 2025; pp. 1–6. [Google Scholar]
- Larouci, N.E.H.; Sahraoui, S.; Djeffal, A. Machine learning based routing protocol (MLBRP) for Mobile Internet of Things networks. J. Netw. Syst. Manag. 2025, 33, 67. [Google Scholar] [CrossRef]
- Mammeri, Z. Reinforcement learning based routing in networks: Review and classification of approaches. IEEE Access 2019, 7, 55916–55950. [Google Scholar] [CrossRef]
- Malhotra, S.; Yashu, F.; Saqib, M.; Mehta, D.; Jangid, J.; Dixit, S. Deep Reinforcement Learning for Dynamic Resource Allocation in Wireless Networks. arXiv 2025, arXiv:2502.01129. [Google Scholar] [CrossRef]
- Donatus, R.C.; Ter, K.; Ajayi, O.O.; Udekwe, D. Multi-Agent Reinforcement Learning in Intelligent Transportation Systems: A Comprehensive Survey. arXiv 2025, arXiv:2508.20315. [Google Scholar] [CrossRef]
- Liu, Q.; Ma, Y. Communication resource allocation method in vehicular networks based on federated multi-agent deep reinforcement learning. Sci. Rep. 2025, 15, 30866. [Google Scholar] [CrossRef]
- Meng, X.; Yu, X.; Chen, W.; Zhao, Y.; Zhang, J. Residual-adaptive key provisioning in quantum-key-distribution enhanced internet of things (q-iot). In Proceedings of the 2020 International Wireless Communications and Mobile Computing (IWCMC), Limassol, Cyprus, 15–19 June 2020; pp. 2022–2027. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).