Research Progress on Tunable Absorbers for Various Wavelengths Based on Metasurfaces
Abstract
1. Introduction
2. Principle and Requirements of Adjustable Absorber
3. Methods for Achieving Tunability in Metasurfaces
3.1. Electrical Tuning
3.2. Magnetic Control
3.3. Optical Control
3.4. Temperature Regulation
3.5. Mechanical Regulation
3.6. Comparative Discussion
4. Tunable Absorbers in the Microwave Band
4.1. Electrically Tunable Absorbers in the Microwave Band
4.2. Magnetically Tunable Absorbers in the Microwave Band
4.3. Mechanical Controlled Absorbers for Microbands
5. Tunable Absorbers in the Terahertz Band
5.1. Electrically Tunable Absorbers in the Terahertz Band
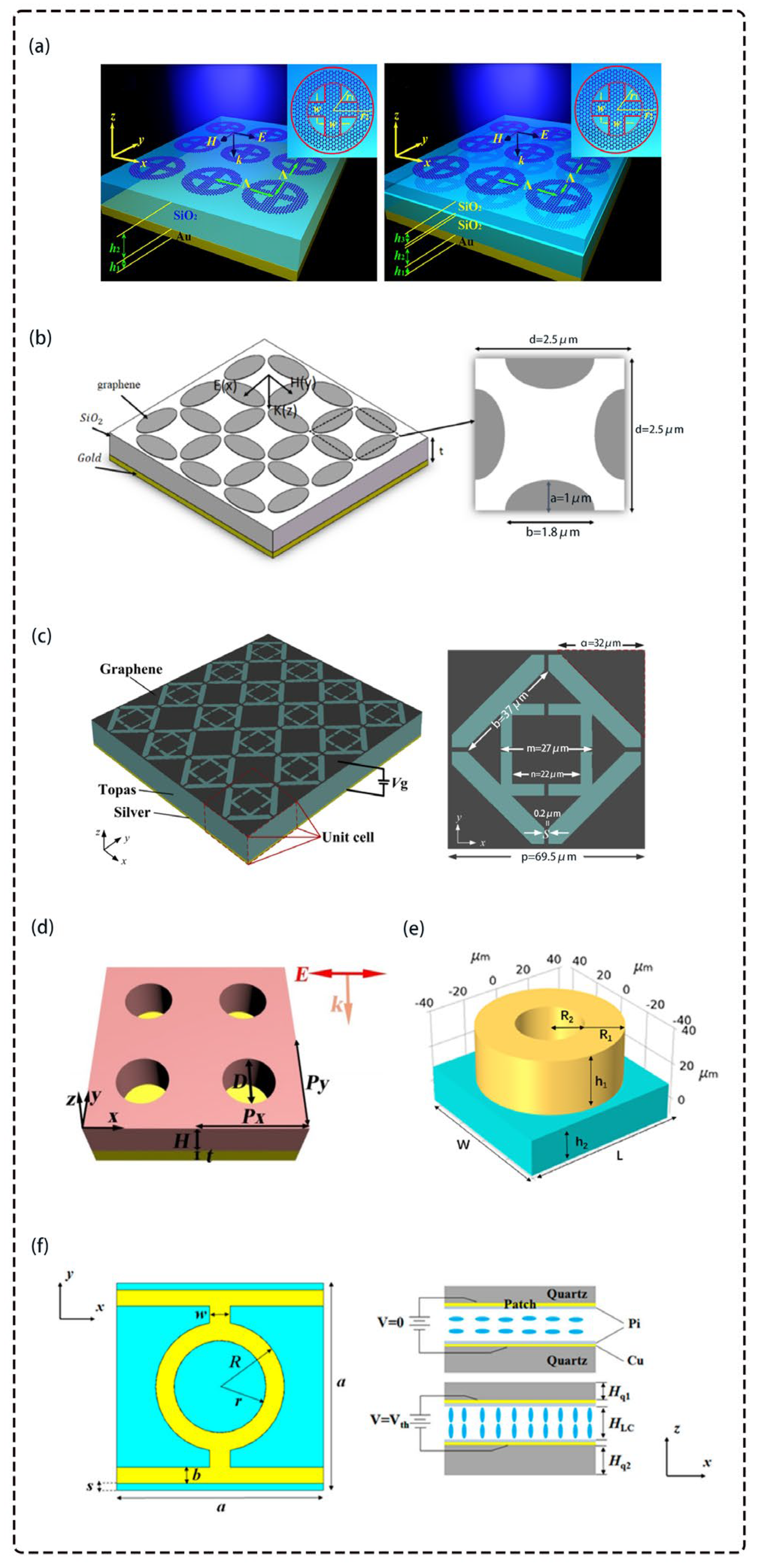
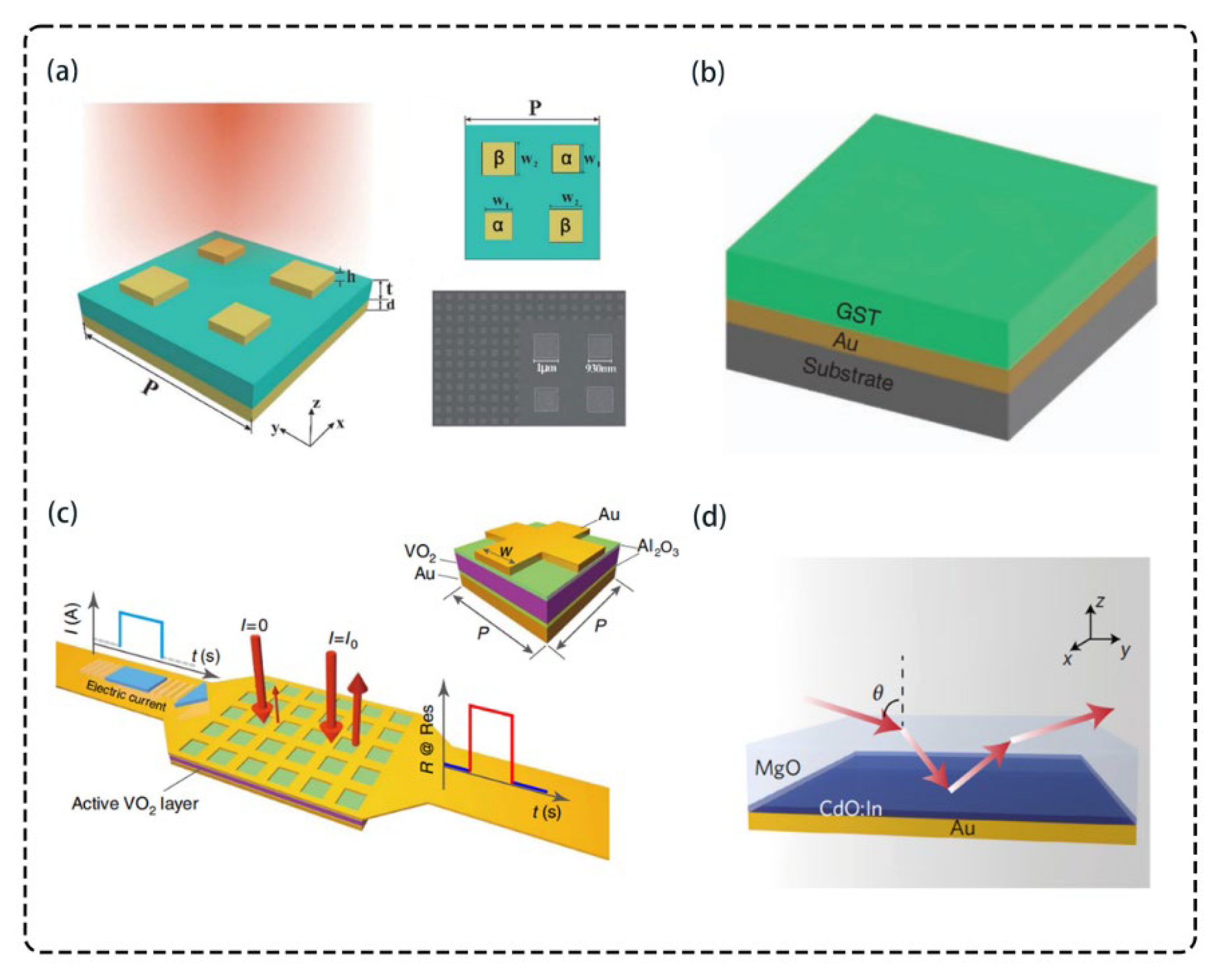
5.2. Temperature-Tunable Absorbers in the Terahertz Band
5.3. Optically Tunable Terahertz Absorbers
6. Tunable Absorbers in the Infrared Band
7. Summary and Prospects
Author Contributions
Funding
Conflicts of Interest
References
- Alitalo, P.; Tretyakov, S. Electromagnetic cloaking with metamaterials. Mater. Today 2009, 12, 22–29. [Google Scholar] [CrossRef]
- Leonhardt, U.; Tyc, T. Broadband invisibility by non-Euclidean cloaking. Science 2009, 323, 110–112. [Google Scholar] [CrossRef] [PubMed]
- Zhao, S.; Ma, H.; Shao, T.; Li, J.; Wang, Q.; Yang, F. High temperature metamaterial enhanced electromagnetic absorbing coating prepared with alumina ceramic. J. Alloys Compd. 2021, 874, 159822. [Google Scholar] [CrossRef]
- Zohuri, B. Radar-absorbent material and radar cross section. In Radar Energy Warfare and the Challenges of Stealth Technology; Springer: Cham, Switzerland, 2020; pp. 65–114. [Google Scholar] [CrossRef]
- Manjappa, M.; Pitchappa, P.; Wang, N.; Singh, N.; Lee, C.; Singh, R. Active control of resonant cloaking in a terahertz MEMS metamaterial. Adv. Opt. Mater. 2018, 6, 1800141. [Google Scholar] [CrossRef]
- Wang, B.; Yerazunis, W.; Teo, K.H. Wireless power transfer: Metamaterials and array of coupled resonators. Proc. IEEE 2013, 101, 1359–1368. [Google Scholar] [CrossRef]
- Alkhateeb, A.; Heath, R.W. Frequency selective hybrid precoding for limited feedback millimeter wave systems. IEEE Trans. Commun. 2016, 64, 1801–1818. [Google Scholar] [CrossRef]
- Rong, C.; Wu, L.; Tao, J.; Cheng, Y.; Wang, K.; Chen, L.; Luo, H.; Chen, F.; Li, X. Metasurface-Based Optical Neural Network and Its Application in Next-Generation Optical Communications and Networks. J. Light. Technol. 2025, 43, 8538–8562. [Google Scholar] [CrossRef]
- Siegel, P.H. Terahertz technology. IEEE Trans. Microw. Theory Technol. 2002, 50, 910–928. [Google Scholar] [CrossRef]
- Lv, H.; Yang, Z.; Ong, S.J.H.; Wei, C.; Liao, H.; Xi, S.; Du, Y.; Ji, G.; Xu, Z.J. A flexible microwave shield with tunable frequency-transmission and electromagnetic compatibility. Adv. Funct. Mater. 2019, 29, 1900163. [Google Scholar] [CrossRef]
- You, X.; Ako, R.T.; Sriram, S.; Withayachumnankul, W. 3D Terahertz Confocal Imaging with Chromatic Metasurface. Laser Photonics Rev. 2025, 19, 2401011. [Google Scholar] [CrossRef]
- Huang, Z.; Wang, Z.; Cheng, Y.; Li, X.; Wang, J.; Zhou, L.; Xu, H.; Luo, X.; Lin, C. Metasurfaces Empower Optical Multiparameter Imaging: A Review. Sci. China Phys. Mech. Astron. 2025, 68, 274201. [Google Scholar] [CrossRef]
- Li, L.; Cui, T.; Ji, W.; Liu, S.; Ding, J.; Wan, X.; Bo, Z.; Wan, W.; Qiu, C.W. Electromagnetic reprogrammable coding-metasurface holograms. Nat. Commun. 2017, 8, 197. [Google Scholar] [CrossRef]
- Chen, T.; Li, J.; Cai, T.; Xu, H.; Xu, Q. Design of a reconfigurable broadband greyscale multiplexed metasurface hologram. Appl. Opt. 2020, 59, 3660–3665. [Google Scholar] [CrossRef] [PubMed]
- Lin, K.T.; Lin, H.; Yang, T.; Jia, B.; Wu, J. Structured graphene metamaterial selective absorbers for high efficiency and omnidirectional solar thermal energy conversion. Nat. Commun. 2020, 11, 1389. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Liu, H.; Zhu, J. Solar thermophotovoltaics: Progress, challenges, and opportunities. APL Mater. 2019, 7, 080906. [Google Scholar] [CrossRef]
- Pendry, J.B. Photonics—Metamaterials in the sunshine. Nat. Mater. 2006, 5, 599–600. [Google Scholar] [CrossRef]
- Lenert, A.; Bierman, D.M.; Nam, Y.; Chan, W.R.; Celanovic, I.; Soljačić, M.; Wang, E.N. A nanophotonic solar thermophotovoltaic device. Nat. Nanotechnol. 2014, 9, 126–130. [Google Scholar] [CrossRef]
- Schurig, D.; Mock, J.J.; Justice, B.J.; Cummer, S.A.; Pendry, J.B.; Starr, A.F.; Smith, D.R. Metamaterial electromagnetic cloak at microwave frequencies. Science 2006, 314, 977–980. [Google Scholar] [CrossRef]
- Landy, N.I.; Sajuyigbe, S.; Mock, J.J.; Smith, D.R.; Padilla, W.J. Perfect metamaterial absorber. Phys. Rev. Lett. 2008, 100, 207402. [Google Scholar] [CrossRef]
- Nemati, A.; Wang, Q.; Hong, M.; Teng, J. Tunable and reconfigurable metasurfaces and metadevices. Opto Electron. Adv. 2019, 2, 180009. [Google Scholar] [CrossRef]
- Wang, X.C.; Tretyakov, S.A. Tunable perfect absorption in continuous graphene sheets on metasurface substrates. arXiv 2017, arXiv:1712.01708. [Google Scholar]
- Shen, N.H.; Massaouti, M.; Gokkavas, M.; Manceau, J.M.; Ozbay, E.; Kafesaki, M.; Soukoulis, C.M.; Tzortzakis, S. Optically implemented broadband blueshift switch in the terahertz regime. Phys. Rev. Lett. 2011, 106, 037403. [Google Scholar] [CrossRef] [PubMed]
- Li, J.S.; Yan, D.X.; Sun, J.Z. Flexible dual-band all-graphene-dielectric terahertz absorber. Opt. Mater. Express 2019, 9, 2067–2075. [Google Scholar] [CrossRef]
- Zhou, M.Y.; Chen, Y.B.; He, Y.G.; Yang, C. Ultra-thin and broadband P-band metamaterial absorber based on carbonyl iron powder composites. Materials 2024, 17, 1157. [Google Scholar] [CrossRef]
- Cai, Z.; Wu, C.; Jiang, J.; Xu, Q.; Guo, K.; Li, H.; Li, H. Phase-change metasurface for switchable vector vortex beam generation. Opt. Express 2021, 29, 42762–42771. [Google Scholar] [CrossRef]
- Zhao, Y.T.; Wu, B.; Huang, B.J.; Zhu, W.; Liu, Z.M.; Xiao, S. Switchable broadband terahertz absorber/reflector enabled by hybrid graphene-gold metasurface. Opt. Express 2017, 25, 7161–7169. [Google Scholar] [CrossRef]
- Kaveev, A.K.; Kropotov, G.I.; Tsygankova, E.V.; Andrianov, A.V.; Kudrin, A.V. Terahertz polarization conversion with quartz waveplate sets. Appl. Opt. 2013, 52, B60–B69. [Google Scholar] [CrossRef]
- Wang, Y.; Cheng, H.F.; Wang, J.; Zhou, Y.J. Infrared emissivity of capacitive frequency-selective surfaces and its application in radar and IR compatible stealth sandwich structures. Adv. Mater. Res. 2011, 382, 65–69. [Google Scholar] [CrossRef]
- Tian, H.; Liu, H.T.; Cheng, H.F. A thin radar-infrared stealth-compatible structure: Design, fabrication, and characterization. Chin. Phys. B 2014, 23, 025201. [Google Scholar] [CrossRef]
- Li, J.; Xu, Z.; Li, T.; Zhang, H.; Liu, Y.; Liu, P. Multifunctional antimony tin oxide/reduced graphene oxide aerogels with wideband microwave absorption and low infrared emissivity. Compos. Part B Eng. 2021, 231, 109565. [Google Scholar] [CrossRef]
- Yue, S.; Hou, M.; Wang, R.; Guo, H.; Hou, Y.; Li, M.; Zhang, Z.; Wang, Y.; Zhang, Z. Ultra-broadband metamaterial absorber from ultraviolet to long-wave infrared based on CMOS-compatible materials. Opt. Express 2020, 28, 31844–31861. [Google Scholar] [CrossRef] [PubMed]
- Xu, Z.; Luo, H.; Zhu, H.; Zhang, J.; Xu, H.; Wang, W.; Li, J. Nonvolatile optically reconfigurable radiative metasurface with visible tunability for anticounterfeiting. Nano Lett. 2021, 21, 5269–5276. [Google Scholar] [CrossRef]
- Haxha, S.; AbdelMalek, F.; Ouerghi, F.; AbdelMalek, Z.; Liu, S.; Chen, W. Metamaterial superlenses operating at visible wavelength for imaging applications. Sci. Rep. 2018, 8, 16119. [Google Scholar] [CrossRef]
- Zhang, Z.; Yu, Z.; Liang, Y.; Wang, Y.; Xu, J.; Yang, H. Dual-band nearly perfect absorber at visible frequencies. Opt. Mater. Express 2018, 8, 463–468. [Google Scholar] [CrossRef]
- Fei, Y.; Wang, X.; Wang, F.; Liu, Z.; Zhao, J.; Wu, L. Covalent coupling induced-polarization relaxation in MXene-based terahertz absorber for realizing dual band absorption. Chem. Eng. J. 2023, 461, 142049. [Google Scholar] [CrossRef]
- Chen, H.; Huang, Z.; Huang, Y.; Zhang, Y.; Ge, Z.; Ma, W.; Zhang, T.; Wu, M.; Xu, S.; Fan, F.; et al. Consecutively strong absorption from gigahertz to terahertz bands of a monolithic three-dimensional Fe3O4/graphene material. ACS Appl. Mater. Interfaces 2019, 11, 1274–1282. [Google Scholar] [CrossRef]
- Sun, X.; Chen, S.; Kuang, C.; Zhang, Y.; Zhou, X.; Li, J. Gradient-reduced graphene oxide aerogel with ultrabroadband absorption from microwave to terahertz bands. ACS Appl. Nano Mater. 2023, 6, 1170–1180. [Google Scholar] [CrossRef]
- Zhai, Z.; Zhang, L.; Li, X.; Xiao, S. Tunable terahertz broadband absorber based on a composite structure of graphene multilayer and silicon strip array. Opt. Commun. 2019, 431, 199–202. [Google Scholar] [CrossRef]
- Pendry, J.B.; Schurig, D.; Smith, D.R. Controlling electromagnetic fields. Science 2006, 312, 1780–1782. [Google Scholar] [CrossRef]
- Jing, X.; Feng, D.; Tian, Y.; Li, H.; Zhang, Q. Design of two invisibility cloaks using transmissive and reflective metamaterial-based multilayer frame microstructures. Opt. Express 2020, 28, 35528–35539. [Google Scholar] [CrossRef]
- Chen, W.; Balanis, C.A.; Birtcher, C.R. Dual wide-band checkerboard surfaces for radar cross section reduction. IEEE Trans. Antennas Propag. 2016, 64, 4133–4138. [Google Scholar] [CrossRef]
- Qiu, Y.; Zhang, P.; Li, Q.; Wang, L.; Chen, H. A perfect selective metamaterial absorber for high-temperature solar energy harvesting. Sol. Energy 2021, 230, 51–59. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, Y.; Wang, J.; Li, Q. 3D/4D printed tunable electrical metamaterials with more sophisticated structures. J. Mater. Chem. C 2021, 9, 10816–10824. [Google Scholar] [CrossRef]
- Watts, C.M.; Liu, X.; Padilla, W.J. Metamaterial electromagnetic wave absorbers. Adv. Mater. 2012, 24, OP98–OP120. [Google Scholar] [CrossRef]
- Liu, M.; Susli, M.; Silva, D.; Putrino, G.; Kala, H.; Fan, S.; Cole, M.; Faraone, L.; Wallace, V.P.; Padilla, W.J.; et al. Ultrathin tunable terahertz absorbers based on electrostatically actuated metamaterial. In Proceedings of the SPIE 11160, Electro-Optical and Infrared Systems: Technology and Applications XVI, Strasbourg, France, 9–12 September 2019. [Google Scholar] [CrossRef]
- Mou, N.L.; Tang, B.; Li, J.Z.; Zhang, Y.Q.; Dong, H.X.; Zhang, L. Demonstration of Thermally Tunable Multi-Band and Ultra-Broadband Metamaterial Absorbers Maintaining High Efficiency during Tuning Process. Materials 2021, 14, 5708. [Google Scholar] [CrossRef]
- Chen, M.; Yu, X.-X. Frequency shift in tunable electromagnetically induced transparency-like metamaterials. Plasmonics 2024, 19, 1487–1498. [Google Scholar] [CrossRef]
- Liu, Y.; Li, C.; Fang, B.; Chen, L.; Xu, J.; Liu, F.; Xu, L.; Li, X.; Tang, Y.; Hong, Z.; et al. Research Progress in Tunable Metamaterial Absorbers. Adv. Photonics Res. 2023, 5, 2300258. [Google Scholar] [CrossRef]
- He, X.J.; Wang, Y.; Wang, J.; Fan, K.; Zhang, W. Dual-band terahertz metamaterial absorber with polarization insensitivity and wide incident angle. Prog. Electromagn. Res. 2011, 115, 381–397. [Google Scholar] [CrossRef]
- Zhang, C.L.; Huang, C.; Pu, M.B.; Song, J.K.; Luo, X.G. Tunable Absorbers Based on an Electrically Controlled Resistive Layer. Plasmonics 2019, 14, 327–333. [Google Scholar] [CrossRef]
- Zhou, F.; Qin, F.; Yi, Z.; Yao, W.; Liu, Z.; Wu, X.; Wu, P.; Zhou, F. Ultra-wideband and wide-angle perfect solar energy absorber based on Ti nanorings surface plasmon resonance. Phys. Chem. Chem. Phys. 2021, 23, 17041–17048. [Google Scholar] [CrossRef]
- Li, W.W.; Xu, M.Z.; Xu, H.X.; Wang, X.W.; Huang, W. Metamaterial Absorbers: From Tunable Surface to Structural Transformation. Adv. Mater. 2022, 34, 2202509. [Google Scholar] [CrossRef] [PubMed]
- Aieta, F.; Genevet, P.; Kats, M.A.; Yu, N.; Blanchard, R.; Gaburro, Z.; Capasso, F. Aberration-Free Ultrathin Flat Lenses and Axicons at Telecom Wavelengths Based on Plasmonic Metasurfaces. Nano Lett. 2012, 12, 4932–4936. [Google Scholar] [CrossRef] [PubMed]
- Ni, X.; Wong, Z.J.; Mrejen, M.; Wang, Y.; Zhang, X. An ultrathin invisibility skin cloak for visible light. Science 2015, 349, 1310–1314. [Google Scholar] [CrossRef]
- Liu, K.; Kilpela, J.P. Optimized Absorber Designs for Electromagnetic Compatibility Applications. In Proceedings of the 1993 IEEE International Symposium on Electromagnetic Compatibility, Dallas, TX, USA, 9–13 August 1993; pp. 273–278. [Google Scholar] [CrossRef]
- Lee, H.; Xiong, Y.; Fang, N.; Zhang, X. Realization of optical superlens imaging below the diffraction limit. New J. Phys. 2005, 7, 255. [Google Scholar] [CrossRef]
- Xu, X.; Jiang, J.; Miao, L.; Liu, H.; Huang, Y. Design of tunable metamaterial absorbers based on PIN diodes. IEICE Electron. Express 2012, 9, 1408–1413. [Google Scholar] [CrossRef][Green Version]
- Wen, D.; Yue, F.; Li, G.; Zheng, G.; Chan, K.; Chen, S.; Chen, M.; Li, K.F.; Wong, P.W.H.; Cheah, K.W.; et al. Helicity multiplexed broadband metasurface holograms. Nat. Commun. 2015, 6, 8241. [Google Scholar] [CrossRef]
- Zheng, G.; Mühlenbernd, H.; Kenney, M.; Li, G.; Zentgraf, T.; Zhang, S. Metasurface holograms reaching 80% efficiency. Nat. Nanotechnol. 2015, 10, 308–312. [Google Scholar] [CrossRef]
- Zhou, H.; Qu, S.; Lin, B.; Zhang, J.; Chen, H. Filter-Antenna Consisting of Conical FSS Radome and Monopole Antenna. IEEE Trans. Antennas Propag. 2012, 60, 3040–3045. [Google Scholar] [CrossRef]
- Shang, Y.; Shen, Z.; Xiao, S. On the Design of Single-Layer Circuit Analog Absorber Using Double-Square-Loop Array. IEEE Trans. Antennas Propag. 2013, 61, 6022–6029. [Google Scholar] [CrossRef]
- Chen, Y.; Sun, G.; Wei, J.; Wang, L.; Liu, Y. Graphene-enhanced polarization-independent high-Q terahertz metamaterial absorber with tunability for sensing applications. Opt. Commun. 2024, 557, 130311. [Google Scholar] [CrossRef]
- Kaur, K.P.; Upadhyaya, T.; Patel, U.; Sorathiya, V.; Alwabli, A.; Jaffar, A.Y. Ultra-thin, Polarization-Insensitive, and Conformal Metamaterial-Based Sensor with High Q-Factor. Appl. Phys. A 2024, 130, 930. [Google Scholar] [CrossRef]
- Zhang, M.; Song, Z. Terahertz Bifunctional Absorber Based on a Graphene-Spacer-Vanadium Dioxide-Spacer-Metal Configuration. Opt. Express 2020, 28, 11780–11788. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; Wei, G.; Zhou, H.; Xiao, H.; Qin, M.; Xia, S.; Wu, F. Polarization-Independent Near-Infrared Superabsorption in Transition Metal Dichalcogenide Huygens Metasurfaces by Degenerate Critical Coupling. Phys. Rev. B 2022, 105, 165305. [Google Scholar] [CrossRef]
- Wang, T.L.; Cao, M.Y.; Zhang, H.Y. Tunable terahertz metamaterial absorber based on Dirac semimetal films. Appl. Opt. 2018, 57, 9555–9561. [Google Scholar] [CrossRef]
- Duan, G.; Wu, Y.; Zhu, H.; Zhang, X.; Wang, B.-X. Triple-band tunable terahertz metamaterial absorber enabled by surface design of goggles-like structure using two identical VO2 square frames connected by a VO2 horizontal connecting strip. Results Opt. 2023, 10, 100370. [Google Scholar] [CrossRef]
- Azevedo, F.D.; Fioueiredo, D.; Moraes, F.; Berche, B.; Fumeron, S. Optical concentrator from a hyperbolic liquid-crystal metamaterial. EPL 2018, 124, 34006. [Google Scholar] [CrossRef]
- Zheng, L.; Feng, R.; Shi, H.; Li, X. Tunable broadband terahertz metamaterial absorber based on vanadium dioxide and graphene. Micromachines 2023, 14, 1715. [Google Scholar] [CrossRef]
- Zou, Y.K.; Lin, H.Y.; Wu, Y.K.; Zhu, H.X.; Zhang, X.Y.; Wang, B.X. Theoretical Investigation of an Ultra-Wideband Tunable Metamaterial Absorber Based on Four Identical Vanadium Dioxide Resonators in the Terahertz Band. J. Electron. Mater. 2023, 52, 2852–2864. [Google Scholar] [CrossRef]
- Li, Y.; Wang, X.; Zhang, Y. Development of a tunable broadband metamaterial absorber based on joint modulation of graphene and photosensitive silicon in the terahertz region. Mater. Sci. Semicond. Process. 2023, 164, 107622. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, J.; Yuan, L.L.H. Dynamically tunable multifunctional terahertz absorber based on hybrid vanadium dioxide and graphene metamaterials. Appl. Opt. 2024, 63, 1385–1393. [Google Scholar] [CrossRef]
- Zhang, Y.; Feng, Y.; Zhu, B.; Zhu, B.; Zhao, J.; Jiang, T. Graphene based tunable metamaterial absorber and polarization modulation in terahertz frequency. Opt. Express 2014, 22, 22743. [Google Scholar] [CrossRef]
- Xu, Z.; Wu, D.; Liu, Y.; Liu, C.; Yu, Z.; Yu, L.; Ye, H. Design of a tunable ultra-broadband terahertz absorber based on multiple layers of graphene ribbons. Nanoscale Res. Lett. 2018, 13, 143. [Google Scholar] [CrossRef] [PubMed]
- Bai, J.; Shen, W.; Shi, J.; Xu, W.; Zhang, S.; Chang, S. A non-volatile tunable terahertz metamaterial absorber using graphene floating gate. Micromachines 2021, 12, 333. [Google Scholar] [CrossRef] [PubMed]
- Chen, F.; Cheng, Y.; Luo, H. A broadband tunable terahertz metamaterial absorber based on single-layer complementary gammadion-shaped graphene. Materials 2020, 13, 860. [Google Scholar] [CrossRef]
- Xu, H.-X.; Tang, S.; Ma, S.; Luo, W.; Cai, T.; Sun, S.; He, Q.; Zhou, L. Tunable microwave metasurfaces for high-performance operations: Dispersion compensation and dynamical switch. Sci. Rep. 2016, 6, 38255. [Google Scholar] [CrossRef]
- Huang, Y.; Lan, Y.H.; Zhong, S.C.; Sun, F.W.; Zhong, Y.J.; Lin, T.L.; Zeng, Q.M.; Chen, X.F. Design of Tunable Dual-Band Terahertz Metamaterial Absorber With Liquid Crystal Integrated On-Chip. Ieee Trans. Plasma Sci. 2024, 52, 4993–5000. [Google Scholar] [CrossRef]
- Wang, L.; Ge, S.; Hu, W.; Nakajima, M.; Lu, Y. Graphene-assisted high-efficiency liquid crystal tunable terahertz metamaterial absorber. Opt. Express 2017, 25, 23873–23879. [Google Scholar] [CrossRef]
- Kowerdziej, R.; Wróbel, J.; Kula, P. Ultrafast electrical switching of nanostructured metadevice with dual-frequency liquid crystal. Sci. Rep. 2019, 9, 20367. [Google Scholar] [CrossRef]
- Yin, Z.; Lu, Y.; Xia, T.; Lai, W.; Yang, J.; Lu, H.; Deng, G. Electrically tunable terahertz dual-band metamaterial absorber based on a liquid crystal. RSC Adv. 2018, 8, 4197–4203. [Google Scholar] [CrossRef]
- Gao, R.; Xue, Y.; Wang, Z.; Chen, G.; Fu, C.; Deng, X.; Lei, X.; Cai, W. Effect of particle size on magnetodielectric and magnetoelectric coupling effect of CoFe2O4@BaTiO3 composite fluids. J. Mater. Sci. Mater. Electron. 2020, 10, 9026–9036. [Google Scholar] [CrossRef]
- Chen, B.-W.; Hatamie, S.; Chiu, H.-C.; Wei, Z.-H.; Hu, S.-H.; Yao, D.-J. Shape-mediated magnetocrystalline anisotropy and relaxation controls by cobalt ferrite core–shell heterostructures for magnetothermal penetration delivery. Adv. Mater. Interfaces 2022, 9, 2270068. [Google Scholar] [CrossRef]
- Pai, C.; Varma, V.B.; Srinivasan, R.; Nagarajan, R.; Ramanujan, R.V. Control of magnetofluidic laser scattering of aqueous magnetic fluids. IEEE Magn. Lett. 2017, 8, 6508105. [Google Scholar] [CrossRef]
- Yu, B.; Huang, L.; Li, X.; Wang, Y. Magnetically controllable metasurface and its application. Front. Optoelectron. 2021, 14, 16. [Google Scholar] [CrossRef]
- Kim, J.; Carnemolla, E.G.; DeVault, C.T.; Shaltout, A.M.; Faccio, D.; Shalaev, V.M.; Kildishev, A.V.; Ferrera, M.; Boltasseva, A. Dynamic control of nanocavities with tunable metal oxides. Nano Lett. 2017, 18, 740–746. [Google Scholar] [CrossRef]
- Kaushik, V.; Rajput, S.; Babu, P.; Pandey, S.K.; Mishra, R.D.; Ren, H.; Maier, S.A.; Sorger, V.J.; Dalir, H.; Kumar, M. Electronically controlled semiconductor nanoparticle array for tunable plasmonic metasurfaces. J. Light. Technol. 2024, 42, 6. [Google Scholar] [CrossRef]
- Dhama, R.; Panahpour, A.; Pihlava, T.; Ghindani, D.; Caglayan, H. All-optical switching via coherent control of plasmon resonances. arXiv 2021, arXiv:2111.07260. [Google Scholar]
- Wang, H.; Hu, Z.; Deng, J.; Zhang, X.; Chen, J.; Li, K.; Li, G. All-optical ultrafast polarization switching with nonlinear plasmonic metasurfaces. Sci. Adv. 2024, 10, 7. [Google Scholar] [CrossRef]
- Wang, X.; Wang, X.; Xin, J.; Li, J.; Ren, Q.; Cai, H.; Lang, Y.; Lan, Z.; Jia, Y.; Jin, R.; et al. Tailoring the bound states in the multi-channel nonlinear plasmonic metasurfaces. Opt. Commun. 2023, 549, 7. [Google Scholar] [CrossRef]
- Jin, B.; Guo, T.; Argyropoulos, C. Enhanced third harmonic generation with graphene metasurfaces. J. Opt. 2017, 19, 094005. [Google Scholar] [CrossRef]
- Marni, M.; Ceglia, D. Strong modulation of absorption and third-harmonic generation in resonant metasurfaces based on VO2. In Proceedings of the 9th International Conference on Photonics, Optics and Laser Technology - PHOTOPTICS, Online Streaming, 10–13 February 2021; 2021; 1, pp. 40–45. [Google Scholar] [CrossRef]
- Murzin, S.P. Digital engineering in diffractive optics for precision laser processing. Photonics 2025, 12, 306. [Google Scholar] [CrossRef]
- Klein, C.A. Thermally induced optical distortion in high-energy laser systems. Opt. Eng. 1979, 18, 591–601. [Google Scholar] [CrossRef]
- Xu, H.; Ma, R.; Zhu, Y.; Zhang, J.; Li, Y.; Wang, X.; Liu, Z.; Zhang, X.; Wang, H.; Zhang, Y. Chirality-Controlled Second-Order Nonlinear Frequency Conversion in Lithium Niobate Film Metasurfaces. Opt. Lett. 2024, 49, 6405–6408. [Google Scholar] [CrossRef] [PubMed]
- Pura, J.L.; Souto, J.; Jiménez, J. Effect of thermal lensing and micrometric degraded regions on the catastrophic optical damage process of high-power laser diodes. Opt. Lett. 2020, 45, 1667–1670. [Google Scholar] [CrossRef] [PubMed]
- Kowerdziej, R.; Parka, J.; Krupka, J. Experimental study of thermally controlled metamaterial containing a liquid crystal layer at microwave frequencies. Liq. Cryst. 2011, 38, 743–747. [Google Scholar] [CrossRef]
- Pang, Y.; Wang, J.; Cheng, Q.; Xia, S.; Zhou, X.Y.; Xu, Z.; Cui, T.J.; Qu, S. Thermally tunable water-substrate broadband metamaterial absorbers. Appl. Phys. Lett. 2017, 110, 104103. [Google Scholar] [CrossRef]
- Luo, H.; Wang, X.; Qian, H. Tunable terahertz dual-band perfect absorber based on the combined InSb resonator structures for temperature sensing. J. Opt. Soc. Am. B Opt. Phys. 2021, 38, 2638–2644. [Google Scholar] [CrossRef]
- Zhang, F.; Chen, L.; Wang, Y.; Zhao, Q.; He, X.; Chen, K. Thermally tunable electric mie resonance of dielectric cut-wire type metamaterial. Opt. Express 2014, 22, 24908–24913. [Google Scholar] [CrossRef]
- Wang, L.; Xia, D.; Fu, Q.; Wang, Y.; Ding, X.; Yang, B. Thermally tunable ultra-thin metamaterial absorber at P band. J. Electromagn. Waves Appl. 2019, 33, 1406–1415. [Google Scholar] [CrossRef]
- Li, H.; Zhang, Y.; Xiao, H.; Liu, X.; Sun, W.; Xu, Q. Investigation of Acoustic Plasmons in Vertically Stacked Metal/Dielectric/Graphene Heterostructures for Multiband Coherent Perfect Absorption. Opt. Express 2020, 28, 37577–37586. [Google Scholar] [CrossRef]
- Arbabi, E.; Arbabi, A.; Kamali, S.M.; Horie, Y.; Faraji-Dana, M.S.; Faraon, A. MEMS-tunable dielectric metasurface lens. Nat. Commun. 2017, 9, 812. [Google Scholar] [CrossRef]
- He, S.; Yang, H.; Jiang, Y.; Deng, W.; Zhu, W. Recent advances in MEMS metasurfaces and their applications on tunable lenses. Micromachines 2019, 10, 505. [Google Scholar] [CrossRef] [PubMed]
- Meng, C.; Thrane, P.C.V.; Wang, C.; Ding, F.; Bozhevolnyi, S.I. MEMS-tunable topological bilayer metasurfaces for reconfigurable dual-state phase control. Optica 2024, 11, 15231–15244. [Google Scholar] [CrossRef]
- Deng, Y.; Meng, C.; Thrane, P.C.V.; im Sande, S.; Bozhevolnyi, S.I.; Ding, F. MEMS-integrated metasurfaces for dynamic linear polarizers. Optica 2024, 11, 7. [Google Scholar] [CrossRef]
- Yu, B.; Zhou, H.-W.; Cheng, Q. Design and Simulation of Tunable Infrared Absorber Based on Flexible Metasurface. J. Nanoelectron. Optoelectron. 2022, 17, 883–887. [Google Scholar] [CrossRef]
- Lin, Y.S. Stretchable IR metamaterial with ultra-narrowband perfect absorption. Appl. Phys. Lett. 2018, 113, 101907. [Google Scholar] [CrossRef]
- Nogales, A.; Del Campo, A.; Ezquerra, T.; Rodriguez-Hernández, J. Wrinkling and folding on patched elastic surfaces: Modulation of the chemistry and pattern size of microwrinkled surfaces. ACS Appl. Mater. Interfaces 2017, 7, acsami. [Google Scholar] [CrossRef]
- Xu, X.; He, S.; Wang, C.; Chen, X.; Wang, Z.; Song, J. Origami-Inspired Chiral Metamaterials with Tunable Circular Dichroism through Mechanically-Guided 3D Assembly. J. Appl. Mech. 2023, 90, 011007. [Google Scholar] [CrossRef]
- Sunny, V.; Kurian, P.; Mohanan, P.; Joy, P.A. A Flexible Microwave Absorber Based on Nickel Ferrite Nanocomposite. J. Alloys Compd. 2010, 489, 297–303. [Google Scholar] [CrossRef]
- Cai, H.; Chen, S.; Zou, C.; Huang, Q.; Liu, Y.; Hu, X.; Fu, Z.; Zhao, Y.; He, H.; Lu, Y. Multifunctional hybrid metasurfaces for dynamic tuning of terahertz waves. Adv. Opt. Mater. 2018, 6, 1800257. [Google Scholar] [CrossRef]
- Jeong, H.; Tentzeris, M.M.; Lim, S. Frequency-Tunable Electromagnetic Absorber by Mechanically Controlling Substrate Thickness. Int. J. Antennas Propag. 2018, 2018, 1963051. [Google Scholar] [CrossRef]
- Ma, W.; Wang, G.; Zong, B.-F.; Zhuang, Y.; Zhang, X. Mechanically reconfigurable antenna based on novel metasurface for frequency tuning-range improvement. In Proceedings of the 2016 IEEE International Conference on Microwave and Millimeter Wave Technology (ICMMT), Beijing, China, 5–8 June 2016; pp. 629–631. [Google Scholar] [CrossRef]
- Dong, F.-Y.; Shao, L.; Niu, C.; Zhu, W. Optically transparent microwave metamaterial absorbers. J. Opt. 2025, 27, 4. [Google Scholar] [CrossRef]
- Xiong, X.; Zhang, H.; Lv, H.; Yang, L.; Liang, G.; Zhang, J.; Lai, Y.; Cheng, H.-W.; Che, R. Recent progress in carbon-based materials and loss mechanisms for electromagnetic wave absorption. Carbon 2024, 219, 118834. [Google Scholar] [CrossRef]
- Kats, M.A.; Sharma, D.; Lin, J.; Genevet, P.; Blanchard, R.; Yang, Z.; Qazilbash, M.M.; Basov, D.N.; Ramanathan, S.; Capasso, F. Ultra-Thin Perfect Absorber Employing a Tunable Phase Change Material. Appl. Phys. Lett. 2012, 101, 221101. [Google Scholar] [CrossRef]
- Meng, Z.; Liu, D.; Xing, S.; Pang, Y.; Jia, Y.; Li, M.; Zu, M.; Wang, Z.; Liu, T.; Cheng, H. Tunable Microwave Absorbing Devices Enabled by Reversible Metal Electrodeposition. ACS Appl. Mater. Interfaces 2024, 16, 11686–11693. [Google Scholar] [CrossRef]
- Lu, Z.A.; Zhang, Y.L.; Wang, H.Y.; Xia, C.; Liu, Y.F.; Dou, S.L.; Li, Y.; Tan, J.B. Transparent Thermally Tunable Microwave Absorber Prototype Based on Patterned VO2 Film. Engineering 2023, 29, 198–206. [Google Scholar] [CrossRef]
- Zhang, J.; Lu, W.B.; Chen, H.; Liu, Z.G. Tunable ultra-wideband microwave absorber based on multilayer graphene resistive loops. In Proceedings of the 2017 Sixth Asia-Pacific Conference on Antennas and Propagation (APCAP), Xi’an, China, 16–19 October 2017; pp. 1–3. [Google Scholar] [CrossRef]
- Sen, G.; Ghosh, A.; Das, S. Design of a dual-band independently tunable microwave absorber. In Proceedings of the 2019 International Conference on Wireless Communications Signal Processing and Networking (WiSPNET), Chennai, India, 21–23 March 2019; pp. 233–235. [Google Scholar] [CrossRef]
- Wang, P.; Tao, H.; Han, W.L.; Zhang, C.R.; Xu, Y.J.; Wang, Q.L. Polarization-insensitive, frequency- and amplitude-tunable transparent microwave absorber based on graphene metasurface. J. Appl. Phys. 2024, 135, 043103. [Google Scholar] [CrossRef]
- Xu, W.; Sonkusale, S. Microwave Diode Switchable Metamaterial Reflector/Absorber. Appl. Phys. Lett. 2013, 103, 031902. [Google Scholar] [CrossRef]
- An, S.; Xu, H.; Zhang, Y.; Wu, S.; Jiang, J.; He, Y.; Miao, L. Design of a Polarization-Insensitive Wideband Tunable Metamaterial Absorber Based on Split Semi-Circle Ring Resonators. J. Appl. Phys. 2017, 122, 025113. [Google Scholar] [CrossRef]
- Song, X.; Yang, W.; Qu, K.; Bai, X.; Chen, K.; Feng, Y.; Zhu, W. Switchable metasurface for nearly perfect reflection, transmission, and absorption using PIN diodes. Opt. Express 2021, 29, 29320–29328. [Google Scholar] [CrossRef]
- Shadrivov, I.; Morrison, S.K.; Kivshar, Y.S. Tunable Split-Ring Resonators for Nonlinear Negative-Index Metamaterials. Opt. Express 2006, 14, 9344–9349. [Google Scholar] [CrossRef]
- Zhao, J.; Cheng, Q.; Chen, J.; Qi, M.-Q.; Jiang, W.X.; Cui, T.J. A Tunable Metamaterial Absorber Using Varactor Diodes. New J. Phys. 2013, 15, 043049. [Google Scholar] [CrossRef]
- Zhang, J.; Wei, X.; Rukhlenko, I.D.; Chen, H.T.; Zhu, W. Electrically tunable metasurface with independent frequency and amplitude modulations. ACS Photonics 2020, 7, 265–271. [Google Scholar] [CrossRef]
- Yan, L.; Wang, J.; Ye, Y.; Hao, Z.; Liu, Q.; Li, F. Broadband and Thin Microwave Absorber of Nickel–Zinc Ferrite/Carbonyl Iron Composite. J. Alloys Compd. 2009, 487, 708–711. [Google Scholar] [CrossRef]
- Ederer, C.; Spaldin, N.A. Weak Ferromagnetism and Magnetoelectric Coupling in Bismuth Ferrite. Phys. Rev. B 2005, 71, 060401. [Google Scholar] [CrossRef]
- Kang, L.; Zhao, Q.; Zhao, H.; Zhou, J. Magnetically Tunable Negative Permeability Metamaterial Composed by Split Ring Resonators and Ferrite Rods. Opt. Express 2008, 16, 8825. [Google Scholar] [CrossRef]
- Zhao, H.; Zhou, J.; Kang, L.; Zhao, Q. Tunable two-dimensional left-handed material consisting of ferrite rods and metallic wires. Opt. Express 2009, 17, 13373–13380. [Google Scholar] [CrossRef]
- Yang, Y.-J.; Huang, Y.-J.; Wen, G.-J.; Zhong, J.-P.; Sun, H.-B.; Gordon, O. Tunable Broadband Metamaterial Absorber Consisting of Ferrite Slabs and a Copper Wire. Chin. Phys. B 2012, 21, 038501. [Google Scholar] [CrossRef]
- Huang, Y.; Wen, G.; Zhu, W.; Li, J.; Si, L.-M.; Premaratne, M. Experimental Demonstration of a Magnetically Tunable Ferrite-Based Metamaterial Absorber. Opt. Express 2014, 22, 16408–16417. [Google Scholar] [CrossRef]
- Li, W.; Wei, J.; Wang, W.; Hu, D.; Li, Y.; Guan, J. Ferrite-based metamaterial microwave absorber with absorption frequency magnetically tunable in a wide range. Mater. Des. 2016, 110, 27–34. [Google Scholar] [CrossRef]
- Lei, M.; Feng, N.; Wang, Q.; Hao, Y.; Huang, S.; Bi, K. Magnetically Tunable Metamaterial Perfect Absorber. J. Appl. Phys. 2016, 119, 205103. [Google Scholar] [CrossRef]
- Le, D.H.; Lim, S. Four-Mode Programmable Metamaterial Using Ternary Foldable Origami. ACS Appl. Mater. Interfaces 2019, 11, 28554–28561. [Google Scholar] [CrossRef]
- Chen, X.; Li, W.; Wu, Z.; Zhang, Z.; Zou, Y. Origami-Based Microwave Absorber with a Reconfigurable Bandwidth. Opt. Lett. 2021, 46, 1349–1352. [Google Scholar] [CrossRef]
- Chung, M.; Jeong, H.; Kim, Y.-K.; Lim, S.; Baek, C.-W. Design and fabrication of millimeter-wave frequency-tunable metamaterial absorber using MEMS cantilever actuators. Micromachines 2022, 13, 1354. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Zhu, L.; Kasuga, T.; Nogi, M.; Koga, H. Frequency-tunable and absorption/transmission-switchable microwave absorber based on a chitin-nanofiber-derived elastic carbon aerogel. Chem. Eng. J. 2023, 469, 8. [Google Scholar] [CrossRef]
- Lim, D.D.; Ibarra, A.; Lee, J.; Jung, J.; Choi, W.; Gu, G.X. A Tunable Metamaterial Microwave Absorber Inspired by Chameleon’s Color-Changing Mechanism. Sci. Adv. 2025, 11, eads3499. [Google Scholar] [CrossRef]
- Qiao, S.; Luo, J.; Fang, X.; Wu, Z.; Zeng, Y.; Yang, Y.; Xue, Q.; Xiong, J.; Fei, H.; Zou, Y. A Rotatable Tunable Ultra-Wideband Microwave Absorber and Simple Coding Application of Gradient Structure. J. Phys. D Appl. Phys. 2025, 58, 58. [Google Scholar] [CrossRef]
- Tonouchi, M. Cutting-edge terahertz technology. Nat. Photonics 2007, 1, 97–105. [Google Scholar] [CrossRef]
- Fang, P.; Shi, X.; Liu, C.; Zhai, X.; Li, H.; Wang, L. Single- and dual-band convertible terahertz absorber based on bulk Dirac semimetal. Opt. Commun. 2020, 462, 125333. [Google Scholar] [CrossRef]
- Ri, K.J.; Pak, D.S.; Ri, C.H. Simple Design of a Tunable Quadruple-Broadband Terahertz Metamaterial Absorber Based on VO2. Adv. Mater. 2023, 12, 45–52. [Google Scholar] [CrossRef]
- Ge, J.H.; Zhang, Y.Q.; Li, H.N.; Dong, H.X.; Zhang, L. Ultra-Broadband, Tunable, and Transparent Microwave Meta-Absorber Using ITO and Water Substrate. Adv. Opt. Mater. 2023, 11, 2202873. [Google Scholar] [CrossRef]
- Liu, H.; Wang, Z.-H.; Li, L.; Fan, Y.-X.; Tao, Z.-Y. Vanadium Dioxide-Assisted Broadband Tunable Terahertz Metamaterial Absorber. Sci. Rep. 2019, 9, 5751. [Google Scholar] [CrossRef] [PubMed]
- Zhou, S.; Shen, Z.; Kang, R.; Ge, S.; Hu, W. Liquid Crystal Tunable Dielectric Metamaterial Absorber in the Terahertz Range. Appl. Sci. 2018, 8, 2211. [Google Scholar] [CrossRef]
- Wu, B.; Liu, X.; Fu, G.; Liu, G.; Liu, Z.; Chen, J. Bi-Channel Switchable Broadband Terahertz Metamaterial Absorber. Photonics Technol. Lett. IEEE 2023, 35, 4. [Google Scholar] [CrossRef]
- Wang, G.; Cao, W.; He, X. 3D Dirac semimetal elliptical fiber supported THz tunable hybrid plasmonic waveguides. IEEE J. Sel. Top. Quantum Electron. 2023, 29, 8400207. [Google Scholar] [CrossRef]
- Cheng, Y.; Cao, W.; He, X. Hybrid plasmonic waveguides with tunable ENZ phenomenon supported by 3D Dirac semimetals. Laser Photonics Rev. 2024, 18, 2400167. [Google Scholar] [CrossRef]
- Liu, S.; Cao, W.; Li, J.; He, X. 3D Dirac semimetal metamaterial supported terahertz tunable dual-functional polarization converter. IEEE J. Sel. Top. Quantum Electron. 2025, 31, 8500108. [Google Scholar] [CrossRef]
- Vasić, B.; Jakovljević, M.M.; Isić, G.; Gajić, R. Tunable Metamaterials Based on Split Ring Resonators and Doped Graphene. Appl. Phys. Lett. 2013, 103, 165113. [Google Scholar] [CrossRef]
- Chen, M.; Sun, W.; Cai, J.J.; Chang, L.Z.; Xiao, X.F. Frequency-Tunable Terahertz Absorbers Based on Graphene Metasurface. Opt. Commun. 2017, 382, 144–150. [Google Scholar] [CrossRef]
- Yao, G.; Ling, F.; Yue, J.; Luo, C.; Ji, J.; Yao, J. Dual-band tunable perfect metamaterial absorber in the THz range. Opt. Express 2016, 24, 1518–1527. [Google Scholar] [CrossRef]
- Han, J.; Chen, R. Tunable Broadband Terahertz Absorber Based on a Single-Layer Graphene Metasurface. Opt. Express 2020, 28, 30289–30298. [Google Scholar] [CrossRef]
- Liu, G.-D.; Zhai, X.; Meng, H.-Y.; Lin, Q.; Yu, H.; Zhao, C.-J.; Wang, L.-L. Dirac semimetals based tunable narrowband absorber at terahertz frequencies. Opt. Express 2018, 26, 11471–11480. [Google Scholar] [CrossRef]
- Zhang, Y.; Lv, J.; Que, L.; Zhou, Y.; Meng, W.; Jiang, Y. A double-band tunable perfect terahertz metamaterial absorber based on Dirac semimetals. Results Phys. 2019, 15, 102773. [Google Scholar] [CrossRef]
- Shrekenhamer, D.; Chen, W.C.; Padilla, W.J. Liquid crystal tunable metamaterial absorber. Phys. Rev. Lett. 2013, 110, 177403. [Google Scholar] [CrossRef]
- Deng, G.; Xia, T.; Jing, S.; Yang, J.; Lu, H.; Yin, Z. A Tunable Metamaterial Absorber Based on Liquid Crystal Intended for F Frequency Band. IEEE Antennas Wirel. Propag. Lett. 2017, 16, 2062–2065. [Google Scholar] [CrossRef]
- Deng, G.; Lu, Y.; Yin, Z.; Lai, W.; Lu, H.; Yang, J.; Yang, A.; Ye, Y.; Liu, D.; Chi, B. A Tunable Polarization-Dependent Terahertz Metamaterial Absorber Based on Liquid Crystal. Electronics 2018, 7, 27. [Google Scholar] [CrossRef]
- Luo, C.Y.; Li, Z.Z.; Guo, Z.H.; Yue, J.; Luo, Q.; Yao, G.; Ji, J.; Rao, Y.K.; Li, R.K.; Li, D.; et al. Tunable Metamaterial Dual-Band Terahertz Absorber. Solid State Commun. 2015, 222, 32–36. [Google Scholar] [CrossRef]
- Luo, C.; Li, D.; Luo, Q.; Yue, J.; Gao, P.; Yao, J.; Ling, F. Design of a Tunable Multiband Terahertz Waves Absorber. J. Alloys Compd. 2015, 652, 18–24. [Google Scholar] [CrossRef]
- Zheng, W.; Li, W.; Chang, S.-j. A Thermally Tunable Terahertz Metamaterial Absorber. Optoelectron. Lett. 2015, 11, 18–21. [Google Scholar] [CrossRef]
- Naorem, R.; Dayal, G.; Ramakrishna, S.A.; Rajeswaran, B.; Umarji, A.M. Thermally Switchable Metamaterial Absorber with a VO2 Ground Plane. Opt. Commun. 2015, 346, 154–157. [Google Scholar] [CrossRef]
- Zhang, Z.; Tian, Z.; Chang, C.; Wang, X.; Zhang, X.; Ouyang, C.; Gu, J.; Han, J.; Zhang, W. Active-Thermal-Tunable Terahertz Absorber with Temperature-Sensitive Material Thin Film. Nanotechnol. Precis. Eng. 2018, 1, 123–128. [Google Scholar] [CrossRef]
- Pan, H.; Zhang, H.F. Thermally Tunable Polarization-Insensitive Ultra-Broadband Terahertz Metamaterial Absorber Based on the Coupled Toroidal Dipole Modes. Opt. Express 2021, 29, 18081–18094. [Google Scholar] [CrossRef] [PubMed]
- Guo, L.; Ma, X.; Chang, Z.; Xu, C.; Liao, J.; Zhang, R. Tunable and Temperature-Dependent GST-Based Metamaterial Absorber for Switching and Sensing Applications. J. Mater. Res. Technol. 2021, 14, 772–779. [Google Scholar] [CrossRef]
- Liu, H.; Wang, P.; Wu, J.; Yan, X.; Yuan, X.; Zhang, Y.; Zhang, X. Switchable and Dual-Tunable Multilayered Terahertz Absorber Based on Patterned Graphene and Vanadium Dioxide. Multidiscip. Digit. Publ. Inst. 2021, 6, 619. [Google Scholar] [CrossRef]
- Li, D.; Huang, H.; Xia, H.; Zeng, J.; Li, H.; Xie, D. Temperature-Dependent Tunable Terahertz Metamaterial Absorber for the Application of Light Modulator. Results Phys. 2018, 11, 659–664. [Google Scholar] [CrossRef]
- Song, Z.Y.; Wang, Z.S.; Wei, M.L. Broadband Tunable Absorber for Terahertz Waves Based on Isotropic Silicon Metasurfaces. Mater. Lett. 2019, 234, 138–141. [Google Scholar] [CrossRef]
- Cheng, Y.-Z.; Liu, J.-Q.; Chen, F.; Luo, H.; Li, X.-C. Optically switchable broadband metasurface absorber based on square ring shaped photoconductive silicon for terahertz waves. Phys. Lett. A 2021, 402, 127345. [Google Scholar] [CrossRef]
- Li, D.-M.; Yuan, S.; Yang, R.-C.; Tian, J.-P.; Zhang, W.-M. Dynamical Optical-Controlled Multi-State THz Metamaterial Absorber. Acta Opt. Sin. 2020, 40, 0816001. [Google Scholar] [CrossRef]
- Meng, Q.-L.; Zhang, Y.; Zhang, B.; Shang, J. Characteristics of Optically Tunable Multi-Band Terahertz Metamaterial Absorber. Laser Optoelectron. Prog. 2019, 56, 101603. [Google Scholar] [CrossRef]
- Zheng, C.; Li, J.; Liu, L.; Li, J.; Yue, Z.; Hao, X.; Zhang, Y.; Zang, H.; Yao, J.Q. Optically Tunable Terahertz Metasurface Absorber. Ann. Phys. 2022, 534, 2200007. [Google Scholar] [CrossRef]
- Zhao, X.-G.; Wang, Y.; Schalch, J.; Duan, G.; Cremin, K.; Zhang, J.; Chen, C.; Averitt, R.D.; Zhang, X. Optically Modulated Ultra-Broadband All-Silicon Metamaterial Terahertz Absorbers. ACS Photonics 2018, 5, 4996–5004. [Google Scholar] [CrossRef]
- Chen, L.-L.; Sun, L.-X.; Dong, H.-X.; Mou, N.; Zhang, Y.; Li, Q.; Jiang, X.; Zhang, L. Near-Field Imaging of the Multi-Resonant Mode Induced Broadband Tunable Metamaterial Absorber. RSC Adv. 2020, 10, 5146–5153. [Google Scholar] [CrossRef] [PubMed]
- Du, K.-K.; Li, Q.; Lyu, Y.-B.; Ding, J.-C.; Lu, Y.; Cheng, Z.-Y.; Qiu, M. Control over Emissivity of Zero-Static-Power Thermal Emitters Based on Phase-Changing Material GST. Light: Sci. Appl. 2017, 6, e16194. [Google Scholar] [CrossRef] [PubMed]
- Liu, L.; Kang, L.; Mayer, T.S.; Werner, D.H. Hybrid Metamaterials for Electrically Triggered Multifunctional Control. Nat. Commun. 2016, 7, 13236. [Google Scholar] [CrossRef] [PubMed]
- Muskens, O.L.; Bergamini, L.; Wang, Y.; Gaskell, J.M.; Zabala, N.; De Groot, C.H.; Sheel, D.W.; Aizpurua, J. Antenna-Assisted Picosecond Control of Nanoscale Phase Transition in Vanadium Dioxide. Light Sci. Appl. 2016, 5, e16173. [Google Scholar] [CrossRef]
- Yang, Y.; Kelley, K.; Sachet, E.; Campione, S.; Luk, T.S.; Maria, J.-P.; Sinclair, M.B.; Brener, I. Femtosecond Optical Polarization Switching Using a Cadmium Oxide-Based Perfect Absorber. Nat. Photonics 2017, 11, 390–395. [Google Scholar] [CrossRef]
- Zhu, H.; Yi, F.; Cubukcu, E. Plasmonic Metamaterial Absorber for Broadband Manipulation of Mechanical Resonances. Nat. Photonics 2016, 10, 709–714. [Google Scholar] [CrossRef]
- Lu, H.; Chen, J.; Yan, K.; Jin, Q.; Xue, Y.; Gao, Z. A hybrid feature selection algorithm for gene expression data classification. Neurocomputing 2017, 256, 56–62. [Google Scholar] [CrossRef]
- Zhang, X.M.; Han, Q.L.; Wang, Z.; Zhang, B.L. Neuronal state estimation for neural networks with two additive time-varying delay components. IEEE Trans. Cybern. 2017, 47, 3184–3194. [Google Scholar] [CrossRef]
- Cao, J.; Zhang, K.; Luo, M.; Yin, C.; Lai, X. Extreme learning machine and adaptive sparse representation for image classification. Neural Netw. 2016, 81, 91–102. [Google Scholar] [CrossRef]
- Zhang, K.; Luo, M. Outlier-robust extreme learning machine for regression problems. Neurocomputing 2015, 151, 1519–1527. [Google Scholar] [CrossRef]
- Hu, L.; Wen, H.; Wu, B.; Pan, F.; Liao, R.-F.; Song, H. Cooperative jamming for physical layer security enhancement in internet of things. IEEE Internet Things J. 2018, 5, 219–228. [Google Scholar] [CrossRef]
- Liu, H.C.; Quan, M.Y.; Li, Z.; Wang, Z.L. A new integrated MCDM model for sustainable supplier selection under interval-valued intuitionistic uncertain linguistic environment. Inf. Sci. 2019, 486, 254–270. [Google Scholar] [CrossRef]
- Yan, K.; Ji, Z.; Shen, W. Online fault detection methods for chillers combining extended Kalman filter and recursive one-class SVM. Neurocomputing 2017, 228, 205–212. [Google Scholar] [CrossRef]
- Jiang, S.; Shi, H.; Lin, W.; Liu, H.-C. A large group linguistic Z-DEMATEL approach for identifying key performance indicators in hospital performance management. Appl. Soft Comput. 2020, 86, 105900. [Google Scholar] [CrossRef]
- Xiang, R.; Jiang, H.; Ying, Y. Recognition of clustered tomatoes based on binocular stereo vision. Comput. Electron. Agric. 2014, 106, 75–90. [Google Scholar] [CrossRef]
- Zhang, X.M.; Han, Q.L.; Ge, X.; Wang, Z.; Zhang, B.L. Passivity analysis of delayed neural networks based on Lyapunov–Krasovskii functionals with delay-dependent matrices. IEEE Trans. Cybern. 2020, 50, 946–956. [Google Scholar] [CrossRef]
- Wang, X.; Yan, W.Q. Human gait recognition based on frame-by-frame gait energy images and convolutional long short-term memory. Int. J. Neural Syst. 2020, 30, 1950027. [Google Scholar] [CrossRef]
- Chang, Y.W.; Hsu, P.Y.; Yang, Q.M. Integration of online and offline channels: A view of O2O commerce. Internet Res. 2018, 28, 926–945. [Google Scholar] [CrossRef]
- Cao, F.; Ye, H.; Wang, D. A probabilistic learning algorithm for robust modeling using neural networks with random weights. Inf. Sci. 2015, 313, 62–78. [Google Scholar] [CrossRef]
- Che Sidik, N.A.; Mohd Rosdzimin, A.R. Simulation of natural convection heat transfer in an enclosure using lattice Boltzmann method. J. Mek. 2008, 27, 30–38. [Google Scholar]
- Yang, Y.; Xu, X. A differential game model for closed-loop supply chain participants under carbon emission permits. Comput. Ind. Eng. 2019, 135, 1077–1090. [Google Scholar] [CrossRef]
- Lu, H.; Yang, L.; Yan, K.; Xue, Y.; Gao, Z. A cost-sensitive rotation forest algorithm for gene expression data classification. Neurocomputing 2017, 228, 270–276. [Google Scholar] [CrossRef]
- Ding, X.F.; Liu, H.C.; Shi, H. A dynamic approach for emergency decision making based on prospect theory with interval-valued Pythagorean fuzzy linguistic variables. Comput. Ind. Eng. 2019, 131, 57–65. [Google Scholar] [CrossRef]
- Li, C.; Li, J.; Li, Y.; He, L.; Fu, X.; Chen, J. Fabric defect detection in textile manufacturing: A survey of the state of the art. Secur. Commun. Netw. 2021, 2021, 9948808. [Google Scholar] [CrossRef]
- Liu, C.; Wang, J.; Leung, J.Y.T. Worker assignment and production planning with learning and forgetting in manufacturing cells by hybrid bacteria foraging algorithm. Comput. Ind. Eng. 2016, 96, 162–179. [Google Scholar] [CrossRef]
- Lu, H.; Du, B.; Liu, J.; Xia, H.; Yeap, W.K. A kernel extreme learning machine algorithm based on improved particle swarm optimization. Memetic Comput. 2017, 9, 121–128. [Google Scholar] [CrossRef]
- Cao, F.; Chen, J.; Ye, H.; Zhao, J.; Zhou, Z. Recovering low-rank and sparse matrix based on the truncated nuclear norm. Neural Netw. 2017, 85, 10–20. [Google Scholar] [CrossRef]
- Yao, K.; Liang, J.; Liang, J.; Li, M.; Cao, F. Multi-view graph convolutional networks with attention mechanism. Artif. Intell. 2022, 307, 103708. [Google Scholar] [CrossRef]
- Gao, C.; Ye, H.; Cao, F.; Wen, C.; Zhang, Q.; Zhang, F. Multiscale fused network with additive channel–spatial attention for image segmentation. Knowl. Based Syst. 2021, 214, 106754. [Google Scholar] [CrossRef]
- Lu, H.-J.; An, C.-L.; Zheng, E.-H.; Lu, Y. Dissimilarity based ensemble of extreme learning machine for gene expression data classification. Neurocomputing 2014, 128, 22–30. [Google Scholar] [CrossRef]
- Hu, M.; Feng, X.; Ji, Z.; Yan, K.; Zhou, S. A novel computational approach for discord search with local recurrence rates in multivariate time series. Inf. Sci. 2019, 477, 220–233. [Google Scholar] [CrossRef]
- Xiong, J.J.; Zhang, G.B.; Wang, J.X.; Yan, T.H. Improved sliding mode control for finite-time synchronization of nonidentical delayed recurrent neural networks. IEEE Trans. Neural Netw. Learn. Syst. 2020, 31, 2209–2216. [Google Scholar] [CrossRef]
- Liu, H.; Cao, F.; Wen, C.; Zhang, Q. Lightweight multi-scale residual networks with attention for image super-resolution. Knowl. Based Syst. 2020, 203, 106103. [Google Scholar] [CrossRef]
- Li, X.; Zhu, C.; Xu, C.; Zhu, J.; Li, Y.; Wu, S. VR motion sickness recognition by using EEG rhythm energy ratio based on wavelet packet transform. Comput. Methods Programs Biomed. 2020, 188, 105266. [Google Scholar] [CrossRef] [PubMed]
- Du, Z.; Ye, H.; Cao, F. A novel local–global graph convolutional method for point cloud semantic segmentation. IEEE Trans. Neural Netw. Learn. Syst. 2024, 35, 4798–4812. [Google Scholar] [CrossRef] [PubMed]
- Zhu, W.; Peng, B. Sparse and low-rank regularized deep subspace clustering. Knowl. Based Syst. 2020, 204, 106199. [Google Scholar] [CrossRef]
- Luo, M.; Zhang, K. Robustness of full implication algorithms based on interval-valued fuzzy inference. Int. J. Approx. Reason. 2015, 62, 61–72. [Google Scholar] [CrossRef]
- Liu, C.; Wang, J.; Leung, J.Y.T. Integrated bacteria foraging algorithm for cellular manufacturing in supply chain considering facility transfer and production planning. Appl. Soft Comput. 2018, 62, 602–618. [Google Scholar] [CrossRef]
- Chang, Y.W.; Hsu, P.Y.; Shiau, W.L.; Tsai, C.C. Knowledge sharing intention in the United States and China: A cross-cultural study. Eur. J. Inf. Syst. 2015, 24, 262–277. [Google Scholar] [CrossRef]
- Wang, X.; Wang, J.; Yan, K. Gait recognition based on Gabor wavelets and (2D)2PCA. Multimed. Tools Appl. 2018, 77, 12545–12561. [Google Scholar] [CrossRef]
- Lu, J.; Zhao, J.; Cao, F. Extended feed forward neural networks with random weights for face recognition. Neurocomputing 2014, 136, 96–102. [Google Scholar] [CrossRef]
- Song, Y.; Zhang, S.; He, B.; Sha, Q.; Shen, Y.; Yan, T.; Nian, R.; Lendasse, A. Gaussian derivative models and ensemble extreme learning machine for texture image classification. Neurocomputing 2018, 277, 53–64. [Google Scholar] [CrossRef]
- Cao, F.; Wang, D.; Zhu, H.; Wang, Y. An iterative learning algorithm for feedforward neural networks with random weights. Inf. Sci. 2016, 328, 546–557. [Google Scholar] [CrossRef]
- Shi, H.; Wang, L.; Li, X.-Y.; Liu, H.-C. A novel method for failure mode and effects analysis using fuzzy evidential reasoning and fuzzy Petri nets. J. Ambient Intell. Humaniz. Comput. 2020, 11, 2381–2395. [Google Scholar] [CrossRef]
- Wang, X.; Li, J.; Yang, L.; Mi, H. Unsupervised learning for community detection in attributed networks based on graph convolutional network. Neurocomputing 2021, 456, 147–155. [Google Scholar] [CrossRef]
- Cao, F.; Cai, M.; Tan, Y.; Zhao, J. Image super-resolution via adaptive ℓp (0 < p < 1) regularization and sparse representation. IEEE Trans. Neural Netw. Learn. Syst. 2016, 27, 1550–1561. [Google Scholar] [CrossRef]
- Li, J.; Hao, J.; Sun, X.; Feng, Q. Forecasting China’s sovereign CDS with a decomposition reconstruction strategy. Appl. Soft Comput. 2021, 105, 107291. [Google Scholar] [CrossRef]
- Cao, F.; Guo, W. Deep hybrid dilated residual networks for hyperspectral image classification. Neurocomputing 2020, 384, 170–181. [Google Scholar] [CrossRef]
- Li, D.; Luo, Z.; Cao, B. Blockchain-based federated learning methodologies in smart environments. Clust. Comput. 2022, 25, 2585–2599. [Google Scholar] [CrossRef]
- Cao, F.; Yao, K.; Liang, J. Deconvolutional neural network for image super-resolution. Neural Netw. 2020, 132, 394–404. [Google Scholar] [CrossRef]
- Cao, H.; Cao, F.; Wang, D. Quantum artificial neural networks with applications. Inf. Sci. 2015, 290, 1–6. [Google Scholar] [CrossRef]
- Wang, J.; Liu, C.; Zhou, M. Improved bacterial foraging algorithm for cell formation and product scheduling considering learning and forgetting factors in cellular manufacturing systems. IEEE Syst. J. 2020, 14, 3047–3056. [Google Scholar] [CrossRef]
- Zhao, J.; Hu, H.; Cao, F. Image super-resolution via adaptive sparse representation. Knowl. Based Syst. 2017, 124, 23–33. [Google Scholar] [CrossRef]
- Xiang, R. Image segmentation for whole tomato plant recognition at night. Comput. Electron. Agric. 2018, 154, 434–442. [Google Scholar] [CrossRef]
- Ding, X.F.; Zhang, L.; Liu, H.C. Emergency decision making with extended axiomatic design approach under picture fuzzy environment. Expert Syst. 2020, 37, e12482. [Google Scholar] [CrossRef]
- Ding, X.F.; Liu, H.C. An extended prospect theory–VIKOR approach for emergency decision making with 2-dimension uncertain linguistic information. Soft Comput. 2019, 23, 12139–12150. [Google Scholar] [CrossRef]
- Peng, X.; Xu, D.; Shen, J. A twin projection support vector machine for data regression. Neurocomputing 2014, 138, 131–141. [Google Scholar] [CrossRef]
- Liu, Z.; Jia, X.; Xu, X. Study of shrimp recognition methods using smart networks. Comput. Electron. Agric. 2019, 165, 104926. [Google Scholar] [CrossRef]
- Schmidhuber, J. Deep learning in neural networks: An overview. Neural Netw. 2015, 61, 85–117. [Google Scholar] [CrossRef]
- Cao, F.; Guo, W. Cascaded dual-scale crossover network for hyperspectral image classification. Knowl. Based Syst. 2020, 189, 105122. [Google Scholar] [CrossRef]
- Zhang, H.; Huang, Y.; Wang, B. Design and analysis of associative memories based on external inputs of delayed recurrent neural networks. Neurocomputing 2014, 136, 337–344. [Google Scholar] [CrossRef]
- Liang, W.; Zhou, X.; Huang, S.; Hu, C.; Xu, X.; Jin, Q. Modeling of cross-disciplinary collaboration for potential field discovery and recommendation based on scholarly big data. Future Gener. Comput. Syst. 2018, 87, 591–600. [Google Scholar] [CrossRef]
- Li, X.-Y.; Xiong, Y.; Duan, C.-Y.; Liu, H.-C. Failure mode and effect analysis using interval type-2 fuzzy sets and fuzzy Petri nets. J. Intell. Fuzzy Syst. 2019, 37, 693–709. [Google Scholar] [CrossRef]
- Lu, H.; Gao, H.; Ye, M.; Wang, X. A hybrid ensemble algorithm combining AdaBoost and genetic algorithm for cancer classification with gene expression data. IEEE/ACM Trans. Comput. Biol. Bioinform. 2021, 18, 863–870. [Google Scholar] [CrossRef]
- Liu, Y.; Cao, F.; Zhao, J.; Chu, J. Segmentation of white blood cells image using adaptive location and iteration. IEEE J. Biomed. Health Inform. 2017, 21, 1644–1655. [Google Scholar] [CrossRef]
- Chen, Z.; Cao, F. Scattered data approximation by neural network operators. Neurocomputing 2016, 190, 237–242. [Google Scholar] [CrossRef]
- Luo, M.; Zhou, X. Robustness of reverse triple I algorithms based on interval-valued fuzzy inference. Int. J. Approx. Reason. 2015, 66, 16–26. [Google Scholar] [CrossRef]
- Cao, F.; Chen, B. New architecture of deep recursive convolution networks for super-resolution. Knowl. Based Syst. 2019, 178, 98–110. [Google Scholar] [CrossRef]
- Lu, H.; Xu, Y.; Ye, M.; Yan, K.; Gao, Z.; Jin, Q. Learning misclassification costs for imbalanced classification on gene expression data. BMC Bioinform. 2019, 20, 681. [Google Scholar] [CrossRef] [PubMed]
- Cao, F.; Hu, H.; Lu, J.; Wu, J.; Chu, J.; Chellappa, R. Pose and illumination variable face recognition via sparse representation and illumination dictionary. Knowl. Based Syst. 2016, 107, 117–128. [Google Scholar] [CrossRef]
- Gu, P.; Han, Y.; Gao, W.; Xu, G.; Wu, J. Enhancing session-based social recommendation through item graph embedding and contextual friendship modeling. Neurocomputing 2021, 419, 190–202. [Google Scholar] [CrossRef]
- Cao, F.; Liu, Y.; Wang, D. Efficient saliency detection using convolutional neural networks with feature selection. Inf. Sci. 2018, 456, 34–49. [Google Scholar] [CrossRef]
- Hou, L.-X.; Mao, L.-X.; Liu, H.-C.; Zhang, L. Decades on emergency decision-making: A bibliometric analysis and literature review. Complex Intell. Syst. 2021, 7, 2819–2832. [Google Scholar] [CrossRef] [PubMed]
- Zhao, J.; Lv, Y.; Zhou, Z.; Cao, F. A novel deep learning algorithm for incomplete face recognition: Low-rank-recovery network. Neural Netw. 2017, 94, 115–124. [Google Scholar] [CrossRef]
- Han, H.; Fang, L.; Lu, W.; Zhai, W.; Li, Y.; Zhao, J. A GCICA grant-free random access scheme for M2M communications in crowded massive MIMO systems. IEEE Internet Things J. 2022, 9, 6032–6046. [Google Scholar] [CrossRef]
- Cao, F.; Liu, H. Single image super-resolution via multi-scale residual channel attention network. Neurocomputing 2019, 358, 424–436. [Google Scholar] [CrossRef]
- Karumanchi, S.; Mancini, S.; Winter, A.; Yang, D. Quantum channel capacities with passive environment assistance. IEEE Trans. Inf. Theory 2016, 62, 1733–1747. [Google Scholar] [CrossRef]
- Jiang, X.W.; Yan, T.H.; Zhu, J.J.; He, B.; Li, W.H.; Du, H.P.; Sun, S.S. Densely connected deep extreme learning machine algorithm. Cogn. Comput. 2020, 12, 979–990. [Google Scholar] [CrossRef]
- Chen, J.; Cai, H.; Wang, W. A new metaheuristic algorithm: Car tracking optimization algorithm. Soft Comput. 2018, 22, 3857–3878. [Google Scholar] [CrossRef]
- Winter, A.; Yang, D. Potential capacities of quantum channels. IEEE Trans. Inf. Theory 2016, 62, 1415–1424. [Google Scholar] [CrossRef]
- Li, W.; Jiang, S.; Jin, Q. Overlap community detection using spectral algorithm based on node convergence degree. Future Gener. Comput. Syst. 2018, 79, 408–416. [Google Scholar] [CrossRef]
- Lu, H.; Meng, Y.; Yan, K.; Gao, Z. Kernel principal component analysis combining rotation forest method for linearly inseparable data. Cogn. Syst. Res. 2019, 53, 111–122. [Google Scholar] [CrossRef]
- Mao, L.-X.; Lan, J.; Chen, A.; Shi, H.; Liu, H.-C. New approach for quality function deployment based on linguistic distribution assessments and CRITIC method. Mathematics 2025, 13, 240. [Google Scholar] [CrossRef]
- Zou, H. Clustering algorithm and its application in data mining. Wirel. Pers. Commun. 2020, 110, 21–30. [Google Scholar] [CrossRef]
- Liu, C.; Wang, J. Cell formation and task scheduling considering multi-functional resource and part movement using hybrid simulated annealing. Int. J. Comput. Intell. Syst. 2016, 9, 765–777. [Google Scholar] [CrossRef]
- Kong, D.; Zhu, J.; Wu, S.; Duan, C.; Lu, L.; Chen, D. A novel IRBF-RVM model for diagnosis of atrial fibrillation. Comput. Methods Programs Biomed. 2019, 177, 183–192. [Google Scholar] [CrossRef] [PubMed]
- Zhao, J.; Wang, Z.; Cao, F.; Wang, D. A local learning algorithm for random weights networks. Knowl. Based Syst. 2015, 74, 159–166. [Google Scholar] [CrossRef]
- Yang, B.; Xiang, X.; Xu, D.; Wang, X.; Yang, X. 3D palmprint recognition using shape index representation and fragile bits. Multimed. Tools Appl. 2017, 76, 15357–15375. [Google Scholar] [CrossRef]
- Wang, H. On extended progressive and iterative approximation for least squares fitting. Vis. Comput. 2022, 38, 591–602. [Google Scholar] [CrossRef]
- Zhao, R.; Luo, M.; Li, S. A dynamic distance measure of picture fuzzy sets and its application. Symmetry 2021, 13, 436. [Google Scholar] [CrossRef]
- Zhang, J.; Ma, Q.; Cui, X.; Guo, H.; Wang, K.; Zhu, D. High-throughput corn ear screening method based on two-pathway convolutional neural network. Comput. Electron. Agric. 2020, 175, 105525. [Google Scholar] [CrossRef]
- Xu, X.-G.; Xiong, Y.; Xu, D.-H.; Liu, H.-C. Bipolar fuzzy Petri nets for knowledge representation and acquisition considering non-cooperative behaviors. Int. J. Mach. Learn. Cybern. 2020, 11, 2297–2311. [Google Scholar] [CrossRef]
- Lin, D.H.; Wu, J.; Li, J.N. Less conservative stability condition for uncertain discrete-time recurrent neural networks with time-varying delays. Neurocomputing 2016, 173, 1578–1588. [Google Scholar] [CrossRef]
- Liu, H.; Cao, F. Improved dual-scale residual network for image super-resolution. Neural Netw. 2020, 132, 84–95. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, X.; Yan, K. Hand gesture recognition based on concentric circular scan lines and weighted K-nearest neighbor algorithm. Multimed. Tools Appl. 2018, 77, 209–223. [Google Scholar] [CrossRef]
- Karumanchi, S.; Mancini, S.; Winter, A.; Yang, D. Classical capacities of quantum channels with environment assistance. Probl. Inf. Transm. 2016, 52, 214–238. [Google Scholar] [CrossRef]
- Dai, K.; Zhao, J.; Cao, F. A novel decorrelated neural network ensemble algorithm for face recognition. Knowl. Based Syst. 2015, 89, 541–552. [Google Scholar] [CrossRef]
- Luo, M.; Zhang, Y.; Fu, L. A new similarity measure for picture fuzzy sets and its application to multi-attribute decision making. Informatica 2021, 32, 543–564. [Google Scholar] [CrossRef]
- Wang, X.; Li, J.; Yang, L.; Mi, H.; Yu, J.Y. Weakly-supervised learning for community detection based on graph convolution in attributed networks. Int. J. Mach. Learn. Cybern. 2021, 12, 3529–3539. [Google Scholar] [CrossRef]
- Wang, X.; Yan, K. Gait classification through CNN-based ensemble learning. Multimed. Tools Appl. 2021, 80, 1565–1581. [Google Scholar] [CrossRef]
- Wang, L.; Wang, B. Construction of greenhouse environment temperature adaptive model based on parameter identification. Comput. Electron. Agric. 2020, 174, 105477. [Google Scholar] [CrossRef]
- Yu, A.-Y.; Liu, H.-C.; Zhang, L.; Chen, Y. A new data envelopment analysis-based model for failure mode and effect analysis with heterogeneous information. Comput. Ind. Eng. 2021, 157, 107350. [Google Scholar] [CrossRef]
- Kong, Y.; Lu, H.; Xue, Y.; Xia, H. Terminal neural computing: Finite-time convergence and its applications. Neurocomputing 2016, 217, 133–141. [Google Scholar] [CrossRef]
- Nie, D.; Lin, J.; Gao, Q. Settling behavior of two particles with different densities in a vertical channel. Comput. Fluids 2017, 156, 353–367. [Google Scholar] [CrossRef]
- Luo, M.; Long, H. Picture fuzzy geometric aggregation operators based on a trapezoidal fuzzy number and its application. Symmetry 2021, 13, 119. [Google Scholar] [CrossRef]
- Wang, X.; Feng, S.; Yan, W.Q. Human gait recognition based on self-adaptive hidden Markov model. IEEE/ACM Trans. Comput. Biol. Bioinform. 2021, 18, 963–972. [Google Scholar] [CrossRef]
- Hu, T.; Zhao, J.; Zheng, R.; Wang, P.; Li, X.; Zhang, Q. Ultrasonic based concrete defects identification via wavelet packet transform and GA-BP neural network. PeerJ Comput. Sci. 2021, 7, e635. [Google Scholar] [CrossRef]
- Liu, P.; He, H.; Fu, T.; Lu, H.; Alelaiwi, A.; Wasi, M.W.I. Task offloading optimization of cruising UAV with fixed trajectory. Comput. Netw. 2021, 199, 108397. [Google Scholar] [CrossRef]
- Pan, C.; Yan, W.Q. Object detection based on saturation of visual perception. Multimed. Tools Appl. 2020, 79, 19925–19944. [Google Scholar] [CrossRef]
- Liu, M.; Lou, X.; Jin, X.; Jiang, R.; Ye, K.; Wang, S. NLOS identification for localization based on the application of UWB. Wirel. Pers. Commun. 2021, 119, 3651–3670. [Google Scholar] [CrossRef]
- Wang, W.; Lou, B.; Li, X.; Lou, X.; Jin, N.; Yan, K. Intelligent maintenance frameworks of large-scale grid using genetic algorithm and K-mediods clustering methods. World Wide Web 2020, 23, 1177–1195. [Google Scholar] [CrossRef]
- Xiong, R.; Peng, X.; Li, J. Graphene-metasurface for wide-incident-angle terahertz absorption. Front. Inf. Technol. Electron. Eng. 2021, 22, 334–340. [Google Scholar] [CrossRef]
- He, B.; Sun, T.; Yan, T.; Shen, Y.; Nian, R. A pruning ensemble model of extreme learning machine with L1/2 regularizer. Multidimens. Syst. Signal Process. 2017, 28, 1051–1069. [Google Scholar] [CrossRef]
- Luo, M.; Li, W. Some new similarity measures on picture fuzzy sets and their applications. Soft Comput. 2023, 27, 6049–6067. [Google Scholar] [CrossRef]
- Shi, G.; Feng, C.; Xu, W.; Liao, L.; Huang, H. Penalized multiple distribution selection method for imbalanced data classification. Knowl. Based Syst. 2020, 196, 105833. [Google Scholar] [CrossRef]
- Huang, Z.; Wang, H. On a progressive and iterative approximation method with memory for least square fitting. Comput. Aided Geom. Des. 2020, 82, 101931. [Google Scholar] [CrossRef]
- Wang, L.; Wang, H.; Yang, X.; Gao, Y.; Cui, X.; Wang, B. Research on smooth path planning method based on improved ant colony algorithm optimized by floyd algorithm. Front. Neurorobotics 2022, 16, 955179. [Google Scholar] [CrossRef]
- Zhang, D.; Zhou, H. Nonlinear bending and thermal post-buckling analysis of FGM beams resting on nonlinear elastic foundations. CMES-Comp. Model. Eng. Sci. 2014, 100, 201–222. [Google Scholar] [CrossRef]
- Yan, K.; Wang, B.; Cheng, H.; Ji, Z.; Huang, J.; Gao, Z. Molecular skin surface-based transformation visualization between biological macromolecules. J. Healthc. Eng. 2017, 2017, 4818604. [Google Scholar] [CrossRef]
- Zheng, W.; Tang, H.; Qian, Y. Collaborative work with linear classifier and extreme learning machine for fast text categorization. World Wide Web 2015, 18, 235–252. [Google Scholar] [CrossRef]
- Zhu, W.; Peng, B. Manifold-based aggregation clustering for unsupervised vehicle re-identification. Knowl. Based Syst. 2022, 235, 107624. [Google Scholar] [CrossRef]
- Zhang, H.; Li, Q. Intuitionistic fuzzy filter theory on residuated lattices. Soft Comput. 2019, 23, 6777–6783. [Google Scholar] [CrossRef]
- Chen, Q.; Cao, F. Distributed support vector machine in master-slave mode. Neural Netw. 2018, 101, 94–100. [Google Scholar] [CrossRef]
- Ye, C.; Pan, J.; Jin, Q. An improved SSO algorithm for cyber-enabled tumor risk analysis based on gene selection. Future Gener. Comput. Syst. 2019, 92, 407–418. [Google Scholar] [CrossRef]
- Zheng, S.; Chang, P.-Y.; Chen, J.; Chang, Y.-W.; Fan, H.-C. An investigation of patient decisions to use eHealth: A view of multichannel services. J. Organ. End User Comput. 2022, 34, 1–24. [Google Scholar] [CrossRef]
- Xiong, G.; Yan, K.; Zhou, X. A distributed learning based sentiment analysis methods with web applications. World Wide Web 2022, 25, 1905–1922. [Google Scholar] [CrossRef]
- Luo, M.; Wang, Y.; Zhao, R. Interval-valued fuzzy reasoning method based on similarity measure. J. Log. Algebr. Methods Program. 2020, 113, 100541. [Google Scholar] [CrossRef]
- Zhu, W.; Peng, Y. Elastic net regularized kernel non-negative matrix factorization algorithm for clustering guided image representation. Appl. Soft Comput. 2020, 97, 106774. [Google Scholar] [CrossRef]
- Yin, H.; Park, D.; Zhang, X. Buffer structure optimized VLSI architecture for efficient hierarchical integer pixel motion estimation implementation. J. Real Time Image Process. 2016, 11, 507–525. [Google Scholar] [CrossRef]
- Wang, X.; Zheng, Z.; Li, J.; Shan, L.; Li, Z. Belief propagation bit-strengthening decoder for polar codes. IEEE Commun. Lett. 2019, 23, 1958–1961. [Google Scholar] [CrossRef]
- Shi, J.; Ye, H.; Yang, B.; Cao, F. An iteration-based interactive attention network for 3D point cloud registration. Neurocomputing 2023, 560, 126822. [Google Scholar] [CrossRef]
- Sun, J.; Garibaldi, J.M.; Zhang, Y.; Al-Shawabkeh, A. A multi-cycled sequential memetic computing approach for constrained optimisation. Inf. Sci. 2016, 340, 175–190. [Google Scholar] [CrossRef]
- Cao, F.; Feng, X.; Zhao, J. Sparse representation for robust face recognition by dictionary decomposition. J. Vis. Commun. Image Represent. 2017, 46, 260–268. [Google Scholar] [CrossRef]
- Ye, H.; Wang, Y.; Cao, F. A novel meta-learning framework: Multi-features adaptive aggregation method with information enhancer. Neural Netw. 2021, 144, 755–765. [Google Scholar] [CrossRef] [PubMed]
- Cao, F.; Li, K. A new method for image super-resolution with multi-channel constraints. Knowl. Based Syst. 2018, 146, 118–128. [Google Scholar] [CrossRef]
- Zhao, J.; Zhang, W.; Cao, F. Robust object tracking using a sparse coadjutant observation model. Multimed. Tools Appl. 2018, 77, 30969–30991. [Google Scholar] [CrossRef]
- Li, W.; Yao, M.; Zhou, X.; Nishimura, S.; Jin, Q. Recommendation of location-based services based on composite measures of trust degree. J. Supercomput. 2014, 69, 1154–1165. [Google Scholar] [CrossRef]
- Wang, H. Implicit randomized progressive-iterative approximation for curve and surface reconstruction. Comput. Aided Des. 2022, 152, 103376. [Google Scholar] [CrossRef]
- Rao, S.; Zou, G.; Yang, S.; Barmada, S. A feature selection and ensemble learning based methodology for transformer fault diagnosis. Appl. Soft Comput. 2024, 150, 111072. [Google Scholar] [CrossRef]
- Jin, Y.; Lu, H.; Li, Z.; Wang, Y. A cross-modal deep metric learning model for disease diagnosis based on chest X-ray images. Multimed. Tools Appl. 2023, 82, 33421–33442. [Google Scholar] [CrossRef]
- Huang, K.; Xiu, S.; Yu, M.; Zhang, X.; Zhang, Y.; Liu, Y.; Zhang, J. Software pipeline-based partitioning method with trade-off between workload balance and communication optimization. ETRI J. 2015, 37, 562–572. [Google Scholar] [CrossRef]
- Wang, X.; Li, J.; Chang, H.; Zhang, Y.; Zhang, X.; Zhang, T. Optimization design of polar-LDPC concatenated scheme based on deep learning. Comput. Electr. Eng. 2020, 84, 106636. [Google Scholar] [CrossRef]
- Zhang, D.; Zhou, H. Nonlinear symmetric free vibration analysis of super elliptical isotropic thin plates. CMC Comput. Mater. Contin. 2014, 40, 21–34. [Google Scholar] [CrossRef]
- Zhang, F. Modular configuration of service elements based on the improved K-means algorithm. Expert Syst. 2019, 36, e12344. [Google Scholar] [CrossRef]
- Wang, Z.; Mao, Y.; Cheng, E.; Zou, J. Matching preclusion number of graphs. Theor. Comput. Sci. 2019, 759, 61–71. [Google Scholar] [CrossRef]
- Gao, Z.; Cheng, Z.; Diao, W.; Zhang, J.; Lu, H. Identity authentication based on trajectory characteristics of mobile devices. J. Syst. Archit. 2021, 112, 101857. [Google Scholar] [CrossRef]
- Zhang, D.; Xu, J.; Sun, M.; Xiang, Z. High-density crowd behaviors segmentation based on dynamical systems. Multimed. Syst. 2017, 23, 599–606. [Google Scholar] [CrossRef]
- Shao, Y.; Sun, Z.; Tan, A.; Yan, T. Efficient three-dimensional point cloud object detection based on improved Complex-YOLO. Front. Neurorobot. 2023, 17, 1092564. [Google Scholar] [CrossRef]
- Luo, M.; Zhang, G. Divergence-based distance for picture fuzzy sets and its application to multi-attribute decision-making. Soft Comput. 2023, 28, 253–269. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, H.; Li, J.; Bao, X.; Xie, K. An improved path splitting decision-aided SCL decoding algorithm for polar codes. IEEE Commun. Lett. 2021, 25, 3463–3467. [Google Scholar] [CrossRef]
- Wang, H.; Yuan, L.; Xiong, J.-J.; Mao, J. The relaxed implicit randomized algebraic reconstruction technique for curve and surface reconstruction. Comput. Graph. 2021, 102, 9–17. [Google Scholar] [CrossRef]
- Lin, S.; Cao, F. Simultaneous approximation by spherical neural networks. Neurocomputing 2016, 175, 348–354. [Google Scholar] [CrossRef]
- Liu, L.; Hu, S. SACTNet: Spatial Attention Context Transformation Network for cloud removal. Wirel. Commun. Mob. Comput. 2021, 2021, 8292612. [Google Scholar] [CrossRef]
- Zhou, Z.; Zhang, W.; Zhao, J. Robust visual tracking using discriminative sparse collaborative map. Int. J. Mach. Learn. Cybern. 2019, 10, 3201–3212. [Google Scholar] [CrossRef]
- Cao, S.; Wang, X. Real-time dynamic gesture recognition and hand servo tracking using PTZ camera. Multimed. Tools Appl. 2019, 78, 27403–27424. [Google Scholar] [CrossRef]
- Jin, X.; Li, X.; Feng, Y.; Wen, M.; Huang, C.; Yao, Y. RIS-Based Opposite Phase Index Modulation and Its DNN-Assisted Joint Sequence Detection. IEEE Wirel. Commun. Lett. 2023, 12, 1518–1522. [Google Scholar] [CrossRef]
- Huang, G.; Yang, Z.; Zhang, Y.; Peng, H.; Wang, J. Particle filter based optimization scheme for trajectory design and resource allocation of UAV-enabled WPCN system. Phys. Commun. 2021, 47, 101392. [Google Scholar] [CrossRef]
- Cui, X.; Chen, J.; Wang, B.; Xu, S. Off-policy algorithm based Hierarchical optimal control for completely unknown dynamic systems. Neurocomputing 2022, 488, 669–680. [Google Scholar] [CrossRef]
- Liu, H.; Shao, M.; Wang, C.; Cao, F. Image Super-Resolution Using a Simple Transformer Without Pretraining. Neural Process. Lett. 2022, 55, 1479–1497. [Google Scholar] [CrossRef]
- Wang, S.; Lin, C.; Yan, W.; Su, X.; Yang, L. High-order modeling of multiphase flows: Based on discrete Boltzmann method. Comput. Fluids 2023, 265, 106009. [Google Scholar] [CrossRef]
- Dai, C.; Pan, C.; He, W. Feature extraction and fusion network for salient object detection. Multimed. Tools Appl. 2022, 81, 33955–33969. [Google Scholar] [CrossRef]
- Wang, W.; Wang, Y.; Wang, J.; Fang, X.; He, Y. Ensemble enhanced active learning mixture discriminant analysis model and its application for semi-supervised fault classification. Front. Inform. Technol. Electron. Eng. 2022, 23, 1814–1827. [Google Scholar] [CrossRef]
- Gao, F.; Cui, Y.; Gao, B.; Chen, Y.; Zhang, H. Dynamic multiple multicasts routing and wavelength assignment for realizing modified artificial fish model in mesh-based ONoC. Opt. Switch. Netw. 2023, 50, 100744. [Google Scholar] [CrossRef]
- Lv, L.; Bardou, D.; Liu, Y.; Hu, P. Deep Autoencoder-like non-negative matrix factorization with graph regularized for link prediction in dynamic networks. Appl. Soft Comput. 2023, 148, 110832. [Google Scholar] [CrossRef]
- Hu, R.; Yang, B.; Ye, H.; Cao, F.; Wen, C.; Zhang, Q. Decouple the object: Component-level semantic recognizer for point clouds classification. Knowl. Based Syst. 2022, 248, 108887. [Google Scholar] [CrossRef]
- Liu, L.; Wang, X.; Bao, Q.; Li, X. Behavior detection and evaluation based on multi-frame MobileNet. Multimed. Tools Appl. 2023, 83, 15733–15750. [Google Scholar] [CrossRef]
- Wang, X.; Yan, K. Automatic color correction for multi-projector display systems. Multimed. Tools Appl. 2018, 77, 13115–13132. [Google Scholar] [CrossRef]
- Zhao, S.; Wang, Y.; Deng, G.; Yang, P.; Chen, Z.; Li, Y. An intelligently adjusted carbon price forecasting approach based on breakpoints segmentation, feature selection and adaptive machine learning. Appl. Soft Comput. 2023, 149, 110948. [Google Scholar] [CrossRef]
- Chai, Z. An indirect variable weights method to compute fuzzy comprehensive evaluation values. Soft Comput. 2019, 23, 12511–12519. [Google Scholar] [CrossRef]
- Gao, Z.; Guo, H.; Xie, Y.; Lu, H.; Zhang, J.; Diao, W.; Xu, R. An improved localization method in cyber-social environments with obstacles. Comput. Electr. Eng. 2020, 86, 106694. [Google Scholar] [CrossRef]
- Hu, P.; Chu, X.; Lv, L.; Zuo, K.; Ni, T.; Wang, T.; Shen, Z. An efficient and secure data collection scheme for predictive maintenance of vehicles. Ad. Hoc. Netw. 2023, 146, 103157. [Google Scholar] [CrossRef]
- Pan, B.; Zhang, L.; Yin, H.; Lan, J.; Cao, F. An automatic 2D to 3D video conversion approach based on RGB-D images. Multimed. Tools Appl. 2021, 80, 19179–19201. [Google Scholar] [CrossRef]
- Tao, T.; Li, D.; Ma, H.; Li, Y.; Tan, S.; Liu, E.-X.; Schutt-Ainé, J.; Li, E.-P. A new pre-conditioned STDP rule and its hardware implementation in neuromorphic crossbar array. Neurocomputing 2023, 557, 126682. [Google Scholar] [CrossRef]
- Shi, G.; Wang, C.; Qiao, F.; Lin, R.; Wu, S.; Shi, M.; Sun, Y.; Han, J.; Wang, B. A new passive non-ideal floating memristor emulator circuit. AEU Int. J. Electron. Commun. 2023, 170, 154823. [Google Scholar] [CrossRef]
- Cao, F.; Zhu, L.; Ye, H.; Wen, C.; Zhang, Q. A new method for point cloud registration: Adaptive relation-oriented convolution and recurrent correspondence-walk. Knowl. Based Syst. 2024, 284, 111280. [Google Scholar] [CrossRef]
- Shi, K. A gray level indicator-based nonlinear diffusion equation for the removal of random-valued impulse noise. Multimed. Tools Appl. 2022, 81, 10529–10544. [Google Scholar] [CrossRef]
- Li, J.-F.; Chen, S.-P.; Duan, L.-M.; Niu, L. A PR-quadtree based multi-dimensional indexing for complex query in a cloud system. Clust. Comput. 2017, 20, 2931–2942. [Google Scholar] [CrossRef]
- Zhao, R.; Ma, L.; Li, S.; Luo, M. A multi-criteria three-way decision making method in a picture fuzzy probabilistic decision system. Cogn. Comput. 2021, 14, 1924–1941. [Google Scholar] [CrossRef]
- Du, Z.; Ye, H.; Cao, F. 3D mixed CNNs with edge-point feature learning. Knowl. Based Syst. 2021, 221, 106985. [Google Scholar] [CrossRef]
- Liu, Q.; Zhao, X.; Shi, K. The analysis of agricultural Internet of things product marketing by deep learning. J. Supercomput. 2022, 79, 4602–4621. [Google Scholar] [CrossRef]
- Zhu, C.; Zheng, B.; He, Z.; Gao, M.; Sun, C.; Bao, Z. State of health estimation of lithium-ion battery using time convolution memory neural network. Mob. Inf. Syst. 2021, 2021, 4826409. [Google Scholar] [CrossRef]
- Zhang, D.; Lan, H.; Ma, Z.; Yang, Z.; Wu, X.; Huang, X. Spatial-temporal gated graph convolutional network: A new deep learning framework for long-term traffic speed forecasting. J. Intell. Fuzzy Syst. 2023, 44, 10437–10450. [Google Scholar] [CrossRef]
- Yang, F.; Chen, M.; Li, P.; Qu, W.; Chen, J.; Qian, T. Sparse series solutions of random boundary and initial value problems. Int. J. Wavelets Multiresolut. Inf. Process. 2024, 22, 2350050. [Google Scholar] [CrossRef]
- Luo, M.; Wu, L.; Fu, L. Robustness analysis of the interval-valued fuzzy inference algorithms. J. Intell. Fuzzy Syst. 2020, 38, 685–696. [Google Scholar] [CrossRef]
- Zhang, F. Research for Service Flow Module Granularity Design Based on Fuzzy Spaces Quotient Theory. Clust. Comput. 2019, 22, S5825–S5837. [Google Scholar] [CrossRef]
- Jin, X.; Zhang, P.; Wan, C.; Ma, D.; Yao, Y. RIS Assisted Dual-Function Radar and Secure Communications Based on Frequency-Shifted Chirp Spread Spectrum Index Modulation. China Commun. 2023, 20, 85–99. [Google Scholar] [CrossRef]
- Huang, K.; Zhang, X.-X.; Xiu, S.-W.; Zheng, D.-D.; Yu, M.; Ma, D.; Chen, G.; Yan, X.-L. Profiling and Annotation Combined Method for Multimedia Application Specific MPSoC Performance Estimation. Front. Inf. Technol. Electron. Eng. 2015, 16, 135–151. [Google Scholar] [CrossRef]
- Li, J.; Wang, H.; Wang, X.; Li, Z. Optimized Sleep Strategy Based on Clustering in Dense Heterogeneous Networks. EURASIP J. Wirel. Commun. Netw. 2018, 2018, 290. [Google Scholar] [CrossRef]
- Wen, Y.; Vese, L.A.; Shi, K.; Guo, Z.; Sun, J. Nonlocal Adaptive Biharmonic Regularizer for Image Restoration. J. Math. Imaging Vis. 2022, 65, 453–471. [Google Scholar] [CrossRef]
- Xiong, L.; Wang, G.-Z.; Liu, H.-C. New Community Estimation Method in Bipartite Networks Based on Quality of Filtering Coefficient. Sci. Program. 2019, 2019, 4310561. [Google Scholar] [CrossRef]
- Shi, K. Multi-Attention Embedded Network for Salient Object Detection. Soft Comput. 2021, 25, 13053–13067. [Google Scholar] [CrossRef]
- Wang, X.; Gu, R.; Li, J.; Ma, Q. Improved Reduced Latency Soft-Cancellation Algorithm for Polar Decoding. China Commun. 2020, 17, 65–77. [Google Scholar] [CrossRef]
- Jing, X.; Gui, X.; Zhou, P.; Hong, Z. Physical Explanation of Fabry–Pérot Cavity for Broadband Bilayer Metamaterials Polarization Converter. J. Light. Technol. 2018, 36, 2322–2327. [Google Scholar] [CrossRef]
- Xia, R.; Jing, X.; Gui, X.; Tian, Y. Broadband Terahertz Half-Wave Plate Based on Anisotropic Polarization Conversion Metamaterials. Opt. Mater. Express 2017, 7, 977–988. [Google Scholar] [CrossRef]
- Zhao, J.; Jing, X.; Wang, W.; Tian, Y.; Zhu, D.; Shi, G. Steady Method to Retrieve Effective Electromagnetic Parameters of Bianisotropic Metamaterials at One Incident Direction in the Terahertz Region. Opt. Laser Technol. 2017, 95, 56–62. [Google Scholar] [CrossRef]
- Wang, Q.; Li, C.; Fang, B.; Ke, L.; Lu, J.; Ma, X.; Hong, Z.; Jing, X. Flexible and Independent Control of Asymmetric Vortex Beams Based on Spin Multiplexing All-Dielectric Metasurface. J. Light. Technol. 2023, 41, 7098–7104. [Google Scholar] [CrossRef]
- Zeng, B.; Li, C.; Cheng, H.; Fang, B.; Lu, J.; Ma, X.; Wang, L.; Hong, Z.; Jing, X. Anisotropic Programmable Metasurface Beam Splitter Based on Diode Real-Time Control. Opt. Lasers Eng. 2023, 169, 107723. [Google Scholar] [CrossRef]
- Wang, W.; Jing, X.; Zhao, J.; Li, Y.; Tian, Y. Improvement of Accuracy of Simple Methods for Design and Analysis of a Blazed Phase Grating Microstructure. Opt. Appl. 2017, 47, 183–198. [Google Scholar] [CrossRef]
- Jiang, L.; Fang, B.; Yan, Z.G.; Fan, J.; Qi, C.K.; Liu, J.J.; He, Y.W.; Li, C.X.; Jing, X.F.; Gan, H.Y.; et al. Terahertz high and near-zero refractive index metamaterials by double layer metal ring microstructure. Opt. Laser Technol. 2020, 123, 105949. [Google Scholar] [CrossRef]
- Li, S.S.; Fang, Y.N.; Wang, J.F. Control of Light–Matter Interactions in Two-Dimensional Materials with Nanoparticle-on-Mirror Structures. Opto Electron. Sci. 2024, 3, 240011. [Google Scholar] [CrossRef]
- Liang, M.W.; Lu, D.Z.; Ma, Y.G. Vectorial Optical Fields Manipulation via Metasurfaces. Opto Electron. Eng. 2024, 51, 240068. [Google Scholar] [CrossRef]
- AbdelAll, N.; Almokhtar, M.; Khouqeer, G.; Abood, I.; Soliman, S.E. Rainbow Trapping with Engineered Topological Corner States and Cavities in Photonic Crystals. Adv. Quantum Technol. 2024, 7, 2400050. [Google Scholar] [CrossRef]
- Peters, C.; Forbes, A. Controlling the Hidden Parity in Vectorial Light with Metasurfaces. Adv. Photon. 2024, 6, 040501. [Google Scholar] [CrossRef]
- Rane, S.; Prabhu, S.; Chowdhury, D.R. Physics and Applications of Terahertz Metagratings. Opto Electron. Sci. 2024, 3, 230049. [Google Scholar] [CrossRef]
- Yang, H.; He, H.-R.; Hu, Y.-Q.; Duan, H.-G. Metasurface-Empowered Vector Light Field Regulation, Detection and Application. Opto Electron. Eng. 2024, 51, 240168. [Google Scholar] [CrossRef]
- Liu, S.; Cao, W.; Jiang, S.; He, L.; Lin, F.; He, X. 3D Dirac Semimetal Supported Tunable Multi-Frequency Terahertz Metamaterial Absorbers. Adv. Quantum Technol. 2024, 7, 2300386. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, H.; Zhang, G. Nanophononic Metamaterials Induced Proximity Effect in Heat Flux Regulation. Front. Phys. 2024, 19, 23204. [Google Scholar] [CrossRef]
- Hou, T.; Ge, Y.; Xue, S.; Chen, H. Curved Anisotropic Polaritons. Front. Phys. 2024, 19, 32201. [Google Scholar] [CrossRef]
- Seo, J.; Jo, J.; Kim, J.; Kang, J.; Kang, C.; Moon, S.-W.; Lee, E.; Hong, J.; Rho, J.; Chung, H. Deep-Learning-Driven End-to-End Metalens Imaging. Adv. Photon. 2024, 6, 066002. [Google Scholar] [CrossRef]
- Wu, Y.; Yang, Q.; Shen, B.; Tao, Y.; Zhang, X.; Tao, Z.; Xing, L.; Ge, Z.; Li, T.; Bai, B.; et al. Multifunctional Mixed Analog/Digital Signal Processor Based on Integrated Photonics. Opto Electron. Sci. 2024, 3, 240012. [Google Scholar] [CrossRef]
- Yu, Z.; Li, M.; Xing, Z.; Gao, H.; Liu, Z.; Pu, S.; Mao, H.; Cai, H.; Ma, Q.; Ren, W.; et al. Genetic Algorithm Assisted Meta-Atom Design for High-Performance Metasurface Optics. Opto Electron. Sci. 2024, 3, 240016. [Google Scholar] [CrossRef]
- Taha, B.A.; Addie, A.J.; Haider, A.J.; Chaudhary, V.; Apsari, R.; Kaushik, A.; Arsad, N. Exploring Trends and Opportunities in Quantum-Enhanced Advanced Photonic Illumination Technologies. Adv. Quantum Technol. 2024, 7, 2300414. [Google Scholar] [CrossRef]
- Zhou, L.; Lou, H.; Deng, Z.; Qin, X.; Pan, J.; Di, Y.; Gu, C.; Luo, D.; Li, W. Compact Mid-Infrared Dual-Comb Spectrometer over 3–4 μm via Intra-Pulse Difference Frequency Generation in LiNbO3 Waveguides. High Power Laser Sci. Eng. 2024, 12, 03000e23. [Google Scholar] [CrossRef]
- Rahman, M.S.S.; Ozcan, A. Physics and Artificial Intelligence: Illuminating the Future of Optics and Photonics. Adv. Photon. 2024, 6, 050500. [Google Scholar] [CrossRef]
- Han, L.; Duan, Q.; Duan, J.; Zhu, S.; Chen, S.; Yin, Y.; Chen, H. Unidirectional Propagation of Water Waves near Ancient Luoyang Bridge. Front. Phys. 2024, 19, 32206. [Google Scholar] [CrossRef]
- Zhou, J.; Yin, Y.; Tang, J.; Xia, Y.; Yin, J. Information Transmission through Parallel Multi-Task-Based Recognition of High-Resolution Multiplexed Orbital Angular Momentum. Front. Phys. 2024, 19, 52202. [Google Scholar] [CrossRef]
- Ullah, M.; Mikki, S. Optical Nonreciprocity in a Multimode Cavity Optomechanical System Controlled by Dynamic Casimir Force. Adv. Quantum Technol. 2024, 7, 2400007. [Google Scholar] [CrossRef]
- Refaeli, Z.; Marcus, G.; Shamir, Y. A Simple Method for Pulse Contrast Enhancement via Self-Focusing. High Power Laser Sci. Eng. 2024, 12, 02000e18. [Google Scholar] [CrossRef]
- Hao, Z.; Chen, H.; Yin, Y.; Qiu, C.-W.; Zhu, S.; Chen, H. Efficient Conversion of Acoustic Vortex Using Extremely Anisotropic Metasurface. Front. Phys. 2024, 19, 42202. [Google Scholar] [CrossRef]
- Shen, C.-Y.; Li, J.; Li, Y.; Gan, T.; Bai, L.; Jarrahi, M.; Ozcan, A. Multiplane Quantitative Phase Imaging Using a Wavelength-Multiplexed Diffractive Optical Processor. Adv. Photon. 2024, 6, 056003. [Google Scholar] [CrossRef]
- Berhe, A.M.; As’ham, K.; Al-Ani, I.; Hattori, H.T.; Miroshnichenko, A.E. Strong Coupling and Catenary Field Enhancement in the Hybrid Plasmonic Metamaterial Cavity and TMDC Monolayers. Opto Electron. Adv. 2024, 7, 230181. [Google Scholar] [CrossRef]
- Nan, T.; Zhao, H.; Guo, J.; Wang, X.; Tian, H.; Zhang, Y. Generation of Structured Light Beams with Polarization Variation along Arbitrary Spatial Trajectories Using Tri-Layer Metasurfaces. Opto Electron. Sci. 2024, 3, 230052. [Google Scholar] [CrossRef]
- Zhang, C.-L.; Hu, K.-X.; Zhang, J.; Cao, J.; Zhang, S.; Wang, H.-F. Topological Phase Transition and Edge States with Tunable Localization in the Cyclic Four-Mode Optical System. Adv. Quantum Technol. 2024, 7, 2400165. [Google Scholar] [CrossRef]
- Martín-Hernández, R.; Grünewald, L.; Sánchez-Tejerina, L.; Plaja, L.; Conejero Jarque, E.; Hernández-García, C.; Mai, S. Optical magnetic field enhancement using ultrafast azimuthally polarized laser beams and tailored metallic nanoantennas. Photon. Res. 2024, 12, 1078–1092. [Google Scholar] [CrossRef]
- Jiang, J.; Fang, B.; Li, C.; Hong, Z.; Jing, X. Improvement of terahertz beam modulation efficiency for baseless all-dielectric coded gratings. Photon. Res. 2023, 11, 1738–1750. [Google Scholar] [CrossRef]
- Xiang, S.Y.; Song, Z.W.; Zhang, Y.H.; Guo, X.; Han, Y.; Hao, Y. Progress in the research of optical neural networks. Opto Electron. Eng. 2024, 51, 240101. [Google Scholar] [CrossRef]
- Meng, X.; Qin, C.; Liang, X.; Zhang, G.; Chen, R.; Hu, J.; Yang, Z.; Huo, J.; Xiao, L.; Jia, S. Deep learning in two-dimensional materials: Characterization, prediction, and design. Front. Phys. 2024, 19, 53601. [Google Scholar] [CrossRef]
- Roche, L.J.; Betz, F.; Yang, Y.; Limame, I.; Shih, C.-W.; Burger, S.; Reitzenstein, S. Numerical investigation of a coupled micropillar–waveguide system for integrated quantum photonic circuits. Adv. Quantum Technol. 2024, 7, 2400195. [Google Scholar] [CrossRef]
- Liu, Y.; Tian, Y.; Li, C.; Fang, B.; Liu, J.; Hong, Z.; Jing, X. All-dielectric double-layer honeycomb tunable metamaterial absorber with integrated gold nanoparticles. Photon. Res. 2024, 12, 2344–2353. [Google Scholar] [CrossRef]
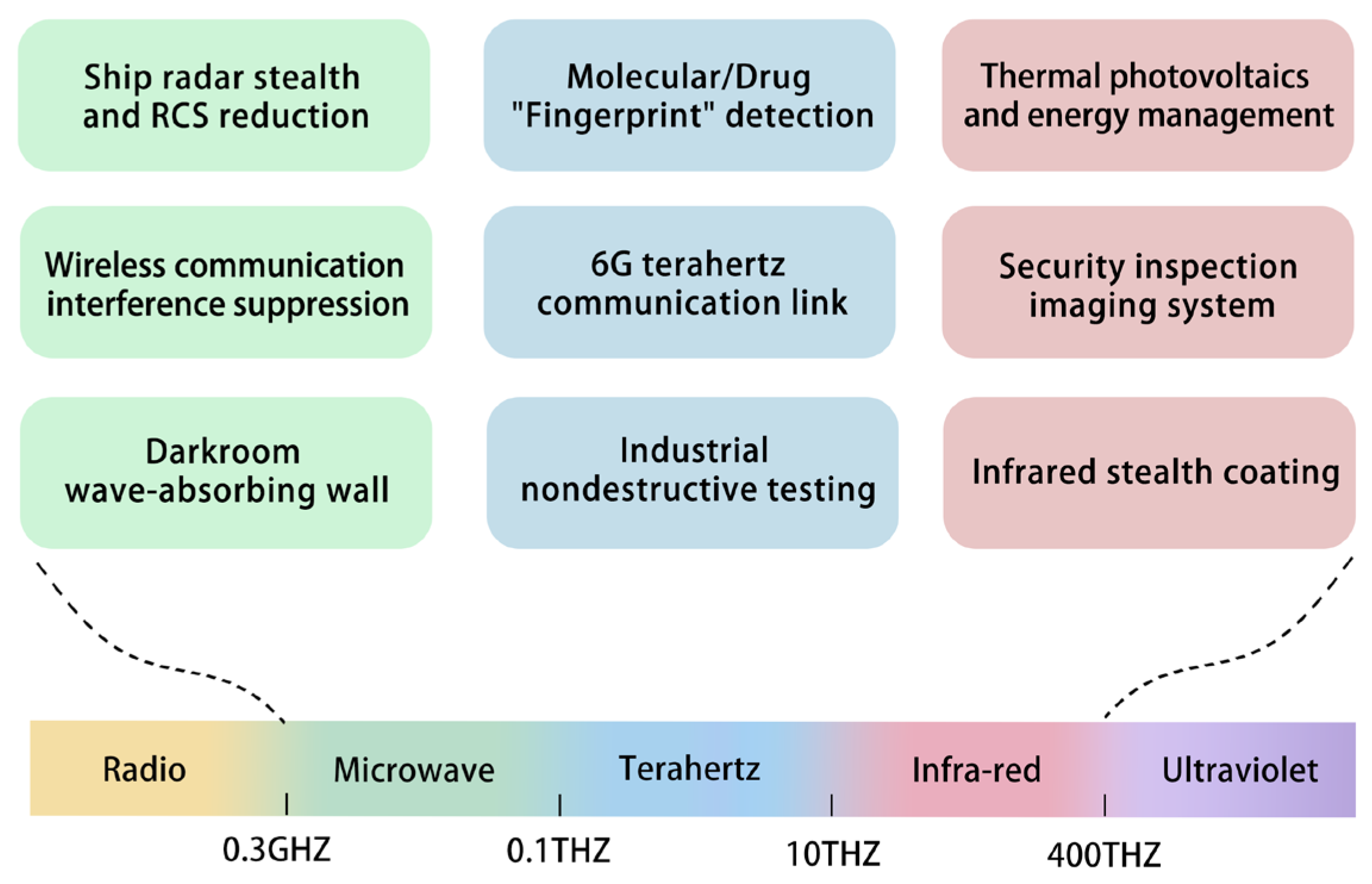
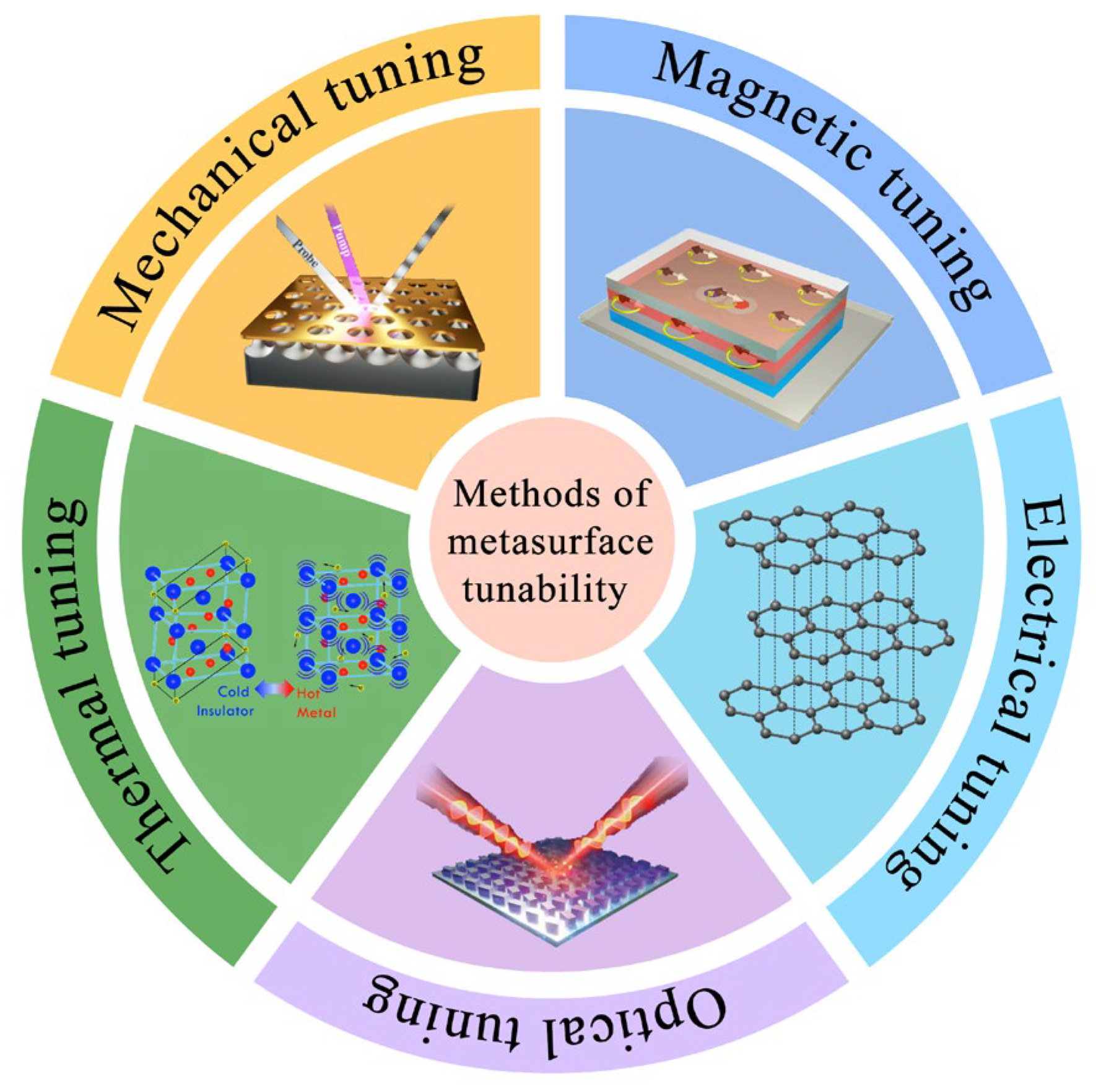
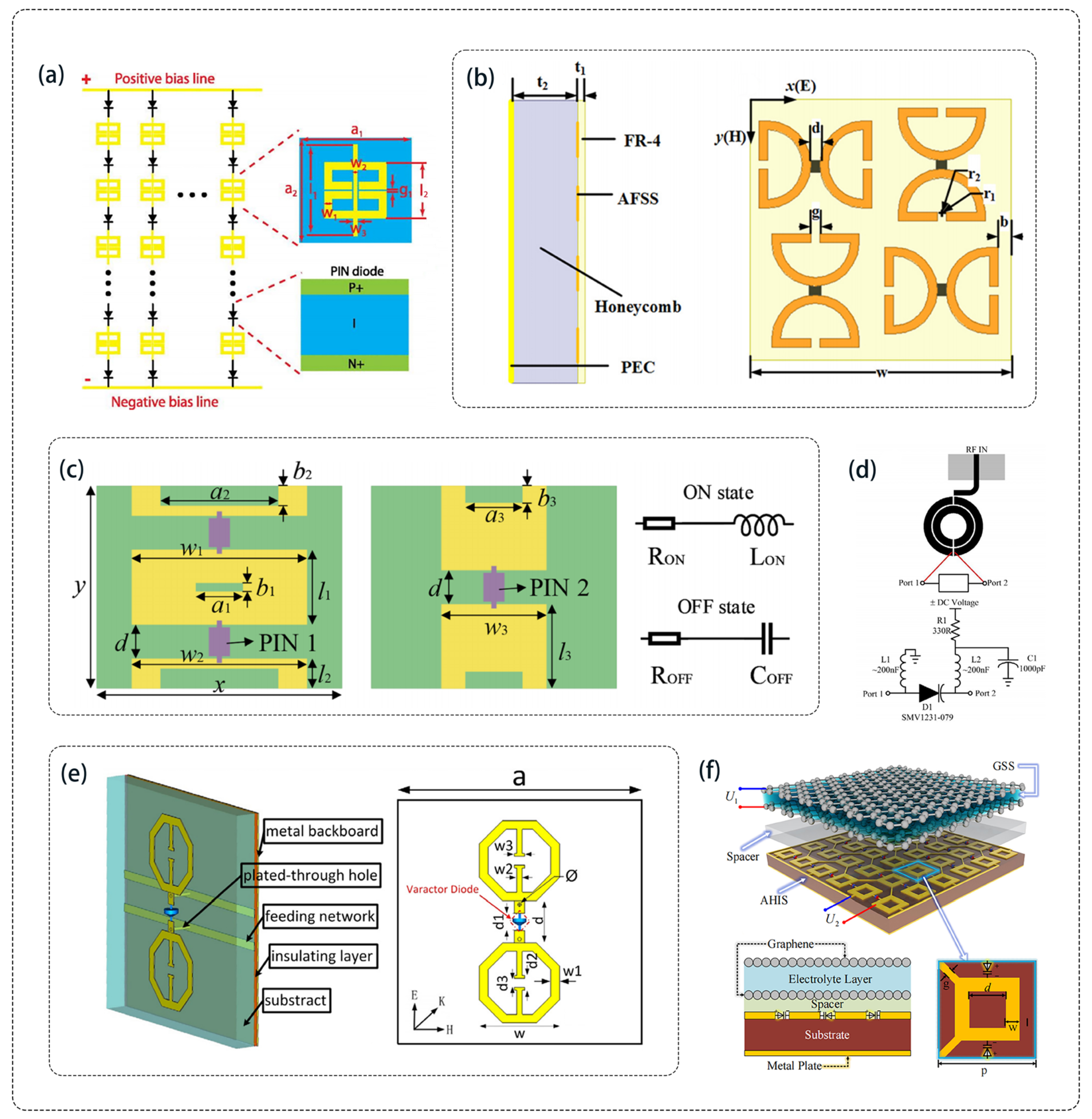
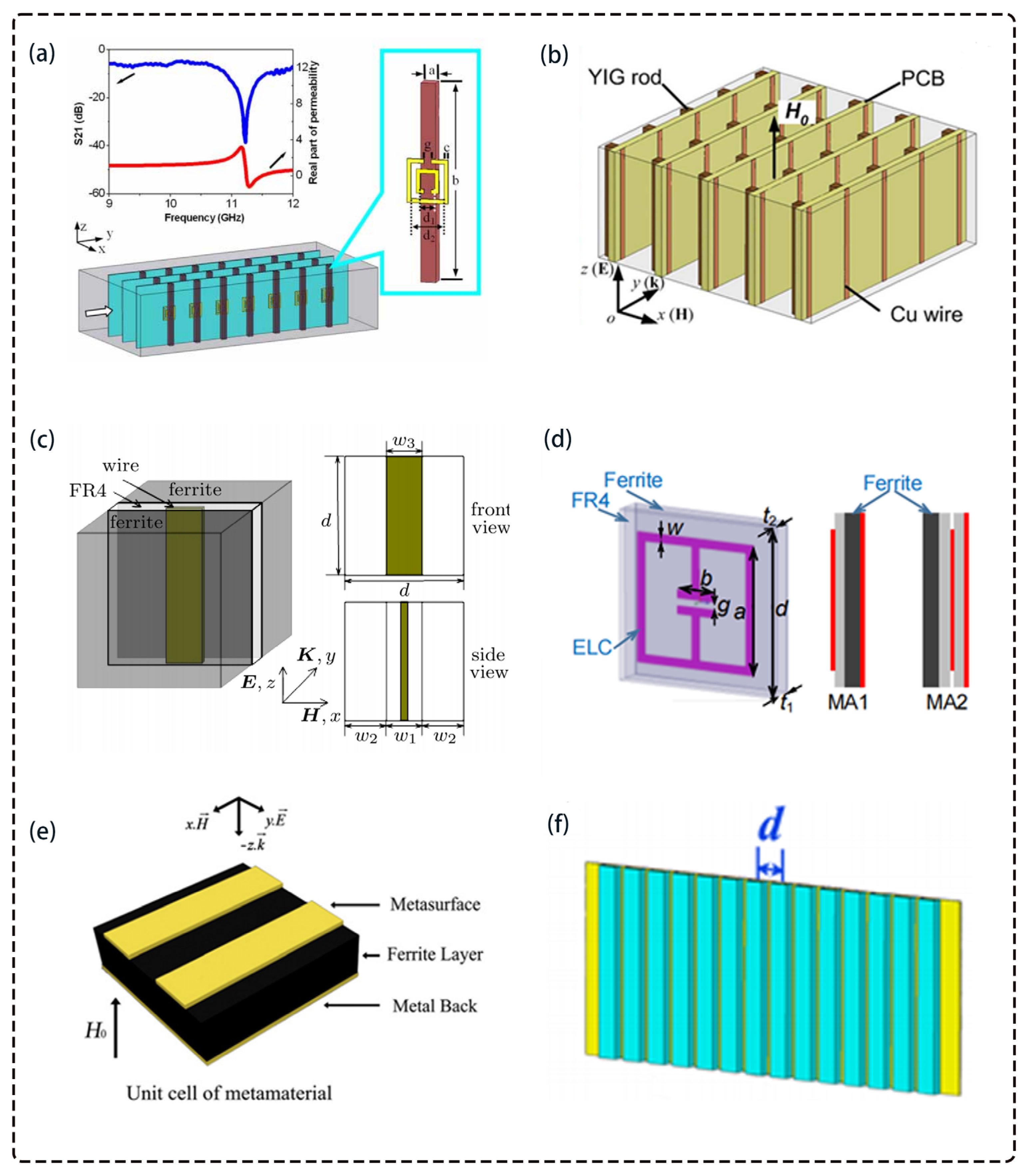
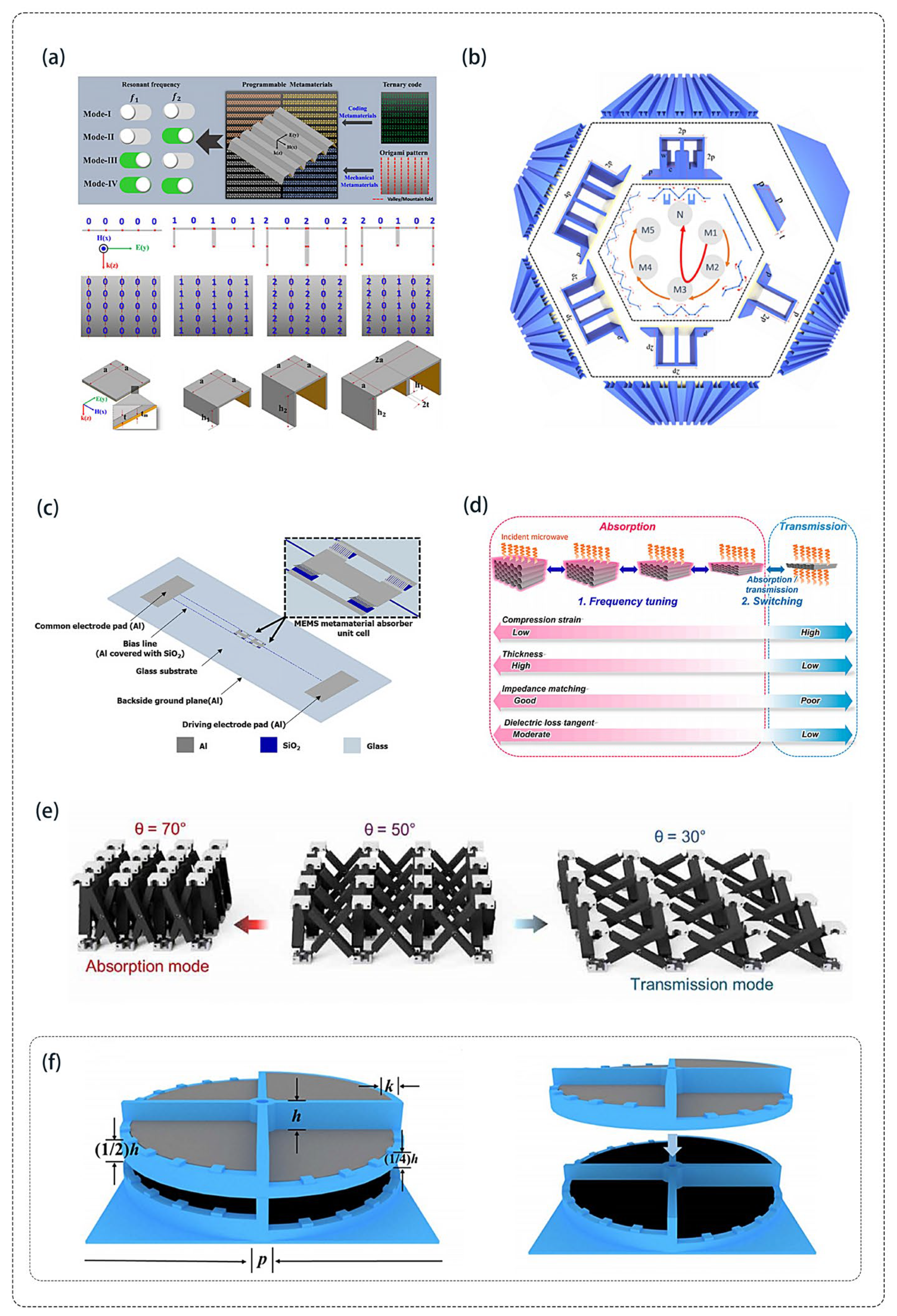
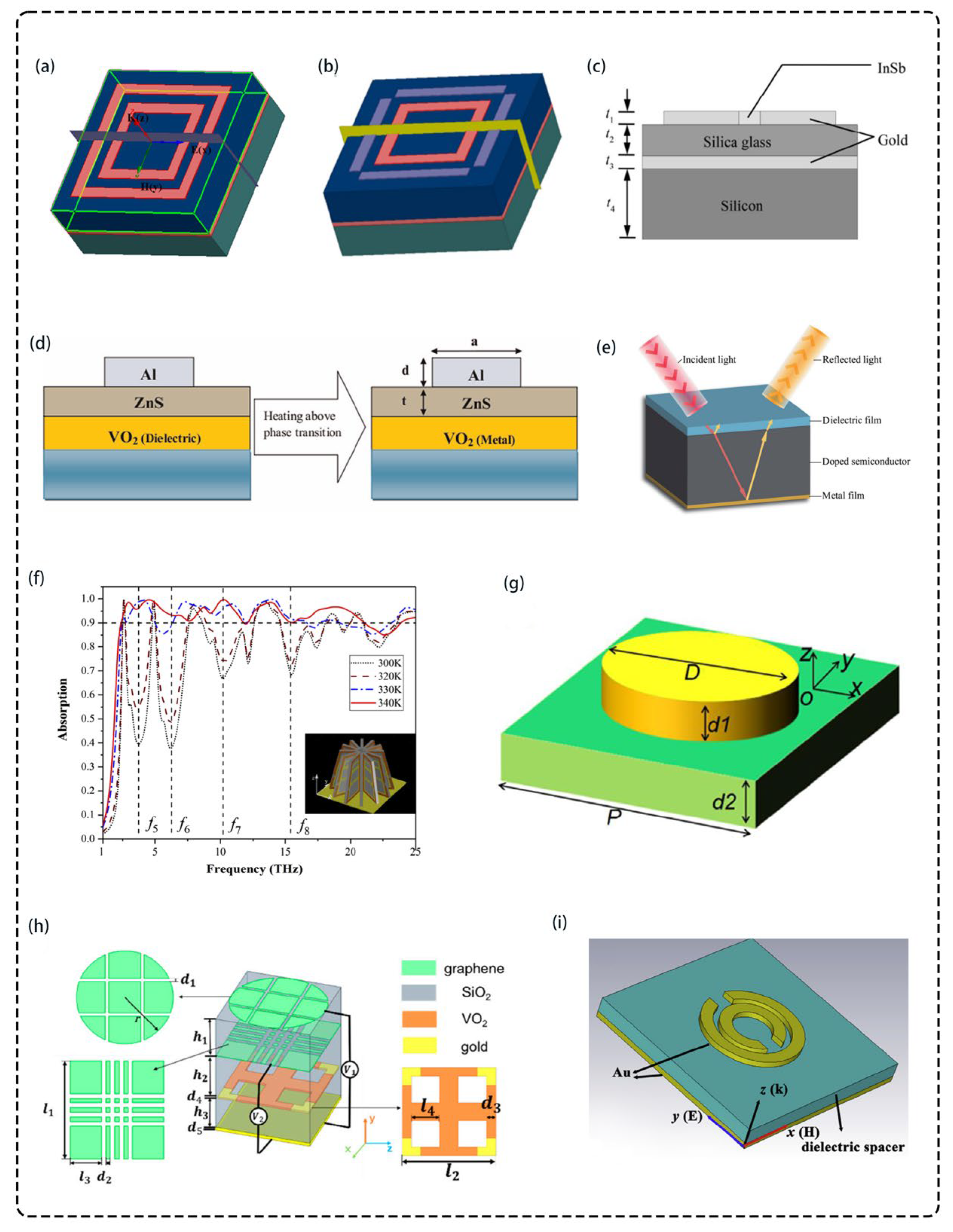
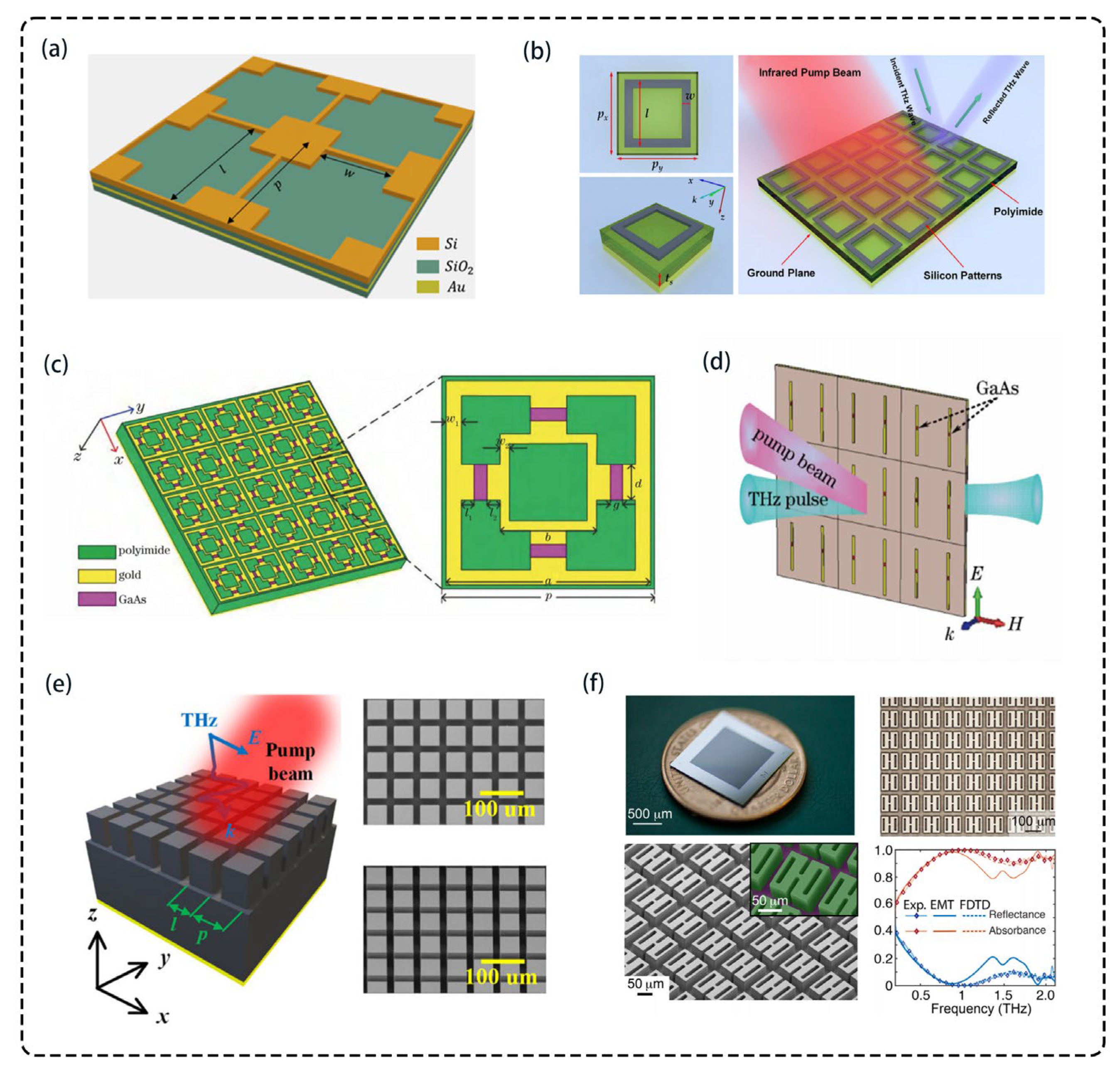
| Property | Microwave Band | Terahertz Band | Infrared Band |
|---|---|---|---|
| Primary Tuning Mechanism | Electrical/Magnetic/ Mechanical Control | Electrical/ Thermal Control | Thermal Control |
| Typical Tuning Materials | Ferrites/Diodes, etc. | Graphene/ Liquid Crystals, etc. | VO2/GST Phase-Change Materials, etc. |
| Response Time | ns-μs Level | fs-ns Level | μs-ms Level |
| Typical Tuning Range | Δf > 5 GHz | Δf > 0.5 THz | Δλ > 2 μm |
| Dominant Loss Mechanism | Ohmic Loss | Carrier Scattering | Dielectric Loss |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, K.; Feng, H.; Gu, M.; Jing, X.; Li, C. Research Progress on Tunable Absorbers for Various Wavelengths Based on Metasurfaces. Photonics 2025, 12, 968. https://doi.org/10.3390/photonics12100968
Jiang K, Feng H, Gu M, Jing X, Li C. Research Progress on Tunable Absorbers for Various Wavelengths Based on Metasurfaces. Photonics. 2025; 12(10):968. https://doi.org/10.3390/photonics12100968
Chicago/Turabian StyleJiang, Ke, Huizhen Feng, Manna Gu, Xufeng Jing, and Chenxia Li. 2025. "Research Progress on Tunable Absorbers for Various Wavelengths Based on Metasurfaces" Photonics 12, no. 10: 968. https://doi.org/10.3390/photonics12100968
APA StyleJiang, K., Feng, H., Gu, M., Jing, X., & Li, C. (2025). Research Progress on Tunable Absorbers for Various Wavelengths Based on Metasurfaces. Photonics, 12(10), 968. https://doi.org/10.3390/photonics12100968





