Abstract
This study evaluates the performance of count regression models in the presence of zero inflation, outliers, and overdispersion using both simulated and real-world maternal mortality dataset. Traditional Poisson and negative binomial regression models often struggle to account for the complexities introduced by excess zeros and outliers. To address these limitations, this study compares the performance of robust zero-inflated (RZI) and robust hurdle (RH) models against conventional models using the Akaike Information Criterion (AIC) and Bayesian Information Criterion (BIC) to determine the best-fitting model. Results indicate that the robust zero-inflated Poisson (RZIP) model performs best overall. The simulation study considers various scenarios, including different levels of zero inflation (50%, 70%, and 80%), outlier proportions (0%, 5%, 10%, and 15%), dispersion values (1, 3, and 5), and sample sizes (50, 200, and 500). Based on AIC comparisons, the robust zero-inflated Poisson (RZIP) and robust hurdle Poisson (RHP) models demonstrate superior performance when outliers are absent or limited to 5%, particularly when dispersion is low (5). However, as outlier levels and dispersion increase, the robust zero-inflated negative binomial (RZINB) and robust hurdle negative binomial (RHNB) models outperform robust zero-inflated Poisson (RZIP) and robust hurdle Poisson (RHP) across all levels of zero inflation and sample sizes considered in the study.
1. Introduction
Excess zeros are common in numerous fields, including healthcare, agriculture, ecology, and manufacturing industries [1,2]. A Zero-Inflated (ZI) model [3] argues that zero counts arise from a combination of two distributions; one distribution generates structural zeros, representing subjects who are not at all at risk of experiencing the event (and thus consistently produce zero counts). For instance, when quantifying specific high-risk behaviors, certain individuals may record a score of zero due to their lack of susceptibility to such health-risk behaviors [4]. The second distribution generates sampling zeros, representing individuals who are at risk but did not experience or report the event during the study period. The justification for categorizing zeros into two categories is that a high proportion of zeros frequently results from the presence of a subgroup of patients who are not at risk for certain outcomes during the study period [3]. The probability of belonging to the zero inflation component is assessed using a Bernoulli model, while a standard count distribution, such as Poisson or negative binomial (NB), represents the counts in the count component [5]. Conversely, a hurdle model [6] claims that all zero observations originate from a singular structural source, comprising a binary component to determine whether the response variable is zero or positive, alongside a truncated model, such as a truncated Poisson or truncated NB distribution, for the positive data. Excess zeros indicate more zeros than the distribution we are modeling would expect. Zero-inflated and hurdle models have been used extensively in various research domains to model such data [2,7]. The traditional models, such as the standard Poisson and NB models, often fail to address the complexity of outliers, overdispersion, and excess zeros simultaneously. The understanding and useful comparison of the robust zero-inflated (RZI) and robust hurdle (RH) models remain largely unexplored, despite substantial advances in statistical modeling methods for count data [1,2]. Although both models address the frequent excess zeros seen in the count data, their fundamental tenets and estimating strategies are different.
Maternal mortality data often exhibit zero inflation, characterized by an excess of zero counts or units reporting no maternal deaths, compared to what standard count models such as Poisson or NB would predict [8,9]. Identifying factors that contribute to maternal mortality and formulating effective interventions are essential to minimize the increase in maternal mortality. In this context, there is a need to employ statistical models that can adequately handle the excessive zeros, overdispersion, and potential outliers that are often observed in maternal mortality [10]. Previous studies that have looked at factors affecting maternal death have used different analysis strategies, with some ignoring the underlying zero inflation [11,12]. There has been considerable interest in the literature in comparing zero-inflated and hurdle models for analyzing count data with excess zeros and outliers [2,10,13]. However, the robustness to outliers that these comparisons frequently neglect can have significant effects on the accuracy and reliability of the models’ results. Robust zero-inflated models and robust hurdle models have been proposed to handle outliers in addition to zero inflation. There is a lack of comprehensive studies that directly examine the performance of robust hurdle and zero-inflated models in the presence of outliers. In addition, there has been little research on the application of these models to maternal mortality data [1,2,12], an important public health indicator. Using simulated data and data on maternal mortality, this study attempts to close these gaps by comparing the robust zero-inflated and hurdle models in the presence of outliers. Through this investigation, the study hopes to shed light on how well these models handle excessive zeros and outliers in count data, with an emphasis on enhancing modeling accuracy and forecasting rates of maternal death.
2. Methods
2.1. Overview of Count Data Models
This section outlines the statistical frameworks employed to model count data, addressing key challenges such as zero inflation, overdispersion, and outliers. Introduces robust extensions of conventional models, specifically robust zero-inflated and hurdle models, which are designed to improve estimation accuracy in the presence of deviations from model assumptions and outliers. These robust models provide a more reliable analytical framework for real-world datasets, particularly in maternal mortality research, where data irregularities are common.
2.2. Classical Zero-Inflated and Hurdle Models
2.2.1. Standard Zero-Inflated (ZI) Models
In the ZI model introduced by [3], zero outcomes can originate from two distinct sources. We have structural zeros, which occur due to an inherent process, and sampling zeros, which arise from a standard count distribution such as Poisson or NB. The general form of a ZI model is as follows:
which combines a degenerate distribution at zero and an untruncated count distribution parameterized by . When the count component follows a Poisson distribution, the model becomes a Zero-Inflated Poisson (ZIP) model:
here, is the Poisson mean and is the probability of structural zeros. The mean and variance of the ZIP model are then given by the following:
To model the count part of a zero inflation, Poisson regression assumes that the mean and variance are equal. However, real-world data often show overdispersion, where the variance exceeds the mean. This may result from unobserved heterogeneity, omitted variables, clustering, or outliers [14,15]. In such cases, the NB model is more appropriate. The ZINB model, which accounts for both excess zeros and overdispersion, is specified as
where is the NB mean, is the structural zero probability, r is the dispersion parameter, and is the gamma function. The mean and variance are as follows:
As , the ZINB model converges to the ZIP model. Smaller values of r indicate higher overdispersion. In practical applications, both and are modeled using explanatory variables. The ZI models can thus be parameterized as
where and are covariate vectors for the count and zero components, respectively, and and are their corresponding coefficients. The covariates for and need not be the same.
2.2.2. Standard Hurdle Models
As an alternative to ZI models, hurdle models [6] are formulated as two component mixture models. They consist of a component that models excess zeros and another that models positive counts using a truncated count distribution, such as the truncated Poisson or truncated NB distribution. Let denote the count response for the i-th observation, where , and n is the total number of observations. The general form of a hurdle model is expressed as
where is the probability of observing a structural zero, and is the probability mass function (PMF) of a standard count distribution parameterized by vector . The denominator, , normalizes the distribution to reflect that only positive counts are considered. If the count component follows a Poisson distribution, the corresponding hurdle Poisson model is
where the denotes the probability of a zero count, is the mean of the underlying Poisson distribution. The mean and variance of the HP are then given by
to handle overdispersion in count data, the positive count component can alternatively follow an NB distribution. The HNB model is then given by
where r is the dispersion parameter and is the mean of the NB distribution, is the is the gamma function, and is the structural zero probability. The mean and variance of the HNB model are given by
As with ZI models, covariates can be incorporated into both the zero and count components. The hurdle model can thus be parameterized as
where and are vectors of regression coefficients for the covariates and , respectively.
2.3. Robust Extensions of Zero-Inflated and Hurdle Models
2.3.1. Robust Zero-Inflated Models
Although ZIP and ZINB models handle excess zeros, they can be sensitive to outliers. The RZIP and RZINB models improve the standard ZI models by incorporating robust estimation techniques. The robust zero-inflated models (RZIP and RZINB), first proposed by [5] and later refined by [16], integrate Huber’s M-estimation into standard ZIP/ZINB structures. The robust approach uses the Huber -function [17], to downweight extreme values during parameter estimation. In the RZI models, the parameters are estimated using a robust Expectation–Maximization (EM) algorithm by [5]. In mixture models like ZI, the EM algorithm is a natural approach for computing maximum likelihood estimates (MLEs) [3]. This algorithm works by introducing latent variables that indicate whether a zero outcome came from the excess zero component or from the count distribution. According to [5] we define when the observation originates from the zero inflation component, and for the non-zero state
With this, the complete data log-likelihood can be expressed as
where . Maximizing this log-likelihood is straightforward because the complete data log-likelihood functions for and , denoted by and , can be optimized separately with respect to their respective parameters using standard methods. The EM algorithm maximizes the log-likelihood of models (10) and (13) through an iterative process consisting of two main steps which is the E-step and the M-step. In the E-step, each latent variable is replaced by its conditional expectation, given the current estimates of . In the M-step, these expected values are treated as fixed, and the complete data log-likelihood is maximized with respect to and . These two steps are repeated alternately until the parameter estimates converge. The algorithm begins with initial values and proceeds iteratively through the following three steps until convergence.
E-step: Estimate by its conditional expectation given the current estimates and
M-step for . Find by maximizing , equivalent to solving
M-step for . For the non-degenerate component, we find by maximizing which is equivalent to solving the estimation ;
Hall [5] proposed in the RES approach that the estimating functions (18) and (19) from the M-step of the EM algorithm can be achieved with robustified estimating functions. That is, we downweight observations in the extreme tails of the Poisson or NB component using a bounded influence function , and apply leverage-based weights . To robustify the estimation, we replace the standard score functions in Equations (18) and (19) with bounded influence versions that combine residual trimming through and leverage weighting via . Specifically, solving for the parameter and in the following Equations (20) and (21). The estimation equation for the zero inflation component parameter is expressed as follows:
where for the non-degenerate Poisson component, and for the negative binomial component, where . The function truncates extreme responses:
with and being the c and quantiles of the non-degenerate distribution (Poisson or NB). The downweighting function is used to reduce the influence of high-leverage points, and is taken as , where is the leverage from the design matrix , with an analogous definition for .
2.3.2. Robust Hurdle Models
The robust hurdle models used in this study build upon the methodology developed by [18], who proposed a robust version of the hurdle models that are based on standard hurdle models by incorporating bounded influence estimation through the -Huber function to mitigate the influence of outliers [19]. For the binary hurdle component, we replace the standard logistic regression with a robust logistic regression using the -Huber function [17]. This ensures that outliers in the binary classification of zeros and non-zeros have less influence.
where are the Pearson residuals, denotes the conditional variance of the positive count component, i.e., the variance of the truncated Poisson or truncated NB distribution, is the Huber function, , and where
ensures that Fisher is consistent with . We have this for the truncated Poisson component
where , variance , and this for the truncated NB component
where , variance , and cutoff points
The classical estimating equations of the quasi-likelihood estimator for GLM imply the structure of (22). These would utilize The function in (22) is responsible for managing deviations in the y-space. To manage deviations in the design space, leverage points are downweighted by adding weights . For instance, , where is the ith diagonal element of the hat matrix. According to the use in linear regression, the estimator produced from (22) is called a Mallows-type estimator. It reduces to a Huber-type estimator for all i when . Note that it is easy to rewrite the estimating equations (22) as
The function reflects the structure of weighted estimating equations involving two types of weights: applied to the residuals and applied to the design matrix.
2.4. Model Comparison
To assess the performance of the six different models (Poisson, NB, RZIP, RZINB, RHP, and RHNB) under different simulation scenarios, the study adopted the widely used model selection criteria: Akaike’s information criteria (AIC) developed by [20]. AIC has been presented as a model selection criterion for comparing non-nested models based on maximum likelihood, utilizing the fitted log-likelihood function to identify the optimal model. The AIC evaluates the relative quality of a statistical model by rewarding goodness of fit while imposing a penalty that increases with the number of estimated parameters. As the log-likelihood is anticipated to rise with the addition of parameters to a model, the AIC criterion imposes a penalty on models with a greater number of parameters (q). The penalty function may also depend on n, the number of observations. This penalty prevents overfitting. Consequently, the AIC is defined as
where L is the maximal likelihood function value for the estimated model, q is the number of degrees of freedom, and 2 is a tuning parameter to balance the information in the model with the residuals, according to the number of degrees of freedom. It is desirable to choose a model with the lowest AIC. Although AIC penalizes the complexity of the model using a constant factor of 2 per parameter, another widely used criterion, the Bayesian Information Criterion (BIC), takes a different approach. Like AIC, BIC rewards goodness of fit but introduces a stronger penalty for model complexity, which makes BIC more conservative. The Bayesian Information Criterion (BIC) is defined as follows:
where L is the likelihood of the model, k is the number of parameters, and n is the sample size. When fitting models, it is possible to increase the likelihood by adding parameters, but doing so may result in overfitting. The BIC addresses this issue by introducing a penalty term for the number of parameters in the model. The penalty term in BIC is larger than the penalty term in AIC.
3. Simulation Study
To assess the performance of standard and robust count regression models under varying levels of overdispersion, zero inflation, and contamination, a structured simulation study was conducted. The dataset was generated from the ZINB model, which is characterized by a mean variance of this form
that allows the variance to be greater than the mean, a common choice for modeling overdispersed count data such as maternal mortality in this study. The simulation design considered combinations of four key factors which are sample size (50, 200, and 500), dispersion levels , i.e., 1 is considered as high dispersion, 3 as moderate, and 5 as low in this study, structural zero proportions (0.5, 0.7, and 0.8), and outlier proportions (0.00, 0.05, 0.10, and 0.15). A summary of the simulation scenarios considered in the study is shown below in Table 1. This produced 3 × 3 × 3 × 4 = 108 distinct simulation scenarios in all. Each scenario was run 1000 times to reduce the influence of simulation error, and the AIC was averaged over the 1000 runs.

Table 1.
Simulation scenarios considered in the simulation study.
For each observation , the response variable was generated from the ZINB model:
with the mean , is the structural zero probability, and dispersion r where with a single continuous covariate drawn independently from a uniform distribution . The intercept was fixed at 1, and the slope coefficient at 1.5, where and To assess the robustness of the models to extreme values, outliers were introduced in the simulated data by randomly selecting a proportion of the observations determined by the specified outlier level (0, 0.05, 0.10, or 0.15), and inflating their outcome values by a factor of 10. Specifically, for a given sample size n, a total of indices were randomly sampled, and the corresponding response values were multiplied by 10. This approach simulates extreme count values that may arise due to data entry errors or rare events, allowing us to evaluate the model’s performance in the presence of such anomalies.
3.1. Simulation Study Findings
3.1.1. Initial Assessment of the Simulation Data
The NB model in Table A2 consistently achieves the lowest AIC across all sample sizes for the initial assessment of the simulation, where the parameters are set to zero, such as the inflation and outliers, confirming it as the best fit for data generated from a ZINB model. As expected, the NB model outperforms the Poisson model, since the data was simulated using an NB model, which is also reflected in its lower AIC value. While robust models like RZIP, RZINB, RHP, and RHNB are designed to handle complexities such as zero inflation and outliers, their AIC values remain higher in this scenario, where no excess zeros or outliers were introduced. These results emphasize the importance of selecting models aligned with the data’s underlying structure, with the NB model excelling in cases of overdispersed count data.
3.1.2. AIC Comparison Across Regression Models
In this section, we describe the analysis of data generated with the ZINB regression model in sixteen different simulation scenarios with varying sample sizes (50, 200, and 500), different levels of outliers (0.0, 0.05, 0.10, and 0.15), and magnitude of dispersion (r = 1, 3, 5). Table A3, Table A4, Table A5, Table A6, Table A7, Table A8, Table A9, Table A10 and Table A11 display the averaged AIC model fit statistics for Poisson, NB, RZIP, RZINB, RHP, and RHNB regression models fitted on data generated with the ZINB regression model with different magnitudes of dispersion, outliers, and sample sizes. The AIC values reveal that the RZINB and RHNB models generally provide the best fit for data generated from a ZINB model, especially under conditions of higher proportions of zeros and levels of outliers. For example, with 5 as the low dispersion level, 0.0% outliers, and a 50% proportion of zeros, the RZIP model achieves a lower AIC than the RZINB model. As the proportion of zeros increases and outliers increases, the RZINB and RHNB models consistently show improved performance, indicating their robustness in handling zero-inflated data. Conversely, the Poisson model and NB have higher AIC values than the other models, reflecting their limitations in scenarios characterized by overdispersion and excess zeros. These results highlight the importance of selecting appropriate modeling techniques that align with the underlying data distribution and characteristics, particularly in the presence of zeros and outliers.
3.1.3. Performance Under Low Outlier Levels and Increasing Dispersion
The RZIP and RHP models, when the dispersion is 5, express superior performance in terms of model fit, particularly under conditions with no outliers (0% outlier level) or a low level of outliers (5% outlier level). This suggests that these models effectively handle zero-inflated datasets with minimal noise. Among them, the RZIP model consistently outperformed the RHP model across varying proportions of zeros (0.5, 0.7, 0.8), achieving the lowest AIC values. This highlights the robustness of RZIP in modeling highly zero-inflated data. These findings emphasize the efficacy of RZIP in accommodating zero inflation and managing datasets with either no or low extreme values. However, when the dispersion reached 3 and the sample size became 200 and above, the RZIP and RHP models demonstrated sensitivity to sample size and data characteristics as they were now outperformed by the RZINB and RHNB models. This reinforces their reliability in scenarios with increased dispersion and low levels of outliers, as evidenced by the results summarized in Table A6, Table A7, Table A8, Table A9, Table A10 and Table A11.
3.1.4. Performance Under Moderate Outlier Levels and Increasing Dispersion
As the level of outliers in the data increases to a moderate threshold of 10–15%, both the RZIP and RHP models show a noticeable decline in performance when compared to more resilient models like the RZINB and RHNB. This trend is evident even when sample size and dispersion remain constant, highlighting the limitations of the RZIP and RHP models in handling moderate to high levels of outliers with low dispersion. As outliers continue to increase and reach 15%, RZIP and RHP persistently lag, suggesting that these models are less effective under conditions with a substantial presence of outliers. In Table A3, Table A4, Table A5, Table A6, Table A7, Table A8, Table A9, Table A10 and Table A11, findings consistently show that RZINB and RHNB outperform other models, especially under moderate and high outlier conditions. This higher performance is consistent across different percentages of zeros and sample sizes, making RZINB and RHNB the most reliable options for dealing with outlier laden data.
As the dispersion parameter in the dataset increased from 3 to 1 and the proportion of outliers escalated from 0% to 5%, 10%, and 15%, notable patterns emerged in model performance. The RZINB model achieved the lowest AIC at outlier thresholds of 0%, 5%, and 10%. However, as the outlier threshold increased to 15%, the RHNB model outperformed RZINB, particularly under higher zero-inflation scenarios. RHNB emerged as the most reliable model under conditions of severe contamination, characterized by high proportions of outliers and substantial overdispersion. Its ability to handle excess zeros while maintaining robustness against noise induced by extreme values highlights its utility in challenging scenarios.
3.1.5. Influence of Sample Size on Model Performance
Examining the performance of RZIP, RHP, RZINB, and RHNB models across sample sizes of 50, 200, and 500 reveals key trends. Model performance varies significantly with sample size, dispersion, and outliers. RZIP and RHP perform well with smaller sample sizes (50) and dispersion of 5, handling outliers up to 5% as shown in Table A3. However, as the sample size and dispersion increase or the outlier proportion exceeds 5%, these models lose accuracy. In contrast, RZINB and RHNB excel under these more challenging conditions, demonstrating superior stability and fit with larger samples, higher dispersion, and more outliers. This comparison emphasizes the importance of aligning model choice with data characteristics. RZIP and RHP are suited for simpler datasets, while RZINB and RHNB are more effective for complex datasets with greater variability and contamination.
4. Application to Maternal Death
4.1. Description of the Study Sample
The real-world dataset comprises records from 222 healthcare facilities in Nairobi, Kenya, which reported maternal health outcomes between October 2021 and January 2022. Each record represents aggregated data at the facility level, not at the patient level. The outcome variable of interest, MaternalDeaths, refers to the number of maternal deaths recorded at each facility, making it appropriate to model this as a count variable. The definition of the variables in the dataset that the study uses includes maternal health outcomes and predictor variables related to delivery characteristics, maternal complications, antenatal care, and stillbirth. The variables used in this study, including maternal health outcomes and predictors related to delivery characteristics, maternal complications, antenatal care, and stillbirths, are described in detail in Table A1 in the Appendix A.
4.2. Exploratory Data Analysis (EDA)
4.2.1. Maternal Mortality Data Overview
The high number of zeros observed in Table 2 justifies the application of robust zero-inflated and hurdle models in this study. These models are designed to handle datasets with excess zeros, outliers, and overdispersion, ensuring a more accurate and robust analysis of maternal mortality data. Maternal death rates are a critical indicator of healthcare quality and access, particularly for women during pregnancy, childbirth, and the postpartum period. Analyzing the frequency distribution of maternal death counts helps us to understand patterns and identify areas for intervention. In this analysis, the study examines a dataset that records the frequency of different maternal death counts. A frequency table of maternal deaths is given in Table 2.

Table 2.
Frequency table of maternal deaths.
The average maternal death count is 1.3198. However, the variance of 14.118 shows a wide range around the mean, indicating significant data dispersion. The median maternal death count is 0, suggesting that there were no maternal deaths in at least half of the recorded instances. This is supported by the mode of zero, which indicates that the most common outcome in the sample is an absence of maternal deaths. With 61.7% of the dependent variable, the number of maternal deaths, being zero, the dataset contains 4.95% outliers, determined by an algorithm based on the 3 rule, which classifies values over three standard deviations from the mean as outliers. Additionally, since the sample variance of the outcome variable (14.118) is higher than the sample mean (1.3198), there is evidence of overdispersion in the data. Thus, our sample dataset clearly shows zero inflation and overdispersion.
In examining the boxplot visualization of the maternal dataset in Figure 1, outliers are observed within the count variable, indicating instances where maternal deaths deviate significantly from the typical distribution. It is essential to recognize and comprehend these outliers, as they may affect the reliability and accuracy of inferences made from the dataset. To provide an accurate evaluation of what is impacting maternal mortality rates using robust count statistical modeling, it is vital to address the existence of outliers.
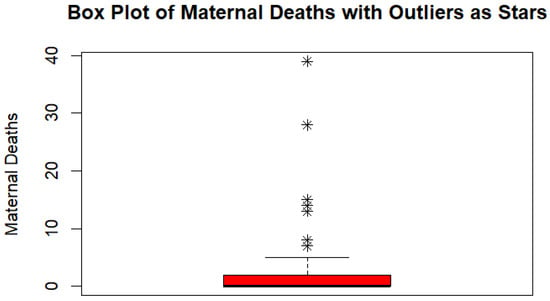
Figure 1.
Visualization of outliers.
4.2.2. Assessment of Multicollinearity Test
The analysis identified substantial correlations among several independent variables, indicating multicollinearity (see Figure 2). This issue arises when predictor variables are highly correlated, leading to redundancy and inflated standard errors in the regression coefficients. As a result, estimates become unstable, and theoretically important variables may appear statistically insignificant, obscuring their true relationships with the outcome.
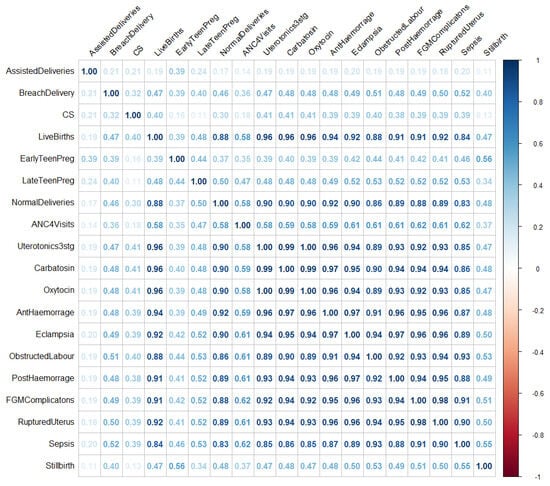
Figure 2.
Visualization indicating multicollinearity patterns.
To mitigate multicollinearity between explanatory variables, a correlation-based feature selection technique was applied [21]. Variables exhibiting high linear correlation (|r| > 0.7) were examined, and from each highly correlated pair, one variable was excluded based on theoretical relevance, interpretability, and contribution to model performance. The updated correlation matrix shown in Figure 3 indicates a significant reduction in multicollinearity, confirming the effectiveness of the selection process. By removing highly correlated variables, the updated model, now free from the detrimental effects of high multicollinearity, provided more reliable and interpretable estimates. The reduction in multicollinearity is expected to improve the stability and reliability of the coefficient estimates. However, it is important to approach the interpretation of the results with caution. The relationships between the predictors and the outcome variable should be evaluated in the context of the selected variables.
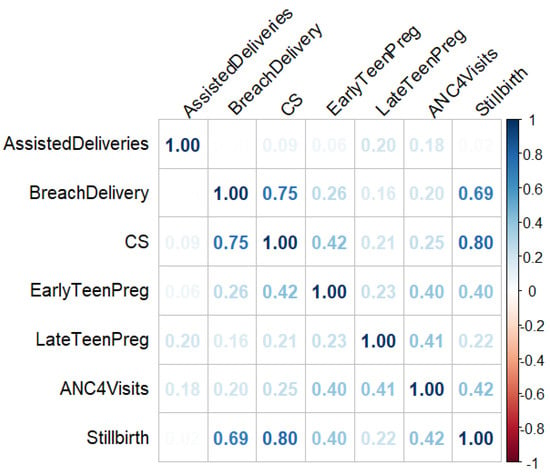
Figure 3.
Retained variables after multicollinearity screening.
4.2.3. Adjustment for Facility Size Through an Offset Term
To account for differences in the number of births handled by each healthcare facility, an offset term was included in all fitted count models. Facilities serving larger populations are naturally expected to record more maternal deaths, independent of underlying risk factors. Without this adjustment, model comparisons could be biased toward facilities with higher patient volumes. The offset term was defined as the natural logarithm of the total number of births recorded at each facility during the study period, denoted as . Including this offset allows the models to estimate maternal mortality rates per birth rather than raw counts, ensuring fair comparisons across facilities of different sizes. Mathematically, the count component of the model becomes the following:
where is the expected number of maternal deaths at facility i, are the predictor variables, and is the fixed offset term. For interpretability, the offset can also be scaled to express rates per 1000 births as . This adjustment ensures that model estimates reflect differences in maternal mortality risk, rather than differences in the volume of births handled by each facility.
4.3. Comparison of the Fitted Count Data Models
This is a comparison of all fitted models for maternal death counts using Akaike information criteria and Bayesian information criteria. Table 3 below provides the AIC and BIC values used to choose the model that best fits the data.

Table 3.
Estimated AIC and BIC for the maternal mortality data.
The comparison of the performance of the model in Table 3 reveals that the RZIP model provided the best fit to the data, outperforming all other models based on AIC and BIC. The NB model showed considerable improvement over the standard Poisson model, indicating its ability to handle overdispersion in the data more effectively. Among the robust models, the RZINB and RHP models showed competitive performance, especially the RZINB, but were still outperformed by the RZIP model. The RHNB model showed a slightly poorer fit compared to the RZIP, RHP, and RZINB models but performed better than the standard count (ZINB and HNB) and traditional (Poisson and NB) models. Looking at the ZINB, showed a better fit over the HNB and traditional models. These findings generally emphasize the suitability of the RZIP model for this dataset, demonstrating its ability to effectively address zero inflation and outliers at approximately 5%.
Figure 4 shows the observed histogram of maternal deaths overlaid with fitted probability curves from six different count regression models (Poisson, NB, RZIP, RZINB, RHP, and RHNB) that included covariates for assisted deliveries, breech delivery, early teen pregnancy, late teen pregnancy, attending at least four ANC visits (ANC4Visits), cesarean section (CS), and stillbirth. For each model, fitted probabilities were computed for individual observations using the estimated parameters and included covariates and then averaged across all observations to generate the marginal predicted distribution. This approach allows for a fair comparison with the empirical distribution of maternal deaths. The observed distribution exhibits significant excess zeros beyond what would be expected under standard count model assumptions, as also shown in Table 2. This zero inflation necessitates the evaluation of models explicitly designed to handle both structural and sampling zeros. The standard Poisson model performs poorly due to its assumption of equidispersion (equal mean and variance), leading it to severely underestimate the frequency of zero outcomes. Although the NB model partially addresses this by accommodating overdispersion, it still lacks a mechanism to model excess structural zeros. In contrast, the robust hurdle models (RHNB and RHP) and robust zero-inflated models (RZINB and RZIP) offer superior fits by explicitly modeling the dual processes that generate zero and positive counts separately. Among these, the RZIP model provides the best overall fit. Its two-part structure, separating the not-at-risk group (structural zeros) from the at-risk group (count component), enables it to accurately capture both the high frequency of zeros and the distribution of non-zero maternal deaths. These results are consistent with those in Table 3, where the RZIP achieved the lowest AIC and BIC scores.
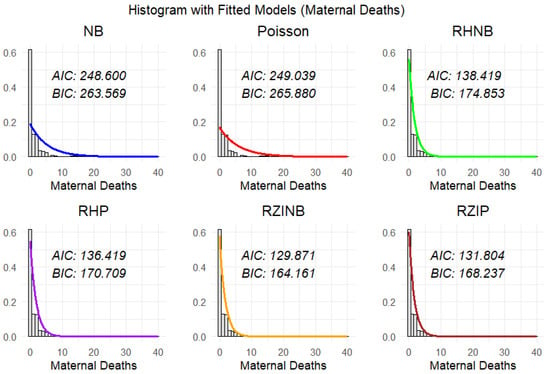
Figure 4.
Probability models for the number of maternal deaths.
4.4. Robust Count Regression Estimation Results
A significant frequency of zero counts and outliers was observed in the maternal mortality data. These observations deviate substantially from the expected patterns of standard count data distributions such as the Poisson and NB models. Such deviations suggest that the data may arise from two latent subpopulations, one that is not at risk of maternal mortality and thus always yields a count of zero, and another that is at risk and generates counts according to a standard count process (possibly zero or positive). In maternal mortality analysis, at-risk facilities are those that conduct deliveries with potential complications, high-risk pregnancies, or limited access to advanced obstetric care, making maternal deaths possible. Not-at-risk facilities are structurally unlikely to report maternal deaths because they either do not offer delivery services, handle only low-risk births, transfer complicated cases, or operate solely as antenatal/postnatal clinics. Furthermore, the presence of outliers in the data requires the use of robust estimation techniques, which the standard count models cannot account for. Given these challenges, an RZIP model is identified as the most appropriate for this analysis, as shown in Figure 4 and supported by model comparison results in Table 3. In the following Table 4, the study displays parameter estimates and the robust standard error of the best-performing model, which is RZIP.

Table 4.
Model estimation of coefficients using robust zero-inflated models.
Table 4 displays the estimated coefficients of the RZIP model for two parts, namely the count model and the zero model. The zero model explains the excess zeros in the data, while the count model concentrates on the count (frequency) of the event, which is maternal mortality in our case. Each component describes a distinct feature of the data. In the count component, the RZIP model estimates the expected number of maternal deaths per 1000 births among the at-risk group. The estimated intercept is , which corresponds to an expected count of 0.4245 maternal deaths when all predictors are at their baseline levels. This significantly lower baseline suggests that, in the absence of specific risk factors, maternal mortality remains below the mean of the sample. Among predictors, BreachDelivery has a statistically significant positive effect on maternal mortality among the at-risk group, with an estimated coefficient of 0.2813 (p = 0.0251), corresponding to a increase in the expected number of maternal deaths per 1000 births , reinforcing its role as a critical risk factor. Conversely, AssistedDeliveries do not exhibit a meaningful impact, with an estimated effect of p = 0.8435), in the at-risk group , corresponding to a 40.13% decrease in the expected number of maternal deaths per 1000 births of an individual being in an at-risk group in maternal mortality, suggesting a limited influence on maternal mortality among individuals at risk. EarlyTeenPreg, however, shows a notable positive association in the at-risk group, with an estimated coefficient of , p = 0.0185), indicating a increase in the expected count of maternal deaths per 1000 births among individuals at risk . The statistical significance of this effect suggests that early teenage pregnancy is an important predictor of maternal mortality within the at-risk group.
LateTeenPreg, on the other hand, has an estimated effect of , p = 0.7900), in the at-risk group corresponding to a 8.26% decrease in the expected count of maternal deaths per 1000 births . However, this effect is not statistically significant ( 0.05), suggesting that late teenage pregnancy may not be a strong predictor of maternal mortality among individuals at risk. ANC4Visits and CS are both negatively associated with maternal mortality among individuals at risk, based on the count component of the model. ANC4Visits shows a statistically significant effect, with a decrease in the expected count of maternal deaths per 1000 births , Although CS is associated with a decrease in the expected number of maternal death per 1000 births , this effect is not statistically significant, indicating limited evidence of its independent contribution within the at-risk population. In contrast, StillBirth shows a positive significant effect, with a increase in the expected count of maternal deaths per 1000 births . This finding strongly strengthens the critical role of stillbirth as a key risk factor for maternal mortality among at-risk individuals and emphasizes the need for targeted interventions addressing this factor to reduce maternal deaths.
The zero inflation component models the log-odds of belonging to the not-at-risk group, those for whom maternal mortality cannot occur (i.e., they always yield a zero count). Among predictors, BreachDelivery has an estimated effect of , p = 0.5500), implying a decreased odds of an individual being in the not-at-risk group , suggesting a limited influence on maternal mortality among individuals that are not-at-risk group. Similarly, AssistedDeliveries has an estimated effect of , p = 0.8560), suggesting a limited influence on maternal mortality among individuals who are not-at-risk group. EarlyTeenPreg has an estimated effect of , p = 0.2140), suggesting that for each unit increase in early teenage pregnancies, the odds of belonging to the not-at-risk group , but there is limited influence on maternal mortality among individuals not-at-risk 0.05) indicating no strong evidence. In contrast, LateTeenPreg demonstrates a significant association in the zero-inflation component, with an estimated coefficient of , p = 0.0306), indicating a increase in the odds of being in the not-at-risk group . This implies that regions with higher late teenage pregnancy rates may be more likely to fall into a subgroup structurally unlikely to report maternal deaths, possibly reflecting reporting differences or underlying protective mechanisms.
ANC4Visits has a statistically significant positive effect, with an estimated coefficient of , p = 0.0164), suggesting that for each unit increase in ANC4Visits pregnancies, the odds of belonging to the not-at-risk group . This result suggests that higher ANC4Visits is associated with a substantially greater probability of avoiding maternal death, indicating that antenatal care may play a protective role in identifying or preventing risk before it manifests. The significance of this effect strengthens the importance of ANC4Visits in reducing the likelihood of being at risk for maternal mortality. CS has an estimated coefficient of , , corresponding to a increase in the odds of being in the not-at-risk group per unit increase . This indicates that individuals with higher values of CS are significantly more likely to be in the not-at-risk group. Similarly, StillBirth has a negative estimated coefficient of , , suggesting a decrease in the odds of being in the not-at-risk group . This estimate is also not statistically significant, and the large standard error reflects substantial uncertainty. Thus, there is no reliable evidence that StillBirth affects the likelihood of being in the not-at-risk group.
4.5. The RZIP Model Validation
The chi-squared test in Table 5 was used to validate the model. The test statistic is 220.203 with 214 degrees of freedom. The p-value is 0.371, which is greater than the typical significance level of 0.05. This indicates that there is no evidence to reject the null hypothesis. Thus, the fit of the model to the data is adequate, and there is no significant lack of fit based on this test.

Table 5.
Model validation results.
4.6. Overview of Application Results
Count part (Poisson mean with offset):
Zero-inflation part (logistic model):
Probability model:
where and are defined above, and is included as an offset to adjust for differences in facility size.
5. Conclusions
This study examined the performance of various count regression models using both simulated and real maternal mortality data. The findings revealed that the RZIP model was the best performer when outlier (0–5%) and dispersion levels were low, making it the most suitable model for such conditions. This result was consistent across both real and simulated data. However, as outlier levels and dispersion increased, the RZINB and RHNB models provided a better fit and predictive accuracy. These models effectively handled datasets with extreme zero inflation and severe outliers, outperforming traditional Poisson and NB models. The AIC and BIC further confirmed the importance of robust zero-inflated models like RZIP in capturing data complexities. In general, RZIP is recommended for datasets with minimal outliers (≤5%), while RZINB and RHNB are better suited for highly dispersed data with severe outliers. These insights highlight the need for researchers to carefully assess model performance and assumptions when analyzing complex count data.
Analysis of the RZIP model showed some statistical significance of maternal mortality. Early teenage pregnancy was associated with a significantly increased risk of maternal death per 1000 births among the at-risk group. This emphasizes a lack of physiological and psychological readiness for childbirth from these young mothers, especially in low-resource settings where access to advanced obstetric care is limited. In alignment with Sustainable Development Goal (SDG) 3.2 [22], which aims to end preventable deaths of newborns and children under five, greater attention must be directed toward maternal health interventions that prioritize early screening and safe delivery methods, such as cesarean sections where medically appropriate. Moreover, the study confirmed that ANC4Visits were statistically significant in both components, positively associated with maternal death in the at-risk group, but also showed a significant increase in the odds of being in the not-at-risk group. In pursuit of the broader SDG 3 goals, health systems should implement tailored strategies that provide adolescent-friendly maternal health services, including education, early risk assessment, and access to skilled birth attendants. Future work should explore the development of a robust hybrid zero inflation model, which combines the strengths of zero-inflated and hurdle frameworks with robust estimation to better handle extreme zero inflation, overdispersion, and outliers. Addressing multicollinearity through techniques such as principal component analysis (PCA) or regularization can further enhance model accuracy.
Author Contributions
Conceptualization, P.P., R.T.C. and C.S.M.; methodology, P.P. and R.T.C.; software, P.P. and R.T.C.; validation, P.P., R.T.C. and C.S.M.; formal analysis, P.P.; investigation, P.P.; resources, P.P.; data curation, P.P.; writing original draft preparation, P.P.; writing review and editing, P.P., R.T.C. and C.S.M.; visualization, P.P.; supervision, R.T.C. and C.S.M.; project administration, R.T.C. and C.S.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by a supervisor-linked bursary from the University’s Research and Innovation Office, which also contributed partial funding for the article processing charges (APC).
Data Availability Statement
Supporting data is accessible at: https://doi.org/10.5061/dryad.zs7h44jdc.
Acknowledgments
The authors would like to express their sincere gratitude to the reviewers and the Editor for their insightful comments and constructive feedback, which significantly contributed in improving the quality of this paper.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A
Appendix A.1
The description of the variables used in this study is defined in the following Table A1.

Table A1.
Descriptions of variables used in the study.
Table A1.
Descriptions of variables used in the study.
| Variable | Description |
|---|---|
| MaternalDeaths | Total number of maternal deaths recorded. |
| AssistedDeliveries | Number of vaginal deliveries conducted with assistance. |
| BreachDelivery | Number of deliveries in breech position. |
| CS | Number of caesarean section deliveries. |
| LiveBirths | Total number of live births. |
| EarlyTeenPreg | Pregnant adolescents aged 10–14 years at their first antenatal care (ANC) visit. |
| LateTeenPreg | Pregnant adolescents aged 15–19 years at their first ANC visit. |
| NormalDeliveries | Number of deliveries without surgical or assisted interventions. |
| ANC4Visits | Number of women who had at least four ANC visits during pregnancy. |
| Uterotonics3stg | Women who received uterotonics during or immediately after the third stage of labor. |
| Carbatosin | Mothers given Carbatosin within one minute after birth. |
| Oxytocin | Mothers given Oxytocin within one minute after birth. |
| Eclampsia | Number of reported cases of eclampsia. |
| AntHaemorrage | Number of cases of antepartum haemorrhage. |
| PostHaemorrage | Number of cases of postpartum haemorrhage. |
| ObstructedLabour | Deliveries complicated by obstructed labor. |
| RupturedUterus | Number of cases involving uterine rupture. |
| Sepsis | Number of maternal sepsis cases. |
| FGMComplicatons | Delivery complications attributed to Female Genital Mutilation (FGM). |
| Stillbirth | Number of macerated stillbirths recorded. |
Appendix A.2
Note: The bold numbers denote the lowest AIC (which determines the best model), while the ones in the block reflect the second-lowest AIC (which determines the second-best model).

Table A2.
Comparing AIC values for models fitted to data generated using an NB model.
Table A2.
Comparing AIC values for models fitted to data generated using an NB model.
| Sample Size | Poisson | NB | RZIP | RZINB | RHP | RHNB |
|---|---|---|---|---|---|---|
| 50 | 266.960 | 153.870 | 268.480 | 199.260 | 268.020 | 199.130 |
| 200 | 589.190 | 461.600 | 489.710 | 470.840 | 488.640 | 469.150 |
| 500 | 1896.760 | 1389.060 | 1650.340 | 1401.300 | 1649.590 | 1400.290 |

Table A3.
AIC fit statistics with varying parameters, a fixed sample size of 50, and a dispersion of 5.
Table A3.
AIC fit statistics with varying parameters, a fixed sample size of 50, and a dispersion of 5.
| Outliers | Prop of Zero | Poisson | NB | RZIP | RZINB | RHP | RHNB |
|---|---|---|---|---|---|---|---|
| 0.0 | 0.5 | 496.377 | 307.548 | 209.245 | 244.406 | 209.406 | 244.489 |
| 0.7 | 382.985 | 295.174 | 203.395 | 250.639 | 203.697 | 250.616 | |
| 0.8 | 299.579 | 250.422 | 164.671 | 189.534 | 166.136 | 189.748 | |
| 0.05 | 0.5 | 892.394 | 619.407 | 221.731 | 408.289 | 225.545 | 408.386 |
| 0.7 | 651.145 | 462.172 | 355.345 | 253.034 | 355.238 | 253.397 | |
| 0.8 | 431.770 | 335.132 | 111.974 | 238.511 | 113.412 | 238.386 | |
| 0.10 | 0.5 | 985.508 | 792.451 | 335.400 | 234.011 | 392.386 | 233.324 |
| 0.7 | 590.654 | 489.585 | 264.072 | 259.122 | 264.009 | 259.544 | |
| 0.8 | 720.789 | 440.900 | 324.987 | 216.363 | 324.780 | 217.951 | |
| 0.15 | 0.5 | 805.736 | 635.367 | 524.872 | 442.714 | 524.771 | 441.866 |
| 0.7 | 864.878 | 786.379 | 529.374 | 362.166 | 529.329 | 362.849 | |
| 0.8 | 802.551 | 656.557 | 506.557 | 321.393 | 506.352 | 319.657 |

Table A4.
AIC fit statistics with varying parameters, a fixed sample size of 200, and a dispersion of 5.
Table A4.
AIC fit statistics with varying parameters, a fixed sample size of 200, and a dispersion of 5.
| Outliers | Prop of Zero | Poisson | NB | RZIP | RZINB | RHP | RHNB |
|---|---|---|---|---|---|---|---|
| 0.0 | 0.5 | 790.969 | 673.619 | 626.241 | 628.711 | 637.4850 | 639.259 |
| 0.7 | 634.526 | 478.498 | 459.158 | 462.408 | 459.250 | 460.426 | |
| 0.8 | 508.746 | 344.618 | 343.351 | 355.219 | 343.578 | 355.186 | |
| 0.05 | 0.5 | 1358.895 | 1081.735 | 699.238 | 705.374 | 703.072 | 781.635 |
| 0.7 | 1071.338 | 602.092 | 490.695 | 594.989 | 500.646 | 595.087 | |
| 0.8 | 767.973 | 499.480 | 362.790 | 482.297 | 368.665 | 482.345 | |
| 0.10 | 0.5 | 1847.062 | 1399.119 | 750.727 | 753.169 | 899.971 | 743.987 |
| 0.7 | 1383.369 | 1119.060 | 887.516 | 519.300 | 887.508 | 521.188 | |
| 0.8 | 1273.901 | 985.569 | 720.022 | 501.215 | 719.685 | 499.567 | |
| 0.15 | 0.5 | 2100.491 | 1650.317 | 792.049 | 782.836 | 796.301 | 783.722 |
| 0.7 | 1758.836 | 1065.086 | 550.029 | 545.644 | 552.289 | 510.068 | |
| 0.8 | 1302.0951 | 999.867 | 707.985 | 425.134 | 707.974 | 410.876 |

Table A5.
AIC fit statistics for models with varying parameters, given a fixed sample size of 500 and dispersion of 5.
Table A5.
AIC fit statistics for models with varying parameters, given a fixed sample size of 500 and dispersion of 5.
| Outliers | Prop of Zero | Poisson | NB | RZIP | RZINB | RHP | RHNB |
|---|---|---|---|---|---|---|---|
| 0.0 | 0.5 | 1952.280 | 1684.040 | 1466.460 | 1579.420 | 1466.680 | 1580.030 |
| 0.7 | 1587.879 | 1208.607 | 1145.725 | 1198.674 | 1146.982 | 1198.491 | |
| 0.8 | 1283.602 | 962.424 | 857.373 | 890.434 | 890.491 | 859.216 | |
| 0.05 | 0.5 | 3352.670 | 2659.260 | 1743.133 | 2173.154 | 1757.532 | 2173.380 |
| 0.7 | 2626.248 | 1847.196 | 1246.235 | 1311.159 | 1244.010 | 1311.525 | |
| 0.8 | 2113.394 | 1338.705 | 960.905 | 1120.507 | 990.635 | 1119.966 | |
| 0.10 | 0.5 | 3666.695 | 2676.751 | 2456.783 | 1854.294 | 2456.701 | 1873.620 |
| 0.7 | 3593.761 | 2316.144 | 1817.978 | 1310.983 | 1709.406 | 1314.567 | |
| 0.8 | 2753.619 | 1978.593 | 1598.149 | 1076.659 | 1598.086 | 1077.034 | |
| 0.15 | 0.5 | 5709.157 | 3974.548 | 2186.390 | 1972.943 | 2186.629 | 1951.884 |
| 0.7 | 4480.317 | 1367.343 | 2745.152 | 1365.166 | 2745.653 | 1361.781 | |
| 0.8 | 3471.394 | 2008.594 | 1899.432 | 1007.210 | 1895.444 | 1006.745 |

Table A6.
AIC fit statistics for models with varying parameters, given a fixed sample size of 50 and dispersion of 3.
Table A6.
AIC fit statistics for models with varying parameters, given a fixed sample size of 50 and dispersion of 3.
| Outliers | Prop of Zero | Poisson | NB | RZIP | RZINB | RHP | RHNB |
|---|---|---|---|---|---|---|---|
| 0.0 | 0.5 | 464.842 | 351.282 | 249.946 | 251.093 | 250.849 | 251.078 |
| 0.7 | 532.040 | 410.725 | 309.592 | 310.436 | 309.739 | 310.684 | |
| 0.8 | 608.652 | 485.119 | 383.096 | 384.573 | 383.288 | 384.762 | |
| 0.05 | 0.5 | 895.515 | 672.718 | 442.356 | 542.138 | 573.728 | 497.223 |
| 0.7 | 782.124 | 650.333 | 413.902 | 496.301 | 442.678 | 499.847 | |
| 0.8 | 694.543 | 472.150 | 328.243 | 370.745 | 399.654 | 369.982 | |
| 0.10 | 0.5 | 954.332 | 742.886 | 593.001 | 332.668 | 512.795 | 416.232 |
| 0.7 | 912.765 | 731.921 | 572.581 | 419.562 | 573.478 | 452.482 | |
| 0.8 | 821.889 | 642.357 | 428.340 | 388.123 | 456.178 | 325.847 | |
| 0.15 | 0.5 | 1064.543 | 834.251 | 673.892 | 489.328 | 578.652 | 390.412 |
| 0.7 | 892.145 | 702.123 | 523.459 | 462.317 | 548.712 | 389.439 | |
| 0.8 | 781.473 | 601.314 | 489.762 | 384.908 | 412.658 | 368.434 |

Table A7.
AIC fit statistics for models with varying parameters, given a fixed sample size of 200 and dispersion of 3.
Table A7.
AIC fit statistics for models with varying parameters, given a fixed sample size of 200 and dispersion of 3.
| Outliers | Prop of Zero | Poisson | NB | RZIP | RZINB | RHP | RHNB |
|---|---|---|---|---|---|---|---|
| 0.0 | 0.5 | 1456.825 | 1302.717 | 1204.150 | 1154.234 | 1205.465 | 1156.786 |
| 0.7 | 1267.547 | 1054.892 | 983.328 | 935.659 | 982.531 | 937.426 | |
| 0.8 | 1098.231 | 856.499 | 785.289 | 751.235 | 783.984 | 652.948 | |
| 0.05 | 0.5 | 2103.451 | 1507.122 | 1376.453 | 1318.224 | 1378.945 | 1321.736 |
| 0.7 | 1896.757 | 1459.478 | 1238.992 | 1189.630 | 1240.713 | 1187.521 | |
| 0.8 | 1768.343 | 1230.549 | 1124.325 | 1070.659 | 1126.277 | 1074.380 | |
| 0.10 | 0.5 | 2450.921 | 1623.450 | 1509.382 | 1459.516 | 1512.872 | 1434.170 |
| 0.7 | 2238.170 | 1498.214 | 1387.415 | 1329.425 | 1390.445 | 1327.236 | |
| 0.8 | 2023.460 | 1357.918 | 1243.356 | 1196.232 | 1246.145 | 1193.704 | |
| 0.15 | 0.5 | 2697.354 | 2078.649 | 1670.475 | 1595.976 | 1673.832 | 1599.870 |
| 0.7 | 2489.998 | 1925.23 | 1512.319 | 1453.178 | 1515.534 | 1450.142 | |
| 0.8 | 2267.102 | 1673.89 | 1378.672 | 1319.982 | 1380.324 | 1317.945 |

Table A8.
AIC fit statistics for models with varying parameters, given a fixed sample size of 500 and dispersion of 3.
Table A8.
AIC fit statistics for models with varying parameters, given a fixed sample size of 500 and dispersion of 3.
| Outliers | Prop of Zero | Poisson | NB | RZIP | RZINB | RHP | RHNB |
|---|---|---|---|---|---|---|---|
| 0.0 | 0.5 | 1903.415 | 1723.187 | 1567.120 | 1517.324 | 1569.687 | 1519.436 |
| 0.7 | 1765.326 | 1498.554 | 1329.762 | 1285.382 | 1331.475 | 1287.767 | |
| 0.8 | 1593.760 | 1245.980 | 1176.340 | 1130.480 | 1178.340 | 1123.210 | |
| 0.05 | 0.5 | 2403.809 | 1824.710 | 1698.325 | 1629.890 | 1701.346 | 1634.780 |
| 0.7 | 2176.450 | 1689.340 | 1568.730 | 1514.380 | 1570.568 | 1512.097 | |
| 0.8 | 1978.230 | 1534.978 | 1432.199 | 1386.786 | 1435.413 | 1380.672 | |
| 0.10 | 0.5 | 2732.435 | 2019.873 | 1902.354 | 1825.364 | 1905.152 | 1820.458 |
| 0.7 | 2508.679 | 1875.768 | 1768.435 | 1703.523 | 1780.547 | 1716.352 | |
| 0.8 | 2304.560 | 1703.234 | 1612.958 | 1550.548 | 1615.340 | 1554.352 | |
| 0.15 | 0.5 | 2954.787 | 2154.322 | 2050.153 | 1969.374 | 2052.78 | 1947.894 |
| 0.7 | 2732.234 | 2013.354 | 1898.261 | 1823.543 | 1901.645 | 1816.976 | |
| 0.8 | 2534.889 | 1845.978 | 1743.584 | 1675.374 | 1746.182 | 1643.389 |

Table A9.
AIC fit statistics for models with varying parameters, given a fixed sample size of 50 and dispersion of 1.
Table A9.
AIC fit statistics for models with varying parameters, given a fixed sample size of 50 and dispersion of 1.
| Outliers | Prop of Zero | Poisson | NB | RZIP | RZINB | RHP | RHNB |
|---|---|---|---|---|---|---|---|
| 0.0 | 0.5 | 364.842 | 301.282 | 275.946 | 251.093 | 278.849 | 269.078 |
| 0.7 | 532.104 | 410.725 | 349.592 | 310.436 | 345.739 | 315.684 | |
| 0.8 | 608.652 | 485.119 | 398.096 | 384.573 | 389.288 | 379.762 | |
| 0.05 | 0.5 | 545.315 | 435.218 | 388.256 | 300.223 | 372.178 | 342.138 |
| 0.7 | 482.124 | 410.333 | 343.902 | 276.847 | 330.678 | 296.301 | |
| 0.8 | 434.543 | 372.150 | 328.243 | 269.982 | 309.654 | 289.745 | |
| 0.10 | 0.5 | 554.332 | 442.886 | 393.001 | 382.668 | 376.232 | 312.795 |
| 0.7 | 512.765 | 431.921 | 372.581 | 272.482 | 349.562 | 303.478 | |
| 0.8 | 421.889 | 372.357 | 338.34 | 285.847 | 318.123 | 306.178 | |
| 0.15 | 0.5 | 664.543 | 534.251 | 473.892 | 390.412 | 459.328 | 328.652 |
| 0.7 | 592.145 | 502.123 | 423.459 | 399.439 | 408.712 | 372.317 | |
| 0.8 | 481.473 | 401.314 | 389.762 | 334.908 | 362.658 | 318.434 |

Table A10.
AIC fit statistics for models with varying parameters, given a fixed sample size of 200 and dispersion of 1.
Table A10.
AIC fit statistics for models with varying parameters, given a fixed sample size of 200 and dispersion of 1.
| Outliers | Prop of Zero | Poisson | NB | RZIP | RZINB | RHP | RHNB |
|---|---|---|---|---|---|---|---|
| 0.0 | 0.5 | 1567.134 | 1328.762 | 1256.455 | 1196.546 | 1258.012 | 1198.832 |
| 0.7 | 1389.345 | 1149.211 | 1087.543 | 1030.213 | 1089.918 | 1032.314 | |
| 0.8 | 1221.788 | 987.485 | 923.678 | 870.568 | 926.34 | 878.845 | |
| 0.05 | 0.5 | 2032.394 | 1534.291 | 1420.789 | 1361.899 | 1423.129 | 1364.329 |
| 0.7 | 1854.678 | 1398.654 | 1289.632 | 1234.456 | 1291.876 | 1231.986 | |
| 0.8 | 1698.455 | 1245.589 | 1143.556 | 1101.765 | 1146.345 | 1087.554 | |
| 0.10 | 0.5 | 2345.687 | 1658.384 | 1556.485 | 1487.832 | 1558.898 | 1489.132 |
| 0.7 | 2187.425 | 1523.958 | 1423.760 | 1365.334 | 1426.142 | 1368.233 | |
| 0.8 | 1999.897 | 1376.435 | 1278.322 | 1223.928 | 1280.607 | 1222.485 | |
| 0.15 | 0.5 | 2598.132 | 1787.344 | 1698.451 | 1627.982 | 1701.126 | 1629.232 |
| 0.7 | 2387.445 | 1645.928 | 1545.768 | 1489.534 | 1548.678 | 1487.761 | |
| 0.8 | 2198.342 | 1498.726 | 1398.245 | 1343.132 | 1400.817 | 1341.627 |

Table A11.
AIC fit statistics for models with varying parameters, given a fixed sample size of 500 and dispersion of 1.
Table A11.
AIC fit statistics for models with varying parameters, given a fixed sample size of 500 and dispersion of 1.
| Outliers | Prop of Zero | Poisson | NB | RZIP | RZINB | RHP | RHNB |
|---|---|---|---|---|---|---|---|
| 0.0 | 0.5 | 4154.748 | 3576.354 | 2454.162 | 2397.192 | 2456.617 | 2398.760 |
| 0.7 | 2899.445 | 2321.687 | 2145.314 | 2204.989 | 2143.938 | 2207.523 | |
| 0.8 | 2643.192 | 2045.898 | 1934.758 | 1889.766 | 1937.374 | 1787.564 | |
| 0.05 | 0.5 | 3521.178 | 2676.435 | 2554.152 | 2489.342 | 2557.839 | 2487.554 |
| 0.7 | 3254.120 | 2439.627 | 2321.495 | 2263.981 | 2324.766 | 2265.321 | |
| 0.8 | 2978.405 | 2178.324 | 2067.514 | 2013.425 | 2070.354 | 2015.236 | |
| 0.10 | 0.5 | 3845.612 | 2789.567 | 2678.458 | 2618.192 | 2681.450 | 2607.341 |
| 0.7 | 3576.334 | 2556.708 | 2434.120 | 2356.980 | 2437.761 | 2375.154 | |
| 0.8 | 3321.415 | 2287.854 | 2176.384 | 2110.213 | 2178.988 | 2116.697 | |
| 0.15 | 0.5 | 4154.898 | 2923.667 | 2812.457 | 2732.728 | 2815.314 | 2724.189 |
| 0.7 | 3898.475 | 2689.232 | 2576.778 | 2512.345 | 2579.989 | 2511.238 | |
| 0.8 | 3627.534 | 2435.412 | 2321.645 | 2267.689 | 2324.781 | 2265.671 |
References
- Shahsavari, S.; Yaseri, M.; Hosseini, M.; Moghimbeigi, A. Robust Inference for Zero-Inflated Models with Outliers Applied to the Number of Involved Lymph Nodes in Patients with Breast Cancer. 2023. Available online: https://doi.org/10.21203/rs.3.rs-2692063/v1 (accessed on 29 May 2025).
- Feng, C.X. A comparison of zero-inflated and hurdle models for modeling zero-inflated count data. J. Stat. Distrib. Appl. 2021, 8, 8. [Google Scholar] [CrossRef] [PubMed]
- Lambert, D. Zero-inflated Poisson regression, with an application to defects in manufacturing. Technometrics 1992, 34, 1–14. [Google Scholar] [CrossRef]
- Min, Y.; Agresti, A. Random effect models for repeated measures of zero-inflated count data. Stat. Model. 2005, 5, 1–19. [Google Scholar] [CrossRef]
- Hall, D.B. Robust estimation for zero-inflated Poisson regression. Scand. J. Stat. 2010, 37, 237–252. [Google Scholar] [CrossRef]
- Mullahy, J. Specification and testing of some modified count data models. J. Econom. 1986, 33, 341–365. [Google Scholar] [CrossRef]
- Tüzen, F. A simulation study for count data models under varying degrees of outliers and zeros. Commun. Stat.—Simul. Comput. 2018, 49, 1078–1088. [Google Scholar] [CrossRef]
- Tawiah, K.; Iddi, S.; Lotsi, A. On Zero-Inflated Hierarchical Poisson Models with Application to Maternal Mortality Data. Int. J. Math. Math. Sci. 2020, 2020, 1407320. [Google Scholar] [CrossRef]
- Bassey, U.E.; Akinyemi, M.I.; Njoku, K.F. On Zero inflated models with applications to maternal healthcare utilization. Int. J. Math. Sci. Optim. Theory Appl. 2021, 7, 65–75. [Google Scholar] [CrossRef]
- Abonazel, M.R.; El-sayed, S.M.; Saber, O.M. Performance of robust count regression estimators in the case of overdispersion, zero inflated, and outliers: Simulation study and application to German health data. Commun. Math. Biol. Neurosci. 2021, 2021, 55. [Google Scholar] [CrossRef]
- Adehi, M.; Yakasai, A.; Dikko, H.; Asiribo, E.; Dahiru, T. Risk of maternal mortality using relative risk ratios obtained from poisson regression analysis. Int. J. Dev. Res. 2017, 7, 15405–15409. [Google Scholar]
- Okello, S.; Otieno Omondi, E.; Odhiambo, C.O. Improving performance of hurdle models using rare-event weighted logistic regression: An application to maternal mortality data. R. Soc. Open Sci. 2023, 10, 221226. [Google Scholar] [CrossRef] [PubMed]
- Chau, A.M.H.; Lo, E.C.M.; Wong, M.C.M.; Chu, C.H. Interpreting poisson regression models in dental caries studies. Caries Res. 2018, 52, 339–345. [Google Scholar] [CrossRef] [PubMed]
- Dean, C.B.; Lundy, E.R. Overdispersion. Wiley StatsRef Stat. Ref. Online 2016, 1–9. [Google Scholar] [CrossRef]
- Payne, E.H.; Hardin, J.W.; Egede, L.E.; Ramakrishnan, V.; Selassie, A.W.; Gebregziabher, M. Approaches for dealing with various sources of overdispersion in modeling count data: Scale adjustment versus modeling. Stat. Methods Med. Res. 2015, 26, 1802–1823. [Google Scholar] [CrossRef] [PubMed]
- Shahsavari, S.; Moghimbeigi, A.; Kalhor, R.; Jafari, A.M.; Bagherpour-kalo, M.; Yaseri, M.; Hosseini, M. Zero-Inflated Count Regression Models in Solving Challenges Posed by Outlier-Prone Data; an Application to Length of Hospital Stay. Arch. Acad. Emerg. Med. 2024, 12, e13. [Google Scholar] [PubMed]
- Huber, P.J. Robust estimation of a location parameter. In Breakthroughs in Statistics: Methodology and Distribution; Springer: Berlin/Heidelberg, Germany, 1992; pp. 492–518. [Google Scholar]
- Cantoni, E.; Zedini, A. A robust version of the hurdlemodel. J. Stat. Plan. Inference 2011, 141, 1214–1223. [Google Scholar] [CrossRef]
- Miranda, M.; Miranda, M.C.; Gomes, M.I. A robust hurdle poisson model in the estimation of the extremal index. In Recent Developments in Statistics and Data Science; Springer: Cham, Switzerland, 2022; pp. 15–28. [Google Scholar] [CrossRef]
- Akaike, H. A new look at the statistical model identification. IEEE Trans. Autom. Control. 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Hall, M.A. Correlation-based feature selection of discrete and numeric class machine learning. In Proceedings of the Seventeenth International Conference on Machine Learning (ICML 2000), Stanford University, Stanford, CA, USA, 29 June–2 July 2000. [Google Scholar]
- GBD 2019 Under-5 Mortality Collaborators. Global, regional, and national progress towards Sustainable Development Goal 3.2 for neonatal and child health: All-cause and cause-specific mortality findings from the Global Burden of Disease Study 2019. Lancet 2021, 398, 870–905. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).