Physics-Informed Machine Learning for Mechanical Performance Prediction of ECC-Strengthened Reinforced Concrete Beams: An Empirical-Guided Framework

Abstract

Predicting the mechanical performance of Engineered Cementitious Composite (ECC)-strengthened reinforced concrete (RC) beams is both meaningful and challenging. Although existing methods each have their advantages, traditional numerical simulations struggle to capture the complex micro-mechanical behavior of ECC, experimental approaches are costly, and data-driven methods heavily depend on large, high-quality datasets. This study proposes a novel physics-informed machine learning framework that integrates domain-specific empirical knowledge and physical laws into a neural network architecture to enhance predictive accuracy and interpretability. The approach leverages outputs from physics-based simulations and experimental insights as weak supervision and incorporates physically consistent loss terms into the training process to guide the model toward scientifically valid solutions, even for unlabeled or sparse data regimes. While the proposed physics-informed model yields slightly lower accuracy than purely data-driven models (mean squared errors of 0.101 VS. 0.091 on the test set), it demonstrates superior physical consistency and significantly better generalization. This trade-off ensures more robust and scientifically reliable predictions, especially under limited data conditions. The results indicate that the empirical-guided framework is a practical and reliable tool for evaluating the structural performance of ECC-strengthened RC beams, supporting their design, retrofitting, and safety assessment.

1. Introduction

Reinforced concrete (RC) members are among the most widely used structural elements in modern civil infrastructure, such as bridges, buildings, and transportation facilities, due to their strength, cost-effectiveness, and ease of construction [1,2]. However, their mechanical performance can deteriorate significantly over time due to factors such as overloading [3], environmental degradation [4], corrosion [5], and seismic actions [6]. This leads to reduced load-bearing capacity and increased safety risks, especially in aging structures [7,8]. To address these, Engineered Cementitious Composites (ECC)—a class of high-performance, fiber-reinforced materials characterized by high ductility, strain hardening, and multiple micro-cracking behavior—have emerged as an effective solution for strengthening and retrofitting RC members [9]. Their unique mechanical properties allow ECC to enhance structural capacity and resilience when used in conjunction with existing concrete [10].

Given the increasing adoption of ECC in structural strengthening, accurately understanding and predicting the mechanical behavior of ECC-strengthened RC members has become essential for design, safety assessment, and life-cycle management [11]. In recent years, several approaches have been developed to capture the performance of such composite systems. Among them, traditional physics-based numerical simulation methods, particularly finite element (FE) modeling, remain the mainstream tools for analyzing the mechanical behavior of RC and composite members [12]. These methods rely on constitutive models, equilibrium conditions, and structural mechanics theory to simulate stress distribution, cracking behavior, and load–displacement relationships [13]. Numerous studies have focused on simulating the flexural and shear behavior of ECC-strengthened beams by developing material models for ECC and bond–slip interfaces [14]. For instance, Qasim et al. [15] performed a finite element-based parametric study on SPH-ECC strengthened RC beams, revealing that reinforcement area in the ECC layer strongly influences flexural capacity. Similarly, Singh et al. [16] developed and validated an ABAQUS-based FE model to assess the flexural behavior of masonry beams strengthened with precast ECC plates. The results confirmed significant improvements in strength and ductility, providing reliable guidance for optimal strengthening design. However, accurately modeling the micro-mechanical behavior of ECC remains difficult due to its complex fiber bridging, strain hardening, and nonlinear interactions with surrounding concrete. These effects are highly sensitive to loading conditions and difficult to capture with simplified constitutive laws, often leading to discrepancies between numerical simulations and observed structural performance, particularly under multi-axial or dynamic loading.

Experimental studies have also played a central role in understanding the mechanical behavior of ECC-strengthened RC specimens [17,18]. Full-scale and laboratory-scale tests have been conducted to examine the flexural strength, crack propagation, load-deflection behavior, energy absorption, and failure modes under various loading schemes [19,20]. Many researchers have confirmed the effectiveness of ECC in improving the ductility and load capacity of RC specimens [10,21]. For example, Qudah et al. [22] examined ECC-enhanced beam–column interior joints and found that replacing conventional concrete in the plastic hinge zone with ECC, along with reduced transverse reinforcement, significantly improved shear resistance, energy dissipation, and crack control. However, experimental investigations are inherently expensive, time-consuming, and constrained by the limitations of test setup, material preparation, and loading protocols. As a result, it is difficult to obtain comprehensive datasets that cover the full range of structural configurations, material properties, and loading conditions relevant to practice.

With the recent development of artificial intelligence (AI) and machine learning (ML) technologies, these data-driven approaches have attracted growing interest for their potential to model complex nonlinear relationships without requiring explicit physical modeling [23,24]. In the field of structural and materials engineering, ML has been applied to predict concrete strength [25], durability [26], failure modes [27], and load-bearing behavior [28]. For instance, artificial neural network (ANN), support vector machine (SVM), decision tree (DT), and ensemble learning (EL) methods have been used to predict compressive strength based on mix design, assess the shear capacity of RC members, and evaluate the residual strength of damaged structures [29,30]. In the context of ECC, some preliminary studies have explored using ML to estimate mechanical properties or classify damage states. For example, Tuken et al. [31] developed an ML model based on the XGBoost algorithm, trained on a comprehensive database comprising experimental results from 217 ECC-strengthened beam specimens. Their work demonstrated the potential of ML to extract meaningful patterns from experimental data and to support predictive analysis of ECC-reinforced systems. However, purely data-driven models rely on large, high-quality labeled datasets to achieve satisfactory accuracy and generalization [32,33]. In the case of ECC-strengthened beams, such datasets are typically scarce due to the novelty of the material and the lack of standardized testing protocols. This data scarcity not only increases the risk of overfitting but also undermines the model’s ability to extrapolate to untested structural configurations or loading scenarios. Moreover, conventional ML models often ignore well-established physical knowledge, such as the monotonic influence of ECC thickness or reinforcement ratio on flexural strength, leading to nonphysical or unstable predictions when data coverage is sparse.

To overcome the limitations of both purely physics-based and purely data-driven approaches, recent advances have introduced physics-informed machine learning (PIML) as a promising hybrid modeling paradigm [34]. PIML aims to incorporate governing equations, physical constraints, and empirical knowledge into neural network architectures or training loss functions to improve accuracy, generalization, and interpretability. In structural engineering, physics-informed neural networks (PINNs) have been applied to simulate deflection profiles [35], dynamic responses [36,37], and failure mechanisms [38] by embedding boundary conditions and differential equations into learning processes. For example, Yu et al. [39] explored the underlying physical relationships between feature parameters and failure modes of RC columns, and embedded this knowledge into a novel physics-supervised ensemble learning model (PELM) for failure mode prediction. Other studies formulated PINNs using classical beam theories—Euler–Bernoulli [40] and Timoshenko—for simulating moving load effects [41], nonlinear buckling behavior [42], and solving both forward and inverse problems in beam systems [43]. In addition, transfer learning has been employed in PINNs to enhance generalization in beam simulations under changing conditions [44]. More recently, Mirsadeghi et al. [45] extended PINNs to bending analysis of two-dimensional nano-beams based on nonlocal strain gradient theory. Teloli et al. [46] further utilized PINNs for model parameter identification of beam-like structures. Bischof and Kraus [47] evaluated various loss-term balancing strategies for PINNs on benchmark PDEs, including Kirchhoff’s plate bending, while Balmer et al. [48] applied PINNs to the analysis and design of reinforced concrete beams using multi-linear material constitutive laws. These PDE-based PINNs are particularly effective when accurate closed-form governing equations are available, as they enable models to learn from both data and scientific principles, reducing the need for large datasets and enhancing robustness under data scarcity.

However, ECC-strengthened RC beams present a more complex challenge: their micro-mechanical behavior is shaped by heterogeneous material composition, hybrid failure mechanisms, and nonlinear ECC–concrete interactions. Deriving explicit PDEs for such systems is often infeasible due to incomplete quantitative understanding of certain ECC-specific relationships. In these cases, empirically established mechanical knowledge—such as typical failure modes, ECC–RC interface behavior, and characteristic load–displacement patterns—offers an alternative, experimentally validated source of domain information. Motivated by these insights, this study proposes a hybrid machine learning framework that integrates physics-based constraints and empirical supervision for predicting the mechanical performance of ECC-strengthened RC beams. The framework uses physics-consistent loss terms and weak supervision from experimental insights to regularize the neural network, enabling robust prediction even in sparse data conditions. The main contributions of this paper are as follows: (1) A novel empirical-guided, physics-informed neural network architecture is developed to capture the flexural performance of ECC-strengthened RC beams; (2) a strategy for incorporating physical and empirical knowledge into the learning process is proposed to improve interpretability and generalization; (3) the model’s accuracy, consistency, and applicability are evaluated through comparison with purely data-driven approaches and tested in realistic engineering scenarios.

2. Empirical-Guided Machine Learning Framework

2.1. Motivation and Concept

Traditional ML approaches rely purely on data-driven fitting and often lack physical interpretability, especially in structural engineering problems where experimental data are sparse and nonlinear behaviors are complex. Such models may generate predictions that violate fundamental engineering principles, limiting their practical reliability.

PINN attempts to address this by embedding governing equations into neural network training. However, for heterogeneous systems like ECC-strengthened RC beams, explicit PDE-based formulations are often unavailable or too simplified to capture mechanisms such as flexure–shear interaction or interface debonding. In contrast, extensive experimental evidence consistently reveals empirical trends—for example, the effect of ECC thickness on flexural capacity, typical load–deflection curve shapes, and known mechanical thresholds. These trends, although not expressible in closed-form equations, provide valuable domain knowledge that can be used to guide learning.

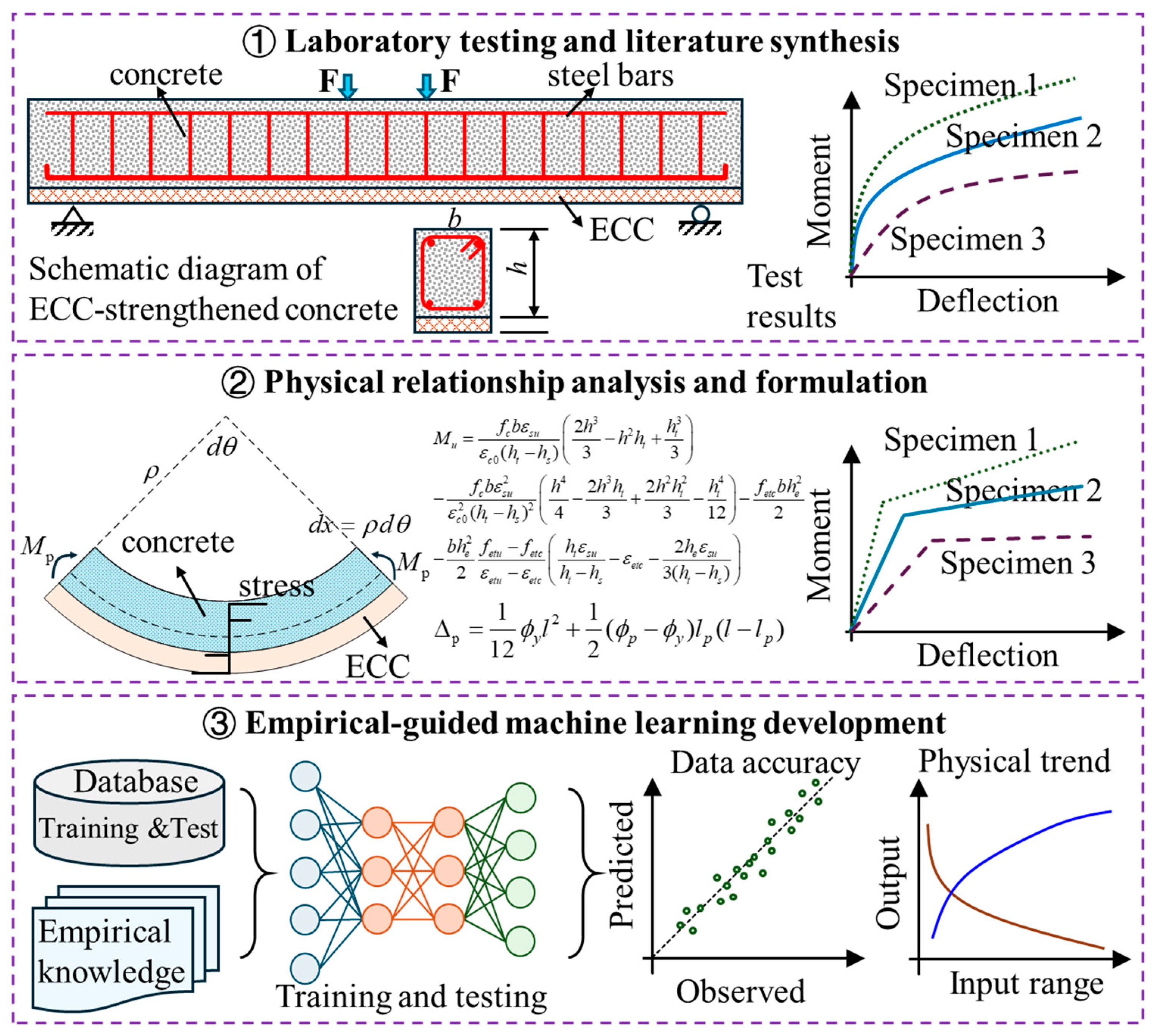
To this end, an empirical-guided machine learning (EGML) framework that incorporates empirical trends and simplified physical insights is proposed. As illustrated in Figure 1, it consists of three interconnected components:

(1) Experimental Study: A comprehensive study of ECC-strengthened RC beams, combining laboratory test data and literature review to identify key influencing parameters (e.g., ECC thickness, reinforcement ratio, bond quality, and concrete grade) and collect corresponding mechanical response data (e.g., load capacity, deflection, and cracking behavior).

(2) Physics-Based Analysis: Establishes approximate relationships among key parameters and mechanical outcomes using simplified theoretical models. Equilibrium equations, stress–strain laws, and physical simulations are used to formulate weak physical constraints that reflect the underlying mechanics.

(3) Empirical-Guided Machine Learning: Trains a neural network using experimental data, while embedding empirical trends as regularization terms and incorporating outputs from physics-based models as weak supervision signals. This enables weak supervision and enhanced interpretability without requiring closed-form physical laws. Model validation is conducted based on both predictive accuracy and adherence to known physical behavior.

The proposed EGML can integrate empirical knowledge—such as monotonicity, typical load–deflection shapes, or known mechanical thresholds—into the learning process as soft constraints. While the empirical trends used in this study are derived from ECC-based systems, the underlying principles of EGML are not system-specific. The framework is designed to accommodate domain-informed constraints in modular and flexible forms, including quantitative inequalities, conditional relationships, or even expert rules. This adaptability makes EGML applicable to a broad range of structural materials and components, such as steel–concrete composites, masonry, and timber structures, where empirical knowledge is available but explicit governing equations are difficult to establish.

2.2. Overview of the Proposed Methodology

The proposed EGML framework enhances a conventional neural network model by embedding domain-specific empirical knowledge directly into its training process. As illustrated in Figure 2, EGML defines the input–output mapping based on engineering relevance (e.g., ECC thickness, reinforcement ratio, concrete strength as inputs; flexural capacity or deflection as outputs), and constructs a feedforward neural network optimized via gradient-based methods.

(1) Standard machine learning pipeline: In a typical supervised learning workflow, the input features $\mathbf{x}=[x_1,x_2,\dots ,x_m]$ and target output y based on the system to be modeled (e.g., ECC thickness, reinforcement ratio, concrete strength as inputs; flexural capacity or deflection as outputs) should be first identified. The core objective is to learn a function $f:\mathbf{x}\to y$ based on observed data $\mathbf{D}=\{{\mathbf{x}}^i,y^i\}$. For example, the neural network architecture is defined by layers of interconnected neurons, where each layer applies linear transformations followed by nonlinear activation functions. The model is trained by minimizing a data-driven loss function loss_data, typically the Mean Squared Error (MSE):

$$los{s}_{\mathrm{data}}={\displaystyle \frac{1}{N_{\mathrm{sample}}}}{\displaystyle \sum _{i=1}^{N_{\mathrm{sample}}}{\left(f({\mathbf{x}}^i,\mathit{\theta })-y^i\right)}^2}$$

(1)

where $\mathit{\theta }$ represents the trainable parameters (weights and biases) of the network; $N_{\mathrm{sample}}$ is the number of samples.

(2) Embedding physics and empirical knowledge into training: To address this challenge, the EGML framework introduces domain knowledge into the training objective. Specifically, the total loss function is reformulated to combine three components:

$$los{s}_{\mathrm{total}}={\lambda }_{\mathrm{data}}\times los{s}_{\mathrm{data}}+{\lambda }_{\mathrm{emp}}\times los{s}_{\mathrm{emp}}$$

(2)

where $los{s}_{\mathrm{phys}}$ denotes the physics-based constraints from simplified theoretical models; $los{s}_{\mathrm{emp}}$ denotes the empirical supervision derived from experimentally observed monotonic or threshold-based behaviors; ${\lambda }_{\mathrm{data}}$ and ${\lambda }_{\mathrm{emp}}$ are tunable hyperparameters that control the balance between data fidelity and physical consistency. These domain-informed constraints act as regularization terms that guide the training toward physically meaningful predictions. By penalizing deviations from known physical and empirical trends, the EGML framework ensures that the trained model not only fits the observed data but also honors established engineering knowledge.

(3) Unified training workflow: The proposed EGML framework follows a structured and interpretable learning pipeline that integrates empirical knowledge and physics-based constraints into data-driven modeling. Input features are defined based on engineering relevance (e.g., ECC layer thickness, concrete strength, reinforcement ratio), and outputs represent key mechanical responses such as flexural capacity, mid-span deflection, or failure mode classification. To address the limitations of purely data-driven models, the EGML framework augments the training objective with additional loss components that encode simplified physics-based relationships and empirically observed mechanical trends. During each training iteration, the neural network performs a forward pass to generate predictions, the data-driven, physics-informed, and empirical loss terms are computed and aggregated into a unified objective function, and the model parameters are iteratively updated using gradient-based optimization.

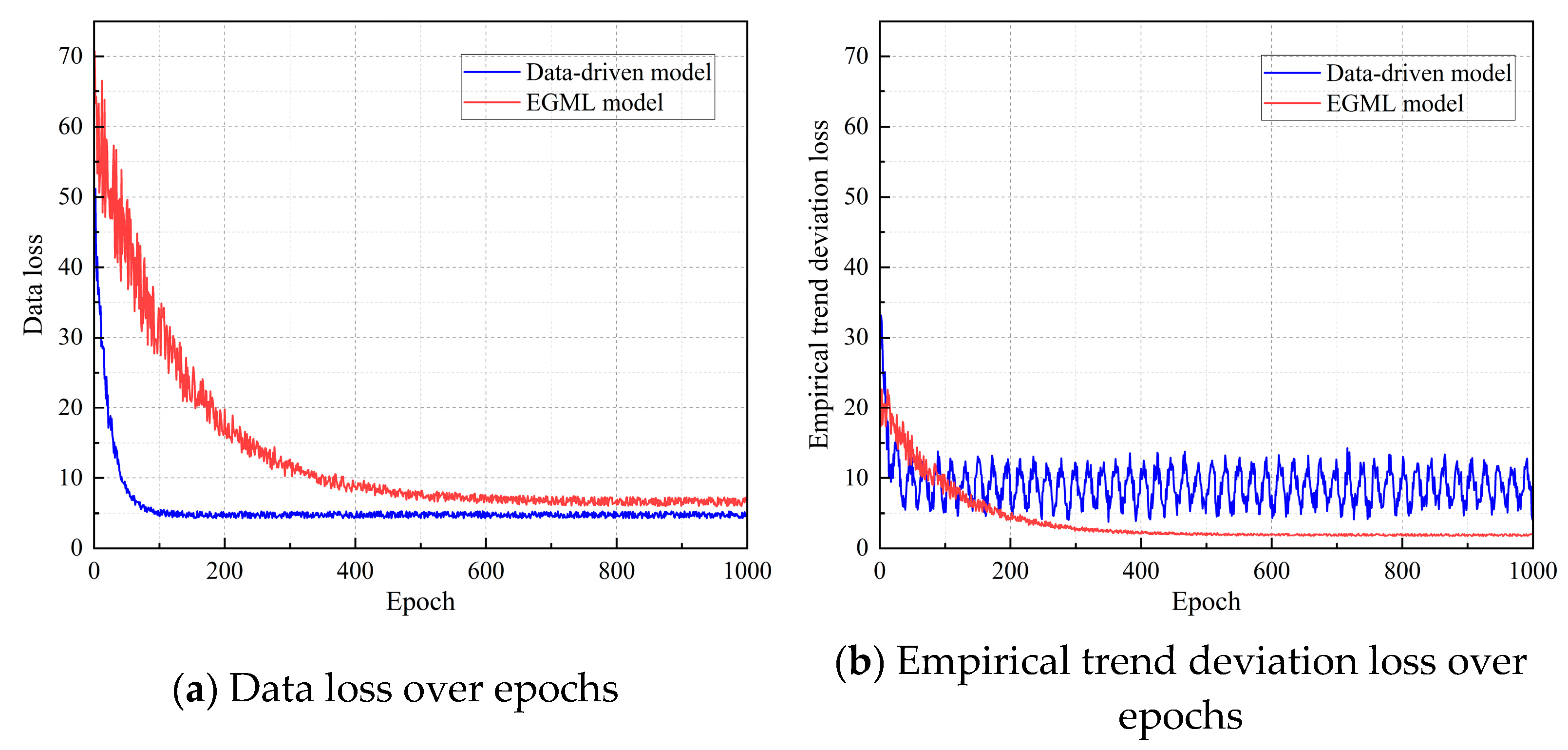
During training, all loss components are combined into a hybrid objective function, and parameters are optimized using gradient descent methods. Model validation is conducted not only in terms of prediction accuracy but also based on the degree to which the predicted outputs adhere to physical and empirical trends. To determine the appropriate weight ${\lambda }_{\mathrm{emp}}$ for the physics-informed loss component, a progressive adjustment strategy is employed: the weight coefficient ${\lambda }_{\mathrm{emp}}$ is gradually increased, and the corresponding decrease in loss_emp is monitored. Once loss_emp plateaus—i.e., further increases in ${\lambda }_{\mathrm{emp}}$ do not result in appreciable improvements in loss_emp—the corresponding ${\lambda }_{\mathrm{emp}}$ value is selected. This strategy allows the model to effectively balance numerical accuracy and physical validity, achieving the best compromise between data fitting and domain knowledge integration. This unified approach enables the trained model to generalize better under data-scarce conditions while maintaining consistency with established engineering principles—making it suitable for practical deployment in performance prediction and design of ECC-strengthened RC structures.

3. Model Development and Implementation

3.1. Experimental Database

The selection of input features is essential for accurately modeling the flexural behavior of ECC-strengthened RC beams. The 14 parameters chosen in this study represent a comprehensive yet practically measurable set of structural, material, and geometric variables that influence flexural capacity. These include properties of concrete, ECC, and reinforcement, as well as cross-sectional dimensions and ECC strengthening thicknesses. Together, they form the input vector:

$$\mathbf{x}=\left\{x_i\right\}=\{b,h,l_0,f_c,f_t,A_s,f_y,f_u,d_t,s_t,f_{t,ECC},f_{c,ECC},t\prime ,t\}, i=1,2, \dots ,14$$

(3)

where each variable, respectively, denotes beam width (b), height (h), span length (l₀), concrete compressive and tensile strengths (f_c and f_t), tensile reinforcement area (A_s), reinforcement yield and ultimate strengths (f_y and f_u), stirrup diameter and spacing (d_t and s_t), ECC tensile and compressive strengths (f_t,ECC and f_c,ECC), and top and bottom ECC thicknesses (t′ and t). This set is derived from standardized testing protocols and engineering design principles, ensuring that all key mechanical contributors are captured for predictive modeling. Including a wide range of factors also facilitates downstream analysis of feature importance and physical interpretability.

The output variable (y) is the ultimate flexural capacity (F_u), chosen due to its central role in assessing structural safety and strengthening effectiveness. Flexural strength directly reflects a beam’s ability to withstand bending under service and extreme conditions. Compared to other possible targets—such as stiffness or crack width—ultimate moment capacity is more commonly reported, easier to measure with consistency, and of greater practical importance for design and retrofitting purposes. Hence, it serves as the primary response variable in this study’s machine learning model.

To develop a robust and interpretable EGML model, a standardized experimental database of ECC-strengthened RC beams was constructed. Given the limited availability of consistent and comprehensive test data in this field, rigorous data inclusion criteria were employed to ensure that the selected samples are both representative and reliable. The following criteria were used to screen experimental studies and construct the database:

• Strengthening Method: Only RC beams strengthened using ECC layers at the top and/or bottom surfaces were included. Side strengthening was excluded to maintain consistency in flexural behavior and load path.
• Geometry: All specimens were required to have a rectangular cross-section, a common and standardized geometry in both research and engineering practice.
• Material Information: Concrete and ECC material properties (compressive and tensile strength) must be reported. Similarly, reinforcement characteristics including yield and ultimate strength are required.
• Loading Protocol: Only monotonic loading tests (e.g., three-point or four-point bending) were considered to ensure a consistent definition of ultimate flexural capacity.
• Data Completeness: Samples must report at least 14 structural, geometric, and material-related features, as well as the ultimate flexural strength, to be included in the final dataset.
• Experimental Conditions: Since factors such as ambient conditions and workmanship quality are rarely reported in existing literature and cannot be quantitatively incorporated as model inputs, only tests conducted under comparable laboratory environments and controlled construction procedures were included to minimize their potential influence on the database.

After filtering based on these criteria, a total of 194 samples were compiled from peer-reviewed experimental studies. The distributions and pairwise correlations of all input and output variables are presented in Figure 3. As shown in the figure, input variables span a wide range. For example, beam width and height range from 100 mm to 200 mm and 60 mm to 300 mm, respectively, reflecting scaled specimens commonly used in laboratory testing; compressive strength of concrete varies from 21.2 MPa to 90 MPa, covering normal and high-strength concrete grades; yield strength of reinforcement steel ranges from 100 MPa to over 1000 MPa, capturing both mild steel and high-strength reinforcement; ECC compressive strength spans 20 MPa to 160 MPa; and top and bottom ECC thicknesses range from 25 mm to 300 mm; samples with 0 mm ECC thickness serve as control RC beams. Despite this wide coverage, several features exhibit skewed or clustered distributions. This non-uniformity poses challenges for purely data-driven learning, making it difficult for conventional machine learning models to generalize well across the input space. The sparsity and heterogeneity of available data further underscore the importance of incorporating physical laws and empirical knowledge—a core advantage of the proposed EGML framework.

3.2. Domain-Specific Empirical Knowledge Formulation

In structural engineering, extensive experimental research and theoretical understanding have led to well-established empirical trends between input parameters and mechanical responses. For ECC-strengthened RC beams, such trends—though not always formally expressed as equations—can provide valuable prior knowledge to guide machine learning models, particularly in data-limited scenarios.

As summarized in

Table 1. Classification of empirical trends and incorporation into the training objective.

Empirical Behavior	Engineering Interpretation	Mathematical Representation
Monotonically Increasing	Output increases as the parameter increases	${\displaystyle \frac{\partial y}{\partial x_i}}\ge 0$
Monotonically Decreasing	Output decreases as the parameter increases	${\displaystyle \frac{\partial y}{\partial x_i}}\le 0$
Weak or Non-monotonic	No consistent directional influence or influence is problem-dependent	$\max \left(\left|{\displaystyle \frac{\partial y}{\partial x_i}}\right|-[\epsilon ],0\right)$

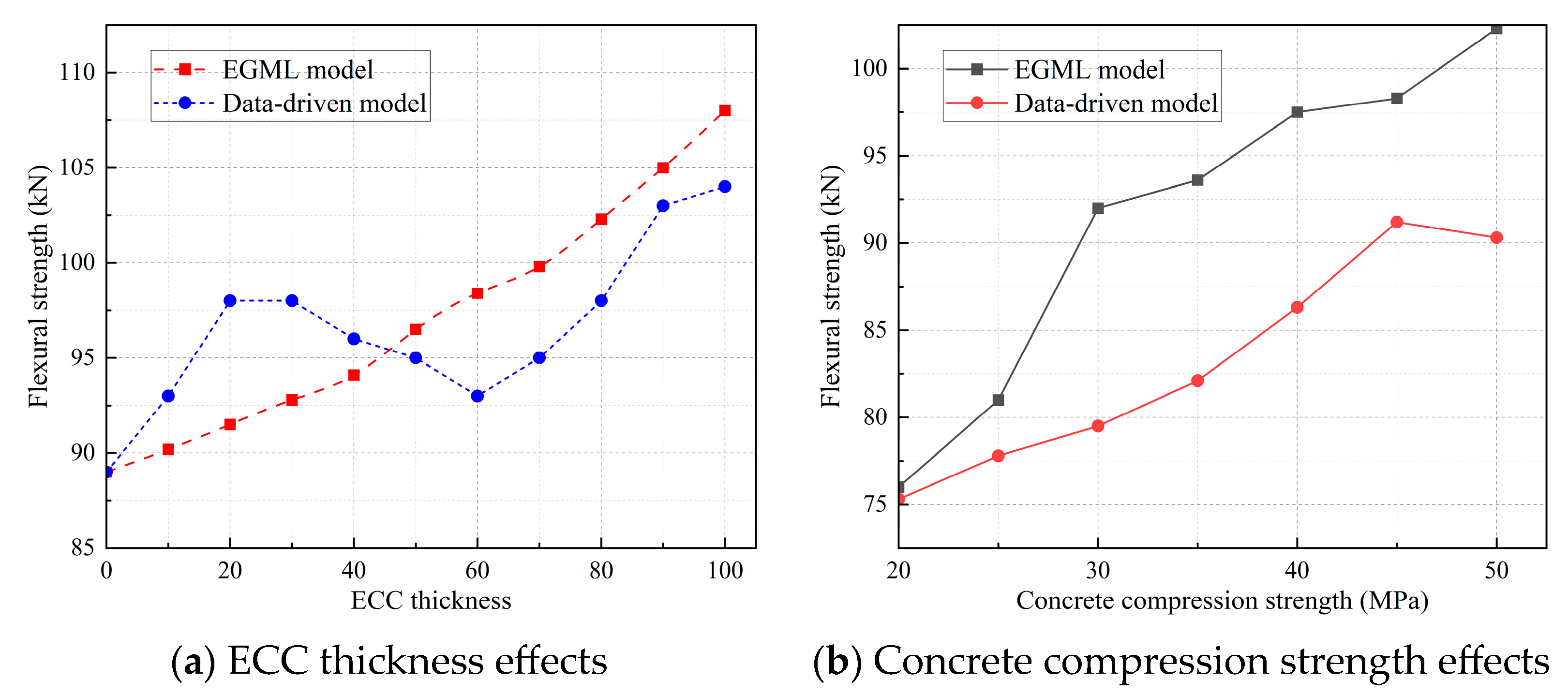
Note: $\left[\epsilon \right]$ is a small constant used to define tolerable derivative bounds, typically set based on engineering judgment or sensitivity analysis.

, the influence of input variables on flexural capacity can be categorized into three general types: monotonically increasing, monotonically decreasing, and weak or non-monotonic. These patterns are distilled from prior literature and expert judgment. For instance, increasing ECC bottom thickness or reinforcement area generally leads to improved flexural strength, while increasing stirrup spacing may reduce confinement and overall capacity. Some parameters, such as stirrup diameter, may have weaker or context-dependent effects.

To integrate these empirical trends into the learning process, custom regularization terms are defined based on the partial derivatives of the model output with respect to each input. If the predicted trend contradicts known engineering expectations (e.g., predicting decreasing strength with increasing ECC thickness), a penalty is imposed through the empirical loss function. Conversely, if the model’s prediction is physically consistent, the regularization term evaluates to zero, allowing standard data-driven learning to proceed unhindered.

$$los{s}_{\mathrm{emp}}={\displaystyle \sum _{j=1}^{N_{\mathrm{emp}}}\mathrm{Re}\mathrm{LU}\left(-s_j\times \frac{\partial f({\mathbf{x}}^j,\mathit{\theta })}{\partial x_j}\right)}$$

(4)

where s_j = +1 for parameters expected to have a monotonically increasing influence, s_j = −1 for parameters expected to have a monotonically decreasing influence, and s_j = 0 for weak or non-monotonic influence. ReLU ensures penalties are only applied when monotonicity is violated. This structure ensures that when the model prediction respects the expected empirical behavior, loss_emp = 0; when the prediction contradicts known physical trends, loss_emp increases sharply, discouraging such behavior.

Optimization algorithms such as Stochastic Gradient Descent (SGD) or Adam are used to update the parameters iteratively:

$$\mathit{\theta }=\mathit{\theta }-\eta \left({\lambda }_{\mathrm{data}}\times {\displaystyle \frac{\partial los{s}_{\mathrm{data}}}{\partial \mathit{\theta }}}+{\lambda }_{\mathrm{emp}}\times {\displaystyle \frac{\partial los{s}_{\mathrm{emp}}}{\partial \mathit{\theta }}}\right)$$

(5)

where $\eta$ is the learning rate. When the model predictions align with engineering expectations, loss_emp vanishes (loss_emp = 0) and training proceeds purely data-driven. When violations occur, the penalty increases sharply, discouraging physically implausible behaviors. This domain-guided supervision enhances interpretability, improves generalization, and reduces the risk of unrealistic predictions, especially under sparse or uneven data distributions.

This structure guarantees that when model predictions are consistent with prior empirical knowledge, the empirical loss becomes zero. When the predictions violate known trends, the loss increases rapidly, discouraging non-physical behaviors. By incorporating these soft constraints, the model is encouraged to follow established engineering relationships, which leads to improved interpretability, enhanced generalization, and reduced risk of physically implausible predictions. This domain-driven supervision forms a core component of the EGML framework and is particularly effective under limited or uneven data distributions.

3.3. Hyper-Parameters Optimization

The training performance of the proposed EGML model depends not only on the effective incorporation of physical and empirical constraints, but also critically on the design of the network architecture and the optimization of associated hyperparameters. These components govern the model’s capacity to learn from limited data while ensuring generalization, interpretability, and compliance with fundamental engineering principles. To achieve this balance, the EGML model is trained under a hybrid supervision strategy guided by a composite loss function that integrates data-driven accuracy, physical laws, and empirical trends.

A feedforward neural network is employed to approximate the nonlinear mapping between the 14 input features and the flexural capacity of ECC-strengthened RC beams. This architecture is chosen due to its universal approximation capability, computational efficiency, and flexibility in integrating physical constraints into custom loss functions. Compared to more complex architectures (e.g., RNNs or CNNs), the fully connected structure allows for easier incorporation of physics-informed terms, such as partial derivatives with respect to specific input parameters—making it particularly suitable for hybrid learning frameworks like EGML that require close interaction between empirical rules, physical consistency, and data-driven learning.

To optimize the architecture and training dynamics of the network, Bayesian Optimization (BO) is adopted. BO is well-suited for high-dimensional hyperparameter spaces and expensive objective evaluations, such as those involving physics-informed loss components. Unlike grid or random search, BO efficiently balances exploration and exploitation by constructing a probabilistic surrogate model (e.g., Gaussian Process) and selecting new hyperparameter candidates through an acquisition function such as Expected Improvement.

The following hyperparameters are tuned within the BO framework: (1) Number of hidden layers: L $\in$ {2, 3, 4, 5}; (2) Neurons per layer: N $\in$ {32, 64, 128, 256}; (3) Activation function: ϕ $\in$ {ReLU, tanh, LeakyReLU}; (4) Learning rate: η $\in$ [10⁻⁴, 10⁻²]; (5) Physics loss weight: λ_emp $\in$ [0.1, 10] (log scale); (6) Empirical loss weight: λ_emp $\in$ [0.1, 10] (log scale). Each configuration is evaluated using a composite validation metric that combines prediction error (RMSE) with penalties for violating known physical constraints and empirical trends. Candidate models are trained using the total loss function. Model training is performed using the Adam optimizer, with early stopping based on validation RMSE and the frequency of constraint violations. To ensure robustness and reproducibility, each training procedure is repeated five times with different random seeds. The best-performing configuration is selected based on the lowest composite score on the validation set.

To systematically search for the optimal EGML model configuration under the hybrid supervision strategy,

Table 2. Pseudocode for Bayesian Hyperparameter Optimization in EGML Training.

# Define input and output Input: Feature vector x ∈ ℝ^14 Output: Predicted flexural capacity $\hat{\mathrm{y}}$ = f_θ(x) # Define loss components Data loss:    L_data = (1/N) * ∑ₙ ($\hat{\mathrm{y}}$⁽ⁿ⁾ − y⁽ⁿ⁾)2 Physics-informed loss:    L_phys = ∑ over constraints [penalty when physical constraint violated] Empirical-guided loss:    For each feature x_j with expected trend s_j ∈ {+1, −1}:       ∂$\hat{\mathrm{y}}$/∂x_j = gradient(f_θ(x), x_j)       L_emp += ReLU(−s_j * ∂$\hat{\mathrm{y}}$/∂x_j) # penalize trend violation Total loss:    L_total = L_data + λ_phys * L_phys + λ_emp * L_emp # Define hyperparameter search space SearchSpace = {    “num_layers”: [2, 3, 4, 5],    “neurons_per_layer”: [32, 64, 128, 256],    “activation”: [“ReLU”, “tanh”, “LeakyReLU”],    “learning_rate”: [1e-4, 1e-2],         # log-uniform    “lambda_phys”: [0.1, 10],             # log-uniform    “lambda_emp”: [0.1, 10]              # log-uniform } # Initialize Bayesian Optimization BO.init(SurrogateModel=“GaussianProcess”, Acquisition=“ExpectedImprovement”) # Begin optimization loop for iteration in range(max_trials):    hparams = BO.suggest_next(SearchSpace)    scores = []    for run in range(num_repeats):       # Build and train EGML model with current hparams       model = build_EGML_model(hparams)       train_model(model,                loss=L_total,                optimizer=“Adam”,                early_stopping=True)       # Evaluate model performance       val_rmse = compute_RMSE(model, val_data)       val_constraint_violation = compute_constraint_violations(model, val_data)       composite_score = val_rmse + α * val_constraint_violation       scores.append(composite_score)    # Update surrogate model in BO    BO.update(hparams, average(scores)) # Return best hyperparameter configuration best_hparams = BO.get_best_configuration()

presents the pseudocode of the Bayesian hyperparameter optimization process. The routine begins by defining the model input (14 structural and material parameters) and output (predicted flexural capacity), as well as the composite loss function that integrates data fitting, physics-based regularization, and empirical trend alignment. The optimization process explores a multi-dimensional hyperparameter space, including network depth, neuron count, activation functions, learning rate, and the relative weights of the physical and empirical loss components. At each iteration, a surrogate model (e.g., Gaussian Process) is updated using the observed validation performance, and a new candidate hyperparameter set is proposed based on an acquisition function that balances exploration and exploitation.

For each candidate configuration, the EGML model is trained and evaluated multiple times to account for stochastic effects. The composite validation score combines root mean square error (RMSE) with penalties for constraint violations. This ensures that the selected model achieves not only high prediction accuracy but also consistency with physical knowledge and empirical observations. The final output is the hyperparameter set that minimizes the composite objective over all iterations. By embedding this automated and knowledge-guided tuning process into the training pipeline, the EGML framework is able to produce physically plausible and robust predictions, even in scenarios with sparse or uneven experimental data.

4. Comparison and Discussion

4.1. Training Process and Computational Efficiency

Both the proposed EGML model and the baseline data-driven neural network were implemented using the same feedforward neural network architecture, with hyperparameters optimized via Bayesian Optimization to ensure fair comparison. Each model was trained using the Adam optimizer, a batch size of 32, and early stopping based on validation loss stagnation.

As illustrated in Figure 4a, the baseline NN achieves fast convergence of the data loss component, stabilizing after approximately 100 epochs. In contrast, the EGML model requires a longer training period—approximately 600 epochs—to reach convergence. This delay stems from the additional computational burden associated with enforcing empirical and physical constraints. Moreover, the final data loss of the EGML model is slightly higher (about 5.6) than that of the baseline NN (about 4.8), reflecting the trade-off between data-fitting accuracy and physical consistency. Importantly, physical consistency is quantified by the empirical trend deviation loss (loss_emp), which penalizes violations of known monotonic or threshold-based mechanical laws. As shown in Figure 4b, for the EGML model, the empirical trend deviation loss decreases steadily and stabilizes at a low value (about 0.9) after 600 epochs, indicating successful enforcement of known engineering behaviors throughout training. Conversely, the empirical loss of the purely data-driven model fails to converge, fluctuating between 5.6 and 14.3 across the entire training process. This fluctuation suggests that, despite its superior data-fitting accuracy, the purely data-driven model frequently produces predictions that violate fundamental engineering trends and may lead to physically implausible outcomes.

In terms of computational efficiency, the EGML model naturally incurs a higher training cost. For a typical architecture with 3 hidden layers and 128 neurons per layer, the average training time per run was approximately 8.5 min on a personal computer equipped with an Intel^® Core™ i7-10750H CPU @ 2.60GHz and 64 GB RAM, compared to 6.1 min for the DNN. This 40% increase is attributable to the additional gradient evaluations and penalty computations required in each epoch. Nevertheless, this increase is considered acceptable and worthwhile, given the significant gains in interpretability, physical reliability, and robustness in prediction—especially for safety-critical structural applications.

4.2. Validation of Prediction Accuracy

To assess the predictive performance of the proposed EGML model, the dataset was split into a training set (80%) and a testing set (20%). The training set was further partitioned into k folds (k = 5 in this study) for cross-validation. In each fold, one subset served as the validation fold while the remaining k – 1 folds were used for model training. This process was iterated k times so that each subset acted as the validation set once. Hyperparameters—including the number of hidden layers, neurons per layer, learning rate, and regularization coefficients—were optimized via Bayesian Optimization using the mean validation error across all folds as the objective function. The same architecture and hyperparameter optimization procedure were applied to both the EGML model and the baseline purely data-driven neural network.

Figure 5a shows performance on the training set. The baseline data-driven DNN yields a lower root-mean-square error (E) of 0.091 for the training set and 0.088 for the testing set, compared with 0.105 (training set) and 0.101 (test set) for the EGML model. Similarly, the Pearson correlation coefficients (ρ) for the training set are 0.981 and 0.975 for the baseline and EGML models, respectively. For the training set, the coefficients of determination (R²) are 0.964 and 0.969 for EGML and the data-driven baseline. These results reflect the baseline model’s stronger fitting ability when evaluated solely by prediction error on known data. On the testing set shown in Figure 5b, the performance gap remains, though it narrows. The EGML model yields an E of 0.101, while the baseline data-driven model achieves 0.088. The ρ values are 0.979 (EGML) and 0.987 (data-driven baseline), respectively. The R² values are 0.968 (EGML) and 0.972 (baseline). This confirms that the purely data-driven model has slightly better generalization performance in terms of numerical accuracy.

4.3. Evaluation of Physical Consistency

To assess the physical consistency of the models, we examined their ability to reproduce well-established mechanical trends as described in Section 3.2. These trends include monotonic relationships, such as increased flexural capacity with greater ECC bottom thickness, larger tensile reinforcement area, and higher concrete compressive strength, as well as a reduction in capacity with increasing stirrup spacing. Such behaviors are grounded in both experimental observations and structural mechanics principles.

To visualize trend adherence, we conducted univariate parametric sweeps using synthetic input scenarios: for a representative RC beam configuration, one input feature was varied across a practical range while all others were held constant. For example, Figure 6a shows the effect of ECC bottom thickness on predicted flexural strength. The baseline configuration used the following fixed values: beam width = 200 mm, height = 300 mm, span length = 2050 mm, concrete compressive strength = 46.2 MPa, tensile reinforcement area = 981.25 mm², reinforcement yield strength = 470 MPa, stirrup diameter = 8 mm, ECC tensile strength = 4.5 MPa, and ECC compressive strength = 38.3 MPa. The ECC bottom thickness was varied from 0 mm (i.e., unstrengthened RC beam) to 90 mm. The results indicate that the EGML model produces smooth and strictly monotonic curves, consistent with engineering expectations. In contrast, the purely data-driven model generates irregular, oscillatory, and occasionally non-physical trends—e.g., decreases in flexural capacity with increasing ECC thickness, which contradicts known structural behavior.

A second trend evaluation was performed for concrete compressive strength, shown in Figure 6b. Here, ECC bottom thickness was fixed at 30 mm, and concrete compressive strength was varied from 20 MPa to 50 MPa, with corresponding tensile strength assumed to be 10% of the compressive strength. Again, the EGML model maintains physically consistent predictions, while the baseline model exhibits trend violations and inconsistent gradients. These experiments demonstrate that, beyond prediction accuracy, EGML offers superior adherence to physical laws and empirical expectations, a critical feature for engineering deployment. In real-world applications, where extrapolation beyond the training data is often necessary, physically inconsistent predictions can lead to unsafe or misleading outcomes.

In summary, the EGML model not only performs competitively in terms of predictive accuracy but also ensures mechanical plausibility, monotonicity, and interpretability—qualities that are vital in structural engineering contexts. The comparison highlights an important trade-off: while pure data-driven models may achieve slightly lower error metrics, they risk generating physically invalid outputs. The incorporation of empirical and physical constraints in EGML mitigates this risk and reinforces the model’s reliability and trustworthiness.

Overall, while the proposed EGML framework exhibits slightly lower numerical accuracy compared to the purely data-driven approach, it consistently enforces physical consistency by embedding domain knowledge into the learning process. Unlike purely data-driven models that may overfit to data idiosyncrasies, the integration of empirical constraints ensures that the predicted responses not only follow the correct overall physical trends but also remain quantitatively aligned with observed data as far as possible. This balance between physical fidelity and data conformity enhances interpretability and strengthens generalization capability across diverse loading and boundary conditions. As demonstrated by the training–testing performance comparison and the evolution of both data-fitting and empirical trend deviation losses, incorporating physical mechanisms effectively mitigates overfitting, ensuring that the model remains robust when applied beyond the training domain.

5. Conclusions

This study proposed an EGML framework for the prediction of flexural capacity in ECC-strengthened RC beams, aiming to bridge the gap between data-driven learning and engineering domain knowledge. The approach integrates experimental evidence, simplified physical models, and well-established empirical trends into the training of a neural network, thereby enhancing both predictive performance and physical interpretability. Key conclusions are as follows:

(1) A comprehensive experimental database was constructed by compiling 194 test samples from literature, encompassing a diverse range of structural, material, and geometric features. Despite its usefulness, the dataset exhibited heterogeneity and imbalance, underscoring the limitations of purely data-driven models.

(2) The EGML framework incorporates physics and empirical supervision through a hybrid loss function. Empirical monotonic trends are transformed into gradient-based soft constraints, while simplified physical relationships serve as weak supervision. This design enables the network to learn not only from data, but also from scientific expectations.

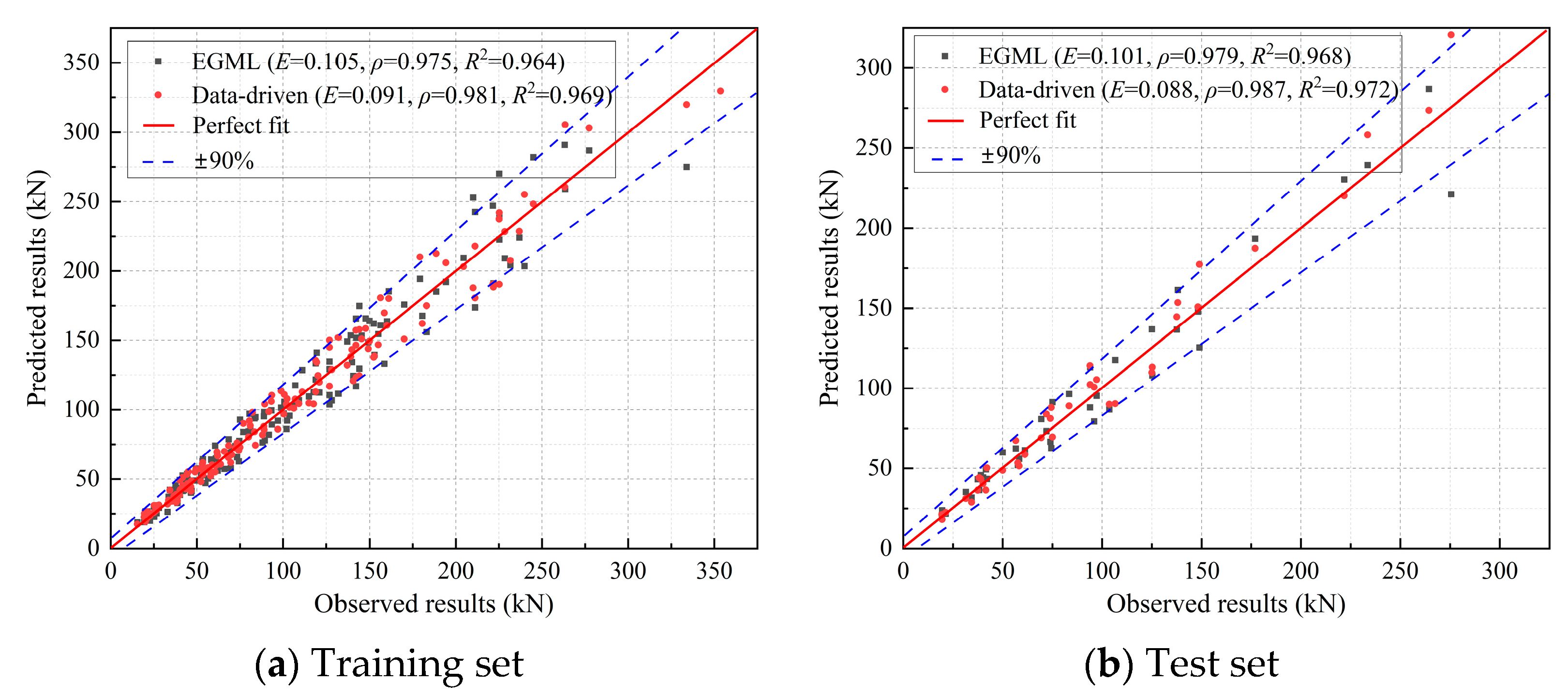
(3) Training results demonstrate that EGML achieves high prediction accuracy, comparable to a purely data-driven model. While the baseline model slightly outperformed EGML in terms of root-mean-square error, it frequently violated physical trends and produced inconsistent predictions—especially in data-sparse regions.

In summary, EGML provides a robust, interpretable approach for structural performance prediction under data scarcity. While current results are limited to ultimate flexural capacity and rely on laboratory-derived datasets, future research will address these limitations by: (i) conducting targeted experiments for underrepresented combinations of structural and material parameters, as well as incorporating field data and material uncertainties through probabilistic modeling, and (ii) expanding the framework to additional mechanical responses such as stiffness degradation, crack development, and energy dissipation. These improvements will advance EGML toward a practical, reliable decision-support tool for performance-based design and construction of ECC-strengthened RC structures.