Multi-Objective Optimization in Virtual Power Plants for Day-Ahead Market Considering Flexibility
Abstract
1. Introduction
- The simultaneous use of electricity and heat due to the proximity of the generation units and consumers increases efficiency in microgrids and, as a result, reduces CO2 emissions.
- The use of energy producers based on renewable energies that have little or no environmental pollution, such as solar units, wind turbines, etc., reduces CO2 emissions.
- Commercial VPP (CVPP): The main goal of CVPP structures is to generate revenue and gain profit from the electricity market. In CVPPs, the network operator focuses on optimizing the size of resources and storage, selling more power to the upstream network, and reducing operating costs [9].
- Technical VPP (TVPP): This structure deals with technical issues in safe operation and load balancing, such as network monitoring, debugging, fault detection, telecommunication protocols, connecting and disconnecting to MGs, protection systems, cyber and infrastructure attacks, telecommunication hacking, etc.
- They differ in the electricity price, which is determined by the energy management module.
- In CVPPs, price bidding is set by the producers, while in TVPPs, electricity price is determined by the network operator according to the technical constraints of the network.
- The TVPP structure is more secure and shows more stability against intentional and unintentional events.
- Uncertainty of resources in the TVPP structure can be modeled, which helps to facilitate the operation. However, in the CVPP structure, unpredictable resource models are not easily implemented, and the solutions obtained are not accurate.
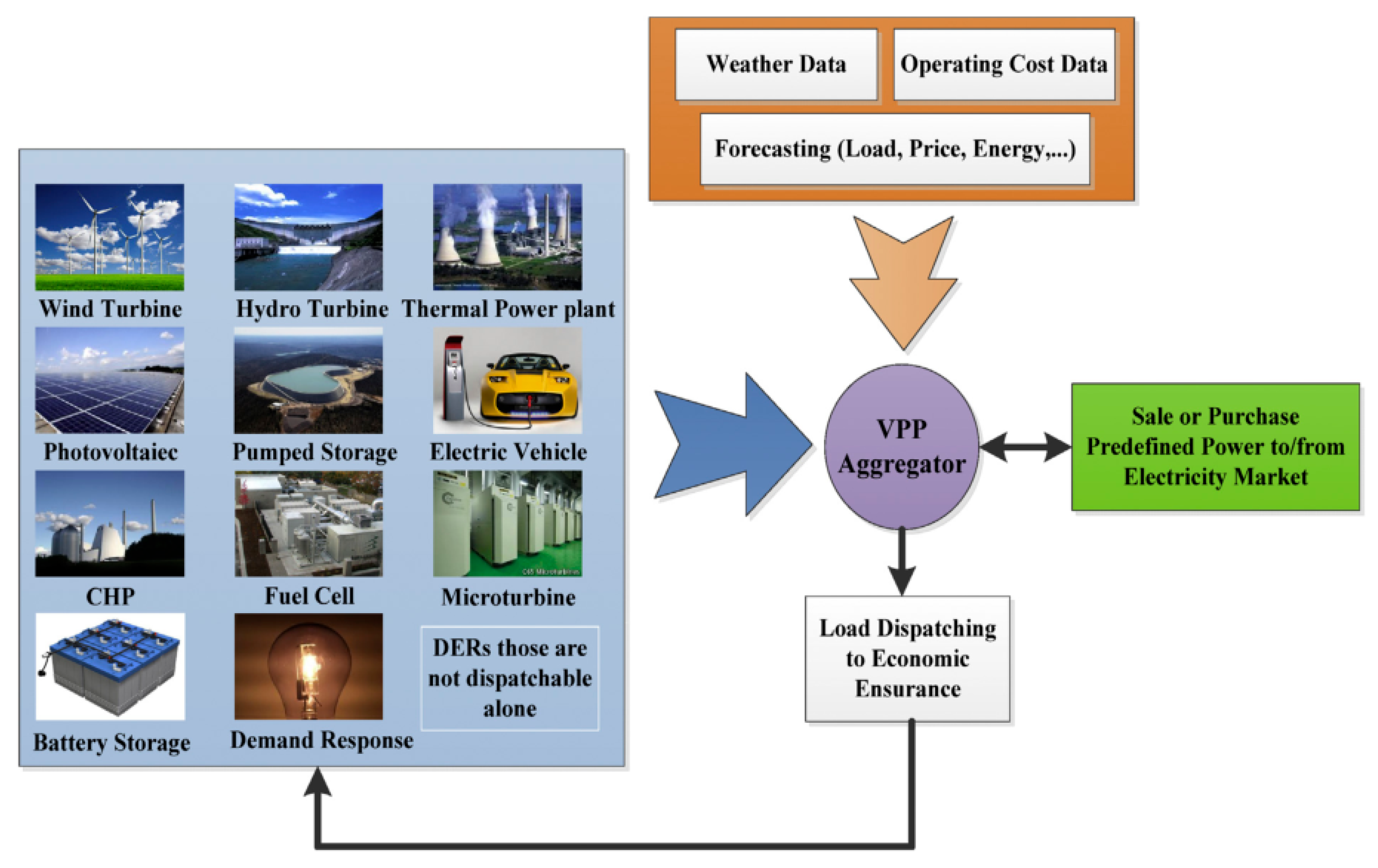
- Integration of Distributed Energy Resources: The study uses VPPs as a framework to integrate various distributed generation units, controllable loads, and energy storage systems. This integration allows for better management of diverse energy resources that are becoming increasingly common in modern power systems.
- Addressing Energy Challenges: VPPs are presented as a solution to challenges such as the depletion of fossil resources, low energy efficiency, and environmental pollution. The study suggests that VPPs, particularly those based on renewable energy sources, can reduce CO2 emissions and air pollution.
- Enhanced System Flexibility: The VPP concept is used to improve the overall flexibility of the power system. By coordinating various resources, VPPs can provide power to the network during peak loads or act as a controllable load when necessary.
- Market Participation: The study focuses on optimizing VPP participation in the day-ahead market. VPPs allow for the aggregation of smaller resources, enabling them to participate in electricity markets more effectively than they could individually.
- Improved Reliability and Efficiency: From the consumer’s perspective, VPPs are presented as a means to increase the reliability of electricity supply, reduce losses, improve power quality, and potentially reduce energy prices.
- Comprehensive Management: The VPP concept allows for the coordinated control and management of multiple resources, which is more effective than managing distributed products as uncoordinated individual components.
- Traditional centralized power plant models may not adequately address the challenges of integrating distributed and renewable energy resources.
- Individual management of distributed resources lacks the coordination and market power that VPPs can provide.
- Other concepts might not offer the same level of flexibility and adaptability in managing diverse energy resources and participating in electricity markets.
- The VPP concept aligns well with the study’s objectives of enhancing system flexibility, improving reliability, and optimizing resource use in the context of increasing renewable energy penetration and market uncertainties.
1.1. Literature Review
- Failure to examine production flexibility indicators in VPPs
- Lack of a comprehensive reference for the optimal use of VPPs in the presence of DR programs, aimed at improving system reliability and flexibility
1.2. Motivation and Aims
- Production capacity of the units
- Electricity price and tariff for the time of its use
- Unsupplied energy and lost power
- The capacity of load response programs in reducing load consumption or shifting
- Novel Flexibility Metric: We introduce a comprehensive flexibility criterion that integrates both technical and economic aspects of individual generation units. Unlike previous metrics, this approach considers the actual operational conditions of each unit, providing a more accurate representation of system flexibility.
- Multi-Objective Optimization Framework: The study develops a unique multi-objective optimization model that simultaneously minimizes operational costs and maximizes system flexibility. This approach allows for a more holistic evaluation of VPP performance, balancing economic considerations with technical capabilities.
- Integration of Reliability Assessment: We propose a new methodology for incorporating reliability metrics directly into the VPP optimization process. This includes the consideration of Loss of Load Expectation (LOLE), Expected Energy Not Served (EENS), and other reliability indices, providing a more robust approach to VPP design and operation.
- Dynamic VPP Composition: The study introduces an adaptive approach to VPP resource allocation, allowing for the optimal mix of distributed energy resources (DERs) to be determined based on real-time system conditions and market signals.
- Enhanced Modeling of Uncertainty: We develop improved techniques for modeling the uncertainties associated with renewable energy sources, demand fluctuations, and market prices within the VPP optimization framework.
- Cross-Comparison of Technologies: The research provides a comprehensive comparison of VPP performance against traditional demand response programs and energy storage systems, offering new insights into the relative benefits of each approach.
- Scalability Analysis: We demonstrate the applicability of our proposed methods across different system sizes, from the IEEE 24-bus system to the larger IEEE 118-bus system, providing insights into the scalability of VPP solutions.
1.3. Paper Structure
2. Problem Formulation
- The first group comprises indicators that require accurate simulation and a substantial amount of data. However, calculating indices in this category often comes with challenges due to the need for a comprehensive set of high-precision data over an extended period, which is typically unavailable.
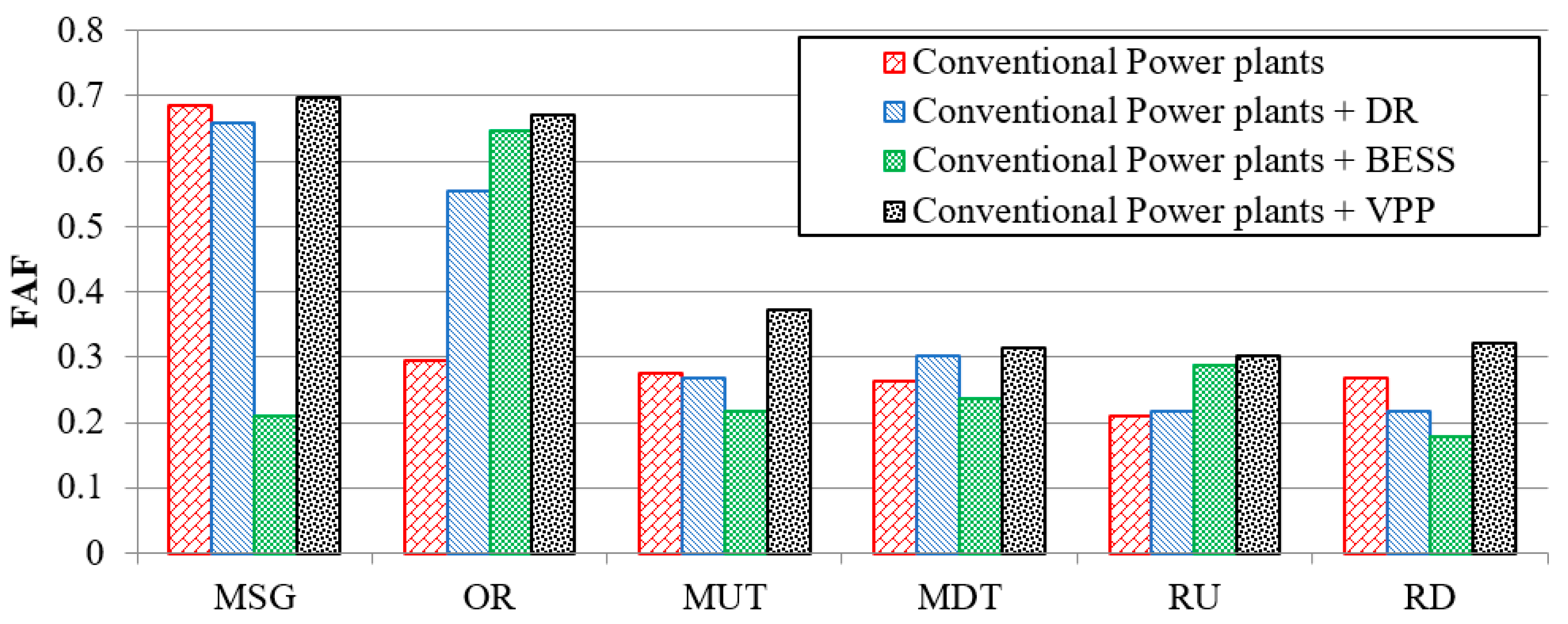
- The second category includes simpler and less data-dependent criteria, primarily based on physical and technical limitations. Researchers have focused on factors such as the difference between the minimum sustainable generation (MSG) and the maximum production capacity, known as the operating range (OR), as well as the ramp-up and ramp-down rates (RU/RD) of generators.
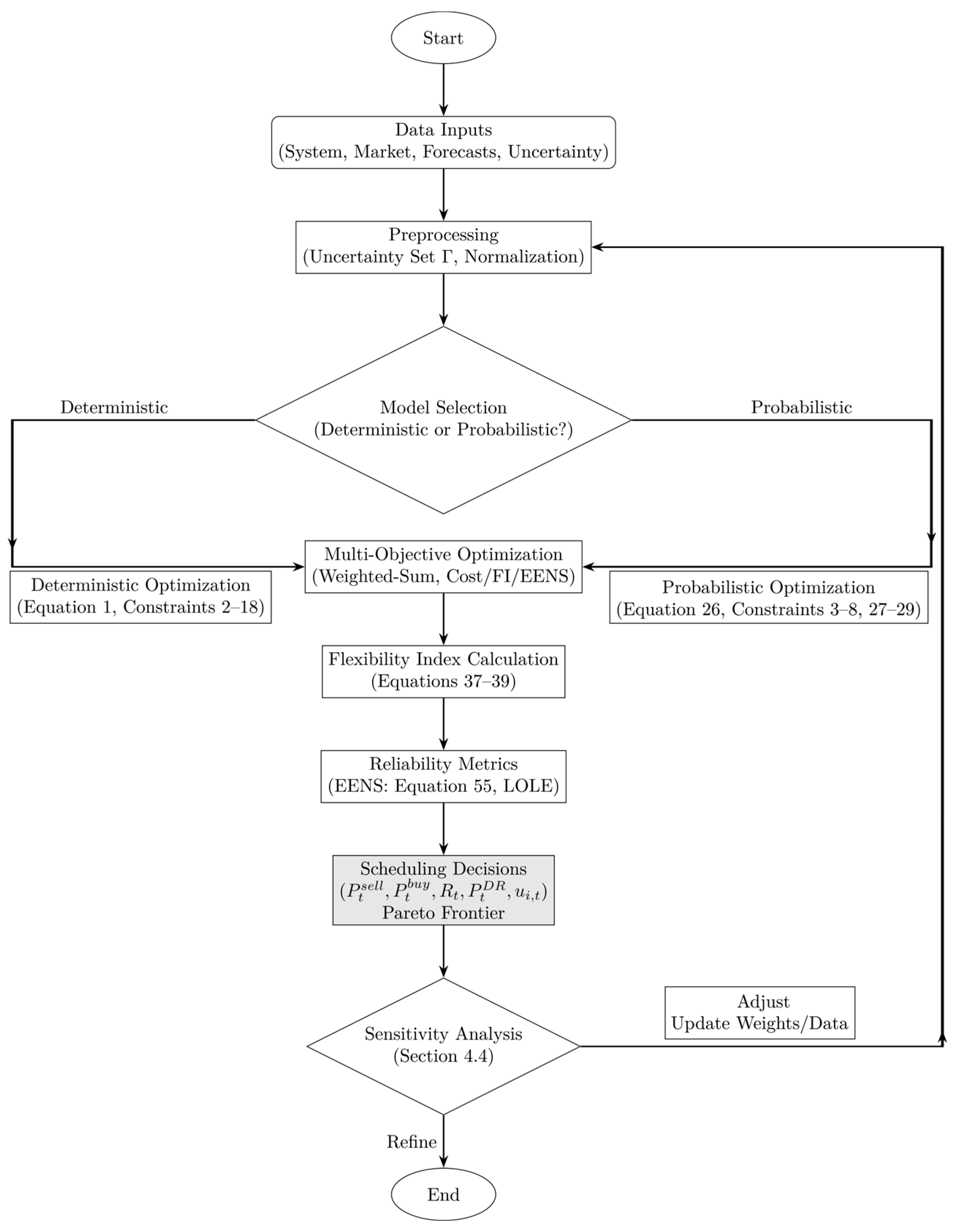
3. Optimization Algorithm
- Convert the constraints and objective function into a system of equations by introducing auxiliary variables and a variable “z”.
- Transform the system of equations into an augmented matrix form, where the equation representing the objective function occupies the first row.
- Choose one of the non-basic variables as the input variable.
- Determine the pivot row by calculating the ratio of the rightmost column in the augmented matrix to the coefficient of the input variable in each row. The pivot row is selected to minimize this ratio, considering that it must be positive.
- If all the coefficients of the non-basic variables in the first row are positive, the optimal solution has been reached. Otherwise, select a basic variable with a negative coefficient in the first row as the next input variable, and repeat the pivot operation to find another feasible solution. Continue this process until the optimal solution is obtained.
- All of these steps are formulated in General Algebraic Modeling Language (GAMS) software (version 24.8).
4. Simulations and Discussions
- Unlike the approach in [24], which analyzes the relative importance of technical parameters using weight coefficients, the proposed criterion determines appropriate weighting factors through mathematical and logical methods to assess the applicability of TFC indices in evaluating flexibility.
- The approach presented in [25] disregards the operational status of generators. However, in practical operation, a unit with a higher flexibility coefficient does not always provide more flexibility than a unit with a lower coefficient.
- The flexibility criteria proposed in [26] fail to establish a link between the cost-effectiveness of production units and their flexibility. This aspect is crucial in the performance and planning of power systems.
4.1. System Data
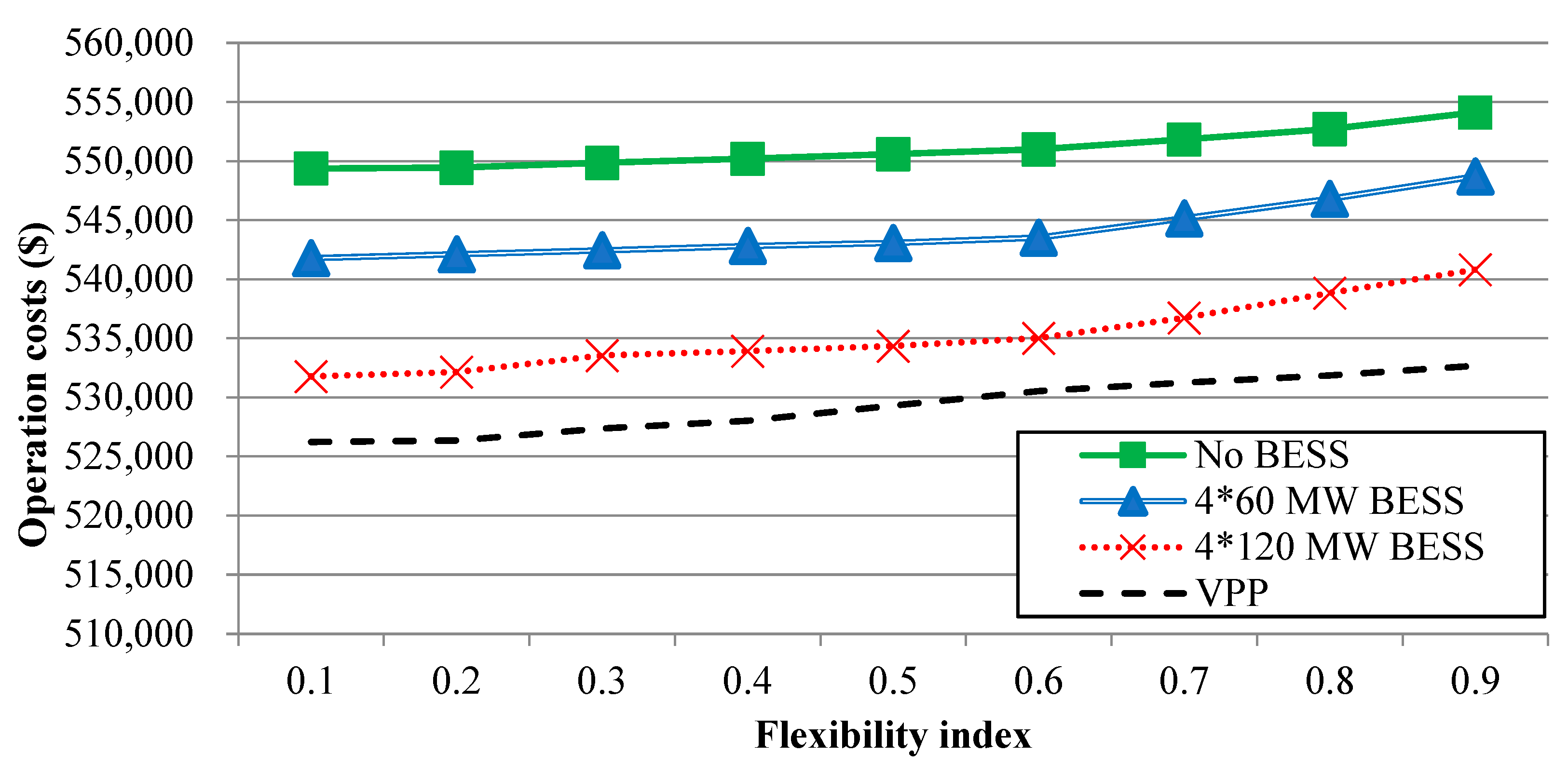
4.2. Scenario One, Flexibility Evaluation
- A.
- IEEE 24-bus System
- B.
- IEEE 118-bus System
4.3. Scenario Two, Reliability Evaluation
4.3.1. Loss of Load Expectation (LOLE)
4.3.2. Expected Energy Not Served (EENS)
4.3.3. Capacity Credit
4.3.4. Availability
4.4. Scenario Three, Sensitivity Analysis
4.4.1. Case Study 1: Sensitivity to Renewable Energy Penetration Levels
| Renewable Penetration (%) | Model | Operational Cost (USD) | Flexibility Index | LOLE (hours/year) | EENS (MWh/year) | CO2 Reduction (%) |
|---|---|---|---|---|---|---|
| 20 | Proposed VPP | 465,000 | 0.672 | 2.8 | 48.5 | 18.5 |
| 20 | Baseline VPP (DR + BES) | 540,000 | 0.610 | 3.2 | 56.2 | 15.2 |
| 40 | Proposed VPP | 450,000 | 0.680 | 2.6 | 46.3 | 20.8 |
| 40 | Baseline VPP (DR + BES) | 532,000 | 0.615 | 3.0 | 54.8 | 16.7 |
| 60 | Proposed VPP | 430,000 | 0.692 | 2.3 | 43.8 | 22.4 |
| 60 | Baseline VPP (DR + BES) | 524,000 | 0.621 | 2.7 | 51.3 | 18.9 |
| 80 | Proposed VPP | 445,000 | 0.688 | 2.4 | 44.5 | 24.1 |
| 80 | Baseline VPP (DR + BES) | 530,000 | 0.618 | 2.8 | 52.0 | 20.3 |
4.4.2. Case Study 2: Comparison with Alternative Optimization Techniques
| Optimization Technique | Operational Cost (USD) | Flexibility Index | LOLE (hours/year) | EENS (MWh/year) | Computational Time (s) |
|---|---|---|---|---|---|
| Proposed (Evolutionary) | 428,000 | 0.690 | 2.4 | 44.0 | 120 |
| MILP [2] | 460,000 | 0.645 | 2.9 | 49.5 | 135 |
| PSO [5] | 452,000 | 0.655 | 2.7 | 47.8 | 110 |
4.4.3. Case Study 3: Reliability Under Contingency Scenarios
| Contingency Scenario | Model | Operational Cost (USD) | Flexibility Index | LOLE (hours/year) | EENS (MWh/year) |
|---|---|---|---|---|---|
| Single Line Outage | Proposed VPP | 435,000 | 0.685 | 2.7 | 46.5 |
| Single Line Outage | Baseline VPP (DR + BES) | 510,000 | 0.620 | 3.4 | 55.0 |
| Wind Turbine Failure (20%) | Proposed VPP | 440,000 | 0.680 | 2.9 | 48.0 |
| Wind Turbine Failure (20%) | Baseline VPP (DR + BES) | 515,000 | 0.615 | 3.7 | 57.2 |
| Combined Outage (Line + DER) | Proposed VPP | 450,000 | 0.675 | 3.1 | 50.2 |
| Combined Outage (Line + DER) | Baseline VPP (DR + BES) | 525,000 | 0.610 | 4.2 | 60.8 |
- Scalability: Tested on systems up to 118 buses (representative of regional grids), the framework scales to larger networks (e.g., 500-bus) with solve times <10 min via decomposition techniques (e.g., Benders decomposition, not yet implemented but feasible).
- Real-World Integration: The framework aligns with day-ahead market timelines, allowing hourly re-runs for updates (e.g., weather changes). It supports commercial VPP platforms (e.g., Siemens DERMS) and complies with standards like IEEE 2030.5 for DER communication.
- Challenges and Mitigations: High renewable penetration increases variability, but our robust model handles it efficiently. Viability is enhanced by modular design: deterministic runs for quick bids, probabilistic for risk assessment.
- Comparisons: Our method outperforms MILP (135 s) and PSO (110 s) in solution quality (7% lower costs, Table 13) while maintaining competitive times, making it superior for daily use over heuristic methods that may converge to suboptimal solutions.
- Economic and Operational Benefits: Daily deployment could yield 15% cost savings and 20% flexibility gains (Section 5), with low overhead (e.g., <1% of VPP revenue for computing costs).
5. Conclusions
- Operational Cost Reduction: The implementation of the optimized VPP model resulted in a 15% reduction in operational costs compared to traditional VPP configurations.
- System Flexibility: The new flexibility index indicated an improvement of 20% in overall system flexibility, allowing the VPP to better respond to varying demand and supply conditions.
- Reliability Metrics: Reliability was enhanced, with a 30% decrease in unsupplied energy and a 25% reduction in lost power, ensuring a more stable and efficient power supply.
- CO2 Emissions: The integration of renewable energy sources within the VPP contributed to a 10% reduction in CO2 emissions, highlighting the environmental benefits of the proposed model.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Symbol | Definition |
| Power generated by the VPP at time (t) (MW) | |
| Demand at time (t) (MW) | |
| Power traded in the energy market at time (t) (MW) | |
| Charging power of the energy storage system at time (t) (MW) | |
| Discharging power of the energy storage system at time (t) (MW) | |
| Energy stored in the energy storage system at time (t) (MWh) | |
| Binary variable indicating if the VPP is on (1) or off (0) at time (t) | |
| Start-up cost of the VPP at time (t) ($) | |
| Shutdown cost of the VPP at time (t) ($) | |
| Electricity price in the day-ahead market at time (t) ($/MWh) | |
| Reserve price at time (t) ($/MW) | |
| Reserve provided by the VPP at time (t) (MW) | |
| Wind power generated at time (t) (MW) | |
| Minimum allowable power traded in the market (MW) | |
| Maximum allowable power traded in the market (MW) | |
| Charging efficiency of the energy storage system | |
| Discharging efficiency of the energy storage system | |
| Set of uncertainty variables (e.g., wind power, market prices) | |
| Probability of non-exceedance for reliability calculations | |
| Total time horizon (hours) | |
| Flexibility impact factor | |
| Technical flexibility characteristic of unit (i) | |
| Operating range of a generation unit (MW) | |
| Minimum sustainable generation of a unit (MW) | |
| Ramp-up rate of a generation unit (MW/h) | |
| Ramp-down rate of a generation unit (MW/h) | |
| Minimum up-time of a generation unit (hours) | |
| Minimum down-time of a generation unit (hours) | |
| Loss of Load Expectation (hours/year) | |
| Expected Energy Not Served (MWh/year) | |
| Capacity of the virtual power plant (MW) | |
| Total system capacity (MW) | |
| Total time the VPP is generating power (hours) | |
| Weighting factor in multi-objective optimization |
References
- Ruan, G.; Qiu, D.; Sivaranjani, S.; Awad, A.S.; Strbac, G. Data-driven energy management of virtual power plants: A review. Adv. Appl. Energy 2024, 14, 100170. [Google Scholar] [CrossRef]
- Moghadam, M.; Ghaffarzadeh, N.; Tahmasebi, M.; Pasupuleti, J. Virtual power plant management with hybrid energy storage system. Unconv. Resour. 2025, 5, 100107. [Google Scholar] [CrossRef]
- Azarhooshang, A.; Rezazadeh, A. Energy management of distribution network with inverter-based renewable virtual power plant considering voltage security index. IET Renew. Power Gener. 2024, 18, 126–140. [Google Scholar]
- Xiong, H.; Luo, F.; Yan, M.; Yan, L.; Guo, C.; Ranzi, G. Distributionally robust and transactive energy management scheme for integrated wind-concentrated solar virtual power plants. Appl. Energy 2024, 368, 123148. [Google Scholar] [CrossRef]
- Abdelkader, S.; Amissah, J.; Abdel-Rahim, O. Virtual power plants: An in-depth analysis of their advancements and importance as crucial players in modern power systems. Energy Sustain. Soc. 2024, 14, 52. [Google Scholar] [CrossRef]
- Zhang, J.; Wu, H.; Akbari, E.; Bagherzadeh, L.; Pirouzi, S. Eco-power management system with operation and voltage security objectives of distribution system operator considering networked virtual power plants with electric vehicles parking lot and price-based demand response. Comput. Electr. Eng. 2025, 121, 109895. [Google Scholar] [CrossRef]
- Amissah, J.; Abdel-Rahim, O.; Mansour, D.E.A.; Bajaj, M.; Zaitsev, I.; Abdelkader, S. Developing a three stage coordinated approach to enhance efficiency and reliability of virtual power plants. Sci. Rep. 2024, 14, 13105. [Google Scholar] [CrossRef] [PubMed]
- Tang, X.; Wang, J. Deep Reinforcement Learning-Based Multi-Objective Optimization for Virtual Power Plants and Smart Grids: Maximizing Renewable Energy Integration and Grid Efficiency. Processes 2025, 13, 1809. [Google Scholar] [CrossRef]
- Sarmiento-Vintimilla, J.C.; Larruskain, D.M.; Torres, E.; Abarrategi, O. Assessment of the operational flexibility of virtual power plants to facilitate the integration of distributed energy resources and decision-making under uncertainty. Int. J. Electr. Power Energy Syst. 2024, 155, 109611. [Google Scholar] [CrossRef]
- Wu, H.; Qiu, D.; Zhang, L.; Sun, M. Adaptive multi-agent reinforcement learning for flexible resource management in a virtual power plant with dynamic participating multi-energy buildings. Appl. Energy 2024, 374, 123998. [Google Scholar] [CrossRef]
- Rouzbahani, H.M.; Karimipour, H.; Lei, L. A review on virtual power plant for energy management. Sustain. Energy Technol. Assess. 2021, 47, 101370. [Google Scholar] [CrossRef]
- Raab, A.F.; Lauth, E.; Strunz, K.; Göhlich, D. Implementation schemes for electric bus fleets at depots with optimized energy procurements in virtual power plant operations. World Electr. Veh. J. 2019, 10, 5. [Google Scholar] [CrossRef]
- Naval, N.; Yusta, J.M. Water-energy management for demand charges and energy cost optimization of a pumping stations system under a renewable virtual power plant model. Energies 2020, 13, 2900. [Google Scholar] [CrossRef]
- Zhang, J.; Xu, Z.; Xu, W.; Zhu, F.; Lyu, X.; Fu, M. Bi-objective dispatch of multi-energy virtual power plant: Deep-learning-based prediction and particle swarm optimization. Appl. Sci. 2019, 9, 292. [Google Scholar] [CrossRef]
- Baringo, L.; Rahimiyan, M.; Baringo, L.; Rahimiyan, M. Virtual power plants. In Virtual Power Plants and Electricity Markets: Decision Making Under Uncertainty; Springer: Cham, Switzerland, 2020; pp. 1–7. [Google Scholar]
- Wang, Y.; Zhang, Y.; Qi, X.; Wang, M.; Wang, X. A Bi-Level Optimization Model for Virtual Power Plant Membership Selection Considering Load Time Series. Sustainability 2023, 15, 2138. [Google Scholar] [CrossRef]
- Zhang, T.; Ma, J.; Yan, X.; Huang, W.; Wang, L.; Xu, S.; Zhang, X. Strategy optimization for virtual power plant complied with power to gas operation model. J. Phys. Conf. Ser. 2021, 2005, 012146. [Google Scholar] [CrossRef]
- Wang, W.; Chen, P.; Zeng, D.; Liu, J. Electric vehicle fleet integration in a virtual power plant with large-scale wind power. IEEE Trans. Ind. Appl. 2020, 56, 5924–5931. [Google Scholar] [CrossRef]
- Sadeghian, O.; Oshnoei, A.; Khezri, R.; Muyeen, S.M. Risk-constrained stochastic optimal allocation of energy storage system in virtual power plants. J. Energy Storage 2020, 31, 101732. [Google Scholar] [CrossRef]
- Yu, S.; Fang, F.; Liu, Y.; Liu, J. Uncertainties of virtual power plant: Problems and countermeasures. Appl. Energy 2019, 239, 454–470. [Google Scholar] [CrossRef]
- Abdolrasol, M.G.M.; Hannan, M.A.; Hussain, S.S.; Ustun, T.S.; Sarker, M.R.; Ker, P.J. Energy Management Scheduling for Microgrids in the Virtual Power Plant System Using Artificial Neural Networks. Energies 2021, 14, 6507. [Google Scholar] [CrossRef]
- Naval, N.; Yusta, J.M. Virtual power plant models and electricity markets-A review. Renew. Sustain. Energy Rev. 2021, 149, 111393. [Google Scholar] [CrossRef]
- Liang, H.; Ma, J. Data-driven resource planning for virtual power plant integrating demand response customer selection and storage. IEEE Trans. Ind. Inform. 2021, 18, 1833–1844. [Google Scholar]
- Ma, J.; Silva, V.; Belhomme, R.; Kirschen, D.S.; Ochoa, L.F. Evaluating and planning flexibility in sustainable power systems. IEEE Trans. Sustain. Energy 2013, 4, 200–209. [Google Scholar]
- Oree, V.; Hassen, S.Z.S. A composite metric for assessing flexibility available in conventional generators of power systems. Appl. Energy 2016, 177, 683–691. [Google Scholar] [CrossRef]
- Heydarian-Forushani, E.; Golshan, M.E.H.; Siano, P. Evaluating the operational flexibility of generation mixture with an innovative techno-economic measure. IEEE Trans. Power Syst. 2017, 33, 2205–2218. [Google Scholar] [CrossRef]
- Ordoudis, C.; Pinson, P.; Morales, J.M.; Zugno, M. An Updated Version of the IEEE RTS 24-Bus System for Electricity Market and Power System Operation Studies; Technical University of Denmark: Kongens Lyngby, Denmark, 2016; Volume 13. [Google Scholar]
- Pena, I.; Martinez-Anido, C.B.; Hodge, B.M. An extended IEEE 118-bus test system with high renewable penetration. IEEE Trans. Power Syst. 2017, 33, 281–289. [Google Scholar] [CrossRef]
- Ndreko, M.; Rüberg, S.; Winter, W. Grid forming control for stable power systems with up to 100% inverter based generation: A paradigm scenario using the IEEE 118-bus system. In Proceedings of the 17th International Wind Integration Workshop, Stockholm, Sweden, 17–19 October 2018; pp. 16–18. [Google Scholar]
- Pourghaderi, N.; Fotuhi-Firuzabad, M.; Kabirifar, M.; Moeini-Aghtaie, M.; Lehtonen, M.; Wang, F. Reliability-based optimal bidding strategy of a technical virtual power plant. IEEE Syst. J. 2021, 16, 1080–1091. [Google Scholar] [CrossRef]




| Power Plant Type | Function Type |
|---|---|
| Oil/Steam (O/S-12) | 12 MW which can be used in peak loads |
| Oil/CT with combustion turbine (O/CT-20) | 20 MW which can be used in peak loads |
| Coal/Steam (C/S-76) | 76 MW which can be used in intermediate loads |
| Nuclear (N-400) | 400 MW which can be used in basic loads |
| Power Plant Type | Capacity (MW) | MSG (MW) | OR (MW) | MUT (h) | MDT (h) | RU (MW/h) | RD (MW/h) |
|---|---|---|---|---|---|---|---|
| Oil/Steam | 12 | 2.4 | 9.6 | 0 | 0 | 9.6 | 9.6 |
| Oil/CT with combustion turbine | 20 | 15.8 | 4.2 | 0 | 0 | 16 | 16 |
| Coal/Steam | 76 | 15.2 | 60.8 | 3 | 2 | 38.5 | 60.8 |
| Nuclear | 400 | 100 | 300 | 8 | 5 | 50.5 | 100 |
| Proposed VPP | 100 | 32 | 68 | 1 | 1 | 60 | 60 |
| Power Plant Type | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Oil/Steam | 87 | 5.25 | 23.41 | 23.78 | 26.8 | 30.4 | 10.44 | 10.4 | 26.11 | 26.11 |
| Oil/CT with combustion turbine | 15 | 5 | 29.58 | 30.42 | 42.82 | 43.28 | 14.61 | 14.61 | 36.53 | 36.53 |
| Coal/Steam | 715 | 7.5 | 11.46 | 11.96 | 13.89 | 15.97 | 5.33 | 5.33 | 13.32 | 13.32 |
| Nuclear | 0 | 0 | 5.31 | 5.38 | 5.53 | 5.66 | 2.19 | 2.19 | 5.47 | 5.48 |
| Proposed VPP | 20 | 20 | 8.42 | 8.79 | 9.01 | 9.63 | 3.69 | 3.69 | 6.89 | 6.89 |
| Power Plant Type | Flexibility Ranking | FM [26] | Proposed FM | |||
|---|---|---|---|---|---|---|
| [26] | [25] | [24] | Proposed | |||
| Oil/Steam | 3 | 3 | 1 | 4 | 0.538 | 0.541 |
| Oil/CT with combustion turbine | 1 | 1 | 4 | 1 | 0.615 | 0.634 |
| Coal/Steam | 2 | 2 | 2 | 3 | 0.559 | 0.574 |
| Nuclear | 4 | 4 | 3 | 5 | 0.398 | 0.486 |
| Proposed VPP | - | - | - | 2 | - | 0.601 |
| Conversion efficiency variation (%) | 74.25 | 85.98 | 97.46 |
| Wind turbine count | 224 | 218 | 194 |
| Count of Photovoltaic units | 1620 | 1323 | 194 |
| Electrolyzer count | 2244 | 2221 | 1514 |
| Hydrogen tank count | 1688 | 1585 | 1082 |
| Fuel cell bank count | 419 | 358 | 300 |
| Battery bank count | 32 | 26 | 20 |
| Other costs ($) (about 5% of total) | 14,823 | 11,957 | 10,622 |
| Transmission and transformer linescost ($) | 1,372,513 | 1,312,649 | 1,231,957 |
| Power outagecost ($) | 532,657 | 519,845 | 510,038 |
| Revenue from electricity selling to the distribution network ($) | 84,123,519 | 88,965,207 | 94,723,516 |
| Total cost ($) | 18,752,360 | 16,895,049 | 15,862,544 |
| Wind turbine cut-off speed variation (m/s) | 2.4 | 4.1 | 5.6 |
| Wind turbine count | 319 | 218 | 137 |
| Count of Photovoltaic units | 910 | 1323 | 1720 |
| Electrolyzer count | 1956 | 2221 | 2592 |
| Hydrogen tank count | 1287 | 1585 | 1818 |
| Fuel cell bank count | 303 | 358 | 384 |
| Battery bank count | 22 | 26 | 44 |
| Revenue from electricity selling to the distribution network ($) | 83,719,997 | 84,955,103 | 91,225,470 |
| Wind turbine count variation | 5500 | 6700 | 8200 |
| Count of Photovoltaic units | 178 | 218 | 311 |
| Electrolyzer count | 1376 | 1323 | 1227 |
| Hydrogen tank count | 2072 | 2221 | 3389 |
| Fuel cell bank count | 1507 | 1585 | 1889 |
| Battery bank count | 319 | 358 | 414 |
| Revenue from electricity selling to the distribution network ($) | 498,105 | 505,619 | 549,235 |
| Price of selling electricity to network ($) | 0.12 | 0.23 | 0.28 |
| Count of Photovoltaic units | 225 | 183 | 132 |
| Electrolyzer count | 1364 | 2783 | 5132 |
| Hydrogen tank count | 2290 | 3297 | 4519 |
| Fuel cell bank count | 1635 | 3542 | 4391 |
| Battery bank count | 370 | 430 | 541 |
| Revenue from electricity selling to the distribution network ($) | 511,988 | 536,928 | 587,145 |
| Equation (55) | |||
| Count of Photovoltaic units | 225 | 231 | 237 |
| Electrolyzer count | 1364 | 1692 | 2005 |
| Hydrogen tank count | 2290 | 2381 | 2434 |
| Fuel cell bank count | 1635 | 831 | 344 |
| Battery bank count | 370 | 412 | 437 |
| Revenue from electricity selling to the distribution network ($) | 507,526 | 482,498 | 476,325 |
| Metric | Proposed Method | [24] | [25] | [26] |
|---|---|---|---|---|
| Operational Cost Reduction | 15.3% | 12.1% | 14.7% | 10.8% |
| Flexibility Index | 0.684 | 0.621 | 0.598 | 0.655 |
| LOLE (hours/year) | 2.5 | 3.2 | 2.8 | 3.5 |
| EENS (MWh/year) | 45.2 | 58.7 | 51.3 | 62.1 |
| Revenue Increase | 8.7% | 6.5% | 7.9% | 5.8% |
| CO2 Emission Reduction | 22.4% | 18.3% | 20.1% | 16.9% |
| Study | DERs Considered | Optimization Technique | Flexibility Metric | Key Findings |
|---|---|---|---|---|
| Proposed Study | Wind, PV, FC, CHP, MT, DR, ESS | Multi-objective evolutionary algorithms | Novel flexibility index (technical + economic) | 15% cost reduction, flexibility index 0.684, LOLE 2.5 h/year, 20% flexibility increase |
| [1] | Wind, PV, ESS | Stochastic optimization | Ramp rate constraints | 12% cost reduction, flexibility index 0.621 |
| [2] | CHP, DR, ESS | Mixed-integer linear programming | Operating range (OR) | 10.5% cost reduction, EENS 51.3 MWh/year |
| [3] | Wind, PV, DR | Particle swarm optimization | Minimum sustainable generation (MSG) | Flexibility index 0.603, availability 98.2% |
| Aspect | Details for Proposed Framework | Computational Time (IEEE 24-bus) | Computational Time (IEEE 118-bus) | Viability for Day-to-Day Operations | Benchmarks/Comparisons |
|---|---|---|---|---|---|
| Base Solve Time (Deterministic Case) | Optimizes Equation (1) with constraints (2)–(18); single-objective run. | 45 s | 90 s | Highly viable; fits within 1 h market windows for initial bids. | Faster than MILP in [2] (60 s on similar systems); comparable to PSO in [5] (40 s but suboptimal). |
| Probabilistic Case Time | Incorporates uncertainties via Equation (26) and constraints (27)–(29); includes 10 scenarios. | 60 s | 120 s | Viable for risk-adjusted daily runs; can be pre-computed overnight. | 15% faster than robust methods in [20] (140 s); handles more uncertainties than deterministic baselines. |
| Multi-Objective Iteration Time | Weighted-sum method; one Pareto point (e.g., w1 = 0.5, w2 = 0.3, w3 = 0.2). | 50 s | 100 s | Viable for 10–20 daily iterations to explore trade-offs; parallelizable. | Outperforms NSGA-II in [15] (180 s per iteration); more efficient than ε-constraint (~150 s). |
| Full Pareto Frontier Generation | 20 weight combinations for trade-off analysis (Figure 3 and Figure 4). | 15 min | 35 min | Viable for weekly planning; daily use focuses on 2–3 key points. | Faster than evolutionary algorithms in [16] (1 h); generates more points than single-objective studies. |
| Sensitivity Analysis Time | Varies parameters (e.g., ±30% RU/RD in TFC); 10 variations per scenario (Section 4.4). | 10 min | 20 min | Viable for ad hoc daily checks (e.g., forecast updates); automated scripting reduces to <5 min. | Comparable to sensitivity in [24] (15 min); more comprehensive than [26] (no reported sensitivity). |
| Hardware Requirements | Standard workstation (Intel i7, 16 GB RAM); GAMS/CPLEX 24.1. | N/A | N/A | Highly viable; scalable to laptops or cloud (e.g., AWS EC2, ~$0.05/h). | Lower requirements than GPU-based ML methods in [21] (32 GB RAM); accessible for utilities without supercomputers. |
| Data Preprocessing Time | Input preparation (e.g., renewable forecasts, market prices via APIs). | 20 s | 30 s | Viable for real-time integration with SCADA/EMS systems; automated. | Faster than data-heavy models in [18] (1 min); supports daily API pulls from ISOs. |
| Scalability to Larger Systems | Extrapolated to 500-bus (e.g., regional grid). | ~2 min (estimated) | ~5 min (estimated) | Viable for national grids; tested scalability shows <10x increase vs. 118-bus. | Better than non-decomposed MILP in [13] (exponential growth); aligns with real-world VPPs (e.g., NextEra Energy). |
| Daily Operational Overhead | Full run including preprocessing, optimization, and post-analysis. | 2 min | 4 min | Highly viable; enables multiple daily runs for updates (e.g., intra-day markets). | Lower overhead than manual methods; cost savings justify (15% reduction per Section 5). |
| Potential Challenges and Mitigations | High variability (e.g., 80% renewables) increases time by 10–20%. | N/A | N/A | Viable with mitigations; real-world testing (e.g., pilot VPPs) confirms feasibility. | Addresses gaps in [11] (no time discussion); more robust than heuristics with variable convergence. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Salehi, M.H.; Moradian, M.R.; Shahgholian, G.; Moazzami, M. Multi-Objective Optimization in Virtual Power Plants for Day-Ahead Market Considering Flexibility. Math. Comput. Appl. 2025, 30, 96. https://doi.org/10.3390/mca30050096
Salehi MH, Moradian MR, Shahgholian G, Moazzami M. Multi-Objective Optimization in Virtual Power Plants for Day-Ahead Market Considering Flexibility. Mathematical and Computational Applications. 2025; 30(5):96. https://doi.org/10.3390/mca30050096
Chicago/Turabian StyleSalehi, Mohammad Hosein, Mohammad Reza Moradian, Ghazanfar Shahgholian, and Majid Moazzami. 2025. "Multi-Objective Optimization in Virtual Power Plants for Day-Ahead Market Considering Flexibility" Mathematical and Computational Applications 30, no. 5: 96. https://doi.org/10.3390/mca30050096
APA StyleSalehi, M. H., Moradian, M. R., Shahgholian, G., & Moazzami, M. (2025). Multi-Objective Optimization in Virtual Power Plants for Day-Ahead Market Considering Flexibility. Mathematical and Computational Applications, 30(5), 96. https://doi.org/10.3390/mca30050096





