Distilling Robust Design Principles of Biocircuits Using Mixed Integer Dynamic Optimization

Abstract

A major challenge in model-based design of synthetic biochemical circuits is how to address uncertainty in the parameters. A circuit whose behavior is robust to variations in the parameters will have more chances to behave as predicted when implemented in practice, and also to function reliably in presence of fluctuations and noise. Here, we extend our recent work on automated-design based on mixed-integer multi-criteria dynamic optimization to take into account parametric uncertainty. We exploit the intensive sampling of the design space performed by a global optimization algorithm to obtain the robustness of the topologies without significant additional computational effort. Our procedure provides automatically topologies that best trade-off performance and robustness against parameter fluctuations. We illustrate our approach considering the automated design of gene circuits achieving adaptation.

1. Introduction

Computer-aided design is a key component for the efficient engineering of biological systems [1,2,3]. The development of functional synthetic biological circuits is usually hampered by the high levels of uncertainty encountered at different scales. As pointed out by Lormeau et al. [4], biological circuits exhibit particularly high parametric uncertainty due to several factors including, on the one hand, imprecise methods to characterize parts and systems and, on the other hand, context related variations concerning circuit, host cell and extracellular conditions. Handling uncertainty has a long history in computer-aided methods for optimal design in engineering [5]. This class of problems is frequently named robust design. Design centering [6] is a related concept that aims to find a design which meets specifications while having a high probability of still doing so in the face of fluctuations in the parameters and/or specifications.

Here, we consider the problem of robust design in synthetic biology, i.e., designing biological circuits with robust behavior against parametric uncertainties. The dynamics are described by parametric nonlinear ordinary differential equations, and we aim to find a robust biocircuit, i.e., one with a large functional parameter space. Robust design has been addressed in recent works by different approaches. Barnes et al. [7] used an Approximate Bayesian Computation sampling-rejection algorithm that computes a Bayesian posterior over possible design parameter values and retrieves quantitative information on the size and shape of the functional parameter space. Woods et al. [8] addressed the question of designing genetic oscillators with arbitrary robustness, and used a Bayesian framework to obtain results for two and three gene oscillators systems. Lormeau et al. [4] proposed an alternative approach that extends the Bayesian topological filtering method (TopoFilter) by Sunnåker et al. [9] to the design of synthetic circuits. The algorithm yields a comprehensive set of functional topologies together with a full characterization of their functional parameter space, which is approximated by ellipsoids by a Monte-Carlo method [10]. TopoFilter reduces computational burden avoiding the exhaustive enumeration of candidate models. Asmus et al. [6] presented an adaptive statistical method to address the problem of design centering, with applications in electronic and biological systems. Despite these advances, the computational cost associated to these methods is very significant and does not seem to scale up well with problem size.

In this study, our goal is to handle the robust design of biocircuits without compromising computational scalability. Our first aim is to address the problem by exploiting the interplay between dynamics and topology considering the multi-objective optimal trade-offs between performance and robustness. In addition, we want to tackle the problem of generating design principles for robustness, which remains a key challenge in this field [11].

To this purpose, we have extended our previous recent works on automated design based on mixed-integer dynamic optimization by taking uncertainty into account. Here, we deal in particular with parametric uncertainty. Further, our new approach enables the distillation of insights from the set of optimal trade-offs (i.e., the Pareto optimal set). Overall, we present a novel optimization-based framework for robust design with the following advantages:

(i)

Robustness is taken into account using a multi-criteria optimal design loop without introducing significant extra computational effort, thus ensuring good scalability.

(ii)

It allows for simultaneous searching through parameter and topology spaces, and it can handle arbitrary topologies with different types of interactions (activation, repression).

(iii)

It generates optimal trade-offs between robustness and user-defined performance metrics, i.e., the so-called Pareto-set of best solutions.

(iv)

Robust design principles can be distilled by post-processing the Pareto set.

The methodology proposed is described in Section 2. As a proof of concept, as presented in Section 3, we used our method to find robust topologies for a case study regarding biochemical adaptation [12].

2. Methods

The approach presented here is based on the following idea: our recent meta-heuristic for solving the design problem via multi-criteria global optimization [13] performs a rather intensive sampling in the design space (i.e., both on topology and kinetic parameters spaces). This sampling can be post-processed to study the robustness of the topologies and provide Pareto-optimal designs trading off user-defined metrics, such as robustness and performance. By exploiting an optimization-based sampling process, our method aims to provide the best topologies (in terms of performance and robustness) while keeping the associated computational effort at relatively modest values.

We formulate the design of biocircuits as a global optimization problem, as in our previous works [13,14,15]. In this new method, the goal is to handle uncertainty, i.e., to design circuits with good performance and, at the same time, robust to variations in the parameters. In general terms, evaluating robustness as an explicit optimization objective in a multi-criteria formulation would require a very intense sampling of the parameter space, making it very computationally costly. To avoid this, we first optimize with respect to performance, and then exploit the sampling obtained during such optimization to evaluate robustness in a post-processing step.

We encode synthetic biochemical networks using a mixed integer framework, where dynamics are described by a system of parametric nonlinear ordinary differential equations (ODEs) of the form:

$$\dot{z}=f(z,w,y,k),z\left(t_0\right)=z_0$$

(1)

where $z\left(t\right)\in {\mathbb{R}}_{\ge 0}^N$ is the species concentration vector, $y\in {\mathbb{Z}}^M$ is an integer vector defining the circuit topology and w and k are, respectively, vectors of tunable and fixed parameters.

Equation (1) can be used to encode different types of kinetics and topologies at various levels of granularity. Starting from a library of synthetic standard parts, in [15], a binary number determines whether a given promoter–transcript pair (from all possible pairs numbered from 1 to M) is actively present in the circuit, such that:

• $y_i=1$ if device i is actively regulating the dynamics; and
• $y_i=0$ otherwise.

In this case, the topology of the circuits (with mass action kinetics) is fully characterized by a binary M-dimensional vector. In other examples endowed with connectionist [16], e.g., Shea–Ackers–Hill or Michaelis–Menten kinetics, topologies are represented by integer numbers such that, for a given pair (species i and species j):

• $y_{ij}=-1$ if species i negatively regulates species j;
• $y_{ij}=+1$ if species i positively regulates species j; and
• $y_{ij}=0$ otherwise (species i does not regulate species j).

Once a target behavior is defined, the circuit performance is evaluated measuring how close is the circuit’s behavior to the target. Target behaviors are usually (but not exclusively) defined in terms of the whole dynamics $z\left(t\right)$, or in terms of the input–output behavior. Let us denote here by $J(\dot{z},z,w,y,k)$ the objective function encoding the distance between the circuit’s and the target performance. The Mixed Integer Dynamic Optimization (MIDO) problem is formulated as finding a vector w of continuous variables and a vector y of integer variables that minimize the objective function $J(\dot{z},z,w,y,k)$:

$$\underset{w,y}{min}J(\dot{z},z,w,y,k)$$

(2)

subject to:

(i)

The dynamics of the biochemical network:

$$f(\dot{z},z,w,y,k)=0,z\left(t_0\right)=z_0$$

(3)

(ii)

Biophysical and/or design requirements in form of additional equality and/or inequality constraints:

$$h(z,w,y,k)=0$$

(4)

$$g(z,w,y,k)\le 0$$

(5)

(iii)

Upper and lower bounds for the decision variables:

$$w_L\le w\le w_U$$

(6)

$$y_L\le y\le y_U$$

(7)

To solve the optimization problem, we use a mixed-integer hybrid global optimization algorithm, combining the advantages of stochastic global and deterministic local solvers. In particular, the combination of eSS [17] and MISQP [18] has shown to work well in our previous studies of automated biocircuit design [13,14]. When evaluating performance of biochemical circuits, we need to define a threshold $ϵ$ such that a circuit is considered to be functional if:

$$J\le ϵ$$

(8)

Generally, there will be infinite functional circuits for a given target behavior, comprising one or a number of different topologies. Some studies (e.g., [4,7,12]) are interested in characterizing the design space providing a comprehensive set of functional structures, evaluating also their robustness. Here, we are interested in finding optimal topologies in terms of global performance and robustness, and, in this sense, we are more interested in exploring the portion of the design space concerning near-optimal solutions. To this purpose, we post-process the set of near optimal solutions (i.e., those with performance value below the threshold $ϵ$ in the convergence curve) to analyze parametric robustness and global performance. Here, is important to remark that the current implementation using eSS and MISQP provides not only the optimal solution but also a number of near-optimal intermediate samples. To enrich the sampling of the near-optimal parameter space, we use multiple runs (i.e., a multi-start strategy) for the meta-heuristic.

To assess the global performance for a given topology $\theta$, we analyze the frequency distribution of the objective function variable J, and approximate the median as a proxy of the topology performance ($PerP$). Assuming that R is the number of functional circuits with topology $\theta$ found by the algorithm, and $J_i$ for $i=1,\dots ,R$ are the corresponding values of the objective function constituting a vector $\widehat{J}$, we define:

$$PerP\left(\theta \right)=\mathcal{M}\left(\widehat{J}\right)|Pr\left(\mathcal{M}\left(\widehat{J}\right)\right)=0.5;$$

(9)

where $\mathcal{M}\left(\widehat{J}\right)$ is the median of the vector $\widehat{J}$ and $Pr$ denotes probability. We are taking the median as a robust estimator of global performance, because the distributions obtained for the performance tend to be skewed towards the optimum (since the sampling is performed during a optimization process, it emphasizes on the near-optimal portion of the design space).

To quantify the robustness of a given topology $\theta$, we evaluate the frequency distribution for each of the parameters along the interval determined by the corresponding lower and upper bounds. As a robustness metric, we use the spread of the distribution of each parameter evaluated as the interquartile range (IQR). Let ${\widehat{w}}_1,\dots ,{\widehat{w}}_P$ be the vectors containing the normalized values of parameters $w_1$ to $w_P$ for each of the functional circuits $i=1,\dots ,R$ with architecture $\theta$ found by the optimization algorithm. We use the following measure as a proxy for robustness of the topology $\theta$:

$$RobP\left(\theta \right)=\frac{{\sum }_{i=1}^{P}IQR\left({\widehat{w}}_i\right)}{P}.$$

(10)

where P is the number of tunable parameters associated to structure $\theta$.

Once we have computed the $PerP$ and $RobP$ for all structures found by the algorithm, we can easily obtain the Pareto front of functional structures that optimally trade-off performance and robustness. We say that a topology ${\theta }^{*}$ is Pareto optimal if no other topology outperforms ${\theta }^{*}$ in terms of robustness and global performance. That is, if for any functional topology $\theta$, $PerP\left({\theta }^{*}\right)\le PerP\left(\theta \right)$ and $RobP\left({\theta }^{*}\right)\ge RobP\left(\theta \right)$, with at least one strict inequality.

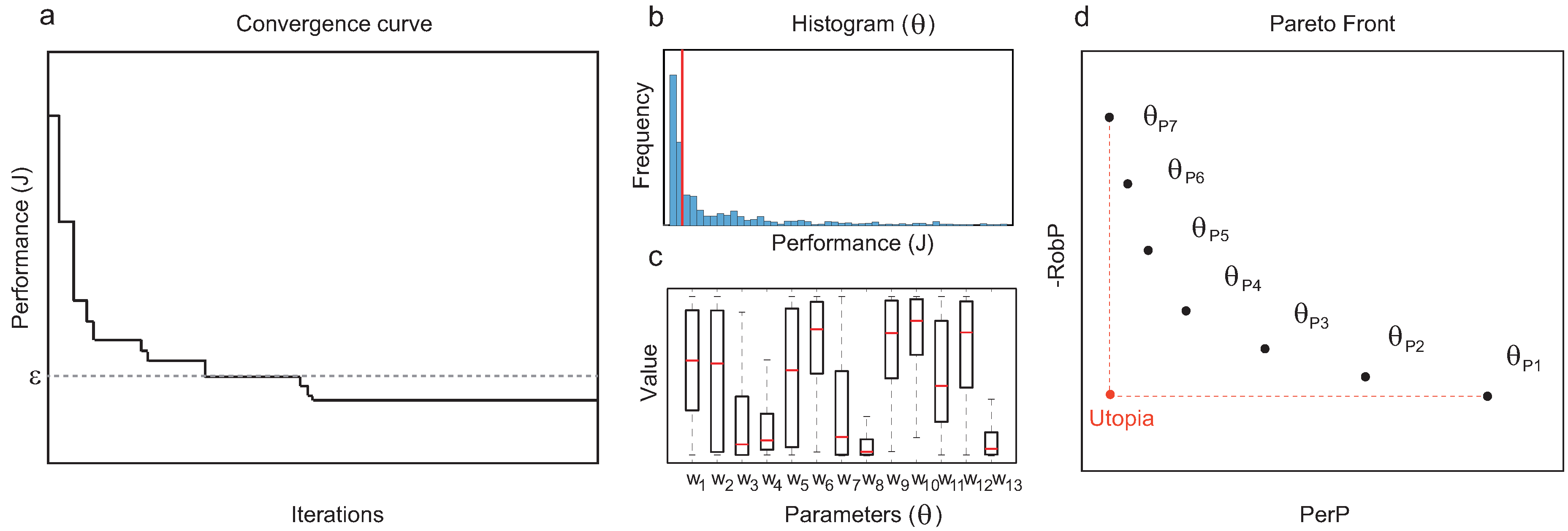
We end the section by summarizing the proposed method with a step-by-step description of the workflow:

Pre-processing:

1.

Encode the dynamics of the biochemical regulation network in a Mixed Integer framework (Equation (1)).

2.

Define the cost function J scoring circuit performance, and the threshold $ϵ$ determining whether a circuit is functional.

3.

Formulate the MIDO optimization problem (2)–(7).

Processing:

4.

Solve the Mixed-Integer Dynamic Optimization problem (2)–(7) using the hybrid meta-heuristic eSS-MISQP. Use multiple runs to ensure a rich enough sampling of the design space.

Post-processing:

5.

Trim the sampling (final and intermediate solutions corresponding to functional circuits) keeping the designs with a performance cost below the threshold $ϵ$ (see Figure 1a).

6.

Classify and analyze the solutions attending to their topology.

7.

For each topology $\theta$, collect all the functional circuits with the same structure and compute $PerP\left(\theta \right)$ and $RobP\left(\theta \right)$ (see Figure 1b,c).

8.

From the set of functional structures, prune the Pareto-optimal topologies in terms of $PerP\left(\theta \right)$ and $RobP\left(\theta \right)$ to obtain a Pareto front (see Figure 1d).

A software implementation of the above method is available from the authors upon request.

In the next section, we illustrate the performance of this method to identify enzyme network topologies capable of achieving adaptation that optimally trade-off performance and robustness against perturbations in the parameters.

3. Results

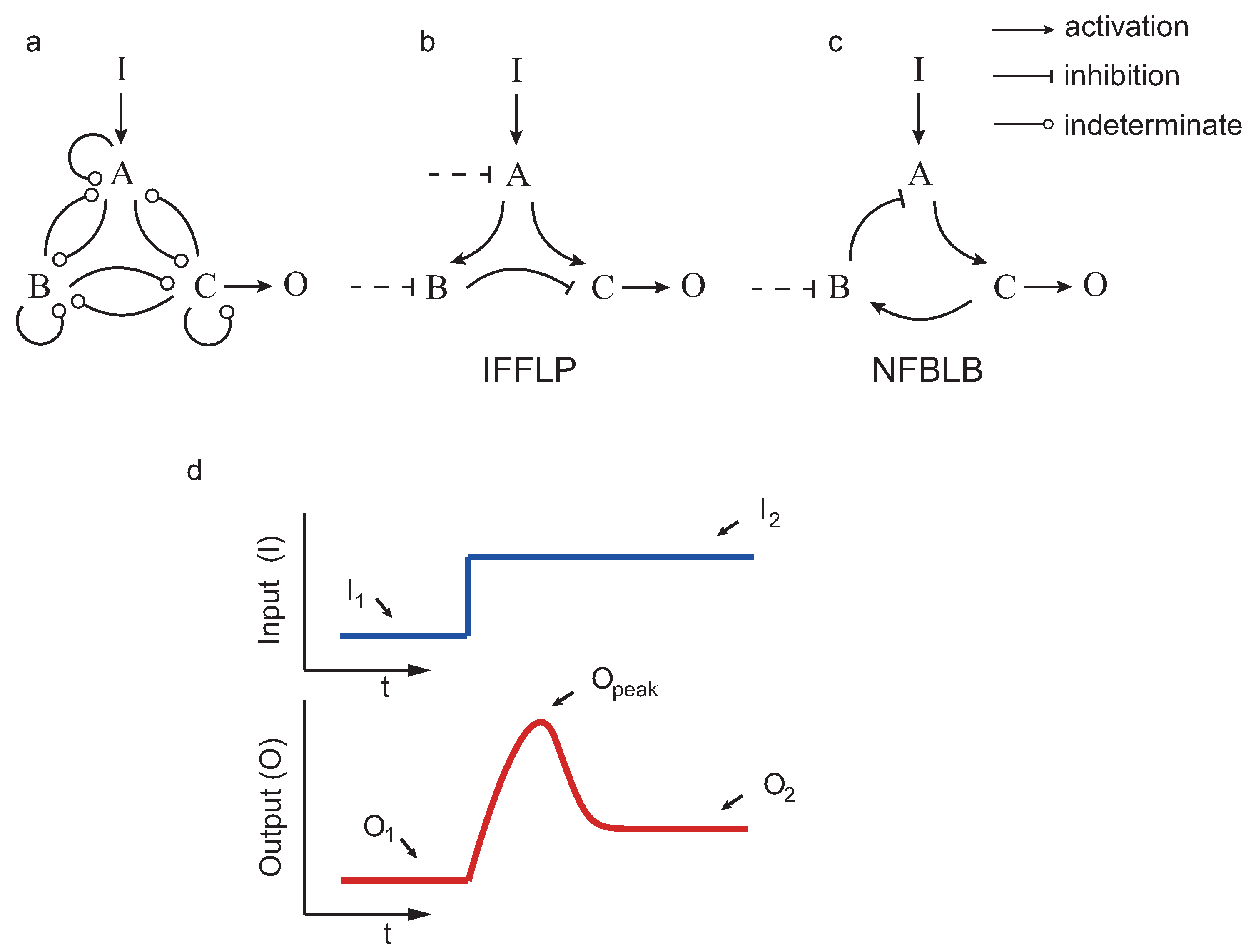
If a system returns (nearly) to the pre-stimulus steady state upon a step input, we say that the system achieves biochemical adaptation. Starting from the three enzyme setup in Figure 2, Ma et al. [12] applied exhaustive exploration to find all the topologies (∼16,000) capable of adapting upon a step input. Those topologies having a proportion of parameter samples with the right behavior were considered robust. The authors concluded, again by exhaustive exploration, that all robust adaptive topologies contain at least one negative feedback loop with a buffering node (NFBLB) or an incoherent feedforward loop with a proportioner node (IFFLP) (see Figure 2).

This problem has also been studied using a Bayesian framework. Barnes et al. [7] explored the functional parameter regions for 11 of the topologies found by Ma et al. [12] using the Approximate Bayesian Computation algorithm. Lormeau et al. [4] used a Bayesian topological filtering method [9], avoiding exhaustive exploration and still providing a comprehensive set of (∼6400) functional topologies. In addition, they evaluated global performance, robustness and feasibility based on a full characterization of the viable parameter space [10]. Plotting the solutions on the corresponding objective spaces, they analyzed the feasibility–performance and robustness–performance trade-offs for the 6434 topologies obtained.

We applied our mixed-integer global optimization approach to find three-node topologies that optimally trade-off robustness and performance.

We considered all possible circuits involving three enzymes A, B and C, shown in Figure 2, such that the enzymes that can repress or activate each other. As in the previous studies, in the case that a node j was not activated (not repressed) by any other, we considered constitutive activation (repression) by an enzyme $E_j$ with fixed concentration. The kinetics were assumed to be, as in the previous studies, of the Michaelis–Menten type.

First, we encoded the dynamics of the enzymatic networks under study using a mixed-integer formulation. The structure was defined by a nine-dimensional integer vector $y=(y_{AA},y_{BA},y_{CA},y_{AB},$$y_{BB},y_{CB},y_{AC},y_{BC},y_{CC})$ such that:

• $y_{kj}=-1$ if enzyme k negatively regulates enzyme j;
• $y_{kj}=+1$ if enzyme k positively regulates enzyme j; and
• $y_{kj}=0$ otherwise (enzyme k does not regulate enzyme j).

In addition, 26 tunable scalar parameters $K_{AA}$, $K_{BA}$, $K_{CA}$, $K_{AB}$, $K_{BB}$, $K_{CB}$, $K_{AC}$, $K_{BC}$, $K_{CC}$, $K_{IA}$, $k_{AA}$, $k_{BA}$, $k_{CA}$, $k_{AB}$, $k_{BB}$, $k_{CB}$, $k_{AC}$, $k_{BC}$, $k_{CC}$, $k_{IA}$, $K_{EA}$, $K_{EB}$, $K_{EC}$, $k_{EA}$, $k_{EB}$, and $k_{EC}$ were contained, in this order, in a real vector w. Note that $k_{kj}$ and $K_{kj}$ correspond, respectively, to the catalytic rate and Michaelis–Menten constants of the Michaelis–Menten expression for the reaction $k\to j$. The subindex E indicates a constitutively active enzyme with fixed concentration (as in [4], when a node is not negatively (positively) regulated by any other enzyme. For example, for the IFFLP topology in Figure 2b, we have: $y_{AB}=y_{AC}=1$, $y_{BC}=-1$ and $y_{AA}=y_{BA}=y_{CA}=y_{BB}=y_{CB}=y_{CC}=0$, leading to:

$$\begin{array}{c}\hfill \frac{dA}{dt}=k_{IA}\frac{I(1-A)}{(1-A)+K_{IA}}-k_{EA}\frac{FA}{A+K_{EA}}\end{array}$$

(11)

$$\begin{array}{c}\hfill \frac{dB}{dt}=k_{AB}\frac{A(1-B)}{(1-B)+K_{AB}}-k_{EB}\frac{BE}{B+K_{EB}}\end{array}$$

(12)

$$\begin{array}{c}\hfill \frac{dC}{dt}=k_{AC}\frac{A(1-C)}{(1-C)+K_{AC}}-k_{BC}\frac{BC}{B+K_{BC}}\end{array}$$

(13)

The design space is given by the vector $\left[wy\right]$. The lower and upper bounds for the real parameters are, respectively, ${10}^{-2}$ and ${10}^1$ for the maximum activation rates and ${10}^{-2}$ and ${10}^2$ for the Michaelis–Menten constants [12].

To evaluate the performance of a given circuit in terms of its capacity to achieve biochemical adaptation, we used the cost function defined by Lormeau et al. [4], which takes into account the sensitivity S, precision P and steady state value $O_2$ of the original work by Ma et al. [12]:

$$J={\left(\frac{1}{\mathcal{S}}\right)}^2+{\left(\frac{10}{\mathcal{P}}\right)}^2+{\left(\frac{0.1}{O_2}\right)}^2$$

(14)

where sensitivity and precision are given by:

$$\mathcal{S}=\left|\frac{(O_{peak}-O_1)/O_1}{(I_2-I_1)/I_1}\right|\mathcal{P}=\left|{\frac{(O_2-O_1)/O_1}{(I_2-I_1)/I_1}}^{-1}\right|$$

(15)

and $I_1$, $I_2$, $O_1$, $O_{peak}$ and $O_2$ are defined in Figure 2. As in [4], a circuit is said to achieve the target performance if $J\le ϵ$ with $ϵ=3$.

We solved the global optimization problem using eSS-MISQP, reaching optimum in less than 4 min of computation time (using Matlab 2015b (Mathworks, Natick, MA, USA) on a PC with Intel 2.8 GHz Xeon processor). To enrich the sampling, multiple runs were executed (around 2000), storing all the solutions achieving the target performance ($ϵ\le 3.0$). This step resulted in 23,273 solutions.

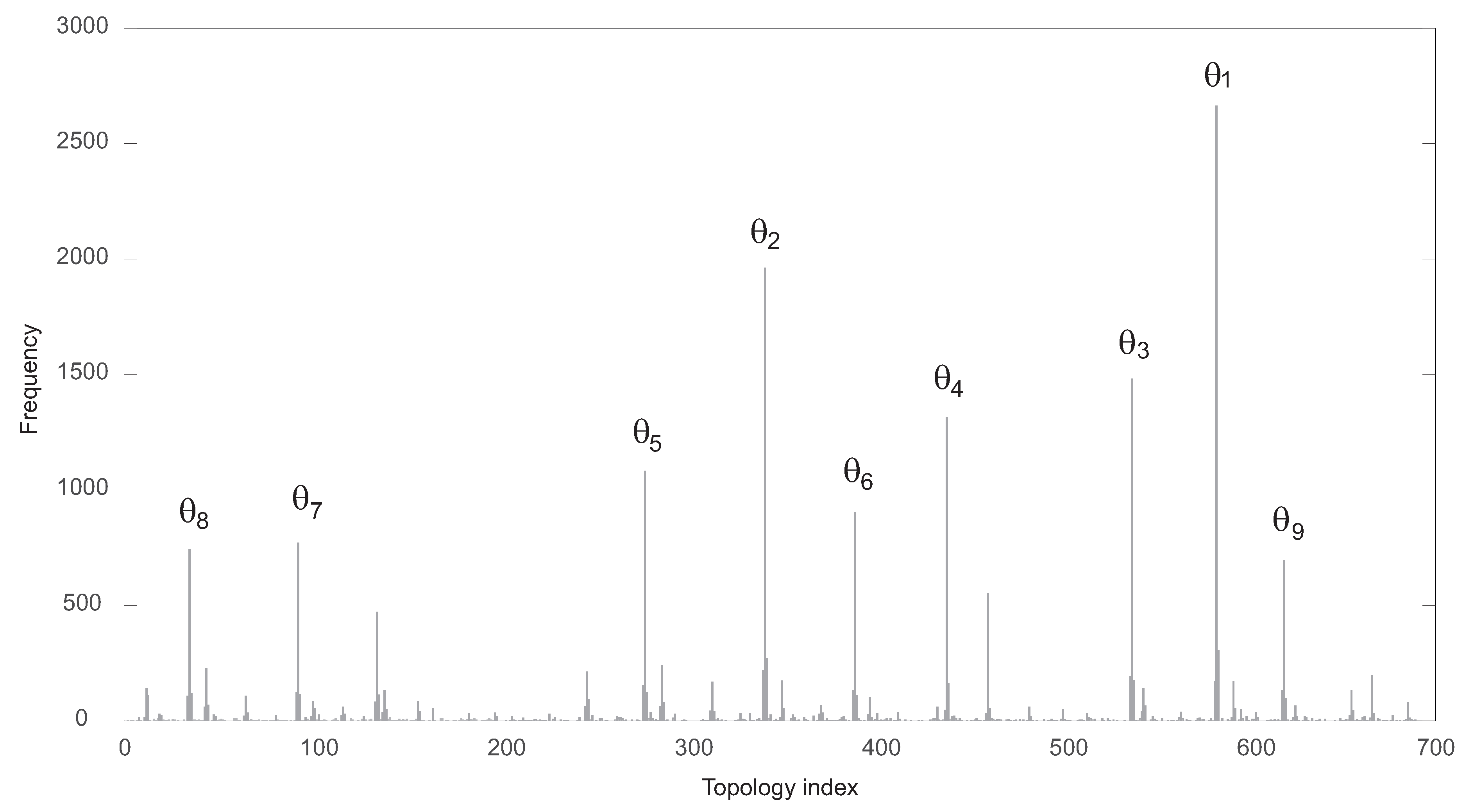
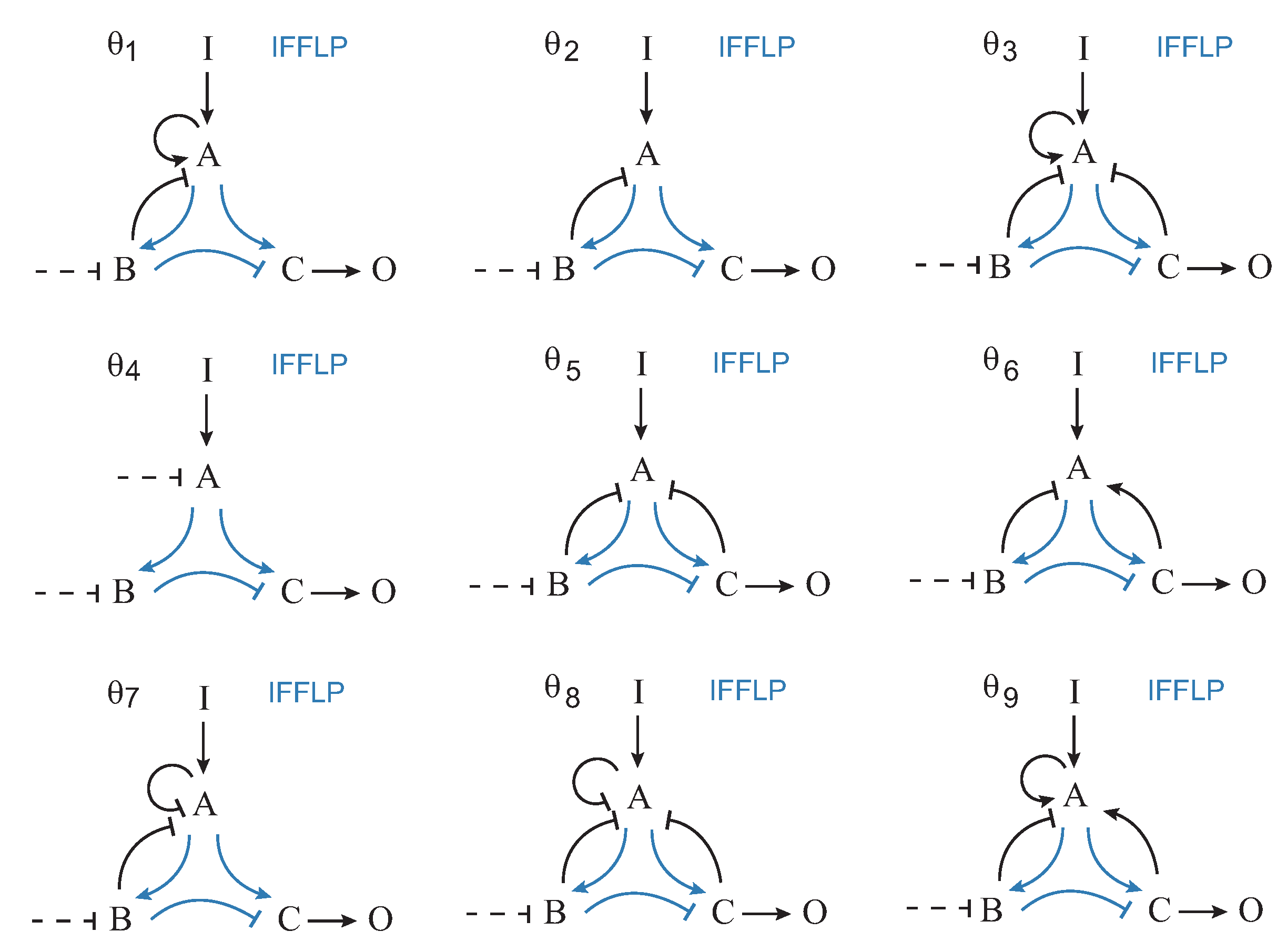
The functional solutions were partitioned attending to their specific topology. There were 689 different topologies. In Figure 3, the corresponding frequency histogram is depicted. The structures are labeled from 1 to 689 according to their respective frequencies. Figure 4 shows the nine most frequent topologies, all of them containing an IFFLP motif.

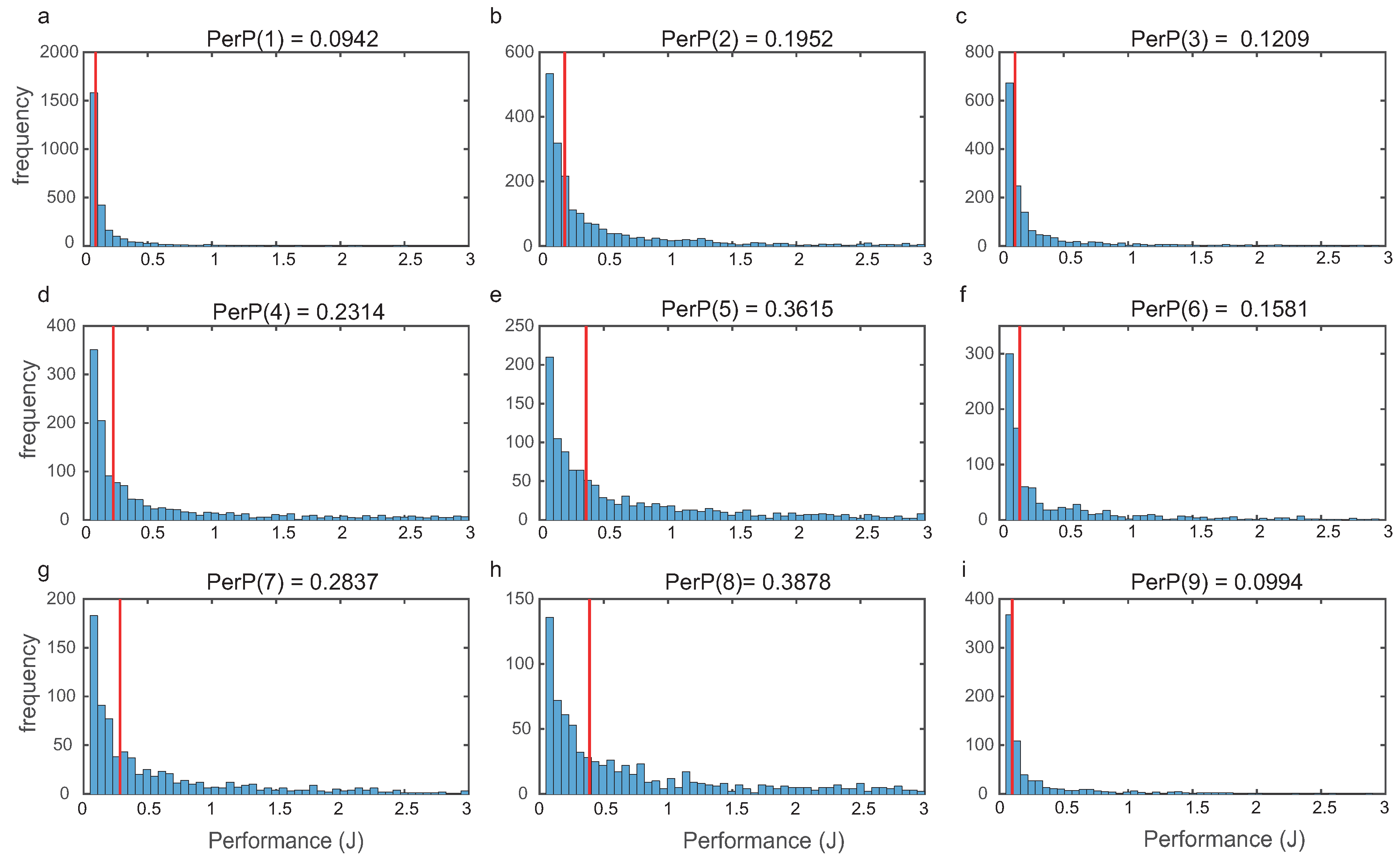
For each topology, we evaluated global performance computing $PerP$ (9) as indicated in Section 2. In Figure 5, we depict the histograms for the nine most frequent structures, showing that the distributions were right tailed.

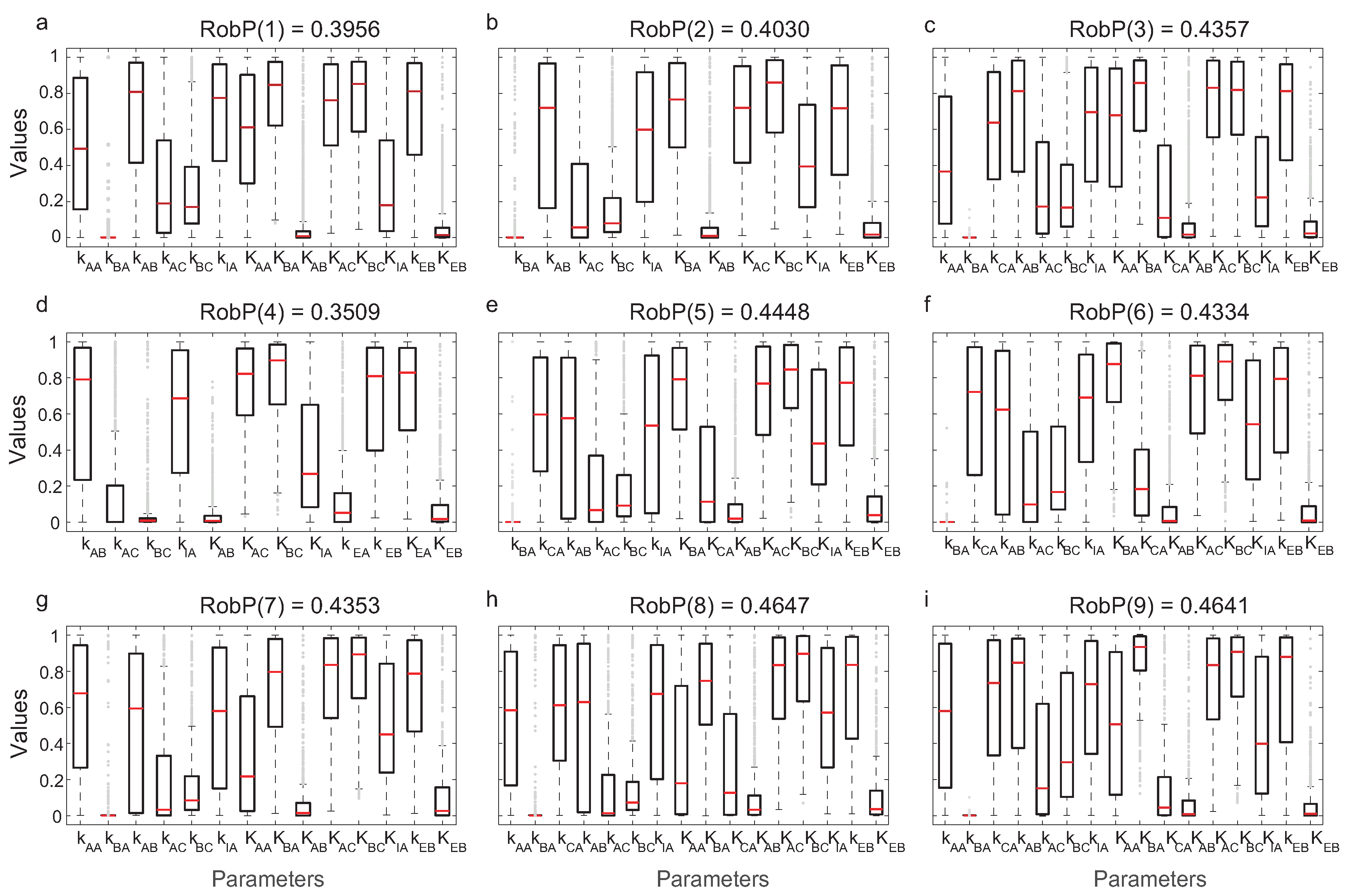
We evaluated the robustness of computing $RobP$ in Equation (10). In Figure 6, the interquartile ranges (IQR) of the parameters for each of the nine most frequent topologies and the corresponding $RobP$ are indicated.

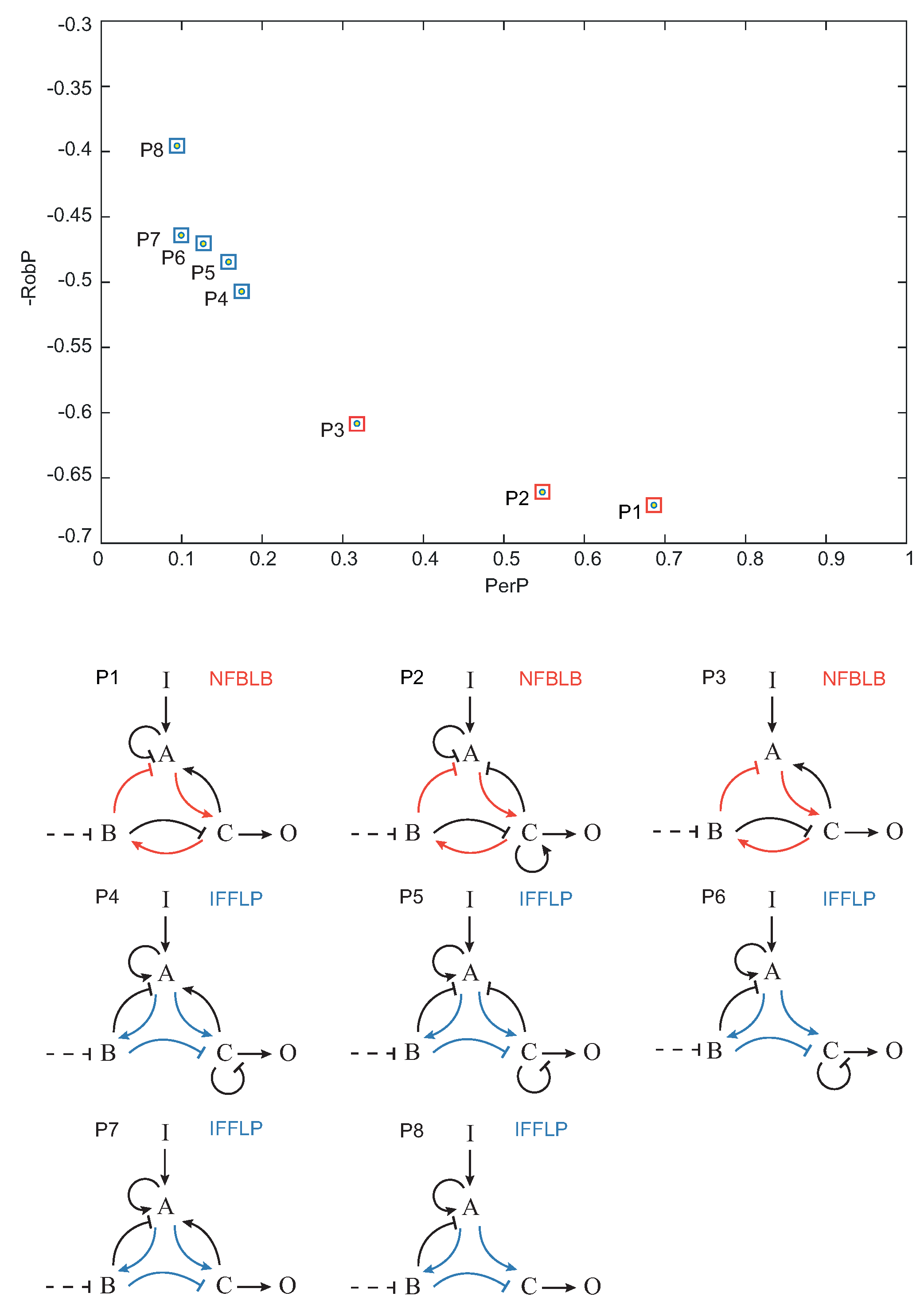
Once each topology was characterized by its global performance ($PerP$) and robustness ($RobP$), we pruned the Pareto optimal solutions among the set of functional topologies, i.e., the topologies that optimally trade-off $PerP$ and $RobP$. In Figure 7, the Pareto optimal topologies $P1$–$P8$ are shown in the objective space. $P1$, $P2$ and $P3$ topologies contain a NFBLB motif, whereas topologies $P4$–$P8$ are of the IFFLP type.

In Figure 8 we depict the dynamics for particular circuits with topologies $P3$ and $P4$, as well as the performance and robustness analyses for the corresponding architecture.

4. Discussion

In this paper, we present a method for the automated design of biocircuits taking into account parameter uncertainty. Our approach is based on the sampling performed during a mixed-integer optimization process taking into account multiple metrics, such as global performance and robustness. This method has been designed to introduce little additional computational effort and is therefore a scalable alternative to more exhaustive analyses based on computational statistics. A second advantage is the simultaneous exploration of the topology and parameter spaces by mixed-integer global optimization methods, and the subsequent distillation of robust design principles from the Pareto optimal solution set.

As a proof of concept, we applied this method to the search of robust biocircuits capable of biochemical adaptation [12]. Our results indicate that only integral feedback control structures are capable of robust adaptation. In particular, we found two different types of motifs, namely incoherent feed-forward loop with a proportioner node (IFFLP) and negative feedback loop with a buffering node (NFBLB), in agreement with previous studies [4,7,12]. We found a set of structures that optimally trade-off performance and robustness and, importantly, both motifs (IFFL and NFBLB) can be distilled from the Pareto optimal set.

Regarding future work, we plan to refine the robustness metric used here, which could over-estimate the viable space for specific nonlinear relationships among parameters. In addition, it is worth mentioning that we suspect there might be significant conceptual similarities between the sampling in our optimization-based approach and those using computational statistics techniques due to the connections between the latter and stochastic global optimization methods [19]. We believe that this topic deserves a more systematic and detailed comparative analysis.