Drilling Rate Prediction Based on Bayesian Optimization LSTM Algorithm with Fusion Feature Selection

Abstract

The Rate of Penetration (ROP), as a core indicator for evaluating drilling efficiency, holds significant importance for optimizing drilling parameter configurations, enhancing drilling efficiency, and reducing operational costs. To address the limitations of existing ROP prediction models—such as difficulties in modeling, solution complexity, and inefficient utilization of field big data—this paper proposes a Bayesian-Optimized LSTM-based ROP prediction model with fused feature selection (BO-LSTM-FS). The model innovatively introduces a sequential-cross-validation fused feature selection framework, which organically integrates Pearson correlation analysis, variance filtering, and mutual information, and incorporates a forward search strategy for final validation. Building on this, the Bayesian optimization algorithm is employed for systematic global optimization of the key hyperparameters of the LSTM neural network. Experimental results demonstrate that the BO-LSTM-FS model achieves significant performance improvements compared to traditional Backpropagation (BP) neural networks, standard LSTM neural networks, and CNN-LSTM models: Mean Absolute Error (MAE) is reduced by 48.0%, 29.3%, and 23.5%, respectively; Root Mean Square Error (RMSE) by 45.5%, 38.5%, and 32.2%, respectively; Mean Absolute Percentage Error (MAPE) by 47.8%, 29.4%, and 22.6%, respectively; and the Coefficient of Determination (R²) is increased by 8.6%, 4.4%, and 3.0%, respectively. The model exhibits high prediction accuracy, fast convergence speed, and strong generalization capability, providing a scientific reference for improving the Rate of Penetration in practical drilling operations.

1. Introduction

Drilling rate, as a core indicator for measuring drilling efficiency, its accurate prediction has important theoretical value and engineering significance for optimizing drilling parameter configuration, improving drilling efficiency, and reducing drilling costs. In modern drilling engineering, how to establish an accurate drilling rate prediction model to achieve intelligent management and real-time optimization of the drilling process has become a research hotspot and difficult problem in the field of petroleum engineering.

Currently, drilling rate prediction models are mainly divided into two categories: One is prediction models based on drilling rate equations, which establish mathematical relationships between drilling rate and various influencing factors based on rock mechanics theory and drilling technology principles. For example, Young established a quantitative relationship between parameters such as weight on bit, drillability, rotary speed and drilling rate [1]; Moraveji et al. introduced multiple variables such as mechanical parameters, hydraulic parameters and rheological parameters to optimize the traditional drilling rate equation [2]; Liu modified the drilling rate equation based on fractal theory to improve prediction accuracy [3]; Zhou et al. further improved the drilling rate prediction model by introducing rock mechanics parameters, pressure and hydraulic parameters [4]. The other category is drilling rate prediction models based on machine learning. With the development of artificial intelligence technology, machine learning algorithms such as neural networks, support vector machines, and random forests have been widely used in drilling rate prediction. Seifabad et al. established a drilling rate regression model for a specific oilfield using fuzzy machine learning algorithms [5]; Zhou et al. systematically summarized the applicability of various machine learning algorithms in drilling engineering [6], providing theoretical guidance for improving the generalization ability and reliability of models.

However, existing ROP prediction methods still suffer from several limitations. Models based on ROP equations, while physically interpretable, face difficulties in modeling and solving under complex geological conditions and exhibit low utilization of field big data. Machine learning-based models, despite their strong nonlinear mapping capabilities, commonly encounter issues such as excessive input parameters, complex model structures, high computational costs, and poor prediction stability. In the field of Enhanced Oil Recovery (EOR), numerical modeling has become a crucial technique for optimizing fluid flow and displacement processes. For instance, Al-Yaari et al. [7] proposed a 3D mathematical model for simulating nanofluid displacement in porous media. This model integrates the effects of temperature and volume fraction on the thermophysical properties of nanofluids, coupling Darcy’s law, mass conservation, and energy equations to achieve accurate prediction of oil recovery. This work provides a recent reference for detailed modeling of fluid flow in complex subsurface media and offers insights for parameter optimization modeling under multi-field coupling conditions in drilling engineering. In recent years, advancements in feature selection techniques and intelligent optimization algorithms have provided new approaches to address these challenges. Tang et al. [8] proposed an ROP prediction model based on the PCA-BP algorithm, improving prediction accuracy by reducing data dimensionality through principal component analysis. Song et al. employed a Bayesian-optimized LSTM neural network for ROP prediction [9], fully leveraging the temporal correlation of sequence data. Xu et al. [10] introduced a fusion feature selection method based on particle swarm optimization, effectively enhancing model generalization capability. Zhou et al. [11] proposed a fused feature selection algorithm combining correlation analysis, variance filtering, and mutual information, offering a new perspective on feature selection for ROP prediction.

To address the limitations of existing methods, this paper proposes a Bayesian-Optimized LSTM-based ROP prediction model with fused feature selection (BO-LSTM-FS). The model first preprocesses the raw data using a combination of wavelet filtering and FFT low-pass filtering [12] to eliminate noise interference. It then applies a fused feature selection algorithm that integrates Pearson correlation analysis (for linear filtering), variance filtering (for screening feature stability), and mutual information (for mining nonlinear dependencies), forming the final feature subset through intersection and union operations. This fused strategy aims to evaluate feature importance from multiple perspectives, thereby compensating for the bias inherent in any single method. Subsequently, the Bayesian optimization algorithm is employed to simultaneously optimize both the feature selection parameters and the LSTM network hyperparameters, constructing an optimal prediction model. Finally, the prediction performance and generalization capability of the model are validated using measured data from multiple wells. The research results can provide a scientific basis for drilling parameter optimization and intelligent decision-making, holding significant engineering application value for improving drilling efficiency and reducing operational costs.

2. BO-LSTM Neural Network Based on Fusion Feature Selection Algorithm

Based on the fusion feature selection algorithm, reducing the dimensionality of the input layer parameters of the BO-LSTM neural network is beneficial to narrowing the search range for the optimal number of hidden layer nodes, reducing computational cost, optimizing the model calculation process, and improving the stability of model prediction results.

2.1. Fusion Feature Selection Algorithm

The fusion feature selection algorithm is based on the idea of fusion learning, combining Pearson correlation analysis, variance filtering, and mutual information methods [11] to remove low-correlation and medium-correlation parameters, and finally select only the intersection parameters of the high-correlation parameter group with drilling rate (ROP) and the parameters selected by variance filtering and mutual information methods as the input feature parameter group of the model.

The core idea of this algorithm is to organically combine multiple feature selection methods, fully utilize the advantages of each method, and achieve efficient feature dimensionality reduction and selection. Pearson correlation analysis can effectively identify feature parameters that have a linear correlation with drilling rate [13]; variance filtering can select discrete features with high discrimination [14]; mutual information method can capture nonlinear relationships between features and drilling rate [15]; forward search strategy further optimizes feature selection results and reduces coupling problems between parameters [16]. The operation steps can be divided into 4 steps (Figure 1).

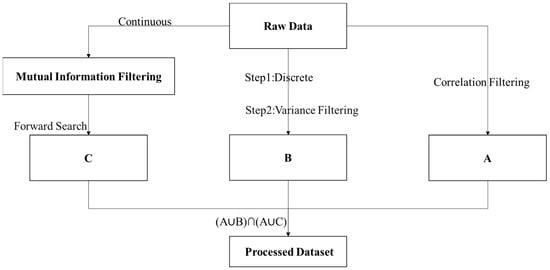
Figure 1. Schematic diagram of the feature selection process.

(1)

Pearson correlation analysis. Perform Pearson correlation calculation on the cleaned data, classify all feature parameters into high-correlation, medium-correlation, and low-correlation parameter groups according to Pearson correlation principles, and then select the high-correlation parameter group with high correlation to drilling rate.

(2)

Variance filtering. Perform variance filtering on discrete-type parameters among all feature parameters according to variance filtering principles, and then select feature parameters with high variance values.

(3)

Mutual information method. Calculate mutual information estimators for continuous-type parameters among all feature parameters according to mutual information calculation principles, sort them by mutual information estimation values, and then use forward search strategy combined with model validation for further feature selection.

(4)

Feature fusion. Take the intersection of the parameter group obtained through correlation filtering with the parameter group obtained through variance filtering and the parameter group obtained through mutual information filtering respectively, and finally take the union of the 2 intersection parameter groups as the final selection result of the fusion algorithm for feature selection.

2.2. LSTM Neural Network

Long Short-Term Memory (LSTM) network is an improved structure of Recurrent Neural Network (RNN), proposed by Hochreiter and Schmidhuber in 1997 [17]. Compared with traditional RNN, LSTM effectively alleviates the problems of gradient vanishing and exploding by introducing gating mechanisms, and can learn long-term dependencies.

The basic unit of LSTM neural network contains a cell state and three gating mechanisms: forget gate, input gate, and output gate. Each gating mechanism controls the flow of information through a sigmoid activation function, which maps the input to a value between 0 and 1, where 0 represents completely closed and 1 represents completely open. The structure diagram of its network unit is shown in Figure 2. In the figure, A on the left represents the cell state and output of the previous time step; A on the right represents the cell state and output of the current time step; Xt represents the input at the current time step.

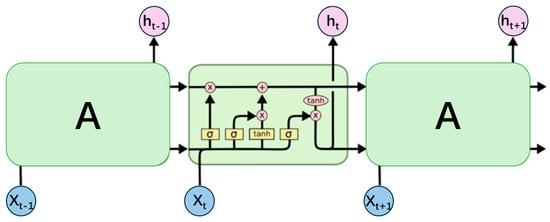
Figure 2. LSTM network unit structure diagram.

2.3. Bayesian Optimization Algorithm

Bayesian optimization algorithm is essentially a global optimization method, whose core idea is to efficiently find the optimal solution within a limited number of evaluations by constructing a probabilistic surrogate model of the objective function and combining it with an intelligent acquisition strategy [18]. Compared with traditional methods such as grid search and random search, Bayesian optimization can fully utilize existing evaluation information, avoid blind search, and thus obtain approximately optimal solutions with less computational cost.

Within the Bayesian optimization framework, a Gaussian Process (GP) is employed as the probabilistic surrogate model. The core assumptions of the Gaussian Process model include: (1) the joint distribution of function values follows a multivariate normal distribution; (2) the smoothness of the function is governed by the kernel function; (3) the model is non-parametric, allowing it to flexibly adapt to complex functional forms. Specifically, the Matérn5/2 kernel function is used to model the prior distribution of the objective function. The mathematical expression of the Matérn kernel is:

$$k(x_i,x_j)={\sigma }^2\left(1+{\displaystyle \frac{\sqrt{5}r}{\mathcal{l}}}+{\displaystyle \frac{5r^2}{3{\mathcal{l}}^2}}\right)\mathrm{e}\mathrm{x}\mathrm{p}\left(-{\displaystyle \frac{\sqrt{5}r}{\mathcal{l}}}\right)$$

(1)

where $r=\parallel x_i-x_j \parallel$ denotes the Euclidean distance between two points in the input space, ${\sigma }^2$ is the signal variance parameter controlling the overall amplitude of function variations, and $\mathcal{l}$ is the characteristic length-scale parameter determining the smoothness of the function. The Matérn5/2 kernel is chosen because it is twice continuously differentiable, enabling it to effectively capture the smooth variations in the objective function. Furthermore, it demonstrates good robustness to hyperparameter settings, making it well-suited for complex black-box optimization problems such as neural network hyperparameter tuning.

For the acquisition function, the Expected Improvement (EI) criterion is adopted. Its calculation formula is:

$$\mathrm{E}\mathrm{I}(x)=\left(\mu \left(x\right)-f\left(x^{+}\right)\right)\mathsf{\Phi }\left({\displaystyle \frac{\mu \left(x\right)-f\left(x^{+}\right)}{\sigma \left(x\right)}}\right)+\sigma (x)\varphi \left({\displaystyle \frac{\mu \left(x\right)-f\left(x^{+}\right)}{\sigma \left(x\right)}}\right)$$

(2)

where $\mu \left(x\right)$ and $\sigma \left(x\right)$ are the predictive mean and standard deviation from the Gaussian Process, respectively; $f\left(x^{+}\right)$ represents the best observed function value found so far; and $\mathsf{\Phi }$ and $\varphi$ denote the cumulative distribution function and probability density function of the standard normal distribution, respectively. The Expected Improvement criterion naturally balances exploration (selecting regions with high uncertainty) and exploitation (selecting regions predicted to be optimal), making it one of the most widely used and effective acquisition strategies in Bayesian optimization.

The basic process of Bayesian optimization is shown in Figure 3, which can be summarized as the following steps: construct a Gaussian process surrogate model using initial sample points; calculate acquisition function values based on the surrogate model and select the most promising evaluation point; perform real function evaluation on this point and add new observations to the sample set; update the surrogate model and repeat the above process until the termination condition is met.

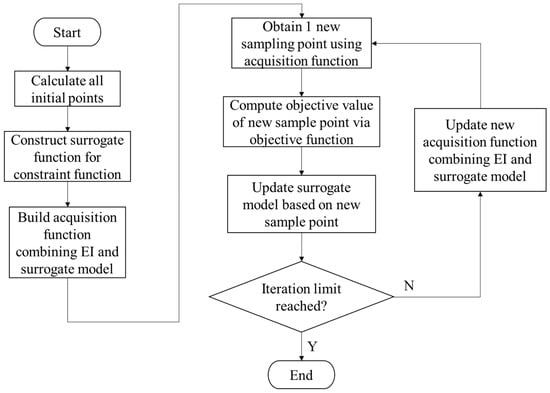
Figure 3. Constrained Bayesian optimization flow chart.

2.4. BO-LSTM-FS Neural Network

The BO-LSTM neural network based on fusion feature selection algorithm (BO-LSTM-FS) is a drilling rate prediction model that combines feature selection, hyperparameter optimization, and deep learning. This model reduces input dimensionality through fusion feature selection algorithm, optimizes the hyperparameters of LSTM neural network using Bayesian optimization algorithm, fully utilizes the advantages of each component, and provides an efficient and accurate solution for drilling rate prediction.

The overall architecture of the BO-LSTM-FS model is shown in Figure 4, which mainly consists of three core parts: data preprocessing module, fusion feature selection module, and Bayesian optimization LSTM prediction module. The data preprocessing module is responsible for cleaning, standardizing, and filtering the original drilling data; the fusion feature selection module selects the optimal feature subset through a combination of Pearson correlation analysis, variance filtering, and mutual information methods; the Bayesian optimization LSTM prediction module uses Bayesian optimization algorithm to optimize the hyperparameters of LSTM neural network and establish a high-precision drilling rate prediction model.

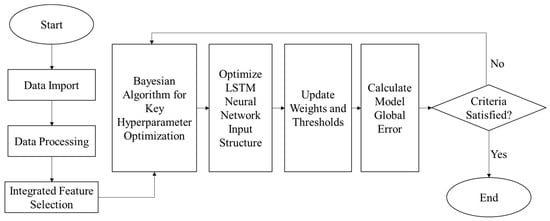
Figure 4. Flow chart of ROP prediction model based on BO-LSTM-FS.

3. Drilling Rate Prediction Modeling Based on BO-LSTM-FS

Traditional drilling rate prediction methods are mainly based on drilling rate equations, which have problems such as difficult modeling, complex solution, and poor adaptability. The BO-LSTM neural network (BO-LSTM-FS) drilling rate prediction model based on fusion feature selection algorithm reduces input dimensionality through fusion feature selection algorithm and optimizes the hyperparameters of LSTM neural network using Bayesian optimization algorithm, providing an efficient and accurate solution for drilling rate prediction.

The modeling steps of drilling rate prediction based on BO-LSTM-FS are as follows: first, preprocess the drilling data to clean up outliers, errors, etc., in the data; second, use fusion feature selection algorithm to perform feature selection on the preprocessed data to reduce the dimensionality of input layer parameters; finally, use the selected feature subset as input parameters of the BO-LSTM neural network and drilling rate as output parameter to conduct drilling rate prediction research.

3.1. Data Preprocessing

Drilling data preprocessing is the basic work of drilling rate prediction modeling, which directly affects the training effect and prediction accuracy of the model. In well sites, logging and well logging data are transmitted through digital circuits. Due to the influence of high-frequency digital frequencies, a large number of abnormal “noises” with spikes or mutations appear in the signals. To improve the information utilization rate in the original data, it is necessary to remove noise interference components.

3.1.1. Data Filtering

Wavelet filtering was employed for data noise reduction, specifically using the Daubechies 4 (db4) wavelet basis function with a decomposition level set to 5. The thresholding process applied the SureShrink adaptive thresholding method. This approach combines the advantages of localization and frequency-adaptive windowing, effectively removing white noise caused by high-frequency components characterized by “high temporal resolution and low frequency resolution.” The basic formula of wavelet transform is:

$$W_f(\tau ,a)={\displaystyle \frac{1}{\sqrt{\left|a\right|}}}{\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}f(t)\psi \left({\displaystyle \frac{t-\tau }{a}}\right)dt$$

(3)

where $W_f(\tau ,a)$ is the denoised data after wavelet transform; $a$ ($a$ > 0) is the scale factor, which is used to realize the scaling transformation of the basic wavelet φ(t); τ is the translation factor, which is used to realize the translation transformation of the basic wavelet on the time axis.

3.1.2. Data Normalization

Due to the large differences between various inputs and outputs, it is necessary to normalize the data. The purpose is to eliminate the dimensional differences between input and output parameters and improve the generalization ability of model data processing. Min-max normalization is used to map the data to the [0, 1] interval, and the formula is:

$$x_{\mathrm{norm}}={\displaystyle \frac{x-x_{\min }}{x_{\max }-x_{\min }}}$$

(4)

where $x_{\mathrm{norm}}$ is the normalized data, $x$ is the original data, $x_{\min }$ is the minimum value of the feature parameter, and $x_{\max }$ is the maximum value of the feature parameter.

3.2. Fusion Feature Selection Analysis

3.2.1. Correlation Analysis

Pearson correlation coefficient is a commonly used indicator to measure the linear correlation degree between two variables, and its value range is [0, 1]. The closer the absolute value of the correlation coefficient is to 1, the stronger the linear correlation between the two variables; the closer the correlation coefficient is to 0, the weaker the linear correlation between the two variables. The calculation formula is:

$${\rho }_{ab}=\mathrm{c}\mathrm{o}\mathrm{v}(a,b)={\displaystyle \frac{{\sum }_{i=1}^n(a_i-\overline{a})(b_i-\overline{b})}{{\sigma }_a{\sigma }_b\sqrt{{\sum }_{i=1}^n{(a_i-\overline{a})}^2}\sqrt{{\sum }_{i=1}^n{(b_i-\overline{b})}^2}}}$$

(5)

where ${\rho }_{ab}$ is the correlation between variables $a$ and $b$; $\mathrm{c}\mathrm{o}\mathrm{v}(a,b)$ is the covariance matrix of variables $a$ and $b$; ${\sigma }_a$, ${\sigma }_b$ are the standard deviations of variables $a$ and $b$ respectively; $a_i$, $b_i$ are the i-th variable values in the datasets of variables $a$ and $b$; $\overline{a}$, $\overline{b}$ are the average values of variables $a$ and $b$; n is the dataset size of variables $a$ and $b$.

The value of ${\rho }_{ab}$ is in the interval [−1, 1]. A positive value indicates a positive correlation between the two parameters, while a negative value indicates a negative correlation between the two parameters. The closer the absolute value of ${\rho }_{ab}$ is to 1, the higher the correlation between $a$ and $b$; the closer it is to 0, the lower the correlation between the two variables. Calculate the correlation between the drilling rate ROP parameter and all other parameters except drilling rate.

3.2.2. Variance Filtering

Variance filtering is a feature selection method based on feature variance, which is mainly used to select discrete features with large variances. The larger the variance of a feature, the more dispersed the values of the feature and the richer the information it contains; the smaller the variance of a feature, the more concentrated the values of the feature and the less information it contains. The formula is:

$$\mathrm{V}\mathrm{a}\mathrm{r}(X)={\displaystyle \frac{1}{n-1}}{\sum }_{i=1}^n{(x_i-\overline{x})}^2$$

(6)

where $\mathrm{V}\mathrm{a}\mathrm{r}\left(X\right)$ is the variance of variable $X$, $x_i$ is the i-th observation value of variable $X$, $\overline{x}$ is the mean value of variable X, and $n$ is the sample size.

In drilling rate prediction modeling, variance calculation is performed on all discrete feature parameters, and then a variance filtering threshold is set, which is set to 0.4 in this study, and feature parameters with variance greater than or equal to 0.4 are selected. Through variance filtering, discrete features with overly concentrated values can be removed, and discrete features containing rich information can be retained.

3.2.3. Mutual Information Analysis

Mutual information is an indicator to measure the nonlinear correlation degree between two variables, which reflects the amount of information that one variable contains about another variable. The value range of mutual information is [0, ∞). The larger the mutual information value, the stronger the correlation between the two variables; a mutual information value of 0 indicates that the two variables are independent of each other. The calculation formula of mutual information is:

$$I(X;Y)=\iint p(x,y)\mathrm{l}\mathrm{o}\mathrm{g}{\displaystyle \frac{p(x,y)}{p\left(x\right)p\left(y\right)}}dxdy$$

(7)

where $p(x,y)$ is the joint probability distribution of $X$ and $Y$; $p\left(x\right)$, $p\left(y\right)$ are the marginal probability distributions.

Discretize the continuous feature parameters, then calculate the mutual information value between each continuous feature parameter and drilling rate, and sort them by the mutual information value. Set a mutual information threshold, which is set to 0.5 in this study, and select feature parameters with mutual information value greater than or equal to 0.5. Through mutual information analysis, the nonlinear relationship between features and drilling rate can be captured, supplementing the shortcomings of Pearson correlation analysis. And through the forward search strategy, the feature subset that contributes the most to model performance is effectively selected.

The results of Pearson correlation analysis are intersected with the results of variance filtering and mutual information analysis respectively to obtain two intermediate feature subsets, and then these two intermediate feature subsets are unioned to obtain the final feature selection result.

3.3. Establishment of BO-LSTM-FS Neural Network

The fusion feature selection algorithm (FS) has been used for parameter optimization, and then these parameters need to be input into the neural network model for training. The model used in this study is improved on the basis of basic prediction using LSTM neural network, adding a Bayesian optimization function to globally optimize the key hyperparameters of LSTM, thereby effectively improving the prediction performance and generalization ability of the model. The framework structure of the prediction model is shown in Figure 5.

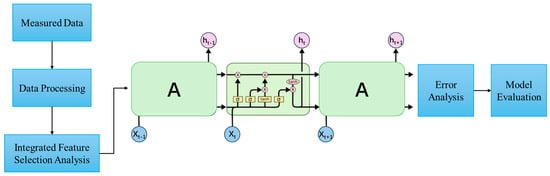
Figure 5. Frame structure of BO-LSTM-FS prediction model.

This paper selects the key hyperparameters that have the most significant impact on the performance of LSTM neural network for Bayesian optimization, mainly including initial learning rate, number of hidden layer neurons, batch size, etc. The parameter constraint ranges are shown in Table 1.

Table 1. Parameter constraint ranges.

Parameter	Range of Values	Before Optimization	After Optimization
InitialLearnRate	[10−3, 1]	0.005	0.0062
NumOfUnits	[10, 100]	32	64
BatchSize	[16, 256]	32	64
Epochs	[50, 500]	200	200
DropoutRate	[0.1, 0.5]	0.2	0.3

The initial learning rate determines the step size of model parameter update. Too large a learning rate easily leads to unstable training, while too small a learning rate results in low training efficiency. The number of hidden layer neurons directly affects the learning ability and complexity of the network. Too few neurons lead to underfitting, while too many neurons easily lead to overfitting. These two parameters are the key to optimization.

The Bayesian optimization process adopts a Sequential Model-Based Optimization (SMBO) strategy, implemented through the following steps. First, five initial sample points are randomly generated within the parameter space to ensure broad coverage. Subsequently, an LSTM model is trained for the hyperparameter combination corresponding to each sample point, and the Root Mean Square Error (RMSE) on the validation set is calculated as the objective function value. Next, a Gaussian Process regression algorithm is used to fit the existing sample points, constructing a probabilistic surrogate model. Then, the L-BFGS-B algorithm is employed to maximize the Expected Improvement acquisition function, thereby selecting the next most promising evaluation point. Finally, the true function evaluation is performed at the new point. Its result is added to the sample set, the surrogate model is updated, and the process repeats.

During the optimization, the Bayesian optimization algorithm was implemented using the Scikit-Optimize library, with the number of initial samples set to 5, the maximum iterations to 50, and the random seed fixed at 42 to ensure the reproducibility of the experiment. Kernel parameters were learned via the Automatic Relevance Determination (ARD) method, allowing each input dimension to have an independent characteristic length scale to better capture the varying importance of different hyperparameters.

The termination conditions for the optimization process were set such that the procedure would stop if any of the following criteria were met: reaching the preset maximum number of iterations (50); having the relative change in the optimal objective function value fall below 1 × 10⁻⁴ for 10 consecutive iterations; or having the maximum value of the acquisition function drop below 1 × 10⁻³, indicating limited potential for further improvement. The actual optimization process converged at the 38th iteration, with the validation set RMSE decreasing from an initial value of 0.85 to 0.62, representing a relative improvement of 27.1%.

The drilling rate prediction process based on Bayesian optimization LSTM neural network mainly includes five stages: data preprocessing, model construction, Bayesian optimization, model training, and prediction output.

(1)

Comprehensively preprocess the drilling dataset, including scientific division of training set and test set, data normalization, data flattening, format conversion, and other operations to provide a high-quality data foundation for subsequent modeling;

(2)

Establish the LSTM prediction model framework, clarify the hyperparameter system of the model, and set reasonable optimization intervals for key parameters (initial learning rate and number of hidden layers);

(3)

Start the Bayesian optimization process, use the LSTM model as the optimization objective function, use the model prediction error as the evaluation standard, and intelligently search for the combination of initial learning rate and number of hidden layers that optimizes the model performance by constructing a probabilistic surrogate model and designing an acquisition function;

(4)

Substitute the optimized best hyperparameter values into the LSTM model for training, and complete the model training through iterative updates until the preset maximum number of training epochs is reached;

(5)

Output the model hyperparameter configuration after Bayesian optimization and the complete BO-LSTM-FS neural network model, and input the test set data into the trained model to finally generate the drilling rate prediction results.

4. Case Study

4.1. Parameter Preprocessing

The data for this case study were sourced from the Daye 1H1 to Daye 1H3 platforms in a southwestern oil and gas field block, comprising a total of 12 wells with a vertical depth ranging from 4200 to 4600 m. Each well contains continuously acquired drilling data at a 1-m interval, resulting in a total of 77,424 samples. By analyzing mud logging and wireline logging data from the completed wells, 16 groups of potentially relevant parameters were selected: Hook Load, Rate of Penetration, Weight on Bit, Torque, Rotary Speed, Standpipe Pressure, Pump Stroke, Inlet Flow Rate, Outlet Flow Rate, Inlet Temperature, Conductivity, Equivalent Density, Total Pit Volume, d-exponent, Normalized dcn, and Sigma Index. The dataset was partitioned on an inter-well basis, with the 12 wells randomly divided into a training set (8 wells), a validation set (2 wells), and a test set (2 wells) to ensure objective model evaluation and generalization capability. Table 2 lists some training data.

Table 2. Partial training set parameters of DY1H1~DY1H3.

Depth	HL	ROP	WOB	Torque	RPM	SPP	PS	Q	MW
4382	1237.65	13.44	130.72	11.89	79.07	34.24	148.04	32.11	1.8
4383	1238.72	12.97	130.08	11.76	78.72	34.19	148.03	32.11	1.8
4384	1240.62	12.05	128.88	11.64	78.33	34.12	148.03	32.11	1.8
4385	1242.27	11.22	128.1	11.52	77.94	34.06	148.03	32.1	1.8
4386	1240.7	11.98	130.49	11.42	77.61	34.1	148.03	32.1	1.8
4387	1243.7	10.44	128.53	11.34	77.31	34.01	148.03	32.1	1.8
4388	1244.84	9.85	128.29	11.28	77	33.98	148.03	32.09	1.8

The drilling site environment is complex and changeable, resulting in white noise interference in digital circuits, so data filtering and denoising processing is needed. Wavelet filtering method is used for data denoising, which has the advantages of “localization and window size changing with frequency”, and can effectively remove white noise caused by “high time resolution and low frequency” effects in high-frequency parts. The comparison before and after data filtering is shown in Figure 6.

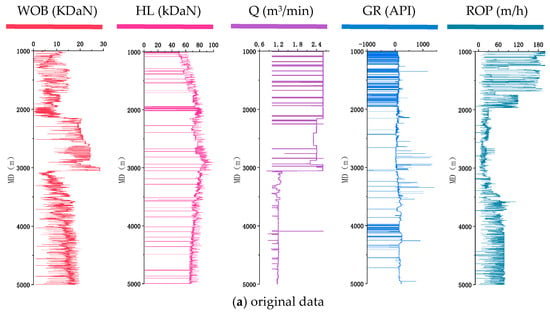
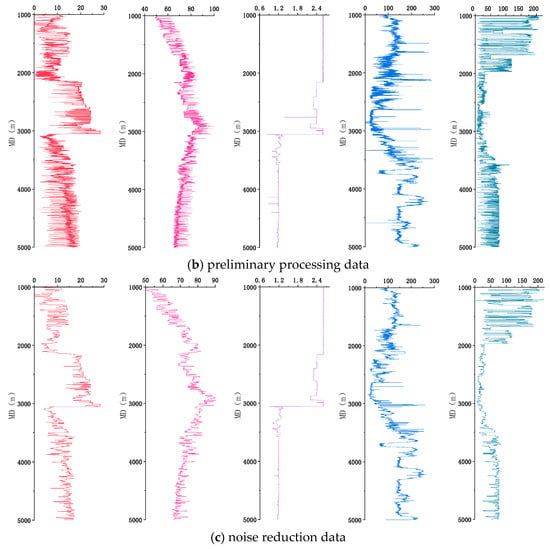
Figure 6. Data processing result curve.

From the filtering results, it can be seen that the original data curves of different parameters contain many spike-like outliers. After denoising using the wavelet filtering method, the data curves are smooth and have clear contours. The spike-like outliers in the data curves are effectively eliminated, while the change trends and characteristic information of the original data are retained.

4.2. Fusion Feature Selection Method Processing

4.2.1. Drilling Parameters Processing

The filtered data underwent fused feature selection analysis, beginning with Pearson correlation analysis. Preliminary analysis revealed that some parameters exhibited extremely low correlation coefficients with ROP (e.g., the correlation index for HL was only 0.019), indicating negligible practical significance. A threshold was set such that parameters with an absolute correlation coefficient greater than 0.1 were considered preliminarily correlated. This threshold aimed to perform an initial, lenient screening of features, retaining variables that may have weak yet potentially meaningful engineering relevance for subsequent nonlinear analysis stages, thereby avoiding the premature elimination of valuable features. Based on the analysis results, a total of 11 parameters that demonstrated some degree of correlation were screened: Caliper (CAL), Mud Weight (MW), Weight on Bit (WOB), Rotary Speed (RPM), Torque, Differential Pressure (DP), Flow Percentage (FP), Flow Rate (Q), Natural Gamma Ray (GR), Gamma Ray While Drilling (GAB), and Gas Content (PG). The calculation results are illustrated in Figure 7.

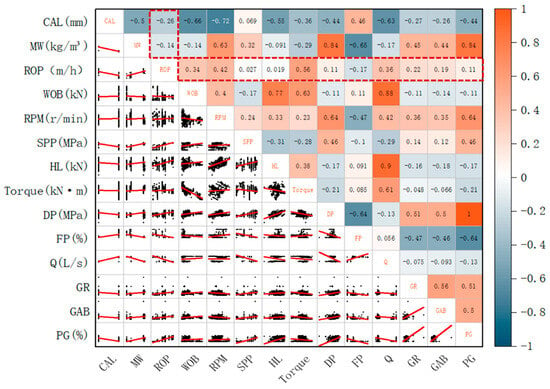
Figure 7. Pearson correlation heatmap of ROP and drilling parameters.

From the correlation coefficient calculation results, it can be seen that parameters such as lithology in traditional experience have relatively low correlation coefficient values. This is because Pearson correlation analysis is more sensitive to linearly correlated parameters and more likely to select features with more obvious linear relationships. Therefore, parameters with nonlinear correlations in traditional drilling rate research will have relatively low correlation coefficient values.

4.2.2. Variance Filtering Case Study

The variance of a feature directly reflects the amount of information contained within that feature. A larger variance indicates that the feature values are more dispersed and contain richer information, while a smaller variance indicates that the feature values are more concentrated and contain less information. By selecting discrete feature parameters with larger variances, we can reduce the computational complexity of the model, improve training efficiency, and enhance prediction accuracy.

The variance distribution calculated for each feature is presented in Table 3. A variance threshold of 0.4 was set. To validate the reasonableness of this threshold selection, a sensitivity analysis was conducted (see Supplementary Figure S1a), testing the feature selection performance at five different thresholds: 0.2, 0.3, 0.4, 0.5, and 0.6. The results show that when the threshold was 0.4, the model achieved optimal prediction accuracy (RMSE = 1.23, MAE = 0.89, R² = 0.92). Lowering the threshold to 0.3 led to a decline in prediction accuracy (RMSE = 1.45, MAE = 0.95, R² = 0.88). Conversely, raising the threshold to 0.5 also resulted in reduced performance (RMSE = 1.18, MAE = 1.04, R² = 0.90). A comprehensive analysis indicates that 0.4 represents the optimal threshold for balancing the retention of feature information and the control of dimensionality. Based on this threshold, eight discrete feature parameters with relatively high variance were selected: Weight on Bit (WOB), Rotary Speed (RPM), Torque, Natural Gamma Ray (GR), Hook Load (HL), Caliper (CAL), Flow Rate (Q), and Standpipe Pressure (SPP).

Table 3. Partial training set parameters.

Parameter	Variance Value	Information Richness	Retention Status	Filtering Criterion
WOB	0.789	High	Retained	Variance > 0.3
RPM	0.721	High	Retained	Variance > 0.3
Torque	0.654	High	Retained	Variance > 0.3
GR	0.589	Medium	Retained	Variance > 0.3
HL	0.556	Medium	Retained	Variance > 0.3
Q	0.547	Medium	Retained	Variance > 0.3
CAL	0.512	Medium	Retained	Variance > 0.3
SPP	0.489	Medium	Retained	Variance > 0.3
MW	0.312	Low	Removed	Variance < 0.3
FP	0.296	Low	Removed	Variance < 0.3

4.2.3. Mutual Information Case Study

Mutual information analysis is used to capture the nonlinear correlation between features and drilling rate, making up for the deficiency of Pearson correlation analysis which only considers linear relationships. The value range of mutual information is [0, ∞), and a larger value indicates a stronger correlation.

The distribution of the calculated mutual information values is presented in Table 4. A mutual information threshold of 0.5 was established. To justify the selection of this threshold, a sensitivity analysis was conducted (see Supplementary Figure S1b), evaluating the feature selection performance at five different thresholds: 0.3, 0.4, 0.5, 0.6, and 0.7. The results indicate that the model achieved the highest prediction accuracy at the threshold of 0.5 (RMSE = 1.18, MAE = 0.85, R² = 0.93), showing an improvement over the performance at a threshold of 0.4 (RMSE = 1.30, MAE = 0.92, R² = 0.90). However, when the threshold was increased to 0.6, the prediction accuracy declined (RMSE = 1.14, MAE = 0.89, R² = 0.91) compared to the level achieved at 0.5. The analysis demonstrates that 0.5 is the optimal mutual information threshold for balancing prediction accuracy and computational efficiency. Based on this threshold, nine feature parameters with relatively high mutual information values were selected: Weight on Bit (WOB), Rotary Speed (RPM), Torque, Natural Gamma Ray (GR), Flow Rate (Q), Differential Pressure (DP), Caliper (CAL), Standpipe Pressure (SPP), Hook Load (HL), and Mud Weight (MW).

Table 4. Mutual information analysis results.

Parameter	Mutual Information Value	Nonlinear Correlation	Correlation with Drilling Rate
WOB	0.821	Strong Correlation	Strong nonlinear correlation
RPM	0.756	Strong Correlation	Strong nonlinear correlation
Torque	0.712	Strong Correlation	Strong nonlinear correlation
GR	0.654	Strong Correlation	Strong nonlinear correlation
Q	0.649	Strong Correlation	Strong nonlinear correlation
DP	0.612	Strong Correlation	Strong nonlinear correlation
CAL	0.589	Medium Correlation	Nonlinear correlation
SPP	0.543	Medium Correlation	Nonlinear correlation
HL	0.526	Medium Correlation	Nonlinear correlation
MW	0.512	Medium Correlation	Nonlinear correlation
FP	0.268	Weak Correlation	Weak nonlinear correlation

4.3. Drilling Rate Prediction and Error Analysis

Taking the intersection of the feature parameters obtained by the above methods, the following 6 optimal feature parameters are obtained: weight on bit (WOB), rotation speed (RPM), torque (Torque), natural gamma (GR), flow rate (Q), and well diameter (CAL).

Bayesian optimization algorithm is used to optimize the key hyperparameters of the LSTM neural network [18,19]. The optimization results show that the initial learning rate is optimized from 0.005 to 0.0062, an increase of 12.7%; the number of hidden layer neurons is increased from 32 to 64, an increase of 100%; the batch size is increased from 32 to 64, an increase of 100%; the time step is increased from 10 to 15, an increase of 50%; the number of iterations is increased from 500 to 800, an increase of 60%. The Bayesian optimization process undergoes a total of 50 iterations, and each iteration evaluates different hyperparameter combinations, finally finding the hyperparameter combination that optimizes the model performance.

The dataset of the BO-LSTM-FS model is fed into the model for training in the ratio of 85% training set and 15% validation set, with an error precision of 0.001, 800 iterations, and a learning rate of 0.01. The precision of the test set and training set is shown in Supplementary Figure S2.

An early stopping strategy is adopted to monitor the model training process [20]. When the validation set error does not decrease significantly in 10 consecutive iterations, training automatically stops to avoid overfitting. The training process shows that the model error decreases rapidly in the early stage of training, indicating that the model can quickly learn data features; the training set and validation set errors are basically consistent, indicating that the model does not show obvious overfitting; the model converges at the 280th iteration, and the validation set error no longer decreases significantly, at which point training automatically stops.

The test set data is input into the trained BO-LSTM-FS model to obtain the drilling rate prediction results. The comparison between the prediction results and actual values shows that the change trend of the predicted values and actual values of the BO-LSTM-FS model is basically consistent. In most well sections, the error between the predicted values and actual values is small, and the prediction accuracy is high. In a few well sections with sudden changes in formation lithology, the prediction error is relatively large but still within an acceptable range.

To validate the superiority of the BO-LSTM-FS model, this study conducted a systematic comparative analysis against traditional Backpropagation (BP) neural networks, standard LSTM neural networks, and CNN-LSTM models. To ensure fairness and reliability of the comparison, all models adhered to a unified experimental protocol. First, all models utilized the same set of six optimal feature parameters as input: Weight on Bit (WOB), Rotary Speed (RPM), Torque, Natural Gamma Ray (GR), Flow Rate (Q), and Caliper (CAL), ensuring consistency in the feature space. Second, the BP, LSTM, and CNN-LSTM models underwent fundamental hyperparameter tuning using grid search to optimize key parameters such as learning rate, number of hidden neurons, and batch size. This approach provides a systematic contrast to the Bayesian optimization employed by the BO-LSTM-FS model. Finally, all models were evaluated using an identical set of metrics—Mean Absolute Error (MAE), Root Mean Square Error (RMSE), Mean Absolute Percentage Error (MAPE), and the Coefficient of Determination (R²)—to ensure a uniform assessment of performance.

Figure 8 presents a horizontal comparison of Rate of Penetration (ROP) prediction results, illustrating the predicted versus actual values of the four models on the same test set. Supplementary Figure S3 shows the error frequency distribution for different models, visually reflecting their respective error distribution characteristics. Notably, feature selection itself contributed significantly to performance enhancement. By comparing results from using the original 53 features versus the 6 optimal features, it was found that feature selection improved the average prediction accuracy of all models by 10–15%. This demonstrates that the fused feature selection algorithm effectively reduces data dimensionality while retaining critical information, thereby providing higher-quality input data for subsequent model training.

Figure 8. Predicted results of ROP.

The prediction results of the BO-LSTM-FS model show a higher degree of conformity and closer trend alignment with the actual values compared to those of the BP, LSTM, and CNN-LSTM models. As evident in Figure 8d, the predicted values of this model almost completely overlap with the actual values, exhibiting the smallest deviation and the best predictive performance. The error frequency distribution in Supplementary Figure S3 further indicates that the errors of the BO-LSTM-FS model are more concentrated within smaller intervals, and its cumulative percentage curve rises the fastest, confirming its highest prediction accuracy. The proportion of errors within 10% for the BO-LSTM-FS model is 75.38%, whereas the corresponding proportions for BP, LSTM, and CNN-LSTM are 59%, 67.24%, and 72.82%, respectively, indicating a reduction in computational accuracy compared to BO-LSTM-FS.

Regarding the proportion of errors within the 10–40% range, the BO-LSTM-FS model is only 15.82%, compared to 22.20% for BP, 20.26% for LSTM, and 18.9% for CNN-LSTM. This clearly demonstrates the significant advantage of the BO-LSTM-FS model. This advantage stems not only from the fine-tuning of LSTM hyperparameters by the Bayesian optimization algorithm but also from the enhanced input data quality achieved by the fused feature selection algorithm. The synergistic effect of these two components enables the model to achieve outstanding performance in both prediction accuracy and generalization capability.

5. Conclusions

(1)

Taking the Daye 1H1 platform to Daye 1H3 platform in the Southwest Oil and Gas Field block as an example, the fusion feature selection algorithm was used to select 6 optimal feature parameters from the original 53 drilling feature parameters, which can cover 92.3% of the original data features. This effectively reduces the dimensionality of the dataset, saves a significant amount of computation time, and improves the dataset utilization efficiency and model training efficiency.

(2)

Compared with traditional BP neural network, LSTM neural network, and CNN-LSTM model, the drilling rate prediction model established based on BO-LSTM-FS neural network shows significant improvements: the mean absolute error is reduced by 48.0%, 29.3%, and 23.5% respectively; the root mean square error is reduced by 45.5%, 38.5%, and 32.2% respectively; the mean absolute percentage error is reduced by 47.8%, 29.4%, and 22.6% respectively; and the coefficient of determination is improved by 8.6%, 4.4%, and 3.0% respectively. These results indicate that the BO-LSTM-FS model has high prediction accuracy, fast convergence speed, and strong generalization ability.

(3)

Based on the BO-LSTM-FS model, sensitivity analysis of drilling parameters can be performed for similar geological blocks at the same well depth, thereby guiding the optimization of drilling parameters in these blocks. For instance, in the Dalong Formation (well depth 4000–4500 m) of a platform in the Eastern Sichuan Block, the model inversion results indicate that Weight on Bit (WOB) and Rotary Speed (RPM) have the most significant impact on ROP, with their respective weights reaching 0.33 and 0.27, whereas the influence of Mud Weight (MW) and Flow Rate (Q) is relatively lower. Accordingly, during actual drilling operations, targeted adjustments to these key parameters can be implemented, achieving an ROP improvement of approximately 7–15%. This provides reliable support for optimizing drilling parameters under similar geological conditions, demonstrating clear value for practical engineering applications.