Comparison of Drag Force Models in Liquid–Solid Mixed Batch Simulations by Observing Off-Bottom Suspension Flow Patterns
Abstract
1. Introduction
1.1. The Lattice Boltzmann Method
1.2. Particle Forces and Drag Force Models
1.3. Validation of Drag Force Models on Engineering Cases
1.4. Off-Bottom Suspension Flow Patterns
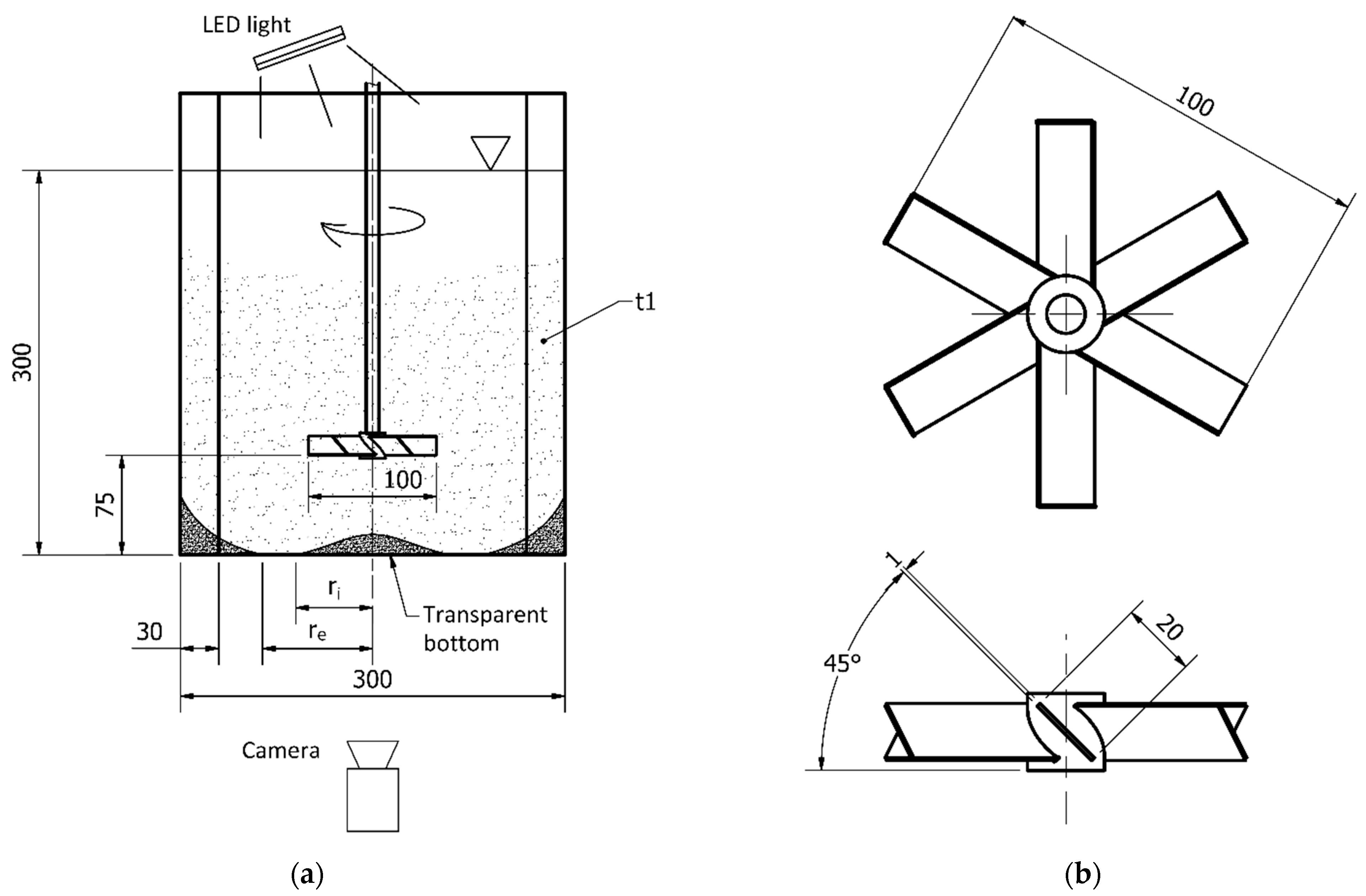
2. Experimental and Numerical Setup and Methods
2.1. Setup of Experiment
2.2. Setup of CFD Simulation
2.2.1. Continuum Model
2.2.2. DEM Model
2.2.3. Simulation Procedure
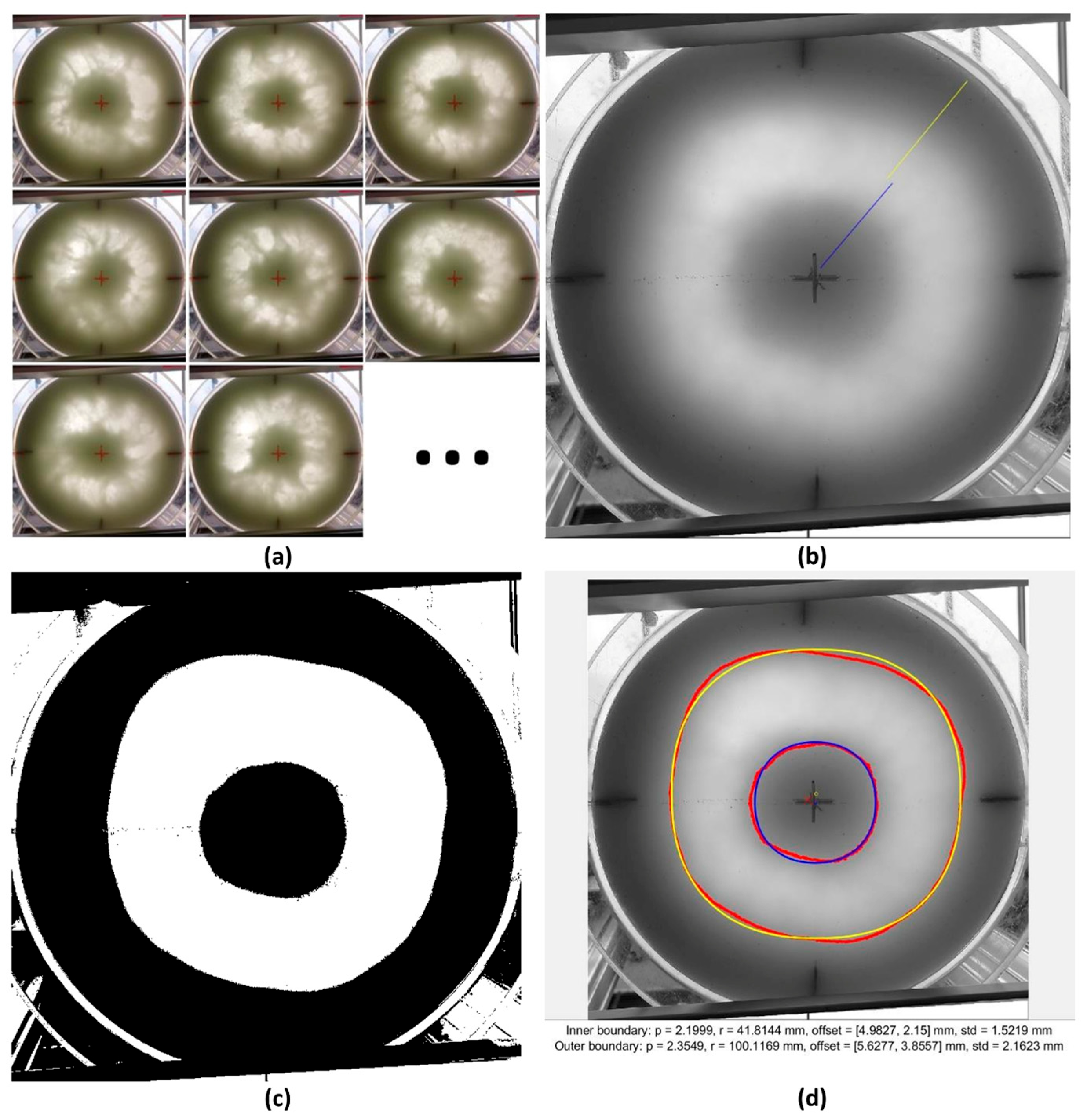
2.3. Visual Comparison Method
2.3.1. Time Averaging of Pictures
2.3.2. Border Detection
2.3.3. Fitting the Shapes
| Baffle plane: | (24) | |
| Mid-baffle plane: | (25) |
3. Results
Sensitivity Tests of the Visual Comparison Method
4. Conclusions
- Lite LBM simulations of an axially mixed liquid–solid batch were carried out for several different particle drag force models, and the results were compared with the experimental findings. The tested models were the Brown and Lawler model [21], Equation (7), and Rong model [27], Equation (13), which are present in the software; as well as the Gidaspow model [28], Equation (14), which was implemented as a user-defined function.
- A simple and accessible comparison method for measuring near-off-bottom suspension flow patterns was newly adapted. The subjectivity of visual reads was eliminated by using computer image processing for both experimental data and simulation result renderings, allowing better comparability.
- It was found that the baffles deform the expected circular patterns when using impeller speeds below the just off-bottom suspension speed in a standard axially mixed baffled tank. The -norm was introduced as an effective tool to describe this phenomenon. It serves to quantify the effect of baffles on the symmetries in the system under different conditions, such as how the outer interface deforms more (p increases) when nearing the baffles at higher impeller speeds. This new two-parameter description can provide the required nuance for more thorough comparisons in the future.
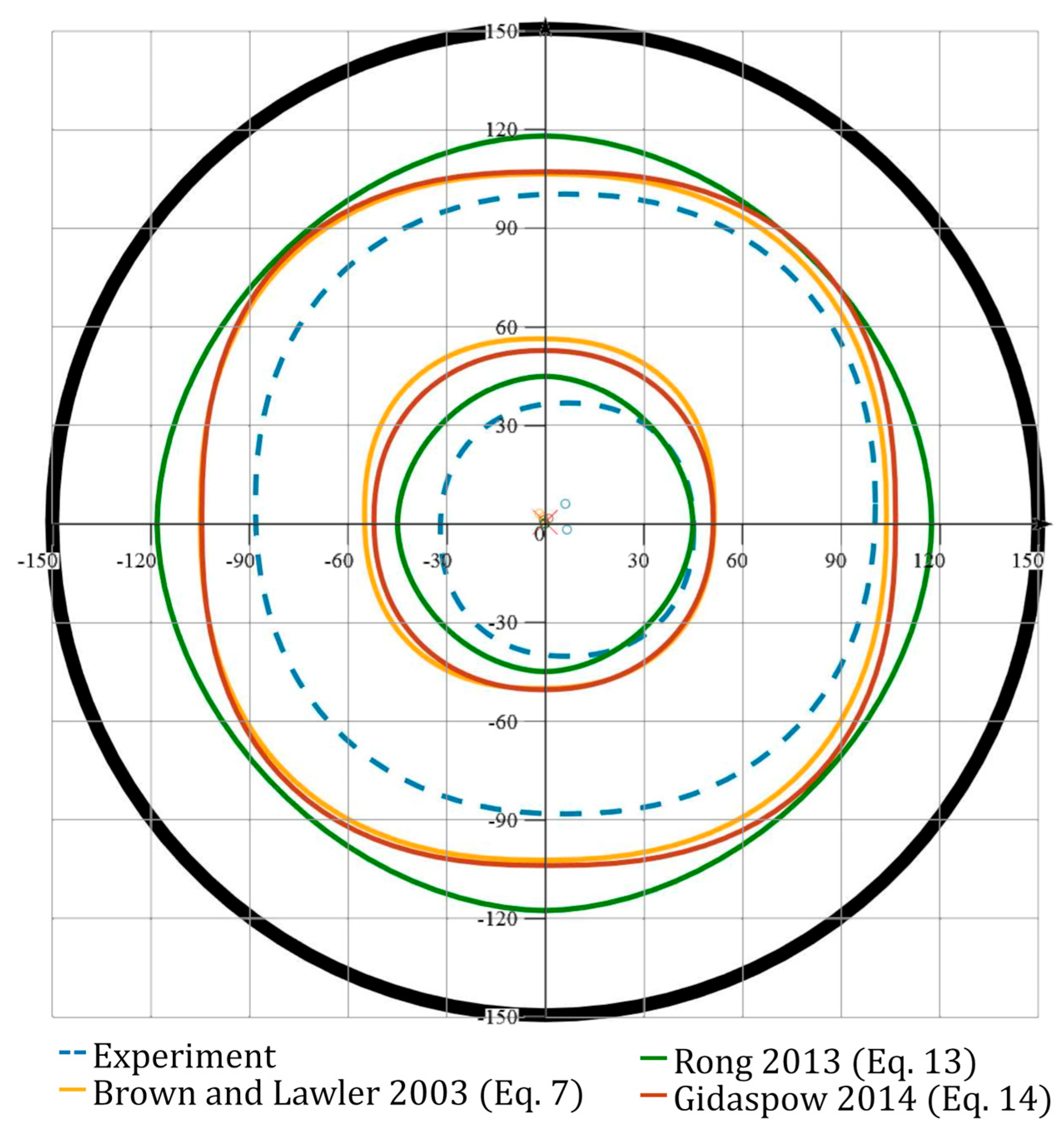
- The simulation succeeded in replicating the flow patterns even without the formulation of the interphase forces considered important for the off-bottom suspension (though with non-negligible average errors of about 20% for the two dilute suspensions and 30% for the dense), underlining our point that the general behavior surrounding the off-bottom suspension comprises more than mechanics of the initial particle lift.
- The simulation results across configurations were generally closer to each other than to experimental data. We consider this a culmination of approximations—both methodical (imperfect calibration of visual conditions and general uncertainties surrounding the visual rendering of simulation results) and numerical (mainly the particle parceling and simplified contact model).
- Despite the simplifications, the Rong model [27], Equation (13), replicated the experiments better overall than the Brown and Lawler model [21], Equation (7), in percentages according to the assumption. The model of Rong [27], Equation (13), however, overestimated the outer interface radius at higher impeller speeds and higher solid fractions. The Gidaspow model [28], Equation (14), behaved well and remained in between the other two models, despite being originally devised for an Euler–Euler description. Its results were closer to the lone particle Brown and Lawler model [21], Equation (7), than to Rong [27], Equation (13). Of course, different regions of the tank may be better described using different models—in our case, it would be possible to conduct a differentiated comparison between the inner and outer shape, which we intend to explore in the future on a more established and rigorous basis. Following these points, the presented method can be a convenient aid for comparing the drag force and other models for different mixing cases.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| Archimedes number | ||
| Smagorinsky coefficient | ||
| drag coefficient | ||
| drag coefficient of a lone steady particle | ||
| tank diameter | ||
| impeller diameter | ||
| particle diameter | ||
| particle drag force | ||
| modified Froude number | ||
| gravitational acceleration | ||
| impeller speed | ||
| just-suspended impeller speed (critical impeller speed) | ||
| p-norm exponent | ||
| interior interface radius of sedimented and mixed particles | ||
| exterior interface radius of sedimented and mixed particles | ||
| empirical proportionality constant for the Zwietering correlation | ||
| timestep | ||
| fluid velocity | ||
| fluid velocity | ||
| mass percentage of suspended solids to liquid in the Zwietering correlation | ||
| grid spacing | ||
| liquid fraction | ||
| solid/particle fraction | ||
| voidage function exponent | ||
| shear rate | ||
| mechanical power dissipation per unit mass of fluid phase | ||
| Kolmogoroff scale of dissipative eddies | ||
| dynamic viscosity | ||
| kinematic viscosity | ||
| liquid density | ||
| particle (solid) density |
References
- Derksen, J.J. Highly resolved simulations of solids suspension in a small mixing tank. AIChE J. 2012, 58, 3266–3278. [Google Scholar] [CrossRef]
- Ayranci, I.; Machado, M.B.; Madej, A.M.; Derksen, J.J.; Nobes, D.S.; Kresta, S.M. Effect of geometry on the mechanisms for off-bottom solids suspension in a stirred tank. Chem. Eng. Sci. 2012, 79, 163–176. [Google Scholar] [CrossRef]
- Derksen, J. Eulerian-Lagrangian simulations of settling and agitated dense solid-liquid suspensions—Achieving grid convergence. AIChE J. 2018, 64, 1147–1158. [Google Scholar] [CrossRef]
- Blais, B.; Lassaigne, M.; Goniva, C.; Fradette, L.; Bertrand, F. Development of an unresolved CFD–DEM model for the flow of viscous suspensions and its application to solid–liquid mixing. J. Comput. Phys. 2016, 318, 201–221. [Google Scholar] [CrossRef]
- Blais, B.; Bertrand, O.; Fradette, L.; Bertrand, F. CFD-dem simulations of early turbulent solid–liquid mixing: Prediction of suspension curve and just-suspended speed. Chem. Eng. Res. Des. 2017, 123, 388–406. [Google Scholar] [CrossRef]
- Tamburini, A.; Cipollina, A.; Micale, G.; Brucato, A.; Ciofalo, M. CFD simulations of dense solid–liquid suspensions in baffled stirred tanks: Prediction of suspension curves. Chem. Eng. J. 2011, 178, 324–341. [Google Scholar] [CrossRef]
- Tamburini, A.; Cipollina, A.; Micale, G.; Ciofalo, M.; Brucato, A. Dense solid–liquid off-bottom suspension dynamics: Simulation and experiment. Chem. Eng. Res. Des. 2009, 87, 587–597. [Google Scholar] [CrossRef]
- Hosseini, S.; Patel, D.; Ein-Mozaffari, F.; Mehrvar, M. Study of solid–liquid mixing in agitated tanks through electrical resistance tomography. Chem. Eng. Sci. 2010, 65, 1374–1384. [Google Scholar] [CrossRef]
- Barigou, M. Particle tracking in opaque mixing systems: An overview of the capabilities of PET and PEPT. Chem. Eng. Res. Des. 2004, 82, 1258–1267. [Google Scholar] [CrossRef]
- Raffel, M.; Willert, C.E.; Scarano, F.; Kähler, C.J.; Wereley, S.T.; Kompenhans, J. Particle Image Velocimetry: A Practical Guide; Springer: Cham, Switzerland, 2018. [Google Scholar]
- M-Star. Available online: https://mstarcfd.com/ (accessed on 31 March 2024).
- Chen, S.; Doolen, G.D. Lattice Boltzmann Method for Fluid Flows. Annu. Rev. Fluid Mech. 1998, 30, 329–364. [Google Scholar] [CrossRef]
- M-Star CFD Documentation. Available online: https://docs.mstarcfd.com/ (accessed on 31 March 2024).
- Sirasitthichoke, C.; Teoman, B.; Thomas, J.; Armenante, P.M. Computational prediction of the just-suspended speed, Njs, in stirred vessels using the lattice Boltzmann method (LBM) coupled with a novel mathematical approach. Chem. Eng. Sci. 2022, 251, 117411. [Google Scholar] [CrossRef]
- Giacomelli, J.J.; Van den Akker, H.E. Time Scales and turbulent spectra above the base of stirred vessels from large eddy simulations. Flow Turbul. Combust. 2020, 105, 31–62. [Google Scholar] [CrossRef]
- Giacomelli, J.J.; Van den Akker, H.E. A spectral approach of suspending solid particles in a turbulent stirred vessel. AIChE J. 2020, 67, e17097. [Google Scholar] [CrossRef]
- Kildashti, K.; Dong, K.; Yu, A. Contact force models for non-spherical particles with different surface properties: A Review. Powder Technol. 2023, 418, 118323. [Google Scholar] [CrossRef]
- Mao, Z.; Yang, C. Challenges in study of single particles and particle swarms. Chin. J. Chem. Eng. 2009, 17, 535–545. [Google Scholar] [CrossRef]
- Schiller, L.; Maumann, A. Über die grundlegenden Berechnungen bei der Schwerkraftaufbereitung. Z. Ver. Dtsch. Ing. 1933, 77, 318–320. [Google Scholar]
- DallaValle, J.M. Micromeritics, the Technology of Fine Particles; Pitman Pub. Corp: New York, NY, USA, 1948. [Google Scholar]
- Brown, P.P.; Lawler, D.F. Sphere drag and settling velocity revisited. J. Environ. Eng. 2003, 129, 222–231. [Google Scholar] [CrossRef]
- Brucato, A.; Grisafi, F.; Montante, G. Particle drag coefficients in turbulent fluids. Chem. Eng. Sci. 1998, 53, 3295–3314. [Google Scholar] [CrossRef]
- Khopkar, A.R.; Kasat, G.R.; Pandit, A.B.; Ranade, V.V. Computational fluid dynamics simulation of the solid suspension in a stirred slurry reactor. Ind. Eng. Chem. Res. 2006, 45, 4416–4428. [Google Scholar] [CrossRef]
- Pinelli, D.; Nocentini, M.; Magelli, F. Solids distribution in stirred slurry reactors: Influence of some mixer configurations and limits to the applicability of a simple model for predictions. Chem. Eng. Commun. 2001, 188, 91–107. [Google Scholar] [CrossRef]
- Fajner, D.; Pinelli, D.; Ghadge, R.S.; Montante, G.; Paglianti, A.; Magelli, F. Solids distribution and rising velocity of buoyant solid particles in a vessel stirred with multiple impellers. Chem. Eng. Sci. 2008, 63, 5876–5882. [Google Scholar] [CrossRef]
- Di Felice, R. The voidage function for fluid-particle interaction systems. Int. J. Multiphas. Flow 1994, 20, 153–159. [Google Scholar] [CrossRef]
- Rong, L.W.; Dong, K.J.; Yu, A.B. Lattice-boltzmann simulation of fluid flow through packed beds of uniform spheres: Effect of porosity. Chem. Eng. Sci. 2013, 99, 44–58. [Google Scholar] [CrossRef]
- Gidaspow, D. Multiphase Flow and Fluidization: Continuum and Kinetic Theory Descriptions; Elsevier Science: St. Louis, MO, USA, 2014. [Google Scholar]
- Ergun, S.; Orning, A.A. Fluid flow through randomly packed columns and Fluidized Beds. Ind. Eng. Chem. 1949, 41, 1179–1184. [Google Scholar] [CrossRef]
- Wen, C.Y.; Yu, Y.H. Mechanics of Fluidization. Chem. Eng. Prog. Symp. Ser. 1966, 162, 100–111. [Google Scholar]
- Wang, H.; Zhang, B.; Li, X.; Xiao, Y.; Yang, C. Modeling total drag force exerted on particles in dense swarm from experimental measurements using an inline image-based method. Chem. Eng. J. 2022, 431, 133485. [Google Scholar] [CrossRef]
- Ochieng, A.; Onyango, M.S. Drag models, solids concentration and velocity distribution in a stirred tank. Powder Technol. 2008, 181, 1–8. [Google Scholar] [CrossRef]
- ANSYS FLUENT 12.0 Theory Guide. Available online: https://www.afs.enea.it/project/neptunius/docs/fluent/html/th/main_pre.htm (accessed on 4 May 2024).
- Špidla, M.; Sinevič, V.; Jahoda, M.; Machoň, V. Solid particle distribution of moderately concentrated suspensions in a pilot plant stirred vessel. Chem. Eng. J. 2005, 113, 73–82. [Google Scholar] [CrossRef]
- Marchelli, F.; Hou, Q.; Bosio, B.; Arato, E.; Yu, A. Comparison of different drag models in CFD-dem simulations of spouted beds. Powder Technol. 2020, 360, 1253–1270. [Google Scholar] [CrossRef]
- Zwietering, T.N. Suspending of solid particles in liquid by agitators. Chem. Eng. Sci. 1958, 8, 244–253. [Google Scholar] [CrossRef]
- Rieger, F.; Ditl, P. Suspension of solid particles. Chem. Eng. Sci. 1994, 49, 2219–2227. [Google Scholar] [CrossRef]
- Jirout, T.; Rieger, F. Impeller design for mixing of suspensions. Chem. Eng. Res. Des. 2011, 89, 1144–1151. [Google Scholar] [CrossRef]
- Grenville, R.K.; Mak, A.T.C.; Brown, D.A.R. Suspension of solid particles in vessels agitated by axial flow impellers. Chem. Eng. Res. Des. 2015, 100, 282–291. [Google Scholar] [CrossRef]
- Jirout, T.; Jiroutová, D. Application of theoretical and experimental findings for optimization of mixing processes and equipment. Processes 2020, 8, 955. [Google Scholar] [CrossRef]
- Jirout, T.; Moravec, J.; Rieger, F.; Sinevič, V.; Špidla, M.; Sobolík, V.; Tihoň, J. Electrochemical Measurement of Impeller Speed For Off-Bottom Suspension. Chem. Process Eng. 2005, 26, 485–497. [Google Scholar]
- Micale, G.; Grisafi, F.; Brucato, A. Assessment of particle suspension conditions in stirred vessels by means of pressure gauge technique. Chem. Eng. Res. Des. 2002, 80, 893–902. [Google Scholar] [CrossRef]
- Teoman, B.; Sirasitthichoke, C.; Potanin, A.; Armenante, P.M. Determination of the just-suspended speed, Njs, in stirred tanks using electrical resistance tomography (ERT). AIChE J. 2021, 67, e17354. [Google Scholar] [CrossRef]
- Rettinger, C.; Rüde, U. A coupled lattice Boltzmann method and discrete element method for discrete particle simulations of particulate flows. Comput. Fluids 2018, 172, 706–719. [Google Scholar] [CrossRef]
- MATLAB Documentation. Available online: https://www.mathworks.com/help/matlab/index.html (accessed on 22 June 2024).
- Otsu, N. A threshold selection method from gray-level histograms. IEEE Trans. Syst. Man Cybern. 1979, 9, 62–66. [Google Scholar] [CrossRef]
- Poodiack, R.D.; Wood, W.E. Squigonometry: The Study of Imperfect Circles; Springer: Cham, Switzerland, 2022. [Google Scholar]
- Lagarias, J.C.; Reeds, J.A.; Wright, M.H.; Wright, P.E. Convergence properties of the Nelder–mead simplex method in low dimensions. SIAM J. Optim. 1998, 9, 112–147. [Google Scholar] [CrossRef]
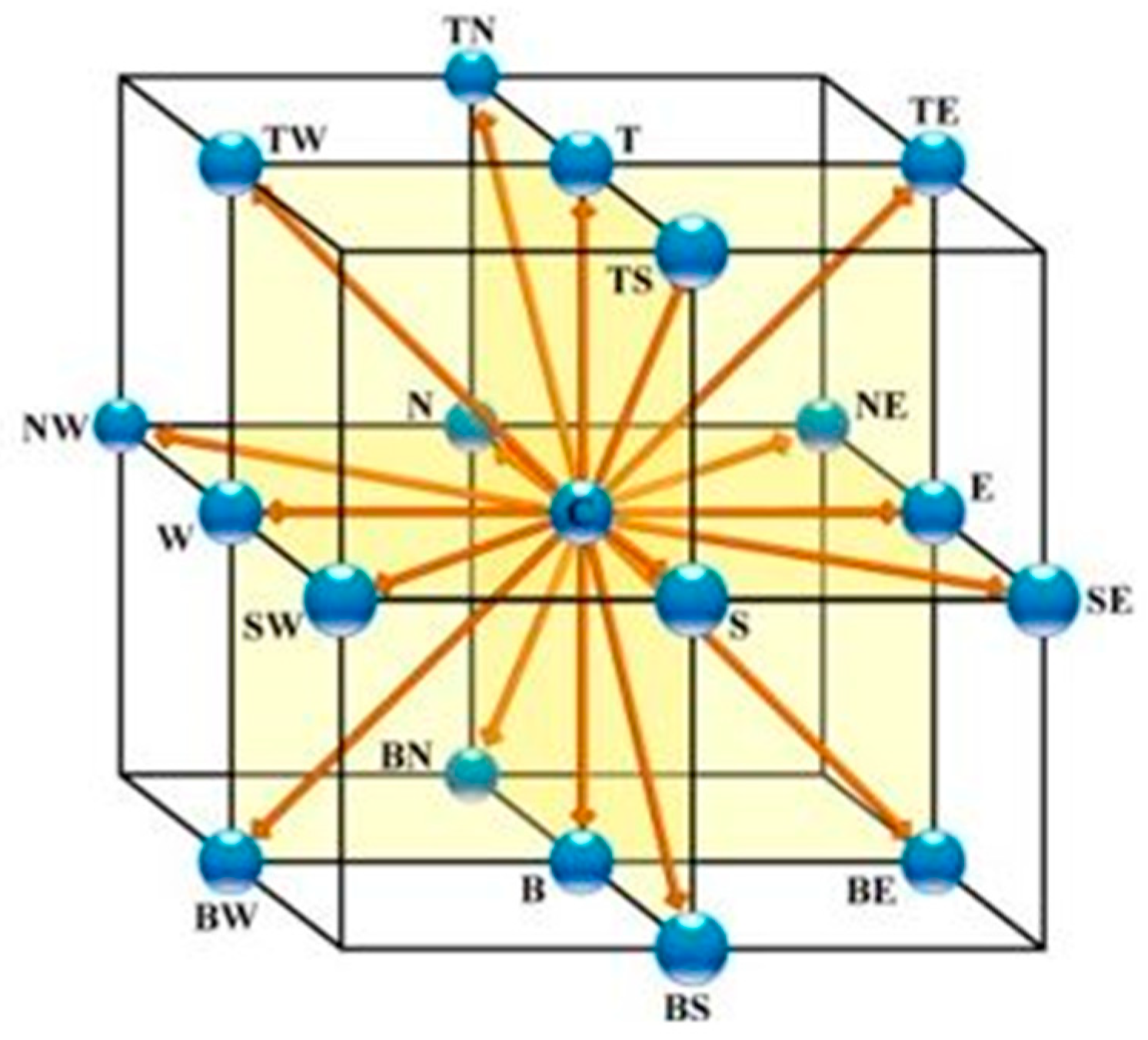
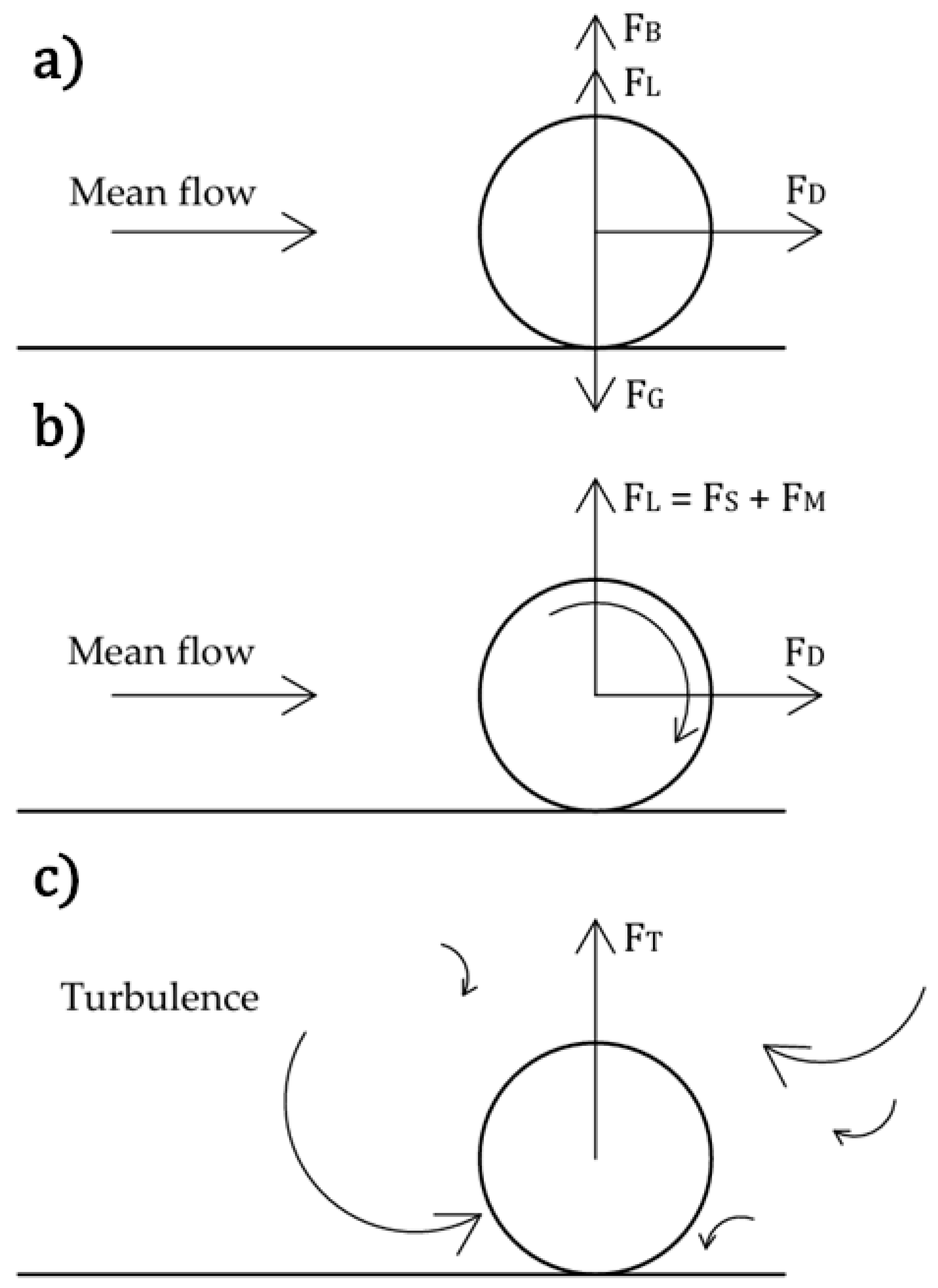
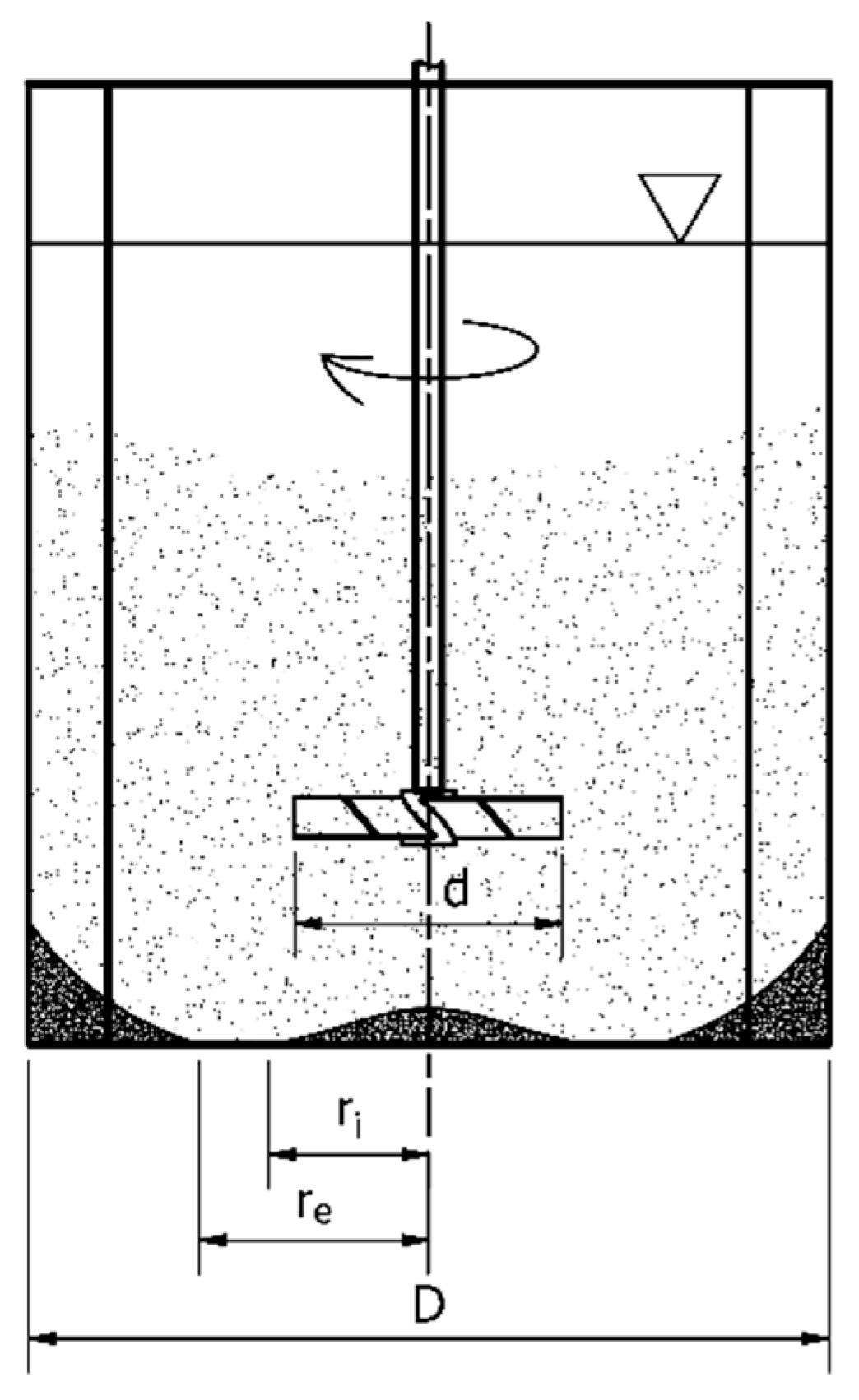
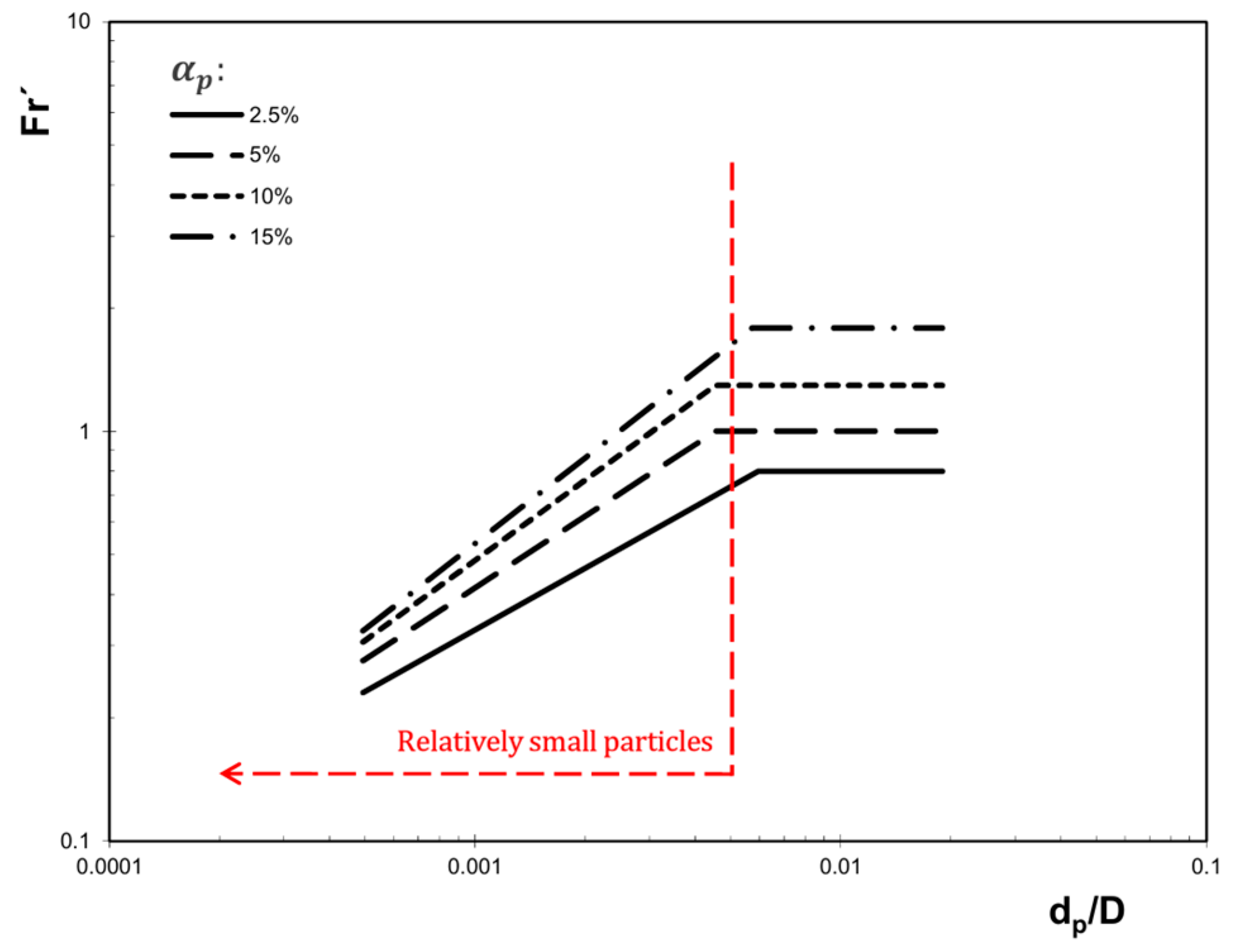





| Category | Ref. | Model Formulation | |
|---|---|---|---|
| Lone steady particle models | [19] | (5) | |
| [20] | (6) | ||
| [21] | (7) | ||
| (a) Models accounting for turbulence | [22] | (8) | |
| [23] | (9) | ||
| [24] | (10) | ||
| [25] | (11) | ||
| (b) Models accounting for other particles | [26] | (12) | |
| [27] | (13) | ||
| [28] | (14) | ||
| [31] | (15) | ||
| Impeller Speed (min−1) | Solid Volume Fraction | ||
|---|---|---|---|
| 2.5% | 5% | 10% | |
| 130 | Evaluated | Evaluated | Shape not clear enough |
| 170 | |||
| 210 | |||
| 250 | |||
| 290 | Evaluated | ||
| 330 | |||
| 370 | Shape lost | ||
| 410 | |||
| 450 | Shape lost | ||
| Contact Model Quantity | Value |
|---|---|
| 0.3 | |
| 0.1 | |
| 0.5 |
| Solid Fraction | Experiment | Simulation |
|---|---|---|
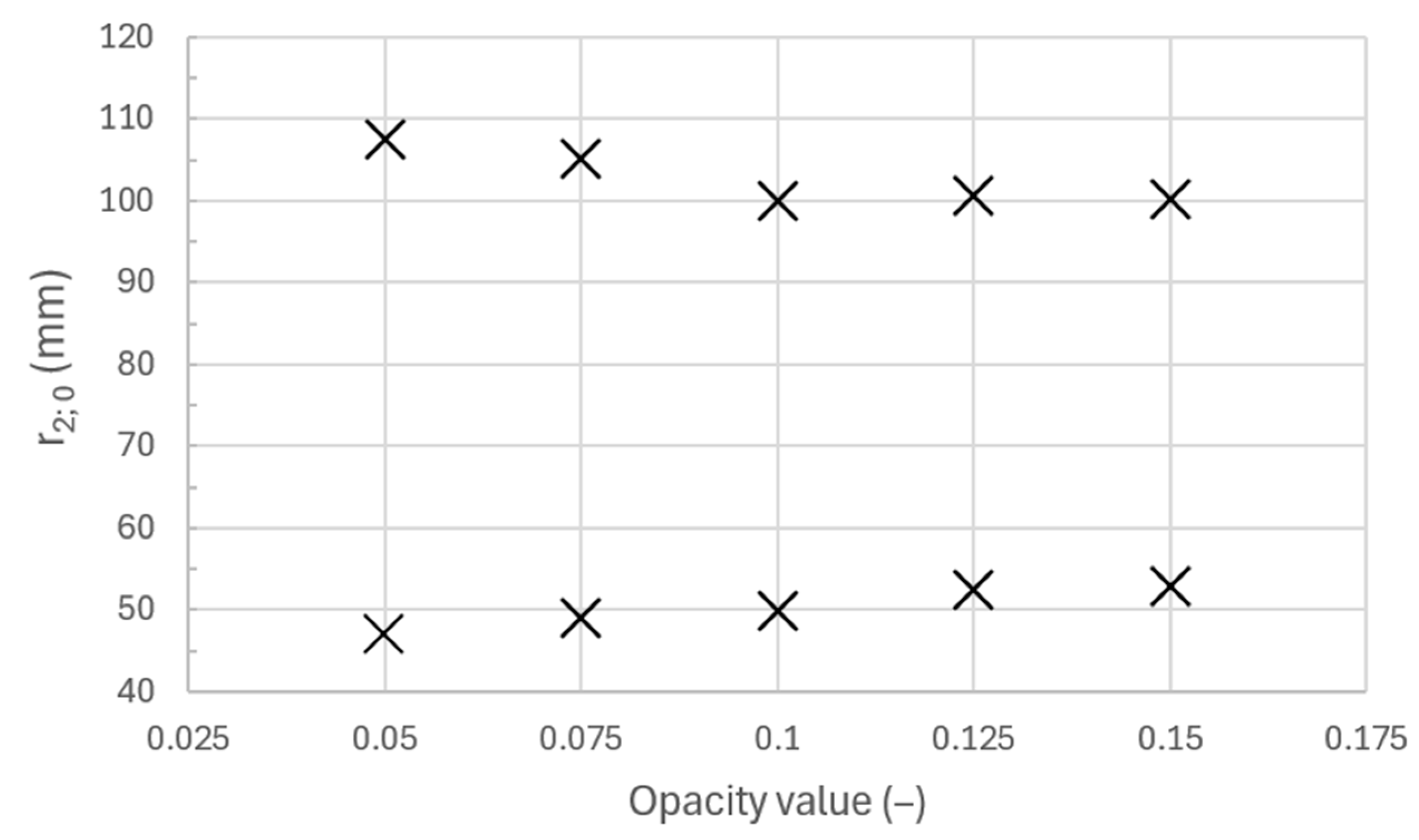
| 2.5% | No light | 50% particle opacity |
| 5% | Studio LED light | 10% particle opacity |
| 10% | Studio LED light | 5% particle opacity |
| Mean Solid Volume Fraction | Average Deviation from Experiment | Brown and Lawler [21] Equation (7) | Rong [27] Equation (13) | Gidaspow [28] Equation (14) |
|---|---|---|---|---|
| 2.5 % | Inner radius | 42.6% (+) | 32.9% (+) | 38.0% (+) |
| Outer radius | 4.2% | 2.7% (−) | 4.2% (−) | |
| Both radii | 23.4% | 17.8% | 21.1% | |
| 5 % | Inner radius | 28.2% (+) | 20.7% | 25.7% (+) |
| Outer radius | 9.8% (+) | 14.7% (+) | 10.7% (+) | |
| Both radius | 19.0% | 17.4% | 18.2% | |
| 10 % | Inner radius | 50.4% | 16.7% | 39.8% |
| Outer radius | 23.3% (+) | 31.3% (+) | 28.0% (+) | |
| Both radii | 36.9% | 24.0% | 33.9% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Randák, F.; Jirout, T. Comparison of Drag Force Models in Liquid–Solid Mixed Batch Simulations by Observing Off-Bottom Suspension Flow Patterns. Processes 2025, 13, 2404. https://doi.org/10.3390/pr13082404
Randák F, Jirout T. Comparison of Drag Force Models in Liquid–Solid Mixed Batch Simulations by Observing Off-Bottom Suspension Flow Patterns. Processes. 2025; 13(8):2404. https://doi.org/10.3390/pr13082404
Chicago/Turabian StyleRandák, Filip, and Tomáš Jirout. 2025. "Comparison of Drag Force Models in Liquid–Solid Mixed Batch Simulations by Observing Off-Bottom Suspension Flow Patterns" Processes 13, no. 8: 2404. https://doi.org/10.3390/pr13082404
APA StyleRandák, F., & Jirout, T. (2025). Comparison of Drag Force Models in Liquid–Solid Mixed Batch Simulations by Observing Off-Bottom Suspension Flow Patterns. Processes, 13(8), 2404. https://doi.org/10.3390/pr13082404






