Simulation Study of Refracturing of Shale Oil Horizontal Wells Under the Effect of Multi-Field Reconfiguration
Abstract
1. Introduction
2. Field Background
3. Materials and Methods
3.1. Three-Dimensional Heterogeneous Geological Modeling
3.2. Three-Dimensional Geomechanical Modeling
3.3. Coupled Seepage Field-Stress Field Modeling
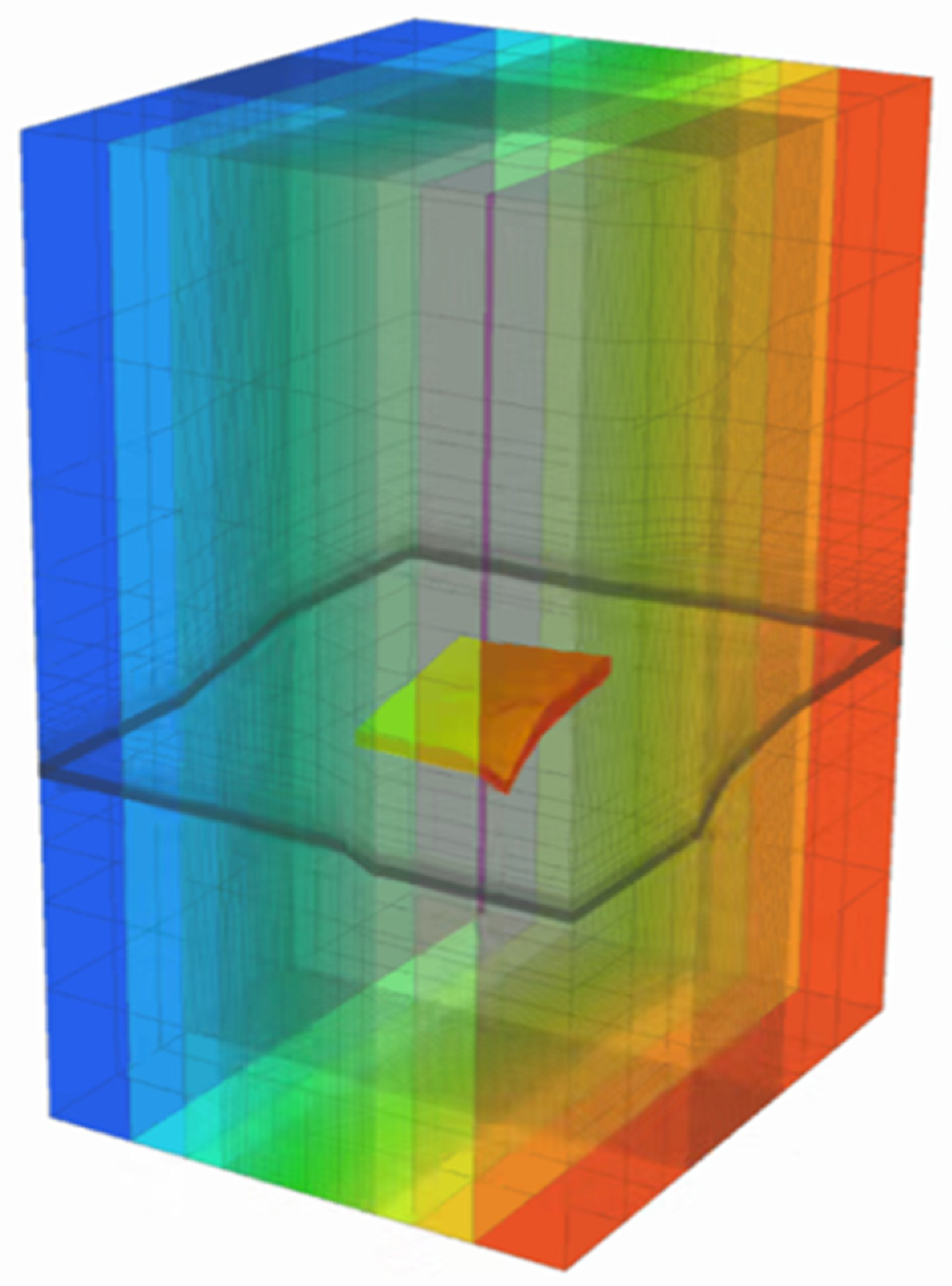
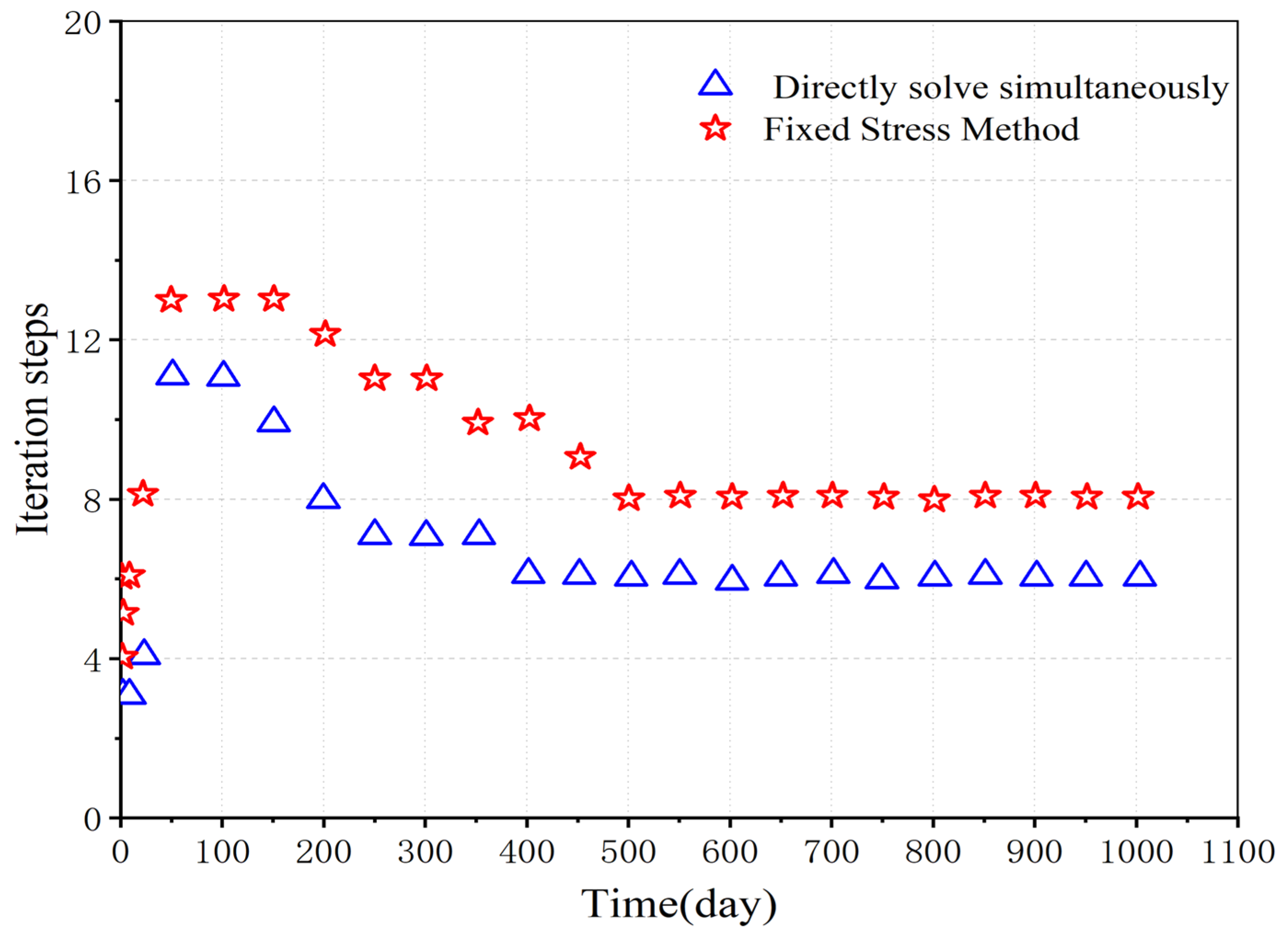
3.4. Refracturing Numerical Simulations
4. Results
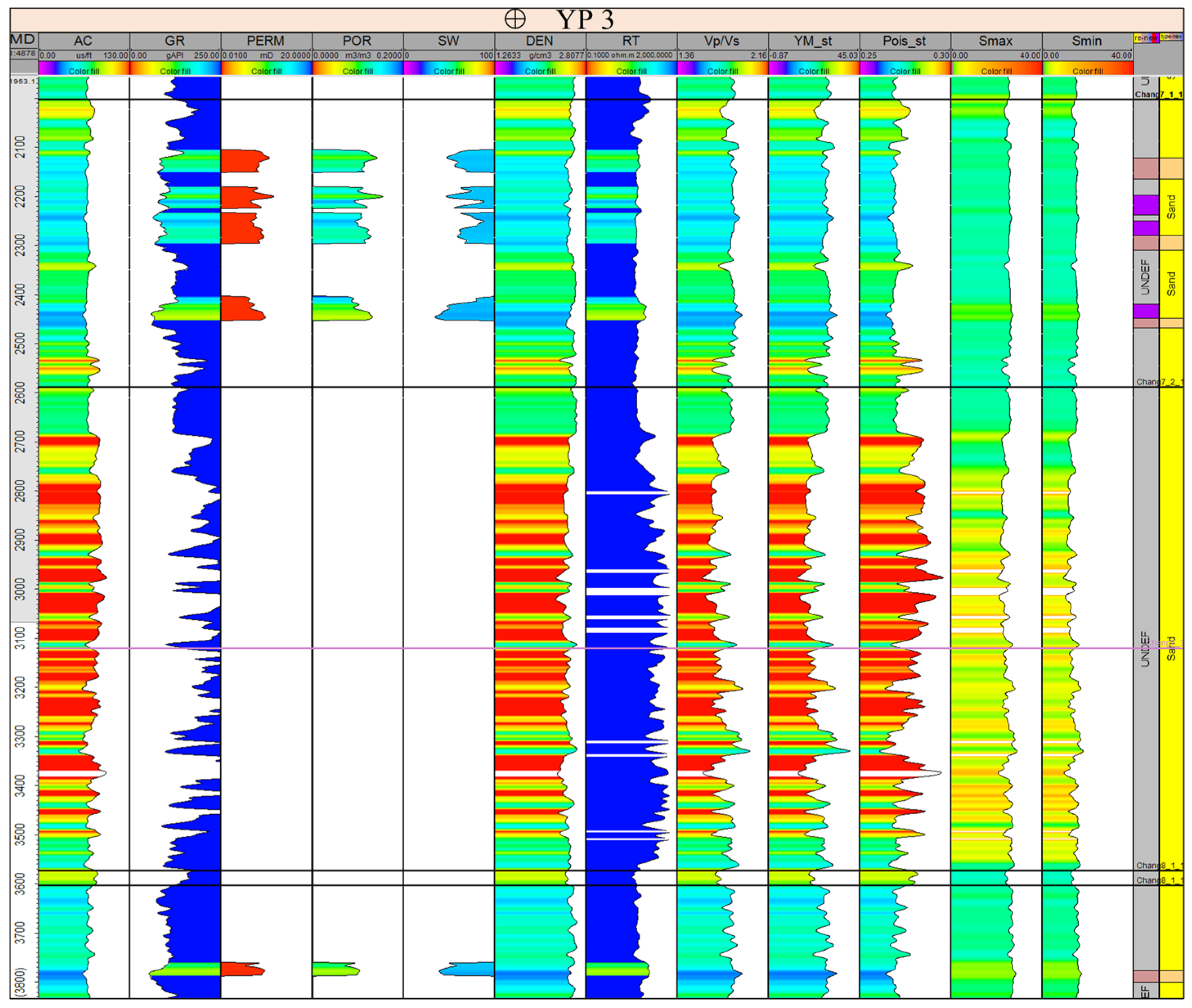
4.1. Three-Dimensional Heterogeneous Geological Model
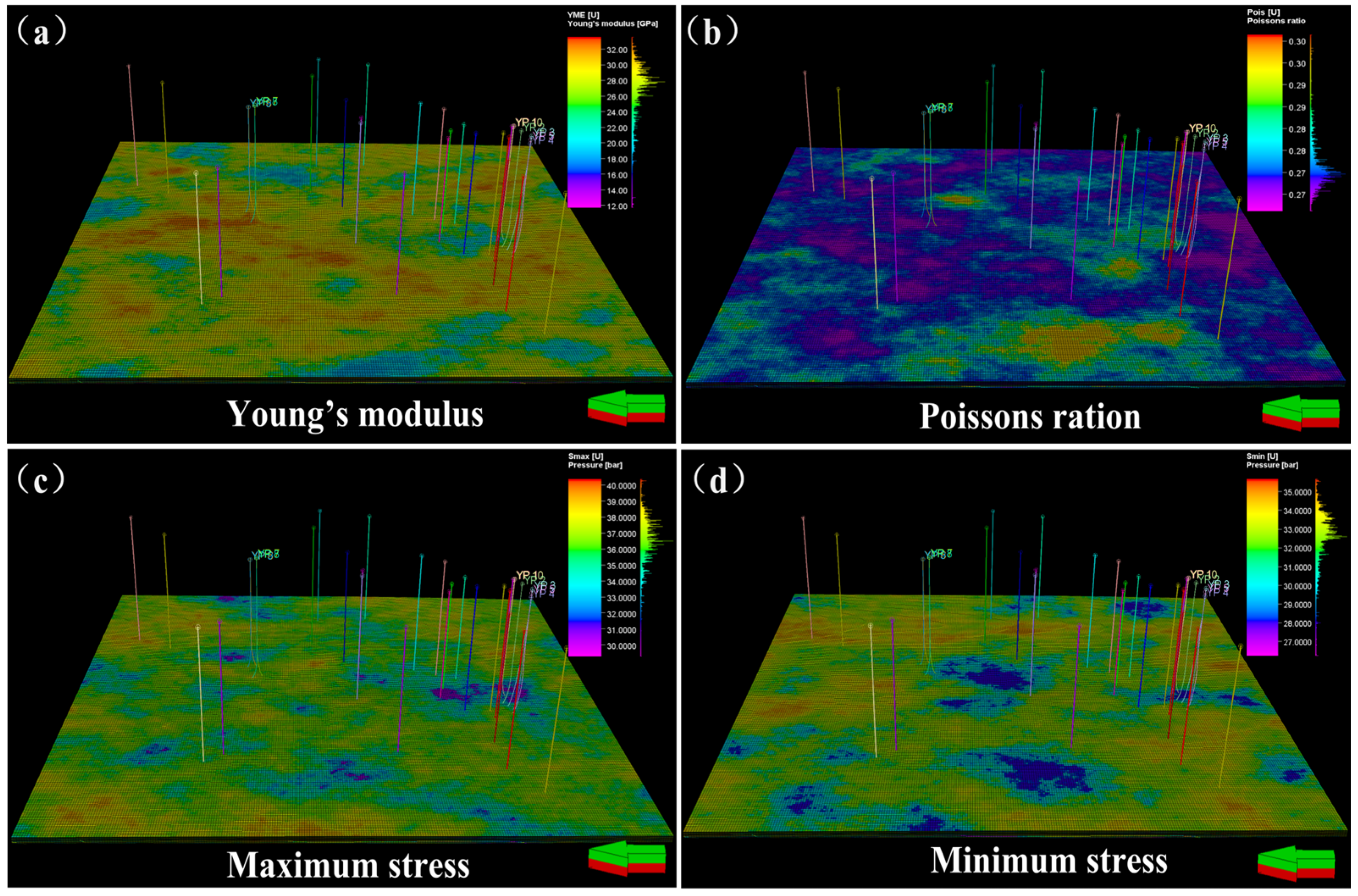
4.2. Three-Dimensional Geomechanical Model
4.3. Analysis of Initial Fracturing, Fracture Propagation, and Oil Well Production Performance
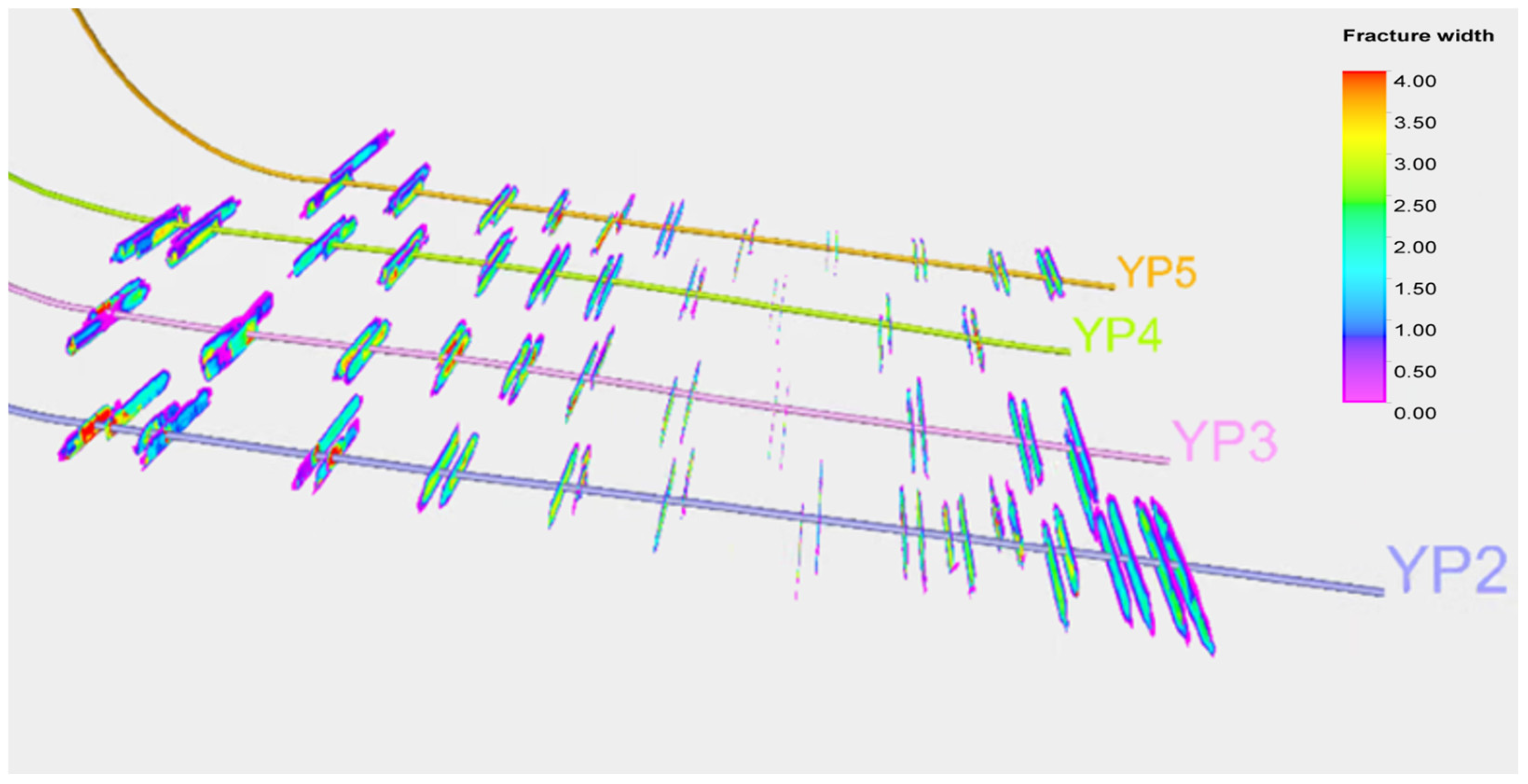
4.3.1. Fracture Propagation of Initial Fracturing
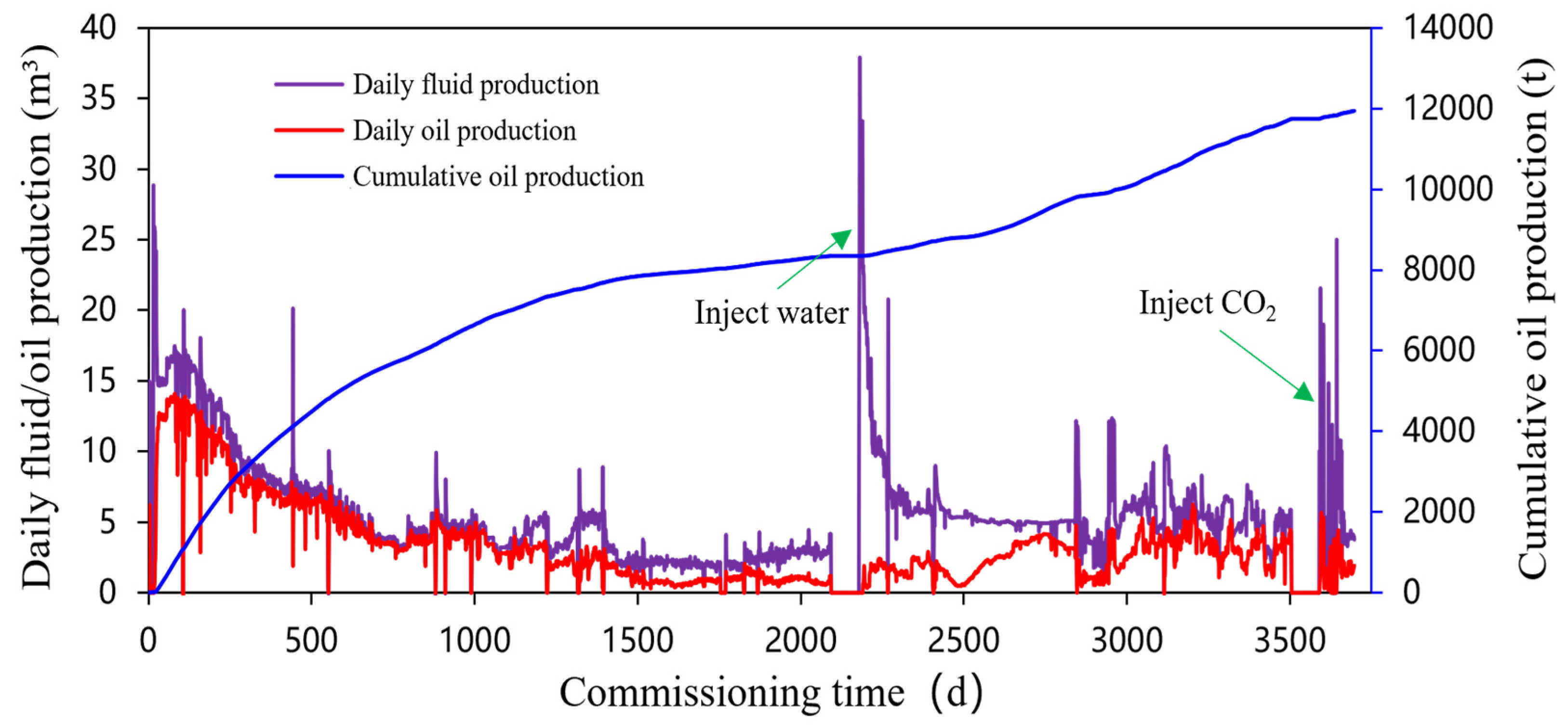
4.3.2. Production Dynamics Analysis of Oil Wells
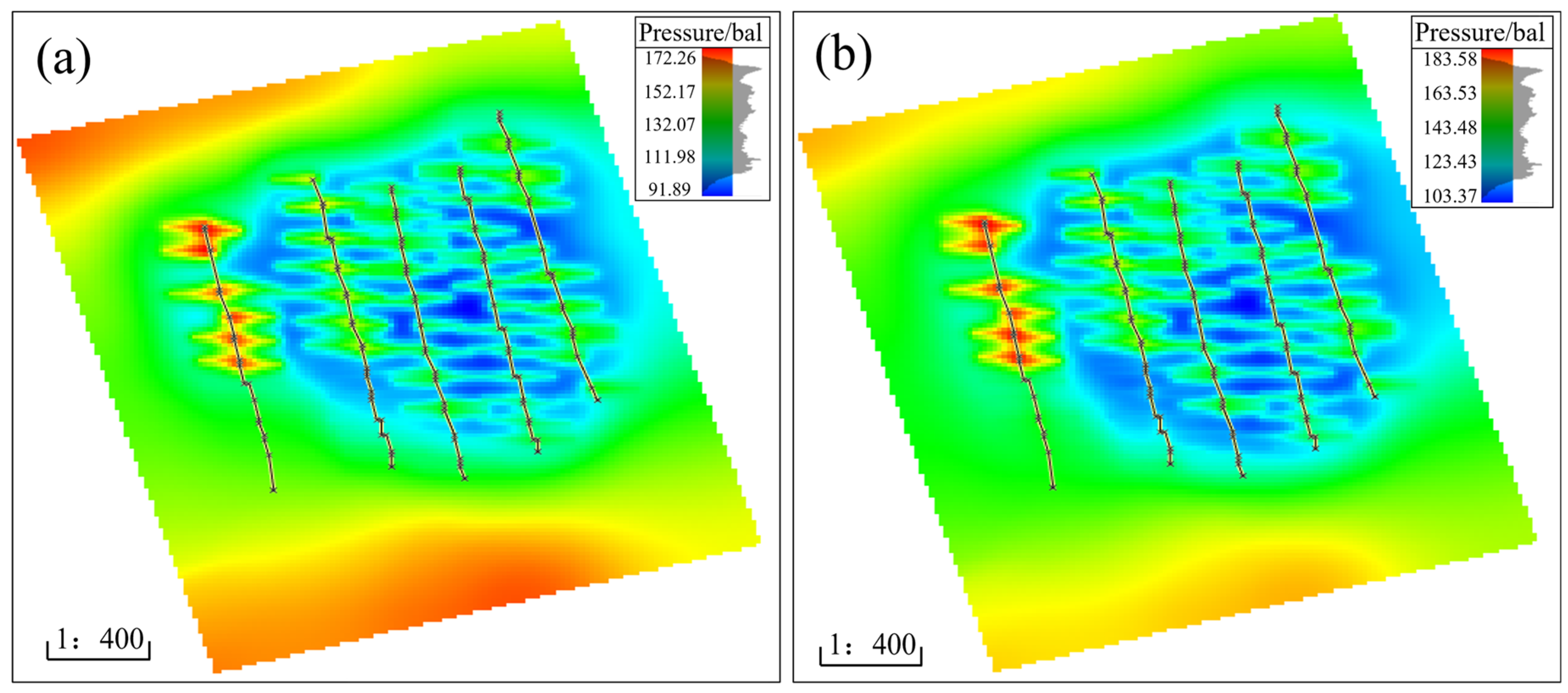
4.3.3. Residual Oil Distribution Pre-Refracturing
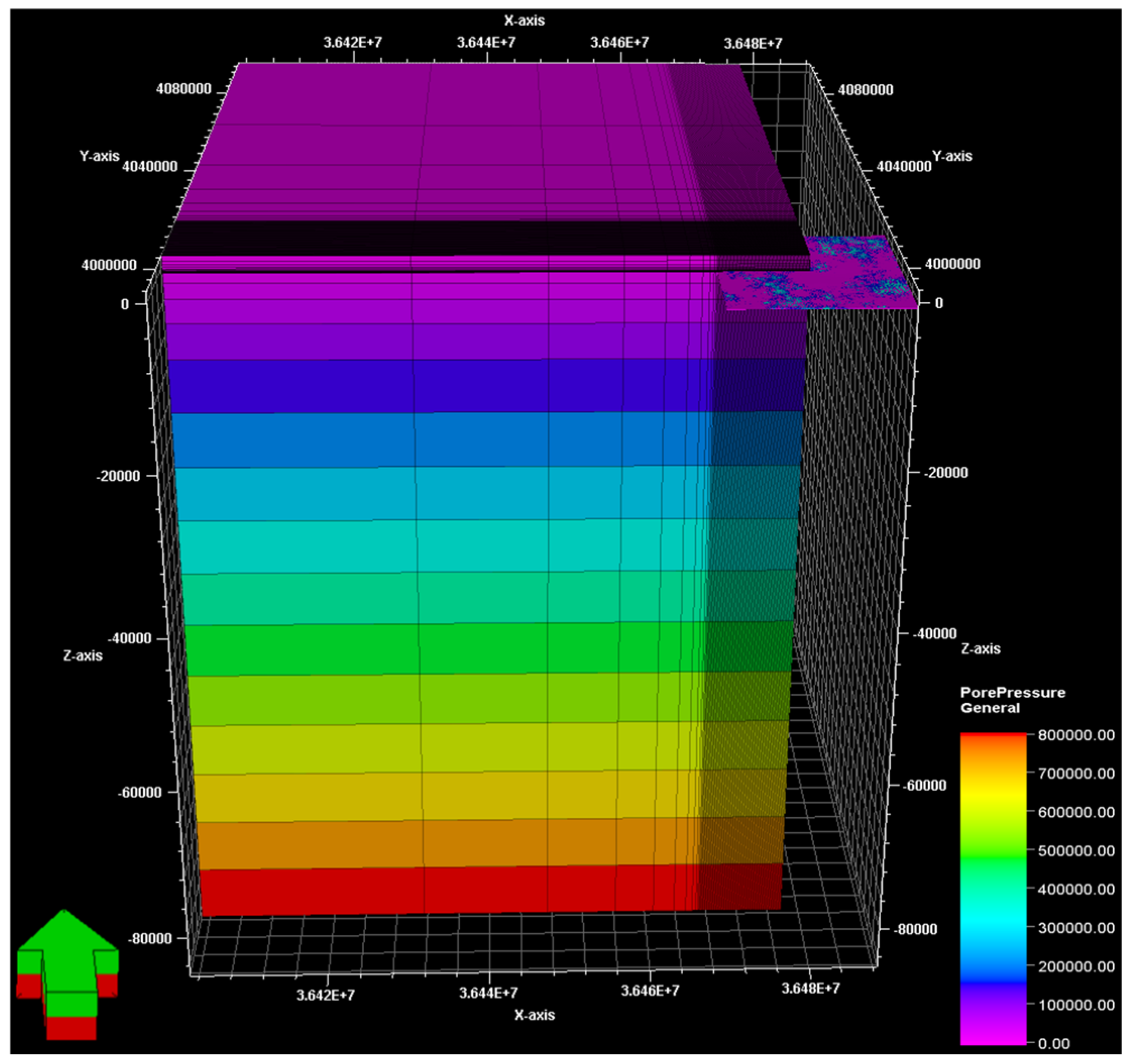
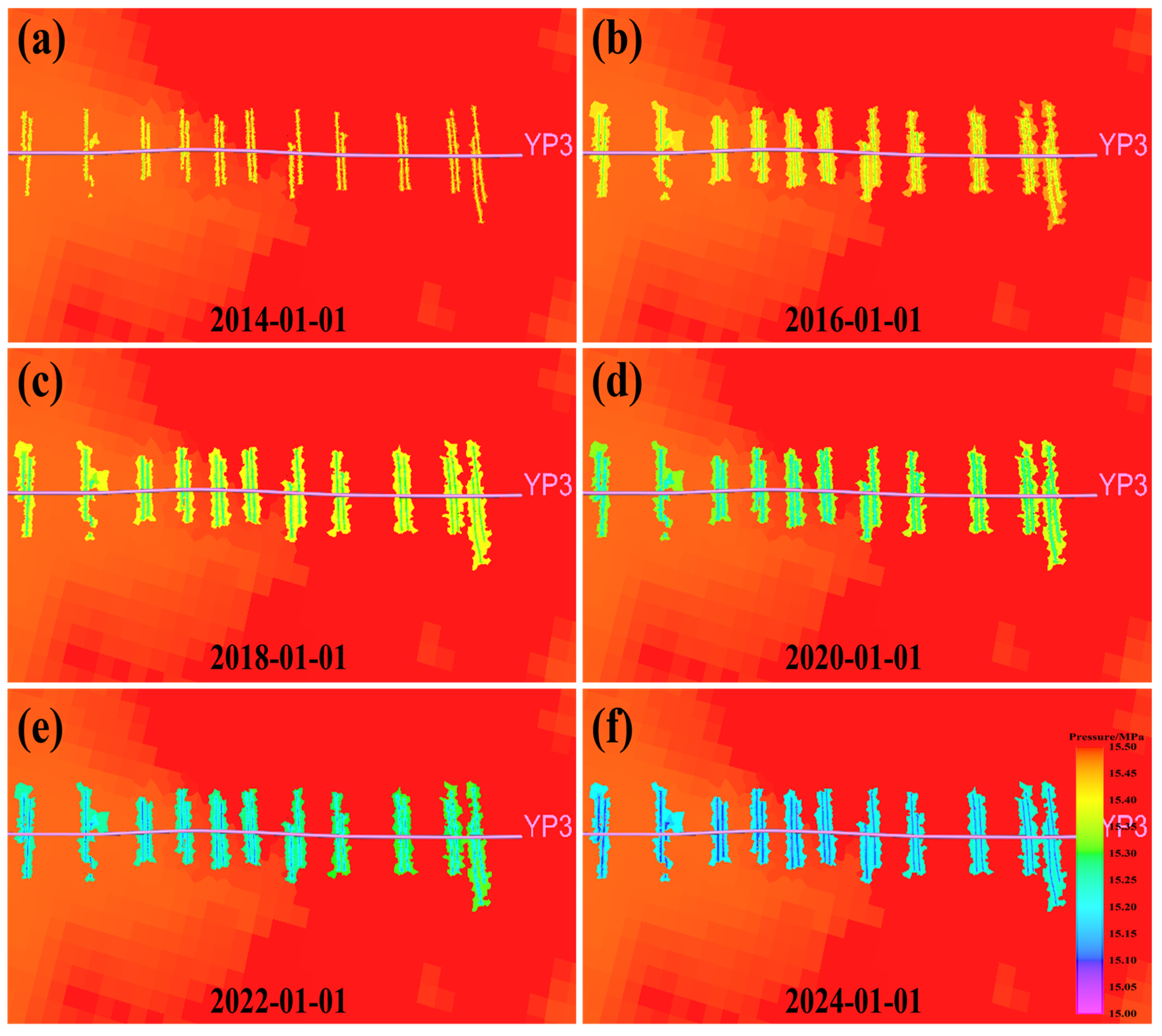
4.4. Four-Dimensional Coupled Seepage–Stress Field Simulation
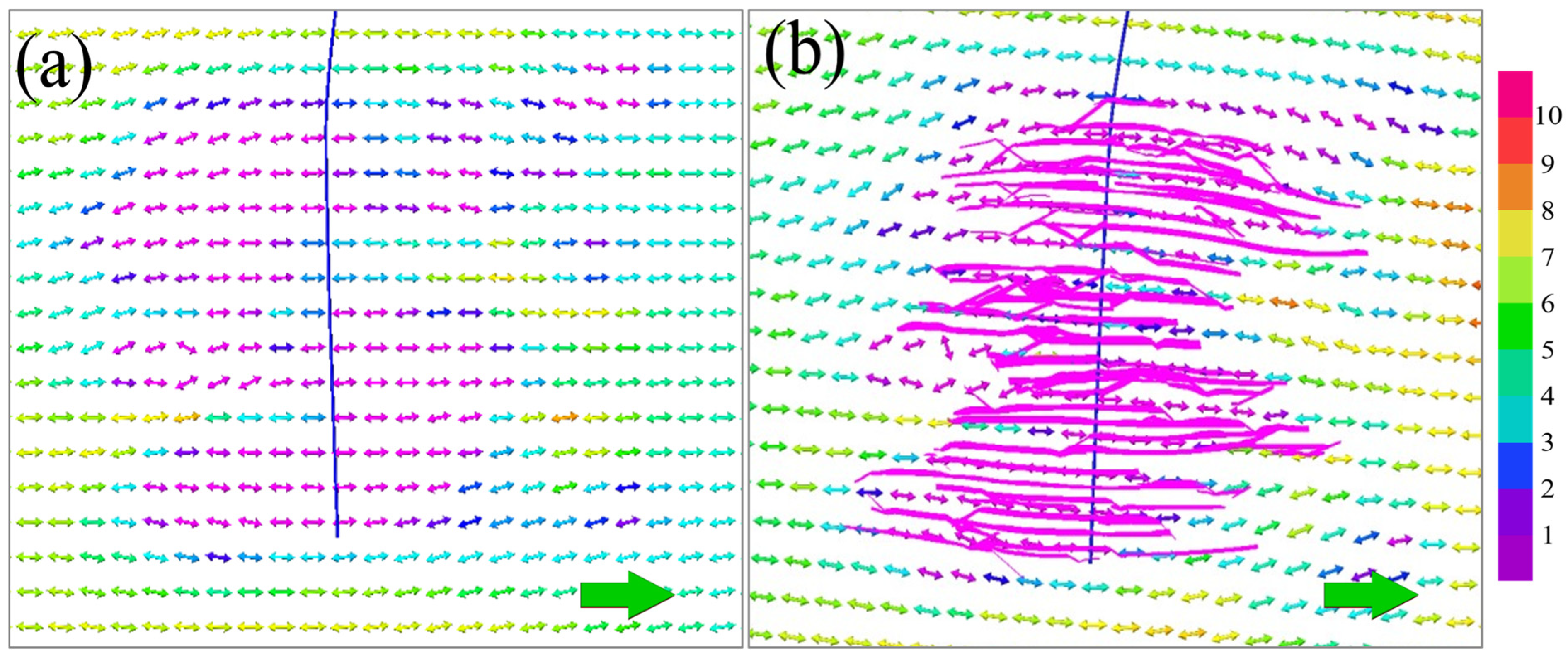
4.5. Fracture Propagation Simulation During Refracturing
4.5.1. Post-Refracturing Simulation
4.5.2. Analysis of Key Controlling Factors in Refracturing
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yang, D.; Moridis, G.J.; Blasingame, T.A. A Fully Coupled Multiphase Flow and Geomechanics Solver for Highly Heterogeneous Porous Media. J. Comput. Appl. Math. 2014, 270, 417–432. [Google Scholar] [CrossRef]
- Rutqvist, J.; Birkholzer, J.; Cappa, F.; Tsang, C.-F. Estimating Maximum Sustainable Injection Pressure during Geological Sequestration of CO2 Using Coupled Fluid Flow and Geomechanical Fault-Slip Analysis. Energy Convers. Manag. 2007, 48, 1798–1807. [Google Scholar] [CrossRef]
- Lewis, R.W.; Sukirman, Y. Finite Element Modelling for Simulating the Surface Subsidence above a Compacting Hydrocarbon Reservoir. Int. J. Numer Anal. Methods Geomech. 1994, 18, 619–639. [Google Scholar] [CrossRef]
- Kidambi, T.; Hanegaonkar, A.; Dutt, A.; Kumar, G.S. A Fully Coupled Flow and Geomechanics Model for a Tight Gas Reservoir: Implications for Compaction, Subsidence and Faulting. J. Nat. Gas Sci. Eng. 2017, 38, 257–271. [Google Scholar] [CrossRef]
- Settari, A.; Walters, D.A.; Behie, G.A. Reservoir Geomechanics: New Approach To Reservoir Engineering Analysis. In Proceedings of the Technical Meeting/Petroleum Conference of The South Saskatchewan Section, Regina, SK, Canada, 18–21 October 1999; PETSOC: Regina, SK, Canada, 1999; p. PETSOC-99-116. [Google Scholar]
- Zhang, D.; Zhang, L.; Tang, H.; Zhao, Y. Fully Coupled Fluid-Solid Productivity Numerical Simulation of Multistage Fractured Horizontal Well in Tight Oil Reservoirs. Pet. Explor. Dev. 2022, 49, 382–393. [Google Scholar] [CrossRef]
- Tutuncu, A.N.; Bui, B.T. A Coupled Geomechanics and Fluid Flow Model for Induced Seismicity Prediction in Oil and Gas Operations and Geothermal Applications. J. Nat. Gas Sci. Eng. 2016, 29, 110–124. [Google Scholar] [CrossRef]
- Pereira, L.C.; Sánchez, M.; Guimarães, L.J.D.N. Uncertainty Quantification for Reservoir Geomechanics. Geomech. Energy Environ. 2016, 8, 76–84. [Google Scholar] [CrossRef]
- Mikelić, A.; Wang, B.; Wheeler, M.F. Numerical Convergence Study of Iterative Coupling for Coupled Flow and Geomechanics. Comput. Geosci. 2014, 18, 325–341. [Google Scholar] [CrossRef]
- Elbel, J.L.; Mack, M.G. Refracturing: Observations and Theories. In Proceedings of the SPE Production Operations Symposium, Oklahoma City, OK, USA, 21–23 March 1993; SPE: Danbury, CT, USA, 1993; p. SPE-25464-MS. [Google Scholar]
- Zhang, G.Q.; Chen, M. Dynamic Fracture Propagation in Hydraulic Re-Fracturing. J. Pet. Sci. Eng. 2010, 70, 266–272. [Google Scholar] [CrossRef]
- Weng, X.; Siebrits, E. Effect of Production-Induced Stress Field on Refracture Propagation and Pressure Response. In Proceedings of the SPE Hydraulic Fracturing Technology Conference, College Station, TX, USA, 19–21 January 2007; SPE: Danbury, CT, USA, 2007; p. SPE-106043-MS. [Google Scholar]
- Wegner, J.; Hagemann, B.; Ganzer, L. Numerical Analysis of Parameters Affecting Hydraulic Fracture Re-Orientation in Tight Gas Reservoirs. In Clean Energy Systems in the Subsurface: Production, Storage and Conversion; Hou, M.Z., Xie, H., Were, P., Eds.; Springer Series in Geomechanics and Geoengineering; Springer: Berlin/Heidelberg, Germany, 2013; pp. 117–130. ISBN 978-3-642-37848-5. [Google Scholar]
- Shan, L.; Guo, B.; Weng, D.; Liu, Z.; Chu, H. Posteriori Assessment of Fracture Propagation in Refractured Vertical Oil Wells by Pressure Transient Analysis. J. Pet. Sci. Eng. 2018, 168, 8–16. [Google Scholar] [CrossRef]
- Roussel, N.P.; Florez, H.A.; Rodriguez, A.A. Hydraulic Fracture Propagation from Infill Horizontal Wells. In Proceedings of the SPE Annual Technical Conference and Exhibition, New Orleans, LA, USA, 30 September–2 October 2013; SPE: Danbury, CT, USA, 2013; p. D031S048R006.W. [Google Scholar]
- Wang, W.; Zhao, H.; Ji, L.; Wang, C.; Zhang, Z.; Xing, X. Research on the Turning Timing of Refracturing in the Hancheng Coal Seam. Saf. Coal Mines 2025, 56, 26–33. [Google Scholar]
- Bi, X.; Li, J.; Lian, C. A Comprehensive Logging Evaluation Method for Identifying High-Quality Shale Gas Reservoirs Based on Multifractal Spectra Analysis. Sci. Rep. 2024, 14, 26107. [Google Scholar] [CrossRef]
- Guo, Q.; Li, S.; Jin, Z.; Zhou, X.; Liu, C. Characteristics and Exploration Targets of Chang 7 Shale Oil in Triassic Yanchang Formation, Ordos Basin, NW China. Pet. Explor. Dev. 2023, 50, 878–893. [Google Scholar] [CrossRef]
- Wu, J.; Zhao, W.; Liu, Y.; Li, H.; Xiao, Y.; Yang, D.; Wang, J. Source-reservoir configuration and hydrocarbon enrichment laws of the Triassic Chang 7 shale in the Yan’an area of the Ordos Basin. Lithol. Reserv. 2025, 37, 170–181. [Google Scholar] [CrossRef]
- Lyu, Q.; Fu, J.; Luo, S.; Li, S.; Zhou, X.; Pu, Y.; Yan, H. Sedimentary characteristics and model of gravity flow channel-lobe complex in a depression lake basin: A case study of Chang 7 Member of Triassic Yanchang Formation in southwestern Ordos Basin, NW China. Pet. Explor. Dev. 2022, 49, 1323–1338. [Google Scholar] [CrossRef]
- Hui, G.; Chen, S.; He, Y.; Wang, H.; Gu, F. Machine Learning-Based Production Forecast for Shale Gas in Unconventional Reservoirs via Integration of Geological and Operational Factors. J. Nat. Gas Sci. Eng. 2021, 94, 104045. [Google Scholar] [CrossRef]
- Lei, Q.; He, Y.; Guo, Q.; Dang, Y.; Huang, T.; Liu, C. Technological Issues in Shale Oil Development Using Horizontal Wells in Ordos Basin, China. J. Nat. Gas Geosci. 2023, 8, 377–387. [Google Scholar] [CrossRef]
- Hui, G.; Chen, Z.; Wang, Y.; Zhang, D.; Gu, F. An Integrated Machine Learning-Based Approach to Identifying Controlling Factors of Unconventional Shale Productivity. Energy 2023, 266, 126512. [Google Scholar] [CrossRef]
- Kumar, K.R.; Honorio, H.; Chandra, D.; Lesueur, M.; Hajibeygi, H. Comprehensive review of geomechanics of underground hydrogen storage in depleted reservoirs and salt caverns. J. Energy Storage 2023, 73, 108912. [Google Scholar] [CrossRef]
- Fu, S.; Fu, J.; Niu, X.; Li, S.; Wu, Z.; Zhou, X.; Liu, J. Reservoir Formation Conditions and Key Technologies for Exploration and Development in Qingcheng Large Oilfield. Pet. Res. 2020, 5, 181–201. [Google Scholar] [CrossRef]
- Zheng, H.; Zhang, J.; Qi, Y. Geology and Geomechanics of Hydraulic Fracturing in the Marcellus Shale Gas Play and Their Potential Applications to the Fuling Shale Gas Development. Energy Geosci. 2020, 1, 36–46. [Google Scholar] [CrossRef]
- Wei, G.; Zheng, B.; Dong, J.; Yang, Y.; Yang, G.; Song, S.; Guo, S.; Qi, S. Research Progress of Three-Dimensional Engineering Geological Evaluation Modeling. Sustainability 2025, 17, 3739. [Google Scholar] [CrossRef]
- Saha, S.; Vishal, V.; Mahanta, B.; Pradhan, S.P. Geomechanical Model Construction to Resolve Field Stress Profile and Reservoir Rock Properties of Jurassic Hugin Formation, Volve Field, North Sea. Geomech. Geophys. Geo-Energy Geo-Resour. 2022, 8, 68. [Google Scholar] [CrossRef]
- Ranjbar, A.; Hassani, H.; Shahriar, K. 3D Geomechanical Modeling and Estimating the Compaction and Subsidence of Fahlian Reservoir Formation (X-Field in SW of Iran). Arab. J. Geosci. 2017, 10, 116. [Google Scholar] [CrossRef]
- Liu, Y.; Ma, X.; Zhang, X.; Guo, W.; Kang, L.; Yu, R.; Sun, Y. 3D Geological Model-Based Hydraulic Fracturing Parameters Optimization Using Geology–Engineering Integration of a Shale Gas Reservoir: A Case Study. Energy Rep. 2022, 8, 10048–10060. [Google Scholar] [CrossRef]
- Yang, J.; Liu, J.; Li, W.; Dai, J.; Xue, F.; Zhuang, X. A Multiscale Poroelastic Damage Model for Fracturing in Permeable Rocks. Int. J. Rock Mech. Min. Sci. 2024, 175, 105676. [Google Scholar] [CrossRef]
- Wan, J.; Durlofsky, L.J.; Hughes, T.J.R.; Aziz, K. Stabilized Finite Element Methods for Coupled Geomechanics–Reservoir Flow Simulations. In Proceedings of the SPE Reservoir Simulation Symposium, Houston, TX, USA, 3–5 February 2003; SPE: Danbury, CT, USA, 2003; p. SPE-79694-MS. [Google Scholar]
- Lei, Q.; Weng, D.; Guan, B.; Shi, J.; Cai, B.; He, C.; Sun, Q.; Huang, R. Shale Oil and Gas Exploitation in China: Technical Comparison with US and Development Suggestions. Pet. Explor. Dev. 2023, 50, 944–954. [Google Scholar] [CrossRef]
- Bao, P.; Hui, G.; Hu, Y.; Song, R.; Chen, Z.; Zhang, K.; Pi, Z.; Li, Y.; Ge, C.; Yao, F.; et al. Comprehensive Characterization of Hydraulic Fracture Propagations and Prevention of Pre-Existing Fault Failure in Duvernay Shale Reservoirs. Eng. Fail. Anal. 2025, 173, 109461. [Google Scholar] [CrossRef]
- Ali, A.M.; Waheed, A.; Shahbaz, M.; Mirani, A.A.; Shahzad, K.; Al-Zahrani, A.A.; Nawaz, A.M.; Mahpudz, A.B. Synergistic Evaluation of Co-Torrefaction Performance of Rice Husk and Coffee Bean Ground Blends for Biosolid Production for Industrial Fuel Sustainability. Fuel 2023, 343, 127891. [Google Scholar] [CrossRef]
- Weng, X.; Kresse, O.; Chuprakov, D.; Cohen, C.-E.; Prioul, R.; Ganguly, U. Applying Complex Fracture Model and Integrated Workflow in Unconventional Reservoirs. J. Pet. Sci. Eng. 2014, 124, 468–483. [Google Scholar] [CrossRef]
- Sun, W.; Fish, J.; Leng, Z.; Ni, P. PD-FEM Chemo-Thermo-Mechanical Coupled Model for Simulation of Early-Age Cracks in Cement-Based Materials. Comput. Methods Appl. Mech. Eng. 2023, 412, 116078. [Google Scholar] [CrossRef]
- Al-Kindi, I.; Babadagli, T. Effect of Wettability on Vaporization of Hydrocarbon Solvents in Capillary Media. SPE J. 2021, 26, 3040–3053. [Google Scholar] [CrossRef]
- Dendumrongsup, N.; Tartakovsky, D.M. Exponential Time Differencing for Problems without Natural Stiffness Separation. Comput. Geosci. 2021, 25, 1667–1679. [Google Scholar] [CrossRef]
- Pi, Z.; Hui, G.; Wang, Y.; Chen, Z.; Li, J.; Qin, G.; Meng, F.; Song, Y.; Yao, F.; Bao, P.; et al. Coupled 4D Flow-Geomechanics Simulation to Characterize Dynamic Fracture Propagation in Tight Sandstone Reservoirs. ACS Omega 2025, 10, 1735–1747. [Google Scholar] [CrossRef]
- Wang, F.; Wu, M.; Wang, Y.; Sun, W.; Chen, G.; Feng, Y.; Shi, X.; Zhao, Z.; Liu, Y.; Lu, S. Prediction of Influencing Factors on Estimated Ultimate Recovery of Deep Coalbed Methane: A Case Study of the Daning–Jixian Block. Processes 2024, 13, 31. [Google Scholar] [CrossRef]
- Voltolini, M. In-Situ 4D Visualization and Analysis of Temperature-Driven Creep in an Oil Shale Propped Fracture. J. Pet. Sci. Eng. 2021, 200, 108375. [Google Scholar] [CrossRef]
- Ma, P.; Tang, S. Simulation of Key Influencing Factors of Hydraulic Fracturing Fracture Propagation in a Shale Reservoir Based on the Displacement Discontinuity Method (DDM). Processes 2024, 12, 1000. [Google Scholar] [CrossRef]
- Lu, C.; Jiang, H.; Qu, S.; Zhang, M.; He, J.; Xiao, K.; Yang, H.; Yang, J.; Li, J. Hydraulic Fracturing Design for Shale Oils Based on Sweet Spot Mapping: A Case Study of the Jimusar Formation in China. J. Pet. Sci. Eng. 2022, 214, 110568. [Google Scholar] [CrossRef]
- Farah, N.; Delorme, M. Unified Fracture Network Model (UFNM) for Unconventional Reservoirs Simulation. J. Pet. Sci. Eng. 2020, 195, 107874. [Google Scholar] [CrossRef]
- Zhu, H.; Song, Y.; Lei, Z.; Tang, X. 4D-Stress Evolution of Tight Sandstone Reservoir during Horizontal Wells Injection and Production: A Case Study of Yuan 284 Block, Ordos Basin, NW China. Pet. Explor. Dev. 2022, 49, 156–169. [Google Scholar] [CrossRef]
- Wang, A.; Chen, Y.; Wei, J.; Li, J.; Zhou, X. Experimental Study on the Mechanism of Five Point Pattern Refracturing for Vertical & Horizontal Wells in Low Permeability and Tight Oil Reservoirs. Energy 2023, 272, 127027. [Google Scholar] [CrossRef]
- Liang, L.; Meng, S.; Tao, J.; Gong, C.; Shen, M.; Jin, X.; Fu, H. Displacement Mechanisms of Modified Carbon Black Nanofluid as a Novel Flooding System in Ultralow-Permeability Reservoirs. SPE J. 2025, 30, 2909–2922. [Google Scholar] [CrossRef]
- Hui, G.; Chen, Z.; Schultz, R.; Chen, S.; Song, Z.; Zhang, Z.; Song, Y.; Wang, H.; Wang, M.; Gu, F. Intricate Unconventional Fracture Networks Provide Fluid Diffusion Pathways to Reactivate Pre-Existing Faults in Unconventional Reservoirs. Energy 2023, 282, 128803. [Google Scholar] [CrossRef]
- Hui, G.; Chen, S.; Gu, F. Strike–Slip Fault Reactivation Triggered by Hydraulic-Natural Fracture Propagation during Fracturing Stimulations near Clark Lake, Alberta. Energy Fuels 2024, 38, 18547–18555. [Google Scholar] [CrossRef]
- He, S.; Huang, T.; Bai, X.; Ren, J.; Meng, K.; Yu, H. Dramatically Enhancing Oil Recovery via High-Efficient Re-Fracturing Horizontal Wells in Ultra-Low Permeability Reservoirs: A Case Study in HQ Oilfield, Ordos Basin, China. Processes 2024, 12, 338. [Google Scholar] [CrossRef]
- Guo, J.; Lu, Q.; He, Y. Key Issues and Explorations in Shale Gas Fracturing. Nat. Gas Ind. B 2023, 10, 183–197. [Google Scholar] [CrossRef]
- Ren, J.; Bai, X.; Tang, S.; Chen, J.; Dong, Q.; Yu, J. Analysis of interwell interference and optimization of well spacing for tight oil based on geologic-engineering integration. Bull. Geol. Sci. Technol. 2024, 43, 271–280. [Google Scholar] [CrossRef]
- Yin, H.; Zhong, G.; Liu, J.; Wu, Y. Quantitative Characterization of Surfactant Displacement Efficiency by NMR—Take the Tight Oil of Chang 8 Member of Yanchang Formation in Fuxian Area, Ordos Basin, as an Example. Energies 2024, 17, 5450. [Google Scholar] [CrossRef]
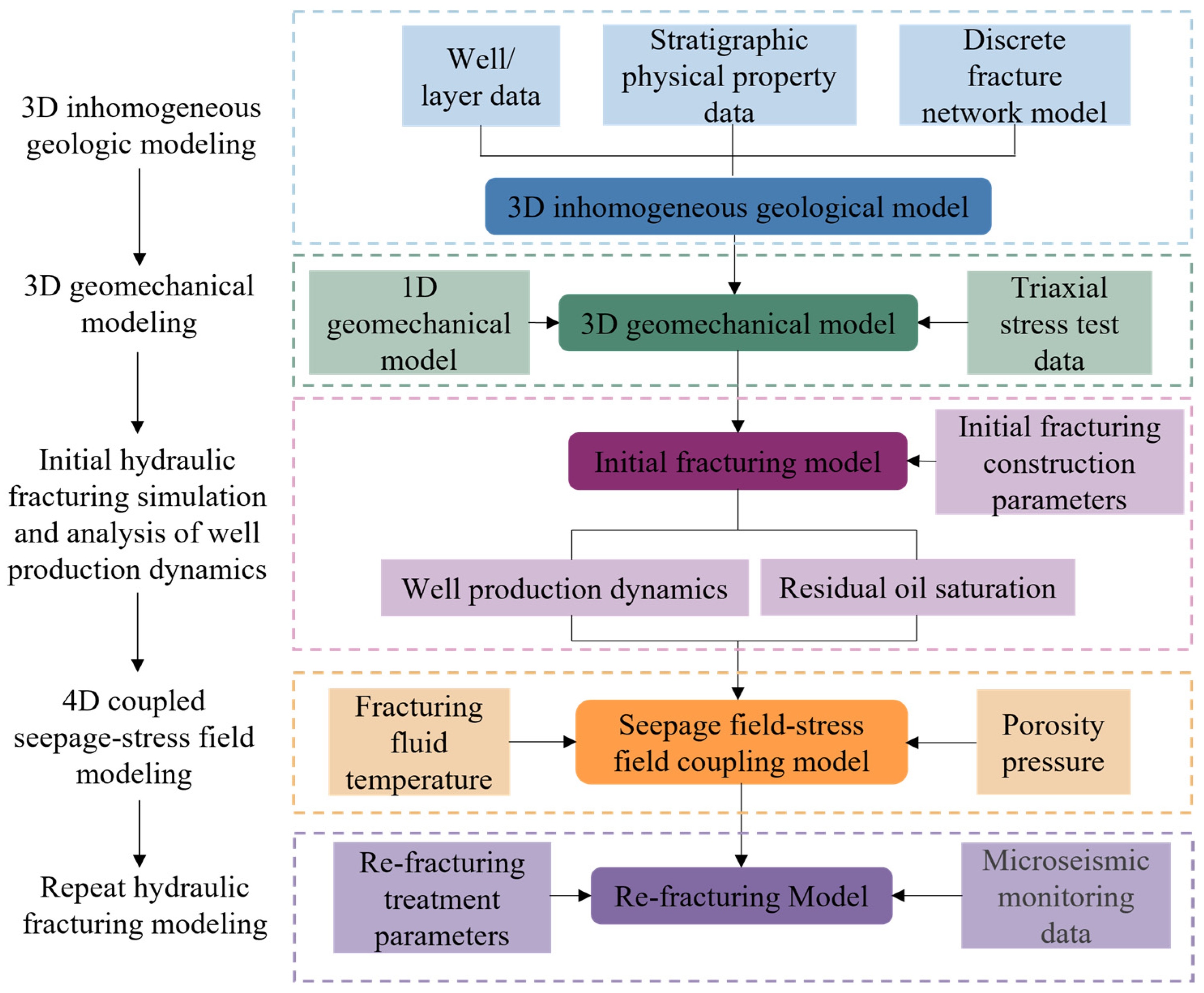

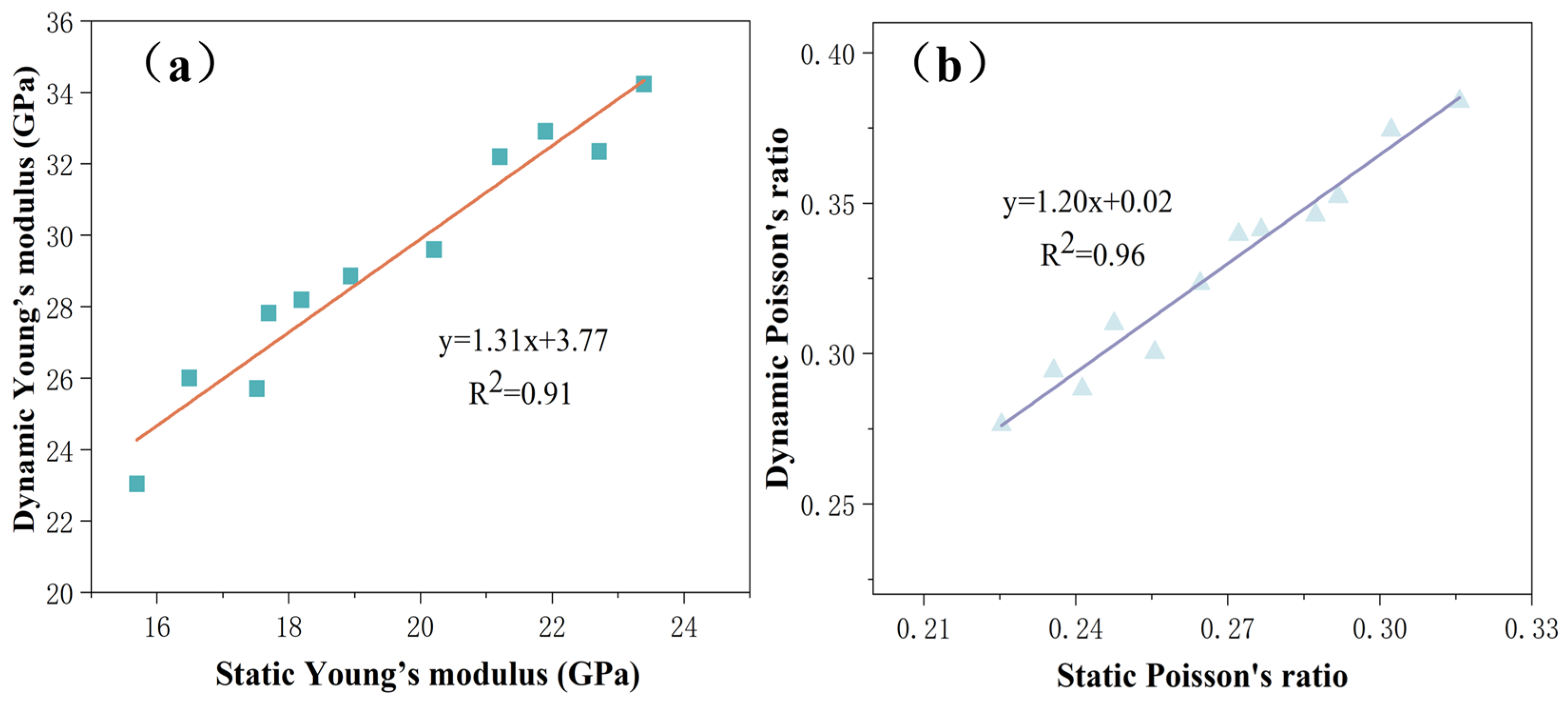






| Initial Fracturing Construction Parameter Design | ||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Construction parameters | stage 1 | stage 2 | stage 3 | stage 4 | stage 5 | stage 6 | stage 7 | stage 8 | stage 9 | stage 10 | stage 11 | |||||||||||
| Tubing | Casing | Tubing | Casing | Tubing | Casing | Tubing | Casing | Tubing | Casing | Tubing | Casing | Tubing | Casing | Tubing | Casing | Tubing | Casing | Tubing | Casing | Tubing | Casing | |
| Treatment pressure/MPa | 44.8 | 37.8 | 39.3 | 34.5 | 53.8 | 34.6 | 45.4 | 35.8 | 48.7 | 35.5 | 48.2 | 31.6 | 48.1 | 30.7 | 44.6 | 30.1 | 45 | 30.9 | 45.4 | 24.9 | 37.9 | 25.1 |
| Sand volume/m3 | 45.1 | 43.7 | 43.9 | 43.4 | 43.7 | 43.5 | 43.7 | 44.5 | 44.3 | 44 | 43.6 | |||||||||||
| Sand Concentration kg/m3 | 155.1 | 165 | 169.2 | 166.4 | 163.8 | 160.7 | 165.4 | 170.4 | 167 | 160.7 | 164.4 | |||||||||||
| Rate m3/min | 2 | 4 | 1.8 | 4.2 | 1.8 | 4.2 | 1.8 | 4.2 | 1.8 | 4.2 | 1.8 | 4.2 | 1.8 | 4.2 | 1.7 | 4.2 | 1.8 | 4.2 | 2 | 4 | 2 | 4 |
| Pad/m3 | 82.1 | 141 | 42.9 | 84.1 | 62.8 | 112.1 | 44.1 | 84.3 | 45.7 | 84.1 | 45.3 | 82.4 | 47.5 | 80.9 | 51.7 | 100.8 | 62.3 | 123.7 | 51 | 88.1 | 54.6 | 79.6 |
| slurry/m3 | 160.7 | 320.2 | 124.5 | 288.2 | 120.6 | 283.4 | 122.8 | 284.1 | 126.4 | 289.8 | 127.7 | 292.1 | 124.4 | 286.8 | 117.9 | 289.8 | 123.3 | 289.1 | 143.3 | 281.7 | 140.2 | 273.6 |
| Flush/m3 | 15.7 | 30.7 | 16.2 | 35.3 | 15.4 | 35.4 | 33.8 | 15.4 | 13.6 | 30.5 | 12.9 | 29.3 | 13.5 | 30.2 | 11.1 | 28.1 | 15.2 | 34.5 | 13.5 | 25.5 | 12 | 23.7 |
| Total fluid/m3 | 259.2 | 466.5 | 183.6 | 380.2 | 198.8 | 403.5 | 200.7 | 357.4 | 185.7 | 377.9 | 185.9 | 376.4 | 185.4 | 371.4 | 180.7 | 391.3 | 200.8 | 420.3 | 207.8 | 368.5 | 206.8 | 350.7 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liang, H.; Bao, P.; Hui, G.; Ma, Z.; Yan, X.; Bai, X.; Ren, J.; Pi, Z.; Li, Y.; Ge, C.; et al. Simulation Study of Refracturing of Shale Oil Horizontal Wells Under the Effect of Multi-Field Reconfiguration. Processes 2025, 13, 1915. https://doi.org/10.3390/pr13061915
Liang H, Bao P, Hui G, Ma Z, Yan X, Bai X, Ren J, Pi Z, Li Y, Ge C, et al. Simulation Study of Refracturing of Shale Oil Horizontal Wells Under the Effect of Multi-Field Reconfiguration. Processes. 2025; 13(6):1915. https://doi.org/10.3390/pr13061915
Chicago/Turabian StyleLiang, Hongbo, Penghu Bao, Gang Hui, Zeyuan Ma, Xuemei Yan, Xiaohu Bai, Jiawei Ren, Zhiyang Pi, Ye Li, Chenqi Ge, and et al. 2025. "Simulation Study of Refracturing of Shale Oil Horizontal Wells Under the Effect of Multi-Field Reconfiguration" Processes 13, no. 6: 1915. https://doi.org/10.3390/pr13061915
APA StyleLiang, H., Bao, P., Hui, G., Ma, Z., Yan, X., Bai, X., Ren, J., Pi, Z., Li, Y., Ge, C., Zhang, Y., Yang, X., Zhang, Y., Lu, Y., Wu, D., & Gu, F. (2025). Simulation Study of Refracturing of Shale Oil Horizontal Wells Under the Effect of Multi-Field Reconfiguration. Processes, 13(6), 1915. https://doi.org/10.3390/pr13061915






