Singular Perturbation Decoupling and Composite Control Scheme for Hydraulically Driven Flexible Robotic Arms
Abstract
1. Introduction
2. Dynamics Modeling of HDFRAs
2.1. Mechanical Subsystem Dynamics Modeling
2.2. Hydraulic Subsystem Modeling
3. The Singular Perturbation Decoupling of HDFRA System
3.1. First-Order Singular Perturbation Decoupling
3.2. Second-Order Singular Perturbation Decoupling
4. Controller Design
4.1. AFTSM-ADRC Design for Second-Order Systems
4.1.1. Design of Tracking Differentiator
4.1.2. Design of the BESO
4.1.3. Design of Adaptive Reaching Law
4.1.4. Design of AFTSM-ADRC
4.2. SMO-ISMCC Design for First-Order Systems
4.2.1. Design of Sliding Mode Observer
4.2.2. Design of Integral Sliding Mode Controller
4.3. Composite Controller (CC)
- (1)
- The tracking errors of SRS and SFS converge to a neighborhood of the equilibrium point within finite time;
- (2)
- FHS satisfies the input-to-state stability (ISS) property, with its states constrained by the boundedness of external inputs;
- (3)
- The closed-loop system is globally asymptotically stable. The composite control strategy collaboratively suppresses uncertainties through fast/slow subsystem coordination, ensuring robust stability, dynamic convergence, and disturbance rejection capability.
5. Simulations
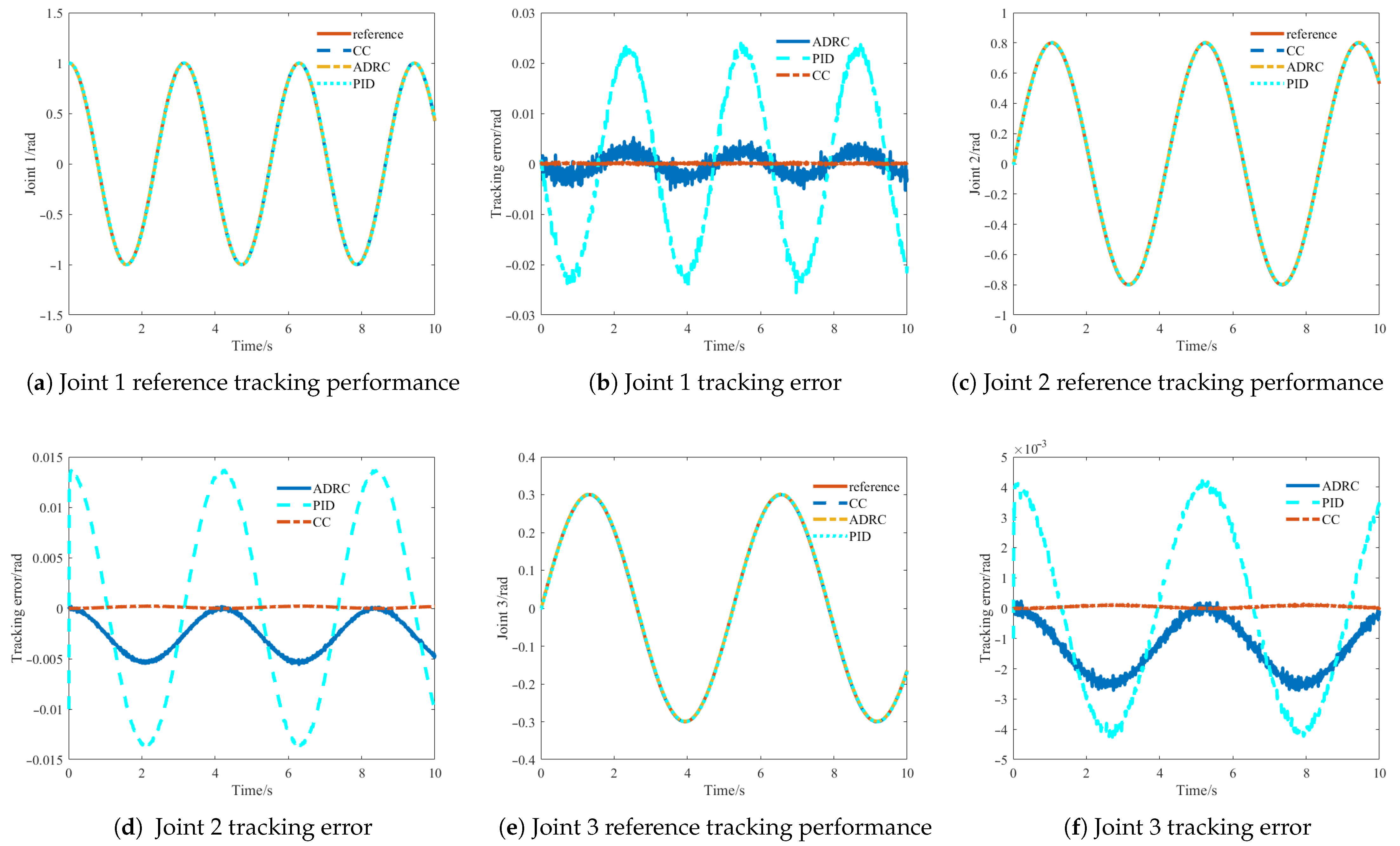
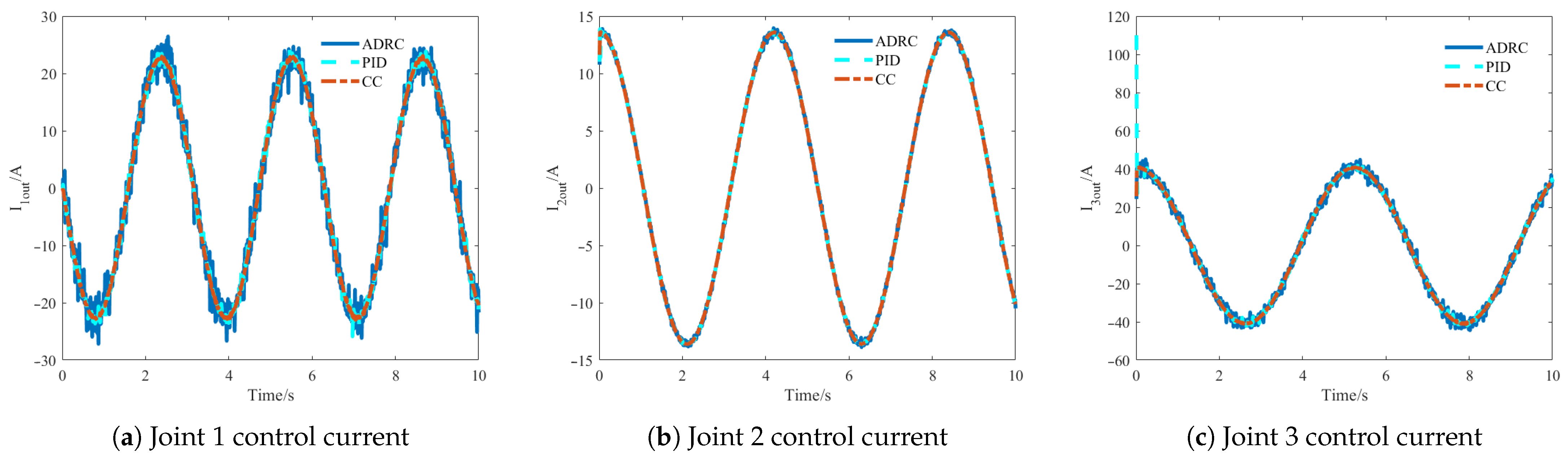
5.1. Trajectory Tracking Comparison Experiment Without Considering Lumped Uncertainties
5.2. Trajectory Tracking Comparison Experiment Considering Lumped Uncertainties
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Liu, Z.; Sun, J.; Yue, D.; Zuo, X.; Gao, H.; Feng, K. A review on integral evolution of electro-hydraulic actuation in three momentous domains: Aerospace, engineering machinery, and robotics. In Proceedings of the Fourth International Conference on Mechanical Engineering, Intelligent Manufacturing, and Automation Technology (MEMAT 2023), Guilin, China, 20–22 October 2023; Volume 13082, pp. 141–159. [Google Scholar]
- Kumar, S.B.; Hossem, M.S.; Sayed, A. A Comprehensive Review of Hydraulic Systems in Aerospace and Construction Engineering. Control Syst. Optim. Lett. 2024, 2, 266–273. [Google Scholar] [CrossRef]
- Vitanov, I.; Farkhatdinov, I.; Denoun, B.; Palermo, F.; Otaran, A.; Brown, J.; Omarali, B.; Abrar, T.; Hansard, M.; Oh, C.; et al. A suite of robotic solutions for nuclear waste decommissioning. Robotics 2021, 10, 112. [Google Scholar] [CrossRef]
- Wei, X.; Ye, J.; Xu, J.; Tang, Z. Adaptive dynamic programming-based cross-scale control of a hydraulic-driven flexible robotic manipulator. Appl. Sci. 2023, 13, 2890. [Google Scholar] [CrossRef]
- Chang, W.; Li, Y.; Tong, S. Adaptive fuzzy backstepping tracking control for flexible robotic manipulator. IEEE/CAA J. Autom. Sin. 2018, 8, 1923–1930. [Google Scholar] [CrossRef]
- Sun, Y.; Wan, Y.; Ma, H.; Liang, X. Real-time force control of hydraulic manipulator arms without force or pressure feedback using a nonlinear algorithm. IEEE Robot. Autom. Lett. 2023, 8, 7146–7153. [Google Scholar] [CrossRef]
- Peng, J.; Xu, W.; Hu, Z.; Liang, B.; Wu, A. Modeling and analysis of the multiple dynamic coupling effects of a dual-arm space robotic system. Robotica 2020, 38, 2060–2079. [Google Scholar] [CrossRef]
- Zhang, F.; Yuan, Z. The study of coupling dynamics modeling and characteristic analysis for flexible robots with nonlinear and frictional joints. Arab. J. Sci. Eng. 2022, 47, 15347–15363. [Google Scholar] [CrossRef]
- Ghorbani, H.; Tarvirdizadeh, B.; Alipour, K.; Hadi, A. Near-time-optimal motion control for flexible-link systems using absolute nodal coordinates formulation. Mech. Mach. Theory 2019, 140, 686–710. [Google Scholar] [CrossRef]
- Wang, B.L.; Cai, Y.; Song, J.C.; Sepehri, N. LuGre model–based robust adaptive control for a pump-controlled hydraulic actuator experiencing friction. Trans. Inst. Meas. Control 2024, 46, 1845–1857. [Google Scholar] [CrossRef]
- Kelkar, R.; Santhya, M.; Kanchan, M.; Powar, O.S. Bond Graph Modeling and Simulation of Hybrid Piezo-Flexural-Hydraulic Actuator. Eng. Proc. 2024, 59, 202. [Google Scholar]
- Xie, Q.; Wang, T.; Zhu, S. Simplified dynamical model and experimental verification of an underwater hydraulic soft robotic arm. Smart Mater. Struct. 2022, 31, 075011. [Google Scholar] [CrossRef]
- Mehrez, M.W.; El-Badawy, A.A. Effect of the joint inertia on selection of under-actuated control algorithm for flexible-link manipulators. Mech. Mach. Theory 2010, 45, 967–980. [Google Scholar] [CrossRef]
- Xu, B.; Yuan, Y. Two performance enhanced control of flexible-link manipulator with system uncertainty and disturbances. Sci. China Inf. Sci. 2017, 60, 050202. [Google Scholar] [CrossRef]
- Wang, C.; Quan, L.; Zhang, S.; Meng, H.; Lan, Y. Reduced-order model based active disturbance rejection control of hydraulic servo system with singular value perturbation theory. ISA Trans. 2017, 67, 455–465. [Google Scholar] [CrossRef]
- Yao, J.; Deng, W.; Jiao, Z. RISE-based adaptive control of hydraulic systems with asymptotic tracking. IEEE Trans. Autom. Sci. Eng. 2015, 14, 1524–1531. [Google Scholar] [CrossRef]
- Yao, J.; Deng, W. Active disturbance rejection adaptive control of hydraulic servo systems. IEEE Trans. Ind. Electron. 2017, 64, 8023–8032. [Google Scholar] [CrossRef]
- Deng, W.; Yao, J. Asymptotic tracking control of mechanical servosystems with mismatched uncertainties. IEEE/ASME Trans. Mechatronics 2020, 26, 2204–2214. [Google Scholar] [CrossRef]
- Won, D.; Kim, W.; Tomizuka, M. High-gain-observer-based integral sliding mode control for position tracking of electrohydraulic servo systems. IEEE/ASME Trans. Mechatronics 2017, 22, 2695–2704. [Google Scholar] [CrossRef]
- Barhaghtalab, M.H.; Meigoli, V.; Haghighi, M.R.G.; Nayeri, S.A.; Ebrahimi, A. Dynamic analysis, simulation, and control of a 6-DOF IRB-120 robot manipulator using sliding mode control and boundary layer method. Methods 2018, 11, 12. [Google Scholar] [CrossRef]
- Ma, T.; Guo, X.; Su, G.; Deng, H.; Yang, T. Research on synchronous control of active disturbance rejection position of multiple hydraulic cylinders of digging-anchor-support robot. Sensors 2023, 23, 4092. [Google Scholar] [CrossRef]
- Chen, Z.; Zhou, S.; Shen, C.; Lyu, L.; Zhang, J.; Yao, B. Observer-based adaptive robust precision motion control of a multi-joint hydraulic manipulator. IEEE/CAA J. Autom. Sin. 2024, 11, 1213–1226. [Google Scholar] [CrossRef]
- Wang, B.L.; Cai, Y.; Song, J.C.; Liang, Q.K. A Singular Perturbation Theory-Based Composite Control Design for a Pump-Controlled Hydraulic Actuator with Position Tracking Error Constraint. Actuators 2023, 12, 265. [Google Scholar] [CrossRef]
- Su, Y.; Müller, P.C.; Zheng, C. Global asymptotic saturated PID control for robot manipulators. IEEE Trans. Control Syst. Technol. 2009, 18, 1280–1288. [Google Scholar] [CrossRef]
- Di Gregorio, R. A geometric and analytic technique for studying multi-DOF planar mechanisms’ dynamics. Mech. Mach. Theory 2022, 176, 104975. [Google Scholar] [CrossRef]
- Kong, X.; Cai, B.; Liu, Y.; Zhu, H.; Liu, Y.; Shao, H.; Yang, C.; Li, H.; Mo, T. Optimal sensor placement methodology of hydraulic control system for fault diagnosis. Mech. Syst. Signal Process. 2022, 174, 109069. [Google Scholar] [CrossRef]
- Zhou, L.; Li, Z.; Yang, H.; Tan, C.; Fu, Y. Adaptive Terminal Sliding Mode Control for High-Speed EMU: A MIMO Data-Driven Approach. IEEE Trans. Autom. Sci. Eng. 2025, 22, 1970–1983. [Google Scholar] [CrossRef]
- Wu, L.; Liu, J.; Vazquez, S.; Mazumder, S.K. Sliding mode control in power converters and drives: A review. IEEE/CAA J. Autom. Sin. 2021, 9, 392–406. [Google Scholar] [CrossRef]
- Huang, X.; Lin, W.; Yang, B. Global finite-time stabilization of a class of uncertain nonlinear systems. Automatica 2005, 41, 881–888. [Google Scholar] [CrossRef]
- Wang, Q.; Lu, G.; Zhao, M.; Sun, J. Finite-time stability and stabilization of discrete-time hybrid systems. Syst. Control Lett. 2024, 189, 105832. [Google Scholar] [CrossRef]
- Zhou, L.; Li, Z.-Q.; Yang, H.; Tan, C. Integral predictive sliding mode control for high-speed trains: A dynamic linearization and input constraint-based data-driven scheme. Control. Eng. Pract. 2025, 154, 106139. [Google Scholar] [CrossRef]
- Xu, J.; Sui, Z.; Wang, W.; Xu, F. An adaptive discrete integral terminal sliding mode control method for a Two-Joint manipulator. Processes 2024, 12, 1106. [Google Scholar] [CrossRef]
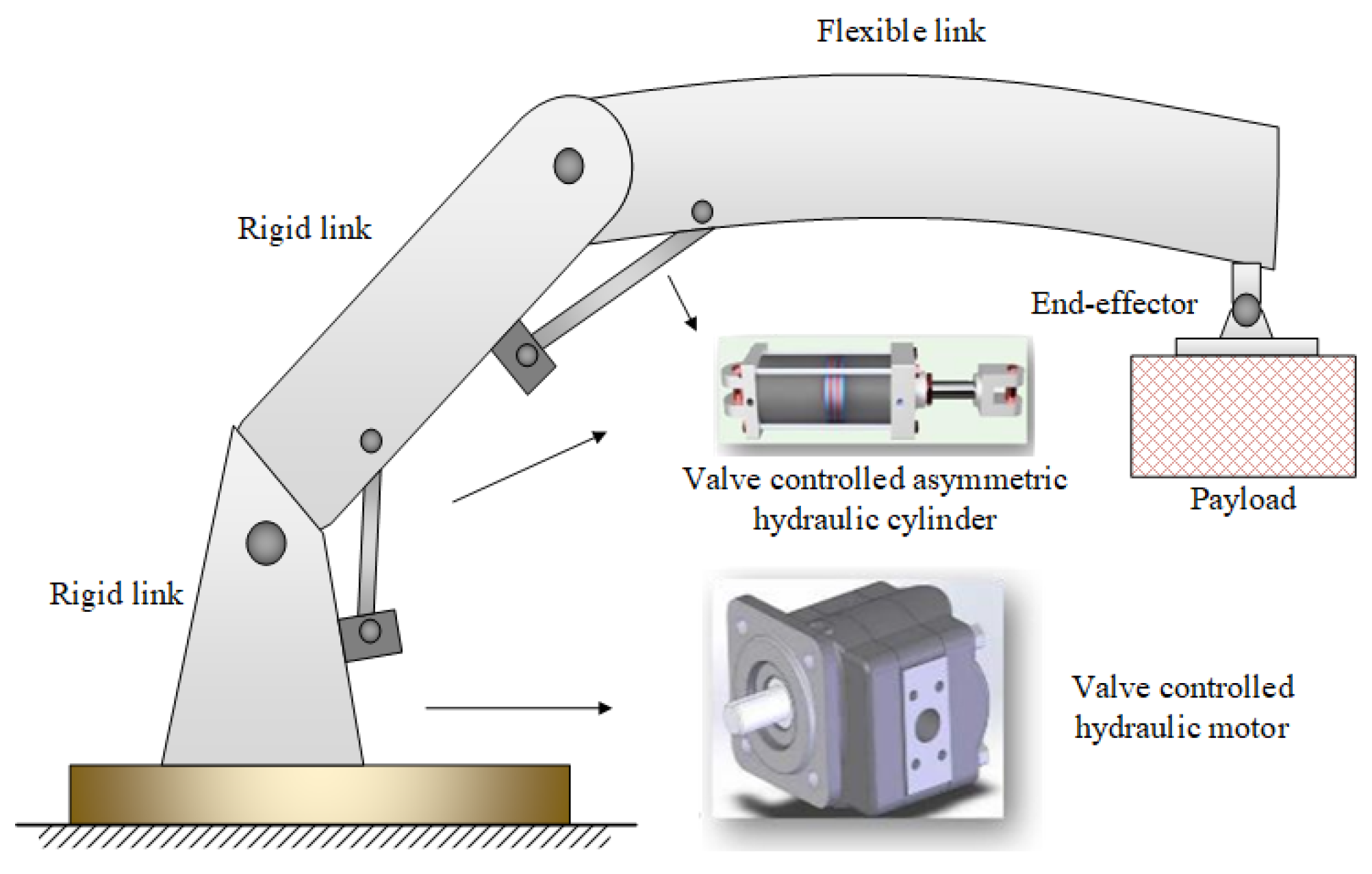

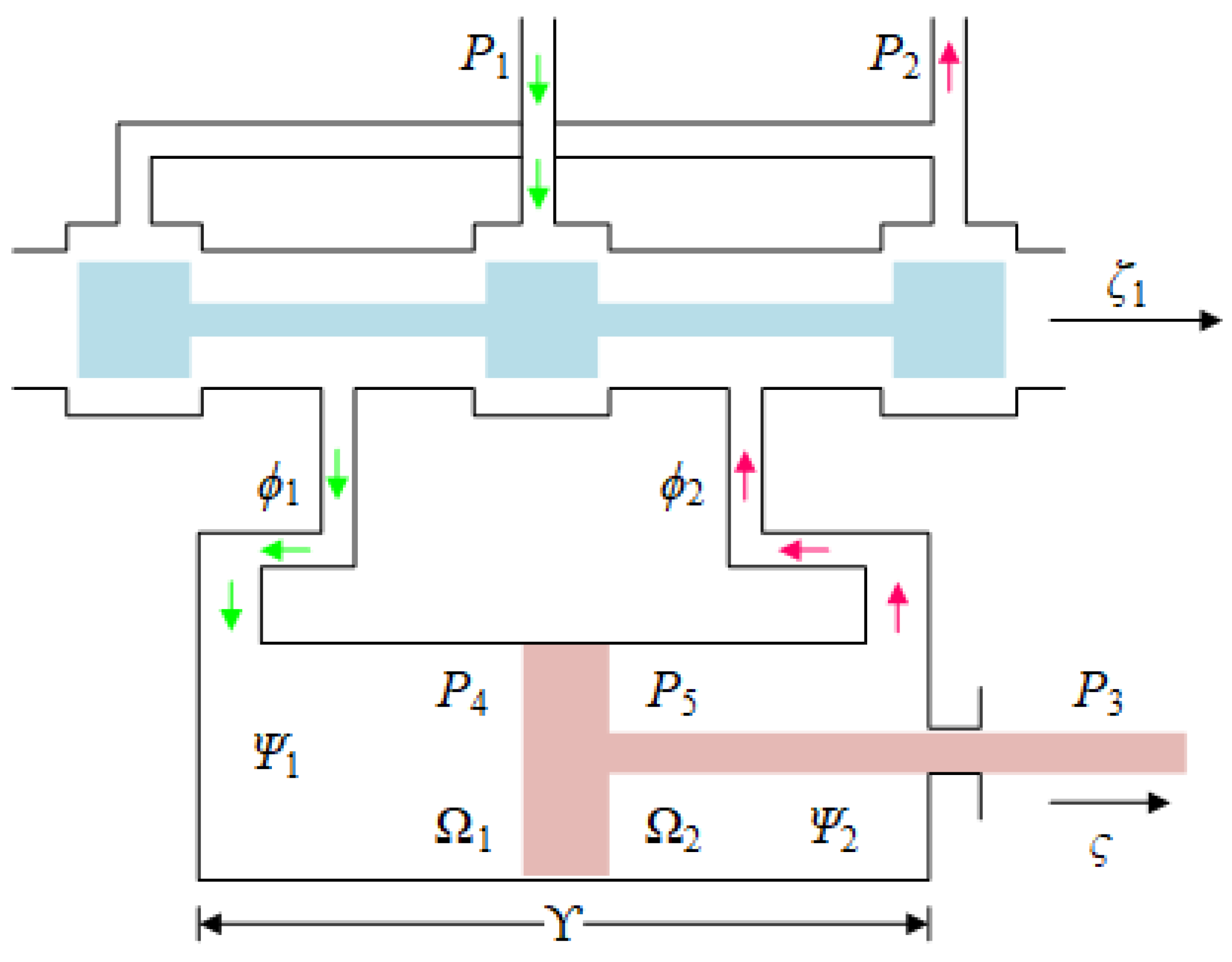




| Symbol | Definition | Symbol | Definition |
|---|---|---|---|
| length of link j | G | payload mass | |
| angle of joint j | g | gravitational acceleration | |
| mass of the actuator j | stiffness coefficient | ||
| top face radial dimension of link 1 | positioning of the primary hydraulic cylinder | ||
| bottom face radial dimension of link 1 | positioning of the secondary hydraulic cylinder | ||
| linear density of link j | oscillation mode characteristic of flexible link 3 | ||
| elastic deflection of compliant link 3 | oscillatory eigenvector element for flexible link 3 |
| Symbol | Definition | Symbol | Definition |
|---|---|---|---|
| supply pressure | equivalent volume | ||
| return pressure | flow/pressure coefficient | ||
| payload pressure | equivalent leakage coefficient | ||
| L/R chamber pressures of the actuator | effective working areas of piston chambers | ||
| real-time flow rates in dual-acting cylinder chambers | left and right hydraulic chamber effective displacement volume | ||
| geometric pumping of the motor | hydraulic throughput amplification factor | ||
| hydraulic orifice flow coefficient | volumetric flow rate to actuator | ||
| area gradient of the valve | valve core travel distance | ||
| electro-hydraulic control signal | actuator rod movement range | ||
| bulk modulus | maximum piston displacement |
| Notation | Value | Unit | Notation | Value | Unit | Notation | Value | Unit |
|---|---|---|---|---|---|---|---|---|
| 1.8 | m | 1 | m | 0.015 | m2 | |||
| 2.5 | m | 0.2 | m | 0.02 | m2 | |||
| 6 | m | 1 | m | Pa | ||||
| 0.2 | m | 0.2 | m | Pa | ||||
| 0.4 | m | 20 | kg m−1 | N m2 | ||||
| 5 | kg | 20 | kg m−1 | 0.002 | m3 | |||
| 8 | kg | 40 | kg m−1 | m3/Pa·s | ||||
| 0.04 | m | 870 | kg m−3 | 0.8 | – | |||
| 1.2 | m | g | 9.8 | m/s2 | N/m2 | |||
| m5/N·s | 8 | cm/A | 0.2 | m2 |
| Notation | Value | Notation | Value | Notation | Value | Notation | Value |
|---|---|---|---|---|---|---|---|
| 0.01 | 0.5 | a | 51 | 20 | |||
| 0.02 | 0.5 | b | 35 | 15 | |||
| 0.05 | 0.7 | c | 2 | 10 | |||
| 1 | 4 | p | 37 | 8 | |||
| 5 | 0.0025 | q | 35 | 0.01 | |||
| 0.5 | 0.1 |
| Performance Metrics | RMSE () | IATER () | IATER () | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Joint | 1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 | |
| without disturbances | CC | 1.23 | 1.26 | 0.63 | 1.339 | 1.074 | 0.408 | 29.225 | 13.323 | 3.200 |
| ADRC | 20.20 | 31.52 | 15.67 | 32.274 | 26.029 | 9.810 | 29.228 | 13.340 | 3.202 | |
| PID | 158.94 | 94.43 | 28.45 | 292.149 | 144.915 | 39.368 | 29.218 | 14.483 | 4.186 | |
| with disturbances | CC | 1.33 | 1.29 | 0.64 | 5.451 | 1.4175 | 1.3806 | 36.561 | 13.542 | 3.972 |
| ADRC | 25.26 | 35.54 | 19.35 | 1374.075 | 137.547 | 135.516 | 237.603 | 26.401 | 23.688 | |
| PID | 165.34 | 101.46 | 30.27 | 794.665 | 171.167 | 85.619 | 90.693 | 16.044 | 9.983 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, J.; Sui, Z.; Wei, X. Singular Perturbation Decoupling and Composite Control Scheme for Hydraulically Driven Flexible Robotic Arms. Processes 2025, 13, 1805. https://doi.org/10.3390/pr13061805
Xu J, Sui Z, Wei X. Singular Perturbation Decoupling and Composite Control Scheme for Hydraulically Driven Flexible Robotic Arms. Processes. 2025; 13(6):1805. https://doi.org/10.3390/pr13061805
Chicago/Turabian StyleXu, Jianliang, Zhen Sui, and Xiaohua Wei. 2025. "Singular Perturbation Decoupling and Composite Control Scheme for Hydraulically Driven Flexible Robotic Arms" Processes 13, no. 6: 1805. https://doi.org/10.3390/pr13061805
APA StyleXu, J., Sui, Z., & Wei, X. (2025). Singular Perturbation Decoupling and Composite Control Scheme for Hydraulically Driven Flexible Robotic Arms. Processes, 13(6), 1805. https://doi.org/10.3390/pr13061805









