Experimental and Numerical Study of Multi-Cluster Fracturing in Horizontal Wells for Low-Permeability Reservoirs
Abstract
1. Introduction
2. Materials and Methods
2.1. Reservoir Characterization and Specimen Preparation
2.2. True Triaxial Hydraulic Fracturing Experiments
2.2.1. Experimental Apparatus
2.2.2. Experimental Design
2.3. Numerical Simulation Using Cohesive Elements
3. Results and Discussion
3.1. Analysis of Multi-Cluster Fracturing Physical Simulation Experiments
3.1.1. Effect of Horizontal In Situ Stress Difference
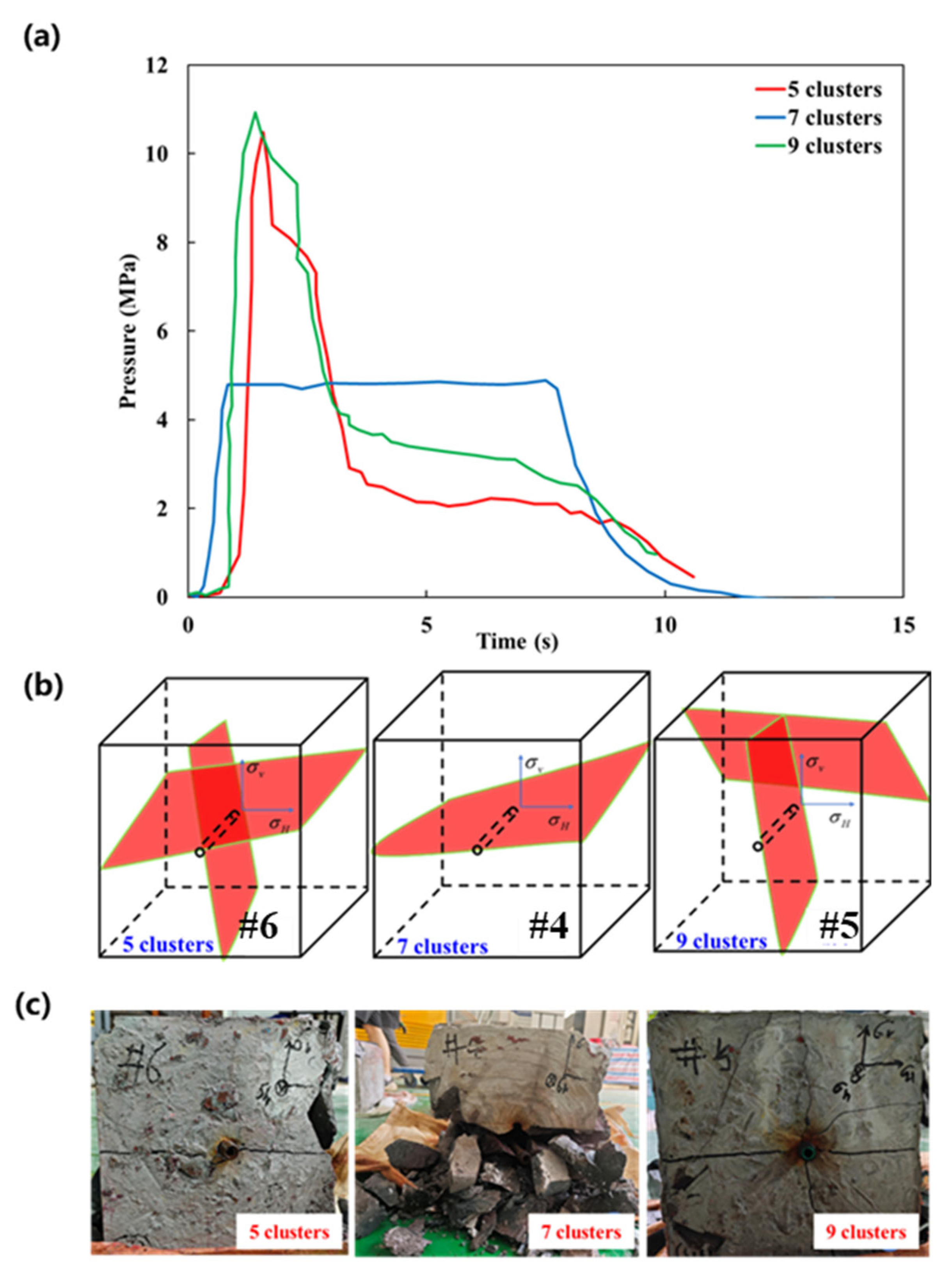
3.1.2. Effect of Perforation Cluster Number
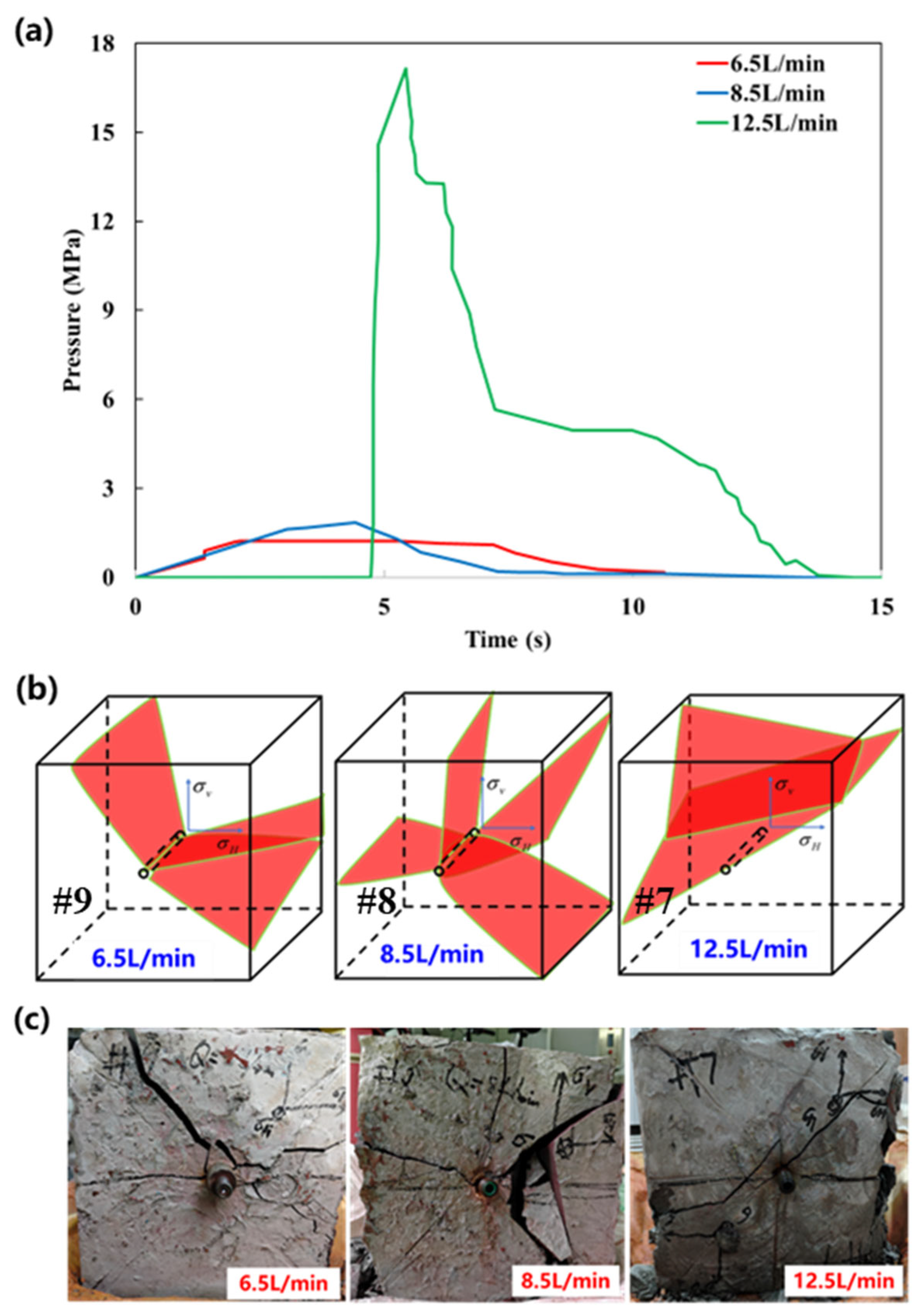
3.1.3. Effect of the Fracturing Fluid Injection Rate
3.1.4. Effect of Fracturing Fluid Viscosity
3.2. Numerical Simulation Results Analysis
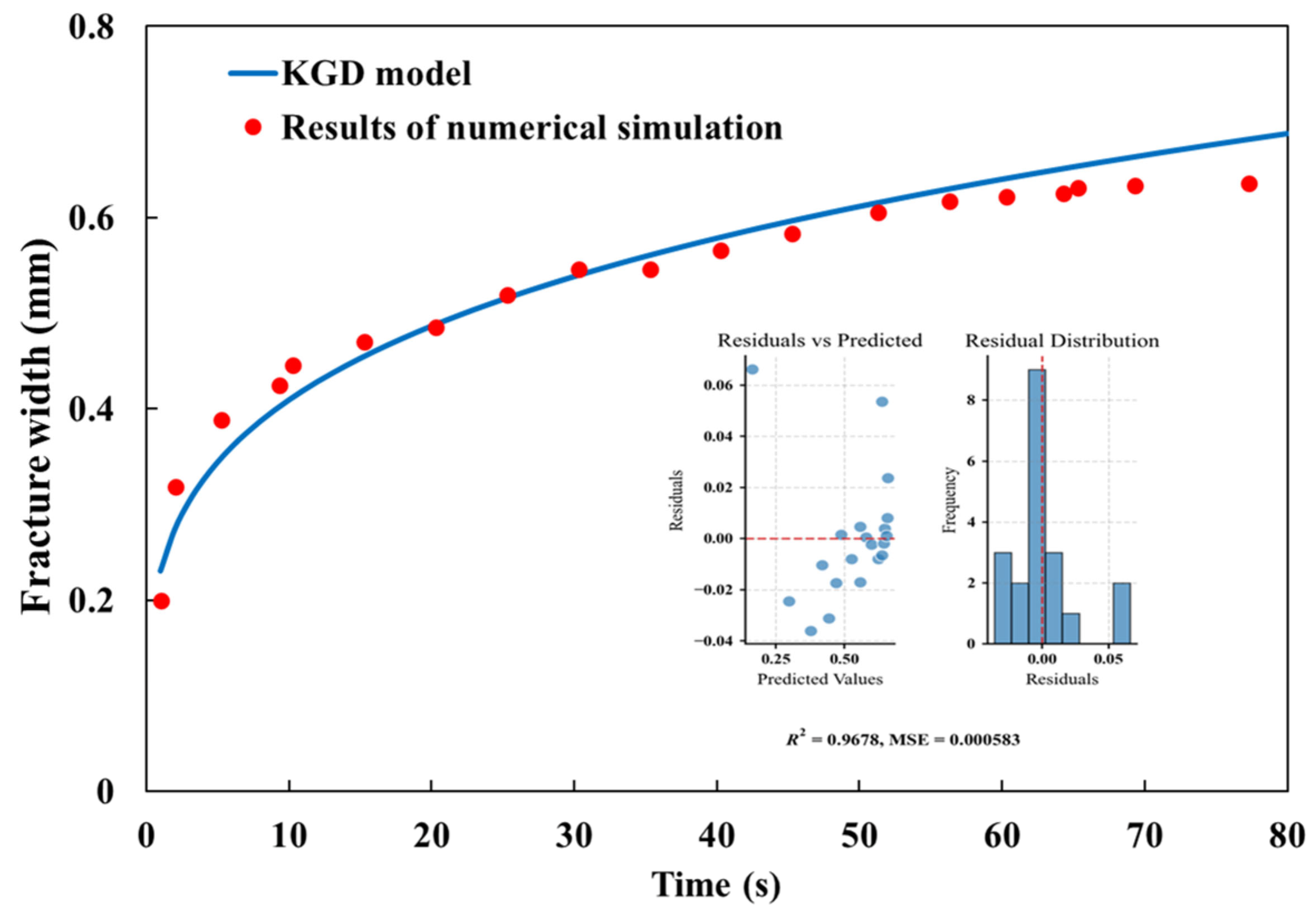
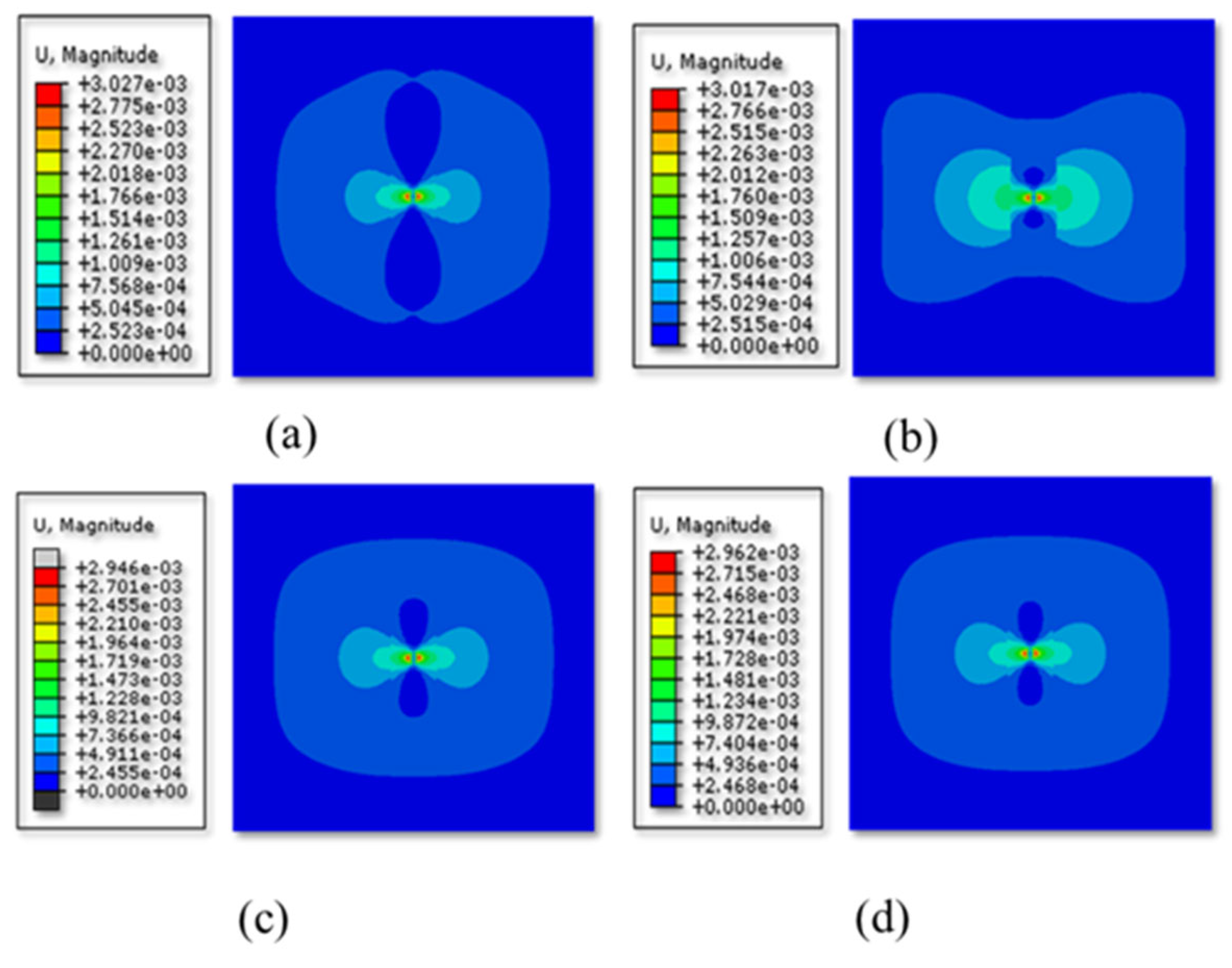
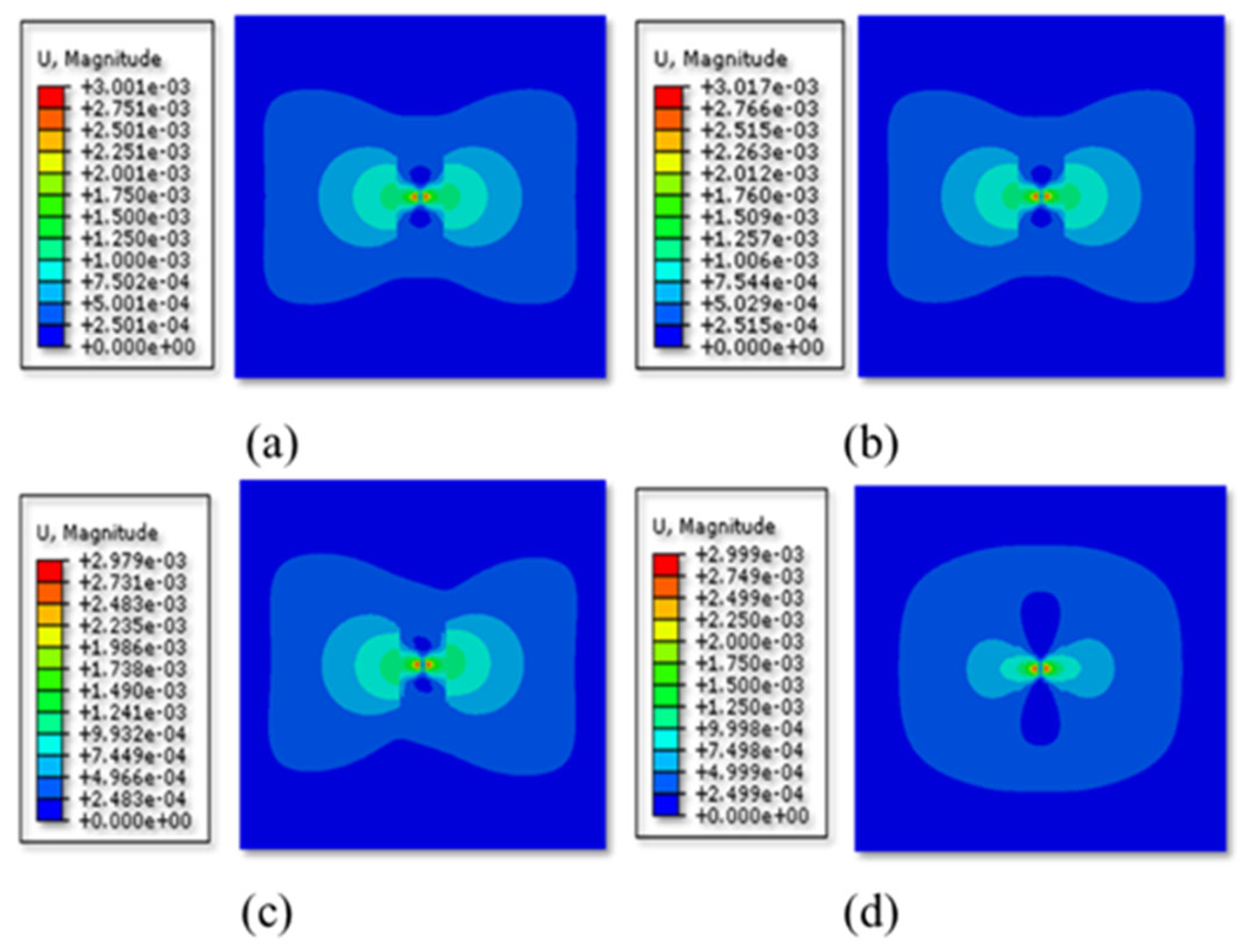
3.2.1. Model Validation
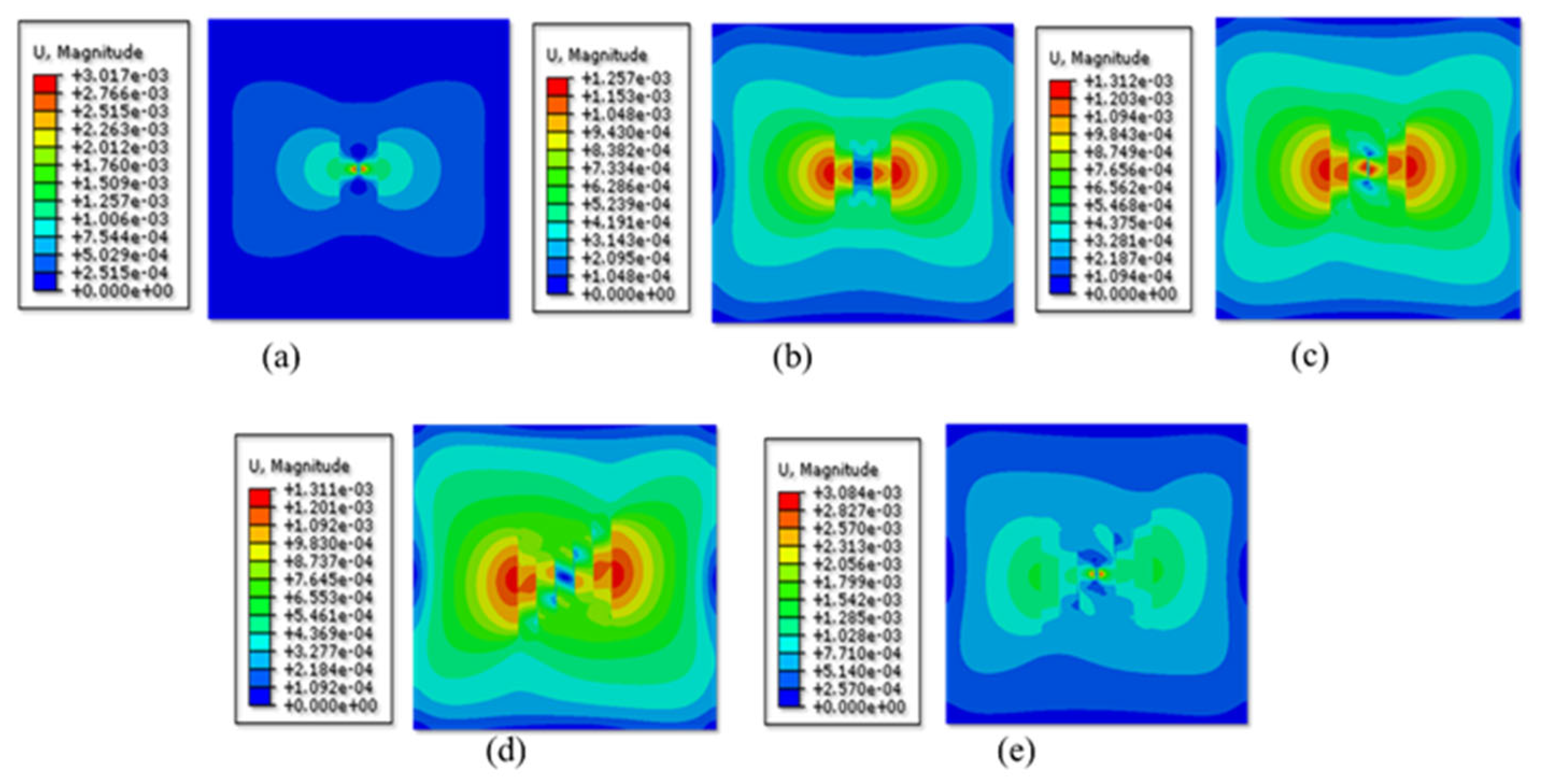
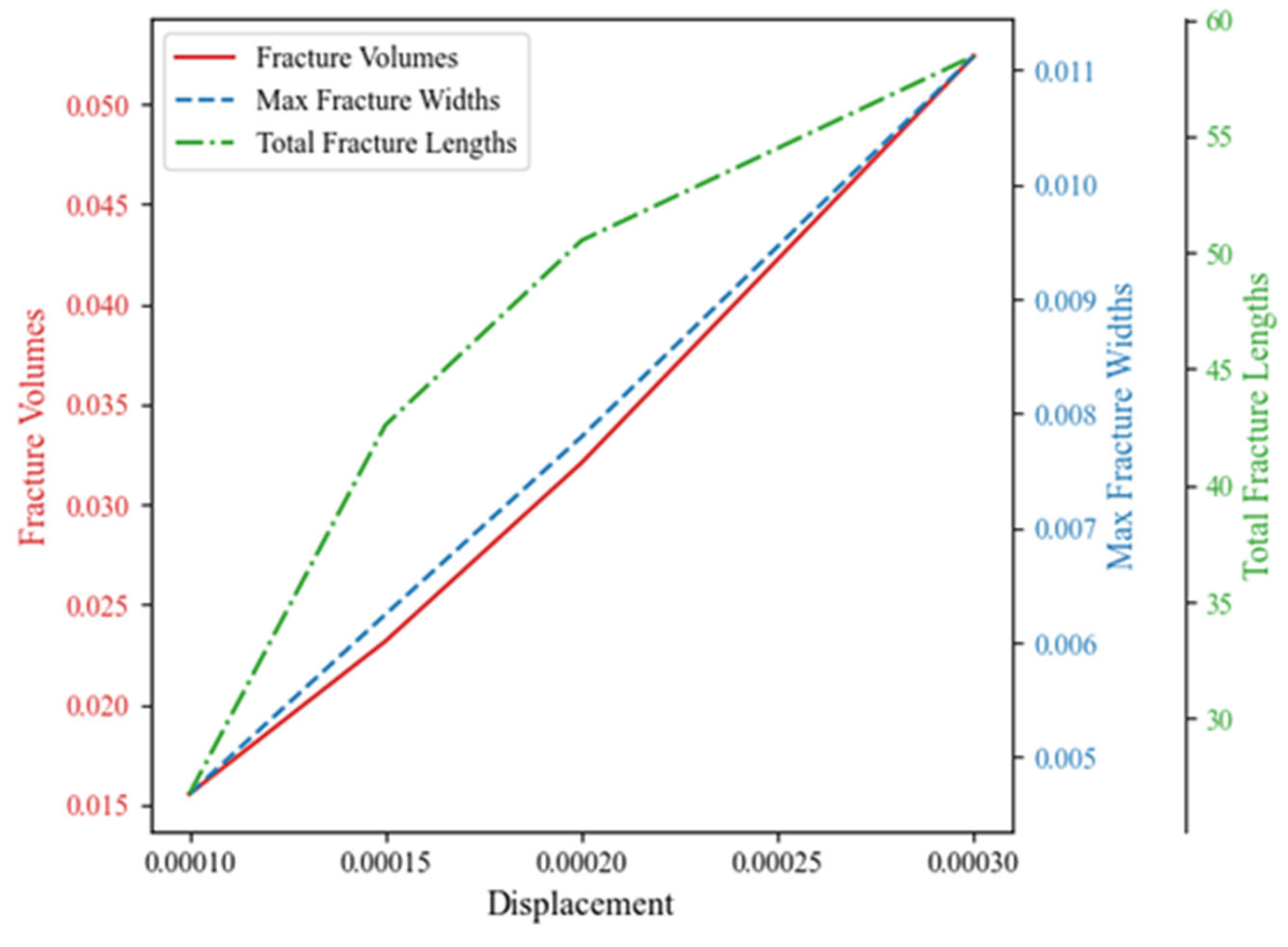
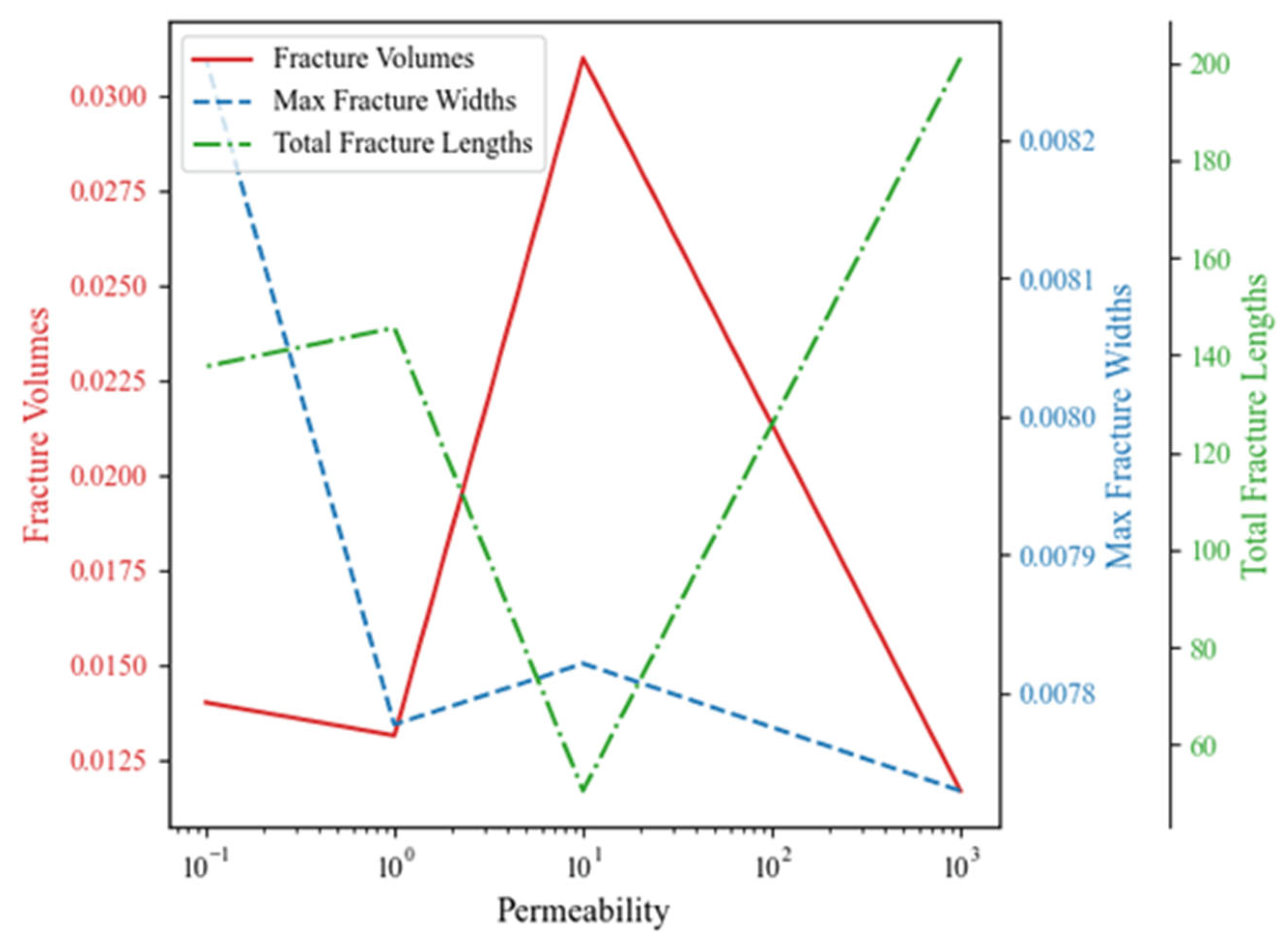
3.2.2. Analysis of Factors Influencing the Fracture Propagation Patterns
- (a)
- Effect of horizontal stress difference
- (b)
- Effect of the number of perforation clusters
- (c)
- Effect of the injection rate
- (d)
- Effect of permeability
- (e)
- Effect of the elastic modulus
- (f)
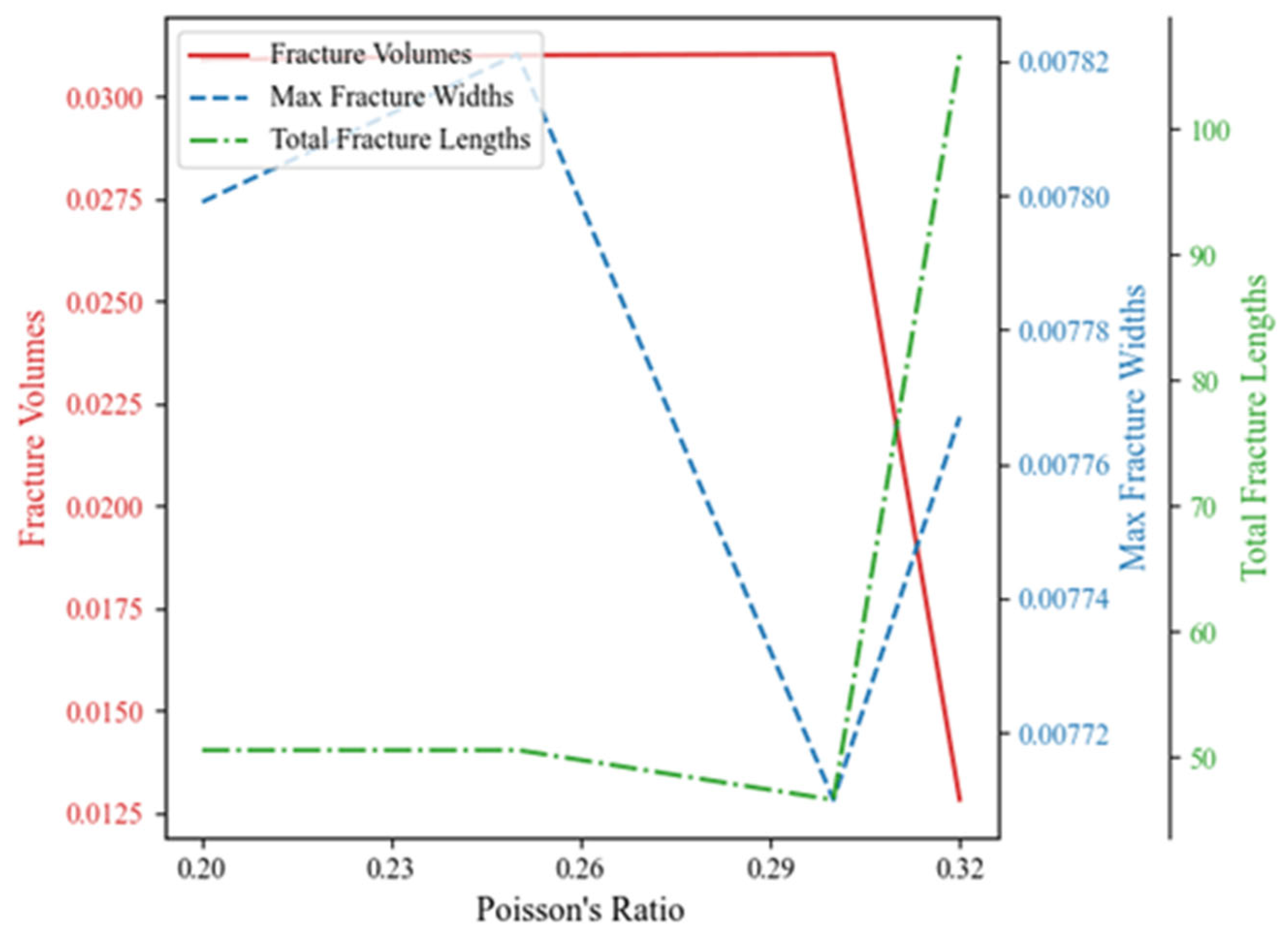
- Effect of Poisson’s ratio
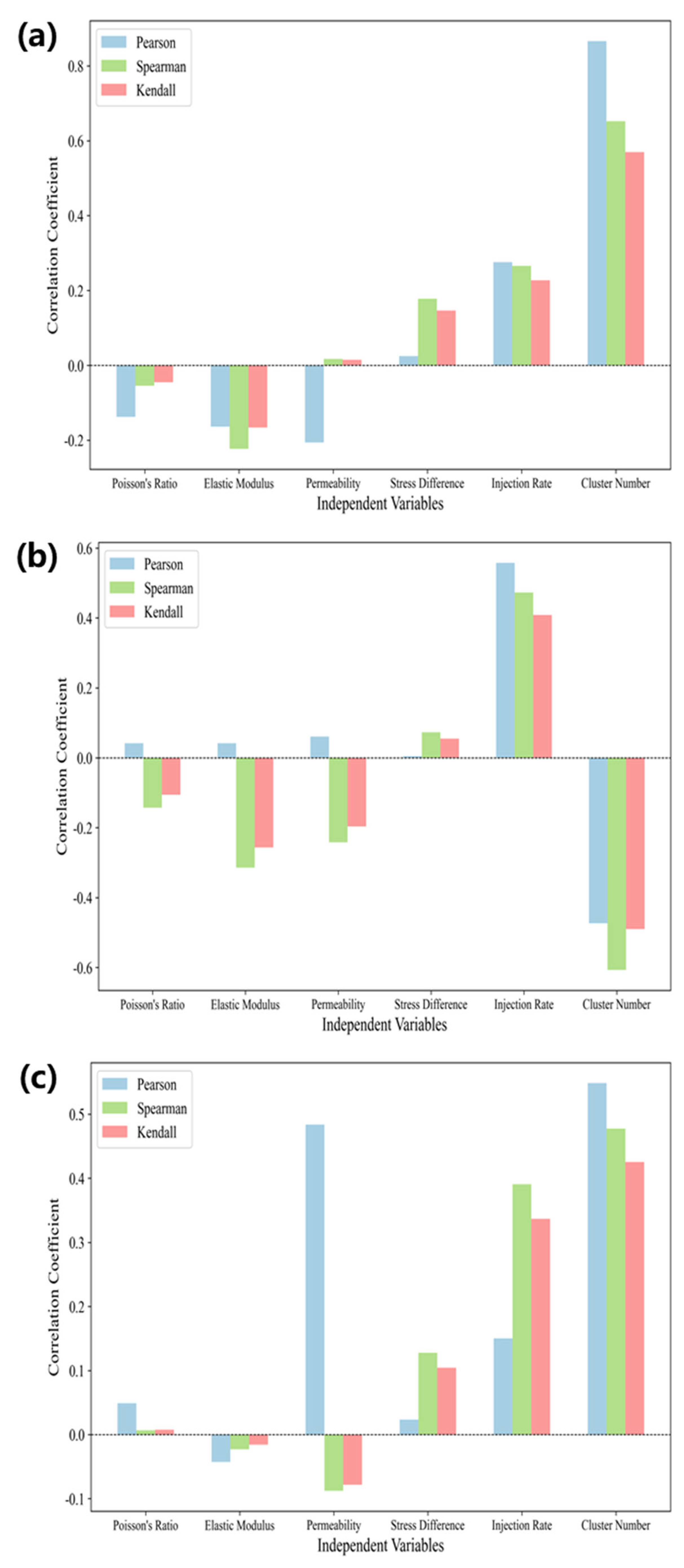
3.3. Dominant Factor Analysis of Fracture Morphology
4. Conclusions
- (1)
- The fracturing pressure curves generally conformed to typical pressure–time characteristics. When the horizontal stress difference coefficient, number of perforation clusters, and fracturing fluid viscosity were relatively low, the fractured specimens predominantly exhibited bi-wing, approximately symmetrical horizontal fractures. In contrast, increasing the injection rate of the fracturing fluid led to the frequent occurrence of vertical fractures. The direction of fracture propagation was strongly affected by the number of perforation clusters and the horizontal stress difference coefficient; specifically, increasing either of these parameters caused noticeable deviation from the initial propagation axis. Additionally, the fracture complexity increased with higher perforation cluster numbers and greater fluid viscosity, reflecting enhanced stress interaction and fluid resistance effects during fracture evolution.
- (2)
- The number of perforation clusters appeared as a significantly dominant factor in determining fracture morphology, reflecting the influence of the fracture spatial distribution characteristics throughout the formation process of stimulated volume, maximum fracture width, and total fracture length. The injection rate, another prominent factor in multiple analyses, reflects the critical influence of external mechanical forces on fracture morphology. Factors such as permeability, elastic modulus, and Poisson’s ratio also appeared to participate in shaping the fracture morphology to varying degrees, interacting with the number of perforation clusters and the injection rate to jointly determine the final fracture morphology.
- (3)
- From the perspective of stimulated volume, increasing the injection rate and the number of perforation clusters was effective to increase the stimulated volume. Specifically, when the injection rate increased from 0.0001 to 0.0003 m3/s, the total fracture length and stimulated volume increased by 118% and 237%, respectively. Similarly, increasing the number of perforation clusters from three to seven resulted in a 263% increase in fracture volume and a 178% increase in total fracture length. However, increasing the number of perforation clusters can lead to stress deflection, resulting in a departure from the symmetrical bi-wing fracture pattern.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Liu, H.; Wang, H.; Liu, R.; Zhao, Q.; Zhang, X.; Yong, H. The present status and essential points of developing the unconventional hydrocarbon resources in China. Nat. Gas Ind. 2009, 29, 113–116+146. [Google Scholar]
- Zou, C.; Zhai, G.; Zhang, G.; Wang, H.; Zhang, G.; Li, J.; Wang, Z.; Wen, Z.; Ma, F.; Liang, Y.; et al. Formation, distribution, potential and prediction of global conventional and unconventional hydrocarbon resources. Pet. Explor. Dev. 2015, 42, 13–25. [Google Scholar] [CrossRef]
- Wang, Y.; Lu, Y.; Li, Y.; Wang, X.; Yan, X.; Zhang, Z. Progress and application of hydraulic fracturing technology in unconventional reservoir. Acta Pet. Sin. 2012, 33, 149–158. [Google Scholar]
- Tan, P.; Xing, Y.; Han, T.; Chen, J.; Xu, H.; Chen, Z. Physical simulation experiments on non-uniform extension of multi-cluster hydraulic fractures under complex fracturing conditions. Chin. J. Rock Mech. Eng. 2025, 1–13. [Google Scholar]
- Li, Y.; Ma, J.; Li, T.; Sun, P. Optimization of Dynamic Fracture Plugging Parameters in Lower Cambrian Qiongzhusi Shale, Southern Sichuan Basin. J. Southwest Pet. Univ. 2024, 46, 137–145. [Google Scholar]
- Wang, C.; Zhang, H.; Zhao, J.; Wang, T. Study on Hydraulic Fracture Propagation in Elastoplastic Reservoir. China Pet. Mach. 2022, 50, 80–88. [Google Scholar] [CrossRef]
- Zhang, Z.; Gao, W.; Ma, X. Energy Dissipation of Hydraulic Fracturing Based on Energy Balance. J. Chongqing Jiaotong Univ. 2017, 36, 54–57. [Google Scholar]
- Song, Y.; Lin, R.; Huang, Y.; Ren, L.; Yue, W.; Sun, Y. Simulation and control of fractures asynchronous initiation-propagation of horizontal well fracturing for deep shale gas. Pet. Geol. Oilfield Dev. Daqing 2022, 41, 145–152. [Google Scholar] [CrossRef]
- Olson, J.E. Multi-fracture propagation modeling: Applications to hydraulic fracturing in shales and tight gas sands. In Proceedings of the 42nd U.S. Rock Mechanics Symposium (USRMS), San Francisco, CA, USA, 29 June 2008. [Google Scholar]
- Nagel, N.B.; Sanchez-Nagel, M. Stress shadowing and microseismic events: A numerical evaluation. In Proceedings of the SPE Annual Technical Conference and Exhibition, Denver, CO, USA, 30 October–2 November 2011. SPE-147363-MS. [Google Scholar]
- Roussel, N.P.; Sharma, M.M. Optimizing fracture spacing and sequencing in horizontal-well fracturing. SPE Prod. Oper. 2011, 26, 173–184. [Google Scholar] [CrossRef]
- Zhao, J.-Z.; Chen, X.-Y.; Liu, C.-Y.; Li, Y.-M.; Li, H.; Cao, X.-J. The Analysis of Crack Interaction in Multi-stage Horizontal Fracturing. Nat. Gas Geosci. 2015, 26, 533–538. [Google Scholar]
- Yan, X.; Wang, Y.; Wang, T.; Zhao, H.; Xu, Y.; Wan, K.; Guo, N. Field application of tight oil factory fracturing in Mahu sag. Reserv. Eval. Dev. 2018, 8, 70–76. [Google Scholar] [CrossRef]
- Zhang, J.; Qi, Y. Impact of in-situ stresses on shale reservoir development and its countermeasures. Oil Gas Geol. 2020, 41, 776–783+799. [Google Scholar]
- Hubbert, M.K.; Willis, D.G. Mechanics of hydraulic fracturing. Trans. AIME 1957, 210, 153–168. [Google Scholar] [CrossRef]
- Wang, B.; Li, L.; Dong, X.; Liu, S.; Zhou, F. Investigation into the controlling factors of the in-stage multi-cluster fracturing effects based on optical fiber monitoring. Pet. Sci. Bull. 2023, 8, 775–786. [Google Scholar]
- Mian, C. Re-orientation and propagation of hydraulic fractures in shale gas reservoir. J. China Univ. Pet. 2013, 37, 88–94. [Google Scholar]
- Wang, C.; Chen, C.; Sun, Y.; Wang, W.; Hong, J.; Gao, S. Simulation of Oil Shale Hydraulic Fracturing in Nong’an and the Experimental Study. Drill. Eng. 2015, 42, 7–11. [Google Scholar]
- Hou, Z.; Yang, C.; Wang, L.; Liu, P.; Guo, Y.; Wei, Y.; Li, Z. Hydraulic fracture propagation of shale horizontal well by large-scale true triaxial physical simulation test. Rock Soil Mech. 2016, 37, 407–414. [Google Scholar] [CrossRef]
- Zheng, Y.; He, R.; Huang, L.; Bai, Y.; Wang, C.; Chen, W.; Wang, W. Exploring the effect of engineering parameters on the penetration of hydraulic fractures through bedding planes in different propagation regimes. Comput. Geotech. 2022, 146, 104736. [Google Scholar] [CrossRef]
- Zhou, T.; Wang, H.; Li, F.; Li, Y.; Zou, Y.; Zhang, C. Numerical simulation of hydraulic fracture propagation in laminated shale reservoirs. Pet. Explor. Dev. 2020, 47, 1039–1051. [Google Scholar] [CrossRef]
- Jafari, A.; Vahab, M.; Khalili, N. Fully coupled XFEM formulation for hydraulic fracturing simulation based on a generalized fluid leak-off model. Comput. Methods Appl. Mech. Eng. 2021, 373, 113447. [Google Scholar] [CrossRef]
- Liu, N.; Zhang, Z.; Zou, Y.; Ma, X.; Zhang, Y. Propagation law of hydraulic fractures during multi-staged horizontal well fracturing in a tight reservoir. Pet. Explor. Dev. 2018, 45, 1059–1068. [Google Scholar] [CrossRef]
- Fu, G.; Wang, Q.; Shi, J. Sealing oil-gas time and ability effectiveness of mudstone caprocks in middle Es1 in Dagang Oilfield. J. Cent. South Univ. 2012, 43, 3142–3148. [Google Scholar]
- Xu, G.; Chen, Y.; Chen, C.; Hu, L.; Liu, Z. Reservoir Characteristics and Reservoir-controlling Factors of Es3 Member in Qi’nan Sag, Huanghua Depression. J. Southwest Pet. Univ. 2023, 45, 31–42. [Google Scholar]
- Jiang, G.; Wang, L.; Zhang, S.; Tang, X.; Guo, H. Drilling fluid technology to protect the formations in low/ultra-low permeability reservoirs. Spec. Oil Gas Reserv. 2014, 21, 113–116+156. [Google Scholar]
- Li, C. Research and Application of Fracture-Induced Stress Field in Tight Oil Reservoirs of Dagang Oilfield. Ph.D. Thesis, Southwest Petroleum University, Chengdu, China, 2016. [Google Scholar]
- Radovitzky, R.; Seagraves, A.; Tupek, M.; Noels, L. A scalable 3D fracture and fragmentation algorithm based on a hybrid, discontinuous Galerkin, cohesive element method. Comput. Methods Appl. Mech. Eng. 2011, 200, 326–344. [Google Scholar] [CrossRef]
- Lu, W.; Lubbad, R.; Løset, S. Simulating ice-sloping structure interactions with the cohesive element method. J. Offshore Mech. Arct. Eng. 2014, 136, 031501. [Google Scholar] [CrossRef]
- Jiang, H.; Meng, D. 3D numerical modelling of rock fracture with a hybrid finite and cohesive element method. Eng. Fract. Mech. 2018, 199, 280–293. [Google Scholar] [CrossRef]
- Camanho, P.P.; Dávila, C.G. Mixed-Mode Decohesion Finite Elements for the Simulation of Delamination in Composite Materials; NASA: Washington, DC, USA, 2002. [Google Scholar]
- Turon, A.; Camanho, P.P.; Costa, J.; Dávila, C.G. A damage model for the simulation of delamination in advanced composites under variable-mode loading. Mech. Mater. 2006, 38, 1072–1089. [Google Scholar] [CrossRef]
- Biao, F.; Liu, H.; Zhang, S.; Zhang, J.; Wang, X. A Numerical Study of Parameter Influences on Horizontal Hydraulic Fracture. Eng. Mech. 2011, 28, 228–235. [Google Scholar]
- Li, B. Research on the Disintegration Study on the Disintegration Mechanism of Mudstone Sample Model Under Freeze-thaw Cycle. Ph.D. Thesis, Shenyang Jianzhu University, Shenyang, China, 2024. [Google Scholar] [CrossRef]
- Wang, H. Study on Hydraulic Fracturing Technology of Top Coal Cross-seam Network in Initial Mining Period Based on Stress Regulation. Ph.D. Thesis, China University of Mining and Technology, Beijing, China, 2024. [Google Scholar]
- Fu, S.; Chen, M.; Xia, Y.; Tan, P.; Zhang, Y.; Li, Y. Hydraulic fracture height growth law for deep coal measures shale reservoir. Fault Block Oil Gas Field 2021, 28, 555–560. [Google Scholar]
- Sobhaniaragh, B.; Trevelyan, J.; Mansur, W.; Peters, F. Numerical simulation of MZF design with non-planar hydraulic fracturing from multi-lateral horizontal wells. J. Nat. Gas Sci. Eng. 2017, 46, 93–107. [Google Scholar] [CrossRef]
- Ahmadi, S.; Khormali, A.; Razmjooie, A. Experimental investigation on separation of water in crude oil emulsions using an oil-soluble demulsifier. Iran. J. Chem. Chem. Eng. Res. Artic. Vol. 2023, 42, 2332–2343. [Google Scholar] [CrossRef]
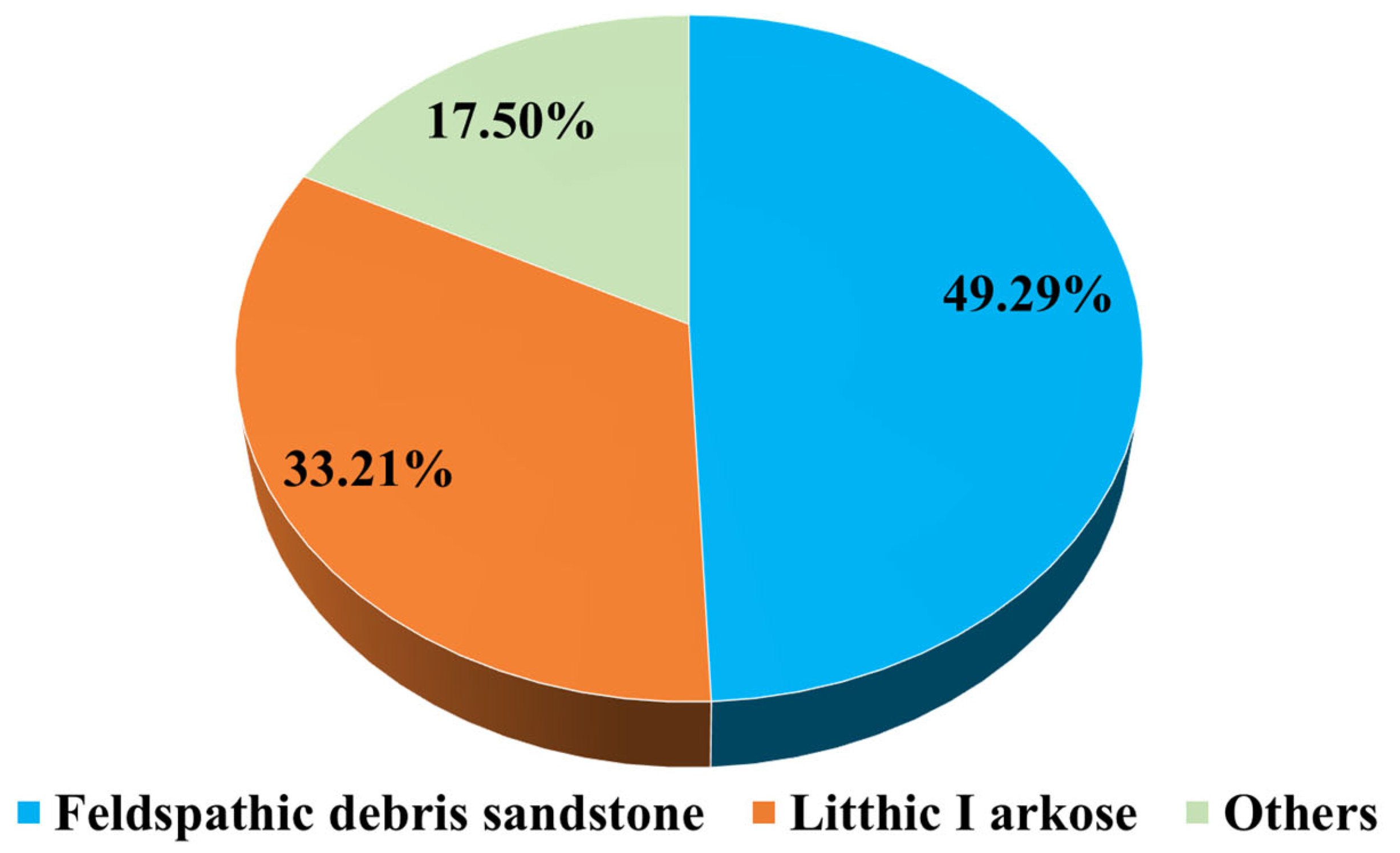
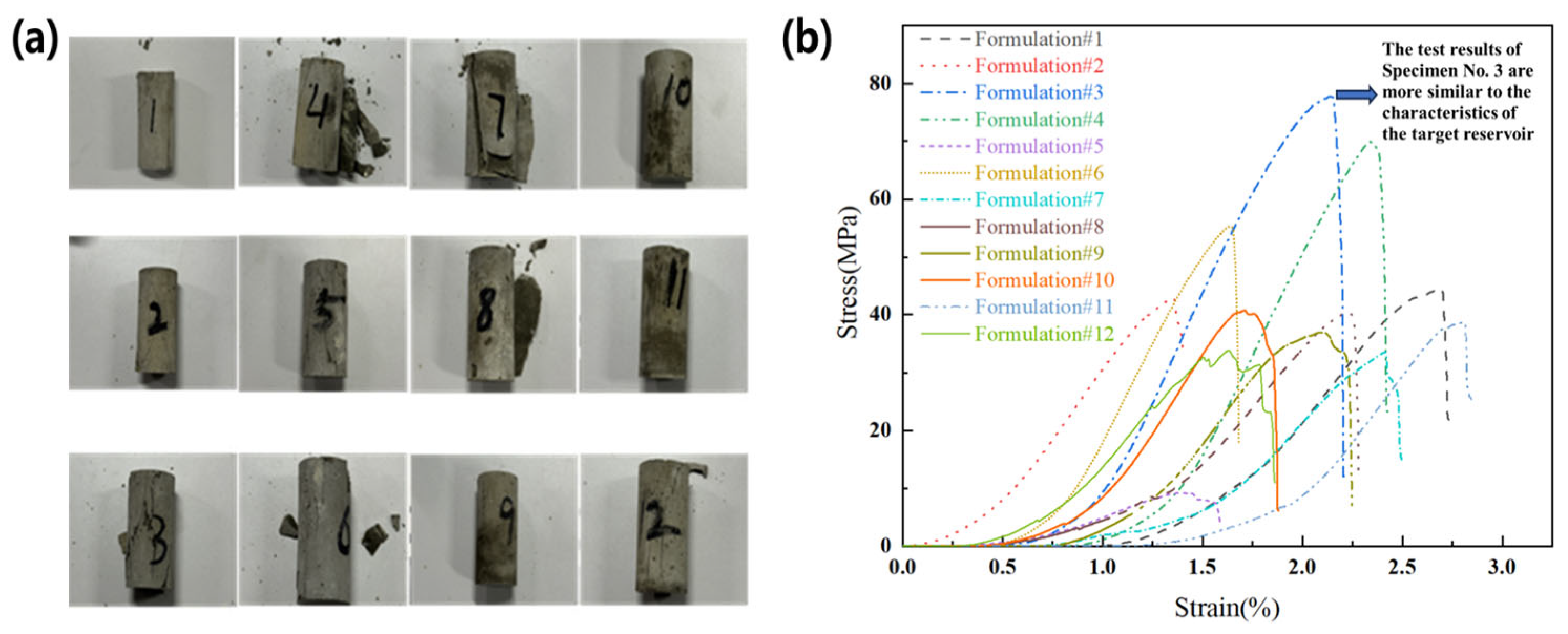


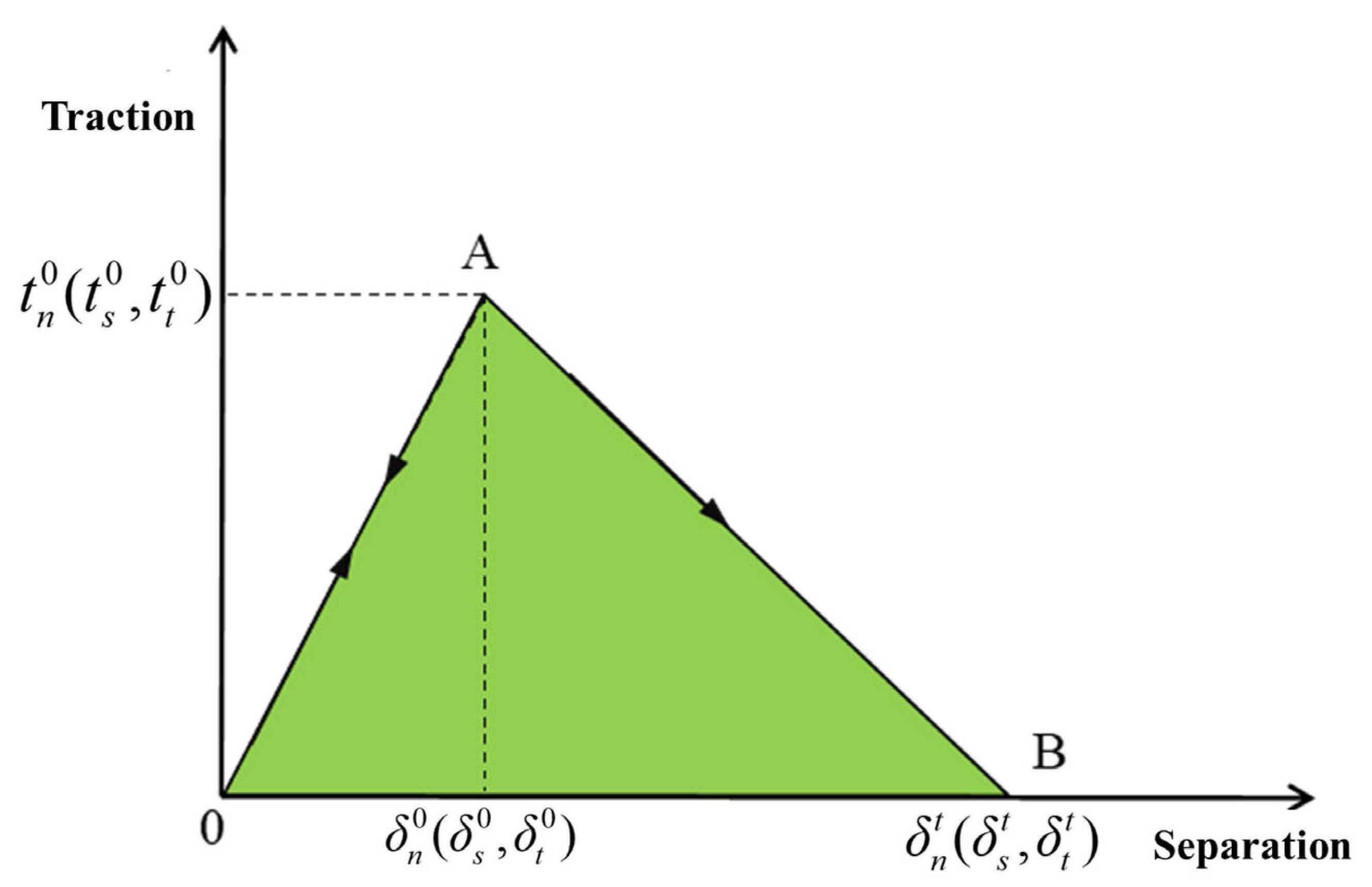
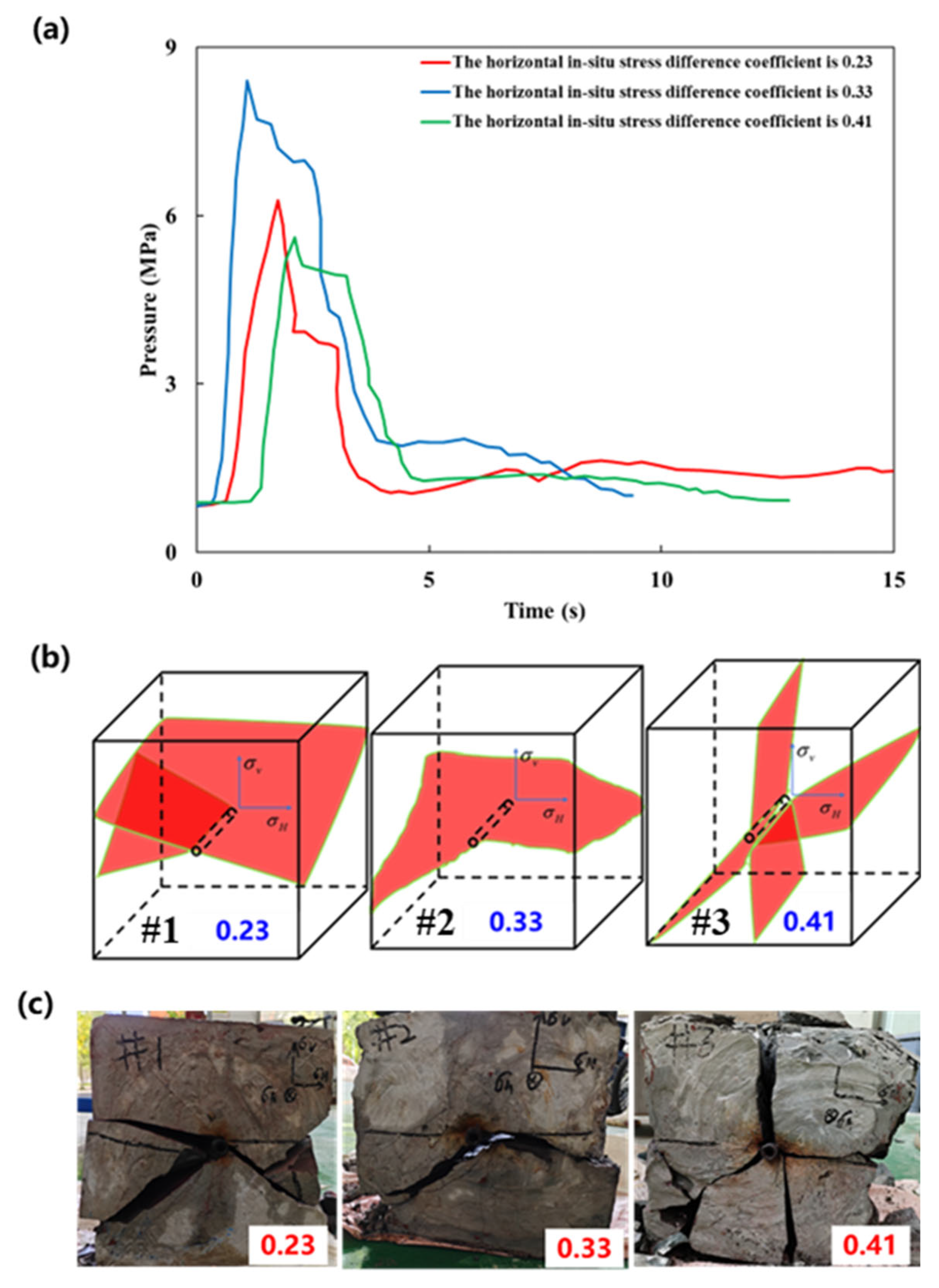









| Parameter | Target Reservoir | Laboratory Specimen | Relative Error (%) |
|---|---|---|---|
| Porosity (%) | 5–25 | 5.77 | 23.07 |
| Uniaxial compressive strength (MPa) | 74 | 77.8 | 5.14 |
| Young’s modulus (GPa) | 16 | 16.47 | 2.94 |
| Permeability (mD) | 0–10 | 1.43 | 42.80 |
| Sample | Test Group | σv/σH/σh | Horizontal In Situ Stress Difference Coefficient () | Number of Perforation Clusters | Pump Displacement (L/min) | Fracturing Fluid Viscosity (cP) |
|---|---|---|---|---|---|---|
| 1 | A | 12/10/7.7 | 0.23 | 7 | 12.5 | 1 |
| 2 | 12/10/6.7 | 0.33 | 7 | 12.5 | 1 | |
| 3 | 12/10/5.9 | 0.41 | 7 | 12.5 | 1 | |
| 4 | B | 12/10/6.7 | 0.33 | 7 | 12.5 | 1 |
| 5 | 12/10/6.7 | 0.33 | 9 | 12.5 | 1 | |
| 6 | 12/10/6.7 | 0.33 | 5 | 12.5 | 1 | |
| 7 | C | 12/10/6.7 | 0.33 | 7 | 12.5 | 1 |
| 8 | 12/10/6.7 | 0.33 | 7 | 8.5 | 1 | |
| 9 | 12/10/6.7 | 0.33 | 7 | 6.5 | 1 | |
| 10 | D | 12/10/6.7 | 0.33 | 7 | 12.5 | 1 |
| 11 | 12/10/6.7 | 0.33 | 7 | 12.5 | 10 | |
| 12 | 12/10/6.7 | 0.33 | 7 | 12.5 | 30 |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Tensile strength | 5 MPa | Cluster spacing | 5 m |
| Maximum horizontal principal stress | 60 MPa | Void ratio | 10% |
| Minimum horizontal principal stress | 60/55/50 MPa | Number of perforation clusters | 3/4/5/6/7 |
| Permeability coefficients | 1 e−5/1 e−7/1 e−8/1 e−9 m/s | Viscosity | 1/10/30 cP |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Elastic modulus | 20 GPa | Injection rate | 0.002 m3/min |
| Poisson’s ratio | 0.25 | Viscosity | 0.001 cP |
| Filtration coefficient | 10−14 cP | Time | 80 s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ji, P.; Qiu, S.; Zhang, H.; Zhou, W.; Song, G.; Wang, Z. Experimental and Numerical Study of Multi-Cluster Fracturing in Horizontal Wells for Low-Permeability Reservoirs. Processes 2025, 13, 1693. https://doi.org/10.3390/pr13061693
Ji P, Qiu S, Zhang H, Zhou W, Song G, Wang Z. Experimental and Numerical Study of Multi-Cluster Fracturing in Horizontal Wells for Low-Permeability Reservoirs. Processes. 2025; 13(6):1693. https://doi.org/10.3390/pr13061693
Chicago/Turabian StyleJi, Peng, Shoumei Qiu, Hao Zhang, Wang Zhou, Guoqiang Song, and Zizhen Wang. 2025. "Experimental and Numerical Study of Multi-Cluster Fracturing in Horizontal Wells for Low-Permeability Reservoirs" Processes 13, no. 6: 1693. https://doi.org/10.3390/pr13061693
APA StyleJi, P., Qiu, S., Zhang, H., Zhou, W., Song, G., & Wang, Z. (2025). Experimental and Numerical Study of Multi-Cluster Fracturing in Horizontal Wells for Low-Permeability Reservoirs. Processes, 13(6), 1693. https://doi.org/10.3390/pr13061693






