Abstract
Today, hydrogen fuel cells occupy a crucial position in sustainable energy systems. However, a precise model of their performance is needed to improve their efficiency and integrate them into hydrogen electric vehicles. This paper presents a hydrogen fuel cell model based on artificial neural networks (ANNs) to predict its performance characteristics. Using experimental data from a PEMFC NEXA 1200 hydrogen fuel cell in the ISA laboratory, an ANN model optimized by deep learning was developed, integrating advanced training techniques. The model’s performance was evaluated on independent test sets, revealing predictive precision with a low mean squared error (MSE) of 0.0429, a low Mean Absolute Percentage Error (MAPE) of 1.05%, a low Root-Mean-Square Error (RMSE) of 0.2071, and a high coefficient of determination (R2) of 0.9071. The model’s development and evaluation will be reviewed here in order to visualize the training progress and the results of the simulation. The main advantages of the proposed ANN model lie in both its flexible architecture, which can capture complex relationships without the need for explicit physical models, and its predictive and optimization capability.
1. Introduction
The global transition to sustainable energy solutions has led to growing interest in hydrogen electric vehicles as a sustainable alternative to fossil fuel transport [1]. With the goal of satisfying adaptability, power, and efficiency requirements, hydrogen fuel cells were designed as a clean energy conversion method operating on the principle of the electrochemical conversion of hydrogen into electricity. They emit only water as a byproduct [2,3,4], making them a clean alternative to conventional combustion engines [5]. The scientific literature on this subject explores various aspects, including the improvement of electrode and electrolyte materials [6], thermal and water management of systems [7], and performance optimization using artificial intelligence and predictive models [8].
Among the various existing technologies [9], fuel cells come in several types, depending on their technology and application: Proton-exchange membrane fuel cells (PEMFCs) are the most common type of fuel cell, notably used in electric vehicles, owing to their low-temperature operation, high power density, and fast response time [10]. Alkaline fuel cells (AFCs), which have historically been used in space missions, offer high efficiency but are sensitive to carbon dioxide, which limits their use in open environments [11]. Phosphoric acid fuel cells (PAFCs) operate at moderate temperatures and are mainly used for combined heat and power generation, as they are highly tolerant of hydrogen impurities [12]. Molten carbonate fuel cells (MCFCs), which operate at high temperatures, are suitable for stationary power plants and can directly use fuels such as natural gas [13]. Finally, solid oxide fuel cells (SOFCs), which operate at even higher temperatures, stand out for their exceptional efficiency and fuel flexibility, making them ideal for industrial applications and distributed power generation [14]. PEMFCs offer many advantages over other types of fuel cells, particularly in applications such as hydrogen vehicles [15]. They start up quickly and operate at relatively low temperatures, making them more practical for mobile applications [16]. They are also lightweight and compact, making them suitable for vehicles, where space and weight are crucial [17]. They require little maintenance, making them attractive for long-term use, and can be fueled by renewable hydrogen sources, helping to reduce dependence on fossil fuels [18]. These advantages make PEMFCs a promising technology for a more sustainable energy future and a transition to clean transport [19,20].
Since their invention in 1839 by William Grove [21], fuel cells have evolved significantly in terms of modeling and control [22]. Initially based on fundamental electrochemical principles, they were used for space applications, with the first simplified mathematical models describing oxidation–reduction reactions and energy losses [23]. In the 1990s, the development of simulation tools enabled the development of more precise dynamic models, integrating water and heat management within PEMFCs. At the same time, the first control strategies, such as PID and predictive control (MPC), were introduced to optimize their performance and durability [24,25]. Then, artificial intelligence revolutionized PEMFC modeling [26], with the use of deep learning techniques for voltage prediction and optimal energy flow management.
Using artificial intelligence, particularly artificial neural networks (ANNs), to model fuel cells (PEMFCs) offers several advantages over traditional electrochemical, empirical, and dynamic models [27]. Unlike electrochemical models, which require complex equations and simplifying assumptions, ANNs can directly capture non-linear relationships between input and output variables. In addition, ANNs offer high computational speed once trained, making them suitable for real-time applications and predictive control of PEMFCs. Another major advantage is their ability to adapt to variations in operating conditions, and to take account of cell aging, unlike rigid physical models [28,29].
The present work deals with the development of an artificial neural network (ANN) model for the voltage prediction of a proton-exchange membrane hydrogen fuel cell (PEMFC). The proposed model was designed to accurately capture non-linear relationships between input and output variables, exploiting deep learning techniques. A comparative analysis was carried out between different optimization algorithms (ADAM, SGDM, and RMSprop) to assess their impact on model accuracy and convergence. The model was implemented and trained in MATLAB R2022b , using experimental data from a NEXA 1200 W hydrogen fuel cell.
The rest of this article is structured as follows: First, we present the theoretical basis and development of the ANN model, detailing its architecture as well as the training process. Then, we move to data acquisition, describing the hardware setup and the data collection methodology for deep learning, followed by an evaluation of the model’s performance, starting with an analysis of the optimization algorithms, along with a presentation of the results and a comparison between optimizers. Finally, the study ends with a conclusion, highlighting the main results.
2. Model Development and Theory
2.1. ANN Model Theory
Artificial neural networks (ANNs) are a category of algorithms inspired by the functioning of the human brain and widely used to model complex, non-linear systems [30]. In the context of PEMFCs, ANNs offer an alternative to electrochemical models, enabling accurate modeling based on experimental data. An artificial neural network is composed of several interconnected layers of neurons, each one playing a specific role in data processing. The input layer receives variables such as current, temperature, and pressure, which influence the operation of the system being modeled. The hidden layers, located between the input and output, apply non-linear transformations to the data using adapted activation functions, enabling the network to learn complex relationships. Finally, the output layer produces predicted values, such as battery voltage, based on the information processed by the previous layers [31].
The process can be explained mathematically as follows: internally, a neuron multiplies all of its inputs (x1, x2, x3… xn) by their associated weights (w1, w2, w3… wn) and adds them all together. A threshold, often known as bias (b), is later applied to this product summation; the basic equation for a neuron is given by
where f is the activation function that the ANN model uses to introduce the non-linearity essential for modeling the complex behavior of PEMFCs; the function used is the Rectified Linear Unit (ReLU) function, defined by
2.2. Proposed ANN Model for Modeling PEMFCs
The artificial neural network model used is a fully connected multi-layer architecture (Figure 1), optimized for PEMFC voltage prediction. It comprises an input layer receiving two input features: current and temperature, followed by four hidden layers composed of 128, 64, 32, and 16 neurons, respectively. Each hidden layer is followed by a ReLU (Rectified Linear Unit) activation function to introduce non-linearity and improve the learning of complex input–output relationships. The output layer contains a single neuron designed to provide the predicted voltage value, while a regression layer is integrated to minimize the error between the predictions and actual values. This architecture enables experimental data to be efficiently exploited to obtain an accurate and generalizable model for PEMFC modeling. The voltage output of a fuel cell is influenced by several interdependent parameters, including temperature, hydrogen and airflow rates, and current density. However, in the current work, only temperature and current density were used as input parameters for the ANN model. This choice was primarily due to the inaccessibility of real-time flow rate measurements in our experimental setup. In sum, the model uses 240 neurons in the hidden layers, plus 1 neuron in the output layer, for a total of 241 neurons used.
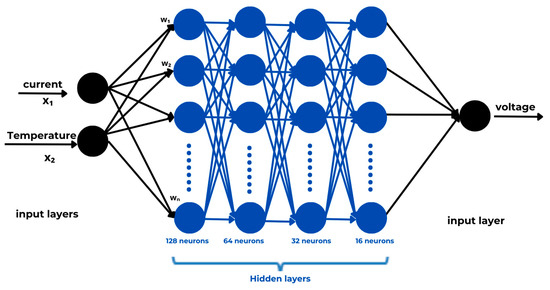
Figure 1.
Artificial neural network architecture.
The choice of the four-hidden-layer architecture (128-64-32-16 neurons) was based on a combination of empirical hyperparameter tuning and support from the previous literature on deep learning modeling of PEMFCs. Provisional tests explored different architectures with varying numbers of layers and neurons. Progressively decreasing layer sizes were chosen to enable the extraction of hierarchical features, which is essential for capturing the complex, non-linear relationships present in PEMFCs’ behavior. Simpler architectures with fewer layers were also evaluated but showed higher validation errors (higher MSE and lower R2), suggesting under-fitting and insufficient modeling capability. Deep architectures with a pyramidal structure (reducing the number of neurons per layer) are commonly used in modeling to promote efficient feature compression and avoid over-parameterization. Iterative manual tuning showed that the four-layer structure offered the best compromise between model complexity, learning time, and predictive performance.
The MATLAB code for modeling hydrogen fuel cells’ voltage based on current and temperature uses multiple linear regression. First, it fits a regression model to linear (I_train, T_train), quadratic (I_train2, T_train2), and interaction (I_train: T_train) data, capturing both linear and non-linear effects of input parameters on fuel cell voltage. Next, a prediction function is applied to the model to estimate the output voltage V_train as a function of the values of I_train and T_train. The advantage of this approach is that it provides a rapid analytical relationship between operating conditions and output voltage, enabling the rapid evaluation of fuel cell performance without the need for costly experimentation.
2.3. ANN Model Training
The training process of the ANN model presented in Figure 2 consists of adjusting the weights of the connections between neurons, starting with the initialization of the weights, followed by the propagation of the input data through the layers of the network to the output, using a specified optimizer. The number of epochs is set at 500, allowing the model to train over several cycles to improve its accuracy. The mini-batch size is set to 64, meaning that optimization is performed on groups of 64 samples at a time, improving the training stability.
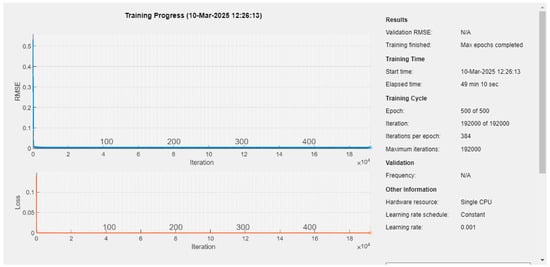
Figure 2.
ANN model training process.
During network training, several evaluation metrics are used to measure the model’s performance and its ability to make accurate predictions. Among the most common are the following:
- Mean squared error (MSE) measures the average squared deviation between the real voltage and predicted voltage . A low MSE value indicates a good model fit, defined as follows [32]:where
- is the real voltage;
- is the predicted voltage;
- is the total number of observations.
- Root-Mean-Square Error (RMSE): A lower RMSE means better precision, defined as follows [33]:
- Mean Absolute Percentage Error (MAPE) measures the average magnitude of the errors between the predicted and actual values, expressed as a percentage of the actual values. The MAPE is calculated using the following formula:
- Coefficient of determination (R2): This metric indicates the percentage of variance explained by the model. A value close to 1 means that the model predicts the data well, while a value close to 0 indicates poor performance, defined as follows [34]:where
- is the real voltage;
- is the predicted voltage;
- is the mean of the real values.
3. Data Acquisition
3.1. Hardware Setup
The experimental bench illustrated in Figure 3 was built to determine the dynamic behavior of the NEXA 1200 PEMFC, as well as the necessary data for modeling hydrogen fuel cells and the ANN model’s training and testing. The bench was designed to evaluate the performance of the hydrogen fuel cell with electric loads under controlled experimental conditions in the ISA laboratory.

Figure 3.
The experimental bench at the ISA laboratory.
The setup included the following: a NEXA 200 fuel cell module (PEMFC) (1), with its monitoring software, three metal hydride canisters from Heliocentris with storage capacities of 800 NL hydrogen (2), a Nexa 1200 DC/DC converter (3), a power supply from BK Precision used for the fuel cell starter (4), Hall effect sensors to measure the voltage and current variables (5) with their AX502 power supply from metrix (6), a programmable DC electronic load (7), and a MicroLabBox-dSPACE (8) with Control Desk software plugged into a personal computer for signal acquisition (9).
3.1.1. Hydrogen Fuel Cell
The fuel cell used in the experimental bench (1) was the Nexa 1200 from Heliocentris, a proton-exchange membrane fuel cell (PEMFC) designed for research and development applications. Its rated power is 1200 W, it operates at 20 to 36 VDC, and it can deliver a maximum current of 60 A. It uses pure hydrogen (99.95% minimum) as fuel, with consumption of around 15 slpm (standard liters per minute). Forced-air cooling provides a 335 m3/h airflow, ensuring stable, efficient operation. In terms of connectivity, it features a DC output via a 16–50 mm2 screw terminal, as well as a hydrogen input via a 6 mm tube. With dimensions of 220 × 400 × 550 mm and a weight of around 22 kg, it is relatively compact and suitable for laboratory environments. The graph below (Figure 4) shows the characteristic curves for the Nexa 1200 fuel cell from Heliocentris, relating power (P) and current (I), as well as voltage (U) and current (I), for the stack and the complete module [35].
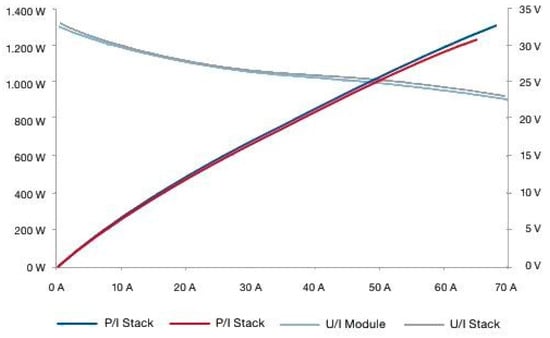
Figure 4.
Characteristic curves for the Nexa 1200 fuel cell.
3.1.2. Programmable DC Electronic Load
The EA-ELR 9250-70 from EA Elektro-Automatik is a programmable DC electronic load with energy recovery, offering a power range from 0 to 3.5 kW, voltage from 0 to 250 V, current from 0 to 70 A, and resistance from 0.09 to 120 Ω. It has an energy efficiency of around 93.5% and weighs 17 kg.
It imposes a controlled current profile on the cell in order to observe its voltage response and acquire accurate data for modeling. The current is progressively increased, and then decreased, while the voltage (V) remains constant at 24 V. Each current step lasts 5 min, allowing for observation of the cell’s response under different loads. The increase in current follows a progression of 5 A per step, reaching a maximum of 35 A, before decreasing in steps of 2.5 A. The evolution of the current, which forms a stepped structure with a step of 5 min, is useful for performance testing of PEMFCs to analyze their electrical behavior. The data collected are then used to train and validate the proposed ANN model, and to predict cell behavior based on applied load.
3.2. Data Acquisition for Deep Learning
The dataset consisted of 35,776 data points collected under carefully controlled experimental conditions. Experiments were carried out at an ambient temperature of 20 °C. Hydrogen and air were supplied at fixed flow rates under ambient pressure. The current varied progressively in the steps, with each step being maintained for 5 min to ensure system stabilization. Data were collected over a period of 1 hour and 5 min to obtain stable behavior at each current level. Repeated tests were run to assess reproducibility, and consistency checks were carried out to validate the data’s stability over time. The data were split at a ratio of 70% and 30% for training and testing, respectively. The division of the obtained data is an indispensable step in the construction of the ANN model to guarantee efficient training and an accurate evaluation. The training set is used for adjusting the model’s parameters, and the test set, representing 30%, is used to evaluate the model’s final performance, ensuring its generalizability. In addition, data normalization was applied to ensure faster and more stable convergence when training the model. Some points representing the current, temperature, and voltage under dynamic conditions of the fuel cell were determined, and they are listed in Table 1:

Table 1.
Some points of the experimental data.
3.3. Results
The current and voltage profiles obtained for the PEMFC are shown in Figure 5 and Figure 6, respectively. Such behavior is consistent with the functioning of a PEMFC (proton-exchange membrane fuel cell). Increasing the current causes a voltage decrease due to internal losses.
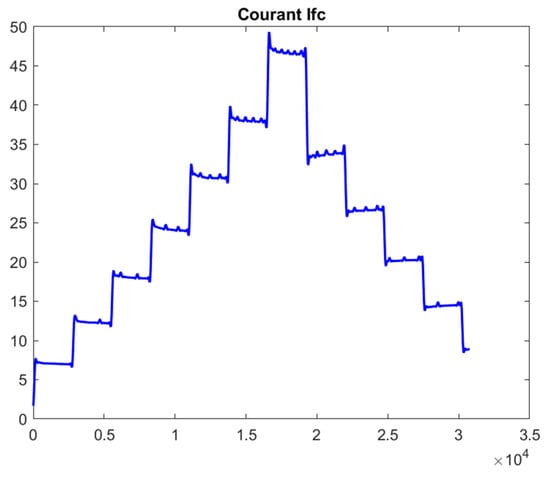
Figure 5.
Current profile of the PEMFC.
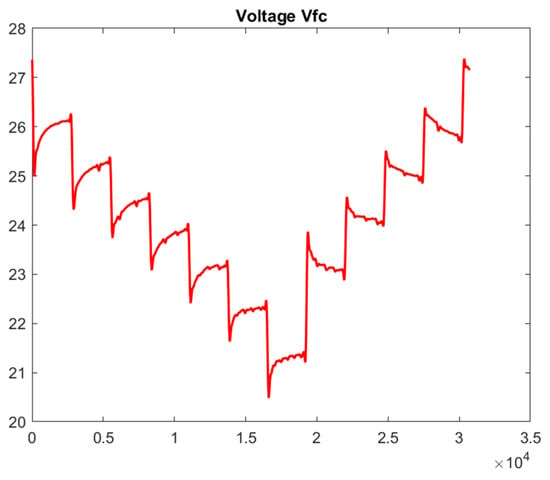
Figure 6.
Voltage profile of the PEMFC.
4. Model Performance and Evaluation
4.1. Optimizer
The choice of optimizer plays a crucial role in the performance of the proposed ANN model and its evaluation [36]. An efficient optimizer enables fast and stable convergence, improving the prediction accuracy while reducing the training time. In this study, we used the Adaptive Moment Estimation (ADAM) optimizer to train the artificial neural network (ANN) applied to the PEMFC modeling.
The ADAM optimizer was chosen due to its recognized performance in deep learning model optimization. It combines the advantages of the Momentum and RMSprop algorithms, enabling it to dynamically adapt the learning rate to each model parameter. This property is particularly advantageous for PEMFC modeling, where stable and rapid convergence is required (Table 2). The ADAM optimizer parameters summarize the main parameters of the ADAM optimizer and their role.

Table 2.
ADAM optimizer parameters.
4.2. Results
The ANN model developed for voltage prediction shows remarkable accuracy, as evidenced by the almost perfect superposition between the predicted and actual voltage curves, as shown in Figure 7. In addition, it can accurately track variations, even during abrupt changes, demonstrating its robustness and ability to adapt to process non-linearities. The results obtained show that the ADAM optimizer considerably improves the convergence and accuracy of the ANN model.
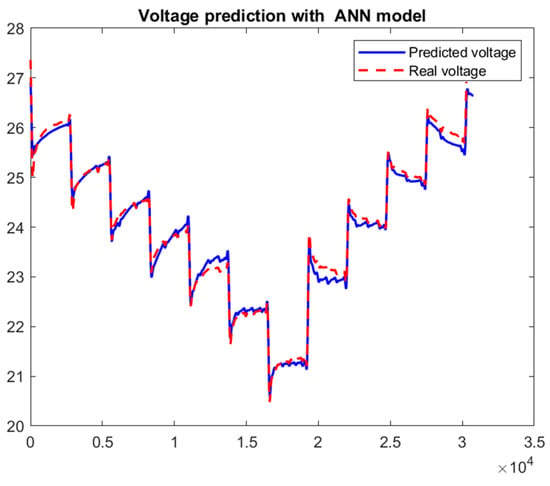
Figure 7.
Voltage prediction with the proposed ANN model–ADAM.
The model’s performances were evaluated by comparing several metrics. The use of ADAM enabled faster model convergence, with reduced values of both MSE (0.0429) and RMSE (0.2071). Also the R2 (0.9071) obtained indicates a strong correlation between the predicted and actual values, validating the robustness of the model, as shown in Figure 8.
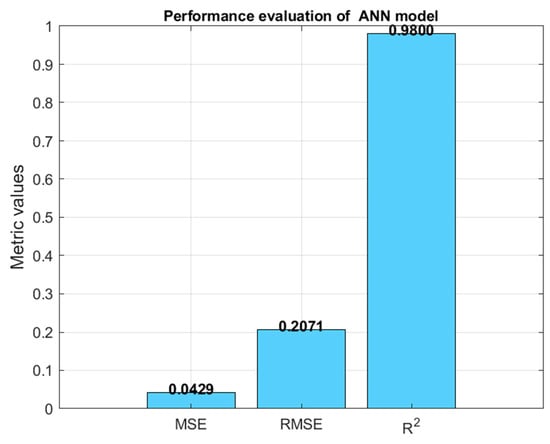
Figure 8.
Proposed ANN model performances.
4.3. Supremacy of the Proposed Model over the ML Models
To validate the effectiveness of our neural network-based prediction model, we compared its performance with that of four popular ML models in the literature [37]: Decision Tree (DT) regression, linear regression (LR), Support Vector Regression (SVR), and Multi-Layer Perceptron (MLP). This comparison, as demonstrated in Table 3, was based on two commonly used indicators: mean squared error (MSE), and the coefficient of determination (R2). These indicators allowed us to quantify the model’s accuracy and highlight the improvements brought about by our approach.

Table 3.
Performance metrics of the proposed model and the ML models.
4.4. Comparative Study Between Different Optimizers
In this section, we evaluate the performance of three different optimization algorithms—Stochastic Gradient Descent with Momentum (SGDM), Root-Mean-Square Propagation (RMSprop), and Adaptive Moment Estimation (ADAM)—to assess their impact on training the proposed artificial neural network (ANN) model. Each optimizer has unique characteristics that influence how the model learns, converges, and generalizes.
SGDM helps accelerate learning by incorporating momentum, which reduces fluctuations in the optimization path and leads to smoother convergence. However, its performance is highly dependent on selecting an appropriate learning rate, making tuning a critical step. RMSprop, in contrast, adapts the learning rate for each parameter based on past gradients, which helps stabilize training in cases where the loss function changes rapidly. While this adaptability improves convergence in some scenarios, it can also introduce instability if not properly configured. Among the three, ADAM stands out as the most robust, as it combines the benefits of both SGDM and RMSprop. By adjusting the learning rate dynamically while leveraging momentum, ADAM often achieves faster convergence and better generalization, making it a preferred choice in many deep learning applications.
To provide a clearer understanding of how these optimizers influence training efficiency and accuracy, a summary of their key parameters and behaviors is presented in Table 4. This comparison helps determine the most suitable optimization strategy for modeling hydrogen fuel cell performance, ensuring a balance between speed, stability, and predictive accuracy. A summary of the parameters of these optimizers is given.

Table 4.
Parameters of the three optimizers.
Figure 9 shows the comparison of voltages predicted by the proposed artificial neural network (ANN) model using three different optimization algorithms: ADAM, SGDM, and RMSprop. The predicted curves were compared with the real voltage to assess the accuracy of each optimizer. It can be observed that the ADAM optimizer provides the closest predictions to the real voltage, indicating better stability and efficient convergence. The SGDM optimizer also follows the real data, but with some more marked deviations at certain points. In contrast, the RMSprop optimizer shows larger fluctuations, suggesting less stable convergence for this application case.
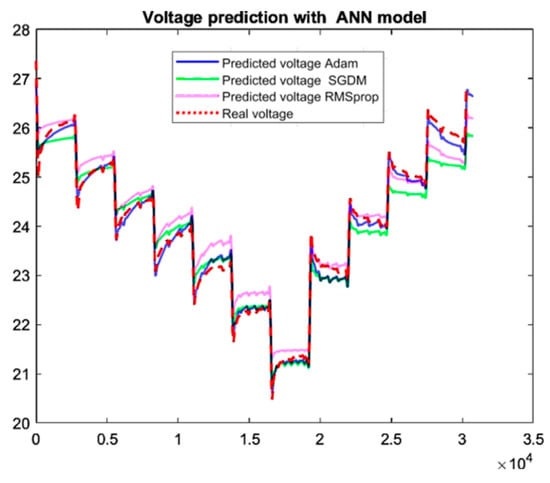
Figure 9.
Comparison of predicted voltages using different optimization methods.
To evaluate these three optimizers, we analyzed several performance metrics, as mentioned in Table 5.

Table 5.
Performance metrics of the three optimizers.
The results confirm that ADAM is the most suitable for voltage modeling of the proton-exchange membrane hydrogen fuel cell using an ANN, due to its better accuracy and robustness against model variations.
5. Conclusions
In conclusion, this work highlights the efficiency of artificial neural networks (ANNs) in modeling the performance of a proton-exchange membrane fuel cell (PEMFC). Using MATLAB, a predictive model was developed to accurately capture non-linear relationships between the input and output variables. A comparison of different optimization algorithms (ADAM, SGDM, and RMSprop) showed that ADAM provided the best performance, offering greater predictive accuracy and better stability. This was due to its ability to dynamically adjust the learning rate, ensuring faster convergence and reduced prediction errors. The results, validated by several metrics, confirm that the proposed model can reliably reproduce the actual behavior of fuel cell voltage. This model serves as a robust tool for performance analysis and optimization, enabling a better understanding and control of PEMFCs’ behavior.
Author Contributions
This paper was developed by a research team from an ISA Laboratory; conceptualization, methodology, and formal analysis, H.A. and H.E.F.; software, A.H. (Anwar Hasni), A.H. (Ahmed Hamed) and Y.E.A.; investigation and resources, A.I., A.H. (Anwar Hasni) and A.F.; writing, H.A. and A.L.; review and supervision, A.L. and H.E.F.; data curation, A.I., Y.E.A. and A.H. (Ahmed Hamed). All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding authors.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Lassioui, A.; Fadil, H.E.; Rachid, A.; El-Idrissi, Z.; Bouanou, T.; Belhaj, F.Z.; Giri, F. Modelling and Sliding Mode Control of a Wireless Power Transfer System for BEV Charger. Int. J. Model. Identif. Control 2020, 34, 171–186. [Google Scholar] [CrossRef]
- Koundi, M.; El Fadil, H.; EL Idrissi, Z.; Lassioui, A.; Intidam, A.; Bouanou, T.; Nady, S.; Rachid, A. Investigation of Hydrogen Production System-Based PEM EL: PEM EL Modeling, DC/DC Power Converter, and Controller Design Approaches. Clean. Technol. 2023, 5, 531–568. [Google Scholar] [CrossRef]
- Hassan, Q.; Azzawi, I.D.J.; Sameen, A.Z.; Salman, H.M. Hydrogen Fuel Cell Vehicles: Opportunities and Challenges. Sustainability 2023, 15, 11501. [Google Scholar] [CrossRef]
- Rachid, A.; El Fadil, H.; Gaouzi, K.; Rachid, K.; Lassioui, A.; El Idrissi, Z.; Koundi, M. Electric Vehicle Charging Systems: Comprehensive Review. Energies 2023, 16, 255. [Google Scholar] [CrossRef]
- Aminudin, M.A.; Kamarudin, S.K.; Lim, B.H.; Majilan, E.H.; Masdar, M.S.; Shaari, N. An Overview: Current Progress on Hydrogen Fuel Cell Vehicles. Int. J. Hydrogen Energy 2023, 48, 4371–4388. [Google Scholar] [CrossRef]
- Sajid, A.; Pervaiz, E.; Ali, H.; Noor, T.; Baig, M.M. A Perspective on Development of Fuel Cell Materials: Electrodes and Electrolyte. Int. J. Energy Res. 2022, 46, 6953–6988. [Google Scholar] [CrossRef]
- Zhang, Z.; Mao, J.; Liu, Z. Advancements and Insights in Thermal and Water Management of Proton Exchange Membrane Fuel Cells: Challenges and Prospects. Int. Commun. Heat. Mass. Transf. 2024, 153, 107376. [Google Scholar] [CrossRef]
- Ghasemi, M.; Nassef, A.M.; Al-Dhaifallah, M.; Rezk, H. Performance Improvement of Microbial Fuel Cell through Artificial Intelligence. Int. J. Energy Res. 2021, 45, 342–354. [Google Scholar] [CrossRef]
- Belhaj, F.Z.; El Fadil, H.; El Idrissi, Z.; Intidam, A.; Koundi, M.; Giri, F. New Equivalent Electrical Model of a Fuel Cell and Comparative Study of Several Existing Models with Experimental Data from the PEMFC Nexa 1200 W. Micromachines 2021, 12, 1047. [Google Scholar] [CrossRef]
- Tellez-Cruz, M.M.; Escorihuela, J.; Solorza-Feria, O.; Compañ, V. Proton Exchange Membrane Fuel Cells (PEMFCs): Advances and Challenges. Polymers 2021, 13, 3064. [Google Scholar] [CrossRef]
- Kordesch, K.; Hacker, V.; Gsellmann, J.; Cifrain, M.; Faleschini, G.; Enzinger, P.; Fankhauser, R.; Ortner, M.; Muhr, M.; Aronson, R.R. Alkaline Fuel Cells Applications. J. Power Sources 2000, 86, 162–165. [Google Scholar] [CrossRef]
- Eapen, D.; Suseendiran, S.; Rengaswamy, R. Phosphoric Acid Fuel Cells. In Compendium of Hydrogen Energy; Elsevier: Amsterdam, The Netherlands, 2016; pp. 57–70. [Google Scholar]
- Dicks, A.L. Molten Carbonate Fuel Cells. Curr. Opin. Solid State Mater. Sci. 2004, 8, 379–383. [Google Scholar] [CrossRef]
- Ramadhani, F.; Hussain, M.A.; Mokhlis, H.; Hajimolana, S. Optimization Strategies for Solid Oxide Fuel Cell (SOFC) Application: A Literature Survey. Renew. Sustain. Energy Rev. 2017, 76, 460–484. [Google Scholar] [CrossRef]
- Cheng, L.; Wu, Z.; Mou, J.; Gu, Y.; Wu, D.; Zhou, P.; Liu, J. Research Progress on Gas Supply System of Proton Exchange Membrane Fuel Cells. Processes 2024, 12, 1224. [Google Scholar] [CrossRef]
- Baroutaji, A.; Arjunan, A.; Robinson, J.; Wilberforce, T.; Abdelkareem, M.A.; Olabi, A.G. PEMFC Poly-Generation Systems: Developments, Merits, and Challenges. Sustainability 2021, 13, 11696. [Google Scholar] [CrossRef]
- Wang, Y.; Pang, Y.; Xu, H.; Martinez, A.; Chen, K.S. PEM Fuel Cell and Electrolysis Cell Technologies and Hydrogen Infrastructure Development–A Review. Energy Environ. Sci. 2022, 15, 2288–2328. [Google Scholar] [CrossRef]
- Segundo, R.-F.; Rocío, P.-C.; Luis, C.-C.; Angelats Silva, L.M. Potential Use of the Fungus Trichoderma Sp. as a Plastic-Reducing Agent and Electricity Generator in Microbial Fuel Cells. Processes 2024, 12, 2904. [Google Scholar] [CrossRef]
- Ogungbemi, E.; Wilberforce, T.; Ijaodola, O.; Thompson, J.; Olabi, A. Selection of Proton Exchange Membrane Fuel Cell for Transportation. Int. J. Hydrogen Energy 2021, 46, 30625–30640. [Google Scholar] [CrossRef]
- Veeranjaneyulu, K.; Joshi, S.; Devalla, V.; Kiran, K.S.; Khushal, K. Recent Advancements of PEMFC in Transport Applications; AIP Publishing: Melville, NY, USA, 2023; Volume 2492. [Google Scholar]
- Tao, S.; Irvine, J.T. Discovery and Characterization of Novel Oxide Anodes for Solid Oxide Fuel Cells. Chem. Rec. 2004, 4, 83–95. [Google Scholar] [CrossRef]
- Nady, S.; Fadil, H.E.; Belhaj, F.Z.; Intidam, A.; Koundi, M.; Idrissi, Z.E. Experimental Validation of an Output Feedback Controller Based on an Integral and Adaptive Backstepping Technique for a Fuel-Cell Power System. Int. J. Model. Identif. Control 2023, 43, 199–214. [Google Scholar] [CrossRef]
- Srinivasan, S. Fuel Cells: From Fundamentals to Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2006; ISBN 0-387-25116-2. [Google Scholar]
- Hamed, A.; El Fadil, H.; Lassioui, A.; Nady, S.; El Jeilani, S.; Bouanou, T. Modeling and Super-Twisting Sliding Mode Control of a Wireless Power Transfer Charger. In Automatic Control and Emerging Technologies, Proceedings of ACET 2023; El Fadil, H., Zhang, W., Eds.; Springer Nature Singapore: Singapore, 2024; pp. 387–395. [Google Scholar]
- Rajashekara, K. Power Conversion and Control Strategies for Fuel Cell Vehicles; IEEE: New York, NY, USA, 2003; Volume 3, pp. 2865–2870. [Google Scholar]
- Vichard, L.; Harel, F.; Ravey, A.; Venet, P.; Hissel, D. Analyse et Modélisation de La Dégradation d’une PEMFC à L’aide D’intelligence Artificielle; CNRS: Paris, France, 2020. [Google Scholar]
- Bicer, Y.; Dincer, I.; Aydin, M. Maximizing Performance of Fuel Cell Using Artificial Neural Network Approach for Smart Grid Applications. Energy 2016, 116, 1205–1217. [Google Scholar] [CrossRef]
- Bhagavatula, Y.S.; Bhagavatula, M.T.; Dhathathreyan, K. Application of Artificial Neural Network in Performance Prediction of PEM Fuel Cell. Int. J. Energy Res. 2012, 36, 1215–1225. [Google Scholar] [CrossRef]
- Lassioui, A.; El Ancary, M.; El Idrissi, Z.; El Fadil, H.; Rachid, K.; Rachid, A. Primary-Side Indirect Control of the Battery Charging Current in a Wireless Power Transfer Charger Using Adaptive Hill-Climbing Control Technique. Processes 2024, 12, 1264. [Google Scholar] [CrossRef]
- Abdolrasol, M.G.M.; Hussain, S.M.S.; Ustun, T.S.; Sarker, M.R.; Hannan, M.A.; Mohamed, R.; Ali, J.A.; Mekhilef, S.; Milad, A. Artificial Neural Networks Based Optimization Techniques: A Review. Electronics 2021, 10, 2689. [Google Scholar] [CrossRef]
- Paturi, U.M.R.; Cheruku, S.; Geereddy, S.R. Process Modeling and Parameter Optimization of Surface Coatings Using Artificial Neural Networks (ANNs): State-of-the-Art Review. Mater. Today Proc. 2021, 38, 2764–2774. [Google Scholar] [CrossRef]
- Köksoy, O. Multiresponse Robust Design: Mean Square Error (MSE) Criterion. Appl. Math. Comput. 2006, 175, 1716–1729. [Google Scholar] [CrossRef]
- Chai, T.; Draxler, R.R. Root Mean Square Error (RMSE) or Mean Absolute Error (MAE)?—Arguments against Avoiding RMSE in the Literature. Geosci. Model. Dev. 2014, 7, 1247–1250. [Google Scholar] [CrossRef]
- Chicco, D.; Warrens, M.J.; Jurman, G. The Coefficient of Determination R-Squared Is More Informative than SMAPE, MAE, MAPE, MSE and RMSE in Regression Analysis Evaluation. Peerj Comput. Sci. 2021, 7, e623. [Google Scholar] [CrossRef]
- Datenblatt_Nexa1200_EN_1109. Available online: https://www.ien.eu/uploads/tx_etim/Datenblatt_Nexa1200_EN_1109.pdf (accessed on 1 May 2025).
- Li, H.; Gao, D.; Shi, L.; Zheng, F.; Yang, B. Parameter Identification of Solid Oxide Fuel Cell Using Elman Neural Network and Dynamic Fitness Distance Balance-Manta Ray Foraging Optimization Algorithm. Processes 2024, 12, 2504. [Google Scholar] [CrossRef]
- Wickramaarachchi, W.A.M.K.P.; Minakshi, M.; Gao, X.; Dabare, R.; Wong, K.W. Hierarchical Porous Carbon from Mango Seed Husk for Electro-Chemical Energy Storage. Chem. Eng. J. Adv. 2021, 8, 100158. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).