Explainable AI and Feature Engineering for Machine-Learning-Driven Predictions of the Properties of Cu-Cr-Zr Alloys: A Hyperparameter Tuning and Model Stacking Approach
Abstract
1. Introduction
2. A Description of the Data
2.1. Feature Description
2.1.1. Input Features
- Aging time (min): This represents the duration of the aging treatment in minutes. Heat treatment significantly influences both a material’s hardness and electrical conductivity by inducing microstructural changes. Its values range from 0 to 90 min.
- Alloy composition (%): This represents the chemical composition of an alloy. This plays a critical role in determining its properties. Key elements include the following:
2.1.2. Output Features
- Hardness (HRC): The primary mechanical property under investigation, measured in Rockwell Hardness C (HRC). Hardness is crucial in preventing wear and deformation under mechanical and thermal stresses in electromechanical applications. It is influenced by the alloying elements and aging time.
- Electrical conductivity (mS/m): The target electrical property, measured in millisiemens per meter (mS/m). Electrical conductivity is essential for electromechanical applications to minimize the power loss and ensure quick signal transfer.
2.2. The Dataset and an Overview of the Feature Analysis
- Feature creation: Both direct and indirect features were created to capture various relationships among the variables, such as interaction terms. Specifically, pairwise interactions between the alloying elements (Cr, Zr, Ce, La) and processing parameters (aging time) were generated to model their synergistic effects. Representative examples such as AgingTime × Ce and Cr × Zr were selected based on the feature importance analysis.
- Feature selection: A mixture of correlation analysis, SHapley Additive exPlanations (SHAP)-based feature importance, and ML-driven feature importance methods was combined to select the relevant predictors. This ensured an appropriate trade-off between the model’s complexity and interpretability.
- Data standardization: The dataset was standardized according to the standard scale method [7] so that every feature could be most equitably scaled across the domains. This was to ensure that one feature did not overshadow all others in the learning process. The transformation was defined by Equation (1), where M is the mean (Equation (2)) and SD is the standard deviation (Equation (3)):
- AgingTime × Ce: This includes the combined effect of the Ce content and heat treatment on the microstructural precipitation and strengthening process;
- Cr × Zr: This testifies to the possible synergy of chromium and zirconium in grain refinement and solid solution strengthening.
3. The Modeling Framework and Methodology
3.1. Overview of Machine Learning and Deep Learning Algorithms
- Linear models (e.g., Ridge, Lasso, ElasticNet) were included to provide interpretable baselines;
- Tree models (e.g., decision trees, random forest, extra trees) were included due to their robustness when dealing with non-linear relationships and feature interactions;
- Boosting models (e.g., XGBoost, LightGBM, CatBoost, AdaBoost, Gradient Boosting) were included due to their current state-of-the-art status with respect to predictions in tabular data;
- Support vector machines and K-nearest neighbors were applied to test the performance concerning margin-based and instance-based learning paradigms;
- DL models (MLP, CNN, and LSTM) were added to serve as a reference and assess the future scalability potential, despite the knowledge that their use with small datasets is not optimal.
3.1.1. Machine Learning Algorithms
3.1.2. Deep Learning Algorithms
3.1.3. Rationale for the Algorithm Selection
3.2. Data Preprocessing and Preparation
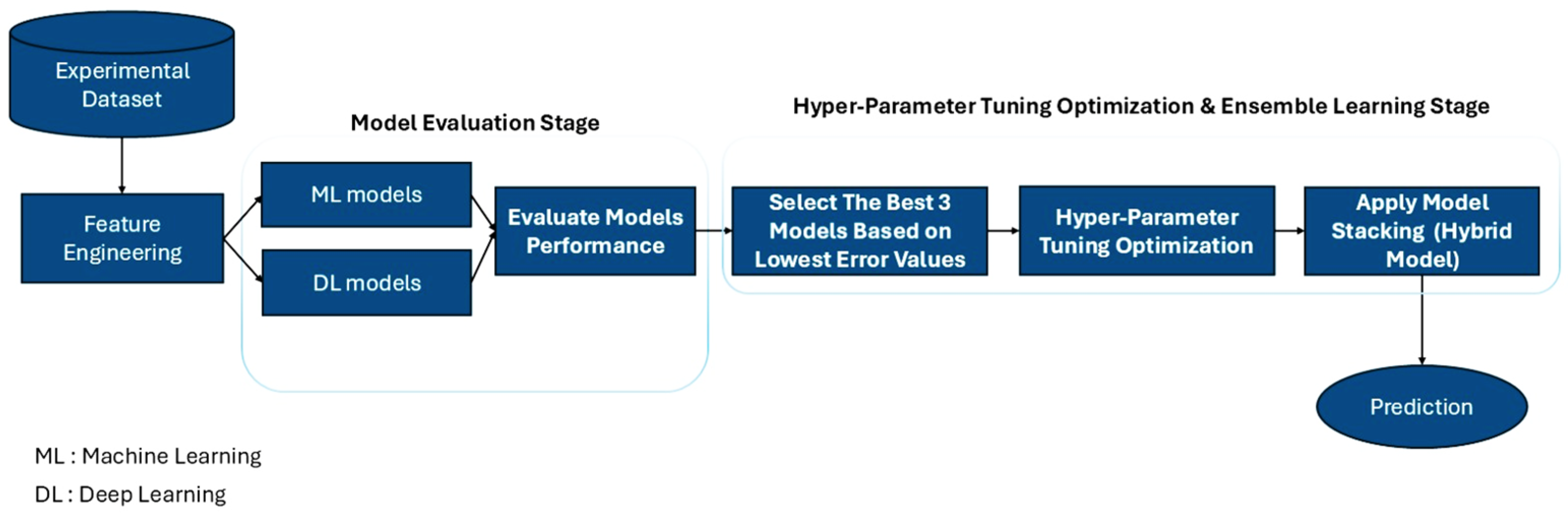
3.3. The Model Selection and Training
3.4. Model Evaluation and Cross-Validation
3.5. Hyperparameter Optimization
3.6. Ensemble Learning and Model Stacking
4. Analysis of Feature Importance
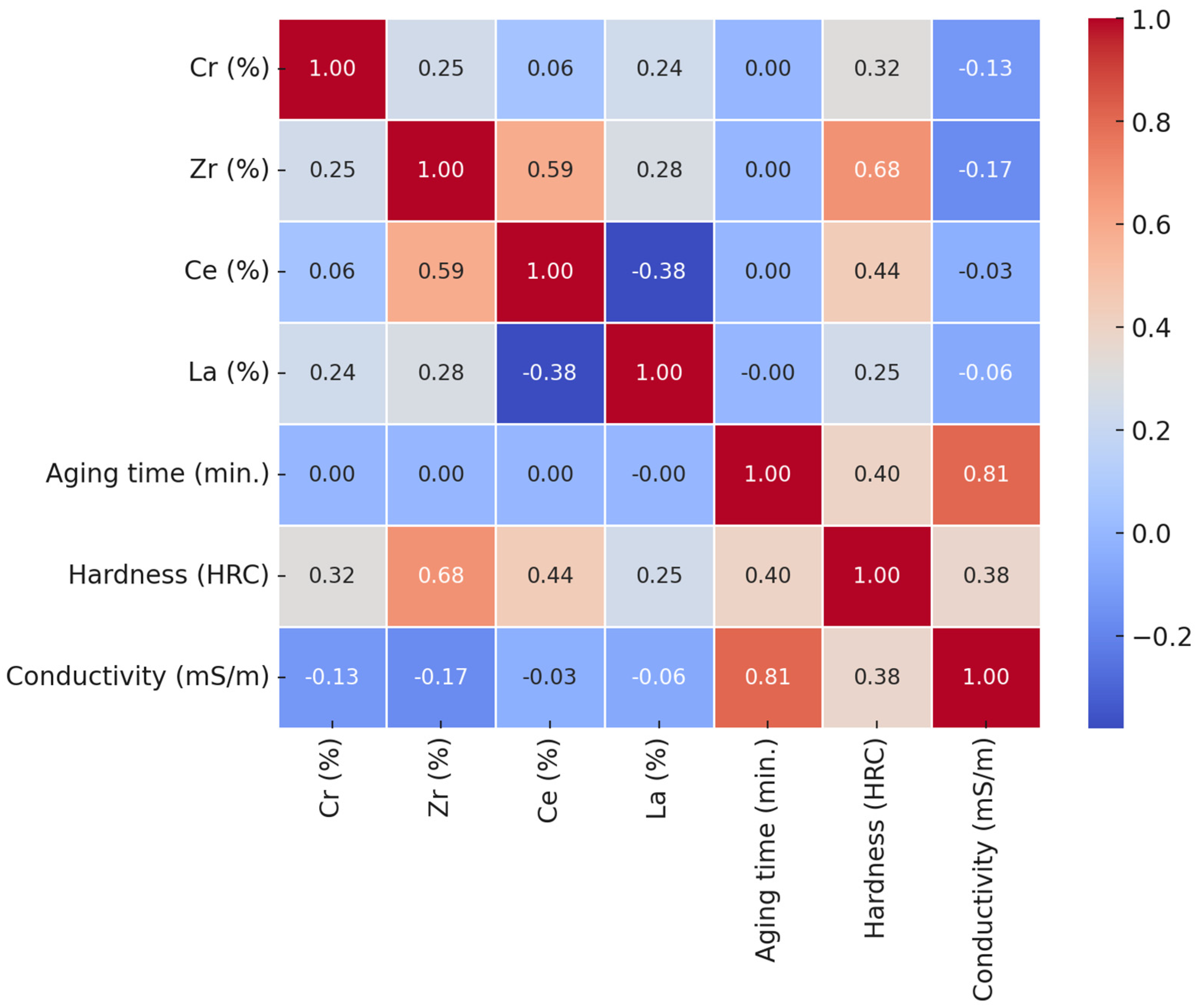
4.1. The Correlation Analysis
4.1.1. Hardness
4.1.2. Electrical Conductivity
- Aging time and electrical conductivity (0.81): The strongest correlation, indicating that this heat treatment is the primary driver of electrical conductivity;
- Cr, Zr, Ce, La vs. electrical conductivity: Weak negative correlations suggest these alloying elements have little effect on the electrical conductivity.
4.2. Hardness Predictions
4.3. Electrical Conductivity Predictions
5. Performance Evaluation
6. Results
6.1. The Initial Predictions of Hardness and Electrical Conductivity Without Feature Engineering and Selection
6.1.1. The Hardness Prediction Performance
6.1.2. The Electrical Conductivity Prediction Performance
6.1.3. Implications and Next Steps
6.2. Predictions with Feature Engineering and Selection
6.2.1. The Hardness Prediction Performance After Feature Engineering
6.2.2. The Electrical Conductivity Prediction Performance After Feature Engineering
6.2.3. Key Takeaways
6.3. Hyperparameter Tuning for Performance Optimization
6.4. Model Stacking for Enhancement of the Final Predictions
7. Discussion and Future Work
7.1. The Impact of the Proposed Framework on Material Property Predictions
7.2. Future Research Directions
- Larger and more diverse datasets: A greater quantity and variety of types of data would equate to significantly better robustness, as well as generalization of ML/DL models into edge case behaviors, thereby reducing the prediction uncertainty.
- Transfer learning: With transfer learning, the learning efficiency and potential of small-data models can be supplemented with prior learned representations through the transfer of knowledge acquired through the application of a larger material science dataset.
- Generative modeling: Using variational autoencoders (VAEs) and Conditional Generative Adversarial Networks (cGANs), among other methods, the authors could synthetically augment the dataset with realistic but novel alloy compositions and their corresponding property patterns.
- Physics-informed modeling: Adopting Physics-Informed Neural Networks (PINNs) allows metallurgical laws (e.g., solid solution strengthening, grain boundary effects) to be embedded directly into the learning process, thereby improving both the accuracy and physical consistency.
- Multi-objective optimization is essential since in reality, any alloy is designed based on multiple conflicting properties. Non-dominated Sorting Genetic Algorithm II (NSGA-II), Bayesian multi-objective optimization, and many such tools could help with reaching comparative solutions suited to each threshold performance across more criteria.
- Uncertainty-aware learning: Introducing predictive uncertainty via Bayesian models, quantile regression, or Monte Carlo dropout would make the model outputs markedly more trustworthy, especially in experimental or safety-critical scenarios.
- Real-time and industrial deployments: Extending this framework for integration with real-time systems in manufacturing or quality control pipelines could help bring predictive alloy modeling into practical industrial use.
8. Conclusions
- Strong agreement was observed between hardness and electrical conductivity in the correlation and SHAP feature importance analyses, with metallurgical concepts bringing strong support for their reliability.
- According to the feature importance analysis, the elements that contribute the most to hardness are Zr content and aging time, whereas second place goes to the Ce content. By contrast, lower contributions to the hardness values come from the Cr and La components.
- Aging time has the largest effect on electrical conductivity, whereas the alloying elements have a minor weak negative effect.
- Feature engineering and selection increased the models’ performance to a very large extent, indicating the need for relevant predictors;
- In terms of high accuracy and quick training times, XGBoost performed well for hardness, but CatBoost was the most successful for electrical conductivity;
- Hyperparameter tuning showed further improvements in the accuracy over that of the ensemble models;
- Model stacking proved to be more efficient than the use of single models for hardness and electrical conductivity predictions;
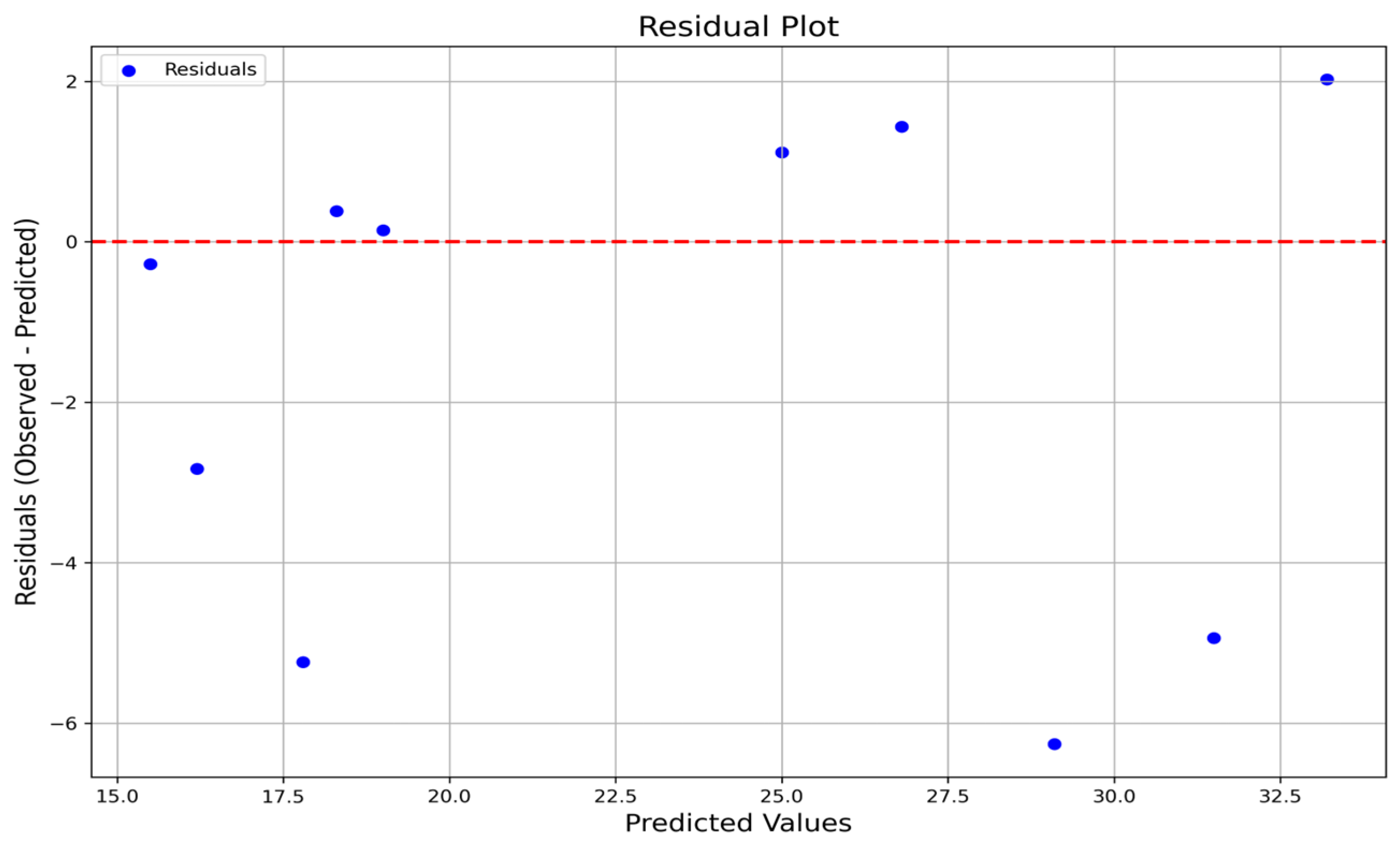
- The residual analysis confirmed that the current data regime was more complicated and showed more significant deviations and indications of heteroscedasticity for hardness;
- Model stacking yielded the best results, outperforming the individual models in both hardness and electrical conductivity predictions;
- The effectiveness of the new stacked models can be seen in R2 scores of 0.8762 for hardness and 0.8132 for electrical conductivity;
- The DL models could not deliver good results due to the size limitations of the dataset.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, C.; Fu, H.; Jiang, L.; Xue, D.; Xie, J. A property-oriented design strategy for high performance copper alloys via machine learning. Npj Comput. Mater. 2019, 5, 87. [Google Scholar] [CrossRef]
- Ibrahim, M.; Reda, R. Tailoring the Composition of the Functional Cu–Cr–Zr–La/Ce Alloys for Electromechanical Applications. Mater. Sci. Technol. 2023, 39, 209–235. [Google Scholar] [CrossRef]
- Ibrahim, M.; Moussa, M.E.; Reda, R. Upgrading the Performance of Functional Cu–Cr–Zr Alloys for Resistance Welding Electrodes. Mater. Sci. Technol. 2022, 38, 484–498. [Google Scholar] [CrossRef]
- Zhao, S.; Li, N.; Hai, G.; Zhang, Z. An improved composition design method for high-performance copper alloys based on various machine learning models. AIP Adv. 2023, 13, 025262. [Google Scholar] [CrossRef]
- Hu, M.; Tan, Q.; Knibbe, R.; Wang, S.; Li, X.; Wu, T.; Jarin, S.; Zhang, M.-X. Prediction of Mechanical Properties of Wrought Aluminium Alloys Using Feature Engineering Assisted Machine Learning Approach. Met. Mater. Trans. A 2021, 52, 2873–2884. [Google Scholar] [CrossRef]
- Zhang, Y.; Dang, S.; Chen, H.; Li, H.; Chen, J.; Fang, X.; Shi, T.; Zhu, X. Advances in machine learning methods in copper alloys: A review. J. Mol. Model. 2024, 30, 398. [Google Scholar] [CrossRef]
- Gal, M.S.; Rubinfeld, D.L. Data standardization. N. Y. Univ. Law Rev. 2019, 94, 30. [Google Scholar] [CrossRef]
- Friedman, J.H. Greedy function approximation: A gradient boosting machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Udousoro, I.C. Machine Learning: A Review. Semicond. Sci. Inf. Devices 2020, 2, 5–14. [Google Scholar] [CrossRef]
- Sarker, I.H. Machine Learning: Algorithms, Real-World Applications and Research Directions. SN Comput. Sci. 2021, 2, 160. [Google Scholar] [CrossRef] [PubMed]
- Geurts, P.; Ernst, D.; Wehenkel, L. Extremely randomized trees. Mach. Learn. 2006, 63, 3–42. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A scalable tree boosting system. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (KDD), San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar] [CrossRef]
- Prokhorenkova, L.; Gusev, G.; Vorobev, A.; Dorogush, A.V.; Gulin, A. CatBoost: Unbiased boosting with categorical features. Adv. Neural Inf. Process. Syst. 2018, 31, 6638–6648. [Google Scholar] [CrossRef]
- Bharadiya, J.P. A Review of Bayesian Machine Learning Principles, Methods, and Applications. Int. J. Innov. Res. Sci. Eng. Technol. 2023, 8, 2033–2038. [Google Scholar] [CrossRef]
- Zou, H.; Hastie, T. Regularization and variable selection via the elastic net. J. R. Stat. Soc. Stat. Methodol. Ser. B 2005, 67, 301–320. [Google Scholar] [CrossRef]
- Feng, Y.; Wu, Q. A statistical learning assessment of Huber regression. J. Approx. Theory 2022, 273, 105660. [Google Scholar] [CrossRef]
- Atiea, M.A.; Shaheen, A.M.; Alassaf, A.; Alsaleh, I. Enhanced solar power prediction models with integrating meteorological data toward sustainable energy forecasting. Int. J. Energy Res. 2024, 2024, 8022398. [Google Scholar] [CrossRef]
- Śmigiel, S. ECG Classification Using Orthogonal Matching Pursuit and Machine Learning. Sensors 2022, 22, 4960. [Google Scholar] [CrossRef]
- Crammer, K.; Dekel, O.; Keshet, J.; Shalev-Shwartz, S.; Singer, Y. Online passive-aggressive algorithms. J. Mach. Learn. Res. 2006, 7, 551–585. [Google Scholar]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar] [CrossRef]
- Ke, G.; Meng, Q.; Finley, T.; Wang, T.; Chen, W.; Ma, W.; Ye, Q.; Liu, T. LightGBM: A highly efficient gradient boosting decision tree. Adv. Neural Inf. Process. Syst. 2017, 30, 3146–3154. [Google Scholar]
- Atiea, M.A.; Adel, M. Transformer-based Neural Network for Electrocardiogram Classification. Int. J. Adv. Comput. Sci. Appl. 2022, 13, 357–363. [Google Scholar] [CrossRef]
- de Andrade, C.H.T.; de Melo, G.C.G.; Vieira, T.F.; de Araújo, Í.B.Q.; Martins, A.d.M.; Torres, I.C.; Brito, D.B.; Santos, A.K.X. How Does Neural Network Model Capacity Affect Photovoltaic Power Prediction? A Study Case. Sensors 2023, 23, 1357. [Google Scholar] [CrossRef]
- Chan, K.Y.; Abu-Salih, B.; Qaddoura, R.; Al-Zoubi, A.M.; Palade, V.; Pham, D.-S.; Del Ser, J.; Muhammad, K. Deep neural networks in the cloud: Review, applications, challenges and research directions. Neurocomputing 2023, 545, 126327. [Google Scholar] [CrossRef]
- Shekar, B.H.; Dagnew, G. Grid search-based hyperparameter tuning and classification of microarray cancer data. In Proceedings of the 2nd International Conference on Advanced Computational and Communication Paradigms (ICACCP), Gangtok, India, 25–28 February 2019. [Google Scholar] [CrossRef]
- Frazier, P.I. A Tutorial on Bayesian Optimization. arXiv 2018, arXiv:1807.02811. [Google Scholar]
- Barton, M.; Lennox, B. Model stacking to improve prediction and variable importance robustness for soft sensor development. Digit. Chem. Eng. 2022, 3, 100034. [Google Scholar] [CrossRef]
- Shcherbakov, M.V.; Brebels, A.; Shcherbakova, N.L.; Tyukov, A.P.; Janovsky, T.A.; Kamaev, V.A. A survey of forecast error measures. World Appl. Sci. J. 2013, 24, 171–176. [Google Scholar]
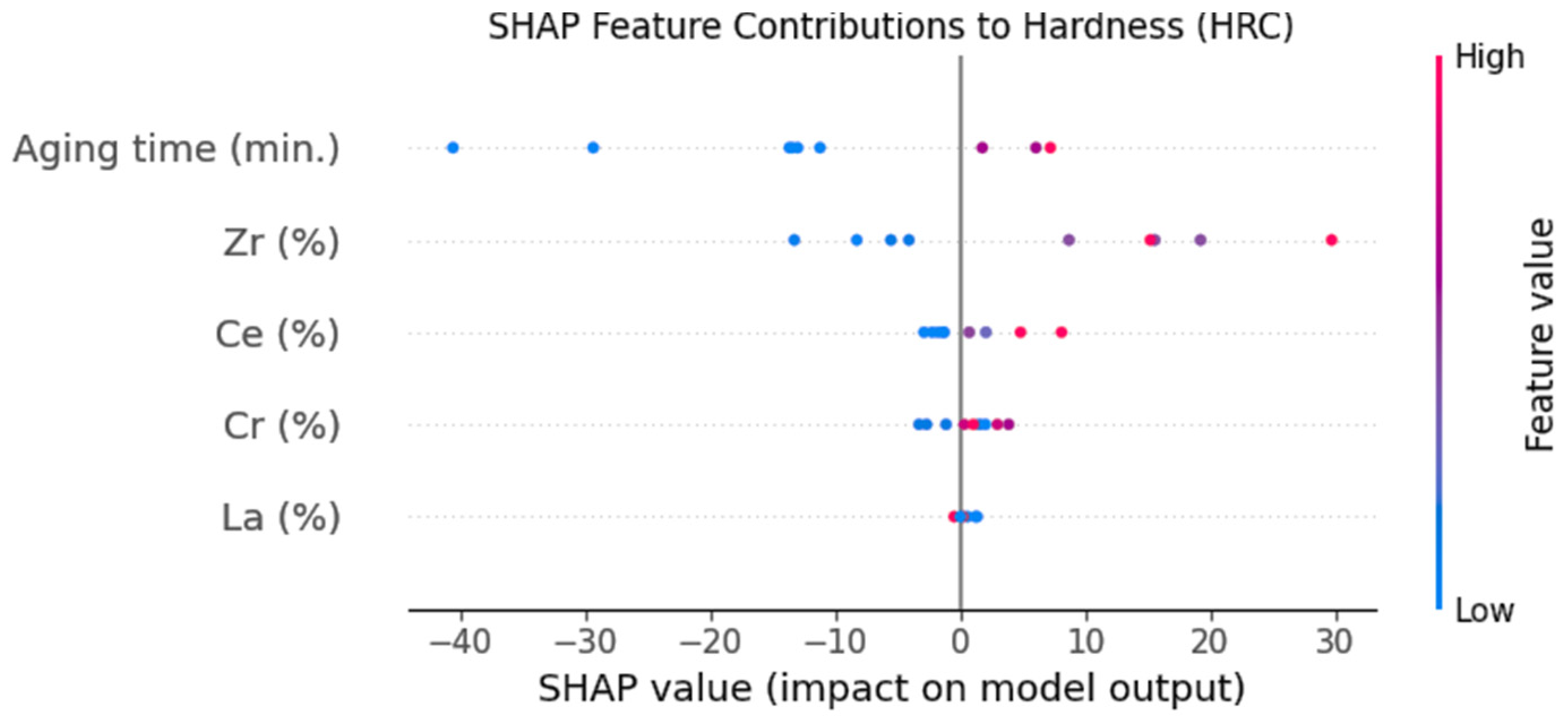

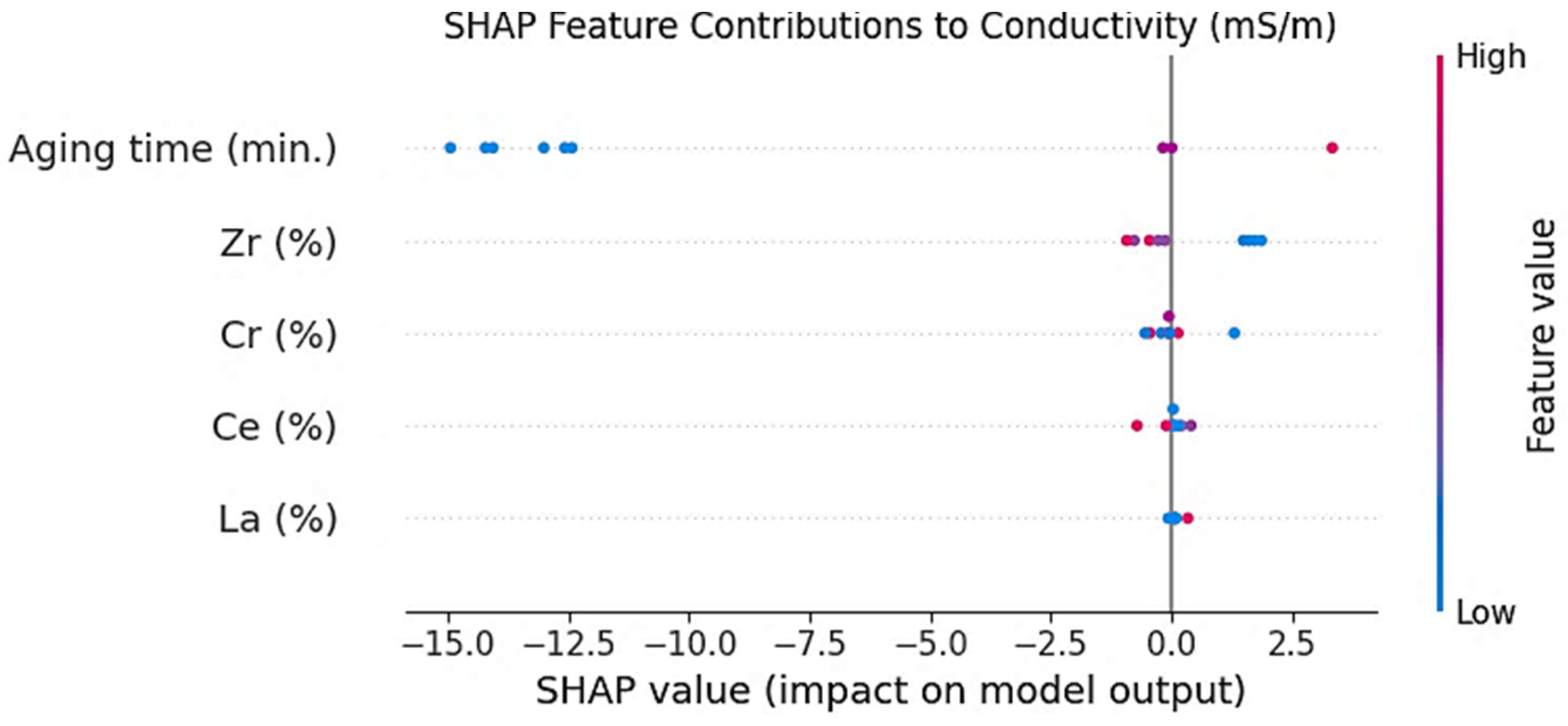


| Feature | SHAP Importance Rank (Hardness) | Pearson’s Correlation with Hardness | SHAP Importance Rank (Conductivity) | Pearson’s Correlation with Conductivity |
|---|---|---|---|---|
| Aging Time | 1 | +0.40 | 1 | +0.81 |
| Zr (%) | 2 | +0.68 | 3 | −0.22 |
| Ce (%) | 3 | +0.44 | 4 | −0.16 |
| Cr (%) | 4 | +0.32 | 2 | −0.21 |
| La (%) | 5 | +0.25 | 5 | −0.17 |
| Model | R2 | RMSE | MAE | Time (s) |
|---|---|---|---|---|
| AdaBoost | 0.6806 | 21.8244 | 15.9758 | 0.327 |
| ET | 0.6475 | 22.9258 | 13.8888 | 0.438 |
| CatBoost | 0.6439 | 23.0438 | 16.0284 | 1.331 |
| XGBoost | 0.6423 | 23.0965 | 15.9762 | 0.208 |
| DT | 0.6091 | 24.1443 | 16.1777 | 0.007 |
| GBR | 0.6075 | 24.1925 | 17.5509 | 0.222 |
| RF | 0.6074 | 24.1964 | 16.5653 | 0.611 |
| BR | 0.5224 | 26.6874 | 24.839 | 0.011 |
| EN | 0.502 | 27.2509 | 24.8831 | 0.008 |
| Ridge | 0.4906 | 27.5603 | 24.8734 | 0.008 |
| PAR | 0.4764 | 27.9412 | 26.5533 | 0.008 |
| HR | 0.4466 | 28.7274 | 25.1102 | 0.029 |
| LASSO | 0.4278 | 29.2106 | 24.5364 | 0.008 |
| LR | 0.427 | 29.2305 | 24.5834 | 0.01 |
| KNN | 0.3948 | 30.0403 | 25.74 | 0.01 |
| MLP | 0.0391 | 37.8528 | 32.1137 | 3.743 |
| Dummy | −0.0005 | 38.6256 | 33.9951 | 0.005 |
| LightGBM | −0.0005 | 38.6256 | 33.9951 | 0.181 |
| OMP | −0.0167 | 38.937 | 30.9779 | 0.008 |
| CNN | −9.4075 | 124.5748 | 118.4372 | 1.359 |
| LSTM | −9.4705 | 124.9516 | 118.8377 | 3.447 |
| Model | R2 | RMSE | MAE | Time (s) |
|---|---|---|---|---|
| CatBoost | 0.6452 | 3.2322 | 2.4843 | 0.338 |
| AdaBoost | 0.6303 | 4.6867 | 3.7656 | 0.381 |
| GBR | 0.6206 | 4.7478 | 3.8211 | 0.244 |
| DT | 0.6146 | 4.7849 | 3.925 | 0.007 |
| RF | 0.6014 | 4.8666 | 3.1853 | 0.611 |
| LASSO | 0.4231 | 5.854 | 5.3156 | 0.009 |
| XGBoost | 0.4145 | 5.8915 | 3.5958 | 0.269 |
| ET | 0.2694 | 3.5903 | 2.7823 | 0.092 |
| EN | 0.0487 | 5.4644 | 4.3068 | 0.022 |
| RR | 0.0157 | 5.2386 | 4.4315 | 0.022 |
| LR | 0.0117 | 5.2766 | 4.4768 | 1.32 |
| BR | 0.0095 | 5.3046 | 4.4264 | 0.028 |
| OMP | −0.0038 | 5.0699 | 4.1033 | 0.024 |
| PAR | −0.0476 | 6.121 | 5.0613 | 0.02 |
| HR | −0.1539 | 5.6234 | 4.7426 | 0.024 |
| MLP | −0.4866 | 5.5228 | 4.7283 | 3.644 |
| KNN | −0.5567 | 7.0426 | 5.3322 | 0.034 |
| LightGBM | −0.5931 | 7.7115 | 6.3372 | 0.36 |
| Dummy | −0.5931 | 7.7115 | 6.3372 | 0.022 |
| CNN | −10.9431 | 26.6373 | 25.4912 | 1.469 |
| LSTM | −11.0996 | 26.8113 | 25.6806 | 4.003 |
| Model | R2 | RMSE | MAE | Time (s) |
|---|---|---|---|---|
| XGBoost | 0.7755 | 18.2959 | 13.2117 | 0.204 |
| DT | 0.7676 | 18.6138 | 13.0222 | 0.007 |
| CatBoost | 0.7421 | 19.612 | 14.1581 | 1.263 |
| AdaBoost | 0.7347 | 19.891 | 14.7487 | 0.327 |
| ET | 0.7158 | 20.587 | 12.8466 | 0.435 |
| RF | 0.6643 | 22.3722 | 15.6268 | 0.608 |
| GBR | 0.62 | 23.8035 | 18.4999 | 0.213 |
| BR | 0.541 | 26.1628 | 21.2371 | 0.011 |
| EN | 0.5297 | 26.4803 | 21.3302 | 0.008 |
| RR | 0.5106 | 27.0143 | 21.4475 | 0.008 |
| HR | 0.4749 | 27.9824 | 21.5282 | 0.027 |
| LASSO | 0.4464 | 28.7312 | 21.8688 | 0.008 |
| LR | 0.444 | 28.7932 | 21.8515 | 0.01 |
| KNN | 0.4403 | 28.8886 | 22.8312 | 0.009 |
| PAR | 0.3362 | 31.4623 | 22.841 | 0.008 |
| OMP | 0.1184 | 36.2571 | 25.6582 | 0.008 |
| MLP | 0.0058 | 38.5027 | 28.7022 | 3.912 |
| Dummy | −0.0005 | 38.6256 | 33.9951 | 0.005 |
| LightGBM | −0.0005 | 38.6256 | 33.9951 | 0.144 |
| CNN | −9.4266 | 124.6896 | 118.5304 | 1.358 |
| LSTM | −9.4755 | 124.9814 | 118.8656 | 3.911 |
| Model | R2 | RMSE | MAE | Time (s) |
|---|---|---|---|---|
| CatBoost | 0.7399 | 2.5616 | 2.0736 | 0.3 |
| DT | 0.6545 | 3.7052 | 2.9362 | 0.022 |
| AdaBoost | 0.6494 | 3.3831 | 2.5718 | 0.05 |
| GBR | 0.6383 | 3.4992 | 2.7524 | 0.05 |
| RF | 0.6064 | 3.5005 | 2.69 | 0.118 |
| LASSO | 0.4524 | 5.1387 | 4.0045 | 0.022 |
| XGBoost | 0.4353 | 5.6883 | 3.0741 | 0.196 |
| MLP | 0.3765 | 6.0862 | 4.9853 | 3.327 |
| ET | 0.2737 | 3.6707 | 2.8467 | 0.09 |
| KNN | 0.1844 | 4.3802 | 3.3835 | 0.028 |
| RR | 0.0674 | 4.9634 | 4.0993 | 0.02 |
| EN | 0.0654 | 5.4055 | 4.1395 | 0.02 |
| BR | 0.0635 | 4.9796 | 4.103 | 0.024 |
| LAR | 0.045 | 4.9771 | 4.1558 | 0.018 |
| OMP | −0.0038 | 5.0699 | 4.1033 | 0.026 |
| PAR | −0.0258 | 5.3578 | 4.3611 | 0.02 |
| HR | −0.0397 | 5.3232 | 4.2347 | 0.024 |
| LightGBM | −0.5931 | 7.7115 | 6.3372 | 0.386 |
| Dummy | −0.5931 | 7.7115 | 6.3372 | 0.02 |
| CNN | −11.0175 | 26.7202 | 25.5921 | 1.4 |
| LSTM | −11.1174 | 26.831 | 25.7001 | 3.513 |
| Model | R2 | RMSE | MAE | Time (s) |
|---|---|---|---|---|
| XGBoost | 0.8222 | 16.2822 | 12.2839 | 0.29 |
| CatBoost | 0.7824 | 18.0141 | 13.7423 | 0.317 |
| DT | 0.7714 | 18.8639 | 14.8355 | 0.02 |
| Model | R2 | RMSE | MAE | Time (s) |
|---|---|---|---|---|
| CatBoost | 0.8080 | 3.1964 | 2.0506 | 0.217 |
| AdaBoost | 0.7827 | 3.6062 | 2.5655 | 0.5 |
| DT | 0.6597 | 3.7052 | 2.9362 | 0.017 |
| Model | R2 | RMSE | MAE | Time (s) |
|---|---|---|---|---|
| Hardness Stacked Model | 0.8762 | 13.5860 | 10.9556 | 1.739 |
| Electrical Conductivity Stacked Model | 0. 8132 | 2.9762 | 2.0341 | 1.091 |
| Metric | Mean (Hardness) | 95% CI (Hardness) | Mean (Conductivity) | 95% CI (Conductivity) |
|---|---|---|---|---|
| R2 | 0.87 | [0.384, 0.940] | 0.81 | [0.467, 0.859] |
| MAE | 10.96 | [6.582, 18.180] | 2.03 | [1.500, 2.520] |
| RMSE | 13.59 | [8.427, 20.795] | 2.98 | [2.100, 3.420] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Atiea, M.A.; Reda, R.; Ataya, S.; Ibrahim, M. Explainable AI and Feature Engineering for Machine-Learning-Driven Predictions of the Properties of Cu-Cr-Zr Alloys: A Hyperparameter Tuning and Model Stacking Approach. Processes 2025, 13, 1451. https://doi.org/10.3390/pr13051451
Atiea MA, Reda R, Ataya S, Ibrahim M. Explainable AI and Feature Engineering for Machine-Learning-Driven Predictions of the Properties of Cu-Cr-Zr Alloys: A Hyperparameter Tuning and Model Stacking Approach. Processes. 2025; 13(5):1451. https://doi.org/10.3390/pr13051451
Chicago/Turabian StyleAtiea, Mohammed A., Reham Reda, Sabbah Ataya, and Mervat Ibrahim. 2025. "Explainable AI and Feature Engineering for Machine-Learning-Driven Predictions of the Properties of Cu-Cr-Zr Alloys: A Hyperparameter Tuning and Model Stacking Approach" Processes 13, no. 5: 1451. https://doi.org/10.3390/pr13051451
APA StyleAtiea, M. A., Reda, R., Ataya, S., & Ibrahim, M. (2025). Explainable AI and Feature Engineering for Machine-Learning-Driven Predictions of the Properties of Cu-Cr-Zr Alloys: A Hyperparameter Tuning and Model Stacking Approach. Processes, 13(5), 1451. https://doi.org/10.3390/pr13051451








