XGBoost and Artificial Neural Networks as Surrogate Models for Vapor–Liquid Equilibrium in PC-SAFT

Abstract

Phase equilibrium calculations are crucial in chemical engineering design and optimization processes. The PC-SAFT equation of state (EoS) can precisely calculate phase equilibrium, but is relatively complex and computationally intensive. Surrogate models are mathematically simple models that map or regress the input–output relationships of more complex, computationally demanding models. This work employs XGBoost and a hybrid XGBoost-artificial neural networks (XGBoost-ANN) model as surrogate models to replace PC-SAFT EoS calculations for the vapor–liquid equilibrium (VLE) of binary associating systems. This work investigates the VLE of five binary associating systems using data generated by the PC-SAFT EoS. The surrogate models take temperature, pressure, liquid phase mole fractions, and the PC-SAFT parameters for binary associating systems as inputs, and predict the vapor phase mole fractions. Both surrogate models significantly reduce the computational time for calculating VLE data compared to the PC-SAFT EoS, while achieving good prediction results.

1. Introduction

The accuracy of phase equilibrium calculations using equations of state (EoS) is crucial for designing and optimizing processes in the process industries. Gross and Sadowski [1] proposed the perturbed-chain statistical associating fluid theory (PC-SAFT), which accurately predicts the phase equilibrium distribution of substances. However, the mathematical formulation of PC-SAFT is significantly more complex than that of the cubic EoSs commonly used in petrochemical processes, such as Soave–Redlich–Kwong (SRK) [2] and Peng–Robinson (PR) [3].

Surrogate models are mathematically simplified representations that map or regress the input–output relationships of more complex, computationally intensive models [4]. Surrogate models can be evaluated more rapidly than rigorous thermodynamic models, yielding a simplified thermodynamic model; however, this approach is applicable only within a limited physical range [5]. In process engineering, surrogate models are widely employed to simplify EoSs and predict thermodynamic parameters [6,7,8,9]. Sun et al. [10] employed graph neural networks (GNNs) to predict vapor–liquid phase equilibrium in binary mixtures (e.g., acid + water, water + ethylene glycol), achieving predictive performance comparable to that of NRTL and Wilson with their developed surrogate model. Ihunde and Olorode [11] employed Physics-Informed Neural Networks (PINN), which are neural networks trained to solve supervised learning tasks while adhering to physical constraints described by general nonlinear partial differential equations [12], and standard deep learning models as surrogate models for the PR EoS, to predict the flash of the methane–propane–tetradecane system. They found that the PINN model achieved a root mean square error (RMSE) approximately two times lower than the standard deep learning model. Recent advances in PINN have largely focused on overcoming the loss-imbalance problem through sophisticated self-adaptive weighting strategies, such as maximum-likelihood-based Gaussian modelling of individual loss terms [13], dynamic minimax-trained weights that act as learnable attention-like masks [14], and the deliberate use of radial basis function activations to faithfully represent nonlocal integral operators in inverse problems [15]. These techniques have dramatically improved convergence, accuracy, and physical consistency for challenging equations, including Navier–Stokes, Allen–Cahn, and peridynamic models. Hakim et al. [16] investigated the liquid–liquid equilibrium of ternary systems composed of aliphatic compounds + aromatic compounds + ionic liquids using a hybrid artificial neural network (ANN) approach that combined backpropagation (BP) and the Group Method of Data Handling (GMDH). The data obtained from the trained neural network were compared with the calculated values from the NRTL and UNIQUAC. The results indicated that the predictions from the BP neural network were more accurate. Despite the promising results achieved by neural networks or machine learning methods in phase equilibrium calculations, most existing studies on surrogate models for phase equilibrium have primarily employed cubic EoSs and activity coefficient models [8,17,18,19,20,21,22], with relatively fewer investigations into SAFT-type EoSs.

Tree boosting is a widely applied and highly effective machine learning method. XGBoost is a scalable machine learning system for tree boosting, frequently integrated with neural networks [23]. In XGBoost, a novel sparsity-aware algorithm is employed to handle sparse data, and a built-in weighted quantile sketch is utilized for approximate learning. These algorithmic improvements have enabled its widespread adoption by data scientists. Despite the growing number of machine learning-based surrogate models for vapour–liquid equilibrium calculations, the vast majority of reported studies have focused on activity coefficient models (NRTL, UNIQUAC, etc.) and cubic EoS. Applications to advanced molecular-based equations such as SAFT-family models remain extremely scarce, primarily because of their considerably higher computational cost and complex residual thermodynamics. The present work fills this gap by developing highly efficient XGBoost- and XGBoost-ANN-based surrogate models trained exclusively on PC-SAFT calculated data. This work investigated the isotherm VLE of five binary associating systems (water + methanol, water + ethanol, water + 1-propanol, water + 2-propanol, and water + 1-butanol) using XGBoost and a hybrid XGBoost-ANN approach (hereafter referred to as XGBoost-ANN). Surrogate models were developed with temperature (T), pressure (P), the mole fraction of the liquid phase ($x_1$), and the PC-SAFT parameters for binary associating systems ($m_i$, ${\sigma }_i$, ${\epsilon }_i/k_B$, ${\kappa }^{A_i{B}_i}$, ${\epsilon }^{A_i{B}_i}/k_B$, $N_{Ai}$, $N_{Bi}$) as inputs, and the mole fraction of the vapor phase as the output. The output is represented by $y_1$. The data used for training and testing the PC-SAFT surrogate models were calculated using PC-SAFT and verified for thermodynamic consistency (comprising a total of 265 data points). Additional details regarding the data are provided in the Supplementary Materials. Furthermore, this work imposed the physical constraint that the output values should lie within the range [0, 1] and customized a loss function for the neural network training in XGBoost-ANN to incorporate this constraint.

2. Method

2.1. PC-SAFT

For the thermodynamic phase equilibrium of two phases (I and II),

$${\mu }_{\mathrm{i}}^I={\mu }_i^{II}(\forall i=1\dots n_c)$$

(1)

$${\widehat{f}}_i^I={\widehat{f}}_i^{II}(\forall i=1\dots n_c)$$

(2)

In Equations (1) and (2), $n_c$ is the number of components, ${\mu }_i$ represents the chemical potential of component i, and ${\widehat{f}}_i$ denotes the fugacity of the i component. The phase equilibrium relationship expressed in terms of fugacity coefficients is given by

$$y_i{\phi }_i^I=x_i{\phi }_i^{II}$$

(3)

In Equation (3), ${\phi }_i$ is the fugacity coefficient of component i. For the binary associating systems investigated in this work, the residual Helmholtz energy (${\tilde{a}}^{res}$) of the PC-SAFT EoS [1] can be expressed as

$${\tilde{a}}^{res}={\tilde{a}}^{hc}+{\tilde{a}}^{disp}+{\tilde{a}}^{assoc}$$

(4)

In Equation (4), ${\tilde{a}}^{hc}$ represents the hard-chain reference contribution, ${\tilde{a}}^{disp}$ is the dispersion contribution. ${\tilde{a}}^{assoc}$ denotes the association contribution.

In the PC-SAFT EoS, the fugacity coefficient is expressed as

$$\ln {\phi }_i={\displaystyle \frac{{\mu }_i^{res}}{k_{B}T}}-\ln Z$$

(5)

$${\displaystyle \frac{{\mu }_i^{res}}{k_{B}T}}={\tilde{a}}^{res}+(Z-1)+{\left({\displaystyle \frac{\partial {\tilde{a}}^{res}}{\partial x_i}}\right)}_{T,V}-{\displaystyle \sum _j^{n_c}\left[x_j{\left(\frac{\partial {\tilde{a}}^{res}}{\partial x_j}\right)}_{T,V}\right]}$$

(6)

In Equations (5) and (6), Z is the compression factor,

$$Z=1+\eta {\left({\displaystyle \frac{\partial {\tilde{a}}^{res}}{\partial \eta }}\right)}_{T,x_i}$$

(7)

In Equation (7), $\eta$ represents the packing fraction. This work utilized the FeOs library [24] in Python 3.10.11 to compute the VLE of binary associating systems using the PC-SAFT EoS. The specific equations of the PC-SAFT EoS and the binary interaction parameters ($k_{ij}$) regressed for each dataset in this work are provided in the Supplementary Materials. In this work, water and alcohols in the considered binary associating systems are modeled using the 2B association scheme, where all site types (A and B) are equally likely to participate in hydrogen bonding [25]. The number of A sites is set to 1 (i.e., $N_A=1$) and the number of B sites to 1 (i.e., $N_B=1$), with the A and B sites illustrated in Figure 1.

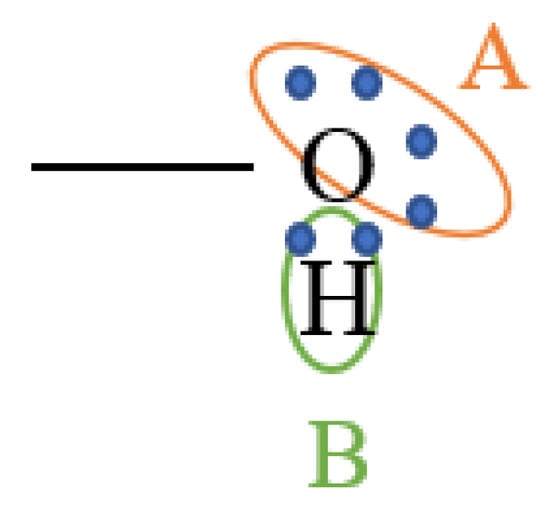
Figure 1. Schematic diagram of the 2B association scheme for water and alcohols.

2.2. XGBoost

2.2.1. Tree Ensemble Model

For regression problems, each regression tree assigns a continuous score to every leaf, with $w_i$ representing by the score associated with the ith leaf. The tree structure is illustrated in Figure 2.

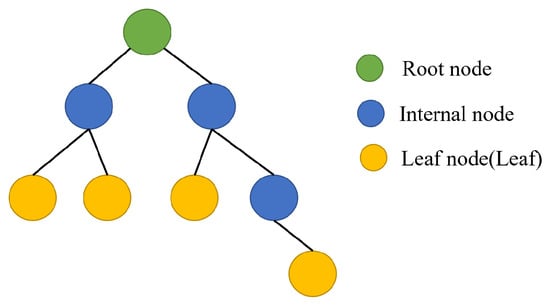
Figure 2. Tree structure.

Figure 3 illustrates the flowchart of the tree ensemble model for regression problems. Initially, training data are input into each tree. The regression trees then assign the corresponding w_i values to the combiner. The combiner performs a weighted sum or average of the w_i values to produce the final output. The regularized objective function of the tree ensemble model is defined as

$$L={\displaystyle \sum _{i}l\left({\widehat{y}}_i,y_i\right)+{\displaystyle \sum _k\Omega (f_k)}}$$

(8)

where

$$\Omega \left(f\right)=\gamma LeavesN+{\displaystyle \frac{1}{2}}\lambda {‖w‖}^2$$

(9)

In Equation (8), $y_i$ and ${\widehat{y}}_i$ represent the true and predicted values, respectively. $l$ is the differentiable convex loss function quantifies the discrepancy between the ${\widehat{y}}_i$ and $y_i$. $\Omega$ is used to penalize the complexity of the tree ensemble model. In Equation (9), LeavesN is the number of leaves in the tree. $\gamma$ and $\lambda$ are penalization parameters.

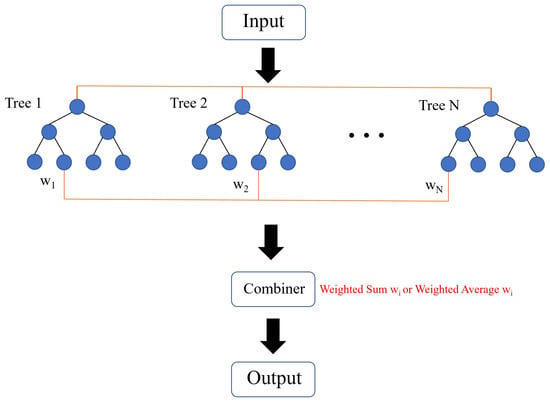
Figure 3. Schematic diagram of the tree ensemble model.

2.2.2. Gradient Tree Boosting

The objective function in Equation (8) cannot be optimized using traditional optimization approaches in Euclidean space. In XGBoost, an iterative objective function based on Equation (8) is employed.

$$L^{(t)}={\displaystyle \sum _{i=1}^{n}l\left(y_i,{\widehat{y}}_i^{(t-1)}+f_t(x_i)\right)+\Omega (f_t)}$$

(10)

In Equation (10), ${\widehat{y}}_i^{(t-1)}$ is the predicted value of the ith instance at the tth iteration. $f_t$ represents an additional perturbation function introduced. To facilitate rapid optimization of the objective function, a second-order approximation is applied to the first term in Equation (10).

$$L^{(t)}={\displaystyle \sum _{i=1}^n\left[l\left(y_i,{\widehat{y}}_i^{(t-1)}\right)+g_i{f}_t(x_i)+\frac{1}{2}{h}_i{f}_t^2(x_i)\right]+\Omega (f_t)}$$

(11)

where

$$g_i={\mathit{\partial }}_{{\widehat{y}}_i^{(t-1)}}l\left(y_i,{\widehat{y}}_i^{(t-1)}\right)$$

(12)

$$h_i={\partial }_{{\widehat{y}}_i^{(t-1)}}^{2}l\left(y_i,{\widehat{y}}_i^{(t-1)}\right)$$

(13)

By further simplifying the constant term $l\left(y_i,{\widehat{y}}_i^{(t-1)}\right)$, the simplified objective function in XGBoost can be obtained.

$$L^{(t)}={\displaystyle \sum _{i=1}^n\left[g_i{f}_t\left(x_i\right)+\frac{1}{2}{h}_i{f}_t^2\left(x_i\right)\right]+\Omega \left(f_t\right)}$$

(14)

If $f_t$ is set to $w_i$, $I_j=\left\{i\right|q(x_i)=j\}$ is the instance set of leaf j, Equation (14) can be rewritten as

$$L^{(t)}={\displaystyle \sum _{j=1}^{LeavesN}\left[\left({\displaystyle \sum _{i\in I_j}{g}_i}\right)w_j+\frac{1}{2}\left({\displaystyle \sum _{i\in I_j}{h}_i+\lambda }\right)w_j^2\right]+\gamma LeavesN}$$

(15)

replace $w_j$ in Equation (15) with

$$w_j^{*}=-{\displaystyle \frac{{\displaystyle \sum _{i\in I_j}{g}_i}}{{\displaystyle \sum _{i\in I_j}{h}_i+\lambda }}}$$

(16)

Hence, Equation (15) can be rewritten as

$$L^{(t)}=-{\displaystyle \frac{1}{2}}{\displaystyle \sum _{j=1}^{LeavesN}\frac{{\left({\displaystyle \sum _{i\in I_j}{g}_i}\right)}^2}{{\displaystyle \sum _{i\in I_j}{h}_i+\lambda }}}+\gamma LeavesN$$

(17)

The schematic diagram of the XGBoost algorithm is presented in Figure 4.

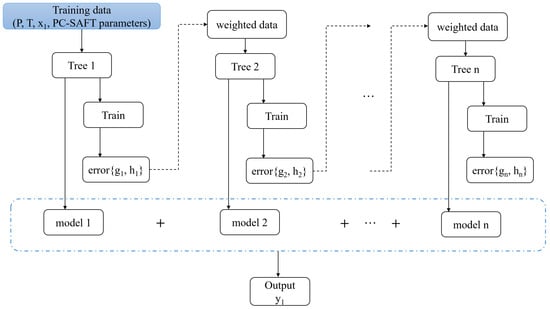
Figure 4. Schematic diagram of XGBoost in this work. The PC-SAFT parameters include $m_i$, ${\sigma }_i$, ${\epsilon }_i/k_B$, ${\kappa }^{A_i{B}_i}$, ${\epsilon }^{A_i{B}_i}/k_B$, $N_{Ai}$, $N_{Bi}$.

2.3. Artificial Neural Networks

In this work, we constructed a custom loss function utilizing the ReLU function to address the scenario where the training data exceeds the physical constraint range of [0, 1]. The mathematical expression of the ReLU function is presented in Equation (18), while Figure 5 illustrates the graphical representation of the ReLU function.

$$\mathrm{ReLU}\left(x\right)=\max \left(0,x\right)$$

(18)

Figure 5. ReLU function.

In this work, the custom loss function is called ConstrainedMSE,

$$ConstrainedMSE=MSE+\mu {\displaystyle \sum _{\mathrm{i}=1}^N\left[\mathrm{ReLU}\left(-{\widehat{y}}_i\right)+\mathrm{Re}\mathrm{LU}\left({\widehat{y}}_i-1\right)\right]}$$

(19)

In Equation (19), N is the number of experimental data. $\mu$ represents the penalty weight. MSE is the mean squared error,

$$MSE={\displaystyle \frac{1}{N}}{\displaystyle \sum _i^N{\left(y_i-{\widehat{y}}_i\right)}^2}$$

(20)

In this work, the ANN was constructed using PyTorch [26], with the Adam optimizer employed and a learning rate set at $1\times {10}^{-4}$. L2 regularization was implemented with a weight decay coefficient of $1\times {10}^{-5}$.

2.4. XGBoost-ANN

The other surrogate model in this work is XGBoost-ANN. The XGBoost-ANN first trains the input data (T, P, $x_1$, PC-SAFT parameters) using XGBoost, and then employs the output from XGBoost as the input for ANN training to obtain the predicted values ($y_1$). The algorithmic schematic of XGBoost-ANN is shown in Figure 6.

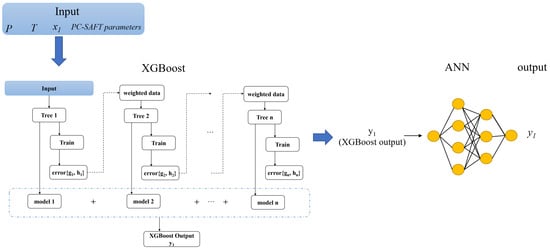
Figure 6. Schematic diagram of XGBoost-ANN. The PC-SAFT parameters include $m_i$, ${\sigma }_i$, ${\epsilon }_i/k_B$, ${\kappa }^{A_i{B}_i}$, ${\epsilon }^{A_i{B}_i}/k_B$, $N_{Ai}$, $N_{Bi}$.

Integrating ANN with ConstrainedMSE into XGBoost in the XGBoost-ANN ensures that the final trained results adhere to the physically constrained range of [0, 1]. Alternative and potentially more principled approaches to enforce the [0, 1] bounds include employing a sigmoid activation at the output layer or predicting logit-transformed targets. These strategies, which eliminate the need for an explicit penalty hyperparameter $\mathsf{\mu }$, will be systematically investigated in our future work.

2.5. Thermodynamic Consistency

Thermodynamic data measured under identical conditions may vary among different researchers. Conducting thermodynamic consistency tests on experimental values is essential [27]. At constant temperature, the Gibbs–Duhem equation for a binary system can be expressed as [28]

$$\left({\displaystyle \frac{V^E}{RT}}\right)\mathrm{dP}=x_{1}d\left(\ln {\gamma }_1\right)+x_{2}d\left(\ln {\gamma }_2\right)$$

(21)

In Equation (21), $V^E$ represents the reduced molar volume, ${\gamma }_i$ denotes the activity coefficient of component i, $R$ is the ideal gas constant, and $x_i$ is the mole fraction of component i. This work employed the PC-SAFT EoS to calculate VLE using the $\phi -\phi$ approach, and Equation (21) can be rewritten as [29,30]

$$\left({\displaystyle \frac{Z-1}{P}}\right)dP=x_{1}d\left(\ln {\phi }_1\right)+x_{2}d\left(\ln {\phi }_2\right)$$

(22)

In this work, we employed the integral form of Equation (22) to conduct thermodynamic consistency tests on isothermal vapor–liquid equilibrium data [27,31].

$${\displaystyle \int \frac{1}{P{y}_2}dP={\displaystyle \int \frac{1-y_2}{y_2(Z-1)}\frac{d{\phi }_1}{{\phi }_1}+{\displaystyle \int \frac{1}{Z-1}\frac{d{\phi }_2}{{\phi }_2}}}}$$

(23)

In Equation (23), the left-hand side term P represents the experimentally measured system pressure, and $y_2$ denotes the experimentally determined vapor-phase mole fraction. On the right-hand side, $y_2$, Z and ${\phi }_i$ are calculated using the PC-SAFT EoS. The basis for deciding thermodynamic consistency is [27,31]

$$\%\Delta A=100\left|{\displaystyle \frac{A_{\phi }-A_P}{A_p}}\right|<20$$

(24)

where

$$A_p={\displaystyle \int \frac{1}{P{y}_2}dP}$$

(25)

$$A_{\phi }={\displaystyle \int \frac{1-y_2}{y_2\left(Z-1\right)}}{\displaystyle \frac{d{\phi }_1}{{\phi }_1}}+{\displaystyle \int \frac{1}{Z-1}\frac{d{\phi }_2}{{\phi }_2}}$$

(26)

The Supplementary Materials provides additional details on the thermodynamic consistency tests.

3. Results and Discussion

This work optimized the hyperparameters n_estimators, max_depth, learning_rate, subsample, colsample_bytree, colsample_bylevel, colsample_bynode, reg_alpha, reg_lambda, min_child_weight, gamma, and max_delta_step of XGBoost using the randomized grid search method from the scikit-learn library [32]. The hyperparameter optimization range for XGBoost is presented in Table 1. Table 2 presents the optimized parameter values obtained through random grid search in this work. Moreover, the neural network architecture of the ANN was optimized using Optuna [33]. A detailed introduction to the Optuna library is provided in the Supplementary Materials. The optimization ranges were set as the number of neural network layers within [1, 5], the number of neurons per layer within [4, 64], with an optimization step size of 4, and the penalty weight $\mu$ within [1, 10,000]. The batch size was selected from the set {16, 32, 64, 128}. The hyperparameters of XGBoost in the XGBoost-ANN framework were adopted from the previously optimized XGBoost hyperparameters, while the optimized parameters for the ANN are presented in Table 3. We utilized thermodynamic consistency data from five binary mixture systems (water + methanol, water + ethanol, water + 1-propanol, water + 2-propanol, and water + 1-butanol) for training the XGBoost and XGBoost-ANN surrogate models. The complete dataset consists of 265 data points. To prevent data leakage and ensure fair evaluation across different binary systems, the dataset was split in a system-stratified manner. For each of the five binary associating systems, 80% of the data points were randomly selected for training (total: 212 points), and the remaining 20% were reserved as the test set (total: 53 points). This stratified splitting guarantees that both training and test sets contain data from all five binary systems in equal proportion.

Table 1. Hyperparameter range for XGBoost optimization in this work.

Hyperparameter	The Range of Hyperparameters	Parameter Usage
n_estimators	[60, 400]	The number of decision trees
max_depth	[3, 10]	The maximum depth of each decision tree
learning_rate	[0.01, 0.06]	Learning rate
subsample	[0.5, 0.9]	The fraction of training data randomly sampled for training each tree
colsample_bytree	[0.6, 0.9]	The fraction of features randomly sampled for constructing each tree
colsample_bylevel	[0.7, 0.9]	The fraction of features sampled at each split within a tree
colsample_bynode	[0.7, 0.9]	The fraction of features sampled for each node split in a tree
reg_alpha	[0.1, 20]	The L1 regularization term on weights
reg_lambda	[0.1, 30]	The L2 regularization term on weights
min_child_weight	[2, 10]	The minimum sum of instance weights needed in a child node
gamma	[0.01, 1.0]	The minimum loss reduction required to make a split on a leaf node of the tree
max_delta_step	[1, 5]	The maximum weight change for each tree’s output

Table 2. The optimized parameters for XGBoost in this work.

Hyperparameter	The Optimized Value
n_estimators	81
max_depth	6
learning_rate	0.0592
subsample	0.7099
colsample_bytree	0.8816
colsample_bylevel	0.7113
colsample_bynode	0.8444
reg_alpha	0.1038
reg_lambda	0.1141
min_child_weight	3
gamma	0.0100
max_delta_step	1

Table 3. The optimized parameters for ANN in this work.

Hyperparameter	The Optimized Value
The number of layers	4
The number of neurons per layer	{64,52,60,8}
Batch size	16
$\mu$	1023.1298

Details of the data used for training and validating the surrogate model are provided in Table S3 of the Supplementary Materials. The binary interaction parameters $k_{ij}$ were regressed based on the PC-SAFT EoS, and the average absolute percentage deviation (%AAD) is presented in Tables S4–S8 of the Supplementary Materials. The loss function for the ANN training set is presented in Figure S1 of the Supplementary Materials.

A comparison of Figure 7 and Figure 8 reveals that the surrogate model based on XGBoost-ANN outperforms the XGBoost surrogate model in terms of $R^2$, RMSE, and MAE (Mean Absolute Error) for both the training and test sets. Additionally, we compared the computational time required to process all data points (265 points) using PC-SAFT, the surrogate model based on XGBoost, and the surrogate model based on XGBoost-ANN, with specific timings presented in Table 4. The computer configuration used for testing computational speed is detailed in Table S9 of the Supplementary Materials. As shown in Table 4, the computational time of the surrogate models is significantly reduced compared to that of the PC-SAFT EoS. The final computational time was determined by averaging the results of three independent measurements. The surrogate model based on XGBoost achieves a computational time reduction of 2918.5 times, while the surrogate model based on XGBoost-ANN achieves a computational time reduction of 973 times.

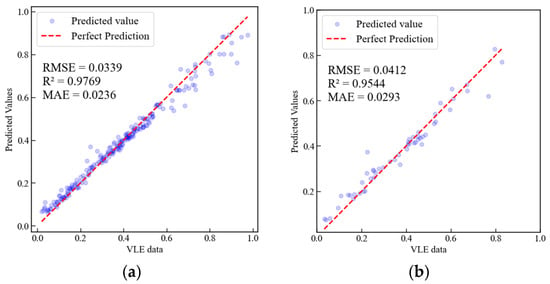
Figure 7. Comparison of predicted values from the surrogate model based on XGBoost with VLE data calculated using PC-SAFT. (a) Training set, (b) Test set.

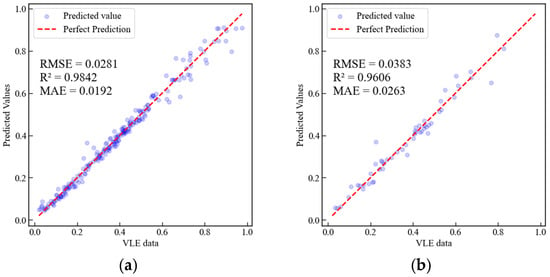
Figure 8. Comparison of predicted values from the surrogate model based on XGBoost-ANN with VLE data calculated using PC-SAFT. (a) Training set, (b) Test set.

Table 4. Computational time required for processing all data points using PC-SAFT, the surrogate model based on XGBoost, and the surrogate model based on XGBoost-ANN.

Model	Computation Time/s
PC-SAFT	2.9185
XGBoost	0.0010
XGBoost-ANN	0.0030

3.1. Water + Methanol

Figure 9 presents the experimental values ($y_1$), PC-SAFT calculated values, and surrogate model predictions at temperatures of 298.144 K, 318 K, 328.126 K, 373.124 K, 388.150 K, and 403.15 K for the water + methanol system. As observed in Figure 9d,f, when the liquid-phase mole fraction ($x_1$) exceeds 0.7, the predictions of the surrogate model based on XGBoost and the surrogate model based on XGBoost-ANN are lower than the PC-SAFT calculated values, with the surrogate model based on XGBoost-ANN predictions being closer to the PC-SAFT values. Table 5 presents the $R^2$ and MSE values for the surrogate model and PC-SAFT calculated values at the temperatures shown in Figure 9. From Table 5, it can be observed that only at temperatures of 298.144 K, 328.136 K, and 388.150 K does the surrogate model based on XGBoost slightly outperform the surrogate model based on XGBoost-ANN, while at all other temperatures, the surrogate model based on XGBoost-ANN yields superior prediction results compared to XGBoost. Table 6 reports the %AAD achieved with PC-SAFT and with the surrogate model, respectively. The $∆\%\mathrm{A}\mathrm{A}\mathrm{D}$ is the absolute deviation between the %AAD of the PC-SAFT calculations and the %AAD of the surrogate model predictions. It is evident from Table 6 that the $∆\%\mathrm{A}\mathrm{A}\mathrm{D}$ for all systems displayed in Figure 9 remains below 5%.

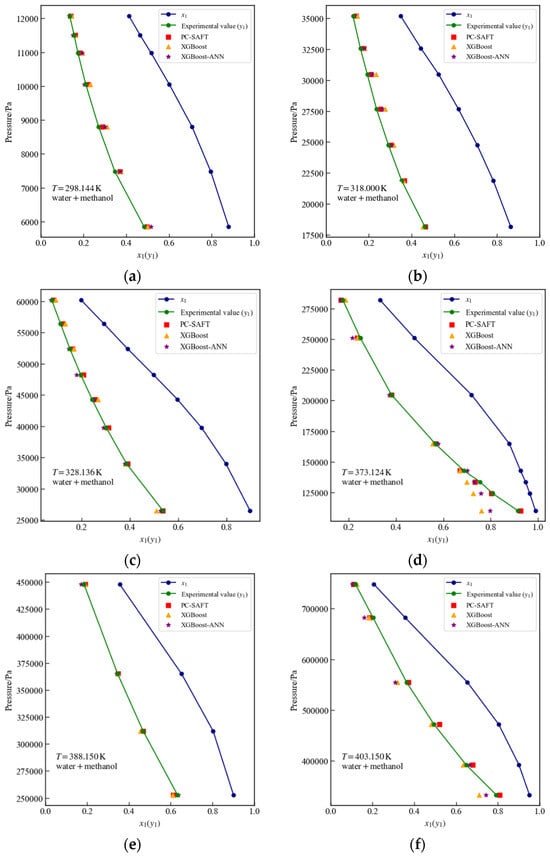
Figure 9. Vapor–liquid equilibrium data for the water + methanol system at different temperatures: comparison of PC-SAFT calculated values with predictions from XGBoost and XGBoost-ANN surrogate models. (a) 298.144 K, (b) 318 K, (c) 328.126 K, (d) 373.124 K, (e) 388.15 K, (f) 403.15 K.

Table 5. Comparison of surrogate models and PC-SAFT calculated values at different temperatures for the water + methanol system.

Temperature/K	XGBoost		XGBoost-ANN
	MSE	${\mathit{R}}^2$	MSE	${\mathit{R}}^2$
298.144	0.0001	0.9929	0.0002	0.9884
318.000	0.0002	0.9832	2.3384 × 10−5	0.9979
328.136	0.0002	0.9918	0.0003	0.9867
373.124	0.0044	0.9328	0.0025	0.9617
388.150	0.0001	0.9979	0.0003	0.9885
403.150	0.0028	0.9563	0.0017	0.9727

Table 6. The %AAD values of the PC-SAFT calculations and those of the surrogate models in Figure 9.

Temperature/K	PC-SAFT	XGBoost		XGBoost-ANN
	%AAD	%AAD	$∆\mathbf{\%}\mathbf{A}\mathbf{A}\mathbf{D}$	%AAD	$∆\mathbf{\%}\mathbf{A}\mathbf{A}\mathbf{D}$
298.144	4.9033	8.3390	3.4357	6.184	1.4151
318.000	6.6105	11.2727	4.6622	6.4610	0.1495
328.136	5.3121	8.4368	3.1247	3.7656	1.5464
373.124	2.1875	6.4645	4.2773	5.9824	3.7952
388.150	1.6987	2.6912	0.9925	2.7253	1.0266
403.150	5.1908	7.2112	2.2004	9.6721	4.4814

3.2. Water + Ethanol

Figure 10 illustrates the liquid-phase mole fraction ($x_1$), experimental values ($y_1$), PC-SAFT calculated values, and surrogate models’ predictions at temperatures of 323.15 K, 328.15 K, 333.15 K, and 423.7 K. As observed in Figure 10d, the surrogate model based on XGBoost-ANN exhibits larger prediction deviations for three points where $y_1$ lies within the range [0.6, 0.8]. Table 7 indicates that at 423.7 K, the surrogate model based on XGBoost provides more accurate predictions, whereas at the other temperatures, the surrogate model based on XGBoost-ANN predictions is closer to the PC-SAFT calculated values. Table 8 indicates that all $∆\%\mathrm{A}\mathrm{A}\mathrm{D}$ values associated with Figure 10 remain below 4%, with the only exception being the surrogate model based on XGBoost-ANN at 423.7 K, which shows substantially greater discrepancies relative to PC-SAFT and experimental data.

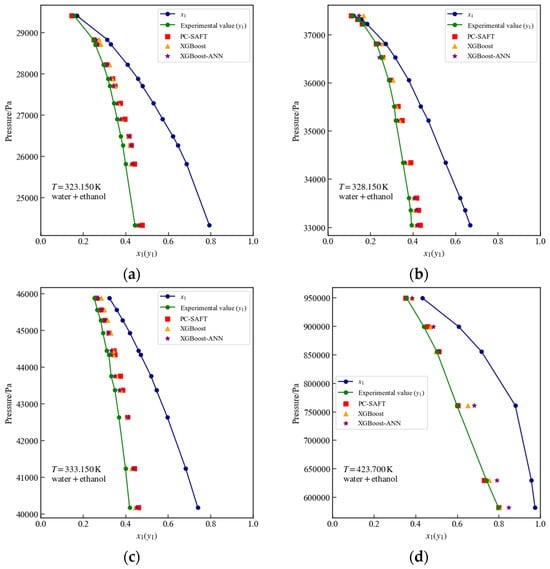
Figure 10. Vapor–Liquid equilibrium data for the water + ethanol system at different temperatures: comparison of PC-SAFT calculated values with predictions from XGBoost and XGBoost-ANN surrogate models. (a) 323.15 K, (b) 328.15 K, (c) 333.15 K, (d) 423.7 K.

Table 7. Comparison of surrogate models and PC-SAFT calculated values at different temperatures for the water + ethanol system.

Temperature/K	XGBoost		XGBoost-ANN
	MSE	${\mathit{R}}^2$	MSE	${\mathit{R}}^2$
323.150	0.0003	0.9658	0.0001	0.9873
328.150	0.0006	0.9519	0.0003	0.9732
333.150	0.0002	0.9510	0.0001	0.9640
423.700	0.0007	0.9703	0.0023	0.9045

Table 8. The %AAD values of the PC-SAFT calculations and those of the surrogate models in Figure 10.

Temperature/K	PC-SAFT	XGBoost		XGBoost-ANN
	%AAD	%AAD	$∆\mathbf{\%}\mathbf{A}\mathbf{A}\mathbf{D}$	%AAD	$∆\mathbf{\%}\mathbf{A}\mathbf{A}\mathbf{D}$
323.150	7.0501	7.7871	0.7380	5.4539	1.5962
328.150	6.0784	9.9871	3.9087	5.6462	0.4322
333.150	9.0990	9.2426	0.1437	7.2375	1.8614
423.700	1.4961	4.4587	2.9626	7.6918	6.1957

3.3. Water + 1-Propanol

Figure 11 presents three data points for the water + 1-propanol system at a temperature of 403.2 K that passed thermodynamic consistency tests. For these points, the surrogate model based on XGBoost yields an MSE of 0.0016 and an $R^2$ of 0.9547, while the surrogate model based on XGBoost-ANN yields an MSE of 0.0013 and an $R^2$ of 0.9627. For all experimental data points of the water + 1-propanol system, the surrogate model based on XGBoost achieves an MSE of 0.0016 and an $R^2$ of 0.9482, whereas the surrogate model based on XGBoost-ANN achieves an MSE of 0.0012 and an $R^2$ of 0.9586. For the water + 1-propanol binary system across all data points, the %AAD values are 4.3023% for PC-SAFT, 4.9932% for the surrogate model based on XGBoost, and 5.1969% for the surrogate model based on XGBoost-ANN, respectively.

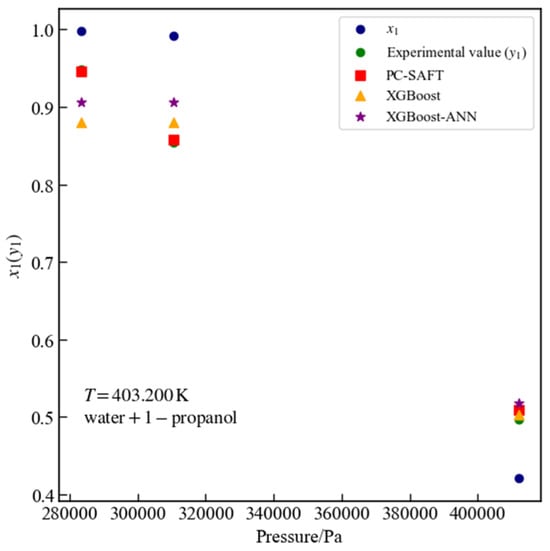
Figure 11. Vapor–liquid equilibrium data for the water + 1-propanol system at 403.2 K: comparison of PC-SAFT calculated values with predictions from XGBoost and XGBoost-ANN surrogate models.

3.4. Water + 2-Propanol

Figure 12 presents three data points for the water + 2-propanol system at a temperature of 353.129 K that passed thermodynamic consistency tests. For these points, the surrogate model based on XGBoost yields an MSE of 0.0007 and an $R^2$ of 0.9669, while the surrogate model based on XGBoost-ANN yields an MSE of 0.0001 and an $R^2$ of 0.9943. For all experimental data points of the water + 2-propanol system, the surrogate model based on XGBoost achieves an MSE of 0.0027 and an $R^2$ of 0.8778, whereas the surrogate model based on XGBoost-ANN achieves an MSE of 0.0025 and an $R^2$ of 0.8865. For the water + 2-propanol binary system across all data points, the %AAD values are 11.7714% for PC-SAFT, 13.2330% for the surrogate model based on XGBoost, and 14.8303% for the surrogate model based on XGBoost-ANN, respectively. Both PC-SAFT and the surrogate models show considerably larger deviations for the VLE experimental data of the water + 2-propanol system.

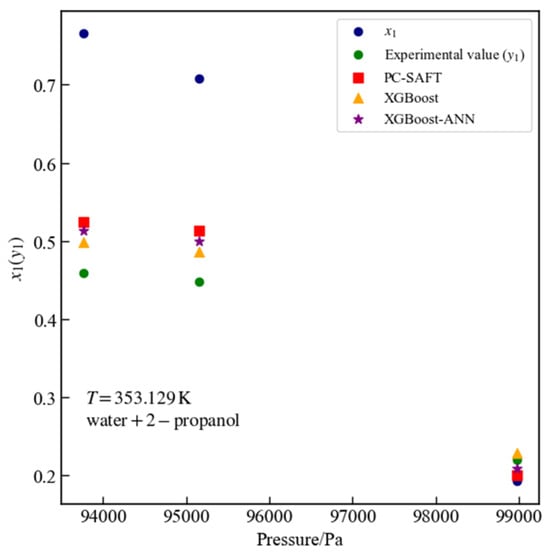
Figure 12. Vapor–Liquid equilibrium data for the water + 2-propanol system at 353.129 K: comparison of PC-SAFT calculated values with predictions from XGBoost and XGBoost-ANN surrogate models.

3.5. Water + 1-Butanol

Figure 13 presents three data points for the water + 1-butanol system at a temperature of 403.118 K that passed thermodynamic consistency tests. For these points, the surrogate model based on XGBoost yields an MSE of 0.0055 and an $R^2$ of 0.7970, while the surrogate model based on XGBoost-ANN yields an MSE of 0.0051 and an $R^2$ of 0.8098. For all experimental data points of the water + 1-butanol system, the surrogate model based on XGBoost achieves an MSE of 0.0057 and an $R^2$ of 0.8670, whereas the surrogate model based on XGBoost-ANN achieves an MSE of 0.0040 and an $R^2$ of 0.9071. For all data of the water + 1-butanol system, the predictions of the surrogate model based on XGBoost-ANN are significantly closer to the PC-SAFT calculated values. For the water + 1-butanol binary system across all data points, the %AAD values are 7.1175% for PC-SAFT, 11.6284% for the surrogate model based on XGBoost, and 9.7374% for the surrogate model based on XGBoost-ANN, respectively.

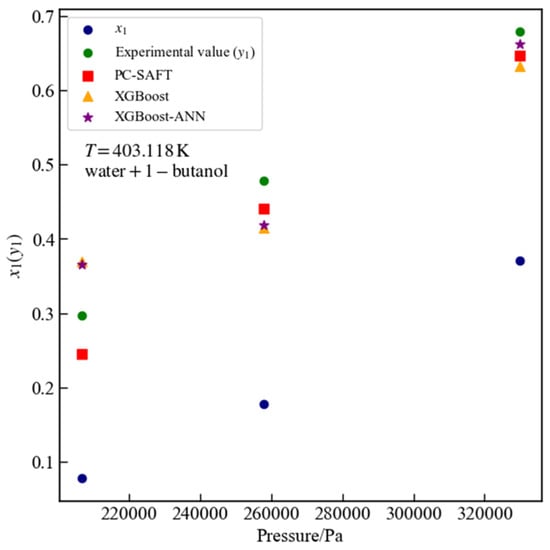
Figure 13. Vapor–liquid equilibrium data for the water + 1-butanol system at 403.118 K: comparison of PC-SAFT calculated values with predictions from XGBoost and XGBoost-ANN surrogate models.

The present study is restricted to binary mixtures. Validation on multicomponent and reactive systems, which is essential for real industrial applications, remains to be conducted and is highlighted as the most important direction for future work. Another important limitation of the current work is the absence of uncertainty quantification. In future work, we will conduct a more comprehensive investigation of PC-SAFT surrogate models by incorporating a broader range of machine learning algorithms as well as uncertainty quantification and analysis. The surrogate models presented in this paper are trained and validated on only five binary associating systems. Defining the precise domain of applicability and safe extrapolation boundaries of the proposed framework will therefore constitute a major focus of our future work, in which a significantly larger and more diverse set of binary and multicomponent systems will be incorporated.

4. Conclusions

This work constructed surrogate models for the VLE of the water + methanol, water + ethanol, water + 1-popanol, water + 2-propanol, and water + 1-butanol binary systems using XGBoost and XGBoost-ANN methods. The models were optimized using randomized grid search and the Optuna library. Both surrogate models significantly reduce the computational time for calculating VLE data compared to the PC-SAFT EoS, while achieving good prediction results. Among the systems investigated, the water + 2-propanol and water + 1-butanol binary mixtures exhibit the largest deviations for both PC-SAFT and all surrogate models. These two systems possess only limited thermodynamically consistent experimental VLE data points 13 for water + 2-propanol and 14 for water + 1-butanol after application of rigorous thermodynamic consistency tests. Even when the binary interaction parameters k_ij of PC-SAFT were regressed against these experimental data, substantial deviations from the measurements persist. Consequently, the relatively poor performance of the surrogate models for these two systems is largely attributable to the scarcity or questionable quality of the underlying experimental database. Improved predictive accuracy of the surrogate models is expected in the future once more reliable and extensive VLE measurements become available for these two challenging binary systems.