Influence of Heterogeneity on Acidizing Performance in Multi-Layered Carbonate Reservoirs

Abstract

Carbonate rocks typically exhibit strong heterogeneity and multi-bedding characteristics, which exert a significant impact on acidification performance. In this study, based on the dual-scale continuum model and the open-source software FMOT, we developed an acidification simulation program suitable for multi-layered rocks, and focused on investigating the influence laws of two representative characteristics—heterogeneity intensity and interlayer permeability difference—on acidification performance. The results show that heterogeneity intensity significantly affects the development morphology of wormholes in high- and low-permeability rocks: under low-heterogeneity intensity conditions, the wormhole morphology in both layers is close to a straight line; under high-heterogeneity intensity conditions, the wormhole morphology exhibits a dendritic shape. When the interlayer permeability difference is 40 mD, the acid breakthrough times of rocks under three heterogeneity intensities (Low, Medium, High) are [476 s, 463 s, 450 s], indicating that the higher the rock heterogeneity intensity, the faster the acid breakthrough speed. In terms of porosity increment, under this condition, the porosity increments of high-permeability rocks are [0.0952, 0.0921, 0.0868], while those of low-permeability rocks are [0.0321, 0.0308, 0.0297]. It is evident that the acidizing effect of high-permeability rocks is significantly superior to that of low-permeability rocks. A further analysis of the influence of interlayer permeability difference shows that reducing the interlayer permeability difference significantly slows down the acid breakthrough speed of rocks, while weakening the acidizing effect of high-permeability rocks and enhancing that of low-permeability rocks; conversely, increasing the interlayer permeability difference accelerates the acid breakthrough of rocks, strengthens the acidizing effect of high-permeability rocks, and inhibits that of low-permeability rocks.

1. Introduction

Carbonate reservoirs account for over 50% of global oil and gas reserves and production [1], playing a pivotal role in energy supply. These reservoirs are characterized by natural fractures, vugs, and strong heterogeneity, making them highly susceptible to formation damage during drilling and production, such as drilling fluid invasion and solid particle plugging. This damage significantly reduces near-wellbore permeability, severely constraining well productivity [2]. Matrix acidizing, a critical stimulation technique, addresses this issue by injecting acid into the formation to chemically react with carbonate minerals, dissolving the rock matrix and creating highly conductive wormhole channels. These wormholes effectively connect the wellbore to deeper reservoir zones, significantly enhancing production capacity [3]. An ideal acidizing process should avoid rapid acid reactions near the wellbore that cause “surface etching” or “dead acid” phenomena, instead promoting deep acid penetration to form interconnected wormhole networks [4,5].

To optimize the matrix acidizing design, extensive experimental studies have systematically revealed the key controlling factors of the acidizing process. Early investigations identified five typical dissolution patterns (uniform dissolution, branched wormholing, dominant wormholing, conical wormholing, and face dissolution) by varying injection rates and acid types [6,7]. Subsequent works further examined the effects of core pore structure, sample size, porosity distribution, and rock permeability on wormhole propagation pathways and the optimal acid injection rate. Studies indicate that wormhole formation is primarily governed by acid–rock reaction kinetics [8], and is significantly influenced by CO₂ gas generated during the reaction [9], as well as by temperature and pressure conditions [10]. Meanwhile, considerable research has been conducted to accurately characterize acid–rock reaction and mass transfer behavior [11,12]. Although these studies have achieved significant progress at the single-core or homogeneous/heterogeneous core scale, their findings are primarily applicable to acidizing mechanisms in isolated reservoir zones. However, in practical oilfield development, carbonate reservoirs often exhibit vertically multi-layered configurations with pronounced property variations. Interlayer differences in permeability and porosity lead to uneven acid distribution, resulting in excessive stimulation of high-permeability layers while low-permeability layers remain poorly contacted. Therefore, there remains a critical need for integrated studies that address acidizing in multi-layered systems to support effective and balanced stimulation design.

Current numerical simulation models for acidizing primarily employ the Two-Scale Continuum (TSC) model [13], which effectively couples pore-scale rock–acid reactions with Darcy-scale fluid flow, enabling accurate simulation of porosity evolution. Petrophysical property variations have been shown to critically influence dissolution patterns [1,14]. Yang, G. et al. [15] demonstrated within the TSC framework that increased heterogeneity leads to more branched and narrower wormholes, shifting the dissolution regime from competitive growth to dominant channel formation. Studies indicate that injecting cooler acid at appropriate rates can enhance acidizing efficiency; moreover, at higher injection rates, the effect of reaction temperature on efficiency becomes more pronounced, and the optimal injection rate increases with rising temperature [14,16,17,18]. Xue et al. [19] incorporated the molar heat of acid–rock reaction into a thermo-hydro-chemical coupling model and found that exothermic reactions can raise the temperature at the wormhole tip by over 11 K, significantly altering macroscopic dissolution morphology. Wang et al. [5] revealed that limestone contributes more to wormhole development under low-temperature conditions (<338 K), whereas dissolution of limestone and dolomite tends to equalize at elevated temperatures (418 K). Shiraz [20] simulated the effects of layer-specific mineral composition and reservoir temperature on final skin factor and dissolution patterns, showing good agreement with field data and providing direct support for customized acidizing design in multi-layered reservoirs. Injection conditions play a critical role in regulating acidizing performance [21]. Furui K. et al. [22] observed that at low injection rates, acid is rapidly depleted near the inlet, whereas high injection rates enable live acid to reach the forefront of dissolution channels. Jia Cunqi et al. [9] highlighted that neglecting mass transfer between phases leads to underestimation of the pore volume required for breakthrough. Tansey J. et al. [23] developed new correlations for mass transfer coefficients and pore merging criteria through finite element simulations, significantly improving the physical fidelity and quantitative accuracy of pore-scale models. Similarly, Bastami, A. et al. [24] systematically accounted for reaction products in spent acid, substantially enhancing model accuracy and revealing feedback mechanisms between dynamic fluid property changes and reactive flow. Chang et al. first conducted a study on the different acidification mechanisms of HCl and diverting acid in carbonate reservoirs with oil saturation [25,26]. On this basis, they developed a PID dynamic boundary correction method to solve the problem of dynamic flow distribution of complex acid fluids in reservoirs with multiple flow units [27]. Furthermore, they carried out additional research on the acid diversion and splitting mechanism in such reservoirs.

In summary, although existing numerical models have made significant progress under the assumptions of single-layer reservoirs or simplified homogeneity, and certain insights have been gained regarding the diversion and splitting mechanisms of acidizing in multi-layered rock, there remains a lack of comprehensive investigation into the influence of multiple heterogeneity factors—such as the combined effects of varying heterogeneity intensity and interlayer property contrasts—on the heterogeneous dissolution behavior of acid fluids. Most prior studies, including recent works on multi-layered systems, e.g., Chang et al., have typically examined these factors in isolation, limiting the understanding of their interactive roles in shaping acid transport and wormhole propagation.

This study uses a numerical simulation framework for multi-layered acidizing based on the TSC model and software FMOT (https://github.com/FMOTs/FMOT_matlab, accessed on 2 October 2025 ). Through a series of cases, the influences of reservoir heterogeneity and interlayer permeability difference on acidification performance in the multi-layered rock acidification process were evaluated, with a particular focus on analyzing the influence laws of these two factors on the wormhole morphology and flow distribution in low-permeability rocks.

2. Mathematical Formulation

This section presents a mathematical framework for simulating reactive acid transport and dissolution processes in carbonate reservoirs at the darcy and pore scales, with particular emphasis on matrix acidizing mechanisms. By adapting the conceptual basis of equivalent continuum approaches, the model formulates coupled flow, solute transport, and chemical reaction equations at the darcy scale, while incorporating pore-scale evolution laws to capture changes in porosity and permeability due to acid–rock interactions, as shown in Figure 1. Additionally, a heat transfer model is integrated to account for thermal variations in both the solid matrix and the fluid phase during the acidization process. The overall system consists of Darcy-scale equations governing fluid flow and acid transport in the porous matrix, pore-scale relationships describing the evolution of rock properties, and energy balance equations for the matrix domain—specifically including equations for acid concentration and rock/fluid temperature dynamics.

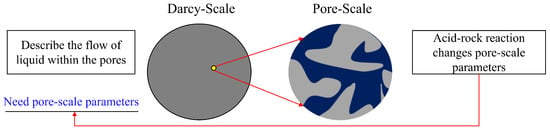
Figure 1. The diagram of the two-scale continuum model.

(1)

Governing equation of Darcy-scale pressure:

Acid is assumed to be an incompressible fluid, so the Darcy-scale pressure equation is

$$\begin{array}{cc}\hfill & {\displaystyle \frac{\partial \varphi }{\partial t}}-\nabla ·v=0\hfill \\ \hfill & v={\displaystyle \frac{\mathit{K}}{\mu }}\nabla P\hfill \end{array}$$

(1)

where $\varphi$ is the porosity of matrix, dimensionless; v is fluid velocity, m/s; $\mathit{K}$ is the permeability of matrix, m²; $\mu$ is the viscosity of the fluid, Pa·s; P is the fluid pressure, Pa.

(2)

Heat transfer model

The two-temperature equation with non-thermal equilibrium state proposed by Kalia [28] are used in this paper. The fluid temperature equation is

$${\displaystyle \frac{\partial }{\partial t}}\left(\varphi {\rho }_f{C}_{p,f}{T}_f\right)+\nabla ·\left(v{\rho }_f{C}_{p,f}{T}_f\right)=\nabla ·\left(\varphi k_{e,f}\nabla T_f\right)+h_c{a}_v\left(T_s-T_f\right)$$

(2)

and the rock temperature equation is

$${\displaystyle \frac{\partial }{\partial t}}\left((1-\varphi ){\rho }_s{C}_{p,s}{T}_s\right)=\nabla ·\left(\left(1-{\varphi }_m\right)k_{e,s}\nabla T_s\right)+\Delta H_r\left(T_s\right)a_{v}R\left(C_s\right)-h_c{a}_v\left(T_s-T_m\right)$$

(3)

where $C_{p,f}$ and $C_{p,s}$ are the specific heat capacity of the acid (fluid) and rock, respectively, J/(kg·K); $T_f$ and $T_s$ are the temperatures of the acid and rock, respectively, K; $k_{e,f}$ and $k_{e,s}$ are the thermal conductivity of the acid and rock, respectively, W/(m·K); $h_c$ is the acid–rock heat transfer coefficient, W/(m²·K); $a_v$ is the interfacial area, m²/m³; $\Delta H_r\left(T_s\right)$ is the acid-rock molar reaction heat, J/mol. According to Kirchhoff’s law, the standard molar reaction heat between HCl and CaCO₃ affected by temperature can be expressed as [29]

$$\Delta H_r\left(T_s\right)=-13692+\left(-6.443\times {10}^{-3}{T}_s^2+16.075T_s-{\displaystyle \frac{17.406\times {10}^5}{T_s}}\right)$$

(4)

(3)

Chemical reaction (acid–rock reaction) equation

Governing equation of acid concentration transport in matrix:

$${\displaystyle \frac{\partial }{\partial t}}\left(\varphi C\right)+\nabla ·\left(vC\right)-\nabla ·\left(\varphi D_m\nabla C\right)+R\left(C_s\right)a_v=0$$

(5)

where C is acid concentration, kmol/m³; $D_m$ is the effective diffusion tensor, m/s; $R\left(C_s\right)$ is reaction kinetics in the matrix and fracture respectively, kmol/(s·m²). Based on the TSC model, the acid–rock reaction eqautions are as follows:

$$R\left(C_s\right)a_v=k_c{a}_v\left(C-C_s\right)$$

(6a)

$$C_s={\displaystyle \frac{C}{\left(1+\frac{k_s}{k_c}\right)}}$$

(6b)

$$R\left(C_s\right)a_v={\displaystyle \frac{k_c{k}_s}{k_c+k_s}}C{a}_v$$

(6c)

where $k_c$ is the mass transfer coefficient, m/s; $k_s$ is reaction rate constant, m/s; $C_s$ represents the mass concentration of acid on the rock surface, kmol/m³. The specific calculation formulas for $k_c$ and $k_s$ are as follows [30]:

$$k_c={\displaystyle \frac{\left(S{h}_{\infty }+\frac{0.7}{m^{\frac{1}{2}}}R{e}_P^{\frac{1}{2}}S{c}^{\frac{1}{3}}\right)D_m}{2r_p}}$$

(7a)

$$k_s=0.015e^{\left(-{\displaystyle \frac{18616}{R{T}_s}}\right)}{C}^{1.1997}$$

(7b)

where R is the gas constant. The constant coefficients of 0.015, 18616, and 1.1997 were determined experimentally, characterizing the acid–rock reaction rate between HCl and limestone [30].

(4)

The pore-scale equation

The pore structure undergoes changes due to the acid–rock reaction. Based on the TSC model, the equations for the quantity of pore-scale updates are as follows:

$${\displaystyle \frac{\partial \varphi }{\partial t}}={\displaystyle \frac{R\left(C_s\right)a_v\alpha }{{\rho }_s}}$$

(8a)

$${\displaystyle \frac{\mathit{K}}{{\mathit{K}}_0}}={\displaystyle \frac{\varphi }{{\varphi }_0}}{\left[{\displaystyle \frac{\varphi \left(1-{\varphi }_0\right)}{{\varphi }_0(1-\varphi )}}\right]}^{2\beta }$$

(8b)

$${\displaystyle \frac{r_p}{r_{p,0}}}=\sqrt{{\displaystyle \frac{\mathit{K}{\varphi }_0}{{\mathit{K}}_0\varphi }}}$$

(8c)

$${\displaystyle \frac{a_v}{a_{v,0}}}={\displaystyle \frac{\varphi r_{p,0}}{{\varphi }_0{r}_p}}$$

(8d)

where the subscript 0 represents initial values of physical quantities; $\beta$ is the pore-broadening parameter; $\alpha$ is the dissolving power of the acid; ${\rho }_s$ is rock density, kg/m³.

3. Numerical Technique

In this section, we present the simulation strategy of the multi-layered rock acidizing problem. All equations and mathematical models mentioned in Section 2 are embedded in the open-source simulation framework FMOT (https://github.com/FMOTs/FMOT_matlab, accessed on 2 October 2025) [25,26].

3.1. Discrete Methods and Algebraic Equations

For the equations in Section 2, the backward Euler scheme, first-order upwind scheme, and central difference scheme are employed for the temporal term, convective term, and Laplacian term, respectively. Furthermore, the Newton iteration method is used to solve the equations that require implicit calculation. Here, the Jacobian matrix (J) and the constant right-hand side (b) are presented directly.

(1)

Governing equation of Darcy-scale pressure:

$$\begin{array}{cc}\hfill & J_P=A_{\mathrm{P}}+A_{\mathrm{N}}\hfill \\ \hfill & A_{\mathrm{P}}=\sum _{f\sim faces}{\left({\displaystyle \frac{\mathit{K}}{\mu }}\right)}_f{\displaystyle \frac{|{\mathit{S}}_f|}{\left|\mathit{d}\right|}}\hfill \\ \hfill & A_{\mathrm{N}}=-\sum _{f\sim faces}{\left({\displaystyle \frac{\mathit{K}}{\mu }}\right)}_f{\displaystyle \frac{|{\mathit{S}}_f|}{\left|\mathit{d}\right|}}\hfill \\ \hfill & b_{P,M}=0\hfill \end{array}$$

(9)

(2)

Heat transfer model

The full coupled method is used to calculate the fluid and rock equations:

$$J_{T_{FC}}=\left[\begin{array}{cc}{J}_{T_f}& J_{fs}\\ J_{sf}& J_{T_s}\end{array}\right]$$

(10a)

$$\begin{array}{cc}\hfill & J_{T_f}=A_{\mathrm{P}}+A_{\mathrm{N}}+A^{\mathrm{up}}\hfill \\ \hfill & A_{\mathrm{P}}=V_{\mathrm{p}}{\varphi }^t+\Delta t\sum _{f\sim faces}{{\varphi }_f}^t{k}_i^t{\displaystyle \frac{|{\mathit{S}}_f|}{\left|\mathit{d}\right|}}+\Delta t{V}_{\mathrm{p}}{h}_c^t{a}_v^t\hfill \\ \hfill & A_{\mathrm{N}}=-\Delta t\sum _{f\sim faces}{{\varphi }_f}^t{k}_{e,f}^t{\displaystyle \frac{|{\mathit{S}}_f|}{\left|\mathit{d}\right|}}\hfill \\ \hfill & A^{\mathrm{up}}=\Delta t\sum _{f\sim faces}{\mathit{F}}_{i,f}^t\hfill \end{array}$$

(10b)

$$\begin{array}{cc}\hfill & J_{T_s}=A_{\mathrm{P}}+A_{\mathrm{N}}\hfill \\ \hfill & A_{\mathrm{P}}=V_{\mathrm{p}}{(1-\varphi )}^t{\rho }_s^t{C}_{p,s}^t+\Delta t\sum _{f\sim faces}{(1-\varphi )}_f^t{k}_{e,s,f}^t{\displaystyle \frac{|{\mathit{S}}_f|}{\left|\mathit{d}\right|}}+\Delta t{V}_{\mathrm{p}}{h}_c^t{a}_v^t\hfill \\ \hfill & A_{\mathrm{N}}=-\Delta t\sum _{f\sim faces}{(1-\varphi )}_f^t{k}_{e,s,,f}^t{\displaystyle \frac{|{\mathit{S}}_f|}{\left|\mathit{d}\right|}}\hfill \end{array}$$

(10c)

$$J_{sf}=J_{fs}=\Delta t{V}_{\mathrm{p}}{h}_c^t{a}_v^t$$

(10d)

$$b_{T_{FC}}=\left[\begin{array}{c}{b}_{T_f}\\ b_{T_s}\end{array}\right]$$

(11a)

$$\begin{array}{cc}\hfill & b_{T_f}=V_{\mathrm{p}}{\varphi }^t{T}_{l,\mathrm{P}}+\Delta t{V}_{\mathrm{p}}{h}_c^t{a}_v^t{T}_{s,\mathrm{P}}^t\hfill \end{array}$$

(11b)

$$\begin{array}{cc}\hfill & b_{T_s}=V_{\mathrm{p}}{(1-\varphi )}^t{\rho }_s^t{C}_{p,s}^t{T}_{s,\mathrm{P}}^t+\Delta t{V}_{\mathrm{p}}{h}_c^t{a}_v^t{T}_l^t\hfill \\ \hfill & -V_{\mathrm{p}}\Delta H_s{\left(T_s\right)}^t{a}_v^t{\displaystyle \frac{k_c^t{k}_s^t}{k_c^t+k_s^t}}{C}_f^{t+\Delta t}\hfill \end{array}$$

(11c)

(3)

Acid concentration transport

$$\begin{array}{cc}\hfill & J_C=A_{\mathrm{P}}+A_{\mathrm{N}}+A^{\mathrm{up}}\hfill \\ \hfill & A_{\mathrm{P}}=V_{\mathrm{p}}{\varphi }^t+\Delta t\sum _{f\sim faces}{{\varphi }_f}^t{\mathit{D}}_{m,f}^t{\displaystyle \frac{|{\mathit{S}}_f|}{\left|\mathit{d}\right|}}\hfill \\ \hfill & A_{\mathrm{N}}=-\Delta t\sum _{f\sim faces}{{\varphi }_f}^t{\mathit{D}}_{m,f}^t{\displaystyle \frac{|{\mathit{S}}_f|}{\left|\mathit{d}\right|}}\hfill \\ \hfill & A^{up}=\Delta t\sum _{f\sim faces}{\mathit{F}}_f^t\hfill \\ \hfill & b_C=V_{\mathrm{p}}{\varphi }^t{C}_{\mathrm{P}}^t-V_{\mathrm{p}}\Delta t{a}_v^t{\displaystyle \frac{k_c^t{k}_s^t}{k_c^t+k_s^t}}{C}_{\mathrm{P}}^t\hfill \end{array}$$

(12)

3.2. Solution Strategy

In this paper, the SIWC (semi-implicit weak coupling solution strategy) and PID (proportional–integral–derivative controller) dynamic pressure control method proposed by Chang [27] is employed to solve the problem of parallel multi-layered rock. The detailed computational procedure is shown in Figure 2. The detailed algorithms of SIWC and PID can be found in Chang’s paper [27], while this paper only presents the main calculation steps.

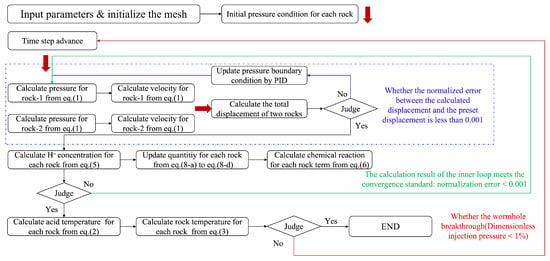
Figure 2. SIWC-PID simulation strategy.

3.3. Model Verification

To validate the accuracy of the model developed in this study, its computational results are compared with those of the two-scale continuum model proposed by Panga [13]. The simulation domain is a two-dimensional homogeneous porous medium with dimensions of 0.05 m in length and 0.02 m in width. Acid is injected at a constant rate from the left boundary, with flow exiting on the right boundary, while the top and bottom boundaries are set as impermeable. Wormhole breakthrough is defined as the moment when the injection pressure drops to 1% of its initial value [13]. The Damköhler number ($Da$) is introduced, defined as $Da={\displaystyle \frac{k_s{a}_{v,0}L}{v_{inj}}}$, $v_{inj}$ is the acid injection rate; L is the length of the model.

By varying the acid injection rate, $Da$ is varied from 1 to 1 × 10⁵, covering a range of conditions from diffusion-dominated to convection-dominated regimes. The simulations reproduce typical dissolution patterns under different values, including face dissolution, conical dissolution, dominant wormholes, ramified channels, and uniform dissolution, as illustrated in Figure 3. As shown in Figure 4, the optimal injection rate predicted by the present model exhibits excellent agreement with the results reported by Panga [13], along with a consistent overall trend. This optimal injection rate corresponds to the minimum volume required for breakthrough, which is a key indicator for evaluating acidizing efficiency. Minor deviations observed in certain ranges can be attributed to the inconsistency between the random porosity distribution adopted in this study and that used by Panga. Nevertheless, the results demonstrate that the proposed model accurately captures acid dissolution behavior in porous media and possesses strong predictive capability and reliability.

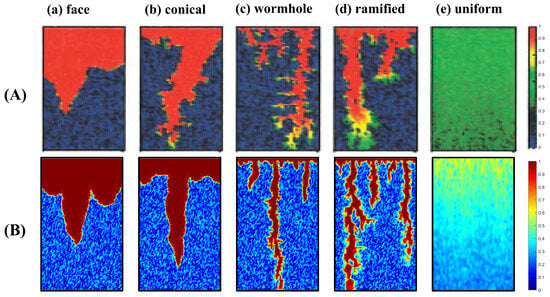
Figure 3. Comparison of simulated acid dissolution patterns: (A) results from Panga [13]; (B) results obtained in this study.

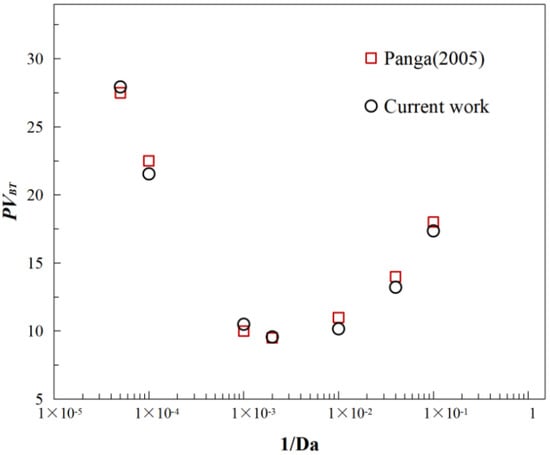
Figure 4. A quantitative comparison of the breakthrough volume predicted by the proposed numerical model and the results reported by Panga [13].

4. Results and Discussion

The objective of this paper is to analyze the effect of heterogeneity on wormhole morphology during the acidizing of multi-layered rock. Therefore, the structure of this chapter is designed as follows:

(1)

Investigate the effect of heterogeneity intensity on acidizing effect under the conditions of the same average permeability and a fixed interlayer permeability difference.

(2)

Investigate the comprehensive effect of interlayer permeability difference and heterogeneity intensity on acidizing performance in multi-layered rock.

In this study, the porosity distribution is obtained by generating normally distributed random numbers, with a mean value of 0.2. The amplitude of porosity fluctuation is used to characterize the heterogeneity intensity of porosity, and this heterogeneity intensity is classified into three levels (low (L), medium (M), and high (H)). Specifically, the fluctuation amplitude ranges corresponding to low, medium, and high heterogeneity intensities are [−5, 5], [−10, 10], and [−15, 20], respectively, and the resulting porosity value intervals generated thereby are [0.15, 0.25], [0.10, 0.30], and [0.05, 0.40] in sequence. Figure 5 shows the porosity distributions corresponding to the three levels of heterogeneity intensity used in this study, where the upper layer is a high-permeability rock and the lower layer is a low-permeability rock. These two rock layers (upper and lower) exhibits the same level of the heterogeneity intensity. Further, permeability is calculated from porosity using the Carman–Kozeny equation, which is given as follows:

$$K={\displaystyle \frac{1}{72\tau }}{\displaystyle \frac{{\varphi }^3{d}_p^2}{{(1-\varphi )}^2}}$$

(13)

where $\tau$ represents the pore tortuosity, and $d_p$ is the pressure drop value. Specifically, by adjusting parameter $d_p$, rocks with the same porosity distribution are made to exhibit different permeability characteristics.

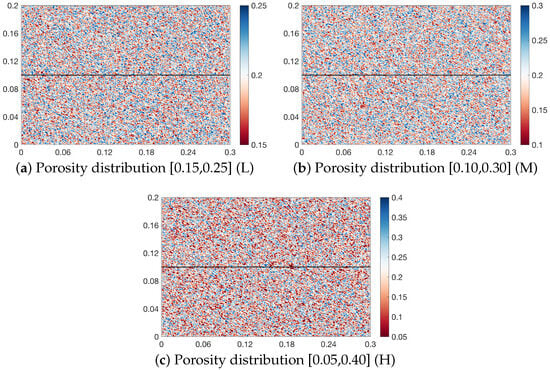
Figure 5. Porosity distribution with three different heterogeneity intensities.

4.1. Effect of Different Heterogeneity Intensity on Acidizing Effect

In this chapter, we set the average permeability of the high-permeability rock to 80 mD, with an interlayer permeability difference of 40 mD. And the values of $d_p$ of the Carman–Kozeny equation corresponding to the three levels of heterogeneity intensity (L, M, H) are [1.50 × 10⁵, 2.11 × 10⁵], [1.35 × 10⁵, 1.88 × 10⁵], and [0.92 × 10⁵, 1.3 × 10⁵], respectively. The case parameter set in this section is shown in Table 1.

Table 1. Parameters of Case 1 to Case 3.

Parameter	Symbol	Case 1	Case 2	Case 3
Permeability of parallel flow units [mD]	[${\mathit{K}}_{upper}$,${\mathit{K}}_{lower}$]	[40, 80]
Interlayer permeability [mD]	${\mathit{K}}_d$	40
Displacement rate [m3/s]	$Q_{inj}$	$1\times {10}^{-5}$
Injection temperature [°C]	$T_{inject}$	60

Figure 6 shows the wormhole morphology under the multi-layered rock are broken through. At a heterogeneity intensity of L, the wormholes in both the upper and lower rock layers exhibit a “straight-line” morphology, with weakly developed branches on the wormhole main trunks. At a heterogeneity intensity of M, the wormholes in the two layers still maintain an approximately “straight-line” shape, but obvious branch structures have emerged. At a heterogeneity intensity of H, the wormhole morphology transitions from “straight-line” to “dendritic,” and a large number of complex-shaped branches develop on the wormhole main trunks. Furthermore, at heterogeneity intensities of L and M, no complex preferential flow paths are formed inside the rock; the acid fluid is mainly concentrated in the wormhole main trunks and advances along the development direction of the trunks. In contrast, at a heterogeneity intensity of H, the difference in acid flow resistance between pores increases significantly, leading to continuous diversion and splitting of the acid fluid. Consequently, the width of the wormholes at a heterogeneity intensity of H is significantly smaller than that at intensities of L and M.

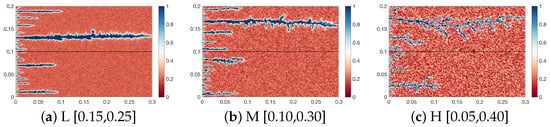
Figure 6. Wormhole morphology of Case 1 to Case 3.

As can be seen from Figure 6, there is a significant difference in the degree of acid dissolution between the upper and lower core layers. This dissolution discrepancy leads to varying degrees of permeability improvement in the two core layers, which in turn results in a differentiation in the acid flow distribution ratio between them. Figure 7 illustrates the results of the comparison of flow diversion. Overall, the flow distribution trends at heterogeneity intensities of L, M, and H are consistent: the flow fraction in the high-permeability rock gradually increases, while that in the low-permeability rock gradually decreases. When the rock experiences breakthrough, the flow distribution in the low-permeability rock drops to 0. As shown in Figure 6, rock heterogeneity mainly affects the flow distribution in the low-permeability rock. At heterogeneity intensities of L and M, the acid fluid diffuses “uniformly” from the wormhole main trunks into the rock interior, which slows down the forward development of wormholes and instead enhances the wormhole development capacity in the low-permeability rock indirectly. Consequently, two wormhole main trunks with similar lengths are observed in the low-permeability rock at intensities of L and M, whereas only one main trunk develops at intensity H. This influence trend leads to two outcomes: first, the decreasing rate of flow distribution in the low-permeability rock at intensity H is significantly faster than that at intensities L and M; second, the breakthrough speed of the high-permeability rock is also faster. In summary, the increase in heterogeneity intensity concentrates more acid fluid in the high-permeability rock, accelerates the acid-rock reaction rate, and simultaneously inhibits the flow distribution in the low-permeability rock.

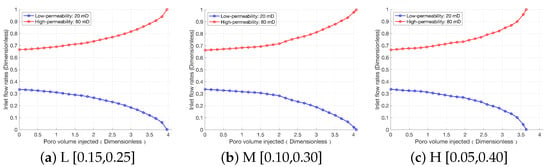
Figure 7. Effect of different heterogeneity intensity on the flow diversion when the interlayer permeability difference is 60 mD: high-permeability core (upper layer) and low-permeability core (lower layer).

Figure 8 displays the comparison of acidizing effect from Case 1 to Case 3. This study conducts analysis from two dimensions: breakthrough time and the porosity increment caused by acid dissolution of rock pores. The results show that when the heterogeneity intensity is L, the acid breakthrough time of the rock is 476 s; when the intensity is M, the breakthrough time is 463 s; and when the intensity is H, the breakthrough time is shortened to 450 s, as shown in Figure 8a. This indicates that the acid breakthrough time of high-permeability rocks decreases with the increase in heterogeneity intensity. This phenomenon indirectly confirms that the higher the heterogeneity intensity, the more prominent the preferential flow paths inside the rock. In addition, under the three heterogeneity intensity conditions, the porosity increments of the two rocks (High- and Low-permeability) are [0.0952, 0.0321], [0.0921, 0.0308], and [0.0868, 0.0297], respectively. The data shows that the porosity increment also decreases with the increase in heterogeneity intensity, as shown in Figure 8b.

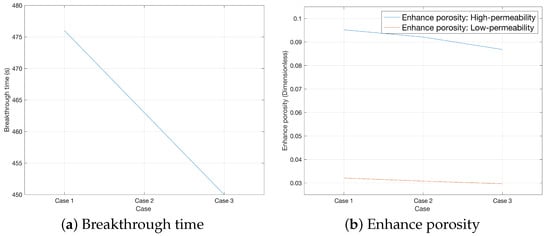
Figure 8. Comparison of acidizing effect from Case 1 to Case 3.

4.2. Effect of Interlayer Permeability Difference on Acidizing Effect

In Section 4.1, a relatively high interlayer permeability difference (60 mD) was set. In this chapter, we further investigate the influence law of heterogeneity intensity on wormhole morphology under different interlayer permeability differences. The average permeability of the high-permeability rock remains at 80 mD, while the average permeability of the low-permeability rock is set to two values: 20 mD and 60 mD. And the values of dp of low-permeability corresponding to the three levels of heterogeneity intensity are [1.07 × 10⁵, 1.86 × 10⁵], [1.93 × 10⁵, 1.64 × 10⁵], and [0.66 × 10⁵, 1.12 × 10⁵], respectively. The case parameter set in this section is shown in Table 2.

Table 2. Parameters of Case 4 to Case 9.

Parameter	Symbol	Case 4	Case 5	Case 6
Permeability of parallel flow units [mD]	[${\mathit{K}}_{upper}$,${\mathit{K}}_{lower}$]	[60, 80]
Interlayer permeability [mD]	${\mathit{K}}_d$	20
Displacement rate [m3/s]	$Q_{inj}$	$1\times {10}^{-5}$
Injection temperature [°C]	$T_{inject}$	60
Parameter	Symbol	Case 7	Case 8	Case 9
Permeability of parallel flow units [mD]	[${\mathit{K}}_{upper}$,${\mathit{K}}_{lower}$]	[20, 80]
Interlayer permeability [mD]	${\mathit{K}}_d$	60
Displacement rate [m3/s]	$Q_{inj}$	$1\times {10}^{-5}$
Injection temperature [°C]	$T_{inject}$	60

Figure 9 shows the wormhole morphology under two interlayer permeability difference conditions. Compared with Figure 7, when the interlayer permeability difference is 20 mD, the wormholes in the low-permeability rock develop longer under the three heterogeneity intensity conditions. When the interlayer permeability difference is 60 mD, the two wormholes that originally had similar lengths under heterogeneity intensities L and M exhibit a significant difference in their development lengths under a 20 mD permeability difference. Furthermore, a decrease in the interlayer permeability difference inhibits the development of wormhole branches in the high-permeability rock: under a 60 mD permeability difference, the development degree of wormholes in the low-permeability rock is greatly weakened, while the wormhole branches in the high-permeability rock are further developed. Meanwhile, the enhancing effect of heterogeneity intensity on the low-permeability rock is significantly reduced.

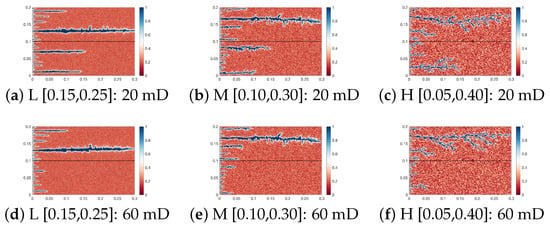
Figure 9. Wormhole morphology of Case 4 to Case 9.

Figure 10 illustrates the results of the comparison of flow diversion. When the interlayer permeability difference is 20 mD, the inhibitory effect of the high-permeability rock on the low-permeability rock weakens, and the initial flow distribution of the low-permeability rock increases from 0.34 (at 60 mD) to 0.44. When the interlayer permeability difference is 60 mD, the flow distribution of the low-permeability rock is significantly inhibited by the high-permeability rock, with its initial flow distribution decreasing to 0.2. Furthermore, the slope of the flow distribution change curve of the low-permeability rock increases with the increase in the interlayer permeability difference; at lower interlayer permeability differences, the decreasing trend of its flow distribution transforms into an approximately linear one. In addition, a larger interlayer permeability difference leads to a higher H⁺ concentration in the high-permeability rock, and the acid–rock reaction rate is accelerated accordingly, resulting in faster breakthrough of the high-permeability rock. Overall, during the acidification of multi-layered rock, the influences of interlayer permeability difference and heterogeneity intensity on acidification performance are mainly reflected in the low-permeability rock: the smaller the interlayer permeability difference, the greater the influence of heterogeneity intensity on the low-permeability rock; the larger the interlayer permeability difference, the smaller the influence of heterogeneity intensity on the low-permeability rock.

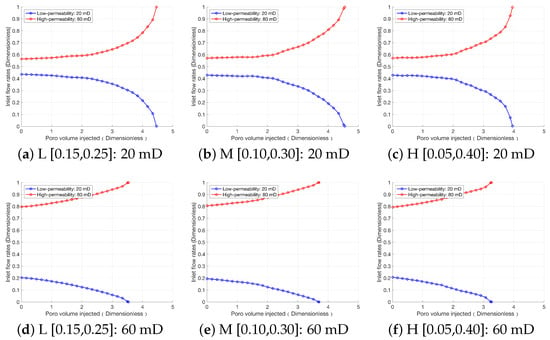
Figure 10. Comprehensive effect of interlayer permeability difference and heterogeneity intensity on the flow diversion.

When the interlayer permeability difference decreases from 40 mD to 20 mD, the acid breakthrough times of rocks under three heterogeneity intensities increase from [476 s, 463 s, 450 s] to [535 s, 522 s, 489 s], as shown in Figure 11a. As can be seen from Figure 10a–c, the reduction in the proportion of acid flow allocated to high-permeability rocks leads to a decrease in the acid–rock reaction rate, which in turn delays the acid breakthrough process of the rocks. In terms of porosity increment, with the decrease of interlayer permeability difference under this condition, the porosity increment of low-permeability rocks increases from [0.0321, 0.0308, 0.0297] to [0.0521, 0.0504, 0.0449], while that of high-permeability rocks decreases from [0.0952, 0.0921, 0.0868] to [0.0907, 0.0874, 0.0812], as shown in Figure 11b. This indicates that the reduction of interlayer permeability difference can enhance the acidizing effect of low-permeability rocks while weakening that of high-permeability rocks.

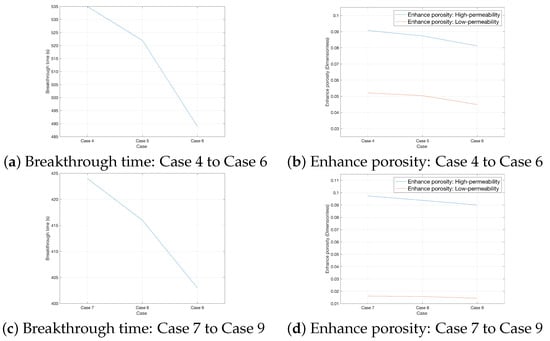
Figure 11. Comparison of acidizing effect from Case 4 to Case 9.

Conversely, when the interlayer permeability difference increases from 40 mD to 60 mD, the acid breakthrough times of rocks under three heterogeneity intensities decrease from [476 s, 463 s, 450 s] to [424 s, 416 s, 403 s], as shown in Figure 11c. At this time, the increase in the proportion of acid flow allocated to high-permeability rocks accelerates the acid–rock reaction rate, thereby speeding up the acid breakthrough of the rocks. Porosity increment data show that the porosity increment of low-permeability rocks decreases significantly from [0.0321, 0.0308, 0.0297] to [0.0161, 0.0157, 0.0144], while that of high-permeability rocks increases from [0.0952, 0.0921, 0.0868] to [0.0974, 0.0938, 0.0900], as shown in Figure 11d. It can be seen that the increase in interlayer permeability difference almost completely inhibits the acidizing effect inside low-permeability rocks.

5. Conclusions

In this study, the SIWC-PID numerical simulation framework for multi-layered rock acidizing was employed to investigate the problem of multi-layered rock acidizing. From two dimensions—wormhole morphology and the flow distribution curve of each rock layer—the influences of both the individual effect of heterogeneity and the synergistic effect of heterogeneity and interlayer permeability difference on the acidizing performance of multi-layered rock were systematically explored. The main important conclusions are as follows:

(1)

The breakthrough times for the three heterogeneity intensities are 476 s, 463 s, and 450 s, respectively. Under the condition of the same interlayer permeability difference, the stronger the rock heterogeneity, the less flow the low-permeability rocks obtain and the faster the high-permeability rocks are broken through. Furthermore, the smaller the flow rate allocated to the rock, the smaller the porosity increase caused by acid dissolution of the rock, and vice versa. The high-permeability rocks inhibit the flow distribution of low-permeability rocks, and the development degree of wormholes in high-permeability rocks is higher than that in low-permeability rocks.

(2)

The interlayer permeability difference significantly affects the degree to which heterogeneity acts on acidification performance: the larger the interlayer permeability difference, the greater the number of wormhole branches and the more complex their morphology in high-permeability rocks, while the development degree of wormholes in low-permeability rocks becomes weaker.

(3)

Comprehensive comparison of flow allocation, breakthrough time, and enhanced porosity reveals that the interlayer permeability difference and reservoir heterogeneity influence the acid–rock reaction rate by altering the flow distribution pattern between high-permeability and low-permeability rocks, and thereby regulating the breakthrough time and acidizing performance of these two types of permeable rocks.