An Intelligent Directional Drill Steering Method Based on Real-Time Adaptive Closed-Loop Control
Abstract
1. Introduction
- (1)
- This study proposes an intelligent closed-loop control method based on online adaptive optimization, which can quickly and dynamically adjust PID control parameters while ensuring control accuracy. This method effectively addresses the issues of error accumulation, response delay, and control instability.
- (2)
- This study proposes a PID parameter optimization model centered on dogleg severity constraints, with online dynamic calibration achieved through a genetic algorithm. This model minimizes trajectory deviation while ensuring trajectory smoothness and precise tracking.
- (3)
- This study develops a real-time control output module, which accurately calculates tool face angle and steering tool force based on real-time attitude data. This module provides intuitive and efficient operational guidance, offering accurate manual intervention solutions for field operators.
2. Methodology
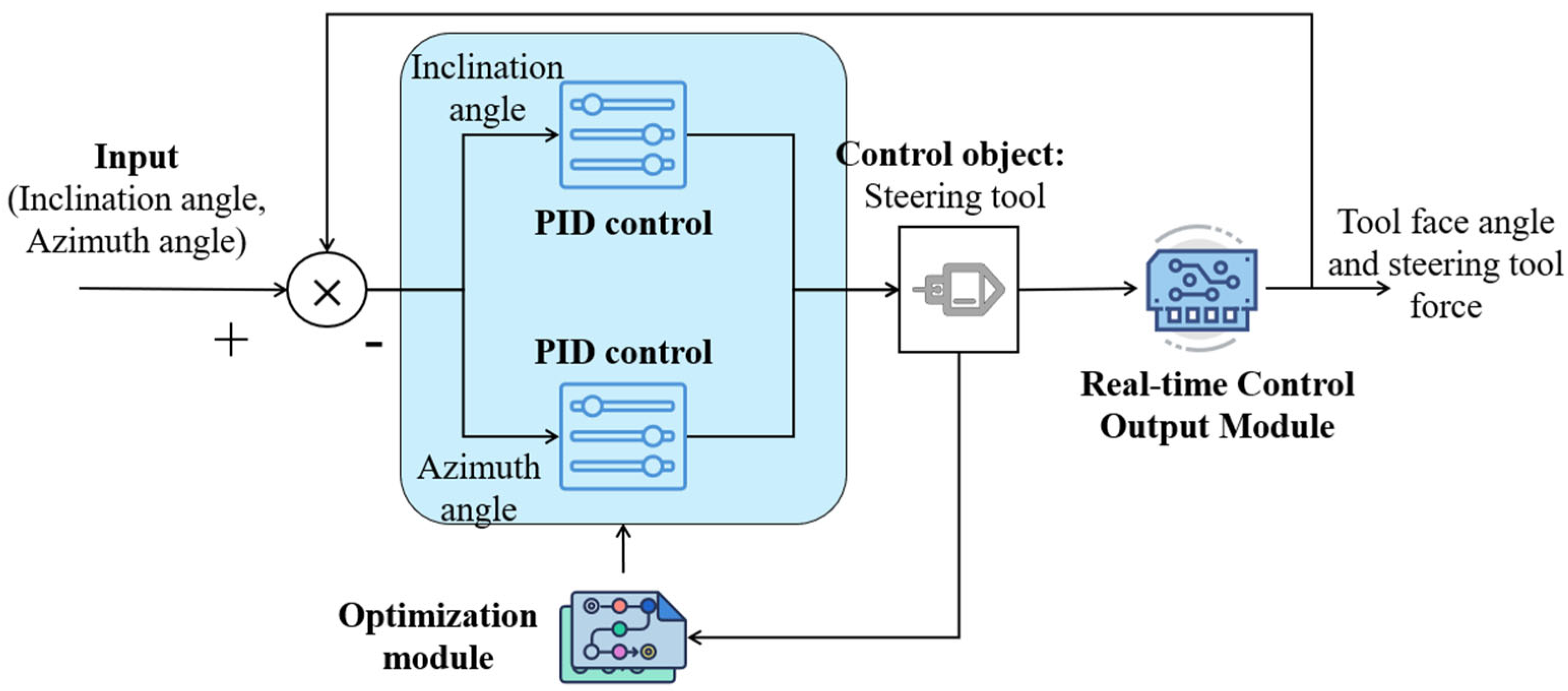
2.1. Framework of This Research
2.2. PID Control Mechanism Based on Three-Dimensional Intelligent Steering
2.3. Online PID Parameter Optimization Mechanism Based on Genetic Algorithm
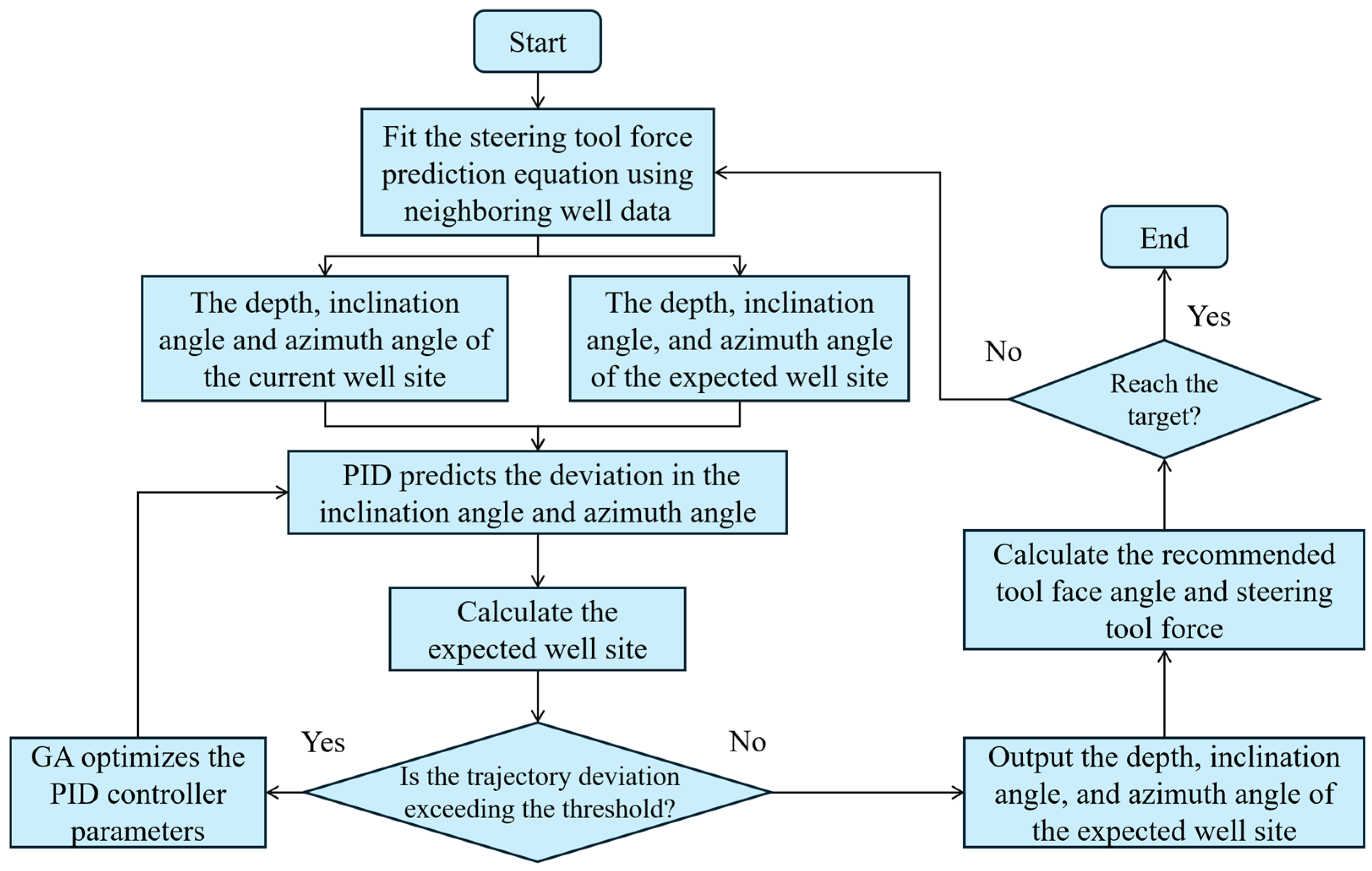
- (1)
- Trigger mechanism improvement: The GA is triggered to run only when the normal distance between the drilling trajectory and the preset trajectory exceeds the threshold, rather than continuously optimizing online, which significantly reduces the computation frequency.
- (2)
- Optimization range reduction: When trajectory deviation occurs, the algorithm selects only a certain range of preset trajectory points near the current drilling position (50 points are selected in this study) for optimization, in order to reduce the computational load.
- (3)
- Early termination strategy: During the optimization process, once a PID parameter causes the normal distance between the predicted trajectory and the preset trajectory to be smaller than the threshold, the optimization is terminated early and the parameter is output, thus avoiding unnecessary computations.
2.4. Control Output Mechanism Based on Real-Time Attitude Data
2.5. Procedure of This Method
3. Geological Characteristics and Simulation Setup
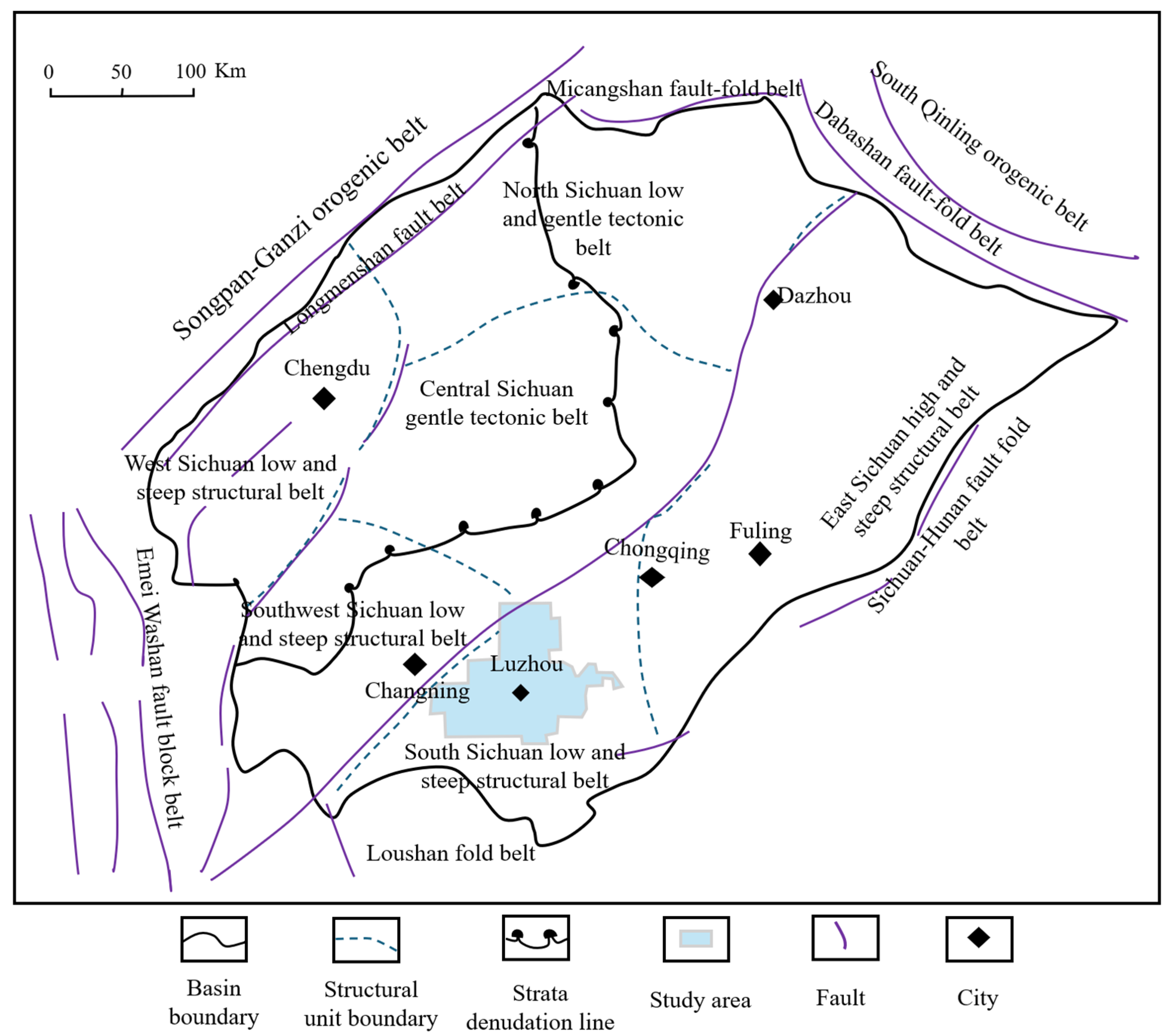
3.1. Stratigraphic Characteristics of Luzhou Block
3.2. Simulation Setup
4. Results Analysis and Discussion
4.1. Comparison of Drilling Trajectories
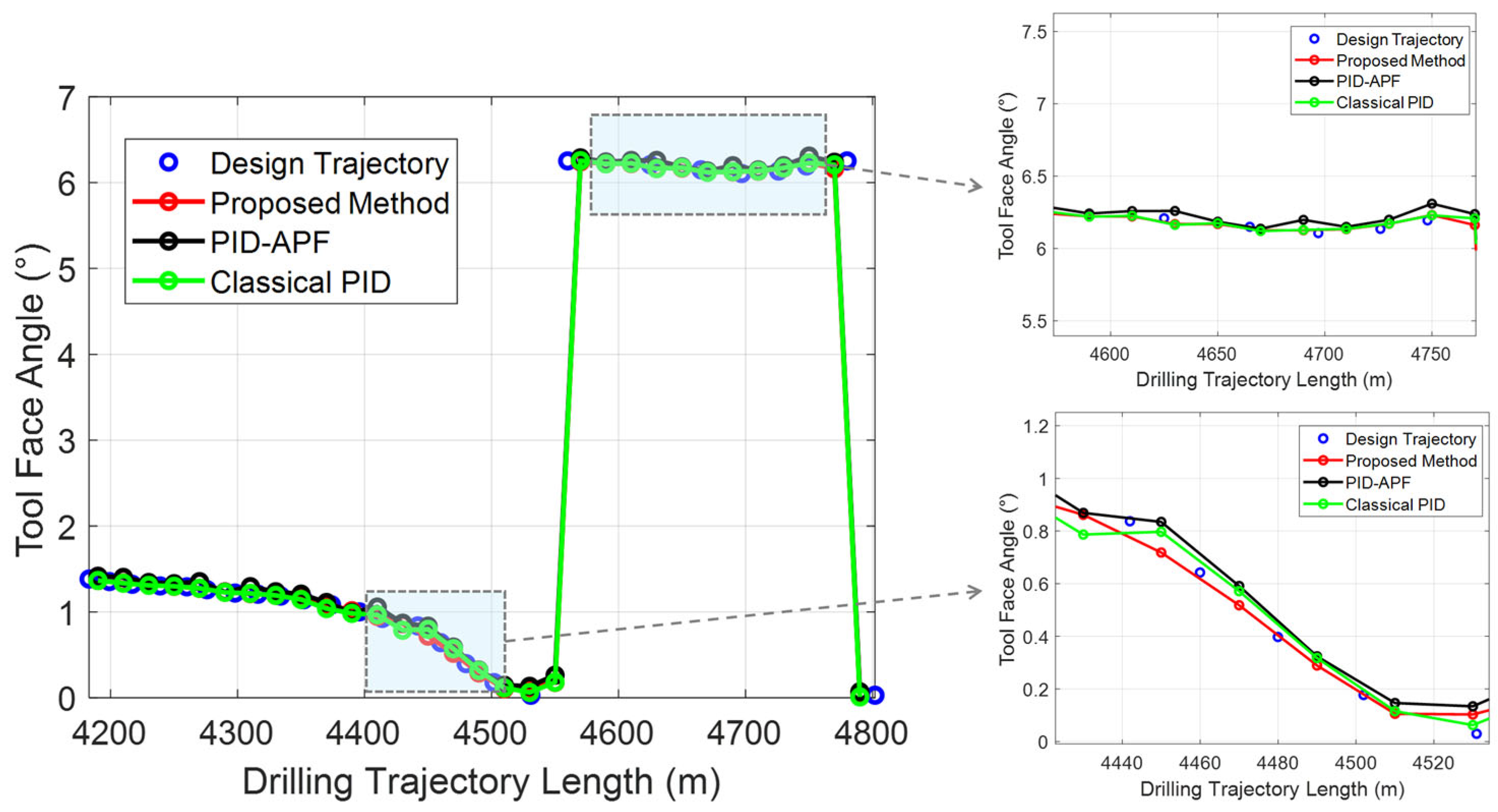
4.2. Analysis of Steering Tool Force and Tool Face Angle
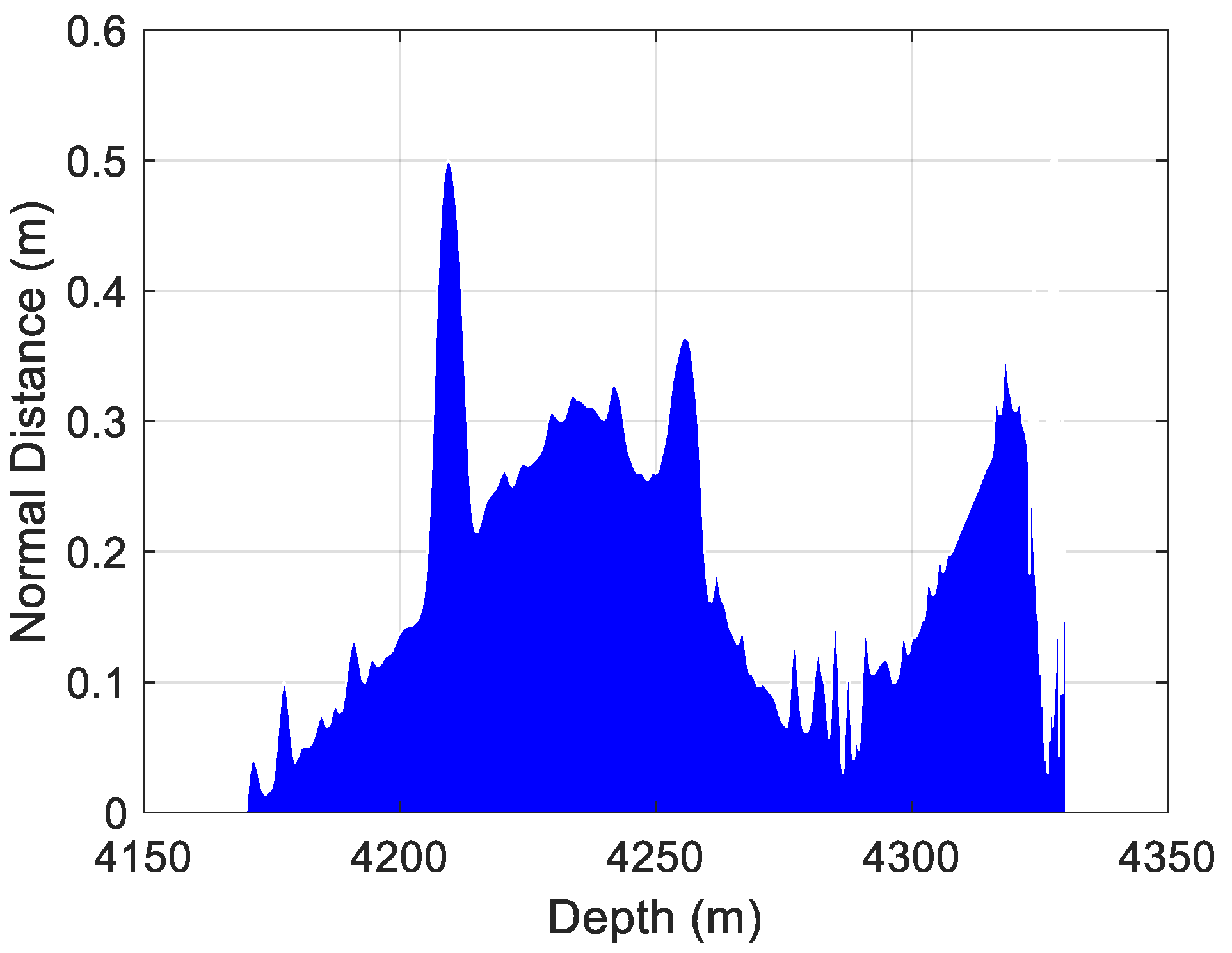
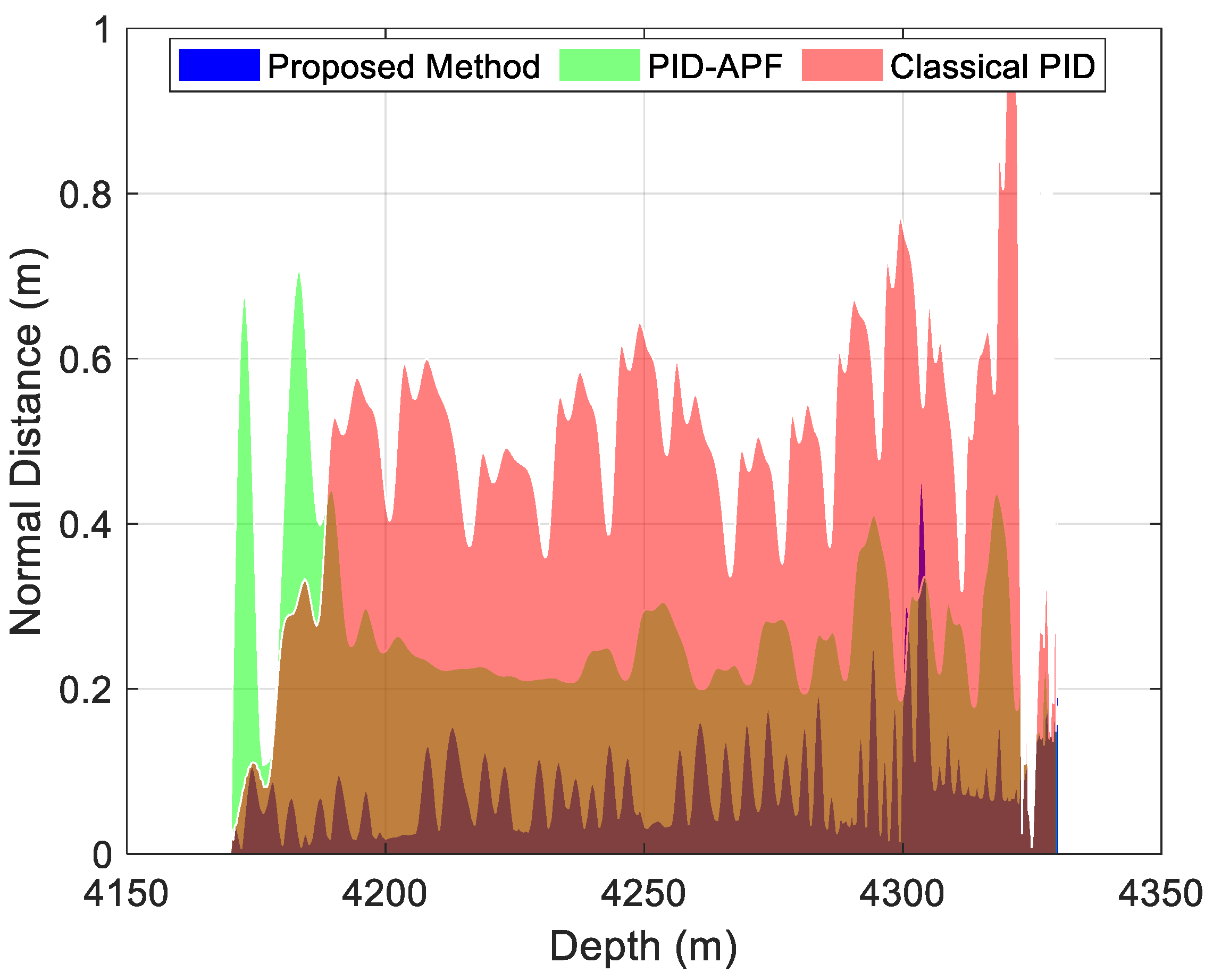
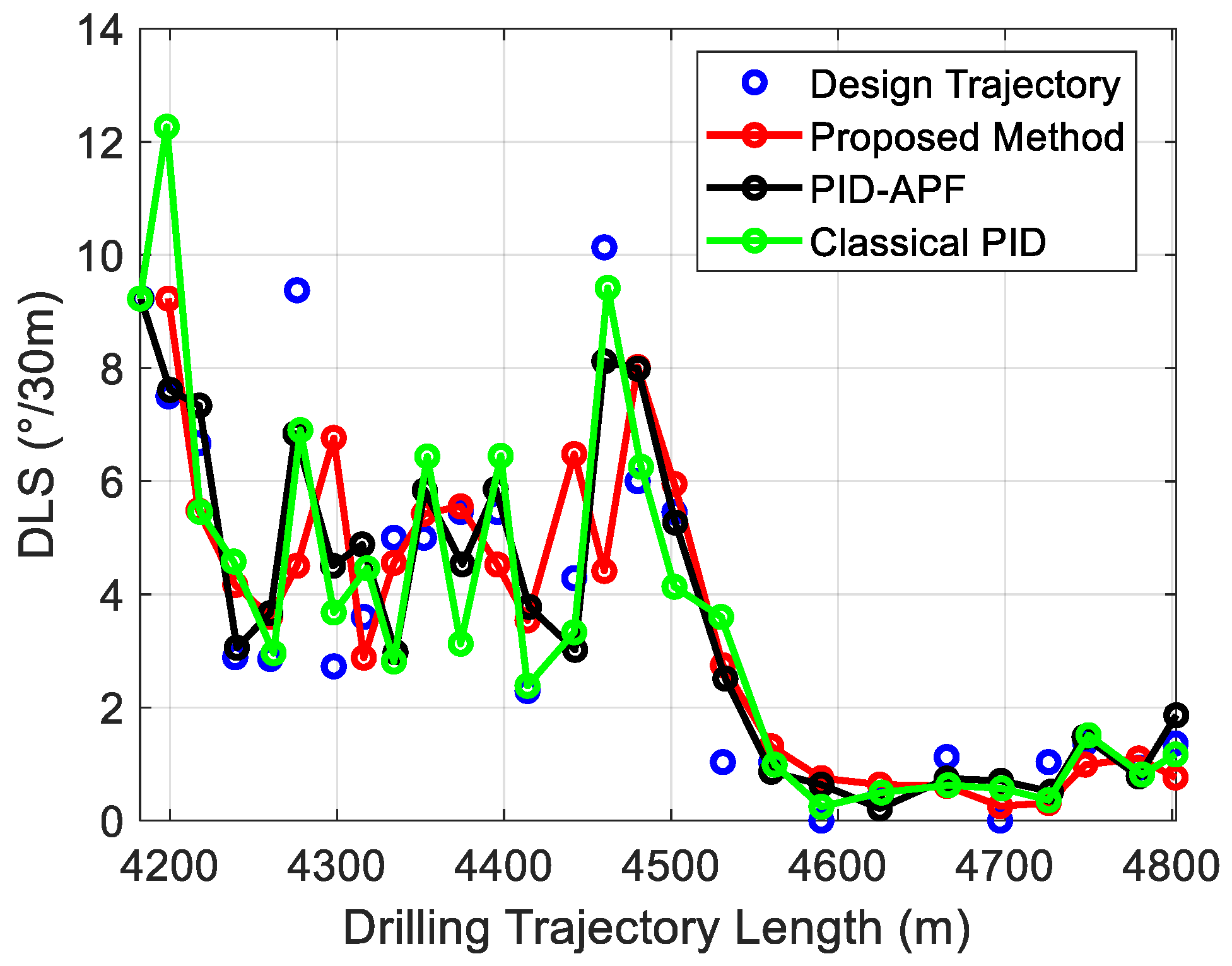
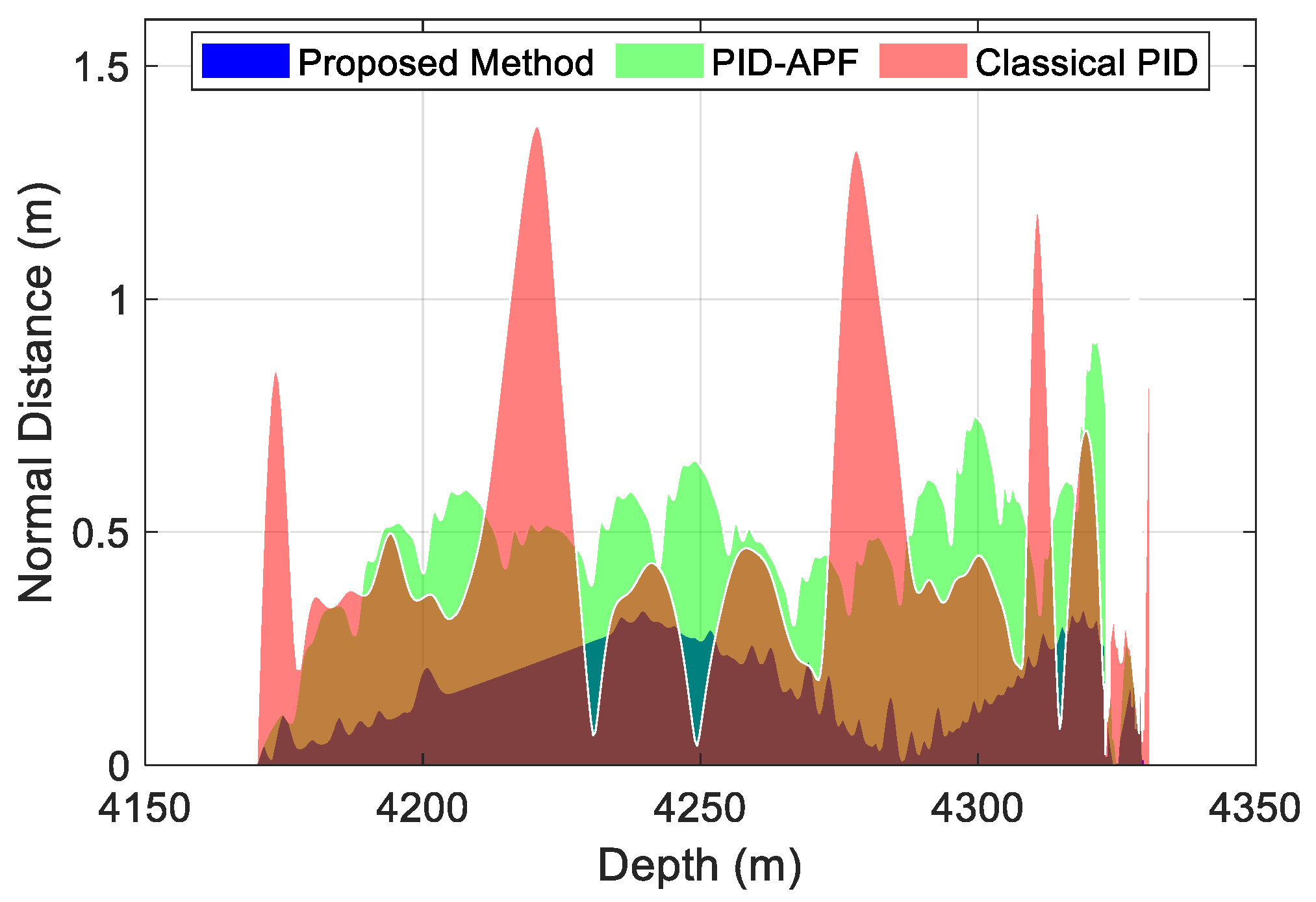
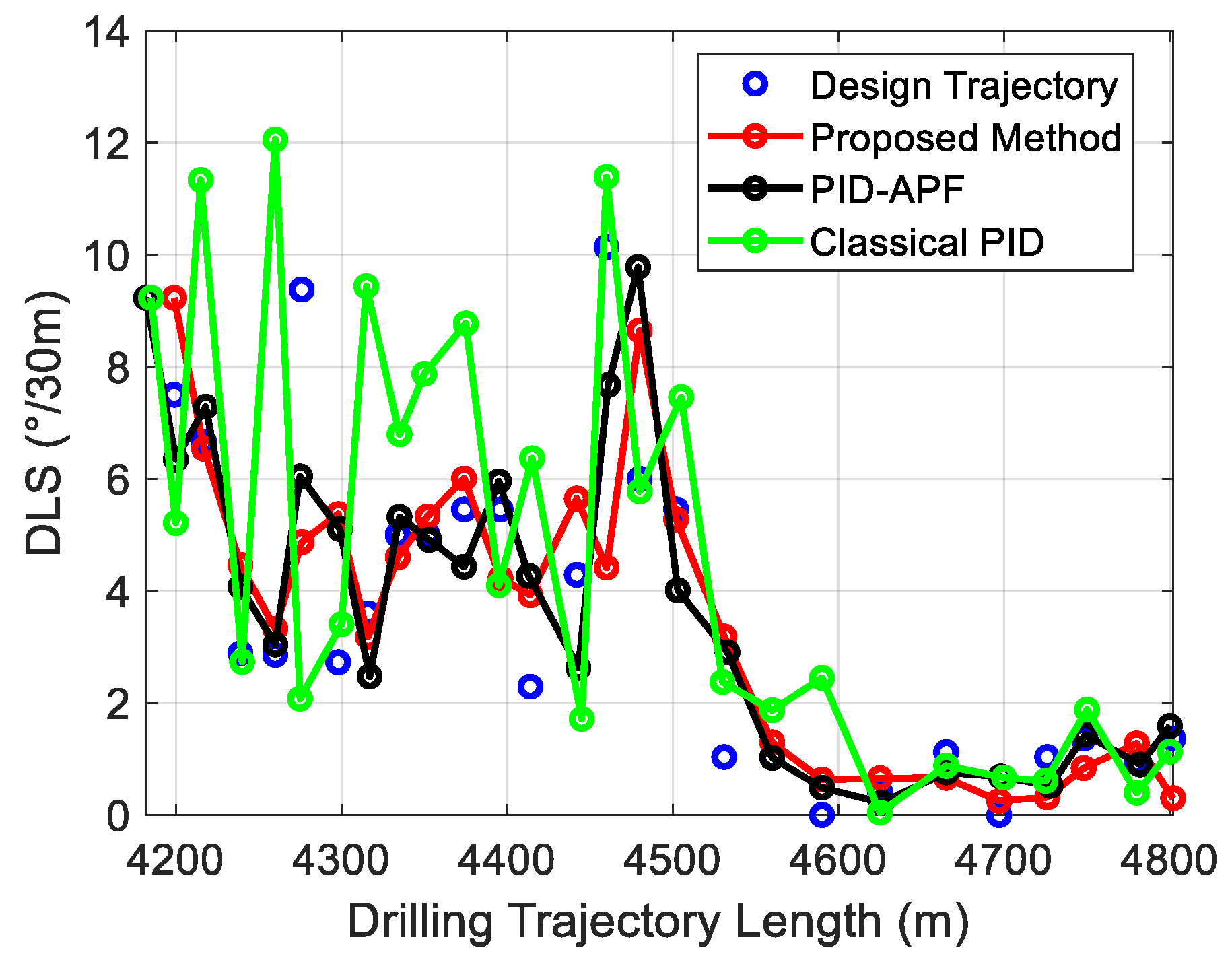
4.3. Comparison of Normal Distance and Dogleg Severity
4.4. Robustness Tests
5. Discussion
6. Conclusions
- (1)
- The proposed method possesses adaptive adjustment capability, enabling real-time response to posture disturbances and thereby enhancing system stability and control accuracy. Compared to the traditional PID and PID-APF methods, the normal distance accuracy improves by 88.89% and 34.02%, respectively, under noise-free conditions; under noise interference, the accuracy improves by 56.73% and 54.97%, respectively.
- (2)
- The proposed method significantly reduces DLS during the drilling process, resulting in a smoother trajectory. Compared to the traditional PID and PID-APF methods, the DLS decreases by 6.30% and 5.81%, respectively, under noise-free conditions; under noise interference, the DLS decreases by 23.38% and 4.85%, respectively.
- (3)
- A control output model based on posture data has been established, which can accurately predict the required force and tool face angle for the steering tool. This enhances the real-time and practical aspects of control quantity calculations, facilitating field guidance and the deployment of automation control systems.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| AA | Azimuth angle |
| DLS | Dogleg severity |
| GA | Genetic algorithm |
| IA | Inclination angle |
| STD | Standard deviation |
| PID | Proportional-integral-derivative |
| PID-APF | PID method based on the artificial potential field |
Appendix A
| Starting Depth (m) | End Depth (m) | Drilled Footage (m) | SIA (°) | SAA (°) | DLS (°/30 m) | STF |
|---|---|---|---|---|---|---|
| 4170 | 4183 | 13 | 31 | 17 | 9.02 | 67% |
| 4183 | 4199 | 16 | 35 | 17 | 9.23 | 77% |
| 4199 | 4217 | 18 | 39 | 17 | 7.50 | 80% |
| 4217 | 4239 | 22 | 43 | 17 | 6.66 | 67% |
| 4239 | 4260 | 21 | 45 | 16 | 2.88 | 58% |
| 4260 | 4276 | 16 | 47 | 16 | 2.85 | 58% |
| 4276 | 4298 | 22 | 52 | 16 | 9.37 | 58% |
| 4298 | 4316 | 18 | 54 | 16 | 2.72 | 58% |
| 4316 | 4334 | 18 | 56 | 15 | 3.60 | 58% |
| 4334 | 4352 | 18 | 59 | 15 | 5.00 | 58% |
| 4352 | 4374 | 22 | 62 | 15 | 5.01 | 45% |
| 4374 | 4396 | 22 | 66 | 15 | 5.45 | 45% |
| 4396 | 4414 | 18 | 70 | 15 | 5.46 | 45% |
| 4414 | 4442 | 28 | 71 | 16 | 2.29 | 54% |
| 4442 | 4460 | 18 | 75 | 16 | 4.28 | 58% |
| 4460 | 4480 | 20 | 81 | 17 | 10.13 | 58% |
| 4480 | 4502 | 22 | 85 | 17 | 6.00 | 54% |
| 4502 | 4531 | 29 | 89 | 17 | 5.45 | 54% |
| 4531 | 4560 | 29 | 90 | 17 | 1.03 | 54% |
| 4560 | 4590 | 30 | 91 | 17 | 1.03 | 54% |
| 4590 | 4625 | 35 | 91 | 17 | 0.68 | 38% |
| 4625 | 4665 | 40 | 91.5 | 17 | 0.42 | 38% |
| 4665 | 4697 | 32 | 93 | 17 | 1.12 | 38% |
| 4697 | 4726 | 29 | 93 | 17 | 0.21 | 38% |
| 4726 | 4748 | 22 | 92 | 17 | 1.03 | 38% |
| 4748 | 4780 | 32 | 91 | 17 | 1.36 | 61% |
| 4780 | 4802 | 22 | 90 | 17 | 0.93 | 61% |
| 4802 | 4835 | 33 | 89 | 17 | 1.36 | 25% |
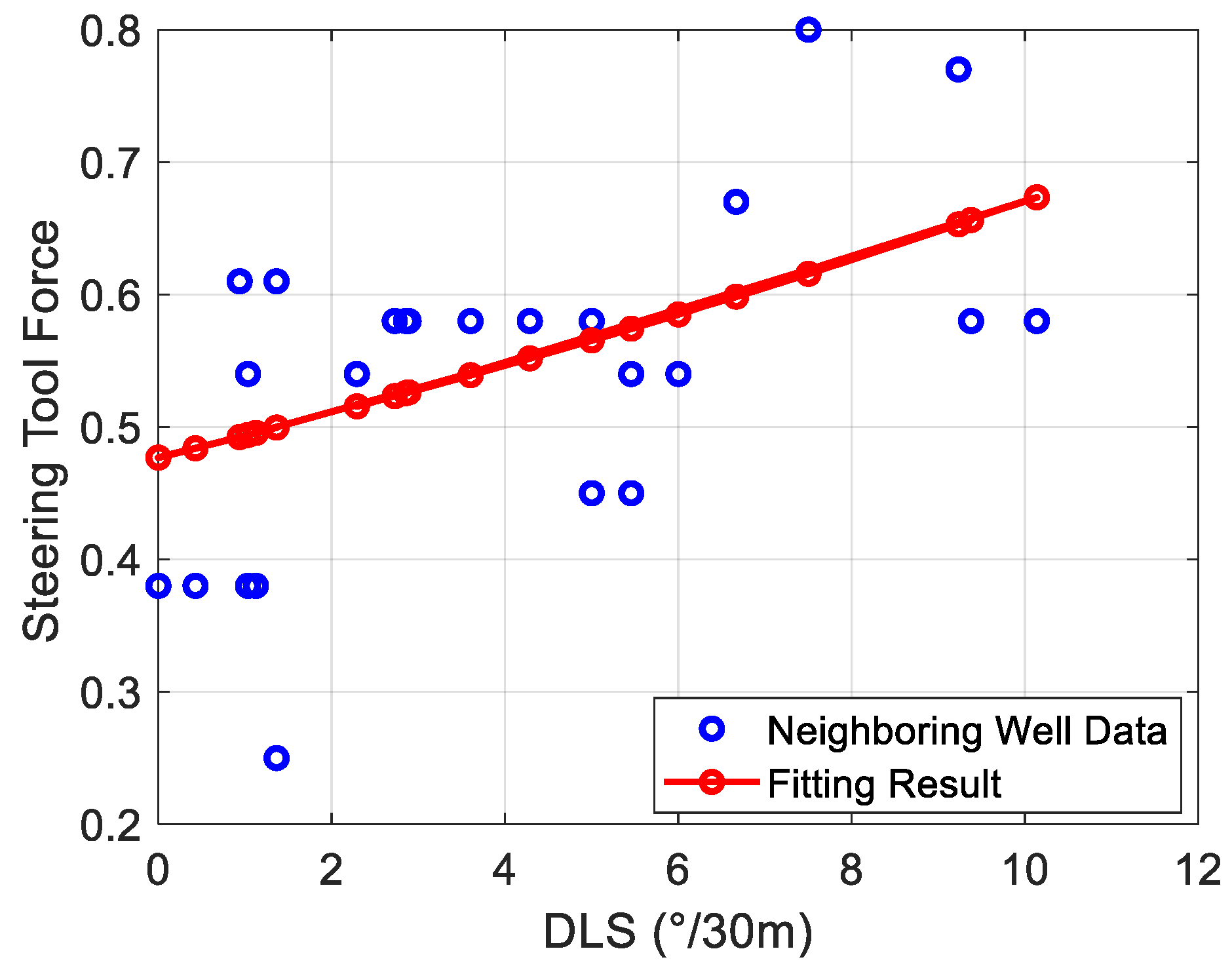
Appendix B
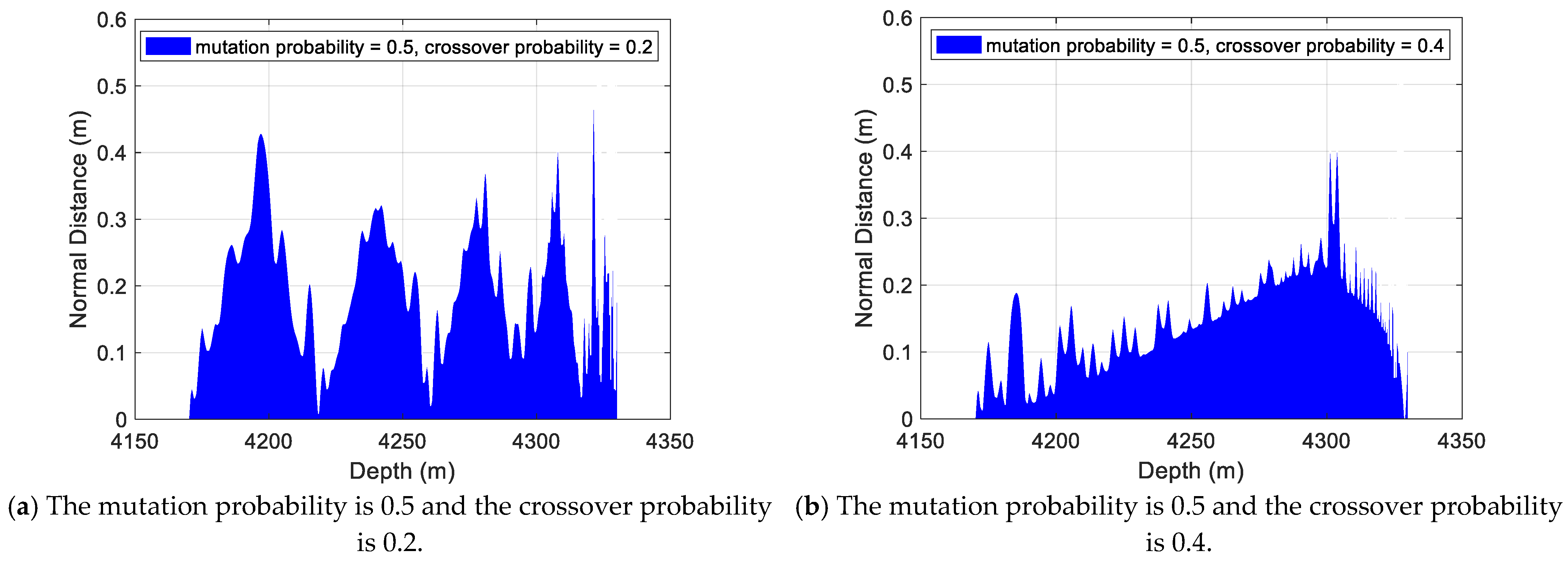

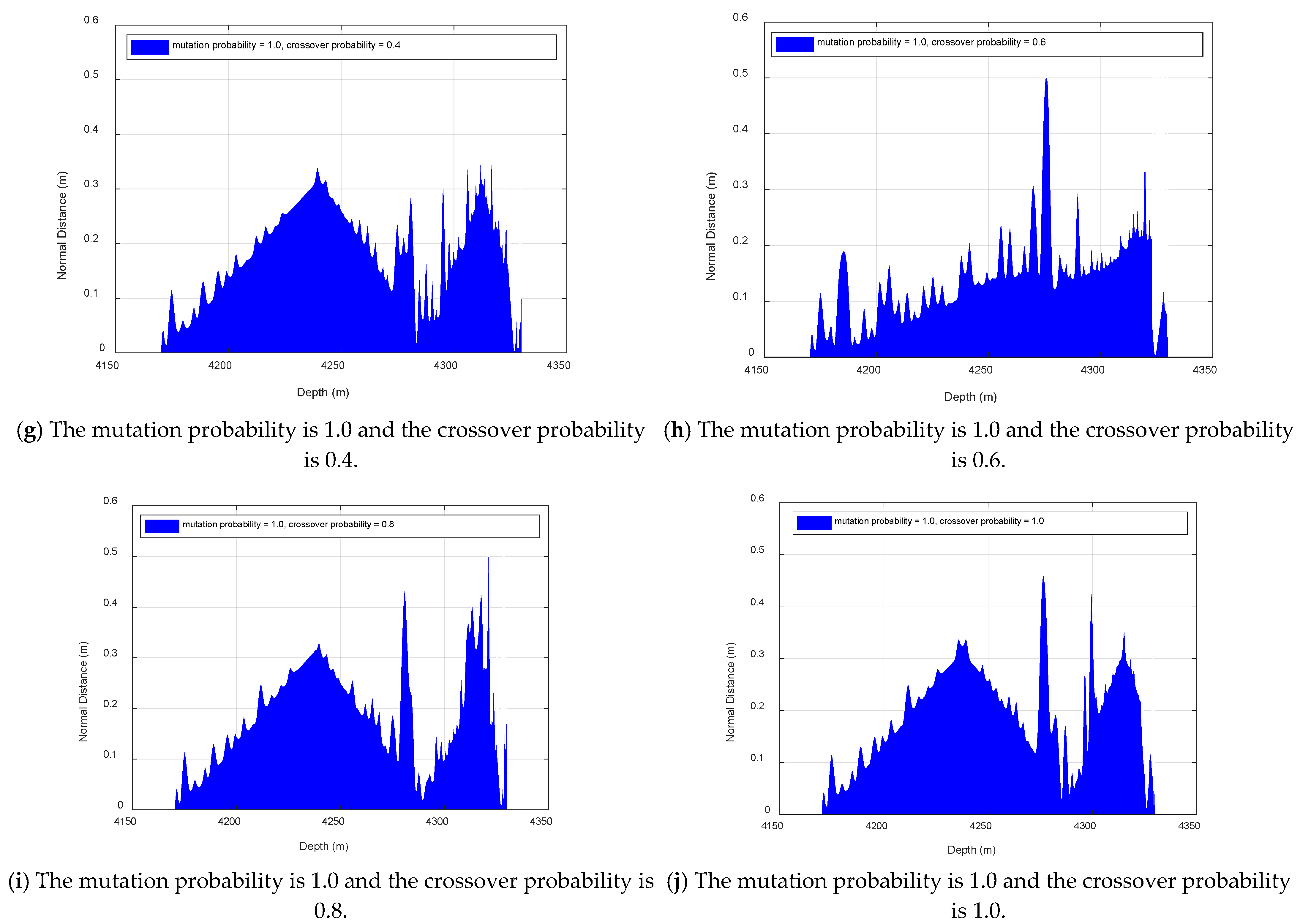
| Parameter Combination | Mean | STD | Parameter Combination | Mean | STD |
|---|---|---|---|---|---|
| CR = 0.2, MU = 0.5 | 0.391 | 0.450 | CR = 0.2, MU = 1.0 | 0.209 | 0.121 |
| CR = 0.4, MU = 0.5 | 0.172 | 0.147 | CR = 0.4, MU = 1.0 | 0.185 | 0.085 |
| CR = 0.6, MU = 0.5 | 0.349 | 0.569 | CR = 0.6, MU = 1.0 | 0.172 | 0.139 |
| CR = 0.8, MU = 0.5 | 0.171 | 0.070 | CR = 0.8, MU = 1.0 | 0.205 | 0.110 |
| CR = 1.0, MU = 0.5 | 0.176 | 0.082 | CR = 1.0, MU = 1.0 | 0.196 | 0.087 |
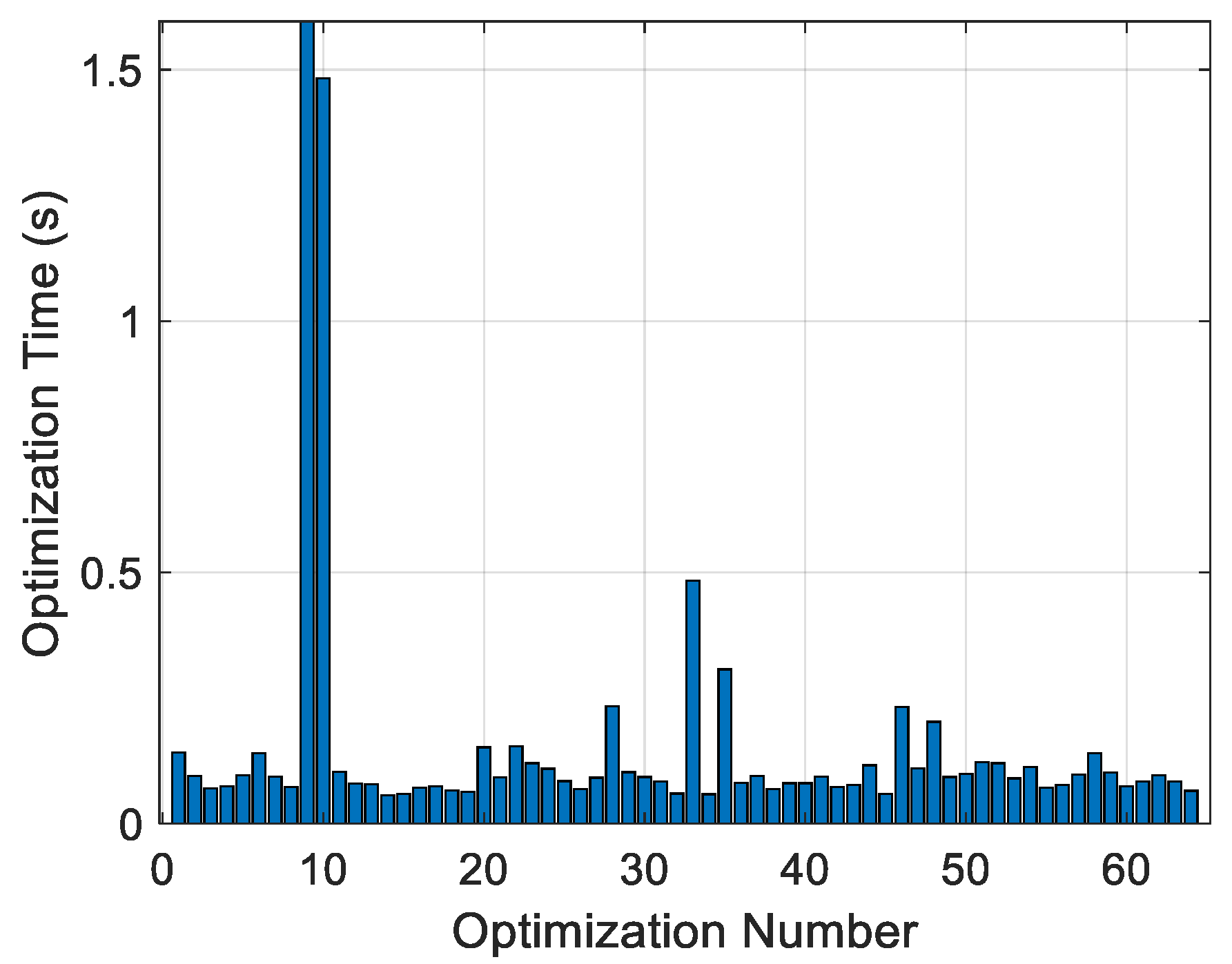
Appendix C
References
- Liu, X.; Jiang, Z.; Wang, Y.; Mo, H.; Li, H.; Guo, J. Research on trajectory control technology for L-shaped horizontal exploration wells in coalbed methane. Sci. Rep. 2024, 14, 11343. [Google Scholar] [CrossRef]
- Zhang, N.; Li, F.; Ren, B.; Liu, Z.; Wang, D.; Chen, J.; Lyu, F. Research on Wellbore Trajectory Control of Rotary Steerable System Using Back-Propagation Neural Network-Fuzzy Method. Geoenergy Sci. Eng. 2025, 257, 214201. [Google Scholar] [CrossRef]
- Gu, H.; Wu, Y.; Li, X.; Hou, Z. Research on Wellbore Trajectory Optimization and Drilling Control Based on the TD3 Algorithm. Appl. Sci. 2025, 15, 7258. [Google Scholar] [CrossRef]
- Li, Z.; Song, X.; Yan, B.; Zhu, Z.; Zhang, C.; Tian, L.; Yu, Q. Fine-Tuning Wellbore Trajectory in Rotary Drilling Using Machine Learning–Based Model Predictive Control. SPE J. 2025, 1–19. [Google Scholar] [CrossRef]
- Chen, S.; Hu, G.; Huang, X.; Zhang, G.; Liu, X. Influence of wellbore dogleg severity on drilling friction in horizontal wells. Geofluids 2023, 2023, 9973863. [Google Scholar]
- Dunn, J. Identifying cumulative TVD error in horizontal wells drilled with rotary steerable systems. In Proceedings of the SPE/IADC Drilling Conference and Exhibition, Galveston, TX, USA, 5–7 March 2024. [Google Scholar]
- Zafarian, H.; Ameri, M.; Vaghasloo, Y.A. Error reduction of tracking planned trajectory in a thin oil layer drilling using smart rotary steerable system. J. Pet. Sci. Eng. 2021, 196, 107668. [Google Scholar] [CrossRef]
- Eltayeb, A.; Ahmed, G.; Imran, I.H.; Alyazidi, N.M.; Abubaker, A. Comparative analysis: Fractional PID vs. PID controllers for robotic arm using genetic algorithm optimization. Automation 2024, 5, 230–245. [Google Scholar] [CrossRef]
- Karam, E.H.; Al-Gburi, A.K.; Abd Mohammed, Y. An Adaptive Robust PID Controller Design for a Single Motorized Robotic Arm. J. Eng. Sustain. Dev. 2025, 29, 682–690. [Google Scholar] [CrossRef]
- Admas, Y.A.; Mitiku, H.M.; Salau, A.O.; Omeje, C.O.; Braide, S.L. Control of a fixed wing unmanned aerial vehicle using a higher-order sliding mode controller and non-linear PID controller. Sci. Rep. 2024, 14, 23139. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Liang, S.; Guo, M.; Wang, H.; Zhang, H. Adaptive multimodal control of trans-media vehicle based on deep reinforcement learning. Eng. Appl. Artif. Intell. 2025, 139, 109524. [Google Scholar] [CrossRef]
- Amertet, S.; Gebresenbet, G.; Alwan, H.M. Modeling of unmanned aerial vehicles for smart agriculture systems using hybrid fuzzy PID controllers. Appl. Sci. 2024, 14, 3458. [Google Scholar] [CrossRef]
- Boonkirdram, S.; Audomsi, S.; Sa-Ngiamvibool, W.; Kasemsin, W. Design of Two-Degree-of-Freedom PID Controllers Optimized by Bee Algorithm for Frequency Control in Renewable Energy Systems. Energies 2025, 18, 4880. [Google Scholar] [CrossRef]
- Lin, J.; Yuan, W.; Hu, Z.; Huang, Z.; Yan, Z.; Huang, H.; Zheng, R. Fuzzy PID Individual Pitch Control with Effective Wind Speed Estimation for Offshore Floating Wind Turbines. Energies 2025, 18, 4812. [Google Scholar] [CrossRef]
- Inyang, I.J.; Whidborne, J.F. Bilinear modelling, control and stability of directional drilling. Control Eng. Pract. 2019, 82, 161–172. [Google Scholar] [CrossRef]
- Hernandez-Suarez, R.; Puebla, H.; Aguilar-Lopez, R.; Hernandez-Martinez, E. An integral high-order sliding mode control approach for stick-slip suppression in oil drillstrings. Pet. Sci. Technol. 2009, 27, 788–800. [Google Scholar] [CrossRef]
- Alvarado-Silva, C.A.; de Oliveira, G.C.R.; Gamboa, A.A.R.; Gaytan-Reyna, K.L.; Guidi, E.S.; Azevedo Silva, F.; Gamarra-Rosado, V.O. A Simulation Study on Pressure Control in Oil Well Drilling Using Gain-Scheduled PID Controllers. Appl. Sci. 2025, 15, 2748. [Google Scholar] [CrossRef]
- Laib, A.; Talbi, B.; Krama, A.; Gharib, M. Hybrid interval type-2 fuzzy PID+ I controller for a multi-DOF oilwell drill-string system. IEEE Access 2022, 10, 67262–67275. [Google Scholar] [CrossRef]
- Zhang, N.; Li, F.; Liu, Z.; Ren, B.; Chen, J. Inclination-holding Control Method for Rotary Steerable System Based on Fuzzy-PID. In Proceedings of the 2024 6th International Conference on Intelligent Control, Measurement and Signal Processing (ICMSP), Xi’an, China, 29 November–1 December 2024; pp. 31–34. [Google Scholar]
- Fang, C.; Wang, Q.; Jiang, H.; Chen, Z.; Wang, Y.; Zhai, W.; Chen, S. Shale wellbore stability and well trajectory optimization: A case study from Changning, Sichuan, China. Pet. Sci. Technol. 2023, 41, 564–585. [Google Scholar] [CrossRef]
- Isaev, A.A.; Aliev, M.M.O.; Drozdov, A.N.; Gorbyleva, Y.A.; Nurgalieva, K.S. Improving the efficiency of curved wells’ operation by means of progressive cavity pumps. Energies 2022, 15, 4259. [Google Scholar] [CrossRef]
- Hu, Y.; Wang, L.; Li, J.; Weng, H.; Zheng, Z.; Wen, G.; Zhang, F. Predicting the Temperature Rise in Oil-Immersed Transformers Based on the Identification of Thermal Circuit Model Parameters. Energies 2025, 18, 4707. [Google Scholar] [CrossRef]
- Liu, X. Directional deflection equations for steerable drilling tools and the control mechanism of wellbore trajectory. Pet. Explor. Dev. 2017, 44, 834–839. [Google Scholar] [CrossRef]
- Liu, Y.; Zhu, R.; Zhai, S.; Li, N.; Li, C. Lithofacies identification of shale formation based on mineral content regression using LightGBM algorithm: A case study in the Luzhou block, South Sichuan Basin, China. Energy Sci. Eng. 2023, 11, 4256–4272. [Google Scholar] [CrossRef]
- Han, L.; Li, X.; Liu, Z.; Duan, G.; Wan, Y.; Guo, X.; Guo, W.; Cui, Y. Influencing factors and prevention measures of casing deformation in deep shale gas wells in Luzhou block, southern Sichuan Basin, SW China. Pet. Explor. Dev. 2023, 50, 979–988. [Google Scholar] [CrossRef]
- Ji, S.; Zhang, C.; Tian, L.; Ran, L.; Yang, Y. Dead reckoning method for tracking wellbore trajectories constrained by the drill pipe length. IEEE Trans. Instrum. Meas. 2024, 73, 1–12. [Google Scholar] [CrossRef]
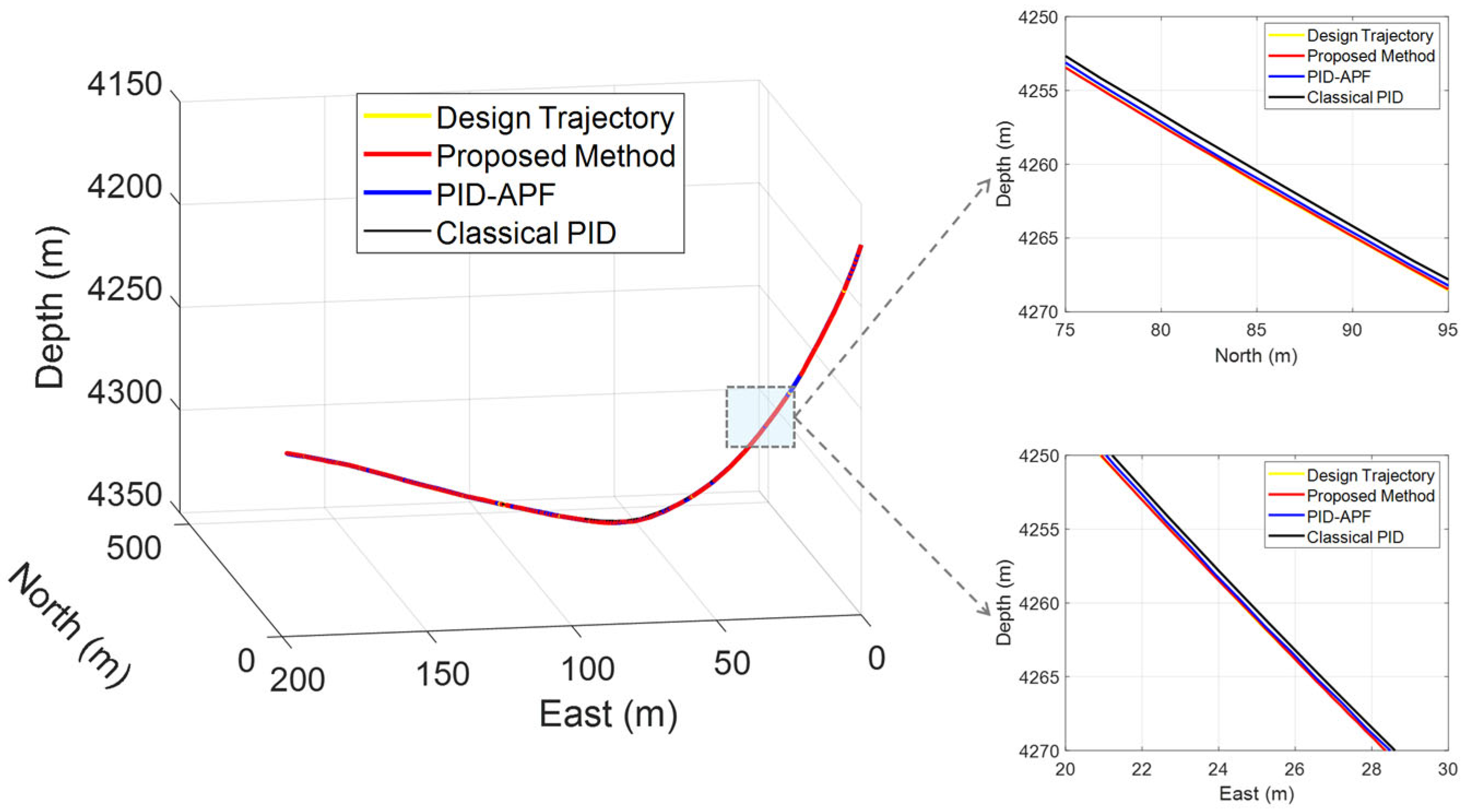
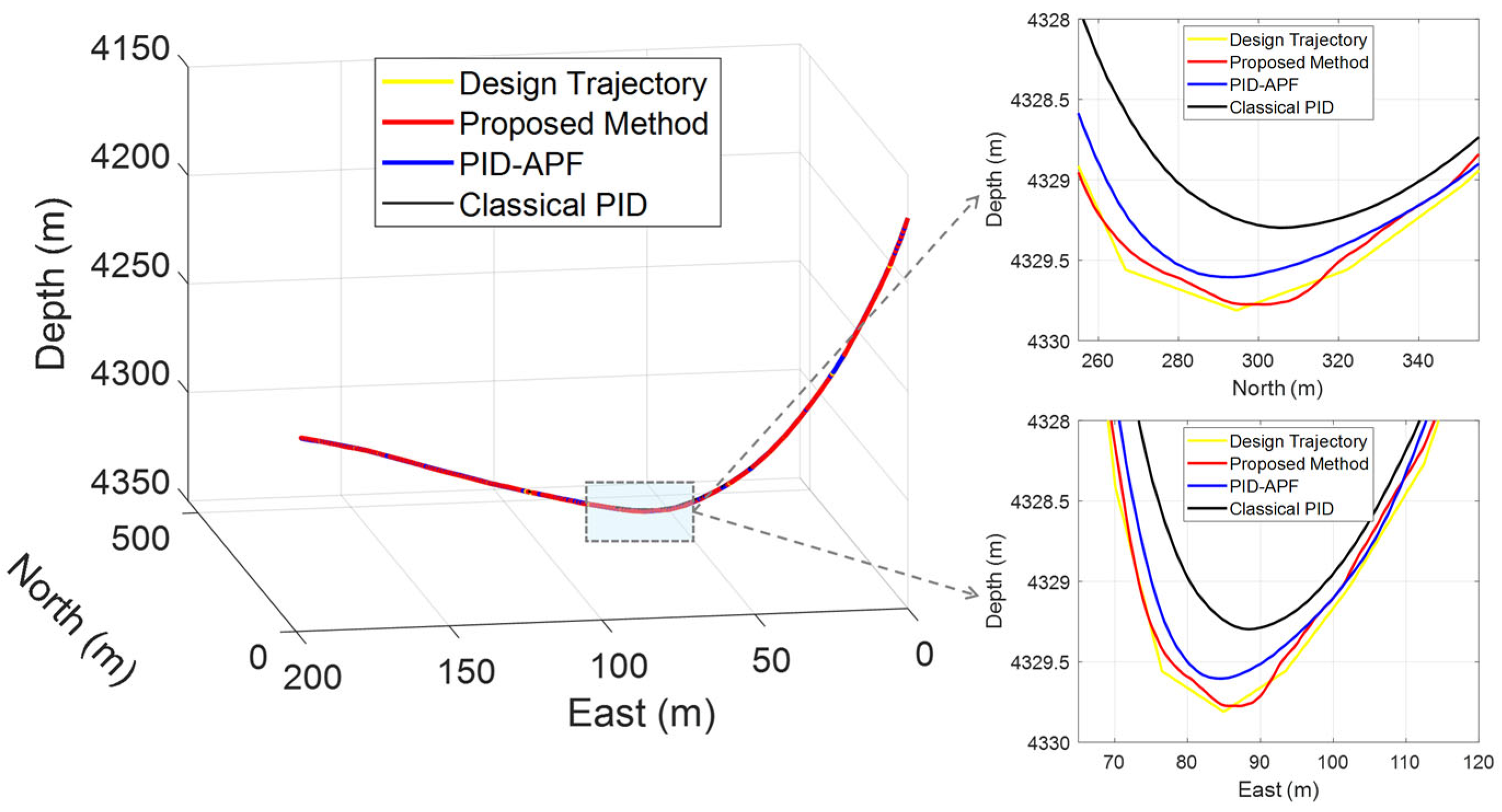
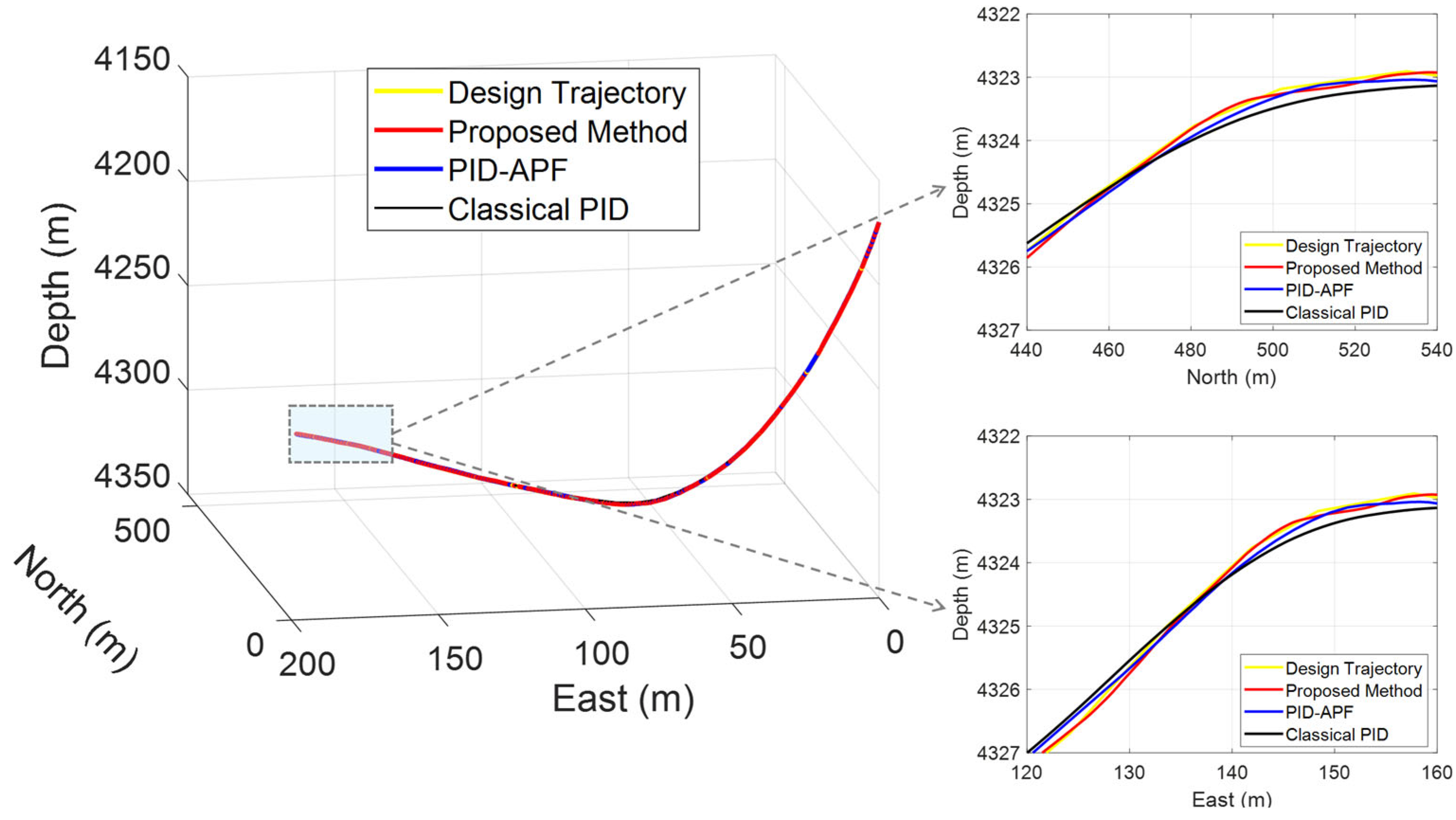
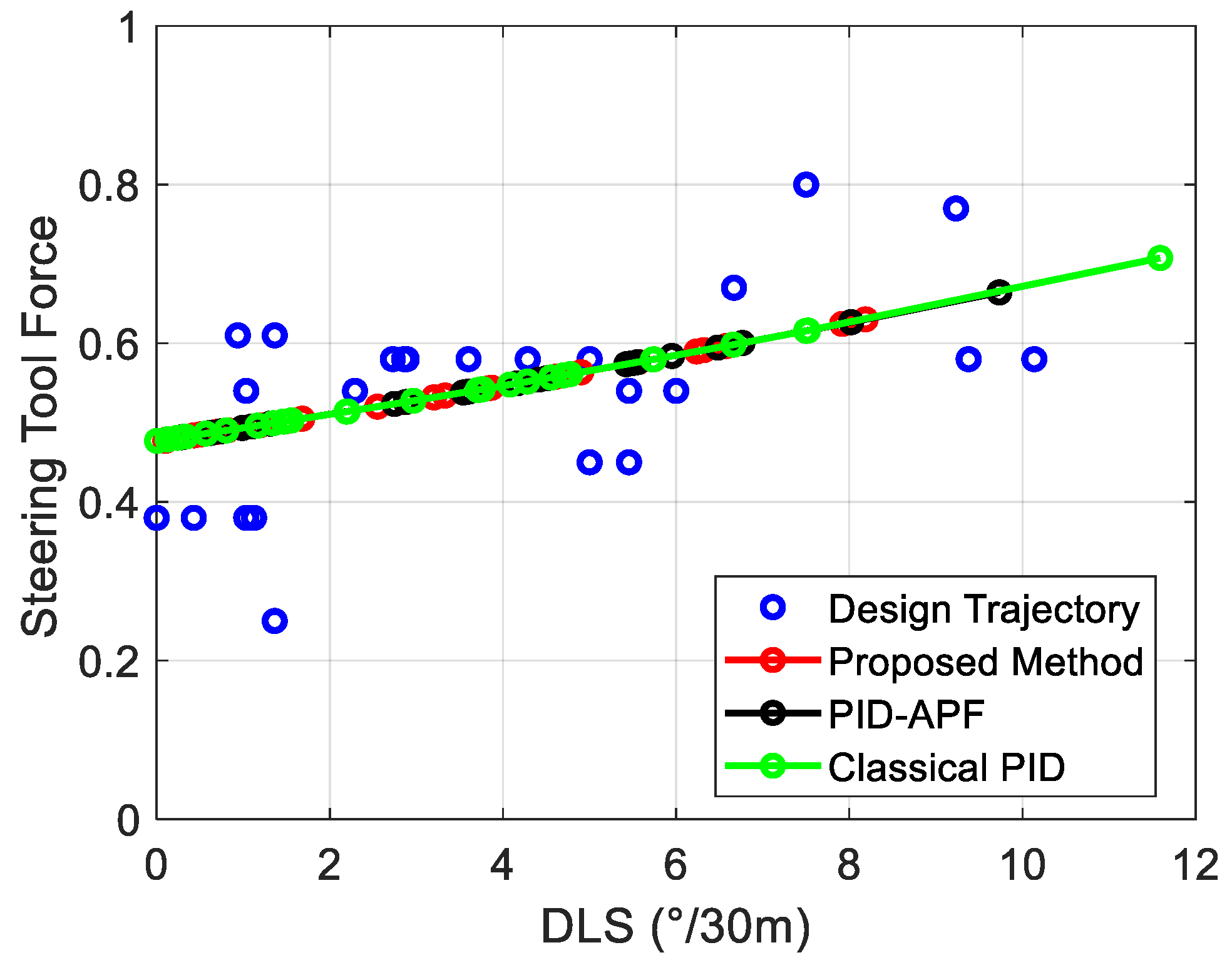
| No. | Design Trajectory | Drilling Information | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| North (m) | East (m) | Depth (m) | IA (°) | AA (°) | North (m) | East (m) | Depth (m) | IA (°) | AA (°) | |
| 1 | 0.00 | 0.00 | 4170.00 | 31 | 17 | 0.00 | 0.00 | 4170.00 | 33.00 | 17 |
| 2 | 27.27 | 8.33 | 4207.25 | 43 | 17 | 27.66 | 8.44 | 4207.53 | 43.78 | 16.83 |
| 3 | 68.13 | 20.19 | 4248.05 | 52 | 16 | 67.29 | 20.04 | 4247.42 | 52.58 | 15.62 |
| 4 | 113.88 | 32.90 | 4281.29 | 59 | 15 | 114.60 | 33.18 | 4281.78 | 60.75 | 14.50 |
| 5 | 167.81 | 47.35 | 4308.03 | 70 | 15 | 166.69 | 46.98 | 4307.61 | 70.37 | 15.66 |
| 6 | 226.77 | 64.26 | 4325.97 | 81 | 17 | 226.32 | 64.53 | 4325.97 | 83.11 | 15.66 |
| 7 | 294.49 | 84.97 | 4329.81 | 90 | 17 | 295.41 | 85.24 | 4329.73 | 90.35 | 17.01 |
| 8 | 384.36 | 112.44 | 4328.27 | 91.5 | 17 | 383.84 | 112.28 | 4328.28 | 92.23 | 17.00 |
| 9 | 480.85 | 141.94 | 4323.76 | 92 | 17 | 481.77 | 142.22 | 4323.72 | 91.49 | 16.99 |
| 10 | 553.52 | 164.16 | 4323.10 | 89 | 17 | 553.25 | 164.04 | 4323.12 | 89.26 | 16.93 |
| No. | Design Trajectory | Drilling Information | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| North (m) | East (m) | Depth (m) | IA (°) | AA (°) | North (m) | East (m) | Depth (m) | IA (°) | AA (°) | |
| 1 | 0.00 | 0.00 | 4170.00 | 31 | 17 | 0.00 | 0.00 | 4170.00 | 33.00 | 17.00 |
| 2 | 27.27 | 8.33 | 4207.25 | 43 | 17 | 28.37 | 8.62 | 4207.62 | 43.75 | 16.40 |
| 3 | 68.13 | 20.19 | 4248.05 | 52 | 16 | 67.81 | 20.08 | 4247.03 | 52.80 | 15.83 |
| 4 | 113.88 | 32.90 | 4281.29 | 59 | 15 | 115.12 | 33.20 | 4281.41 | 61.07 | 15.04 |
| 5 | 167.81 | 47.35 | 4308.03 | 70 | 15 | 167.32 | 47.26 | 4307.18 | 70.04 | 15.53 |
| 6 | 226.77 | 64.26 | 4325.97 | 81 | 17 | 228.15 | 64.77 | 4325.26 | 83.13 | 16.85 |
| 7 | 294.49 | 84.97 | 4329.81 | 90 | 17 | 293.94 | 84.81 | 4329.30 | 90.07 | 16.99 |
| 8 | 384.36 | 112.44 | 4328.27 | 91.5 | 17 | 385.73 | 112.86 | 4327.91 | 92.20 | 16.99 |
| 9 | 480.85 | 141.94 | 4323.76 | 92 | 17 | 480.33 | 141.78 | 4323.91 | 91.30 | 17.00 |
| 10 | 553.52 | 164.16 | 4323.10 | 89 | 17 | 553.77 | 164.48 | 4323.28 | 90.42 | 17.00 |
| No. | Design Trajectory | Drilling Information | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| North (m) | East (m) | Depth (m) | IA (°) | AA (°) | North (m) | East (m) | Depth (m) | IA (°) | AA (°) | |
| 1 | 0.00 | 0.00 | 4170.00 | 31 | 17 | 0.00 | 0.00 | 4170.00 | 33.00 | 17.00 |
| 2 | 27.27 | 8.33 | 4207.25 | 43 | 17 | 27.69 | 8.50 | 4207.92 | 41.11 | 17.01 |
| 3 | 68.13 | 20.19 | 4248.05 | 52 | 16 | 69.58 | 20.63 | 4249.03 | 50.17 | 15.97 |
| 4 | 113.88 | 32.90 | 4281.29 | 59 | 15 | 113.74 | 32.86 | 4281.17 | 57.06 | 15.01 |
| 5 | 167.81 | 47.35 | 4308.03 | 70 | 15 | 169.54 | 47.85 | 4308.45 | 68.60 | 15.09 |
| 6 | 226.77 | 64.26 | 4325.97 | 81 | 17 | 228.56 | 64.84 | 4325.88 | 79.24 | 16.62 |
| 7 | 294.49 | 84.97 | 4329.81 | 90 | 17 | 293.41 | 84.64 | 4329.30 | 89.52 | 17.00 |
| 8 | 384.36 | 112.44 | 4328.27 | 91.5 | 17 | 385.20 | 112.70 | 4328.14 | 91.40 | 17.00 |
| 9 | 480.85 | 141.94 | 4323.76 | 92 | 17 | 480.74 | 141.91 | 4323.76 | 92.50 | 16.99 |
| 10 | 553.52 | 164.16 | 4323.10 | 89 | 17 | 553.41 | 164.12 | 4323.10 | 89.65 | 16.99 |
| Metric | Proposed Method | Classical PID | PID-APF | |
|---|---|---|---|---|
| Normal Distance (m) | mean | 0.1534 | 1.3812 | 0.2325 |
| Reduction Rate | -- | 88.89% | 34.02% | |
| STD | 0.0921 | 0.7556 | 0.0988 | |
| DLS (°/30 m) | mean | 3.6378 | 3.8824 | 3.8620 |
| Reduction Rate | -- | 6.30% | 5.81% | |
| STD | 2.5673 | 2.7574 | 3.1348 | |
| Metric | Proposed Method | Classical PID | PID-APF | |
|---|---|---|---|---|
| Normal Distance (m) | mean | 0.1791 | 0.4139 | 0.3979 |
| Reduction Rate | -- | 56.73% | 54.97% | |
| STD | 0.1078 | 0.3400 | 0.2247 | |
| DLS (°/30 m) | mean | 3.6339 | 4.7425 | 3.8191 |
| Reduction Rate | -- | 23.38% | 4.85% | |
| STD | 2.5844 | 3.8097 | 2.7682 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, Y.; Shao, K.; Wang, Z.; Fan, Y.; Chen, D. An Intelligent Directional Drill Steering Method Based on Real-Time Adaptive Closed-Loop Control. Processes 2025, 13, 3798. https://doi.org/10.3390/pr13123798
Sun Y, Shao K, Wang Z, Fan Y, Chen D. An Intelligent Directional Drill Steering Method Based on Real-Time Adaptive Closed-Loop Control. Processes. 2025; 13(12):3798. https://doi.org/10.3390/pr13123798
Chicago/Turabian StyleSun, Yan, Kun Shao, Zhaojun Wang, Yongtao Fan, and Dong Chen. 2025. "An Intelligent Directional Drill Steering Method Based on Real-Time Adaptive Closed-Loop Control" Processes 13, no. 12: 3798. https://doi.org/10.3390/pr13123798
APA StyleSun, Y., Shao, K., Wang, Z., Fan, Y., & Chen, D. (2025). An Intelligent Directional Drill Steering Method Based on Real-Time Adaptive Closed-Loop Control. Processes, 13(12), 3798. https://doi.org/10.3390/pr13123798





