Identification of Key Parameters for Fracturing and Driving Oil in Low-Permeability Offshore Reservoirs Based on Fuzzy Analytic Hierarchy Process and Numerical Simulation
Abstract
1. Introduction
2. Methods
2.1. Fuzzy Analytic Hierarchy Process
2.2. Reservoir Numerical Simulation
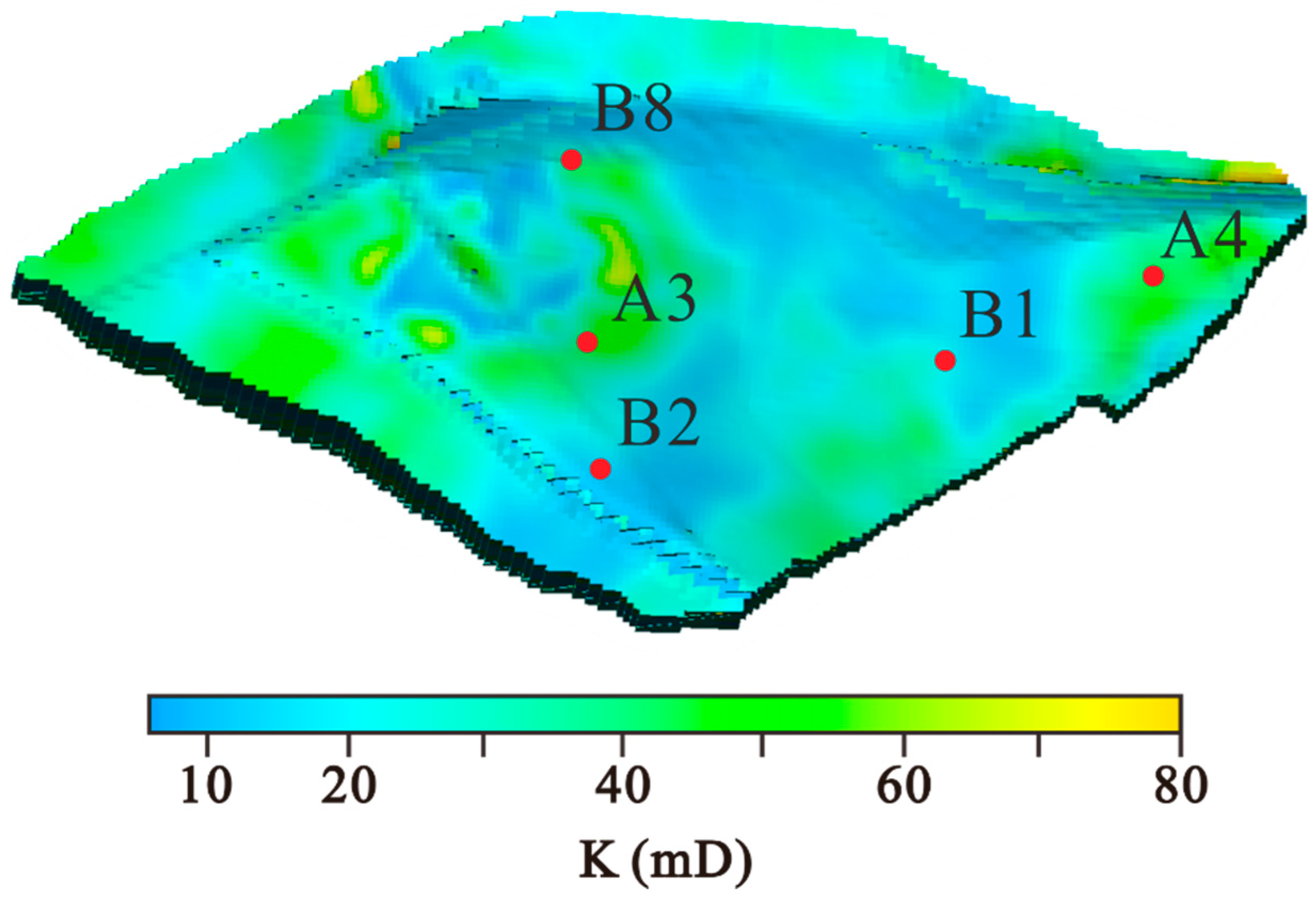
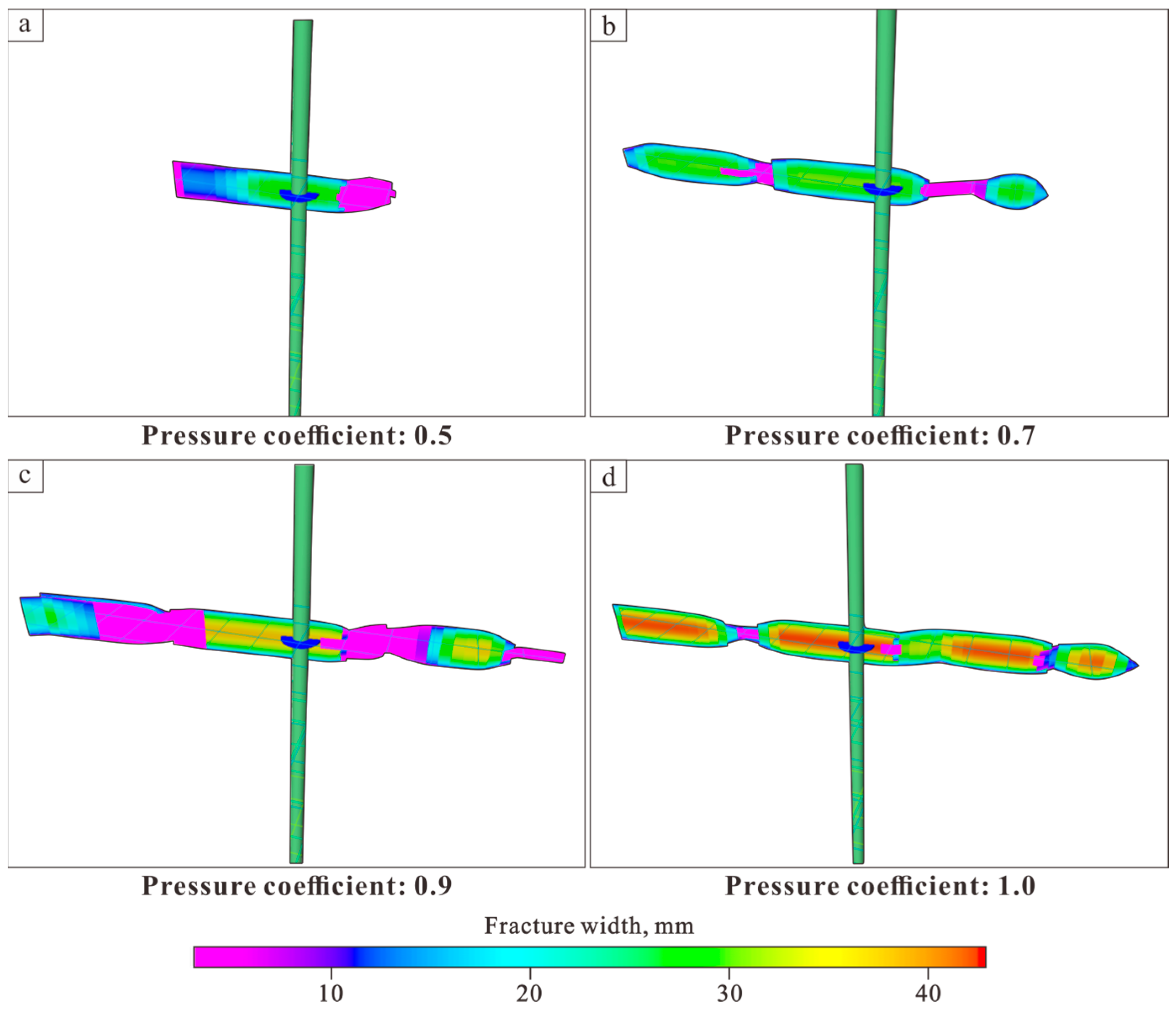
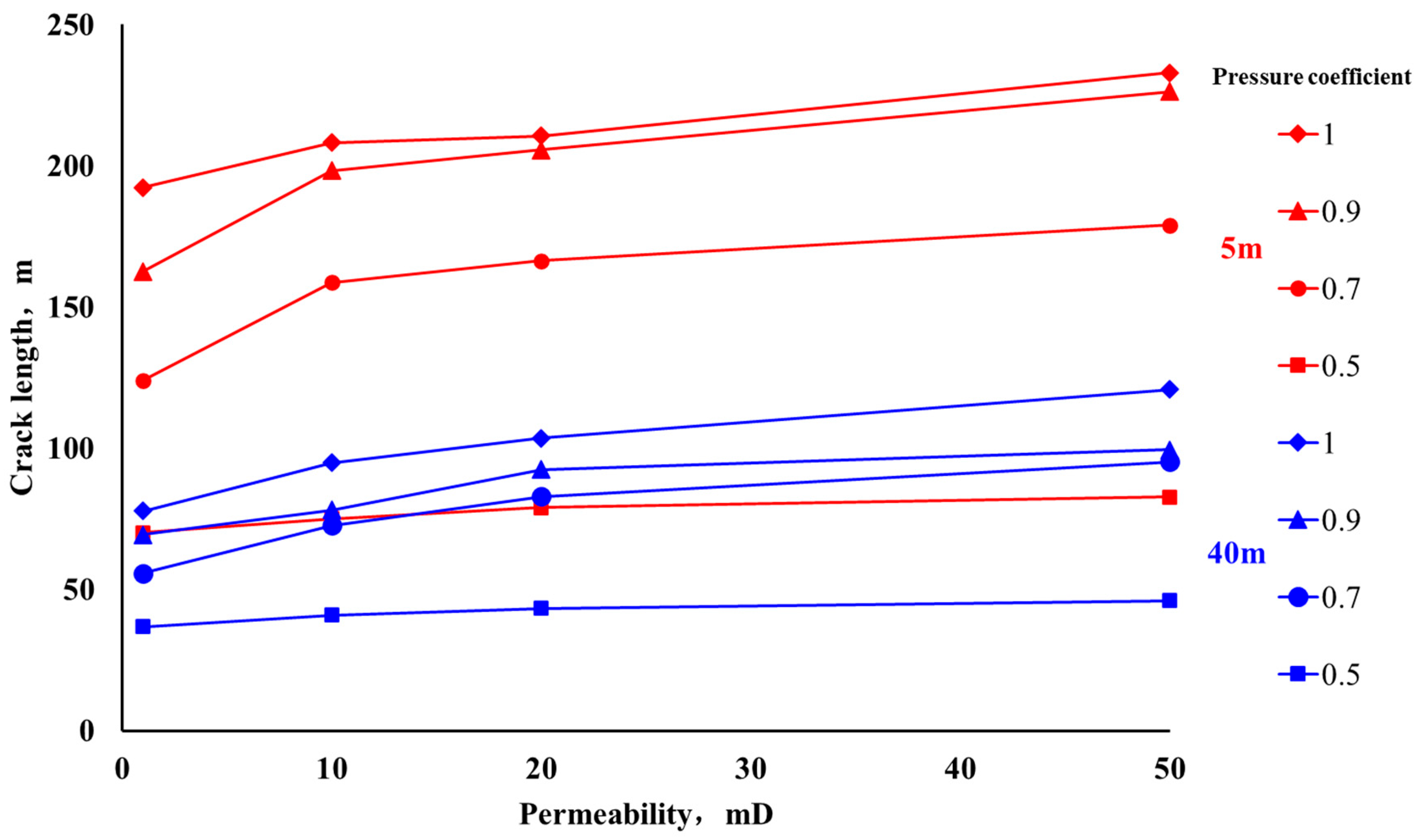
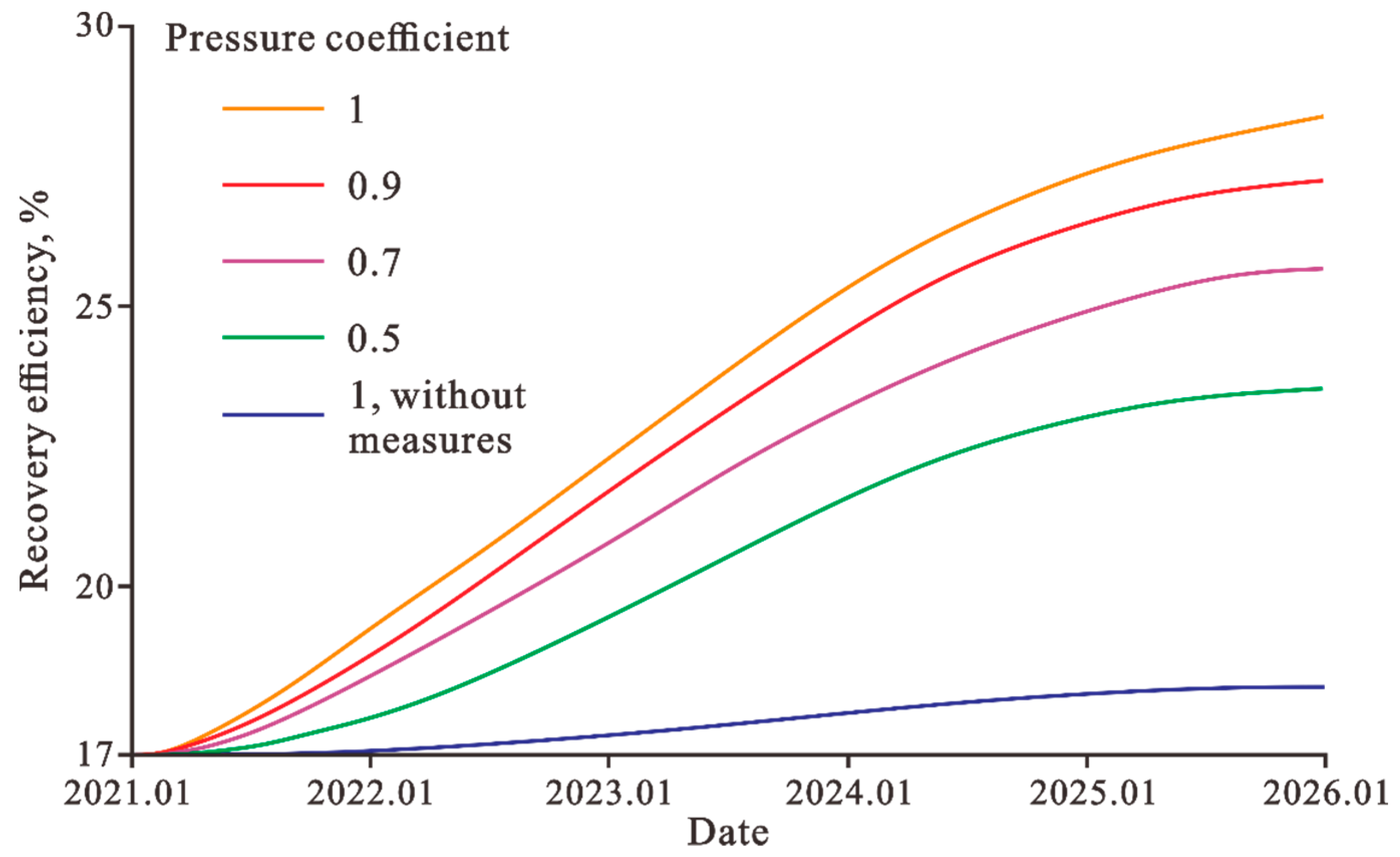
3. Results
3.1. Parameter Evaluation Results
3.2. Numerical Simulation Results
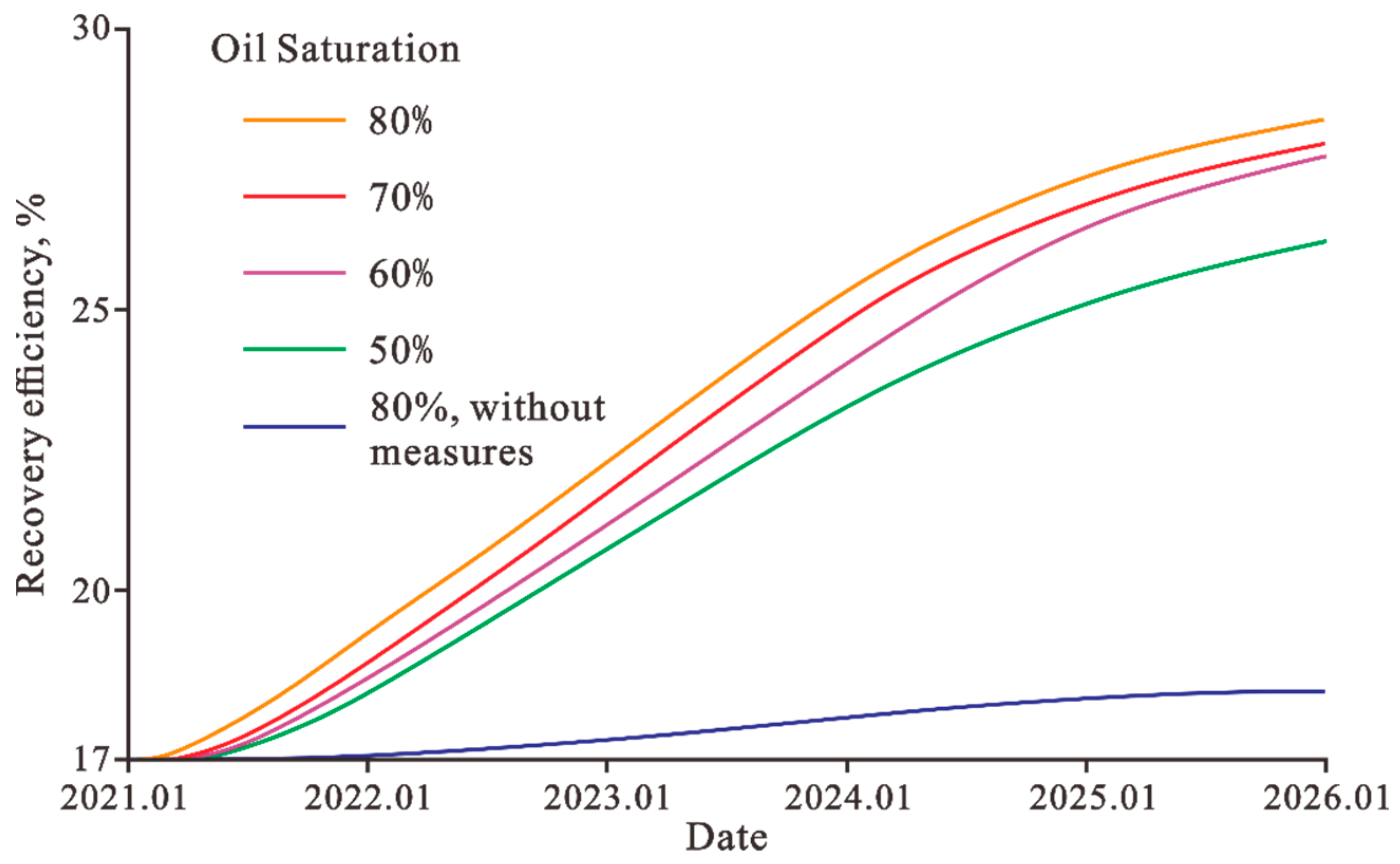
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhao, M.W.; Song, X.G.; Zhou, D.; Lv, W.; Dai, C.; Yang, Q.; Li, Y.; Zhang, B.; Zhao, Y.; Wu, Y. Study onthe reducing injection pressure regulation of hydrophobic carbon nanoparticles. Langmuir 2020, 36, 3989–3996. [Google Scholar] [CrossRef]
- Su, H.; Lei, Z.D.; Li, J.C.; Gong, B.; Zhao, W.; Ju, B.; Zhang, D.; Qin, H. An effective numerical simulation model of multi-scale fractures in reservoir. Acta Pet. Sin. 2019, 40, 587–593. [Google Scholar] [CrossRef]
- Bai, X.; Qi, Y.; He, S.; Zhu, X.; Hou, Z.; Zhang, Y. Integrated re-stimulating technology of fracturing-replenishment-displacement ofhorizontal wells in tight reservoirs. Fault-Block Oil Gas Field 2021, 28, 63–67. [Google Scholar] [CrossRef]
- Zhao, L.Q.; Chen, Y.X.; Du, J.; Liu, P.; Li, N.; Luo, Z.; Zhang, C.; Huang, F. Experimental study on a new type of self-propping fracturing technology. Energy 2019, 183, 249–261. [Google Scholar] [CrossRef]
- Liu, Y.K.; Wang, F.J.; Wang, Y.M.; Li, B.; Zhang, D.; Yang, G.; Zhi, J.; Sun, S.; Wang, X.; Deng, Q.; et al. The mechanism of hydraulic fracturing assisted oil displacement to enhanceoil recovery in low and medium permeability reservoirs. Pet. Explor. Dev. 2022, 49, 864–873. [Google Scholar] [CrossRef]
- Ma, Y.X.; Zhang, Q.L.; Lu, R.B.; Yu, C.C.; Ruan, H.J.; Tang, X.; Wu, S.; Sun, S. Progress and development direction of development technology for low-permeability oil field in complex fault blocks in the western South China Sea. China Pet. Explor. 2024, 29, 1–9. [Google Scholar] [CrossRef]
- Huang, Z.G.; Mao, J.C.; Cun, M.; Yang, X.; Lin, C.; Zhang, Y.; Zhang, H.; Mao, J.; Wang, Q.; Zhang, Q.; et al. Polyhydroxy cationic viscoelastic surfactant for clean fracturing fluids: Study on the salt tolerance and the effect of salt on the high temperature stability of wormlike micelles. J. Mol. Liq. 2022, 366, 120354. [Google Scholar] [CrossRef]
- Zhao, M.W.; Dai, C.L.; Liu, P. Characteristics and efficient imbibitionoil displacement mechanism of gemini surlactant slickwater for integrated fracturing flooding technology. Acta Pet. Sin. 2024, 45, 1409–1421. [Google Scholar] [CrossRef]
- Cui, C.Z.; Wang, J.K.; Wu, Z.W.; Li, J.; Li, J.; Qian, Y. Analysis of unsteady pressure characteristics of fracturingllooding water injection wells in low permeability heterogeneous reservoirs. Acta Pet. Sin. 2025, 46, 938–952. [Google Scholar] [CrossRef]
- Zhang, M.L.; Zhang, T.Y.; Fan, J.Y. Calculation and Analysis of Fracture Extension Parameters Based on PKN Model. Sci. Technol. Eng. 2019, 19, 116–123. [Google Scholar]
- Wu, X.Y.; Liu, X.W.; Liu, F.F. Mechanism of pressure flooding development technology in deep ultra-low permeability reservoir and its application research. Lnner Mong. Petro-Chem. Ind. 2021, 47, 66–69. [Google Scholar]
- Cui, C.Z.; Wang, J.K.; Wu, Z.W.; Sui, Y.F.; Li, J.; Lu, S.Q.S. Establishment and Application of Pressure Drive Dynamic Fracture Model for Tight Oil Reservoirs. Spec. Oil Gas Reserv. 2023, 30, 87–95. [Google Scholar] [CrossRef]
- Cao, H.; Zhang, G.Q.; Li, S.Y. A hydraulic fracture extension model for fracturing and enhanced oil recovery considering the influence of the fracture process zone and its application. Rock Soil Mech. 2025, 46, 798–810. [Google Scholar] [CrossRef]
- Guo, J.C.; Ma, L.; Lu, C. Progress and development directions of fracturing flooding technology for tight reservoirs in China. Acta Pet. Sin. 2022, 43, 1788–1797. [Google Scholar] [CrossRef]
- Ouyang, W.P.; Zhang, M.; Sun, H.; Zhang, Y.; Chi, X. Numerical simulation of oil displacement by fracturing imbibition in horizontal shale oil wells. Pet. Drill. Tech. 2021, 49, 143–149. [Google Scholar] [CrossRef]
- Zhou, Y.H.; Liu, S.Y.; Qing, Y.P.; Zheng, T.Y.; Chen, K.X.; Song, J.; Song, M.L. CADP: Towards Better Centralized Learning for Decentralized Execution in MARL. In Proceedings of the 34th International Joint Conference on Artificial Intelligence, Montreal, QC, Canada, 16–22 August 2025; pp. 2838–2840. [Google Scholar]
- Chen, H.; Tang, H.; Wu, T.; Liu, T.Y.; Du, Y.J. Big data technology and its application in fine reservoir description. Pet. Geol. Recovery 2022, 29, 11–20. [Google Scholar] [CrossRef]
- Ji, B.; Zhang, W.; He, G.; Duan, T.Z.; Liu, H. Connotation and development trend of integrated reservoir geological modeling and numerical simulation. Chin. J. Pet. 2024, 45, 1152–1162. [Google Scholar]
- Sircar, A.; Yadav, K.; Rayavarapu, K.; Bist, N.; Oza, H. Application of machine learning and artificial intelligence in oil and gas industry. Pet. Res. 2021, 6, 379–391. [Google Scholar] [CrossRef]
- Al-Fattah, S.M.; Startzman, R.A. Predicting natural gas production using artificial neural network. In Proceedings of the SPE Hydrocarbon Economics and Evaluation Symposium, Dallas, TX, USA, 2–3 April 2001; Society of Petroleum Engineers. 2001; pp. 1–10. [Google Scholar]
- Noshi, C.I.; Schubert, J.J. The role of machine learning in drilling operations; a review. In Proceedings of the SPE/AAPG Eastern Regional Meeting, Pittsburgh, PA, USA, 7–11 October 2018; Society of Petroleum Engineers. 2018. [Google Scholar]
- Sheng, X.; Jin, Z.; Xu, Z.; Jiang, H. Uncertainty analysis in geological risk assessment. Pet. Exp. Geol. 2014, 36, 633–641. [Google Scholar] [CrossRef]
- Yang, P.; Zhan, S.; Li, M.; Li, L.; Guo, R.; Shang, M.Q.; Tao, C.F. Research and practice of artificial intelligence earthquake interpretation model based on dream cloud. China Pet. Explor. 2020, 25, 89–96. [Google Scholar] [CrossRef]
- Lu, H.; Huang, K.; Azimi, M.; Guo, L. Blockchain technology in the oil and gas industry: A review of applications, opportunities, challenges, and risks. IEEE Access 2019, 7, 41426–41444. [Google Scholar] [CrossRef]
- Liang, Y.F.; Wu, B.; Wang, J.J.; Li, C.H.; Suo, X.; Zhang, K. Optimization of recharge parameters for foundation pit engineering based on orthogonal test and fuzzy analytical hierarchy process-value engineering method. Tunn. Constr. 2021, 41, 1492. [Google Scholar]
- Saaty, T.; Kearns, K. Analytic Hierarchy Process. Anal. Plan. 1985, 63–86. [Google Scholar] [CrossRef]
- Jie, Y.; Yang, J.; Zhou, D.; Wang, H.; Zou, Y.; Liu, Y.; Zhang, Y. Study on the Optimal Volume Fracturing Design for Horizontal Wells in Tight Oil Reservoirs. Sustainability 2022, 14, 15531. [Google Scholar] [CrossRef]
- Yu, H.Y.; Du, X.L.; Li, Y.; Qin, S.Q.; Wang, J.F.; Li, Y.F.; Ma, B. Application and mechanism analysis of surfactants in enhanced oil recovery of low permeability reservoirs. Chem. Bioeng. 2025, 42, 41–45. [Google Scholar] [CrossRef]
- Gao, F.; Song, Z.Z. Mechanism of surfactant flooding in low-permeability oilfields. J. China Univ. Pet. 2012, 36, 160–165. [Google Scholar] [CrossRef]
- Liu, J.X.; Li, Z.; He, X.; Lu, X.G.; Chen, C.; Liu, Y.G.; Lan, X.T.; Zhang, L.P.; Ju, J.C.; Hong, X.J.; et al. Effect Evaluation and Process Parameter Optimization of Synergistic Pressure Flooding in Low Permeability Reservoir of Bohai B Oilfield. Oilfield Chem. 2025, 42, 244–253. [Google Scholar] [CrossRef]
- Liu, B.; Zhang, W.; Bie, M.J.; Yang, Z.C.; Zhai, Z.Z. Study on the strategy of restoring formation pressure and field application in offshore L oilfield. Xinjiang Oil Gas 2020, 16, 78–82. [Google Scholar]
- Zhu, Z.; Dang, H.L.; Cui, P.X.; Dang, K.Y.; Bai, P.; Zhao, Y.N. Numerical simulation of the pressure law of energy charging and permeability enhancement in low permeability reservoirs. Xinjiang Oil Gas 2023, 19, 56–62. [Google Scholar] [CrossRef]
- Lin, H.; Zhang, S.C.; Wang, F.; Pan, Z.; Zhang, Y.; Chen, Y. Optimization of hydraulic fracture parameters for low-permeability condensate reservoir in Jilin Oilfield. J. Xi’Shiyou Univ. (Nat. Sci. Ed.) 2016, 31, 62–67. [Google Scholar] [CrossRef]
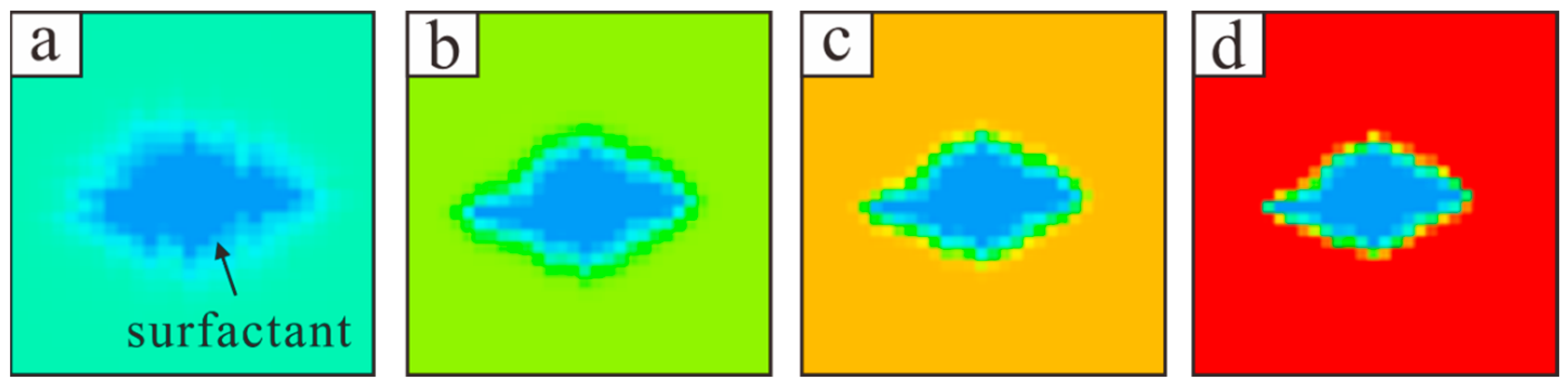
| Relative Importance | Definition |
|---|---|
| 0.1 | Objective i is more important than objective j in absolute terms |
| 0.2 | Goal i is significantly more important than goal j |
| 0.3 | Goal i is more important than goal j |
| 0.4 | Goal i is slightly more important than goal j |
| 0.5 | Goal i is equally important as goal j |
| 0.6 | Target j is slightly more important than target i |
| 0.7 | Target j is more important than target i |
| 0.8 | Goal j is significantly more important than goal i |
| 0.9 | Target j is more absolutely important than target i in comparison |
| Model Parameters | Numerical Value |
|---|---|
| Formation pressure | 32 MPa |
| Saturation pressure | 24.43 MPa |
| Average depth of reservoir | 2955 m |
| Volume coefficient of stratum crude oil | 1.4135 |
| Original dissolved gas–oil ratio | 177 m3/m3 |
| Viscosity of formation crude oil | 8.3 mPa·s |
| Density of ground crude oil | 0.86 g/cm3 |
| Rock compression coefficient | 8.6 × 10−4 MPa−1 |
| Ground temperature gradient | 3.86 °C/100 m |
| Stratigraphic Young’s modulus | 57 GPa |
| Poisson’s ratio | 0.28 |
| Horizontal Stress Difference | 18.2 MPa |
| Total amount of surface activator injected | 12,000 m3 |
| Injection rate of surface activator | 400 m3/d |
| Total amount of fracturing fluid injected | 500 m3 |
| Fracturing fluid injection rate | 96 m3/d |
| Fracturing Fluid | Displacement (m3/min) | Volume (m3) | Water Consumption (m3) | Sand Ratio (kgPA) | Sand Addition (kg) | Pumping Time (min) |
|---|---|---|---|---|---|---|
| Pre-liquid | 0.07 | 250 | 225 | 0 | 0 | 3571.43 |
| Sand Carrying Liquid | 0.07 | 250 | 225 | 0.4 | 100 | 3571.43 |
| Total volume | 500 | 425 | Total quality | 100 | ||
| Layer Type | Layer Name | Included Elements and Description |
|---|---|---|
| Target layer (T) | Key parameters of fracturing and oil removal in offshore low-permeability oilfields | Overall objective, overseeing the guideline and indicator layers. |
| Criteria layer (S) | Efficiency of Fracturing (S1) | Core criterion, reflecting the ability of the parameter to enhance crude oil recovery, corresponding to indicators I1, I2, I3, I4. |
| Construction feasibility (S2) | Constraints reflecting the impact of the parameter on construction safety and operational difficulties, corresponding to the indicator I1 (fracture formation capacity) | |
| Economic cost (S3) | Constraint criterion reflecting the impact of the parameter on the construction cost, corresponding to indicator I2 (surface activator accounts for more than 30% of the cost of the fracturing fluid) | |
| Indicator layer (I) | Pressure coefficient (I1) | Ratio of formation pressure to fracture pressure during fracturing, range 0.5~1.0 |
| Surfactant concentration (I2) | Mass fraction of surface activator in fracturing fluid, range 0.1~0.5% | |
| Residual oil saturation (I3) | Unused crude oil in the reservoir, range 50% to 80% | |
| Effective thickness (I4) | Reservoir thickness with industrial capacity, range 5~40 m |
| T | S1 | S2 | S3 |
|---|---|---|---|
| S1 | (0.5, 0.5, 0.5) | (0.7, 0.8, 0.9) | (0.8, 0.9, 1.0) |
| S2 | (0.1, 0.2, 0.3) | (0.5, 0.5, 0.5) | (0.6, 0.7, 0.8) |
| S3 | (0.1, 0.2, 0.3) | (0.2, 0.3, 0.4) | (0.5, 0.5, 0.5) |
| S1 | I1 | I2 | I3 | I4 |
|---|---|---|---|---|
| I1 | (0.5, 0.5, 0.5) | (0.6, 0.7, 0.8) | (0.4, 0.5, 0.6) | (0.7, 0.8, 0.9) |
| I2 | (0.2, 0.3, 0.4) | (0.5, 0.5, 0.5) | (0.3, 0.4, 0.5) | (0.6, 0.7, 0.8) |
| I3 | (0.4, 0.5, 0.6) | (0.5, 0.6, 0.7) | (0.5, 0.5, 0.5) | (0.8, 0.9, 1.0) |
| I4 | (0.1, 0.2, 0.3) | (0.2, 0.3, 0.4) | (0.0, 0.1, 0.2) | (0.5, 0.5, 0.5) |
| AS1-I | I1 | I2 | I3 | I4 | KS1-I | I1 | I2 | I3 | I4 |
|---|---|---|---|---|---|---|---|---|---|
| I1 | 1.000 | 0.952 | 0.933 | 0.976 | I1 | 0.500 | 0.700 | 0.500 | 0.800 |
| I2 | 0.048 | 1.000 | 0.905 | 0.952 | I2 | 0.300 | 0.500 | 0.400 | 0.700 |
| I3 | 0.067 | 0.095 | 1.000 | 0.992 | I3 | 0.500 | 0.600 | 0.500 | 0.900 |
| I4 | 0.024 | 0.048 | 0.008 | 1.000 | I4 | 0.200 | 0.300 | 0.100 | 0.500 |
| GS1-I | I1 | I2 | I3 | I4 |
|---|---|---|---|---|
| I1 | 0.500 | 0.826 | 0.490 | 0.872 |
| I2 | 0.174 | 0.500 | 0.385 | 0.826 |
| I3 | 0.510 | 0.615 | 0.500 | 0.956 |
| I4 | 0.128 | 0.174 | 0.044 | 0.500 |
| Criteria Layer | Criterion Layer Weight | Indicator Layer | Indicator Layer Weight | Comprehensive Weight |
|---|---|---|---|---|
| S1 | 0.625 | I1 | 0.28 | 0.175 |
| I2 | 0.19 | 0.119 | ||
| I3 | 0.35 | 0.219 | ||
| I4 | 0.18 | 0.113 | ||
| S2 | 0.275 | I1 | 1.00 | 0.275 |
| S3 | 0.1 | I2 | 1.00 | 0.100 |
| Well Name | Pressure Coeffcient | Surfactant Concentration (%) | Residual Oil Saturation (%) | Effective Thickness (m) | Numerical Simulation of Increasing Oil Volume (104 m3) | Actual Increasing Oil Volume (104 m3) | Data Error |
|---|---|---|---|---|---|---|---|
| C1 | 0.81 | 0.30% | 0.51 | 12.7 | 6.6 | 5.87 | 11.06% |
| C2 | 0.73 | 0.30% | 0.56 | 41.4 | 7.78 | 6.84 | 12.08% |
| C3 | 0.56 | 0.30% | 0.57 | 23.4 | 4.24 | 3.72 | 12.26% |
| C4 | 0.75 | 0.30% | 0.64 | 33.6 | 7.87 | 6.59 | 16.26% |
| C5 | 0.68 | 0.30% | 0.61 | 25.7 | 8.14 | 7.26 | 10.81% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, D.; Zhou, Y.; Zhang, H.; Ge, Y.; Liu, L.; Li, Z. Identification of Key Parameters for Fracturing and Driving Oil in Low-Permeability Offshore Reservoirs Based on Fuzzy Analytic Hierarchy Process and Numerical Simulation. Processes 2025, 13, 3312. https://doi.org/10.3390/pr13103312
Wang D, Zhou Y, Zhang H, Ge Y, Liu L, Li Z. Identification of Key Parameters for Fracturing and Driving Oil in Low-Permeability Offshore Reservoirs Based on Fuzzy Analytic Hierarchy Process and Numerical Simulation. Processes. 2025; 13(10):3312. https://doi.org/10.3390/pr13103312
Chicago/Turabian StyleWang, Dianju, Yanfei Zhou, Haixiang Zhang, Yan Ge, Lingtong Liu, and Zhandong Li. 2025. "Identification of Key Parameters for Fracturing and Driving Oil in Low-Permeability Offshore Reservoirs Based on Fuzzy Analytic Hierarchy Process and Numerical Simulation" Processes 13, no. 10: 3312. https://doi.org/10.3390/pr13103312
APA StyleWang, D., Zhou, Y., Zhang, H., Ge, Y., Liu, L., & Li, Z. (2025). Identification of Key Parameters for Fracturing and Driving Oil in Low-Permeability Offshore Reservoirs Based on Fuzzy Analytic Hierarchy Process and Numerical Simulation. Processes, 13(10), 3312. https://doi.org/10.3390/pr13103312





